Fast Equipartition of Complex 2D Shapes with Minimal Boundaries †
Abstract
1. Introduction
- A region-growing-based method that solves the general version of 2D-SEP problem called SEP-RG;
- A sequential selection method that efficiently solves the problem under the constraint that the intrinsic boundaries are line segments called SEP-ILS.
- A 2D Shape Equipartition algorithm based on a fast balanced clustering method (SEP-FBC);
- A Particle Swarm Optimization (PSO) method that uses the SEP-FBC method, called SEP-PSO FBC.
- To the best of our knowledge, this is the first work that extensively studies the 2D-SEP problem under the minimum intrinsic boundary length.
- We study for the first time basic problem instances, providing the optimal 2D-SEP problem solutions of partitioning of a square and circle into two, three, four, and five equal-area regions and analyzing the case of partitioning of a plane into a high number of equal-area regions.
- We study for the first time the properties of 2D-SEP, including the total intrinsic boundaries’ length of the optimal 2D-SEP solution as a sequence of N.
- We propose a fast balanced clustering method (SEP-FBC) that can be combined with a Particle Swarm Optimization (PSO) framework, due to its lower computational cost compared to the baselines from the literature, to efficiently solve the general version of the 2D-SEP problem.
- The quantitative results obtained on more than 2800 2D shapes included in two standard datasets quantify the outer performance of the proposed methods from baselines of the literature.
2. Related Work
- The problem of minimum error, where the error (e.g., boundary length) is minimized given the number of segments N.
- The problem of the minimum number of segments, where the approximation error is bounded, and the goal is to find the minimum number of segments (N) that gives an error lower than the given error.
- Hierarchical clustering algorithms recursively find nested clusters in either an agglomerative (bottom-up) mode or in a divisive (top-down) mode.
- According to partitional clustering algorithms, the clusters are simultaneously computed as a partition of the data. Usually, the partition is based on a local optimization of a given criterion.
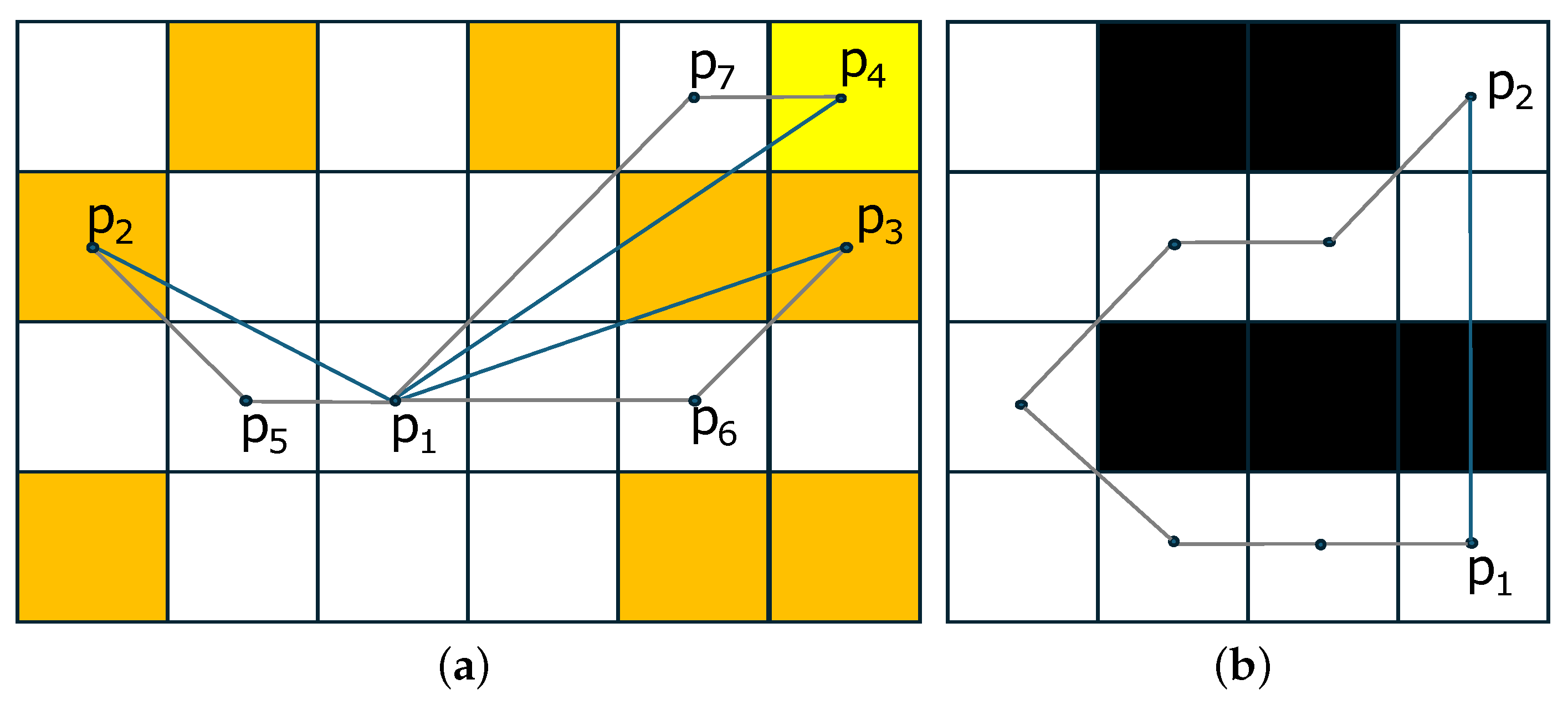
3. Problem Formulation
4. 2D-SEP Instances and Properties
4.1. Plane Partition
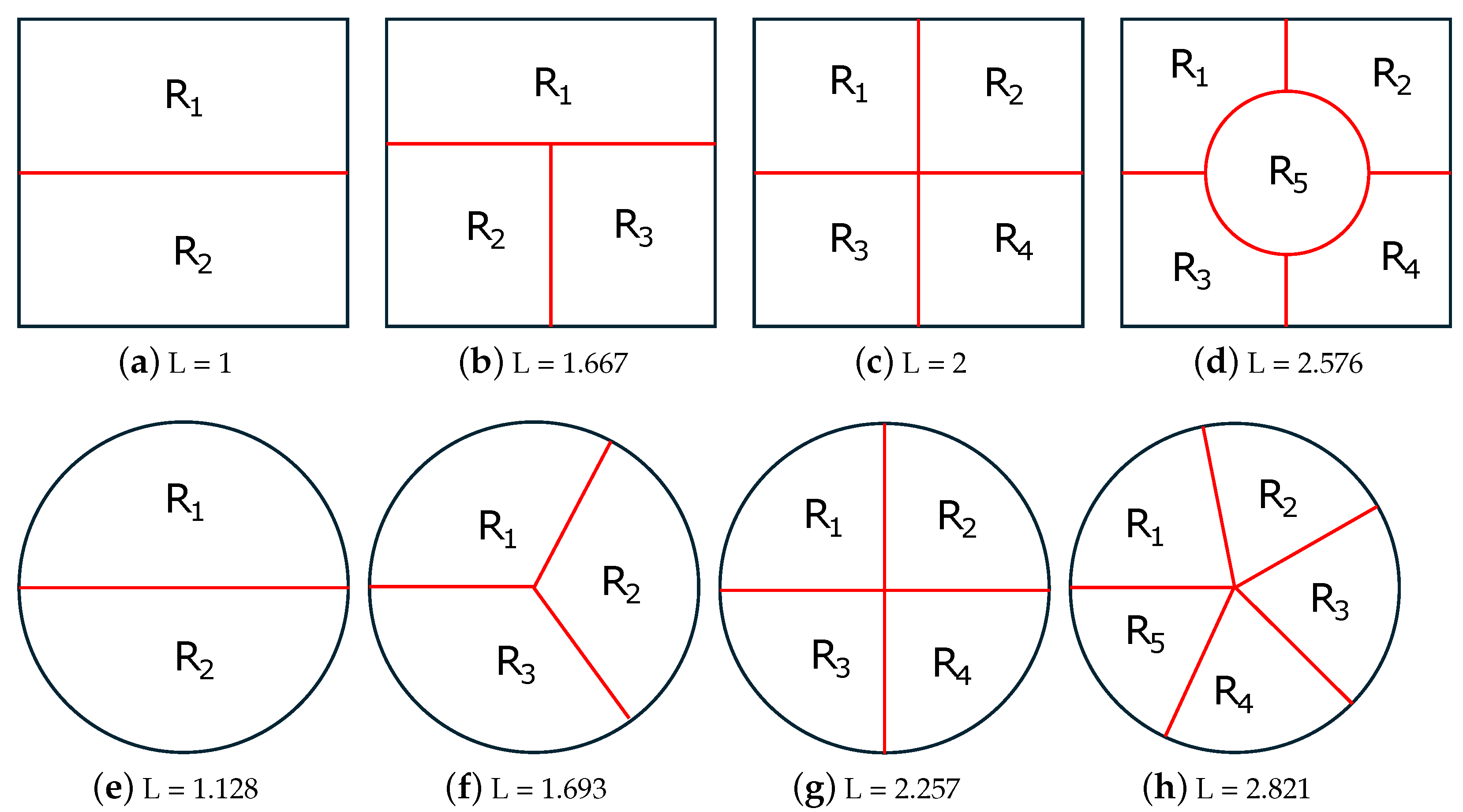
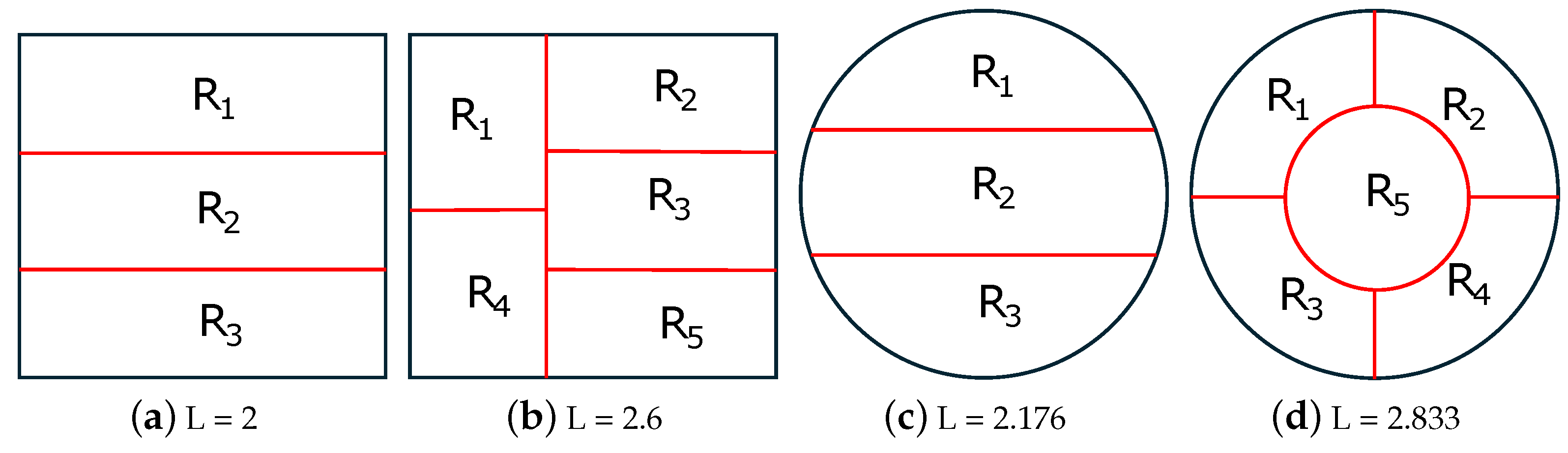
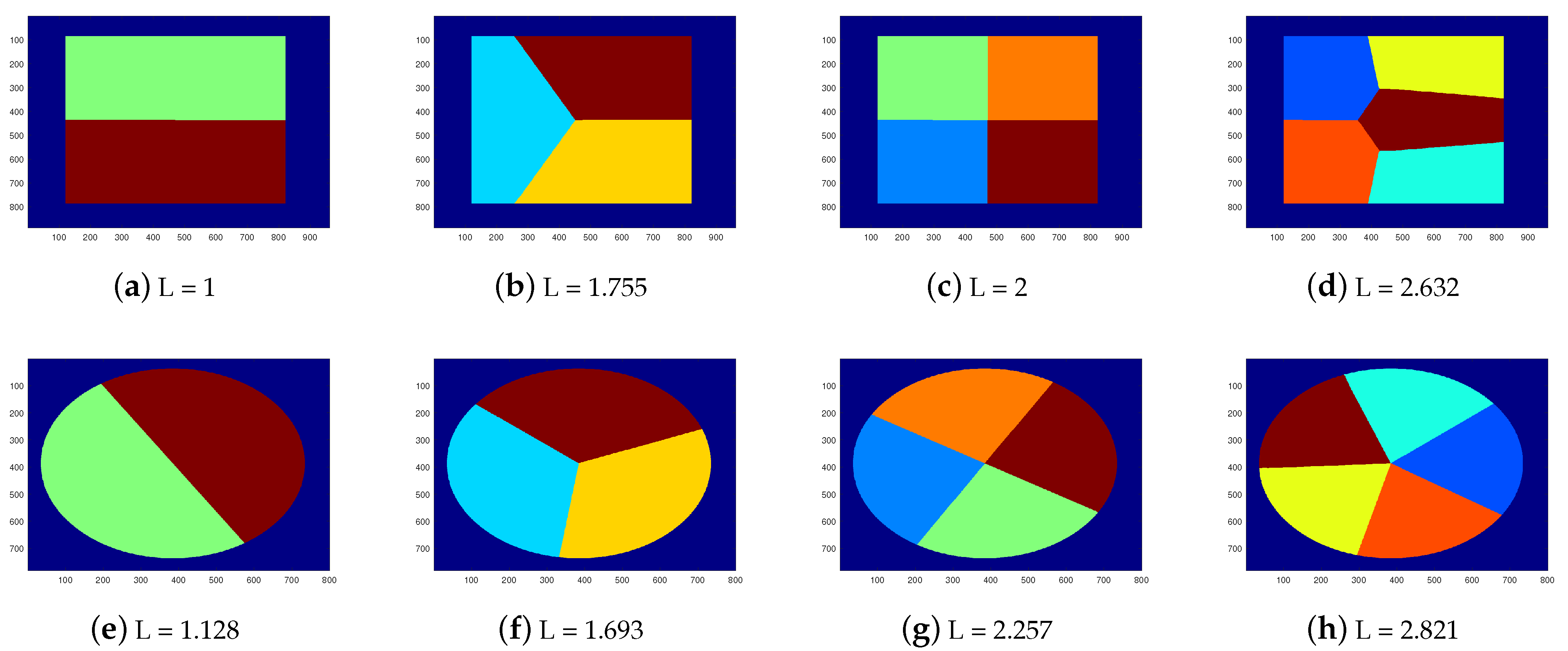
4.2. 2D-SEP of Square and Circle
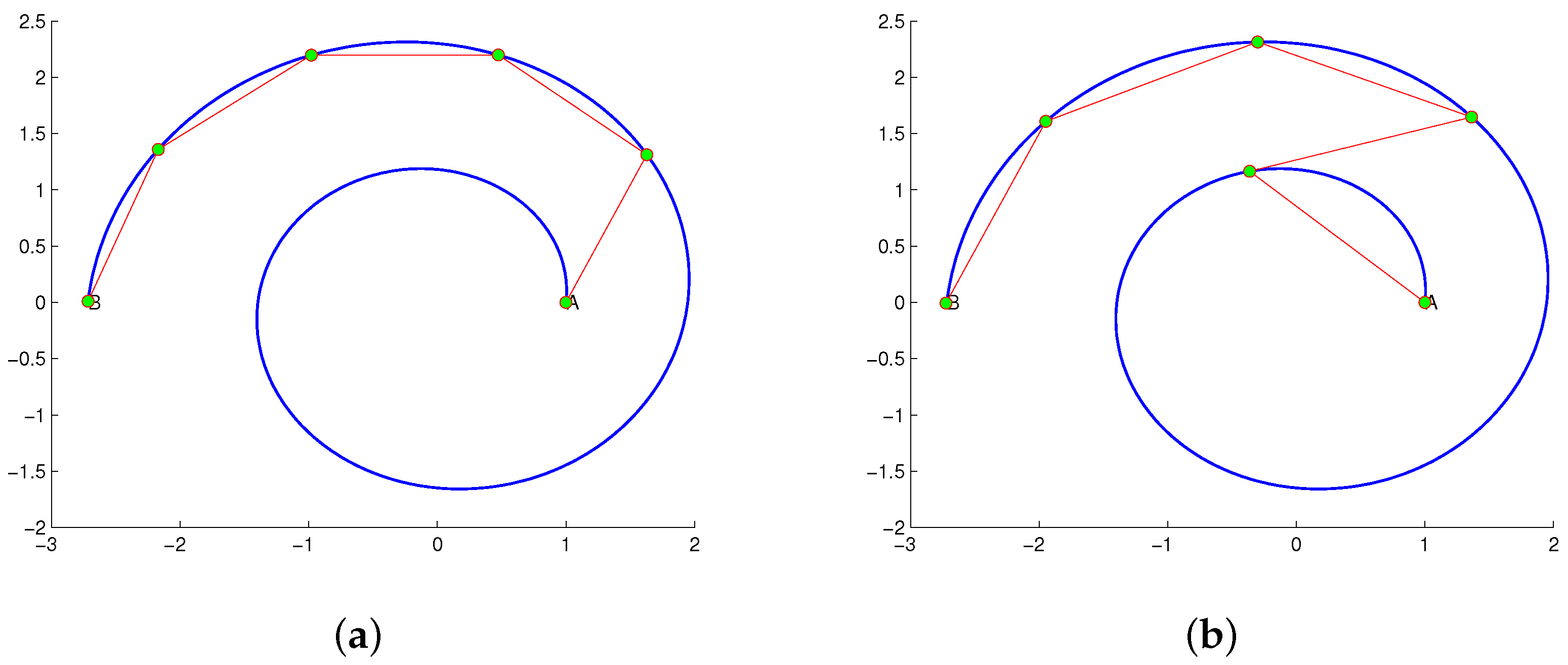
- When N = 2 (see Figure 5a,e), the optimal solution of 2D-SEP under the square and circle is given by the horizontal line that passes from the square centroid () and the diameter of the circle (), respectively.
- When N = 3 (see Figure 5b,f), the optimal solution of 2D-SEP under the square is given by two suitable vertical lines that divide the square into three rectangles , , with . The optimal solution of 2D-SEP under the circle is given by the boundary of the three radiuses that passes from the center with .
- When N = 4 (see Figure 5c,g), the optimal solution of 2D-SEP under the square is given by two suitable vertical lines that cross at the square centroid and divide the square into four equal squares, with . The optimal solution of 2D-SEP under the circle is given similarly by two vertical diameters with .
- When N = 5 (see Figure 5d,h), the optimal solution of 2D-SEP under the square is given by a circle of the radius ( plus four suitable vertical lines of length (), with . The optimal solution of 2D-SEP under the circle is given by five radiuses with , which is slightly lower than the corresponding solution of Figure 6d with .
- For , SEP-FBC yields , which is higher than the corresponding optimal L of Figure 5d. In this case, a part of the intrinsic boundaries of the optimal solution is a circle. The reason why both proposed methods do not find it is that the intrinsic boundaries provided by the proposed method should be polygonal lines.
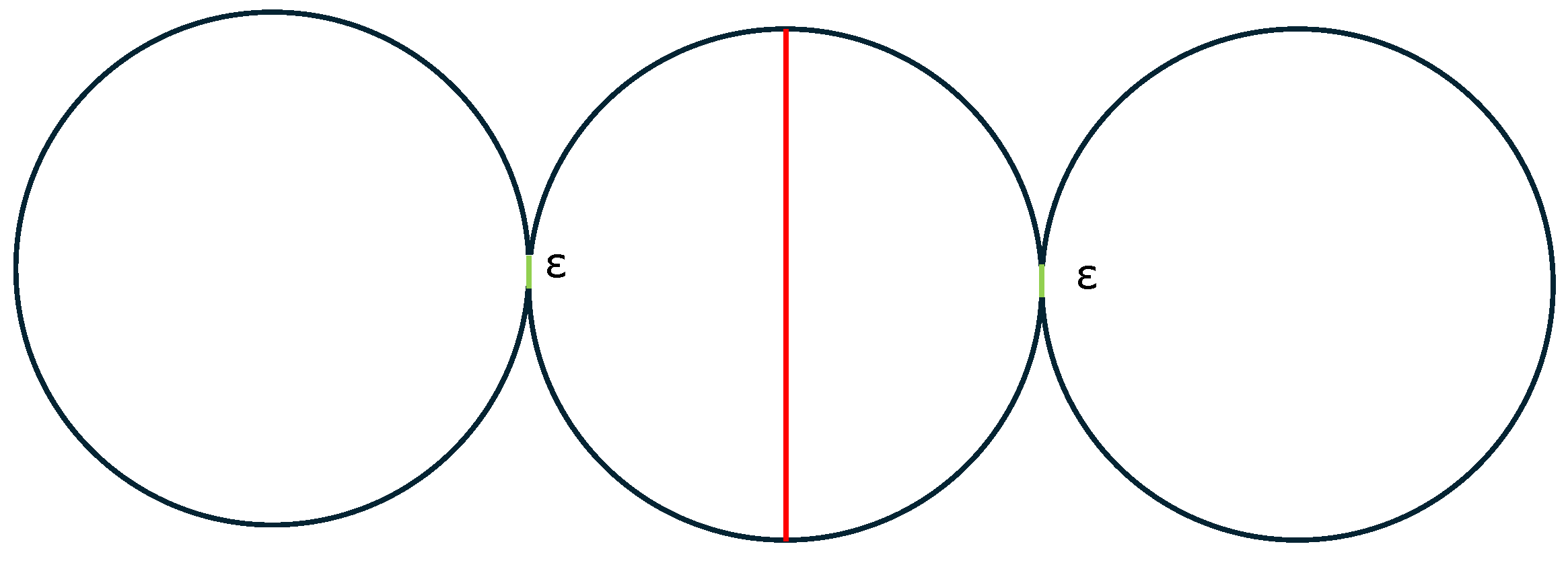
4.3. Intrinsic Boundaries’ Length
5. Methodology
5.1. SEP-Fast Balanced Clustering
| Algorithm 1: The proposed SEP-FBC method |
 |
- Initially, a graph G of the connected pixels from the 2D image space of shape S is computed using eight pixel connectivity. This graph is used to approximate the shortest path distance between the shape points of the complete graph (see Appendix A).
- Then, an initial estimation of the centroids of the N clusters () is calculated by the k-means++ method [26] (with computational cost ) followed by the round operation to adjust C to the space of the image coordinates (see line 1 of Algorithm 1). In the case where does not belong in shape S (), is set to the nearest shape pixel. This is conducted by the get_closest_point procedure (see line 5 of Algorithm 1 and Equation (9)).where the centroid corresponds to the region .
- Furthermore, we initialize each region and compute for each region the vector with all the eight-connectivity graph-based distances between the centroid and the shape points (see lines 7–8 Algorithm 1 and procedure distances(G,)) (the computational cost of this process is using the Dijkstra algorithm with the Adjacency List and Heap, since it is executed N times and the number of edges of the graph G is , due to the fact that each node of the graph has a limited number of neighbors (up to eight neighbors)). The initial clustering of shape pixels is performed using an approximation by the combination of the Euclidean distance and (see line 12 of Algorithm 1) of the graph-based distance of a complete graph of shape S. The use of graph-based distances for clustering provides better image component connectivity for clusters compared with the use of the pure Euclidean distance. This is due to the fact that graph-based distances take into account the component connectivity, while the pure Euclidean distance is directly computed from the pixels’ coordinates (see Figure A1b of Appendix A). The sum of the boundaries’ lengths of the resulting segmentation is low due to the distance-based clustering procedure, but the clusters’ sizes may not be equal.
- Initially, we ensure that all the clusters (regions) consist of connected pixels by assigning non-connected pixels to the smallest neighbor region. This is performed by the procedure correctConnectedComponets(R) (in line 17 of Algorithm 1). Additionally, we smooth the region boundaries by reassigning the pixels of each region boundary to the region that has the most neighbors which is carried out by the procedure smoothBoundaries(R) of line 18 of Algorithm 1.
- Finally, we perform an iterative process that in each iteration grows the smallest region (areaGrow procedure) until the inequality (4) is satisfied (see lines 20–23 of Algorithm 1). The symmetric matrix that counts the number of pixel reassignments between two regions is initialized to zero. The areaGrow procedure uniformly grows the smallest region c by applying the dilation operation with an open disk of radius one. The procedure prevents infinite loops by adding the extra pixels p in a descending way according to expression , where denotes the area of the region to which p belonged, and is the number of reassignments between the regions c and the region that p belonged (). The procedure can stop before growth has finished only if the current area of the region is at least . The computational cost of this stage is according to the procedures of lines 17–19 of Algorithm 1. The iterative step of lines 20–23 of Algorithm 1 has a computational cost of .
5.2. SEP-PSO Fast Balanced Clustering
6. Experimental Evaluation
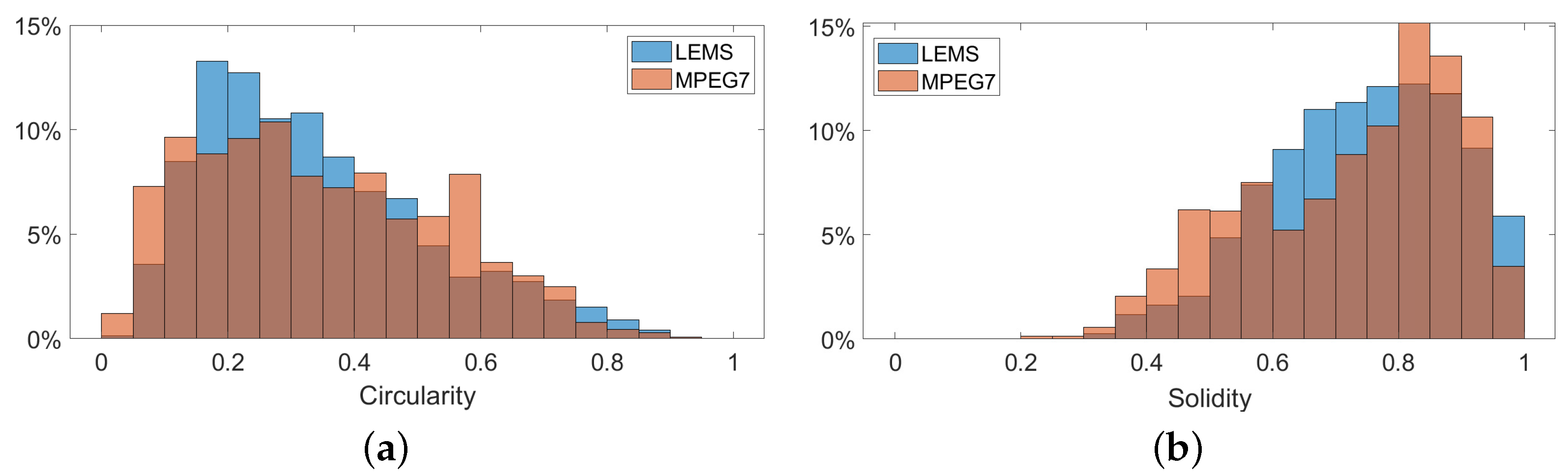
6.1. Datasets
6.2. Baseline Methods
6.3. Evaluation Metrics
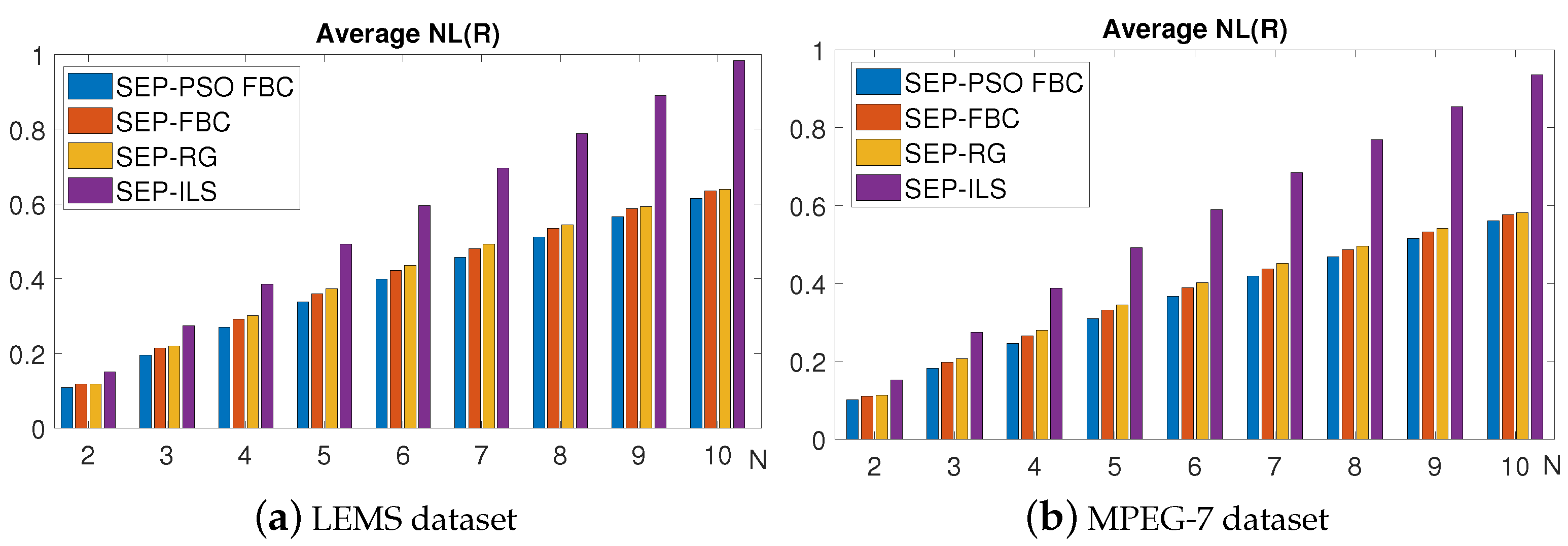
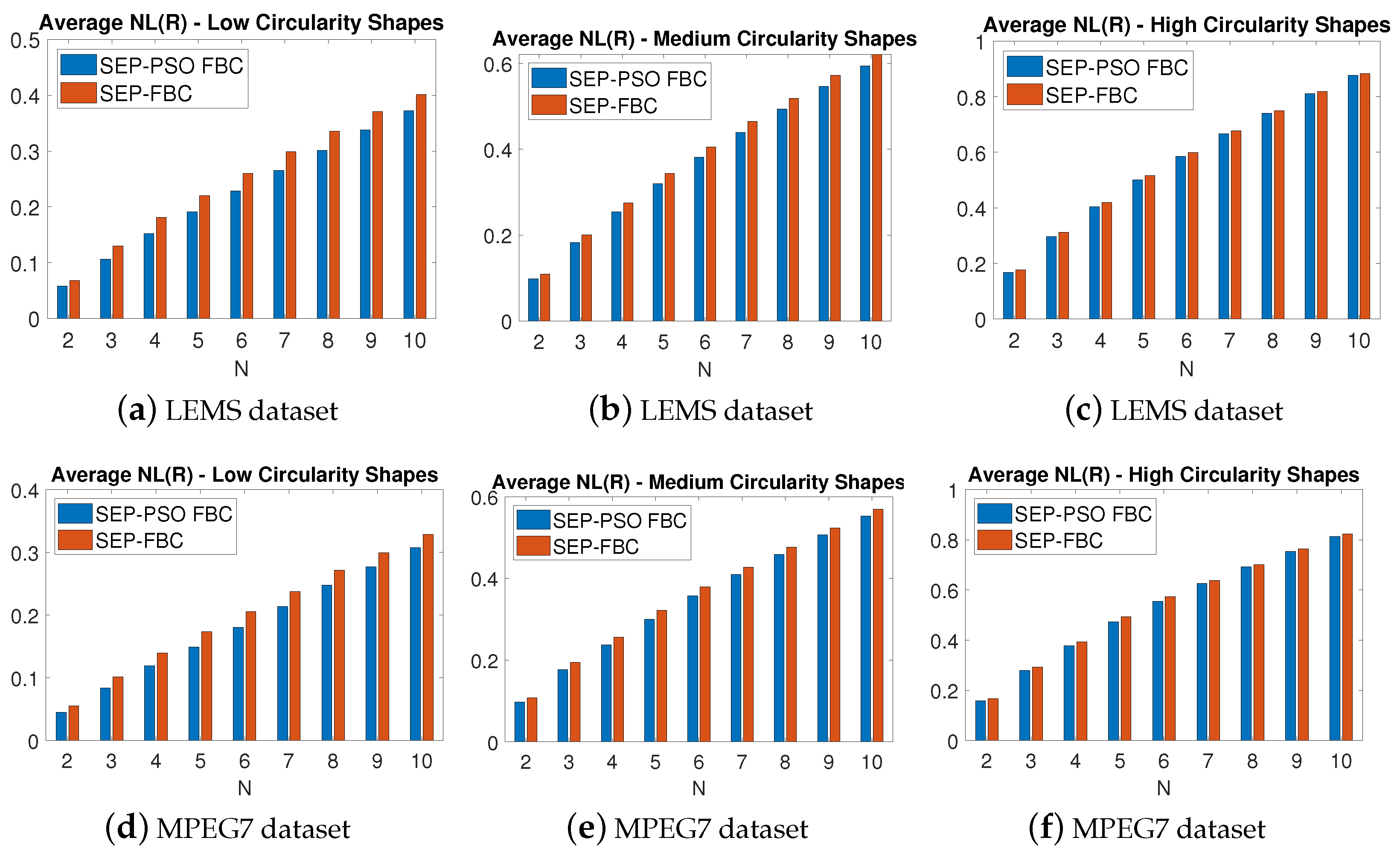
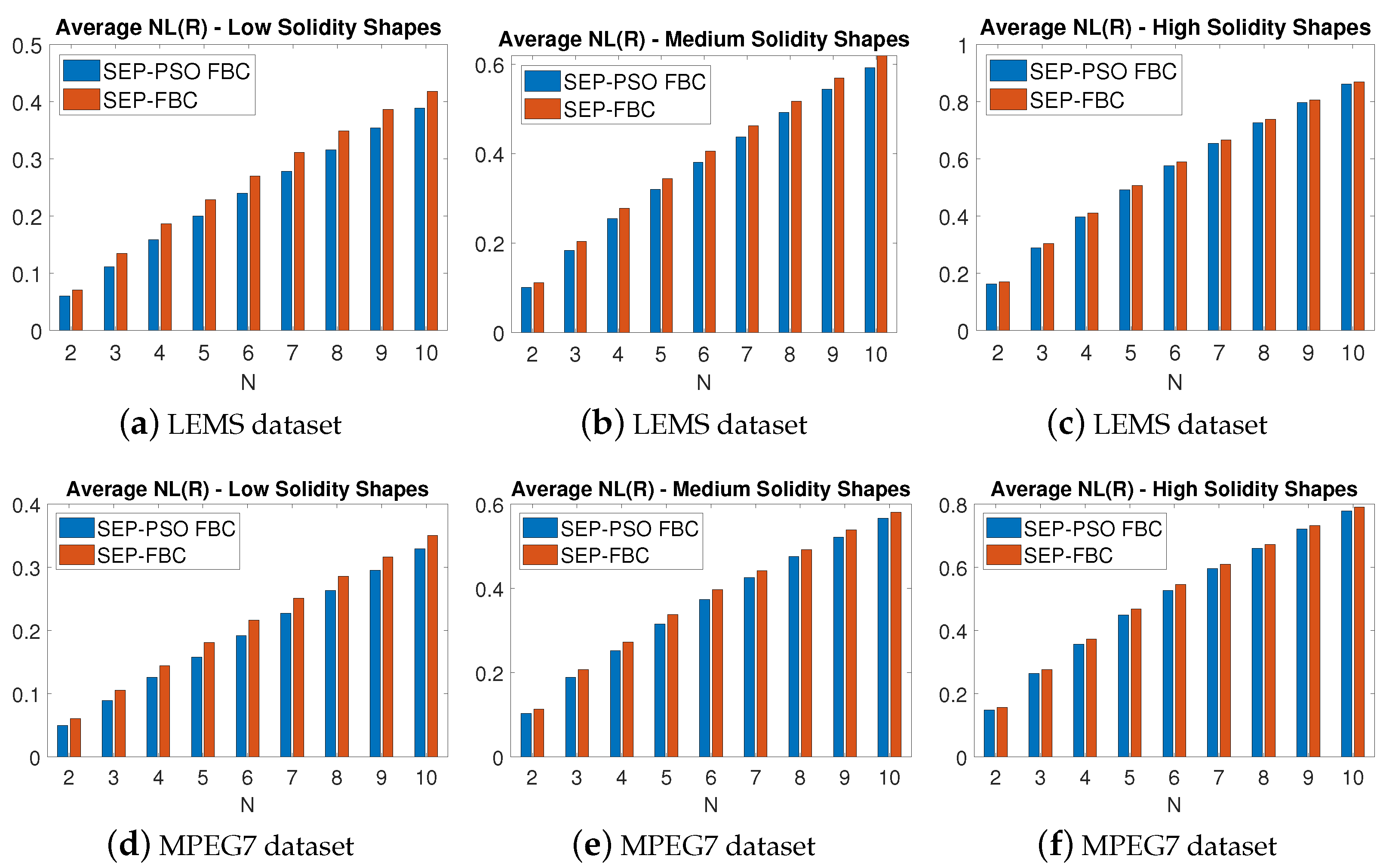
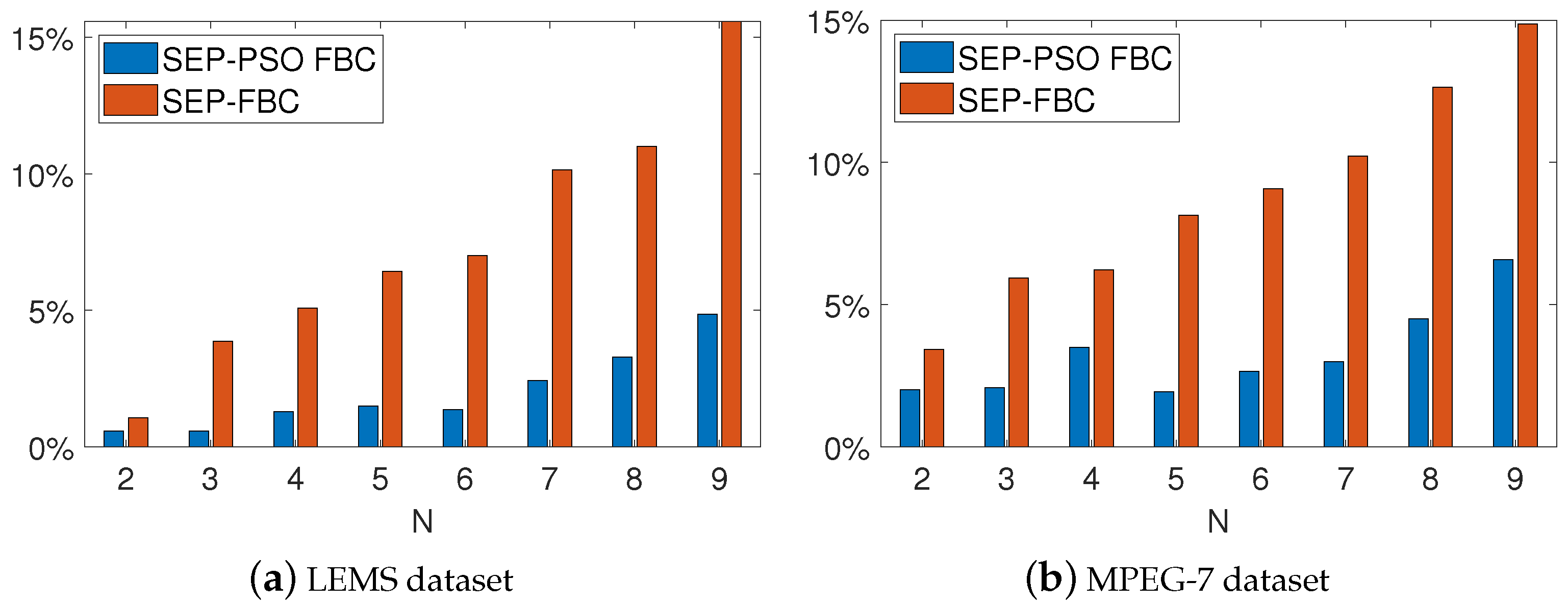
6.4. Comparisons on LEMS and MPEG7 Datasets
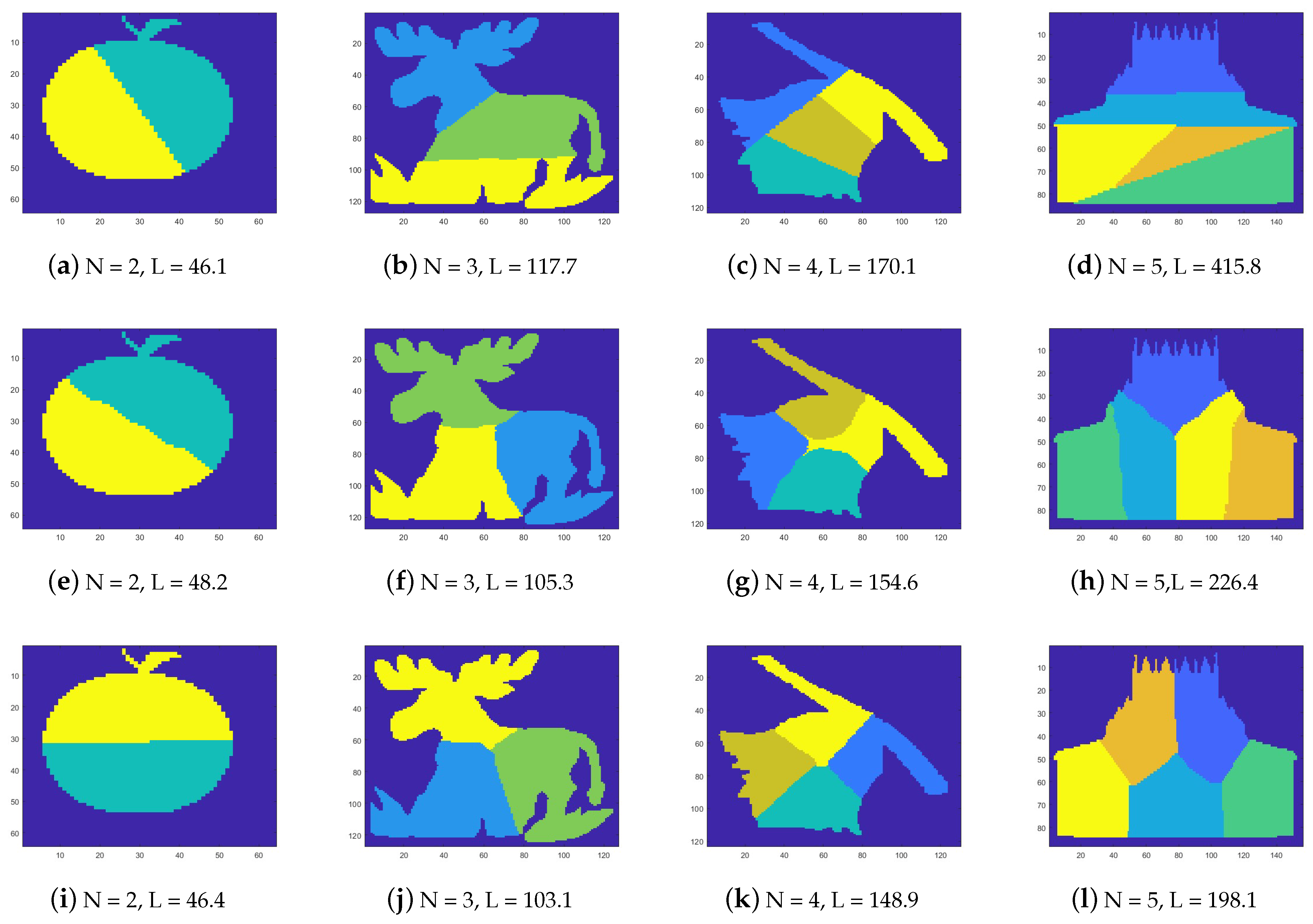
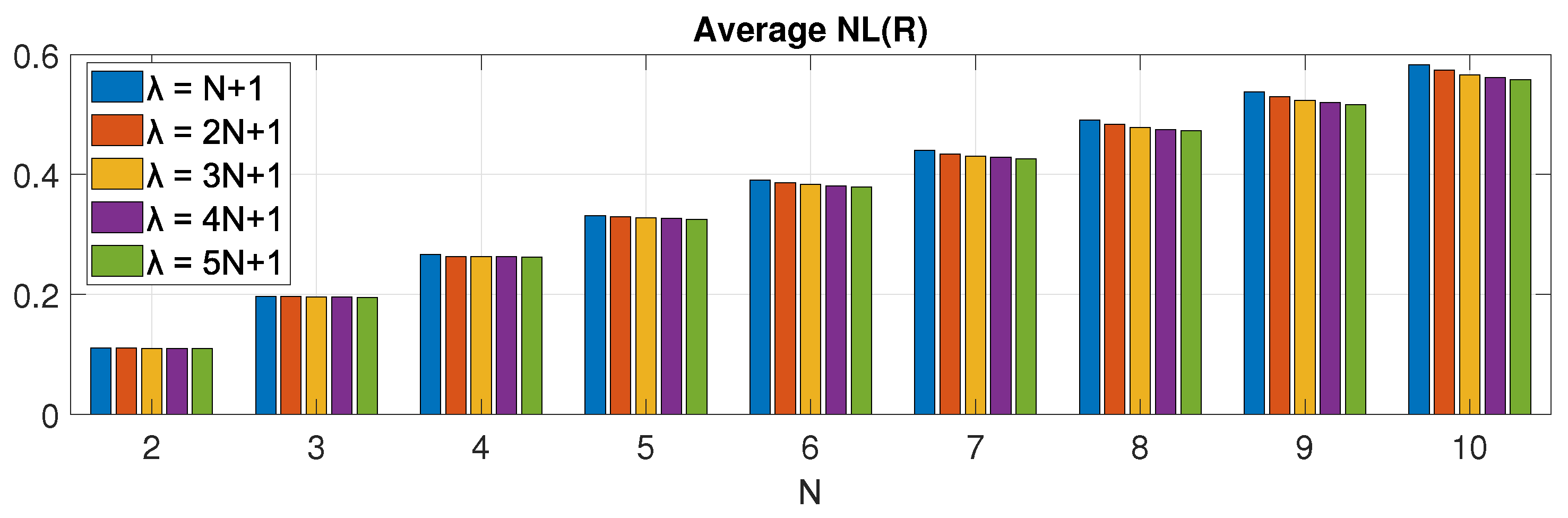
6.5. Evaluation of the Proposed Methods
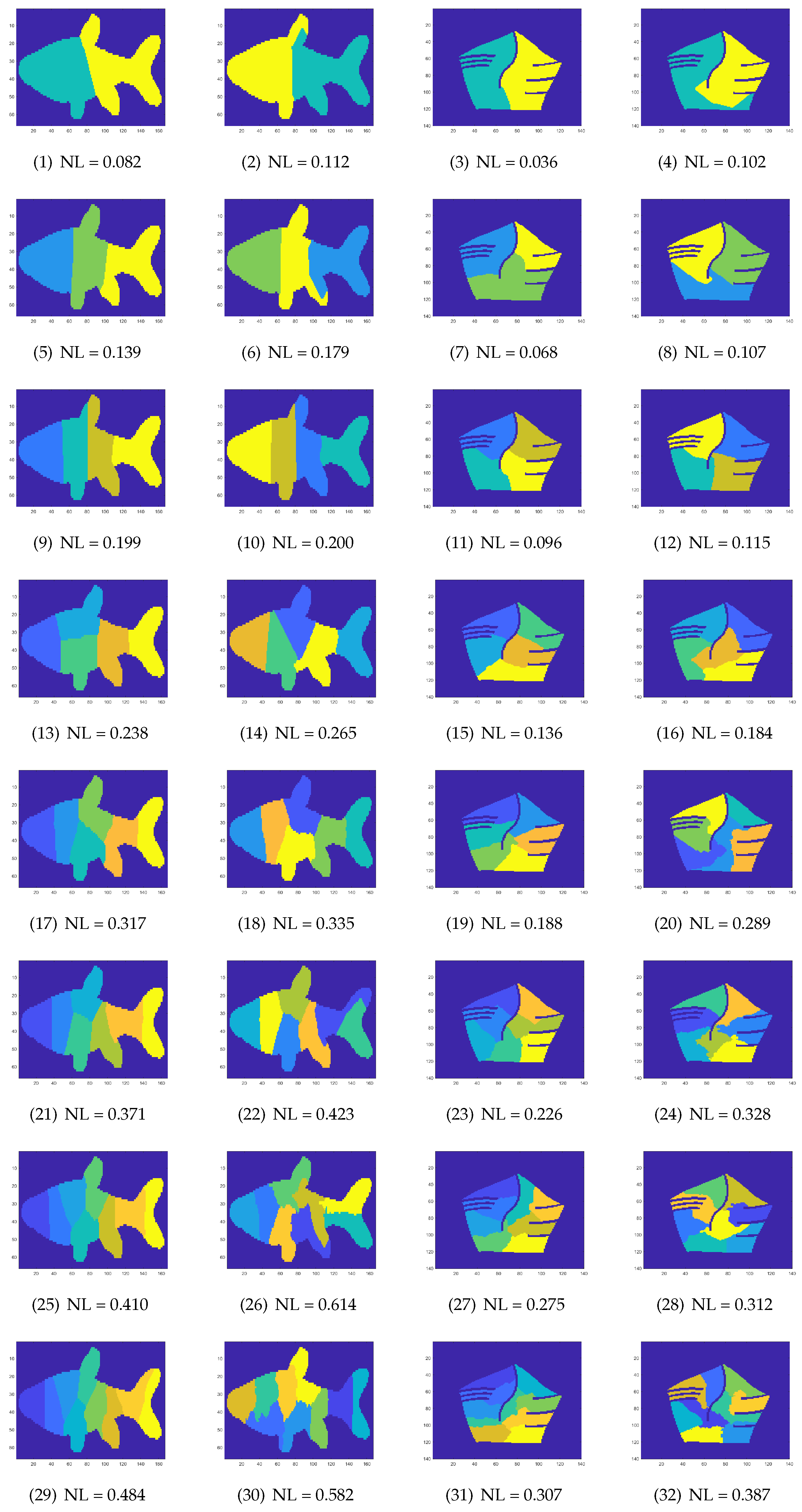
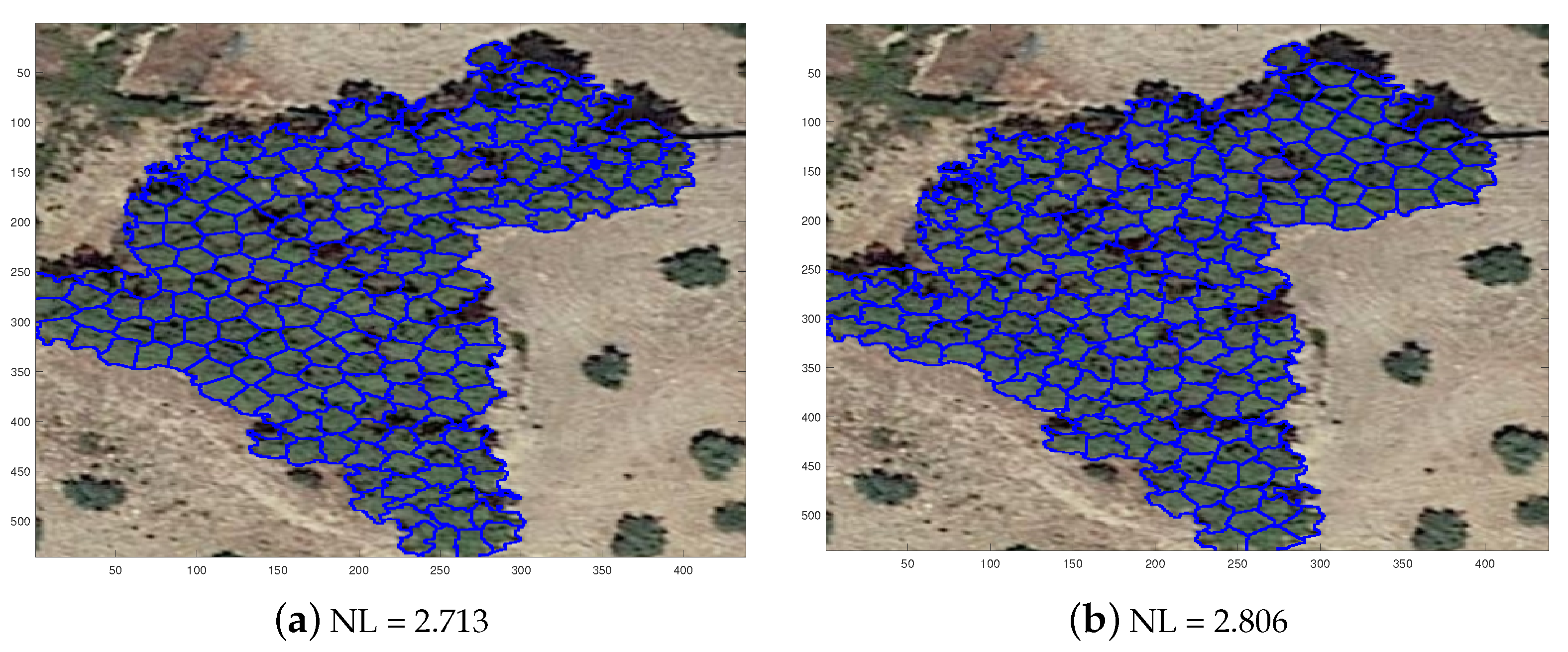
6.6. Applications of the Proposed Methods
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Jiang, D.; Li, G.; Tan, C.; Huang, L.; Sun, Y.; Kong, J. Semantic segmentation for multiscale target based on object recognition using the improved Faster-RCNN model. Future Gener. Comput. Syst. 2021, 123, 94–104. [Google Scholar] [CrossRef]
- Yi, Y.; Zhang, Z.; Zhang, W.; Zhang, C.; Li, W.; Zhao, T. Semantic segmentation of urban buildings from VHR remote sensing imagery using a deep convolutional neural network. Remote Sens. 2019, 11, 1774. [Google Scholar] [CrossRef]
- Li, H.; Zhao, X.; Su, A.; Zhang, H.; Liu, J.; Gu, G. Color space transformation and multi-class weighted loss for adhesive white blood cell segmentation. IEEE Access 2020, 8, 24808–24818. [Google Scholar] [CrossRef]
- Panagiotakis, C.; Athanassopoulos, K.; Tziritas, G. The equipartition of curves. Comput. Geom. 2009, 42, 677–689. [Google Scholar] [CrossRef]
- Shapira, L.; Shamir, A.; Cohen-Or, D. Consistent mesh partitioning and skeletonisation using the shape diameter function. Vis. Comput. 2008, 24, 249–259. [Google Scholar] [CrossRef]
- Markaki, S.; Panagiotakis, C. Unsupervised Tree Detection and Counting via Region-Based Circle Fitting. In Proceedings of the ICPRAM, Lisbon, Portugal, 22–24 February 2023; pp. 95–106. [Google Scholar]
- Panagiotakis, C. The 2D Shape Equipartition Problem Under Minimum Boundary Length. In Proceedings of the International Conference on Pattern Recognition, Kolkata, India, 1–5 December 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 64–79. [Google Scholar]
- Ostu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62. [Google Scholar]
- Zheng, J.; Gao, Y.; Zhang, H.; Lei, Y.; Zhang, J. OTSU multi-threshold image segmentation based on improved particle swarm algorithm. Appl. Sci. 2022, 12, 11514. [Google Scholar] [CrossRef]
- Preetha, M.M.S.J.; Suresh, L.P.; Bosco, M.J. Image segmentation using seeded region growing. In Proceedings of the 2012 International Conference on Computing, Electronics and Electrical Technologies (ICCEET), Nagercoil, Tamil Nadu, India, 21–22 March 2012; pp. 576–583. [Google Scholar]
- Lv, X.; Persello, C.; Li, W.; Huang, X.; Ming, D.; Stein, A. Deep Merge: Deep-Learning-Based Region Merging for Remote Sensing Image Segmentation. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5614120. [Google Scholar] [CrossRef]
- Dhanachandra, N.; Manglem, K.; Chanu, Y.J. Image segmentation using K-means clustering algorithm and subtractive clustering algorithm. Procedia Comput. Sci. 2015, 54, 764–771. [Google Scholar] [CrossRef]
- Grau, V.; Mewes, A.; Alcaniz, M.; Kikinis, R.; Warfield, S.K. Improved watershed transform for medical image segmentation using prior information. IEEE Trans. Med Imaging 2004, 23, 447–458. [Google Scholar] [CrossRef]
- Kornilov, A.; Safonov, I.; Yakimchuk, I. A review of watershed implementations for segmentation of volumetric images. J. Imaging 2022, 8, 127. [Google Scholar] [CrossRef] [PubMed]
- Chan, T.F.; Vese, L.A. Active contours without edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef] [PubMed]
- Niazi, M.; Rahbar, K.; Taheri, F.; Sheikhan, M.; Khademi, M. Delicate image segmentation based on cosine kernel graph cut. J. Vis. Commun. Image Represent. 2025, 108, 104430. [Google Scholar] [CrossRef]
- Minaee, S.; Wang, Y. An ADMM approach to masked signal decomposition using subspace representation. IEEE Trans. Image Process. 2019, 28, 3192–3204. [Google Scholar] [CrossRef]
- Minaee, S.; Boykov, Y.; Porikli, F.; Plaza, A.; Kehtarnavaz, N.; Terzopoulos, D. Image segmentation using deep learning: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3523–3542. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, E.; Zhu, Y. Image segmentation evaluation: A survey of methods. Artif. Intell. Rev. 2020, 53, 5637–5674. [Google Scholar] [CrossRef]
- Khan, J.F.; Bhuiyan, S.M. Weighted entropy for segmentation evaluation. Opt. Laser Technol. 2014, 57, 236–242. [Google Scholar] [CrossRef]
- Panagiotakis, C. Particle Swarm Optimization-Based Unconstrained Polygonal Fitting of 2D Shapes. Algorithms 2024, 17, 25. [Google Scholar] [CrossRef]
- Lempitsky, V.; Blake, A.; Rother, C. Image segmentation by branch-and-mincut. In Proceedings of the Computer Vision–ECCV 2008: 10th European Conference on Computer Vision, Marseille, France, 12–18 October 2008; Proceedings, Part IV 10. Springer: Berlin/Heidelberg, Germany, 2008; pp. 15–29. [Google Scholar]
- Jain, A. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Ikotun, A.M.; Ezugwu, A.E.; Abualigah, L.; Abuhaija, B.; Heming, J. K-means clustering algorithms: A comprehensive review, variants analysis, and advances in the era of big data. Inf. Sci. 2023, 622, 178–210. [Google Scholar] [CrossRef]
- MacQueen, J.B. Some Methods for Classification and Analysis of MultiVariate Observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1965 and 27 December 1965–7 January 1966; Volume 1, pp. 281–297. [Google Scholar]
- Arthur, D.; Vassilvitskii, S. k-means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Theodoridis, S.; Koutroumbas, K. Pattern Recognition, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2006; p. 635. [Google Scholar]
- Malinen, M.I.; Fränti, P. Balanced k-means for clustering. In Proceedings of the Structural, Syntactic, and Statistical Pattern Recognition: Joint IAPR InternationalWorkshop, S+ SSPR 2014, Joensuu, Finland, 20–22 August 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 32–41. [Google Scholar]
- Lin, W.; He, Z.; Xiao, M. Balanced Clustering: A Uniform Model and Fast Algorithm. In Proceedings of the IJCAI, Macao, 10–16 August 2019; pp. 2987–2993. [Google Scholar]
- Hales, T.C. The honeycomb conjecture. Discret. Comput. Geom. 2001, 25, 1–22. [Google Scholar] [CrossRef]
- Oikonomidis, I.; Kyriazis, N.; Argyros, A.A. Efficient model-based 3D tracking of hand articulations using Kinect. In Proceedings of the BMVC, Dundee, UK, 29 August–2 September 2011; Volume 1, p. 3. [Google Scholar]
- Farshi, T.R.; Drake, J.H.; Özcan, E. A multimodal particle swarm optimization-based approach for image segmentation. Expert Syst. Appl. 2020, 149, 113233. [Google Scholar] [CrossRef]
- Gad, A.G. Particle swarm optimization algorithm and its applications: A systematic review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Kimia, B. A Large Binary Image Database, LEMS Vision Group at Brown University. 2002. Available online: http://www.lems.brown.edu/~dmc/ (accessed on 7 May 2024).
- Latecki, L.J.; Lakamper, R.; Eckhardt, T. Shape descriptors for non-rigid shapes with a single closed contour. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Head, SC, USA, 13–15 June 2000; Volume 1, pp. 424–429. [Google Scholar]
- Bai, X.; Yang, X.; Latecki, L.J.; Liu, W.; Tu, Z. Learning context-sensitive shape similarity by graph transduction. Pattern Anal. Mach. Intell. IEEE Trans. 2010, 32, 861–874. [Google Scholar]
- Zdilla, M.J.; Hatfield, S.A.; McLean, K.A.; Cyrus, L.M.; Laslo, J.M.; Lambert, H.W. Circularity, solidity, axes of a best fit ellipse, aspect ratio, and roundness of the foramen ovale: A morphometric analysis with neurosurgical considerations. J. Craniofacial Surg. 2016, 27, 222–228. [Google Scholar] [CrossRef]
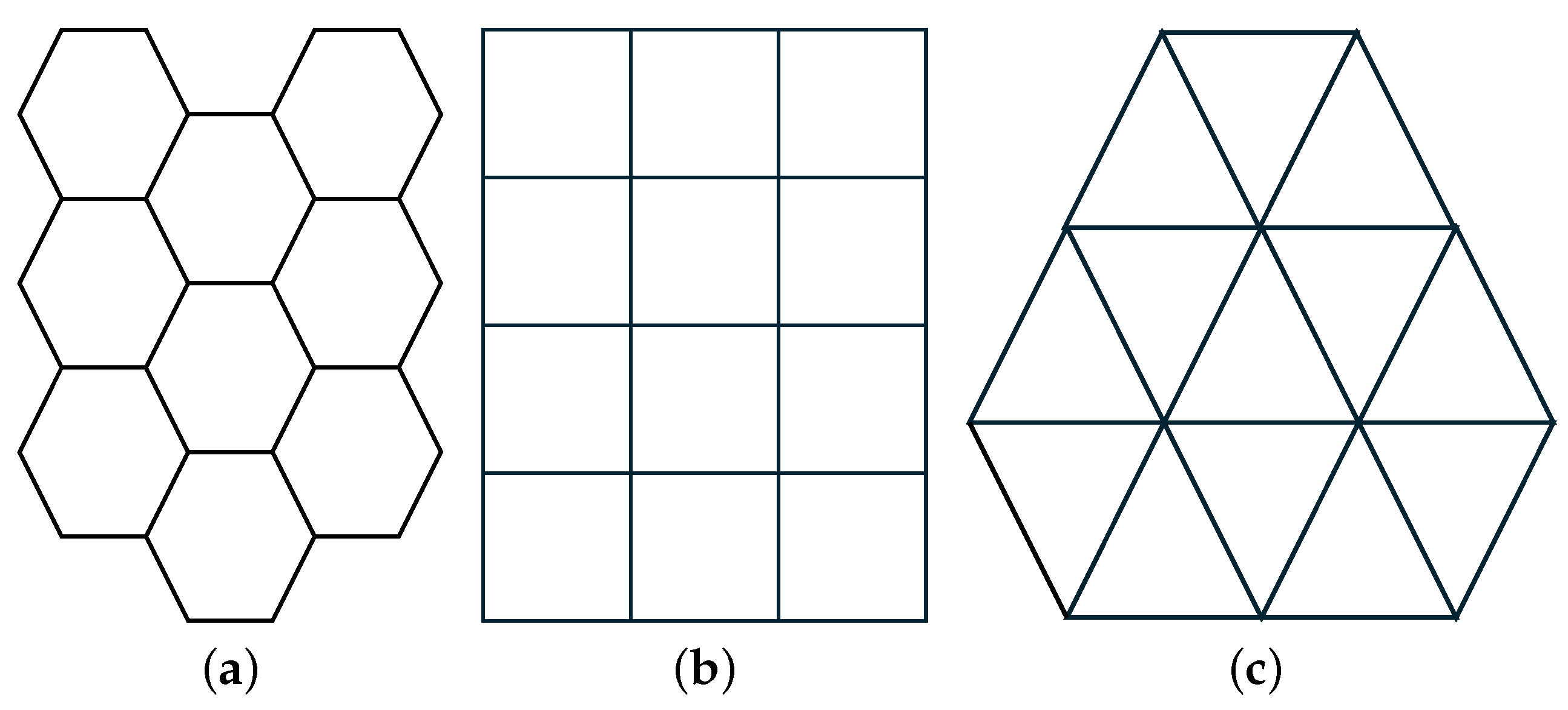


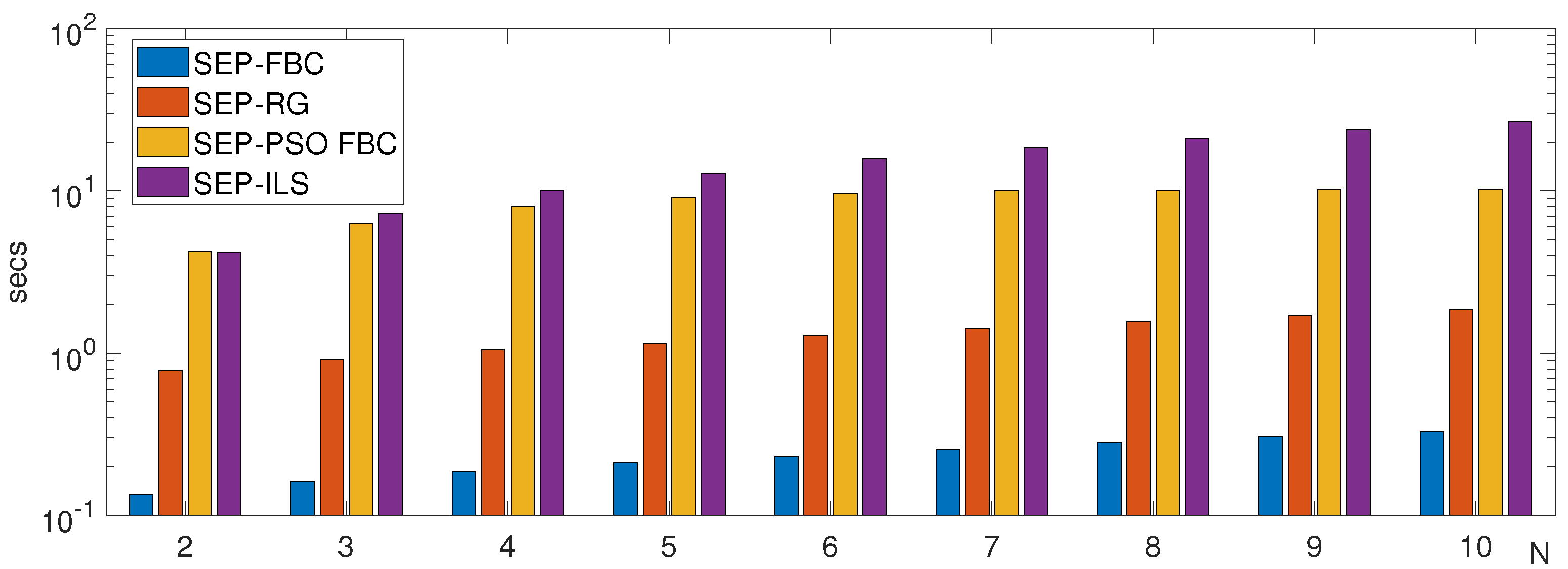
| Shape | Perimeter |
|---|---|
| hexagon | |
| square | |
| equilateral triangle |
| LEMS Dataset | MPEG7 Dataset | |||||
|---|---|---|---|---|---|---|
| Methods | NL | Pr (m/NL) | AET | NL | Pr (m/NL) | AET |
| SEP-PSO FBC | 0.384 | 76.89% | 11.26 | 0.350 | 74.48% | 6.049 |
| SEP-FBC | 0.405 | 12.33% | 0.28 | 0.368 | 13.42% | 0.184 |
| SEP-RG | 0.413 | 8.11% | 1.46 | 0.378 | 8.46% | 1.145 |
| SEP-ILS | 0.584 | 1.12% | 21.49 | 0.572 | 0.96% | 9.727 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panagiotakis, C. Fast Equipartition of Complex 2D Shapes with Minimal Boundaries. Algorithms 2025, 18, 277. https://doi.org/10.3390/a18050277
Panagiotakis C. Fast Equipartition of Complex 2D Shapes with Minimal Boundaries. Algorithms. 2025; 18(5):277. https://doi.org/10.3390/a18050277
Chicago/Turabian StylePanagiotakis, Costas. 2025. "Fast Equipartition of Complex 2D Shapes with Minimal Boundaries" Algorithms 18, no. 5: 277. https://doi.org/10.3390/a18050277
APA StylePanagiotakis, C. (2025). Fast Equipartition of Complex 2D Shapes with Minimal Boundaries. Algorithms, 18(5), 277. https://doi.org/10.3390/a18050277







