Forecasting Cancer Incidence in Canada by Age, Sex, and Region Until 2026 Using Machine Learning Techniques
Abstract
1. Introduction
2. Related Works
3. Materials and Methods
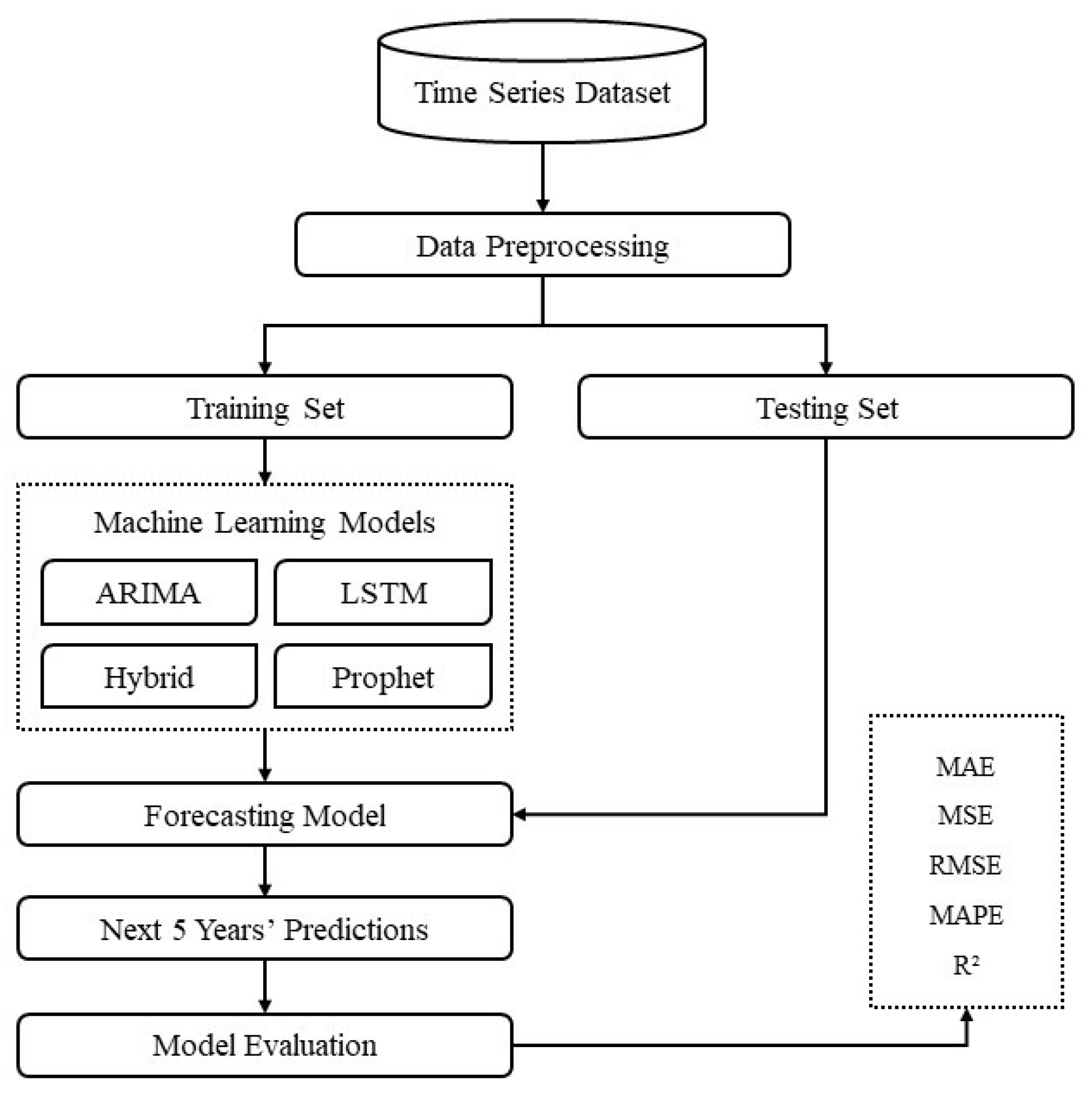
3.1. Research Design
3.2. Data Source
3.3. Data Preprocessing
3.3.1. Handling Missing Data
3.3.2. Normalization
3.3.3. Temporal Indexing
3.3.4. Stationarity Checks
3.4. Model Selection
3.4.1. Long Short-Term Memory (LSTM)
3.4.2. Facebook Prophet Forecasting Model
3.4.3. Autoregressive Integrated Moving Average (ARIMA)
3.4.4. ARIMA-LSTM Hybrid Model
3.5. Evaluation Metrics
3.5.1. Mean Absolute Error (MAE)
3.5.2. Mean Squared Error (MSE)
3.5.3. Root Mean Squared Error (RMSE)
3.5.4. Mean Absolute Percentage Error (MAPE)
3.5.5. Coefficient of Determination (R2)
4. Results
4.1. Performance of the Models
4.1.1. Error Rates for Geography Categories
4.1.2. Error Rates for Age Categories
4.1.3. Error Rates for Sex Categories
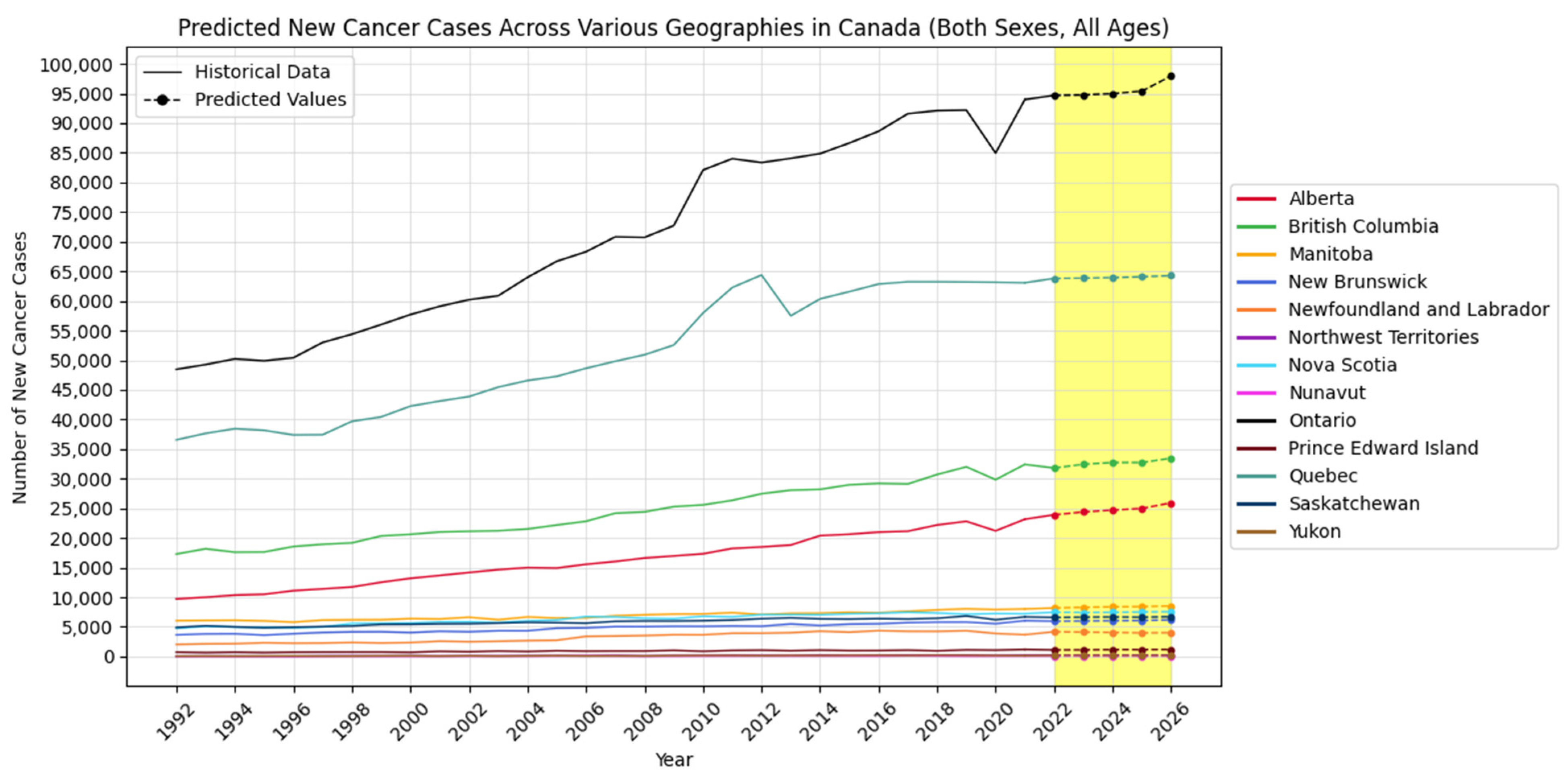
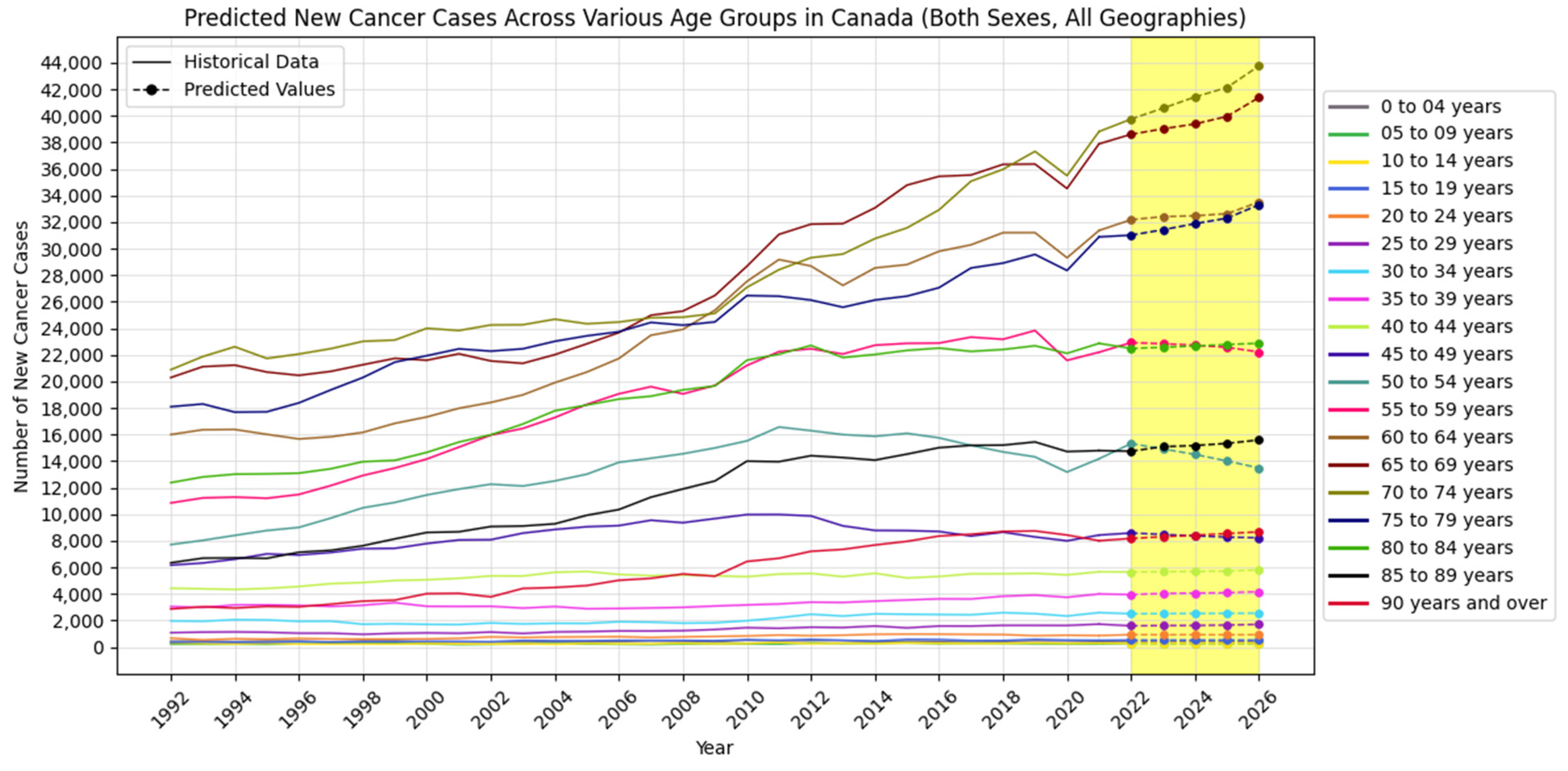
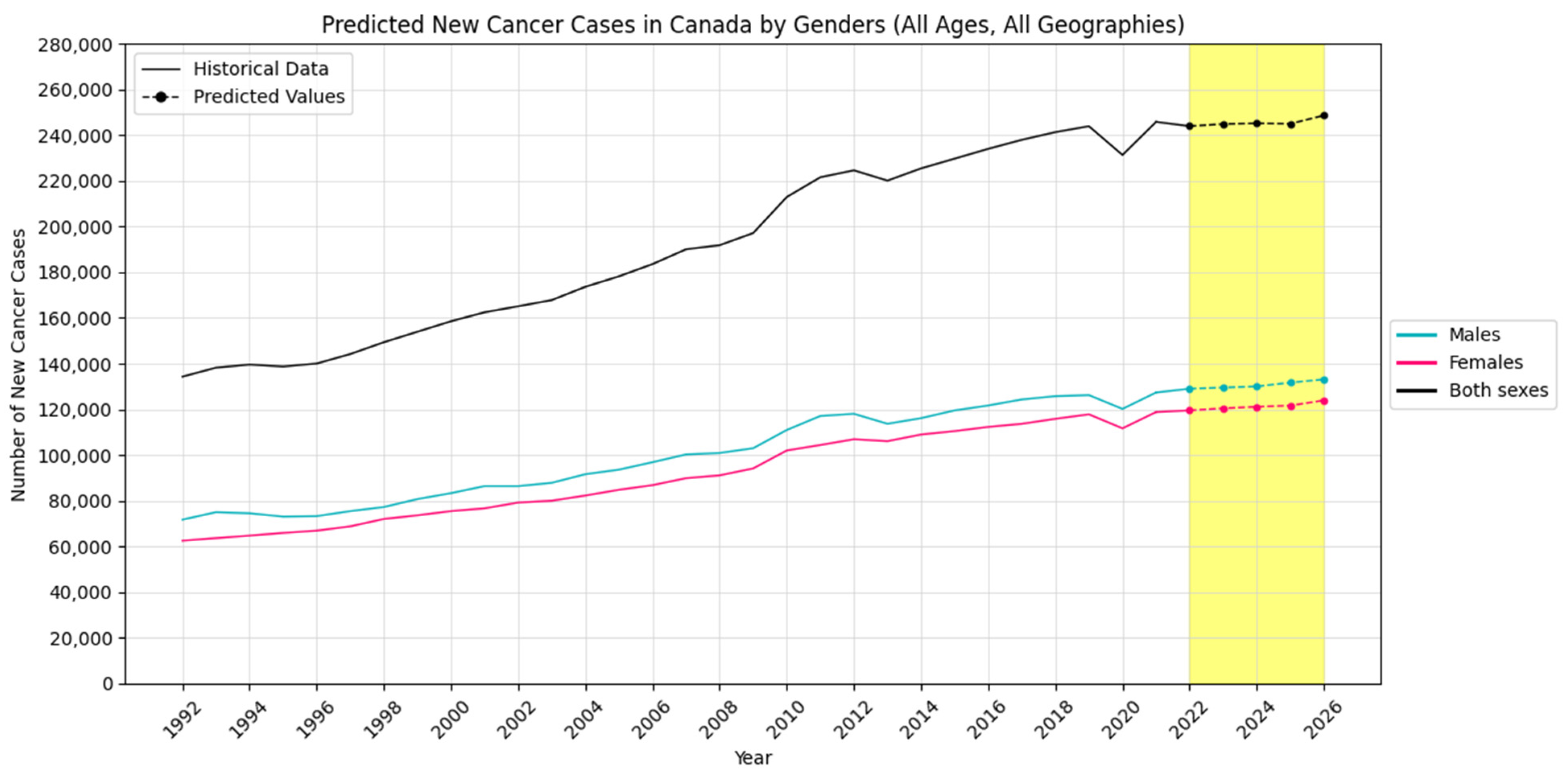
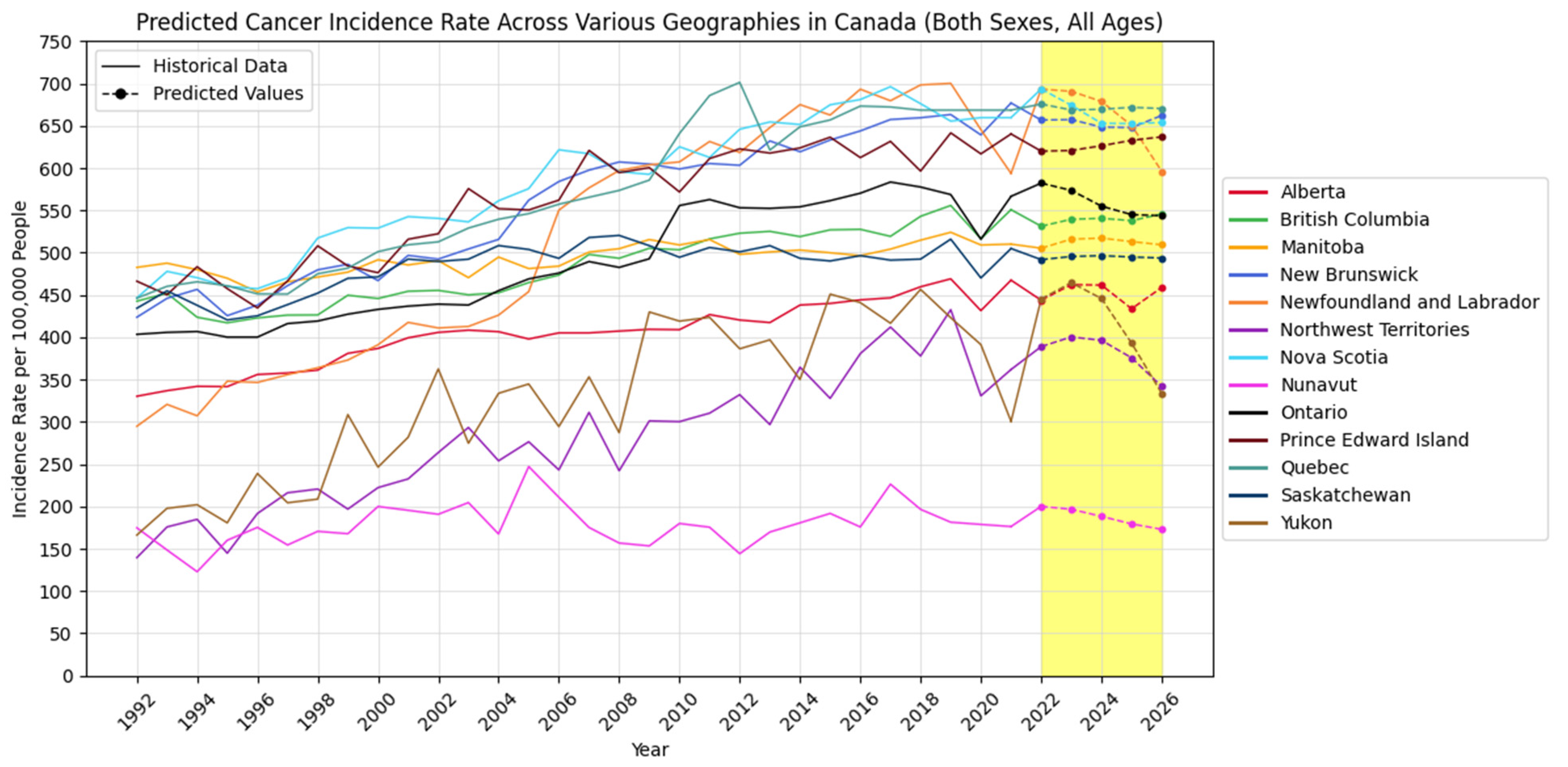
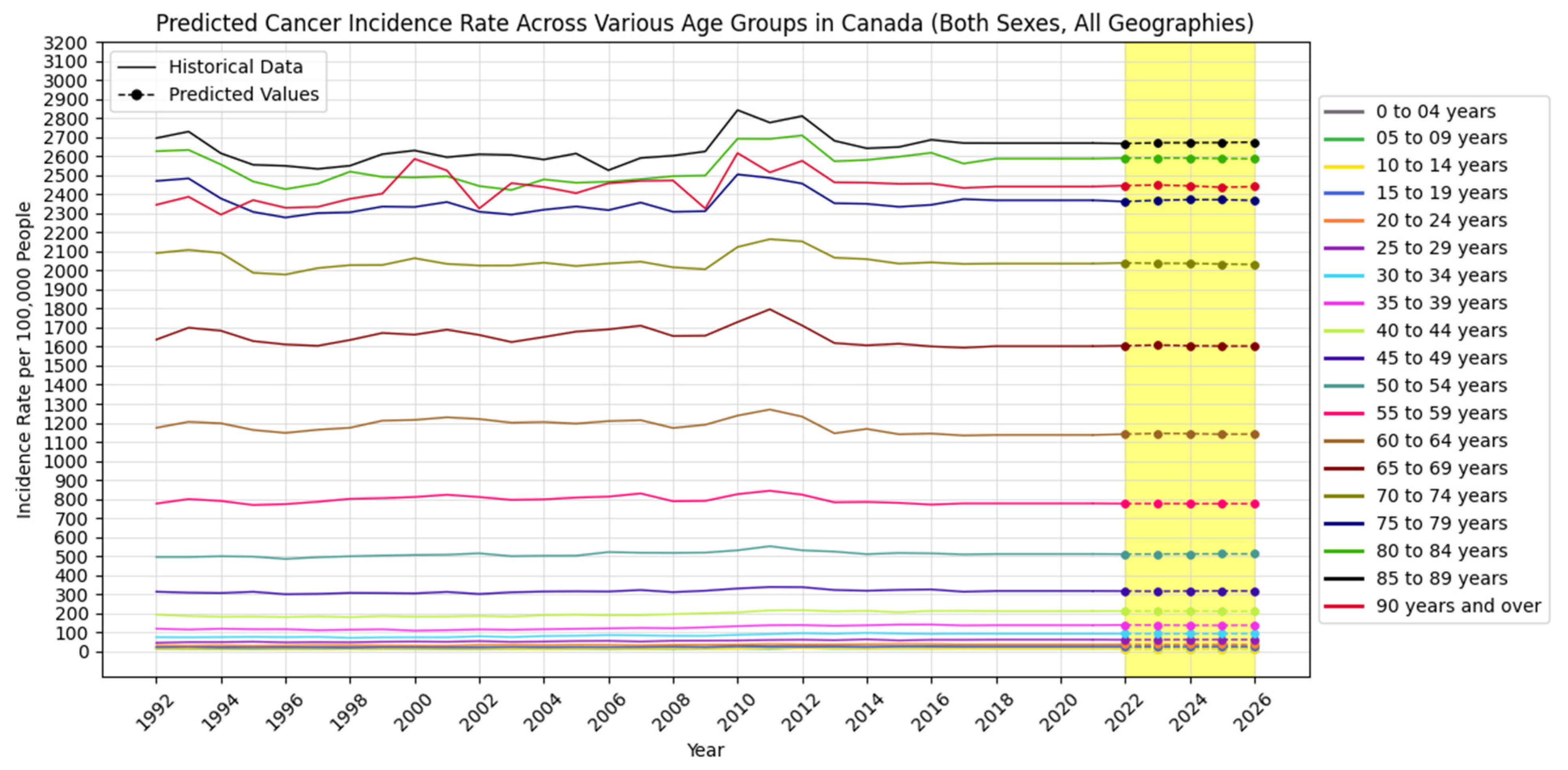
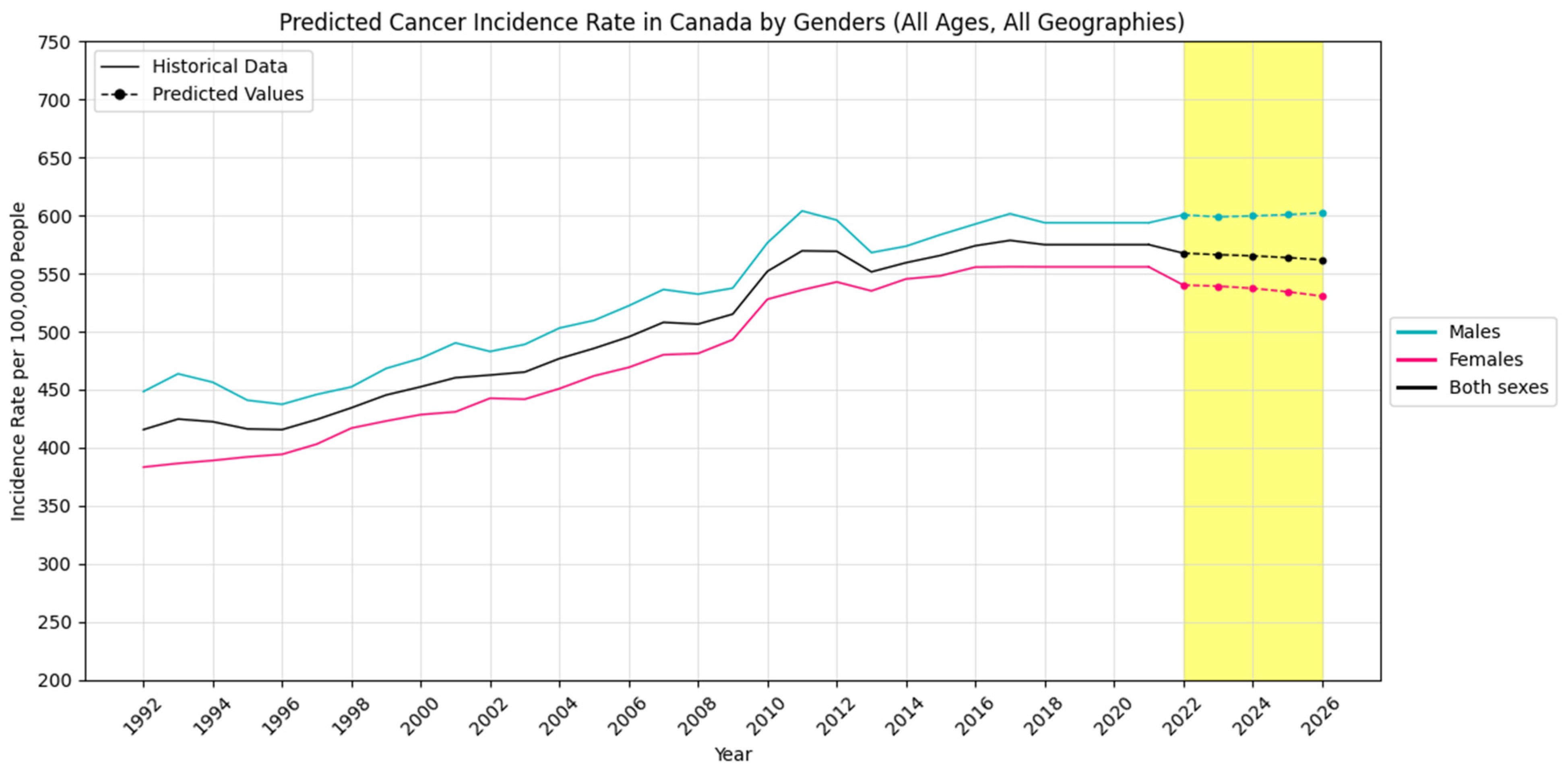
4.2. Forecasting New Cancer Cases and Incidence Rate
4.3. Visualization Insights
5. Discussion
5.1. Model Performance Across Demographics and Regions
5.2. Implications for Public Health and Cancer Prevention
5.3. Limitations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kibbe, W.A.; Klemm, J.D.; Quackenbush, J. Cancer Informatics: New Tools for a Data-Driven Age in Cancer Research. Cancer Res. 2017, 77, e1–e2. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Biemar, F.; Foti, M. Global progress against cancer—Challenges and opportunities. Cancer Biol. Med. 2013, 10, 183–186. [Google Scholar] [CrossRef] [PubMed]
- Sikora, K. Developing a global strategy for cancer. Eur. J. Cancer 1999, 35, 24–31. [Google Scholar] [CrossRef] [PubMed]
- Ivanović, M.; Radovanović, M. Modern machine learning techniques and their applications. In Electronics, Communications and Networks IV; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar] [CrossRef]
- Rathor, A.; Gyanchandani, M. A review at Machine Learning algorithms targeting big data challenges. In Proceedings of the 2017 International Conference on Electrical, Electronics, Communication, Computer, and Optimization Techniques (ICEECCOT), Mysuru, India, 15–16 December 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Nguyen, G.T.; Dlugolinsky, S.; Bobák, M.; Tran, V.D.; López García, Á.; Heredia, I.; Malík, P.; Hluchý, L. Machine Learning and Deep Learning frameworks and libraries for large-scale data mining: A survey. Artif. Intell. Rev. 2019, 52, 77–124. [Google Scholar] [CrossRef]
- Udousoro, I.C. Machine Learning: A Review. Semicond. Sci. Inf. Devices 2020, 2, 5–14. [Google Scholar] [CrossRef]
- Verma, M.; Khoury, M.J.; Ioannidis, J.P. Opportunities and Challenges for Selected Emerging Technologies in Cancer Epidemiology: Mitochondrial, Epigenomic, Metabolomic, and Telomerase Profiling. Cancer Epidemiol. Biomark. Prev. 2012, 22, 189–200. [Google Scholar] [CrossRef]
- Berger, M.L.; Curtis, M.D.; Smith, G.; Harnett, J.; Abernethy, A.P. Opportunities and challenges in leveraging electronic health record data in oncology. Future Oncol. 2016, 12, 1261–1274. [Google Scholar] [CrossRef]
- Gupta, S.; Gupta, A.; Kumar, Y. Artificial intelligence techniques in Cancer research: Opportunities and challenges. In Proceedings of the 2021 International Conference on Technological Advancements and Innovations (ICTAI), Tashkent, Uzbekistan, 10–12 November 2021; pp. 411–416. [Google Scholar] [CrossRef]
- Schlick, C.J.; Castle, J.P.; Bentrem, D.J. Utilizing Big Data in Cancer Care. Surg. Oncol. Clin. N. Am. 2018, 27, 641–652. [Google Scholar] [CrossRef]
- Shweta; Riya; Kumar, A. Cancer Prediction Using Machine Learning Algorithm. Int. J. Sci. Res. (IJSR) 2022, 11, 873–875. [Google Scholar] [CrossRef]
- Kaur, I.; Doja, M.N.; Ahmad, T. Data mining and machine learning in cancer survival research: An overview and future recommendations. J. Biomed. Inform. 2022, 128, 104026. [Google Scholar] [CrossRef]
- Shruti Trivedi, N.K. Predictive Analytics in Healthcare using Machine Learning. In Proceedings of the 2023 14th International Conference on Computing Communication and Networking Technologies (ICCCNT), Delhi, India, 6–8 July 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Meropol, N.J.; Donegan, J.; Rich, A.S. Progress in the Application of Machine Learning Algorithms to Cancer Research and Care. JAMA Netw. Open 2021, 4, e2116063. [Google Scholar] [CrossRef] [PubMed]
- Brenner, D.R.; Poirier, A.; Woods, R.R.; Ellison, L.F.; Billette, J.M.; Demers, A.A.; Zhang, S.X.; Yao, C.; Finley, C.; Fitzgerald, N.; et al. Canadian Cancer Statistics Advisory Committee. Projected estimates of cancer in Canada in 2022. CMAJ 2022, 194, E601–E607. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Brenner, D.R.; Weir, H.K.; Demers, A.A.; Ellison, L.F.; Louzado, C.; Shaw, A.; Turner, D.; Woods, R.R.; Smith, L.M. Projected estimates of cancer in Canada in 2020. Can. Med. Assoc. J. 2020, 192, E199–E205. [Google Scholar] [CrossRef] [PubMed]
- Brenner, D.R.; Gillis, J.; Demers, A.A.; Ellison, L.F.; Billette, J.-M.; Zhang, S.X.; Liu, J.L.; Woods, R.R.; Finley, C.; Fitzgerald, N.; et al. Projected estimates of cancer in Canada in 2024. Can. Med. Assoc. J. 2024, 196, E615–E623. [Google Scholar] [CrossRef]
- Table 13-10-0394-01: Leading Causes of Death, Total Population, by Age Group. Statistics Canada: Ottawa, ON, Canada, 2025; Available online: https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310039401 (accessed on 4 August 2018).
- Canadian Cancer Statistics Advisory Committee in Collaboration with the Canadian Cancer Society Statistics Canada and the Public Health Agency of Canada. Canadian Cancer Statistics; Canadian Cancer Society: Toronto, ON, Canada, 2021; Available online: www.cancer.ca/Canadian-Cancer-Statistics-2021-EN (accessed on 28 March 2022).
- Xie, L.; Semenciw, R.; Mery, L. Cancer incidence in Canada: Trends and projections (1983–2032). Health Promot. Chronic Dis. Prev. Can. 2015, 35 (Suppl. S1), 2–186. [Google Scholar] [CrossRef]
- de Oliveira, C.; Weir, S.; Rangrej, J.; Krahn, M.D.; Mittmann, N.; Hoch, J.S.; Chan, K.K.W.; Peacock, S. The economic burden of cancer care in Canada: A population-based cost study. CMAJ Open 2018, 6, E1–E10. [Google Scholar] [CrossRef]
- Qiu, Z.; Hatcher, J. Cancer Projection Analytical Network Working Team CANPROJ: The Rpackage of Cancer Projection Methods Based on Generalized Linear Models for Age Period/or Cohort Version, I; Alberta Health Services: Edmonton, AB, Canada, 2013. [Google Scholar]
- Government of Canada, S.C. Cancer Incidence in Canada, 2021. The Daily. Available online: https://www150.statcan.gc.ca/n1/daily-quotidien/240131/dq240131d-eng.htm (accessed on 31 January 2024).
- Government of Canada, S.C. Canadian Cancer Registry—Age-Standardization: Incidence; Government of Canada, Statistics Canada: Ottawa, ON, Canada, 2025; Available online: https://www.statcan.gc.ca/en/statistical-programs/document/3207_D12_V4 (accessed on 17 November 2021).
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Emmert-Streib, F.; Yang, Z.; Feng, H.; Tripathi, S.; Dehmer, M. An Introductory Review of Deep Learning for Prediction Models with Big Data. Front. Artif. Intell. 2020, 3, 4. [Google Scholar] [CrossRef]
- Kaninde, S.; Mahajan, M.; Janghale, A.; Joshi, B. Stock Price Prediction using Facebook Prophet. ITM Web Conf. 2022, 44, 3060. [Google Scholar] [CrossRef]
- Korstanje, J. The Prophet Model. In Advanced Forecasting with Python; Apress: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Shen, J.; Valagolam, D.; McCalla, S. Prophet forecasting model: A machine learning approach to predict the concentration of air pollutants (PM2.5, PM10, O3, NO2, SO2, CO) in Seoul, South Korea. PeerJ 2020, 8, e9961. [Google Scholar] [CrossRef]
- Rundo, F.; Trenta, F.; di Stallo, A.L.; Battiato, S. Machine learning for quantitative finance applications: A survey. Appl. Sci. 2019, 9, 5574. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. A comparison of ARIMA and LSTM in forecasting time series. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 1394–1401. [Google Scholar]
- Kontopoulou, V.I.; Panagopoulos, A.D.; Kakkos, I.; Matsopoulos, G.K. A Review of ARIMA vs. Machine Learning Approaches for Time Series Forecasting in Data Driven Networks. Future Internet 2023, 15, 255. [Google Scholar] [CrossRef]
- Sima, S.N.; Akbar, S.N. Forecasting Economics and Financial Time Series: ARIMA vs. LSTM. arXiv 2018, arXiv:1803.06386. [Google Scholar] [CrossRef]
- Kulshreshtha, S.; Vijayalakshmi, A. An ARIMA-LSTM hybrid model for stock market prediction using live data. J. Eng. Sci. Technol. Rev. 2020, 13, 117–123. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Maxim, S.; Adriaan, B.; Shcherbakova, N.L.; Anton, T.; Janovsky, T.A.; Kamaev, V.A. A survey of forecast error measures. World Appl. Sci. J. 2013, 24, 171–176. [Google Scholar]
- Cheng, C.; Shalabh Garg, G. Coefficient of determination for multiple measurement error models. J. Multivar. Anal. 2014, 126, 137–152. [Google Scholar] [CrossRef]
- Goel, H.; Melnyk, I.; Banerjee, A. R2N2: Residual Recurrent Neural Networks for Multivariate Time Series Forecasting. arXiv 2017, arXiv:1709.03159. [Google Scholar]
- Chatfield, C. Model uncertainty and forecast accuracy. J. Forecast. 1996, 15, 495–508. [Google Scholar] [CrossRef]
- Hewamalage, H.; Bergmeir, C.; Bandara, K. Recurrent Neural Networks for Time Series Forecasting: Current Status and Future Directions. arXiv 2019, arXiv:1909.00590. [Google Scholar] [CrossRef]
- Kim, T.; Leybourne, S.J.; Newbold, P. Asymptotic mean-squared forecast error when an autoregression with linear trend is fitted to data generated by an I(0) or I(1) process. J. Time Ser. Anal. 2004, 25, 583–602. [Google Scholar] [CrossRef]
| Geography | Category | Model | MSE | MAE | RMSE | MAPE | R2 |
|---|---|---|---|---|---|---|---|
| Alberta | New Cancer Cases | ARIMA | 0.0028 | 0.0377 | 0.0528 | 0.0444 | 0.6795 |
| LSTM | 0.0028 | 0.0379 | 0.0527 | 0.0452 | 0.6905 | ||
| Hybrid | 0.0015 | 0.0344 | 0.0385 | 0.0402 | 0.8296 | ||
| Prophet | 0.0032 | 0.0509 | 0.0564 | 0.0596 | 0.3438 | ||
| Cancer Incidence Rate | ARIMA | 0.0102 | 0.0629 | 0.1012 | 0.0786 | 0.0832 | |
| LSTM | 0.0081 | 0.0671 | 0.0907 | 0.0820 | 0.0898 | ||
| Hybrid | 0.0013 | 0.0293 | 0.0357 | 0.0315 | 0.8651 | ||
| Prophet | 0.0051 | 0.0568 | 0.0714 | 0.0656 | 0.3887 | ||
| British Columbia | New Cancer Cases | ARIMA | 0.0032 | 0.0383 | 0.0567 | 0.0468 | 0.6612 |
| LSTM | 0.0028 | 0.0416 | 0.0525 | 0.0491 | 0.7100 | ||
| Hybrid | 0.0018 | 0.0317 | 0.0419 | 0.0382 | 0.8151 | ||
| Prophet | 0.0038 | 0.0544 | 0.0614 | 0.0665 | 0.3208 | ||
| Cancer Incidence Rate | ARIMA | 0.0112 | 0.0816 | 0.0961 | 0.0935 | 0.0659 | |
| LSTM | 0.0091 | 0.0769 | 0.0954 | 0.0934 | 0.1547 | ||
| Hybrid | 0.0064 | 0.0628 | 0.0799 | 0.0766 | 0.3516 | ||
| Prophet | 0.0071 | 0.0595 | 0.0845 | 0.0765 | 0.0301 | ||
| Manitoba | New Cancer Cases | ARIMA | 0.0092 | 0.0762 | 0.0960 | 0.0844 | 0.4569 |
| LSTM | 0.0047 | 0.0547 | 0.0687 | 0.0677 | 0.6866 | ||
| Hybrid | 0.0004 | 0.0169 | 0.0205 | 0.0199 | 0.9752 | ||
| Prophet | 0.0061 | 0.0583 | 0.0779 | 0.0661 | 0.5133 | ||
| Cancer Incidence Rate | ARIMA | 0.0148 | 0.0910 | 0.1218 | 0.1202 | 0.1289 | |
| LSTM | 0.0054 | 0.0564 | 0.0732 | 0.0598 | 0.2090 | ||
| Hybrid | 0.0015 | 0.0240 | 0.0390 | 0.0279 | 0.8844 | ||
| Prophet | 0.0089 | 0.0877 | 0.1174 | 0.0922 | −1.7234 | ||
| New Brunswick | New Cancer Cases | ARIMA | 0.0059 | 0.0705 | 0.0768 | 0.0835 | 0.3275 |
| LSTM | 0.0038 | 0.0493 | 0.0619 | 0.0613 | 0.5627 | ||
| Hybrid | 0.0018 | 0.0258 | 0.0427 | 0.0343 | 0.7917 | ||
| Prophet | 0.0048 | 0.0594 | 0.0694 | 0.0726 | 0.4504 | ||
| Cancer Incidence Rate | ARIMA | 0.0060 | 0.0605 | 0.0776 | 0.0657 | 0.4920 | |
| LSTM | 0.0023 | 0.0350 | 0.0480 | 0.0433 | 0.5112 | ||
| Hybrid | 0.0011 | 0.0252 | 0.0325 | 0.0281 | 0.7727 | ||
| Prophet | 0.0068 | 0.0741 | 0.0823 | 0.0851 | −1.1331 | ||
| Newfoundland and Labrador | New Cancer Cases | ARIMA | 0.0062 | 0.0634 | 0.0790 | 0.0748 | 0.2867 |
| LSTM | 0.0155 | 0.0778 | 0.1244 | 0.0997 | 0.6262 | ||
| Hybrid | 0.0003 | 0.0141 | 0.0169 | 0.0154 | 0.9763 | ||
| Prophet | 0.0122 | 0.0816 | 0.1105 | 0.0895 | −2.8241 | ||
| Cancer Incidence Rate | ARIMA | 0.0060 | 0.0658 | 0.0776 | 0.0718 | 0.3345 | |
| LSTM | 0.0119 | 0.0692 | 0.1093 | 0.0844 | 0.7782 | ||
| Hybrid | 0.0007 | 0.0211 | 0.0274 | 0.0222 | 0.9157 | ||
| Prophet | 0.0109 | 0.0766 | 0.1046 | 0.0819 | −0.3781 | ||
| Northwest Territories | New Cancer Cases | ARIMA | 0.0194 | 0.1343 | 0.1394 | 0.1676 | 0.1355 |
| LSTM | 0.0128 | 0.0908 | 0.1132 | 0.1170 | 0.6193 | ||
| Hybrid | 0.0052 | 0.0601 | 0.0721 | 0.0842 | 0.8061 | ||
| Prophet | 0.0252 | 0.1397 | 0.1589 | 0.1923 | 0.1366 | ||
| Cancer Incidence Rate | ARIMA | 0.0200 | 0.0995 | 0.1414 | 0.1293 | 0.07207 | |
| LSTM | 0.0164 | 0.0809 | 0.1279 | 0.1113 | 0.2239 | ||
| Hybrid | 0.0076 | 0.0672 | 0.0869 | 0.0922 | 0.5949 | ||
| Prophet | 0.0155 | 0.1101 | 0.1245 | 0.1375 | 0.3650 | ||
| Nova Scotia | New Cancer Cases | ARIMA | 0.0062 | 0.0634 | 0.0790 | 0.0748 | 0.2867 |
| LSTM | 0.0004 | 0.0163 | 0.0206 | 0.0119 | 0.7926 | ||
| Hybrid | 0.0002 | 0.0118 | 0.0139 | 0.0125 | 0.8699 | ||
| Prophet | 0.0091 | 0.0694 | 0.0951 | 0.0767 | 0.4746 | ||
| Cancer Incidence Rate | ARIMA | 0.0054 | 0.0661 | 0.0737 | 0.0780 | 0.6996 | |
| LSTM | 0.0087 | 0.0866 | 0.0939 | 0.0960 | 0.3972 | ||
| Hybrid | 0.0003 | 0.0145 | 0.0165 | 0.0164 | 0.9188 | ||
| Prophet | 0.0058 | 0.0641 | 0.0990 | 0.0735 | −1.7068 | ||
| Nunavut | New Cancer Cases | ARIMA | 0.0038 | 0.0379 | 0.0617 | 0.0826 | 0.3726 |
| LSTM | 0.0030 | 0.0431 | 0.0549 | 0.0744 | 0.9006 | ||
| Hybrid | 0.0022 | 0.0289 | 0.0469 | 0.0557 | 0.9356 | ||
| Prophet | 0.0309 | 0.1348 | 0.1757 | 0.2021 | 0.2435 | ||
| Cancer Incidence Rate | ARIMA | 0.0010 | 0.0255 | 0.0260 | 0.0566 | 0.4159 | |
| LSTM | 0.0041 | 0.0373 | 0.0640 | 0.0837 | 0.7505 | ||
| Hybrid | 0.0009 | 0.0233 | 0.0298 | 0.0422 | 0.9471 | ||
| Prophet | 0.0231 | 0.1117 | 0.1521 | 0.1067 | 0.1507 | ||
| Ontario | New Cancer Cases | ARIMA | 0.0081 | 0.0614 | 0.0901 | 0.0693 | 0.3200 |
| LSTM | 0.0043 | 0.0496 | 0.0658 | 0.0563 | 0.2001 | ||
| Hybrid | 0.0019 | 0.0283 | 0.0436 | 0.0329 | 0.6904 | ||
| Prophet | 0.0035 | 0.0517 | 0.0589 | 0.0570 | 0.1763 | ||
| Cancer Incidence Rate | ARIMA | 0.0191 | 0.0910 | 0.1083 | 0.0936 | 0.55701 | |
| LSTM | 0.0107 | 0.0631 | 0.1035 | 0.0840 | 0.4479 | ||
| Hybrid | 0.0021 | 0.0344 | 0.0459 | 0.0388 | 0.6580 | ||
| Prophet | 0.0128 | 0.1011 | 0.1212 | 0.1162 | −0.5615 | ||
| Prince Edward Island | New Cancer Cases | ARIMA | 0.0110 | 0.0776 | 0.1047 | 0.0879 | 0.3742 |
| LSTM | 0.0187 | 0.0693 | 0.1368 | 0.0784 | 0.1700 | ||
| Hybrid | 0.0036 | 0.0451 | 0.0604 | 0.0632 | 0.8212 | ||
| Prophet | 0.0227 | 0.1229 | 0.1507 | 0.1065 | 0.2397 | ||
| Cancer Incidence Rate | ARIMA | 0.0059 | 0.0588 | 0.0767 | 0.0613 | 0.1394 | |
| LSTM | 0.0039 | 0.0623 | 0.0626 | 0.0654 | 0.1945 | ||
| Hybrid | 0.0035 | 0.0469 | 0.0590 | 0.0532 | 0.2424 | ||
| Prophet | 0.0181 | 0.1059 | 0.1347 | 0.1042 | −2.7544 | ||
| Quebec | New Cancer Cases | ARIMA | 0.0084 | 0.0511 | 0.0919 | 0.0558 | 0.1893 |
| LSTM | 0.0020 | 0.0398 | 0.0444 | 0.0440 | 0.5558 | ||
| Hybrid | 0.0006 | 0.0242 | 0.0250 | 0.0260 | 0.5084 | ||
| Prophet | 0.0052 | 0.0488 | 0.0719 | 0.0522 | −0.6552 | ||
| Cancer Incidence Rate | ARIMA | 0.0007 | 0.0250 | 0.0267 | 0.0271 | 0.2899 | |
| LSTM | 0.0012 | 0.0353 | 0.0408 | 0.0996 | 0.6675 | ||
| Hybrid | 0.0005 | 0.0161 | 0.0231 | 0.0207 | 0.8603 | ||
| Prophet | 0.0112 | 0.0918 | 0.1061 | 0.1077 | −3.3572 | ||
| Saskatchewan | New Cancer Cases | ARIMA | 0.0115 | 0.0741 | 0.1075 | 0.0958 | 0.4375 |
| LSTM | 0.0111 | 0.0865 | 0.1052 | 0.1005 | 0.1892 | ||
| Hybrid | 0.0048 | 0.0486 | 0.0691 | 0.0607 | 0.3505 | ||
| Prophet | 0.0086 | 0.0688 | 0.0929 | 0.0845 | 0.2633 | ||
| Cancer Incidence Rate | ARIMA | 0.0179 | 0.1095 | 0.1340 | 0.1652 | 0.1713 | |
| LSTM | 0.0208 | 0.1249 | 0.1442 | 0.1869 | 0.3781 | ||
| Hybrid | 0.0122 | 0.0716 | 0.1103 | 0.0965 | 0.2076 | ||
| Prophet | 0.0143 | 0.0848 | 0.1194 | 0.1119 | −0.5023 | ||
| Yukon | New Cancer Cases | ARIMA | 0.0106 | 0.0862 | 0.1030 | 0.1074 | 0.5719 |
| LSTM | 0.0160 | 0.1135 | 0.1145 | 0.0911 | 0.8823 | ||
| Hybrid | 0.0026 | 0.0344 | 0.0513 | 0.0449 | 0.8793 | ||
| Prophet | 0.0137 | 0.1021 | 0.1169 | 0.1293 | 0.3063 | ||
| Cancer Incidence Rate | ARIMA | 0.0205 | 0.1055 | 0.1432 | 0.1283 | 0.3311 | |
| LSTM | 0.0044 | 0.0361 | 0.0664 | 0.0483 | 0.8559 | ||
| Hybrid | 0.0016 | 0.0311 | 0.0395 | 0.0451 | 0.9427 | ||
| Prophet | 0.0263 | 0.1244 | 0.1621 | 0.1606 | −1.1203 |
| Age Group | Category | Model | MSE | MAE | RMSE | MAPE | R2 |
|---|---|---|---|---|---|---|---|
| 0 to 04 years | New Cancer Cases | ARIMA | 0.0186 | 0.1079 | 0.1362 | 0.1765 | 0.1522 |
| LSTM | 0.0198 | 0.1249 | 0.1407 | 0.2338 | 0.4500 | ||
| Hybrid | 0.0178 | 0.1267 | 0.1333 | 0.2349 | 0.1454 | ||
| Prophet | 0.1187 | 0.2956 | 0.3445 | 0.6277 | −6.2204 | ||
| Cancer Incidence Rate | ARIMA | 0.0019 | 0.0343 | 0.0436 | 0.0956 | 0.2485 | |
| LSTM | 0.0080 | 0.0689 | 0.0896 | 0.1696 | 0.1359 | ||
| Hybrid | 0.0003 | 0.0124 | 0.0169 | 0.0270 | 0.1520 | ||
| Prophet | 0.0961 | 0.2822 | 0.3100 | 0.2458 | −1.9227 | ||
| 05 to 09 years | New Cancer Cases | ARIMA | 0.0445 | 0.1901 | 0.2108 | 0.4117 | 0.1155 |
| LSTM | 0.0554 | 0.2000 | 0.2353 | 0.4075 | 0.0097 | ||
| Hybrid | 0.0237 | 0.1442 | 0.1541 | 0.3136 | 0.3751 | ||
| Prophet | 0.1057 | 0.2656 | 0.3251 | 0.4799 | −2.0613 | ||
| Cancer Incidence Rate | ARIMA | 0.0020 | 0.0417 | 0.0453 | 0.0712 | 0.2856 | |
| LSTM | 0.0018 | 0.0310 | 0.0420 | 0.0497 | 0.3977 | ||
| Hybrid | 0.0010 | 0.0280 | 0.0319 | 0.0344 | 0.1493 | ||
| Prophet | 0.0148 | 0.0859 | 0.1215 | 0.1345 | −1.4655 | ||
| 10 to 14 years | New Cancer Cases | ARIMA | 0.0112 | 0.0929 | 0.1056 | 0.1679 | 0.0206 |
| LSTM | 0.0140 | 0.1061 | 0.1183 | 0.1846 | 0.0688 | ||
| Hybrid | 0.0101 | 0.0845 | 0.1004 | 0.1504 | 0.0770 | ||
| Prophet | 0.0273 | 0.143 | 0.1652 | 0.1652 | −0.9431 | ||
| Cancer Incidence Rate | ARIMA | 0.0058 | 0.0572 | 0.0761 | 0.1240 | 0.3283 | |
| LSTM | 0.0079 | 0.0639 | 0.0890 | 0.1169 | 0.2946 | ||
| Hybrid | 0.0029 | 0.0456 | 0.0537 | 0.0632 | 0.6257 | ||
| Prophet | 0.0317 | 0.1619 | 0.1780 | 0.2154 | −1.0946 | ||
| 15 to 19 years | New Cancer Cases | ARIMA | 0.0257 | 0.1459 | 0.1571 | 0.1969 | 0.0586 |
| LSTM | 0.0270 | 0.1365 | 0.1642 | 0.1846 | 0.1824 | ||
| Hybrid | 0.0256 | 0.1341 | 0.1601 | 0.1792 | 0.2258 | ||
| Prophet | 0.0769 | 0.2243 | 0.2774 | 0.3919 | −0.6949 | ||
| Cancer Incidence Rate | ARIMA | 0.0019 | 0.0428 | 0.0443 | 0.0536 | 0.2529 | |
| LSTM | 0.0215 | 0.1133 | 0.1467 | 0.1521 | 0.2127 | ||
| Hybrid | 0.0012 | 0.0264 | 0.0348 | 0.0279 | 0.3815 | ||
| Prophet | 0.0293 | 0.1462 | 0.1711 | 0.1793 | −0.5151 | ||
| 20 to 24 years | New Cancer Cases | ARIMA | 0.0082 | 0.0584 | 0.0909 | 0.0682 | 0.2217 |
| LSTM | 0.0135 | 0.1071 | 0.1160 | 0.1310 | 0.5725 | ||
| Hybrid | 0.0018 | 0.0361 | 0.0420 | 0.0436 | 0.8290 | ||
| Prophet | 0.0256 | 0.1309 | 0.1601 | 0.1498 | −2.2898 | ||
| Cancer Incidence Rate | ARIMA | 0.0045 | 0.0517 | 0.0675 | 0.0704 | 0.2005 | |
| LSTM | 0.0147 | 0.1144 | 0.1214 | 0.1427 | 0.4443 | ||
| Hybrid | 0.0021 | 0.0352 | 0.0453 | 0.0392 | 0.4128 | ||
| Prophet | 0.0319 | 0.1595 | 0.1784 | 0.2025 | −1.7085 | ||
| 25 to 29 years | New Cancer Cases | ARIMA | 0.0091 | 0.0931 | 0.0999 | 0.1045 | 1.5091 |
| LSTM | 0.0045 | 0.0501 | 0.0672 | 0.0660 | 0.5181 | ||
| Hybrid | 0.0039 | 0.0465 | 0.0625 | 0.0620 | 0.6534 | ||
| Prophet | 0.0207 | 0.1293 | 0.1440 | 0.1597 | −1.8633 | ||
| Cancer Incidence Rate | ARIMA | 0.0017 | 0.0407 | 0.0413 | 0.0447 | 0.6333 | |
| LSTM | 0.0104 | 0.0715 | 0.1020 | 0.0866 | 0.3196 | ||
| Hybrid | 0.0002 | 0.0130 | 0.0143 | 0.0154 | 0.5169 | ||
| Prophet | 0.0103 | 0.0776 | 0.1016 | 0.0942 | −0.162 | ||
| 30 to 34 years | New Cancer Cases | ARIMA | 0.0212 | 0.1211 | 0.1457 | 0.1536 | 0.2017 |
| LSTM | 0.0134 | 0.0966 | 0.1159 | 0.1141 | 0.1338 | ||
| Hybrid | 0.0079 | 0.0721 | 0.0889 | 0.0849 | 0.1797 | ||
| Prophet | 0.3214 | 0.2738 | 0.3214 | 0.3220 | −1.5855 | ||
| Cancer Incidence Rate | ARIMA | 0.0015 | 0.0367 | 0.0396 | 0.0447 | 0.2534 | |
| LSTM | 0.0164 | 0.1075 | 0.1282 | 0.1244 | 0.4915 | ||
| Hybrid | 0.0004 | 0.0170 | 0.0205 | 0.0198 | 0.4139 | ||
| Prophet | 0.0185 | 0.1128 | 0.1360 | 0.1310 | −0.6678 | ||
| 35 to 39 years | New Cancer Cases | ARIMA | 0.0040 | 0.0504 | 0.0635 | 0.0698 | 0.8737 |
| LSTM | 0.0115 | 0.0984 | 0.1070 | 0.1378 | 0.5311 | ||
| Hybrid | 0.0039 | 0.0484 | 0.0627 | 0.0679 | 0.8771 | ||
| Prophet | 0.0052 | 0.0602 | 0.0724 | 0.0865 | 0.7172 | ||
| Cancer Incidence Rate | ARIMA | 0.0029 | 0.0438 | 0.0543 | 0.0494 | 0.5215 | |
| LSTM | 0.0114 | 0.1009 | 0.1065 | 0.1131 | 0.0491 | ||
| Hybrid | 0.0014 | 0.0282 | 0.0368 | 0.0310 | 0.2678 | ||
| Prophet | 0.0254 | 0.1307 | 0.1594 | 0.1395 | −0.3627 | ||
| 40 to 44 years | New Cancer Cases | ARIMA | 0.0077 | 0.1023 | 0.1329 | 0.1390 | 0.6226 |
| LSTM | 0.0036 | 0.0574 | 0.0598 | 0.0685 | 0.4477 | ||
| Hybrid | 0.0015 | 0.0331 | 0.0391 | 0.0371 | 0.5223 | ||
| Prophet | 0.0200 | 0.1269 | 0.1416 | 0.1641 | 0.1681 | ||
| Cancer Incidence Rate | ARIMA | 0.0024 | 0.0466 | 0.0499 | 0.0540 | 0.1890 | |
| LSTM | 0.0098 | 0.0893 | 0.0990 | 0.0981 | 0.1507 | ||
| Hybrid | 0.0001 | 0.0072 | 0.0105 | 0.0074 | 0.2190 | ||
| Prophet | 0.0112 | 0.0855 | 0.1058 | 0.1006 | −1.7236 | ||
| 45 to 49 years | New Cancer Cases | ARIMA | 0.0070 | 0.0592 | 0.0835 | 0.0989 | 0.8396 |
| LSTM | 0.0035 | 0.0545 | 0.0590 | 0.0900 | 0.2453 | ||
| Hybrid | 0.0020 | 0.0370 | 0.0450 | 0.0613 | 0.7002 | ||
| Prophet | 0.0554 | 0.1919 | 0.2355 | 0.1978 | −0.3463 | ||
| Cancer Incidence Rate | ARIMA | 0.0067 | 0.0566 | 0.0823 | 0.1302 | 0.2436 | |
| LSTM | 0.0122 | 0.0805 | 0.1106 | 0.1737 | 0.0910 | ||
| Hybrid | 0.0001 | 0.0084 | 0.0100 | 0.0174 | 0.9899 | ||
| Prophet | 0.0135 | 0.0998 | 0.1286 | 0.2087 | −1.6021 | ||
| 50 to 54 years | New Cancer Cases | ARIMA | 0.0053 | 0.0660 | 0.0727 | 0.0903 | 0.3711 |
| LSTM | 0.0055 | 0.0491 | 0.0742 | 0.0736 | 0.2727 | ||
| Hybrid | 0.0020 | 0.0328 | 0.0448 | 0.0444 | 0.8250 | ||
| Prophet | 0.1113 | 0.3037 | 0.3336 | 0.3778 | −0.7868 | ||
| Cancer Incidence Rate | ARIMA | 0.0002 | 0.0137 | 0.0144 | 0.0355 | 0.4636 | |
| LSTM | 0.0074 | 0.0578 | 0.0859 | 0.1351 | 0.2222 | ||
| Hybrid | 0.0001 | 0.0034 | 0.0039 | 0.0098 | 0.9734 | ||
| Prophet | 0.0320 | 0.1613 | 0.1790 | 0.1922 | −3.2580 | ||
| 55 to 59 years | New Cancer Cases | ARIMA | 0.0053 | 0.0542 | 0.0726 | 0.0574 | 0.6032 |
| LSTM | 0.0056 | 0.0504 | 0.0750 | 0.0578 | 1.2721 | ||
| Hybrid | 0.0023 | 0.0368 | 0.0475 | 0.0401 | 0.1101 | ||
| Prophet | 0.0230 | 0.1342 | 0.1518 | 0.1448 | −1.794 | ||
| Cancer Incidence Rate | ARIMA | 0.0068 | 0.0542 | 0.0829 | 0.0341 | 0.4939 | |
| LSTM | 0.0043 | 0.0483 | 0.0655 | 0.0897 | 0.6194 | ||
| Hybrid | 0.0002 | 0.0112 | 0.0150 | 0.0292 | 0.7621 | ||
| Prophet | 0.0122 | 0.0926 | 0.1106 | 0.1004 | −0.8536 | ||
| 60 to 64 years | New Cancer Cases | ARIMA | 0.0044 | 0.0595 | 0.0665 | 0.0642 | 0.7781 |
| LSTM | 0.0034 | 0.0463 | 0.0586 | 0.0510 | 0.2373 | ||
| Hybrid | 0.0023 | 0.0231 | 0.0481 | 0.0262 | 0.5316 | ||
| Prophet | 0.0026 | 0.0406 | 0.0513 | 0.0462 | 0.6347 | ||
| Cancer Incidence Rate | ARIMA | 0.0048 | 0.0639 | 0.0739 | 0.0402 | 0.4163 | |
| LSTM | 0.0093 | 0.0861 | 0.0963 | 0.0426 | 0.5478 | ||
| Hybrid | 0.0002 | 0.0142 | 0.0150 | 0.0182 | 0.5654 | ||
| Prophet | 0.0119 | 0.0987 | 0.1103 | 0.0743 | 0.2763 | ||
| 65 to 69 years | New Cancer Cases | ARIMA | 0.0083 | 0.0662 | 0.0914 | 0.0772 | 0.3804 |
| LSTM | 0.0071 | 0.0643 | 0.0840 | 0.0786 | 0.2028 | ||
| Hybrid | 0.0030 | 0.0473 | 0.0546 | 0.0546 | 0.6826 | ||
| Prophet | 0.0434 | 0.1977 | 0.2083 | 0.1373 | −7.8478 | ||
| Cancer Incidence Rate | ARIMA | 0.0049 | 0.0701 | 0.0867 | 0.0423 | 0.7709 | |
| LSTM | 0.0008 | 0.0226 | 0.0278 | 0.0313 | 0.3561 | ||
| Hybrid | 0.0001 | 0.0070 | 0.0083 | 0.0235 | 0.6739 | ||
| Prophet | 0.0069 | 0.0612 | 0.0845 | 0.0679 | 0.5764 | ||
| 70 to 74 years | New Cancer Cases | ARIMA | 0.0080 | 0.0806 | 0.0892 | 0.0931 | 0.2429 |
| LSTM | 0.0039 | 0.0520 | 0.0627 | 0.0634 | 0.8156 | ||
| Hybrid | 0.0031 | 0.0459 | 0.0559 | 0.0620 | 0.8845 | ||
| Prophet | 0.0579 | 0.2302 | 0.2409 | 0.1138 | −2.4798 | ||
| Cancer Incidence Rate | ARIMA | 0.0001 | 0.0101 | 0.0116 | 0.0327 | 0.4240 | |
| LSTM | 0.0045 | 0.0498 | 0.0672 | 0.1582 | −0.4997 | ||
| Hybrid | 0.0001 | 0.0086 | 0.0117 | 0.0275 | 0.2875 | ||
| Prophet | 0.0056 | 0.0725 | 0.0935 | 0.2287 | −1.1505 | ||
| 75 to 79 years | New Cancer Cases | ARIMA | 0.0035 | 0.0524 | 0.0592 | 0.0669 | 0.7772 |
| LSTM | 0.0061 | 0.0757 | 0.0778 | 0.0964 | 0.5426 | ||
| Hybrid | 0.0033 | 0.0512 | 0.0572 | 0.0584 | 0.5831 | ||
| Prophet | 0.0054 | 0.0633 | 0.0732 | 0.0903 | 0.4110 | ||
| Cancer Incidence Rate | ARIMA | 0.0018 | 0.0218 | 0.0422 | 0.0563 | 0.0188 | |
| LSTM | 0.0023 | 0.0326 | 0.0479 | 0.0835 | 0.3755 | ||
| Hybrid | 0.0010 | 0.0205 | 0.0316 | 0.0465 | 0.4501 | ||
| Prophet | 0.0125 | 0.0835 | 0.11201 | 0.0843 | 0.5386 | ||
| 80 to 84 years | New Cancer Cases | ARIMA | 0.0023 | 0.0442 | 0.0476 | 0.0462 | 0.9672 |
| LSTM | 0.0024 | 0.0407 | 0.0485 | 0.0428 | 0.7745 | ||
| Hybrid | 0.0007 | 0.0196 | 0.0261 | 0.0210 | 0.8385 | ||
| Prophet | 0.0267 | 0.0500 | 0.0634 | 0.0575 | 0.1867 | ||
| Cancer Incidence Rate | ARIMA | 0.0013 | 0.0358 | 0.0363 | 0.0623 | 0.2378 | |
| LSTM | 0.0042 | 0.0620 | 0.0650 | 0.1096 | 0.5701 | ||
| Hybrid | 0.0002 | 0.0126 | 0.0154 | 0.0130 | 0.6267 | ||
| Prophet | 0.0076 | 0.0694 | 0.0869 | 0.1163 | 0.5425 | ||
| 85 to 89 years | New Cancer Cases | ARIMA | 0.0040 | 0.0524 | 0.0629 | 0.0538 | 0.2693 |
| LSTM | 0.0023 | 0.0398 | 0.0480 | 0.0425 | 0.1433 | ||
| Hybrid | 0.0019 | 0.0355 | 0.0432 | 0.0376 | 0.1592 | ||
| Prophet | 0.0056 | 0.0568 | 0.0745 | 0.0601 | −1.6369 | ||
| Cancer Incidence Rate | ARIMA | 0.0093 | 0.0950 | 0.0963 | 0.2053 | 0.0619 | |
| LSTM | 0.0105 | 0.0884 | 0.1027 | 0.2135 | 0.2379 | ||
| Hybrid | 0.0014 | 0.0286 | 0.0375 | 0.0650 | 0.2018 | ||
| Prophet | 0.0192 | 0.1139 | 0.1386 | 0.1236 | 8.1164 | ||
| 90 years and over | New Cancer Cases | ARIMA | 0.0099 | 0.0671 | 0.0995 | 0.0737 | 4.7627 |
| LSTM | 0.0094 | 0.0799 | 0.0969 | 0.0894 | 1.5906 | ||
| Hybrid | 0.0032 | 0.0479 | 0.0564 | 0.0536 | 0.4497 | ||
| Prophet | 0.0182 | 0.1257 | 0.1350 | 0.1387 | −2.9161 | ||
| Cancer Incidence Rate | ARIMA | 0.0011 | 0.0258 | 0.0338 | 0.0560 | 0.5235 | |
| LSTM | 0.0037 | 0.0450 | 0.0607 | 0.0956 | 0.4617 | ||
| Hybrid | 0.0003 | 0.0155 | 0.0184 | 0.0327 | 0.6609 | ||
| Prophet | 0.0076 | 0.0714 | 0.0874 | 0.0755 | −0.6405 |
| Sex | Category | Model | MSE | MAE | RMSE | MAPE | R2 |
|---|---|---|---|---|---|---|---|
| Males | New Cancer Cases | ARIMA | 0.0061 | 0.0506 | 0.0781 | 0.0552 | 0.0908 |
| LSTM | 0.0023 | 0.0219 | 0.0481 | 0.0244 | 0.5148 | ||
| Hybrid | 0.0029 | 0.0364 | 0.0537 | 0.0399 | 0.3304 | ||
| Prophet | 0.0031 | 0.0433 | 0.0557 | 0.0478 | 0.4621 | ||
| Cancer Incidence Rate | ARIMA | 0.0069 | 0.0728 | 0.0833 | 0.0772 | 0.1768 | |
| LSTM | 0.0022 | 0.0415 | 0.0465 | 0.0454 | 0.0470 | ||
| Hybrid | 0.0036 | 0.0491 | 0.0600 | 0.0530 | 0.0662 | ||
| Prophet | 0.0093 | 0.0827 | 0.0967 | 0.08276 | −1.8708 | ||
| Females | New Cancer Cases | ARIMA | 0.0055 | 0.0484 | 0.0740 | 0.0529 | 0.4091 |
| LSTM | 0.0019 | 0.0248 | 0.0436 | 0.0288 | 0.3378 | ||
| Hybrid | 0.0019 | 0.0259 | 0.0437 | 0.0292 | 0.3402 | ||
| Prophet | 0.0021 | 0.0338 | 0.0463 | 0.0377 | 0.5566 | ||
| Cancer Incidence Rate | ARIMA | 0.0058 | 0.0714 | 0.0761 | 0.0714 | 0.1504 | |
| LSTM | 0.0017 | 0.0324 | 0.0413 | 0.0329 | 0.2201 | ||
| Hybrid | 0.0045 | 0.0606 | 0.0672 | 0.0626 | 0.8291 | ||
| Prophet | 0.0065 | 0.0582 | 0.0805 | 0.0587 | −0.1023 | ||
| Both Sexes | New Cancer Cases | ARIMA | 0.0054 | 0.0445 | 0.0741 | 0.0489 | 0.5487 |
| LSTM | 0.0021 | 0.0226 | 0.0454 | 0.0258 | 0.4082 | ||
| Hybrid | 0.0024 | 0.0297 | 0.0493 | 0.0330 | 0.3410 | ||
| Prophet | 0.0032 | 0.0478 | 0.0562 | 0.0532 | 0.3917 | ||
| Cancer Incidence Rate | ARIMA | 0.0036 | 0.0520 | 0.0603 | 0.0532 | 0.0001 | |
| LSTM | 0.0013 | 0.0292 | 0.0366 | 0.0301 | 0.0165 | ||
| Hybrid | 0.0038 | 0.0562 | 0.0618 | 0.0592 | 0.3813 | ||
| Prophet | 0.0075 | 0.0679 | 0.0867 | 0.0703 | −0.6117 |
| Geography/Predicted Years | 2022 | 2023 | 2024 | 2025 | 2026 | |
|---|---|---|---|---|---|---|
| Alberta | New Cancer Cases | 23,907 | 24,387 | 24,702 | 24,975 | 25,927 |
| Cancer Incidence Rate | 443.8 | 462.2 | 461.7 | 433.7 | 458.9 | |
| British Columbia | New Cancer Cases | 31,801 | 32,438 | 32,729 | 32,728 | 33,456 |
| Cancer Incidence Rate | 531.3 | 539.5 | 540.6 | 537.9 | 545.7 | |
| Manitoba | New Cancer Cases | 8181 | 8300 | 8374 | 8418 | 8530 |
| Cancer Incidence Rate | 505.3 | 516.0 | 517.2 | 513.1 | 509.3 | |
| New Brunswick | New Cancer Cases | 5959 | 5999 | 6033 | 6076 | 6187 |
| Cancer Incidence Rate | 656.8 | 657.3 | 648.5 | 647.9 | 662.2 | |
| Newfoundland and Labrador | New Cancer Cases | 4171 | 4116 | 4062 | 3976 | 4012 |
| Cancer Incidence Rate | 693.4 | 690.7 | 678.8 | 650.3 | 596.1 | |
| Northwest Territories | New Cancer Cases | 241 | 237 | 244 | 240 | 263 |
| Cancer Incidence Rate | 389.0 | 400.4 | 396.4 | 375.7 | 341.8 | |
| Nova Scotia | New Cancer Cases | 7467 | 7434 | 7445 | 7511 | 7562 |
| Cancer Incidence Rate | 693.5 | 674.2 | 652.9 | 652.6 | 653.8 | |
| Nunavut | New Cancer Cases | 84 | 79 | 77 | 79 | 81 |
| Cancer Incidence Rate | 200.1 | 196.7 | 188.3 | 179.4 | 173.0 | |
| Ontario | New Cancer Cases | 94,677 | 94,763 | 94,975 | 95,398 | 97,951 |
| Cancer Incidence Rate | 582.2 | 573.6 | 555.0 | 545.0 | 543.7 | |
| Prince Edward Island | New Cancer Cases | 1102 | 1111 | 1157 | 1161 | 1181 |
| Cancer Incidence Rate | 620.0 | 620.8 | 626.4 | 632.8 | 636.9 | |
| Quebec | New Cancer Cases | 63,803 | 63,841 | 63,932 | 64,073 | 64,264 |
| Cancer Incidence Rate | 675.7 | 668.7 | 669.5 | 671.8 | 670.4 | |
| Saskatchewan | New Cancer Cases | 6585 | 6636 | 6666 | 6624 | 6716 |
| Cancer Incidence Rate | 491.8 | 495.5 | 496.5 | 494.9 | 493.7 | |
| Yukon | New Cancer Cases | 199 | 198 | 188 | 183 | 188 |
| Cancer Incidence Rate | 445.4 | 464.5 | 445.8 | 393.0 | 333.6 | |
| Age Group/Predicted Years | 2022 | 2023 | 2024 | 2025 | 2026 | |
|---|---|---|---|---|---|---|
| 0 to 4 years | New Cancer Cases | 453 | 454 | 452 | 450 | 450 |
| Cancer Incidence Rate | 23.2 | 23.4 | 23.4 | 23.4 | 23.4 | |
| 5 to 9 years | New Cancer Cases | 280 | 270 | 265 | 264 | 266 |
| Cancer Incidence Rate | 13.8 | 13.9 | 13.8 | 13.8 | 13.8 | |
| 10 to 14 years | New Cancer Cases | 286 | 290 | 291 | 286 | 290 |
| Cancer Incidence Rate | 13.2 | 13.5 | 13.3 | 13.4 | 13.5 | |
| 15 to 19 years | New Cancer Cases | 534 | 531 | 535 | 537 | 530 |
| Cancer Incidence Rate | 24.4 | 24.1 | 24.1 | 24.1 | 24.2 | |
| 20 to 24 years | New Cancer Cases | 937 | 929 | 936 | 930 | 935 |
| Cancer Incidence Rate | 36.4 | 35.7 | 35.8 | 35.9 | 35.9 | |
| 25 to 29 years | New Cancer Cases | 1605 | 1625 | 1633 | 1665 | 1715 |
| Cancer Incidence Rate | 59.6 | 60.1 | 60.4 | 60.5 | 60.3 | |
| 30 to 34 years | New Cancer Cases | 2514 | 2526 | 2536 | 2545 | 2555 |
| Cancer Incidence Rate | 91.4 | 90.9 | 90.7 | 91.1 | 91.5 | |
| 35 to 39 years | New Cancer Cases | 3960 | 4040 | 4073 | 4095 | 4179 |
| Cancer Incidence Rate | 137.6 | 136.9 | 135.8 | 135.5 | 136.0 | |
| 40 to 44 years | New Cancer Cases | 5660 | 5678 | 5705 | 5732 | 5808 |
| Cancer Incidence Rate | 210.2 | 210.4 | 210.1 | 209.5 | 209.3 | |
| 45 to 49 years | New Cancer Cases | 8595 | 8489 | 8379 | 8287 | 8234 |
| Cancer Incidence Rate | 315.5 | 314.2 | 315.8 | 316.5 | 315.9 | |
| 50 to 54 years | New Cancer Cases | 15,325 | 14,930 | 14,509 | 14,018 | 13,488 |
| Cancer Incidence Rate | 509.6 | 510.0 | 510.6 | 510.9 | 510.9 | |
| 55 to 59 years | New Cancer Cases | 22,931 | 22,845 | 22,740 | 22,576 | 22,228 |
| Cancer Incidence Rate | 775.0 | 775.4 | 774.7 | 774.8 | 774.6 | |
| 60 to 64 years | New Cancer Cases | 32,186 | 32,419 | 32,481 | 32,641 | 33,517 |
| Cancer Incidence Rate | 1140.0 | 1144.1 | 1142.8 | 1139.6 | 1140.5 | |
| 65 to 69 years | New Cancer Cases | 38,617 | 39,032 | 39,397 | 39,965 | 41,398 |
| Cancer Incidence Rate | 1604.8 | 1608.2 | 1604.8 | 1603.0 | 1603.0 | |
| 70 to 74 years | New Cancer Cases | 39,764 | 40,584 | 41,431 | 42,145 | 43,771 |
| Cancer Incidence Rate | 2040.0 | 2037.9 | 2037.4 | 2033.9 | 2031.8 | |
| 75 to 79 years | New Cancer Cases | 31,024 | 31,431 | 31,890 | 32,303 | 33,313 |
| Cancer Incidence Rate | 2362.2 | 2369.2 | 2372.2 | 2372.2 | 2368.4 | |
| 80 to 84 years | New Cancer Cases | 22,494 | 22,578 | 22,682 | 22,787 | 22,883 |
| Cancer Incidence Rate | 2590.6 | 2591.1 | 2590.8 | 2588.9 | 2586.9 | |
| 85 to 89 years | New Cancer Cases | 14,756 | 15,094 | 15,181 | 15,342 | 15,602 |
| Cancer Incidence Rate | 2667.2 | 2671.3 | 2671.5 | 2672.3 | 2674.6 | |
| 90 years and above | New Cancer Cases | 8185 | 8311 | 8432 | 8550 | 8685 |
| Cancer Incidence Rate | 2446.3 | 2449.3 | 2444.8 | 2437.5 | 2440.8 | |
| Sex/Predicted Years | 2022 | 2023 | 2024 | 2025 | 2026 | |
|---|---|---|---|---|---|---|
| Males | New Cancer Cases | 129,012 | 129,515 | 130,009 | 131,690 | 133,088 |
| Cancer Incidence Rate | 600.6 | 598.9 | 599.7 | 600.8 | 602.3 | |
| Females | New Cancer Cases | 119,514 | 120,428 | 121,119 | 121,614 | 123,904 |
| Cancer Incidence Rate | 540.1 | 539.2 | 537.3 | 534.4 | 530.6 | |
| Both Sexes | New Cancer Cases | 244,007 | 244,941 | 245,242 | 245,051 | 248,705 |
| Cancer Incidence Rate | 567.6 | 566.3 | 565.3 | 563.8 | 561.8 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaviani, E.; Passi, K. Forecasting Cancer Incidence in Canada by Age, Sex, and Region Until 2026 Using Machine Learning Techniques. Algorithms 2025, 18, 265. https://doi.org/10.3390/a18050265
Kaviani E, Passi K. Forecasting Cancer Incidence in Canada by Age, Sex, and Region Until 2026 Using Machine Learning Techniques. Algorithms. 2025; 18(5):265. https://doi.org/10.3390/a18050265
Chicago/Turabian StyleKaviani, Ehsan, and Kalpdrum Passi. 2025. "Forecasting Cancer Incidence in Canada by Age, Sex, and Region Until 2026 Using Machine Learning Techniques" Algorithms 18, no. 5: 265. https://doi.org/10.3390/a18050265
APA StyleKaviani, E., & Passi, K. (2025). Forecasting Cancer Incidence in Canada by Age, Sex, and Region Until 2026 Using Machine Learning Techniques. Algorithms, 18(5), 265. https://doi.org/10.3390/a18050265






