Abstract
The reduction in mass and surface of antennas and scattering structures is an important task in designing electromagnetic devices. To solve this task, we present a novel algorithm based on the optimal current grid approximation for generating sparse scattering structures and evaluating their effectiveness. The main contributions of the work include analyzing the performance of the optimal current grid approximation and its modifications in generating sparse antennas, as well as demonstrating the effectiveness of the algorithm in generating sparse scattering structures using a scattering plate and corner reflectors as an example. To validate the accuracy of the algorithm, we compared the scattering properties of the obtained sparse scattering structures. The results show that the algorithm worked accurately and effectively in generating sparse scattering structures while reducing their mass and surface.
1. Introduction
Antennas and scattering structures are widely used in various fields, from civil [1,2,3,4,5] to military [6,7,8,9,10]. With the continuous advancement of science, the demand for producing compact antennas and scatterers with intelligent designs is increasing [11,12,13,14]. Designing those structures to achieve required properties while maintaining low production costs necessitates high-accuracy simulation software with low computational costs. Simulating structures significantly reduces production costs, allowing for the assessment and optimization of structural properties before manufacturing. Additionally, it helps avoid technical errors during production [15]. Thus, simulation becomes an essential part of the design process for antennas and scattering structures [16,17]. However, accurate modeling may require intensive computations, especially when analyzing complex structures. In the meantime, the proper choice of numerical methods for modeling can significantly impact the cost and efficiency of the design process.
One of the common methods for analyzing antenna and scatterer structures is the method of moments (MoM) [18,19,20,21,22]. MoM is based on transforming the integral equations of the electric field into a system of linear algebraic equations, and then the current distribution in the structure is determined by inverting the impedance matrix [23,24]. MoM is considered to have a simple algorithm and low computational costs compared to other methods, while allowing for acceptable simulation results. Based on MoM, many new approaches to modeling antennas and scatterers have been developed [25,26,27,28,29]. One prominent method is the surface approximation of structures using wire grid (WG). This approach simplifies the surface shape, making the implementation of modeling in source code easier. Multiple studies on modeling antenna and scattering structures have been conducted taking advantage from this approach (WG based on MoM) [30,31,32,33,34].
The reduction in antenna mass is an important factor in many engineering fields [35,36]. Low mass and compact size not only reduce transportation costs (for example, into space [37,38]), but also simplify installation and maintenance, and can minimize negative environmental impacts on the structure (for instance, wind and rain).
Similarly, in the field of interferometric synthetic aperture radar (InSAR), corner reflectors (CRs) are a typical example of scattering structures [39,40,41,42]. These structures are prominent because they are easy to fabricate and feature significant scattering capabilities over a wide range for incident plane waves. However, a clear disadvantage is that the size of CRs is often quite large (for example, a trihedral CR can have edge lengths of up to 2.5 m [43]). In addition, their weight is also relatively heavy, mainly due to the use of conductive metal materials. Therefore, reducing the mass of these structures to facilitate transportation, installation, and maintenance is an important issue that needs to be solved.
Several methods have emerged to reduce the weight and size of these structures. One example is the use of silver-coated textiles [44]; however, a disadvantage of this method is that the conductive material is susceptible to environmental factors. In addition, the silver-coated technology is complex and expensive. Another method is the use of structures with a perforated plate [45]. Although this method significantly reduces the weight of the entire structure and improves drainage of accumulated rainwater [46], the perforation process complicates manufacturing and increases costs [47]. Moreover, perforation can often cause surface deformation [43]. Therefore, there is a need to develop new methods to reduce the weight of such structures.
To reduce antenna mass and surface, we [38] developed a technique that uses optimal current grid approximation (OCGA) based on MoM and WG. This technique allows for easy implementation of algorithms to create sparse structures by removing wires with low current magnitudes from the structure. The application of OCGA not only significantly reduces the mass and surface of the structures but also decreases computational costs, including calculation time and the necessary computer memory. When it is necessary to reduce the mass and surface of scattering devices, the use of OCGA to design sparse scatterer structures becomes truly essential. However, the biggest difference between antenna and scattering structures is the characteristics of the excitation source. In antennas, the source is typically fixed [6], while in scattering devices, the source depends on many parameters of the incident wave, for example, direction, polarization, and wave front (spherical, plane, etc.) [48,49]. Therefore, applying OCGA to scattering structure presents more challenges.
CR structures are composed of flat metal plates with various shapes [50,51]. Therefore, reducing the mass and surface of rectangular flat scattering plates will be considered a preliminary study to apply the OCGA algorithm to more complex scattering structures in the future. In addition, the synthesis and review of the results related to the reduction in antenna mass and surface based on OCGA will provide more insight into the effectiveness of this algorithm. This will facilitate the application of OCGA to reduce the mass and surface of scattering structures. Therefore, the aim of this paper is to present the results of sparse antennas generation summarized from previous studies and developed algorithm for generating sparse scattering structures based on OCGA.
This paper is organized as follows. Section 2 presents a comprehensive review of approaches for reducing mass and surface of various antenna structures using the OCGA. Section 3 presents the results of validating scattering characteristics for the plate scatterer structure, obtained using MoM with pulse basis function (PBF) based on WG. Section 4 introduces an algorithm to sparse the scattering structure when it is excited by an incident wave at a specific direction. Section 5 presents another algorithm to generate sparse scattering structures and analyze their scattering properties when the specific excitation region of the incident wave is unknown through the scattering plate example. Section 6 analyzes it when this region is known. Section 7 presents the results of generating a sparse structure of a dihedral and circular trihedral corner reflector. Section 8 summarizes and discusses the results obtained and highlights the points to consider in future studies, followed by conclusions in Section 9.
2. Review of Approaches for Reducing Mass and Surface of Various Antenna Structures Using the OCGA
The MoM is widely used for modeling different antenna designs with low computational cost and optimizing their designs to meet specific requirements. A review of the MoM-enhanced antenna modeling history and the potential of using WG to approximate the solid metallic surface of different antenna types is presented in [38]. To further reduce the antenna mass, surface, and computational cost, sparsifying WG antenna structure by using OCGA was firstly proposed in [38]. The OCGA works based on obtaining the current distribution in a WG structure. After this, the current magnitudes in each wire are normalized by their average or maximum value. Then, all wires with current magnitudes less than a certain threshold are eliminated since their contribution to the radiation is negligible. This threshold is called the grid element elimination tolerance (GEET) and can be adjusted according to each specific requirement. The result is a sparse WG structure that includes only wires with large currents. Compared with the original WG structure, the sparse WG structure has lower antenna mass and surface as well as its modeling cost.
To generate sparse WG structures using OCGA, it is necessary to accurately approximate the solid metal surface of the antenna using WG. Many recommendations have been proposed in the past for approximating metal surfaces using WG. However, they are not complete and are not suitable for creating an original WG structure to which OCGA can be applied to create a sparse structure. The suitability and inadequacy of the previous recommendations are presented in detail in [52]. Therefore, new recommendations were proposed in [52] for approximating the solid surface of horn structures using WG, which can be used as an original structure for applying OCGA to create a sparse structure. An approximate comparison of antenna surface using WG with different cell types such as square and trapezoidal was carried out. Antenna surface approximation using WG and OCGA to create sparse structures was compared in different computer-aided design systems such as TUSUR.EMC [53], MMANA-GAL [54], and 4NEC2 [55]. In addition, an optimization method based on OCGA was proposed in [56] to generate sparse WG structures that meet the given criteria. The algorithmic details of this optimization method were presented, and software with a user-friendly interface was developed based on this method.
However, the WG structure obtained after OCGA encounters difficulties in fabricating unprinted antennas because it has wires that are not connected to the structure (free wires). To overcome these difficulties, a modification of OCGA to create a sparse WG structure with connected current paths was proposed in [38]. This modified approach is referred to as “Connecting” OCGA (COCGA), and its main idea is to recover radial wires to create a current path between the free wires and the structure, since for radial structures these wires usually carry large currents. The algorithm details of the OCGA and COCGA approaches were presented in detail in [38]. The OCGA and COCGA approaches have been applied to a reflector antenna (5.1–5.9 GHz), a horn antenna at 8 GHz, perforated X-band horn antenna (8–12 GHz), and a conical horn antenna at 8 GHz. A comparative analysis of the sparse structures obtained after applying OCGA and COCGA to these types of antennas was presented in [57] in detail. The comparative analysis shows that COCGA generally results in antenna characteristics closer to the original structure, demonstrating higher accuracy in preserving the original characteristics, while OCGA also demonstrates the possibility of reducing the antenna mass and surface as well as the time and memory requirements for subsequent modeling. In addition, [58] presented details on the classification of hidden antenna types and the possibility of using sparse WG structures to design hidden antennas that meet specific requirements.
Since the current distribution on the obtained WG structure is different at different frequencies in the operating frequency range, the effect of frequency selection on the obtained sparse structure after OCGA and COCGA application on the horn antenna X-band (8–12 GHz) was analyzed in [59]. The analysis results show that the sparse structures obtained based on the current distribution at the lowest frequency in the operating frequency range provide antenna characteristics closer to those of the original antenna and less dependent on the GEET value, compared to the other structures. In addition, at the highest frequency in the operating frequency range, the sparse structures obtained after COCGA provide results with minimal differences compared to the original structure.
The sparse structure obtained after COCGA has antenna characteristics close to those obtained for the original structure. However, it recovers a large number of radial wires to maintain the current paths in the structure and its continuity, which leads to a nonoptimal reduction in mass and simulation cost. Therefore, OCGA modifications were proposed in [60] to create a sparse WG structure with all wires interconnected. These approaches were referred to as “Eliminating” OCGA (EOCGA) and “Near-Connecting” OCGA (NCOCGA). To provide a current path in the sparse WG structure, EOCGA eliminates all free wires in the sparse WG structure obtained after OCGA, while NCOCGA restores only those wires that are necessary to connect these free wires to the structure. The algorithms of these approaches were discussed in detail, and their performance was verified on different types of antennas.
However, the algorithms of these approaches were based on the geometric position of the wires in the grid, which limits their accuracy. Furthermore, they are only applicable to radial WG designs such as antenna reflectors and conical horn antennas. Therefore, new algorithms were proposed in [61] to improve the OCGA and its modifications. Its aim is to use the start and end coordinates of the wires in combination with an algorithm for finding free wires and determining the shortest path to connect them. The results obtained after applying the modernized algorithms were compared with the results of the previous algorithm. The comparison results showed that these new algorithms had higher accuracy, efficiency, and flexibility and could be applied to many different types of WG structures.
The OCGA, EOCGA, and NCOGA with the modernized algorithms have shown to be effective in creating sparse structures on various types of antennas operating at various frequency bands. A series of prototypes, original WG and sparse WG structures obtained after applying various approaches on various types of antennas are presented in Table 1. The improvements in antenna mass and surface, memory and time cost in subsequent modeling for various sparse structures were obtained after applying different approaches to different types of antennas compiled from different works and presented in Table 2. Moreover, Table 2 also summarizes the maximum differences in characteristics of these sparse antennas compared to the original antenna in the operating frequency range. Then, comparative analyses were performed to analyze the effect of frequency selection on the sparse structure generated after applying different approaches.

Table 1.
Prototype, original WG structure and sparse structures obtained after applying different approaches to different types of antennas.

Table 2.
The improvements and maximum differences from the original sparse structure after applying different approaches to different antenna types.
After the comparative analysis, these works provide conclusions and recommendations about the following:
- The approach that provides better reduction in antenna mass, surface, and cost for subsequent modeling (approach for reduction);
- The approach that provides the best antenna characteristics (approach for characteristics);
- The frequency at which the sparse structure is created is based on the current distribution at the frequency that has the best characteristics (current distribution for sparse structure);
- The frequency at which the antenna characteristics of the sparse structure are obtained is least dependent on the GEET value (frequency for characteristics).
The sparse WG structures presented in Table 1 demonstrate the accuracy of various approaches. OCGA excluded the wires with normalized smaller current magnitudes than a given GEET value and obtained the corresponding sparse WG structures. However, it can be seen that some free wires appear in the sparse structures after OCGA. Therefore, EOCGA eliminated them while NCOCGA recovered the necessary wires to connect them to the WG structure. The sparse structures obtained after EOCGA and NCOCGA had no free wires. This confirms the correct performance of the modernized algorithms, since they can be applied to various antenna structures. The results summarized in Table 3 show that the greatest value of antenna mass and surface reduction and simulation cost is usually obtained after OCGA and EOCGA, and the smallest value of the maximum antenna characteristic difference when compared with the results obtained for the original structure is usually obtained for the sparse structure after NCOCGA. Comparing the sparse structures obtained based on the current distribution at different frequencies, it can be noticed that virtually all works recommend that the sparse structures are generated based on the current distribution at the lowest or center frequency in the operating frequency range. Moreover, when comparing the antenna characteristics obtained at different frequencies for sparse structures, the antenna characteristics obtained at the highest frequency in the operating frequency range are stable and less dependent on the GEET value than at other frequencies.

Table 3.
The conclusions and recommendations are given after comparative analysis of the sparse WG structures in different works.
All the results obtained after applying OCGA and its modifications on different antenna structures operating at different frequencies demonstrate the effectiveness of these approaches in creating sparse structures. The sparse antenna structures have lower mass, surface, and modeling cost than the original structure, while the antenna characteristics are maintained. Sparse antenna structures can be used to fulfill various requirements, such as in IoT devices or space applications where there are severe specifications on antenna mass and size. In addition, they can be used in applications that require hidden antennas so as not to affect the overall landscape.
The conditions for performing antenna measurements must fully meet the requirements and criteria specified in [62]. WG antenna structures have been widely developed and studied in previous studies, and the far zone was considered for these types of antennas. Although there are changes in the number of wires in sparse WG antenna structures, they are basically not much different from the original WG structure. Therefore, the measurement conditions and far zone requirements for these structures are still the same as those for the original WG structures; they can be measured in an anechoic chamber or in outdoor areas, depending on the purpose of testing the real-life performance of the antenna.
Figure 1 presents the setup for antenna measurements, the configuration of the sparse antennas, and the results of main characteristic measurements for both sparse and original antennas.
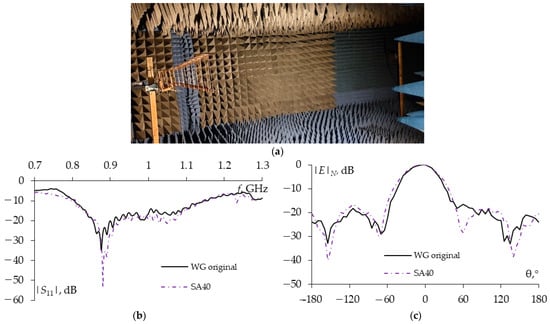
Figure 1.
Setup for sparse antenna measurement (a), the frequency dependence of the measured |S11| (b) and measured RPs in the E planes at 0.915 GHz (c) for the original and sparse WG antennas [63].
In [63], we created actual sparse horn antennas based on OCGA using the horn antenna from [64] operating in the UHF band with a central frequency of 0.915 GHz. A total of 1062 copper wires are employed to form the WG structure. To connect the WG structure and the excitation wires, a 50-Ohm SMA connector is used. To meet the far-field conditions, the UHF dipole antenna is placed 4 m away from the horn antenna. The characteristics of the antenna are measured using a vector network analyzer R4M in an anechoic chamber to enhance accuracy. Based on the sparse WG structures obtained from simulations, the corresponding wires in the initial WG structure are cut using simple tools.
Sparse WG structure with GEET = 40% was created. When using OCGA with GEET = 40%, some free wires appeared in the sparse structure, so the modified OCGA was used to connect free wires to the WG structure. The main characteristics were measured for the sparse WG structure and compared with experimental results for the original WG structure in the operating frequency range of 0.7–1.3 GHz. In [63], it is noted that when a lightmass antenna is required while maintaining acceptable main characteristics, GEET = 40% is reasonable choice. This structure is up to 1.41 times lighter than the original WG structure and up to 7.63 times lighter than the solid structure. This is extremely important in modern devices and systems, particularly in satellite or military applications.
3. Verification of the Modeling Results for Scattering Plate Using MoM with PBF Based on WG Model
Section 2 demonstrated the effectiveness of using OCGA and its modifications in generating sparse antenna structures. Therefore, it is reasonable to apply this approach to develop algorithms for generating sparse scattering structures. However, first, to verify the accuracy of using MoM with PBF based on WG in scatterer analysis, we verify the scattering field results obtained for a flat plate scattering structure.
The shape of the rectangular perfect electrically conductive plate scatterer from [65] is illustrated in Figure 2a. The plate is positioned in the xOz plane and is orthogonal to the Oy-axis. The origin of the coordinate system coincides with the center of the plate. The structure has a length of H = 3λ and a width of W = 2λ. Figure 2b depicts the plate from Figure 2a, approximated using a WG in this study. The WG structure consists of the same square cells: 30 cells along the H edge and 20 cells along the W edge, while Δ represents the edge length of all the WG cells, which is equal to the length of each cell wire. Each of the four wires forming the WG cells is represented by a single segment. This approach simplifies the construction of the structure and complies with the recommendations that no basis function passes through the intersection points of the segments.
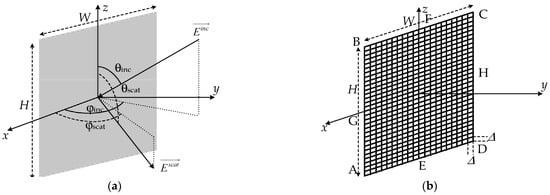
Figure 2.
Rectangular scattering plate (a) and its equivalent WG structure (b).
In the process of modeling the rectangular plate scatterer, the segment length (Δ = λ/10) and the wire radius (a = Δ/2π) were calculated based on the findings of previous publications. Specifically, at the excitation frequency f = 300 MHz, the dimensions of the plate were H = 3 m, W = 2 m, Δ = 0.1 m, and a = 0.016 m. A plane wave with θ-polarization was utilized for excitation at the incident angles θinc, φinc. When calculating the backscattering cross section (BSCS), the scattered field was considered at the angles θscat = θinc, φscat = φinc.
In this work, the BSCS of the structure was calculated using MoM with PBF based on WG and compared with numerical simulation results using MoM with piecewise-sinusoidal (PWS) basis functions, as well as with experimental results from [65] (Figure 3). The obtained results coincided well with each other. In fact, the BSCS results using MoM with PBF based on WG matched even more closely with the measured results than those obtained with MoM using PWS, particularly when the direction of the incident wave changes in the xOy plane. Observing Figure 3, it can be seen that there are differences in the results in the side lobes, possibly due to the measurement conditions and imperfections of the flat plate surface. However, the results in the main lobe of BSCS generally agree well with each other with a deviation at maximum magnitude BSCS of 0.55 dB. Additionally, when the incident wave was perpendicular to the surface of the plate, the scattered field reached its maximum; specifically, the BSCS magnitude at θ = 90°, φ = 90° were 26.8 dBsm (MoM with PBF based on WG) and 26.25 dBsm (experimentally and MoM with PWS). Note that the width of the main lobe (–3 dBsm from the maximum BSCS level) obtained in the xOy plane (12°) was larger than that in the yOz plane (8°), which was consistent with the fact that the width of the plate (W = 2 m) was smaller than its length (H = 3 m). These findings demonstrate the accuracy of using MoM-based WG with PBF for analyzing scattering plate structures.
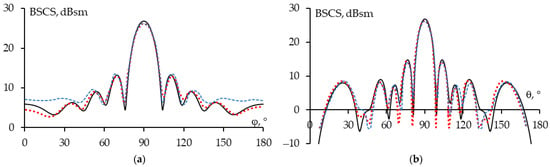
Figure 3.
Measured (•••) and calculated BSCS results for the scatterer in the xOy (a) and yOz (b) plane using MoM with PBF (−−) and PWS (---).
4. The OCGA for Creating Sparse Scatterers When It Is Excited by an Incident Wave at a Specific Direction
The results obtained in Section 3 have verified the accuracy of approximating the perfect conducting flat plate using the WG structure. However, as mentioned above, it is not necessary to use all the wires of the grid to simulate the plate. Therefore, in this section, we present an OCGA-based approach for the initial WG scattering structure when the incident wave is at a fixed direction, aiming to achieve a sparse WG structure.
Since OCGA is based on the characteristics of surface current, it is essential to analyze the current distribution in the structure when it is excited by a plane wave. In this section, we assume that the incident wave has θ-polarization perpendicular to the plate, which means that the horizontal wires are completely unaffected by the incident plane wave. As a result, the current that appears on the horizontal wires is very small compared to that on the vertical wires. Figure 4 presents the magnitude of the obtained current distribution (|I|) at the left vertical edge (AB) and along the central vertical line (EF) of the plate. It is observed that |I| along the plate at the edge ( = 1.23 mA) reaches a higher value compared to that at the center line of the plate ( = 0.68 mA).
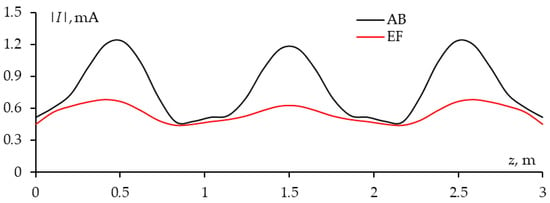
Figure 4.
The dependences of |I| on coordinates along the AB and EF of considered structure when θinc = φinc = 90°.
According to electromagnetic theory, the tangential component of an electric field must be continuous across the boundary between two media (in this case, the surface of the plate). However, the sudden changes in geometric shape at the edges of the plate caused significant variations in the electromagnetic field. Specifically, in the central region of the plate, the electromagnetic field is distributed uniformly across the surface, while at the edges, the electric field was more intensely excited. This phenomenon leads to high accumulation of electric charge at the edges, resulting in high current at these locations (edges AB and CD). In contrast, the current distribution obtained in the central region of the plate surface is lower.
We developed the OCGA algorithm to create a sparse scatterer structure (Figure 5). After applying MoM with PBF based on WG to the plate, |I| was obtained for all wire segments. The obtained |I| was then normalized by its maximum value (|I|max). Subsequently, the normalized current results (Inor) were compared with GEET. Segments with Inor values smaller than GEET were removed from the initial WG structure. As a result, the obtained sparse structure consists only of segments with Inor values greater than GEET. The indices of the segments in the sparse structure were stored in a matrix denoted as Ms, which has the size of 1 × Ns where Ns is the total number of segments in the sparse structure.
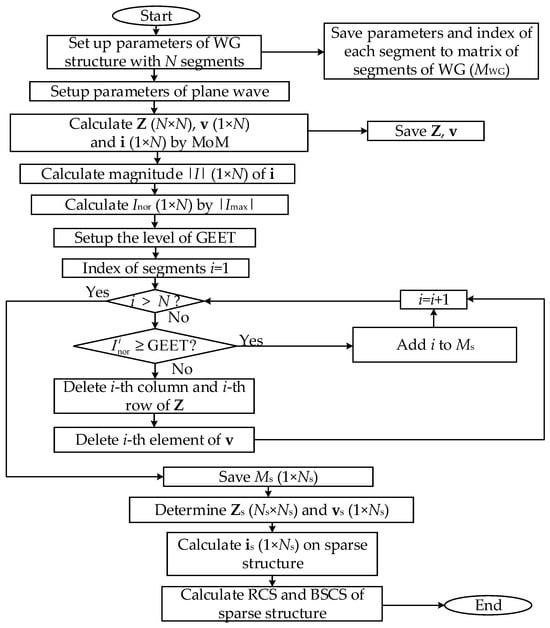
Figure 5.
The OCGA algorithm for creating sparse scatterers when the incident wave is excited in a fixed direction.
Then, we calculated the impedance matrix (Zs) and excitation vector (vs) for the sparse scatterer to determine the scattering characteristics of the structure. There are two approaches to achieve this.
The first approach involves recalculating the elements of Zs and vs directly using MoM with PBF for the sparse structure. This approach is easy to implement in code. However, as mentioned earlier, actual scattering structures are electrically large (much larger than λ), which means that their modeling using WG requires a significant number of segments (N) (potentially reaching tens of thousands). Even after sparsing the structure, there are still quite a few segments to consider. Therefore, recalculating Zs and vs using this approach significantly increases the computational cost.
The second approach leverages a significant advantage related to the formation of the initial impedance matrix (Z) using MoM with PBF. When an i-th segment is removed from the structure, it is sufficient to eliminate the corresponding i-th row and i-th column in matrix Z. In other words, the existence of each individual segment is independent of the others, which contrasts with the use of basis functions constructed from points along the wire (e.g., triangular functions). Therefore, this approach is considered more optimal in this context. Furthermore, this approach not only accelerates Zs computation but also facilitates the rapid identification of the vs element by removing the i-th elements (corresponding to the index i of the removed segment) from v (the excitation vector for the initial WG). As a result, the computational cost of analyzing the scattering characteristics of the sparse structure is significantly reduced.
Next, we analyzed the results of using OCGA to sparse the considered WG structure. In previous publications [66,67], the scattering characteristics of the rectangular plate, as represented by the radar cross section (RCS), are typically examined when the incident wave is directed orthogonally to the plate (θinc = φinc = 90°). Therefore, in this section, we first investigated the variation in the RCS maximum magnitude (RCSmax) (when θscat = φscat = 90°) for the plate when the GEET value changed (Figure 6).
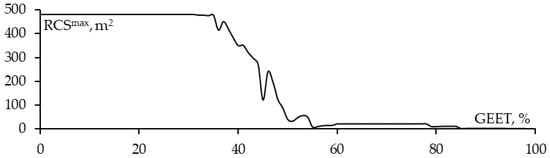
Figure 6.
The dependence of RCSmax on GEET when θinc = φinc = 90°.
From Figure 6, it can be observed that when GEET is set to 0–34%, the RCSmax value remains largely unchanged. This is because, in addition to the horizontal segments, which do not contribute to the scattering field, the |I| of the vertical segments is generally greater than GEET (exceeding 34% of |I|max). Specifically, as seen in Figure 6, |I|min on segment EF is 0.44 mA, which is still greater than approximately 34% of |I|max on segment AB (1.23 × 0.34 = 0.41 mA).
When GEET increases to 34–55%, RCSmax decreases sharply. This can be explained by the fact that |I| on the vertical wires in the middle of the plate is smaller than the GEET value and leads to the removal of the wires. Furthermore, from Figure 6, it can be noted that |I| of the vertical wires in the middle of the plate is approximately equal, so even a slight increase in GEET within the range of 34–55% results in the removal of a significant number of vertical segments in that region. Unlike the case when GEET = 0–34%, the removal of a large number of horizontal wires does not affect the scattering properties. However, the sudden decrease in the number of mid-plate segments (where |I| is not small) in this case leads to a sharp decrease in the scattering field, resulting in a rapid decrease in RCSmax in this range (Figure 6).
When GEET reaches 45%, RCSmax decreases significantly (down to 120 m2) and then increases again when GEET is at 46% (up to 240 m2). This phenomenon can depend on the phase of the current in the removed wires. The amplitude characterizes the strength of the scattered field created by that wire, while the phase characterizes how the scattered fields created by these wires combine with each other and thus also affect the RCSmax value. When GEET is set to 56–100%, RCSmax drops to a very low value. This is because most of the segments in the middle of the plate have been removed, leaving only a few segments at the edges. Although the |I| in the remaining segments at the edges is large, the number of those segments is clearly insufficient to generate such a substantial scattering field as the field that is contributed by the segments in the middle of the plate.
From the above observations, it is clear that the number of wires removed from the WG structure depends on the GEET value: as the GEET value increases, the number of wires removed also increases. This directly impacts the mass and surface of the structure as well as the computational cost required for modeling the scatterer, such as the time and memory needed for subsequent simulations. According to [38], the time cost to solve a linear algebraic system of N order (using Gaussian elimination) scales with the cube of its order, O(N3); and the memory cost is O(N2). Consequently, the reduction in scatterer volume is proportional to N/Ns, while the time reduces as (N/Ns)3 and the memory requirement decreases as (N/Ns)2, where N is the total number segments of the WG structure, and Ns—of sparse structure.
The dependence of the reduction in scatterer mass and surface, as well as the time and memory required for subsequent simulations, on GEET is illustrated in Figure 7. As noted, when GEET is very small (1%), the horizontal wires are removed from the structure. Meanwhile, the numbers of horizontal and vertical wires are nearly equal; thus, horizontal wire removal results in approximately a 2-time reduction in the mass and surface of the plate, which corresponds to about 8-time decrease in simulation time and 4-time reduction in memory usage. When GEET increases to 34%, these reductions remain constant, as previously mentioned (the vertical wires are largely retained).
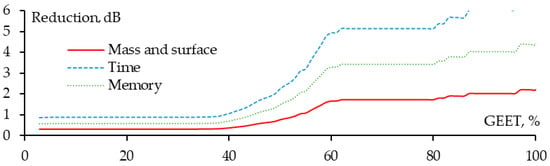
Figure 7.
The GEET dependences of the sparse WG reduction in scatterer mass and surface, and in the time and memory on subsequent simulations after OCGA.
When GEET is in the range of 34–55%, these reduction values decrease more rapidly because of the removal of many vertical segments in the middle of the plate. For GEET > 55%, the reduction values still increase but not as rapidly, as the increase in GEET can only eliminate a certain number of vertical segments located at the edges of the plate.
However, as previously mentioned, changes in the number of wires in the WG structure directly affect the scattering characteristics of the structure. Therefore, this factor must be carefully analyzed before implementing sparse scatterers in production.
The GEET value can be adjusted according to the specific conditions and requirements of the manufacturer. When adjusting GEET, it is necessary to consider the scattering properties and the mass and surface of the model. A higher GEET will help reduce the mass of the structure, but at the same time it may reduce the scattering efficiency. On the contrary, when GEET is low, the scattering properties of the sparse structure will be similar to the original WG but may reduce the effectiveness of mass and surface reduction. Therefore, GEET should be carefully adjusted according to specific practical applications. If the goal is to optimize the structural mass, for example, in designs that require a lightweight structure and are less affected by external factors (such as wind resistance), a GEET value should be high. On the contrary, if the scattering properties of the structure should be similar to the original structure, a low GEET value will be a reasonable choice. In addition, the choice of GEET also affects other factors such as cost, hiding and durability of the structure.
Although we have broadly outlined the characteristics and variations in the scattering field as GEET changes, the analysis thus far has focused only on RCSmax. Consequently, we will next analyze the RCS and BSCS of the sparse structure at various GEET values.
Specifically, we selected the GEET values of 35% (the point at which RCSmax begins to decline), 40% (the value within the decreasing range of RCSmax), and 50% (the value with significant reduction in RCSmax). The models of the sparse WG structure obtained at 300 MHz in MATLAB R2022a, after applying OCGA with GEET values of 35% (S35), 40% (S40), and 50% (S50), are presented in Figure 8.
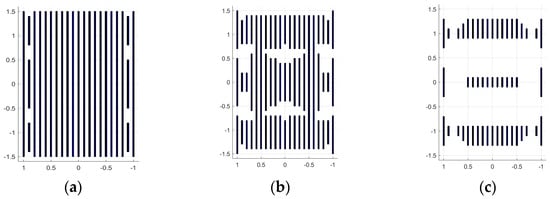
Figure 8.
The MATLAB models of S35 (a), S40 (b), and S50 (c).
It is observed that when the incident wave is perpendicular to the plate, all segments of the vertical wires will exhibit the same potential. Therefore, the obtained |I| of the segments on the plate surface is also symmetric, which means that the sparse structure is also symmetric.
The number of wires that remained in the sparse WG structure using OCGA with GEET values of 35, 40, and 50% were 614, 484, and 174, respectively, while the original structure comprised 1250 wires. Consequently, the scatterer mass and surface were reduced by factors of 2.035, 2.583, and 7.183, while memory usage decreased by factors of 4.14, 6.67, and 51.6 times, and computation time was reduced by factors of 8.427, 17.23, and 370.6 times. It can be observed that the reductions achieved with GEET = 50% are superior to those with GEET = 40%, and the reductions with GEET = 35% were the least significant.
However, the characteristics for these sparse scatterers must also be compared with those for the original WG scatterer. The far-field characteristics obtained (RCSs and BSCSs) at 300 MHz in the xOy and xOz planes for S35, S40, S50, and the original WG structure are illustrated in Figure 9. The deviations in the scattering characteristics for the sparse structures compared to those for the original scatterer at 300 MHz are summarized in Table 4.
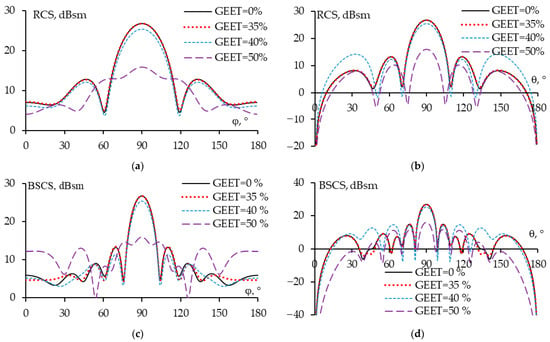
Figure 9.
The obtained RCSs (a,b) and BSCSs (c,d) for original and sparse structures in xOy (a,c) and yOz (b,d) planes.

Table 4.
RCSs, BSCSs, and bandwidth deviations for S35, S40, and S50.
The data from Figure 9 demonstrate that the obtained scattering characteristics from the S50 exhibit the greatest deviation from the original WG structure, followed by S40, while S35 shows the smallest deviation. The scattered field in the main lobe direction in Figure 9 indicates that the results for the sparse structures S35 and S40 match well with those of the original structure. The side lobes of RCSs illustrate that S35 again produces results that are nearly indistinguishable from those of the original WG, while the scattering field from S40 shows a more significant deviation. For the S50 structure, both the main lobe and side lobes of the scattered field demonstrate considerable differences compared to the original WG structure. A similar conclusion is drawn regarding the bandwidth (BW) of S50, which deviates significantly more than that of S35 and S40.
Similar conclusions can also be drawn based on the data presented in Table 4. Overall, S40 provides scattering characteristics with lower accuracy compared to S35, but these can still be considered acceptable when weighing the advantages of reduced scatterer mass, surface, and computational costs for subsequent simulations. Manufacturers can choose an appropriate sparse structure depending on their specific applications and design requirements. If they need the performance that is closely aligned with the original structure, OCGA can be applied with GEET = 35% or lower. When they seek for a scatterer with reduced mass, surface, and modeling costs, OCGA with a higher GEET value (40%) may be applied to the original WG structure.
Figure 9a,b demonstrates that when the incident wave is excited at θinc = φinc = 90°, the RCS for S35 closely matches that of the original WG structure. However, when the BSCS graphs (Figure 9c,d) illustrate that as the incident wave deviates from θinc = φinc = 90°, the side lobes of the S35 BSCS also exhibit greater deviation compared to those of the original WG structure. This can be attributed to the fact that the current sparse structure has only been evaluated based on the impact of the incident wave at a specific direction (θinc = φinc = 90°) on the original WG structure, while the influence of excitation from other directions has not yet been considered. Additionally, it is observed that the differences in the side lobes of the BSCS for the sparse scatterer compared to the original WG structure also increase as GEET increases (in the cases of GEET = 40% and 50%). The development of sparse scatterer structures considering the influence of incident waves from various directions will be examined and analyzed in more detail in the following section.
5. The OCGA for Creating Sparse Scatterers Excited in Unknown Region Through the Scattering Plate Example
As mentioned, in the study of scattering structures, it is essential to consider not only the case when the incident wave is perpendicular to the structure but also various excitation directions. It is important to note that when the incident wave excites the original WG structure from different directions, vector v in each case will vary, while matrix Z remains the same across all scenarios. As a result, the obtained vector i will differ for each case. Consequently, we will consider a sparse scattering structure for each direction of the incident plane wave.
In the general case, when the specific excitation region of the incident wave is not determined, it is necessary to consider the impact of all incident angles (θ = 0–359° and φ = 0–359°) on the original WG structure, followed by the creation of a sparse structure. Conversely, if a specific excitation region is identified, it suffices to create the sparse scattering structure based on the angles within the effective range of the incident wave. The algorithm for generating this structure is illustrated in Figure 10. Below, we will explain the main steps involved in developing the sparse scattering structure when the specific excitation region of the incident wave is not determined in advance. For the cases when the excitation region has been identified, the process of creating the sparse scattering structure will follow a similar logic.
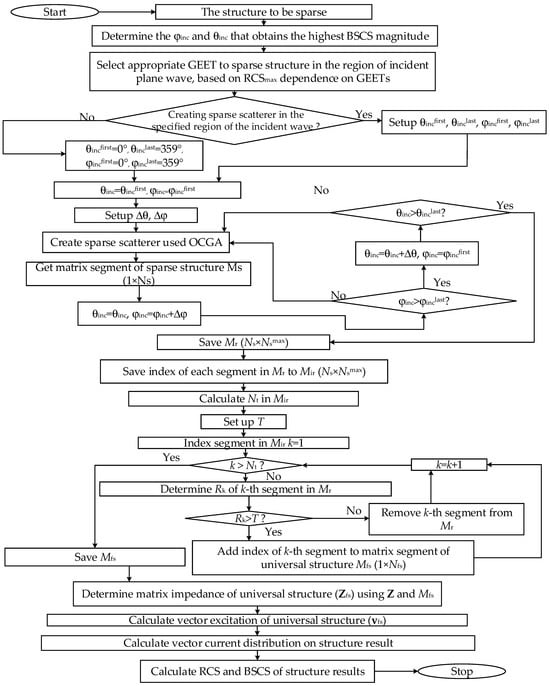
Figure 10.
The OCGA algorithm for creating final sparse scatterers when the incident wave is excited in region direction.
After determining the shape of the initial structure, the next step is to identify the direction of the incident wave where the BSCS of the structure achieves its maximum magnitude (in this work, at θinc = φinc = 90°). Based on the graph showing the relationship between RCSmax and GEET (for example, Figure 6), a suitable GEET value is chosen to create the final sparse (FS) structure (in this study, use GEET = 40%). Subsequently, the original WG structure is sparsified while systematically varying the excitation direction in increments Δθ, Δφ according to θ and φ based on the OCGA and GEET, as outlined in the algorithm in Figure 4.
When considering all excitation directions of the incident wave (θinc = 0–359° and φinc = 0–359°) with Δθ = Δφ = 1°, a total of 360 × 360 = 129,600 sparse structures would be generated. However, the considered plate structure is symmetrical (specifically, the scattering characteristics when the plane is excited from the front are identical to those when excited from the back). Therefore, this study focuses only on θinc = 0–180° and φinc = 0–180° (i.e., exciting the front face of the plate). This results in 181 × 181 = 32,761 unique sparse structures. This approach significantly reduces the computational time and memory required for generating scattering structures (approximately by about 4 times).
However, during the simulation, it became apparent that the number of structures (32,761) was still quite large, leading to significant computational time. This is because we not only aim to create sparse structures for each direction of the incident wave but also need to determine the scattering characteristics of each sparse structure.
One important point to note is that when the incident wave direction changes slightly, its influence on the wire grid is almost identical (i.e., V is similar), resulting in similar values of i. Consequently, the resulting sparse scattering structure also has a comparable shape. Therefore, it can be concluded that there is no need to create and analyze all 32,000 structures to find a sparse structure. Based on this observation, we can consider the original WG structure with larger increments in the incident wave direction (Δθ > 1°, Δφ > 1°) to be sparse. However, it is also important to note that if the increment between incident directions is too large, the shape of the resulting sparse structure may differ significantly between two adjacent incident directions, leading to inaccuracies in creating the final sparse structure. In this work, we examined the incident wave directions at θinc = 0, 2, 4, …, 178, 180° and φinc = 0, 2, 4, …, 178, 180° (i.e., Δθ = 2°, Δφ = 2°). As a result, the number of sparse structures was reduced to 91 × 91 = 8281 (a reduction of about 4 times compared to 32,761 structures).
On each sparse structure obtained for different incident wave directions, we determined which segments remained and which were discarded. The characteristics of the remained segments were saved in a matrix called “segments remained” (Mr) with dimensions Na × Nsmax (where Na is the number of excitation directions, and Nsmax is the number of segments of the sparse structure with maximum remaining segment in the region direction). Subsequently, the indices of the segments for each sparse structure were saved in a matrix called “index segments remained” (Mir).
We calculated the total number of different segments (Nt) in the Mir matrix. We then determined the number of repetitions of each segment (Rk) in the Mir matrix and compared Rk for each k-th index segment with a predefined threshold value (T). Any index segment with Rk less than T was discarded. The result was a collection of indices corresponding to segments that exceed the threshold, which was saved in a matrix called “final segments” (Mfs) with dimensions 1 × Nfs where Nfs is the number of segments in the final sparse structure.
Using the indices of these segments, we constructed the final sparse structure. Finally, based on the indices of the segments in the final sparse structure, we determined the impedance matrix of the final structure (Zfs) by retaining the corresponding rows and columns in Z. We also calculated the excitation vector for the final structure (vfs). The scattering characteristics of the structure can then be determined by solving the linear algebraic equations to find Ifs.
It is important to consider the threshold value T when creating the final structure. If small values of Δθ and Δφ are used, the number of repeated segments will be significantly higher compared to the cases when larger Δθ and Δφ are used. Consequently, the choice of T for generating the final structure with smaller Δθ and Δφ will be higher than those when using larger Δθ and Δφ.
Using this algorithm, we obtained the final structure with T = 50 (FS50), 100 (FS100), 200 (FS200), and 300 (FS300), as illustrated in Figure 11. Additionally, we considered the scattering characteristics of the structure that retained the most segments after sparsing the original WG scatterer during the change in the wave excitation direction. The reason for investigating this structure is that it may exhibit scattering properties similar to those of the original structure. After calculations, we found that the structure with the incident wave directed at θinc = φinc = 90° (S40) retained the most segments after the excitation direction change.
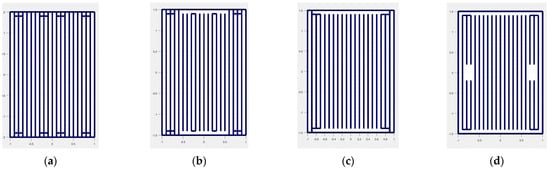
Figure 11.
The MATLAB models of FS50 (a), FS100 (b), FS200 (c), and FS300 (d).
The obtained BSCSs for the final structures and S40 in the xOy and yOz planes were then compared with those for the original WG structure (Figure 12). Additionally, the deviations in the maximum magnitude of BSCSs and the maximum BSCS deviation between the results are summarized in Table 5.
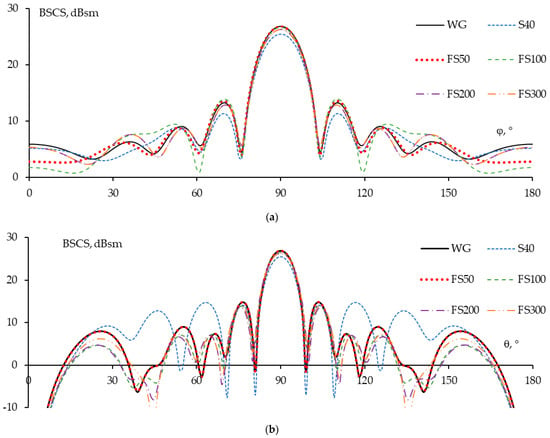
Figure 12.
The obtained BSCSs for original and sparse structures in xOy (a) and yOz (b) planes.

Table 5.
BSCS (dBsm) deviations for S40, FS50, FS100, FS200, and FS300.
Figure 12 and Table 5 demonstrate that the BSCS for FS50 in the xOy and yOz planes matches very well with that of the original WG structure. Specifically, in the xOy plane, the BSCS matches well in the range of φ = 20–160°, while in the yOz plane, there is almost no deviation between the obtained results. The structures FS100, FS200, and FS300 also achieve good similarity with the WG structure, although not as good as FS50.
The S40 structure shows the greatest deviation in the BSCS compared to the WG structure, with a clear difference observed in the yOz plane. However, in the range of φ = 0–20° in the xOy plane, the S40 BSCS aligns better with that of the WG structure than FS50. Overall, the scattering characteristics of the FS structures align well with those of the original WG structure, and this alignment decreases as the threshold T value increases.
All these observations demonstrate the effectiveness of the OCGA method in creating sparse structures when the specific direction of incoming waves is not known.
6. The OCGA for Creating Sparse Scatterers Excited in Specific Region Through the Scattering Plate Example
In practice, scattering structures are often studied when excited by incoming waves directed at a specific region. Therefore, in this section, we discuss generating sparse structures in this context. More specifically, using GEET = 40%, we created sparse scatterers while varying the incoming wave direction in ranges of θ = 60–120° and φ = 60–120°. The analysis steps were carried out as described in the algorithm in Figure 9, with Δθ = Δφ = 1°. At this point, the BSCS characteristics were determined over the entire region corresponding to the incident wave angles (with BSCS include of 61 × 61 = 3721 values).
In this section, we also discuss the influence of T on the FS scattering characteristics. To do this, we first obtained matrix Mr for the 61 × 61 = 3721 sparse structures and then changed the value of T to create different FSs. Logically, when applying various T values, the final structure will have various shapes, and consequently, their scattering characteristics will also differ. Since the BSCS contains many values (3721), comparing the BSCS between all the obtained sparse structures (for example, if the T change step is 10, we would get approximately 372 FSs) and the original WG structure based on their graphs is nearly impossible. Therefore, to analyze the similarity of the BSCSs for FSs and the original WG structure as T changes, we calculated the similarity coefficients for the BSCS for each FS and the BSCS for WG and analyzed them using different correlation coefficients to determine the overall assessment. Specifically, we used the following coefficients to evaluate the similarity: the Pearson, Spearman’s rank, Cosine, Euclidean correlation coefficient, and standard deviation of the difference between two vectors.
The Pearson correlation coefficient reflects the linear correlation between two vectors [68,69,70] (in this case, the BSCS for each FS and WG):
In this equation, a and b are the vectors being considered (BSCS for each FS and WG), n is the total number of elements in each vector, Xa,i and Yb,i are the i-th elements X, Y of vectors a and b, and , are the mean values of vectors a and b.
Spearman’s rank correlation coefficient is similar to the Pearson coefficient in assessing the degree of correlation between two vectors. If the value is close to +1, it indicates a strong positive correlation. Conversely, if the value is close to –1, it signifies a strong negative correlation [71]. However, one of the primary benefits of Spearman’s coefficient benefits is its non-parametric nature, which means it does not require the assumption of a linear relationship between variables [72,73]. Additionally, Spearman’s correlation coefficient is less sensitive to strong outliers compared to the Pearson correlation coefficient [74]:
where d is the difference between the two ranks of two vectors a and b.
The Cosine coefficient measures the similarity between two vectors by calculating the angle between them [75,76]. The value of this coefficient also ranges from –1 to +1 [76]. Coefficients with values within this range will be collectively referred to as group 1 coefficients.
where , .
The Euclidean coefficient [77,78] is commonly used to compare the differences between the element values of vectors. This coefficient is easy to understand and intuitive, reflecting the actual distance between points in a multidimensional space:
The standard deviation of the difference between the two vectors indicates the degree of dispersion of the values in the difference vector of the two BSCS vectors:
A low standard deviation suggests that the elements in the two vectors are relatively close to each other, meaning that their similarity is high. Conversely, a high standard deviation indicates a significant difference between the elements, meaning the two vectors are not similar. The values of the Euclidean coefficient and standard deviation range from 0 to +∞, with values closer to 0 indicating greater similarity between the two vectors. These coefficients were categorized into group 2.
Figure 13 illustrates the dependence of the correlation coefficients on T with a step size of T equal to 10. It can be observed that the Pearson and Cosine coefficients show a good match with each other, while the Spearman and Kendall coefficients have a similar shape but differ in value. Similarly, the Euclidean and standard deviation coefficients exhibit a similar shape but differ in magnitude (the Euclidean coefficient is significantly higher than the standard deviation).
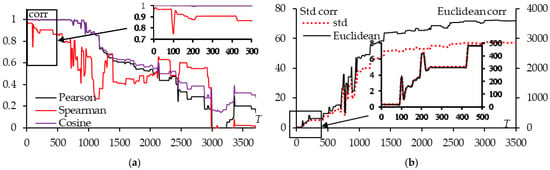
Figure 13.
The dependence of correlation coefficient of group 1 (a) and group 2 (b) on T.
In general, Figure 13 indicates that when T < 400, the correlation coefficients demonstrate that the FS BSCSs are similar to the WG BSCS in the region of θ = 60–120° and φ = 60–120°. However, at T = 100 (or T = 200), the Spearman and Kendall coefficients show a significant drop (or the Euclidean and standard deviation coefficients increase rapidly), indicating that the FS BSCSs at T = 100 (or T = 200) differs from the WG BSCS more than at other T within this range. This again may be explained by the fact that the phase of i on the removed wires were not considered. Overall, it can be concluded that in the case when the incoming wave excites in the region of θ = 60–120° and φ = 60–120°, to create a FS that achieves scattering characteristics similar to the original WG, T < 400 should be considered (except for T = 100 or 200).
Additionally, the dependence of the reduction in mass and computational cost on T is illustrated in Figure 14. Similarly to the GEET value, as T increased, the number of segments decreased, resulting in a reduction in mass, surface, and computational cost. When T = 0 (meaning no segments were removed from each structure after sparsing at each direction excitation), the structure mass and surface nearly halved, indicating that in the considered region, many horizontal wire segments were not considered for creating the sparse structure. Furthermore, Figure 14 depicts that when T < 400, the reduction in mass and surface is almost consistent, suggesting that in this range of T values, the number of segments removed when applying different T is quite similar.
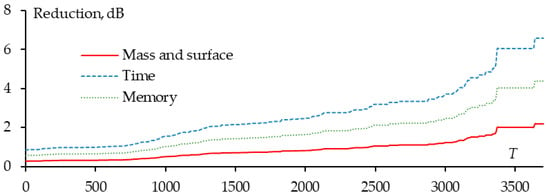
Figure 14.
T dependences of the sparse WG reduction in scatterer mass and surface, and in the time and memory on subsequent simulations after OCGA.
To verify the observations, the FS scattering characteristics based on the correlation, we examined the FS BSCSs when T = 50 (FSr50), 100 (FSr100), 200 (FSr200), and 300 (FSr300). The shapes of the FSr50, FSr100, FSr200, and FSr300 structures are presented in Figure 15.
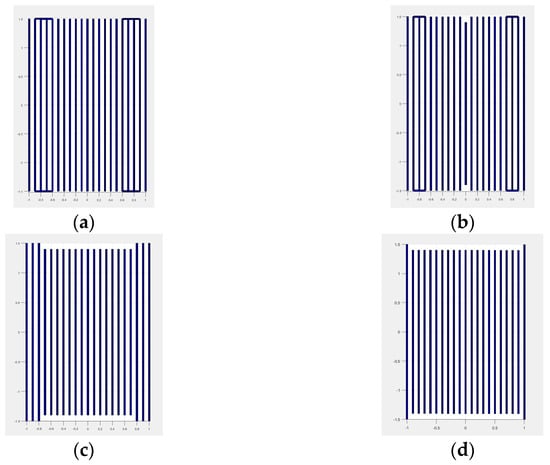
Figure 15.
The MATLAB models of FSr50 (a), FSr100 (b), FSr200 (c), and FSr300 (d).
Similar to Section 3, when T is small, the FS still has more segments than S40 (the sparse structure with the most segments when changing the excitation direction of the incoming wave). This can be explained by the fact that with GEET = 40%, when the incoming wave changed direction, other segments (in addition to those present in S40) were also considered. Additionally, some horizontal segments were present in the final structure because when the incoming wave is deflected away from the yOz and xOy planes, its polarization may no longer be perpendicular to the horizontal wires, leading to a greater current appearing on them. However, this phenomenon only occurred with the horizontal wires at the edge of the plate, not in the middle. Furthermore, it is observed that both FSr50 and FSr100 contained horizontal segments, while FSr200 and FSr300 did not. This is likely because horizontal segments are still less affected by the incoming wave compared to vertical segments, even at different angles of excitation.
The obtained BSCSs for S40, FSr50, FSr100, FSr200, and FSr300 were then compared with the WG BSCS in the region of θ = 60–120° and φ = 60–120°, as well as in the xOy and yOz planes. In the region of θ = 60–120° and φ = 60–120°, comparing the 3D graph (representing the obtained BSCS) for the structures is quite challenging; therefore, we converted it into a 2D plot to make the comparison easier. In this graph, the vertical axis represents the BSCS magnitude in dBsm, while the horizontal axis combines the θ and φ values (with a total of 3721 values). Specifically, 0–61° corresponds to θ = 0° and φ = 60–120°; 62–123° corresponds to θ = 1° and φ = 60–120°; …; 3660–3721° corresponds to θ = 120° and φ = 60–120°. However, accurate comparison of the BSCS values is quite difficult due to the abrupt variations in the graph, so we used the function “smooth” in MATLAB to smooth the obtained BSCS magnitudes, making it easier to observe (Figure 16). Additionally, the discrepancies in BSCSs for S40, FSr50, FSr100, FSr200, and FSr300 in the region of θ = 60–120° and φ = 60–120° (actual values, not smoothed) and in the xOy and yOz planes compared to the WG structure are presented in Table 6.
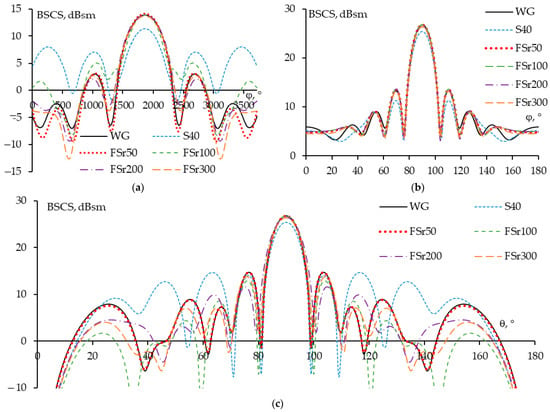
Figure 16.
The obtained BSCSs for original (smoothing value) and sparse structures in region θ = 60–120°, φ = 60–120° (a), xOy (b), and yOz (c) plane.

Table 6.
BSCS (dBsm) deviations for S40, S50, S100, S200, and S300.
From Figure 16a, it can be seen that the obtained BSCS for FSr50 matches best with that of the WG scatterer, followed by FSr300 and FSr200. The FSr100 BSCS deviates more compared to the other FS structures, indicating that the use of the Spearman, Kendall, Euclidean, and standard deviation coefficients accurately predicted the similarity of the BSCS for the sparse structure with that of the WG. This also explains why the FSr300 BSCS is slightly better than the FSr200 BSCS. The maximum FS BSCS values deviate more as T increases. Additionally, it is observed that S40 has a much greater BSCS deviation compared to the other sparse structures.
From Figure 16a, when θ approaches 60° or 120°, which are the boundaries of the excitation region (represented in the graph as approximately 0–700 and 3000–3721), the BSCSs of the resulting FS structures show significant differences from the WG. This may be explained by the fact that as θ nears the boundary values of the excitation region, the θ-polarization significantly affects the horizontal wires, leading to higher currents on these wires at these angles. Consequently, the sparse structures at these positions tend to include horizontal wires, although the quantity of horizontal wires may not be substantial (i.e., these horizontal wires do not repeat frequently in the sparse structures). Therefore, when using the threshold T, these horizontal wires are inadvertently excluded, preventing them from contributing to the scattering characteristics of the FS.
Figure 16b illustrates that the BSCSs of all FS structures match closely with each other and match well with that of the WG structure, while S40 shows significantly more deviation not only at the main direction but also at the first side lobe and across the region of φ = 0–45°. Similar observations can be made from Figure 16c; however, as T changes, the deviations in the BSCSs for the FS structures from that of the WG also vary.
Similar findings are reflected in Table 6. Clearly, among all the structures, the FSr50 BSCS most closely resembles the WG BSCS compared to the other FS structures. Moreover, as mentioned earlier, when T < 400, the reduction in mass for the FS does not change significantly. Therefore, FSr50 can be selected for production when the incident wave excited in the region of θ = 60–120° and φ = 60–120°.
7. Generation of Sparse Dihedral and Trihedral Corner Reflector
In this section, to increase the versatility of our algorithm, we applied it to the dihedral (DCR) and trihedral (TCR) corner reflector as a practical scattering structure commonly used in the calibration and validation of the SAR system [79,80,81,82]. The shape of the DCR and its WG model in MATLAB are shown in Figure 17. The DCR is composed of two orthogonal square plates with the sides of 5.6088λ and operates at 9.4 GHz (Figure 17b) [83]. In the WG structure, the DCR is divided into 2178 square cells with the side length equal to the segment length of 0.16λ, and the wire radius is determined by equal area rule.

Figure 17.
The actual DCR structure [79] (a) and its equivalent WG MATLAB model (b).
For the DCR as in Figure 17b, BSCS achieves the magnitude maximum at θ = 90°, φ = 0°. The dependence of RCSmax, as well as the reduction in mass, surface, and required computational cost, on GEET is shown in Figure 18. It is seen that when GEET = 20%, the RCSmax of the structure does not change much compared to the original WG, while the mass was reduced by about 1.9 times. Therefore, we choose GEET = 20% to create sparse DCR when the direction of the incident wave changes.
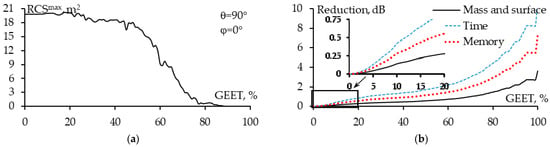
Figure 18.
The GEET dependence of RCSmax when θinc = 90°, φinc = 0° (a) and the sparse DCR reduction in mass, surface, and computation cost (b).
Now the DCR is sparsed when the excitation wave is at φinc = 0–360° and θinc = 0–360°. The reduction in mass, surface, and computation cost depending on T for this sparse DCR is shown in Figure 19. As mentioned, when T increases, the number of remaining wires of the sparse structure decreases, so the mass, surface, and computation cost also decrease. From Figure 19, it can be seen that when T ≤ 600, the mass and surface of the structure decrease by less than 2.1 times, when T > 600, the mass and surface decrease faster. To analyze the influence of mass and surface reduction on the scattering properties of the DCR, we consider the BSCS for the sparse DCR at T = 0, 500, 600, and 700 (the mass and surface reduction compared to the original WG are 1.16, 1.9, 2.1, and 6.18, respectively). The shapes of the sparse DCR are presented in Figure 20.
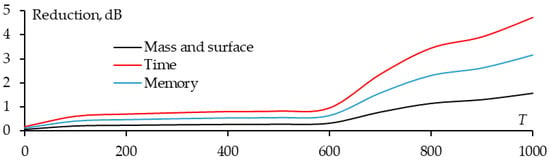
Figure 19.
T dependences of the reduction in mass and surface, in the time and memory for the sparse DCR.
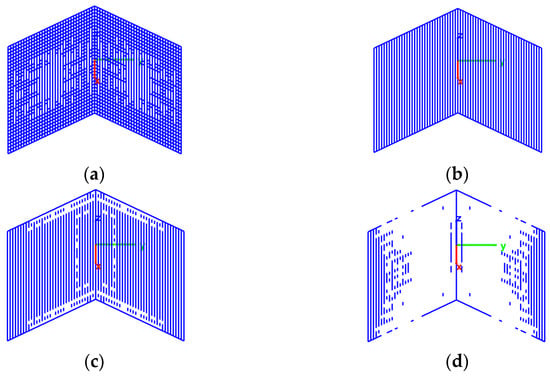
Figure 20.
The MATLAB models of the sparse DCR when φinc = 0–360°, θinc = 0–360° at T = 0 (a), 500 (b), 600 (c), and 700 (d).
The characteristics of sparse DCRs are shown in Figure 21. The WG and sparse structures in the region θ = 90° and φ = 0–55° have almost no difference with the measurement results. In the region θ = 90° and φ = 55–90°, this deviation increases more with an average deviation of about 0.2 dB (for the results using WG-model and measurement results). As in the case of flat plate, this deviation can be due to errors in the structure fabrication and measurement conditions. In addition, at high frequencies, this deviation also increases. It can be seen that when T = 0, the BSCS is in very good agreement with the WG DCR and solid DCR in both θ = 90° and φ = 0° planes. When T = 500, 600, the BSCS in θ = 90° plane is still in good agreement with it for WG; however, in φ = 0° plane, the side lobes of the BSCS are more deviated than those of the WG. This deviation increases as T increases. When T = 700, the BSCS for sparse DCR is completely inconsistent with the BSCS for the original WG. Therefore, when φinc = 0–360° and θinc = 0–360°, T = 500 can be chosen to balance the mass and surface reduction and the scattering properties of the sparse structure.
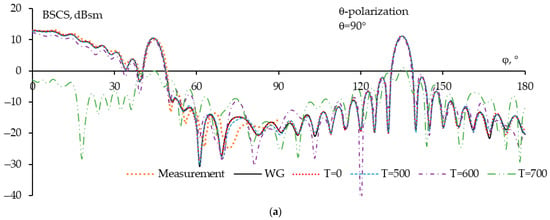
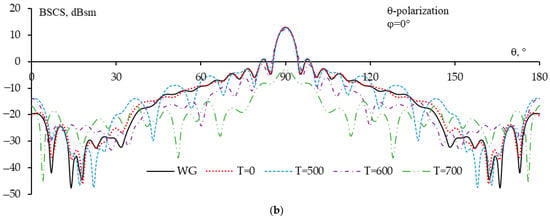
Figure 21.
The obtained BSCSs for the original DCR [83] and sparse DCR in θ = 90° (a) and φ = 0° (b) planes when φinc = 0–360° and θinc = 0–360°.
Next, we created the sparse DCR when θinc = 84–96° and φinc = –40–40° (BSCS main lobe of DCR). The dependence of reduction in mass, surface, computational cost, and correlation coefficient of BSCS for the sparse and original DCRs on T is shown in Figure 22. It can be seen that when T = 600, 700, the BSCS for the sparse structure still agrees quite well with the original WG, while the mass reduction is 1.92 and 2.27 times, respectively. When T = 800, although the mass reduction is high (5.44 times), the BSCS for the sparse DCR deviates quite a lot from that for the WG.
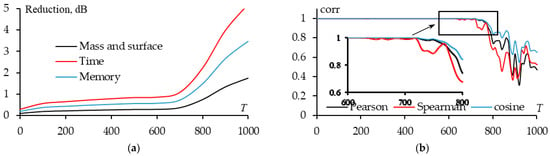
Figure 22.
T dependences of the reduction in mass, surface, computation cost for the sparse DCR (a) and of correlation coefficient of group 1 (b).
The shapes of the sparse structures and their backscatter fields at different T values (T = 600, 700, and 800) are shown in Figure 23. Consistent with the values of the correlation coefficients, when T = 600 and 700, the BSCS of the sparse DCR agrees quite well with the original WG. When T = 800, the backscatter field deviates significantly from the original WG.
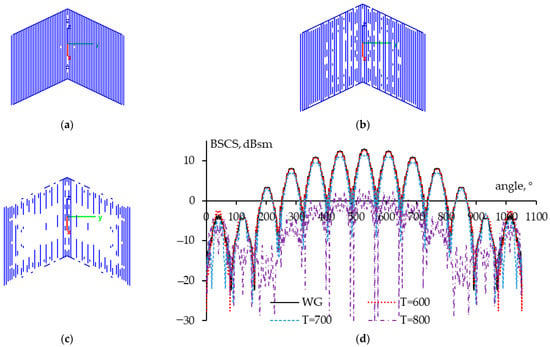
Figure 23.
The MATLAB models of the sparse DCR when φinc = –40–40° and θinc = 84–96° at T = 600 (a), 700 (b), and 800 (c) and the obtained BSCSs for original and sparse DCRs (d).
In some civil and military maritime applications, TCR and their variants are commonly used [84,85,86,87,88]. One of the popular types of TCR is the circular TCR (CTCR), which is formed by orthogonally joining quarter circular faces [89,90,91]. To further assess the effectiveness of the proposed algorithm, we applied OCGA to a CTCR with orthogonal edge lengths of 0.2 m at the X-band f = 9 GHz [44]. The BSCS results obtained in the θ = 90° plane using the WG model are compared with those obtained using CST and measured in [44] (Figure 24). In the WG structure, the CTCR is divided into 2178 cells with the side length equal 0.17λ. The BSCS results show a good agreement between the methods.
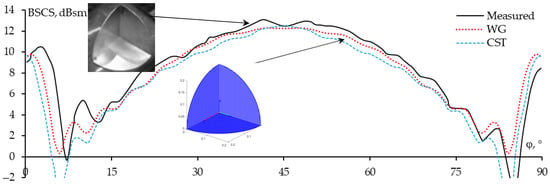
Figure 24.
BSCS for CTCR in θ = 90° plane.
From Figure 24, the difference between the average BSCS obtained from the WG-model and the measured results is 0.3 dB, while the average difference between the CST and the measured results is 1.5 dB. It can be seen that the simulation results using the WG-model match well with the measured results. A slight difference between these results due to manufacturing imperfections in the structure, include non-ideal orthogonal surfaces and surfaces that are not perfectly smooth [44].
For the TCR, the maximum BSCS is obtained at θ = 55°, φ = 45°. Therefore, when the incident wave excites at θ = 55°, φ = 45°, we calculate the BSCS in the θ = 55°, φ = 45° planes while varying the GEET. The shape of the sparse CTCR and the corresponding BSCS results are shown in Figure 25. The mass reduction for GEET values of 15%, 25%, and 35% are 1.06, 1.15, and 1.3, respectively. It is observed that when GEET = 15%, the BSCS of the sparse CTCR matches quite well with that of the WG. As GEET increases, the BSCS of the sparse CTCR deviates more from the WG. However, after balancing the mass reduction and the BSCS deviation of the sparse structure compared to the original WG, we chose GEET = 25% to create the sparse structure when the incident wave changes its excitation direction.
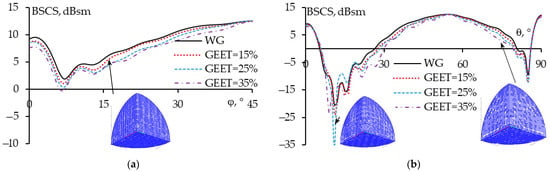
Figure 25.
The obtained BSCSs for original and sparse CTCR in θ = 55° (a) and φ = 45° (b) planes.
When θinc = 0–360°, φinc = 0–360°, the dependence of mass and surface, computational cost reduction, and correlation coefficient on T is shown in Figure 26. Based on the correlation coefficient, it is predicted that when T = 800, the BSCS of the sparse CTCR still matches that of the original CTCR. The shape and BSCS of the sparse structures at the θ = 55°, φ = 45° planes are shown in Figure 27. It is observed that when T = 800, the characteristics of the sparse CTCR align well with the original WG (Figure 27c), while the mass reduction is 1.45 times. When T = 900, the mass reduction of the structure is about 1.5 times, but the BSCS of the sparse CTCR at the θ = 55°, φ = 45° is slightly reduced compared to the original WG (Figure 27d). Therefore, selecting the sparse CTCR with T = 800 is entirely reasonable in this case.
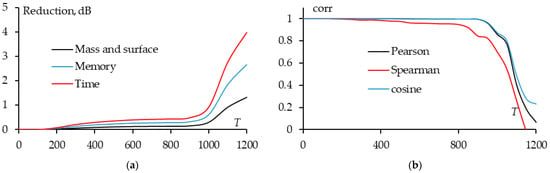
Figure 26.
T dependences of the reduction in mass, surface, computation cost for the sparse SCTCR (a) and of correlation coefficient of group 1 (b) when θinc = 0–360°, φinc = 0–360°.
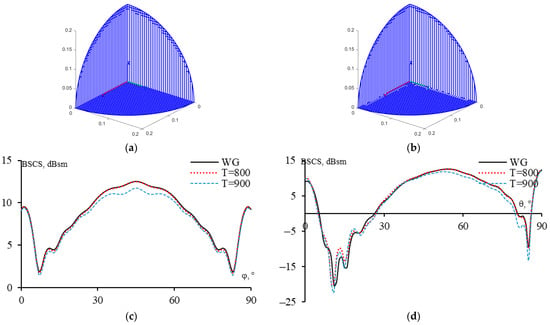
Figure 27.
The MATLAB models of the sparse CTCR when φinc = 0–360° and θinc = 0–360° at T = 800 (a), 900 (b), and the obtained BSCSs for original and sparse CTCRs in θ = 55° (c) and φ = 45° (d) planes.
Next, when the plane wave excites in the main lobe (θinc = 40–67° and φinc = 27–63°), we created the sparse CTCR. Dependences of reduction in mass, surface, computational cost and correlation coefficient of BSCS for the sparse and original CTCRs on T are shown in Figure 28. The shapes of the sparse structures and their backscatter fields at different T values (T = 600, 700, and 800) are shown in Figure 29. It can be seen that when T = 600, 700, the BSCS for the sparse structure still agrees quite well with the original WG, while the mass reduction is 1.44 and 1.51 times, respectively. When T = 800, the mass reduction is 1.6 times, but the BSCS for the sparse DCR deviates quite a lot from that for the WG. Therefore, in this case, T = 700 can be chosen to create a sparse CTCR structure with reasonable mass reduction and scattering properties.
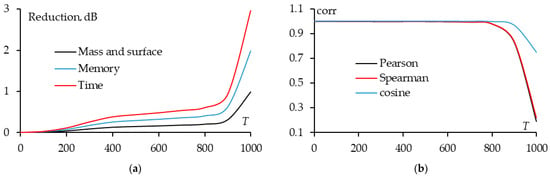
Figure 28.
T dependences of the reduction in mass, surface, computation cost for the sparse SCTCR (a) and of correlation coefficient of group 1 (b) when θinc = 40–67° and φinc = 27–63°.
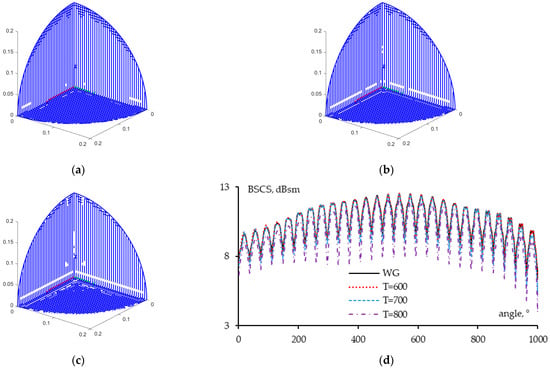
Figure 29.
The MATLAB models of the sparse CTCR when θinc = 40–67° and φinc = 27–63° at T = 600 (a), 700 (b), and 800 (c) and the obtained BSCSs for original and sparse CTCRs (d).
All these observations demonstrate the effectiveness of the proposed algorithm in creating sparse DCR and CTCR structures.
8. Discussion
Being newly developed for difference scattering structures, the sparse scatterer structure generation algorithm that uses the OCGA approach has proven effective in reducing the mass and surface of the original WG structure by nearly 1.5–2 times while maintaining its scattering properties.
Initial processing of the free wires can be performed by choosing a small GEET value, creating a sparse structure without free wires, which enhances the reliability of the structure. Various algorithms for connecting free wires to the WG structure after OCGA have been used for sparse antennas. As shown in Section 2, these algorithms have demonstrated their accuracy while maintaining mass reduction efficiency in both real measurements and simulations. Therefore, it is quite possible to confidently apply this algorithm to sparse scatterers in the future, especially when GEET and T are large.
The comparison of the computational cost shows that the proposed algorithm allows more reduction in the cost than the existing methods. Specifically, when compared with the perforated structure (usually using holes with diameters of about λ/6 corresponding to the cell size used for WGs), the classical method such as MoM requires computational complexity O(N3) and memory O(N2) when solving a system of equations with N unknowns (N basis functions). When the number of unknowns is large, this significantly increases the computational cost. However, this paper considers each wire in the WG as a segment, which significantly reduces the number of unknowns compared to the perforated structure using the RWG function for analysis. The last case uses more small triangles at the holes (where the boundary conditions change abruptly), which results in an increase in the number of unknowns and requires more cost for the analysis. For the method using silver-coated textiles, MoM is often used in combination with the volume integral equation, making the problem more complicated. In addition, the number of unknowns to be solved also increases because the mesh grid is not only on the surface but also in the structure.
The nature of the current distribution results for sparse structures is obtained from solving the MoM system of equations, so it can be affirmed that the obtained current results are completely accurate. Not only that, taking advantage of PBF when calculating the current for sparse structures also helps reduce the required computational resources. This is because the time to solve the MoM linear system of equations is shortened, and there is no need to recalculate the impedance matrices and excitation vectors from scratch, as mentioned in Section 4.
In this paper, we have obtained sparse scatterers for complex original scatterers such as DCR and CTCR with different sizes at different frequency bands and commonly used in practice. The obtained sparse structures have demonstrated effective mass reduction and retained important scattering properties of OCGA. Meanwhile, we also have performed detailed analysis of the properties of sparse structures when GEET and the excitation direction of the incident wave are varied. This analysis is conducted on a wide range of structures, from simple to complex, in order to clarify the nature and effectiveness of the presented algorithm.
The choice of the threshold value T assumes that the contribution of each sparse structure (corresponding to each incident wave direction) to the resulting final sparse structure is uniform. This simplification, as demonstrated in Section 5, Section 6 and Section 7, does not significantly affect the accuracy of the resulting sparse structure in both simple and complex structures. Meanwhile, it helps to increase the computational efficiency and reduce the algorithmic complexity in the process of determining T. In the following studies, we will consider the separate contribution of each sparse structure and integrate this factor into the process of determining the threshold value T, in order to analyze its influence on the resulting sparse structure.
The algorithm presented in this study has the potential to be applied in reality. In particular, the fabrication of metal wire grid plates has been studied and applied for a long-time using techniques such as welding or 3D metal printing. These methods can be easily implemented in industrial production at a relatively low cost and increase the feasibility of the algorithm in practice. Once the process of creating a metal grid plate is completed, the presented algorithm can be used to identify and remove wires that have low influence on the scattering field. Finally, these unneeded wires in the original WG structure can be removed using a simple cutting technique without causing deformation of the structure surface, which is a significant advantage compared to creating a perforated structure. This not only helps to optimize the structure parameters but also saves materials.
To demonstrate this conclusion, in this paper, we considered the actual sparse horn antenna and measured its characteristics. This antenna can be considered as representing complex structures due to its design, which involves the assembly of rectangular and trapezoidal facets with different angles and dimensions. Furthermore, the analysis of sparse structures with different shapes, when GEET and T threshold are varied, also leads to complex shapes. These shapes arise from the combination of many cells of different shapes in different sparse configurations.
The result of using OCGA for horn antenna is that the mass of sparse antennas has been reduced by about 1.4 times compared to WG original through a simple low-cost wire cutting process without deforming the surface, which increases the practicality of the proposed method. Even some actual sparse structures achieve better characteristics than the original WG structure. The obtained actual model contributes to increasing the scientific basis of the paper and helps to strengthen the reliability and capability of the algorithm under real conditions, making the algorithm performance obvious and fully applicable in fields requiring high precision such as telecommunications and military purposes.
Although the measurement results for the sparse scatterer structures are not presented in this paper, the agreement between the WG-model results and the measured BSCS for the original structure has demonstrated that our scattering characteristic analysis software achieves an acceptable level of accuracy. The measurement results for the sparse scatterer structures will be presented in future work.
9. Conclusions
In this study, we proposed a novel algorithm based on the OCGA method to generate sparse scattering structures using examples of flat plates, dihedral, and trihedral CRs. The algorithm allows for the reduction in the mass and surface area of the original wire grid structure while maintaining key radiation and scattering characteristics (at least for structures considered properly in this paper). The algorithm demonstrated the ability to reduce the mass and surface area of plate and CR structures by up to two times without altering the scattering properties compared to the original structure in two cases: when the excitation region of the incident wave is unknown and when the wave is excited in a specific region.
Moreover, the algorithm proved to be computationally efficient compared to traditional methods such as perforation or using silver-coated textiles. It significantly reduces the number of unknowns and computational complexity, thus saving computational costs. By optimizing structural parameters (the number of wires after sparsing), the algorithm also helps save materials without deforming the structure.
The obtained results were further validated by comparison using MoM with PBF-based WG, showing that the scattering properties of the sparse structures remained consistent with the original WG structure, confirming the accuracy and stability of the algorithm in practice. Additionally, the selection of GEET values and thresholds for creating final structures was discussed based on manufacturing conditions. Clearly, the proposed algorithm is effective in generating sparse plate, dihedral, and trihedral corner reflector structures at low manufacturing cost using simple manufacturing techniques.
However, this first step in investigating the new algorithm opens some directions of studies relevant in the future. Specifically, the algorithm has potential applications for more complex scattering structures. Finally, a more detailed study of GEET influence on the scattering characteristics would be valuable for real-world applications. Future research will also focus on refining the algorithm to free-wire connections and improving the speed of sparse structure generation when the wave is excited in a wide region.
Author Contributions
Conceptualization, T.P.D. and A.F.A.H.; methodology, T.P.D. and M.T.N.; software, T.P.D. and M.T.N.; validation, T.P.D., M.T.N. and A.F.A.H.; formal analysis, T.P.D., M.T.N. and A.F.A.H.; investigation, A.F.A.H. and T.R.G.; resources, T.R.G.; data curation, T.P.D., M.T.N. and T.R.G.; writing—original draft preparation, T.P.D., M.T.N. and T.R.G.; writing—review and editing, T.P.D., M.T.N. and T.R.G.; visualization, T.P.D. and M.T.N.; supervision, A.F.A.H. and T.R.G.; project administration, A.F.A.H. and T.R.G.; funding acquisition, T.R.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Higher Education of the Russian Federation project FEWM-2023-0014.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the funding organization policy.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cao, W.; Xiang, F.; Ma, P. A Circularly Polarized Antenna Design for 5G Mobile Communication. In Proceedings of the 2023 IEEE 5th International Conference on Civil Aviation Safety and Information Technology, Dali, China, 11–13 October 2023. [Google Scholar] [CrossRef]
- Ayukov, B.A.; Kryachko, A.F.; Medzigov, A.V.; Revunov, G.M. About Scattering Properties of Civil Aviation Aircraft Antennas. In Proceedings of the 2024 Systems of Signal Synchronization, Generating and Processing in Telecommunications, Vyborg, Russia, 1–3 July 2024. [Google Scholar] [CrossRef]
- Patruno, J.; Fitrzyk, M.; Delgado Blasco, J.M. Monitoring and Detecting Archaeological Features with Multi-Frequency Polarimetric Analysis. Remote Sens. 2020, 12, 1. [Google Scholar] [CrossRef]
- El Gharbi, M.; Fernández-García, R.; Ahyoud, S.; Gil, I. A Review of Flexible Wearable Antenna Sensors: Design, Fabrication Methods, and Applications. Materials 2020, 13, 3781. [Google Scholar] [CrossRef]
- Choo, H. Antenna Design for Microwave and Millimeter Wave Applications: Latest Advances and Prospects. Appl. Sci. 2021, 11, 5556. [Google Scholar] [CrossRef]
- Karli, R.; Becquaert, M.; Bontemps, L. Assessment of the Antenna Mounting Location on a Military Vehicle for Jamming Applications Based on Computational Electromagnetics. In Proceedings of the 2023 International Conference on Military Communications and Information Systems, Skopje, North Macedonia, 16–17 May 2023. [Google Scholar] [CrossRef]
- Osman, H.; Bray, J.R. Backscatter Radar Cross Section Analysis of Chaff Using the Sequential Loading Method. IEEE Trans. Antennas Propagat. 2024, 72, 6151–6155. [Google Scholar] [CrossRef]
- Carneiro, A.F.A.; Torres, J.P.N.; Baptista, A.; Martins, M.J.M. Smart Antenna for Application in UAVs. Information 2018, 9, 328. [Google Scholar] [CrossRef]
- Lee, H.; Tak, J.; Choi, J. Wearable Antenna Integrated into Military Berets for Indoor/Outdoor Positioning System. Antennas Wirel. Propag. Lett. 2017, 16, 1919–1922. [Google Scholar] [CrossRef]
- Nahar, T.; Rawat, S. A Survey on Wearable Antenna Used for Defense Applications. Lect. Notes Electr. Eng. 2022, 863, 121–130. [Google Scholar] [CrossRef]
- Rasilainen, K.; Phan, T.D.; Berg, M.; Pärssinen, A.; Soh, P.J. Hardware Aspects of Sub-THz Antennas and Reconfigurable Intelligent Surfaces for 6G Communications. IEEE J. Sel. Areas Commun. 2023, 41, 2530–2546. [Google Scholar] [CrossRef]
- Singh, H.; Mittal, N.; Gupta, A.; Kumar, Y.; Woźniak, M.; Waheed, A. Metamaterial Integrated Folded Dipole Antenna with Low SAR for 4G, 5G and NB-IoT Applications. Electronics 2021, 10, 2612. [Google Scholar] [CrossRef]
- Hao, J.; Wang, X.; Yang, S.; Gao, H.; Yu, C.; Xing, W. Intelligent Target Design Based on Complex Target Simulation. Appl. Sci. 2022, 12, 8010. [Google Scholar] [CrossRef]
- Iizuka, T.; Kosaka, N.; Hisada, M.; Kawahara, Y.; Sasatani, T. Trimmed Aperture Corner Reflector for Angle-Selective Chipless RFID. Antennas Wirel. Propag. Lett. 2023, 22, 2537–2541. [Google Scholar] [CrossRef]
- Koziel, S.; Ogurtsov, S. Antenna Design by Simulation-Driven Optimization; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Fedeli, A.; Montecucco, C.; Gragnani, G.L. Open-Source Software for Electromagnetic Scattering Simulation: The Case of Antenna Design. Electronics 2019, 8, 1506. [Google Scholar] [CrossRef]
- Vasylchenko, A.; Schols, Y.; De Raedt, W.; Vandenbosch, G.A.E. Quality Assessment of Computational Techniques and Software Tools for Planar-Antenna Analysis. IEEE Antennas Propag. Mag. 2009, 51, 23–38. [Google Scholar] [CrossRef]
- Werner, D.H. A Method of Moments Approach for the Efficient and Accurate Modeling of Moderately Thick Cylindrical Wire Antennas. IEEE Trans. Antennas Propagat. 1998, 46, 373–382. [Google Scholar] [CrossRef]
- Sawaya, K. Antenna Design by Using Method of Moments. IEICE Trans. Commun. 2005, E88-B, 1766–1773. [Google Scholar] [CrossRef]
- Rashid, A.K.; Zhang, Q. An Efficient Method of Moments for Thick-Wire Antennas. IEEE Trans. Antennas Propagat. 2022, 70, 12399–12404. [Google Scholar] [CrossRef]
- Steinberg, B.Z.; Leviatan, Y. On the Use of Wavelet Expansions in the Method of Moments (EM Scattering). IEEE Trans. Antennas Propagat. 1993, 41, 610–619. [Google Scholar] [CrossRef]
- Lakhtakia, A. Strong and Weak Forms of the Method of Moments and the Coupled Dipole Method for Scattering of Time-Harmonic Electromagnetic Fields. Int. J. Mod. Phys. C 1992, 3, 583–603. [Google Scholar] [CrossRef]
- Harrington, R.F. Matrix Methods for Field Problems. Proc. IEEE 1967, 55, 136–149. [Google Scholar] [CrossRef]
- Harrington, R.; Mautz, J. Straight Wires with Arbitrary Excitation and Loading. IEEE Trans. Antennas Propagat. 1967, 15, 502–515. [Google Scholar] [CrossRef]
- Ilic, M.M.; Djordjevic, M.; Ilic, A.Z.; Notaro, B.M. Higher Order Hybrid FEM-MoM Technique for Analysis of Antennas and Scatterers. IEEE Trans. Antennas Propagat. 2009, 57, 1452–1460. [Google Scholar] [CrossRef]
- Djordjevic, M.; Notaros, B.M. Higher Order Hybrid Method of Moments-Physical Optics Modeling Technique for Radiation and Scattering from Large Perfectly Conducting Surfaces. IEEE Trans. Antennas Propagat. 2005, 53, 800–813. [Google Scholar] [CrossRef]
- Hua, M.; He, S. Efficient EM Scattering Modeling from Metal Targets Coated with Anisotropic Thin Layers. Electronics 2024, 13, 536. [Google Scholar] [CrossRef]
- Yu, H.; Liao, C.; Feng, J.; Du, W.; Zhong, X. Analysis of Radar Target Scattering Echo With Surface Ducting in Large-Scale Environments Based on the PE-MoM Hybrid Method. Antennas Wirel. Propag. Lett. 2023, 22, 2295–2299. [Google Scholar] [CrossRef]
- Mastorakis, E.; Papakanellos, P.J.; Anastassiu, H.T.; Tsitsas, N.L. Analysis of Electromagnetic Scattering from Large Arrays of Cylinders via a Hybrid of the Method of Auxiliary Sources (MAS) with the Fast Multipole Method (FMM). Mathematics 2022, 10, 3211. [Google Scholar] [CrossRef]
- Yuan, W.; Li, E. Accuracy Investigation of the Wire-grid Model in EM Scattering Analysis with the MoM. Micro. Opt. Technol. Lett. 2005, 46, 259–263. [Google Scholar] [CrossRef]
- Topa, T.; Karwowski, A.; Noga, A. Using GPU With CUDA to Accelerate MoM-Based Electromagnetic Simulation of Wire-Grid Models. Antennas Wirel. Propag. Lett. 2011, 10, 342–345. [Google Scholar] [CrossRef]
- Richmond, J. A Wire-Grid Model for Scattering by Conducting Bodies. IEEE Trans. Antennas Propagat. 1966, 14, 782–786. [Google Scholar] [CrossRef]
- Nakano, H.; Kawano, T.; Kozono, Y.; Yamauchi, J. A Fast MoM Calculation Technique Using Sinusoidal Basis and Testing Functions for a Wire on a Dielectric Substrate and Its Application to Meander Loop and Grid Array Antennas. IEEE Trans. Antennas Propagat. 2005, 53, 3300–3307. [Google Scholar] [CrossRef]
- Vipiana, F.; Francavilla, M.A.; Vecchi, G.; Wilton, D.R. Analysis of Large Multi-Scale Wire-Surface Structures with a Fast Hierarchical MoM Approach. In Proceedings of the 2010 IEEE Antennas and Propagation Society International Symposium, Toronto, ON, Canada, 11–17 July 2010. [Google Scholar] [CrossRef]
- Aragbaiye, Y.M.; Isleifson, D. Mass Reduction Techniques for Short Backfire Antennas: Additive Manufacturing and Structural Perforations. Sensors 2023, 23, 8765. [Google Scholar] [CrossRef]
- Pietrenko-Dabrowska, A.; Koziel, S. Cost-Efficient EM-Driven Size Reduction of Antenna Structures by Multi-Fidelity Simulation Models. Electronics 2021, 10, 1536. [Google Scholar] [CrossRef]
- Unified Product and Component Portal for the Rocket and Space Industry Glavkosmos Website. Available online: https://trade.glavkosmos.com/ru (accessed on 15 November 2024).
- Alhaj Hasan, A.; Nguyen, T.M.; Kuksenko, S.P.; Gazizov, T.R. Wire-Grid and Sparse MoM Antennas: Past Evolution, Present Implementation, and Future Possibilities. Symmetry 2023, 15, 378. [Google Scholar] [CrossRef]
- Froese, C.; Poncos, V.; Skirrow, R.; Mansour, M.; Martin, D. Characterizing complex deep seated landslide deformation using corner reflector InSAR (CR-INSAR): Little Smoky Landslide, Alberta. In Proceedings of the 4th Canadian Conference on Geohazards, Dartmouth, NS, Canada, 20–24 May 2008; pp. 1–4. [Google Scholar]
- Gisinger, C.; Willberg, M.; Balss, U.; Klügel, T.; Mähler, S.; Pail, R.; Eineder, M. Differential Geodetic Stereo SAR with TerraSAR-X by Exploiting Small Multi-Directional Radar Reflectors. J. Geod. 2016, 91, 53–67. [Google Scholar] [CrossRef]
- Jauvin, M.; Yan, Y.; Trouvé, E.; Fruneau, B.; Gay, M.; Girard, B. Integration of Corner Reflectors for the Monitoring of Mountain Glacier Areas with Sentinel-1 Time Series. Remote Sens. 2019, 11, 988. [Google Scholar] [CrossRef]
- Lin, S.-Y. A Function Design for a Power-Generation Corner Reflector for SAR Analysis. In Proceedings of the 2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022. [Google Scholar] [CrossRef]
- Garthwaite, M.C.; Nancarrow, S.; Hislop, A.; Thankappan, M.; Dawson, J.H.; Lawrie, S. The Design of Radar Corner Reflectors for the Australian Geophysical Observing System: A Single Design Suitable for InSAR Deformation Monitoring and SAR Calibration at Multiple Microwave Frequency Bands. Geosci. Aust. 2015, 3, 490. [Google Scholar] [CrossRef]
- Yazdani Mianroodi, R.; Heidar, H.; Mohseni Armaki, H. Expandable Shipboard Decoy Including Adequate RCS by Using Trihedral Corner Reflectors. IET Sci. Meas. Technol. 2016, 10, 485–491. [Google Scholar] [CrossRef]
- Gu, J.; Dai, F.; Chen, Q.; Gu, D.; Liao, Y.; Wang, B. Research on RCS Calculation and Weight Loss Method of Radar Angle Reflector. In Proceedings of the 2022 3rd China International SAR Symposium, Shanghai, China, 2–4 November 2022. [Google Scholar] [CrossRef]
- Garthwaite, M.C. On the Design of Radar Corner Reflectors for Deformation Monitoring in Multi-Frequency InSAR. Remote Sens. 2017, 9, 648. [Google Scholar] [CrossRef]
- Algafsh, A.; Inggs, M.; Mishra, A.K. The Effect of Perforating the Corner Reflector on Maximum Radar Cross Section. In Proceedings of the 2016 16th Mediterranean Microwave Symposium, Abu Dhabi, United Arab Emirates, 14–16 November 2016. [Google Scholar] [CrossRef]
- Mahadevan, K.; Auda, H.A.; Glisson, A.W. Scattering from a Thin Perfectly-Conducting Square Plate. IEEE Antennas Propag. Mag. 1992, 34, 26–32. [Google Scholar] [CrossRef]
- Godin, O.A. Scattering of a Spherical Wave by a Small Sphere: An Elementary Solution. J. Acoust. Soc. Am. 2011, 130, 135–141. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Zhu, K.; Zhang, X.; Sun, H. Classification of Plates and Trihedral Corner Reflectors Based on Linear Wavefront Phase-Modulated Beam. Electronics 2022, 11, 4044. [Google Scholar] [CrossRef]
- Nasucha, M.; Sri Sumantyo, J.T.; Santosa, C.E.; Sitompul, P.; Wahyudi, A.H.; Yu, Y.; Widodo, J. Computation and Experiment on Linearly and Circularly Polarized Electromagnetic Wave Backscattering by Corner Reflectors in an Anechoic Chamber. Computation 2019, 7, 55. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Hasan, A.F.A.; Gazizov, T.R. Recommendations on Modeling Wire Grid Horn Structures for Sparse Antenna Generation. In Proceedings of the 2024 International Ural Conference on Electrical Power Engineering, Magnitogorsk, Russia, 27–29 September 2024. [Google Scholar] [CrossRef]
- TUSUR.EMC System. Available online: https://talgat.org/talgat-software/ (accessed on 21 November 2024).
- MMANA-GAL. Available online: http://gal-ana.de/basicmm/en/ (accessed on 17 November 2024).
- 4NEC2. Available online: https://www.qsl.net/4nec2/ (accessed on 25 November 2024).
- Nguyen, M.T.; Alhaj Hasan, A.F.; Gazizov, T.R. Optimal Sparse Wire Grid Structures: Development and Verification of an OCGA-Based Algorithm. In Proceedings of the 2024 International Conference on Engineering Management of Communication and Technology, Vienna, Austria, 16–18 October 2024. [Google Scholar] [CrossRef]
- Alhaj Hasan, A.F.; Nguyen, M.T.; Gazizov, T.R. Modelling and Designing Wire-Grid Sparse Antennas Using MoM-Based Approaches for Enhanced Performance and Reduced Cost. Microw. Rev. 2023, 29, 83–94. [Google Scholar] [CrossRef]
- Gazizov, T.R.; Hasan, A.A.; Nguyen, M.T. A Simple Modeling Methodology for Creating Hidden Antennas. In Proceedings of the 2023 International Conference on Industrial Engineering, Applications and Manufacturing, Sochi, Russia, 15–19 May 2023. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Alhaj Hasan, A.F.; Gazizov, T.R. Comparative Analysis of C/OCGA Sparse Horn Antenna Structures at Different Frequencies. In Proceedings of the 2023 IEEE XVI International Scientific and Technical Conference Actual Problems of Electronic Instrument Engineering, Novosibirsk, Russia, 10–12 November 2023. [Google Scholar] [CrossRef]
- Hasan, A.A.; Nguyen, T.M.; Gazizov, T.R. Novel MoM-Based Approaches for Generating Wire-Grid Sparse Antenna Structures. In Proceedings of the 2023 IEEE 24th International Conference of Young Professionals in Electron Devices and Materials, Novosibirsk, Russia, 29 June–3 July 2023. [Google Scholar] [CrossRef]
- Nguyen, M.T. Innovative approaches to the design of sparse wire-grid antennas: Development of algorithms and evaluation of their effectiveness. Syst. Control Commun. Secur. 2024, 4, 1–47. (In Russian) [Google Scholar] [CrossRef]
- IEEE Std 149-2021 (Revision of IEEE Std 149-1977); IEEE Recommended Practice for Antenna Measurements. IEEE: New York, NY, USA, 2022; pp. 1–207. [CrossRef]
- Nguyen, M.T.; Alhaj Hasan, A.F.; Gazizov, T.R. Generating sparse wire-grid antennas using maximum current-based optimal current grid approximation. IEEE Open J. Antennas Propag. 2025. accepted. [Google Scholar] [CrossRef]
- Kumar, H.; Kumar, G. Coaxial Feed Pyramidal Horn Antenna with High Efficiency. IETE J. Res. 2017, 64, 51–58. [Google Scholar] [CrossRef]
- Wang, N.; Richmond, J.; Gilreath, M. Sinusoidal Reaction Formulation for Radiation and Scattering from Conducting Surfaces. IEEE Trans. Antennas Propagat. 1975, 23, 376–382. [Google Scholar] [CrossRef]
- Hongo, K.; Serizawa, H. Diffraction of Electromagnetic Plane Wave by a Rectangular Plate and a Rectangular Hole in the Conducting Plate. IEEE Trans. Antennas Propagat. 1999, 47, 1029–1041. [Google Scholar] [CrossRef]
- Sevgi, L.; Rafiq, Z.; Majid, I. Radar Cross Section (RCS) Measurements [Testing Ourselves]. IEEE Antennas Propag. Mag. 2013, 55, 277–291. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef]
- MathWorks MATLAB. Available online: https://www.mathworks.com/help/stats/corr.html (accessed on 20 November 2024).
- Lee Rodgers, J.; Nicewander, W.A. Thirteen Ways to Look at the Correlation Coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Hauke, J.; Kossowski, T. Comparison of Values of Pearson’s and Spearman’s Correlation Coefficients on the Same Sets of Data. QUAGEO 2011, 30, 87–93. [Google Scholar] [CrossRef]
- Bocianowski, J.; Wrońska-Pilarek, D.; Krysztofiak-Kaniewska, A.; Matusiak, K.; Wiatrowska, B. Comparison of Pearson’s and Spearman’s Correlation Coefficients Values for Selected Traits of Pinus sylvestris L. Biom. Letters. 2024, 61, 115–135. [Google Scholar] [CrossRef]
- Puth, M.-T.; Neuhäuser, M.; Ruxton, G.D. Effective Use of Spearman’s and Kendall’s Correlation Coefficients for Association between Two Measured Traits. Anim. Behav. 2015, 102, 77–84. [Google Scholar] [CrossRef]
- De Winter, J.C.F.; Gosling, S.D.; Potter, J. Comparing the Pearson and Spearman Correlation Coefficients across Distributions and Sample Sizes: A Tutorial Using Simulations and Empirical Data. Psychol. Methods 2016, 21, 273–290. [Google Scholar] [CrossRef] [PubMed]
- Sohangir, S.; Wang, D. Improved sqrt-cosine similarity measurement. J. Big Data 2017, 4, 25. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pei, J. Getting to Know Your Data. In Data Mining, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2012; Chapter 2; pp. 39–82. [Google Scholar] [CrossRef]
- Liberti, L.; Lavor, C. Euclidean Distance Geometry; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Korenius, T.; Laurikkala, J.; Juhola, M. On Principal Component Analysis, Cosine and Euclidean Measures in Information Retrieval. Inf. Sci. 2007, 177, 4893–4905. [Google Scholar] [CrossRef]
- Jayasri, P.V.; Niharika, K.; Yedukondalu, K.; Sita Kumari, E.V.S.; Prasad, A.V.V. Radar cross section characterization of corner reflectors in different frequency bands and polarizations. Int. Arch. Photogramm. Remote Sens. Spat. Inf. 2018, XLII–5, 637–642. [Google Scholar] [CrossRef]
- Algafsh, A. A Comprehensive Literature Review of SAR Polarimetric Calibration for Waseda SAR Sensor. Master’s thesis, Department of Electrical Engineering, University of Cape Town, Cape Town, South Africa. 2015. Available online: http://hdl.handle.net/11427/13645 (accessed on 22 November 2024).
- Liu, J.; Li, T.; Ma, S.; Wen, Y.; Xu, Y.; Nie, G. Analysis of the Dihedral Corner Reflector’s RCS Features in Multi-Resource SAR. Appl. Sci. 2024, 14, 5054. [Google Scholar] [CrossRef]
- Jayasri, P.V.; Niharika, K.; Ryali, H.S.V.U.S.; Kumari, E.V.S.S. Synthetic Aperture Radar (SAR) Data Calibration and Validation. In Spaceborne Synthetic Aperture Radar Remote Sensing; CRC Press: Boca Raton, FL, USA, 2023; pp. 393–412. [Google Scholar] [CrossRef]
- Griesser, T.; Balanis, C. Backscatter analysis of dihedral corner reflectors using physical optics and the physical theory of diffraction. IEEE Trans. Antennas Propagat. 1987, 35, 1137–1147. [Google Scholar] [CrossRef]
- Munir, A.; Taufiq, S.; Utoro, S. Design of Trihedral Corner Reflector for Shipboard Navigation Systems. In Proceedings of the 2011 International Symposium on Antennas and Propagation, Jeju, Republic of Korea, 25–28 October 2011. [Google Scholar]
- Wang, M.; Xie, M.; Su, Q.; Fu, X. Identification of Ship and Corner Reflector Based on Invariant Features of the Polarization. In Proceedings of the 2019 IEEE 4th International Conference on Signal and Image Processing, Wuxi, China, 19–21 July 2019. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, J.; Li, C.; Li, S.; Lan, C. Combined Jamming Method of Chaff and Corner Reflector Against Anti-Ship Missiles. In Proceedings of the 2024 IEEE 7th Advanced Information Technology, Electronic and Automation Control Conference, Chongqing, China, 15–17 March 2024. [Google Scholar] [CrossRef]
- Zhu, J.X.; Pei, Z.B.; Qu, S.B. Design of novel trihedral corner reflector loaded with meta-material absorbing body. Electron. Compon. Mater. 2013, 32, 52–54. [Google Scholar] [CrossRef]
- Kang, H.-J.; Yang, H.-K.; Jo, M.-C.; Kim, K.-H. Feasibility Study of Corner Reflector for Radar Countermeasures and Deception for Conventional Forces. J. Korean Soc. Mar. Eng. 2017, 41, 171–175. [Google Scholar] [CrossRef]
- Armin, W.D. Reflectors for SAR Performance Testing, 2nd ed.; Sandia National Laboratories: Albuquerque, NM, USA, 2014. [Google Scholar]
- Unal, I.; Gulum, T.O.; Bayramoglu, E.C. Investigations of Electrical Size Effects on Radar Cross Section for Orthogonally Distorted Corner Reflectors. In Proceedings of the 2015 IEEE Radar Conference, Arlington, VA, USA, 10–15 May 2015. [Google Scholar] [CrossRef]
- Ying, L.; Lixin, G.; Yanchun, Z. Investigations of Effects of Geometric Characteristics on RCS for Corner Reflectors. In Proceedings of the 2019 IEEE International Conference on Computational Electromagnetics, Shanghai, China, 20–22 March 2019. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).