An Alternative Estimator for Poisson–Inverse-Gaussian Regression: The Modified Kibria–Lukman Estimator

Abstract

Poisson regression is used to model count response variables. The method has a strict assumption that the mean and variance of the response variable are equal, while, in practice, the case of overdispersion is common. Also, in multicollinearity, the model parameter estimates obtained with the maximum likelihood estimator are adversely affected. This paper introduces a new biased estimator that extends the modified Kibria–Lukman estimator to the Poisson–Inverse-Gaussian regression model to deal with overdispersion and multicollinearity in the data. The superiority of the proposed estimator over the existing biased estimators is presented in terms of matrix and scalar mean square error. Moreover, the performance of the proposed estimator is examined through a simulation study. Finally, on a real dataset, the superiority of the proposed estimator over other estimators is demonstrated.

1. Introduction

Count models are considered for regression analysis when the response variable only consists of non-negative integers. These models are useful in identifying the factors that could have a major effect on the non-negative response variable [1]. The Poisson regression model is a popular count model that assumes the variance equals the mean (equi-dispersed). Count variables can occasionally show over- or under-dispersion, meaning that the variance is either higher than the mean or lower than the mean; as a result, the Poisson model produced inaccurate results. Therefore, when count data are over- or under-dispersed, the Poisson model is substituted with the negative binomial, Conway–Maxwell–Poisson, or Poisson–Inverse-Gaussian (PIG) models, among others [2,3,4].

Heavy-tailed count data are prevalent in various disciplines, including biology, computer science, actuarial science, electronic engineering, and medical research [5,6]. These datasets are characterized by a predominance of values close to zero, accompanied by a small proportion of exceptionally large integer values. Effectively modeling such data requires a distribution that can accommodate both the heavy tail and the concentration of smaller values. One such model is the PIG distribution, a special case of the Sichel distribution with two parameters. Like the negative binomial (NB) distribution, the PIG model can be expressed as a mixture; however, while the NB distribution assumes a gamma mixing component, the PIG distribution is derived from a Poisson and inverse-Gaussian mixture [7,8]. This distinction allows the PIG model to capture heavy tails and high kurtosis, making it a more flexible alternative to the NB distribution, particularly for datasets with a high initial peak and right-skewed distributions [9,10].

The PIG Maximum Likelihood Estimator (PIGMLE) is commonly used to estimate the parameters of the PIG regression model. One significant drawback of PIGMLE is its susceptibility to unreliable inference and predictions in multicollinearity, as the high variance in regression estimates can lead to instability and reduced accuracy [11].

To address the challenges posed by multicollinearity, researchers have developed alternative estimators that introduce a controlled bias to stabilize estimates, thereby mitigating the adverse effects [12]. Several biased estimators have been proposed for linear regression models, including the James–Stein estimator [13], ridge regression estimator [14,15], Liu and Liu-type estimators [16,17,18], and Kibria–Lukman estimator [19]. These estimators have also been extended to nonlinear regression models, such as gamma regression, to improve estimation efficiency in multicollinearity [20,21,22,23].

Building on the work of Kibria and Lukman [19] and Aladeitan et al. [24], we developed a new way to address multicollinearity in the PIG regression model. The remaining part of this article follows this pattern: Section 2 presents the fundamentals of the PIG regression model, reviews existing estimators, and introduces the PIG-MKL estimators. Section 3 provides a theoretical comparison of the estimators, while Section 4 evaluates their performance through a Monte Carlo simulation study. In Section 5, the proposed estimators are applied to real-world data. Finally, Section 6 summarizes the key findings and conclusions.

2. Methodology

2.1. Poisson–Inverse-Gaussian Regression Model (PIGM)

Holla [25] proposed the PIG distribution as a mixture of the Poisson and inverse-Gaussian distributions. The resulting probability mass function is defined as follows:

$$\mathrm{p}\left(\mathrm{Y}=\mathrm{y}|\mu ,\omega \right)=\sqrt{{\displaystyle \frac{2}{\pi \omega }}}{\displaystyle \frac{e^{{\left(\omega \mu \right)}^{-1}}}{y!}}{\left(\sqrt{2\omega (1+{\displaystyle \frac{1}{2\omega {\mu }^2}})}\right)}^{-\left(y-0.5\right)}{K}_{y-0.5}\left(\sqrt{{\displaystyle \frac{2}{\omega }}(1+{\displaystyle \frac{1}{2\omega {\mu }^2}})}\right),$$

(1)

for $\mathrm{y}$ = 0, 1, 2, …, $\mu >0$ is the mean parameter, $\omega >0$ is the dispersion parameter, $K_{y-0.5}\left(.\right)$ represents the modified Bessel function of the second kind [26]. The mean and variance are $E\left(y\right)=\mu$ and $V\left(y\right)=\mu +{\displaystyle \frac{{\mu }^3}{\omega }}$, respectively. The linear predictor is defined as

$${\mu }_i=\exp \left(x_i^{’}\beta \right) i=\mathrm{1,2},\dots ,n,$$

(2)

where $x_{ij}$ is the matrix of the explanatory variables and $\beta$ is the vector of regression parameters.

The maximum likelihood estimator (MLE) method is widely employed for estimating regression parameters due to its desirable statistical properties, such as consistency, efficiency, and asymptotic normality. This method determines the parameter values that maximize the log-likelihood function, identifying the values that best explain the observed data. For the regression model specified in Equation (1), the corresponding log-likelihood function is formulated as follows:

$$\mathcal{l}\left(\beta ,\omega \mid y_i\right)={\sum }_{i=1}^n\left[{\displaystyle \frac{1}{2}}\mathrm{l}\mathrm{n}\left({\displaystyle \frac{2}{\pi \omega }}\right)+{\left(\omega \mu \right)}^{-1}-\ln (y_i!)-\left(y-0.5\right)\left(\sqrt{2\omega \left(1+{\displaystyle \frac{1}{2\omega {\mu }^2}}\right)}\right)+K_{y-0.5}\left(\sqrt{{\displaystyle \frac{2}{\omega }}(1+{\displaystyle \frac{1}{2\omega {\mu }^2}})}\right)\right]$$

(3)

The partial derivative of the log-likelihood function is given as:

$$S\left(\beta \right)={\displaystyle \frac{\partial \mathcal{l}\left(\beta ,\omega \mid y_i\right)}{\partial {\beta }_j}}=0$$

(4)

The solution to Equation (4) requires numerical methods such as the Newton–Raphson method and Fisher score method [26,27]. The Fisher scoring algorithm is commonly employed for estimating the parameters ${\beta }_j,j=\mathrm{1,2},\dots ,q$. Let ${\widehat{\beta }}^l$ denotes the maximum likelihood estimator after $l$ iterations, then ${\beta }^l$ is given as follows:

$${\widehat{\beta }}^{l+1}={\widehat{\beta }}^l+{\left(I\left({\beta }^l\right)\right)}^{-1}S\left({\beta }^l\right)$$

(5)

where $l$ is the number of iterations until convergence is reached and $I\left({\beta }^l\right)=-E\left({\displaystyle \frac{{\partial }^{2}l\left(\beta \right)}{\partial {\beta }_j{\beta }_h}}\right)$ is the Fisher information matrix. The iterations terminate when ${\widehat{\beta }}^l-{\widehat{\beta }}^{l+1}<ϵ$ where $ϵ$ is a specified small value and usually equals ${10}^{-6}$. The final estimate algorithm form is then combined with iterative reweighted least squares as follows, with a few modifications:

$${\widehat{\beta }}^{PIG-MLE}={\left(X\prime \widehat{W}X\right)}^{-1}\left(X\prime \widehat{W}\varphi \right)$$

(6)

where $\widehat{W}$ is a $\left(n\times n\right)$ diagonal matrix with its diagonal elements ${\widehat{w}}_i={\widehat{\mu }}_i+{\displaystyle \frac{{\mu }_i^3}{\omega }},i=\mathrm{1,2},\dots ,n$ and $\varphi =\mathrm{l}\mathrm{n}{\widehat{\mu }}_i+{\displaystyle \frac{y_i-{\widehat{\mu }}_i}{{\widehat{\mu }}_i+\frac{{\mu }_i^3}{\omega }}}$. The dispersion parameter $\omega$ is defined as follows:

$$\widehat{\omega }={\displaystyle \frac{1}{n-p}}{\sum }_{i=1}^n{\displaystyle \frac{{\left(y_i-{\widehat{\mu }}_i\right)}^2}{Var\left({\widehat{\mu }}_i\right)}}$$

In this study, the matrix mean squared error (MMSE) and scalar mean squared error (SMSE) are primarily used to evaluate the performance of the estimator $\tilde{\tau }$. The MMSE and SMSE are defined as follows:

$$\begin{array}{c}MMSE\left(\tilde{\tau }\right)=\mathrm{c}\mathrm{o}\mathrm{v}\left(\tilde{\tau }\right)+\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left(\tilde{\tau }\right)\prime \mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left(\tilde{\tau }\right)\\ SMSE\left(\tilde{\tau }\right)=\mathrm{t}\mathrm{r}\left[\mathrm{c}\mathrm{o}\mathrm{v}\left(\tilde{\tau }\right)\right]+\mathrm{t}\mathrm{r}\left[\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}{\left(\tilde{\tau }\right)}^{\prime }\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left(\tilde{\tau }\right)\right],\end{array}$$

where $\mathrm{t}\mathrm{r}\left(\cdot \right)$ is the trace operator of a matrix.

The MMSE and the SMSE for the estimators are obtained using spectral decomposition of the estimated weighted information matrix ($X\prime \widehat{W}X)$. Assuming the existence of an orthogonal matrix $\theta$ such that $\theta (X\prime \widehat{W}X)\theta \prime =\Lambda , \mathrm{s}\mathrm{o} X\prime \widehat{W}X=\theta \prime \Lambda \mathsf{\theta }$. Here, $\Lambda =\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\lambda }_j\right)$ contains the ordered eigenvalues ${\lambda }_1\ge {\lambda }_2\ge \dots \ge {\lambda }_q$, we define $Z=X\prime \theta$ and $\alpha =\theta \prime \beta$, then $\theta \left(X\prime \widehat{W}X\right){\theta }^{\prime }=Z^{\prime }Z=\Lambda$. The MMSE and the SMSE for ${\widehat{\beta }}^{PIG-MLE}$ are:

$$MMSE\left({\widehat{\alpha }}^{PIG-MLE}\right)=\widehat{\omega }{\Lambda }^{-1}$$

(7)

$$SMSE\left({\widehat{\alpha }}^{PIG-MLE}\right)=\mathrm{t}\mathrm{r}\left(MMSE\left({\widehat{\alpha }}^{PIG-MLE}\right)\right)=\widehat{\omega }{\sum }_{j=1}^q{\displaystyle \frac{1}{{\lambda }_j}}$$

(8)

PIG-MLE exhibits high variance and instability in multicollinearity, highlighting the need for alternative estimators. We discuss the alternative methods in the next Section.

2.2. Biased Estimators

When multicollinearity is found in the data, corrective measures ought to be implemented to mitigate its effects. Multicollinearity poses a serious threat to the estimates of the regression coefficients [28,29], as it can lead to inflated variances of the estimated parameters. Consequently, the precision of these estimates is reduced. One approach to addressing multicollinearity is removing highly correlated regressors. However, an alternative is to retain all regressors and employ a biased estimator rather than the maximum likelihood estimator, which may offer advantages in certain contexts.

Biased estimators have been proposed to increase the accuracy of the parameter estimate in the model when multicollinearity exists, especially when the parameter estimation is the focus of the regression analysis. Following the work of James and Stein [13], Ashraf et al. [4] extended the James–Stein estimator to the Poisson–Inverse-Gaussian (PIG) regression model as:

$${\widehat{\beta }}^{PIG-JSE}=c{\widehat{\beta }}^{PIG-MLE}, 0<c<1$$

(9)

where

$$c={\displaystyle \frac{{\widehat{\beta }}^{PIG-MLE}\prime {\widehat{\beta }}^{PIG-MLE}}{{{\widehat{\beta }}^{PIG-MLE}}^{\prime {\widehat{\beta }}^{PIG-MLE}}+\widehat{\psi }\mathrm{t}\mathrm{r}\left(\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\beta }}^{PIG-MLE}\right)\right)}}·$$

The MMSE and SMSE for ${\widehat{\beta }}^{PIG-JSE}$ are defined as follows:

$$MMSE\left({\widehat{\alpha }}^{PIG-JSE}\right)=c^2\widehat{\omega }{\Lambda }^{-1}+\left(c-1\right)\alpha \prime \alpha \left(c-1\right)$$

(10)

$$SMSE\left({\widehat{\alpha }}^{PIG-JSE}\right)=c^2\widehat{\omega }{\sum }_{j=1}^q{\displaystyle \frac{1}{{\lambda }_j}}+{\left(c-1\right)}^2{\sum }_{j=1}^q{\alpha }_j^2$$

(11)

Hoerl and Kennard [14] developed the ridge estimator to address multicollinearity in the linear regression model. Batool et al. [11] extended the ridge regression estimator to the Poisson–Inverse-Gaussian (PIG) regression model as:

$${\widehat{\beta }}^{PIG-RRE}={\Lambda }_{k^{+}}^{-1}\left(X\prime \widehat{W}X\right){\widehat{\beta }}^{PIG-MLE}, k>0$$

(12)

where ${{\Lambda }_{k^{+}}^{-1}=\left(X\prime \widehat{W}X+kI\right)}^{-1}$.

The MMSE and SMSE for ${\widehat{\beta }}^{PIG-RRE}$ are defined as follows:

$$MMSE\left({\widehat{\alpha }}^{PIG-RRE}\right)=\widehat{\omega }{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}+k^2{\Lambda }_{k^{+}}^{-1}\alpha \prime \alpha {\Lambda }_{k^{+}}^{-1}$$

(13)

$$SMSE\left({\widehat{\alpha }}^{PIG-RRE}\right)=\widehat{\omega }{\sum }_{j=1}^q{\displaystyle \frac{{\lambda }_j}{{\left({\lambda }_j+k\right)}^2}}+k^2{\sum }_{j=1}^q{\displaystyle \frac{{\alpha }_j^2}{{\left({\lambda }_j+k\right)}^2}}$$

(14)

Following Hoerl and Kennard [14], Liu [16] introduced a biased estimator that competes favorably with the ridge at reducing the impact of collinearity. Ashraf et al. [4] proposed the adjusted Liu estimator, which is defined as follows:

$${\widehat{\beta }}^{PIG-LE}={\Lambda }_I^{-1}{\Lambda }_{d^{+}}{\widehat{\beta }}^{PIG-MLE} 0\le d<1$$

(15)

where ${\Lambda }_I^{-1}={\left(X\prime \widehat{W}X+I\right)}^{-1}, {\Lambda }_{d^{+}}=(X\prime \widehat{W}X+dI)$. Hence, the MMSE and SMSE for ${\widehat{\beta }}^{PIG-LE}$ are defined as follows:

$$MMSE\left({\widehat{\alpha }}^{PIG-LE}\right)=\widehat{\omega }{\Lambda }_I^{-1}{\Lambda }_{d^{+}}{\Lambda }^{-1}{\Lambda }_{d^{+}}{\Lambda }_I^{-1}+{(d-1)}^2{\Lambda }_I^{-1}\alpha \prime \alpha {\Lambda }_I^{-1}$$

(16)

$$SMSE\left({\widehat{\alpha }}^{PIG-LE}\right)=\widehat{\omega }{\sum }_{j=1}^q{\displaystyle \frac{{({\lambda }_j+d)}^2}{{\left({\lambda }_j+1\right)}^2{\lambda }_j}}+{(d-1)}^2{\sum }_{j=1}^q{\displaystyle \frac{{\alpha }_j^2}{{\left({\lambda }_j+1\right)}^2}}$$

(17)

Based on the research of Özkale and Kaçıranlar [30] and Akram et al. [31], Alrweili [32] introduced a new method for the PIG regression model with two parameters as follows:

$${\widehat{\beta }}^{PIG-TPE}={\Lambda }_{k^{+}}^{-1}{\Lambda }_{kd}{\widehat{\beta }}^{PIG-MLE} 0\le d<1, 0<k$$

(18)

where ${\Lambda }_{kd}=(X\prime \widehat{W}X+kdI)$. Hence, the MMSE and SMSE for ${\widehat{\beta }}^{PIG-TPE}$ are defined as follows:

$$MMSE\left({\widehat{\alpha }}^{PIG-TPE}\right)=\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{kd}{\Lambda }^{-1}{\Lambda }_{kd}{\Lambda }_{k^{+}}^{-1}+{(d-1)}^2{k}^2{\Lambda }_{k^{+}}^{-1}\alpha \prime \alpha {\Lambda }_{k^{+}}^{-1}$$

(19)

$$SMSE\left({\widehat{\alpha }}^{PIG-TPE}\right)=\widehat{\omega }{\sum }_{j=1}^q{\displaystyle \frac{{({\lambda }_j+kd)}^2}{{\left({\lambda }_j+k\right)}^2{\lambda }_j}}+{(d-1)}^2{k}^2{\sum }_{j=1}^q{\displaystyle \frac{{\alpha }_j^2}{{\left({\lambda }_j+k\right)}^2}}·$$

(20)

2.3. Suggested Biased Estimators

In this paper, we present a novel biased estimator that expands on the Kibria–Lukman estimator ${\widehat{\beta }}^{PIG-KLE}$. Firstly, the Kibria–Lukman estimator was developed especially for the linear regression model by Kibria and Lukman [19], the suggested ${\widehat{\beta }}^{PIG-KLE}$ to the PIG regression model can be obtained as

$${\widehat{\beta }}^{PIG-KLE}={\Lambda }_{k^{+}}^{-1}{\Lambda }_k^{-}{\widehat{\beta }}^{PIG-MLE} k>0$$

(21)

where ${\Lambda }_k^{-}=\left(X\prime \widehat{W}X-kI\right)$. Thus, the MMSE and SMSE of ${\widehat{\beta }}^{PIG-KLE}$ is given by

$$MMSE\left({\widehat{\alpha }}^{PIG-KLE}\right)=\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_k^{-}{\Lambda }^{-1}{\Lambda }_k^{-}{\Lambda }_{k^{+}}^{-1}+4k^2{\Lambda }_{k^{+}}^{-1}\alpha \prime \alpha {\Lambda }_{k^{+}}^{-1}$$

(22)

$$SMSE\left({\widehat{\alpha }}^{PIG-KLE}\right)=\widehat{\omega }{\sum }_{j=1}^q{\displaystyle \frac{{({\lambda }_j-k)}^2}{{\left({\lambda }_j+k\right)}^2{\lambda }_j}}+4k^2{\sum }_{j=1}^q{\displaystyle \frac{{\alpha }_j^2}{{\left({\lambda }_j+k\right)}^2}}$$

(23)

Aladeitan et al. [24] introduced the modified Kibria–Lukman estimator for the Poisson regression model. We proposed this method in this study because it dominates the estimators we reviewed. Thus, ${\widehat{\beta }}^{PIG-\mathrm{M}KLE}$ is given by:

$${\widehat{\beta }}^{PIG-MKLE}={\Lambda }_{k^{+}}^{-1}{\Lambda }_k^{-}{\widehat{\beta }}^{PIG-RRE} , k>0$$

(24)

where ${{\Lambda }_{k^{-}}^{-1}=\left(X\prime \widehat{W}X-kI\right)}^{-1}$ and ${\Lambda }_{k^{+}}^{-1}$ as defined before, then:

$$MMSE\left({\widehat{\alpha }}^{PIG-\mathrm{M}KLE}\right)=\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}+k^2{\Lambda }_{k^{+}}^{-2}(3\Lambda +kI)\alpha \prime \alpha (3\Lambda +kI){\Lambda }_{k^{+}}^{-2}$$

(25)

$$SMSE\left({\widehat{\alpha }}^{PIG-\mathrm{M}KLE}\right)=\widehat{\omega }{\sum }_{j=1}^q{\displaystyle \frac{{{\lambda }_j({\lambda }_j-k)}^2}{{\left({\lambda }_j+k\right)}^4}}+k^2{\sum }_{j=1}^q{\displaystyle \frac{{(3{\lambda }_j+k)}^2{\alpha }_j^2}{{\left({\lambda }_j+k\right)}^4}}$$

(26)

3. Theoretical Comparisons Between Estimators

For a novel estimator to be considered a significant contribution, it must demonstrate clear advantages over existing methodologies. A rigorous theoretical framework is essential for establishing its superiority, providing a foundation for comparative analysis. Theoretical investigations enable a precise understanding of the conditions under which the new estimator outperforms or underperforms relative to conventional approaches. This, in turn, aids practitioners in determining when to adopt the new estimator and when traditional methods remain preferable.

Lemma 1. 

Let  $B$ be a positive definite matrix, $\zeta$ be a vector of nonzero constants and $\nu$ be a positive constant, then $\nu B-\zeta \zeta ’>0$ if and only if   ${\zeta }^{’}{B}^{-1} \zeta <\nu$ [33].

Definition 1. 

Let  ${\widehat{\theta }}_1, {\widehat{\theta }}_2$be two estimators of $\theta$, the estimator ${\widehat{\theta }}_1$ is superior to the estimator ${\widehat{\theta }}_2$ in the sense of MMSE criterion, if and only if

$$∆\left({\widehat{\theta }}_1,{\widehat{\theta }}_2\right)=MMSE\left({\widehat{\theta }}_1\right)-MMSE\left({\widehat{\theta }}_2\right)>0$$

Lemma 2. 

Let ${\widehat{\theta }}_1, {\widehat{\theta }}_2$be two estimators of $\theta$, ${\widehat{\theta }}_1=A_{1}y$, and ${\widehat{\theta }}_2=A_{2}y$. Assume that $\psi =cov\left({\widehat{\theta }}_1\right)-cov\left({\widehat{\theta }}_2\right)>0$, where $cov\left({\widehat{\theta }}_1\right), cov\left({\widehat{\theta }}_2\right)$represent the covariance matrices of the estimators  ${\widehat{\theta }}_1, {\theta }_2$, respectively. Then,

$$\begin{array}{c}∆\left({\widehat{\theta }}_1,{\widehat{\theta }}_2\right)=MMSE\left({\widehat{\theta }}_1\right)-MMSE\left({\widehat{\theta }}_2\right)=cov\left({\widehat{\theta }}_1\right)+a_1{a}_1^{\prime }-cov\left({\widehat{\theta }}_2\right)-a_2{a}_2^{\prime }\\ ∆\left({\widehat{\theta }}_1,{\widehat{\theta }}_2\right)=\psi +a_1{a}_1^{\prime }-a_2{a}_2^{\prime }>0\end{array}$$

if and only if

$$a_2\prime \left(\psi +a_1{a}_1\prime \right)a_2<1$$

where $a_1,a_2$ denote the bias vectors of the estimators ${\widehat{\theta }}_1, {\widehat{\theta }}_2$, respectively [33,34].

Theorem 1.

The estimator ${\widehat{\alpha }}^{PIG-MKLE}$ is superior to the estimator ${\widehat{\alpha }}^{PIG-MLE}$ in the sense of MMSE criterion, i.e., $MMSE\left({\widehat{\alpha }}^{PIG-MLE}\right)-MMSE\left({\widehat{\alpha }}^{PIG-MKLE}\right)>0$ if and only if

$$\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\alpha }}^{PIG-\mathrm{M}KLE}\right)\prime \left[\widehat{\omega }{\Lambda }^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\right]bias\left({\widehat{\alpha }}^{PIG-\mathrm{M}KLE}\right)<1$$

Proof. 

The difference between $\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-\mathrm{M}LE}\right)$ and $\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-\mathrm{M}KLE}\right)$ is as follows:

$$\begin{array}{c}\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-\mathrm{M}LE}\right)-\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-\mathrm{M}KLE}\right)=\widehat{\omega }{\Lambda }^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\\ \mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-\mathrm{M}LE}\right)-\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MKLE}\right)=\widehat{\omega } \mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}{\left\{{\displaystyle \frac{1}{{\lambda }_j}}-{\displaystyle \frac{{{\lambda }_j({\lambda }_j-k)}^2}{{\left({\lambda }_j+k\right)}^4}}\right\}}_{j=1}^q\end{array}$$

Since $\mathrm{B}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\alpha }}^{PIG-MKLE}\right)\mathrm{B}\mathrm{i}\mathrm{a}\mathrm{s}{\left({\widehat{\alpha }}^{PIG-MKLE}\right)}^{\prime }$ is non-negative definite, then the difference matrix $\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MLE}\right)-\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MKLE}\right)$ is positive definite if and only if

${\left({\lambda }_j+k\right)}^4>{{\lambda }_j^2({\lambda }_j-k)}^2$, for $k>0$. Thus, $\widehat{\omega }{\Lambda }^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}$ is positive definite, which means that ${\widehat{\alpha }}^{PIG-MKLE}$ is better than ${\widehat{\alpha }}^{PIG-\mathrm{M}LE}$ since it has a smaller covariance matrix. □

Theorem 2.

The estimator ${\widehat{\alpha }}^{PIG-MKLE}$ is superior to the estimator ${\widehat{\alpha }}^{PIG-JSE}$ in the sense of MMSE criterion, i.e., $MMSE\left({\widehat{\alpha }}^{PIG-JSE}\right)-MMSE\left({\widehat{\alpha }}^{PIG-MKLE}\right)>0$ if and only if

$$\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\alpha }}^{PIG-MKLE}\right)\prime \left[c^2\widehat{\omega }{\Lambda }^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\right]\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\alpha }}^{PIG-MKLE}\right)<1$$

Proof. 

The difference between $\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-\mathrm{M}LE}\right)$ and $\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MKLE}\right)$ is as follows:

$$\begin{gathered} \mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-JSE}\right)-\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MKLE}\right)=c^2\widehat{\omega }{\Lambda }^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1} \\ \mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-JSE}\right)-\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MKLE}\right)=\widehat{\omega } \mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}{\left\{{\displaystyle \frac{c^2}{{\lambda }_j}}-{\displaystyle \frac{{{\lambda }_j({\lambda }_j-k)}^2}{{\left({\lambda }_j+k\right)}^4}}\right\}}_{j=1}^q \end{gathered}$$

Since $\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\alpha }}^{PIG-MKLE}\right)\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}{\left({\widehat{\alpha }}^{PIG-MKLE}\right)}^{\prime }$ is non-negative definite, then the difference matrix $\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-JSE}\right)-\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MKLE}\right)$ is positive definite if and only if

${c^2\left({\lambda }_j+k\right)}^4>{{\lambda }_j^2({\lambda }_j-k)}^2$, for $k>0 and 0<c<1$. Thus, $c^2\widehat{\omega }{\Lambda }^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}$ is positive definite, which means that ${\widehat{\alpha }}^{PIG-\mathrm{M}KLE}$ is better than ${\widehat{\alpha }}^{PIG-JSE}$ since it has a smaller covariance matrix. □

Theorem 3.

The estimator ${\widehat{\alpha }}^{PIG-MKLE}$ is superior to the estimator ${\widehat{\alpha }}^{PIG-RRE}$ in the sense of MMSE criterion, i.e., $MMSE\left({\widehat{\alpha }}^{PIG-RRE}\right)-MMSE\left({\widehat{\alpha }}^{PIG-MKLE}\right)>0$ if and only if

$$\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\alpha }}^{PIG-MKLE}\right)\prime \left[\widehat{\omega }{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\right]\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\alpha }}^{PIG-MKLE}\right)<1$$

Proof. 

The difference between $\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-RRE}\right)\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MKLE}\right)$ is as follows:

$$\begin{gathered} \mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-RRE}\right)-\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MKLE}\right)=\widehat{\omega }{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1} \\ \mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-RRE}\right)-\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MKLE}\right)=\widehat{\omega } \mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}{\left\{{\displaystyle \frac{{\lambda }_j}{{\left({\lambda }_j+k\right)}^2}}-{\displaystyle \frac{{{\lambda }_j({\lambda }_j-k)}^2}{{\left({\lambda }_j+k\right)}^4}}\right\}}_{j=1}^q \end{gathered}$$

Since $\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\alpha }}^{PIG-MKLE}\right)\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}{\left({\widehat{\alpha }}^{PIG-\mathrm{M}KLE}\right)}^{\prime }$ is non-negative definite, then the difference matrix $\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-RRE}\right)-\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-\mathrm{M}KLE}\right)$ is positive definite if and only if

${\left({\lambda }_j+k\right)}^2>{({\lambda }_j-k)}^2$, for $k>0$. Thus, $\widehat{\omega }{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}$ is positive definite, which means that ${\widehat{\alpha }}^{PIG-\mathrm{M}KLE}$ is better than ${\widehat{\alpha }}^{PIG-RRE}$ since it has a smaller covariance matrix. □

Theorem 4.

The estimator ${\widehat{\alpha }}^{PIG-MKLE}$ is superior to the estimator ${\widehat{\alpha }}^{PIG-RRE}$ in the sense of MMSE criterion, i.e., $MMSE\left({\widehat{\alpha }}^{PIG-LE}\right)-MMSE\left({\widehat{\alpha }}^{PIG-MKLE}\right)>0$ if and only if

$$\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\alpha }}^{PIG-MKLE}\right)\prime \left[\widehat{\omega }{\Lambda }_I^{-1}{\Lambda }_{d^{+}}{\Lambda }^{-1}{\Lambda }_{d^{+}}{\Lambda }_I^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\right]\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\alpha }}^{PIG-MKLE}\right)<1$$

Proof. 

The difference between $cov\left({\widehat{\alpha }}^{PIG-LE}\right)andcov\left({\widehat{\alpha }}^{PIG-MKLE}\right)$ is as follows:

$$\begin{gathered} cov\left({\widehat{\alpha }}^{PIG-LE}\right)-cov\left({\widehat{\alpha }}^{PIG-MKLE}\right)=\widehat{\omega }{\Lambda }_I^{-1}{\Lambda }_{d^{+}}{\Lambda }^{-1}{\Lambda }_{d^{+}}{\Lambda }_I^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1} \\ \mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-LE}\right)-\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MKLE}\right)=\widehat{\omega } \mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}{\left\{{\displaystyle \frac{{({\lambda }_j+d)}^2}{{\left({\lambda }_j+1\right)}^2{\lambda }_j}}-{\displaystyle \frac{{{\lambda }_j({\lambda }_j-k)}^2}{{\left({\lambda }_j+k\right)}^4}}\right\}}_{j=1}^q \end{gathered}$$

Since $\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\alpha }}^{PIG-MKLE}\right)\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}{\left({\widehat{\alpha }}^{PIG-MKLE}\right)}^{\prime }$ is non-negative definite, then the difference matrix $\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-LE}\right)-\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-\mathrm{M}KLE}\right)$ is positive definite if and only if

$${\left({\lambda }_j+k\right)}^4{({\lambda }_j+d)}^2>{{\lambda }_j^2({\lambda }_j-k)}^2{\left({\lambda }_j+1\right)}^2, \mathrm{for} k>0 \mathrm{a}\mathrm{n}\mathrm{d} 0<d<1$$

Thus, $\widehat{\omega }{\Lambda }_I^{-1}{\Lambda }_{d^{+}}{\Lambda }^{-1}{\Lambda }_{d^{+}}{\Lambda }_I^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}$ is positive definite, which means that ${\widehat{\alpha }}^{PIG-\mathrm{M}KLE}$ is better than ${\widehat{\alpha }}^{PIG-LE}$ since it has a smaller covariance matrix. □

Theorem 5.

The estimator ${\widehat{\alpha }}^{PIG-MKLE}$ is superior to the estimator ${\widehat{\alpha }}^{PIG-ILE}$ in the sense of MMSE criterion, i.e., $MMSE\left({\widehat{\alpha }}^{PIG-ILE}\right)-MMSE\left({\widehat{\alpha }}^{PIG-MKLE}\right)>0$ if and only if

$$\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\alpha }}^{PIG-MKLE}\right)\prime \left[\widehat{\omega }{\Lambda }_I^{-1}{\Lambda }_{d^{-}}{\Lambda }^{-1}{\Lambda }_{d^{-}}{\Lambda }_I^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\right]\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\alpha }}^{PIG-MKLE}\right)<1$$

Proof. 

The difference between $\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-ILE}\right)and\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MKLE}\right)$ is as follows

$$\begin{gathered} \mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-ILE}\right)-\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MKLE}\right)=\widehat{\omega }{\Lambda }_I^{-1}{\Lambda }_{d^{-}}{\Lambda }^{-1}{\Lambda }_{d^{-}}{\Lambda }_I^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1} \\ \mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-ILE}\right)-\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MKLE}\right)=\widehat{\omega } \mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}{\left\{{\displaystyle \frac{{({\lambda }_j-d)}^2}{{\left({\lambda }_j+1\right)}^2{\lambda }_j}}-{\displaystyle \frac{{{\lambda }_j({\lambda }_j-k)}^2}{{\left({\lambda }_j+k\right)}^4}}\right\}}_{j=1}^q \end{gathered}$$

Since $\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\alpha }}^{PIG-MKLE}\right)\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}{\left({\widehat{\alpha }}^{PIG-MKLE}\right)}^{\prime }$ is non-negative definite, then the difference matrix $\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-ILE}\right)-\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-\mathrm{M}KLE}\right)$ is positive definite if and only if

$${\left({\lambda }_j+k\right)}^4{({\lambda }_j-d)}^2>{{\lambda }_j^2({\lambda }_j-k)}^2{\left({\lambda }_j+1\right)}^2, \mathrm{for} k>0 \mathrm{a}\mathrm{n}\mathrm{d} 0<d<1$$

Thus, $\widehat{\omega }{\Lambda }_I^{-1}{\Lambda }_{d^{-}}{\Lambda }^{-1}{\Lambda }_{d^{-}}{\Lambda }_I^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}$ is positive definite, which means that ${\widehat{\alpha }}^{PIG-\mathrm{M}KLE}$ is better than ${\widehat{\alpha }}^{PIG-ILE}$ since it has a smaller covariance matrix. □

Theorem 6. 

The estimator ${\widehat{\alpha }}^{PIG-MKLE}$ is superior to the estimator ${\widehat{\alpha }}^{PIG-TPE}$ in the sense of MMSE criterion, i.e., $MMSE\left({\widehat{\alpha }}^{PIG-TPE}\right)-MMSE\left({\widehat{\alpha }}^{PIG-MKLE}\right)>0$ if and only if

$$\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\alpha }}^{PIG-MKLE}\right)\prime \left[\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{kd}{\Lambda }^{-1}{\Lambda }_{kd}{\Lambda }_{k^{+}}^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\right]\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\alpha }}^{PIG-MKLE}\right)<1$$

Proof. 

The difference between $\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-TPE}\right)\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MKLE}\right)$ is as follows:

$$\begin{gathered} \mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-TPE}\right)-\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MKLE}\right)=\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{kd}{\Lambda }^{-1}{\Lambda }_{kd}{\Lambda }_{k^{+}}^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1} \\ \mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-TPE}\right)-\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MKLE}\right)=\widehat{\omega } \mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}{\left\{{\displaystyle \frac{{({\lambda }_j+kd)}^2}{{\left({\lambda }_j+k\right)}^2{\lambda }_j}}-{\displaystyle \frac{{{\lambda }_j({\lambda }_j-k)}^2}{{\left({\lambda }_j+k\right)}^4}}\right\}}_{j=1}^q \end{gathered}$$

Since $\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}\left({\widehat{\alpha }}^{PIG-MKLE}\right)\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}{\left({\widehat{\alpha }}^{PIG-MKLE}\right)}^{\prime }$ is non-negative definite, then the difference matrix $\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-TPE}\right)-\mathrm{c}\mathrm{o}\mathrm{v}\left({\widehat{\alpha }}^{PIG-MKLE}\right)$ is positive definite if and only if

$${\left({\lambda }_j+k\right)}^2{({\lambda }_j+kd)}^2>{{\lambda }_j^2({\lambda }_j-k)}^2, \mathrm{for} k>0 \mathrm{a}\mathrm{n}\mathrm{d} 0<d<1$$

Thus, $\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{kd}{\Lambda }^{-1}{\Lambda }_{kd}{\Lambda }_{k^{+}}^{-1}-\widehat{\omega }{\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}\Lambda {\Lambda }_{k^{+}}^{-1}{\Lambda }_{k^{-}}{\Lambda }_{k^{+}}^{-1}$ is positive definite, which means that ${\widehat{\alpha }}^{PIG-\mathrm{M}KLE}$ is better than ${\widehat{\alpha }}^{PIG-TPE}$ since it has a smaller covariance matrix. □

4. Simulation Study

This Section outlines a Monte Carlo simulation designed to evaluate the performance of the estimators under different levels of multicollinearity and dispersion. The predictors are generated using the following equation:

$$x_{ij}={(1-{\gamma }^2)}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{z}_{ij}+\gamma z_{i,q },i=\mathrm{1,2},\dots ,n, j=\mathrm{1,2},3,\dots ,q$$

(27)

where $z_{ij}$ indicates independent standard normal random numbers, and $\gamma$ panels the degree of correlation among predictors. We examined the following levels of multicollinearity: $\gamma =0.80, 0.90, 0.95 \mathrm{and} 0.99$. The response variable $y_i$ is drawn from the Poisson–Inverse-Gaussian distribution, where ${\mu }_i=\exp \left(x_i^T\beta \right)\mathrm{and}$ $\omega$ represents the dispersion parameter, with $\omega =\mathrm{2,4},6$. The sample sizes are set to $n=30, 50, 100$, and $200$, and the predictors were taken to be $q=4, q=8$ and $q=12$. The regression coefficients were chosen such that ${\beta }^{\prime }\beta =1$ [35]. The performance of the estimators was compared using the estimated mean squared error (MSE) in Equation (28).

$$MSE={\displaystyle \frac{1}{1000}}{\sum }_{r=1}^{1000}{\sum }_{j=1}^p{({\widehat{\beta }}_{rj}-{\beta }_j)}^2$$

(28)

where ${\widehat{\beta }}_{rj}$ denotes the estimate obtained in the $r^{th}$ replication of the simulation, and ${\beta }_j$ is the vector of the true regression parameters. Each simulation is replicated 1000 times. The MixPoissonReg package in R is an explicit tool for fitting and analyzing mixed Poisson regression models, specifically those involving over-dispersed count data [36]. It is constructed to handle models where the response variable follows a Poisson distribution mixed with another distribution to account for over-dispersion. The package supports two common mixed Poisson distributions: the Poisson–Inverse-Gaussian regression and Negative Binomial (NB) regression models.

We summarized the simulation algorithms as follows:

Step (1): Initialize Parameters:

-

Set the sample size $n$.

-

Define the total number of replications of the simulation, $r=1, 2,\dots , 1000$.

-

Specify the number of predictors $p$.

-

Define the true regression coefficients $\beta$.

Step (2): Set the replication counter: Let r = 1.

Step (3): Generate data with varying degrees of correlation using Equation (27).

Step (4): Estimates the parameters using the estimators under study.

Step (5): Evaluate the estimators’ performance using $MSE$, using Equation (28).

Step (6): Iterate Until Completion:

-

Increment the replication counter: r = r + 1.

-

If r = 1000, stop the simulation; otherwise, return to Step 3.

The simulation results are summarized in

Table 1. Estimated MSE values for $q=4$.

$\omega$	$2$				$4$				$6$
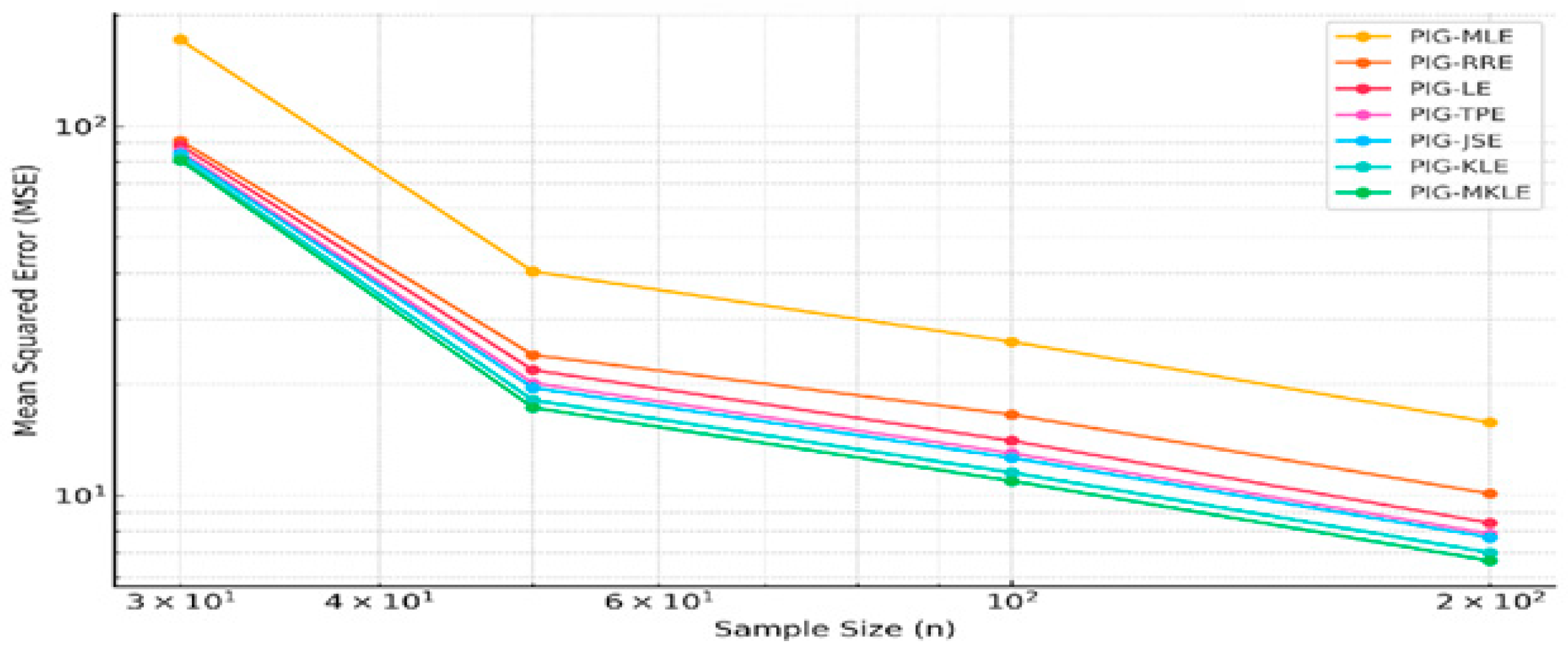
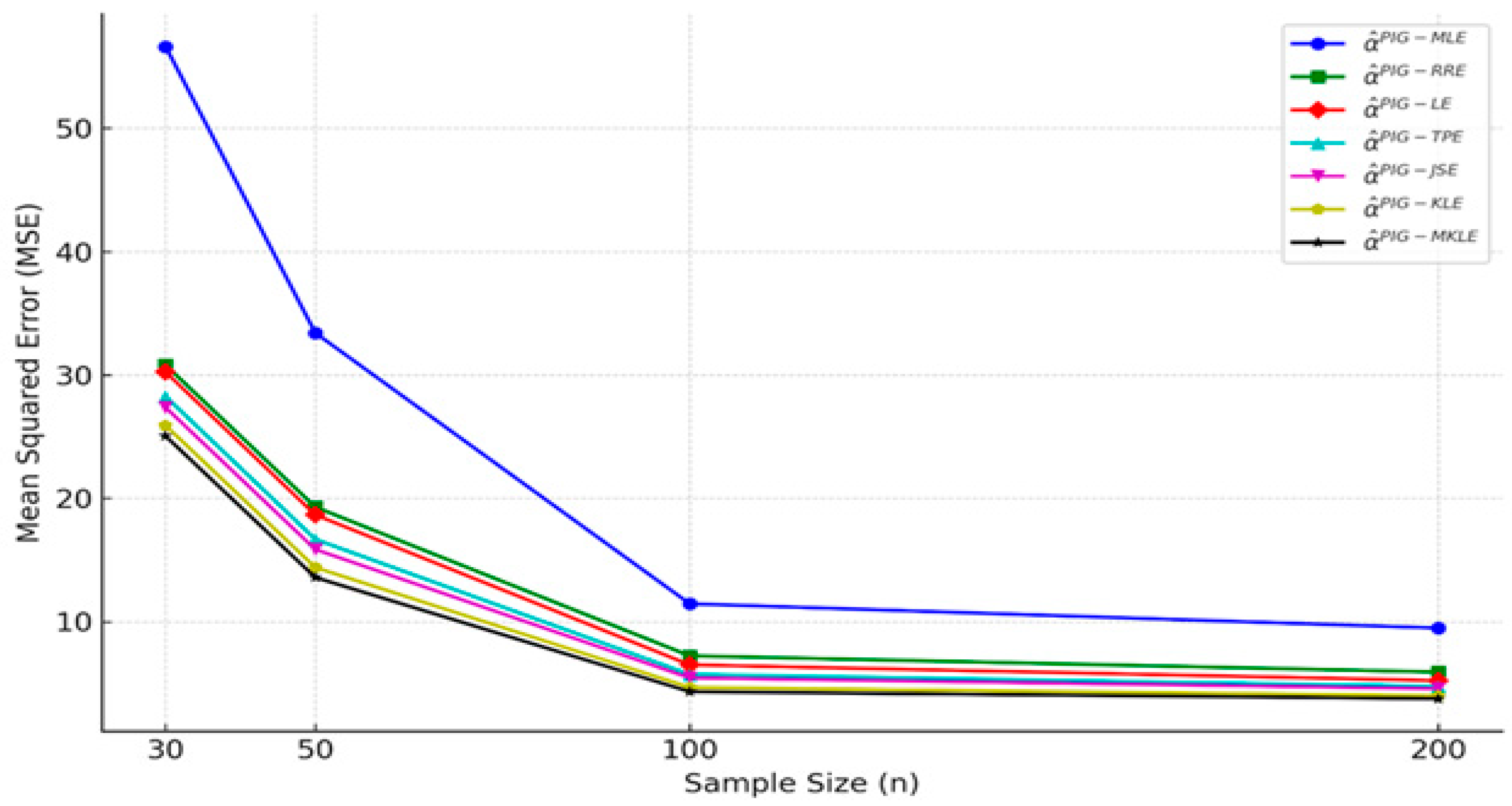
n	30	50	100	200	30	50	100	200	30	50	100	200
	$\gamma =0.8$				$\gamma =0.8$				$\gamma =0.8$
${\widehat{\alpha }}^{PIG-MLE}$	2.563	1.956	1.892	1.814	2.656	1.984	1.960	1.906	2.704	2.007	1.993	1.982
${\widehat{\alpha }}^{PIG-RRE}$	1.347	0.965	0.925	0.919	1.531	0.981	0.957	0.939	1.680	1.000	0.981	0.972
${\widehat{\alpha }}^{PIG-LE}$	1.328	0.975	0.935	0.904	1.524	0.988	0.957	0.925	1.899	1.000	0.990	0.964
${\widehat{\alpha }}^{PIG-JSE}$	1.281	0.958	0.957	0.946	1.327	0.962	0.963	0.960	1.451	1.004	0.986	0.976
${\widehat{\alpha }}^{PIG-TPE}$	1.267	0.982	0.914	0.902	1.294	0.995	0.986	0.929	1.309	1.006	1.000	0.974
${\widehat{\alpha }}^{PIG-KLE}$	1.126	0.952	0.919	0.906	1.251	0.976	0.947	0.914	1.008	1.000	0.963	0.955
${\widehat{\alpha }}^{PIG-MKLE}$	1.096	0.931	0.908	0.901	1.103	0.948	0.947	0.918	1.201	0.965	0.952	0.949
$\gamma =0.9$					$\gamma =0.9$				$\gamma =0.9$
${\widehat{\alpha }}^{PIG-MLE}$	3.933	2.229	1.952	1.895	4.830	2.253	1.993	1.937	4.993	2.714	2.022	2.019
${\widehat{\alpha }}^{PIG-RRE}$	2.268	1.140	0.952	0.921	2.927	1.197	0.977	0.940	3.061	1.289	0.999	0.986
${\widehat{\alpha }}^{PIG-LE}$	2.209	1.150	0.958	0.920	2.900	1.212	0.986	0.938	3.036	1.305	1.003	0.988
${\widehat{\alpha }}^{PIG-JSE}$	1.964	1.134	0.976	0.948	2.411	1.156	0.996	0.968	2.492	1.171	1.011	1.009
${\widehat{\alpha }}^{PIG-TPE}$	1.914	1.136	0.956	0.953	2.298	1.169	1.002	0.976	2.369	1.179	1.015	1.015
${\widehat{\alpha }}^{PIG-KLE}$	1.628	1.024	0.956	0.906	1.913	1.105	0.972	0.940	1.992	1.120	1.003	0.990
${\widehat{\alpha }}^{PIG-MKLE}$	1.549	0.952	0.935	0.902	1.784	1.008	0.945	0.928	1.897	1.699	0.971	0.950
$\gamma =0.95$					$\gamma =0.95$				$\gamma =0.95$
${\widehat{\alpha }}^{PIG-MLE}$	7.203	3.286	2.193	2.130	9.763	4.081	2.380	2.172	10.407	4.932	2.645	2.220
${\widehat{\alpha }}^{PIG-RRE}$	4.251	1.819	1.072	1.038	5.757	2.454	1.104	1.041	6.187	3.045	1.184	1.140
${\widehat{\alpha }}^{PIG-LE}$	4.133	1.805	1.072	1.032	5.603	2.381	1.127	1.041	6.006	2.935	1.205	1.162
${\widehat{\alpha }}^{PIG-JSE}$	3.596	1.642	1.096	1.065	4.873	2.038	1.110	1.061	5.195	2.462	1.210	1.122
${\widehat{\alpha }}^{PIG-TPE}$	3.436	1.614	1.103	1.071	4.650	1.967	1.115	1.098	5.960	2.354	1.125	1.117
${\widehat{\alpha }}^{PIG-KLE}$	2.911	1.367	1.042	1.036	4.118	1.622	1.016	1.075	5.330	1.919	1.113	1.100
${\widehat{\alpha }}^{PIG-MKLE}$	2.732	1.305	1.034	1.032	3.876	1.519	1.100	1.047	4.071	1.779	1.105	1.076
$\gamma =0.99$					$\gamma =0.99$				$\gamma =0.99$
${\widehat{\alpha }}^{PIG-MLE}$	45.884	20.772	7.035	5.806	53.706	25.398	9.405	7.780	56.620	33.407	11.446	9.476
${\widehat{\alpha }}^{PIG-RRE}$	25.701	12.607	4.332	3.484	29.055	15.021	6.001	4.843	30.797	19.288	7.225	5.906
${\widehat{\alpha }}^{PIG-LE}$	24.798	11.718	3.866	3.093	28.652	14.309	5.382	4.212	30.233	18.652	6.495	5.215
${\widehat{\alpha }}^{PIG-TPE}$	22.897	10.367	3.512	2.899	26.800	12.675	4.695	3.884	28.254	16.671	5.713	4.730
${\widehat{\alpha }}^{PIG-JSE}$	22.063	9.816	3.396	2.834	25.978	11.995	4.461	3.766	27.361	15.848	5.433	4.560
${\widehat{\alpha }}^{PIG-KLE}$	20.575	8.621	2.925	2.509	24.672	10.689	3.771	3.310	25.896	14.385	4.662	3.987
${\widehat{\alpha }}^{PIG-MKLE}$	19.771	8.045	2.738	2.381	23.869	10.005	3.485	3.113	25.036	13.575	4.317	3.740

,

Table 2. Estimated MSE values for $q=8$.

$\omega$	$2$				$4$				$6$
n	30	50	100	200	30	50	100	200	30	50	100	200
	$\gamma =0.8$				$\gamma =0.8$				$\gamma =0.8$
${\widehat{\alpha }}^{PIG-MLE}$	6.478	2.036	1.964	1.866	8.074	2.092	1.982	1.918	9.105	2.277	2.010	1.995
${\widehat{\alpha }}^{PIG-RRE}$	3.460	1.012	0.914	0.899	4.491	1.105	0.970	0.910	5.004	1.185	1.000	0.972
${\widehat{\alpha }}^{PIG-LE}$	3.473	1.054	0.947	0.927	4.392	1.081	0.966	0.983	4.908	1.249	0.989	0.985
${\widehat{\alpha }}^{PIG-JSE}$	3.234	1.018	0.943	0.931	4.030	1.046	0.982	0.957	4.545	1.137	1.005	0.999
${\widehat{\alpha }}^{PIG-TPE}$	3.206	1.024	0.953	0.936	3.966	1.055	0.986	0.969	4.492	1.141	1.013	1.002
${\widehat{\alpha }}^{PIG-KLE}$	2.984	0.977	0.924	0.903	3.708	1.002	0.940	0.897	4.218	1.030	0.996	0.983
${\widehat{\alpha }}^{PIG-MKLE}$	2.889	0.956	0.918	0.902	3.587	0.980	0.964	0.959	4.092	0.996	0.985	0.982
$\gamma =0.9$					$\gamma =0.9$				$\gamma =0.9$
${\widehat{\alpha }}^{PIG-MLE}$	16.613	2.844	2.419	2.050	16.705	3.951	2.891	2.086	20.355	4.371	3.504	2.093
${\widehat{\alpha }}^{PIG-RRE}$	9.046	1.404	1.144	0.996	9.316	2.132	1.436	0.997	11.408	2.515	1.818	0.998
${\widehat{\alpha }}^{PIG-LE}$	8.804	1.501	1.238	1.013	8.978	2.168	1.531	1.039	11.002	2.473	1.907	1.050
${\widehat{\alpha }}^{PIG-JSE}$	8.291	1.421	1.209	1.025	8.337	1.973	1.444	1.043	10.158	2.182	1.750	1.046
${\widehat{\alpha }}^{PIG-TPE}$	8.191	1.430	1.221	1.031	8.191	1.963	1.452	1.052	9.961	2.159	1.749	1.058
${\widehat{\alpha }}^{PIG-KLE}$	7.732	1.304	1.128	1.011	7.788	1.761	1.307	1.017	9.444	1.920	1.544	1.110
${\widehat{\alpha }}^{PIG-MKLE}$	6.495	1.266	1.104	0.990	7.590	1.687	1.264	1.007	9.165	1.832	1.478	1.011
$\gamma =0.95$					$\gamma =0.95$				$\gamma =0.95$
${\widehat{\alpha }}^{PIG-MLE}$	28.105	5.684	4.395	2.131	42.217	9.106	6.266	2.429	47.142	10.507	8.554	2.752
${\widehat{\alpha }}^{PIG-RRE}$	15.747	3.182	2.341	1.036	23.076	5.348	3.593	1.154	25.580	6.252	5.118	1.307
${\widehat{\alpha }}^{PIG-LE}$	14.869	3.158	2.349	1.049	22.415	5.082	3.438	1.226	24.810	5.924	4.741	1.423
${\widehat{\alpha }}^{PIG-JSE}$	14.026	2.838	2.195	1.065	21.067	4.545	3.128	1.214	23.524	5.244	4.270	1.375
${\widehat{\alpha }}^{PIG-TPE}$	13.800	2.803	2.186	1.073	20.672	4.458	3.088	1.224	23.169	5.111	4.190	1.386
${\widehat{\alpha }}^{PIG-KLE}$	13.139	2.473	1.951	1.015	19.837	3.996	2.699	1.160	22.349	4.593	3.678	1.274
${\widehat{\alpha }}^{PIG-MKLE}$	12.786	2.353	1.867	1.006	19.334	3.799	2.550	1.143	21.874	4.361	3.468	1.242
$\gamma =0.99$					$\gamma =0.99$				$\gamma =0.99$
${\widehat{\alpha }}^{PIG-MLE}$	171.420	40.414	26.096	15.786	225.455	58.279	39.836	20.008	247.230	71.848	56.252	21.255
${\widehat{\alpha }}^{PIG-RRE}$	91.340	24.024	16.571	10.114	117.311	33.219	24.659	11.340	127.790	42.226	33.631	13.572
${\widehat{\alpha }}^{PIG-LE}$	88.722	21.862	14.071	8.431	115.666	31.413	21.324	10.849	126.440	38.562	30.151	11.425
${\widehat{\alpha }}^{PIG-TPE}$	85.541	20.168	13.024	7.879	112.503	29.082	19.880	9.985	123.360	35.854	28.071	10.608
${\widehat{\alpha }}^{PIG-JSE}$	84.340	19.572	12.662	7.710	111.383	27.246	19.310	9.671	122.330	34.748	28.246	10.338
${\widehat{\alpha }}^{PIG-KLE}$	82.218	18.115	11.545	7.010	109.448	25.429	17.864	9.072	120.550	32.492	26.535	9.401
${\widehat{\alpha }}^{PIG-MKLE}$	80.789	17.299	10.949	6.661	108.081	24.335	17.036	8.704	119.240	31.090	25.499	8.912

and

Table 3. Estimated MSE values for $q=12$.

$\omega$	$2$				$4$				$6$
n	30	50	100	200	30	50	100	200	30	50	100	200
	$\gamma =0.8$				$\gamma =0.8$				$\gamma =0.8$
${\widehat{\alpha }}^{PIG-MLE}$	18.197	4.901	2.011	1.871	22.662	10.091	2.027	1.904	29.077	11.399	2.300	1.985
${\widehat{\alpha }}^{PIG-RRE}$	9.630	2.537	0.956	0.915	12.012	5.592	0.977	0.937	15.433	6.476	1.057	0.995
${\widehat{\alpha }}^{PIG-LE}$	9.433	2.626	1.008	0.927	11.796	5.456	1.037	0.941	15.057	6.189	1.201	0.981
${\widehat{\alpha }}^{PIG-JSE}$	9.080	2.447	1.005	0.935	11.309	5.037	1.013	0.952	14.510	5.689	1.149	0.992
${\widehat{\alpha }}^{PIG-TPE}$	9.008	2.446	1.014	0.940	11.212	4.989	1.025	0.955	14.402	5.627	1.162	0.995
${\widehat{\alpha }}^{PIG-KLE}$	8.819	2.276	0.972	0.929	10.910	4.684	0.993	0.947	14.108	5.287	1.080	0.980
${\widehat{\alpha }}^{PIG-MKLE}$	8.713	2.212	0.937	0.925	10.755	4.545	0.986	0.936	13.942	5.123	1.055	0.950
$\gamma =0.9$					$\gamma =0.9$				$\gamma =0.9$
${\widehat{\alpha }}^{PIG-MLE}$	36.880	10.744	2.778	1.998	38.850	22.156	3.691	2.015	39.860	27.797	5.009	2.025
${\widehat{\alpha }}^{PIG-RRE}$	19.263	6.032	1.285	0.971	20.521	12.565	1.809	0.977	21.356	15.929	2.601	0.996
${\widehat{\alpha }}^{PIG-LE}$	19.008	5.809	1.437	0.998	20.117	11.935	1.960	1.000	20.788	15.050	2.696	1.018
${\widehat{\alpha }}^{PIG-JSE}$	18.403	5.362	1.388	0.999	19.386	11.057	1.843	1.007	19.890	13.871	2.501	1.012
${\widehat{\alpha }}^{PIG-TPE}$	18.265	5.304	1.401	1.008	19.206	10.882	1.853	1.013	19.680	13.643	2.504	1.023
${\widehat{\alpha }}^{PIG-KLE}$	17.975	4.907	1.307	0.981	18.810	10.248	1.689	0.986	19.163	12.921	2.263	0.997
${\widehat{\alpha }}^{PIG-MKLE}$	17.574	4.729	1.277	0.945	17.799	9.924	1.631	0.948	18.879	12.544	2.173	0.975
$\gamma =0.95$					$\gamma =0.95$				$\gamma =0.95$
${\widehat{\alpha }}^{PIG-MLE}$	66.641	30.079	6.278	2.287	85.710	46.629	9.247	2.635	89.977	57.280	13.434	3.068
${\widehat{\alpha }}^{PIG-RRE}$	34.588	17.375	3.445	1.089	45.226	26.555	5.347	1.292	46.842	32.207	7.943	1.396
${\widehat{\alpha }}^{PIG-LE}$	34.213	16.021	3.363	1.155	44.240	24.953	5.020	1.357	46.258	30.496	7.269	1.599
${\widehat{\alpha }}^{PIG-JSE}$	33.254	15.010	3.134	1.143	42.769	23.269	4.616	1.317	44.898	28.583	6.705	1.533
${\widehat{\alpha }}^{PIG-TPE}$	32.980	14.776	3.118	1.155	42.363	22.838	4.559	1.333	44.534	28.072	6.601	1.550
${\widehat{\alpha }}^{PIG-KLE}$	32.492	13.972	2.822	1.101	41.555	21.743	4.105	1.238	43.850	26.860	6.023	1.423
${\widehat{\alpha }}^{PIG-MKLE}$	32.165	13.546	2.703	1.046	41.053	21.117	3.906	1.111	43.409	26.149	5.752	1.384
$\gamma =0.99$					$\gamma =0.99$				$\gamma =0.99$
${\widehat{\alpha }}^{PIG-MLE}$	306.507	183.213	56.727	13.293	375.705	254.194	57.365	19.084	383.607	323.779	111.401	24.977
${\widehat{\alpha }}^{PIG-RRE}$	154.971	100.452	34.761	8.242	190.652	135.672	35.063	12.210	197.565	170.258	64.316	15.799
${\widehat{\alpha }}^{PIG-LE}$	154.611	95.371	30.083	7.086	189.952	131.931	30.675	10.177	194.846	167.306	58.826	13.420
${\widehat{\alpha }}^{PIG-TPE}$	152.947	91.424	28.308	6.635	187.477	126.844	28.627	9.525	191.421	161.567	55.590	12.465
${\widehat{\alpha }}^{PIG-JSE}$	152.599	89.952	27.650	6.534	186.913	125.012	27.897	9.361	190.396	159.480	54.318	12.212
${\widehat{\alpha }}^{PIG-KLE}$	151.808	87.232	25.980	5.933	185.773	121.917	26.073	8.570	188.554	156.134	51.715	11.151
${\widehat{\alpha }}^{PIG-MKLE}$	151.189	85.386	24.991	5.648	184.901	119.712	25.000	8.179	187.200	153.668	50.016	10.617

.

The performance of the estimators is assessed based on their MSE values across different sample sizes, multicollinearity levels, dispersion parameters, and numbers of predictors. The results presented in Table 1, Table 2 and Table 3 reveal a consistent trend, where the estimator with the lowest MSE is preferred due to its higher estimation accuracy and efficiency. This is supported by Figure 1 and Figure 2. As the dispersion parameter increases from $\omega =2$ to $\omega =4 \mathrm{and} 6$, the MSE also rises. A notable trend across all tables is the decline in MSE as the sample size increases, emphasizing the benefits of larger datasets. This pattern remains consistent across varying levels of multicollinearity and dispersion, indicating that a larger sample size effectively reduces estimator variance and enhances overall performance. Conversely, smaller sample sizes (e.g., $n=30$) result in higher MSEs, particularly in cases of severe multicollinearity (e.g., $\gamma =0.99$) and overdispersion. Under these conditions, the performance differences between estimators become more pronounced, with the proposed estimator demonstrating greater adaptability than its counterparts.

Increasing the number of predictors from q = 4 (Table 1) to q = 12 (Table 3) leads to higher MSE values across all conditions. The superiority of the proposed estimator is particularly evident in smaller sample sizes, where it demonstrates strong resistance to both multicollinearity and dispersion effects. Although the performance gap diminishes as the sample size grows, the proposed estimator dominates the alternatives, underscoring its robustness and efficiency across varying model complexities and data conditions.

5. Real Data Application

We performed a thorough examination of the nut’s dataset in this application, following Hardin and Hilbe’s [7] documentation and Lukman et al.’s [35] recent adoption. The dataset is accessible through the COUNT library in the R program. The data collection, which includes fifty-two observations and four (4) predictors. In particular, the number of cones that squirrels remove is represented by the response variable. The predictors are the number of DBH (diameter at breast height) per plot ($x_1$), mean tree height per plot ($x_2$), canopy closure (as a percentage) ($x_3$), and standardized number of trees per plot ($x_4$). To determine which model was best suited for the dataset, we fitted the Poisson regression model (PRM), negative binomial regression model (NBRM), and Poisson–Inverse-Gaussian regression model (PIGMR). The results are shown in

Table 4. Model Adequacy Check.

Metrics	$\mathit{P}\mathit{R}\mathit{M}$	$\mathit{N}\mathit{B}\mathit{R}\mathit{M}$	$\mathit{P}\mathit{I}\mathit{G}\mathit{R}\mathit{M}$
Residual Variance	661.2	661.2	0.5498
AIC	873.1	397.9	406.0

. The PIGRM provides the best fit based on residual variance, as it has significantly smaller errors. In terms of AIC, NBRM is marginally better than PIGRM, but the substantial reduction in residual variance for the PIGRM suggests that it may offer a better model despite the slightly higher AIC. PRM performs worse on both metrics, making it the least desirable model. Furthermore, over-dispersion was discovered in the model using the dispersion test, which made the Poisson regression model inappropriate for this dataset [35].

Furthermore, the estimated variance inflation factors are 40.89, 39.61, 16.332, and 4.474, which clearly show that the model contains correlated regressors. This leads to both multicollinearity and over-dispersion in the model.

Table 5. Squirrel dataset estimated regression coefficients.

Coef.	${\widehat{\mathit{\alpha }}}^{\mathit{P}\mathit{I}\mathit{G}-\mathit{M}\mathit{L}\mathit{E}}$	${\widehat{\mathit{\alpha }}}^{\mathit{P}\mathit{I}\mathit{G}-\mathit{R}\mathit{R}\mathit{E}}$	${\widehat{\mathit{\alpha }}}^{\mathit{P}\mathit{I}\mathit{G}-\mathit{L}\mathit{E}}$	${\widehat{\mathit{\alpha }}}^{\mathit{P}\mathit{I}\mathit{G}-\mathit{J}\mathit{S}\mathit{E}}$	${\widehat{\mathit{\alpha }}}^{\mathit{P}\mathit{I}\mathit{G}-\mathit{T}\mathit{P}\mathit{E}}$	${\widehat{\mathit{\alpha }}}^{\mathit{P}\mathit{I}\mathit{G}-\mathit{K}\mathit{L}\mathit{E}}$	${\widehat{\mathit{\alpha }}}^{\mathit{P}\mathit{I}\mathit{G}-\mathit{M}\mathit{K}\mathit{L}\mathit{E}}$
$x1$	0.5436	0.0001	0.1434	0.0010	−0.0296	0.0430	−0.0001
$x2$	0.4398	0.0002	0.1440	0.0008	0.2138	0.0348	−0.0002
$x3$	−0.3814	−0.0002	−0.1318	−0.0007	−0.2544	−0.0302	0.0002
$x4$	0.8503	0.0001	0.2116	0.0016	−0.1302	0.0672	−0.0001
SMSE	987.4608	18.0435	17.5653	1.3558	171.9145	7.3136	1.3578
PMSE	453.3143	446.1027	448.5152	446.1133	450.5399	446.6592	446.0973
PMAE	16.1498	15.9001	15.9847	15.9005	16.0511	15.9198	15.8999

displays the estimated regression coefficients derived from the various estimators examined in this study. We assessed the estimator’s performance using the SMSE, prediction mean squared error (PMSE), and prediction mean absolute error (PMAE). The dataset was randomly split into 80% training and 20% test sets. We estimated the model parameters on the training set and calculated the performance criteria on the test set. The results revealed that ${\widehat{\alpha }}^{PIG-MLE}$ exhibits poor performance in handling multicollinearity within the PIG regression model, as evidenced by its high SMSE, PMSE, and PMAE. The proposed estimator is the most preferred among the shrinkage estimators, achieving lower PMSE and PMAE.

6. Conclusions

The PIG regression model is widely used for modeling count data with overdispersion. The model regression estimates are mostly estimated using the PIGMLE. However, multicollinearity is a threat to the performance of PIGMLE. To address this issue, we proposed a novel biased estimator: the modified Kibria–Lukman estimator (${\widehat{\alpha }}^{PIG-MKLE})$. Through theoretical analysis and extensive simulations, we evaluate their performance. The results demonstrate that the proposed estimator exhibits superior efficiency, as evidenced by a reduced MSE compared to traditional approaches. These findings suggest that our proposed estimators provide a more robust alternative for PIG regression in the presence of multicollinearity.

An example study was conducted, examining squirrel behavior and forest characteristics across different plots in Abernethy Forest, Scotland. The proposed estimator has the lowest PMSE and PMAE among the shrinkage estimators. The findings further support the superiority of the proposed method in handling multicollinearity while maintaining predictive accuracy. Our findings enhance the existing research on count regression models and provide valuable analytical tools for researchers across various disciplines seeking robust estimation methods. In future studies, we aim to enhance the effectiveness of these estimators by incorporating techniques such as partial least squares and principal component regression.