1. Introduction
The rapid advancement of engineering and technological fields has significantly transformed the landscape of design and problem-solving. As industries push the boundaries of innovation, they face increasingly intricate and multifaceted design problems that demand not only creativity but also rigorous analytical methods [
1]. Traditional optimization techniques often fall short in addressing these complex challenges due to the inherent nature of modern design problems. These problems are frequently characterized by high dimensionality, where the number of variables or parameters involved is vast, leading to a highly intricate solution space [
2]. Additionally, the non-linearity of these problems means that the relationships between variables are not straightforward or proportional, further complicating the optimization process. Moreover, multiple constraints, such as resource limitations, regulatory requirements, and environmental considerations, add layers of complexity to the problem [
3].
To effectively tackle such challenges, there is a growing need for advanced optimization algorithms that can navigate these complexities with precision and efficiency. This is where hybrid optimization methods come into play. These methods represent a sophisticated approach that merges the strengths of various algorithms, each contributing its unique capabilities to the overall process [
4]. For instance, hybrid methods may combine global optimization techniques, which are adept at exploring large and complex solution spaces, with local optimization techniques, which excel at fine-tuning solutions within a specific region of the search space. By integrating these approaches, hybrid optimization methods can offer a more balanced and robust solution strategy, addressing both the broad exploration of potential solutions and the detailed refinement of those solutions [
5].
The power of hybrid optimization lies in its ability to enhance both performance and reliability. Performance is improved by combining different algorithms that can adapt to various aspects of the problem and avoid common pitfalls, such as becoming trapped in local optima [
6]. Reliability is achieved by leveraging the complementary strengths of the algorithms, leading to more consistent and dependable results. This holistic approach not only improves the efficiency of finding optimal solutions but also ensures that the solutions are more applicable and practical in real-world scenarios. As engineering and technological fields continue to evolve, the role of hybrid optimization methods becomes increasingly crucial in addressing the sophisticated and dynamic nature of modern design problems [
7].
In this paper, we introduce a hybrid optimization framework called JADEDO, designed to address both benchmark-driven and practical optimization challenges. JADEDO combines the strengths of two established metaheuristics, namely, (1) dandelion optimizer (DO): Inspired by the dispersal of dandelion seeds, DO employs a sequence of stages (dispersal, propagation, and competition) that collectively push the search process toward promising regions while maintaining the potential to escape local optima. (2) Adaptive differential evolution (JADE): Known for its adaptive mutation strategies and crossover operators, JADE dynamically adjusts parameter settings (e.g., mutation factor and crossover rate) to balance exploration and exploitation over the course of the search.
By merging these two paradigms, JADEDO leverages DO’s robust dispersal mechanisms to broaden global exploration, while JADE’s adaptive operators refine local searches effectively. The resultant synergy endows JADEDO with heightened flexibility and robustness across different problem landscapes—unimodal, multimodal, and hybrid.
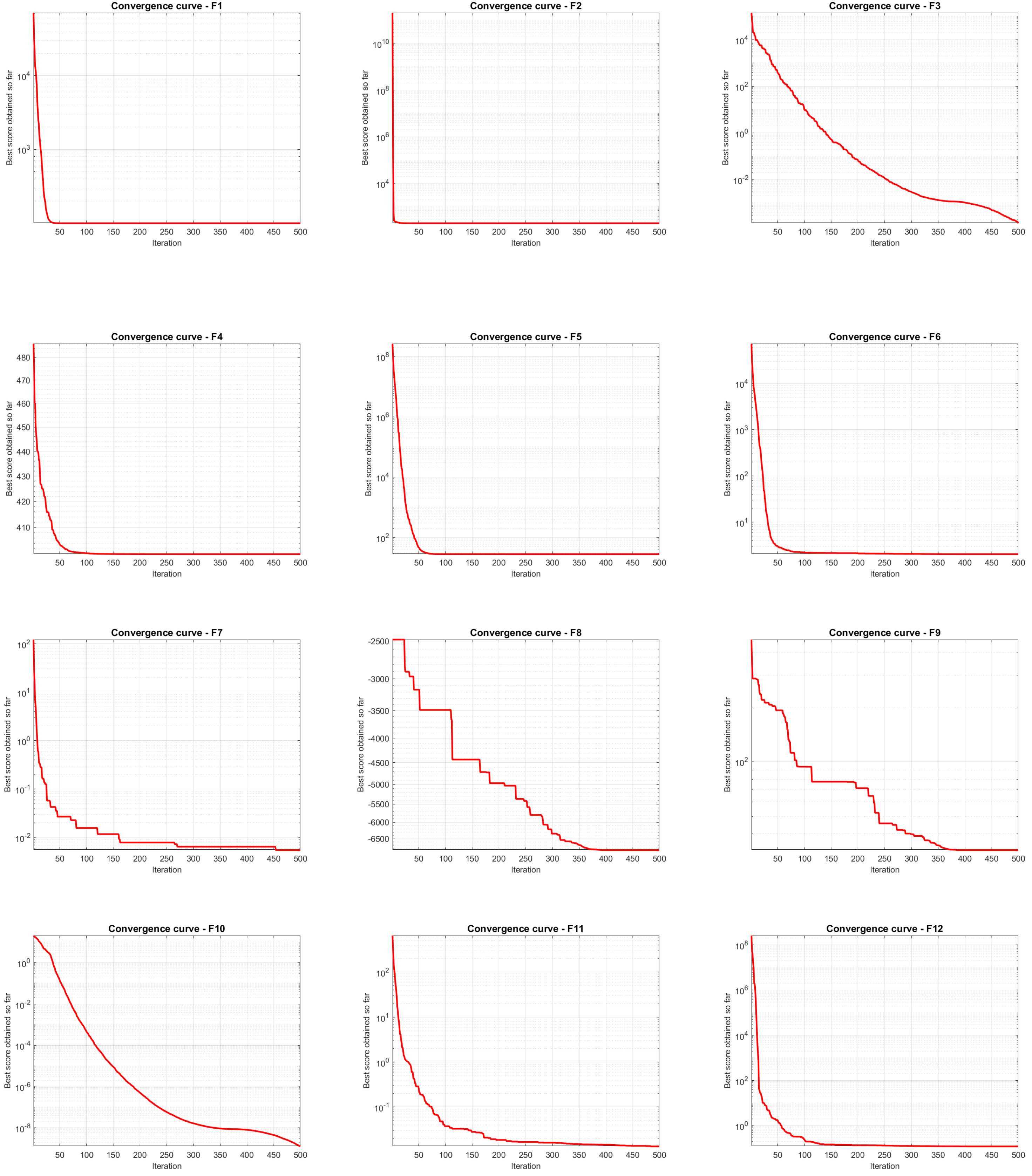
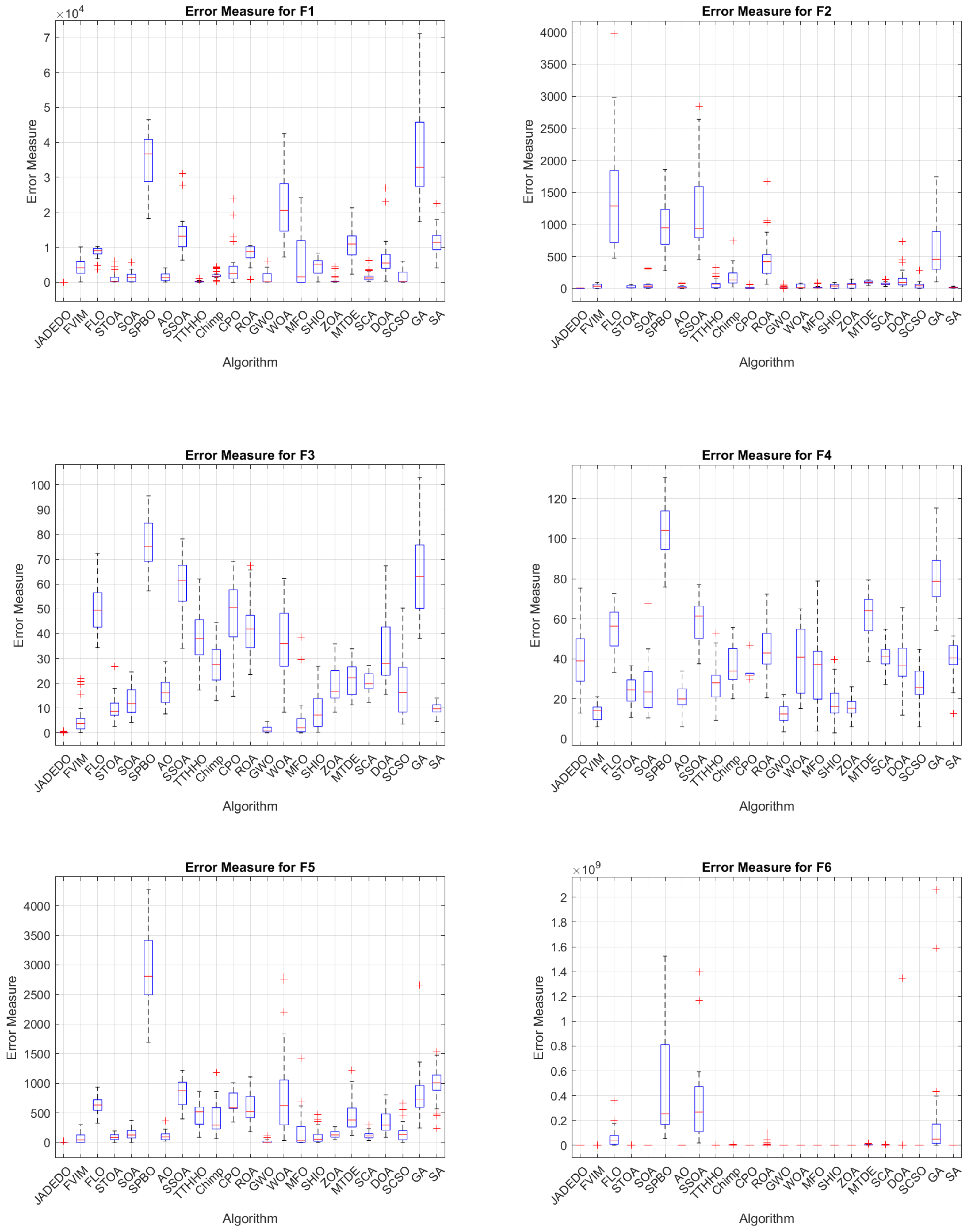
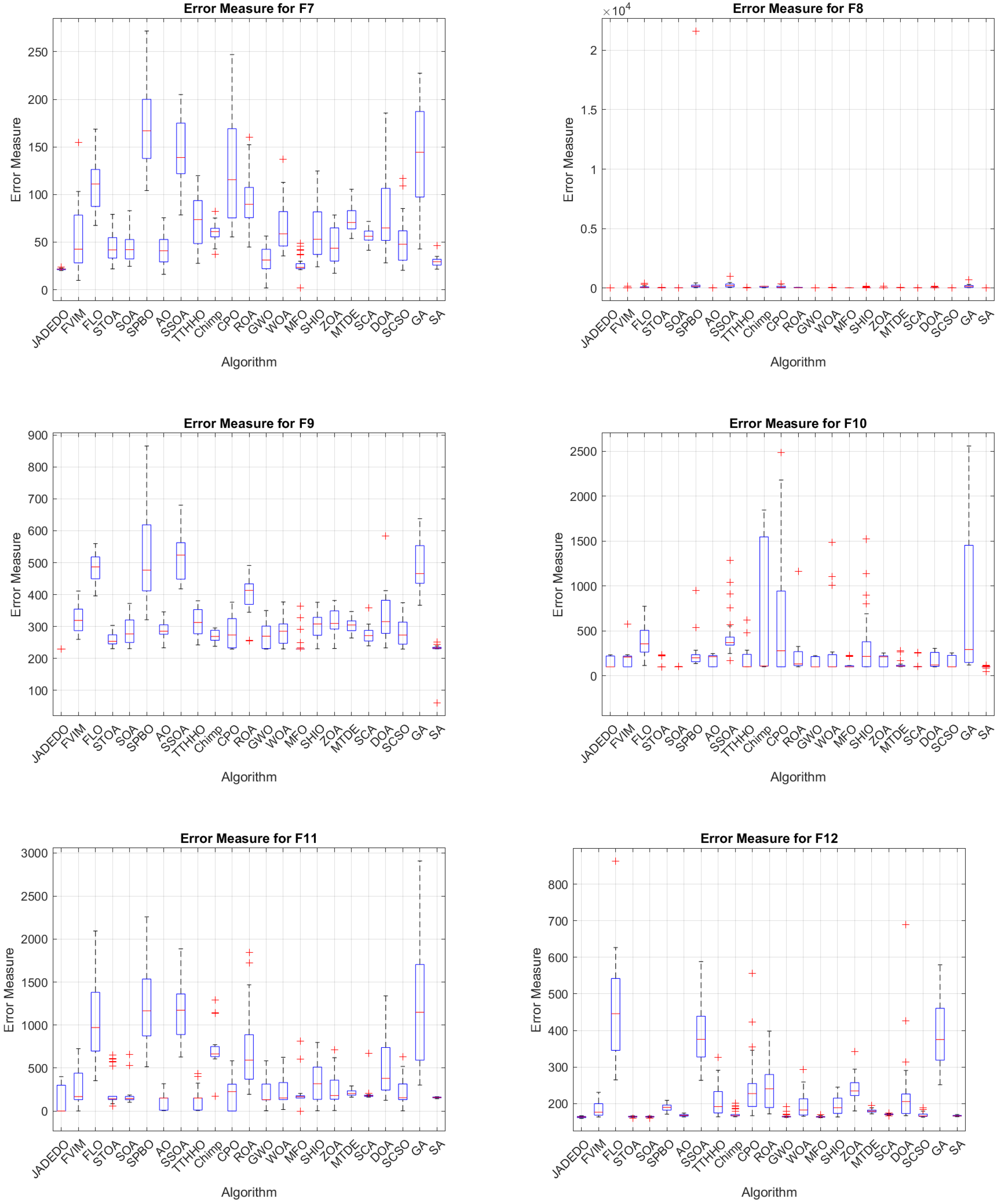
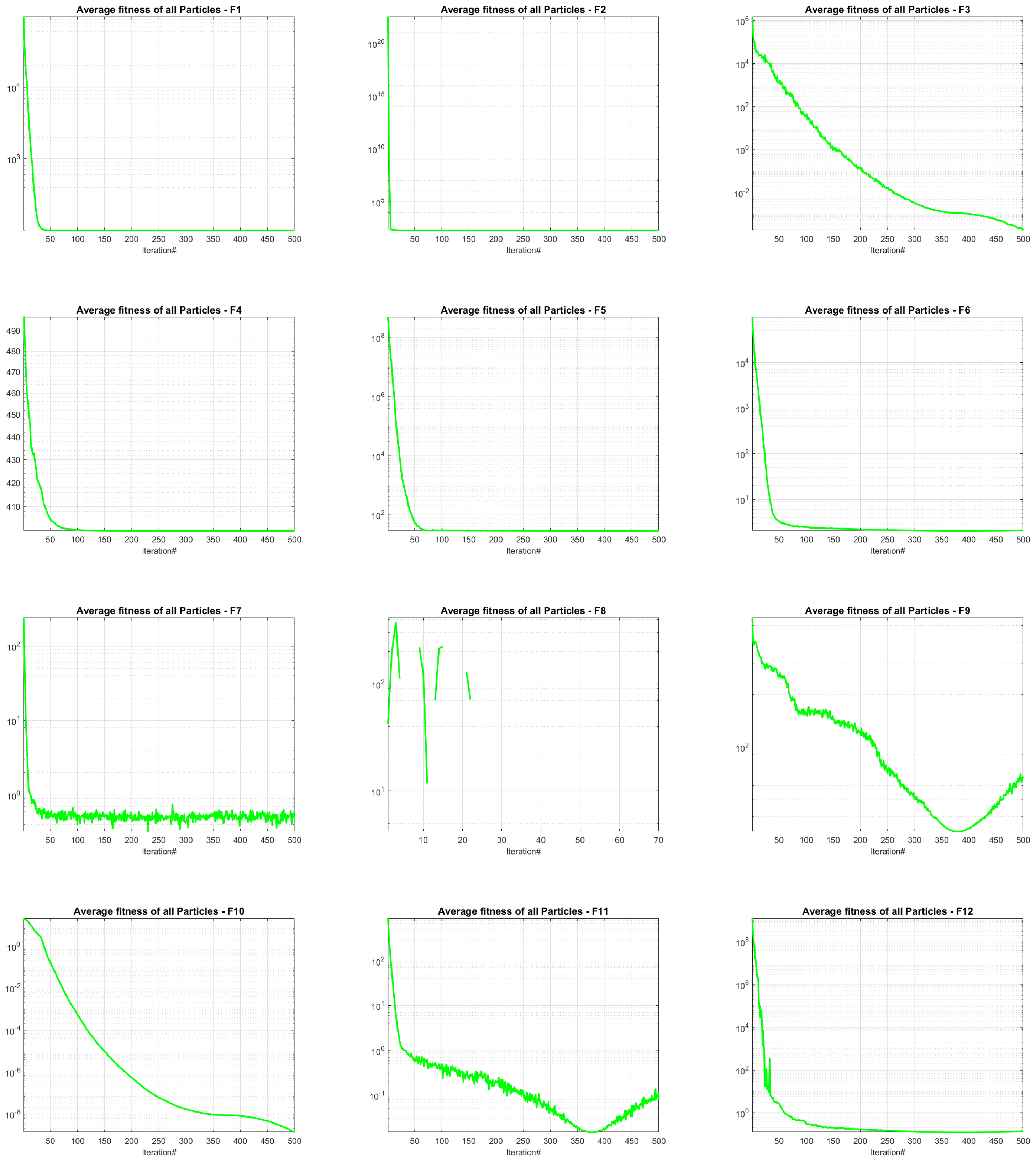
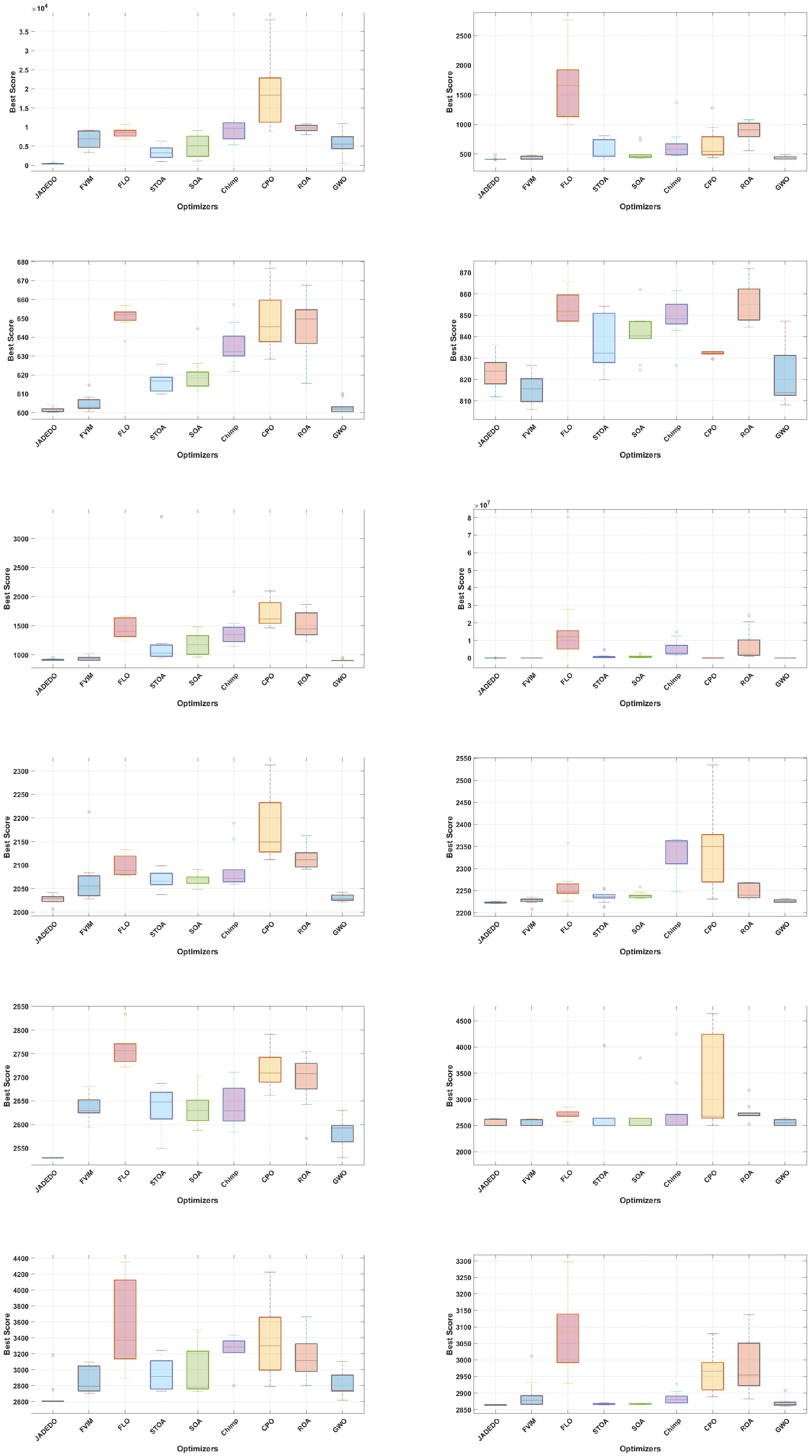
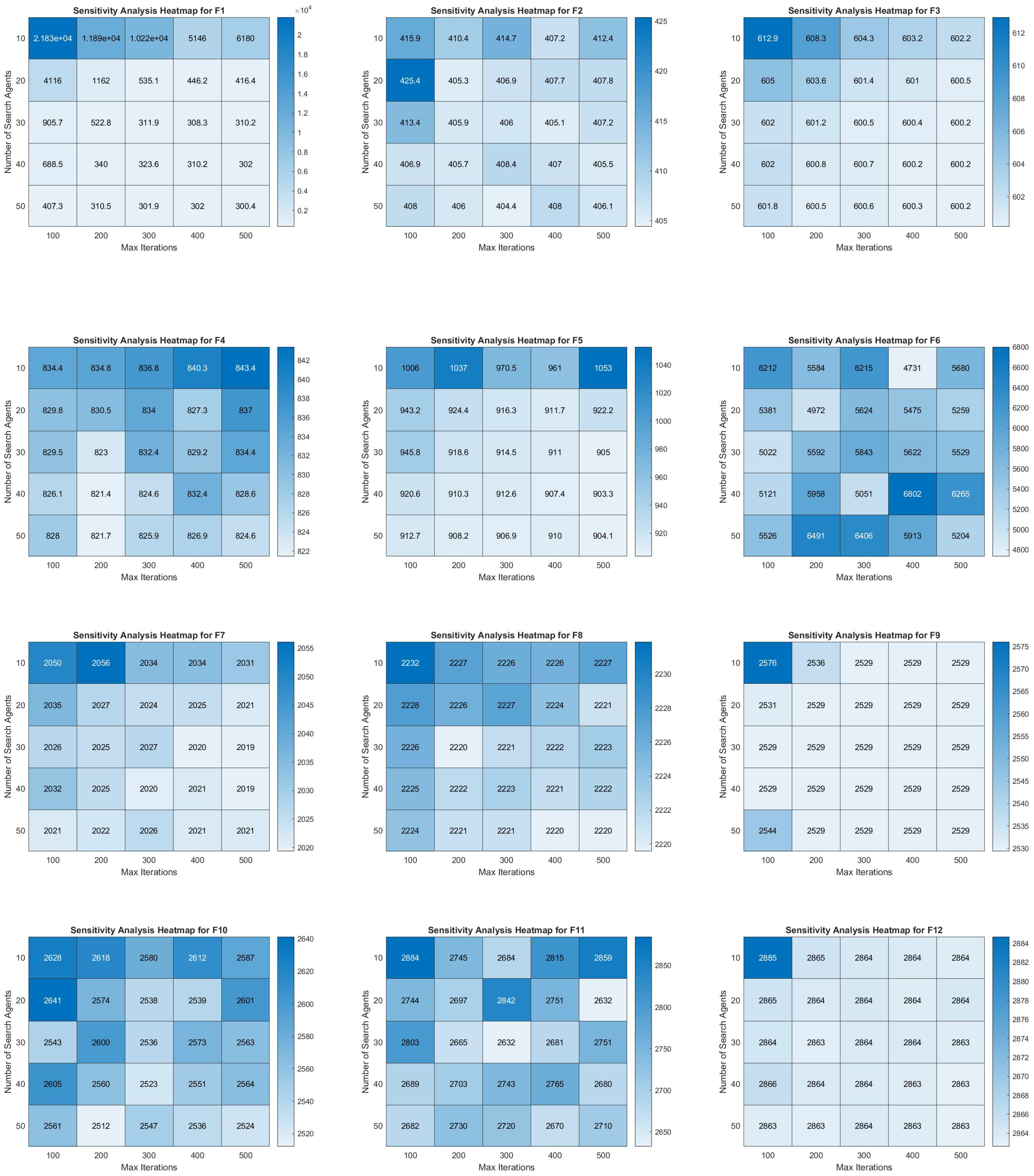
To validate its performance, JADEDO is extensively benchmarked against a suite of well-known and cutting-edge metaheuristics using the IEEE CEC2022 test functions. These functions impose diverse optimization challenges, ranging from simple unimodal functions that test convergence speed to intricate multimodal and hybrid landscapes that stress exploration capabilities. The experiments highlight that JADEDO achieves competitive or superior results in terms of both solution quality (precision) and convergence speed. Statistical significance, assessed via the Wilcoxon sum-rank test, underscores JADEDO’s consistent advantage over several established optimizers.
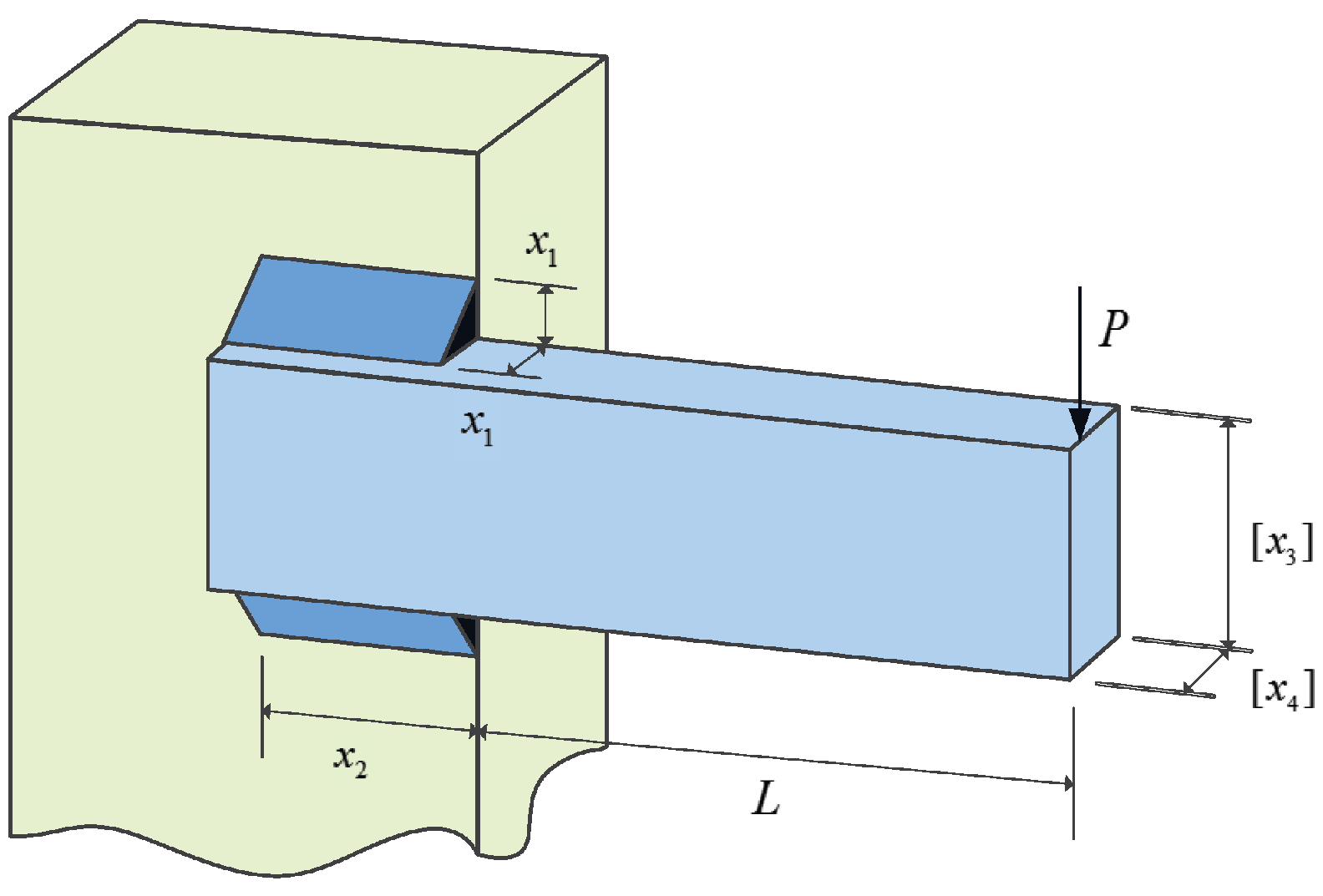
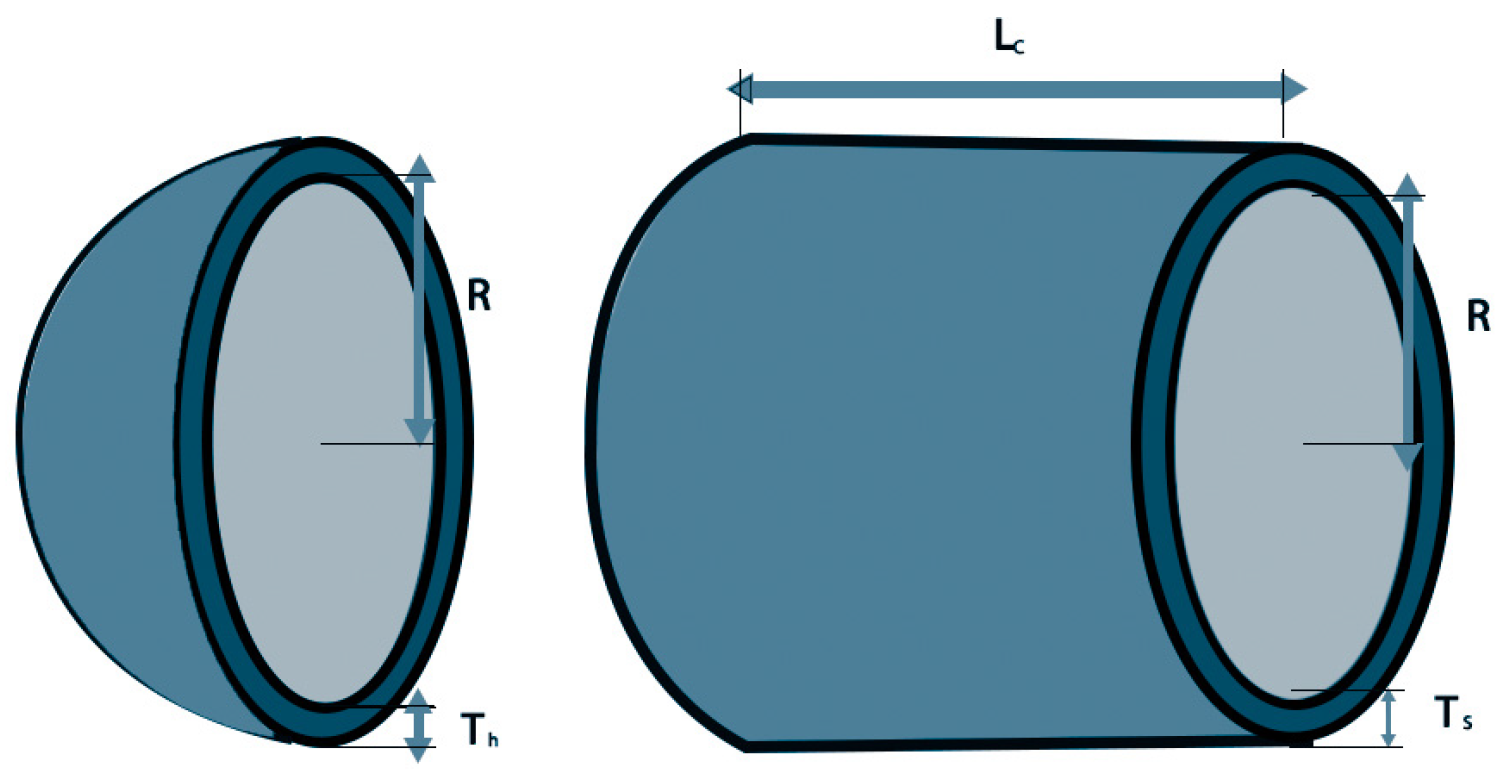
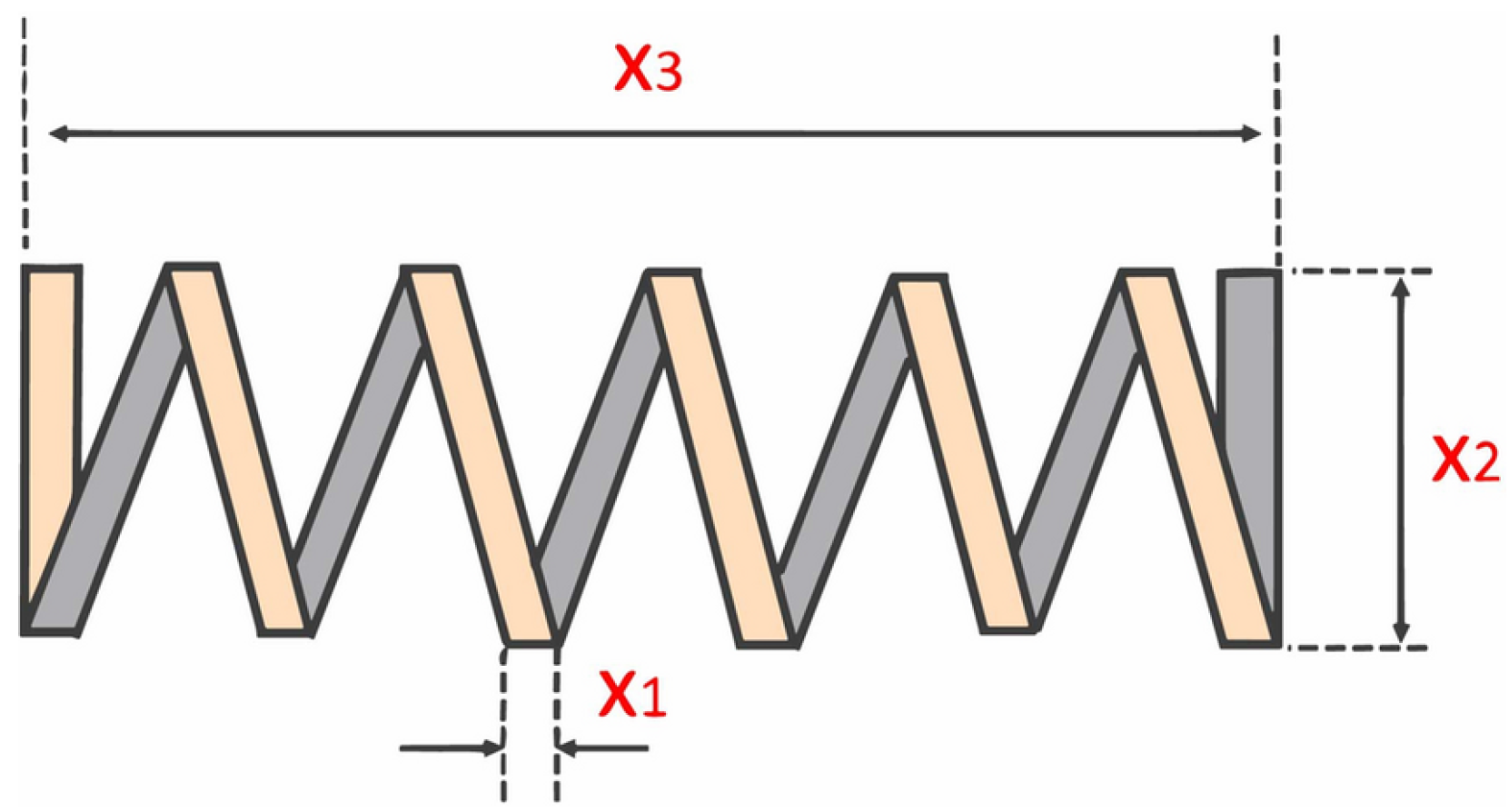
Beyond synthetic benchmarks, we demonstrate the practical value of JADEDO in two domains. First, we address three engineering design problems with high stakes and multiple constraints: the pressure vessel, the spring, and the speed reducer. In each case, JADEDO attained highly competitive designs, underscoring its potential to reduce costs, maintain reliability, and meet strict physical constraints. Second, we apply JADEDO to an attack-response optimization problem, where timely and cost-effective countermeasures against potential threats must be identified. JADEDO excels in this domain by swiftly converging on strategies that minimize both risk and resource expenditure.
Key Contributions
Proposal of a novel hybrid method: We introduce JADEDO, a new optimization algorithm that fuses the dispersal stages of the dandelion optimizer with the adaptive mutation and crossover mechanisms of JADE, aiming to leverage both global exploration and local exploitation in a unified framework.
Benchmark validation: Comprehensive experiments on the IEEE CEC2022 benchmark functions, encompassing unimodal, multimodal, and hybrid landscapes, demonstrate JADEDO’s superior or highly competitive performance in terms of solution accuracy, convergence speed, and robustness.
Real-world applicability: We validate JADEDO on three engineering design problems (pressure vessel, spring, and speed reducer) and an attack-response optimization scenario. In each case, JADEDO identifies effective solutions under strict constraints, highlighting its capacity to handle high-stakes, complex optimization tasks.
2. Literature Review
Recent advancements in optimization techniques have increasingly focused on hybrid algorithms to solve complex engineering design problems, capitalizing on the strengths of multiple approaches to enhance solution quality and convergence speed. Verma and Parouha [
8] introduced an advanced hybrid algorithm, haDEPSO, which integrates differential evolution (aDE) with particle swarm optimization (aPSO). The aDE component prevents premature convergence through novel mutation, crossover, and selection strategies, while aPSO utilizes gradually varying parameters to avoid stagnation. This hybrid approach was validated on five engineering design problems, demonstrating superior convergence characteristics through extensive numerical, statistical, and graphical analyses.
Panagant et al. [
9] introduced HMPANM, a hybrid optimization algorithm combining Marine Predators Optimization with the Nelder–Mead method to improve local exploitation capabilities. This algorithm was applied to the structural design optimization of automotive components, proving its effectiveness in achieving optimal designs under competitive industrial conditions. Yildiz and Mehta [
10] further explored hybrid metaheuristics for automotive engineering design, applying the hybrid Taguchi Salp Swarm–Nelder–Mead algorithm (HTSSA-NM) and manta ray foraging optimization (MRFO) to optimize the structure of automobile brake pedals. The results showed HTSSA-NM’s superiority in minimizing mass while achieving better shape optimization compared to other algorithms.
Duan and Yu [
11] introduced a collaboration-based hybrid grey wolf optimizer and sine cosine algorithm (cHGWOSCA), which enhances global exploration through SCA while maintaining a balance with exploitation via a weight-based position update mechanism. This algorithm demonstrated high performance on IEEE CEC benchmarks and real-world engineering problems. Similarly, Barshandeh et al. [
12] proposed the hybrid multi-population algorithm (HMPA), combining artificial ecosystem-based optimization (AEO) with Harris Hawks optimization (HHO). HMPA employs strategies like a Lévy flight, local search mechanisms, and quasi-oppositional learning, resulting in improved exploration and exploitation.
Su et al. [
13] introduced the hybrid political algorithm (HPA), which enhances the political optimizer’s exploration process for global optima by improving particle movement during computation. HPA was tested on engineering optimization problems, outperforming other algorithms in avoiding local optima. Uray et al. [
14] presented a Taguchi method-integrated hybrid harmony search algorithm (HHS), focusing on parameter optimization through statistical estimation of control parameter values, achieving rapid convergence in engineering design problems.
Fakhouri et al. [
15] introduced PSOSCANMS, a hybrid algorithm that integrates PSO with the sine cosine algorithm (SCA) and the Nelder–Mead simplex (NMS) technique. This approach addresses PSO’s drawbacks, such as low convergence rates and local minima entrapment, by enhancing exploration–exploitation balance through mathematical formulations from SCA and NMS. The algorithm was benchmarked on various optimization problems, demonstrating significant improvements over traditional PSO.
Kumar et al. [
16] introduced a hybrid algorithm that integrates quantum-behaved particle swarm optimization (QPSO) with a binary tournament technique to tackle bound-constrained optimization problems. This algorithm demonstrated superior performance on several benchmark problems and engineering design challenges, offering promising results. Hu et al. [
17] developed the hybrid CSOAOA algorithm, combining the arithmetic optimization algorithm (AOA) with point set, optimal neighborhood learning, and crisscross strategies. CSOAOA was highly effective, with improved precision, faster convergence rates, and better solution quality.
Bose [
18] conducted an experimental study on hybrid composite materials using laser engineering net shaping (LENS) and applied optimization techniques like desirable gray relational analysis (DGRA) to improve material properties. The optimized parameters led to significant improvements in cooling rate and hardness, contributing to material engineering advancements. Wang [
19] explored genetic hybrid optimization for multi-objective engineering project management, showcasing the advantages of hybrid optimization in handling complex, multi-objective tasks.
Li and Ma [
20] proposed a hybrid algorithm, CWDEPSO, integrating differential evolution concepts into PSO to prevent premature convergence and enhance local search. Pham et al. [
21] introduced nSCA, an enhancement to the sine cosine algorithm, by incorporating roulette wheel selection and opposition-based learning. nSCA outperformed leading-edge methods like genetic algorithms and PSO across various optimization problems, making it a strong candidate for complex engineering challenges.
2.1. Overview of Adaptive Differential Evolution with an Optional External Archive (JADE)
Adaptive differential evolution with an optional external archive, usually referred to as JADE, is an improved variant of differential evolution (DE). Its design focuses on increasing convergence speed and maintaining solution diversity. JADE accomplishes these goals by adapting two central parameters—the scale factor and crossover probability—and by keeping an external archive of solutions. This archive retains historical information that can help the algorithm explore the search space more effectively.
JADE employs a special mutation strategy referred to as
current-to-pbest. Equation (24) shows how the mutant vector
is formed from the target vector
at generation
G.
In Equation (24), is the mutant vector, is the current (target) vector, and is the scale factor for the ith individual. The vector is randomly selected from the top best solutions in the current population. The parameter p is a small positive constant (for instance, ) controlling how many top solutions can be chosen as . The vectors and are selected randomly from the population and from the union of the population and an external archive, respectively. This archive, denoted by , stores older solutions that were replaced in previous generations.
After producing the mutant vector, JADE relies on binomial crossover to generate a trial vector
by mixing the components of
and
. The crossover step is illustrated in Equation (16).
In Equation (16), is the dth component of the trial vector . The term represents the dth component of the mutant vector , while is the dth component of the target vector . The quantity is the crossover probability for the ith individual, and is a uniformly distributed random number in . The index ensures that at least one component of is inherited from the mutant vector.
The selection step compares
against
and keeps the superior one according to Equation (
3).
Equation (
3) indicates that
is the solution that exhibits the better (or equal) objective function value among
and
. If
replaces
, the replaced vector
may be stored in the archive
. Thus, the archive collects solutions that have been displaced during the evolutionary process, which can help retain search diversity in subsequent generations.
One of JADE’s core strengths is the adaptation of the scale factor
and crossover probability
. The means of these parameters,
and
, are updated dynamically as indicated in Equations (
4) and (
5).
In Equations (
4) and (
5),
c is a small constant (for instance,
) that controls how much emphasis is placed on newly gathered information. The sets
and
contain the scale factors and crossover probabilities that produced improvements in the current generation. The function
typically denotes the Lehmer mean, used for
F, while
represents the arithmetic mean, used for
. By sampling
and
from probability distributions centered around
and
and then adaptively updating those means based on successful parameter values, JADE steers its parameters toward beneficial settings over time.
In summary, JADE proceeds by generating new mutant vectors according to Equation (24), performing crossover as shown in Equation (16), selecting superior solutions using Equation (
3), and adapting its key parameters with Equations (
4) and (
5). The external archive
and the adaptive parameter control both serve to balance exploration and exploitation. As a result, JADE can converge more quickly and locate better-quality solutions than basic differential evolution for many types of real-valued optimization tasks.
2.2. Overview of Dandelion Optimizer
The dandelion optimizer (DO) is a nature-inspired optimization algorithm based on the dispersal process of dandelion seeds. This process models the way dandelion seeds are carried by the wind, allowing them to explore new areas and settle in fertile ground. The DO algorithm translates this natural phenomenon into an optimization framework that balances exploration and exploitation, making it well-suited for solving complex and high-dimensional optimization problems.
The dandelion optimizer operates in the following three main stages: the rising stage, the decline stage, and the landing stage. Each stage represents a different phase of the optimization process, facilitating both exploration and exploitation of the search space.
In this stage, dandelion seeds (solutions) are dispersed into the air, mimicking the exploration phase. The algorithm introduces randomness through parameters such as the angle
, scaling factor
, and a randomly generated vector NEW. The position of each seed is updated as shown in Equation (
6):
where
is a scaling factor;
and are velocity components;
is a random scaling factor;
NEW is a randomly generated vector.
This stage allows the algorithm to explore new areas of the search space, mimicking the dispersal of seeds by the wind.
After the seeds have risen, they begin to descend, symbolizing the transition from exploration to exploitation. In this stage, the population is adjusted based on the mean position of the seeds and a random factor
, ensuring that seeds settle closer to promising areas, as shown in Equation (
7):
Here, represents the mean position of the population, and is a random factor that controls the descent. This stage refines the search and exploits the best-found solutions.
In the final stage, the seeds land and settle into optimal positions. This stage is driven by a Lévy flight mechanism, which enhances global exploration by introducing larger, random steps. The position update in the landing stage is given, as shown in Equation (61):
where
represents the best individuals in the population;
is a step size determined by the Lévy flight distribution;
l is the current iteration, and is the maximum number of iterations.
This stage ensures thorough exploration of the search space and helps avoid premature convergence.
The dandelion optimizer effectively balances exploration and exploitation through its three-stage process. The rising stage emphasizes exploration by allowing the algorithm to search new regions of the search space. The decline and landing stages shift the focus toward exploitation, refining the solutions, and converging toward optimal results. This balance is crucial for solving complex optimization problems, as it prevents the algorithm from becoming trapped in local optima while still ensuring convergence.
A key feature of the dandelion optimizer is the incorporation of the Lévy flight mechanism in the landing stage. Lévy flights introduce randomness with a probability distribution that allows for large, random steps, helping the algorithm escape local optima and explore new areas of the search space. This mechanism is particularly beneficial in high-dimensional and multimodal optimization problems, where the search space is vast and complex.
The dandelion optimizer can be summarized mathematically through the following steps:
The dandelion optimizer has been shown to perform well on a variety of benchmark optimization problems, particularly those that are high-dimensional and multimodal. Its ability to balance exploration and exploitation, combined with the Lévy flight mechanism, makes it a robust and versatile algorithm for solving complex real-world problems.
2.3. Limitations of Dandelion Optimizer (DO)
DO often encounters challenges in escaping local optima, particularly within complex and multi-modal landscapes. This difficulty can result in suboptimal outcomes and stagnation during optimization. Although DO emulates the dispersal strategy of dandelion seeds, its exploration mechanism may not always be well-balanced with exploitation, potentially leading to inefficient searches, especially in high-dimensional contexts. Furthermore, DO’s performance is highly dependent on control parameters, such as the dispersal ratio; inadequate tuning of these parameters can significantly diminish the algorithm’s effectiveness across various problem domains. Finally, DO’s efficiency may decline when addressing large-scale optimization problems with numerous decision variables, rendering it less suitable for such applications.
2.4. Limitations of JADE Algorithm
JADE enhances differential evolution (DE) by incorporating self-adaptive control parameters. However, inadequate adaptation can lead to slow convergence or stagnation, particularly in complex optimization scenarios. When confronted with abrupt landscape variations, JADE may require numerous iterations to refine solutions effectively, making it unsuitable for real-time applications. Additionally, the self-adaptive parameter mechanism does not always guarantee sufficient diversity in the early stages, which can cause premature convergence and limit exploration of the search space. Furthermore, JADE employs an external archive to maintain diversity, but the computational burden of managing this archive increases as problem complexity escalates.
3. Proposed Hybrid JADE–DO Algorithm
This section presents a novel hybrid optimization algorithm that integrates the dandelion optimizer (DO) with JADE, an adaptive variant of differential evolution augmented by an optional external archive. The primary objective of this hybridization is to balance exploration and exploitation by merging DO’s global search mechanisms with JADE’s adaptive parameter control. As a result, the proposed hybrid JADE–DO method aims to achieve faster convergence while maintaining robustness in complex optimization tasks.
3.1. Algorithmic Overview
The hybrid JADE–DO algorithm begins by randomly initializing a population of candidate solutions within predefined lower and upper bounds. Each individual in this population is then evaluated according to the specified objective function. Within each iteration, JADE’s mutation, crossover, boundary handling, and selection procedures are applied. These steps include the adaptive tuning of crossover probabilities and scaling factors based on the performance of the most successful individuals in the population. Following the JADE procedure, the dandelion optimizer (DO) stages (rising, decline, and landing) refine the population further. This integration helps maintain exploration (global search) and exploitation (local search) in a synergistic manner. After updating the best solution in each iteration, the algorithm proceeds until the maximum number of iterations is reached or some other stopping criterion is met.
3.2. Mathematical Formulation of the Hybrid JADE–DO Method
The sections below describe the Hybrid JADE–DO algorithm in detail, including initialization, the main iterative steps, and the final outputs, it also present the pseudocode as shown in Algorithm 1.
3.2.1. Initialization
The iteration counter is initially set to . The JADE-related parameters are also defined: the mean crossover probability is , and the mean scaling factor is . The percentage of top individuals in the population is , and the number of these top individuals is , where pop denotes the population size. The JADE archive is initialized as with an archive size counter . Two arrays, curve and , record the convergence of the best fitness values and the exploitation metric, respectively, over time.
The population P is then randomly initialized within the bounds . Each row represents a candidate solution, and lb and ub are the lower and upper bounds of the search space.
3.2.2. Main Loop
The main loop repeats until the maximum number of iterations, , is reached. Each iteration proceeds with the following steps.
- (1)
Fitness evaluation
Every individual
i in the population is evaluated as follows:
where
f is the objective function.
- (2)
Parameter sampling
For each individual
i, the crossover rate
is sampled from a normal distribution,
and the scaling factor
is sampled from a Cauchy distribution:
Both and are constrained to ensure that they lie within permissible ranges.
- (3)
Mutation and crossover (JADE)
A mutant vector
for individual
i is generated as follows:
where
is a randomly selected individual from the top
of the population, and
and
are randomly chosen solutions drawn from the population and the archive
A, respectively.
Crossover produces a trial vector
according to the following:
where jrand is a randomly chosen index that ensures at least one component comes from
.
- (4)
Boundary handling and selection
The trial vectors
U are restricted to
by
where the max and min operations are applied element-wise. If the fitness of
is better than
, the trial vector replaces the original vector. In such cases, the associated
and
are labeled as successful.
- (5)
Adaptation (JADE)
The mean crossover probability
and mean scaling factor
are updated after each iteration using the following:
where
c is a learning rate parameter, Scr is the set of successful crossover rates, and Sf is the set of successful scaling factors from the current iteration.
3.2.3. Dandelion Optimizer Integration
After the JADE procedure, the dandelion optimizer (DO) is applied to the population via three stages: rising, decline, and landing. The DO stages promote enhanced exploration and controlled convergence.
The population is updated using a mechanism inspired by dandelion seed dispersal:
where
is a scaling factor,
and
are velocity components, and
is the value of a log-normal PDF at
. The vector Best is the best individual found so far.
Each individual converges toward the population mean according to the following:
where
is a uniformly distributed random factor within
, and
is the
j-th component of the population mean.
A final update step based on a Lévy flight refines the population:
where
is the
j-th component of the best solution found so far. The term
is a Lévy-distributed step size, and
l denotes the current iteration number.
3.2.4. Termination and Output
At the end of each iteration, the best fitness value is updated and recorded in the curve. The exploitation metric, defined as the difference between consecutive best fitness values, is also updated and stored in
. The algorithm terminates when
is reached or if another stopping criterion is satisfied. Upon termination, the Hybrid JADE–DO algorithm returns:
Here,
is the best solution found,
is the corresponding objective value.
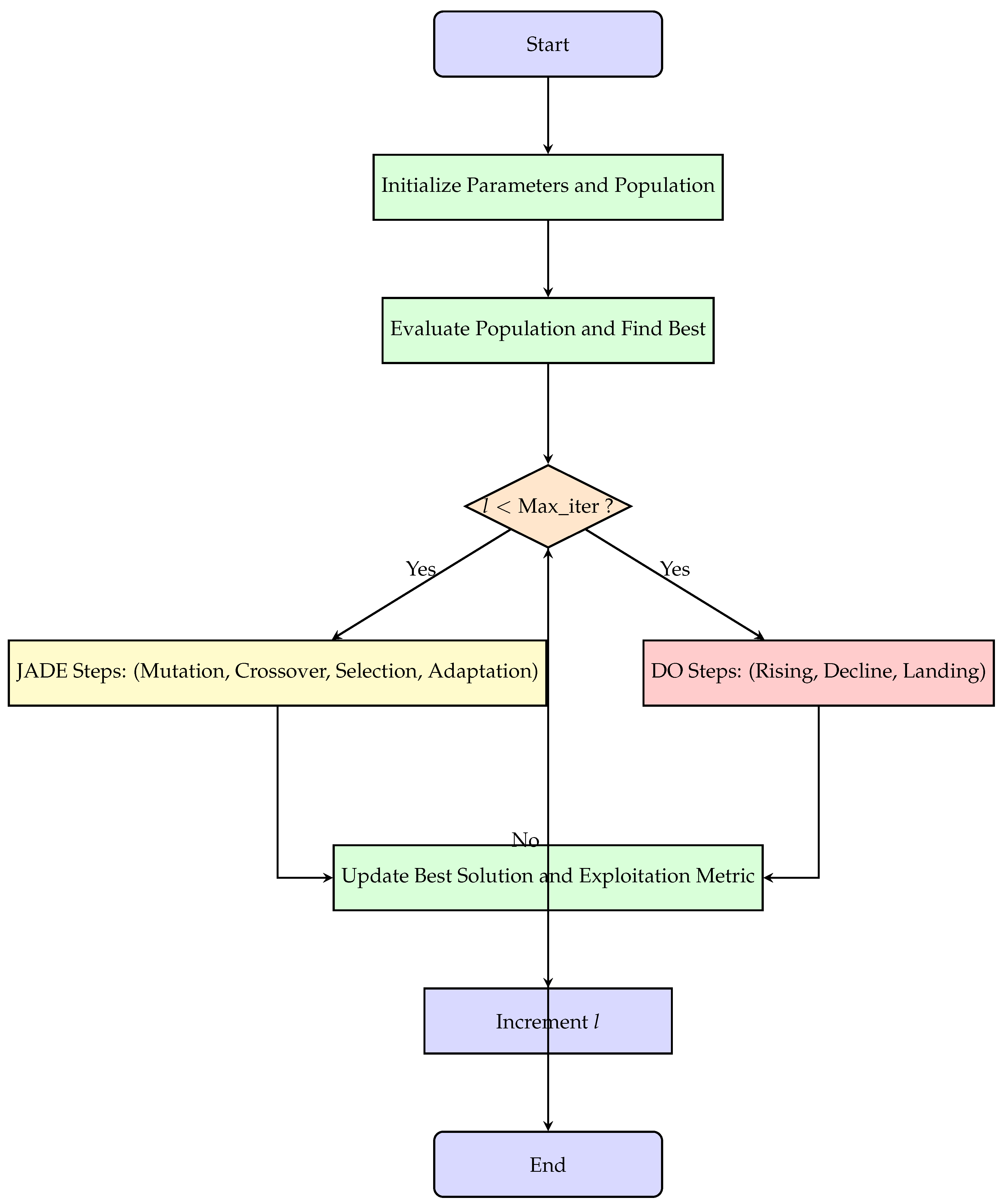
JADEDO flowchart (See
Figure 1) begins with the initialization of parameters and the random population generation. The population is then evaluated to find the current best solution. If the iteration counter
l has not reached
, the algorithm executes two main stages in parallel: the JADE steps (
yellow box) and the DO steps (
red box). The JADE steps carry out mutation, crossover, selection, and adaptive parameter updates, while the DO steps implement the rising, decline, and landing phases. After these stages, the best solution is updated, the exploitation metric is calculated, and the iteration counter
l is incremented. This process continues until the maximum number of iterations is reached, at which point the algorithm terminates and outputs the final best solution.
| Algorithm 1 Hybrid JADEDO algorithm |
- 1:
Input: Objective function , bounds , population size pop, maximum iterations , ratio , learning rate c, DO scaling factor , initial means , , DO velocity components , , and any other DO-specific parameters. - 2:
Output: Best solution , best fitness - 3:
Initialization: Set iteration counter . Initialize , . Define . Initialize archive ; set archive size counter . Initialize arrays and . Randomly initialize population P in . Evaluate each by (see Equation ( 12)). Identify and from the initial population. - 4:
Main Loop (while ): JADE Steps: - 5:
for to pop do - 6:
Draw from a normal distribution with mean (refer to Equation ( 13)) and clip to . - 7:
Draw from a Cauchy distribution with location (refer to Equation ( 14)) and clip to a valid range. - 8:
Generate mutant vector (see Equation ( 15)) using , , and (which can come from ). - 9:
Perform crossover to create trial vector (see Equation (16)). - 10:
Apply boundary handling (refer to Equations ( 17) and (18)). - 11:
Evaluate . - 12:
Compare with ; if is better, replace and update archive A as needed. - 13:
end for - 14:
Adapt and using successful and F (Equations ( 19) and (20)). Dandelion optimizer (DO) integration: - 15:
Rising stage: Update via a random dispersal process (Equation ( 21)), then re-evaluate fitness. - 16:
Decline stage: Move solutions toward the mean (Equation ( 22)), then re-evaluate fitness. - 17:
Landing stage: Refine solutions using Lévy flights around the elite (Equation ( 23)), then re-evaluate fitness. Update best solutions: - 18:
Identify any improvement in and update if found. - 19:
Compute exploitation metric as the difference in consecutive best fitness values. - 20:
Append to curve and the exploitation metric to . - 21:
Increment . - 22:
End While - 23:
Return ,
|
3.3. Exploration and Exploitation Behavior
The hybrid JADEDO algorithm is designed to balance exploration and exploitation effectively throughout the optimization process. Exploration refers to the algorithm’s ability to investigate diverse regions of the search space, while exploitation focuses on refining solutions in promising areas.
In the
mutation and crossover phase of JADE, the generation of mutant vectors
introduces diversity by combining information from the current population and top-performing individuals. Specifically, Equation (24) utilizes the scaling factor
and differences between individuals to explore new regions:
where
is the mutant vector for individual
i;
is the current individual;
is the scaling factor;
is a randomly selected individual from the top
best individuals; and
and
are randomly selected individuals from the population and the archive
A, respectively.
The
adaptation mechanism in JADE adjusts the mean crossover rate
and mean scaling factor
based on successful parameters from previous generations, enhancing exploitation by fine-tuning the parameters to focus on promising regions. This is shown in Equations (
25) and (
26):
where
is the updated mean crossover rate;
c is the learning rate; and
is the mean of successful crossover rates Scr.
where
is the updated mean scaling factor; and Sf is the set of successful scaling factors.
The integration of the dandelion optimizer introduces additional exploration and exploitation behaviors. In the
rising stage (Equation (
27)), the algorithm simulates the dispersal of dandelion seeds to explore new areas:
where
is the
i-th individual in the population;
is a scaling factor;
and
are velocity components in the
x and
y directions;
is a log-normal random Xwith parameter
; and Best is the best individual found so far.
In the
decline stage (Equation (
28)), the algorithm exploits the information gathered by converging toward the mean position
:
where
is the
j-th component of individual
i;
is a random factor between 0 and 1;
is the scaling factor; and
is the
j-th component of the mean position of the population.
Finally, the
landing stage (Equation (
29)) employs a Lévy flight mechanism to refine solutions, enhancing exploitation:
where
is the
j-th component of the elite (best) individual;
is a step length determined by the Lévy distribution;
is the scaling factor;
l is the current iteration number; and
is the maximum number of iterations.
3.4. Computational Complexity Analysis
The computational complexity of the hybrid JADEDO algorithm can be analyzed by examining the operations performed in both the JADE (adaptive differential evolution) and dandelion optimizer (DO) phases. In each iteration, the algorithm executes a series of operations whose computational costs depend on the population size N and the dimensionality of the problem d.
In the JADE phase, the key operations are mutation, crossover, and selection. Each of these operations involves processing all
N individuals in the population, and for each individual, the computational cost is proportional to the dimensionality
d. Therefore, the computational complexity of the JADE phase per iteration is as follows:
Similarly, the DO phase consists of the rising, decline, and landing stages. Each stage also processes all
N individuals, with operations proportional to
d per individual. Hence, the computational complexity of the DO phase per iteration is as follows:
Combining both phases, the total computational complexity per iteration of the hybrid JADEDO algorithm is as follows:
Since constants are ignored in Big-O notation, the combined complexity remains per iteration.
If the algorithm runs for
T iterations, the total computational complexity is as follows:
This indicates that the computational complexity of the hybrid JADEDO algorithm scales linearly with the population size N, the problem dimensionality d, and the number of iterations T.
While the hybrid approach introduces additional computational overhead compared to standalone methods, it enhances optimization performance, particularly in high-dimensional and multimodal problems. The increased computational cost is justified by the improved convergence speed and solution quality achieved through the effective combination of exploration and exploitation mechanisms in both the JADE and DO phases.
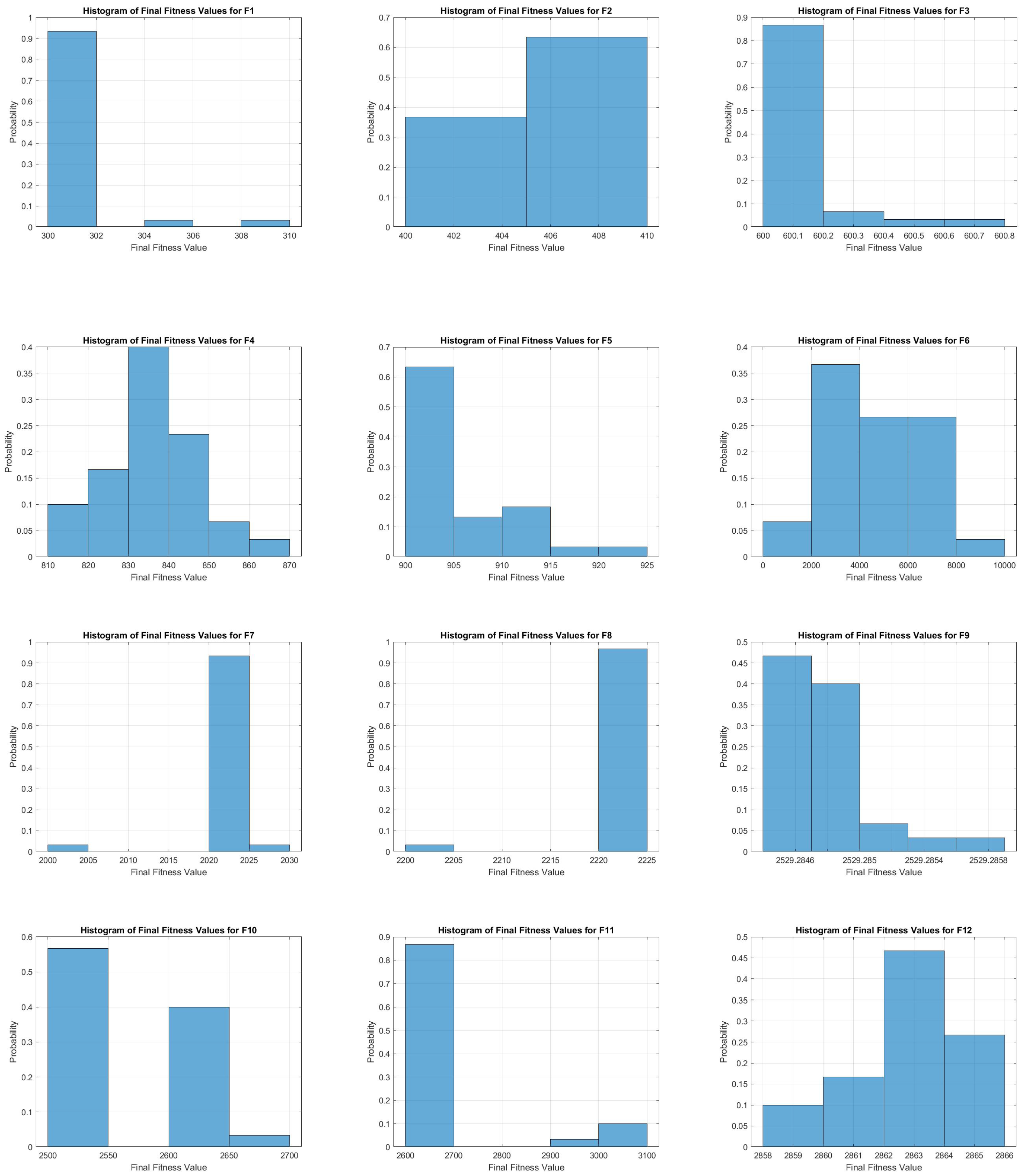
12. Problem Formulation
We assume there are candidate responses, each with a corresponding base cost, base effectiveness, base risk, and duration. Let be a binary decision variable for response i, where if response i is chosen and otherwise. The total cost, total risk, and the maximum duration among the chosen responses must each not exceed specified limits. A random threat factor scales the base effectiveness of each response, so the realized effectiveness of response i is .
The goal is to
maximize total effectiveness while remaining within a cost limit, a risk limit, and a time limit. In practice, we
minimize the negative effectiveness plus large penalty terms for any constraint violations. Specifically, we define the following:
If any limit is exceeded, a penalty term is added. For example, exceeding the cost limit (CostLimit) by
results in a penalty proportional to
with a large penalty coefficient,
. Similar penalties are applied to the risk and time constraints. The composite objective function then becomes as follows:
We then minimize this objective with respect to the binary vector . Because of its combinatorial structure and the uncertain threat factor, , we employ metaheuristic solvers to find good solutions.
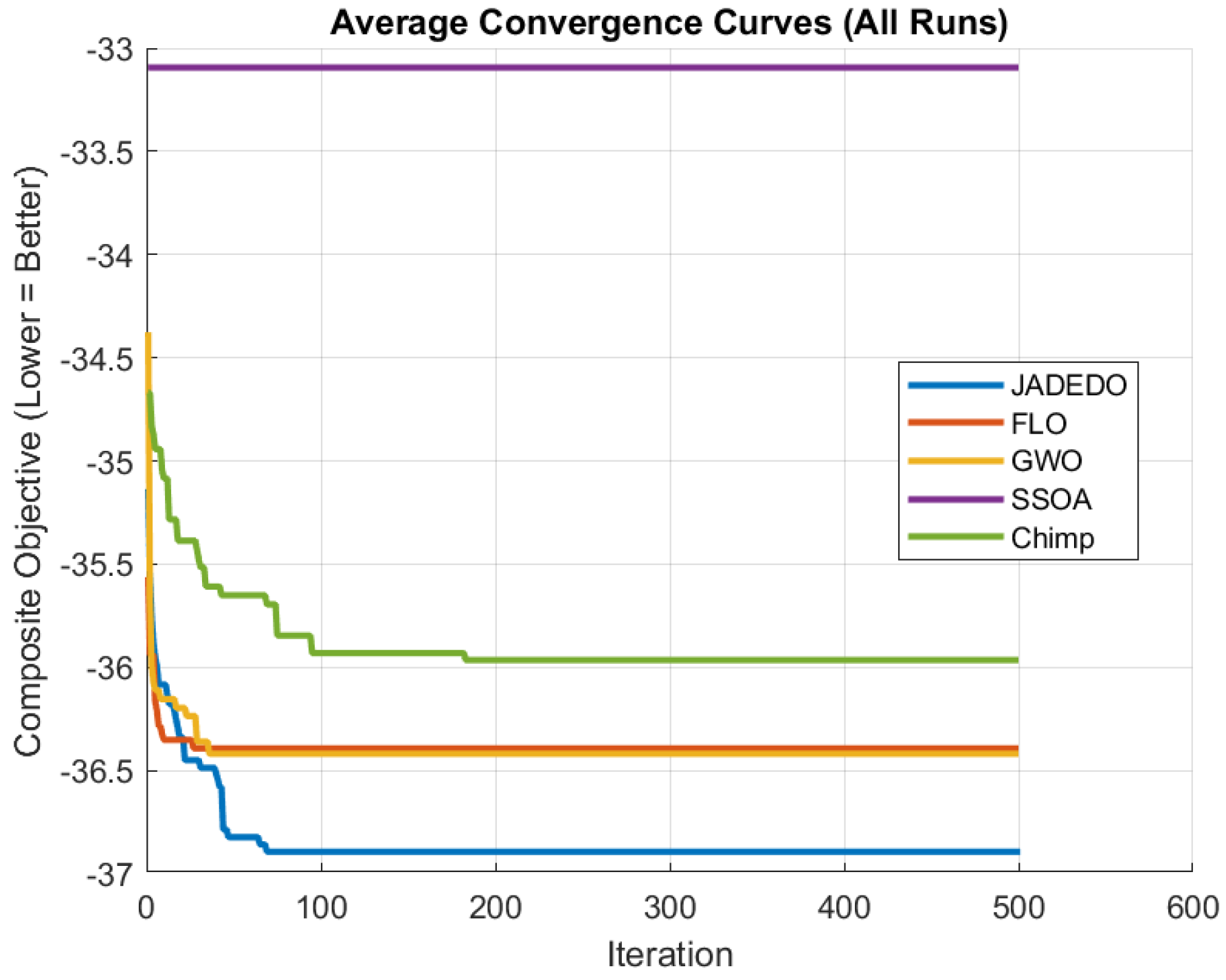
15. Conclusions
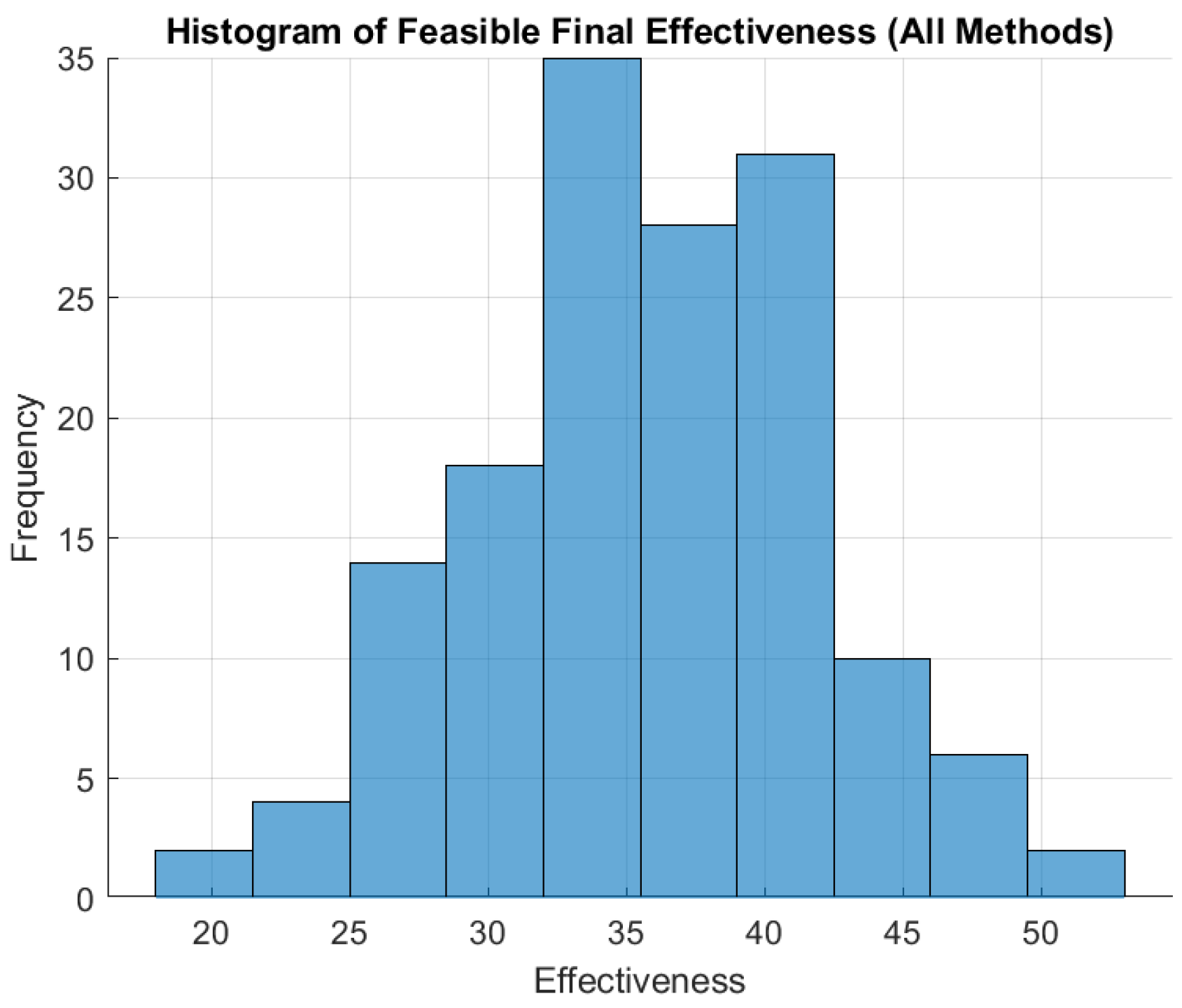
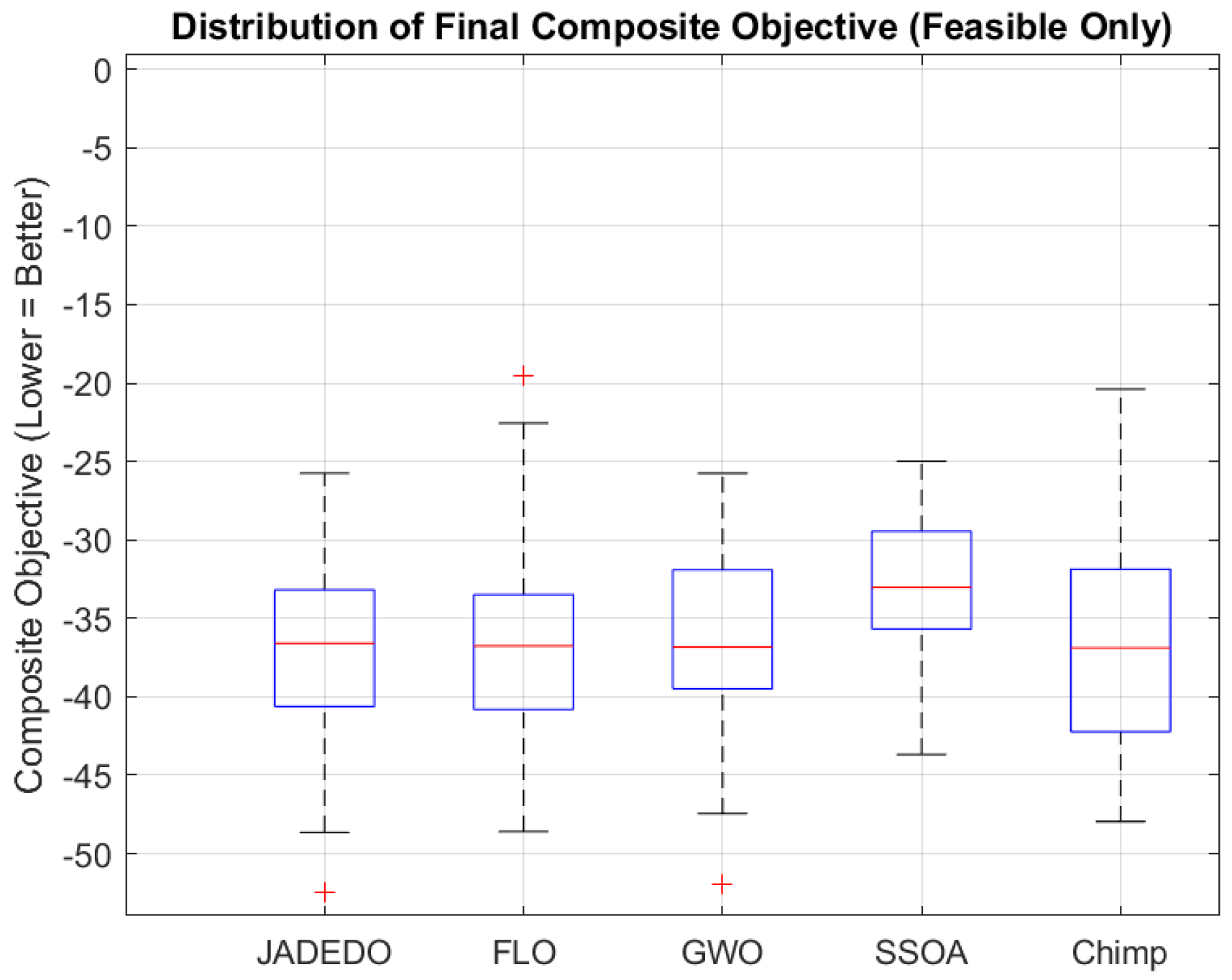
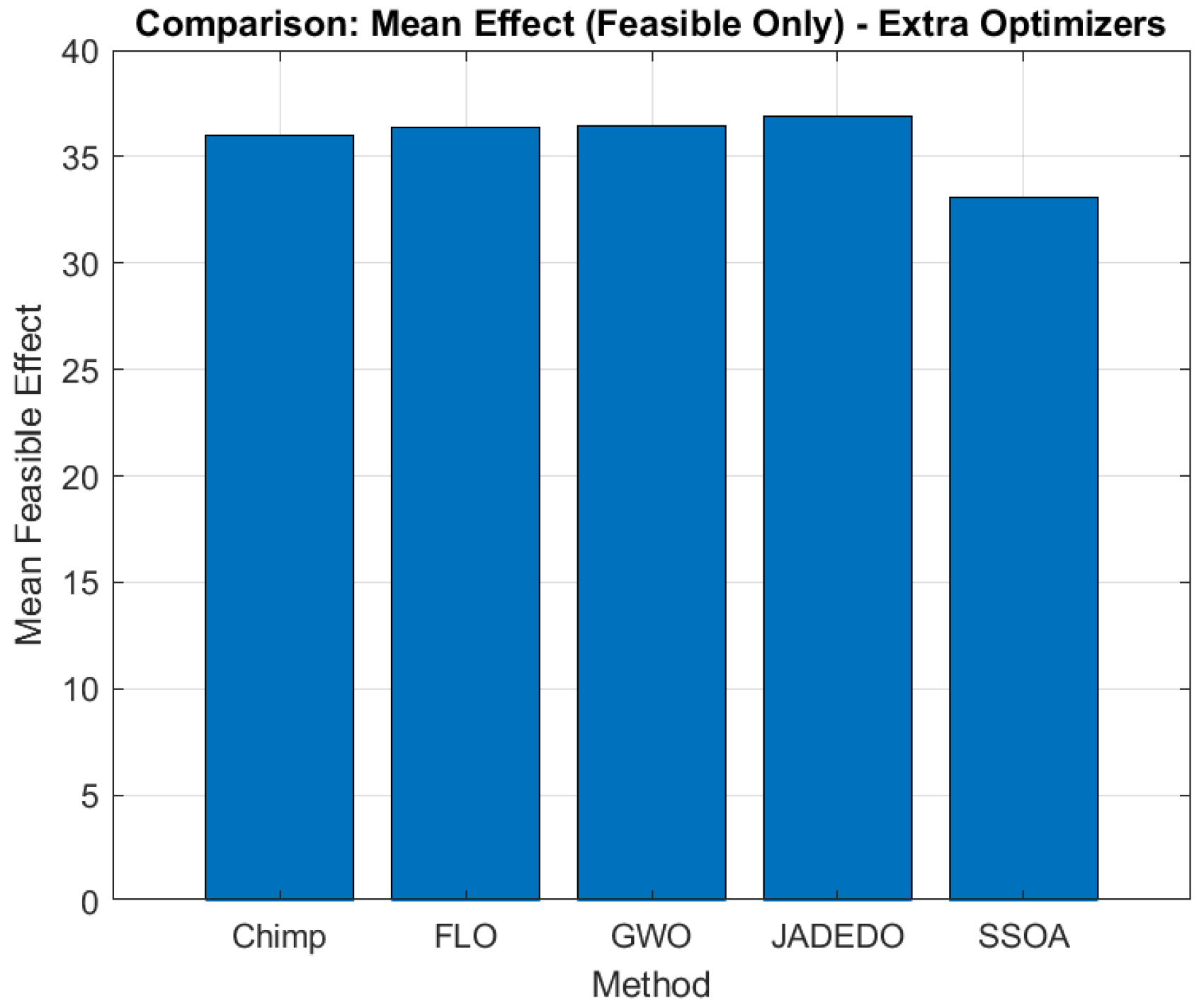
This work introduced JADEDO, a hybrid evolutionary optimizer that merges the biologically inspired dispersal stages of the dandelion optimizer (DO) with the adaptive parameter control mechanisms of JADE (adaptive differential evolution). Extensive experiments were conducted on diverse optimization scenarios, including the CEC2022 benchmark suite, a security-oriented attack-response (or cloud) optimization problem, and several engineering design tasks (pressure vessel, spring, and speed reducer). For the CEC2022 benchmarks, JADEDO ranked among the top performers across unimodal, multimodal, composition, and hybrid functions. Its capacity to balance global exploration and local exploitation was evident in the consistently high rankings. Statistical evaluations via Wilcoxon sum-rank tests further confirmed its robust and reliable performance, emphasizing JADEDO’s proficiency in navigating complex, high-dimensional search spaces. In the attack-response optimization problem, JADEDO demonstrated its adaptability by efficiently finding feasible, high-effectiveness defensive strategies under strict cost, risk, and time constraints. Compared with several state-of-the-art algorithms—such as FLO, GWO, and Chimp—JADEDO frequently emerged as a leading method. Its strong performance underscored the potential of combining DO’s explorative power with JADE’s adaptive mechanisms, particularly in security or cloud-based contexts where robust and rapid convergence can be crucial. JADEDO also excelled in engineering design challenges. In the pressure vessel problem, it achieved an excellent mean cost (6067.595) while attaining the lowest recorded cost of 5885.334, proving its ability to handle the stringent constraints typical in real-world industrial scenarios. For the spring design problem, JADEDO consistently reached near-optimal results, marked by a low mean objective () and minimal standard deviations, underscoring its reliability in complex mechanical systems. Although JADEDO did show abnormal values in one speed reducer experiment—suggesting that parameter tuning and constraint handling need careful attention—its competitive outcomes in other cases indicate its promise for such gear-design tasks when properly configured.