SA-Net: Leveraging Spatial Correlations Spatial-Aware Net for Multi-Perspective Robust Estimation Algorithm
Abstract
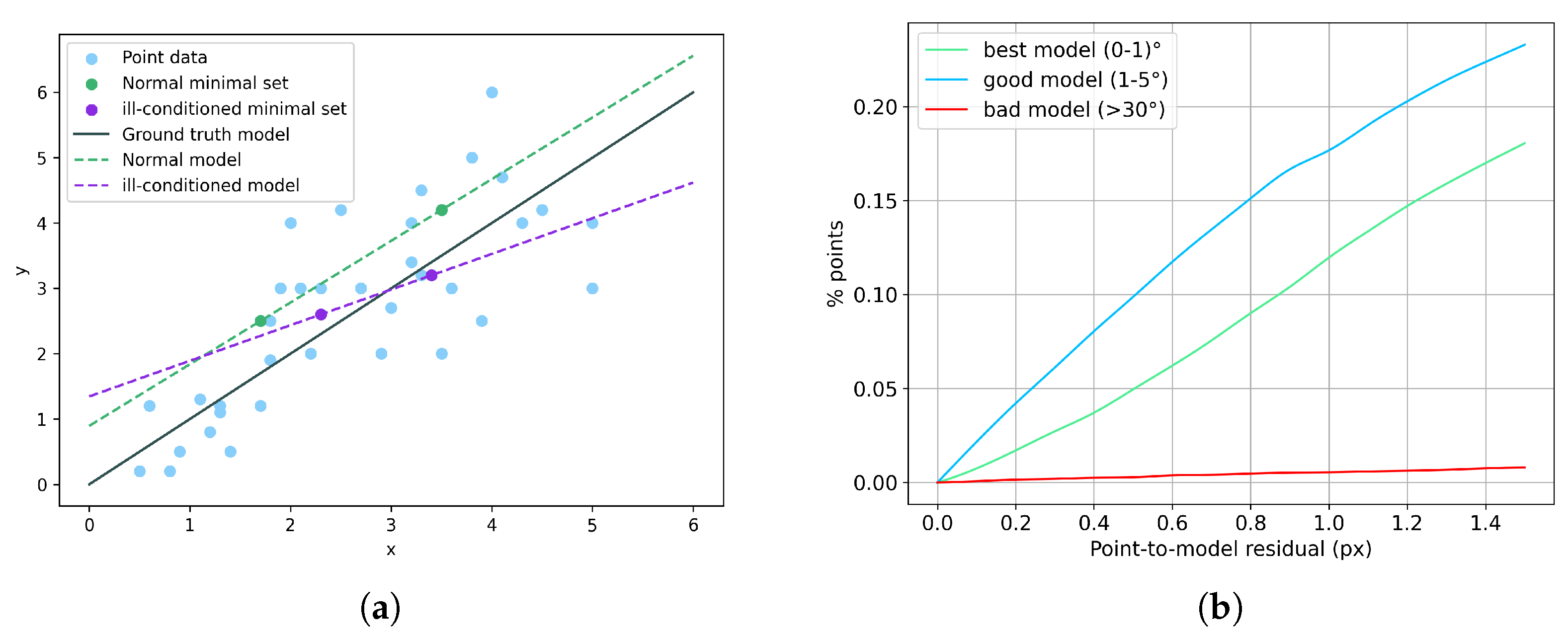
1. Introduction
- We reveal the suboptimality in robust estimation models that rely solely on confidence for evaluation. To address this, we propose SA-Net, a dual-branch network that integrates spatial distribution information, mitigating over-reliance on confidence to improve optimization.
- To improve the model’s spatial perception, we introduce the Cluster-based Mapping and FPS Aggregate Dispatch block, which explore feature point relationships from both global and local perspectives. Additionally, we utilize Chamfer Loss to constrain the sampling distribution.
- Compared with state-of-the-art methods, SA-Net achieves superior results in real-world scenarios on fundamental and essential matrix estimation.
2. Related Works
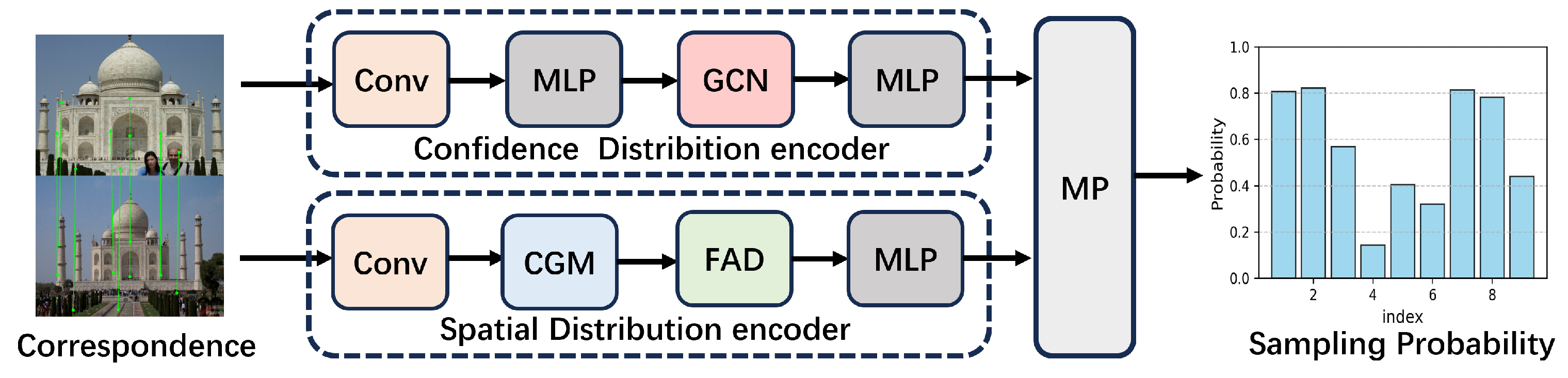
3. Methods
3.1. Confidence Distribution Encoder
3.2. Spatial Probability Distribution Encoder
3.3. Loss Function
4. Experiments
4.1. Fundamental Matrix Estimation
4.2. Essential Matrix Estimation
4.3. Ablation Study
4.4. Visualization
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| RANSAC | Random Sample Consensus |
| MAGSAC++ | Marginalizing Sample Consensus plus plus |
| LO-RANSAC | Locally Optimized Random Sample Consensus |
| GroupSAC | Group Sample Consensus |
| GC-RANSAC | Graph-Cut Random Sample Consensus |
| NG-RANSAC | Neural-Guided Random Sample Consensus |
| BANSAC | Bayesian Network Random Consensus |
| PARSAC | Parallel Sample Consensus |
| CDF | Cumulative Distribution Functions |
| CGM | Cluster-based Graph Mapping Block |
| CL | Chamfer Loss |
| MAGSAC | Marginalizing Sample Consensus |
| NAPSAC | N Adjacent Points Sample Consensus |
| PROSAC | Progressive Sample Consensus |
| USAC | Universal Sample Consensus |
| DSAC | Differentiable Random Sample Consensus |
| D-RANSAC | Generalized Differentiable Random Sample Consensus |
| NeFSAC | Neurally Filtered Sample Consensus |
| CDE | Confidence Distribution Encoder |
| FAD | FPS Aggregation Dispatch Block |
References
- Torr, P.H.; Murray, D.W. Outlier detection and motion segmentation. In Proceedings of the Sensor Fusion VI. SPIE, Boston, MA, USA, 7–10 September 1993; Volume 2059, pp. 432–443. [Google Scholar]
- Schönberger, J.L.; Zheng, E.; Frahm, J.M.; Pollefeys, M. Pixelwise view selection for unstructured multi-view stereo. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 201; Proceedings, Part III 14. pp. 501–518.
- Ding, L.; Sharma, G. Fusing structure from motion and lidar for dense accurate depth map estimation. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 1283–1287. [Google Scholar]
- Schonberger, J.L.; Frahm, J.M. Structure-from-motion revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Capel, D. Image mosaicing. In Image Mosaicing and Super-Resolution; Springer: Berlin/Heidelberg, Germany, 2004; pp. 47–79. [Google Scholar]
- Chen, Z.; Liu, T.; Huang, J.J.; Zhao, W.; Bi, X.; Wang, M. Invertible Mosaic Image Hiding Network for Very Large Capacity Image Steganography. In Proceedings of the ICASSP 2024–2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 4520–4524. [Google Scholar]
- Mei, X.; Ramachandran, M.; Zhou, S.K. Video background retrieval using mosaic images. In Proceedings of the ICASSP 2005–2005 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Philadelphia, PA, USA, 18–23 March 2005; Volume 2, pp. ii-441–ii-444. [Google Scholar]
- Barath, D.; Matas, J.; Noskova, J. MAGSAC: Marginalizing sample consensus. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10197–10205. [Google Scholar]
- Barath, D.; Noskova, J.; Ivashechkin, M.; Matas, J. MAGSAC++, a fast, reliable and accurate robust estimator. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WC, USA, 14–19 June 2020; pp. 1304–1312. [Google Scholar]
- Cavalli, L.; Pollefeys, M.; Barath, D. NeFSAC: Neurally filtered minimal samples. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 351–366. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Chum, O.; Matas, J.; Kittler, J. Locally optimized RANSAC. In Proceedings of the Pattern Recognition: 25th DAGM Symposium, Magdeburg, Germany, 10–12 September 2003; Proceedings 25. pp. 236–243. [Google Scholar]
- Torr, P.H.; Zisserman, A. MLESAC: A new robust estimator with application to estimating image geometry. Comput. Vis. Image Underst. 2000, 78, 138–156. [Google Scholar] [CrossRef]
- Torr, P.H.; Nasuto, S.J.; Bishop, J.M. Napsac: High noise, high dimensional robust estimation-it’s in the bag. In Proceedings of the British Machine Vision Conference (BMVC), Cardiff, UK, 2–5 September 2002; Volume 2, p. 3. [Google Scholar]
- Ni, K.; Jin, H.; Dellaert, F. GroupSAC: Efficient consensus in the presence of groupings. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 2193–2200. [Google Scholar]
- Raguram, R.; Chum, O.; Pollefeys, M.; Matas, J.; Frahm, J.M. USAC: A universal framework for random sample consensus. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 2022–2038. [Google Scholar] [CrossRef] [PubMed]
- Brachmann, E.; Krull, A.; Nowozin, S.; Shotton, J.; Michel, F.; Gumhold, S.; Rother, C. Dsac-differentiable ransac for camera localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6684–6692. [Google Scholar]
- Barath, D.; Matas, J. Graph-cut RANSAC. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 6733–6741. [Google Scholar]
- Brachmann, E.; Rother, C. Neural-guided RANSAC: Learning where to sample model hypotheses. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 4322–4331. [Google Scholar]
- Wei, T.; Patel, Y.; Shekhovtsov, A.; Matas, J.; Barath, D. Generalized differentiable RANSAC. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 17649–17660. [Google Scholar]
- Piedade, V.; Miraldo, P. BANSAC: A dynamic BAyesian Network for adaptive SAmple Consensus. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 3738–3747. [Google Scholar]
- Chum, O.; Matas, J. Matching with PROSAC-progressive sample consensus. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–26 June 2005; Volume 1, pp. 220–226. [Google Scholar]
- Rydell, F.; Torres, A.; Larsson, V. Revisiting sampson approximations for geometric estimation problems. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 4990–4998. [Google Scholar]
- Jang, E.; Gu, S.; Poole, B. Categorical reparameterization with gumbel-softmax. arXiv 2016, arXiv:1611.01144. [Google Scholar]
- Nie, C.; Wang, G.; Liu, Z.; Cavalli, L.; Pollefeys, M.; Wang, H. RLSAC: Reinforcement Learning enhanced Sample Consensus for End-to-End Robust Estimation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 9891–9900. [Google Scholar]
- Ding, Y.; Vávra, V.; Bhayani, S.; Wu, Q.; Yang, J.; Kukelova, Z. Fundamental matrix estimation using relative depths. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Berlin/Heidelberg, Germany, 2025; pp. 142–159. [Google Scholar]
- Fan, Z.; Pan, P.; Wang, P.; Jiang, Y.; Xu, D.; Wang, Z. POPE: 6-DoF Promptable Pose Estimation of Any Object in Any Scene with One Reference. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 7771–7781. [Google Scholar]
- Fan, Z.; Cai, Z. Random epipolar constraint loss functions for supervised optical flow estimation. Pattern Recognit. 2024, 148, 110141. [Google Scholar] [CrossRef]
- Kluger, F.; Rosenhahn, B. PARSAC: Accelerating Robust Multi-Model Fitting with Parallel Sample Consensus. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, USA, 20–27 February 2024; Volume 38, pp. 2804–2812. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Zhao, C.; Ge, Y.; Zhu, F.; Zhao, R.; Li, H.; Salzmann, M. Progressive correspondence pruning by consensus learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 6464–6473. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Arandjelović, R.; Zisserman, A. Three things everyone should know to improve object retrieval. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2911–2918. [Google Scholar]
- Jin, Y.; Mishkin, D.; Mishchuk, A.; Matas, J.; Fua, P.; Yi, K.M.; Trulls, E. Image Matching across Wide Baselines: From Paper to Practice. Int. J. Comput. Vis. 2020, 129, 517–547. [Google Scholar] [CrossRef]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 2, pp. 1150–1157. [Google Scholar]








| Scene/Method | RANSAC | MAGSAC++ | OANet | CLNet | NG-RANSAC | RLSAC | D-RANSAC | SA-Net |
|---|---|---|---|---|---|---|---|---|
| Taj Mahal | 42.21 | 58.63 | 54.13 | 56.22 | 57.65 | 54.98 | 59.66 | 60.51 |
| Sacre Coeur | 45.83 | 52.11 | 47.28 | 48.10 | 51.03 | 53.71 | 53.09 | 55.08 |
| Trevi Fountain | 31.77 | 35.93 | 29.32 | 30.07 | 36.25 | 34.89 | 35.97 | 39.45 |
| Pantheon Exterior | 58.20 | 63.44 | 51.39 | 55.79 | 59.81 | 61.49 | 65.38 | 66.97 |
| Brandenburg Gate | 36.95 | 39.32 | 37.03 | 38.48 | 39.20 | 41.94 | 41.43 | 44.91 |
| Colosseum Exterior | 46.80 | 51.34 | 43.58 | 47.87 | 53.21 | 56.86 | 55.43 | 56.08 |
| Buckingham Palace | 25.65 | 29.76 | 25.93 | 27.81 | 29.88 | 29.13 | 30.71 | 33.79 |
| Grand Place Brussels | 29.75 | 33.84 | 29.56 | 33.52 | 35.39 | 34.35 | 35.56 | 37.52 |
| Palace of Westminster | 31.73 | 33.85 | 31.65 | 32.72 | 35.12 | 34.27 | 34.92 | 39.88 |
| Prague Old Town Square | 35.56 | 38.73 | 34.32 | 37.34 | 39.43 | 38.31 | 39.72 | 41.23 |
| Notre-Dame Front Facade | 37.93 | 39.84 | 34.58 | 36.85 | 39.74 | 39.47 | 43.51 | 45.63 |
| Westminster Abbey | 52.06 | 52.89 | 43.38 | 49.03 | 51.27 | 50.41 | 52.04 | 52.57 |
| Avg | 39.54 | 44.14 | 38.51 | 41.15 | 44.00 | 44.15 | 45.61 | 47.80 |
| Method | AUC@5° | AUC@10° | AUC@20° | Run-Time (ms) |
|---|---|---|---|---|
| LMEDS | 0.237 | 0.292 | 0.345 | 21 |
| RANSAC | 0.251 | 0.334 | 0.394 | 42 |
| GC-RANSAC | 0.315 | 0.375 | 0.413 | 81 |
| MAGSAC | 0.355 | 0.405 | 0.457 | 102 |
| MAGSAC++ | 0.354 | 0.411 | 0.459 | 68 |
| OANet | 0.259 | 0.323 | 0.374 | 25 |
| CLNet | 0.334 | 0.395 | 0.449 | 31 |
| NG-RANSAC | 0.369 | 0.413 | 0.464 | 52 |
| D-RANSAC | 0.394 | 0.426 | 0.501 | 61 |
| SA-Net | 0.436 | 0.442 | 0.524 | 78 |
| CDE | CGM | FAD | CL | AUC | ||
|---|---|---|---|---|---|---|
| @5° | @10° | @20° | ||||
| ✔ | 0.378 | 0.421 | 0.483 | |||
| ✔ | ✔ | 0.412 | 0.428 | 0.513 | ||
| ✔ | ✔ | ✔ | 0.401 | 0.434 | 0.517 | |
| ✔ | ✔ | ✔ | ✔ | 0.436 | 0.442 | 0.524 |
| Settings/Metric | F1 Score (%) | Med. Epi. Error (px) | Run-Time (ms) |
|---|---|---|---|
| 44.29 | 2.61 | 21 | |
| 47.50 | 1.83 | 25 | |
| 49.31 | 1.07 | 34 | |
| 43.77 | 4.12 | 46 | |
| 34.81 | 13.23 | 73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, Y.; Zhou, L.; Li, X.; Feng, C.; Jin, X. SA-Net: Leveraging Spatial Correlations Spatial-Aware Net for Multi-Perspective Robust Estimation Algorithm. Algorithms 2025, 18, 65. https://doi.org/10.3390/a18020065
Shao Y, Zhou L, Li X, Feng C, Jin X. SA-Net: Leveraging Spatial Correlations Spatial-Aware Net for Multi-Perspective Robust Estimation Algorithm. Algorithms. 2025; 18(2):65. https://doi.org/10.3390/a18020065
Chicago/Turabian StyleShao, Yuxiang, Longyang Zhou, Xiang Li, Chunsheng Feng, and Xinyu Jin. 2025. "SA-Net: Leveraging Spatial Correlations Spatial-Aware Net for Multi-Perspective Robust Estimation Algorithm" Algorithms 18, no. 2: 65. https://doi.org/10.3390/a18020065
APA StyleShao, Y., Zhou, L., Li, X., Feng, C., & Jin, X. (2025). SA-Net: Leveraging Spatial Correlations Spatial-Aware Net for Multi-Perspective Robust Estimation Algorithm. Algorithms, 18(2), 65. https://doi.org/10.3390/a18020065






