Robust Client Selection Strategy Using an Improved Federated Random High Local Performance Algorithm to Address High Non-IID Challenges
Abstract
1. Introduction
2. Materials and Methods
2.1. Exploring Issues of Client Selection Methods
2.2. Developing the Improved Federated RHLP Algorithm for Efficient Client Selection
| Algorithm 1: Improved Federated RHLP algorithm. | |
| 1: | ServerExecute: |
| 2: | = Initial parameters of the CNNs model |
| 3: | N = Total number of clients |
| 4: | C1 = Fraction of candidate clients |
| 5: | C2 = Fraction of selected clients |
| 6: | m1 = Number of candidate clients |
| 7: | m2 = Number of selected clients |
| 8: | nk = Number of samples of client k |
| 9: | lk = Label diversity of client k |
| 10: | d_train_proportion = Proportion of local training samples |
| 11: | d_test_proportion = Proportion of local testing samples |
| 12: | For t = 1 to T do |
| 13: | m1 = N·C1 |
| 14: | Ct = {random set of candidate (m1) clients based on = , } |
| 15: | For k ∈ Ct in Parallel do |
| 16: | |
| 17: | |
| 18: | End for |
| 19: | For k ∈ Ct do |
| 20: | = |
| 21: | .append() |
| 22: | End for |
| 23: | St = {random set of higher local performance (m2) clients based on
,} |
| 24: | |
| 25: | End for |
| 26: | ClientUpdate_TestLP(k, w): |
| 27: | d_train, d_test = TrainTestSplit(dk, d_train_proportion, d_test_proportion) |
| 28: | B = (Split d_train into batches) |
| 29: | For i = 1 to E do |
| 30: | For b ∈ B do |
| 31: | |
| 32: | End for |
| 33: | End for |
| 34: | |
| 35: | Return w, LP to the server |
2.3. Experiment Setup
2.3.1. Dataset Preparation
2.3.2. Setting up Algorithms, CNN Model Structures, and Hardware Specifications
- Setting Up Algorithms
- 2.
- Setting Up CNN Model Structures
- 3.
- Setting Up Hardware Component Specifications
2.3.3. Algorithm Performance Evaluation
3. Results
4. Discussion and Conclusions
5. Future Works
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tahir, M.; Ali, M.I. Multi-Criterion Client Selection for Efficient Federated Learning. In Proceedings of the AAAI Symposium Series, Stanford, CA, USA, 20 May 2024; Volume 3, pp. 318–322. [Google Scholar]
- de Souza, A.M.; Maciel, F.; da Costa, J.B.; Bittencourt, L.F.; Cerqueira, E.; Loureiro, A.A.; Villas, L.A. Adaptive client selection with personalization for communication efficient Federated Learning. Ad Hoc Netw. 2024, 157, 103462. [Google Scholar] [CrossRef]
- Zhou, T.; Lin, Z.; Zhang, J.; Tsang, D.H. Understanding and improving model averaging in federated learning on heterogeneous data. IEEE Trans. Mob. Comput. 2024, 23, 12131–12145. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A. Communication-efficient learning of deep net-works from decentralized data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017; PMLR: Birmingham, UK, 2017; pp. 1273–1282. [Google Scholar]
- Putra, M.A.; Putri, A.R.; Zainudin, A.; Kim, D.S.; Lee, J.M. ACS: Accuracy-based client selection mechanism for federated industrial IoT. Internet Things 2023, 21, 100657. [Google Scholar] [CrossRef]
- Schoinas, I.; Triantafyllou, A.; Ioannidis, D.; Tzovaras, D.; Drosou, A.; Votis, K.; Lagkas, T.; Argyriou, V.; Sarigiannidis, P. Federated learning: Challenges, SoTA, performance improvements and application do-mains. IEEE Open J. Commun. Soc. 2024, 5, 5933–6017. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Lin, J.; Zhang, Q. A multi-agent reinforcement learning approach for efficient client selection in federated learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Pittsburgh, PA, USA, 28 June 2022; Volume 36, pp. 9091–9099. [Google Scholar]
- Zhou, H.; Lan, T.; Venkataramani, G.; Ding, W. On the Convergence of Heterogeneous Federated Learning with Arbitrary Adaptive Online Model Pruning. arXiv 2022, arXiv:2201.11803. [Google Scholar]
- Mu, X.; Shen, Y.; Cheng, K.; Geng, X.; Fu, J.; Zhang, T.; Zhang, Z. FedProc: Prototypical contrastive federated learning on non-IID data. Future Gener. Comput. Syst. 2023, 143, 93–104. [Google Scholar] [CrossRef]
- Cho, Y.J.; Wang, J.; Joshi, G. Client selection in federated learning: Convergence analysis and power-of-choice se-lection strategies. arXiv 2020, arXiv:2010.01243. [Google Scholar]
- Zeng, Y.; Teng, S.; Xiang, T.; Zhang, J.; Mu, Y.; Ren, Y.; Wan, J. A Client Selection Method Based on Loss Function Optimization for Federated Learning. Comput. Model. Eng. Sci. 2023, 137, 1047–1064. [Google Scholar] [CrossRef]
- Sittijuk, P.; Tamee, K. Fed-RHLP: Enhancing Federated Learning with Random High-Local Performance Client Selection for Improved Convergence and Accuracy. Symmetry 2024, 16, 1181. [Google Scholar] [CrossRef]
- Kairouz, P.; McMahan, H.B.; Avent, B.; Bellet, A.; Bennis, M.; Bhagoji, A.N.; Bonawitz, K.; Charles, Z.; Cormode, G.; Cummings, R.; et al. Advances and open problems in federated learning. Found Trends Mach Learn. 2021, 14, 1–210. [Google Scholar] [CrossRef]
- Le, D.D.; Tran, A.K.; Dao, M.S.; Nguyen-Ly, K.C.; Le, H.S.; Nguyen-Thi, X.D.; Pham, T.Q.; Nguyen, V.L.; Nguyen-Thi, B.Y. Insights into multi-model federated learning: An advanced approach for air quality index forecasting. Algorithms 2022, 15, 434. [Google Scholar] [CrossRef]
- Yang, H.; Li, J.; Hao, M.; Zhang, W.; He, H.; Sangaiah, A.K. An efficient personalized federated learning approach in heterogeneous environments: A reinforcement learning perspective. Sci. Rep. 2024, 14, 28877. [Google Scholar] [CrossRef] [PubMed]
- Iyer, V.N. A review on different techniques used to combat the non-IID and heterogeneous nature of data in FL. arXiv 2024, arXiv:2401.00809. [Google Scholar]
- Hu, M.; Yue, Z.; Xie, X.; Chen, C.; Huang, Y.; Wei, X.; Lian, X.; Liu, Y.; Chen, M. Is aggregation the only choice? Federated learning via layer-wise model recombination. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 25 August 2024; pp. 1096–1107. [Google Scholar]
- Zhang, L.; Fu, L.; Liu, C.; Yang, Z.; Yang, J.; Zheng, Z.; Chen, C. Towards Few-Label Vertical Federated Learning. ACM Trans. Knowl. Discov. Data 2024, 18, 1–21. [Google Scholar] [CrossRef]
- Xu, Y.; Liao, Y.; Wang, L.; Xu, H.; Jiang, Z.; Zhang, W. Overcoming Noisy Labels and Non-IID Data in Edge Federated Learning. IEEE Trans. Mob. Comput. 2024, 23, 11406–11421. [Google Scholar] [CrossRef]
- Li, A.; Zhang, L.; Tan, J.; Qin, Y.; Wang, J.; Li, X.-Y. Sample-level data selection for federated learning. In Proceedings of the IEEE INFOCOM 2021—IEEE Conference on Computer Communications, Vancouver, BC, Canada, 10–13 May 2021; pp. 1–10. [Google Scholar] [CrossRef]
- Yan, R.; Qu, L.; Wei, Q.; Huang, S.-C.; Shen, L.; Rubin, D.L.; Xing, L.; Zhou, Y. Label-Efficient Self-Supervised Federated Learning for Tackling Data Heterogeneity in Medical Imaging. IEEE Trans. Med. Imaging 2023, 42, 1932–1943. [Google Scholar] [CrossRef]
- Gu, W.Y.; Zhang, L.X. Strong law of large numbers for m-dependent and stationary random variables under sub-linear expectations. arXiv 2024, arXiv:2404.01118. [Google Scholar]
- Khalil, A.; Wainakh, A.; Zimmer, E.; ParraArnau, J.; Fernandez Anta, A.; Meuser, T.; Steinmetz, R. Label-aware aggregation for improved federated learning. In Proceedings of the 2023 Eighth International Conference on Fog and Mobile Edge Computing (FMEC), Tartu, Estonia, 18–20 September 2023; pp. 216–223. [Google Scholar]
- Alhijawi, B.; Awajan, A. Genetic algorithms: Theory, genetic operators, solutions, and applications. Evol. Intell. 2024, 17, 1245–1256. [Google Scholar] [CrossRef]
- Tirumalapudi, R.; Sirisha, J. Onward and Autonomously: Expanding the Horizon of Image Segmentation for Self-Driving Cars through Machine Learning. Scalable Comput. Pract. Exp. 2024, 25, 3163–3171. [Google Scholar] [CrossRef]
- Singh, G.; Sood, K.; Rajalakshmi, P.; Nguyen, D.D.; Xiang, Y. Evaluating Federated Learning Based Intrusion Detection Scheme for Next Generation Networks. IEEE Trans. Netw. Serv. Manag. 2024, 21, 4816–4829. [Google Scholar] [CrossRef]
- Shi, X.; Zhang, W.; Wu, M.; Liu, G.; Wen, Z.; He, S.; Shah, T.; Ranjan, R. Dataset Distillation-based Hybrid Federated Learning on Non-IID Data. arXiv 2024, arXiv:2409.17517. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. Proc. Mach. Learn. Syst. 2020, 2, 429–450. [Google Scholar]
- Ren, H.; Deng, J.; Xie, X. GRNN: Generative regression neural network—A data leakage attack for federated learning. ACM Trans. Intell. Syst. Technol. 2022, 13, 1–24. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, L.; Bae, J.; Chow, K.H.; Iyengar, A.; Pu, C.; Wei, W.; Yu, L.; Zhang, Q. Demystifying learning rate policies for high accuracy training of deep neural networks. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; IEEE: New York, NY, USA, 2019; pp. 1971–1980. [Google Scholar]
- Zhai, R.; Jin, H.; Gong, W.; Lu, K.; Liu, Y.; Song, Y.; Yu, J. Adaptive client selection and model aggregation for heterogeneous federated learning. Multimed. Syst. 2024, 30, 211. [Google Scholar] [CrossRef]
- Casella, B.; Esposito, R.; Sciarappa, A.; Cavazzoni, C.; Aldinucci, M. Experimenting with normalization layers in federated learning on non-IID scenarios. IEEE Access 2024, 12, 47961–47971. [Google Scholar] [CrossRef]
- Juan, P.H.; Wu, J.L. Enhancing Communication Efficiency and Training Time Uniformity in Federated Learning through Multi-Branch Networks and the Oort Algorithm. Algorithms 2024, 17, 52. [Google Scholar] [CrossRef]
- Tariq, A.; Serhani, M.A.; Sallabi, F.M.; Barka, E.S.; Qayyum, T.; Khater, H.M.; Shuaib, K.A. Trustworthy federated learning: A comprehensive review, architecture, key challenges, and future research prospects. IEEE Open J. Commun. Soc. 2024, 5, 4920–4998. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, D.; Tao, L.; Wang, K.; Qiao, S.; Zeng, X.; Tan, C.W. A credible and fair federated learning framework based on blockchain. IEEE Trans. Artif. Intell. 2024, 1–15. [Google Scholar] [CrossRef]
- Al-Betar, M.A.; Abasi, A.K.; Alyasseri, Z.A.; Fraihat, S.; Mohammed, R.F. A Communication-Efficient Federated Learning Framework for Sustainable Development Using Lemurs Optimizer. Algorithms 2024, 17, 160. [Google Scholar] [CrossRef]
- Nabavirazavi, S.; Taheri, R.; Iyengar, S.S. Enhancing federated learning robustness through randomization and mixture. Future Gener. Comput. Syst. 2024, 158, 28–43. [Google Scholar] [CrossRef]
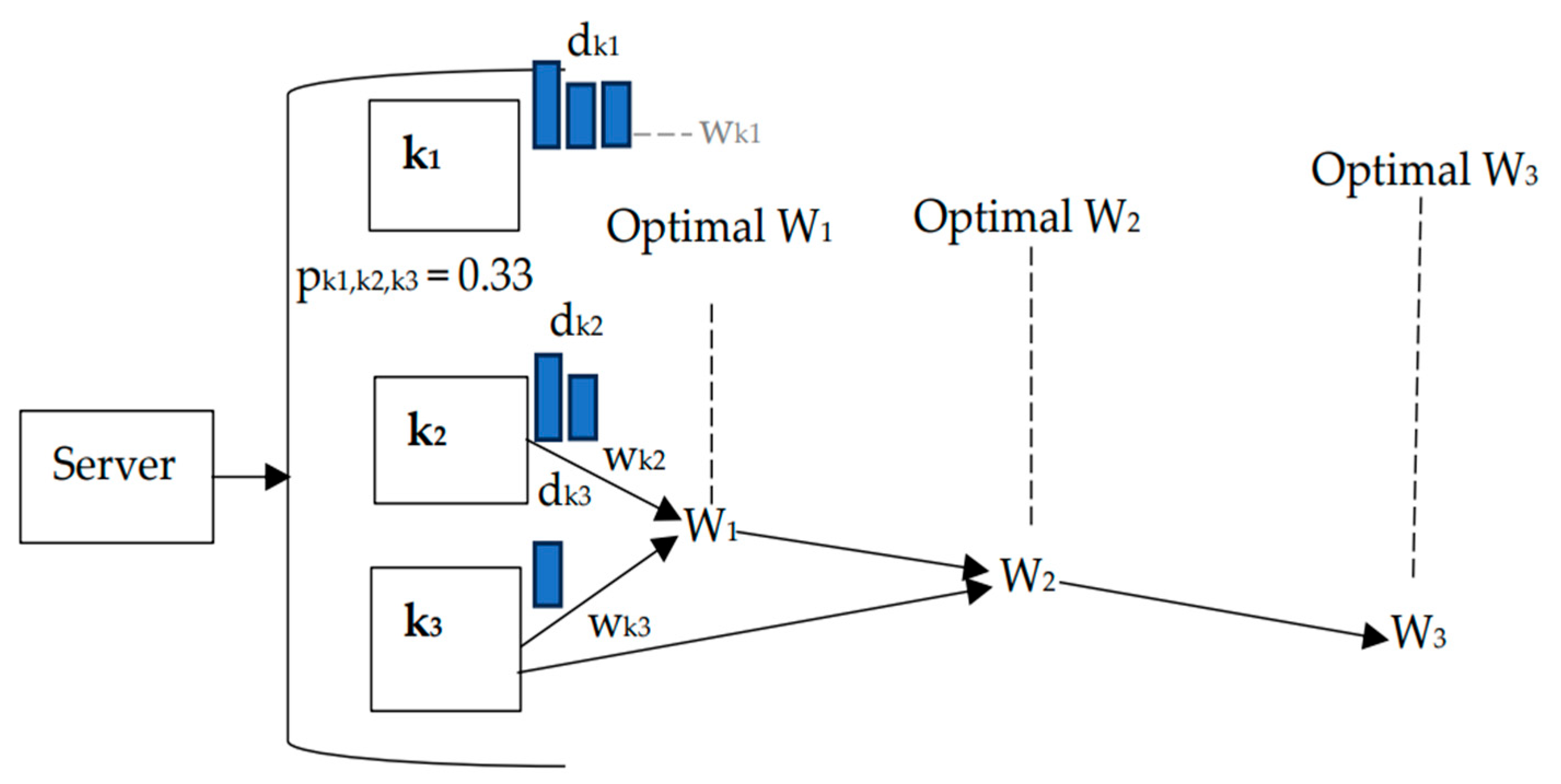

 : the green-colored section represents the local training samples of candidate clients (d_traink1, d_traink2, and d_traink3), and the sky-blue section represents the local testing samples of candidate clients (d_testk1, d_testk2, and d_testk3).
: the green-colored section represents the local training samples of candidate clients (d_traink1, d_traink2, and d_traink3), and the sky-blue section represents the local testing samples of candidate clients (d_testk1, d_testk2, and d_testk3).
 : the green-colored section represents the local training samples of candidate clients (d_traink1, d_traink2, and d_traink3), and the sky-blue section represents the local testing samples of candidate clients (d_testk1, d_testk2, and d_testk3).
: the green-colored section represents the local training samples of candidate clients (d_traink1, d_traink2, and d_traink3), and the sky-blue section represents the local testing samples of candidate clients (d_testk1, d_testk2, and d_testk3).





| Device | Specification |
|---|---|
| Central Processing Unit | 11th Gen Intel(R) Core(TM) i5-11400F 2.59 GHz |
| Graphics Processing Unit | Radeon (TM) RX 480 Graphics |
| Random Access Memory | 32.0 GB |
| Operating System | Windows 11 |
| Software Environment | Python 3.7.2 with the Pytorch framework |
| Algorithm | Issue Level | Accuracy of Global Model | Convergence Rounds and Time (Seconds) with Different Accuracy | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 60% | 70% | 80% | 90% | |||||||
| Round | Time | Round | Time | Round | Time | Round | Time | |||
| improved Fed-RHLP | High | 96.49% | 6 | 633.6 | 11 | 1161.6 | 19 | 2006.4 | 41 | 4329.6 |
| Low | 98.91% | 3 | 486 | 3 | 486 | 6 | 972 | 10 | 1620 | |
| FedAvg | High | 86.18% | 32 | 1747.2 | 74 | 4040.4 | 126 | 6879.6 | - | - |
| Low | 98.03% | 9 | 680.4 | 12 | 907.2 | 12 | 907.2 | 52 | 3931.2 | |
| PoC | High | 90.31% | 43 | 3947.4 | 57 | 5232.6 | 85 | 7803 | 185 | 16,983 |
| Low | 98.76% | 3 | 451.8 | 5 | 753 | 8 | 1204.8 | 15 | 2259 | |
| FedChoice | High | 87.80% | 40 | 3816 | 60 | 5724 | 92 | 8776.8 | - | - |
| Low | 98.78% | 3 | 464.4 | 5 | 774 | 8 | 1238.4 | 14 | 2167.2 | |
| Algorithm | Issue Level | Accuracy of Global Model | Convergence Rounds and Time (Seconds) with Different Accuracy | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 60% | 70% | 80% | 90% | |||||||
| Round | Time | Round | Time | Round | Time | Round | Time | |||
| improved Fed-RHLP | High | 89.06% | 6 | 1288.8 | 11 | 2362.8 | 15 | 3222 | - | - |
| Low | 90.97% | 1 | 328.2 | 2 | 656.4 | 7 | 2297.4 | 48 | 15,753.6 | |
| FedAvg | High | 83.68% | 13 | 2386.8 | 23 | 4222.8 | 55 | 10,098 | - | - |
| Low | 90.59% | 3 | 747 | 3 | 747 | 3 | 747 | 83 | 20,667 | |
| PoC | High | 85.79% | 8 | 1929.6 | 9 | 2170.8 | 39 | 9406.8 | - | - |
| Low | 90.77% | 3 | 1072.8 | 5 | 1788 | 6 | 2145.6 | 85 | 30,396 | |
| FedChoice | High | 87.90% | 8 | 1934.4 | 12 | 2901.6 | 21 | 5077.8 | - | - |
| Low | 90.63% | 2 | 714 | 4 | 1428 | 6 | 2142 | 59 | 21,063 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sittijuk, P.; Petrot, N.; Tamee, K. Robust Client Selection Strategy Using an Improved Federated Random High Local Performance Algorithm to Address High Non-IID Challenges. Algorithms 2025, 18, 118. https://doi.org/10.3390/a18020118
Sittijuk P, Petrot N, Tamee K. Robust Client Selection Strategy Using an Improved Federated Random High Local Performance Algorithm to Address High Non-IID Challenges. Algorithms. 2025; 18(2):118. https://doi.org/10.3390/a18020118
Chicago/Turabian StyleSittijuk, Pramote, Narin Petrot, and Kreangsak Tamee. 2025. "Robust Client Selection Strategy Using an Improved Federated Random High Local Performance Algorithm to Address High Non-IID Challenges" Algorithms 18, no. 2: 118. https://doi.org/10.3390/a18020118
APA StyleSittijuk, P., Petrot, N., & Tamee, K. (2025). Robust Client Selection Strategy Using an Improved Federated Random High Local Performance Algorithm to Address High Non-IID Challenges. Algorithms, 18(2), 118. https://doi.org/10.3390/a18020118






