A Scalable Framework with Modified Loop-Based Multi-Initial Simulation and Numerical Algorithm for Classifying Brain-Inspired Nonlinear Dynamics with Stability Analysis

Abstract

The principal problem with the analysis of nonlinear dynamical systems is that it is repetitive and inefficient to simulate every initial condition and parameter configuration individually. This not only raises the cost of computation but also constrains scalability in the exploration of a large parameter space. To solve this, we restructured and extended the computational framework so that variation in the parameters and initial conditions can be automatically explored in a unified structure. This strategy is implemented in the brain-inspired nonlinear dynamical model that has three parameters and multiple coupling strengths. The framework enables detailed categorization of the system responses through statistical analysis and through eigenvalue-based assessment of the stability by considering multiple initial states of the system. These results reveal clear differences between periodic, divergent, and non-divergent behavior and show the extent to which the strength of the coupling $k_{ij}$ can drive transitions to stable periodic behavior under all conditions examined. This method makes the analysis process easier, less redundant, and provides a scalable tool to study nonlinear dynamics. In addition to its computational benefits, the framework provides a general method that can be generalized to models with more parameters or more complicated network structures.

1. Introduction

Nonlinear dynamical systems are objects of study that must be explored carefully in terms of parametric variations and sensitivity to initial conditions. Traditional methods tend to examine each of the initial conditions individually, which may be ineffective and redundant. To fix this, we present an automated and unified exploration model that systematically evaluates the system over a wide set of parameters and initial conditions. In this method, the internal parameters $a_1$, $b_1$, and $c_1$ are varied within a defined search space, with different initial conditions placed inside the same computational structure. This combined design means that there is no longer a requirement to run a particular script or manually simulate a specific case, and it provides a consistent and comprehensive evaluation of the system’s behavior across the parameter space. The time dependence of each set of parameters and initial conditions is simulated and categorized by the quality of the stability of the trajectories using eigenvalue analysis and statistics of the trajectories. The suggested methodology is an efficient and scalable way of classifying the behavior of systems by iterating numeric algorithms to classify them using parameters and an initial state. This not only reduces redundancy in the calculations, but it also offers a systematic framework within which one can study nonlinear systems to become dynamic under different conditions. This kind of methodology has two benefits. First, it removes redundancy and manual effort from the process. Second, it offers a systematic and scalable basis on which critical transitions can be determined, stability regimes can be identified, and behaviors at various coupling strengths can be compared. Therefore, it becomes efficient, reproducible, and understandable to study nonlinear dynamics, which leads to a framework and makes it feasible to study more deeply than traditional case-by-case methods.

Nonlinear dynamical systems have been central to the consideration of the complex behavior of natural and engineered systems. Such models can be very sensitive to parameters and initial conditions, exhibit periodicity, and demonstrate chaos. The properties of systematizing and graphically visualizing these kinds of behavior in a large parameter space are fundamental to the search for the underlying organization of such systems and the subsequent application of such systems to disciplines such as neuroscience, physics, and control theory. They have the properties needed for these models in that they describe how the state of a system varies with time; e.g., differential equations, which can be used to model both a natural system and an engineered system [1]. A property of dynamical systems is that they are largely sensitive to internal parameters, and this may cause them to be either stable, periodic, unstable, or chaotic. The slight changes in the parameters can result in significant changes in behavior, which are called bifurcations [2]. It is this sensitivity that makes it particularly important to determine how the dynamics depend on the system’s parameters in order to perform a parameter-space analysis.

In practice, there is a need to understand the way in which the dynamics of global systems are changing within the whole spectrum of parameters. Analytical methods can only be limited to exceptional cases or idealized situations in the case of nonlinear systems. Thus, computational tools are needed to look at a broader parameter space. A parametric classification of the sets of behavior can be used to determine the boundaries between qualitatively different sets of behavior, e.g., between chaotic and non-chaotic regions or between a set of fixed points and a set of limit cycles [3]. Such classifications are very handy in the design of control systems, in stability analysis, signal processing, and even in interpreting such complex biological rhythms or population dynamics.

2. Literature Review

The identification and analysis of parameters of dynamical systems have been central subjects in the study of complex systems. More recent studies have been conducted on creating systematic, multidimensional, and data-driven techniques that can be used to investigate the parameter space of such systems. The most common approach in traditional studies has been to test the effect of one or two parameters separately, which can provide valuable but limited information on the behavior of the system. Stuart et al. pointed out the significance of parameter-space classification of a dynamical system in order to comprehend its overall behavior. Their analysis [4] was devoted to systematic coverage of the parameter space instead of an analysis of the system with particular or randomly chosen parameters. This is yet another innovative aspect of the present work, as it is not a case-based search but rather a methodological determination of systematic and multidimensional categorization of parameters. Behrisch et al. discuss the dynamics theory of describing dynamical systems in terms of category theory, which offers a single and abstract picture for researching the behavior of systems. They demonstrate that categorical constructions can describe changes, compositions, and interactions between dynamical systems in a mathematically consistent manner [5]. Abarbanel et al. provided a systematic solution to the estimation of both internal states and unknown parameters of nonlinear dynamical systems in the case of observational data [6]. Their approach is a combination of data assimilation and optimization strategies to create consistency between model development and observations. Patel et al. experimentally [7] observed extreme multi-stability in a pair of coupled Rössler electronic circuits, finding that the system is able to transition to a large number of different attractors with a significant dependence on initial conditions. The article also emphasized the importance of small changes in initial conditions in producing radically different long-term dynamics in coupled oscillator systems. It is based on short-term prediction and integrates neural networks and Markov theory to introduce promising effects of modeling a system. It works in systems that exhibit periodic, limit cycle, and chaotic behavior [8].

The analysis of complex dynamics according to the diligent study [9] of parameter spaces has been considered in the last few years. A general classification of multi-stability and Lyapunov exponents pertaining to nonlinear Schrödinger systems was proposed. Chaotic attractors, bifurcation analysis, and Poincaré maps equations have been used in this work to find areas where complex dynamics are present and why more than one stable state can be present within the parameter space. An international standard method of analysis of the stability of multi-stable dynamical systems was proposed in [10]. Not only did they highlight the importance of coming up with effective classification schemes in large parameter spaces, but they also provided the computational tools that allowed the researcher to visualize the basins of attraction and quantify global stability in an informed way. They proposed applying geometric principles to machine learning techniques in modeling dynamical systems. A framework [11] offered by Azizi et al. relates machine learning algorithms to the theory of dynamical systems, demonstrating that learning processes may be considered trajectories changing with time. They study the stability, convergence, and behavior of learning models based on nonlinear dynamics tools.

The transition of systems between conservative and dissipative dynamics was analyzed in a detailed multiparameter way in [12]. Initial conditions and parameter values have been known to affect transitions and are also useful in indicating methods for determining points of bifurcation and regime changes in the space of systems. The existence of multiple stable states that can be reached within a set of parameters, along with the possibility of transitions among them, constitutes the phenomenon of multi-stability, which has a wide variety of applications, from neural networks to ecological models. Pisarchik et al. in [13] survey the problem of the emergence of multi-stability in nonlinear dynamical systems and how one can seek to determine such complex behaviors in both natural and engineered systems. This is essential in terms of realizing that the systems could move to different operational states upon perturbation. Transitions, such as bifurcation or phase transitions, are dynamic processes and are important in the evolution of systems over time. The dynamic transition theory is used to investigate transitions in dissipative systems in [14], detailing its mathematical background and history of development.

In other parts of the classification scheme of partially observed dynamical systems, the noise in the data was corrected with Bayesian inference and posterior distribution [15] to deal with insufficient sampling. The technique facilitated a syntactically viable categorization of the conduct of the system, which was provided with imperfect information, which is common in experiments and practical systems. In [16], a more theoretical contribution has been presented, which discussed singularities and transition delays in a dynamical system. It is the first work to have qualified a framework to discuss how bottlenecks and time-sensitive phenomena emerge due to initial states and constraints on the abilities of a system, providing some data on the dynamics of bottlenecks and time-sensitive bifurcations. In [17], the role of stochastic differential equations (SDEs) in the estimation of robust parameter values for noisy systems has been discussed. Schittkowski explains the use of numerical approaches [18] to parameter estimation in dynamics with emphasis on optimization-based approaches. The way in which system parameters can be determined through the minimization of the difference between actual data and model values has been discussed. A study [19] of the Mackey–Glass delayed system mapped regions in the parameter space, zones of multi-stable states. By examining the basins of attraction, they provided us with insight into the control and synchronization of delayed systems, showing how sensitivity to parameter changes could produce radical changes in long-term behavior.

In [20], the non-smooth dynamical system shows the coexistence of strange and non-chaotic, as well as quasi-periodic, attractors. Their attraction domains are used to analyze the global behavior with multiple attractors at the same parameter values. The authors in [21] examined the dynamics of discontinuous jerk-type systems, in which multi-stability and attraction are present within certain parameter windows. It has been revealed that various attractor types, that is, periodic, chaotic, or a combination of two or more, are allowed to coexist in the phase space, regardless of whether they are self-excitable or inhibited. Based on the literature review, this work applies a better framework to systematically search the parameter space and categorize system dynamics in a more efficient and general manner.

Using a computational pipeline capable of classifying behavior in the entire parameter grid $3D$, the current research will close that gap. The fact that the study’s generalizations can be applied to large nonlinear dynamical systems is the most significant finding. The paper’s analysis and computation techniques can be applied to more complicated and complex systems. Such systems are most frequently found in biological, physical, and engineering systems. The study of these systems must focus on understanding how the parameters affect the predictability and control of the behavior. A systematic understanding of how the parameter space can be separated into different dynamical regimes, whether they be multi-stable, chaotic, periodic, or stable, is made possible by this parameter space structure. In addition to aiding in the discovery of undiscovered dynamical structures, it also contributes to the development of stronger models and more advantageous tactics that may be used in an effort to control and improve systems. This paper is structured as follows. Its main results are shown in Section 3, which starts with the algorithm suggested for parameter space exploration and classification (Section 3.1) and then proceeds to its application (Section 3.2). According to the coupling strength, the application is further separated into three cases: Case 1 with $k_{ij}=0\%$ (Section 3.2.1), Case 2 with $k_{ij}=10\%$ (Section 3.2.2), and Case 3 with $k_{ij}=20\%$ (Section 3.2.3). The parametric space definition (Section 3.3.1), statistical property-based categorization (Section 3.3.2), distribution chart analysis (Section 3.3.3), and coordinate plots (Section 3.3.4) are all included in the systematic parameter space categorization presented in Section 3.3. The eigenvalue-based classification is presented in Section 3.4. An overview of the main conclusions and methodological advancements is provided at the end of the paper.

3. Main Result

In order to address the inefficiencies of exploring the parameter space by analyzing each initial condition one at a time, we have designed a loop-based approach for the systematic exploration and categorization of the parameter space. In this section, a detailed description of the method is provided, outlining the steps starting with the definition of the search space and ending with the classification of system behaviors. The method integrates numerical algorithms with iterative looping so that the combinations of initial parameters are systematically surveyed. The methodology enables the automation of the simulation process, thereby improving redundancy and scalability, and offers a stable framework for dynamical analysis.

Table 1. Comparison of traditional approaches and the proposed loop-based methodology.

Steps	Inefficiencies	Proposed Improvements
Defining Parameter Space	Parameters and initial conditions are often tested manually with limited coverage of the parameter space.	Systematic definition of parameter ranges and initial conditions; full exploration of parameter space using loops.
Control Variables	External variables (e.g., coupling strength $k_{ij}$) adjusted separately for each run.	External control variables are integrated directly into the loop, allowing simultaneous evaluation.
Simulation Execution	Separate code or repeated manual runs required for each initial condition and parameter set.	Unified loop structure automates simulations for all parameter–initial condition combinations in a single run.
Classification	Stability analysis performed in isolation, often only for selected trajectories; risk of inconsistency.	Automated classification of all cases based on statistical properties and eigenvalue analysis; consistent labeling.
Result Storage	Results stored case-by-case; hard to reproduce and time-consuming for large data sets.	Automated storage of results into structured files, ensuring reproducibility and scalability.

is a comparison between traditional case-by-case methods and the proposed loop-based framework, and demonstrates how the new framework surpasses inefficiencies in parameter exploration, simulation, and classification.

3.1. Algorithm: General Framework for Parameter Space Exploration and Categorization

The suggested framework is extensible since it is model-independent. It is also meant to be used on a nonlinear dynamical system through the redefinition of the governing equations and parameter ranges; that is, each step, such as the definition of parameters and their classification, is a standalone module. The algorithm enables simulations to be parallelized across multiple cores or nodes, enabling an effective exploration of higher-dimensional parameter spaces of interest. As an illustration, the same framework can be used with the Rossler system as well as with other systems, without making any changes to the basic framework. This scalability to higher-dimensional systems and larger networks is guaranteed by this modular design and computational flexibility. The framework is designed as a sequence of systematic steps that mutually allow for efficient exploration of parameters and categorization of stability, beginning with the definition of parameter space and leading to the classification and storage of results.

• Defining Parameter Space

The methodology starts with the definition of the parameter space in which an analysis will be performed. This includes specifying the ranges of all system parameters $(a_1,b_1,c_1)$, the choice of appropriate initial conditions, and the choice of sampling. The sampling plan or step size is selected carefully to trade off between computational feasibility and the resolution required to resolve key transitions in the system behavior.

• Setting Control Variables

After defining the parameter space, the external control variables, including the strength of the coupling $k_{ij}$, are prescribed. The data structures at this level are also ready to hold the results of simulations and related classifications. It is an organization that makes all results available for analysis later and prevents redundancy in the iterative process.

• Automated Simulation Loop

The fundamental structure of the framework is a systematic exploration loop through a parameter space that is automated. Each control variable $k_{ij}$ is tested in each entry of all triplets of parameters $(a_1,b_1,c_1)$. The simulation is either a combination of the system trajectories or a calculation of the Jacobian at every point, and the resultant eigenvalue or trajectory data are saved to be used later. This removes the issue of individual codes or the manual execution of individual cases.

• Classification Step

Once the data are collected, they undergo a classification scheme in order to differentiate the various types of system behavior. Statistical parameters such as growth, decay, and periodicity are investigated when these are based on trajectories. Alternatively, using the eigenvalue analysis, the Jacobian matrix is obtained, and its eigenvalues are evaluated to obtain the type of stability of the system. All cases are then defined by the dynamics they exhibit; that is, divergent, non-divergent, periodic, or certain types of stability, namely, $B1$ and $B2$.

• Result Storage

All parameter sets, initial conditions, and their corresponding categories are stored in well-formatted forms to facilitate reproducibility and scalability. It is possible to export the results to CSV files or other standard storage systems, and thus efficiently retrieve, share, and process further with additional statistics without repeating the simulations.

• Visualization

Lastly, the results are categorized and visualized to provide clear information on the system’s behavior in the parameter space. Scatter plots, distribution charts, and coordinate plots are used to draw attention to trends and changes in dynamical regimes. These visualizations help us to understand the complicated parameters, initial conditions, and relationships between the outcomes of the system.

3.2. Application

In this paper, a brain-inspired dynamical system is a term used to describe a mathematical model that recapitulates important dynamic properties of a brain activity, including oscillations, synchronization, and chaotic transitions. This study was based on the Rossler system, which is chaotic in nature. It was initially generalized to a 360-node network with each node modeling an individual Rossler oscillator that interacts with the others via coupling terms. Such a network configuration allowed for the achievement of a wide range of complex collective behaviors, including synchronization and phase correlations among nodes. However, here in the current study, the emphasis is on one node of the system to examine the behavior of the node itself and to obtain the local properties of the system in the context of the network.

The given case study is devoted to the Rossler system as one of the representatives of the nonlinear ODEs, due to the wide variety of dynamic behaviors that can be observed in the system; thus, it serves as a suitable test case for the proposed framework in the exploration and classification of the parameter space. The selection of one system was aimed at providing a strong and descriptive illustration of the procedure and its working process. However, the framework itself is model-independent and can be applied directly to other nonlinear dynamical systems, e.g., the Lorenz, Chen, or Hindmarsh–Rose models, by merely redefining the governing equations and parameter ranges. This flexibility is used to ensure that the approach is always general and applicable in real life within different fields of science and engineering. The dynamical system taken into account in this work is provided by the following set of corresponding nonlinear differential equations [22].

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_i& =-y_i-z_i+\sum _{j=1}^{360}{k}_{ij}^{\left(xx\right)}(x_j-x_i),\hfill \\ \hfill {\dot{y}}_i& =x_i+a_i{y}_i+\sum _{j=1}^{360}{k}_{ij}^{\left(yy\right)}(y_j-y_i),\hfill \\ \hfill {\dot{z}}_i& =b_i-c_i{z}_i+x_i{z}_i+\sum _{j=1}^{360}{k}_{ij}^{\left(zz\right)}(z_j-z_i).\hfill \end{array}\right.$$

(1)

The variables $x_i$, $y_i$, and $z_i$ represent the dynamic states of the i-th unit in the network and evolve over time. This set of control coefficients incorporates the local control coefficients, where the self-feedback of $y_i$ is provided by $a_i$, a constant external feed to $z_i$ is provided by $b_i$, and the decay rate of $z_i$ is provided by $c_i$. An interaction between the components $x_i$ and $z_i$ has a nonlinear term in the equation. The diffusion conditions are represented in summation terms that indicate the interconnectivity of the nodes. The products $k_{ij}^{\left(xx\right)}$, $k_{ij}^{\left(yy\right)}$, and $k_{ij}^{\left(zz\right)}$ indicate the intensity of association between the nodes i and j. Using a combination of these, we can obtain a very highly flexible system that can display many different behaviors, and all this depends on the parameter values, as well as the strengths of the interactions. The dynamical system studied in this paper originates from a brain-inspired nonlinear circuit model, and it is constructed from a number of locally interconnected nonlinear ordinary differential equations that model the time-dependent behavior of three state variables $x_i$, $y_i$, and $z_i$ at node i. Such variables are states of electricity in a simplified circuit model of a neural unit using circuit analogs, capacitors, and resistors. The system exhibits a wide range of dynamics, including local feedback, nonlinearity, and inter-node coupling.

We examine a nonlinear dynamical system represented as a network of interconnected components. Each unit of the network is described by three state variables that capture its behavior under different conditions. The internal parameters of the system, $a_i$, $b_i$, and $c_i$, are systematically varied over a wide range $[0,6]$ to explore the response of the system across diverse parameter settings. The strength of the interaction $k_{ij}$ controls the coupling between the units, indicating the level of influence they exert on each other. Three coupling strengths are considered: 0% (no coupling), 10% (moderate coupling), and 20% (strong coupling) to study how different levels of interaction affect the overall dynamics of the system.

The external nodes have fixed values, and for the purpose of studying the internal behavior, we set $x_j=\alpha =5$, $y_j=\beta =6$, and $z_j=\gamma =7$. These act as constant injections or background inputs from neighboring areas and, in effect, create a closed system in which the dynamics of the local nodes can be observed and classified.

We also performed a systematic sweep of initial conditions to enable a finer analysis of the system’s sensitivity to initial conditions, as well as the resulting dynamical behaviors. Specifically, the initial conditions of the form $x_1$, $y_1$, and $z_1$ are varied using a discrete grid with a step of 0.3 in the domain [−0.2, 0.2]. In order to study the behavior of the system under any of these initial conditions, we introduce an automatic structure of simulations, where all the possible consistent dynamical trajectories and their indexed results can be constructed during a single run. This also eliminates the necessity of handling each initial condition separately with manual analysis and allows all of the relevant parametric behavior to be plotted simultaneously, saving significantly on computing and visualization expenses, with much of the systematic exploration preserved. A direct choice of the parameter ranges and initial conditions was made to be consistent with the original system specification in the reference model [22]. The parameters $a_i$, $b_i$, and $c_i$ used in that model are positive control coefficients that should act within a reasonably positive range. Therefore, the range $[0,6]$ was adopted to encompass the entire meaningful operating space, as well as to permit systematic exploration. Similarly, the reference model specifies that the starting conditions applied in its simulations were randomly chosen within the interval [−0.2, 0.2] for each state variable and were maintained the same in the current work. On the whole, these options allow for maintaining the parameters of the original formulation in balance, in addition to enabling a complete exploration of the dynamics of the system.

Table 2. Parameter values used in the dynamical system analysis.

Parameter Set
$k_{ij}$	$a_1$	$b_1$	$c_1$	$x_j=\alpha$	$y_j=\beta$	$z_j=\gamma$
0.0 (0%)	[0, 6]	[0, 6]	[0, 6]	5	6	7
0.1 (10%)	[0, 6]	[0, 6]	[0, 6]	5	6	7
0.2 (20%)	[0, 6]	[0, 6]	[0, 6]	5	6	7

illustrates the ranges and fixed values of the parameters involved in the analysis of the dynamical system with different coupling strengths $k_{ij}$, which set the shape parameters.

Table 3. Initial conditions used in the dynamical system simulation.

Variable	Range	Step Size
$x_1$	$-0.2$ to $0.2$	0.3
$y_1$	$-0.2$ to $0.2$	0.3
$z_1$	$-0.2$ to $0.2$	0.3

provides the initial conditions used in the simulation, including the range and step size of each state variable $(x_1,y_1,z_1)$.

In order to investigate the stability behavior of the nonlinear dynamical system, we perform an eigenvalue analysis by computing the Jacobian matrix at the chosen initial conditions for each combination of parameters. The system is linearized around the sampled initial states instead of determining the explicit equilibrium point, and the local response of the system to small disturbances at these points is determined. That way, we obtain the information on whether the local flow around the initial state is divergent, non-divergent, or periodic, which aids in categorizing the behavior in the parameter space. Once the Jacobian J has been calculated at every sampled point, the characteristic equation is solved to extract the eigenvalues, and then these eigenvalues are used to classify the local linear behavior of the system. In a three-variable system whose state variables are $x_1,y_1,z_1$, the Jacobian matrix will acquire the general form:

$$J=\left[\begin{array}{ccc}{\displaystyle \frac{\partial {\dot{x}}_1}{\partial x_1}}& {\displaystyle \frac{\partial {\dot{x}}_1}{\partial y_1}}& {\displaystyle \frac{\partial {\dot{x}}_1}{\partial z_1}}\\ {\displaystyle \frac{\partial {\dot{y}}_1}{\partial x_1}}& {\displaystyle \frac{\partial {\dot{y}}_1}{\partial y_1}}& {\displaystyle \frac{\partial {\dot{y}}_1}{\partial z_1}}\\ {\displaystyle \frac{\partial {\dot{z}}_1}{\partial x_1}}& {\displaystyle \frac{\partial {\dot{z}}_1}{\partial y_1}}& {\displaystyle \frac{\partial {\dot{z}}_1}{\partial z_1}}\end{array}\right].$$

(2)

Once the Jacobian is calculated, we find the eigenvalues using the characteristic polynomial, which is obtained through the following determinant equation:

$$\det (J-\lambda I)=0.$$

(3)

where $\lambda$ represents the eigenvalues and I is the identity matrix. When the real parts of all the eigenvalues are negative, the system is locally stable; if there is one eigenvalue with a positive real part, the system is unstable. Imaginary eigenvalues completely solve a problem that is oscillatory or periodic. Such an eigenvalue-based classification systematizes and makes rigorous the analysis of the dynamic behavior of the system across parameter regimes.

3.2.1. Case 1: $k_{ij}=0\%$

When there is no coupling of nodes, the coefficient $k_{ij}$ assumes a value of zero. This disconnects the system node from the network, and only its internal dynamics are governed by the parameters $a_1,b_1,c_1\in [0,6]$. The resulting system is as follows:

$$\begin{array}{cc}\hfill {\dot{x}}_1& =-y_1-z_1,\hfill \\ \hfill {\dot{y}}_1& =x_1+a_1{y}_1,\hfill \\ \hfill {\dot{z}}_1& =b_1-c_1{z}_1+x_1{z}_1.\hfill \end{array}$$

(4)

In order to analyze the local behavior of this system in the parameter space, a Jacobian matrix is computed as such at the chosen initial conditions. The eigenvalues of this Jacobian determine whether the local flow around those locations is rotational, contracting, or divergent. The classification of eigenvalues allows us to plot the various types of responses within the range of parameters being investigated.

3.2.2. Case 2: $k_{ij}=10\%$

In this case, the coupling is moderate, and $k_{ij}=0.1$. The internal parameters belong to the interval $[0,6]$. The external node values are assigned as $x_j=\alpha =5$, $y_j=\beta =6$, and $z_j=\gamma =7$. Replacing them in the system, we obtain the following:

$$\begin{array}{cc}\hfill {\dot{x}}_1& =-y_1-z_1+35.9(5-x_1),\hfill \\ \hfill {\dot{y}}_1& =x_1+a_1{y}_1+35.9(6-y_1),\hfill \\ \hfill {\dot{z}}_1& =b_1-c_1{z}_1+x_1{z}_1+35.9(7-z_1).\hfill \end{array}$$

(5)

The stability behavior of this case is also evaluated in the same way. The Jacobian is evaluated at the selected initial states, and the eigenvalues obtained characterize the local dynamics of each simulation parameter combination.

3.2.3. Case 3: $k_{ij}=20\%$

Here, the coupling effect is considered stronger with $k_{ij}=0.2$. The internal parameters are now in the range [0, 6], and the external parameters are set to the same values as before: $x_j=\alpha =5$, $y_j=\beta =6$, and $z_j=\gamma =7$. The results of substitution are as follows:

$$\begin{array}{cc}\hfill {\dot{x}}_1& =-y_1-z_1+71.8(5-x_1),\hfill \\ \hfill {\dot{y}}_1& =x_1+a_1{y}_1+71.8(6-y_1),\hfill \\ \hfill {\dot{z}}_1& =b_1-c_1{z}_1+x_1{z}_1+71.8(7-z_1).\hfill \end{array}$$

(6)

At higher coupling strengths, the obtained expressions are discussed using the same Jacobian-based procedure employed throughout this paper. The local eigenvalues that are calculated in the sampled states show how strong the coupling is and how it shifts the immediate tendencies of the system.

3.3. Systematic Parameter Space Categorization

A systematic investigation of how system responses change as important parameters and initial conditions change is necessary to comprehend the dynamic behavior of nonlinear systems. In order to thoroughly map the dynamics of a brain-inspired nonlinear system, we use a methodical parameter space classification approach in this study. We are able to capture a large range of potential system behaviors by building a grid in a three-dimensional parameter space, specified by $a_1$, $b_1$, and $c_1$, each of which ranges from 0 to 6. Critical transitions and areas of qualitative change in system dynamics, such as bifurcations, stability loss, and oscillation beginning, can be detected using this grid-based method. To demonstrate the sensitivity of the system to initial conditions, we chose three representative initial states from a large number of conditions $[-0.20,-0.20,-0.20]$, $[-0.20,-0.20,0.10]$, and $[-0.20,0.10,-0.20]$. These have been selected as examples to show the range of behavior levels. Two distinct methodologies are employed within this framework to categorize system behavior.

• Analysis of Statistical Behavior: This method assesses the system time-series trajectories to identify if the behavior is periodic, non-divergent, or diverging. It provides a global view of the long-term behavior of the system by concentrating on how it changes over time under various circumstances. This approach demonstrates how changes to the initial conditions or parameters affect the trajectory results.

• Eigenvalue Classification: The Jacobian matrix is calculated at the local behavior of the system under the chosen initial conditions. The eigenvalues of this Jacobian explain the response of the system to small disturbances around the sampled states. Having sorted the eigenvalues into real, complex, positive, negative, or zero, we can deduce the existence of tendencies in the general behavior of the parameter space, e.g., divergence, non-divergence, or periodicity.

3.3.1. Parametric Space

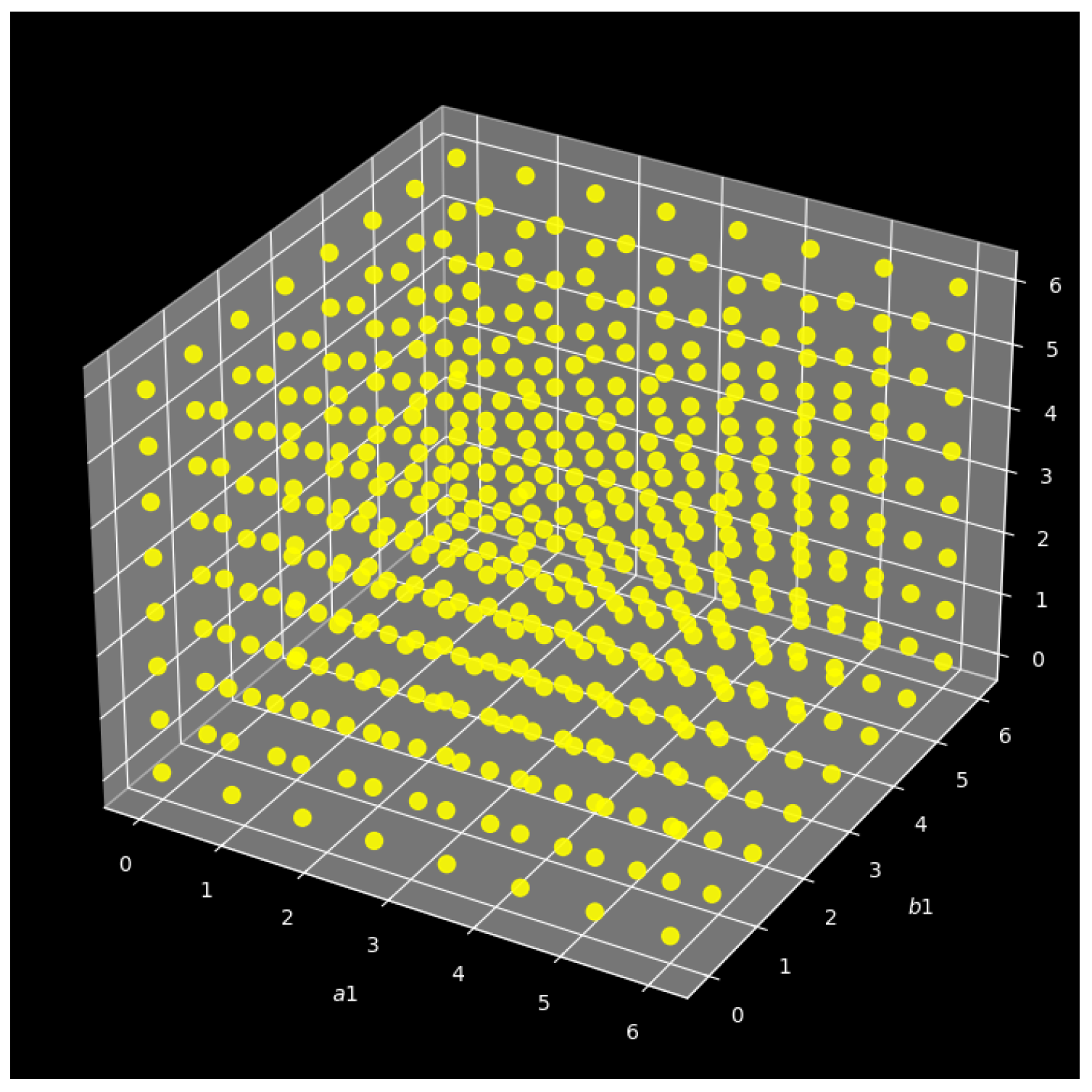
We constructed a thorough three-dimensional parameter space for searching in order to methodically investigate the multidimensional nature of the nonlinear dynamical system that our model equations specify. This is accomplished by specifying discrete sets of intervals, created using locations that are equidistant by 8, in which the values of the system parameters vary: $a_1$, $b_1$, and $c_1$, individually within the range $[0,6]$. With different configurations $8\times 8\times 8$ = 512, the resulting parametric grid then enables us to investigate a wide range of dynamical behaviors. The $8\times 8\times 8$ grid was chosen as a convenient sampling option in order to sample a large parameter space in three dimensions and have the simulations manageable, since each parameter combination was also sampled in a variety of initial conditions and coupling strengths. Simulation behaviors are classified and characterized under a variety of initial conditions to achieve robustness. Dynamics that are not visible in a single-trajectory analysis can be revealed with the use of this multi-initial condition technique. Figure 1 provides a graphic representation of the parametric space generated, with each point denoting a specific set of parameter values selected within the given limits. This hierarchical structure makes it possible to directly comprehend how modifications to the parameters impact the behavior of the system.

3.3.2. Categorization Based on Statistical Properties

In this analysis, we will explore the effect of the coupling strength ($k_{ij}$) and the varying initial conditions on the long-term dynamics of a nonlinear dynamic system. We shall similarly vary ($k_{ij}$) and run the system under initial conditions that differ substantially and seek to discern the impact of $k_{ij}$ on how the trajectories evolve within a three-dimensional parameter space spanned by $a_1$, $b_1$, and $c_1$. Every trajectory is classified according to the statistical behavior, which is periodic, divergent, or non-divergent. Constant displays this type of classification through $3D$ scatter plots in which every point within the parameter space is colored according to the behavior produced. The results are obtained for three coupling strength values ($k_{ij}=0$, 0.1 and 0.2) and three representative initial conditions [$-0.20,-0.20,-0.20$], [$-0.20,-0.20,0.10$], and [$-0.20,0.10,-0.20$]. This twofold variation enables us to measure the sensitivity of the system to either internal structure or external coupling and to measure how the dynamics are stabilized into periodic attractors by the growing coupling across a wide range of initial set-ups. The complete ODE-based behavioral classification, a processor of all trajectories, took an average of 8 min of computational time. Figure 2 shows the classification of the behavior of the system according to the parameter statistics in the parameter space under varying initial conditions and coupling strengths.

Table 4. Category and description of system behavior.

Category	Description
Total	Total number of cases analyzed.
Diverging	$x_{max}$, $x_{min}$, $y_{max}$, $y_{min}$, $z_{max}$, $z_{min}$ exceed the threshold ${10}^6$.
Non-diverging	$x_{max}-x_{min}$, $y_{max}-y_{min}$, $z_{max}-z_{min}$ are all below the threshold ${10}^{-3}$.
Periodic	Repeating oscillatory behavior (range is moderate).

shows the category and description of system behavior.

Table 5. Behavior categorization summary across initial conditions and $k_{ij}$ values.

Initial Condition	${\mathit{k}}_{\mathit{ij}}$ = 0	${\mathit{k}}_{\mathit{ij}}$ = 0.1	${\mathit{k}}_{\mathit{ij}}$ = 0.2
$[-0.20,-0.20,-0.20]$	Periodic: 452, Diverging: 60	Periodic: 512	Periodic: 512
$[-0.20,-0.20,0.10]$	Periodic: 508, Diverging: 4	Periodic: 512	Periodic: 512
$[-0.20,0.10,-0.20]$	Diverging: 347, Periodic: 165	Periodic: 512	Periodic: 512

shows the summary of the behavior categorization across the initial conditions and the values $k_{ij}$. A tabulated summary of the behavior of the system in terms of the initial conditions and the strength of the coupling among various combinations can be obtained in

Table 6. Summary of behavior across initial conditions and coupling strengths.

Initial Condition	${\mathit{k}}_{\mathit{ij}}$	Behavior	Color	Interpretation
$[-0.20,-0.20,-0.20]$	0.0	Mixed: Periodic + Diverging	Green + Red	System is unstable without coupling; divergence appears in several regions.
$[-0.20,-0.20,-0.20]$	0.1	Fully Periodic	Pink	Moderate coupling eliminates divergence completely.
$[-0.20,-0.20,-0.20]$	0.2	Fully Periodic	Yellow	Stronger coupling enforces periodicity across the full parameter space.
$[-0.20,-0.20,0.10]$	0.0	Mostly Periodic	Green	Almost all regions are periodic; few small divergent spots.
$[-0.20,-0.20,0.10]$	0.1	Fully Periodic	Pink	Coupling removes remaining divergence.
$[-0.20,-0.20,0.10]$	0.2	Fully Periodic	Yellow	Higher coupling maintains periodicity.
$[-0.20,0.10,-0.20]$	0.0	Mostly Diverging	Red	System is highly unstable with many diverging trajectories.
$[-0.20,0.10,-0.20]$	0.1	Fully Periodic	Pink	Coupling significantly stabilizes the system.
$[-0.20,0.10,-0.20]$	0.2	Fully Periodic	Yellow	Periodicity dominates, confirming strong influence of coupling.

.

• Subfigures (a–c): Initial condition = [−0.20, −0.20, −0.20]

  (a)

  When $k_{ij}=0$, a large number of red points can be seen (divergence), as well as green (periodic). This is a sign that the system, in which there is no coupling, is unstable in many places.

  (b)

  $k_{ij}=0.1$, all points turn pink, indicating complete periodicity. This is a stabilizing influence brought about by the coupling.

  (c)

  With $k_{ij}=0.2$, the preponderance is overtaken by yellows. The system is fully periodic, which means that a greater coupling results in uniform boundedness.

• Subfigures (d–f): Initial condition = [−0.20, −0.20, 0.10]

  (d)

  When $k_{ij}=0$, the parameter space is already mostly filled with periods (green), and the remaining divergent points are only small.

  (e)

  When $k_{ij}=0.1$, the whole system is periodic (pink). The divergence is destroyed by coupling.

  (f)

  At $k_{ij}=0.2$, fully periodic (yellow), but with even more extreme coupling, indicating a highly robust regime.

• Subfigures (g–i): Initial condition = [−0.20, 0.10, −0.20]

  (g)

  At $k_{ij}=0$, they have a heavy red presence: most of the space is diverging. The outcome of this inability to couple is a set of highly unstable trajectories.

  (h)

  $k_{ij}=0.1$, fully periodic (pink) dramatic stabilization through coupling.

  (i)

  With $k_{ij}=0.2$, the entire parameter space changes again to periodic (yellow) and confirms that consistency and robustness are rooted in coupling.

• Notable Outcomes
  • Effect of Initial Conditions: The initial conditions have a great influence on the long-term behavior of the system in the absence of coupling. An example is the initial condition $[-0.20,0.10,-0.20]$, see Figure 2g, which shows a high divergence in the case of no coupling.
  • Coupling Strength Effect (${\mathit{k}}_{\mathit{ij}}$): By altering the coupling strength between the interacting systems, from $k_{ij}=0$ to finally $k_{ij}=0.2$, the system moves through a mixed or divergent behavior into a complete periodic behavior. This indicates the fact that coupling creates a stabilizing factor of the dynamics.

3.3.3. Distribution Chart

In this section, we analyze in a systematic way how parameter setting and the coupling strength $k_{ij}$ affect the long-term behavior of the system, which can take one of three forms: diverging, periodic, and non-diverging. The rationale for this analysis is to gain additional insight into how sensitive the system is to the inter-node interactions and initial states, which are diagnostic issues in nonlinear and brain-inspired dynamics. For this purpose, we simulate the system in a three-dimensional parameter space $(a_1,b_1,c_1)$ and produce 512 different parameter points for each combination of the coupling coefficient and initial condition. These results are plotted as a bar graph where three different values of the coupling coefficient are considered, namely $k_{ij}=0$ (no coupling), $k_{ij}=0.1$ (moderate coupling), and $k_{ij}=0.2$ (strong coupling). It is such a systematic comparison that will enable us to assess the effects of introducing and increasing the coupling on the stability and periodicity of the system within the entire parameter space. By studying how the behavior changes from divergence to periodicity as $k_{ij}$ assumes larger values, we obtain clear indications of how controllable and robust the system is. The findings may be relevant, especially where one wishes to have a stable or oscillatory system, e.g., in designing neuromorphic circuits or in adaptive control of large systems. Figure 3 indicates the bar charts of the categorized behavior (diverging, periodic, non-diverging) of the system for the different values of $k_{ij}$ and different initial conditions.

Table 7. Summary of key observations.

Observation	Description
Sensitivity at $k_{ij}=0$	Behavior varies widely with initial conditions; divergence is common.
Stability at $k_{ij}=0.1$	All cases become periodic; divergence is fully suppressed.
Robustness at $k_{ij}=0.2$	Uniform periodic behavior across all conditions and parameters.
The Effect of Coupling	Coupling suppresses divergence and stabilizes dynamics.
Parameter Space Consistency	Coupling ensures consistent behavior across all 512-parameter combinations.

summarizes the key observations drawn from the behavioral analysis across different coupling strengths.

• Behavior counts of $k_{ij}=0$.

The figure indicates the distribution of the behavior under three initial conditions when no coupling is taken into account ($k_{ij}=0$). The initial condition $[-0.20,-0.20,0.10]$ provides the principal period behavior since it is manifested by the high yellow bump. In reverse, the initial conditions $[-0.20,0.10,-0.20]$ lead to a much higher amount of divergence behavior, as illustrated by the red bars. This implies that the system is quite sensitive to the initial state or slight variation, and without coupling, the system will jump between stable oscillations and unstable divergence. It can also be observed that there is practically no non-divergent behavior considered under this setting, which indicates that local feedback is not enough to stabilize the system.

• Behavior counts of $k_{ij}=0.1$.

A significant change in behavior is recorded with a moderate degree of coupling ($k_{ij}=0.1$). The three initial conditions yield 512 periodic behaviors that are all represented by uniformly tall bars of pink color. This result demonstrates that system responses move to limit cycle oscillations as inter-node coupling is introduced and that inter-node coupling prevents divergence (and fixed-point convergence). This kind of convergence of initial conditions implies that even a moderate coupling causes a decrease in the sensitivity of the system to changes in the initial state, such that robust, rhythmic dynamics occur over the entire parameter space.

• Behavior counts of $k_{ij}=0.2$.

With high coupling strength ($k_{ij}=0.2$), the system experiences another qualitative change—this time, fully periodic behavior in all initial conditions. This can be seen by the fact that the solid green bars show that in all 512 simulations, each initial condition converges to a limit cycle. As opposed to moderate coupling territory, where there was also dominance in periodicity, this behavior is even more stable and regular, with no indication of divergence or convergence toward a fixed point. What this means is that strong coupling does not just inhibit instability, but also, in fact, increases the robustness of the oscillatory process so that it is completely persistent, irrespective of initial conditions.

3.3.4. Coordinate Plots

The parallel coordinate plots showing the classification of system behavior for various values of the coupling factor $k_{ij}$, under identical initial conditions $[-0.20,-0.20,-0.20]$, $[-0.20,-0.20,0.10]$, and $[-0.20,0.10,-0.20]$ are represented by Figure 4. By mapping the normalized values of the parameters and coloring the trajectory according to the behavior, each graph illustrates how the parameters $a_1$, $b_1$, and $c_1$ affect the behavior of the dynamical system, whether it is divergent, non-divergent, or periodic. These visualizations provide a concise representation of how the system will develop in relation to different internal parameters, focusing on the effect that initial conditions and coupling have on the dynamical characteristics of the system. The results of the classification of behavior into coordinate graphs are provided in

Table 8. Coordinate plot observations based on coupling strength $k_{ij}$ and initial conditions.

Subfigure	Initial Condition	${\mathit{k}}_{\mathit{ij}}$	Dominant Colors	Description
(a)	[0.20, 0.20, 0.20]	0.0	Blue + Red	Indicates a mix of periodic and diverging regions; absence of coupling leads to instability.
(b)	[0.20, 0.20, 0.20]	0.1	Yellow	Complete periodic behavior; mild coupling drives uniform bounded dynamics.
(c)	[0.20, 0.20, 0.20]	0.2	Purple	Strong coupling sustains full periodicity, confirming stability.
(d)	[0.20, 0.20, 0.10]	0.0	Mostly Blue	High level of periodicity, even without coupling; low divergence present.
(e)	[0.20, 0.20, 0.10]	0.1	Yellow	Coupling enforces total periodicity across the parameter space.
(f)	[0.20, 0.20, 0.10]	0.2	Purple	Periodic behavior remains dominant with enhanced robustness.
(g)	[0.20, 0.10, 0.20]	0.0	Red + Blue	Major divergence dominates, indicating unstable dynamics without coupling.
(h)	[0.20, 0.10, 0.20]	0.1	Yellow	Stable periodic regime induced by weak coupling.
(i)	[0.20, 0.10, 0.20]	0.2	Purple	Consistent periodicity confirms stable dynamics under strong coupling.

and represent how the various combinations of initial values, values of the coupling parameters, and strengths result in behavior.

• Subfigures (a–c): Initial condition = [−0.20, −0.20, −0.20]

  (a)

  $k_{ij}=0$, IC: [−0.20, −0.20, −0.20]

  There is a strong occurrence of blue (periodic) and some red, which implies that, in the absence of coupling, the system can access chaotic and unstable regions. The parametric space has sensitive dynamics due to the absence of interaction.

  (b)

  $k_{ij}=0.1$, IC: [−0.20, −0.20, −0.20]

  Yellow is overwhelming in the plot; this signifies that the system turns completely periodic with weak coupling. This demonstrates moderate stabilization that verifies that the existence of external node information is sufficient to overcome the effect of divergence.

  (c)

  $k_{ij}=0.2$, IC: [−0.20, −0.20, −0.20]

  Purple sweeps it away entirely, indicating very regular periodic behavior, which can even be symmetrical. This signifies a healthy stabilization, in the sense that the coupling is so tight that bounded, repeated behavior holds in larger parameter intervals as well.

• Subfigures (d–f): Initial condition = [−0.20, −0.20, 0.10]

  (d)

  $k_{ij}=0$, IC: [−0.20, −0.20, 0.10]

  The predominance of blue indicates that the system is largely periodic, likely due to the chosen initial condition. This IC makes the system very periodic, even though it is not coupled.

  (e)

  $k_{ij}=0.1$, IC: [−0.20, −0.20, 0.10]

  The completely yellow region indicates a uniform periodic regime with particularly strong convergence across the parameter space. This periodicity is further enhanced by coupling.

  (f)

  $k_{ij}=0.2$, IC: [−0.20, −0.20, 0.10]

  The fully purple region indicates that under strong coupling, the dynamics move to a symmetric periodic regime, which may also include a decay or uniform cycle formation.

• Subfigures (g–i): Initial condition = [−0.20, 0.10, −0.20]

  (g)

  $k_{ij}=0$, IC: [−0.20, 0.10, −0.20]

  There is a predominance of blue and red; this indicates a chaotic or divergent regime; thus, without coupling, such an initial condition results in unstable behavior throughout most of the parameter space.

  (h)

  $k_{ij}=0.1$, IC: [−0.20, 0.10, −0.20]

  The completely yellow region indicates that periodic dynamics are in control, implying that, in the case of unstable ICs, even weak coupling can induce order, eliminating divergence.

  (i)

  $k_{ij}=0.2$, IC: [−0.20, 0.10, −0.20]

  Again, completely purple, indicating that in the case of strong coupling, periodicity is strengthened, and all instability is eliminated. The complete boundedness and repeatability are confirmed.

3.4. Categorization Based on Eigenvalues

To study the stability and dynamical character of the system in parameter space, we obtain the Jacobian matrix based on the structure of the system provided in Equations (4)–(6) for the following values of $k_{ij}$: 0, $0.1$, and $0.2$, respectively. We compute the Jacobian matrix under the initial conditions of each chosen triplet of parameters $(a_1,b_1,c_1)$ and compute the eigenvalues of the Jacobian matrices in the provided ranges. Such eigenvalues characterize the local behavior of the system with each parameter setting and enable us to categorize the resulting dynamical tendencies. This is done three times with three representative initial conditions. The behavior of the system is sensitive to its internal parameters, and initial states are determined. This is represented by a scatter plot $3D$ in which each colored point denotes the qualitative behavior class of the eigenvalue point. The eigenvalue analysis of the same set of parameter combinations using the Jacobian needed about 2 min of computation time. Figure 5 shows the classification of system behavior as a function of eigenvalue based on three initial conditions and varying coupling strengths $k_{ij}$ to demonstrate stability patterns among system configurations. The classification labels applied in describing the eigenvalues of the Jacobian matrix are listed in

Table 9. Eigenvalue category definitions.

Label	Description
B1	All eigenvalues real and positive
B2	All eigenvalues real and negative
B3	Real eigenvalues with mixed signs
B4	Two eigenvalues are zero, one is non-zero
B5	One zero eigenvalue, others real with ± signs
D	All eigenvalues are purely imaginary
BD1	Complex eigenvalues with positive real parts
BD2	Complex eigenvalues with negative real parts
BD3	One real eigenvalue and one complex conjugate pair with opposite signs
Z	All eigenvalues are exactly zero

.

Table 10. Dominant eigenvalue categories and observations across coupling strengths and initial conditions.

Initial Condition	${\mathit{k}}_{\mathit{ij}}=0.0$	${\mathit{k}}_{\mathit{ij}}=0.1$	${\mathit{k}}_{\mathit{ij}}=0.2$
$[-0.20,-0.20,-0.20]$	B3, BD3	B2, BD3	B2, BD3
$[-0.20,-0.20,0.10]$	B3, BD3	B2, BD3	B2, BD3
$[-0.20,0.10,-0.20]$	BD3, B3	BD3, B2	BD3, B2

summarizes the main categories of eigenvalues obtained through local Jacobian analysis under different starting conditions and varying coupling strengths.

• Subfigures (a–c): Initial condition = [−0.20, −0.20, −0.20]

  (a)

  $k_{ij}=0$, IC: [−0.20, −0.20, −0.20]

  Yellow (B3: real mixed-sign eigenvalues) and purple (BD3: real and complex opposite) prevail, denoting unstable manifold dynamics that exhibit saddle-like divergence behavior and chaotic tendencies, as they lack coupling.

  (b)

  $k_{ij}=0.1$, IC: [−0.20, −0.20, −0.20]

  Green (B2: all real $<0$) and purple (BD3) become dominant, implying that with weak coupling, damping is added and some stabilization occurs, but complex dynamics remain because this regime involves coexisting BD3 structures.

  (c)

  $k_{ij}=0.2$, IC: [−0.20, −0.20, −0.20]

  Blue (B2: all real $<0$) and light pink (BD3) prevail, and it is indeed true that another characteristic that becomes apparent is that strong coupling has a stabilizing effect, suppresses instability, and instead produces more regular decaying orbits.

• Subfigures (d–f): Initial condition = [−0.20, −0.20, 0.10]

  (d)

  $k_{ij}=0$, IC: [−0.20, −0.20, 0.10]

  Once again, both yellow (B3) and purple (BD3) dominate, and their dynamics are prone to mixture with mixed real eigenvalues and complex elements, supporting the statement that no coupling can produce rich but inconsistent behavior.

  (e)

  $k_{ij}=0.1$, IC: [−0.20, −0.20, 0.10]

  Green prevails (B2) and purple (BD3), demonstrating a slight coupling restriction of the dynamics, with emerging convergence areas while maintaining oscillatory elements.

  (f)

  $k_{ij}=0.2$, IC: [−0.20, −0.20, 0.10]

  The space is dominated by blue (B2) and light pink (BD3), creating a very wet system in which most eigenvalues are negative with little oscillation, resulting in behavior with minimal irregularity.

• Subfigures (g–i): Initial condition = [−0.20, 0.10, −0.20]

  (g)

  $k_{ij}=0$, IC: [−0.20, 0.10, −0.20]

  Yellow (B3), dominated by purple (BD3), indicates that the system is sensitive and unstable, with dubious eigenvalue signs, and repulsive behavior by itself, and does not influence coupling.

  (h)

  $k_{ij}=0.1$, IC: [−0.20, 0.10, −0.20]

  When green (B2) emerges with purple (BD3), we see the onset of damping; this is evidence of low divergence and high occurrence of convergent solutions.

  (i)

  $k_{ij}=0.2$, IC: [−0.20, 0.10, −0.20]

  It then becomes blue (B2) and then light pink (BD3), which is a highly damped and stable regime whose trajectories tend to move toward steady-state or bounded oscillation regions.

4. Conclusions

In this work, we propose a general and extensible model for examining the nonlinear dynamics of a brain-inspired system by exploring how variations in parameters and initialization influence system behavior. Using statistical classification and eigenvalue-based stability analysis, we methodically classify the responses of the system as periodic, divergent, and non-divergent in a three-dimensional parameter space ($a_1$, $b_1$, and $c_1$). The findings of our results indicate the role of coupling strength in determining the stability of the system, where the strong coupling system always tends towards uniform periodic behavior regardless of the initial condition. Certain visual tools, such as $3D$ coordinate plots and distribution graphs, were also utilized, which show changes in dynamics as coupling was added. One key contribution of the current work to the field consists of the simulation methodology itself. Whereas previous methods forced the user to send multiple different scripts or to run a single analysis multiple times to obtain multiple different initial conditions, the loop-based implementation we propose in this paper allows multiple initial conditions to be simulated in a single cohesive explanation (a detailed comparison is provided in

Table 11. Comparison between existing studies and the proposed framework.

Aspect	Existing Studies	Present Work (Proposed Framework)
Parameter Exploration	Typically constrained to a single or two parameters that must be manually changed.	Automated scanning of complete three-dimensional parameter space $(a_1,b_1,c_1)$.
Automation	Often manual or semi-automated processes.	Completely automated simulation framework loop.
Sampling Method	Random or case-specific sampling.	Organized a grid of parameters so that the space is fully covered.
Initial Conditions	Typically fixed or single trajectory tested.	Multiple initial conditions are tested automatically in the same framework.
Output Type	Qualitative trajectory or phase-space plots.	Quantitative classification of regimes (diverging, periodic, non-divergent).
Data Handling	Manual inspection and result extraction.	Automatic data generation, classification, and organized storage for later analysis.
Computational Efficiency	High computational cost for large parameter sweeps.	Parallelizable structure producing large datasets efficiently.
General Applicability	Model-specific (e.g., Lorenz, Rössler only).	Model-independent and adaptable to any nonlinear ODE system.
Novel Contribution	Focus on parameter sensitivity or bifurcation analysis.	Unified, scalable framework integrating parameter exploration, classification, and visualization.

). Innovation not only increases the efficiency of computation but also enables the investigation of the dynamics of the system on a wider scale in a more automated manner. Consequently, in addition to enhancing the knowledge of local and global system dynamics, this framework also lays the groundwork for future studies on larger complex networks whose nodes and interconnections are heterogeneous and presents possible applications for neuromorphic computing, networked control systems, and brain-like modeling.