Prioritizing Longitudinal Gene–Environment Interactions Using an FDR-Assisted Robust Bayesian Linear Mixed Model
Abstract
1. Introduction
2. Materials and Methods
2.1. The Robust Linear Mixed Model
2.2. A Bayesian Formulation of the Robust Linear Mixed Model
2.3. Robust Sparse Bayesian Linear Mixed Model
2.4. Robust Variable Selection with Bayesian False Discovery Rates
2.5. Gibbs Sampling Algorithm
- Define . Then, the full conditional distribution of follows with meanand variance
- Denote the partial residual after excluding environmental main effect as , then the full conditional distribution of is with meanand variance
- To obtain the full conditional distribution of , which represents the main genetic effects, we first define and . Then, the posterior distribution of given the rest of the parameters follows a spike-and-slab distribution:whereand the posterior mixture proportion isThe posterior distribution of is a mixture component distrinbution consisting of a normal distribution and a point mass at 0. At each MCMC iteration, is drawn from with probability , and set to 0 otherwise. If = 0, then we have . Otherwise, .
- We show the full conditional distribution of denoting the effect size of , the interaction between the omics features and environmental factors, . With a partial residual and , the posterior distribution of is expressible as follows:where mean vector and covariance arerespectively, and the posterior mixture proportion is
- The full conditional distributions of and areand
- The full conditional distributions of and areand
- The full conditional distributions of and areand
- The full conditional distribution of :
- The full conditional distribution of :
- The full conditional distribution of random effects iswhere
- Finally, the full conditional distribution of is
| Algorithm 1. Gibbs Sampler for Bayesian Inference |
Output: Posterior samples for . |
3. Results
3.1. Simulation
3.2. Case Study
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANOVA | Analysis of Variance |
| FDR | False Discovery Rate |
| GWAS | Genome-wide association studies |
| MCMC | Markov chain Monte Carlo |
| PIP | Posterior inclusion probability |
Appendix A
Appendix A.1. Additional Numeric Results
| Error | Method | TP | FP | F1 | MCC | Estimation Error |
|---|---|---|---|---|---|---|
| RBLSS | 19.78 (0.46) | 1.52 (1.23) | 0.96 (0.03) | 0.95 (0.03) | 2.01 (0.55) | |
| RBL | 19.48 (0.68) | 3.30 (1.84) | 0.91 (0.04) | 0.90 (0.05) | 14.14 (1.05) | |
| BLSS | 19.88 (0.33) | 0.94 (0.84) | 0.97 (0.02) | 0.97 (0.02) | 1.72 (0.41) | |
| BL | 19.66 (0.56) | 1.96 (1.68) | 0.95 (0.04) | 0.94 (0.04) | 13.35 (1.00) | |
| RBLSS | 17.52 (1.37) | 0.62 (0.81) | 0.92 (0.05) | 0.91 (0.05) | 2.98 (0.78) | |
| RBL | 16.48 (1.54) | 1.04 (1.01) | 0.88 (0.05) | 0.87 (0.05) | 14.56 (1.06) | |
| BLSS | 12.12 (3.33) | 0.28 (0.54) | 0.73 (0.14) | 0.75 (0.12) | 5.22 (1.76) | |
| BL | 12.76 (2.43) | 3.04 (2.51) | 0.71 (0.11) | 0.69 (0.12) | 23.70 (6.15) | |
| RBLSS | 19.36 (0.83) | 0.86 (0.81) | 0.96 (0.03) | 0.96 (0.04) | 2.22 (0.65) | |
| RBL | 18.56 (0.97) | 2.10 (1.46) | 0.91 (0.04) | 0.90 (0.04) | 14.13 (1.09) | |
| BLSS | 16.96 (1.46) | 0.44 (0.73) | 0.91 (0.05) | 0.90 (0.05) | 3.56 (1.01) | |
| BL | 16.40 (1.59) | 2.66 (1.89) | 0.84 (0.06) | 0.82 (0.07) | 20.08 (2.44) | |
| ) | RBLSS | 17.92 (1.23) | 1.10 (0.89) | 0.92 (0.05) | 0.91 (0.05) | 3.18 (0.77) |
| RBL | 16.66 (1.36) | 1.96 (1.28) | 0.86 (0.05) | 0.85 (0.06) | 15.82 (1.02) | |
| BLSS | 17.16 (1.33) | 0.72 (0.57) | 0.90 (0.04) | 0.90 (0.05) | 3.31 (0.72) | |
| BL | 16.42 (1.16) | 2.62 (1.72) | 0.84 (0.05) | 0.83 (0.06) | 19.22 (1.39) |
| Error | Method | TP | FP | F1 | MCC | Estimation Error |
|---|---|---|---|---|---|---|
| RBLSS | 19.40 (0.67) | 1.84 (1.58) | 0.94 (0.04) | 0.94 (0.04) | 2.29 (0.65) | |
| RBL | 16.88 (1.19) | 2.20 (1.47) | 0.86 (0.04) | 0.86 (0.05) | 23.05 (1.42) | |
| BLSS | 19.48 (0.65) | 0.76 (0.82) | 0.97 (0.03) | 0.97 (0.03) | 1.91 (0.47) | |
| BL | 17.48 (1.11) | 1.06 (1.11) | 0.91 (0.04) | 0.90 (0.04) | 20.96 (1.34) | |
| RBLSS | 18.16 (1.13) | 0.70 (0.81) | 0.93 (0.04) | 0.93 (0.04) | 2.84 (0.85) | |
| RBL | 15.06 (1.68) | 1.00 (0.97) | 0.83 (0.06) | 0.83 (0.06) | 24.32 (1.44) | |
| BLSS | 11.90 (4.57) | 0.14 (0.40) | 0.71 (0.23) | 0.75 (0.17) | 5.65 (2.60) | |
| BL | 8.80 (3.57) | 1.46 (1.85) | 0.56 (0.20) | 0.60 (0.17) | 42.45(17.73) | |
| RBLSS | 19.34 (0.66) | 0.94 (0.93) | 0.96 (0.03) | 0.96 (0.03) | 2.21 (0.55) | |
| RBL | 17.06 (1.38) | 1.62 (1.24) | 0.88 (0.05) | 0.88 (0.05) | 24.31 (1.57) | |
| BLSS | 17.66 (1.39) | 0.66 (0.75) | 0.92 (0.05) | 0.92 (0.05) | 3.47 (1.01) | |
| BL | 13.64 (1.85) | 1.88 (2.13) | 0.77 (0.08) | 0.77 (0.08) | 34.34 (4.74) | |
| ) | RBLSS | 17.04 (1.62) | 1.10 (1.05) | 0.89 (0.06) | 0.89 (0.06) | 3.50 (0.98) |
| RBL | 14.18 (1.47) | 1.34 (1.14) | 0.80 (0.05) | 0.80 (0.05) | 25.21 (1.52) | |
| BLSS | 15.54 (1.79) | 0.48 (0.79) | 0.86 (0.06) | 0.86 (0.06) | 3.87 (0.85) | |
| BL | 12.46 (1.82) | 1.32 (1.11) | 0.74 (0.08) | 0.74 (0.08) | 32.00 (2.15) |
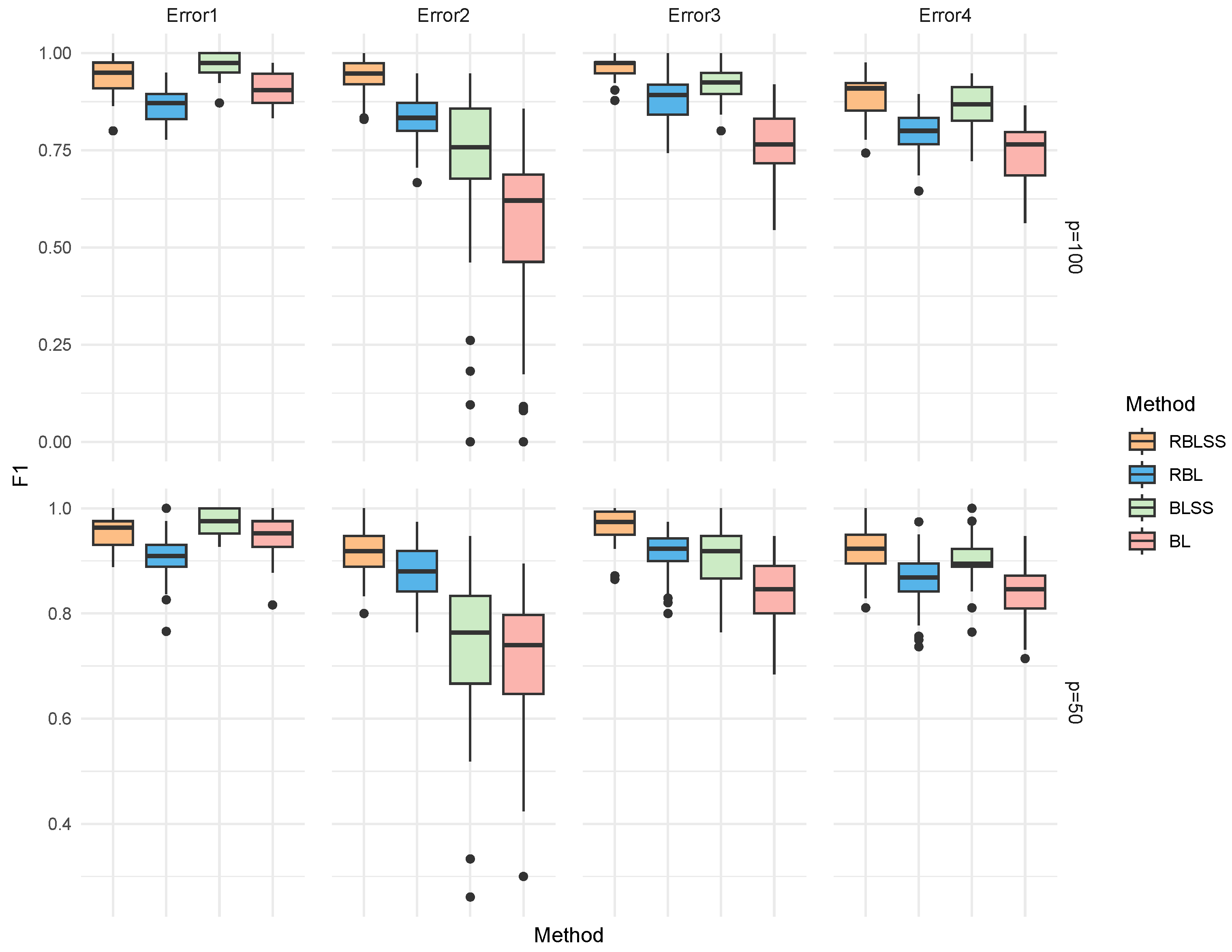
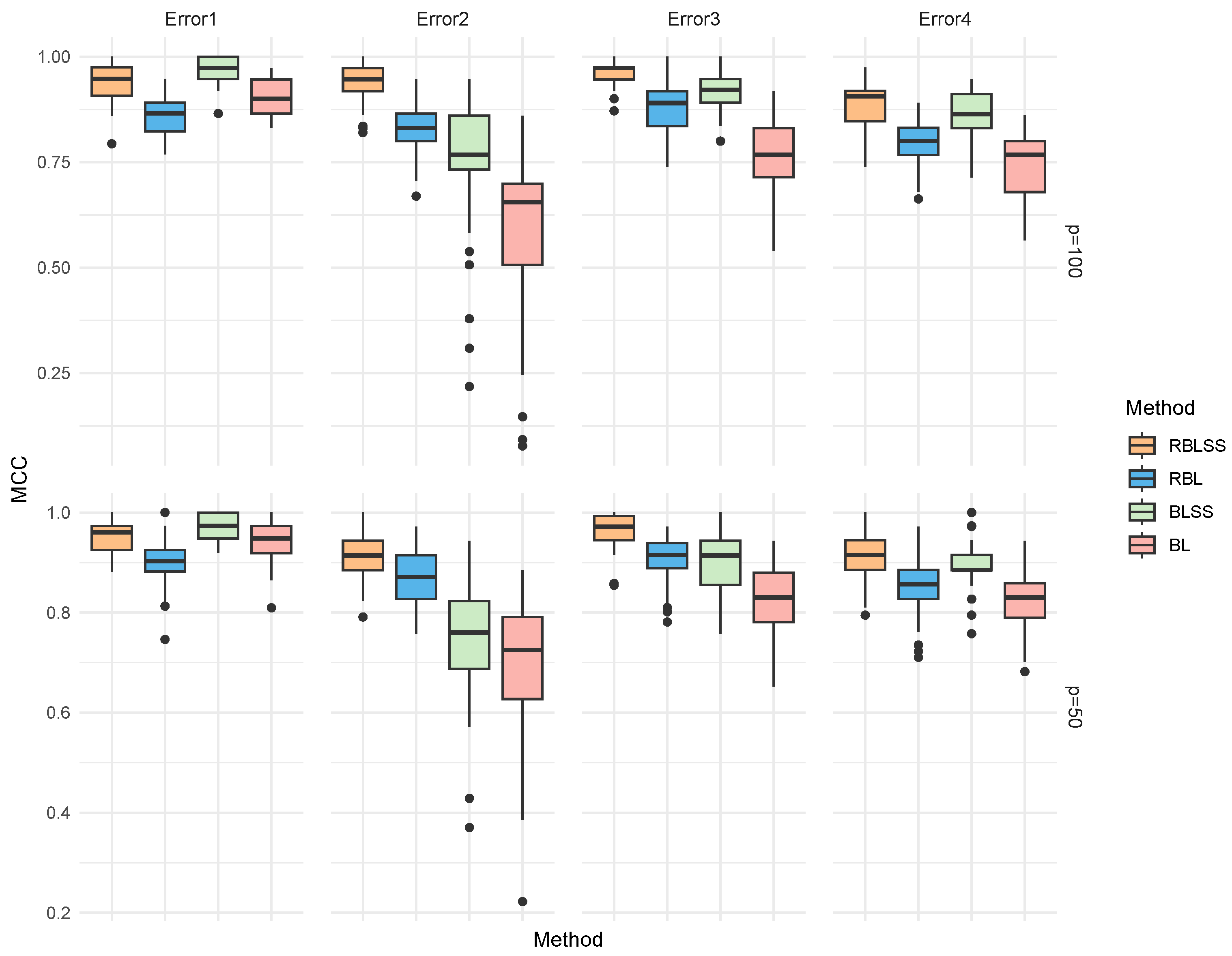

| Error | Method | TP | FP | F1 | MCC | Estimation Error |
|---|---|---|---|---|---|---|
| RBLSS | 19.56 (0.73) | 1.76 (0.85) | 0.95 (0.03) | 0.94 (0.04) | 2.30 (0.60) | |
| RBL | 19.00 (1.07) | 3.68 (1.99) | 0.89 (0.06) | 0.88 (0.06) | 14.39 (1.07) | |
| BLSS | 19.84 (0.37) | 0.94 (0.74) | 0.97 (0.02) | 0.97 (0.02) | 1.90 (0.45) | |
| BL | 19.02 (0.98) | 2.00 (1.32) | 0.93 (0.04) | 0.92 (0.04) | 13.54 (0.88) | |
| RBLSS | 17.28 (1.69) | 0.70 (0.79) | 0.91 (0.06) | 0.90 (0.06) | 3.28 (0.88) | |
| RBL | 15.88 (1.73) | 1.42 (1.18) | 0.85 (0.06) | 0.84 (0.06) | 15.22 (1.25) | |
| BLSS | 11.22 (4.16) | 0.28 (0.50) | 0.69 (0.21) | 0.73 (0.13) | 5.90 (1.85) | |
| BL | 11.48 (3.56) | 2.66 (2.87) | 0.66 (0.18) | 0.66 (0.14) | 24.50 (4.82) | |
| RBLSS | 19.08 (0.90) | 0.78 (0.91) | 0.96 (0.03) | 0.95 (0.03) | 2.38 (0.70) | |
| RBL | 18.10 (1.16) | 1.46 (1.39) | 0.92 (0.05) | 0.91 (0.05) | 14.58 (1.28) | |
| BLSS | 15.94 (2.03) | 0.54 (0.86) | 0.87 (0.07) | 0.87 (0.07) | 4.26 (1.19) | |
| BL | 15.50 (1.63) | 2.22 (1.80) | 0.82 (0.07) | 0.81 (0.08) | 21.61 (3.12) | |
| ) | RBLSS | 17.88 (1.45) | 0.76 (0.69) | 0.92 (0.05) | 0.92 (0.05) | 3.24 (0.92) |
| RBL | 16.68 (1.57) | 1.48 (1.33) | 0.87 (0.06) | 0.86 (0.06) | 15.97 (1.21) | |
| BLSS | 16.60 (1.55) | 0.38 (0.60) | 0.90 (0.05) | 0.89 (0.05) | 3.61 (0.91) | |
| BL | 15.96 (1.59) | 2.20 (1.54) | 0.84 (0.06) | 0.82 (0.07) | 20.12 (1.66) |
| Error | Method | TP | FP | F1 | MCC | Estimation Error |
|---|---|---|---|---|---|---|
| RBLSS | 19.34 (0.69) | 1.40 (1.12) | 0.95 (0.03) | 0.95 (0.04) | 2.24 (0.58) | |
| RBL | 17.38 (1.18) | 2.40 (1.65) | 0.87 (0.05) | 0.87 (0.05) | 23.69 (1.40) | |
| BLSS | 19.58 (0.61) | 0.48 (0.65) | 0.98 (0.02) | 0.98 (0.03) | 1.84 (0.44) | |
| BL | 17.98 (1.20) | 1.00 (0.97) | 0.92 (0.04) | 0.92 (0.04) | 21.22 (1.17) | |
| RBLSS | 17.28 (1.40) | 0.78 (1.06) | 0.91 (0.05) | 0.90 (0.05) | 3.32 (0.93) | |
| RBL | 13.58 (1.93) | 1.20 (1.37) | 0.78 (0.07) | 0.78 (0.07) | 25.01 (1.93) | |
| BLSS | 10.44 (3.39) | 0.22 (0.46) | 0.66 (0.17) | 0.69 (0.14) | 6.52 (2.15) | |
| BL | 8.24 (3.01) | 1.84 (2.38) | 0.53 (0.17) | 0.57 (0.15) | 43.24(14.10) | |
| RBLSS | 19.32 (0.91) | 0.70 (0.84) | 0.97 (0.03) | 0.96 (0.03) | 2.30 (0.66) | |
| RBL | 15.58 (2.04) | 1.26 (1.19) | 0.84 (0.07) | 0.84 (0.07) | 24.06 (1.51) | |
| BLSS | 15.30 (2.73) | 0.48 (0.68) | 0.85 (0.10) | 0.85 (0.09) | 4.55 (1.69) | |
| BL | 11.90 (2.24) | 1.24 (1.30) | 0.71 (0.09) | 0.72 (0.09) | 34.67 (4.79) | |
| ) | RBLSS | 15.94 (1.60) | 0.92 (0.80) | 0.86 (0.06) | 0.86 (0.06) | 4.03 (1.02) |
| RBL | 12.56 (1.64) | 1.36 (1.24) | 0.74 (0.07) | 0.74 (0.07) | 25.56 (1.63) | |
| BLSS | 14.22 (1.79) | 0.50 (0.68) | 0.82 (0.07) | 0.82 (0.06) | 4.66 (1.06) | |
| BL | 10.68 (1.96) | 1.10 (1.07) | 0.67 (0.09) | 0.68 (0.08) | 32.21 (2.23) |
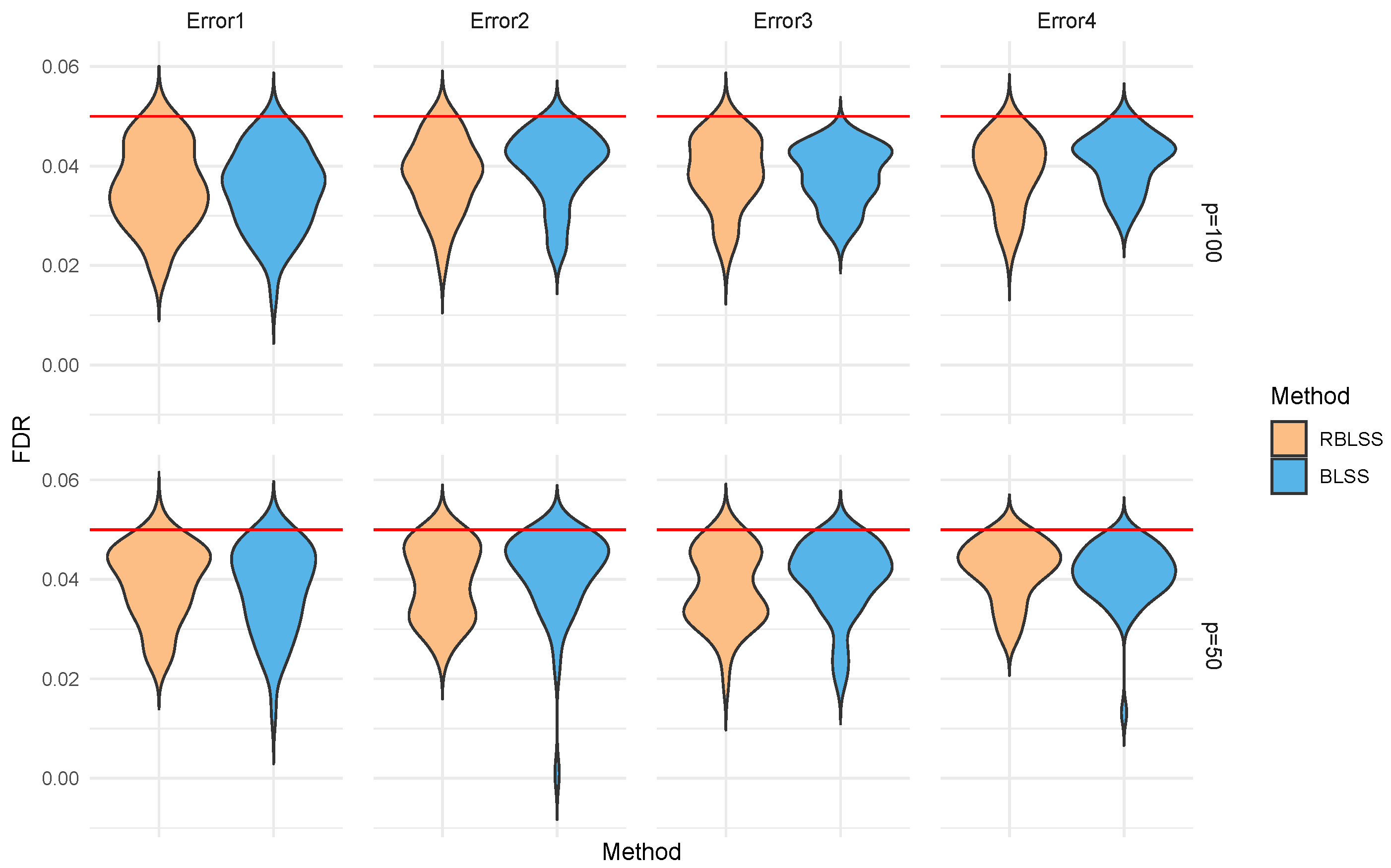
Appendix A.2. Additional Results on FDR Control


Appendix A.3. Sensitivity Analysis
| Error | Prior | TP | FP | F1 | MCC | Estimation Error |
|---|---|---|---|---|---|---|
| 19.24 (0.98) | 1.60 (1.31) | 0.94 (0.04) | 0.94 (0.05) | 2.39 (0.64) | ||
| 19.18 (0.96) | 1.42 (1.03) | 0.94 (0.04) | 0.94 (0.04) | 2.40 (0.59) | ||
| 19.32 (0.89) | 1.50 (1.15) | 0.95 (0.04) | 0.94 (0.04) | 2.40 (0.61) | ||
| 19.26 (0.99) | 1.44 (1.01) | 0.95 (0.04) | 0.94 (0.04) | 2.37 (0.57) | ||
| 19.36 (0.85) | 1.92 (1.24) | 0.94 (0.04) | 0.93 (0.04) | 2.46 (0.67) | ||
| 18.70 (1.15) | 0.70 (0.93) | 0.95 (0.04) | 0.94 (0.04) | 2.70 (0.66) | ||
| 18.58 (1.20) | 0.66 (0.75) | 0.95 (0.04) | 0.94 (0.04) | 2.74 (0.70) | ||
| 18.78 (0.93) | 0.72 (0.90) | 0.95 (0.03) | 0.95 (0.04) | 2.66 (0.61) | ||
| 18.50 (1.05) | 0.76 (0.89) | 0.94 (0.04) | 0.94 (0.04) | 2.80 (0.62) | ||
| 18.90 (0.97) | 1.04 (1.24) | 0.95 (0.04) | 0.94 (0.05) | 2.80 (0.79) | ||
| 19.10 (1.02) | 0.88 (0.82) | 0.96 (0.04) | 0.95 (0.04) | 2.43 (0.69) | ||
| 19.14 (0.88) | 0.86 (0.93) | 0.96 (0.03) | 0.95 (0.04) | 2.41 (0.60) | ||
| 19.16 (1.09) | 0.90 (0.95) | 0.96 (0.04) | 0.95 (0.05) | 2.39 (0.74) | ||
| 19.18 (0.85) | 0.72 (0.95) | 0.96 (0.04) | 0.96 (0.04) | 2.40 (0.77) | ||
| 19.26 (0.88) | 1.22 (0.93) | 0.95 (0.03) | 0.95 (0.04) | 2.46 (0.70) | ||
| 16.46 (2.17) | 0.88 (1.06) | 0.88 (0.08) | 0.87 (0.09) | 3.55 (1.16) | ||
| 16.22 (2.06) | 0.78 (1.00) | 0.87 (0.08) | 0.87 (0.08) | 3.65 (1.17) | ||
| 16.48 (1.92) | 0.72 (0.78) | 0.88 (0.07) | 0.88 (0.07) | 3.51 (1.06) | ||
| 16.28 (1.95) | 0.72 (0.78) | 0.88 (0.07) | 0.87 (0.07) | 3.59 (1.00) | ||
| 16.70 (1.95) | 1.14 (0.95) | 0.88 (0.07) | 0.87 (0.08) | 3.69 (1.18) |
| Error | Prior | TP | FP | F1 | MCC | Estimation Error |
|---|---|---|---|---|---|---|
| 19.28 (0.88) | 1.34 (1.17) | 0.95 (0.04) | 0.94 (0.05) | 2.35 (0.63) | ||
| 19.18 (0.96) | 1.42 (1.03) | 0.94 (0.04) | 0.94 (0.04) | 2.40 (0.59) | ||
| 19.36 (0.78) | 1.94 (1.30) | 0.94 (0.03) | 0.93 (0.04) | 2.41 (0.55) | ||
| 19.24 (0.87) | 1.26 (1.01) | 0.95 (0.03) | 0.95 (0.04) | 2.29 (0.53) | ||
| 18.92 (1.05) | 1.02 (1.02) | 0.95 (0.04) | 0.94 (0.05) | 2.38 (0.69) | ||
| 18.72 (1.03) | 0.68 (1.00) | 0.95 (0.04) | 0.95 (0.04) | 2.73 (0.68) | ||
| 18.58 (1.20) | 0.66 (0.75) | 0.95 (0.04) | 0.94 (0.04) | 2.74 (0.70) | ||
| 18.66 (1.24) | 1.12 (1.14) | 0.94 (0.05) | 0.93 (0.05) | 2.85 (0.79) | ||
| 18.44 (1.13) | 0.66 (0.80) | 0.94 (0.04) | 0.94 (0.04) | 2.80 (0.73) | ||
| 18.24 (1.13) | 0.46 (0.71) | 0.94 (0.04) | 0.94 (0.04) | 2.86 (0.75) | ||
| 19.26 (0.88) | 0.78 (0.82) | 0.96 (0.03) | 0.96 (0.04) | 2.37 (0.64) | ||
| 19.14 (0.88) | 0.86 (0.93) | 0.96 (0.03) | 0.95 (0.04) | 2.41 (0.60) | ||
| 19.16 (0.82) | 1.08 (1.01) | 0.95 (0.03) | 0.95 (0.04) | 2.42 (0.69) | ||
| 19.02 (0.96) | 0.84 (0.87) | 0.95 (0.03) | 0.95 (0.04) | 2.44 (0.63) | ||
| 18.90 (1.28) | 0.60 (0.73) | 0.96 (0.04) | 0.95 (0.05) | 2.45 (0.84) | ||
| 16.42 (2.00) | 0.84 (0.93) | 0.88 (0.07) | 0.87 (0.08) | 3.65 (1.25) | ||
| 16.22 (2.06) | 0.78 (1.00) | 0.87 (0.08) | 0.87 (0.08) | 3.65 (1.17) | ||
| 16.82 (1.91) | 1.02 (0.89) | 0.89 (0.07) | 0.88 (0.07) | 3.51 (1.08) | ||
| 16.14 (2.06) | 0.78 (0.95) | 0.87 (0.08) | 0.86 (0.08) | 3.75 (1.18) | ||
| 15.82 (1.87) | 0.76 (0.82) | 0.86 (0.06) | 0.86 (0.07) | 3.90 (1.13) |
References
- Hunter, D.J. Gene–environment interactions in human diseases. Nat. Rev. Genet. 2005, 6, 287–298. [Google Scholar] [CrossRef] [PubMed]
- Cornelis, M.C.; Tchetgen Tchetgen, E.J.; Liang, L.; Qi, L.; Chatterjee, N.; Hu, F.B.; Kraft, P. Gene-environment interactions in genome-wide association studies: A comparative study of tests applied to empirical studies of type 2 diabetes. Am. J. Epidemiol. 2012, 175, 191–202. [Google Scholar] [CrossRef] [PubMed]
- Han, S.S.; Chatterjee, N. Review of statistical methods for gene-environment interaction analysis. Curr. Epidemiol. Rep. 2018, 5, 39–45. [Google Scholar] [CrossRef]
- Zhou, F.; Ren, J.; Lu, X.; Ma, S.; Wu, C. Gene–environment interaction: A variable selection perspective. Epistasis Methods Protoc. 2021, 2212, 191–223. [Google Scholar]
- Murcray, C.E.; Lewinger, J.P.; Gauderman, W.J. Gene-environment interaction in genome-wide association studies. Am. J. Epidemiol. 2009, 169, 219–226. [Google Scholar] [CrossRef]
- Wu, C.; Cui, Y. A novel method for identifying nonlinear gene–environment interactions in case–control association studies. Hum. Genet. 2013, 132, 1413–1425. [Google Scholar] [CrossRef]
- Tyrrell, J.; Wood, A.R.; Ames, R.M.; Yaghootkar, H.; Beaumont, R.N.; Jones, S.E.; Tuke, M.A.; Ruth, K.S.; Freathy, R.M.; Davey Smith, G.; et al. Gene–obesogenic environment interactions in the UK Biobank study. Int. J. Epidemiol. 2017, 46, 559–575. [Google Scholar] [CrossRef]
- Wang, X.; Lim, E.; Liu, C.T.; Sung, Y.J.; Rao, D.C.; Morrison, A.C.; Boerwinkle, E.; Manning, A.K.; Chen, H. Efficient gene–environment interaction tests for large biobank-scale sequencing studies. Genet. Epidemiol. 2020, 44, 908–923. [Google Scholar] [CrossRef]
- Lin, W.Y.; Chan, C.C.; Liu, Y.L.; Yang, A.C.; Tsai, S.J.; Kuo, P.H. Performing different kinds of physical exercise differentially attenuates the genetic effects on obesity measures: Evidence from 18,424 Taiwan Biobank participants. PLoS Genet. 2019, 15, e1008277. [Google Scholar] [CrossRef]
- Lin, W.Y. Gene-Environment Interactions and Gene–Gene Interactions on Two Biological Age Measures: Evidence from Taiwan Biobank Participants. Adv. Biol. 2024, 8, 2400149. [Google Scholar] [CrossRef]
- Wu, C.; Ma, S. A selective review of robust variable selection with applications in bioinformatics. Briefings Bioinform. 2015, 16, 873–883. [Google Scholar] [CrossRef]
- Huber, P.J. Robust statistics. In International Encyclopedia of Statistical Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1248–1251. [Google Scholar]
- Koenker, R. Quantile Regression; Cambridge University Press: Cambridge, UK, 2005; Volume 38. [Google Scholar]
- Han, A.K. Non-parametric analysis of a generalized regression model: The maximum rank correlation estimator. J. Econom. 1987, 35, 303–316. [Google Scholar] [CrossRef]
- Wang, H.; Li, G.; Jiang, G. Robust regression shrinkage and consistent variable selection through the LAD-Lasso. J. Bus. Econ. Stat. 2007, 25, 347–355. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Y. Variable selection in quantile regression. Stat. Sin. 2009, 19, 801–817. [Google Scholar]
- Alfons, A.; Croux, C.; Gelper, S. Sparse least trimmed squares regression for analyzing high-dimensional large data sets. Ann. Appl. Stat. 2013, 7, 226–248. [Google Scholar] [CrossRef]
- Chai, H.; Zhang, Q.; Jiang, Y.; Wang, G.; Zhang, S.; Ahmed, S.E.; Ma, S. Identifying gene-environment interactions for prognosis using a robust approach. Econom. Stat. 2017, 4, 105–120. [Google Scholar] [CrossRef]
- Wu, C.; Shi, X.; Cui, Y.; Ma, S. A penalized robust semiparametric approach for gene–environment interactions. Stat. Med. 2015, 34, 4016–4030. [Google Scholar] [CrossRef]
- Wu, C.; Jiang, Y.; Ren, J.; Cui, Y.; Ma, S. Dissecting gene-environment interactions: A penalized robust approach accounting for hierarchical structures. Stat. Med. 2018, 37, 437–456. [Google Scholar] [CrossRef]
- Ren, M.; Zhang, S.; Ma, S.; Zhang, Q. Gene–environment interaction identification via penalized robust divergence. Biom. J. 2022, 64, 461–480. [Google Scholar] [CrossRef]
- Dezeure, R.; Bühlmann, P.; Meier, L.; Meinshausen, N. High-dimensional inference: Confidence intervals, p-values and R-software hdi. Stat. Sci. 2015, 30, 533–558. [Google Scholar] [CrossRef]
- Bühlmann, P.; Kalisch, M.; Meier, L. High-dimensional statistics with a view toward applications in biology. Annu. Rev. Stat. Appl. 2014, 1, 255–278. [Google Scholar] [CrossRef]
- Chernozhukov, V.; Chetverikov, D.; Kato, K.; Koike, Y. High-dimensional data bootstrap. Annu. Rev. Stat. Appl. 2023, 10, 427–449. [Google Scholar] [CrossRef]
- Fan, K.; Subedi, S.; Yang, G.; Lu, X.; Ren, J.; Wu, C. Is Seeing Believing? A Practitioner’s Perspective on High-Dimensional Statistical Inference in Cancer Genomics Studies. Entropy 2024, 26, 794. [Google Scholar] [CrossRef]
- Liang, W.; Zhang, Q.; Ma, S. Hierarchical false discovery rate control for high-dimensional survival analysis with interactions. Comput. Stat. Data Anal. 2024, 192, 107906. [Google Scholar] [CrossRef] [PubMed]
- Sun, N.; Chu, J.; He, Q.; Wang, Y.; Han, Q.; Yi, N.; Zhang, R.; Shen, Y. BHAFT: Bayesian heredity-constrained accelerated failure time models for detecting gene-environment interactions in survival analysis. Stat. Med. 2024, 43, 4013–4026. [Google Scholar] [CrossRef] [PubMed]
- Sun, N.; Han, Q.; Wang, Y.; Sun, M.; Sun, Z.; Sun, H.; Shen, Y. BHCox: Bayesian heredity-constrained Cox proportional hazards models for detecting gene-environment interactions. BMC Bioinform. 2025, 26, 58. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Fan, K.; Ren, J.; Wu, C. Identifying gene–environment interactions with robust marginal Bayesian variable selection. Front. Genet. 2021, 12, 667074. [Google Scholar] [CrossRef]
- Ren, J.; Zhou, F.; Li, X.; Ma, S.; Jiang, Y.; Wu, C. Robust Bayesian variable selection for gene–environment interactions. Biometrics 2023, 79, 684–694. [Google Scholar] [CrossRef]
- Zhou, F.; Ren, J.; Ma, S.; Wu, C. The Bayesian regularized quantile varying coefficient model. Comput. Stat. Data Anal. 2023, 187, 107808. [Google Scholar] [CrossRef]
- Fan, R.; Albert, P.S.; Schisterman, E.F. A discussion of gene-gene and gene-environment interactions and longitudinal genetic analysis of complex traits. Stat. Med. 2012, 31, 2565. [Google Scholar] [CrossRef]
- Liang, K.Y.; Zeger, S.L. Longitudinal data analysis using generalized linear models. Biometrika 1986, 73, 13–22. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, J.; Qu, A. Penalized generalized estimating equations for high-dimensional longitudinal data analysis. Biometrics 2012, 68, 353–360. [Google Scholar] [CrossRef] [PubMed]
- Fitzmaurice, G.M.; Laird, N.M.; Ware, J.H. Applied Longitudinal Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Qu, A.; Lindsay, B.G.; Li, B. Improving generalised estimating equations using quadratic inference functions. Biometrika 2000, 87, 823–836. [Google Scholar] [CrossRef]
- Zhou, F.; Ren, J.; Li, G.; Jiang, Y.; Li, X.; Wang, W.; Wu, C. Penalized variable selection for lipid–environment interactions in a longitudinal lipidomics study. Genes 2019, 10, 1002. [Google Scholar] [CrossRef]
- Zhou, F.; Lu, X.; Ren, J.; Fan, K.; Ma, S.; Wu, C. Sparse group variable selection for gene–environment interactions in the longitudinal study. Genet. Epidemiol. 2022, 46, 317–340. [Google Scholar] [CrossRef]
- Jiang, J. Linear and Generalized Linear Mixed Models and Their Applications; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Diggle, P. Analysis of Longitudinal Data; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- O’hara, R.B.; Sillanpää, M.J. A review of Bayesian variable selection methods: What, how and which. Bayesian Anal. 2009, 4, 85–117. [Google Scholar] [CrossRef]
- Mitchell, T.J.; Beauchamp, J.J. Bayesian variable selection in linear regression. J. Am. Stat. Assoc. 1988, 83, 1023–1032. [Google Scholar] [CrossRef]
- George, E.I.; McCulloch, R.E. Variable selection via Gibbs sampling. J. Am. Stat. Assoc. 1993, 88, 881–889. [Google Scholar] [CrossRef]
- Zhang, S.; Xue, Y.; Zhang, Q.; Ma, C.; Wu, M.; Ma, S. Identification of gene–environment interactions with marginal penalization. Genet. Epidemiol. 2020, 44, 159–196. [Google Scholar] [CrossRef]
- Barbieri, M.M.; Berger, J.O. Optimal predictive model selection. Ann. Stat. 2004, 32, 870–897. [Google Scholar] [CrossRef]
- Barbieri, M.M.; Berger, J.O.; George, E.I.; Ročková, V. The median probability model and correlated variables. Bayesian Anal. 2021, 16, 1085–1112. [Google Scholar] [CrossRef]
- Zhang, L.; Baladandayuthapani, V.; Mallick, B.K.; Manyam, G.C.; Thompson, P.A.; Bondy, M.L.; Do, K.A. Bayesian hierarchical structured variable selection methods with application to molecular inversion probe studies in breast cancer. J. R. Stat. Soc. Ser. C Appl. Stat. 2014, 63, 595–620. [Google Scholar] [CrossRef] [PubMed]
- Morris, J.S.; Brown, P.J.; Herrick, R.C.; Baggerly, K.A.; Coombes, K.R. Bayesian analysis of mass spectrometry proteomic data using wavelet-based functional mixed models. Biometrics 2008, 64, 479–489. [Google Scholar] [CrossRef] [PubMed]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B Methodol. 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Storey, J.D.; Tibshirani, R. Statistical significance for genomewide studies. Proc. Natl. Acad. Sci. USA 2003, 100, 9440–9445. [Google Scholar] [CrossRef]
- Newton, M.A.; Noueiry, A.; Sarkar, D.; Ahlquist, P. Detecting differential gene expression with a semiparametric hierarchical mixture method. Biostatistics 2004, 5, 155–176. [Google Scholar] [CrossRef]
- King, B.S.; Lu, L.; Yu, M.; Jiang, Y.; Standard, J.; Su, X.; Zhao, Z.; Wang, W. Lipidomic profiling of di-and tri-acylglycerol species in weight-controlled mice. PLoS ONE 2015, 10, e0116398. [Google Scholar] [CrossRef]
- Fan, K.; Jiang, Y.; Ma, S.; Wang, W.; Wu, C. Robust sparse Bayesian regression for longitudinal gene–environment interactions. J. R. Stat. Soc. Ser. C Appl. Stat. 2025, 74, qlaf027. [Google Scholar] [CrossRef]
- Kozumi, H.; Kobayashi, G. Gibbs sampling methods for Bayesian quantile regression. J. Stat. Comput. Simul. 2011, 81, 1565–1578. [Google Scholar] [CrossRef]
- Chiu, C.y.; Yuan, F.; Zhang, B.s.; Yuan, A.; Li, X.; Fang, H.B.; Lange, K.; Weeks, D.E.; Wilson, A.F.; Bailey-Wilson, J.E.; et al. Linear mixed models for association analysis of quantitative traits with next-generation sequencing data. Genet. Epidemiol. 2019, 43, 189–206. [Google Scholar] [CrossRef]
- Jiang, Y.; Chiu, C.Y.; Yan, Q.; Chen, W.; Gorin, M.B.; Conley, Y.P.; Lakhal-Chaieb, M.L.; Cook, R.J.; Amos, C.I.; Wilson, A.F.; et al. Gene-based association testing of dichotomous traits with generalized functional linear mixed models using extended pedigrees: Applications to age-related macular degeneration. J. Am. Stat. Assoc. 2021, 116, 531–545. [Google Scholar] [CrossRef]
- Park, T.; Casella, G. The bayesian lasso. J. Am. Stat. Assoc. 2008, 103, 681–686. [Google Scholar] [CrossRef]
- Müller, P.; Parmigiani, G.; Rice, K. FDR and Bayesian Multiple Comparisons Rules. In Bayesian Statistics 8: Proceedings of the Eighth Valencia International Meeting; Oxford University Press: Oxford, UK, 2007; pp. 359–380. [Google Scholar] [CrossRef]
- Calder, P.C. Functional roles of fatty acids and their effects on human health. J. Parenter. Enter. Nutr. 2015, 39, 18–32. [Google Scholar] [CrossRef] [PubMed]
- Harayama, T.; Riezman, H. Lipid remodeling factors in membrane homeostasis. Nat. Rev. Mol. Cell Biol. 2018, 19, 389–403. [Google Scholar]
- Stanford, K.I.; Goodyear, L.J. Exercise and metabolic health: Interactions among skeletal muscle, adipose tissue, and inflammation. Cell Metab. 2018, 27, 10–22. [Google Scholar] [CrossRef]
- Bien, J.; Taylor, J.; Tibshirani, R. A lasso for hierarchical interactions. Ann. Stat. 2013, 41, 1111. [Google Scholar] [CrossRef]
- Lin, W.Y. Detecting gene–environment interactions from multiple continuous traits. Bioinformatics 2024, 40, btae419. [Google Scholar] [CrossRef]
- Benjamini, Y.; Yekutieli, D. The control of the false discovery rate in multiple testing under dependency. Ann. Stat. 2001, 29, 1165–1188. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, Y.; Du, Y.; Zhao, Y.; Ren, J.; Ma, S.; Wu, C. Identification of prognostic genes and pathways in lung adenocarcinoma using a Bayesian approach. Cancer Inform. 2017, 16, 1176935116684825. [Google Scholar] [CrossRef]

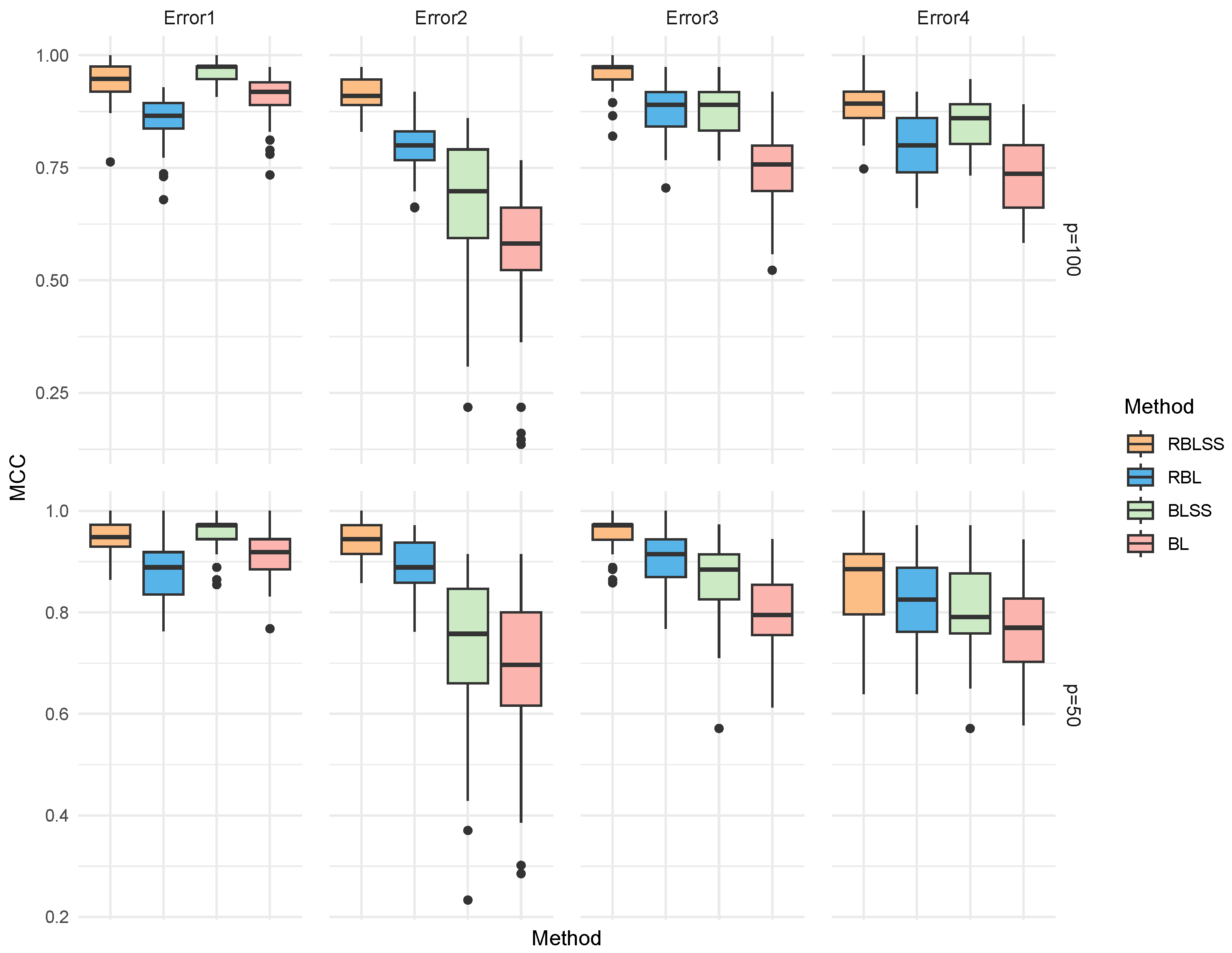
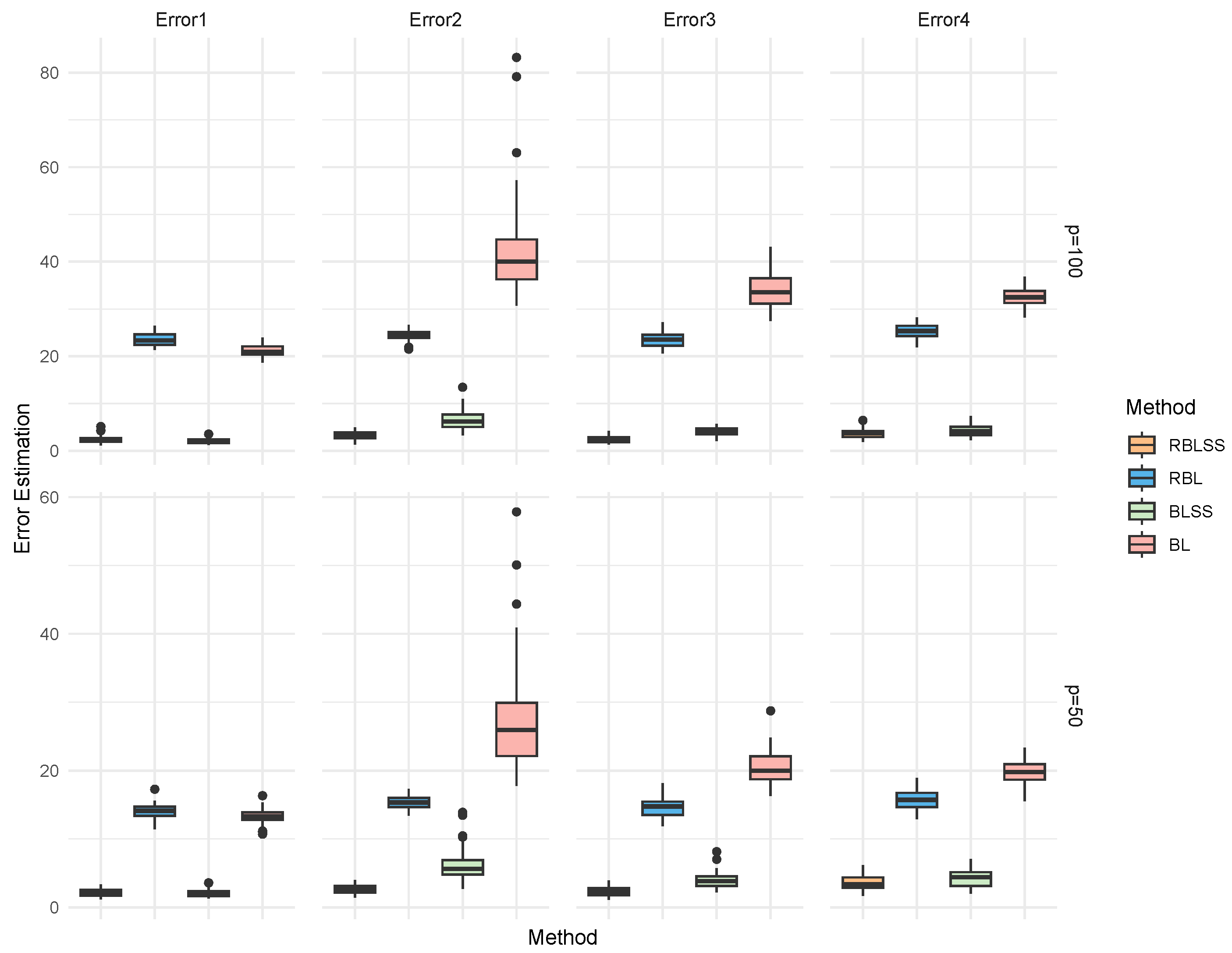
| Error | Method | TP | FP | F1 | MCC | Estimation Error |
|---|---|---|---|---|---|---|
| RBLSS | 19.38 (0.78) | 1.36 (1.12) | 0.95 (0.03) | 0.95 (0.04) | 2.21 (0.55) | |
| RBL | 18.66 (1.12) | 3.10 (1.99) | 0.89 (0.05) | 0.88 (0.05) | 14.08 (1.09) | |
| BLSS | 19.32 (0.84) | 0.80 (0.86) | 0.96 (0.03) | 0.96 (0.04) | 2.10 (0.53) | |
| BL | 18.76 (1.10) | 2.04 (1.71) | 0.92 (0.04) | 0.91 (0.05) | 13.29 (1.13) | |
| RBLSS | 18.66 (0.94) | 0.72 (0.73) | 0.95 (0.03) | 0.94 (0.04) | 2.68 (0.61) | |
| RBL | 17.32 (1.30) | 1.30 (1.13) | 0.90 (0.05) | 0.89 (0.05) | 15.41 (0.99) | |
| BLSS | 11.68 (3.99) | 0.42 (0.64) | 0.71 (0.18) | 0.72 (0.15) | 6.27 (2.44) | |
| BL | 12.62 (3.52) | 2.96 (2.44) | 0.70 (0.16) | 0.68 (0.15) | 27.65 (8.11) | |
| RBLSS | 19.10 (1.04) | 0.88 (0.82) | 0.96 (0.04) | 0.95 (0.04) | 2.40 (0.72) | |
| RBL | 18.08 (1.18) | 1.56 (1.39) | 0.91 (0.05) | 0.90 (0.05) | 14.65 (1.35) | |
| BLSS | 16.06 (2.11) | 0.46 (0.81) | 0.88 (0.08) | 0.87 (0.07) | 3.95 (1.15) | |
| BL | 15.18 (1.99) | 2.12 (1.86) | 0.81 (0.07) | 0.80 (0.07) | 20.49 (2.36) | |
| ) | RBLSS | 16.38 (2.01) | 0.90 (0.99) | 0.88 (0.08) | 0.87 (0.08) | 3.61 (1.09) |
| RBL | 15.50 (2.03) | 1.46 (1.03) | 0.84 (0.07) | 0.83 (0.08) | 15.70 (1.44) | |
| BLSS | 14.12 (2.62) | 0.36 (0.60) | 0.81 (0.09) | 0.81 (0.09) | 4.21 (1.33) | |
| BL | 14.40 (2.19) | 2.06 (1.63) | 0.79 (0.09) | 0.77 (0.09) | 19.80 (1.70) |
| Error | Method | TP | FP | F1 | MCC | Estimation Error |
|---|---|---|---|---|---|---|
| RBLSS | 19.16 (0.84) | 1.56 (1.37) | 0.94 (0.04) | 0.94 (0.05) | 2.46 (0.75) | |
| RBL | 17.02 (1.53) | 2.34 (1.61) | 0.86 (0.05) | 0.86 (0.05) | 23.47 (1.41) | |
| BLSS | 19.40 (0.73) | 0.58 (0.76) | 0.97 (0.02) | 0.97 (0.02) | 2.06 (0.48) | |
| BL | 17.38 (1.34) | 1.04 (1.18) | 0.90 (0.05) | 0.90 (0.05) | 21.15 (1.28) | |
| RBLSS | 17.28 (1.33) | 0.46 (0.68) | 0.91 (0.04) | 0.91 (0.04) | 3.26 (0.80) | |
| RBL | 13.68 (1.87) | 0.66 (0.92) | 0.79 (0.07) | 0.80 (0.06) | 24.41 (1.25) | |
| BLSS | 10.16 (3.37) | 0.48 (0.84) | 0.65 (0.17) | 0.68 (0.14) | 6.86 (2.29) | |
| BL | 7.86 (2.84) | 1.58 (2.14) | 0.52 (0.17) | 0.56 (0.15) | 44.21(14.99) | |
| RBLSS | 19.12 (0.90) | 0.64 (0.78) | 0.96 (0.04) | 0.96 (0.04) | 2.31 (0.71) | |
| RBL | 16.42 (1.46) | 0.96 (0.95) | 0.88 (0.05) | 0.88 (0.05) | 23.73 (1.66) | |
| BLSS | 16.04 (1.68) | 0.40 (0.67) | 0.88 (0.06) | 0.88 (0.05) | 4.06 (0.95) | |
| BL | 12.28 (1.95) | 1.08 (1.24) | 0.73 (0.08) | 0.74 (0.08) | 33.93 (3.81) | |
| ) | RBLSS | 17.00 (1.50) | 0.86 (0.99) | 0.90 (0.05) | 0.89 (0.05) | 3.67 (1.06) |
| RBL | 14.16 (1.84) | 1.20 (1.29) | 0.80 (0.07) | 0.80 (0.07) | 25.37 (1.50) | |
| BLSS | 15.18 (1.80) | 0.36 (0.69) | 0.85 (0.06) | 0.85 (0.06) | 4.27 (1.21) | |
| BL | 12.12 (2.22) | 1.08 (0.97) | 0.73 (0.09) | 0.73 (0.08) | 32.41 (2.11) |
| Lipid | Main PIP | Interaction PIP |
|---|---|---|
| C18:2/16:1 | 0.9597 | - |
| C18:2/18:1 | 0.9752 | - |
| C22:7/16:0 | - | 0.9087 |
| C16:0/18:1 | - | 0.9501 |
| C18:3/18:1 | - | 1.0000 |
| C18:2/20:4 | - | 0.9248 |
| Lipid | Main PIP | Interaction PIP |
|---|---|---|
| C20:6/16:0 | 0.9863 | - |
| C18:3/18:1 | - | 1.0000 |
| C18:2/20:4 | - | 0.9578 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Fan, K.; Wu, C. Prioritizing Longitudinal Gene–Environment Interactions Using an FDR-Assisted Robust Bayesian Linear Mixed Model. Algorithms 2025, 18, 728. https://doi.org/10.3390/a18110728
Li X, Fan K, Wu C. Prioritizing Longitudinal Gene–Environment Interactions Using an FDR-Assisted Robust Bayesian Linear Mixed Model. Algorithms. 2025; 18(11):728. https://doi.org/10.3390/a18110728
Chicago/Turabian StyleLi, Xiaoxi, Kun Fan, and Cen Wu. 2025. "Prioritizing Longitudinal Gene–Environment Interactions Using an FDR-Assisted Robust Bayesian Linear Mixed Model" Algorithms 18, no. 11: 728. https://doi.org/10.3390/a18110728
APA StyleLi, X., Fan, K., & Wu, C. (2025). Prioritizing Longitudinal Gene–Environment Interactions Using an FDR-Assisted Robust Bayesian Linear Mixed Model. Algorithms, 18(11), 728. https://doi.org/10.3390/a18110728







