Abstract
This study presents a fuzzy-Apriori model that analyses student background data, along with end-of-lesson student-generated questions, to identify interpretable rules. After linguistic and semantic preprocessing, questions are represented in a fuzzy form and combined with background and performance variables to generate association rules, including support, confidence, and lift. The dataset includes 202 students, parent reports from 174 families, 5832 student-generated questions, and 510 teacher-generated questions collected in regular lessons in grades 7–8. The model also incorporates a topic-level dynamic updating step that refreshes the rule set over time. The findings indicate descriptive associations between background characteristics, question complexity and alignment, and classroom performance. It is essential to note that this phase explores possibilities rather than providing a validated instructional method. Question coding inevitably involves subjective elements, and while we conducted the study in real classroom settings, we did not perform causal analyses at this stage. The next step will be developing reliability metrics through longitudinal studies across multiple classroom environments. Future work will test whether using these patterns can inform instructional adjustments and support student learning.
1. Introduction
Across many countries, assessment is moving toward acknowledging individual learner differences and tailoring evaluation to them. Conventional approaches, written tests and oral exams—often miss what matters most: students’ true understanding and motivation, their diverse backgrounds, and whether teaching strategies actually work. In response, technology-enhanced assessment frameworks have emerged that apply AI to help teachers make better, data-informed decisions [1,2,3]. One novelty of this study is the presentation of an algorithmic approach that, by combining fuzzy logic [4,5,6,7] and Apriori association rule mining [8,9,10], is capable of generating interpretable, decision-support rules from student background data and questions generated by students at the end of the lesson. In our model, pedagogical constructs such as Bloom’s taxonomy, cognitive depth, and student reflection serve as heuristic reference frames rather than absolute measures. Recent evidence suggests that the surrounding learning environment influences the quality of student questions and their level of engagement. Meta-analytic work links teacher-student relationships and teachers’ provision of classroom structure with students’ engagement and achievement beyond individual knowledge states [11,12]. Contemporary reviews of teacher expectations also report meaningful downstream effects on participation and performance, which can indirectly shape the kinds of questions students ask [13]. We interpret student questioning not as a direct and exclusive sign of understanding, but as one observable dimension of engagement and reasoning. We therefore treat student-generated questions as context-sensitive data to be analysed for potential patterns, rather than as fixed evaluative indicators. The advantage of fuzzy logic lies in its ability to handle uncertain, non-exact data and its suitability for modelling complex human characteristics [14,15,16]. A central role in the research is played by our system called WTCAi, which has already proven its suitability for student profiling and predictive assessment in previous developments [3]. However, the improved version presented in this article processes not only numerical and social background data, but also takes into account students’ active cognitive engagement through the questions formulated at the end of lessons. Investigating question generation offers a useful pedagogical lens from multiple perspectives. On one hand, it provides feedback on the depth of comprehension of the material; on the other hand, it offers the teacher information about the interpretability of the lesson’s structure and content, as well as the students’ levels of interpretation [17].
This study processes a corpus of naturally formulated questions using linguistic and semantic methods, then transforms them into fuzzy variables, which serve as the basis for rule mining. Fuzzy modelling enables a gradual, multi-dimensional evaluation of student activities, which better reflects real learning processes than binary or point-based measurement models [6,7,18,19]. The extended version of the model does not use a static rule set, but is capable of temporal adaptation. Based on data from student activities and new questions, it cyclically reweights the rules, allowing pedagogical interpretation to follow changes in learning patterns sensitively. The dynamic interpretation of the fuzzy-Apriori combination enables the creation of a model that can be applied in complex decision-making situations, while remaining transparent and pedagogically interpretable in an educational context [20,21,22].
The research aims to identify rules using the fuzzy-Apriori algorithm that are suitable for exploring associations related to student performance and for suggesting potential pedagogical intervention points. The paper provides insight into the methodology used, presents the main results, and provides methodological context and refers readers to prior benchmarking for predictive comparisons [23].
2. Related Research
Artificial intelligence and data mining methods are increasingly present in educational systems. Within the fields of Educational Data Mining (EDM) and Learning Analytics (LA), there is a growing emphasis on approaches that can map and predict the quality of the learning process through the analysis of student activities, performance, and background data [1,2].
Fuzzy logic-based systems have proven particularly useful in this area, as they enable the description of characteristics that cannot be reduced to precise numerical categories [4,5,16]. Student motivation, interest, social background, or classroom activity are examples of subjective features that fuzzy sets are well-suited to handle [6,19]. Fuzzy-based decision support systems thus offer opportunities not only for nuanced interpretation of performance but also for the personalisation of pedagogical interventions [14,15,18]. Association rule mining, especially the Apriori algorithm [8,9], has been widely applied in educational data mining to uncover interpretable relations among student, teacher, and task variables. Student question generation can be viewed through a structured network perspective, where the evolving rule set functions as an adaptive network that is incrementally optimised as new patterns emerge. The rule-based structure of the fuzzy-Apriori system, which combines graded relationships and frequency-based associations, is conceptually related to the P-graph and S-graph methodologies associated with Ferenc Friedler, which are based on logical and discrete element-based network construction used in industrial systems [24]. This structured yet flexible approach also effectively models the nonlinear, iterative nature of student thinking. Previous studies have often used these techniques to model academic performance, subject preferences, or dropout risks [3]. The algorithm enables the identification of frequent regularities that reveal hidden connections between student characteristics and behavioural patterns. However, the combined application of fuzzy logic and the Apriori algorithm has so far appeared relatively rarely in educational contexts, especially in cases where student background data and individual cognitive activities, such as end-of-lesson question generation, are examined in an integrated manner. This research offers novelty in that regard: we apply a fuzzy-Apriori-based algorithm, similar to the FARM-HPT system [25], to explore the regularities characterising student question generation and its background. From a pedagogical perspective, question generation is of significant importance, as it develops critical thinking, supports self-regulated learning, and reflects the active mental processing of the learning material [3,17]. International studies have also highlighted that the depth and structure of student questions correlate with the level of understanding [3]. Nevertheless, these linguistic contents rarely form part of machine learning analyses and are even less frequently processed within a fuzzy logic framework. At the same time, based on research by international experts, the effective possibilities of using interactive machine learning can be utilized even before elementary school studies [26].
The aim of the present study is therefore not merely to extend previous models, but to develop an interpretable and transparent rule-based framework capable of jointly processing student questions and background data, thereby contributing to a deeper understanding of the learning process and enabling targeted pedagogical support.
3. Applied Methodology
3.1. Data Analysis and Preprocessing
The foundation of the research is an empirical dataset that is partly based on the results of previous studies and partly on new data collected within the framework of the present study. A total of 174 parents [23,27,28] and 202 students participated in the data collection. These students belonged to different grade levels and took part in lessons across various subject areas (e.g., digital culture, science, physics). The data collection aimed to cover the broadest possible spectrum of student background and classroom activity, with particular emphasis on the questions formulated by the students.
The data were categorized into three main groups:
- Background variables include parental education level, learning habits, the extent of support for learning at home, and sleep duration (see Appendix A for a complete list of variables). These attributes primarily assist in interpreting student motivation and learning capacity.
- Classroom performance indicators, including achieved scores, the number of absences, and teacher-assessed classroom activity.
- Students recorded open-ended questions at the end of every lesson, phrased in their own words. This elicitation provided a direct window into the depth of their understanding, areas of interest, and how they were cognitively processing the topic.
During preprocessing, numerical and categorical variables were transformed into fuzzy logic-based sets. The attributes were typically classified into three fuzzy categories (e.g., low, medium, high), although the granularity of the scale depended on the specific characteristics of each attribute. Membership functions were defined using triangular and trapezoidal mappings, following standard practices in the field of fuzzy logic literature. The student-generated questions were recorded in textual form and then underwent multi-step linguistic and semantic preprocessing.
This included:
- Descriptive categorisation of the questions (e.g., factual, conceptual, application-level questions).
- Determination of complexity level.
- Examination of content overlap with the topics outlined by the teacher.
We classified questions as factual, conceptual, or analytical and mapped them to Bloom’s taxonomy. This classification process is inherently interpretive and may vary across different teachers, subject areas, and student age groups. We mitigated this by using a shared rubric and calibration examples prior to coding. Disagreements were resolved through discussion until a working consensus was reached. We did not compute a formal inter-rater coefficient in this phase. Any κ values reported later refer to agreement among weighting models, not to inter-rater coding reliability. Fuzzy membership values quantify graded measurement uncertainty in the variables we define; however, they do not resolve conceptual divergence among human coders. This divergence reflects interpretive, not statistical uncertainty and will therefore require explicit coder training, as well as formal reliability procedures in later phases. Future iterations will include reliability statistics and expanded training for coders. The ultimate goal was to create a data structure that, for each student, contained a set of fuzzy attributes reflecting characteristics of their background, performance, and question-generation patterns. This served as the foundation for generating subsequent fuzzy transactions and association rules. Predictive benchmarking results for the current pipeline are available in a separate evaluation study [23]; here, we restrict our reporting to interpretability-oriented indicators defined in Equations (11)–(13) and the cohort-level coverage definition in Fuzzy Rule Generation and Evaluation. Data were collected during regular lessons in digital culture, science, and physics in grades 7 and 8. Teachers explained the activity to students and made it clear that questions would not be graded. In addition to quantitative indicators, we collected brief, anonymised reflections from participants to document classroom interpretation. One teacher remarked, “Students’ end-of-lesson questions were sometimes deeper than the ones I had planned, which made me revisit how I scaffold questioning”. A student similarly noted, “When we could ask our own questions, I tried to connect today’s topic to what we learned last week”. We obtained written consent from parents, and students could withdraw at any time. Both teachers and students were aware that the questions would be used for research and analysed at the school level. No individual feedback or labels were displayed to students. The study complied with institutional guidelines and GDPR requirements.
3.2. Description of the Fuzzy-Apriori Algorithm
The goal of the algorithmic model applied in this research is to identify interpretable, pedagogically relevant, and sufficiently frequent patterns within the student population, based on background variables and the characteristics of end-of-lesson question generation. We provide a compact flowchart (Figure 1) that summarises the end-to-end pipeline from raw inputs to mined rules, with each block aligned to the mathematical operators defined below. To complement the formal description, we include a brief worked example. Consider a student with the background profile {parental support: medium, homework regularity: high} and an end-of-lesson question coded as conceptual with above-average abstraction. After linguistic preprocessing and fuzzy transformation, the resulting transaction contains medium and high membership values for the corresponding background and question features. Using the α-cut defined in Equation (5), the active fuzzy subsets enter the transaction database, and the Apriori step yields an interpretable rule such as {homework regularity = high, question abstraction = high} ⇒ {performance = above-median}, with support, confidence, and lift computed as in Equations (11)–(13). This walk-through mirrors the full pipeline while keeping the mathematical details in the main equations. These patterns could help us better understand how learning actually happens.
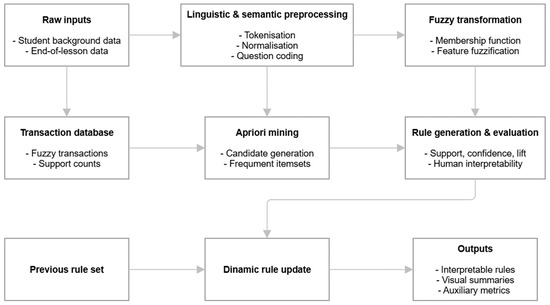
Figure 1.
End-to-end pipeline from student background data and end-of-lesson questions to fuzzy transactions and mined association rules.
The model, expanding on the previous two-level approach, operates in four main phases:
- Transformation of input data based on fuzzy logic.
- Computation of cognitive alignment between teacher and student questions.
- Generation of fuzzy transactions.
- Generation of association rules using a modified Apriori procedure, which is based on the fuzzy adaptation of the algorithm introduced by Agrawal and Srikant [8].
The model enables the simultaneous examination of the relationships between student background characteristics, cognitive levels of question generation, and instructional intent. The system not only generates rules but also supports pedagogical reflection by revealing potential discrepancies between students’ approaches and teachers’ expectations.
3.2.1. Fuzzy Transformation
One of the fundamental assumptions of the model is that student data and responses are not interpreted solely as numerical values, but also in terms of linguistic categories that can incorporate gradation [19]. For example, “motivation” or “evaluation of textbook usage” should not be viewed merely as numbers on a 1–5 scale, but can also be described using natural language classifications such as “very low”, “low”, “medium”, “high”, and “very high”. Since these are not mutually exclusive categories, a student can belong to multiple fuzzy subsets simultaneously, to varying degrees.
Based on the real-world data, the following attributes were included in the fuzzy transformation:
Student Background Variables:
- Homework completion: {yes, no, not_assigned}
- Extra credit task: {yes, no, not_assigned}
- Textbook evaluation: 1–5 scale → fuzzy sets: {very poor, poor, average, good, excellent}
- Number of questions (quantitative indicator)
- Consistency of question complexity (internal standard deviation, normalised value)
- Question-Specific Attributes:
- Difficulty level: 1–5 scale, based on subjective scoring
- Question type: {factual, conceptual, application, analysis, evaluation}
- Content overlap: the degree to which the question aligns with the teacher’s instructional focus
During the fuzzy transformation, each attribute is assigned individual fuzzy subsets, to which membership functions are defined (in trapezoidal or triangular form). The membership values are evaluated based on a predefined threshold (α-cut). If the membership value exceeds this threshold, the corresponding subset is considered active in the transaction. Formally, let be the set of students, and the set of attributes.
For each attribute , there are associated fuzzy subsets:
The corresponding membership functions are as follows:
The type of membership function can be triangular or trapezoidal, depending on the nature of the given attribute.
Triangular membership function:
where the membership value is one at point , and zero at the endpoints and .
Trapezoidal membership function:
where . In this case, the membership value is one on the interval , which represents the zone of full membership.
The fuzzy transaction is assigned to the student in the following way:
where α-cut∈ [0, 1] is a predefined threshold value.
One of the novel elements of the model is that it examines not only the number or type of questions posed by students but also their cognitive complexity. The difficulty level of the questions is scaled based on Bloom’s taxonomy. We define the complexity function as follows:
where is the set of questions, and the interval corresponds to the six levels of Bloom’s taxonomy. However, in the real data, we observed significant subjectivity: the same question was evaluated at different levels by different students. For example, the question “How did Miklós Zrínyi die?” was classified by the teacher as level 1 (remembering), while two different student groups rated it at levels 2 and 3, respectively. This kind of discrepancy reinforces the justification for using fuzzy modelling, especially given that the aggregation of fuzzy values from pairwise comparisons can also be examined using geometric methods, complemented with consistency analysis [29]. The complexity value is not a single-point number, but can be associated with multiple levels to varying degrees.
The average complexity of the question set is:
The degree of alignment between the teacher’s question set and the student’s question set is:
The above value is converted into natural language categories.
Calculating the cognitive complexity of student and teacher questions is a non-trivial task, as the pedagogical distance between different Bloom levels is not necessarily linear [9,10]. To address this, we implemented three different weighting approaches: empirical, logarithmic, and adaptive, which align with weighting logics based on the principles of hierarchical decision-making [18,29]. The demand for automated handling of question complexity also appears in AI-based question generation research, such as in the works of Muse et al. [30] and Bulathwela et al. [31], and already in the work of Heilman et al. [32], where scalable generative models are applied for the personalised generation of educational questions.
Our models were validated using real-world data:
- Empirical model (E-model)—Assigns complexity values to Bloom levels based on expert assessments conducted by teachers. The distances between levels are not equal; for example, the transition between “understanding” and “application” is less distinct than that between “application” and “analysis”. The empirical model is therefore nonlinear but aligns well with teachers’ subjective evaluations. The weighting logic corresponds to the axiomatic foundations of the AHP method, which aims to organise priorities into a consistent and interpretable structure [21]. The resulting alignment categories and their value ranges in the empirical model are summarised in Table 1.
 Table 1. E-Model Alignment Categories and Value Ranges.
Table 1. E-Model Alignment Categories and Value Ranges. - Logarithmic model (L-model)—As cognitive levels increase, the values assigned to each level grow proportionally according to a logarithmic curve.
- Adaptive model (A-model)—This hybrid approach considers differences in subject area and age group. For example, the model applies different weightings in a 7th-grade physics lesson compared to an 8th-grade literature class. The adaptive model automatically adjusts the scale based on prior grade-level data and teacher patterns.
- To address the weighting differences between cognitive levels, we incorporated scaling principles based on hierarchical decision-making logics during the design of the weighting scales, which are related to Saaty’s priority method [21].
The three weighting approaches were validated on 510 teacher-generated and 5832 student-generated questions (Table 2).

Table 2.
Comparison of Weighting Models (κ values indicate agreement among weighting models rather than inter-rater coding reliability).
3.2.2. Fuzzy Rule Generation and Evaluation
One of the most important components of the model is its ability to generate association rules based on the resulting fuzzy transactions. The aim is not merely the automatic detection of frequent patterns, but also their pedagogical interpretability, that is, to ensure that the generated rules provide feedback on students’ thinking, the effectiveness of classroom strategies, or even on which types of learners require special attention.
The general form of a fuzzy rule is [8]:
where is the set of antecedent fuzzy attributes [15], for example:
Moreover, is the consequent, which often corresponds to a fuzzy category related to a student type or behavioural pattern.
The rules are evaluated using three main fuzzy metrics: support, confidence, and lift [4,5,15,16]. These are calculated based on the following formulas, which are also widely used in traditional data mining practices, especially in Apriori-type algorithms [8,9]:
Support:
Confidence:
where the sum in the denominator must not be zero. If for all i, then the rule is not interpretable.
Lift:
where
In this formalism, is the minimum membership value among the fuzzy sets included in the antecedent , concerning student :
The “minimum intersection” principle originates from classical fuzzy logic and aims to model the dominance of the weakest link within a rule [4,5,16,33]. During the aggregation of fuzzy rules, the use of OWA weights with minimal variance can further enhance the stability and interpretability of the metrics [6].
Based on real-world data, the following types can be distinguished, for example, along the fuzzy regulation of student behaviour patterns:
- Performance-based rule pattern: The simultaneous presence of low motivation and low Complexity may indicate a problematic student pattern: {Homework: no} ∧ {Complexity: very_low} ∧ {Alignment: divergent} ⇒ {Student_profile: problematic}.
- Motivational rule pattern: The relationship between student effort and autonomy: {Textbook_evaluation: high} ∧ {Complexity: high} ∧ {Question_consistency: low} ⇒ {Student_type: enthusiastic_but_unstructured}.
- Subject-specific rule pattern, which may reveal learning style characteristics within a given subject: {Subject: history} ∧ {Question_type: factual > 80%} ∧ {Complexity: low} ⇒ {Learning_style: memorization_based}.
These rules are not static. The model is capable of learning and updating itself based on new student data. The resulting fuzzy rule system is suitable not only for classification, but also for differentiation, intervention, and assessment [18], similar to the fuzzy educational model applied in a higher education context as presented by Teng [25]. During the formulation of rules, decisions are made with consideration of multiple, often competing, pedagogical objectives, which are based on the weighing of preferences and trade-offs [22].
3.2.3. Topic-Based Dynamic Updating
One of the model’s most significant advantages is that it is not static, but capable of adapting to the temporally changing pedagogical environment. Students do not revisit the same topics year after year, as they typically pose questions within a given content area only once, following a linear progression of learning. Consequently, the rule system should not be updated individually by a student or sporadically, but rather in a topic-specific and grade-level manner. This approach enables educational experiences to build upon one another through a form of generational learning, meaning that a new cohort’s question generation does not start from scratch but instead shapes the new rule system in combination with previously observed patterns.
After generating fuzzy transactions from the current grade level’s student data, a new set of rules is constructed:
where is the database containing the fuzzy transactions generated within a given topic, and is the new set of rules derived from it. During the update process, the existing rules are not simply replaced; instead, they are combined with the new patterns using weighted merging. This ensures that infrequent but pedagogically important rules are not lost. The weighting is performed formally as follows: if a rule appears in both the previous set ( and the new set ():
where is a weighting parameter that controls the degree to which new patterns are preferred over old ones, the use of the min and max functions ensures that the resulting values remain within the [0, 1] interval.
If the rule appears only in the new set, then:
If the rule appears only in the old rule set, then:
3.2.4. Rule Set Updating
A rule can remain active in the following year if it meets the minimum required support and confidence thresholds.
The minimum thresholds can also change dynamically: if too many rules are generated, the thresholds become stricter; if too few, they are relaxed. This supports scalability and helps manage the increasing complexity that comes with database growth.
3.2.5. Adaptive Question Generation
One of the most exciting capabilities offered by the intelligent assessment system is its ability to suggest new questions [30,31,32]. In our method, this is done not only based on learning objectives defined by the teacher but also in response to student interest. This adaptive question generation enables question selection to be dynamic, context-aware, and personalised, rather than static.
The model operates with two sources of questions:
- : the set of teacher-generated questions,
- : the set of student-generated questions.
Each question is assigned multiple features, the most important of which are:
- : the complexity level of the question according to Bloom’s taxonomy,
- : the relevance of the question in relation to the current rule set ().
The goal of the selection process is to compile a balanced question set that considers both the teacher’s and the student’s intentions. In our current research, the method does not aim for a perfect solution; instead, it applies a fast, heuristic, near-optimal selection process through the following steps. Here, we use the term ‘heuristic’ in its computational sense, that is, as a practical, near-optimal selection method, rather than as a pedagogical heuristic for student thinking.
Step-by-step operation of the algorithm:
- Weight calculation: For each question, a weight is calculated based on the following factors:
- Its complexity (γ);
- Its relevance to the curriculum (ρ);
- Pedagogical priority in the case of teacher-generated questions;
- Frequency in the case of student-generated questions (i.e., the number of students who posed a similar question).
- Ranking: The questions are sorted in descending order based on their weight values, with the most important ones at the top.
- Selection: The system selects the top questions in order until a predefined target number is reached (e.g., 10 questions).
- Diversity check: The selected question set is reviewed to ensure that all Bloom levels (ranging from 1 to 6) are adequately represented. If any level is missing, the system replaces specific questions to maintain a balanced distribution of cognitive levels (Figure 2).
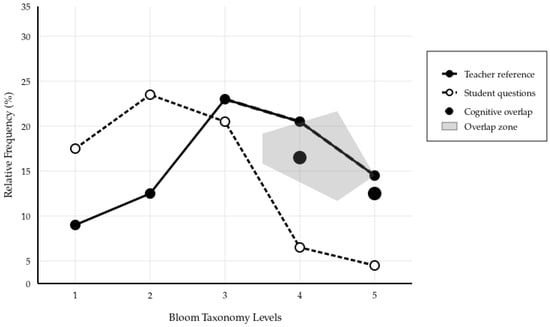 Figure 2. Cognitive overlap phenomenon analysis (Teacher vs. Student Question Complexity Patterns).
Figure 2. Cognitive overlap phenomenon analysis (Teacher vs. Student Question Complexity Patterns).
Table method is fast, well-suited for classroom environments, and takes into account teacher goals, student activity, and cognitive diversity. Additionally, it provides feedback; for example, if students consistently ask low-level Bloom questions, this may prompt a reconsideration of the instructional focus or teaching strategies.
3.3. Analysis of Question Generation
The analysis of student-generated questions has become one of the most sensitive indicators of how students interpret the curriculum content and the internal mental operations through which they process it. A single question does not merely signal what the student does not understand; it also reveals what they are curious about, what connections they perceive, and what relationships they are trying to comprehend or even reconstruct. In this sense, student questions are not passive, reactive responses but active attempts at knowledge construction, reflecting individual cognitive patterns. During the research, these questions were recorded in textual form, typically after each lesson concluded. Data collection took place through an online platform, allowing students to formulate their questions voluntarily and at their own pace. The system did not assign any direct evaluative function to the questions, which reduced the influence of conformity or formal subject-specific pressure. This made it possible for the responses to more accurately reflect the students’ actual level of understanding and focus of interest. Natural language processing analysis identified three types of questions. The first group includes factual questions, which inquire about specific, clear-cut information, data, or facts. These showed simpler linguistic structures and often consisted of a single sentence. The second type, conceptual questions, addressed relationships between concepts, sometimes assuming prior knowledge. The third category is analytical questions, which extend beyond basic understanding and aim to evaluate and interpret. These tended to be longer, more complex, and reflected thought processes that surpassed simple recall of the material.
The structural features associated with each question type showed clear correlations with student performance indicators. Analytical questions appeared more frequently among students who achieved higher scores in classroom assessments, whereas factual questions were more dominant among students with lower results. This supports the assumption that question generation may reflect not only stylistic differences but also substantive distinctions in depth of understanding. Each question was linked to a student identifier, subject, and timestamp, allowing for temporal and subject-based comparisons. The use of different weighting models enabled assessments tailored to specific topics and student groups. Complexity weighting was thus not treated as an absolute value, but always adjusted to the local context. The fuzzy logic-based classification of questions reflects this gradual and layered approach. These choices reflect the exploratory nature of this phase and will be extended in subsequent iterations.
4. Results
The application of the fuzzy-Apriori algorithm led to the identification of association rules that proved not only statistically valid but also pedagogically interpretable, describing patterns that reflect aspects of the learning process. A distinctive feature of the model is that it did not treat question-generation-related student characteristics in isolation, but rather as part of the broader learning context. This means that the interpretation of the rules goes beyond simple predictive relationships. One of the strongest and most frequently recurring rules is captured by the following association. If a student can formulate high-abstraction-level questions despite having low parental support, their classroom performance tends to exceed expectations and typically falls within the mid-to-high range.
The rule, expressed in fuzzy logic, can be formulated as follows:
{Support: low, Abstraction: high} ⇒ Performance: good
The support value for this rule was 0.34, its confidence level was 0.72, and its lift value was 1.48. The latter indicates that the relationship is informative, meaning it is not merely the result of random co-occurrence between variables. The use of fuzzy representation made it possible to identify rules that handle “partial truths”, building on Zadeh’s theoretical framework [4], which is exceptionally well-suited to the subjective characteristics of educational contexts [5,19]. A similarly significant rule emerged, indicating that students with moderate motivation, if capable of formulating conceptual-level questions, generally achieve average or better classroom performance. The interpretation of this rule suggests that an outstanding motivational background is not necessary for a student to process content through interpretive questioning successfully. This finding is particularly relevant for differentiated pedagogical practices, as it reinforces the idea that question complexity, as a metric variable, could serve as a new indicator of student development [3]. The distribution of student question cluster difficulty across the participating disciplines is summarised in Figure 3.
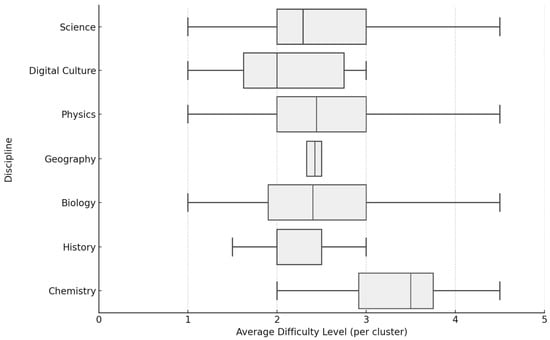
Figure 3.
Distribution of the difficulty levels of student question clusters across different disciplines; different shades of green are used only for visual distinction between disciplines and do not represent additional variables.
The rules generated based on student question generation also made it possible to group students using fuzzy clustering. This was not based on discrete types but rather on partial membership to various characteristics. Four distinct, partially overlapping student types emerged. The first type included students who, despite low background support and relatively modest prior performance, were able to formulate complex, analytical questions. These students typically engage in higher-level cognitive processing and reflect indirectly, through their questions, on the quality of the educational environment. The second type consisted of students who, even with moderate to high classroom support, tended to generate superficial and simple questions. Their performance, accordingly, was weaker than expected. This type highlights the fact that the mere presence of external resources does not guarantee the use of deeper learning strategies [1]. The third group comprised students whose questions were predominantly conceptual in structure, though intermediate categories also appeared frequently among their questions. In general, they were susceptible to the classroom environment, the teacher’s style, and the group dynamics. The fourth type included students who consistently demonstrated high complexity in question generation, addressing multiple conceptual layers and often incorporating interdisciplinary connections. Their performance, according to the analysed data, was consistently high, and they were often those who even exceeded the complexity level of the teacher’s questions [3]. An exciting finding from a pedagogical perspective was the observed trend that more frequent and more complex questions were typically generated during lessons where the teacher actively used visual tools, cooperative learning techniques, or interdisciplinary references. This confirms that the teaching methodology and tools employed influence both the frequency and complexity of student question generation. As one teacher summarised, “Using visual prompts and short pair-shares reliably drew out more ‘why/what-if’ questions than my usual routine”. This observation is consistent with our quantitative finding that richer methodological support co-occurred with more complex student-generated questions, suggesting that the classroom context contributes to part of the observed complexity. As such, question generation is a kind of implicit pedagogical feedback system [3,17]. The automatic classification of questions was performed using a natural language processing (NLP) module, which was capable of identifying syntactic and semantic differences among the three main question types [2]. This approach enabled the development of scalable and reproducible interpretive structures alongside traditional content analysis techniques. By jointly processing linguistic features, fuzzy logic evaluation, and student background data, an analytical horizon was created that is sensitive even to the more subtle qualitative dimensions of the learning process. The system’s dynamic nature was also evident in its ability to regenerate the rule set with each new student question submitted. The weighted updating mechanism ensures that the experiences of previous cohorts are not lost, while also incorporating the emerging patterns of new generations into the system. In the temporal adaptation of rules, both stability and flexibility are maintained. Student profiles are not static categories, but continuously evolving fuzzy clusters, shaped by tracking the individual learning paths of students [6,19].
In evaluating the predictive performance of the model, the fuzzy-Apriori approach was compared with two other algorithms: random forest and logistic regression. We intentionally refrain from reframing the rule set as a predictive classifier in this article. A dedicated predictive benchmarking of the pipeline against random forest and logistic regression is reported in a separate study by our group [23]. In the present manuscript, we quantify the mined patterns with indicators intrinsic to association analysis and pedagogical interpretability, namely support, confidence, lift, and cohort coverage. As discussed in prior benchmarking [23], tree-based ensembles may limit interpretability, whereas logistic regression offers a simpler decision surface but may underperform on specific subgroups. In this article, we therefore emphasise interpretability and restrict reporting to support, confidence, lift, and cohort coverage. Accordingly, the results highlight interpretable associations among background variables, question characteristics, and performance, and illustrate how the model can sensitively surface feedback patterns within the pedagogical context [1,2,3,23].
5. Discussion
The algorithmic model presented in this research is a technological development with pedagogical interpretive potential. Our findings are descriptive and correlational. Accordingly, fuzziness should be understood as modelling measurement imprecision, not as compensating for interpretive disagreement between raters. The rules reveal interpretable associations between background variables, question characteristics, and performance; however, we do not claim to have tested instructional effects. At this stage, the model serves as an interpretable hypothesis generator for teachers and researchers. Future work will include classroom interventions and longitudinal tracking to examine whether using these rules supports instructional adaptation and improves learning trajectories. While accuracy-style indicators are helpful for specific applications, our study emphasises interpretability; readers interested in predictive metrics can consult our separate benchmarking report [23]. These plans align with the scope of the present study, which focuses on a development stage rather than a validated intervention. To illustrate this context-sensitive reading more concretely, consider a rule of the form {Moderate motivation + conceptual (“why”-type) questions ⇒ average-or-better performance}. In a classroom climate where the teacher routinely legitimises exploratory questioning (by giving time, modelling, and acknowledging students’ attempts), this rule can be read as an argument for sustaining conceptual questioning even among only moderately motivated learners—here, the context amplifies the pedagogical value of the configuration. In a more time-pressured or strongly assessment-oriented lesson structure, however, the same rule signals a fragile opportunity. Unless the teacher deliberately protects space for such questions, the configuration may not reappear, and the associated performance benefit may not materialise. Thus, the rule’s significance is not determined solely by the data pattern, but is shaped by how the surrounding practices support or suppress it. A second example is a rule of the form {Predominantly factual questions + low alignment with the lesson focus ⇒ below-median performance}. In a class where peers occasionally model higher-order questions and the teacher uses short think-alouds, this rule can be interpreted as a prompt to insert a brief reframing activity (e.g., pair-share, “what would change if…?”), because the social and instructional context can realistically lift students out of factual questioning. In a less supportive context, however, the same pattern is read more cautiously, as an indicator of a broader misalignment between task demands and students’ current questioning repertoire. In both cases, the context does not merely surround the rule; it tells the teacher which instructional response is proportionate. The interpretive meaning of the discovered fuzzy rules depends strongly on the classroom context. Teacher expectations, peer dynamics, and the emotional climate of lessons may amplify or moderate the strength and direction of these associations. For example, links between question complexity and performance can reflect not only individual cognitive tendencies but also how the teacher scaffolds questioning or how peers value deeper inquiry. In supportive and structured environments, students with initially lower confidence may still formulate higher-order questions, leading to stronger fuzzy alignment scores. This suggests that contextual sensitivity is not an external add-on but an inherent dimension of the pedagogical interpretation of the model; consequently, the rules are best read as context-conditioned hypotheses rather than context-free regularities. When the model surfaces patterns such as {Moderate motivation + conceptual questioning ⇒ average-or-better performance}, teachers may treat this as a prompt to sustain and scaffold conceptual questioning—even when overt motivation appears modest—because classroom structures (clear routines, feedback norms, and peer support) can enable the emergence of deeper inquiry that the fuzzy measures capture. The adaptive logic of the fuzzy-Apriori-based model aligns well with educational innovations that aim for real-time feedback and student engagement. For example, the research by Katona and Gyönyörű examined the integration of an AI-based adaptive learning system with the flipped classroom model [34]. It demonstrated that personalised feedback improves both learning outcomes and learner autonomy. The combination of fuzzy logic and association rule mining enables student characteristics to be represented not in rigid, discrete categories, but rather in gradual, nuanced structures that reflect degrees of belonging. This is especially important in educational environments where student responses are often subjective, fragmented, or context-dependent. In addition to the subjectivity of coding, the study faces further constraints that are relevant for interpretation. Linguistic grouping of student questions can introduce bias because similar intents may be phrased with different lexical choices, and student-generated wording reflects individual style. Several background variables rely on self-reported information, which can add noise and social desirability effects to the mined patterns. Finally, while the present dataset fits comfortably within our computational budget, scaling to substantially larger cohorts will require more aggressive preprocessing and distributed association-rule mining, given the combinatorial growth of candidates. These constraints do not alter the descriptive scope of the study but delineate its present boundaries and inform the future work plan.
A key advantage of the model is its ability to handle non-exact, uncertain, or ambiguous student data, not only from a technical perspective but also from a didactic one. This makes it possible to uncover relationships that are difficult to interpret using classical statistical baselines, such as logistic regression, or more opaque ensemble models, like random forest. In contrast, the present approach offers a transparent and interpretable rule-based system, in which every decision can be traced back to concrete dimensions of classroom reality. Baranyi [35] demonstrated that fuzzy rule systems can be scaled while maintaining interpretability, an idea that conceptually aligns with the goals of our dynamically updatable, profile-tracking fuzzy-Apriori model. The textual form of fuzzy rules allows learning patterns to be approached linguistically, which is especially useful in pedagogical decision-making.
Within this framework (Figure 4), student-generated questioning is not merely interpreted as a cognitive performance but also as a form of reflective indicator. The structural characteristics of questions, such as their level of complexity, type, or content focus, provide direct feedback on what students considered relevant, what they understood, or what they expressed doubt about. Suppose a student group generates factual, primarily questions that are associated with lower performance scores. In that case, this may indicate that the lesson’s concept formation did not offer sufficient interpretive depth. In contrast, students who pose analytical, interdisciplinary, or abstract questions often go beyond the lesson structure, reinterpret the content, and restructure the material according to their cognitive patterns. Thus, question generation functions as a sensitive feedback mechanism, not only in terms of comprehension but also in terms of lesson engagement, emotional relevance, and content focus. During the study, a clear trend emerged: in lessons where the teacher employed visual tools, cooperative learning techniques, or real-life examples, both the number and complexity of student questions increased significantly.
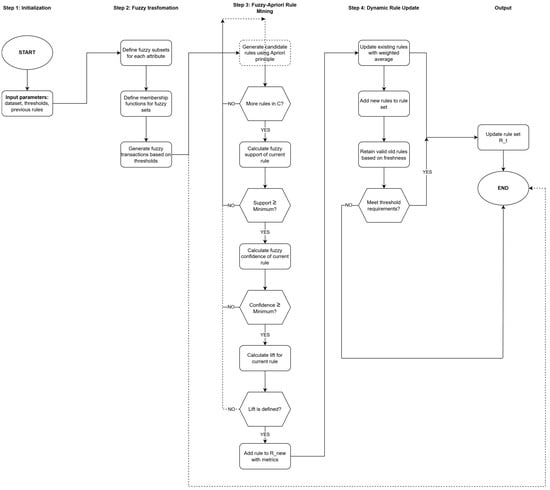
Figure 4.
Fuzzy-Apriori-Based Algorithmic Model for Pedagogical Evaluation.
In contrast, those content areas deemed professionally important by the teacher but not addressed by students’ questions often pointed to a need to reconsider the instructional approach or contextual framing. The model can provide interpretive insight not only from the students’ perspective but also offers didactic feedback to the teacher. It may help identify “silent” content areas and may map potential gaps between teaching intentions and student perception. Thanks to its dynamically updatable rule set, the model enables not only the tracking of student development but also the evaluation of the effectiveness of pedagogical interventions. The analysis of temporal patterns in student questions supports longitudinal monitoring of learning progress, and the rules can be differentiated by subject area. One promising direction for future research is the structural analysis of teacher-generated questions, as these not only guide student thinking but also directly influence the structure and quality of student-generated questions.
Overall, the presented model and empirical findings suggest that the algorithm is a transparent and interpretable tool that may inform educational assessment. Several limitations should be noted. Question coding involves subjective judgments that can vary across teachers, subjects, and grade levels. The fuzzy representation reduces the impact of such uncertainty but does not eliminate it. The present study does not include classroom interventions or causal analyses; therefore, the reported rules are descriptive associations that serve to formulate testable hypotheses. The sample originates from a single institutional context, which limits its generalisability. Future work will incorporate reliability indices, broader contexts, and classroom trials to examine whether using these rules supports instructional adaptation and improves learning trajectories. These directions are aligned with the conclusions outlined below. The integration of student-generated questions as an assessment dimension, combined with the fuzzy logic-based processing of data, may help educational practice become more reflective, adaptive, and interpretable, from both the students’ and the teachers’ perspectives.
6. Conclusions
These conclusions should be read in light of the above constraints, as the model is reported at a developmental stage and its educational effects require further testing. The approach should not be regarded as a finished and validated educational tool. It reflects a development stage in which the method exposes interpretable patterns that invite further testing. The next step is to conduct classroom trials and longitudinal follow-ups to determine whether the discovered rules can meaningfully support instructional decisions and student development. For current classroom use, the descriptive rules can already inform reflective practice. For example, when a pattern such as {Low parental support + high question abstraction ⇒ good performance} appears repeatedly, a teacher might respond by preserving space for end-of-lesson student questions, grading for question quality in formative rather than summative ways, and offering optional extension tasks that reward conceptual exploration rather than homework volume. Likewise, suppose the system surfaces {Predominantly factual questions + low alignment with instructional focus ⇒ below-median performance}. In that case, a teacher might introduce brief think-aloud modelling of conceptual questions, use pair-share prompts (“What would change if…?”), or add a mid-lesson pause for re-framing the learning goal. These are illustrative uses of descriptive associations—not validated interventions—but they demonstrate how the present findings can already guide low-risk, context-sensitive adjustments to instruction. By integrating the analysis of student background data, classroom performance, and independently formulated end-of-lesson questions, the model offers an exploratory perspective on the learning process, particularly regarding the depth, focus, and structure of student thinking.
This study was conducted with the participation of 202 Hungarian elementary school students, supported by background data provided by 174 parents, as documented in our previous studies [23,27,28]. It involved the analysis of 5832 student-generated questions and 510 teacher-generated questions from 7 educators. One of the most significant findings is that an identifiable group of students regularly formulated more complex and abstract questions at the end of the lesson than those posed by the teachers about the same curriculum content. These student questions correspond to higher levels in Bloom’s taxonomy, and often represent interdisciplinary or reinterpretive directions. While the phenomenon is not universal, it emerged as a recurring pattern among students who demonstrated greater classroom engagement and independent thinking. This result suggests that student question generation, at least for specific learner profiles, does not merely reflect understanding but also can restructure the curriculum and transcend the cognitive frames defined by the teacher. The model is thus capable of interpreting not only the alignment between teacher and student questions but also cases where students formulate questions that exceed the complexity level of the teacher’s questions, which may indicate creativity and depth of thinking. At the same time, student-generated questions also serve as a form of didactic feedback. They reveal which parts of the curriculum trigger interest and question formation, and which remain “unresponsive”. For teachers, this provides valuable feedback that can support the rethinking of instructional delivery, contextual framing, or emphasis within the curriculum. In this way, student-generated questions become not only a tool for assessing knowledge and thinking, but also a means of evaluating the quality of lessons.
A key advantage of the model is that it is rule-based yet non-static: it can adapt to temporal changes in the learning environment and dynamically reweight the rule set based on newly submitted questions. The fuzzy clusters do not represent rigid learner types, but instead reflect partial and nuanced affiliations, which more closely resemble real classroom experiences than traditional binary models. From a practical standpoint, it is important to highlight that the algorithm is not only suitable for scientific analysis but also for school-level pedagogical development. The integrated analysis of individual learner background data and student-generated questions provides a foundation for subject-level diagnostics, identifying pedagogical intervention points, and supporting the targeted development of classroom methodologies. The algorithm supports learner differentiation, encourages self-regulated learning processes, and facilitates motivation-driven instructional design. At the institutional level, the model offers data-driven feedback on the impact of teacher-generated questions, the pedagogical effectiveness of specific curriculum units, and the development of cognitive depth in student thinking. Altogether, this may contribute to the emergence of a school culture in which learning processes are not only measurable but also interpretable, thereby supporting the growth of a reflective and adaptive pedagogical practice.
In summary, the research illustrates that algorithmic, fuzzy logic-based processing of student-generated questions offers a plausible, exploratory approach that may inform educational assessment. The model provides a transparent feedback framework that is interpretable by teachers, thereby supporting the development of a differentiated, learner-centred pedagogical culture, particularly in primary education, where student interest, engagement, and reflection are critical in shaping long-term learning motivation.
Author Contributions
Conceptualization, É.K. and G.M.; methodology, É.K.; software, É.K.; validation, É.K. and G.M.; formal analysis, É.K.; investigation, É.K.; resources, É.K. and G.M.; data curation, É.K.; writing-original draft preparation, É.K.; writing-review and editing, É.K. and G.M.; visualization, É.K. and G.M.; supervision, G.M.; project administration, É.K. and G.M.; funding acquisition, G.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. The authors’ institutions funded the APC.
Data Availability Statement
The data underlying this study contain student information and cannot be made publicly available due to privacy and ethical restrictions. Anonymised and aggregated data may be available from the corresponding author upon reasonable request and with the prior approval of the relevant institutional bodies.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Structured Table of Variables with Explanations 1.
Table A1.
Structured Table of Variables with Explanations 1.
| Variable Name | Explanation |
|---|---|
| Grade level | Student’s current school grade |
| Age | Student’s age in years |
| Gender | Student’s gender |
| Type of residence | Type of student’s place of residence |
| Family size | Number of people in the household |
| Parents’ marital status | “0”—married/living together; “1”—divorced; “2”—single parent |
| Mother’s education level | 0: none, 1: primary, 2: secondary, 3: higher education |
| Mother’s occupation | Public sector, private sector, education, unemployed |
| Mother takes regular medication | Whether the mother takes medication regularly |
| Mother smokes | Whether the mother smokes |
| Mother consumes alcohol regularly | Whether the mother drinks alcohol regularly |
| Father’s education level | 0: none, 1: primary, 2: secondary, 3: higher education |
| Father’s occupation | Public sector, private sector, education, unemployed |
| Father takes regular medication | Whether the father takes medication regularly |
| Father smokes | Whether the father smokes |
| Father consumes alcohol regularly | Whether the father drinks alcohol regularly |
| Legal guardian | Mother, Father, Both, Grandparent(s), Other |
| Travel time to school | 1: <15 min, 2: 15–30 min, 3: 30–60 min, 4: >1 h |
| Family relationship quality | 1: very poor—5: excellent |
| Weekly study hours | 1: <2 h, 2: 2–5 h, 3: 5–10 h, 4: >10 h |
| Number of failed subjects | 0: never failed; 1: 1 subject; 2: 2 subjects; 3: more than 2 |
| Attends remedial classes | Whether the student attended remedial instruction |
| Remedial subjects | If yes: subject name(s) |
| Type of remedial class | Institutional, private tutor, or not applicable |
| Plans to continue education | Whether parents want their child to attend secondary education |
| Home internet access | Whether the household has internet access |
| Computer for learning | Whether student has a computer available for study |
| Own room | Whether the student has a private room |
| Own desk | Whether the student has a dedicated study desk |
| Free time | 1: very little—5: very much |
| Has a hobby | Whether the student has a personal hobby |
| Time with friends | 1: very little—5: a lot |
| Learning difficulty | 0: no; 1: SEN; 2: LD (BTMN); 3: other |
| Student smokes (per parent) | Whether the parent believes the student smokes |
| Absences per month | Number of classes missed monthly |
| Fatigue level during learning | 1: very easily—5: hardly ever |
| Preferred assessment method | 1: written, 2: oral, 3: unspecified |
| Exam anxiety | 1: yes, 2: no, 3: unspecified |
| Learning approach | 1: rote, 2: detail-focused, 3: meaning-oriented |
| Self-image | 1: positive, 2: negative, 3: unstable |
| Self-assessment | 1: underestimates, 2: overestimates, 3: realistic |
| Strongest subjects | Subject names (e.g., math, physics, etc.) |
| Weakest subjects | Subject names (e.g., math, physics, etc.) |
| Main interest area | 0: none, 1: arts, 2: languages, 3: engineering, 4: science, 5: humanities, 6: sports, 7: other |
| Extracurricular activity | 0: none, 1: sport, 2: arts, 3: other |
| Daily screen time | 0: none, 1: <1 h, 2: <2 h, 3: >2 h |
| Engages in music or dance | Whether the student practices music or dance |
| Music preference | 1: pop, 2: rock, 3: folk, 4: classical |
| Relationship with adults | 1: no interest—5: prefers adult company |
| Relationship with peers | 1: avoids peers—5: prefers peer company |
| Role in the school group | 1: sociable, 2: leader, 3: outsider, 4: none |
| Number of school conflicts | 1: low, 2: moderate, 3: high |
Appendix B
This appendix presents the complete pseudocode of the adaptive fuzzy-Apriori algorithm developed in the study. The algorithm combines fuzzy logic-based data transformation with association rule mining and dynamic rule adaptation. It operates in two main phases: initial rule generation and iterative updating based on new student question data. The fuzzy logic components enable the handling of imprecise input values, while the Apriori-based mechanism ensures the generation of interpretable rule sets for pedagogical decision-making.
| Algorithm A1: Adaptive Fuzzy-Apriori Rule Mining for Pedagogical Evaluation. |
| Input: D_t: Student dataset at time t (background data + question complexity) α_fuzzy: Membership threshold (default: 0.6) minSupp: Minimum support threshold minConf: Minimum confidence threshold R_{t-1}: Rule set from previous time period (t-1) α_update: Freshness parameter for dynamic update (default: 0.7) Output: R_t: Updated rule set at time t BEGIN AdaptiveFuzzyApriori(D_t, α_fuzzy, minSupp, minConf, R_{t-1}, α_update) // Step 1: Fuzzy Transformation FOR each attribute A_j in D_t DO Define fuzzy subsets: {Ã_j^1, Ã_j^2, …, Ã_j^{k_j}} Define membership functions: μ_{Ã_j^k}: Dom(A_j) → [0, 1] END FOR // Step 2: Generate Fuzzy Transactions T ← ∅ // Initialise transaction database FOR each student x_i ∈ D_t DO T_i ← ∅ // Initialise transaction for student i FOR each attribute A_j DO FOR each fuzzy subset Ã_j^k DO IF μ_{Ã_j^k}(x_i) ≥ α_fuzzy THEN T_i ← T_i ∪ {(Ã_j^k, μ_{Ã_j^k}(x_i))} END IF END FOR END FOR T ← T ∪ {T_i} // Add transaction to database END FOR // Step 3: Mine Fuzzy-Apriori Rules R_new ← MineRules(T, minSupp, minConf) // Step 4: Dynamic Rule Update R_t ← UpdateRuleSet(R_{t-1}, R_new, α_update, minSupp, minConf) RETURN R_t END AdaptiveFuzzyApriori FUNCTION MineRules(T, minSupp, minConf) R_new ← ∅ // Initialize new rule set C ← GenerateCandidateRules(T) // Generate candidate rules X ⇒ Y FOR each candidate rule R: X ⇒ Y in C DO // Calculate fuzzy support supp_R ← CalculateFuzzySupport(R, T) IF supp_R ≥ minSupp THEN // Calculate fuzzy confidence conf_R ← CalculateFuzzyConfidence(R, T) IF conf_R ≥ minConf THEN // Calculate lift lift_R ← CalculateLift(R, T, conf_R) IF lift_R is defined THEN R_new ← R_new ∪ {(R, supp_R, conf_R, lift_R)} END IF END IF END IF END FOR RETURN R_new END MineRules FUNCTION CalculateFuzzySupport(R: X ⇒ Y, T) support_sum ← 0 n ← |T| // Number of transactions FOR each transaction T_i in T DO μ_X ← min{μ_{Ã_j^k}(x_i) | Ã_j^k ∈ X} μ_Y ← μ_{Ã_l^t}(x_i) // where Y = Ã_l^t support_sum ← support_sum + min{μ_X, μ_Y} END FOR RETURN support_sum/n END CalculateFuzzySupport FUNCTION CalculateFuzzyConfidence(R: X ⇒ Y, T) numerator ← 0 denominator ← 0 FOR each transaction T_i in T DO μ_X ← min{μ_{Ã_j^k}(x_i) | Ã_j^k ∈ X} μ_Y ← μ_{Ã_l^t}(x_i) // where Y = Ã_l^t numerator ← numerator + min{μ_X, μ_Y} denominator ← denominator + μ_X END FOR IF denominator > 0 THEN RETURN numerator/denominator ELSE RETURN 0 END IF END CalculateFuzzyConfidence FUNCTION CalculateLift(R: X ⇒ Y, T, confidence_R) support_Y ← 0 n ← |T| FOR each transaction T_i in T DO support_Y ← support_Y + μ_Y(x_i) END FOR support_Y ← support_Y/n IF support_Y > 0 THEN RETURN confidence_R/support_Y ELSE RETURN undefined END IF END CalculateLift FUNCTION UpdateRuleSet(R_old, R_new, α, minSupp, minConf) R_updated ← ∅ // Process rules in both sets FOR each rule R in (R_old ∩ R_new) DO supp_updated ← α × supp_new(R) + (1-α) × supp_old(R) conf_updated ← α × conf_new(R) + (1-α) × conf_old(R) // Ensure values stay in [0, 1] supp_updated ← min(1, max(0, supp_updated)) conf_updated ← min(1, max(0, conf_updated)) R_updated ← R_updated ∪ {(R, supp_updated, conf_updated)} END FOR // Process rules only in new set FOR each rule R in (R_new \ R_old) DO supp_updated ← α × supp_new(R) conf_updated ← α × conf_new(R) IF supp_updated ≥ minSupp AND conf_updated ≥ minConf THEN R_updated ← R_updated ∪ {(R, supp_updated, conf_updated)} END IF END FOR // Process rules only in old set FOR each rule R in (R_old \ R_new) DO supp_updated ← (1-α) × supp_old(R) conf_updated ← (1-α) × conf_old(R) IF supp_updated ≥ minSupp AND conf_updated ≥ minConf THEN R_updated ← R_updated ∪ {(R, supp_updated, conf_updated)} END IF END FOR RETURN R_updated END UpdateRuleSet FUNCTION GenerateCandidateRules(T) // Generate frequent itemsets using the Apriori principle L_1 ← FindFrequent1Itemsets(T) L ← {L_1} k ← 2 WHILE L_{k-1} ≠ ∅ DO C_k ← AprioriGen(L_{k-1}) // Generate k-itemset candidates // Count support for candidates FOR each transaction t in T DO C_t ← Subset(C_k, t) FOR each candidate c in C_t DO c.count ← c.count + 1 END FOR END FOR // Keep frequent itemsets L_k ← {c ∈ C_k | c.count/|T| ≥ minSupp} L ← L ∪ {L_k} k ← k + 1 END WHILE // Generate rules from frequent itemsets Rules ← ∅ FOR each itemset I in L with |I| ≥ 2 DO FOR each non-empty subset X ⊂ I DO Y ← I \ X Rules ← Rules ∪ {X ⇒ Y} END FOR END FOR RETURN Rules END GenerateCandidateRules |
References
- Molnár, G.; Szűts, Z. Use of Artificial Intelligence in Electronic Learning Environments. In Proceedings of the 2022 IEEE 5th International Conference and Workshop Óbuda on Electrical and Power Engineering (CANDO-EPE), Budapest, Hungary, 21–22 November 2022; pp. 000137–000140. [Google Scholar] [CrossRef]
- Molnar, G.; Jozsef, C.; Eva, K. Evaluation and Technological Solutions for a Dynamic, Unified Cloud Programming Development Environment: Ease of Use and Applicable System for Uniformized Practices and Assessments. In Proceedings of the 2023 IEEE 21st World Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 19–21 January 2023; pp. 000237–000240. [Google Scholar] [CrossRef]
- Karl, É.; Nagy, E.; Molnár, G.; Szűts, Z. Supporting the Pedagogical Evaluation of Educational Institutions with the Help of the WTCAi System. Acta Polytech. Hung. 2024, 21, 125–142. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Operations on Fuzzy Numbers. Int. J. Syst. Sci. 1978, 9, 613–626. [Google Scholar] [CrossRef]
- Fullér, R.; Majlender, P. On Obtaining Minimal Variability OWA Operator Weights. Fuzzy Sets Syst. 2003, 136, 203–215. [Google Scholar] [CrossRef]
- Karl, É. Analytic Hierarchy Process. Ph.D. Thesis, Széchenyi István University, Doctoral School of Multidisciplinary Engineering Sciences, Győr, Hungary, 2022. [Google Scholar]
- Agrawal, R.; Srikant, R. Fast Algorithms for Mining Association Rules in Large Databases. In Proceedings of the 20th International Conference on Very Large Data Bases, Santiago, Chile, 12–15 September 1994; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1994; pp. 487–499. [Google Scholar]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques, 3rd ed.; Morgan Kaufmann Series in Data Management Systems; Elsevier: Amsterdam, The Netherlands; Morgan Kaufmann: Boston, MA, USA, 2012; ISBN 9780123814791. [Google Scholar]
- Jha, J.; Ragha, L. Educational Data Mining using Improved Apriori Algorithm. Int. J. Inf. Comput. Technol. 2013, 3, 411–418. [Google Scholar]
- Li, J.; Xue, E. Dynamic Interaction between Student Learning Behaviour and Learning Environment: Meta-Analysis of Student Engagement and Its Influencing Factors. Behav. Sci. 2023, 13, 59. [Google Scholar] [CrossRef] [PubMed]
- Patall, E.A.; Yates, N.; Lee, J.; Chen, M.; Bhat, B.H.; Lee, K.; Beretvas, S.N.; Lin, S.; Yang, S.M.; Jacobson, N.G.; et al. A Meta-Analysis of Teachers’ Provision of Structure in the Classroom and Students’ Academic Competence Beliefs, Engagement, and Achievement. Educ. Psychol. 2024, 59, 42–70. [Google Scholar] [CrossRef]
- Rubie-Davies, C.M.; Hattie, J.A.C. The Powerful Impact of Teacher Expectations: A Narrative Review. J. R. Soc. N. Z. 2024, 55, 343–371. [Google Scholar] [CrossRef] [PubMed]
- Buckley, J.J. Fuzzy Hierarchical Analysis. Fuzzy Sets Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- Van Laarhoven, P.J.M.; Pedrycz, W. A Fuzzy Extension of Saaty’s Priority Theory. Fuzzy Sets Syst. 1983, 11, 229–241. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Preface. In Mathematics in Science and Engineering; Elsevier: Amsterdam, The Netherlands, 1980; Volume 144, pp. xv–xvi. ISBN 9780122227509. [Google Scholar]
- Karl, É.; Molnár, G. IKT-vel támogatott STEM készségek fejlesztésének lehetőségei a tanulók körében. In Proceedings of the XXXVIII, Kandó Konferencia 2022, Hungary, Budapest, 3–4 November 2022; Óbudai Egyetem, Kandó Kálmán Villamosmérnöki Kar: Budapest, Hungary, 2022; pp. 144–155, ISBN 978-963-449-298-6. [Google Scholar]
- Carlsson, C.; Fullér, R. Problem Solving with Multiple Interdependent Criteria. In Consensus Under Fuzziness; Kacprzyk, J., Nurmi, H., Fedrizzi, M., Eds.; Springer: Boston, MA, USA, 1997; Volume 10, pp. 231–246. ISBN 9781461379089. [Google Scholar] [CrossRef]
- Carlsson, C.; Fullér, R. Multiobjective Linguistic Optimization. Fuzzy Sets Syst. 2000, 115, 5–10. [Google Scholar] [CrossRef]
- Saaty, T.L. A Scaling Method for Priorities in Hierarchical Structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Saaty, T.L. Axiomatic Foundation of the Analytic Hierarchy Process. Manag. Sci. 1986, 32, 841–855. [Google Scholar] [CrossRef]
- Keeney, R.L.; Raiffa, H.; Rajala, D.W. Decisions with Multiple Objectives: Preferences and Value Trade-Offs. IEEE Trans. Syst. Man Cybern. 1979, 9, 403. [Google Scholar] [CrossRef]
- Karl, É. Examining the Relationship Between the WTCAi System and Student Background Data in Modern Educational Assessment. J. Appl. Tech. Educ. Sci. 2024, 14, 389. [Google Scholar] [CrossRef]
- Friedler, F.; Tarjan, K.; Huang, Y.W.; Fan, L.T. Combinatorial Algorithms for Process Synthesis. Comput. Chem. Eng. 1992, 16, S313–S320. [Google Scholar] [CrossRef]
- Teng, F. Fuzzy Association Rule Mining for Personalized Chinese Language and Literature Teaching from Higher Education. Int. J. Comput. Intell. Syst. 2024, 17, 266. [Google Scholar] [CrossRef]
- Li, D. An interactive teaching evaluation system for preschool education in universities based on machine learning algorithm. Comput. Hum. Behav. 2024, 157, 108211. [Google Scholar] [CrossRef]
- Karl, É.; Molnár, G.; Cserkó, J.; Orosz, B.; Nagy, E. Supporting the Pedagogical Assessment Process in Educational Institutions with Social Background Data Analysis and WTCAi System Integration. In Proceedings of the 2025 IEEE 23rd World Symposium on Applied Machine Intelligence and Informatics (SAMI), Stará Lesná, Slovakia, 23–25 January 2025; pp. 000071–000076. [Google Scholar] [CrossRef]
- Karl, É.; Nagy, E.; Molnár, G. Advanced Examination Systems: Applying Fuzzy Logic and Machine Learning Methods in Education. In Proceedings of the 2025 IEEE 12th International Conference on Computational Cybernetics and Cyber-Medical Systems (ICCC), Maui, HI, USA, 9–11 April 2025; pp. 231–236. [Google Scholar] [CrossRef]
- Ramík, J.; Korviny, P. Inconsistency of Pair-Wise Comparison Matrix with Fuzzy Elements Based on Geometric Mean. Fuzzy Sets Syst. 2010, 161, 1604–1613. [Google Scholar] [CrossRef]
- Muse, H.; Bulathwela, S.; Yilmaz, E. Pre-Training with Scientific Text Improves Educational Question Generation. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 22 February–1 March 2022. [Google Scholar] [CrossRef]
- Bulathwela, S.; Muse, H.; Yilmaz, E. Scalable Educational Question Generation with Pre-Trained Language Models. In Artificial Intelligence in Education; Wang, N., Rebolledo-Mendez, G., Matsuda, N., Santos, O.C., Dimitrova, V., Eds.; Springer: Cham, Switzerland, 2023; Volume 13916, pp. 327–339. [Google Scholar] [CrossRef]
- Heilman, M.; Smith, N.A. Good Question! Statistical Ranking for Question Generation. In Proceedings of the Human Language Technologies: The 2010 Annual Conference of the North American Chapter of the Association for Computational Linguistics, Los Angeles, CA, USA, 2–4 June 2010; Kaplan, R., Burstein, J., Harper, M., Penn, G., Eds.; Association for Computational Linguistics: Los Angeles, CA, USA, 2010; pp. 609–617. [Google Scholar]
- Zimmermann, H.-J. Fuzzy Set Theory-and Its Applications; Springer: Dordrecht, The Netherlands, 1996; ISBN 9789401587044. [Google Scholar]
- Katona, J.; Gyönyörű, K.I.K. Integrating AI-Based Adaptive Learning into the Flipped Classroom Model to Enhance Engagement and Learning Outcomes. Comput. Educ. Artif. Intell. 2025, 8, 100392. [Google Scholar] [CrossRef]
- Baranyi, P. Relaxed TS Fuzzy Model Transformation to Improve the Approximation Accuracy/Complexity Tradeoff and Relax the Computation Complexity. IEEE Trans. Fuzzy Syst. 2024, 32, 5237–5247. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).