A Multi-Branch Convolutional Neural Network for Student Graduation Prediction

Abstract

Accurate prediction of student graduation status is crucial for higher education institutions to implement timely interventions and improve student success. While existing methods often rely on single data sources or generic model architectures, this paper proposes a novel Multi-Branch Convolutional Neural Network (MBCNN) that systematically integrates multi-dimensional factors influencing student outcomes. The model employs eight dedicated branches to capture both subjective and objective features from four key dimensions: student characteristics, school resources, family environment, and societal factors. Through robust normalization and hierarchical feature fusion, MBCNN effectively learns discriminative representations from these heterogeneous data sources. Evaluated on a real-world dataset from Polytechnic Institute of Portalegre, our approach demonstrates superior performance compared to traditional and up-to-date machine learning methods, achieving improvements of 4.07–17.35% in accuracy, 4.60–20.19% in weighted precision, 4.07–17.35% in weighted recall, and 4.59–18.73% in weighted F1-score. The results validate that domain-specific neural architectures, designed to align with the inherent structure of educational data, significantly enhance prediction accuracy and generalization capability.

1. Introduction

Student academic completion status serves as a critical indicator for evaluating the effectiveness of higher education and tracking individual student development [1]. Nevertheless, higher education institutions worldwide continue to face persistent challenges related to academic non-completion, including student dropout and delayed graduation. Traditional prediction methods predominantly rely on lagging indicators such as final examination results or mid-term evaluations, which fail to provide adequate lead time for meaningful early intervention. The emergence of educational data mining and learning analytics has created new opportunities for leveraging multi-dimensional, temporal data generated during students’ enrollment—including course grades, library usage patterns, and digital learning platform activities—to enable proactive prediction. Deep neural networks, particularly Convolutional Neural Networks (CNNs), present a powerful technical framework for extracting meaningful patterns from this complex educational data due to their exceptional capability in feature extraction and hierarchical representation learning [2].

The accurate prediction of student graduation status carries substantial theoretical and practical significance. From an institutional perspective, it enables early identification of at-risk students, allowing educational administrators to implement targeted academic support and psychological counseling interventions, thereby effectively enhancing graduation rates and educational quality. Concurrently, it empowers students with valuable insights for self-assessment and academic planning. Methodologically, by systematically analyzing the key determinants of academic performance, the findings can inform data-driven decisions regarding teaching resource allocation and curriculum optimization.

Despite these promising applications, developing accurate student graduation prediction systems confronts several fundamental challenges. The primary obstacle lies in data heterogeneity—student-related information originates from diverse sources encompassing personal academic records, institutional resource utilization, family background, and social engagement. These datasets exhibit significant variations in structure, scale, and semantic meaning, making effective data integration and alignment particularly demanding.

The evolution of student prediction models has progressed from conventional approaches like logistic regression and decision trees to more sophisticated ensemble and deep learning methodologies [3]. However, current research remains constrained by a critical limitation: the prevailing modeling paradigms largely overlook the multi-dimensional nature of student development. Student graduation outcomes inherently result from complex interactions among multiple factors, including individual characteristics, institutional environments and resources, family background, and broader societal contexts [4,5,6]. Unfortunately, most existing models are constructed without adequate consideration of this fundamental premise, frequently employing generic architectures that process limited data sources and failing to systematically integrate the four crucial dimensions of influence. This oversimplified modeling approach inevitably compromises the comprehensiveness of student representation, ultimately constraining prediction accuracy.

To address this gap, our research is fundamentally motivated by the need to establish a holistic modeling framework that captures the dynamic interplay of factors spanning the “Student, School, Family, Society” dimensions. This comprehensive perspective recognizes that student success is influenced not only by academic performance but also by institutional contexts, family support structures, and broader societal factors. In methodological response to this conceptual framework, we propose a novel Multi-Branch Convolutional Neural Network (MBCNN) architecture specifically designed to model diverse feature interactions in a structured manner. By explicitly aligning our model with this multi-dimensional understanding of learning, we aim to advance beyond grade-centric prediction paradigms toward more comprehensive and educationally meaningful analytics.

The main contributions of this work are summarized as follows:

• Holistic Student Modeling through Novel Eight-Branch CNN Architecture: We propose a dedicated deep learning framework that advances beyond generic models by incorporating eight distinct branches to explicitly capture and integrate subjective and objective features across student characteristics, school resources, family environment, and societal factors. This architecture directly addresses key limitations in existing works by modeling the synergistic effects of multi-domain influences, establishing a more accurate and interpretable foundation for graduation prediction.
• Comprehensive Performance Evaluation Using Real-World Dataset: We conduct extensive experiments to validate the proposed MBCNN framework on a real-world dataset from the Polytechnic Institute of Portalegre [7]. The results demonstrate the framework’s superior prediction accuracy and confirm its effectiveness as a high-performance practical solution for modern educational data mining challenges.

The remainder of this paper is organized as follows: Section 2 reviews the related literature on student performance prediction. Section 3 details the architecture of the proposed Multi-Branch Convolutional Neural Network (MBCNN). Section 4 presents the experimental setup and evaluation results. Section 5 provides a comprehensive analysis and discussion of the findings. Section 6 examines the study’s limitations and suggests future research directions, while Section 7 concludes the paper with final remarks.

2. Related Work

The accurate prediction of student academic status holds exceptional importance due to its significant implications for enhancing educational outcomes and optimizing institutional resource allocation. However, traditional statistical learning methods have demonstrated limited effectiveness in addressing the inherent complexity and heterogeneity of educational data. This limitation has motivated researchers to investigate various machine learning algorithms, resulting in the development of diverse predictive frameworks for student academic success and dropout risk assessment. Roslan et al. [8] conducted a comparative analysis of Decision Trees (DTs) and Logistic Regression (LR) for predicting student dropout in a Malaysian private university, revealing that the DT algorithm achieved marginally superior performance. Similarly, Haron et al. [9] evaluated RepTree, K-Nearest Neighbour (kNN), and Naïve Bayes (NB), determining that RepTree attained the highest accuracy while KNN demonstrated the weakest performance. The learning analytic framework proposed by Alalawi et al. [10] implemented LR, Support Vector Machine (SVM), DT, KNN and NB for the course-specific predicting.

Guided by the “No Free Lunch” theorem [11], which establishes that no single algorithm can maintain optimal performance across all problem domains, researchers have increasingly adopted ensemble learning methodologies. These approaches strategically combine multiple base predictors to enhance the accuracy and robustness of student status prediction. Zerkouk et al. [12] implemented an eXtreme Gradient Boosting (XGB)-based framework utilizing gradient boosting with multiple decision trees for dropout prediction in a Canadian distance learning platform. Delogu et al. [13] conducted a comprehensive evaluation of machine learning algorithms, including RF, Gradient Boosting Machines (GBM), DNN, and the Least Absolute Shrinkage and Selection Operator (LASSO), using Italian undergraduate data, highlighting the potential of machine learning as an early warning system. Kok et al. [14] employed Random Forest (RF) to improve prediction accuracy through the combination of multiple DT, while Hassan et al. [15] analyzed national survey data using seven distinct algorithms and demonstrated RF’s superior accuracy in dropout prediction. Noviandy et al. [16] developed a stacked ensemble combining LightGBM and RF with LR meta-classification, achieving slight performance improvements over individual algorithms. Okoye et al. [17] exploited Bagging with KNN meta-classification for predicting student retention and graduation outcomes.

While these studies establish valuable foundations, they predominantly rely on traditional machine learning frameworks that, despite capturing fundamental data patterns, often fail to extract the deeper latent features influencing academic performance. This recognition has prompted an investigation into deep learning applications for educational data mining. Mustofa et al. [18] proposed a hybrid architecture integrating LR with DNN, achieving 96% accuracy in binary dropout classification. Shoaib et al. [19] designed a two-stage predictor utilizing Convolutional Neural Networks (CNNs) for feature extraction followed by Bayesian-averaged ensemble classification. Kukkar [20] employed Recurrent Neural Networks (RNNs) and Long Short-Term Memory (LSTM) for feature selection combined with conventional classifiers (e.g., DT, SVM, NB, and RF) for grade prediction. Rabelo and Zárate [21] developed an ensemble model combining LR, Multi-Layer Perceptron (MLP), and Classification And Regression Tree (CART) with voting integration for dropout prediction in higher education. Huynh-Cam et al. [22] employed DT, MLP, and LR to develop early prediction models and identify key contributing factors associated with first-year university student dropout risk. These models were evaluated using a real-world dataset from a private university in Taiwan.

Existing research has predominantly applied generic machine learning techniques while overlooking the multifaceted nature of factors influencing student academic outcomes, resulting in limited predictive accuracy and generalizability. To address this fundamental limitation, our work adopts a holistic perspective that conceptualizes student achievement as the synergistic influence of individual, institutional, familial, and societal dimensions. This theoretical foundation motivates the design of our novel multi-branch deep learning architecture, which systematically models these diverse factors through dedicated network pathways while preserving their distinctive characteristics and enabling effective cross-domain feature integration.

3. Multi-Branch CNN for Academic Graduation Prediction

Existing models for predicting student graduation often suffer from a narrow modeling perspective. Student academic outcomes are not determined solely by individual academic performance but result from the complex interplay of multi-dimensional factors, including personal characteristics, institutional resources and environment, family background and support, and broader societal circumstances. However, most studies employ generic model architectures to process single or simply concatenated data sources, failing to effectively capture and interpret the deep, specific patterns within these heterogeneous data.

To address this, this section proposes a novel Multi-Branch Convolutional Neural Network (MBCNN). The core motivation for this model is: To utilize dedicated branch structures to separately and deeply learn feature representations from both subjective and objective factors within four key dimensions (Student, School, Family, and Society), and ultimately achieve more accurate three-class prediction of student graduation status (e.g., On-time Graduation, Delayed Graduation, and Dropout) through hierarchical feature fusion.

The overall architecture of the MBCNN is a meticulously designed eight-branch network. Its data processing and flow are illustrated in Figure 1, with the specific composition presented below.

Figure 1. The neural network of multi-branch CNN. (N is the number of features).

The model’s input corresponds to the raw data vectors for the eight branches. To ensure numerical stability and training efficiency, we apply Robust Normalization to all input data. This method uses the median and interquartile range for scaling, effectively reducing the influence of outliers. The calculation is as follows:

$$x_{scaled}={\displaystyle \frac{x-x_{1/2}}{x_{3/4}-x_{1/4}}},$$

(1)

where $x_{1/4}$, $x_{1/2}$ and $x_{3/4}$ are the first, second, and third quartiles of the data, and thus $x_{3/4}-x_{1/4}$ is the interquartile range (IQR).

The model comprises eight branches with identical structures but independent parameters. Each branch is responsible for processing data from one specific aspect (e.g., Student subjective factors, School objective resources, etc.). The specific structure of each branch is as follows:

• First Convolutional Layer: Employs multiple one-dimensional convolutional kernels to slide over the input vector, capturing local feature patterns and interactions, followed by a ReLU activation function to introduce non-linearity.
• Second Convolutional Layer: Further combines and abstracts low-level features to form higher-level semantic features, also followed by a ReLU activation function.
• Feature Flattening and Fully Connected Layer: The output feature map from the convolutional layers is flattened into a one-dimensional vector and fed into a fully connected layer. This fully connected layer has 4 neurons, producing a 4-dimensional feature vector. This 4-dimensional vector is regarded as the deep feature embedding for the dimension (Student, School, Family, and Society) corresponding to that branch.

After the eight branches generate their respective 4-dimensional deep feature representations, these specialized vectors are concatenated to form a unified 32-dimensional feature vector (8 branches × 4 dimensions). This comprehensive representation effectively captures the multifaceted information influencing student development from all considered perspectives.

Subsequently, a fully connected classification layer processes this integrated representation. The layer maps the 32-dimensional features to 3 output neurons, corresponding to the three target categories (On-time Graduation, Delayed Graduation, and Dropout). Final classification probabilities are obtained through a Softmax activation function, providing a probabilistic assessment of each student’s likely outcome.

The cross-entropy loss function is employed in this study, augmented with an L2 regularization term to mitigate potential overfitting. The complete objective function combining cross-entropy loss and L2 regularization is formulated as follows:

$$L=-{\displaystyle \frac{1}{S}}\sum _{i=1}^S\sum _{j=1}^3{y}_{ij}log\left({\widehat{y}}_{ij}\right)+\lambda ·{\displaystyle \frac{1}{2}}\sum _{k=1}^W{w}_k^2,$$

(2)

where S is the number of samples. $y_{ij}$ is the ground truth label for the i-th sample in the j-th class (one-hot encoded). ${\widehat{y}}_{ij}$ is the predicted probability for the i-th sample in the j-th class. The 3 target classes are the Dropout ($j=1$), Enrolled ($j=2$) and Graduate ($j=3$). $\lambda$ is the regularization strength hyperparameter. $w_k$ is the k-th trainable weight parameter in the model. W is the number of all trainable weight parameters.

The proposed MBCNN architecture offers several significant advantages over conventional approaches:

First, by implementing a hierarchical feature learning pipeline comprising “convolutional layers + dedicated fully connected layers”, our model achieves deeper and more specific feature extraction from multi-source data compared to simple feature concatenation. The resulting 4-dimensional embeddings from each branch represent highly condensed and abstract representations of the original data, providing information-rich features for the final classification decision.

Second, the branch structure naturally enhances model interpretability. Researchers can qualitatively or quantitatively analyze the impact of various factors (Student, School, Family, and Society) on prediction outcomes by examining feature strength variations across branches or conducting ablation studies. This capability significantly aids educational decision-making by providing insights into the relative importance of different influencing factors.

Third, the independent branch architecture helps mitigate gradient interference between heterogeneous data sources during initial training phases, promoting faster and more stable convergence. Additionally, the robust normalization of inputs and carefully designed network depth effectively address vanishing/exploding gradient concerns, further enhancing training efficiency and model robustness.

Finally, the eight-branch framework maintains principled flexibility. In practical applications, specific branches can be enhanced or streamlined based on data availability. The architecture also supports future expansion, allowing for seamless incorporation of additional data dimensions through new branches, thus ensuring long-term scalability and adaptability.

In the training process, the time complexity of MBCNN primarily depends on the computational load of forward and backward propagation. Each branch has an input feature size of N, and both the convolutional and fully connected layers have an input and output channel size of 1. The computation for a single sample in each branch includes two convolutional layers (each with a kernel size of $3\times 1$) and one fully connected layer (with an output size of 4). Then, the forward propagation complexity for a single branch is approximately $O\left(N\right)$. With 8 branches, the total computational load for the branches is $O\left(8N\right)=O\left(N\right)$. The fusion layer consists of two fully connected layers (the top two layers in Figure 1; one has an input size of 32 and output size of 4, while the other has an input size of 4 and output size of 3), with a constant computational load of $O\left(1\right)$. Therefore, the complexity of a single training step (forward and backward propagation) for one sample is $O\left(N\right)$. The total training time is influenced by the number of epochs E and the training set size S, resulting in an overall training complexity of $O\left(ESN\right)$, which is identical to a single-branch CNN that has a similar structure. MBCNN has a higher constant factor (due to the multiple branches), but the overall complexity remains linear.

During the inference phase, the forward propagation complexity of MBCNN for a single sample is also $O\left(N\right)$, specifically derived from the convolutional and fully connected operations of each branch (each branch $O\left(N\right)$, with 8 branches operating in parallel) and the constant computation of the fusion layer $O\left(1\right)$. Thus, the inference complexity is $O\left(N\right)$, exhibiting a linear relationship with the input feature size N, which is also the same as the single-branch CNN.

4. Performance Evaluation

This section aims to systematically evaluate the performance of the proposed Multi-Branch Convolutional Neural Network (MBCNN) model through comprehensive experiments. We will provide detailed descriptions of the dataset used, the baseline algorithms selected for comparison, and the performance metrics employed for evaluation, laying the groundwork for subsequent results analysis and discussion.

4.1. Dataset

This study utilizes a real-world dataset from the Polytechnic Institute of Portalegre [7] for experimental validation. This dataset contains anonymized student information spanning multiple years, covering multiple dimensions such as individual student characteristics, school resources, family background, and societal factors. The dataset comprises a total of 4424 student samples (enrolled between the academic years 2008/2009 to 2018/2019). Each sample consists of 36 raw features and one academic status. The features primarily consist of information known at the time of student enrollment, including aspects such as academic background, demographic profiles, and socioeconomic factors, along with records of academic performance at the conclusion of the first and second semesters. This comprehensive dataset effectively captures multiple contextual dimensions influencing student academic progression. The academic status is categorized into three distinct outcomes: Dropout, Enrolled, and Graduate. This classification effectively captures the key transitional states in a student’s academic journey. Specifically, “Dropout” refers to students who discontinue their studies before completing the program. “Enrolled” describes students who are actively continuing their education but have not yet met all graduation requirements. “Graduate” denotes students who have successfully fulfilled all academic criteria and have been awarded their degree. This clear three-class categorization is crucial for the predictive modeling task, as it allows for the development of targeted intervention strategies and provides a comprehensive view of student progression.

Robust Normalization was applied to all numerical features to eliminate scale differences and mitigate the impact of outliers. For categorical features, one-hot encoding was used. To ensure unbiased evaluation and statistical significance, the dataset was randomly split into a training set and an independent test set in an 8:2 ratio. The training set was used for model parameter training, while the test set was strictly reserved for the final performance evaluation.

4.2. Comparison Algorithms

To comprehensively assess the performance of the MBCNN model, we selected several representative classical machine learning and deep learning algorithms as baseline models for comparison. These algorithms cover different modeling paradigms.

• K-Nearest Neighbors (KNN) [9,10]: An instance-based, lazy learning algorithm that classifies samples based on proximity in the feature space.
• Support Vector Classifier (SVC) [10]: A powerful classifier based on the maximum margin principle, particularly suitable for handling high-dimensional data. The RBF kernel was used in the experiments.
• Decision Tree (DT) [8,10,22]: An easily interpretable tree-structured model that makes predictions through a series of decision rules.
• Bagging [13]: An ensemble learning method that constructs multiple base classifiers (using decision trees as base classifiers in this experiment) via bootstrap sampling and uses their voting results for the final prediction, aiming to reduce model variance.
• Random Forest (RF) [13,14]: An extension of Bagging that additionally introduces feature randomness during training, further enhancing the model’s generalization ability and robustness.
• eXtreme Gradient Boosting (XGB) [12]: An advanced gradient boosting framework that iteratively trains a series of weak learners and employs regularization strategies to control model complexity, demonstrating exceptional performance in practice.
• Deep Neural Network (DNN) [18,21,22]: A standard fully connected feed-forward neural network with multiple hidden layers, serving as a fundamental deep learning baseline for comparison.
• Convolutional Neural Network (CNN) [19]: A traditional single-branch CNN model used for comparison to highlight the advantage of our proposed multi-branch architecture in feature extraction.

4.3. Performance Metrics

To comprehensively evaluate the performance of the proposed model in the three-class classification task, we employ the following four core evaluation metrics: Accuracy, Weighted Precision, Weighted Recall, and Weighted F1-score. These metrics effectively reflect the model’s overall performance, particularly in scenarios where class imbalance may be present in the dataset.

• Accuracymeasures the overall proportion of correct predictions made by the model. The formula is defined as follows:

  $$Accuracy={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

  (3)

  where $TP$, $TN$, $FP$ and $FN$ represent True Positives, True Negatives, False Positives, and False Negatives, respectively. In the multi-class context, this metric calculates the proportion of correctly predicted samples across all classes.
• Weighted Precision accounts for the varying number of samples in each class by computing a support-weighted average:

  $$Weighted-Precision=\sum _{i=1}^C{\displaystyle \frac{n_i}{N}}·{\displaystyle \frac{T{P}_i}{T{P}_i+F{P}_i}},$$

  (4)

  where C denotes the total number of classes (in this study, $C=3$), and $n_i$ is the true number of samples in class i and N is the total number of samples. Then $n_i/N$ represents the weight for the i-th class.
• Weighted Recall employs class-weighted averaging to assess the model’s ability to identify positive instances:

  $$Weighted-Recall=\sum _{i=1}^C{\displaystyle \frac{n_i}{N}}·{\displaystyle \frac{T{P}_i}{T{P}_i+F{N}_i}}.$$

  (5)
  This metric ensures that classes with fewer samples receive appropriate consideration during evaluation.
• Weighted F1-Score provides a single composite metric with the harmonic mean of precision and recall:

  $$Weighted-F1=\sum _{i=1}^C{\displaystyle \frac{n_i}{N}}·{\displaystyle \frac{2·Precisio{n}_i·Recal{l}_i}{Precisio{n}_i+Recal{l}_i}}.$$

  (6)
  When class distribution is imbalanced, this metric offers a more reliable assessment of model performance than accuracy alone.

These weighted metrics ensure that both majority and minority classes are given equal importance during model evaluation, thereby providing a fairer performance comparison. To ensure the statistical significance and robustness of our experimental results, we conducted a comprehensive statistical validation. All performance metrics are reported as mean across 10 independent runs with different random seeds and data partitions. Furthermore, we performed paired t-tests between MBCNN and each baseline method. The results demonstrate that the performance advantages of MBCNN are statistically significant ($p<0.01$) across all evaluation metrics, confirming that the observed improvements are consistent and not attributable to random variations in training or testing splits.

4.4. Results

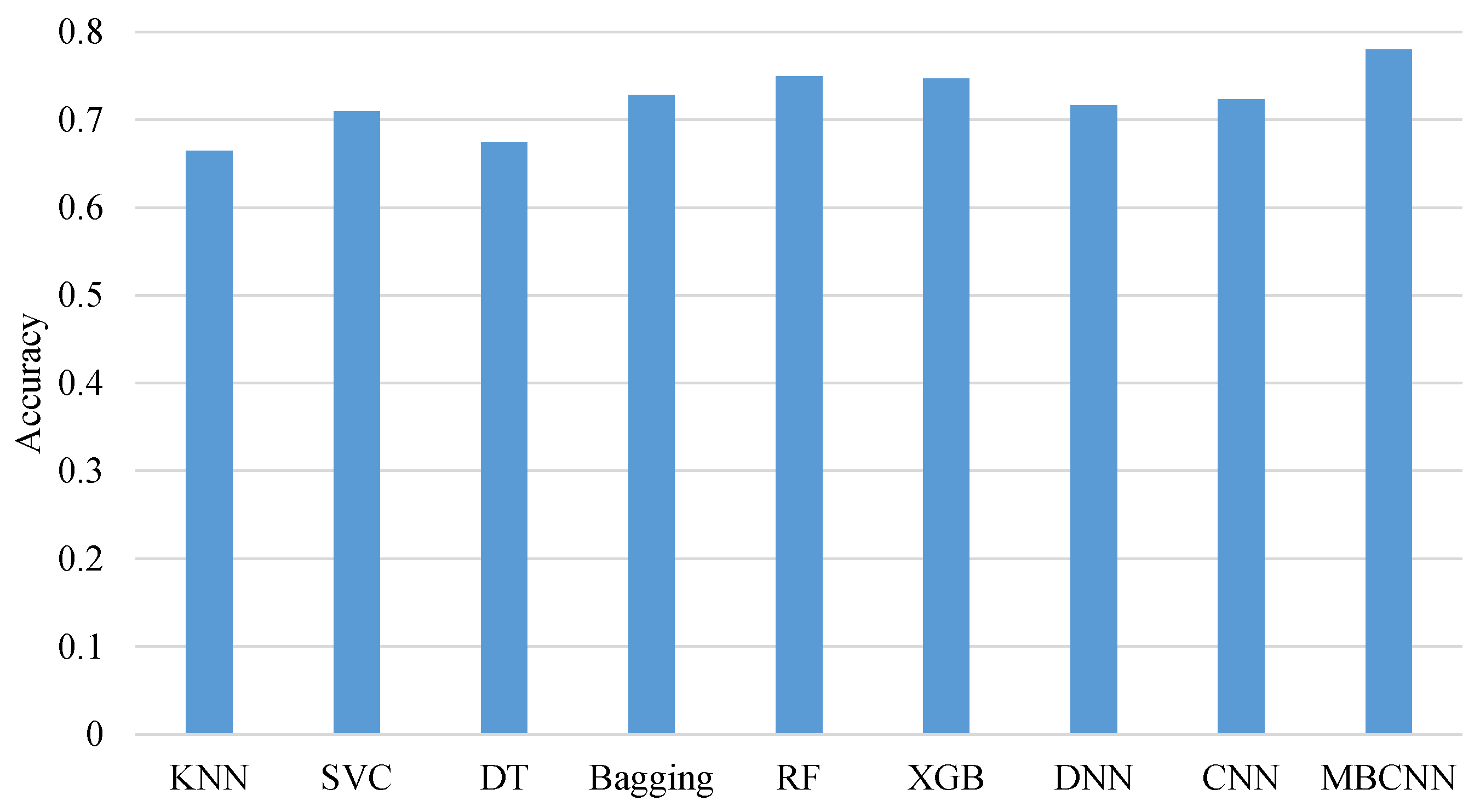
The confusion matrices achieved by various prediction algorithms are given in Figure 2. The values of accuracy, weighted precision, weighted recall, and weighted F1-score achieved by these prediction algorithms are shown in Figure 3, Figure 4, Figure 5 and Figure 6, respectively. As evidenced by these experimental results, the proposed MBCNN model achieves optimal values across all four evaluation metrics. Compared with other algorithms, MBCNN has 4.07–17.35% better accuracy, 4.60–20.19% better weighted precision, 4.07–17.35% better weighted recall, and 4.59–18.73% better weighted F1-score. This demonstrates that our multi-branch architecture possesses significant advantages in capturing the multi-dimensional factors influencing student academic status. The primary reasons can be attributed to the following aspects: Firstly, through its unique eight-branch design, the MBCNN model can learn more discriminative feature representations from both subjective and objective factors across four dimensions: student characteristics, school resources, family environment, and social circumstances. Compared to traditional single-architecture models, each branch in MBCNN can focus on feature extraction from specific data sources, effectively preventing interference between features from different origins. Secondly, through the later feature fusion layer, the model successfully integrates these heterogeneous information sources, enabling a more comprehensive and accurate assessment of student development status. Additionally, the robust normalization and L2 regularization strategies employed by the model contribute to enhanced generalization capability, effectively preventing overfitting to the training data.

Figure 2. The confusion matrices achieved by various prediction algorithms: (a) KNN. (b) SVC. (c) DT. (d) RF. (e) XGB. (f) Bagging. (g) DNN. (h) CNN. (i) MBCNN.

Figure 3. The accuracy rates achieved by various algorithms.

Figure 4. The weighted precisions achieved by various algorithms.

Figure 5. The weighted recalls achieved by various algorithms.

Figure 6. The weighted F1-scores achieved by various algorithms.

Compared to DNN and CNN, the proposed MBCNN achieves substantial improvements across all evaluation metrics: 7.81–8.83% increase in accuracy, 9.82–9.86% in weighted precision, 7.81–8.83% in weighted recall, and 8.65–9.09% in weighted F1-score. Notably, the improvements in weighted precision and weighted F1-score are relatively pronounced. These experimental results strongly demonstrate the effectiveness of our multi-branch architecture in capturing the complex, multifaceted nature of factors influencing student academic outcomes. This finding provides valuable inspiration for designing deep learning solutions: rather than employing generic, one-size-fits-all network structures, we should deliberately design neural architectures that specifically align with the characteristics of the target problem. The significant performance gains of MBCNN underscore the importance of developing domain-specific network topologies that can effectively model the inherent structure and relationships within educational data, particularly when dealing with heterogeneous information sources from multiple dimensions.

The superior performance of deep learning algorithms (DNN and CNN) over traditional methods like KNN, SVC, and DT validates the effectiveness of employing deep learning techniques for predicting student academic status. The primary reasons are threefold: Firstly, deep neural networks possess powerful automatic feature extraction capabilities, eliminating the heavy reliance on manual feature engineering required by traditional algorithms. Through multi-layer non-linear transformations, they can effectively learn complex feature interactions from raw data. Secondly, these models demonstrate exceptional performance in processing high-dimensional data, effectively mitigating the curse of dimensionality that severely impacts distance-based algorithms like KNN. Furthermore, their layered structure enables progressive learning of hierarchical feature representations, capturing both local patterns and global trends within the educational data. This outcome demonstrates that deep learning architectures possess superior capability in modeling complex educational data patterns compared to conventional algorithms. These findings strongly support the continued development of specialized neural network structures for educational prediction tasks, particularly those capable of handling the multi-dimensional nature of student information.

The superior performance of ensemble learning algorithms (Bagging, RF, XGB) over other traditional machine learning methods, with some (RF and XGB) even surpassing deep learning algorithms (DNN and CNN), demonstrates the exceptional capability of ensemble methods in handling complex educational prediction tasks. This can be primarily attributed to their inherent advantages: ensemble methods effectively mitigate overfitting through mechanisms like bootstrap sampling and feature randomness, automatically capture complex non-linear relationships and feature interactions through tree-based structures, and demonstrate stronger robustness when dealing with heterogeneous, multi-source tabular data. These findings provide valuable inspiration for our future research, suggesting that instead of solely pursuing more complex deep learning architectures, we could explore hybrid approaches that integrate the strengths of both ensemble and deep learning methods, or investigate designing more efficient ensemble strategies specifically tailored for educational data characteristics.

The K-Nearest Neighbors (KNN) algorithm demonstrated the poorest performance among all compared methods, primarily due to its inherent limitations in handling high-dimensional data and capturing complex feature relationships. As a distance-based algorithm, KNN suffers from the curse of dimensionality when processing our multi-branch feature set and lacks the capability to automatically learn discriminative feature representations. Furthermore, its sensitivity to data noise and poor handling of class imbalance significantly constrained its predictive accuracy in this educational context. These fundamental shortcomings highlight why KNN was substantially outperformed by more sophisticated approaches like our proposed MBCNN architecture.

Figure 7 presents the loss function convergence curves of the three deep learning approaches (DNN, CNN, and MBCNN). The graph clearly demonstrates that MBCNN achieves significantly faster convergence compared to the other two models. This indicates that our multi-branch architecture facilitates more stable gradient flow and more efficient parameter optimization during the training process, enabling the model to rapidly approach a favorable optimization region.

Figure 7. The convergence curves of neural network-based algorithms.

While both CNN and MBCNN eventually converge to similar final loss values, MBCNN achieves better performance on evaluation metrics. This suggests that MBCNN discovers a superior solution in the parameter space, one that not only minimizes the training loss but also possesses stronger generalization capability and produces more discriminative feature representations for the classification task.

Interestingly, DNN achieves a lower final loss value than MBCNN yet demonstrates inferior performance. This apparent paradox highlights that lower training loss does not necessarily translate to better generalization, and may indicate that the DNN model has overfitted the training data, capturing noise rather than meaningful patterns. In contrast, MBCNN’s architectural constraints and regularization effects help it learn more robust representations that generalize better to unseen data.

These experimental findings further validate the importance of designing specialized network architectures tailored to the specific characteristics of the problem domain, rather than relying on generic models. The superior performance of MBCNN, despite similar final loss values to other models, underscores that the quality of the learned representations matters more than simply achieving minimal training loss.

5. Discussion

The consistent outperformance of our proposed MBCNN across all evaluation metrics demonstrates the critical importance of architectural design in deep learning applications for educational prediction. The significant improvements over both traditional machine learning methods and conventional deep learning architectures underscore that the multi-branch design effectively addresses the fundamental challenge of integrating heterogeneous educational data sources. Unlike generic models that attempt to process concatenated features uniformly, MBCNN’s dedicated branches enable specialized feature learning from each data domain while maintaining the capacity to capture cross-domain interactions through late fusion. This approach proves particularly valuable in educational contexts where different types of factors (personal, institutional, familial, and societal) may exhibit distinct patterns and require customized processing.

The performance hierarchy observed across different algorithm categories reveals important insights. Traditional algorithms like KNN and DT showed limited capability in handling the complex, high-dimensional educational data, primarily due to their inability to learn sophisticated feature interactions. Ensemble methods, particularly XGB and RF, demonstrated remarkable effectiveness, likely attributable to their built-in feature selection mechanisms and robustness to noisy educational data. However, their performance plateau suggests limitations in learning deep hierarchical representations.

The comparison between standard deep learning models and MBCNN is particularly illuminating. While DNN and CNN showed improvements over traditional methods, their performance gap with MBCNN highlights that simply applying deep learning is insufficient. The performance improvement achieved by MBCNN emphasizes that success in educational prediction requires not just deep learning capabilities, but specifically designed architectures that align with the multi-source nature of educational data.

The convergence behavior observed in Figure 7 provides additional evidence for MBCNN’s advantages. The faster convergence suggests more stable optimization dynamics, possibly due to the decomposed learning objectives across branches. More importantly, the dissociation between loss values and final performance between DNN and MBCNN offers a crucial insight: in educational prediction tasks, lower training loss does not necessarily indicate better generalization. This underscores the importance of proper architectural regularization through domain-informed design, rather than relying solely on explicit regularization techniques.

These findings have significant implications for educational data mining practice. First, they validate that student outcomes are indeed influenced by multiple interconnected factors that require specialized modeling approaches. Second, the results suggest that predictive performance in education depends heavily on how well the model architecture captures the inherent structure of educational data, rather than simply increasing model complexity. Third, the superior performance of MBCNN supports the development of explainable AI in education, as the branch structure naturally facilitates the interpretation of different factor contributions.

While MBCNN demonstrates promising results, several limitations warrant attention. The current architecture requires careful balancing of branch contributions, and the fixed branch design may not optimally adapt to varying data availability across different educational contexts. Future work should explore adaptive branching mechanisms that can dynamically adjust to data characteristics. Additionally, incorporating temporal dynamics through recurrent connections could capture evolving student trajectories more effectively. The integration of attention mechanisms may further enhance interpretability by explicitly quantifying the importance of different factors in final predictions.

In conclusion, this study establishes that purpose-built deep learning architectures, specifically designed to align with the multi-faceted nature of educational data, significantly outperform both traditional methods and generic deep learning models. The MBCNN framework provides a foundation for developing more sophisticated, effective, and interpretable educational prediction systems that can better support student success initiatives.

6. Limitations and Future Directions

6.1. Limitations

While the proposed MBCNN framework demonstrates promising performance in student performance prediction, several limitations warrant careful consideration:

• Data Dependency and Generalization Constraints: Although the model achieves strong performance on the specific institutional dataset used in this study, its direct transferability to other educational contexts requires further verification. Like most data-driven approaches in educational data mining, the model remains susceptible to dataset shift and would necessitate retraining when applied to different institutions or temporal contexts.
• Temporal Modeling Constraints: The current architecture primarily processes static feature representations and may not adequately capture the evolving temporal dynamics of student learning behaviors throughout their academic journey.
• Potential Data Biases: As with most data-driven approaches, the model may inherit and potentially amplify biases present in the training data, particularly concerning feature selection and representation, which could impact fairness across different student demographics.
• Feature Engineering Requirements: The effectiveness of our multi-branch architecture depends substantially on meaningful feature grouping, which currently requires considerable domain expertise. This may limit immediate applicability in contexts where feature semantics are ambiguous or interdisciplinary in nature.
• Computational Considerations: While MBCNN introduces only moderate computational overhead compared to standard MLPs, the parallel branch processing and associated hyperparameter optimization demand more resources than simpler baseline models, which could affect deployment in resource-constrained environments.

6.2. Future Research Directions

Building upon the current work and addressing the identified limitations, we outline several promising research directions:

• Cross-Institutional Validation: We plan to conduct comprehensive validation across multiple educational institutions with diverse demographic and pedagogical characteristics to rigorously assess the framework’s broader applicability and generalization capabilities.
• Temporal Generalization Studies: Future work will investigate model performance across different academic years, with particular focus on robustness to temporal shifts such as those induced by the pandemic-induced transition to online learning.
• Architectural Enhancements: We will explore hybrid architectures integrating LSTM modules for capturing temporal dynamics in learning trajectories, attention mechanisms for adaptive feature weighting and noise reduction, and transfer learning techniques to improve model portability across institutional contexts.
• Beyond-Supervised Learning: Recognizing the practical challenges of obtaining comprehensive labeled educational data, we will investigate semi-supervised and self-supervised approaches that can effectively leverage unlabeled student data, thus bridging methodological gaps between data-rich and data-scarce educational environments [23,24].
• Explainability and Fairness Enhancement: Future iterations will incorporate explicit model interpretation techniques to identify stable, transferable feature interactions and ensure algorithmic fairness across different student demographic groups.

While the current implementation provides a solid foundation for structured educational data modeling, pursuing these future directions will significantly enhance the framework’s practical utility and strengthen its methodological contributions to the educational data mining community.

7. Conclusions

This study demonstrates the superior effectiveness of the proposed Multi-Branch Convolutional Neural Network (MBCNN) in predicting student graduation status by explicitly modeling multi-dimensional factors, including student characteristics, school resources, family environment, and societal influences. Experimental results show that MBCNN outperforms traditional machine learning methods and standard deep learning models, achieving improvements in accuracy, weighted precision, weighted recall and weighted F1-score. These gains highlight the importance of designing domain-specific neural architectures that align with the inherent structure of educational data, rather than relying on generic models. The work underscores the potential of tailored deep learning frameworks to enhance predictive accuracy and interpretability in educational data mining, while also providing a foundation for future research into adaptive and explainable student success systems.