Foundational Algorithms for Modern Cybersecurity: A Unified Review on Defensive Computation in Adversarial Environments
Abstract
1. Introduction
Review Methodology
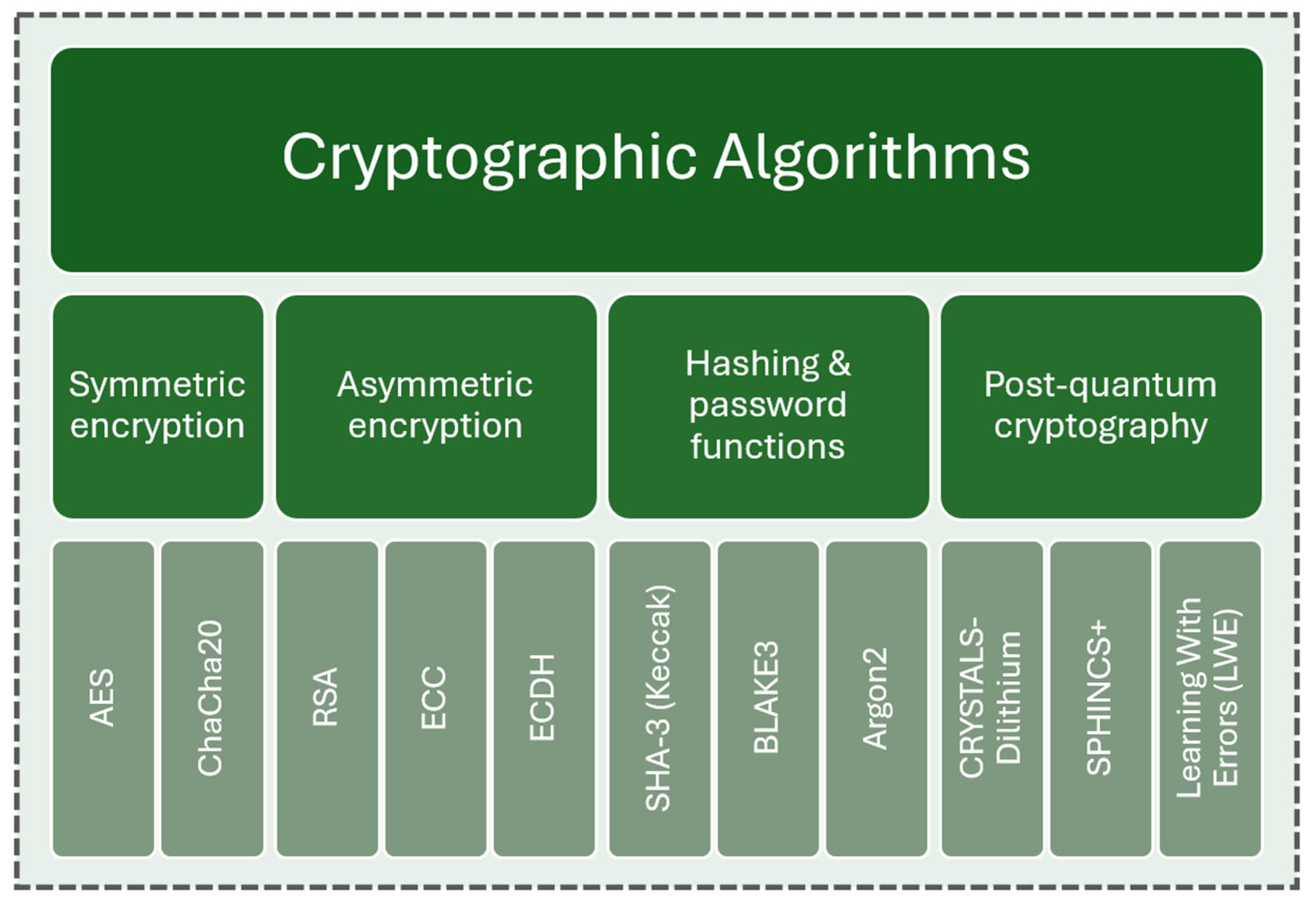
2. Cryptographic Algorithms: Confidentiality and Integrity
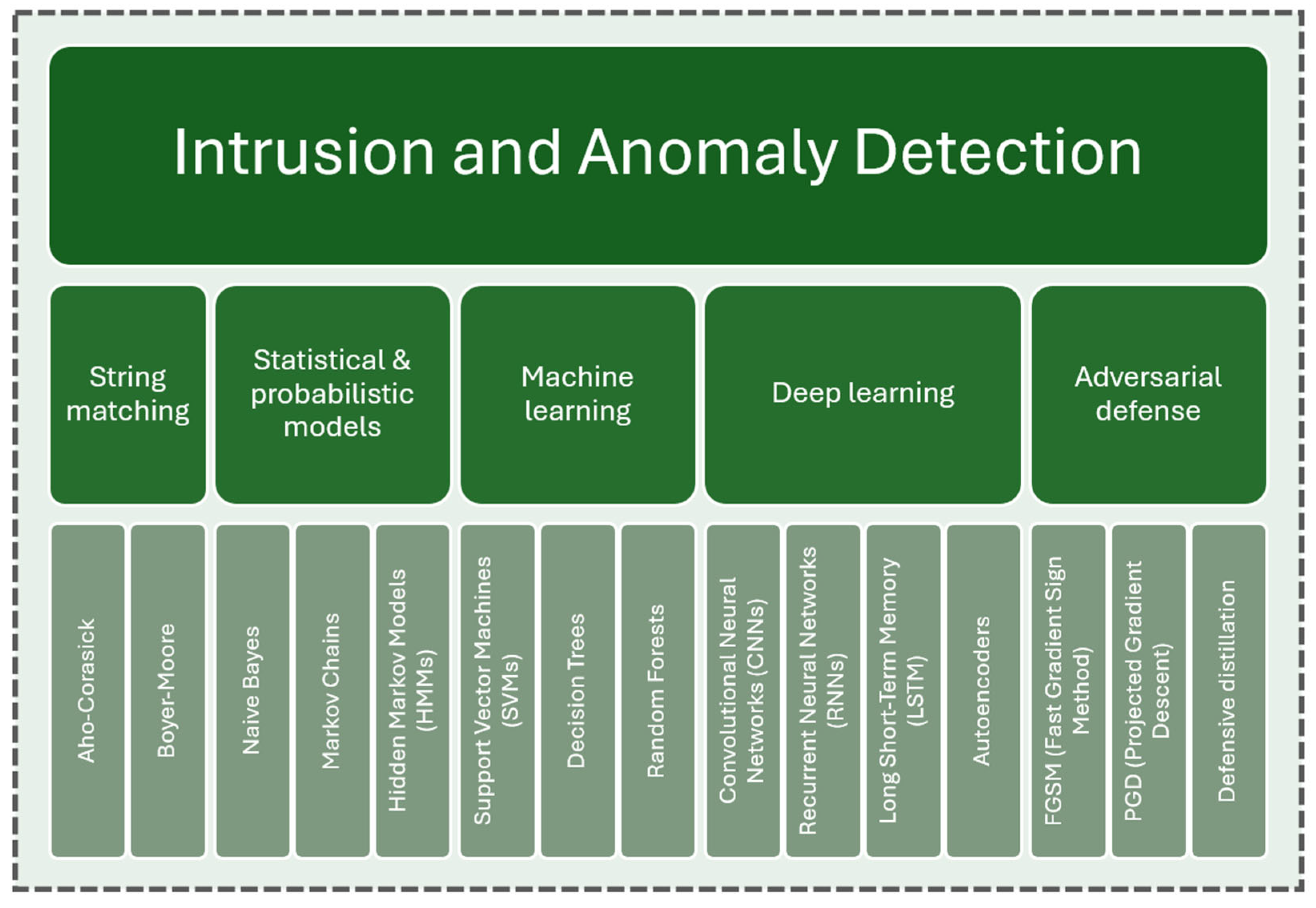
3. Algorithms for Intrusion and Anomaly Detection
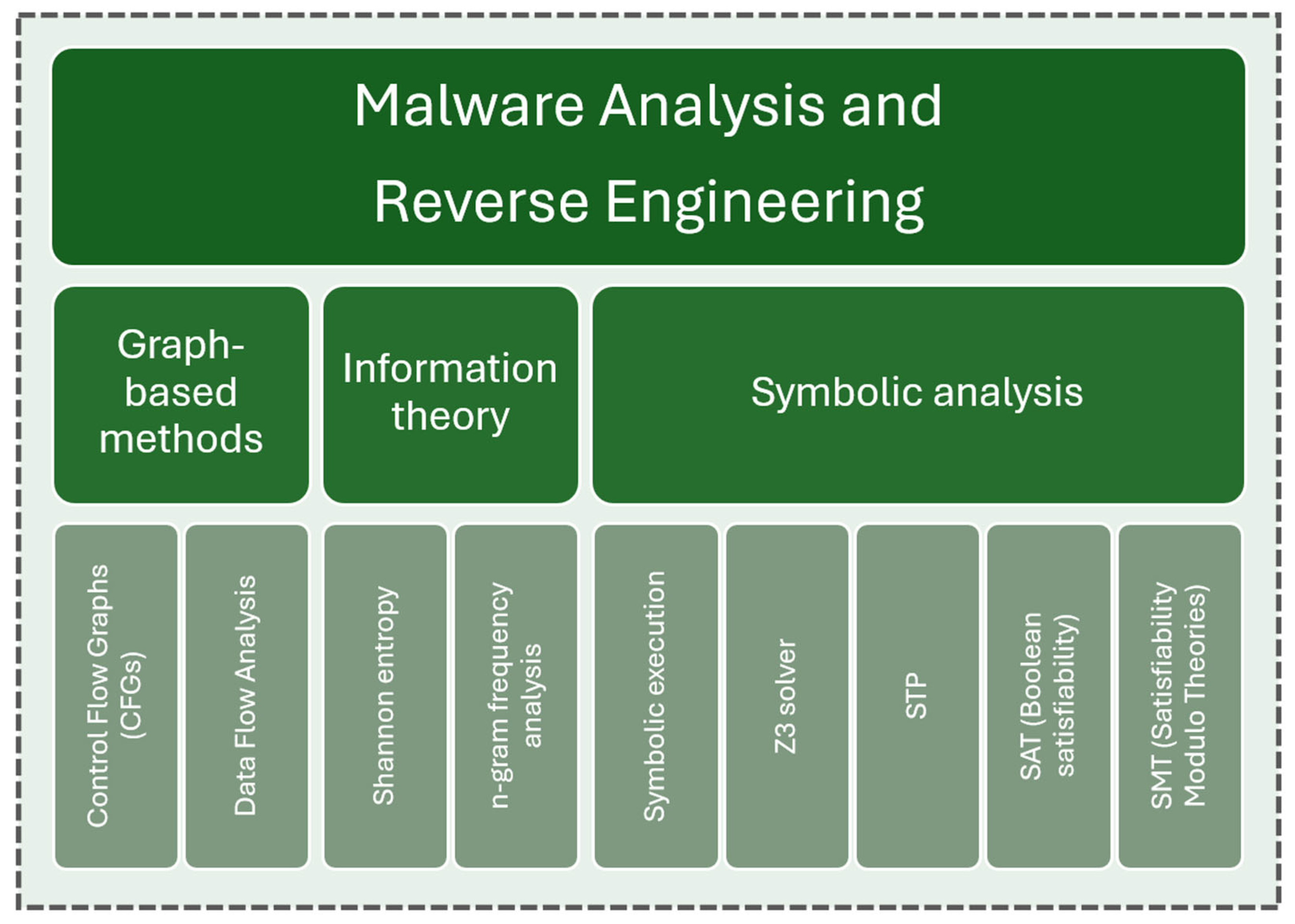
4. Algorithms in Malware Analysis and Reverse Engineering
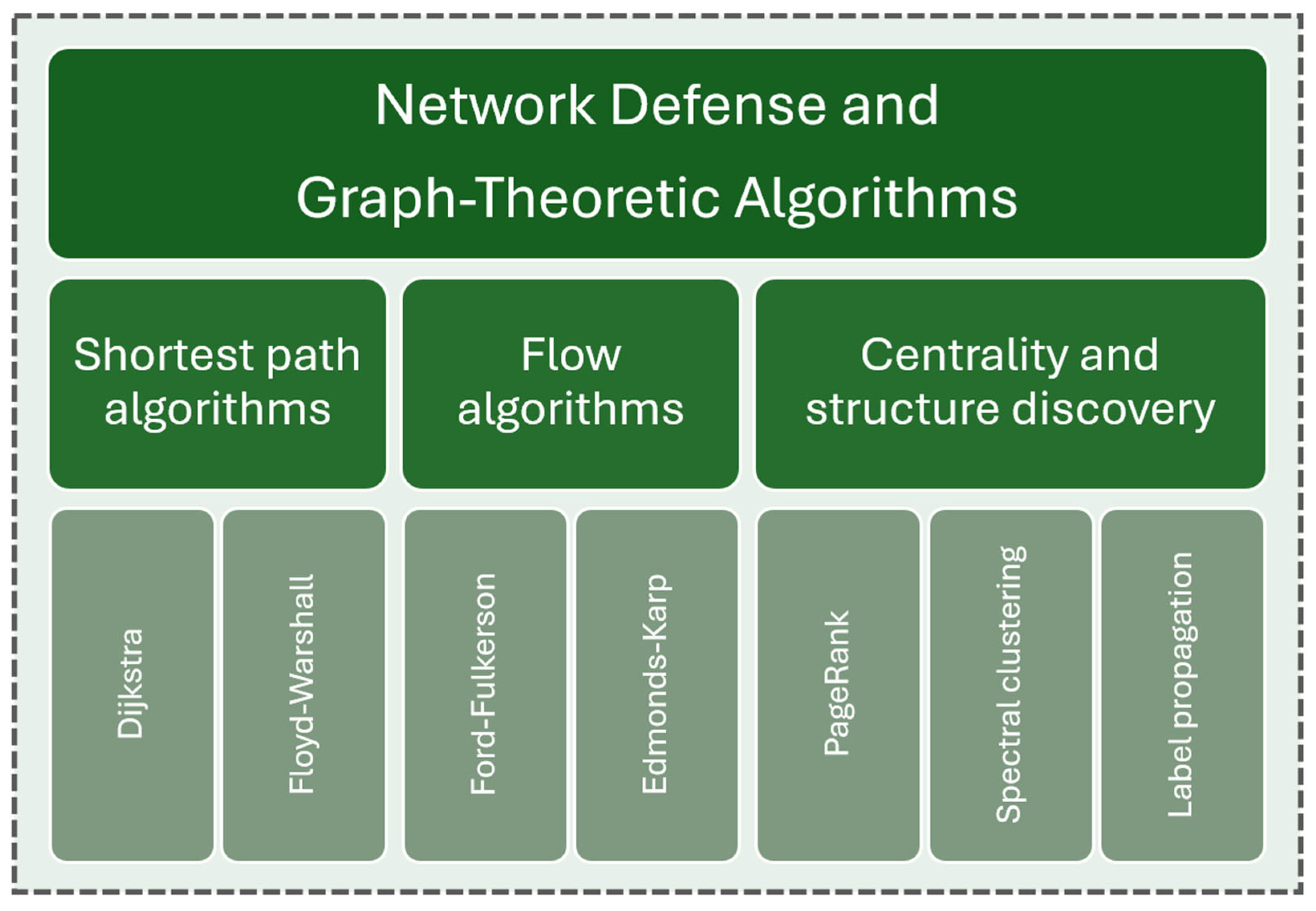
5. Network Defense and Graph-Theoretic Algorithms
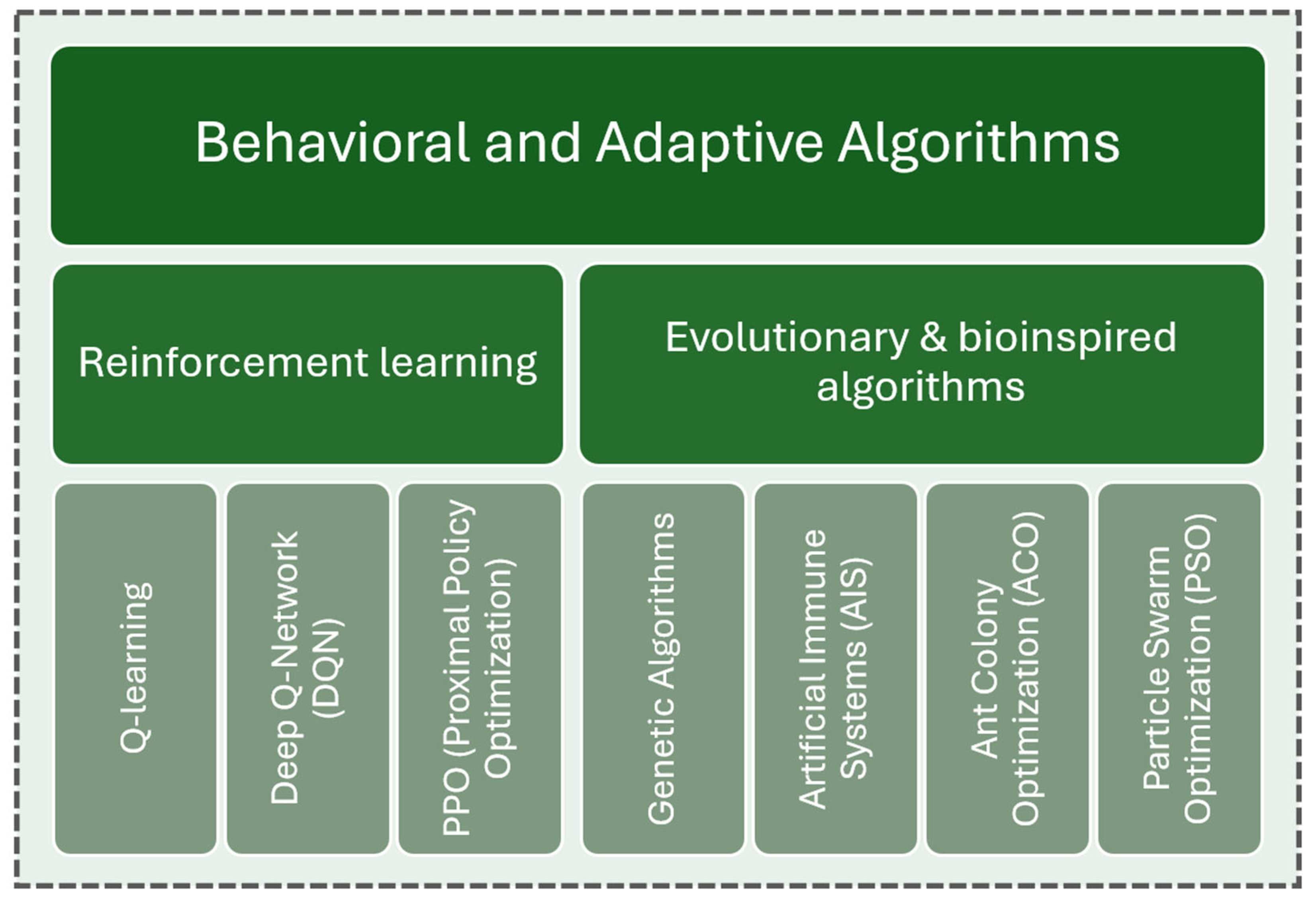
6. Behavioral and Adaptive Algorithms
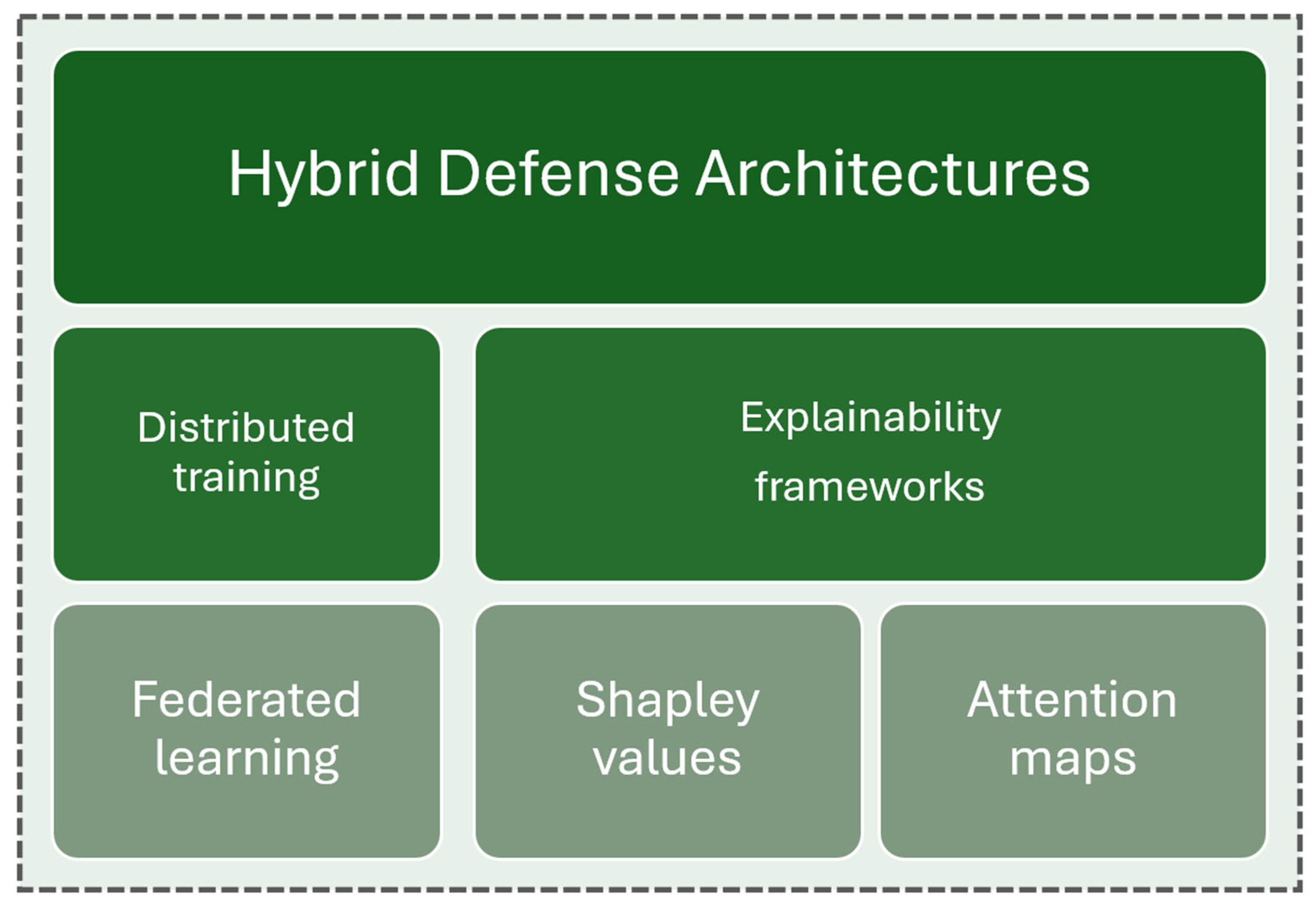
7. Algorithmic Integration and Hybrid Defense Architectures
8. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AES | Advanced Encryption Standard |
| ECC | Elliptic Curve Cryptography |
| RSA | Rivest-Shamir-Adleman |
| ECDH | Elliptic Curve Diffie-Hellman |
| HMM | Hidden Markov Model |
| CNN | Convolutional Neural Network |
| RNN | Recurrent Neural Network |
| LSTM | Long Short-Term Memory |
| SIEM | Security Information and Event Management |
| DQN | Deep Q-Network |
| AIS | Artificial Immune System |
| ACO | Ant Colony Optimization |
| PSO | Particle Swarm Optimization |
| CFG | Control Flow Graph |
| DFG | Data Flow Graph |
| SAT | Boolean Satisfiability Problem |
| SMT | Satisfiability Modulo Theories |
| XAI | Explainable Artificial Intelligence |
| PQC | Post-Quantum Cryptography |
| SHA | Secure Hash Algorithm |
| DHT | Distributed Hash Table |
| HIDS | Host-Based Intrusion Detection System |
| NIDS | Network-Based Intrusion Detection System |
Appendix A
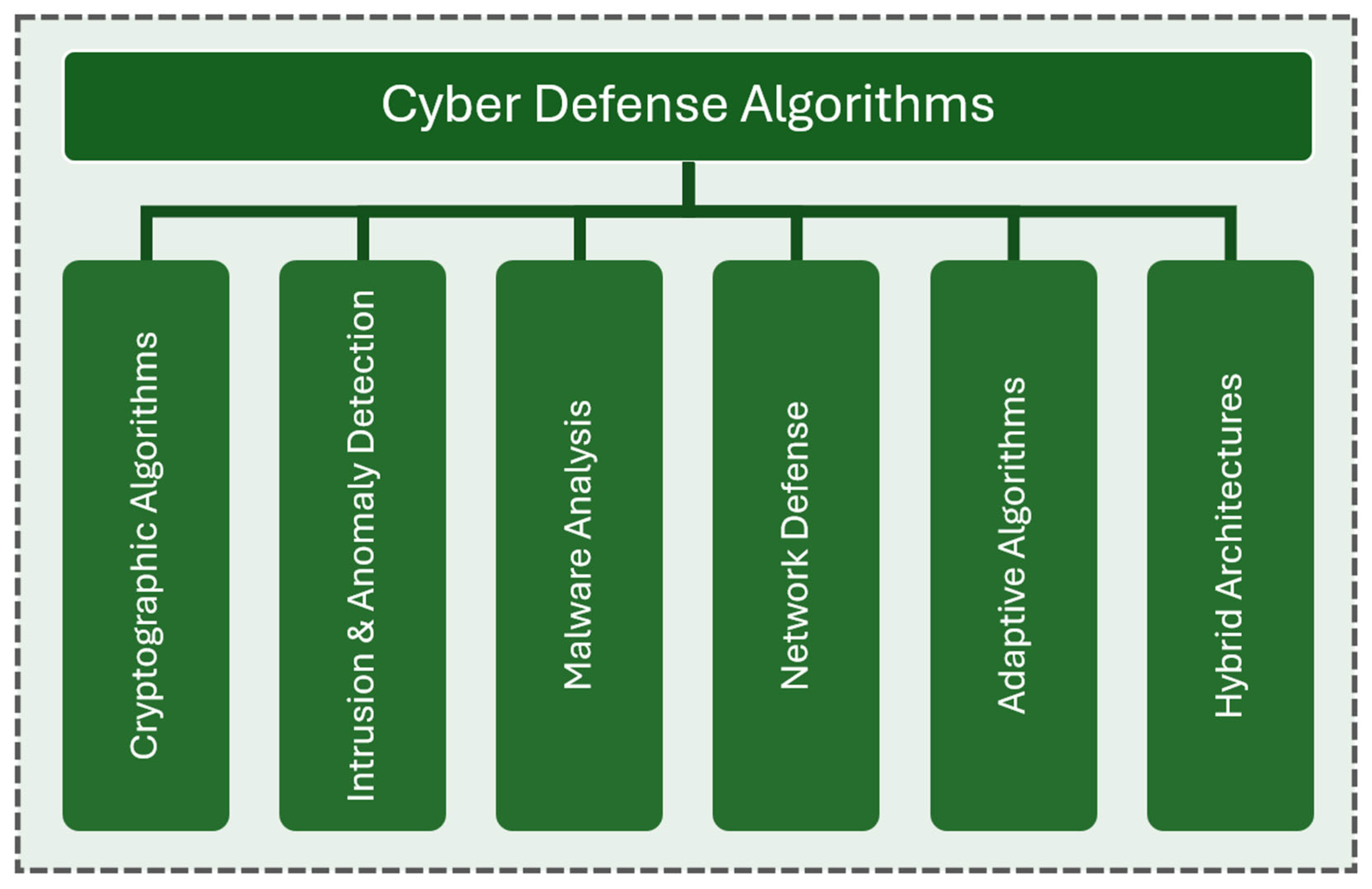
Taxonomic Rationale
References
- Bishop, M. Security, Computer Security: Art and Science, 2nd ed.; Addison-Wesley: Boston, MA, USA, 2018. [Google Scholar]
- Paul, A.G. Antivirus Engines: From Methods to Innovations and Applications; Elsevier Syngress: Burlington, MA, USA, 2024; pp. 1–656. [Google Scholar]
- Stallings, W. Cryptography and Network Security: Principles and Practice, 8th ed.; Pearson: London, UK, 2023. [Google Scholar]
- Axelsson, S. The base-rate fallacy and its implications for the difficulty of intrusion detection. ACM Trans. Inf. Syst. Secur. 1999, 3, 186–205. [Google Scholar] [CrossRef]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Song, Y. Application of Deep Learning in Malware Detection: A. Review. J. Big Data 2025, 12, 57. [Google Scholar] [CrossRef]
- Rivest, R.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Ozkan-Okay, M.; Akin, E.; Aslan, Ö.; Kosunalp, S.; Iliev, T.; Stoyanov, I.; Beloev, I. A Comprehensive Survey: Evaluating the Efficiency of Artificial Intelligence and Machine Learning Techniques on Cyber Security Solutions. IEEE Access 2024, 12, 12252–12278. [Google Scholar] [CrossRef]
- Boneh, D.; Shoup, V. A Graduate Course in Applied Cryptography; Stanford University: Stanford, CA, USA, 2020. [Google Scholar]
- Carlini, N.; Wagner, D. Towards evaluating the robustness of neural networks. In Proceedings of the IEEE Symposium on Security and Privacy, San Jose, CA, USA, 22–26 May 2017; pp. 39–57. [Google Scholar]
- Schneier, B. Applied Cryptography: Protocols, Algorithms, and Source Code in C, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Daemen, J.; Rijmen, V. The Design of Rijndael: AES—The Advanced Encryption Standard; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- FIPS PUB 197; Advanced Encryption Standard (AES). National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2001.
- Bernstein, D.J. ChaCha, a Variant of Salsa20 Workshop Record of SASC 2008; The State of the Art of Stream Ciphers; The University of Illinois at Chicago: Chicago, IL, USA, 2008. [Google Scholar]
- Williams, H.C. A Modification of the RSA Public-Key Encryption Procedure. IEEE Trans. Inf. Theory 1980, 26, 726–729. [Google Scholar] [CrossRef]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Miller, V.S. Use of Elliptic Curves in Cryptography. Advances in Cryptology—CRYPTO ’85 Proceedings; Springer: Berlin/Heidelberg, Germany, 1986; pp. 417–426. [Google Scholar]
- Bertoni, G.; Daemen, J.; Peeters, M.; Van Assche, G. Keccak. In Advances in Cryptology—EUROCRYPT 2013; Johansson, T., Nguyen, P.Q., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7881, pp. 313–314. [Google Scholar]
- O’Connor, J.; Aumasson, J.P.; Neves, S.; Wilcox-O’Hearn, Z. BLAKE3: One Function, Fast Everywhere Cryptology ePrint Archive, Report 2020/014. 2020. Available online: https://autoblog.suumitsu.eu/autoblogs/sebsauvagenetlinks_f5730e92d2c28615f2f44758a6d249f605e9c0ae/media/f32098b6.blake3.pdf (accessed on 20 October 2025).
- Biryukov, A.; Dinu, D.; Khovratovich, D. Argon2: The memory-hard function for password hashing and other applications. In Proceedings of the IEEE EuroS&P, Saarbruecken, Germany, 21–24 March 2016; pp. 292–302. [Google Scholar]
- Leo, D.; Tancrede, L.; Vadim, L.; Peter, S.; Gregor, S.; Damien, S. CRYSTALS—Dilithium: Digital Signatures from Module Lattices. IACR ePrint Archive, 2017/633. 2017. Available online: https://eprint.iacr.org/2017/633 (accessed on 12 January 2025).
- Bernstein, D.J.; Dobraunig, C.; Eichlseder, M.; Fluhrer, S.; Gazdag, S.-L.; Hülsing, A.; Kampanakis, P.; Kölbl, S.; Lange, T.; Lauridsen, M.M.; et al. SPHINCS+: Submission to the NIST Post-Quantum Cryptography Project; NIST PQC Round 3 Submission; Eindhoven University of Technology: Eindhoven, The Netherlands, 2020. [Google Scholar]
- Peikert, C. A decade of lattice cryptography. Found. Trends Theor. Comput. Sci. 2016, 10, 283–424. [Google Scholar]
- Farhan, M.; Waheed Ud Din, H.; Ullah, S.; Hussain, M.S.; Khan, M.A.; Mazhar, T.; Jaghdam, I.H. Network-based intrusion detection using deep learning technique. Sci. Rep. 2025, 15, 25550. [Google Scholar] [CrossRef]
- Aho, A.V.; Corasick, M.J. Efficient string matching: An aid to bibliographic search. Commun. ACM 1975, 18, 333–340. [Google Scholar] [CrossRef]
- Boyer, R.S.; Moore, J.S. A fast string searching algorithm. Commun. ACM 1977, 20, 762–772. [Google Scholar] [CrossRef]
- Panda, M.; Patra, M.R. Network intrusion detection using Naive Bayes. Int. J. Comput. Sci. Netw. Secur 2007, 7, 258–263. [Google Scholar]
- Gagniuc, P.A. Markov Chains: From Theory to Implementation and Experimentation; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Kim, K.L.; Kuperman, B.A. Using Hidden Markov Models for intrusion detection. In Proceedings of the IEEE Systems Man and Cybernetics Society, Taipei, Taiwan, 8–11 October 2006; pp. 1756–1761. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- An, J.; Cho, S. Variational Autoencoder Based Anomaly Detection Using Reconstruction Probability; SNU Data Mining Center Technology Report; Seoul National University: Seoul, Republic of Korea, 2015. [Google Scholar]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. In Proceedings of the ICLR, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Altaha, S.J.; Aljughaiman, A.; Gul, S. A Survey on Android Malware Detection Techniques Using Supervised Machine Learning. IEEE Access 2024, 12, 173168–173191. [Google Scholar] [CrossRef]
- Kruegel, C.; Kirda, E.; Mutz, D.; Robertson, W.; Vigna, G. Polymorphic worm detection using structural information of executables. In Proceedings of the RAID, Seattle, WA, USA, 7–9 September 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 207–226. [Google Scholar]
- Nielson, F.; Nielson, H.R.; Hankin, C. Principles of Program Analysis; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Vasudevan, A. Re-inforced Stealth Breakpoints. In Proceedings of the 2009 Fourth International Conference on Risks and Security of Internet and Systems (CRiSIS 2009), Toulouse, France, 19–22 October 2009; pp. 59–66. [Google Scholar]
- Lyda, R.; Hamrock, J. Using entropy analysis to find encrypted and packed malware. IEEE Secur. Privacy 2007, 5, 40–45. [Google Scholar] [CrossRef]
- Christodorescu, M.; Jha, S. Static analysis of executables to detect malicious patterns. In Proceedings of the USENIX Security Symposium, Washington, DC, USA, 4–8 August 2003; pp. 169–186. [Google Scholar]
- Aboaoja, F.A.; Zainal, A.; Ghaleb, F.A.; Al-Rimy, B.A.S.; Eisa, T.A.E.; Elnour, A.A.H. Malware Detection Issues, Challenges, and Future Directions: A Survey. Appl. Sci. 2022, 12, 8482. [Google Scholar] [CrossRef]
- Berrios, S.; Leiva, D.; Olivares, B.; Allende-Cid, H.; Hermosilla, P. Systematic Review: Malware Detection and Classification in Cybersecurity. Appl. Sci. 2025, 15, 7747. [Google Scholar] [CrossRef]
- Moura, L.; Bjørner, N. Z3: An Efficient SMT Solver. In Proceedings of the TACAS, Budapest, Hungary, 29 March–6 April 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 337–340. [Google Scholar]
- Eén, N.; Sörensson, N. An Extensible SAT-Solver. In Proceedings of the SAT, Santa Margherita Ligure, Italy, 5–8 May 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 502–518. [Google Scholar]
- Salwan, J.; Bardin, S.; Potet, M.L. Symbolic Deobfuscation: From Virtualized Code Back to the Original. In DIMVA 2018: Detection of Intrusions and Malware, and Vulnerability Assessment; Springer: Berlin/Heidelberg, Germany, 2018; pp. 372–392. [Google Scholar]
- Dullien, T. Graph-Based Comparison of Executable Objects (Reloaded). In Proceedings of the Symposium Sur la Sécurité des Technologies de L’information et des Communications, Rennes, France, 30 May–1 June 2007. [Google Scholar]
- Newman, M. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Barbarossa, S.; Scutari, G. Distributed signal processing in self-organizing sensor networks. IEEE J. Sel. Areas Commun. 2007, 24, 775–786. [Google Scholar]
- Zhong, X.; Sun, Y.; Li, Q. A Survey on Graph Neural Networks for Intrusion Detection Systems: Methods, Trends and Challenges. Comput. Secur. 2024, 125, 103152. [Google Scholar] [CrossRef]
- Floyd, R.W. Algorithm 97: Shortest path. Commun. ACM 1962, 5, 345. [Google Scholar] [CrossRef]
- Shapiro, J.; Sandhu, R.S. A Weighted Shortest-Path Approach to Network Security Metrics. In Proceedings of the IEEE International Conference on Communications, Cape Town, South Africa, 23–27 May 2010; pp. 1642–1647. [Google Scholar]
- Ford, L.R.; Fulkerson, D.R. Maximal flow through a network. Canad. J. Math. 1956, 8, 399–404. [Google Scholar] [CrossRef]
- Edmonds, J.; Karp, R.M. Theoretical improvements in algorithmic efficiency for network flow problems. J. ACM 1972, 19, 248–264. [Google Scholar] [CrossRef]
- Sperotto, A.; Schaffrath, G.; Sadre, R.; Morariu, C.; Pras, A.; Stiller, B. Flow-Based Intrusion Detection: From Theory to Practice. In Proceedings of the International Workshop on Recent Advances in Intrusion Detection (RAID), Dublin, Ireland, 23–27 May 2011; pp. 1–17. [Google Scholar]
- Yu, S.Z.; Zhang, Y.X.; Wang, C. Botnet detection using improved PageRank algorithm. J. Netw. Comput. Appl. 2013, 36, 1441–1450. [Google Scholar]
- Girvan, M.; Newman, M.E. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, S. Detecting coordinated attacks in large networks using community detection. IEEE Trans. Inf. Forensics Secur. 2019, 14, 1533–1547. [Google Scholar]
- Dainotti, A.; Pescape, A.; Claffy, K.C. Issues and future directions in traffic classification. IEEE Netw. 2012, 26, 35–40. [Google Scholar] [CrossRef]
- Nguyen, H.; Altman, E.; Nain, P. Reinforcement learning in network security: A comprehensive survey. IEEE Commun. Surv. Tutor. 2021, 23, 1649–1697. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Watkins, C.J.H.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Hassabis, D. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, W.; Kim, H. Adaptive cyber defense using deep reinforcement learning. In Proceedings of the IEEE Security Privacy Workshops (SPW), Genoa, Italy, 21 May 2020; pp. 8–14. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- De Castro, L.N.; Von Zuben, F.J. Artificial Immune Systems: Part I—Basic Theory and Applications; Technical Report TR-DCA 01/99; State University: Campinas, Brazil, 1999. [Google Scholar]
- Forrest, S.; Perelson, A.S.; Allen, L.; Cherukuri, R. Self-Nonself Discrimination in a Computer. In Proceedings of the IEEE Symposium Security Privacy, Oakland, CA, USA, 16–18 May 1994; pp. 202–212. [Google Scholar]
- Dorigo, M.; Stützle, T. Ant Colony Optimization; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Paranjape, S.; Chandane, P.; Chatur, P. A hybrid swarm intelligence approach for network intrusion detection. Expert Syst. Appl. 2022, 206, 118011. [Google Scholar]
- Bridges, S.M.; Vaughn, R.B. Fuzzy data mining and genetic algorithms applied to intrusion detection. In Proceedings of the 12th Annual Canadian Information Technology Security Symposium. Workshop, Baltimore, MD, USA, 16–19 October 2000; pp. 109–122. [Google Scholar]
- Cohen, D.; Te’eni, D.; Yahav, I.; Zagalsky, A.; Schwartz, D.; Silverman, G.; Makowski, J. Human–AI Enhancement of Cyber Threat Intelligence. Int. J. Inf. Secur. 2025, 24, 99. [Google Scholar] [CrossRef]
- Lilhore, U.K.; Simaiya, S.; Alroobaea, R.; Baqasah, A.M.; Alsafyani, M.; Alhazmi, A.; Khan, M.M. SmartTrust: A hybrid deep learning framework for real-time threat detection in cloud environments using Zero-Trust Architecture. J. Cloud Comput. 2025, 14, 35. [Google Scholar] [CrossRef]
- Kim, S.; Shin, J.; Kim, H. Hybrid intrusion detection using deep neural networks and Markov models. IEEE Access 2021, 9, 73182–73193. [Google Scholar]
- Ye, Y.; Li, T.; Adjeroh, D.; Iyengar, S.S. A survey on malware detection using data mining and machine learning. ACM Comput. Surv. 2017, 50, 41. [Google Scholar]
- Han, Z.; Niyato, D.; Saad, W.; Başar, T. Game Theory for Next Generation Wireless and Communication Networks; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Konečný, J.; McMahan, H.B.; Ramage, D.; Richtárik, P. Federated Optimization: Distributed Machine Learning for on-Device Intelligence. arXiv 2016, arXiv:1610.02527. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated machine learning: Concept and applications. ACM Trans. Intell. Syst. Technol. 2019, 10, 12. [Google Scholar] [CrossRef]
- Mo, K.; Tang, W.; Li, J.; Yuan, X. Cloud-based distributed intrusion detection using ensemble learning. IEEE Trans. Dependable Secur. Comput. 2022, 19, 233–247. [Google Scholar]
- Guo, W.; Mu, D.; Xu, J.; Su, P.; Wang, G.; Xing, X. LEMNA: Explaining Deep Learning based Security Applications. In Proceedings of the 2018 ACM SIGSAC Conference on Computer & Communications Security (CCS ’18), Toronto, ON, Canada, 15 October 2018; pp. 364–379. [Google Scholar]
- Biggio, B.; Roli, F. Wild patterns: Ten years after the rise of adversarial machine learning. Pattern Recognit. 2018, 84, 317–331. [Google Scholar] [CrossRef]
- Buczak, A.; Guven, E. A survey of data mining and machine learning methods for cyber security intrusion detection. IEEE Commun. Surv. Tutor. 2016, 18, 1153–1176. [Google Scholar] [CrossRef]
- Tagarev, T.; Sharkov, G. Computationally Intensive Functions in Designing and Operating Distributed Cyber Secure and Resilient Systems. In Proceedings of the 20th International Conference on Computer Systems and Technologies (CompSysTech), New York, NY, USA, 21–22 June 2019; pp. 8–18. [Google Scholar]
- Chunawala, H.; Kumbhar, S.; Pandey, A.; Rajput, B.J.; Sahu, G.; Guru, A. A Survey of Anomaly Detection in Graphs: Algorithms and Applications. In Graph Mining; Bhattacharya, R., Rathore, Y.K., Tran, T.A., Swarnkar, S.K., Eds.; Springer: Cham, Switzerland, 2025. [Google Scholar]
- Ali, S.; Wadho, S.A.; Talpur, K.R.; Talpur, B.A.; Alshudukhi, K.S.; Humayun, M.; Shah, A. Next-generation quantum security: The impact of quantum computing on cybersecurity-Threats, mitigations, and solutions. Comput. Electr. Eng. 2025, 128, 110649. [Google Scholar] [CrossRef]
- Lima, M.; Viana, C.; Santos, W.R.; Neves, F.; Campos, J.R.; Aires, F. Toward using cyber threat intelligence with machine and deep learning for IoT security: A comprehensive study. J. Supercomput. 2025, 81, 1404. [Google Scholar] [CrossRef]
- Moriano, P.; Hespeler, S.C.; Li, M.; Mahbub, M. Adaptive anomaly detection for identifying attacks in cyber-physical systems: A systematic literature review. Artif. Intell. Rev. 2025, 58, 283. [Google Scholar] [CrossRef]
- Bogdan, I.C.; Simion, E. Cybersecurity Assessment and Certification of Critical Infrastructures. Univ. Politeh. Buchar. Sci. Bull. Ser. C 2024, 86, 4. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gagniuc, P.A. Foundational Algorithms for Modern Cybersecurity: A Unified Review on Defensive Computation in Adversarial Environments. Algorithms 2025, 18, 709. https://doi.org/10.3390/a18110709
Gagniuc PA. Foundational Algorithms for Modern Cybersecurity: A Unified Review on Defensive Computation in Adversarial Environments. Algorithms. 2025; 18(11):709. https://doi.org/10.3390/a18110709
Chicago/Turabian StyleGagniuc, Paul A. 2025. "Foundational Algorithms for Modern Cybersecurity: A Unified Review on Defensive Computation in Adversarial Environments" Algorithms 18, no. 11: 709. https://doi.org/10.3390/a18110709
APA StyleGagniuc, P. A. (2025). Foundational Algorithms for Modern Cybersecurity: A Unified Review on Defensive Computation in Adversarial Environments. Algorithms, 18(11), 709. https://doi.org/10.3390/a18110709





