Explainable AI for Coronary Artery Disease Stratification Using Routine Clinical Data

Abstract

Background: Coronary artery disease (CAD) remains a leading cause of morbidity and mortality. Early diagnosis reduces adverse outcomes and alleviates the burden on healthcare, yet conventional approaches are often invasive, costly, and not always available. In this context, machine learning offers promising solutions. Objective: The objective of this study is to evaluate the feasibility of reliably predicting both the presence and the severity of CAD. The analysis is based on a harmonized, multi-center UCI dataset that includes cohorts from Cleveland, Hungary, Switzerland, and Long Beach. The work aims to assess the accuracy and practical utility of models built exclusively on routine tabular clinical and demographic data, without relying on imaging. These models are designed to improve risk stratification and guide patient routing. Methods and Results: The study is based on a uniform and standardized data processing pipeline. This pipeline includes handling missing values, feature encoding, scaling, an 80/20 train–test split and applying the SMOTE method exclusively to the training set to prevent information leakage. Within this pipeline, a standardized comparison of a wide range of models (including gradient boosting, tree-based ensembles, support vector methods, etc.) was conducted with hyperparameter tuning via GridSearchCV. The best results were demonstrated by the CatBoost model: accuracy—0.8278, recall—0.8407, and F1-score—0.8436. Conclusions: A key distinction of this work is the comprehensive evaluation of the models’ practical suitability. Beyond standard metrics, the analysis of calibration curves confirmed the reliability of the probabilistic predictions. Patient-level interpretability using SHAP showed that the model relies on clinically significant predictors, including ST-segment depression. Calibrated and explainable models based on readily available data are positioned as a practical tool for scalable risk stratification and decision support, especially in resource-constrained settings.

1. Introduction

Coronary artery disease (CAD) is the leading cause of morbidity and mortality worldwide and the most common type of cardiovascular disease (CVD), affecting high-, low, and middle-income countries alike [1,2]. Its prevalence is steadily increasing due to population aging, lifestyle changes, and risk factors such as hypertension, diabetes, and smoking, creating a significant burden on healthcare systems and economies [3,4,5].

Epidemiological data show that while CAD is widespread, its patterns vary based on geographic and socioeconomic factors [6]. Developing countries are experiencing a sharp rise in CAD prevalence due to urbanization and unhealthy lifestyles [7,8]. In contrast, developed nations are seeing an increase in the absolute number of cases, mainly because of an aging population and improved survival rates [5,9]. Socioeconomic and gender disparities in disease rates are also evident [4,10].

Early diagnosis of CAD is critical for improving patient outcomes but remains a significant challenge [2]. Key difficulties include the disease’s wide spectrum of clinical presentations and its often silent or asymptomatic nature in the early stages. Additional challenges arise from the inherent limitations of current diagnostic methodologies [11,12]. Furthermore, inconsistencies between anatomical, functional, and biomarker tests complicate an accurate and timely diagnosis [13].

The UCI Heart Disease dataset has become the gold standard for testing predictive models for coronary artery disease (CAD). It includes several subsets, the most well-known of which is the Cleveland subset, containing data from 303 patients with 14 clinical and demographic variables [14,15]. Many studies using this dataset report accuracy in the range of 80–95%, which has made it the de facto standard for evaluating models [14,16].

Despite its widespread use, approaches to analyzing this dataset vary significantly, which makes a direct comparison of results difficult. The work by Teja and Rayalu (2025) conducted a broad comparative analysis of 15 ML models with an emphasis on performance metrics [17]. Another approach was proposed by Ahmad and Polat (2023), who focused on feature selection to improve accuracy [18]. In turn, Akella and Akella (2021) focused on creating an open-source solution but, like many others, limited their scope to standard metrics [14]. These approaches are part of a broader spectrum of research that, despite its value, exhibits a set of interrelated limitations that reduce the credibility of conclusions and the generalizability of models [19]. Key problems remain the small size and insufficient representativeness of the data. The 303 records of the Cleveland dataset are often insufficient for training deep learning models, which require large volumes of data for effective generalization [15,20]. Many studies rely on small, single-center samples, which increases the risk of overfitting and prevents a robust assessment of model stability on external cohorts [19,21]. Furthermore, datasets often suffer from demographic and class imbalance, such as the underrepresentation of women or younger individuals [14,22]. This imbalance systematically distorts evaluation metrics and reduces sensitivity to rare yet clinically significant cases [19,23]. Finally, the data often contain biases related to the source and collection protocols. These biases cause a distribution shift between training and test sets and reduce the transferability of models in real-world clinical settings [23,24]. The complexity and high cost of medical data annotation also limit the availability of high-quality samples and reduce the reproducibility of research [23,25].

Our study aims to overcome these limitations and evaluate the feasibility of reliably predicting both the presence and the severity of CAD. The analysis is based exclusively on routine tabular clinical and demographic data, without reliance on imaging. The novelty of this work lies in several aspects. Firstly, we use a harmonized, multi-center UCI dataset that includes cohorts from Cleveland, Hungary, Switzerland, and Long Beach. This approach enhances representativeness and allows for the assessment of model generalizability across heterogeneous populations. Secondly, the target variable is defined to support both a binary task (presence/absence of CAD) and a multiclass task (with gradations of severity). This increases the practical applicability of the models for risk stratification and patient routing. Thirdly, we apply a uniform and standardized data processing pipeline. This pipeline includes detecting and handling missing or incorrect values, encoding categorical features, scaling the data, and performing an 80/20 train–test split. To combat class imbalance, the SMOTE method is applied exclusively to the training subset to prevent information leakage. Within this pipeline, a standardized comparison of several widely used methods is conducted—gradient boosting, tree-based ensembles, nearest neighbor and support vector methods, as well as logistic regression—with hyperparameter tuning via GridSearchCV. Accordingly, the central research question of this study is whether an explainable and well-calibrated machine learning model can accurately predict the presence and severity of CAD while maintaining transparency at the patient level. We hypothesize that integrating machine learning algorithms with SHAP-based interpretability will provide both high predictive accuracy and meaningful insights. This approach aims to bridge the existing gap between algorithmic performance and medical interpretability. The distinct contribution of this work lies in its methodological rigor, which includes multi-center data harmonization, standardized preprocessing pipelines, and comprehensive model calibration. It also emphasizes explainability as a core design principle rather than a secondary component. To the best of our knowledge, this study represents the first comprehensive application of SHAP-based explainable artificial intelligence for CAD stratification using the UCI multi-center dataset. The proposed framework establishes a reproducible, transparent, and interpretable approach that can guide the development of future AI-driven diagnostic systems in cardiovascular medicine.

2. Materials and Methods

2.1. Dataset Description

The dataset used in this study was obtained from the publicly available UCI Machine Learning Repository, which is widely recognized as one of the most authoritative platforms for benchmark datasets in machine learning. Specifically, the dataset employed is the Heart Disease Dataset, a classical and extensively utilized resource for cardiovascular research, particularly in the prediction of CAD. Its open accessibility, standardized structure, and frequent use in prior studies make it a reliable foundation for testing and evaluating machine learning models in the medical domain [26].

The dataset contains records of 303 patients, each described by a set of demographic and clinical attributes that are considered critical in the diagnosis of heart disease. The dataset records each patient’s age and sex. It also includes clinical measurements such as resting blood pressure, serum cholesterol level, and fasting blood sugar. Cardiovascular indicators are captured through the results of the resting electrocardiogram (ECG), the maximum heart rate achieved, and the presence of exercise-induced angina. Additional diagnostic features include ST-segment depression (old peak), the slope of the ST-segment, the number of major vessels identified by fluoroscopy, and the thalassemia indicator. Together, these variables represent a diverse range of physiological and clinical factors that provide comprehensive insights into cardiovascular health.

The target variable (num) indicates the presence and severity of heart disease. A value of 0 denotes the absence of CAD, while values from 1 to 4 reflect increasing levels of disease severity. This enables the dataset to be approached both as a binary classification problem (disease vs. no disease) and as a multiclass classification task (different severity levels).

To illustrate the structure of the dataset, a subset of five patient records is presented in

Table 1. Sample of Patient Records with Variables and Target Outcome (UCI Heart Disease Dataset).

Age	Sex	Dataset	Cp	Trestbps	Chol	Fbs	Restecg	Thalch	Exang	Oldpeak	Slope	Ca	Thal	Num
63	Male	Cleveland	typical angina	145	233	True	lv hypertrophy	150	False	2.3	downsloping	0	fixed defect	0
67	Male	Cleveland	asymptomatic	120	229	False	lv hypertrophy	108	True	1.5	flat	3	normal	2
67	Male	Cleveland	asymptomatic	120	229	False	lv hypertrophy	129	True	2.6	flat	2	reversible defect	1
37	Male	Cleveland	non-anginal	130	250	False	normal	187	False	3.5	downsloping	0	normal	0
41	Female	Cleveland	atypical angina	130	204	False	lv hypertrophy	172	False	1.4	upsloping	0	normal	0

. These records include demographic, clinical, and diagnostic variables, along with the target outcome indicating the presence and severity of coronary artery disease.

Importantly, the dataset was compiled from multiple clinical centers, including Cleveland, Hungarian, Swiss, and VA Long Beach cohorts. This diversity enhances the dataset’s representativeness and allows for the evaluation of model generalization across heterogeneous populations. CAD presence was derived from the angiographic field num (attribute 58): 1 if num ≥ 1 (≥50% stenosis in any major vessel), otherwise 0 (num = 0). For severity, we mapped num to 1-vessel (1), 2-vessel (2), and ≥3-vessel (3–4). Per-vessel codes (attributes 59–68) were used only to cross-check labels; num remained the ground truth. The ca field (attribute 44) was not used for outcome definition, and records without a valid num were excluded. Because of these characteristics, the UCI Heart Disease Dataset is widely trusted by researchers. It serves as a common benchmark for developing machine learning algorithms. Researchers use it to compare models for coronary artery disease (CAD) prediction and early diagnosis.

2.2. Data Preprocessing

The raw dataset obtained from the UCI Machine Learning Repository was not ready for direct use in machine learning models and therefore required several preprocessing steps. Data preprocessing is a critical stage in the research workflow, as the quality and consistency of the data directly determine the reliability of model performance.

The first step consisted of encoding categorical variables. Machine learning algorithms require numerical input, and categorical or Boolean attributes must therefore be transformed into numeric representations. In this study, Label Encoding was employed, converting each category into an integer value [27]. Variables such as chest pain type, resting electrocardiogram results, sex, and thalassemia indicators were transformed in this way. This step standardized the data and enabled the model to interpret categorical features in a structured manner.

Feature scaling represented the next stage of preprocessing. Since variables were measured in different units, there was a risk that attributes with larger magnitudes could dominate the learning process. To resolve this, Z-score standardization was applied, which centers each feature at a mean of zero with a standard deviation of one [28]. The Z-score formula is expressed as

$$z={\displaystyle \frac{x-\mu }{\sigma }}$$

(1)

where x is an individual value, μ is the mean of the feature, and σ is the standard deviation. This transformation placed all features on a comparable scale and ensured a balanced contribution to the model training process.

After completing all preprocessing steps, the dataset was prepared for model training. To further understand the relevance of individual features in predicting heart disease, a mutual information (MI) analysis was conducted [29].

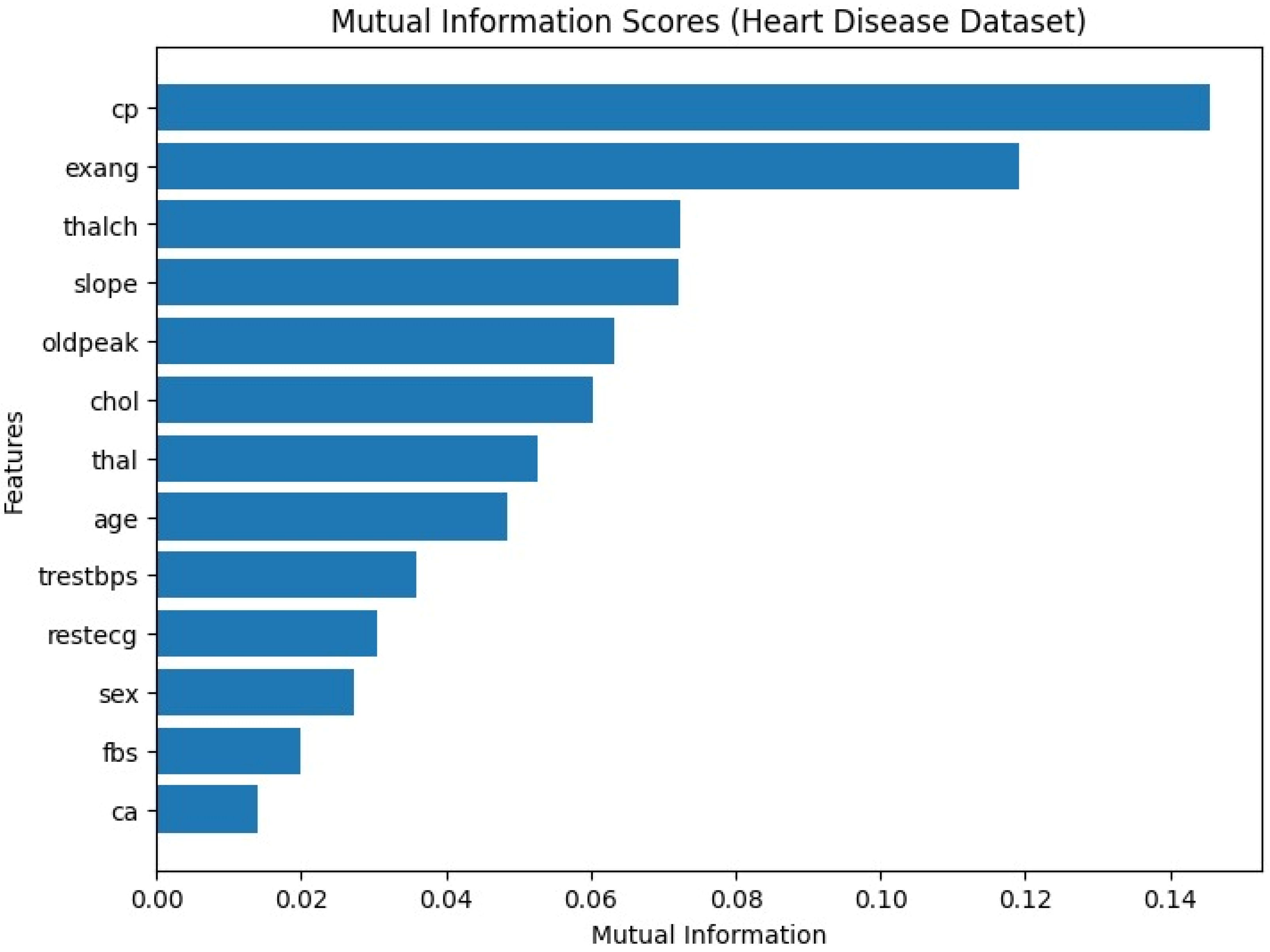
As shown in Figure 1 above, features such as chest pain type (cp), slope of the ST segment (slope), and ST depression induced by exercise (oldpeak) demonstrated the highest mutual information scores, indicating a strong relationship with the target variable. Conversely, attributes like resting electrocardiographic results (restecg) and resting blood pressure (trestbps) had relatively low scores, suggesting a weaker contribution to prediction. This analysis highlights which clinical and demographic features may carry the greatest predictive value, providing additional interpretability and clinical insight.

The next step involved splitting the dataset into training and testing subsets. Using the train_test_split method, 80% of the data was allocated to training and 20% to testing [30]. Such a division allowed for assessing the generalization ability of the models while reducing the risk of overfitting. The test set provided an independent basis for evaluating predictive accuracy under conditions resembling real-world applications.

To address the issue of class imbalance, the Synthetic Minority Oversampling Technique (SMOTE) was applied to the training data [31]. By generating synthetic samples of the minority class, SMOTE balanced the outcome distribution and improved the model’s ability to identify less frequent clinical cases. This approach reduced bias toward the majority class and strengthened the robustness of predictive performance. Importantly, oversampling was performed only on the training set to prevent information leakage, thereby preserving the independence of the test evaluation.

Through these preprocessing steps, the dataset was transformed into a consistent and structured format suitable for machine learning analysis. The resulting dataset facilitated the development of robust models and ensured that the outcomes were both statistically valid and clinically interpretable.

2.3. Machine Learning Classification

A diverse set of machine learning algorithms was applied to predict the presence and severity of coronary artery disease (CAD), allowing for a comprehensive comparison of different approaches. The use of multiple architectures made it possible to highlight the strengths and limitations of each model.

Boosting-based algorithms such as XGBoost [32], CatBoost [33], LightGBM [34], and HistGradientBoosting demonstrated strong predictive performance by building ensembles of decision trees and iteratively correcting errors [35]. CatBoost is particularly robust in handling categorical variables, LightGBM is optimized for large-scale data with fast computation, and HistGradientBoosting reduces memory usage through histogram-based binning, making it efficient for high-dimensional datasets.

Ensemble tree-based methods, including RandomForest and ExtraTrees [36,37], were also employed. RandomForest constructs multiple independent decision trees and combines their outputs through majority voting, thereby reducing variance and improving model stability. ExtraTrees introduces additional randomness in the construction process, increasing diversity among trees and enhancing generalization. As a simple baseline, the Decision Tree model was included [38], offering interpretability but showing limitations in handling complex, non-linear relationships.

Distance and margin-based models were further considered. The KNeighbors algorithm classifies new samples based on the most frequent label among their nearest neighbors [39]. While easy to understand and implement, KNN can be computationally demanding on large datasets. The Support Vector Machine (SVM) algorithm was also tested, which identifies an optimal hyperplane to maximize the margin between classes [22]. With its ability to use kernel functions, SVM is effective in modeling both linear and non-linear boundaries, making it well-suited for complex medical data.

Finally, Logistic Regression served as a classical statistical model, offering interpretability [40], efficiency, and reliability in binary classification tasks. Its established role in medical research provided a valuable baseline for comparison with more complex algorithms.

Taken together, this collection of models ensured a balanced evaluation, capturing both linear and non-linear patterns within the dataset. By integrating boosting, ensemble, distance-based, margin-based, and statistical methods, the analysis provided a strong benchmark for prediction and clinical insight.

Hyperparameter optimization was performed using GridSearchCV [41]. We implemented a leakage-safe pipeline comprising median imputation, SMOTE oversampling, feature scaling, and the classifier. Hyperparameter tuning was carried out with GridSearchCV (inner 3-fold) and generalization was estimated with an outer stratified 5-fold CV. All preprocessing (imputation, SMOTE, scaling) was fit inside training folds only.

The primary selection metric in GridSearchCV was Accuracy. The CatBoost search space was iterations ∈ {300, 500, 700}, depth ∈ {4, 6, 8}, learning_rate ∈ {0.01, 0.05, 0.1} (with random_state = 42, verbose = 0). Cross-validated performance was summarized over the outer folds for Accuracy, Precision, Recall, and F1. This method systematically evaluates combinations of parameter values under cross-validation to identify the configuration that yields the best performance. Effective hyperparameter tuning significantly improved model accuracy and reduced the risk of overfitting.

We addressed class imbalance using SMOTE applied strictly within training folds via imbalanced-learn’s Pipeline combined with GridSearchCV. All preprocessing (median imputation, standardization) and resampling were encapsulated in a single pipeline to avoid information leakage. Because SMOTE relies on k-nearest neighbors in feature space [42], features were standardized before oversampling. Model selection was performed inside an inner cross-validation loop, while the outer StratifiedKFold (5 folds, shuffled) provided an unbiased performance estimate (nested CV).

The models were evaluated using several widely accepted performance metrics [30]. Accuracy reflects the overall proportion of correctly classified samples and is given by:

$$\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

(2)

Precision measures the proportion of positive predictions that are truly correct:

$$\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}={\displaystyle \frac{TP}{TP+FP}}$$

(3)

Recall, or sensitivity, quantifies the proportion of actual positives correctly identified by the model:

$$\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}={\displaystyle \frac{TP}{TP+FN}}$$

(4)

The F1-score provides a harmonic mean of precision and recall, balancing the trade-off between them:

$$F1=2\times {\displaystyle \frac{\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\times \mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}}{\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}+\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}}}$$

(5)

Here, TP denotes true positives, TN true negatives, FP false positives, and FN false negatives. These metrics provide a solid numerical foundation for evaluating model quality, yet they alone cannot fully capture the nuances of prediction performance.

To complement these measures, the confusion matrix was analyzed, offering a more intuitive visualization of classification outcomes [43]. This matrix summarizes the counts of true positives, true negatives, false positives, and false negatives, thereby revealing where the models excel and where misclassifications occur. This analysis is especially important in medical applications. It emphasizes the need to correctly identify patients with CAD. At the same time, it aims to minimize false alarms for healthy individuals. By examining the confusion matrix, the trade-off between sensitivity and specificity becomes clearer before progressing to more advanced evaluation metrics.

Beyond these standard metrics, models were further assessed using the ROC-AUC curve [30]. The Receiver Operating Characteristic (ROC) curve illustrates the trade-off between the true positive rate (TPR) and the false positive rate (FPR) across varying threshold values. The area under the curve (AUC) serves as a global measure of discriminative ability, with 0.5 representing random guessing and 1.0 indicating perfect classification. The ROC-AUC score thus provides a comprehensive evaluation of a model’s ability to distinguish between positive and negative cases.

Calibration analysis was also performed using the reliability curve [44]. This plot compares the predicted probabilities of positive outcomes against their observed frequencies. An ideally calibrated model will produce probabilities that align closely with actual outcomes, represented by the diagonal line in the calibration plot. For example, if the model predicts a 0.8 probability of disease, then approximately 80% of those cases should indeed have CAD. Calibration plots are particularly valuable in clinical decision-making, where probability estimates guide diagnostic and therapeutic strategies.

The Brier Score evaluates a probabilistic classifier’s calibration and absolute accuracy (lower is better). It is computed as

$$BS={\displaystyle \frac{1}{N}}\sum _{i=1}^N{(\widehat{p_i}-y_i)}^2$$

(6)

where $\widehat{p_i}$ is the predicted probability for the positive class and $y_i\in \left\{0,1\right\}$ is the true label.

Predicted probabilities were used to quantify whether they reflected true risk (good calibration), complementing rating measures such as ROC-AUC, and supporting a robust clinical risk-based decision-making process.

To enhance interpretability, SHAP (SHapley Additive Explanations) analysis was employed [45]. SHAP values are grounded in cooperative game theory and assign an additive contribution of each feature to the final prediction. This allows for a transparent understanding of the relative importance of variables such as age, cholesterol, blood pressure, ST-segment changes, and exercise-induced angina. SHAP not only identifies which features drive predictions but also quantifies their impact for each individual patient. This interpretability builds clinical trust and offers physicians actionable insights, bridging prediction with medical relevance.

The study combined multiple models to enhance reliability and applied rigorous hyperparameter tuning with comprehensive evaluation metrics. It further used ROC-AUC curves, calibration plots, and SHAP analysis to support detailed assessment, creating a cohesive and robust framework for evaluating predictive performance. This evaluation strategy emphasized not only the numerical accuracy of the models but also their reliability, clinical applicability, and transparency.

3. Results

The comparison of different machine learning models provided valuable insights into their effectiveness in predicting coronary artery disease (CAD). The dataset was preprocessed and each model was trained and evaluated under the same conditions. Performance was assessed using four key metrics: Accuracy, representing the overall proportion of correctly classified cases; Precision, reflecting the proportion of predicted positives that were correct; Recall, indicating the ability of the model to identify actual positive cases; and F1 Score, which balances precision and recall into a single measure. These metrics are particularly important in the medical domain, where both false negatives and false positives carry significant implications [46].

Ensemble and boosting approaches demonstrated stronger performance compared to simpler linear or single-tree models. This highlights the advantage of ensemble learning in capturing complex relationships within clinical data. In particular, RandomForest, CatBoost, and HistGradientBoosting achieved the highest levels of balanced performance, combining strong accuracy with robust recall and precision. In contrast, simpler models such as Logistic Regression and Decision Tree produced lower scores, although they remain useful for interpretability and as baseline comparisons. The KNeighbors classifier showed relatively strong precision but reduced recall, underlining its limitations in consistently identifying all positive cases.

The detailed results for each model are summarized in

Table 2. Classification results of various machine learning models with 95% confidence intervals calculated using the Bootstrap method.

Model	Accuracy	Precision	Recall	F1 Score
XGBoost	0.8217 [0.7946, 0.8467]	0.8436 [0.8139, 0.8755]	0.8288 [0.7949, 0.8619]	0.8371 [0.8122, 0.8596]
CatBoost	0.8278 [0.8011, 0.8522]	0.8467 [0.8135, 0.8767]	0.8407 [0.8095, 0.8717]	0.8436 [0.8167, 0.8669]
KNeighbors	0.8190 [0.7946,0.8424]	0.8574 [0.8263, 0.8877]	0.8064 [0.7723, 0.8384]	0.8310 [0.8045, 0.8541]
ExtraTrees	0.8216 [0.8076, 0.8544]	0.8423 [0.8212, 0.8825]	0.8314 [0.8082, 0.8704]	0.8367 [0.8215, 0.8699]
LGBMClassifier	0.8191 [0.7924, 0.8435]	0.8407 [0.8091, 0.8718]	0.8308 [0.7960, 0.8630]	0.8356 [0.8085, 0.8585]
RandomForest	0.8186 [0.7945, 0.8424]	0.8257 [0.7926, 0.8580]	0.8524 [0.8223, 0.8816]	0.8386 [0.8147, 0.8626]
Decision Tree	0.7579 [0.7293, 0.7837]	0.7818 [0.7459, 0.8161]	0.7799 [0.7442, 0.8128]	0.7807 [0.7528, 0.8073]
HistGradientBoosting	0.8132 [0.7880, 0.8380]	0.8378 [0.8057, 0.8707]	0.8213 [0.7886, 0.8517]	0.8293 [0.8038, 0.8526]
Logistic Regression	0.8142 [0.7891, 0.8380]	0.8490 [0.8160, 0.8776]	0.8077 [0.7736, 0.8410]	0.8277 [0.8012, 0.8516]
SVM	0.8230 [0.7978, 0.8479]	0.8405 [0.8079, 0.8713]	0.8393 [0.8158, 0.8724]	0.8398 [0.8158, 0.8646]

.

This table presents the classification results of various machine learning models, with 95% confidence intervals calculated using the Bootstrap method. The table includes the metrics Accuracy, Precision, Recall, and F1 Score, which reflect the average performance of each model, and the confidence intervals allow for assessing the variability of model performance.

The XGBoost model shows deviations of (+/−0.0339) for Accuracy, (+/−0.0329) for Precision, (+/−0.0480) for Recall, and (+/−0.0328) for F1 Score. The model demonstrates very stable performance with high reliability.

The CatBoost model shows deviations of (+/−0.0272) for Accuracy, (+/−0.0238) for Precision, (+/−0.0407) for Recall, and (+/−0.0267) for F1 Score. This model also performs well, but slightly lower than XGBoost.

The KNeighbors model shows deviations of (+/−0.0193) for Accuracy, (+/−0.0169) for Precision, (+/−0.0341) for Recall, and (+/−0.0205) for F1 Score. The model’s performance is at a moderate level.

The ExtraTrees model shows deviations of (+/−0.0277) for Accuracy, (+/−0.0249) for Precision, (+/−0.0421) for Recall, and (+/−0.0271) for F1 Score. This model demonstrates stable and high performance.

The LGBMClassifier model shows deviations of (+/−0.0177) for Accuracy, (+/−0.0160) for Precision, (+/−0.0472) for Recall, and (+/−0.0206) for F1 Score. This model also exhibits high performance.

The RandomForest model shows deviations of (+/−0.0352) for Accuracy, (+/−0.0280) for Precision, (+/−0.0458) for Recall, and (+/−0.0328) for F1 Score. The model performs well but exhibits slightly higher deviations compared to others.

The Decision Tree model shows deviations of (+/−0.0232) for Accuracy, (+/−0.0258) for Precision, (+/−0.0968) for Recall, and (+/−0.0358) for F1 Score. The Recall is high, but other metrics are lower.

The HistGradientBoosting model shows deviations of (+/−0.0252) for Accuracy, (+/−0.0331) for Precision, (+/−0.0483) for Recall, and (+/−0.0249) for F1 Score. This model also produces good results.

The Logistic Regression model shows deviations of (+/−0.0455) for Accuracy, (+/−0.0343) for Precision, (+/−0.0602) for Recall, and (+/−0.0454) for F1 Score. The Recall is very high, but other metrics are slightly lower.

The SVM model shows deviations of (+/−0.0232) for Accuracy, (+/−0.0209) for Precision, (+/−0.0242) for Recall, and (+/−0.0210) for F1 Score. This model performs at the lowest level compared to the others.

The CatBoost model was identified as the best-performing approach for predicting coronary artery disease (CAD). Its consistent results across various evaluation metrics, including Accuracy, Precision, Recall, and F1 Score, highlighted its ability to effectively capture complex, non-linear relationships within clinical and demographic data. The CatBoost model outperformed other models in supporting medical decision-making. It provided stable and reliable predictions across diverse patient populations, demonstrating its superior potential for clinical application. These characteristics indicate that CatBoost is not only effective in detecting the presence of CAD but also holds promise for evaluating its severity. This makes it a highly valuable tool for clinical applications, early diagnosis, and risk stratification in healthcare practice, where its stable performance offers great potential for real-world implementation.

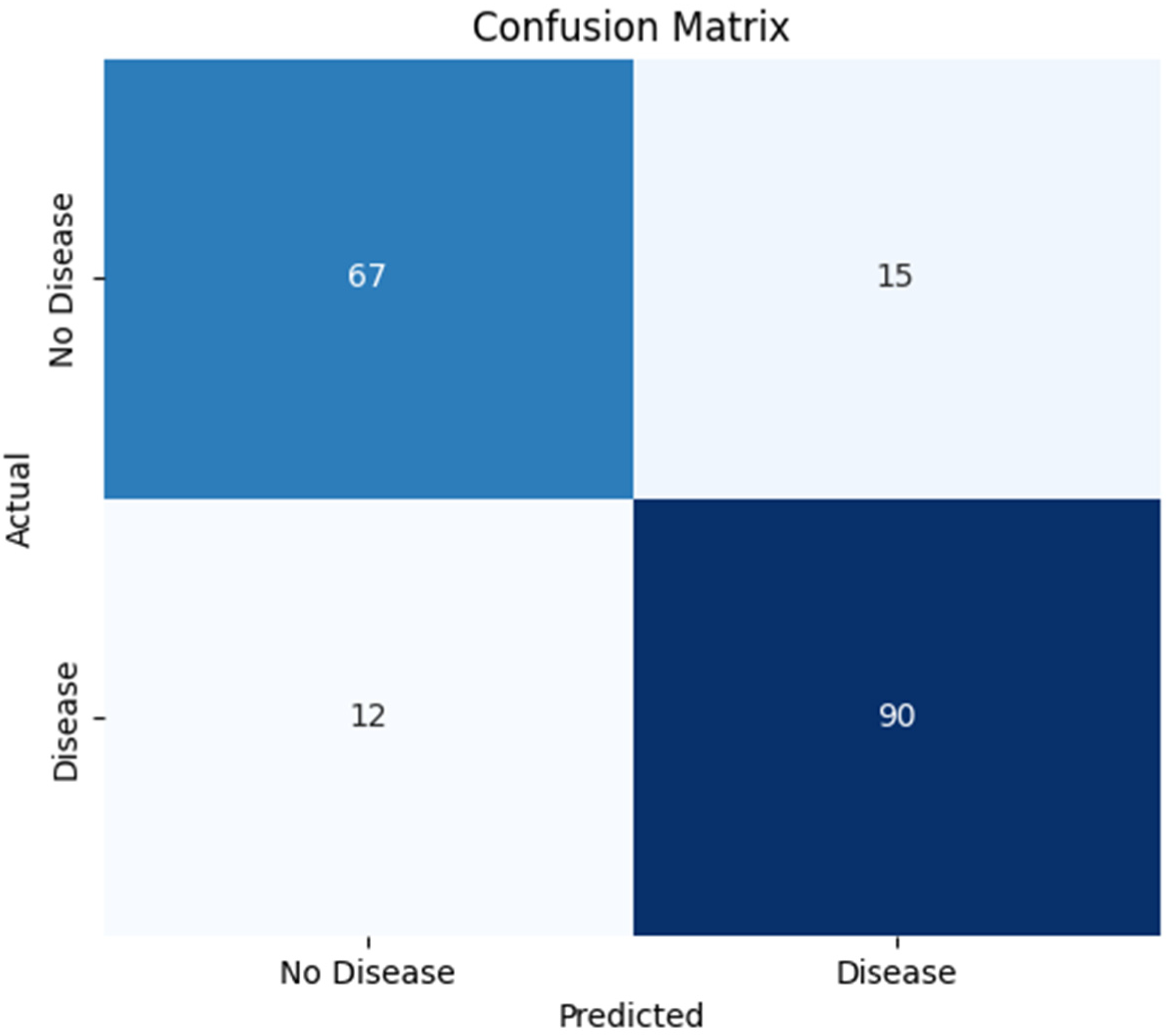
The Confusion Matrix, in Figure 2, is a widely used tool for evaluating the performance of classification models. It allows for a comparison between correct and incorrect predictions. The key metrics include True Positive (TP), True Negative (TN), False Positive (FP), and False Negative (FN). This method provides insights into accuracy, sensitivity (recall), specificity, and the overall error rate.

The confusion matrix of the CatBoost model shows that it correctly identified 67 patients as not having CAD (true negatives) and 90 patients as having CAD (true positives). The number of misclassifications was relatively low: 15 cases were incorrectly predicted as having CAD when they did not (false positives), and 12 patients with CAD were incorrectly classified as healthy (false negatives). These outcomes indicate that the CatBoost classifier maintains a solid trade-off between sensitivity and specificity.

In particular, the low number of false negatives highlights the model’s clinical value by ensuring that most patients with CAD are accurately detected, minimizing the chance of undiagnosed conditions. Meanwhile, the moderate false positive rate suggests that the model limits over-diagnosis and avoids unnecessary follow-up procedures. Overall, this confusion matrix demonstrates the robustness and reliability of the CatBoost algorithm, underscoring its potential for real-world clinical decision support in identifying coronary artery disease [30].

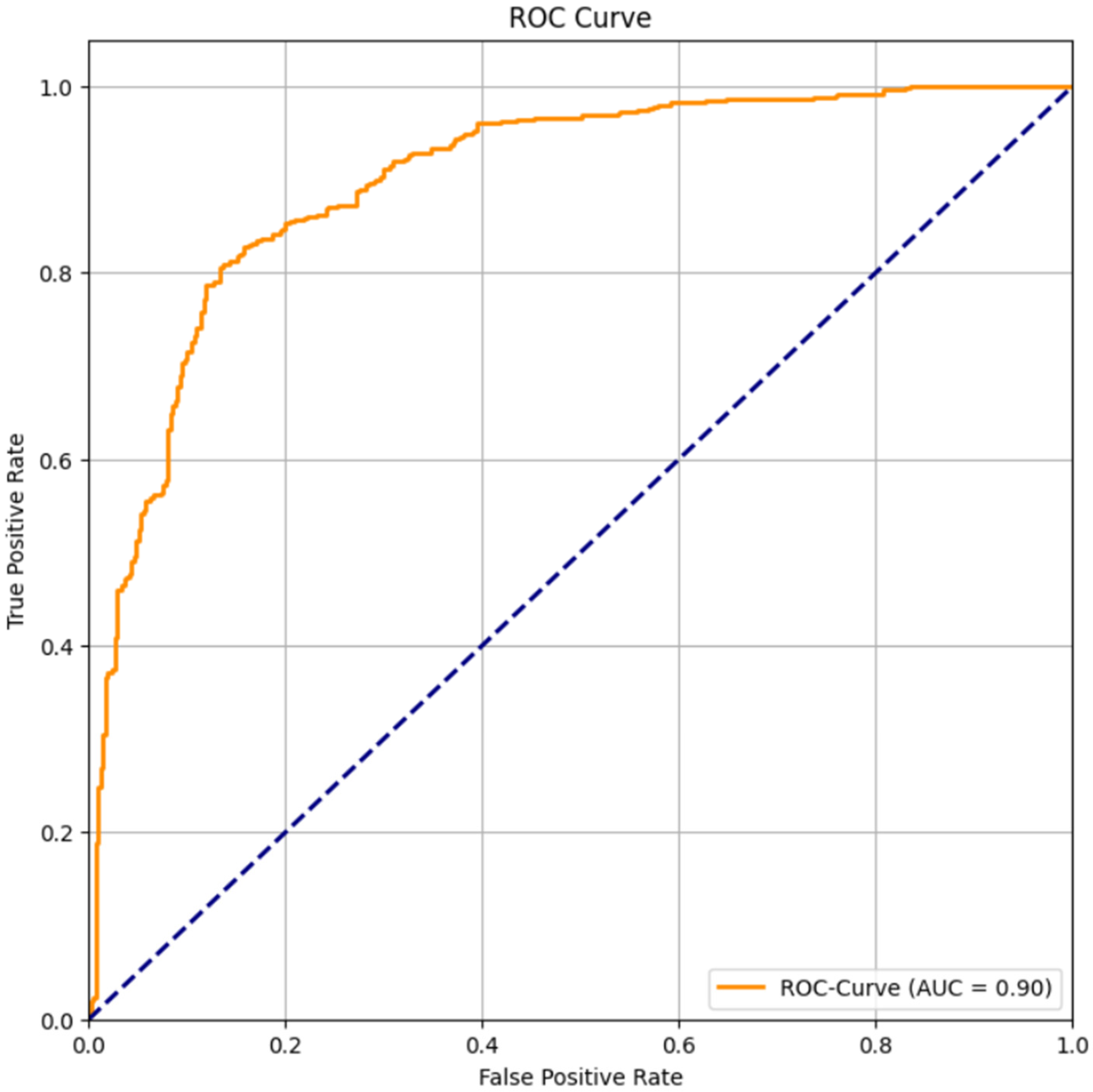
The Receiver Operating Characteristic (ROC) Curve is used to evaluate a classifier’s performance across different threshold values. It represents the trade-off between the true positive rate (sensitivity) and the false positive rate (1-specificity). The Area Under the Curve (AUC) quantifies the overall discriminatory power of the model: 0.5 indicates random performance, while 1.0 indicates a perfect classifier.

The ROC curve obtained for the CatBoost classifier yielded an AUC value of 0.90, demonstrating an excellent ability to discriminate between patients with and without CAD. In Figure 3, the curve lies well above the diagonal baseline, confirming that the CatBoost model performs significantly better than random guessing. This high AUC value indicates that CatBoost can accurately identify both CAD-positive and CAD-negative individuals, showing a reliable balance between sensitivity and specificity. From a clinical perspective, such model performance is highly valuable as it enhances early disease detection and reduces misclassification risks. AUC values exceeding 0.9 are generally considered outstanding in medical diagnostics, highlighting CatBoost’s robustness and reliability. Therefore, the ROC curve results suggest that the CatBoost classifier is a powerful predictive model for CAD diagnosis and has strong potential for deployment in real-world clinical decision-support systems.

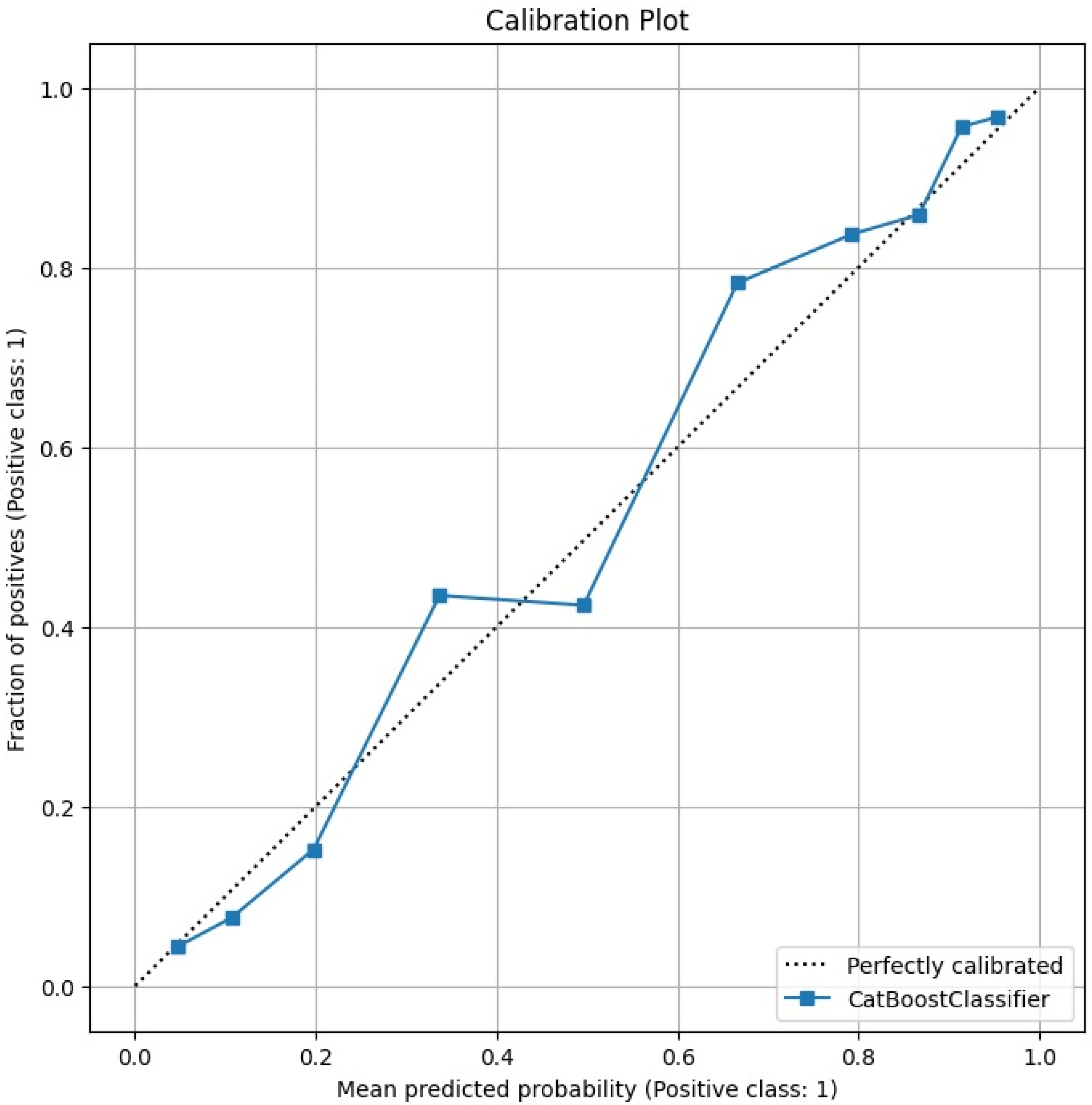
The Calibration Plot in Figure 4 assesses how well the predicted probabilities of the model correspond to actual outcomes. It compares the predicted probability with the observed frequency of positive cases. Ideally, the calibration curve should align with the diagonal line, indicating perfect calibration.

The calibration plot of the CatBoost model shows that the predicted probabilities are well aligned with the observed fraction of positive cases. The curve closely follows the diagonal reference line, which represents perfect calibration. This alignment indicates that the CatBoost classifier produces probability estimates that are both accurate and interpretable. This alignment suggests that the model’s confidence reliably reflects the true likelihood of coronary artery disease (CAD).

From a clinical perspective, such well-calibrated probability outputs are highly valuable, as they enable physicians to make informed, risk-based decisions. For example, patients with higher predicted probabilities of CAD can be prioritized for additional testing or preventive treatment.

The quantitative assessment supports the visual impression: the Brier Score is 0.1252, indicating a low mean squared error of the predicted probabilities and overall good calibration. These calibration results confirm that the CatBoost model not only delivers strong classification performance but also provides trustworthy probability estimates, reinforcing its suitability for real-world diagnostic and decision-support applications.

SHAP (SHapley Additive exPlanations) is a method that explains model predictions by attributing contributions of each feature through Shapley values. It quantifies how each variable influences the model’s output. In medical applications, SHAP is particularly useful for interpreting the clinical and demographic factors that drive the prediction.

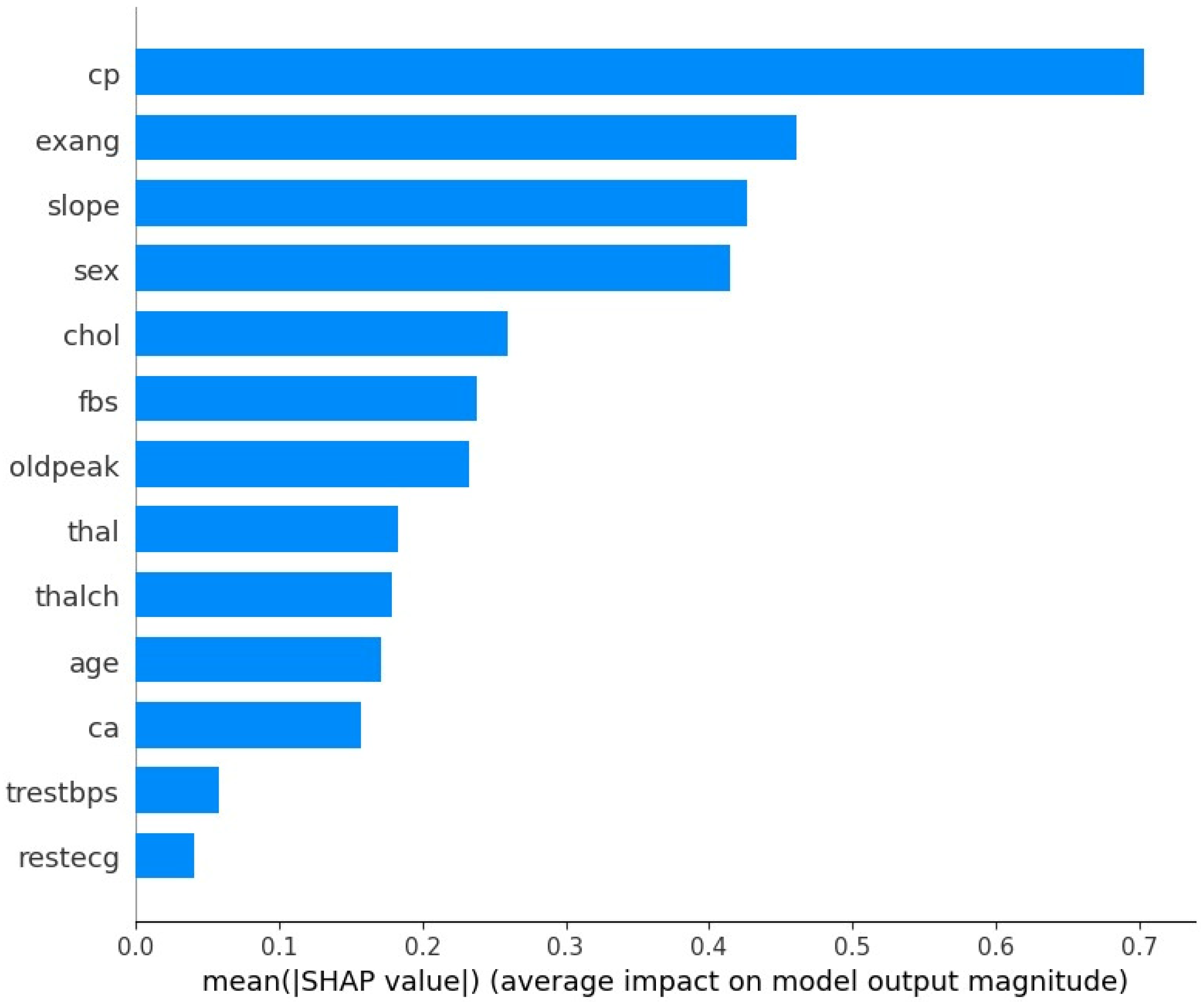
The SHAP feature importance analysis, in Figure 5, for the CatBoost model highlights several clinical and demographic variables as the most influential predictors of coronary artery disease (CAD). Variables such as chest pain type (cp), exercise-induced angina (exang), and slope of the peak exercise ST segment (slope) emerged as the most impactful predictors. This finding is consistent with established medical knowledge, as these factors are recognized as key risk indicators for CAD. The SHAP plot not only ranks the features but also provides insight into the direction of their impact, demonstrating how changes in these variables influence the likelihood of CAD. This interpretability is crucial for clinical applications, as it enables healthcare professionals to validate model predictions based on domain expertise and communicate risk factors effectively to patients [47]. The results underscore the robustness of the CatBoost model by confirming that its predictions are driven by medically relevant features, making it a reliable tool for CAD diagnosis.

The findings of this study clearly demonstrate the effectiveness of machine learning algorithms in predicting the presence and severity of coronary artery disease (CAD) based on clinical and demographic data. A comparison of different models, as presented in the table, showed that the CatBoost ensemble and boosting approach achieved the highest performance, outperforming other methods including XGBoost, LightGBM, and SVM. CatBoost recorded the best Accuracy (0.8278) and the highest F1 Score (0.8436).

These results highlight the advantage of advanced ensemble models in capturing complex, non-linear relationships. Specifically, the strong predictive performance of CatBoost, along with other high-performing models like KNeighbors (Accuracy 0.8190) and ExtraTrees (Accuracy 0.8216), suggests their capability to predict not only the presence of CAD but also its severity with high precision. Integrating such powerful models into diagnostic workflows can enable earlier detection, more precise risk stratification, and ultimately better patient outcomes.

4. Discussion

Among the machine learning models compared, the CatBoost model demonstrated the best balance of performance, with its F1 Score being 0.8436 (confidence interval: [0.8167, 0.8669]). The model’s Accuracy was 0.8278 (confidence interval: [0.8011, 0.8522]). This performance suggests potential for clinical screening diagnosis of CAD, especially where it is critical not to miss true CAD cases (i.e., high Recall). The deviations for the CatBoost model based on the confidence interval are (0.02555) for Accuracy and (0.0251) for F1 Score, indicating its stable and reliable performance.

The CatBoost model demonstrated a high degree of discriminatory power, evidenced by a ROC–AUC of 0.90. This result signifies the model’s excellent ability to distinguish between patients with and without CAD.

The confusion matrix further supports these findings: the model correctly identified 90 patients as having CAD (True Positives) and 67 patients as not having CAD (True Negatives). The number of misclassifications was relatively low: 15 cases were incorrectly predicted to have CAD when they did not (False Positives), and 12 patients with CAD were incorrectly classified as healthy (False Negatives).

This matrix shows a favorable trade-off between sensitivity and specificity, supported by the low number of false negatives (12). Minimizing false negatives is crucial for frontline use as it reduces the chance of overlooking patients who require further investigation. Clinical prediction papers increasingly recommend reporting both discrimination and calibration together (e.g., calibration plots and Brier score) to ensure probabilities can be interpreted as risk, not only ranks.

CatBoost’s advantage likely arises from its ability to capture non-linear relationships and higher-order interactions that are common in tabular clinical data. The gradient boosting approach employed by CatBoost helps model complex decision boundaries while maintaining good generalization when hyperparameters are tuned via cross-validation. Other ensemble learners, such as Random Forest and XGBoost, also showed competitive performance. However, the CatBoost model demonstrated the most robust performance profile. It achieved the highest F1 Score (0.8436) and maintained a stable balance between sensitivity and specificity in our experimental setting. This stability is critical when a model is intended to support early risk stratification rather than definitive diagnosis. On tabular clinical datasets, tree-based boosting methods frequently outperform deep or linear baselines, reinforcing our choice of CatBoost for structured CAD risk factors.

From a clinical decision-making perspective, the error profile is encouraging. The relatively low number of false negatives reduces the chance of overlooking patients who may require further investigation, while the moderate number of false positives limits unnecessary downstream testing. In practice, the operating threshold can be adjusted to prioritize either sensitivity or specificity depending on the intended use case. Because the AUC is high, the model affords headroom to shift the threshold toward even lower false negatives in screening scenarios without catastrophic loss of precision. To quantify whether a chosen operating point would improve outcomes versus “treat-all” or “treat-none,” decision-curve analysis (net benefit) is recommended alongside ROC metrics [48].

A noteworthy limitation, identified in the introduction as a challenge for prior research, is the modest sample size and class imbalance common to many benchmark medical datasets, including the UCI cohorts. While the present study employed a harmonized, multi-center dataset to enhance representativeness, these constraints directly informed the study’s methodological design. The critique regarding small sample sizes is particularly pertinent to data-intensive deep learning approaches. Consequently, this work deliberately focused on machine learning algorithms renowned for their strong performance and robustness on smaller, imbalanced and tabular datasets, specifically gradient boosting [49] and ensemble learning models [49,50,51]. To simultaneously address the co-existing challenge of class imbalance, the SMOTE was applied. Critically, this was performed exclusively on the training subset as part of a standardized processing pipeline. This methodological step is essential for preventing information leakage and avoiding the over-optimistic bias that can arise from improper oversampling. The superior results demonstrated by CatBoost validate this combined approach. Moreover, the objective of this study was not merely to achieve incremental gains in standard accuracy metrics, a focus of many preceding studies. The primary contribution lies in the application of this rigorous, standardized processing pipeline and a comprehensive evaluation of the model’s technical performance and potential utility. By moving beyond standard metrics to analyze probability calibration curves and patient-level SHAP explainability, this study demonstrates that it is possible to develop a reliable and interpretable model, even within the constraints of limited data.

While many studies, such as those by Teja and Rayalu (2025) [17] and Akella and Akella (2021) [14], focus primarily on standard performance metrics like accuracy, our work emphasizes model reliability and interpretability. The central research question was not just whether we could predict CAD but also whether we could do so in a reliable and transparent manner. This study’s key distinction lies in its comprehensive evaluation of model calibration and explainability. We confirmed through calibration plots that the CatBoost model’s probability estimates are reliable and well-aligned with actual patient outcomes. This is a crucial, often-overlooked step that is essential for building clinical trust, as it validates the trustworthiness of the model’s risk predictions. Moreover, our use of SHAP bridges the “black box” gap by demonstrating that the model’s predictions are driven by clinically significant predictors, such as chest pain type (cp), exercise-induced angina (exang), and slope of the peak exercise ST segment—factors well-established in clinical practice. This explainability is a first step toward building the clinical trust required for potential adoption.

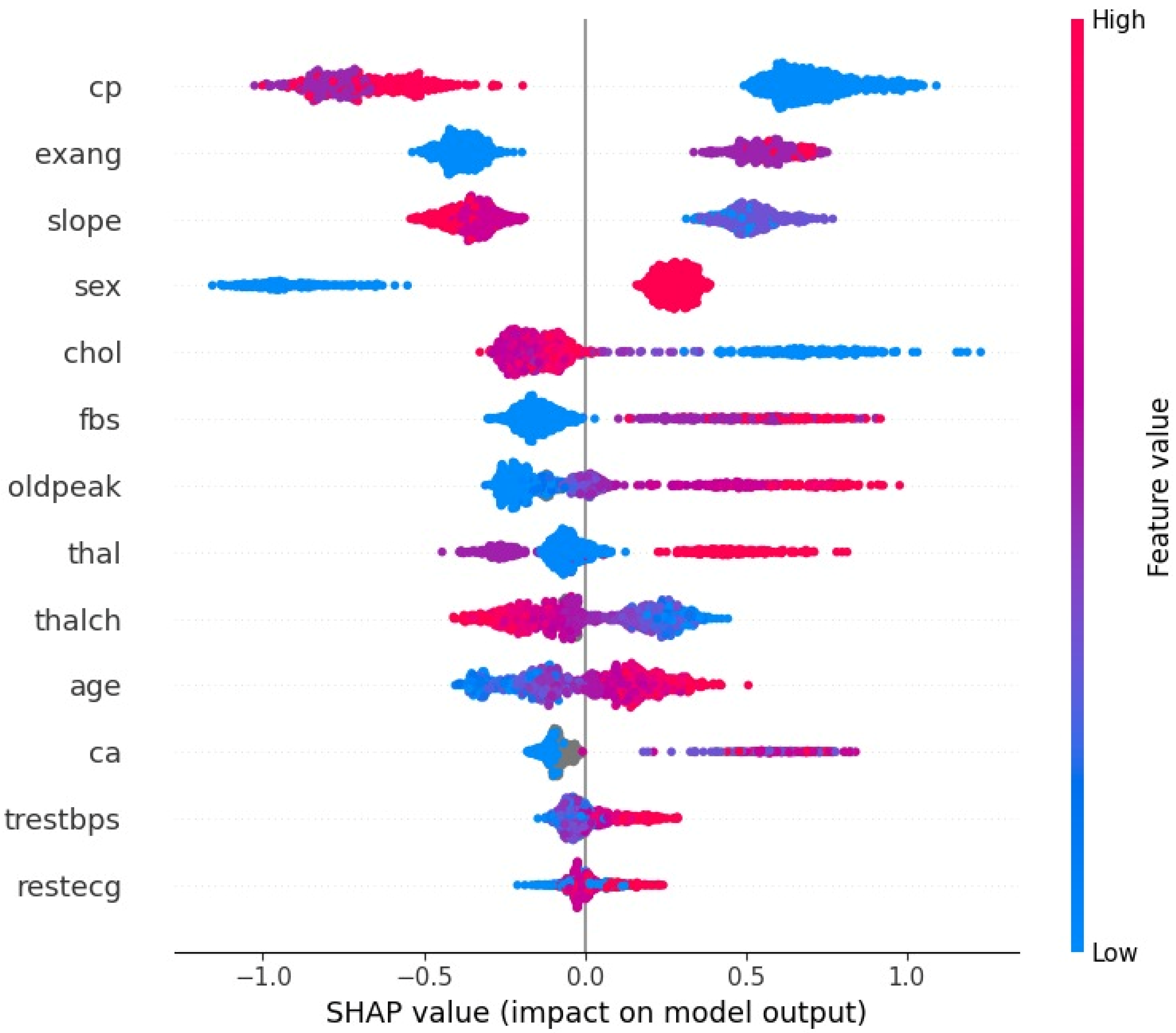
As shown by the SHAP summary plot in Figure 6, variables such as cp (chest pain type), exang (exercise-induced angina), slope (slope of the peak exercise ST segment), and sex exert a significant and directional influence on the model’s output. Specifically, oldpeak, exang, and ca are among the most important factors. Higher values of the oldpeak variable (indicating greater post-exercise ST-segment depression) are clustered with positive SHAP values (increasing the predicted probability of CAD), which aligns with clinical evidence that ST depression is a hallmark of obstructive coronary disease. The presence of exang (yes/true) and an increase in ca (the number of major vessels visualized by fluoroscopy) also push predictions toward CAD, consistent with the clinical meaning of multivessel involvement and higher risk. Furthermore, lower values of the slope variable (downsloping or flat ST segment) increase the risk of CAD, while a higher value of the sex variable (1 = male) indicates an increased risk of CAD. This concordance between SHAP patterns and cardiology fundamentals indicates that the model is leveraging clinically meaningful signals. The factors such as high oldpeak, the presence of exang, and ca ± 1 reliably shift a patient into a high-risk stratum.

These findings are broadly consistent with prior reports that ensemble tree methods tend to perform strongly on structured clinical datasets and that classic risk factors and stress-test markers dominate model importance. The present work adds to that literature by coupling strong discrimination with careful calibration assessment and case-level interpretability. In cardiology, SHAP has already been shown to enhance interpretation of model drivers and to support expert review of predictions [52].

Several limitations warrant consideration. First, although the dataset is multi-center and heterogeneous, it remains an open repository; external, geographically distinct validation is necessary before routine deployment. Second, the feature set does not include contemporary imaging metrics or advanced biomarkers, which may capture phenotypes not fully represented here. Third, class imbalance was addressed with SMOTE on the training split only, which is methodologically appropriate but can still distort decision boundaries; prospective evaluation is needed. Resampling to fix class imbalance (e.g., SMOTE) can worsen calibration and overestimate minority-class risk if applied incautiously, so recalibration and careful audit are needed after any oversampling [53]. Fourth, while the target allows gradations of disease severity, most analyses focus on a binary endpoint; a dedicated severity model should be developed and assessed. Finally, potential domain differences between contributing centers suggest that performance audits by site and subgroup fairness analyses by age and sex are important next steps.

5. Conclusions

This study successfully demonstrated that an explainable machine learning framework can reliably predict the presence of CAD using only routine clinical and demographic data from a harmonized, multi-center UCI repository. Through a standardized and methodologically rigorous pipeline, we demonstrated that the CatBoost algorithm yields strong predictive performance, achieving an F1-score of 0.8436, an accuracy of 0.8278, and an excellent discriminatory capacity with a ROC-AUC of 0.90.

Crucially, we moved beyond standard performance metrics to address the clinical requirement for trust and interpretability. The comprehensive SHAP explainability analysis confirmed the reliability of the model’s decisions. The results showed that the model’s predictions are influenced by key factors such as chest pain type, exercise-induced angina, and the slope of the peak exercise ST segment. Furthermore, analysis of the calibration curve confirmed that the model’s predicted probabilities are reliable and well-aligned with observed patient outcomes.

The findings carry significant implications for clinical practice and resource management. The ability of an interpretable model, built exclusively on inexpensive, routine tabular data, to achieve high performance suggests a scalable solution for initial risk stratification. In settings where advanced, costly, or invasive diagnostic tools such as angiography and advanced imaging are scarce or inaccessible, this predictive framework can act as a low-cost triage tool. The model can assist front-line clinicians in prioritizing patients who require immediate and costly specialist referral. It can also help identify patients who may be safely managed through conservative follow-up. This approach can optimize resource allocation and reduce diagnostic delays in clinical practice. The established link between the model’s feature importance (via SHAP) and clinical knowledge also serves to build the necessary physician confidence, paving the way for the eventual integration of such tools into electronic health record decision-support systems.

Despite the promising results and strong internal validation, the limitations of this work, which relies on a historical, open-source dataset, define a clear roadmap for subsequent research. Future work should therefore prioritize external and prospective validation, decision-curve analysis to quantify net clinical benefit, formal threshold setting aligned with care pathways, and subgroup fairness audits. Methodologically, isotonic or Platt scaling could further refine calibration, and multimodal extensions that integrate imaging and laboratory biomarkers may improve sensitivity for atypical or silent presentations. A pilot implementation within an electronic health record to assess workflow fit, alert fatigue, and time-to-diagnosis could provide the strongest evidence of clinical utility.