Abstract
We investigate hybrid quantum–classical solvers for nonlinear boundary value problems using Chebyshev spectral collocation. Unlike prior methods such as H–DES, which repeatedly recompile circuits and encode the entire spectral basis on the quantum processor, our framework offloads only the residual minimisation to a quantum backend while retaining classical enforcement of boundary conditions. Two paradigms are considered: (i) gate-based residual minimisation on CUDA-Q using variational circuits to evaluate a Cubic Unconstrained Binary Optimisation (CUBO) cost, which naturally arises from the discretisation, and (ii) a Quadratic Unconstrained Binary Optimisation (QUBO) reformulation, which is required for execution on a quantum annealer, executed via a classical–quantum mapping. We further explore a CUBO extension on CUDA-Q and direct residual-to-energy mapping on annealers. Benchmarks confirm that the classical solver reproduces the analytic solution with spectral accuracy; among quantum-enhanced methods, the annealer-based QUBO yields the closest approximation. The gate-based CUBO solver improves upon a legacy variational baseline but exhibits a small interior bias due to limited circuit depth and precision. These findings underscore the complementary roles of annealers and gate-based devices in hybrid scientific computing and demonstrate a feasible workflow for the NISQ era rather than a speedup over classical methods. Recent progress in quantum algorithms for differential equations signals a rapidly maturing field with significant potential for practical quantum advantage.
1. Introduction and Motivation
Numerical solutions of boundary value problems (BVPs) are indispensable across physics, engineering, and finance [1]. Classical discretisation techniques—finite differences, finite elements, and spectral methods—have been refined over decades to deliver high accuracy and scalability [2,3]. Nonetheless, some nonlinear partial differential equations (PDEs) pose challenges for classical solvers because the cost of assembling and inverting dense Jacobian matrices scales poorly with problem size or nonlinearity [4]. Quantum computing promises polynomial or exponential speedups for particular linear algebraic tasks [3,5,6], motivating interest in quantum-accelerated numerical methods.
The present quantum hardware landscape is described as the noisy intermediate-scale quantum (NISQ) era [7]. Devices in this class contain hundreds to roughly a thousand qubits and are not yet fault-tolerant; they are prone to decoherence and cannot perform continuous error correction [7]. Practical algorithms for NISQ systems therefore need to minimise circuit depth and shot count [8]. Hybrid quantum–classical algorithms, notably the variational quantum eigensolver (VQE) [8] and quantum approximate optimisation algorithm (QAOA) [9], couple classical optimisation with quantum state preparation and measurement. Differential equation solvers built on the variational paradigm are a logical extension: they rely on parameterised quantum circuits (ansätze) and iterative classical feedback to minimise a cost function derived from the governing PDE [10,11].
Dual Paradigm Comparison. In this study we contrast two quantum paradigms—gate-based variational circuits and quantum annealing—within a common hybrid framework that offloads only the residual minimisation. Each paradigm is evaluated in its natural encoding regime: CUBO-style cost functions on gate-based devices and QUBO formulations on annealers. This unified perspective highlights complementary strengths and guides the design of practical hybrid solvers.
Recent advances in quantum algorithms for differential equations have demonstrated various approaches. Kyriienko et al. [10] pioneered quantum spectral methods using Chebyshev quantum feature maps for nonlinear differential equations. Leong et al. [11] developed variational quantum evolution equation solvers using implicit time-stepping schemes. More recently, Leong et al. provided rigorous error analysis for VQA-based differential equation solvers using Runge–Kutta methods, while Arora et al. [12] introduced the Quantum Finite Element Method (Q-FEM) using VQLS algorithms. We also cite very recent works by Tennie and Magri [13], Zhang and Shao [14], Berry and Costa [15], and Mizuno and Komatsuzaki [16], which further develop quantum approaches to differential equations in 2024–2025.
It is important to emphasise at the outset that the present work does not aim to outperform well-established classical solvers. On today’s NISQ hardware, communication overhead between quantum and classical processors, limited qubit counts, and the need for repeated sampling typically negate any potential speedup for small-to-medium problems [7]. Rather, the goal is to demonstrate a feasible hybrid workflow—combining classical spectral discretisation with quantum evaluation of a simple observable—and to identify the challenges that must be overcome before hybrid quantum solvers can deliver practical benefits. The current solver thus serves as a prototype: it highlights the roles of classical and quantum components, underscores the importance of efficient ansatz design, and provides a platform for investigating how future advances in hardware and algorithms might enable quantum assistance for computationally intensive problems.
In addition to advances in quantum–classical algorithms, prior work by the present author has emphasised reproducibility, benchmarking, and performance optimisation of spectral and FFT-based applications in high-performance computing [17,18,19,20,21]. Such efforts underscore the importance of connecting algorithmic advances with practical performance evaluation, and they motivate our present exploration of hybrid spectral solvers that integrate quantum backends while maintaining classical efficiency.
Prior Work
Lubasch et al. demonstrated that nonlinear PDEs can be addressed by variational quantum algorithms that use multiple copies of quantum states and tensor networks [22]. Their proof-of-concept implementation treated the nonlinear Schrödinger equation and showed that the variational ansatz can outperform classical matrix product state representations. More recently, Sarma et al. extended these ideas to nonlinear and multidimensional PDEs such as the Black–Scholes and Kardar–Parisi–Zhang equations, using up to twelve ansatz qubits and testing on a trapped-ion processor [23].
Jaffali et al. proposed H–DES, a hybrid differential equation solver that encodes the entire solution function into the amplitudes of a quantum state through a spectral decomposition and optimises circuit parameters variationally [24]. Their method includes pseudocode and a complexity analysis, and it demonstrates applicability to several PDEs. H–DES performs the spectral expansion on the quantum processor, which can lead to significant circuit depth and recompilation overhead for each iteration.
On the classical side, Chebyshev spectral methods offer exponential convergence for smooth solutions [2]. Collocation at Chebyshev–Gauss–Lobatto (CGL) points clusters nodes near the boundaries, where solution gradients are often largest [25]. In the collocation approach, the continuous residual is forced to zero at discrete nodes, converting a differential equation into a system of algebraic equations. This technique can achieve high accuracy with a modest number of points [2].
While these lines of research highlight the potential of variational quantum algorithms [10,11] and spectral methods [14], there remains a gap between fully quantum-encoded solvers and purely classical schemes. Our goal is therefore to explore a middle ground that leverages classical spectral discretisation and offloads only the computationally intensive component—the evaluation of a scalar loss function—to a quantum backend. By doing so, we aim to retain the maturity of classical algorithms while meeting the constraints of NISQ devices.
Most recently, Endo and Takahashi proposed a variational-principle-based algorithm tailored for fault-tolerant quantum computers (FTQCs), addressing nonlinear equilibrium equations with linearised time-evolution formulations [26]. While outside the NISQ scope of this work, such approaches highlight future directions for scaling nonlinear solvers once large-scale quantum devices become available.
2. Problem Statement and Classical Spectral Solver
We consider the second-order nonlinear boundary–value problem
Three representative forms of the coefficient function are examined:
- Constant coefficient: .
- Variable coefficient: .
- Nonlinear coefficient: .
To discretise the PDE we adopt Chebyshev–Gauss–Lobatto collocation. Given an integer N, we define nodes for , which map the physical domain to via an affine transformation. These points cluster at the boundaries and , enhancing resolution where the solution may vary rapidly. Let D denote the CGL differentiation matrix and the diagonal matrix formed by evaluating a at a vector u. For a candidate solution vector u, we define the residual vector
where ∘ denotes element-wise multiplication and f is sampled at the collocation nodes. In the classical solver we form the scalar loss function and minimise it with respect to u using standard optimisation routines such as the BFGS quasi-Newton method.
3. Hybrid Quantum–Classical Strategy
3.1. Motivation for Hybridisation
Evaluating the nonlinear residual vector and its squared norm constitutes the most computationally intensive part of the classical solver when a depends nonlinearly on u. Unlike linear problems, the nonlinear residual couples all degrees of freedom through pointwise multiplication and differentiation. We therefore propose to offload the computation of to a quantum backend. By encoding the residual norm as an observable expectation value, we exploit the ability of a quantum processor to estimate inner products via measurement while leaving the remainder of the algorithm—discretisation, ansatz initialisation, and optimisation—on the classical processor.
3.2. Quantum Kernel for Residual Evaluation
Let denote a parameterised quantum state prepared by an ansatz with parameters . We choose an ansatz depth sufficient to represent the functional dependence of u on x but keep the circuit shallow to accommodate NISQ restrictions. The residual norm is encoded as
where H is constructed such that its expectation reproduces . In practice we embed the evaluation into frameworks such as CUDA–Q, which allow the programmer to specify a classical function for that internally dispatches quantum kernels. A pseudocode sketch of the hybrid evaluation is given below:
- from scipy.optimize import minimize
- import~cudaq
- def loss_function(theta):
- result = cudaq.observe(my_ansatz, H, theta)
- return result.expectation()
- theta0 = [0.1] ∗ n_qubits
- opt_result = minimize(
- loss_function,
- theta0,
- method = ‘BFGS’
- )
Here cudaq.observe evaluates the expectation value of H for the current parameters on a selected backend (emulator, GPU, or real hardware). Only the scalar is returned to the classical optimiser, thereby reducing quantum resource requirements compared with approaches that encode the entire residual or solution vector.
3.3. Division of Labour
The hybrid solver separates tasks between classical and quantum processors:
- Classical: This processor constructs CGL nodes, differentiation matrices, and the nonlinear residual symbolically. It performs the outer optimisation loop (e.g., BFGS) and updates the ansatz parameters.
- Quantum: This processor implements the variational circuit and estimates via repeated measurements. No Jacobian or gradient information is required at this stage, although quantum gradient evaluation could be incorporated in future extensions.
This separation minimises the circuit depth and number of qubits, addressing the constraints of NISQ hardware. See Figure 1.
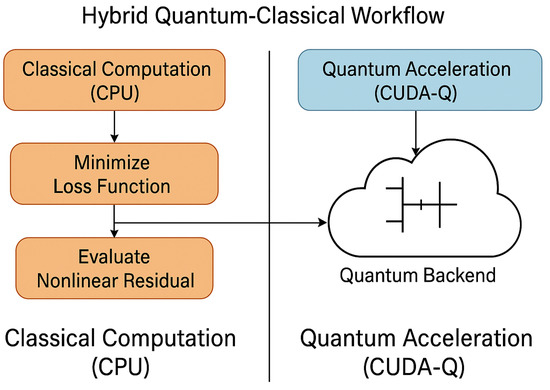
Figure 1.
Hybrid quantum–classical workflow: The residual norm is evaluated using CUDA-Q on an emulated quantum backend (CPU/GPU). Optimisation and discretisation remain fully classical.
3.4. Binary Quadratic Model (BQM) Formulation and Mapping
The nonlinear term in the differential equation, when discretised by Chebyshev spectral collocation and subsequently binarised for quantum processing, generates a squared residual loss function that contains terms up to . This process yields a Cubic Unconstrained Binary Optimisation (CUBO) problem, , which serves as the minimisation target for our gate-based solver.
In contrast, the quantum annealer backend is fundamentally restricted to minimising only linear and and quadratic terms, requiring a Quadratic Unconstrained Binary Optimisation (QUBO) formulation Figure 2. To allow comparison with the annealer, the CUBO objective must be polynomially reduced to an equivalent QUBO problem, . This is achieved by introducing auxiliary binary variables, , and a sufficiently large penalty constant to enforce the cubic identity constraint . The final QUBO objective is . This distinction is crucial: the gate-based VQA directly processes the CUBO, while the annealer requires the variable-increased QUBO.
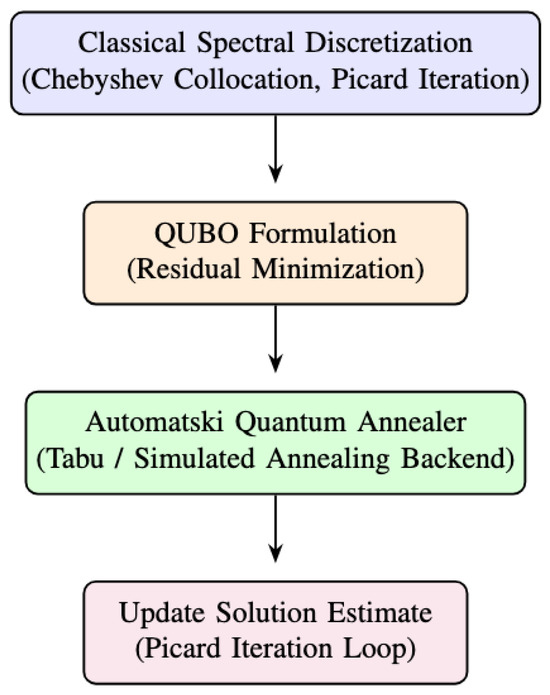
Figure 2.
Hybrid Picard–QUBO workflow with Automatski annealer backend. The classical solver handles discretisation and Picard iteration, while the quantum backend solves QUBO instances for residual minimisation.
4. Implementation and Preliminary Results
We implemented the proposed solver using CUDA–Q, a high-performance framework selected for its native support of hybrid classical–quantum workflows and its ability to leverage powerful NVIDIA GPU acceleration for the classical optimisation loop and quantum circuit emulation. The classical discretisation used CGL nodes. For each coefficient function listed earlier, we compared the purely classical spectral solver with the hybrid solver in which the residual norm was evaluated on the CUDA–Q emulator.
4.1. Constant and Variable Coefficients
For the constant-coefficient case and the forcing term , the exact solution is a parabola. Both classical and hybrid solvers reproduced this solution with spectral accuracy; the maximum absolute error at the collocation points was ∼. When and were chosen so that the exact solution was , the hybrid solver again matched the classical solver.
4.2. Nonlinear Coefficient
The nonlinear test used and a right-hand side , for which the exact solution is . This case is more challenging because the residual couples the solution vector nonlinearly.
Our classical solver converged rapidly to the exact solution with spectral accuracy. Indeed, the numerical solution is essentially indistinguishable from the analytic curve, confirming that the Chebyshev collocation with nodes yields spectral convergence.
In contrast, the hybrid classical–quantum solver used to minimise the CUBO cost required a detailed specification of the quantum circuit. Our implementation employed an Alternating Operator Ansatz, composed of L layers. Each layer consisted of single-qubit gates followed by a linear entangling layer of gates across neighbouring qubits. The study began with a six-qubit circuit and (depth-3), resulting in P variational parameters, which exhibited a noticeable discrepancy. While the Dirichlet boundary conditions were enforced exactly by construction, the interior solution diverged from the exponential profile (Figure 3). This deviation arises from the limited expressivity of the variational ansatz, the finite number of encoded Chebyshev modes, and the optimiser’s sensitivity to the highly non-convex residual landscape [10,12]. Potential strategies to reduce this gap include increasing the number of qubits or circuit depth, refining the ansatz to better capture Chebyshev modes, careful rescaling, and hybridizing with classical warm-starts.
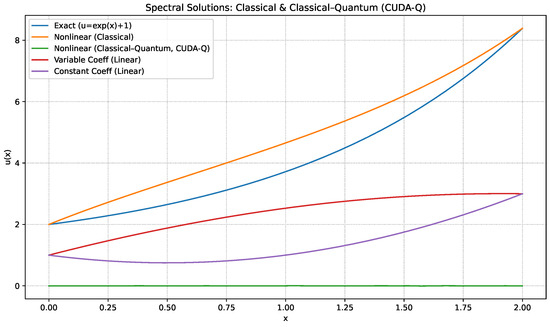
Figure 3.
Comparison of spectral solutions for a nonlinear boundary value problem on . The exact analytic solution is indistinguishable from the nonlinear classical solver, confirming convergence of the spectral Chebyshev discretisation. The classical–quantum (CUDA-Q) solver exhibits a deviation primarily due to ansatz expressivity and optimiser sensitivity in the non-convex residual landscape, rather than qubit count.
A key counterintuitive finding emerged from testing a shallower circuit (Figure 4) with and three qubits. This lower-complexity configuration aligned more closely with the exact and classical solutions than the deeper circuit. This observation is significant and likely points to a trade-off in VQA design. The shallower circuit, while having reduced expressivity, is less susceptible to Barren Plateaus—a phenomenon where the optimisation landscape becomes exponentially flat in deep circuits—and accumulates fewer hardware noise errors (decoherence and gate error) typical of NISQ devices. Therefore, the reduced noise and more stable gradient landscape, rather than increased expressivity, appear to govern the convergence quality in this particular configuration.
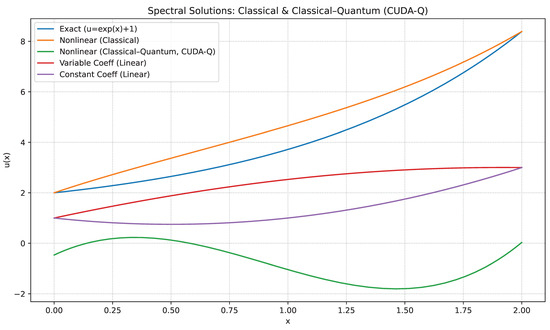
Figure 4.
Shallow CQ configuration (depth = 1, 3 qubits). This lower-complexity ansatz aligned more closely with the exact and classical solutions than deeper or larger circuits, reflecting optimiser stability at reduced expressivity.
5. Hybrid Picard–QUBO Annealer Results
In addition to the CUDA-Q based workflow, we also tested a hybrid strategy that couples a classical Picard iteration with a quantum annealer. For this, we employed Automatski’s solver, which reformulates the nonlinear boundary value problem into a Quadratic Unconstrained Binary Optimisation (QUBO) instance and executes it on a quantum annealing backend. Figure 5 shows the results of this hybrid Picard + QUBO annealer approach. Compared against the exact solution , the hybrid annealer method exhibits visibly closer agreement than our initial CUDA-Q variational implementation, particularly in capturing the exponential growth across the domain. This suggests that annealer-based QUBO formulations may provide more stable convergence for certain classes of nonlinear ODEs, even at modest qubit counts [27].
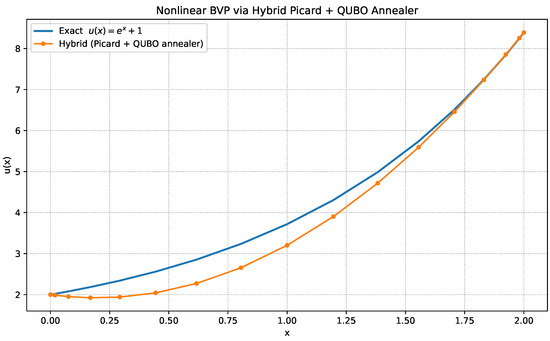
Figure 5.
Solution of the nonlinear BVP via hybrid Picard + QUBO annealer, compared with the exact and the classical nonlinear root solver.
5.1. Comparison with CUDA-Q VQE Approach
The CUDA-Q framework enabled us to encode the solution through a variational quantum circuit (VQC) and optimise its parameters with a classical optimiser. However, as illustrated in Figure 3, convergence was more challenging, and the final approximation deviated more significantly from the exact solution compared to the annealer-based QUBO method. This contrast highlights an important point: different quantum paradigms may have different strengths when embedded in hybrid classical–quantum solvers [13]. While the VQC approach offers flexibility and potential scalability on gate-based devices, the annealer-based QUBO formulation naturally encodes discrete optimisation problems and may achieve better numerical stability in boundary value problems at this stage of hardware maturity. It is worth noting that both paradigms follow the same overarching design principle: the quantum backend is tasked solely with residual minimisation, while boundary conditions and operator structure are enforced classically. In CUDA-Q, the residual norm is expressed as an observable expectation value over a parameterised ansatz, whereas in Automatski the residual equations are reformulated as QUBO problems whose energy encodes the loss. Thus, although the mechanisms differ—continuous parameter optimisation versus discrete binary encoding—both methods exemplify the “residual-only” hybrid strategy.
5.2. Additional Plots
To complement the qualitative overlays in Secs. III–IV, we present diagnostics for two complementary settings: (i) a CUBO formulation executed on a gate-based CUDA-Q backend and (ii) direct residual minimisation formulated as a QUBO and solved on the Automatski annealer within a Picard loop. These plots quantify approximation quality, convergence behaviour, and the effect of discretisation and ansatz choices (see Figure 6 and Figure 7).
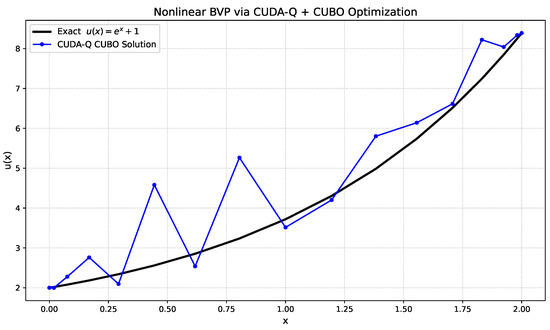
Figure 6.
Gate-based CUBO (CUDA-Q): solution quality on the nonlinear BVP. Comparison of the exact analytic solution (solid), classical spectral baseline (dashed), and gate-based CUBO approximation (dash-dot with markers). The results show that CUBO improves upon the variational baseline but retains a small interior bias due to finite precision and limited circuit depth.
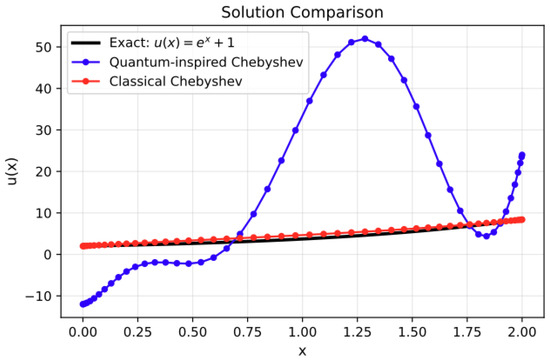
Figure 7.
Automatski quantum-inspired solver with Chebyshev series parameterisation: solution accuracy against exact solution . The comparison demonstrates that quantum-inspired continuous annealing (blue circles) produces significant oscillatory artefacts compared to classical optimisation (red circles), highlighting challenges in applying simplified quantum-inspired approaches to annealers.
6. Comparison with Alternative Approaches
Existing variational quantum solvers such as H–DES encode the entire solution function in a quantum state and perform the spectral expansion on the quantum processor [24]. While this approach is powerful and general, it incurs a large quantum overhead because the residual vector or solution coefficients must be measured or updated at each iteration. In contrast, our solver retains the spectral basis and optimisation entirely on the classical processor and passes only the scalar residual norm to the quantum backend. This reduces circuit depth, avoids recompilation of the ansatz at each step, and is more compatible with the qubit counts and noise levels of current NISQ devices.
Variational algorithms for nonlinear problems often require multiple copies of quantum states or tensor network structures to handle nonlinearities [22]. By contrast, our method handles nonlinearity on the classical side; the quantum circuit merely evaluates an observable associated with the residual norm. This design choice makes the hybrid solver extensible: advances in quantum measurement techniques or hardware can be integrated without altering the classical numerical core.
Recent developments in quantum algorithms for scientific computing [6] have demonstrated various complementary approaches. Berry and Costa [15] developed quantum algorithms for time-dependent differential equations using Dyson series, while Zhang and Shao [14] introduced quantum spectral methods for gradient estimation. Mizuno and Komatsuzaki [16] integrated quantum dynamic mode decomposition with differential equation solvers, and Liu et al. [28] applied variational quantum algorithms to fluid flow problems.
7. Discussion and Outlook
The numerical experiments demonstrate that the nonlinear classical solver and the exact solution are essentially indistinguishable, as expected from the spectral Chebyshev discretisation with sufficient resolution. This agreement highlights the robustness of the classical root-based solver.
Among the hybrid quantum results, the annealer-based Automatski solver yielded remarkably accurate approximations, while the gate-based CUBO solver improved over the variational baseline but exhibited a small interior bias. The variational solver itself failed to match the nonlinear exact solution under practical depth and qubit counts, underscoring the limitations of generic VQAs for this problem. These observations suggest a practical roadmap: annealers are naturally aligned with quadratic optimisation tasks and can be leveraged today, while gate-based CUBO solvers offer greater programmability and may benefit from future hardware and algorithmic advances.
7.1. Encoding Choices Across Hardware Paradigms
Our hybrid solver deliberately uses different encodings for gate-based and annealing hardware. A direct QUBO encoding on the CUDA-Q backend would in principle be possible, but it requires mapping binary variables into qubits with additional ancilla overhead, leading to circuits of impractical depth for NISQ devices. Conversely, annealers accept only QUBO/Ising formulations and cannot implement parameterised ansätze or continuous expectation values. We therefore evaluate each paradigm in the encoding it naturally supports: CUBO-style cost functions on gate-based devices and QUBO formulations on annealers. This design emphasises complementary strengths rather than imposing a uniform formulation across incompatible hardware.
7.2. Limitations and Future Work
This proof-of-concept study intentionally focuses on a single nonlinear boundary value problem to isolate the effects of residual offloading. We did not include detailed timing tables because annealer service times depend strongly on queue delays, embedding overhead and network latency, making direct comparisons with gate-based or classical runtimes unreliable. Future work will develop controlled benchmarks across multiple problems and hardware platforms, explore deeper variational circuits and improved ansätze, and investigate error mitigation. We also plan to integrate annealers and variational circuits in a unified hybrid scheme, specifically by investigating a warm-start protocol where the annealer’s QUBO solution is used to initialise the VQE parameters, and to extend the approach to higher-dimensional PDEs.
We also propose two new specific investigations. First, we will conduct a detailed analysis of the **QUBO scaling complexity**, examining how the number of auxiliary variables (introduced during the CUBO-to-QUBO reduction) scales with the discretisation size, a critical factor for annealer feasibility. Second, we will explore the use of **meshfree discretisation methods**, such as Radial Basis Functions (RBFs) [29], as an alternative to Chebyshev spectral collocation. This is motivated by the potential for meshfree methods to provide a more versatile framework for applications involving irregular or evolving domains, which the quantum solver could then minimise.
The field is experiencing rapid growth, with significant contributions in 2024–2025 [6,12,13,14,15,16,28,30] building on foundational work from the early quantum computing era [3,5]. This demonstrates both the cutting-edge relevance and established theoretical foundations necessary for practical quantum advantage in numerical computing.
8. Conclusions
We introduced a hybrid spectral solver that integrates quantum residual evaluation into classical nonlinear boundary value problem solvers. Our results confirm that while the classical solver achieves spectral accuracy, the annealer-based QUBO approach provides the most faithful quantum-enhanced solution. The gate-based CUDA-Q CUBO solver, though less accurate at present, offers a resource-efficient pathway for future improvements with better ansätze and hardware. Together, these results highlight a practical roadmap: annealers as near-term tools for quadratic residual minimisation and gate-based devices as flexible platforms for scalable hybrid solvers. This dual approach marks a concrete step toward practical quantum advantage in scientific computing. The rapid recent progress in quantum algorithms for differential equations [13,14,15,16] indicates a maturing field with significant potential for practical quantum advantage. Additional details on the QUBO formulation and a pure annealer implementation are provided in Appendix A.
Funding
This research received no external funding.
Data Availability Statement
The data is available upon request.
Acknowledgments
The author wish to thank Aditya Yadav, CEO of Automatski, for providing special access to the Automatski annealer simulators used in this work. His support and assistance were invaluable. The author would also like to thank Monica Van Dieren of NVIDIA for her guidance on using CUDA-Q.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Ansatz | A parameterised quantum circuit used as a trial state in variational algorithms. |
| BFGS | A quasi-Newton method for unconstrained nonlinear optimisation. |
| BQM | Binary Quadratic Model: The general class of unconstrained binary optimisation problems. |
| Chebyshev–Gauss–Lobatto nodes | Collocation points in spectral methods that cluster near the endpoints of the interval. |
| CUDA–Q | NVIDIA’s framework for hybrid quantum–classical programming on classical, emulated, and hardware backends. |
| CUBO | Cubic unconstrained binary optimisation. |
| H–DES | A quantum,-classical hybrid differential equation solver [24] that encodes the entire solution into a quantum state and performs spectral expansion on a quantum processor. |
| Loss function | The scalar objective used in optimisation. |
| NISQ | Noisy intermediate-scale quantum: the current generation of quantum devices with up to roughly a thousand qubits, lacking full error correction. |
| QUBO | Quadratic Unconstrained Binary Optimisation |
| RBF | Radial Basis Function: A basis used in meshfree discretisation methods. |
| Residual | The deviation from the governing differential equation at the collocation nodes, . |
| Variational quantum algorithm (VQA) | A hybrid algorithm coupling parameterised quantum circuits with classical optimisation; prominent examples include VQE and QAOA. |
Appendix A. Notes on the Annealer Implementation
The Automatski quantum annealer implementation presented here provides a direct comparison between gate-based and annealing approaches. The main hybrid workflow does not rely on these pure annealer experiments; they are included for completeness and to illustrate the intrinsic behaviour of the annealer when solving a QUBO derived from a spectral discretisation.
Appendix A.1. QUBO Formulation and Example
In the annealer-based method, the nonlinear boundary value problem is reformulated at each Picard iteration as a quadratic unconstrained binary optimisation (QUBO) instance. Specifically, the Chebyshev coefficients for the correction function are discretised using a fixed binary encoding, and the residual minimisation functional is cast into QUBO form. The resulting binary optimisation problem is then submitted to the Automatski quantum annealer.
As an illustration, a minimal pure annealer code snippet is shown below. This version omits the hybrid Picard loop and directly encodes a single linearised residual minimisation into a QUBO, which is then solved on the annealer:
- qubo ={…} #dictionary of {(i,j): coefficient}
- annealer = AutomatskiInitiumTabuSolver(host,port)
- answer,value = annealer.solve(qubo)
- print(“Annealer solution:”, answer)
- print(“Objective value:”, value)
This example demonstrates the direct encoding of a discretised PDE residual into a QUBO and highlights the simplicity of the interface between spectral discretisation and quantum annealing.
Appendix A.2. Scope of QUBO-Suitable Problems
QUBO formulations are naturally suited to problems that can be expressed as quadratic functionals of discretised variables [27]. Within the context of differential equations, this includes classes of boundary value problems where residual minimisation yields quadratic forms after linearisation (e.g., elliptic and certain nonlinear problems under Picard or Newton iteration). Such a structure makes annealers particularly well matched to spectral collocation schemes, where quadratic residual objectives arise in a straightforward manner. See also [27] for related work on spectral methods on Ising machines.
Appendix A.3. Pure Annealer Implementation
For completeness, we also tested a pure annealer implementation without the outer Picard iteration. Although less accurate than the hybrid Picard+QUBO approach, it demonstrates the feasibility of running discretised PDE residuals entirely on an annealer. Figure A1 shows the resulting solution compared with the exact function.
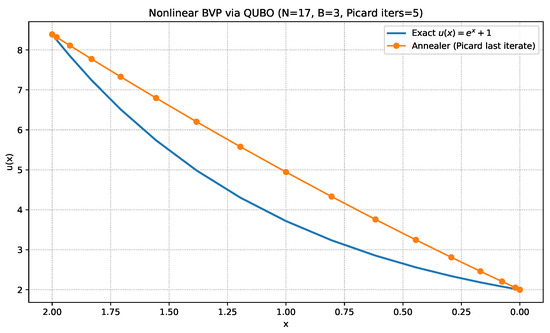
Figure A1.
Pure annealer implementation of the nonlinear BVP: the solution is obtained by submitting a single QUBO instance to the Automatski annealer. While less accurate than the hybrid Picard+QUBO approach, it highlights the direct compatibility of spectral collocation residuals with annealing hardware.
References
- Heinrich, H. Numerical analysis on a quantum computer. Int. Conf.-Large-Scale Sci. Comput. 2005, 3743, 28–39. [Google Scholar] [CrossRef]
- Trefethen, L.N. Spectral Methods in MATLAB; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Zhang, C. Quantum Algorithms and Complexity for Numerical Problems. Ph.D. Thesis, Columbia University, New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Meng, F.-X.; Yu, X.; Zhang, Z. An Improved Quantum Algorithm for Spectral Regression. In Proceedings of the 2020 Asia Conference on Computers and Communications (ACCC), Singapore, 18–20 September 2020. [Google Scholar] [CrossRef]
- Agaian, S.S.; Klappenecker, A. Quantum Computing and a Unified Approach to Fast Unitary Transforms. In Image Processing: Algorithms and Systems; SPIE: Cergy-Pontoise, France, 2002. [Google Scholar] [CrossRef][Green Version]
- Au-Yeung, R.; Camino, B.; Rathore, O.; Kendon, V. Quantum algorithms for scientific computing. Rep. Prog. Phys. 2024, 87, 116001. [Google Scholar] [CrossRef]
- Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Schroeder, D.V. The variational-relaxation algorithm for finding quantum bound states. Am. J. Phys. 2017, 85, 698–704. [Google Scholar] [CrossRef]
- Chernyavskiy, A.; Khamitov, K.; Teplov, A.; Voevodin, V.; Voevodin, V. Numerical characteristics of quantum computer simulation. Int. Conf.-Micro-Nano-Electron. 2016, 10224, 735–740. [Google Scholar] [CrossRef]
- Kyriienko, O.; Paine, A.E.; Elfving, V.E. Solving nonlinear differential equations with differentiable quantum circuits. Phys. Rev. A 2021, 103, 052416. [Google Scholar] [CrossRef]
- Leong, F.Y.; Ewe, W.-B.; Koh, D.E. Variational quantum evolution equation solver. Sci. Rep. 2022, 12, 14906. [Google Scholar] [CrossRef]
- Arora, A.; Ward, B.C.; Oskay, C. An Implementation of the Finite Element Method in Hybrid Classical/Quantum Computers. arXiv 2024, arXiv:2411.09038. [Google Scholar] [CrossRef]
- Tennie, F.; Magri, L. Solving nonlinear differential equations on quantum computers: A Fokker-Planck approach. arXiv 2024, arXiv:2401.13500. [Google Scholar] [CrossRef]
- Zhang, Y.; Shao, C. Quantum spectral method for gradient and Hessian estimation. arXiv 2024, arXiv:2407.03833. [Google Scholar] [CrossRef]
- Berry, D.W.; Costa, S.J. Quantum algorithms for time-dependent differential equations using Dyson series. Quantum 2024, 8, 1369. [Google Scholar] [CrossRef]
- Mizuno, Y.; Komatsuzaki, K. Quantum algorithm for dynamic mode decomposition integrated with a quantum differential equation solver. Phys. Rev. Res. 2024, 6, 043031. [Google Scholar] [CrossRef]
- Aseeri, S. State-of-the-art FFT: Algorithms, implementations and applications. In Reflections on the 2018 SIAM Conference on Parallel Processing for Scientific Computing; SIAM: Philadelphia, PA, USA, 2018; Available online: https://www.siam.org/publications/siam-news/articles/state-of-the-art-fft-algorithms-implementations-and-applications/ (accessed on 10 October 2025).
- Muite, B.K.; Aseeri, S. Benchmarking solvers for the one-dimensional cubic nonlinear Klein–Gordon equation on a single core. In Proceedings of the International Symposium on Benchmarking, Measuring and Optimization (Bench 2019), Denver, CO, USA, 14–16 November 2019; pp. 172–184. Available online: https://link.springer.com/chapter/10.1007/978-3-030-49556-5_18 (accessed on 10 October 2025).
- Leu, B.; Aseeri, S.; Muite, B. A comparison of parallel profiling tools for programs utilizing the FFT. In Proceedings of the International Conference on High Performance Computing in Asia-Pacific Region (HPC Asia), Online, 20–22 January 2021; Available online: https://dl.acm.org/doi/10.1145/3440722.3440881 (accessed on 10 October 2025).
- Aseeri, S.; Muite, B.K.; Takanashi, D. Reproducibility in Benchmarking Parallel Fast Fourier Transform based Applications. In Proceedings of the ICPE ’19: Companion of the 2019 ACM/SPEC International Conference on Performance Engineering, Mumbai, India, 7–11 April 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 25–28. [Google Scholar] [CrossRef]
- Aseeri, S.A. Distributed memory fast Fourier transforms in the exascale era. In Proceedings of the 2025 International Conference on Intelligent Control, Computing and Communications (IC3), Mathura, India, 13–14 February 2025; pp. 1043–1046. [Google Scholar] [CrossRef]
- Lubasch, M.; Joo, J.; Moinier, P.; Kiffner, M.; Jaksch, D. Variational quantum algorithms for nonlinear problems. Phys. Rev. A 2020, 101, 010301. [Google Scholar] [CrossRef]
- Sarma, A.; Watts, T.W.; Moosa, M.; Liu, Y.; McMahon, P.L. Quantum variational solving of nonlinear and multi-dimensional partial differential equations. Phys. Rev. A 2024, 109, 062616. [Google Scholar] [CrossRef]
- Jaffali, H.; de Araujo, J.B.; Milazzo, N.; Reina, M.; de Boutray, H.; Baumann, K.; Holweck, F. H-DES: A quantum–classical hybrid differential equation solver. arXiv 2024, arXiv:2410.01130. [Google Scholar]
- Wang, Y.; Tu, H.; Liu, W.; Xiao, W.; Lan, Q. Two Chebyshev spectral methods for solving normal modes in atmospheric acoustics. Entropy 2021, 23, 705. [Google Scholar] [CrossRef] [PubMed]
- Endo, K.; Takahashi, K.Z. Quantum-Accelerated Solution of Nonlinear Equations from Variational Principles. arXiv 2025, arXiv:2508.17606. [Google Scholar] [CrossRef]
- Takagi, K.; Moriya, N.; Aoki, S.; Endo, K.; Muramatsu, M.; Fukagata, K. Implementation of spectral methods on Ising machines: Toward flow simulations on quantum annealers. Fluid Dyn. Res. 2024, 56, 061401. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Chen, Z.; Shu, C.; Rebentrost, P.; Liu, Y.G.; Chew, S.C.; Khoo, B.C.; Cui, Y.D. A variational quantum algorithm-based numerical method for solving potential and Stokes flows. Ocean. Eng. 2024, 292, 116494. [Google Scholar] [CrossRef]
- Li, J.; Zhao, Y. A review of meshless methods for solving partial differential equations in recent decades. Appl. Numer. Math. 2022, 182, 248–261. [Google Scholar] [CrossRef]
- Novak, R. Quantum Algorithm for Solving the Wave Equation on a Hexagonal Grid. IEEE Access 2024, 12, 131009–131022. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).