MORA: A Multicriteria Optimal Resource Allocation and Decision Support Toolkit for Wildfire Management
Abstract
1. Introduction
2. Related Work
2.1. The Role of GIS Spatial Analysis and Modeling for Decision Support Systems
2.2. Forecasting Wildfire Spread Methods and Models
2.3. Resource Allocation and Cost Minimization
2.3.1. Linear Programming Based Optimization
2.3.2. Search-Based Optimization and Heuristic-Based Approaches
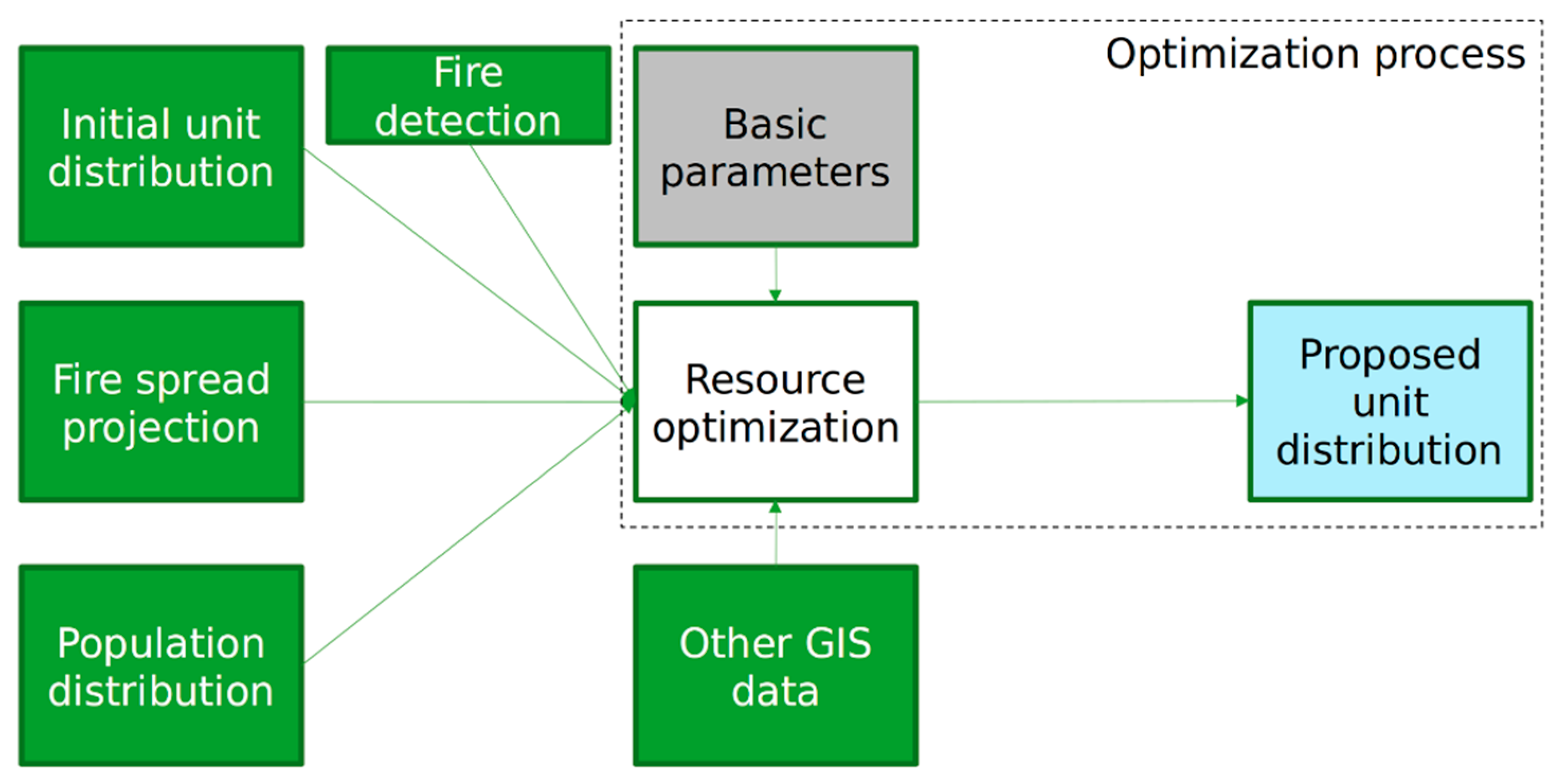
3. System Architecture, Concept of Operation and Contributions of This Work
3.1. System Architecture and Concept of Operation
3.2. Contributions of This Work
4. Multicriteria Optimization Based Resource Allocation (MORA)
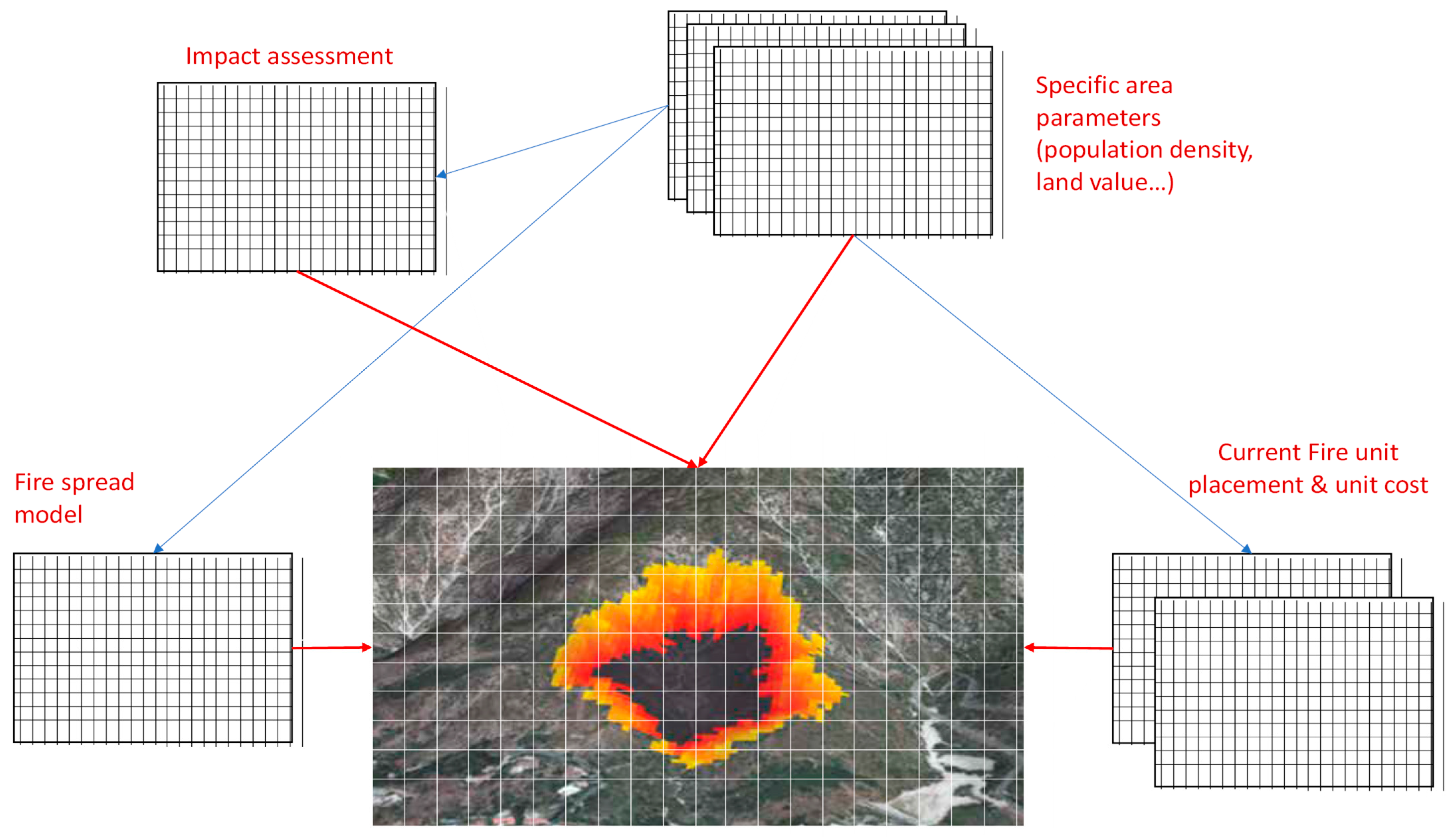
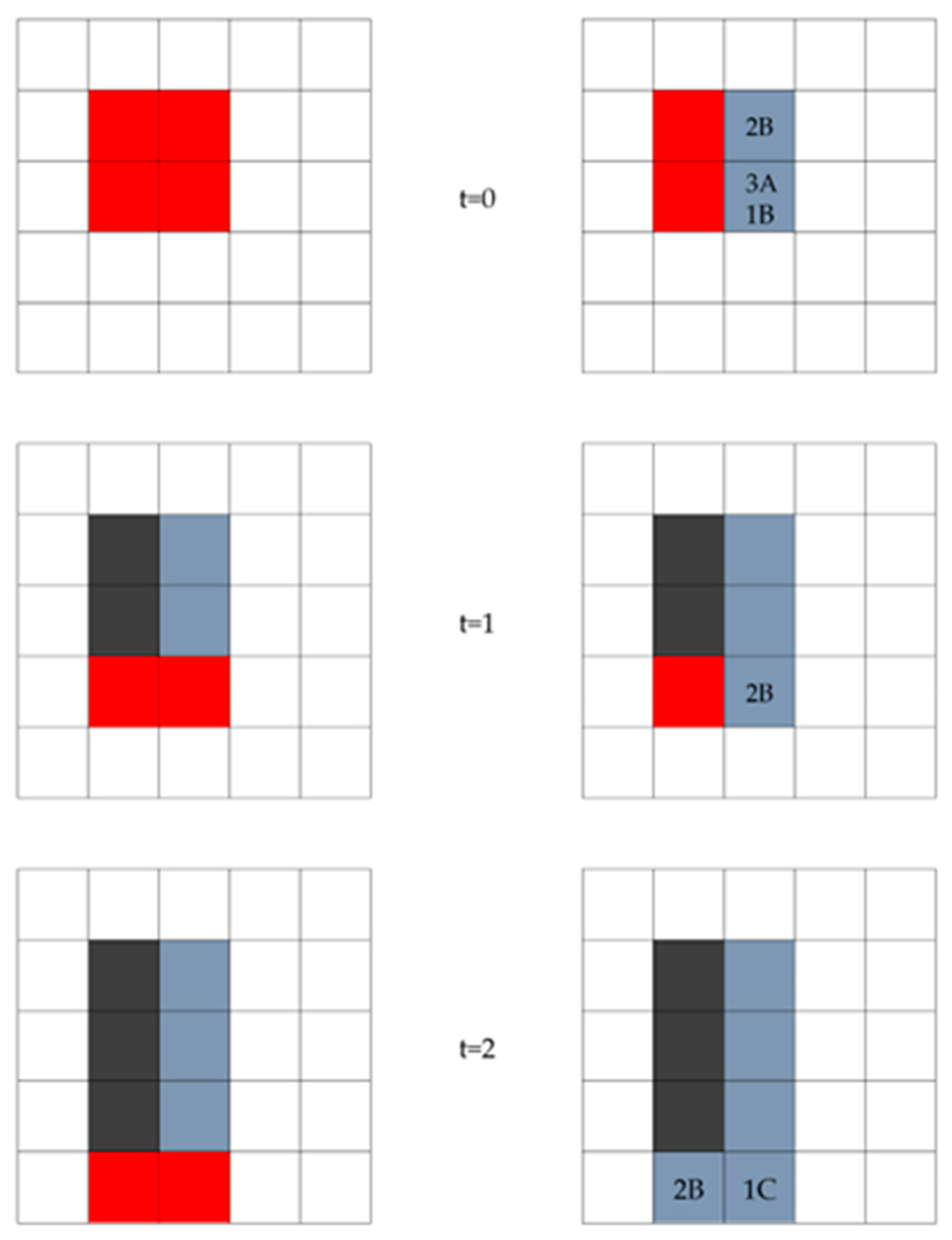
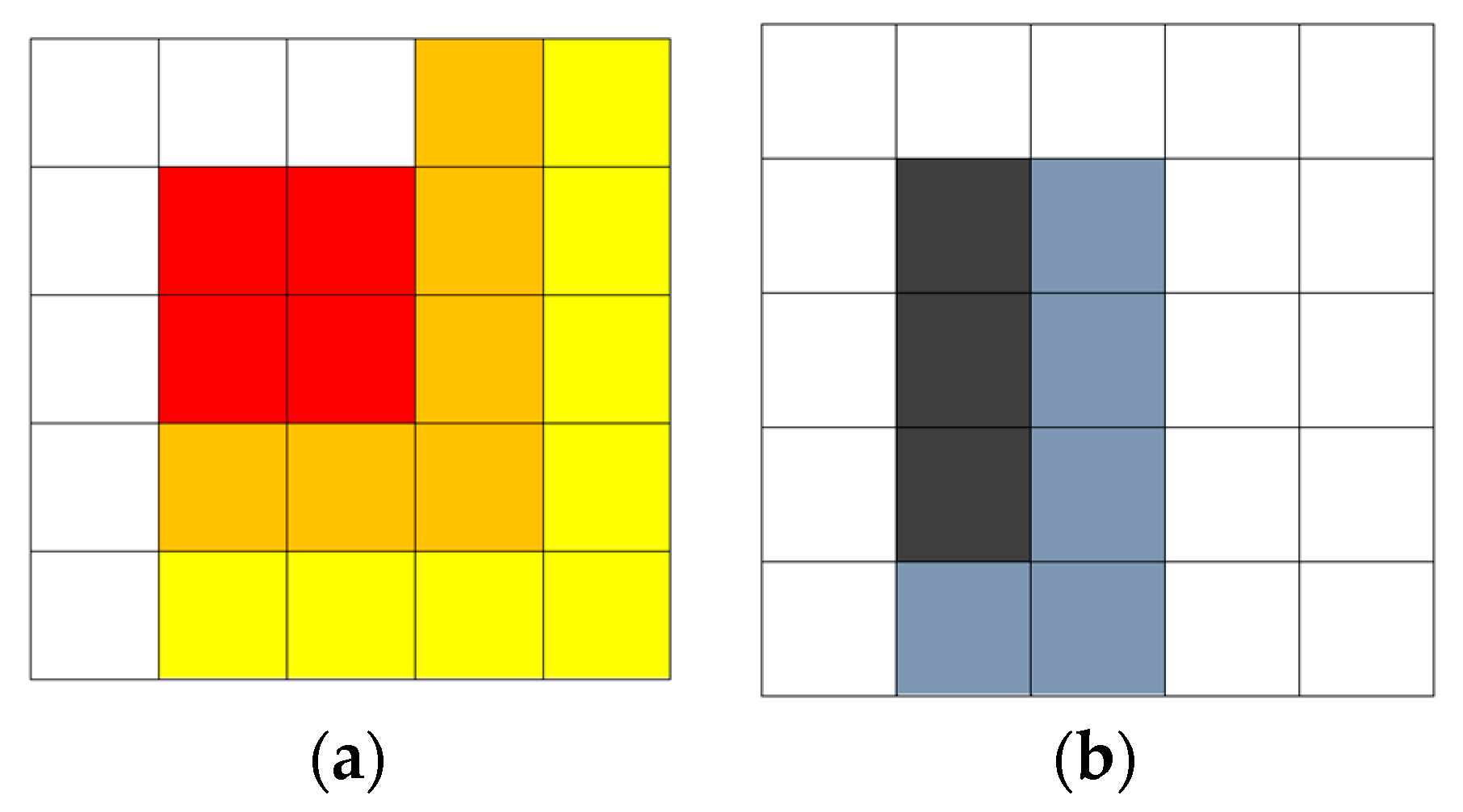
4.1. Model Assumptions and Data Sources
- The total population in risk.
- The total land/property losses.
- The total cost of resource units.
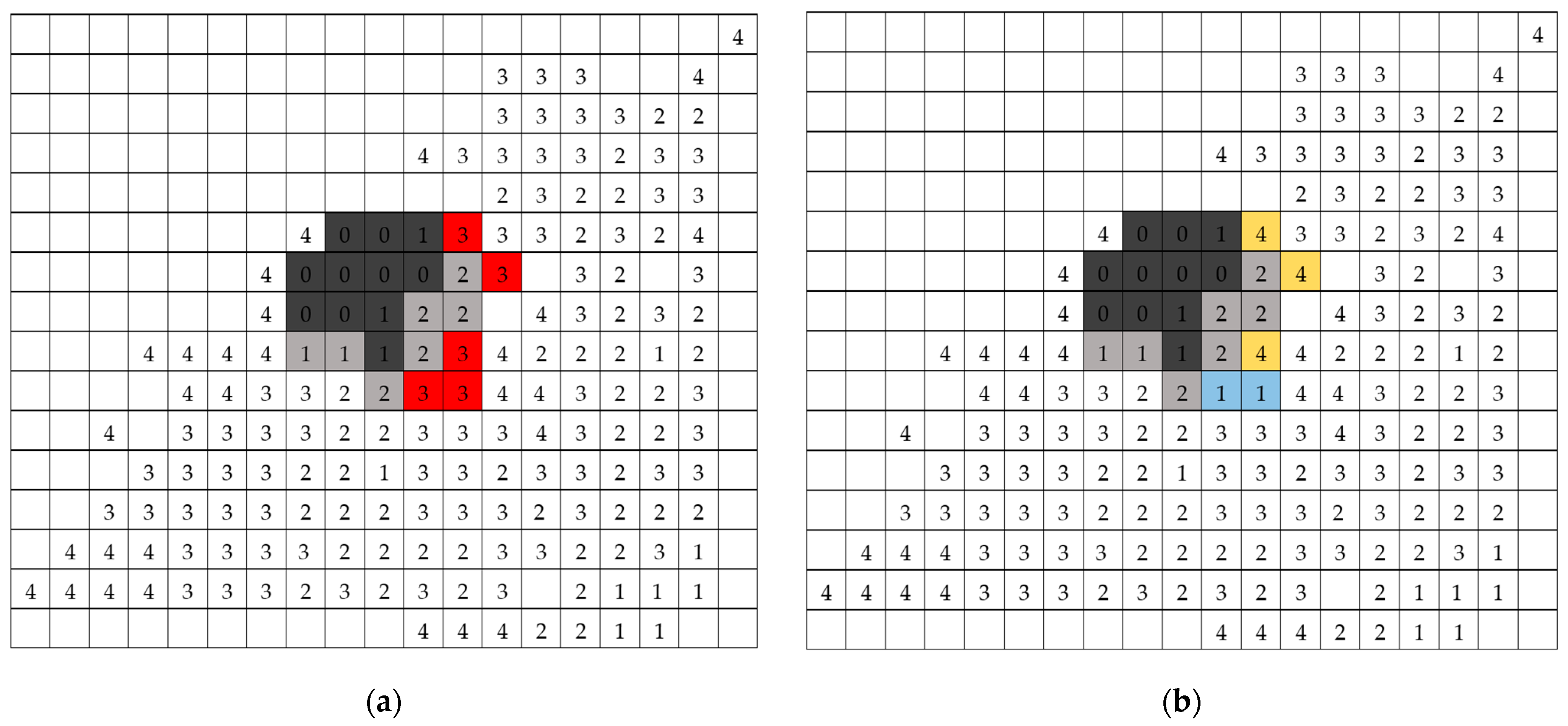
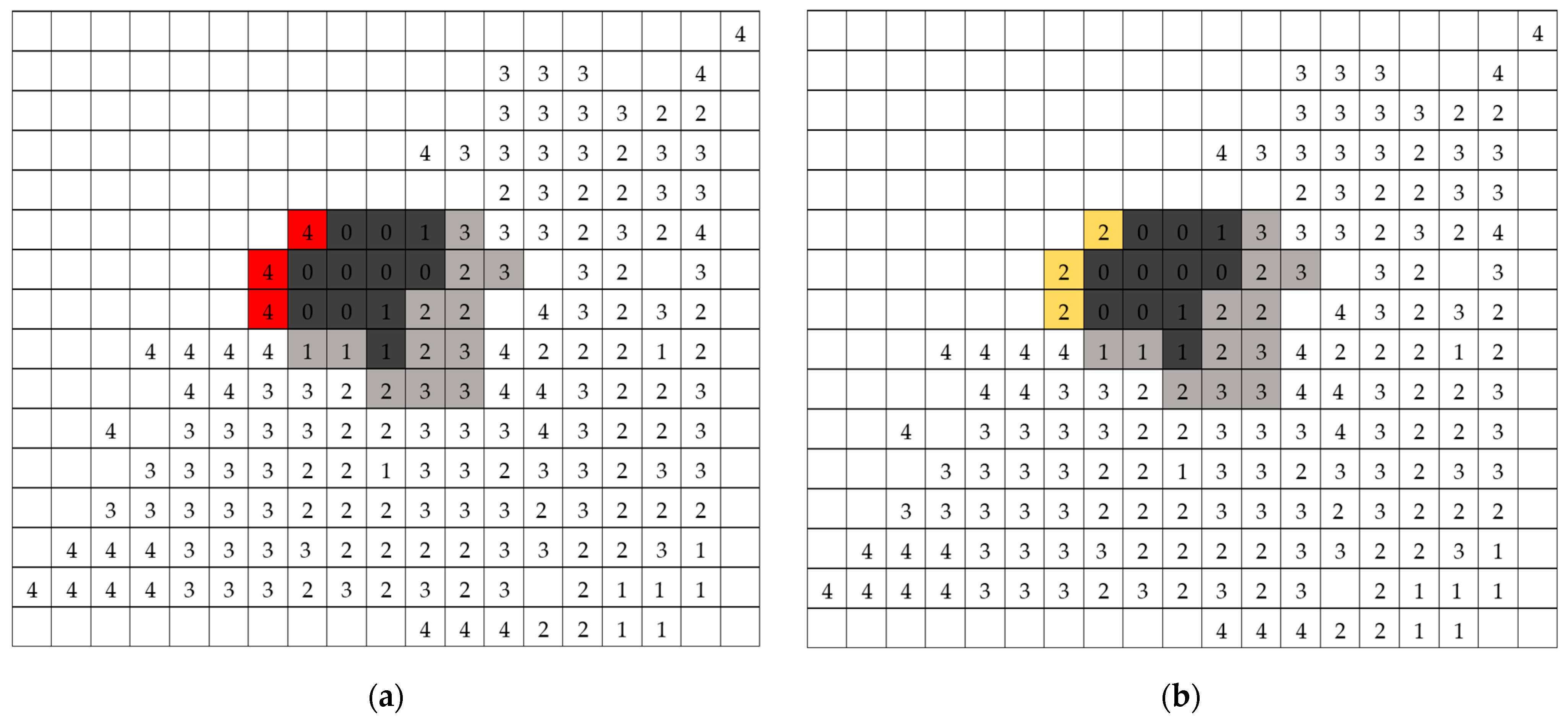
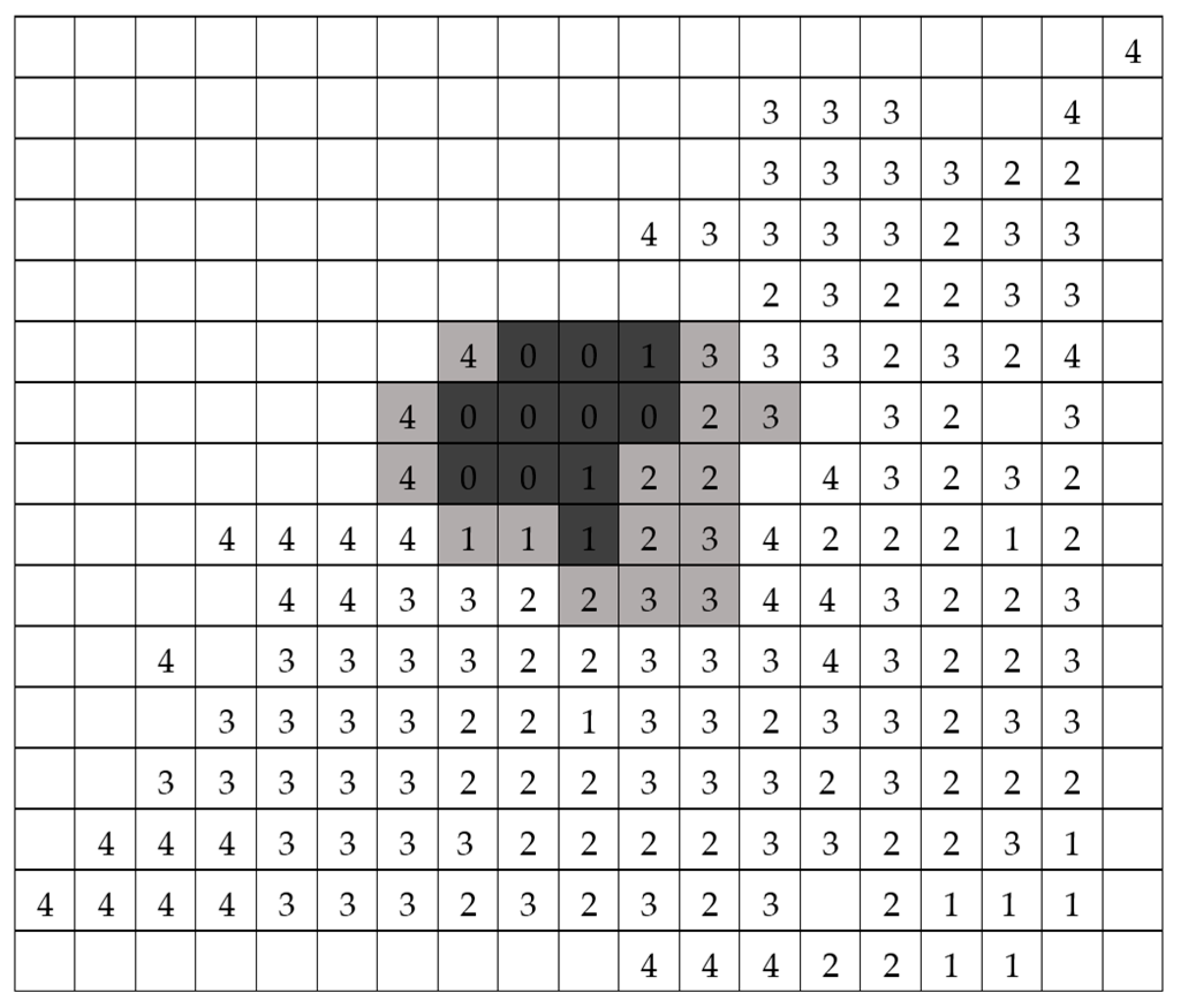
- High-risk: The cell is about to be affected by the fire or has been partially on fire.
- Burnt: The cell has been fully burnt and cannot be treated.
- Treated: The cell is treated by response teams.
- It should have at least one burnt cell neighbor.
- It should not have been a burnt cell before.
- It should have never been treated before.
4.2. Model Formulation
4.2.1. Sets
- A: Set of cells in consideration, indexed by a.
- I: Set of resource types, indexed by i.
- T: Set of discrete time periods, indexed by t.
4.2.2. Parameters
- B: Budget for resource units. This is a control parameter that sets an upper bound to the total cost of resources. Obviously, with an infinite amount of budget there would not be a need to optimize the use of resources, but this is not the case in practice.
- R: Minimum required suppression rate for each cell (chains/hour). This can be provided as a projection by some of the fire spread models like Flammap.
- Pa: Population Density at cell α. This is provided by GIS models like Worldpop.
- Va: Property and land value at cell a. This could be provided by GIS models developed and maintained specifically by authorities like civil protection agencies, etc.
- Si: Suppression rate of resource i. This is known for each type of unit depending on the water tank capacity of a truck, a plane or helicopter etc.
- Ci: Unit cost of resource i. This cost is not necessarily expressed solely in monetary terms. It could also be related to other conditions, including the risk of reserving resources in an event, leaving other high-risk areas unprotected, increasing the utilization of units with high cost and long delay in their maintenance, etc. It is directly related to the way of expressing the total available budget B.
- Ki,t: Capacity (availability) of resource i in period t. This is provided by the firefighting authorities and civil protection agencies, and it is known by the incident commanders. Their availability and geographical dispersion is also facilitated by real-time connectivity through an IoT infrastructure, which is becoming widespread lately.
- Ha,t: Binary parameter defining whether cell a will be high-risk in period t. The conditions for this were explained in Section 4.1 above.
- Ga: Binary parameter defining whether cell a is accessible. This is again related to GIS data and expresses the condition that a road is available (and free of danger) so that land units and troops can reach this area.
- Mi: Binary parameter defining whether resource i has accessibility constraints (i.e., land vs. aerial units).
4.2.3. Decision Variables
- xi,a,t: Number of resources i sent to cell a in period t.
- µa,t: Binary variable defining whether cell a becomes high-risk in period t.
- ka,t: Binary variable defining whether cell a becomes fully burnt in period t.
- ɸa,t: Binary variable defining whether cell a starts to be treated in period t.
- Zi,a,t: Binary variable defining whether resource i is allocated to cell a in period t.
4.2.4. Objective Functions
- O1: Total number of people in fire risk.
- O2: Total land/property losses.
- O3: Total cost of resource units.
4.2.5. Constraints
- Total budget for resources must not be exceeded:
- For each period and for each resource type, the total number of resources must not exceed the capacity (availability):
- All resources sent to each cell are sufficient to contain the fire in this cell:
- Resource allocation depends on accessibility:
- Only high-risk cells will be treated:
- If a cell is a high-risk in t − 1 and is not treated in t − 1, then it will become a fully burnt cell in t:
- Each cell can become a high-risk cell, a burnt cell or a treated cell at most once:
- Each burnt cell or treated cell needs to be a high-risk cell previously:
- If a cell has fully burnt, it will never be treated in the future and the opposite:
- Each high-risk cell must become a treated cell or a burnt cell in the end:
- To become high-risk, a cell must have at least one fully burnt cell neighbor:
- Nonnegativity of the number of resources:
- Binary variables limitations:
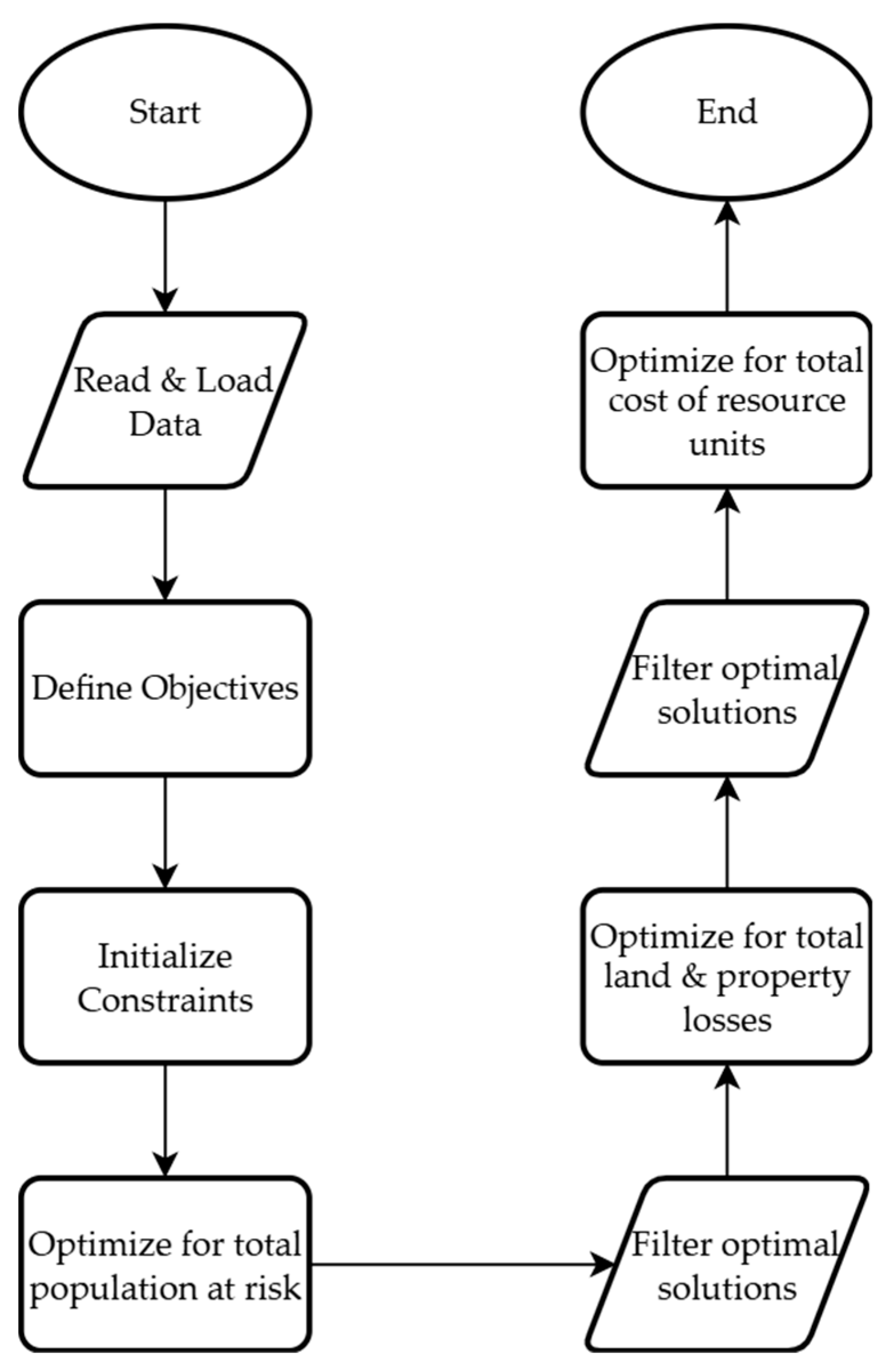
5. Model Demonstration and Validation
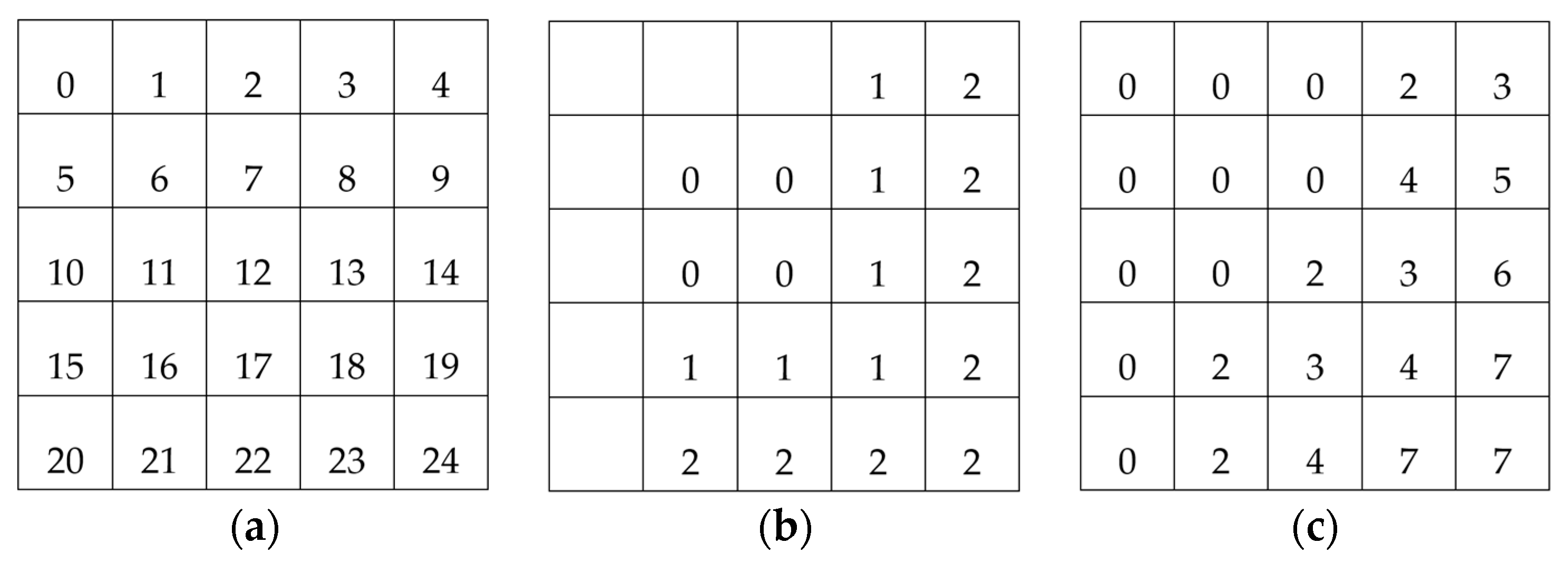
5.1. Model Demonstration
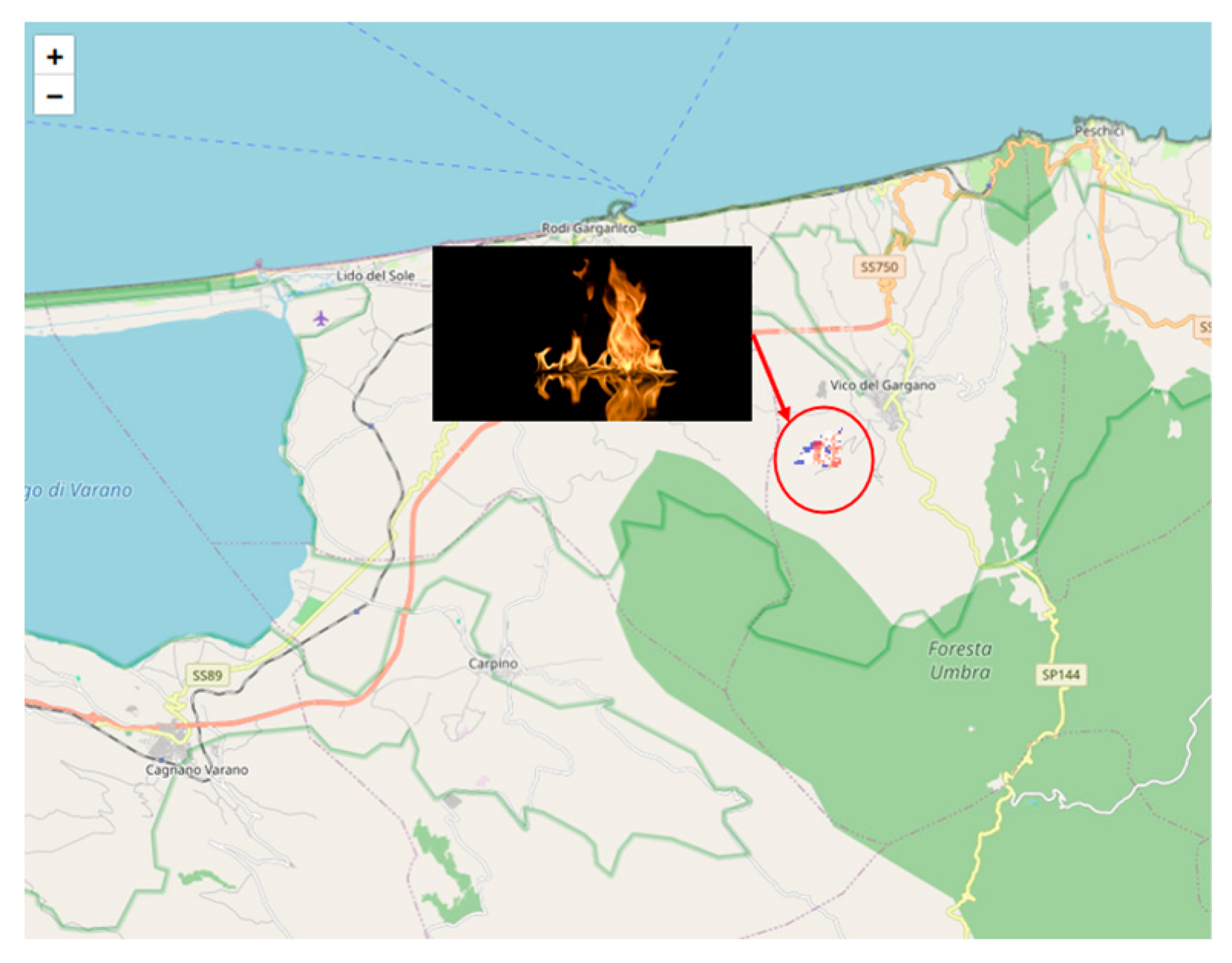
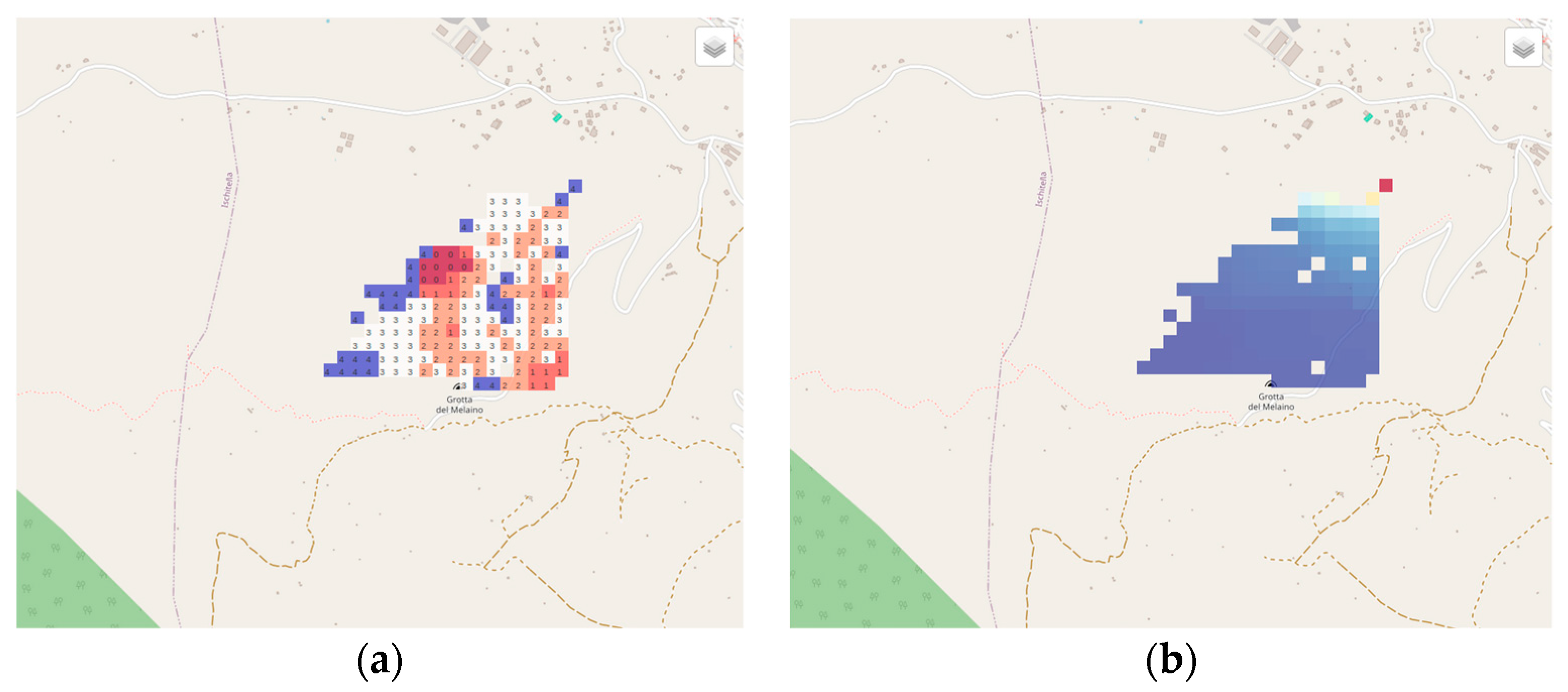
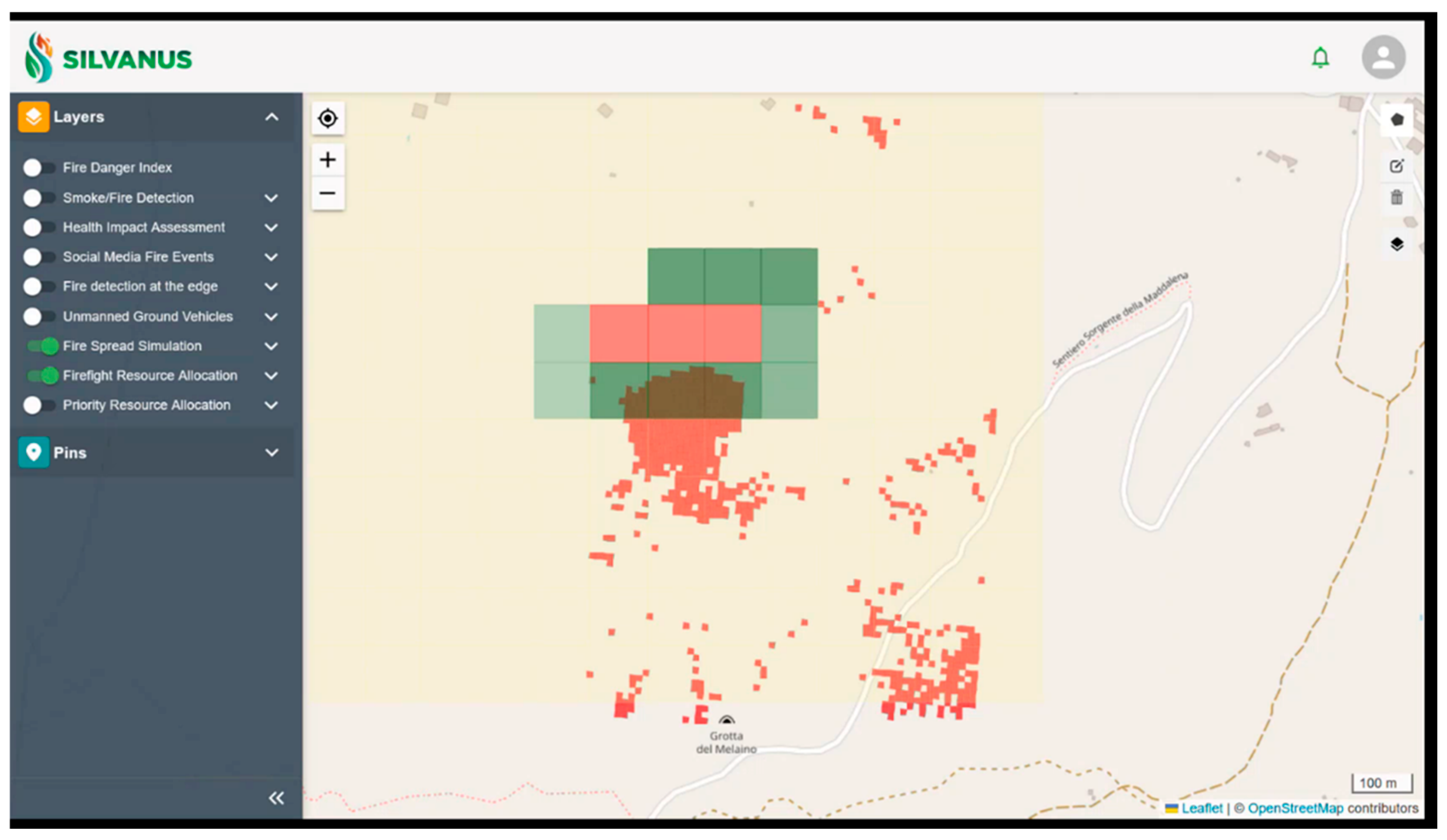
5.2. Model Validation in in the Gargano, Italy Scenario
5.3. Model Integration
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krsnik, G.; Busquets Olivé, E.; Piqué Nicolau, M.; Larrañaga, A.; Cardil, A.; García-Gonzalo, J.; González Olabarría, J.R. Regional level data server for fire hazard evaluation and fuel treatments planning. Remote Sens. 2020, 12, 4124. [Google Scholar] [CrossRef]
- Oliveras Menor, I.; Prat-Guitart, N.; Spadoni, G.L.; Hsu, A.; Fernandes, P.M.; Puig-Gironès, R.; Ascoli, D.; Bilbao, B.A.; Bacciu, V.; Brotons, L.; et al. Integrated fire management as an adaptation and mitigation strategy to altered fire regimes. Commun. Earth Environ. 2025, 6, 202. [Google Scholar] [CrossRef]
- Marić, L.; Chandramouli, K.; Martinez, J.R.; Maslioukova, M.I.; Christodolou, G.; Avgerinakis, K.; Kosmides, P. Advancement of an Integrated Technological Platform for Wildfire Management Through Edge Computing. In Proceedings of the 8th International Conference on Smart and Sustainable Technologies (SpliTech), Split/Bol, Croatia, 20–23 June 2023; pp. 1–6. [Google Scholar]
- Tezcan, B.; Eren, T. Forest fire management and fire suppression strategies: A systematic literature review. Nat. Hazards 2025, 121, 10485–10515. [Google Scholar] [CrossRef]
- Granda, B.; León, J.; Vitoriano, B.; Hearne, J. Decision Support Models and Methodologies for Fire Suppression. Fire 2023, 6, 37. [Google Scholar] [CrossRef]
- Zehra, S.N.; Wong, S.D. Systematic review and research gaps on wildfire evacuations: Infrastructure, transportation modes, networks, and planning. Transp. Plan. Technol. 2024, 47, 1364–1398. [Google Scholar] [CrossRef]
- Minas, J.P.; Hearne, J.W.; Martell, D.L. A spatial optimization model for multi period landscape level fuel management to mitigate wildfire impacts. Eur. J. Oper. Res. 2014, 232, 412–422. [Google Scholar] [CrossRef]
- Minas, J.P.; Hearne, J.W.; Martell, D.L. An integrated optimization model for fuel management and fire suppression preparedness planning. Ann. Oper. Res. 2015, 232, 201–215. [Google Scholar] [CrossRef]
- Rashidi, E.; Medal, H.; Gordon, J.; Grala, R.; Varner, M. A maximal covering location based model for analyzing the vulnerability of landscapes to wildfires: Assessing the worst case scenario. Eur. J. Oper. Res. 2017, 258, 1095–1105. [Google Scholar] [CrossRef]
- You, W.; Lin, L.; Wu, L.; Ji, Z.; Yu, J.A.; Zhu, J.; Fan, Y.; He, D. Geographical information system-based forest fire risk assessment integrating national forest inventory data and analysis of its spatiotemporal variability. Ecol. Indic. 2017, 77, 176–184. [Google Scholar] [CrossRef]
- Tien, D.; Van Le, H.; Hoang, N. GIS-based spatial prediction of tropical forest fire danger using a new hybrid machine learning method. Ecol. Inform. 2018, 48, 104–116. [Google Scholar] [CrossRef]
- Yuana, K.A.; Kusrini, K.; Setyanto, A.; Laksito, A.D.; Maruf, Z.R.; Johari, M.Z.F.; Adninda, G.B.; Kartikakirana, R.A.; Nucifera, F.; Widayani, W.; et al. GIS data support technique for forest fire management and decision support system: A Sebangau National Park, Kalimantan case. In Proceedings of the 6th International Conference on Information and Communications Technology (ICOIACT) 2023, Hybrid Conference, Yogyakarta, Indonesia, 10–11 November 2023. [Google Scholar]
- Silva, J.; Marques, J.; Gonçalves, I.; Brito, R.; Teixeira, S.; Teixeira, J.; Alvelos, F. A Systematic Review and Bibliometric Analysis of Wildland Fire Behavior Modeling. Fluids 2022, 7, 374. [Google Scholar] [CrossRef]
- Andrews, P.L. The Rothermel Surface Fire Spread Model and Associated Developments: A Comprehensive Explanation; General Technical Report RMRS-GTR-371; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2018; 121p. [Google Scholar]
- Cruz, M.G.; Alexander, M.E.; Sulivan, A.L.; Gould, J.S.; Kilinc, M. Assessing improvements in models used to operationally predict wildland fire rate of spread. Env. Mod. Softw. 2018, 105, 54–63. [Google Scholar] [CrossRef]
- FlamMap Updates for Next-Generation Fire Modeling. Available online: https://www.fs.usda.gov/sites/default/files/fire-management-today/00313%20FS%20Pubs%20FMT%2078%283%29_final%20508-Web.pdf (accessed on 10 August 2025).
- Mell, W.; Maranghides, A.; McDermott, R.; Manzello, S.L. Numerical simulation and experiments of burning Douglas fir trees. Combust. Flame 2009, 156, 2023–2041. [Google Scholar] [CrossRef]
- Coen, J.L.; Cameron, M.; Michalakes, J.; Patton, E.G.; Riggan, P.J.; Yedinak, K.M. WRF-Fire: Coupled Weather–Wildland Fire Modeling with the Weather Research and Forecasting Model. J. Appl. Meteor. Climatol. 2013, 52, 16–38. [Google Scholar] [CrossRef]
- Alexandridis, A.; Russo, L.; Vakalis, D.; Bafas, G.V.; Siettos, C.I. Wildland fire spread modelling using cellular automata: Evolution in large-scale spatially heterogeneous environments under fire suppression tactics. Int. J. Wildland Fire 2011, 20, 633–647. [Google Scholar] [CrossRef]
- Dorrer, G.; Yarovoy, S. Use of Agent-Based Modeling for Wildfire Situations Simulation. In Proceedings of the 2018 3rd Russian-Pacific Conference on Computer Technology and Applications (RPC) 2018, Vladivostok, Russia, 18–25 August 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Xu, Z.; Li, J.; Cheng, S.; Rui, X.; Zhao, Y.; He, H.; Guan, H.; Sharma, A.; Erxleben, M.; Chang, R.; et al. Deep learning for wildfire risk prediction: Integrating remote sensing and environmental data. ISPRS J. Photogramm. Remote Sens. 2025, 227, 632–677. [Google Scholar] [CrossRef]
- Andrianarivony, H.S.; Akhloufi, M.A. Machine Learning and Deep Learning for Wildfire Spread Prediction: A Review. Fire 2024, 7, 482. [Google Scholar] [CrossRef]
- Zou, Y.; Sadeghi, M.; Liu, Y.; Puchko, A.; Le, S.; Chen, Y.; Andela, N.; Gentine, P. Attention-Based Wildland Fire Spread Modeling Using Fire-Tracking Satellite Observations. Fire 2023, 6, 289. [Google Scholar] [CrossRef]
- Ejaz, N.; Choudhury, S. A comprehensive survey of the machine learning pipeline for wildfire risk prediction and assessment. Ecol. Inform. 2025, 90, 103325. [Google Scholar] [CrossRef]
- Kale, M.P.; Meher, S.S.; Chavan, M.; Kumar, V.; Sultan, M.A.; Dongre, P.; Narkhede, K.; Mhatre, J.; Sharma, N.; Luitel, B.; et al. Operational Forest-Fire Spread Forecasting Using the WRF-SFIRE Model. Remote Sens. 2024, 16, 2480. [Google Scholar] [CrossRef]
- Donovan, G.H.; Rideout, D.B. An integer programming model to optimize resource allocation for wildfire containment. For. Sci. 2003, 49, 331–335. [Google Scholar] [CrossRef]
- Arrubla, J.A.; Ntaimo, L.; Stripling, C. Wildfire initial response planning using probabilistically constrained stochastic integer programming. Int. J. Wildland Fire 2014, 23, 825–838. [Google Scholar] [CrossRef]
- Zhou, S.; Erdogan, A. A spatial optimization model for resource allocation for wildfire suppression and resident evacuation. Comput. Ind. Eng. 2019, 138, 106101. [Google Scholar] [CrossRef]
- Granda, B.; Vitoriano, B.; Figueira, J.R. A mathematical programming approach for a wildfire suppression problem. Oper. Res. 2025, 25, 16. [Google Scholar] [CrossRef]
- Tezcan, B.; Eren, T. Forest fire resource planning with integer programming: An application in Turkey. For. Sci. Technol. 2025, 21, 318–325. [Google Scholar] [CrossRef]
- Petersen, J.E.; Kapur, S.; Gkantonas, S.; Mastorakos, E.; Giusti, A. Modelling and optimisation of extinction actions for wildfire suppression. Combust. Sci. Technol. 2023, 195, 3584–3595. [Google Scholar] [CrossRef]
- Renkas, A.; Popovych, V.; Rudenko, D. Optimization of Fire Station Locations to Increase the Efficiency of Firefighting in Natural Ecosystems. J. Environ. Res. Eng. Manag. 2022, 78, 97–104. [Google Scholar] [CrossRef]
- Trachanatzi, D.; Rigakis, M.; Marinaki, M.; Marinakis, Y. A modified Ant Colony System for the asset protection problem. Swarm Evol. Comput. 2022, 73, 101109. [Google Scholar] [CrossRef]
- Lankipalle, V. SwarmFusion: Revolutionizing Disaster Response with Swarm Intelligence and Deep Learning. arXiv 2025, arXiv:2507.00005. [Google Scholar] [CrossRef]
- de Azevedo Dantas, A.F.O.; Maitelli, A.L.; da Silva Linhares, L.L.; de Araujo, F.M.U. A Modified Matricial PSO Algorithm Applied to System Identification with Convergence Analysis. J. Control Autom. Electr. Syst. 2015, 26, 149–158. [Google Scholar] [CrossRef]
- Paiva, E.J.; Matos, M.A.; Rocha, A.M.A.C. A Simulation-Based Optimization Approach to the Firefighting Resource Scheduling Problem. In Computational Science and Its Applications—ICCSA 2024 Workshops; Lecture Notes in Computer Science 2024; Gervasi, O., Murgante, B., Garau, C., Taniar, D.C., Rocha, A.M.A., Faginas Lago, M.N., Eds.; Springer: Cham, Switzerland, 2024; Volume 14816. [Google Scholar] [CrossRef]
- Akopov, A.S. MBHGA: A Matrix-Based Hybrid Genetic Algorithm for Solving an Agent-Based Model of Controlled Trade Interactions. IEEE Access 2025, 13, 26843–26863. [Google Scholar] [CrossRef]
- SILVANUS Consortium. Deliverable D5.3: Demonstration of SILVANUS Decision Support System for Response Coordination; SILVANUS Project, Grant Agreement No. 101037247 (H2020-LC-GD-2020-3); Horizon 2020 EU. Available online: https://silvanus-project.eu/wp-content/uploads/2023/12/SILVANUS-D5.3.pdf (accessed on 10 August 2025).
- Chen, R.; Yan, H.; Liu, F.; Du, W.; Yang, Y. Multiple Global Population Datasets: Differences and Spatial Distribution Characteristics. ISPRS Int. J. Geo-Inf. 2020, 9, 637. [Google Scholar] [CrossRef]
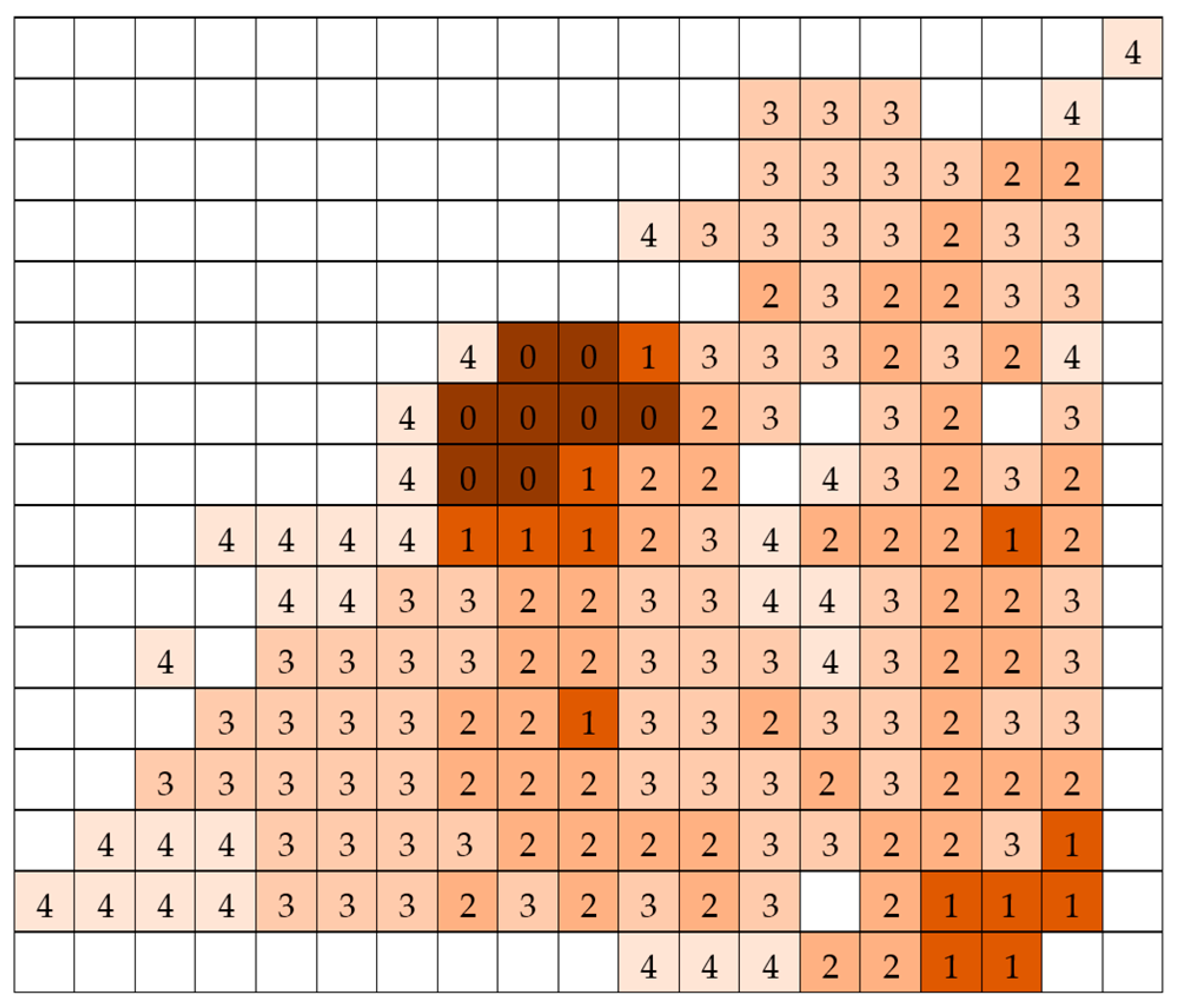
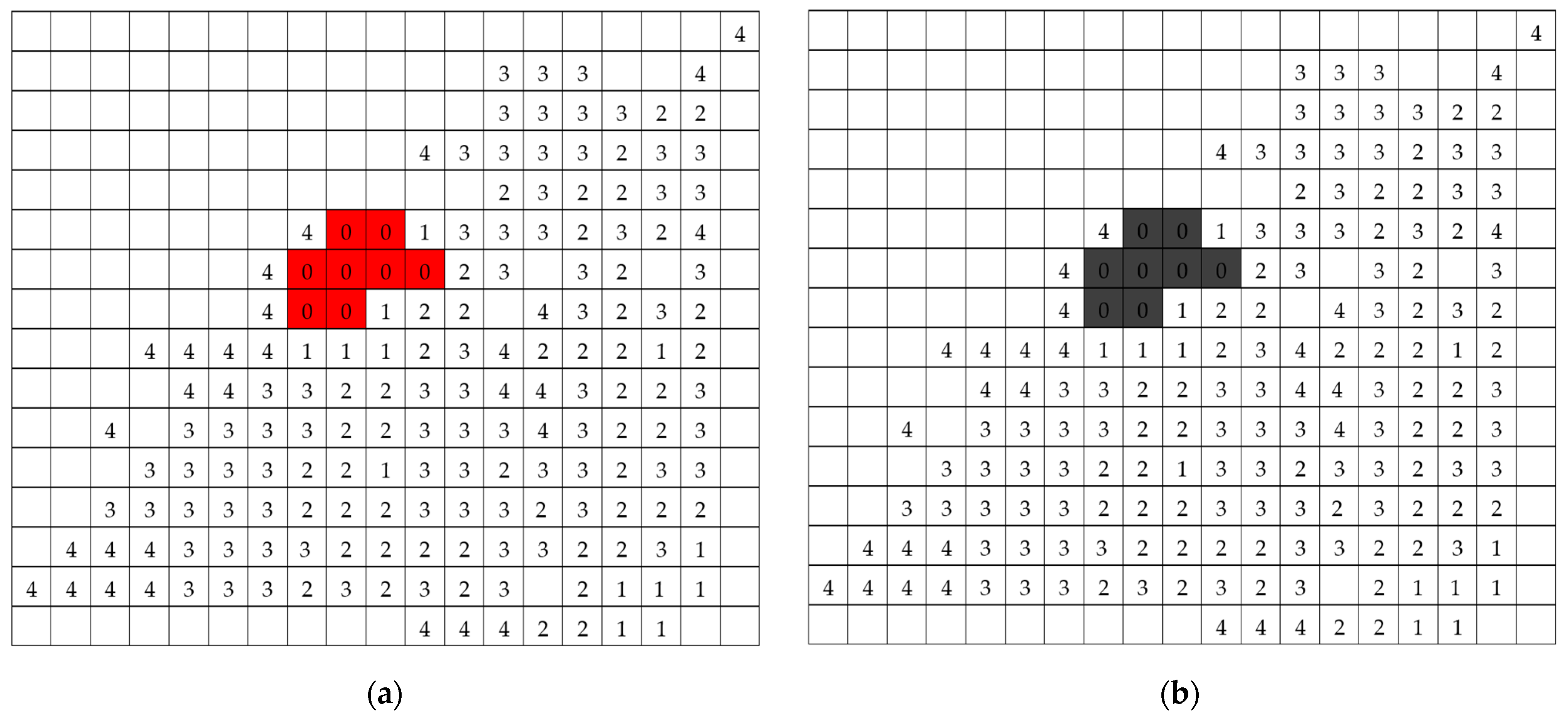
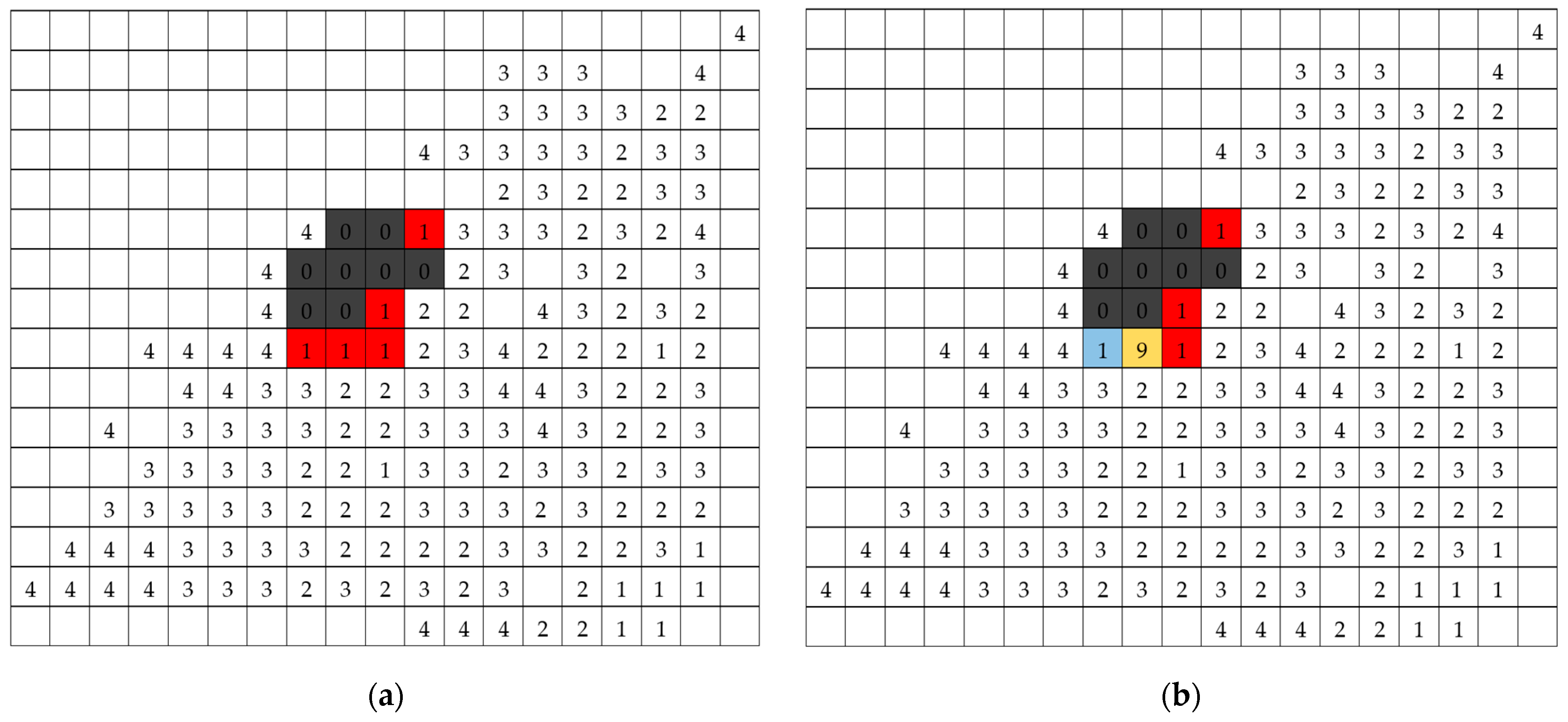
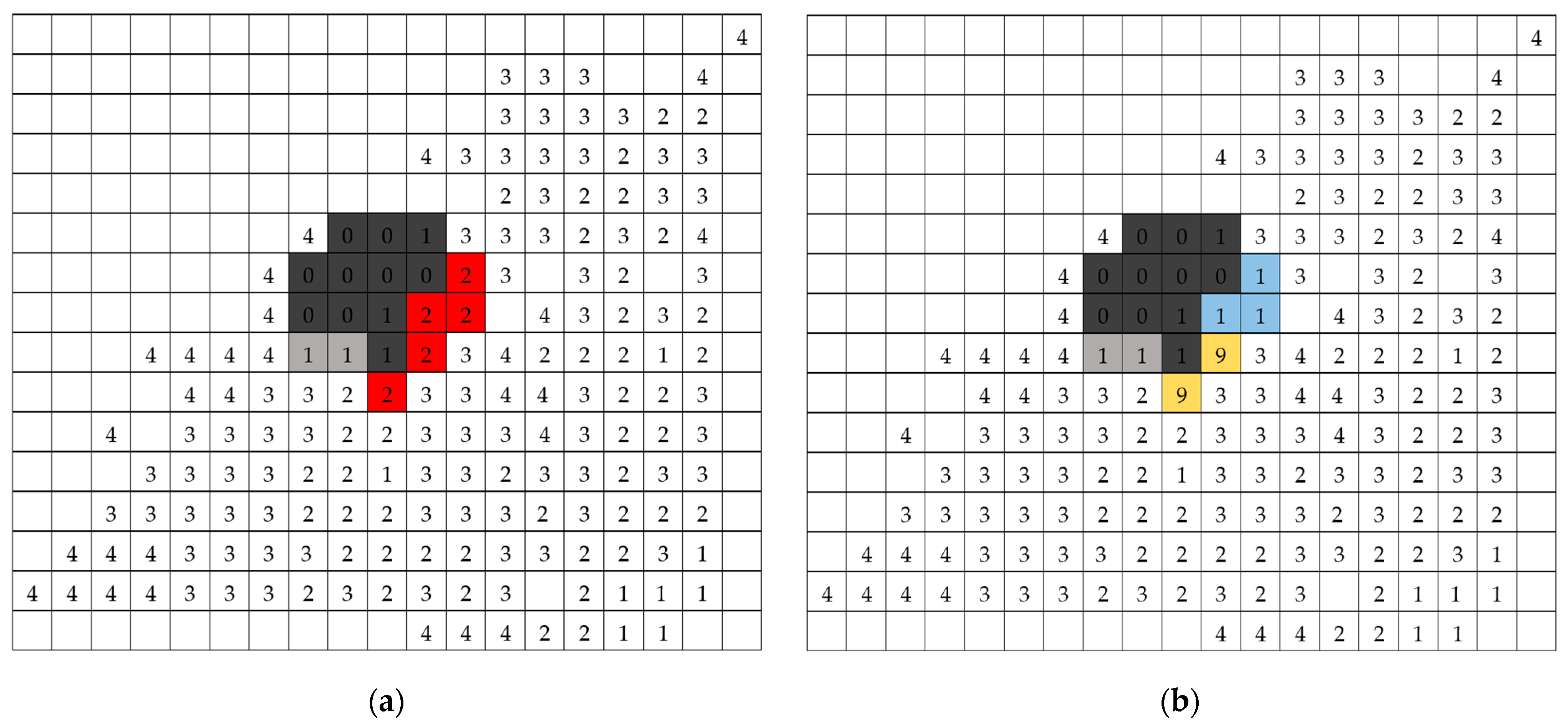
| Resource Type | Suppression Rate | Cost | Capacity (vs. Availability at Different Timeslots) |
|---|---|---|---|
| A | 2 | t = 0:4 | |
| 5 | t = 1:4 | ||
| t = 2:4 | |||
| B | 5 | t = 0:3 | |
| 15 | t = 1:2 | ||
| t = 2:4 | |||
| C | 10 | 20 | t = 0:0 t = 1:0 |
| t = 2:1 |
| Resource Type | Suppression Rate (Chains/Hour) | Cost | Capacity (vs. Availability at Different Timeslots) |
|---|---|---|---|
| Hand Crew | 1 | t = 0:0 | |
| 2 | t = 1:10 | ||
| t = 2:18 t = 3:20 t = 4:8 | |||
| Engine Crew | 9 | 6 | t = 0:0 |
| t = 1:1 | |||
| t = 2:3 t = 3:2 t = 4:1 | |||
| Helicopter | 15 | 10 | t = 0:0 t = 1:0 |
| t = 2:0 t = 3:0 t = 4:1 |
| Time Period | Time (Min) | Minimum Suppression Rate (Chains/Hour) |
|---|---|---|
| 0 | 0 | 9 |
| 1 | 15 | 9 |
| 2 | 30 | 9 |
| 3 | 60 | 4 |
| 4 | 120 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orphanoudakis, T.; Betzelos, C.; Leligou, H.C. MORA: A Multicriteria Optimal Resource Allocation and Decision Support Toolkit for Wildfire Management. Algorithms 2025, 18, 677. https://doi.org/10.3390/a18110677
Orphanoudakis T, Betzelos C, Leligou HC. MORA: A Multicriteria Optimal Resource Allocation and Decision Support Toolkit for Wildfire Management. Algorithms. 2025; 18(11):677. https://doi.org/10.3390/a18110677
Chicago/Turabian StyleOrphanoudakis, Theofanis, Christos Betzelos, and Helen Catherine Leligou. 2025. "MORA: A Multicriteria Optimal Resource Allocation and Decision Support Toolkit for Wildfire Management" Algorithms 18, no. 11: 677. https://doi.org/10.3390/a18110677
APA StyleOrphanoudakis, T., Betzelos, C., & Leligou, H. C. (2025). MORA: A Multicriteria Optimal Resource Allocation and Decision Support Toolkit for Wildfire Management. Algorithms, 18(11), 677. https://doi.org/10.3390/a18110677






