1. Introduction
Every chemical molecule can be abstracted as a molecular graph, in which atoms correspond to the vertices and chemical bonds correspond to the edges of the graph [
1]. For example, a fullerene can be regarded as a 3-regular planar connected molecular graph composed of pentagonal and hexagonal faces [
2]. Topological indices are measures that use the structural parameters of molecular graphs to study the physicochemical properties of molecules, and constitute an important direction in mathematical chemistry. Experimental studies have further shown that the stability of fullerenes is closely related to their Kekulé structure number (i.e., the number of perfect matchings in graph theory) [
3,
4,
5] and to invariants such as the permanental polynomial [
6,
7].
In 2004, after Xie et al. [
8] captured the fullerene
, Tong et al. [
9] calculated, from a mathematical perspective, the coefficients of the permanental polynomial of all 271 isomers of
, and found that the sum of the absolute values of the coefficients of the permanental polynomial of
was the smallest among all 271
isomers. They also pointed out that the coefficients of the permanental polynomial are related to the stability of fullerenes. To study this phenomenon from the viewpoint of graph theory, Wu and Lai [
10] proposed the permanental sum as a topological index, defining it as the sum of the absolute values of all coefficients of the permanental polynomial. Since its introduction, has attracted significant attention from researchers. For example, Li et al. [
11] studied the properties of the permanental sum of octagonal chains; Wu et al. [
12] provided upper and lower bounds for the permanental sum of helical hexagonal chains; and Wei Li et al. [
13] determined the permanental sum of planar quadrilateral linear chains and cylindrical quadrilateral linear rings. For more results on the permanental sum, see [
14,
15].
Since the computation of the permanental sum is inherently difficult, Wu and So [
16] showed that calculating the permanental sum is equivalent to computing a matrix permanent. To evaluate the permanent, several classical algorithms have been developed, including Ryser’s algorithm [
17], the R–NW algorithm [
18], and Kallman’s algorithm [
19]. Ryser’s algorithm converts the permanent computation into a weighted sum over all subsets of columns and has a time complexity of
. Based on this method, Nijenhuis and Wilf proposed the R–NW algorithm, which optimizes the computation range and subset traversal, reducing the complexity to
. Kallman’s algorithm, on the other hand, decomposes, reduces, and simplifies the matrix rows recursively, transforming the original problem into smaller subproblems that can be solved using a closed-form formula, with a complexity of
. These classical exact algorithms lay the theoretical foundation for the exponential complexity of permanent computation. Over the past two decades, research on permanent algorithms has evolved in more diverse directions. In the domain of approximation algorithms, Jerrum et al. [
20] proposed a fully polynomial time-randomized approximation scheme based on Markov chain Monte Carlo methods for computing the permanent of nonnegative matrices. In addition, Anari et al. [
21] developed a deterministic approximation algorithm for the permanent of positive semidefinite (PSD) matrices. In the study of parameterized complexity, Curticapean et al. [
22] conducted a systematic analysis of the permanent problem, exploring the complexity boundaries within the fixed-parameter tractable (FPT) framework based on various structural parameters, including graph genus, excluded minors, and modular evaluation. Recent research on permanent algorithms has thus formed a diversified framework encompassing exact computation, approximation methods, and parameterized analysis. Although permanent computation remains #P-complete in general, efficiently solvable subclasses for specific matrix structures or graph families, as well as effective approximation algorithms, continue to emerge. Against this background, designing structure-aware exact algorithms for chemical molecular graphs—particularly the sparse and highly symmetric (3,6)-fullerenes—has significant theoretical and practical value.
On the other hand, the Hosoya index is an important topological descriptor for studying molecular matching properties. According to the relationship between the permanental sum and the Hosoya index derived by Wu and Jiu [
23], the Hosoya index can be regarded as a component of the permanental sum. However, the computational methods for the Hosoya index remain scarce. Manuel et al. [
24] proposed a recursive algorithm that first sorts the edge set and constructs an edge adjacency matrix, then recursively accumulates the sizes of independent edge sets to obtain the Hosoya index. Jerrum [
25] proved that computing the Hosoya index is a #NP-complete problem. Given its high computational complexity, developing efficient algorithms for the Hosoya index is also of significant interest.
In summary, research on the computational algorithms for the permanental sum and the Hosoya index remains insufficient. From an algorithmic perspective, this paper proposes two unified computational methods and applies them to the topological structure analysis and synthesis prediction of small-molecule (3,6)-fullerenes.
Although various algorithms for computing the permanental sum and the Hosoya index have been developed, the existing studies still exhibit the following three limitations when applied to chemical molecular graphs:
(1) Most algorithms are designed for general matrices or tree-like graphs and lack structural optimization tailored to sparse and highly symmetric molecular graphs (such as (3,6)-fullerenes); (2) classical algorithms (e.g., Ryser and R–NW algorithms) can compute the permanent exactly but their time complexity grows exponentially, making them impractical for medium-scale molecular systems; and (3) existing recursive algorithms for the Hosoya index incur significant computational and memory costs when the number of edges increases and are highly sensitive to edge ordering.
To overcome these limitations, this study proposes two types of structure-aware algorithms:
Permanental sum algorithm: based on Kallman’s closed-form formula and GPU array computation, the algorithm combines binary encoding of matrix rows with structural pruning, reducing the computational complexity from the traditional to approximately ;
Hosoya index algorithm: incorporates bitmask representation and memoized dynamic programming to effectively control the state space while maintaining exactness.
Under a unified framework, these two algorithms achieve efficient topological computation for chemical molecular graphs, providing theoretical support for the synthesis prediction of small-molecule (3,6)-fullerenes and offering new insights for the further development of topological index algorithms.
The remainder of this paper is organized as follows.
Section 2 introduces the fundamental graph-theoretic definitions and topological indices as preliminary knowledge.
Section 3 and
Section 4 present the algorithms for calculating the permanental sum and Hosoya index, respectively.
Section 5 combines both algorithms to calculate the permanental sum and Hosoya index of small (3,6)-fullerenes for synthesis prediction.
Section 6 provides conclusions, and
Section 7 discusses the limitations of this study.
3. Permanental Sum Algorithm
This section mainly introduces an algorithm for computing the permanental sum. Before that, we first present some related lemmas.
Lemma 1 ([
31])
. If a matrix has two rows , then Lemma 2 ([
31])
. Let , where is a singleton row, and for any , have or . Then, Lemma 3 ([
31])
. If some row is a universal row (equal to the union of all rows), thenwhere denotes the number of 1s in . Based on the above lemmas, using Kallman’s closed formulas [
31] together with above Formula (
2), and combined with GPU array computation, we design an algorithm for computing the permanental sum of (0,1)-matrices. The Algorithm 1 steps are as follows:
| Algorithm 1: Permanental Sum Algorithm |
![Algorithms 18 00673 i001 Algorithms 18 00673 i001]() |
Parameter Description: row threshold
: only rows with a number of nonzero elements greater than this threshold are retained; column threshold
: only columns with a number of nonzero elements greater than this threshold are retained; Typically,
, which significantly reduces the computational dimension while maintaining structural completeness. Lemmas 2 and 3 are applied to identify structurally redundant row vectors, enabling effective pruning. For matrices with
, the permanent is computed directly using the explicit closed-form expression.
The GPU-accelerated component of the permanental sum algorithm was implemented using the MATLAB R2023a GPU Computing Toolbox, and all computations were performed on a local computer, an ASUS laptop (ASUSTeK Computer Inc., Taipei, Taiwan) equipped with an Intel Core i5-7200U processor (2.71 GHz) and an NVIDIA GeForce 940MX GPU (2 GB GDDR5 memory). The input adjacency matrix A was transferred to GPU memory via the gpuArray structure, and matrix operations such as sum(A_gpu, 2) and sum(A_gpu, 1) were executed directly on the GPU. These operations are automatically parallelized within the CUDA kernel, enabling implicit multithreaded computation without the need for explicit kernel programming. After the threshold filtering process, the processed submatrix was transferred back to the CPU, where a custom function was invoked to compute the permanental sum.
The proposed algorithm for the permanental sum employs binary encoding and sorting of matrix rows during preprocessing and structural ordering, with complexity of approximately . For pruning, Lemma 2 and Lemma 3 are utilized for structural pruning with a complexity of . During GPU-accelerated submatrix screening, row and column sums are used to filter out submatrices with negligible contributions, further reducing computation. In the inclusion–exclusion aggregation step, the permanental sum of submatrices are weighted and combined to ensure accuracy without redundancy. The overall computational complexity is approximately , which is significantly more efficient than the traditional Ryser algorithm.
4. Hosoya Index Algorithm
This section presents algorithms for computing the Hosoya index and begins with a review of existing research.
The Hosoya index is a classical topological index in chemical graph theory, defined as the total number of independent edge sets (matchings) in a graph [
26]. For trees, it can be computed via dynamic programming on vertex subsets, a method that has been described in detail in the literature [
32]. In addition, [
33,
34] computed the Hosoya index for pristine coronoid systems and condensed hexagonal systems, respectively.
Existing algorithms can be broadly divided into two categories: (i) vertex–subset dynamic programming methods [
32], which are suitable for trees and some sparse graph structures and can effectively reduce computational complexity and memory usage; and (ii) edge–set recursion methods [
24], which involve extensive operations on edge sets during computation. The latter approach leads to significantly increase the complexity when the graph is large or dense, tends to incur high memory usage, and is sensitive to the ordering of edges.
To address the limitations of the algorithm by Manuel et al., we optimize the computation of the Hosoya index. Within a dynamic programming framework, we represent vertex subsets by binary bitmasks and employ memoization to reduce both time and space complexity. The Algorithm 2 proceeds as follows:
| Algorithm 2: Hosoya Index Algorithm |
- Input:
Adjacency matrix of a simple undirected graph without loops or multiple edges - Output:
Hosoya index and the running time of the program - 1
Step 1: Adjacency preprocessing; - 2
For each vertex v, record its neighbor set ; - 3
Convert each neighbor set into a bitmask (the i-th bit equals 1 iff vertex i is a neighbor) and store them for fast matching checks; - 4
Step 2: Dynamic programming; - 5
Define a function , where is an n-bit integer indicating the set of currently available vertices (1 means that the vertex has not been matched; 0 means that the vertex has already been matched); - 6
Base case: if , return 1; - 7
Transition: choose the smallest-index available vertex v; the count equals the sum of the following two cases:; - 8
(a) Exclude v: compute ; - 9
(b) Include v: iterate over all vertices u adjacent to v that are available in , compute , and sum the results; - 10
Memoization: cache results of already computed states to avoid recomputation; - 11
Step 3: Computing the Hosoya index; - 12
Initialize with all vertices available and call ; - 13
The result is the Hosoya index ; - 14
return and the running time
|
Notes on parameters: Bitmask of neighbor sets: represent vertex adjacencies in binary to speed up matching checks. Memoization cache: store the computed values of
to reduce redundant computation.
The Hosoya index computation algorithm proposed in this paper, during the adjacency preprocessing phase, traverses each vertex in the graph along with its adjacency relations, and stores them in a compressed form using bitmasks. The complexity of this phase is approximately , where n is the number of vertices. In the recursive search and memoization phase, bitwise operations are used to quickly extract the lowest-numbered vertex and its neighbor set in the current state, and two types of computations are performed separately: “Excluding the vertex” and “Including the vertex”. For each vertex, the complexity of vertex selection and neighbor iteration is , where is the degree of the current vertex. Since memoization is employed, each vertex is computed only once, avoiding the exponential accumulation of repeated subproblems. Therefore, the overall computational complexity of the algorithm is .
5. Synthesis Prediction of Small-Molecule (3,6)-Fullerenes
The permanental sum and Hosoya index, as important topological indices for studying chemical molecules. In this section, we used the above two algorithms to identify the molecular graphs with the minimum permanental sum and Hosoya index, providing guidance for the synthesis of small-molecule (3,6)-fullerenes.
For a positive integer
, a (
k,6)-fullerene graph is defined as a 3-regular (each vertex of degree 3) planar graph whose faces consist of only
k-gons and hexagons. According to Euler’s formula
, such (
k,6)-fullerene graphs exist only for
. Among them, (5,6)-fullerene graphs correspond to classical fullerene molecules (e.g.,
), while (4,6)-fullerene graphs correspond to boron–nitrogen fullerene molecules (e.g.,
). In the approximately forty years since the discovery of
fullerene in 1985, researchers have successfully synthesized large carbon-cage fullerenes (with more than 70 carbon atoms), such as
,
,
,
,
, and
[
35,
36,
37,
38,
39,
40]. Troshin [
41] and Qian [
42] synthesized non-classical fullerene derivatives
and
(containing non-pentagonal or non-hexagonal faces). In addition, Chen et al. [
43] systematically studied 31 isomers of the boron–nitrogen fullerene
and identified its most stable structure. Compared to the extensive research on (5,6)-fullerenes and (4,6)-fullerenes, (3,6)-fullerenes have not yet been synthesized experimentally, and theoretical studies are also limited. Due to their unique geometric configurations, (3,6)-fullerenes may exhibit physicochemical properties distinct from those of (5,6)-fullerenes and (4,6)-fullerenes. However, the existing research on the structural prediction, stability analysis, and synthesis pathways of (3,6)-fullerenes is extremely limited, restricting their potential applications in nanomaterials, catalysts, and energy storage. Inspired by the studies on (5,6)-fullerenes and (4,6)-fullerenes, this paper investigates the synthesis prediction of small molecule (3,6)-fullerenes from a mathematical perspective, which is of considerable value and can provide theoretical guidance for their synthesis.
Although (3,6)-fullerenes have not yet been synthesized experimentally, their structural characteristics have been extensively studied by both mathematicians and chemists. For instance, Motzkin et al. [
44] deduced that the number of vertices in a (3,6)-fullerene must be a multiple of 4. Shabbir et al. [
45] further established the relations among the number of vertices
n, the number of edges
m, the radius
r, and the Step
S as
. Combined with Euler’s formula
, it follows that a (3,6)-fullerene graph with
n vertices contains exactly 4 triangular faces and
hexagonal faces [
46]. Therefore, the connectivity of such graphs is either 2 or 3.
Yang and Zhang [
47] characterized the structure of (3,6)-fullerenes with connectivity 2.
Lemma 4 ([
47])
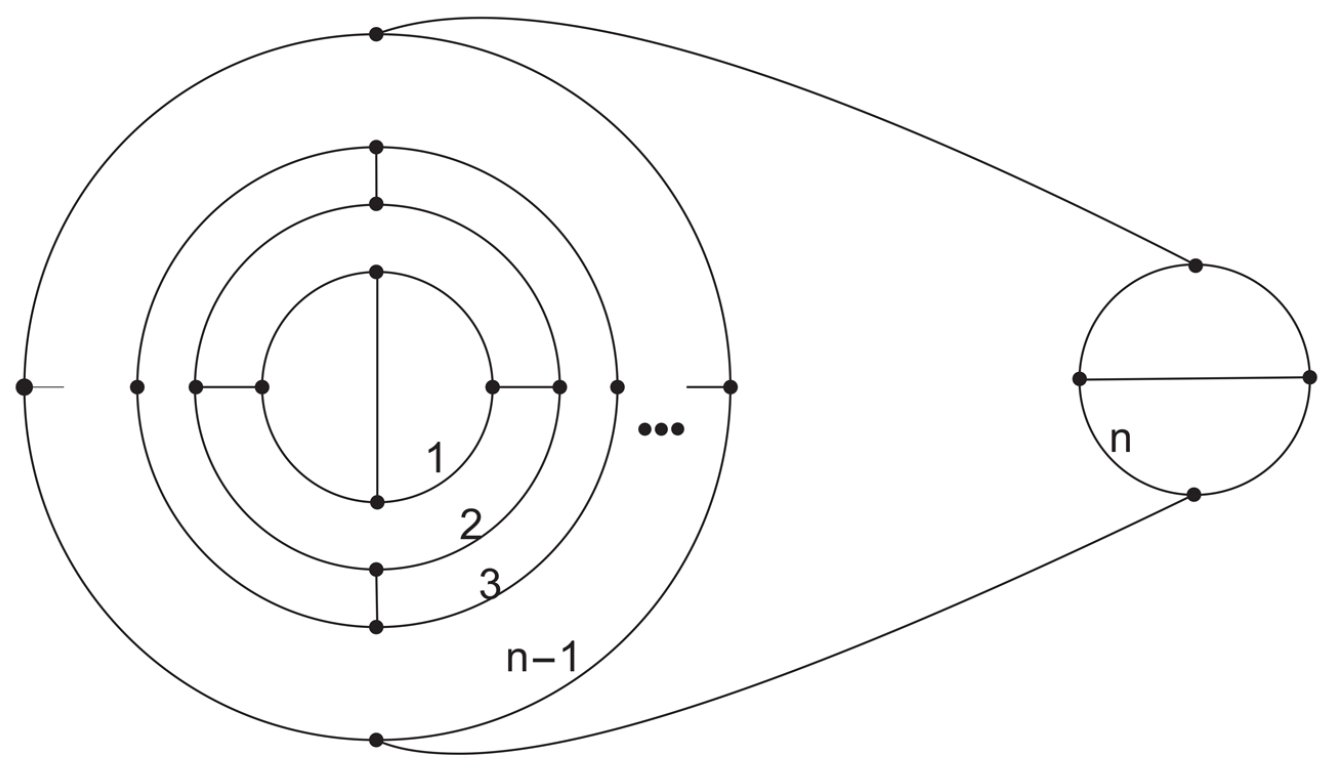
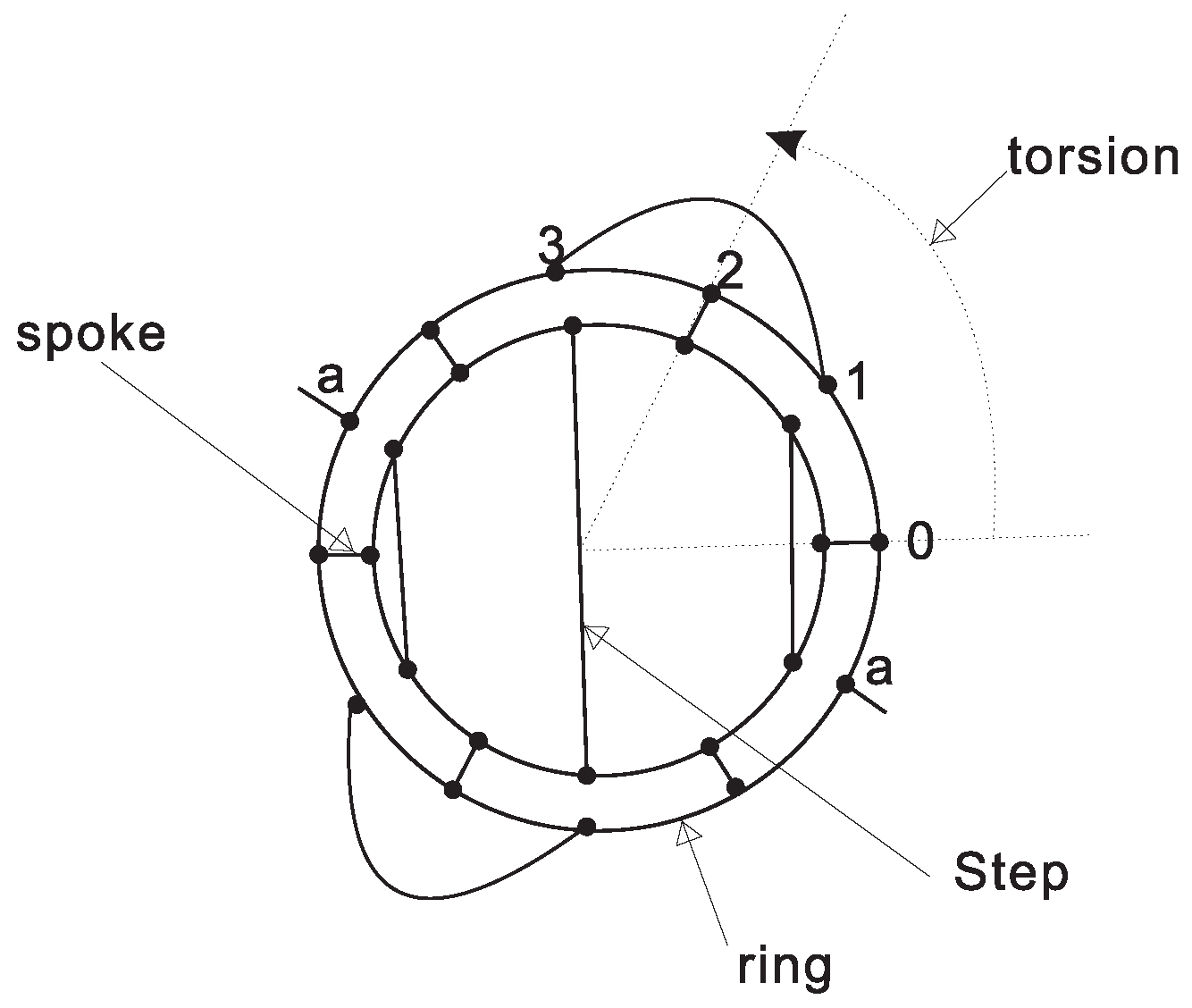
. A (3,6)-fullerene graph G has connectivity 2 if and only if . Where n() is an integer, and is constructed from n concentric layers of hexagons capped at both ends with a pair of triangles (see Figure 1). The structure of (3,6)-fullerene with connectivity 3 is determined by three parameters:
r,
S, and
t. Here,
denotes the radius, which is the number of circles.
S represents the Step, defined as the number of spokes in each layer
, where
and is even. Finally,
t is the torsion or twist, satisfying
and
. Based on these parameters, the specific topological structure of (3,6)-fullerene can be constructed. For example,
Figure 2 shows the topological structure of a 3-connected (3,6)-fullerene with parameters
.
Based on the above structural properties, it can be seen that the minimum number of vertices of (3,6)-fullerene is 4, at this point, the corresponding graph is a regular tetrahedron. By graph theoretical analysis, we obtained the number of isomers of (3,6)-fullerenes with
vertices, as shown in
Table 1.
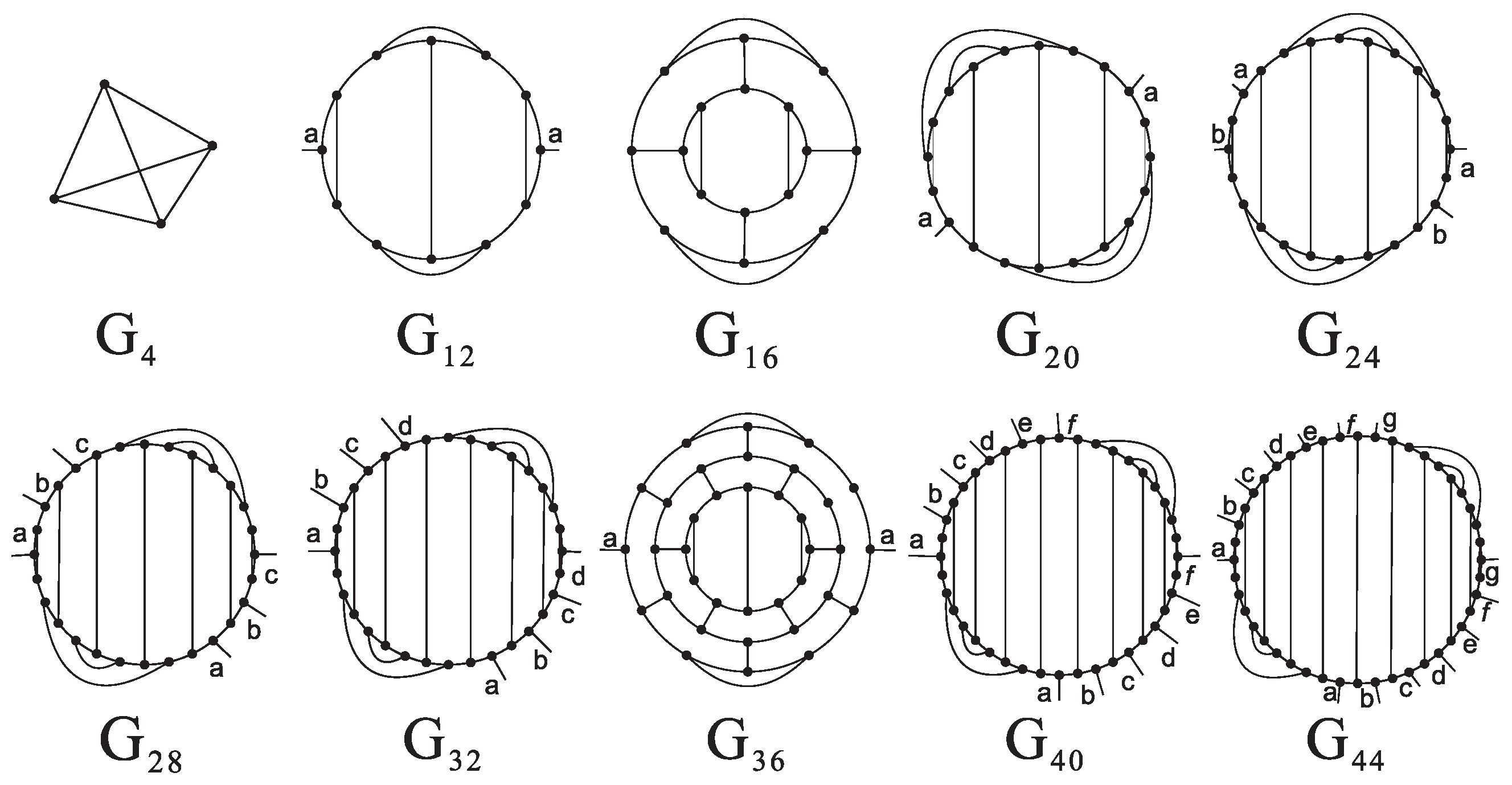
Let
denote a (3,6)-fullerene graph with
n vertices. Based on the above structural properties of (3,6)-fullerenes, and by applying the algorithms presented earlier (See Algorithm 1), we calculated the minimum permanental sum values of (3,6)-fullerene isomers with
n vertices
(see
Table 2), and determined that their corresponding graph structures are
, as illustrated in
Figure 3.
The structure shown in
Figure 3 corresponds to the permanental sum and minimal (3,6)-fullerene molecule
calculated in
Table 2. Its local topological features are the primary factors leading to the minimal permanental sum. Based on the findings of Xie et al. [
8], these (3,6)-fullerene structures can be regarded as candidate molecular structure models with potential synthetic feasibility in theory. However, the minimality of the permanental sum does not imply that the structure has been successfully synthesized, and its actual feasibility still requires further validation through quantum chemical calculations and experimental studies by chemists.
Furthermore, by analyzing the graph structures of (3,6)-fullerenes with minimum permanental sum, we summarized the following relationships among the structural parameters r, S, and t for any (3,6)-fullerene with vertices when its permanental sum reaches the minimum value:
When the step , the torsion ;
When the step , the torsion .
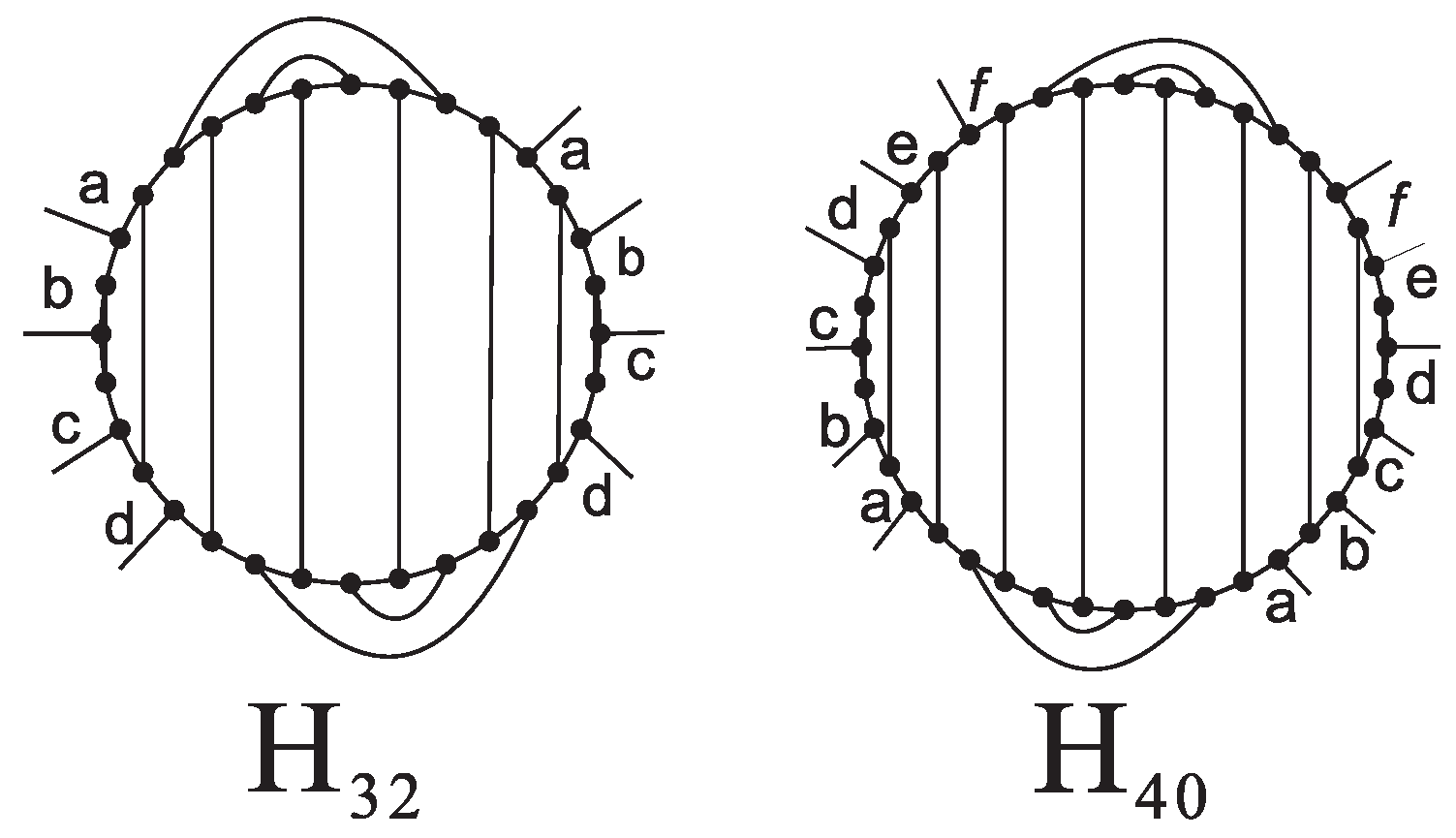
The Hosoya index, as a special chemical topological index, is closely related to the permanental sum. Using the algorithms provided earlier (See Algorithm 2), we computed the minimum Hosoya index values of (3,6)-fullerene isomers with
n vertices
(see
Table 3), and further determined their corresponding molecular graph structures. Specifically, for
, the (3,6)-fullerene molecular structures with minimum permanental sum are identical to those with minimum Hosoya index; however, for
and
, the (3,6)-fullerene molecular structures corresponding to the minimum permanental sum and minimum Hosoya index differ, as shown in
Figure 4. To distinguish them, we denote the (3,6)-fullerene structures corresponding to the minimum Hosoya indices as
.
Through the preceding analysis, we found that the (3,6)-fullerene molecular structures corresponding to the minimum values of the Hosoya index and the permanental sum are highly consistent. This result theoretically strengthens the rationale for prioritizing the (3,6)-fullerene structures that share the same minimal values of these two indices in studies of structural stability and synthetic feasibility. However, their actual synthesizability still requires further verification through quantitative calculations and experimental investigations. In particular, when and 44, the (3,6)-fullerene molecular structures corresponding to the minimal values of the permanent sum and the Hosoya index are completely identical, suggesting that these structures may possess higher synthetic potential.
7. Limitations
Although the algorithms proposed in this study provide an effective computational framework for evaluating the permanental sum and Hosoya index of molecular graphs, several limitations remain that need to be addressed in future research.
First, the computational complexity of both algorithms is inherently exponential. The computation of the permanental sum belongs to the class of #P-complete problems, and the Hosoya index is known to be #NP-complete. Despite the incorporation of recursive decomposition, pruning strategies, and GPU acceleration, the time and memory requirements still increase exponentially with the number of vertices. Therefore, the proposed algorithms are mainly practical for small- and medium-sized molecular systems, and further optimization or approximation techniques are required for large-scale graphs.
Second, the chemoinformatic predictions derived from the minimal permanental sum and Hosoya index are theoretical and speculative. The correlations between these topological indices and molecular stability are based purely on mathematical structures. Hence, the predicted synthesizability of small (3,6)-fullerenes should be regarded as a theoretical hypothesis rather than an experimentally verified conclusion. Future work should integrate the presented computational framework with quantum chemical simulations or experimental studies to validate these theoretical predictions.
Overall, these limitations define the theoretical scope of the present work and provide directions for extending the applicability of the proposed algorithms and models.