Abstract
In response to the issues of premature convergence and insufficient parameter control in Particle Swarm Optimization (PSO) for high-dimensional complex optimization problems, this paper proposes a Multi-Strategy Topological Particle Swarm Optimization algorithm (MSTPSO). The method builds upon a reinforcement learning-driven topological switching framework, where Q-learning dynamically selects among fully informed topology, small-world topology, and exemplar-set topology to achieve an adaptive balance between global exploration and local exploitation. Furthermore, the algorithm integrates differential evolution perturbations and a global optimal restart strategy based on stagnation detection, together with a dual-layer experience replay mechanism to enhance population diversity at multiple levels and strengthen the ability to escape local optima. Experimental results on 29 CEC2017 benchmark functions, compared against various PSO variants and other advanced evolutionary algorithms, show that MSTPSO achieves superior fitness performance and exhibits stronger stability on high-dimensional and complex functions. Ablation studies further validate the critical contribution of the Q-learning-based multi-topology control and stagnation detection mechanisms to performance improvement. Overall, MSTPSO demonstrates significant advantages in convergence accuracy and global search capability.
1. Introduction
Optimization techniques play a central role in fields such as engineering design, machine learning, artificial intelligence, and operations research. From parameter optimization of complex mechanical structures to hyperparameter tuning of deep learning models, efficient optimization algorithms are the key to solving practical problems. Current mainstream optimization algorithms include differential evolution (DE) [1,2], Genetic Algorithm (GA) [3], Bayesian Optimization (BO) [4], and Artificial Bee Colony (ABC) algorithm [5], among which Particle Swarm Optimization (PSO) has been widely applied due to its simple structure, easy parameter adjustment, and convenient implementation [6,7,8]. Since its introduction by Kennedy and Eberhart in 1995, PSO has simulated the social behavior of biological populations to perform optimization search and has spawned numerous improved variants [6]. However, traditional PSO still suffers from significant limitations: most variants are effective only for specific problem types, PSO tends to fall into local optima in high-dimensional multimodal functions, and fixed topology structures limit population diversity [9,10]. To overcome these bottlenecks, researchers have systematically improved PSO in several directions.
First, hybrid strategies integrate the strengths of different algorithms to enhance search performance. Recent studies include GWOPSO, which combines Grey Wolf Optimization (GWO) with PSO by leveraging PSO’s population collaboration mechanism and GWO’s hierarchical hunting strategy [11]; ECCSPSOA, which integrates chaotic crow search with PSO to improve the diversity of initial solutions for feature selection problems [12]; and HGSPSO, which merges gravitational search with PSO to optimize particle interactions via a gravity model [13]. In particular, hybridization of PSO and differential evolution (DE) has become a research hotspot: heterogeneous DE-PSO improves exploitation through local search [14], while Mutual Learning DE-PSO enhances global exploration by knowledge sharing among swarms [15]. These hybrid approaches have demonstrated significant advantages in complex function optimization tasks, as validated on CEC2017 benchmarks [16,17].
Second, learning strategies focus on building efficient guidance mechanisms. Liu et al. proposed simplified PSO models with cognitive, social, and temporal-hierarchical strategies (THSPSO), which dynamically update learning patterns to improve optimization efficiency and significantly shorten convergence time compared with standard PSO in complex function optimization [10]. Huang et al. introduced the LRMODE algorithm, which incorporates ruggedness analysis of the fitness landscape to refine particle learning directions [18]. Lu et al. employed reinforcement learning to guide particle behavior, integrating historical successful experiences into wastewater treatment control optimization [19]. Zhao et al. proposed the mean-hierarchy PSO (MHPSO), which stratifies particles according to population mean fitness and uses stochastic elite neighbor selection to maintain diversity [20]. Wang et al. developed the SCDLPSO algorithm with self-correction and dimension-wise learning ability to strengthen links between individual and global bests for solving complex multimodal problems [21]. Other studies have enhanced adaptability at different stages by introducing adaptive inertia weights and learning factors [22,23]. These methods dynamically adjust learning exemplars to strengthen PSO’s adaptability to complex problems.
Third, neighborhood topology innovations are critical to improving PSO performance. While traditional global topology risks premature convergence and local topology converges slowly [24], dynamic topologies provide balance. For example, SWD-PSO employs small-world networks with dense short-range links and random long-range connections to accelerate global information exchange [25]. DNSPSO adapts neighborhood range via dynamic switching mechanisms [26], while MNPSO applies distance-adaptive neighborhoods to improve nonlinear equation solving [27]. Pyramid PSO (PPSO) enhances population diversity through competition-cooperation strategies and multi-behavior learning [28]. Liang et al. proposed NRLPSO, a neighborhood differential mutation PSO guided by reinforcement learning, with a dynamic oscillatory inertia weight to adapt particle motion [29]. Jiang et al. developed HPSO-TS, a hybrid PSO with time-varying topology and search perturbation, which uses K-medoids clustering to dynamically divide the swarm into heterogeneous subgroups, facilitating intra-group information flow and global-local search transitions [30]. Zeng et al. further proposed a dynamic-neighborhood switching PSO (DNSPSO) with a novel velocity update rule and switching strategy, showing excellent performance on multimodal optimization problems [26]. These topology improvements have greatly enhanced search capability in high-dimensional spaces.
Finally, adaptive parameter control in PSO has evolved from heuristic rules to intelligent learning strategies. Tatsis et al. introduced an online adaptive parameter method that combines performance estimation with gradient search, significantly improving robustness in complex environments [31]. Chen et al. developed MACPSO, which applies multiple Actor-Critic networks to optimize parameters in continuous space, balancing global exploration and local exploitation [16]. Liu et al. proposed QLPSO, where Q-learning trains parameters and Q-tables guide particle actions based on states, improving search efficiency in complex solution spaces [32]. A deep reinforcement learning-based PSO (DRLPSO) [33] employs neural networks to learn state-action mappings and dynamically adjust parameters for high-dimensional tasks. Hamad et al. proposed QLESCA, which introduces Q-learning into the sine cosine algorithm (SCA) to achieve adaptive tuning of key parameters, significantly improving convergence speed and solution accuracy. Subsequent studies applied QLESCA to high-dimensional COVID-19 feature selection, verifying its potential in high-dimensional problems; however, the overall optimization strategy remains primarily parameter-focused [34,35]. RLPSO algorithm employs a reinforcement learning strategy to adaptively control the hierarchical structure of the swarm, adjusting search modes across different levels to balance exploration and exploitation [36]. Most existing RL-PSO methods still concentrate on parameter-level adaptation. Although this improves convergence performance to some extent, little work has addressed adaptive control of the swarm topology. As topology determines the interaction pattern among particles, it plays a crucial role in maintaining population diversity and balancing exploration and exploitation. Therefore, introducing reinforcement learning for dynamic topology selection remains an area requiring further investigation. Based on this background, the main contributions of this paper are as follows:
- A reinforcement learning-based topology switching strategy is proposed, enabling particles to dynamically select among FIPS, small-world, and exemplar-set topologies to balance global exploration and local exploitation.
- A dual-layer Q-learning experience replay mechanism is designed, integrating short-term and long-term memories to stabilize parameter control and improve learning efficiency.
- A stagnation detection mechanism is constructed and combined with differential evolution perturbations and a global restart strategy to enhance population diversity and improve the ability to escape local optima.
Compared with existing RL-PSO methods that mainly focus on parameter adaptation, the proposed MSTPSO applies reinforcement learning to adaptive control of swarm topology, optimizing the information exchange pattern at the structural level and thereby improving convergence efficiency and robustness. The remainder of this paper is organized as follows: Section 2 reviews PSO and reinforcement learning–related theories. Section 3 describes the design and implementation of MSTPSO. Section 4 presents performance validation on the CEC2017 benchmark and ablation analysis of each component. Section 5 concludes the study and outlines future research directions.
2. Background Information
2.1. Particle Swarm Optimization
The Particle Swarm Optimization (PSO) algorithm was proposed by Kennedy and Eberhart in 1995 [7], inspired by the foraging behavior of bird flocks. In PSO, each individual in the population is abstracted as a “particle”, and each particle’s position corresponds to a potential solution to the optimization problem. Through cooperation and information sharing within the swarm, global optimal search can be achieved. In a standard PSO, a particle swarm consisting of N particles is described by two vector quantities: velocity vector v and position vector x. For a D-dimensional search space, the velocity and position of the i-th particle are defined as
Equation (1) represents the velocity vector of the particle in D-dimensional space, while Equation (2) denotes its position in the search space. Each particle has a memory ability and can store the best position it has visited so far, referred to as the individual best position . Among all individual bests , the best one is selected as the global best position . The velocity and position of particles are updated iteratively using the following equations:
In the above: is the inertia weight, which maintains the particle’s previous momentum and balances exploration and exploitation; and are cognitive and social acceleration coefficients, representing the particle’s self-learning and swarm-learning abilities, respectively; are random numbers uniformly distributed within , introducing stochasticity to avoid premature convergence; h is the iteration index; and represent the velocity and position of the i-th particle at the h-th iteration, respectively. The PSO mechanism is driven by a dual principle of “individual experience + group cooperation”, enabling particles to update their positions by considering both their historical best positions and the global best position , thereby forming a self-organizing search process. This mechanism allows PSO to dynamically balance global exploration and local exploitation through a simple structure and parameter configuration. However, traditional PSO often uses fixed parameter settings, which limits its adaptability. This paper designs an adaptive multi-strategy inertia weight adjustment mechanism based on particle state feedback to achieve dynamic balance. Moreover, coefficients such as and are linearly adjusted to enhance convergence capability and address the parameter sensitivity issue in standard PSO.
2.2. Reinforcement Learning
Reinforcement learning (RL) is a key branch of machine learning that focuses on enabling intelligent agents to make sequential decisions in dynamic environments. Its core objective is to learn optimal or near-optimal policies through interactions with the environment to maximize expected cumulative long-term rewards. This process can be modeled as a Markov Decision Process (MDP), formally defined as a quadruple [37], where S represents the set of states, describing all possible situations the agent may encounter; A denotes the action set available to the agent; is the state transition probability function, describing the probability of transitioning from one state to another given an action; is the reward function, quantifying the immediate feedback received by the agent for performing an action in a given state.
Through continuous interaction with the environment, the agent receives a sequence of observations and generates an experience trajectory , where the cumulative discounted return at time t is defined as
where is the discount factor, used to balance the importance between immediate and future rewards. The core objective of RL is to find the optimal policy that maximizes the expected cumulative return
To achieve this, RL commonly defines a state-value function and an action-value function , as follows:
When the optimal policy is achieved, the action-value function satisfies the Bellman optimality condition, which forms the theoretical foundation of the Q-learning algorithm [38].
2.3. Q-Learning
Q-learning, a representative algorithm in reinforcement learning (RL), aims to learn the optimal action-selection policy in an environment by maximizing the expected cumulative reward. RL typically models the learning process through continuous interactions between the agent and the environment, based on three key elements: state, action, and reward. The theoretical basis of Q-learning was proposed by Watkins in 1989 [39], which focuses on estimating the value (Q-value) of performing an action in a specific state without requiring a model of the environment’s dynamics. Q-learning uses an iterative update rule to approximate the optimal Q-value function, with the update equation given as
where is the learning rate, controlling how much newly acquired information overrides the old one; is the discount factor, controlling the importance of future rewards; is the immediate reward received after performing action in state ; represents the maximum estimated future return from the next state , assuming the best action is taken.
This update process is an off-policy method that uses the greedy policy to update Q-values while allowing exploratory behavior during the learning process through strategies such as -greedy selection. The algorithm bootstraps its Q-value estimations, progressively improving policy performance through value iteration. The core architecture of the Q-learning model is illustrated in Figure 1, and its workflow can be summarized as a closed-loop cycle of state perception → action selection → environment interaction → reward acquisition → Q-table update. This mechanism aligns well with the dynamic parameter adjustment requirements of Particle Swarm Optimization (PSO); by defining the search states of PSO (such as particle distribution and fitness variation) as RL states and defining parameter combinations as RL actions, Q-learning enables online optimization of PSO parameters through its adaptive updating capability [40].
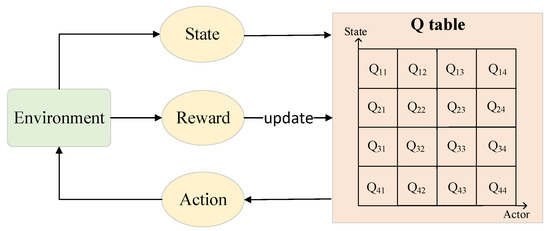
Figure 1.
The model of Q-learning.
3. Multi-Strategy Topology PSO
This paper proposes a multi-topology Particle Swarm Optimization algorithm integrated with reinforcement learning, and its workflow is illustrated in Figure 2. In each iteration, the Q-learning agent selects the topology and parameter configuration according to the current state, after which particles update their velocities and positions and perform fitness evaluation. Stagnation detection is then carried out: if swarm stagnation is detected, a partial restart based on the global best is triggered, while individual stagnation activates a differential evolution–based perturbation. The Q-table is updated in every iteration using immediate feedback, whereas prioritized experience replay from the dual-layer experience pool is triggered periodically to further optimize the strategy.
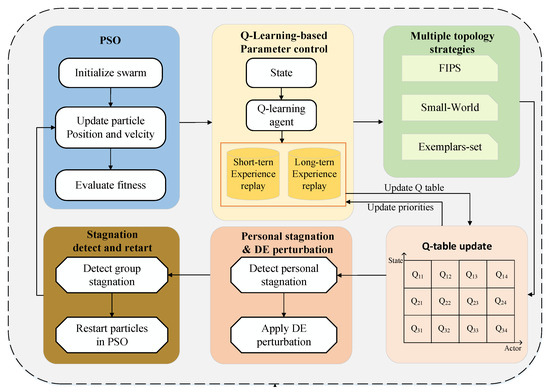
Figure 2.
Algorithmic flow diagram.
3.1. State
Under the Q-learning framework, the state space needs to simultaneously reflect both the convergence trend of individual particles and the diversity of the entire swarm, thereby characterizing the dynamic balance between exploration and exploitation. In this paper, the state is designed with two complementary components: the fitness improvement state and the diversity shrinkage state. For particle i at generation t, the change in fitness is defined as
where denotes the fitness of particle iii at generation t. According to the value of , the base state of particle i, denoted as , is categorized as
where the threshold is commonly used in swarm intelligence optimization to distinguish between significant and non-significant improvements, ensuring the stability and robustness of numerical judgment. The states correspond respectively to significant degradation, slight degradation, no change, and improvement. To quantify the diversity of the swarm distribution, Shannon entropy is introduced,
where M = 10 denotes the number of partitions of the search space, and represents the proportion of particles falling into the j-th interval. According to the entropy value, the diversity level is categorized as
These correspond to low, medium, and high diversity, respectively. Shannon entropy has been widely applied in PSO to measure the distribution and convergence behavior of the swarm [32].
3.2. Action Design
This study selects three representative topologies as reinforcement learning actions: Fully-Informed Particle Swarm Topology (FIPS) [41], small-world topology [25], and exemplar-set topology [42]. Figure 3 shows the three topological structures adopted in this work. These topologies have been demonstrated to significantly enhance global searchability and convergence efficiency in multimodal and complex optimization problems. Their corresponding velocity update mechanisms are described below.
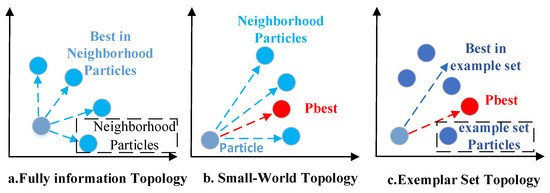
Figure 3.
Topology comparison chart.
Under the FIPS topology, the velocity of particle i is influenced by all its neighborhood members with additional weights. Its update equation is
where denotes the set of neighbors of particle i, is an additional weight factor, and is a random weight. The inertia weight is linearly decreased,
where T is the maximum number of iterations, and t is the current iteration index. This design balances global exploration in early iterations and local exploitation in later stages. Under the small-world topology, particles mainly interact with nearby neighbors while introducing long-distance links with a small probability. Its velocity update is
where is the best solution among neighbors, and the learning factors , vary linearly,
Under the exemplar-set topology, each particle dynamically selects exemplars from the constructed exemplar set as reference points to enhance diversity and effectively avoid premature convergence. Its velocity update is
where denotes the best individual in the exemplar set. This strategy introduces diverse references, strengthening swarm diversity and improving the ability to escape local optima.
In summary, combining the three topological structures with the dynamic adjustment mechanism of , and provides Q-learning with a set of structural actions, achieving a balance between exploration and exploitation. The FIPS topology strengthens fully informed aggregation to improve global convergence; the small-world topology balances information transmission and convergence speed, enhancing search robustness; and the exemplar-set topology maintains swarm diversity through diversified reference individuals, reducing the risk of premature convergence.
3.3. Reward Function
In the MSTPSO algorithm, the reward function is designed to quantify the search performance after executing the current strategy, and it serves as the updating signal for the Q-learning module. The design of the reward comprehensively considers both the improvement of particle fitness and the maintenance of population diversity, thereby guiding the search in the desired direction and avoiding premature convergence and local stagnation. Specifically, the reward of a particle in each generation consists of two parts: (1) the fitness improvement, which reflects the enhancement of a particle’s solution quality, and (2) the diversity maintenance, which encourages exploration behavior. The reward is defined as follows:
where represents the fitness improvement between the current solution and the historical best of particle i, and denotes the diversity contribution of the swarm. In terms of weight setting, this study refers to the related work of Liu et al. [32], in which a reinforcement learning-based PSO parameter control adopts a uniform weighting strategy to balance different optimization objectives. Accordingly, this paper sets , thereby establishing a stable balance between fitness improvement and diversity maintenance.
The reward is then used to update the Q-value function, following the rule
where is the learning rate and is the discount factor.
To balance the rapid response to new information and the long-term stability derived from past experiences, MSTPSO adopts a dual experience replay mechanism. The short-term memory (STM) stores the most recent samples of particle state transitions for rapid adaptation, while the long-term memory (LTM) preserves older and more stable samples to enhance the robustness of strategy learning. Each sample consists of and its corresponding priority. The prioritized update rule is defined as
where , , and are coefficients corresponding to error, fitness improvement, and diversity contribution, respectively, denotes the temporal-difference () error of the i-th sample, and is a smoothing term to avoid zero priority. The coefficients are set as , , and , respectively.
During the search, STM and LTM are updated at fixed intervals (every 500 evaluations). A replacement strategy with a ratio of 0.7:0.3 is applied, where 70% of new samples replace those in STM, while 30% are promoted to LTM. In addition, the top 10% of high-priority samples in STM are transferred into LTM to preserve valuable experience, ensuring long-term diversity maintenance in strategy learning.
3.4. Stagnation Detection and Hierarchical Response Mechanism
To address the potential issues of premature convergence and search stagnation during the iterative process of Particle Swarm Optimization, this paper proposes a hierarchical response mechanism based on stagnation detection. The mechanism first determines the level at which stagnation occurs (population or individual) and subsequently triggers either a partial restart strategy based on the global best neighborhood or a differential evolution (DE)-based perturbation mechanism, thereby enhancing global exploration capability while maintaining local exploitation performance.
In each iteration, if the improvement of the global-best fitness over 20 consecutive iterations is less than , or if the velocity magnitude of all particles falls below the lower bound , the population is deemed stagnant and the restart strategy is executed. If an individual particle’s personal best position remains unchanged for 10 consecutive generations, the particle is considered individually stagnant, and the DE-based perturbation mechanism is activated.
3.4.1. Global-Best-Oriented Restart Strategy
When population stagnation is detected, a partial restart strategy centered on the global-best neighborhood is employed: 20% of the particles are randomly selected for position and velocity reinitialization within an adaptive radius around the global best, thereby restoring search diversity. The new position is generated as
where denotes the coordinate of the global best in dimension d, and represents a uniformly distributed random number. This method redistributes particles around the global best within an adaptive radius, helping the swarm escape stagnation caused by local clustering and velocity decay.
3.4.2. DE-Based Perturbation Mechanism
For particles identified as individually stagnant, a DE-based perturbation mechanism is integrated into the stagnation detection framework to enhance diversity and promote escape from local optima. As shown in Figure 4, the specific operation is as follows:
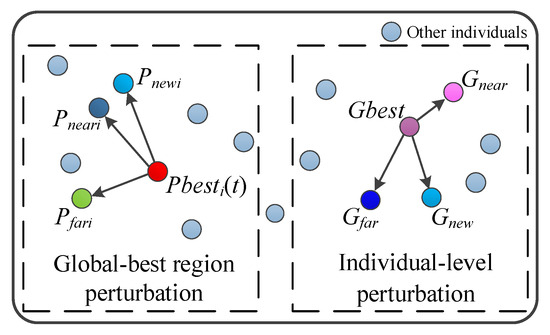
Figure 4.
Differential evolutionary perturbations.
- (1)
- Global-best region perturbation.
Based on Euclidean distance, the closest and farthest particles from the global best are selected to generate a new candidate,
where F denotes the differential evolution scaling factor, set to F = 0.6 in our experiments. If the fitness of is better than that of , the latter is replaced by the new one.
- (2)
- Individual-level perturbation.
For each stagnant particle, the nearest and farthest neighbors and relative to are selected,
If is better, it updates ; otherwise, it replaces the farthest neighbor to increase local diversity.
3.5. Summary and Complexity Analysis
The MSTPSO algorithm begins with the initialization of particles, PSO parameters, the Q-table, and short-term and long-term experience buffers. In each iteration, particle states are obtained, topology actions are selected through the policy on the Q-table, and particle velocities and positions are updated accordingly. Fitness is then evaluated, personal and global bests are updated, and rewards with transitions are stored into replay buffers. The Q-table is updated regularly with prioritized experience replay. Stagnation detection is performed, and restart or DE-based perturbation strategies are applied when necessary. After completing the iterations, the algorithm returns the global best solution.
As shown in Algorithm 1, the computational complexity of MSTPSO consists of five components: fitness evaluation, Q-learning-based topology selection and particle swarm update, diversity entropy calculation, restart and DE perturbation, and the dual-layer experience replay mechanism.
Fitness evaluation is performed for N particles and costs O(), where N is the swarm size and is the cost of a single fitness computation. On CEC benchmark functions, = , with D denoting the problem dimension. In the Q-learning–controlled particle swarm update, each generation each particle selects one of three topologies. For FIPS and small-world topologies, the update is . When the exemplar-set topology is chosen, it needs to select from msl = [0.1N] exemplars, incurring an additional cost. The diversity entropy module relies on Shannon entropy statistics: interval frequency counting for N particles over D dimensions is . Restart and DE perturbation are triggered only when stagnation occurs, with amortized complexity . The dual-layer experience replay comprises a short-term memory (STM, size 2N) and a long-term memory (LTM, size 5N), with storage complexity . Each generation writes N transitions into STM and computes priorities in constant time, giving per generation. When replay is triggered, B = 3N samples are drawn and the Q-table is updated, costing . Amortized over all generations, this remains linear and negligible compared with the main terms. Considering the entire evolutionary process, the overall time complexity of MSTPSO is .
| Algorithm 1 MSTPSO Algorithm |
Input: population size N, dimension D, maximum iterations T Output: global best solution 1: Initialize particle positions, velocities, and the Q-table. 2: Create dual-layer replay buffers. 3: Evaluate initial fitness and determine . 4: for to T do 5: for each particle do 6: Select topology using Q-learning policy. 7: Update and according to the selected topology by (15), (17), and (20). 8: end for 9: Evaluate fitness and update personal and global bests. 10: If stagnation is detected, apply perturbation or restart strategy. 11: end for 12: Return . |
4. Numerical Experiments
4.1. Experimental Settings and Comparison Methods
In this experiment, the performance of the proposed MSTPSO algorithm is evaluated using 30 benchmark functions from the CEC2017 [40] test suite. Since function shows instability in high-dimensional cases, it is excluded from the analysis. Table 1 lists the detailed information of these functions, which are divided into four categories: unimodal functions (), multimodal functions (–), hybrid functions (–), and composition functions (–). Extensive numerical experiments are conducted to validate the effectiveness of MSTPSO.

Table 1.
The information of the test suite on CEC2017.
For comparative studies, MSTPSO is benchmarked against nine mainstream PSO variants, including DQNPSO [43], APSO_SAC [44], EPSO [45], KGPSO [46], XPSO [22], MSORL [47], DRA [48], RFO [49], and RLACA [50]. The detailed information of these algorithms is given in Table 2. All functions are independently executed 51 times according to the CEC standard, with the termination condition set as the maximum number of evaluations equal to , where D is the problem dimension.

Table 2.
Parameter settings for the nine compared algorithms.
To comprehensively evaluate the effectiveness of MSTPSO, experiments are conducted on the CEC2017 test suite in 10, 30, 50 and 100 dimensions, and the results are compared with the above-mentioned algorithms. Table 3, Table 4, Table 5 and Table 6 present the mean and standard deviation of the solution errors obtained after 51 runs. In addition, as shown in Table 7, the results of the Wilcoxon signed-rank test demonstrate the statistical significance of the algorithm. The data indicate that MSTPSO demonstrates significant advantages over existing PSO variants, confirming its superior performance.

Table 3.
The comparative results of MSTPSO and advanced algorithms on 10-D using the CEC2017 benchmark suite.

Table 4.
The comparative results of MSTPSO and advanced algorithms on 30-D using the CEC2017 benchmark suite.

Table 5.
The comparative results of MSTPSO and advanced algorithms on 50-D using the CEC2017 benchmark suite.

Table 6.
The comparative results of MSTPSO and advanced algorithms on 100-D using the CEC2017 benchmark suite.

Table 7.
Wilcoxon signed-rank test results of ten algorithms versus MSTPSO on CEC 2017 (counts over functions).
4.2. Performance Comparison Across Different Dimensions
In the 10-dimensional tests, Table 3 reports the mean and standard deviation of solution errors after 51 independent runs. For the unimodal functions and , the proposed algorithm ranks first on and second on , with only a small gap from the top, reflecting its effectiveness in solving unimodal problems. For the multimodal functions (–), MSTPSO achieves the best results on –, which not only demonstrates its excellent global search ability but also highlights the effectiveness of its reinforcement learning strategy and perturbation mechanism in escaping local optima. In the hybrid (–) and composition functions (–), MSTPSO also achieves first place on , , , , –, , and .
In the 30-dimensional case, Table 4 presents the mean and standard deviation of solution errors after 51 runs. MSTPSO ranks second on the unimodal functions and , slightly behind RLACA. For the multimodal functions (–), MSTPSO maintains stable rankings, demonstrating its competitiveness in handling multimodal optimization problems. For the hybrid and composition functions (–), MSTPSO shows significant improvement; however, experiences a performance drop, indicating its sensitivity to dimensionality, while other functions achieve notable gains. Specifically, MSTPSO ranks first on , , , and , underscoring its strong global search ability and remarkable performance in complex hybrid problems.
In the 50-dimensional case, Table 5 shows the mean and standard deviation of solution errors after 51 runs. MSTPSO achieves a significant improvement on unimodal functions, rising to first place on . For the multimodal functions (–), MSTPSO obtains the best results on six functions (–) and ranks third on , reflecting its robustness in escaping local optima under complex conditions. For the hybrid and composition functions (–), MSTPSO achieves overall improvement, ranking first on 14 out of 20 functions, which demonstrates its powerful global search capability in high-dimensional settings.
In the 100-dimensional case, Table 6 presents the mean and standard deviation of solution errors, as well as the average rankings over 51 independent runs. MSTPSO achieves the best result on the unimodal function . For multimodal functions, MSTPSO maintains optimal performance on to and ranks second on . In hybrid and composition functions, MSTPSO maintains stable rankings, while other RL-PSO variants show significant performance degradation, fully demonstrating the robustness and stability of the topology structure in high-dimensional complex optimization tasks. Overall, compared with several state-of-the-art PSO algorithms, the results indicate that MSTPSO ranks first across the 10-D, 30-D, 50-D, and 100-D CEC 2017 test suites, highlighting its superior performance.
4.3. Convergence Curves and Dynamic Performance Analysis
To further evaluate the convergence performance of MSTPSO, convergence curves are plotted. It should be noted that due to minor differences in initialization strategies, the early-stage convergence behavior of different algorithms may vary. Figure 5 illustrates the convergence processes for functions – in 50 dimensions. The proposed method achieves the fastest convergence on , demonstrating significant advantages in solving unimodal functions through multi-agent reinforcement learning-based parameter training. For multimodal functions, MSTPSO consistently shows the fastest convergence on –. For hybrid functions, MSTPSO also converges quickly on –, –, with strong capability to escape local optima. These results confirm that MSTPSO possesses strong global search ability and robustness in solving complex hybrid optimization problems.
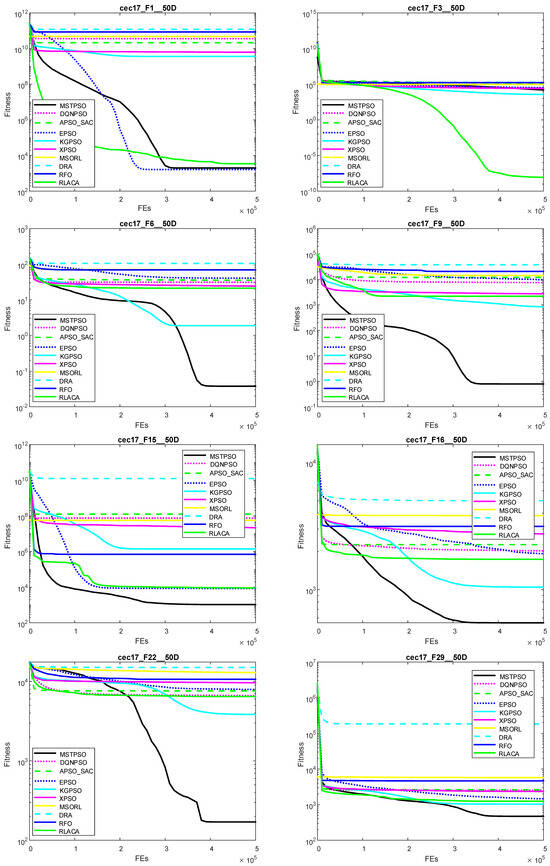
Figure 5.
The convergence curves of MSTPSO with PSO variants in the CEC2017 (50-D).
4.4. Boxplot Analysis and Robustness Evaluation
As shown in Figure 6, the boxplot analysis, indicates that MSTPSO demonstrates varying performance across functions. For unimodal function , it shows strong convergence and stability, approaching the optimal solution quickly with almost no outliers. For multimodal functions , , , and , MSTPSO effectively avoids local optima, although a few outliers appear on , indicating occasional influence by local traps. For hybrid functions , , , and , MSTPSO maintains good solution quality and stability, with only minor fluctuations on but avoiding many outliers overall. For composition functions and , especially under high-dimensional complex conditions, MSTPSO shows strong global search capability, successfully escaping local optima with fast convergence and fewer outliers. In summary, MSTPSO demonstrates excellent performance across different optimization problems, particularly excelling on unimodal, multimodal, and composition functions.
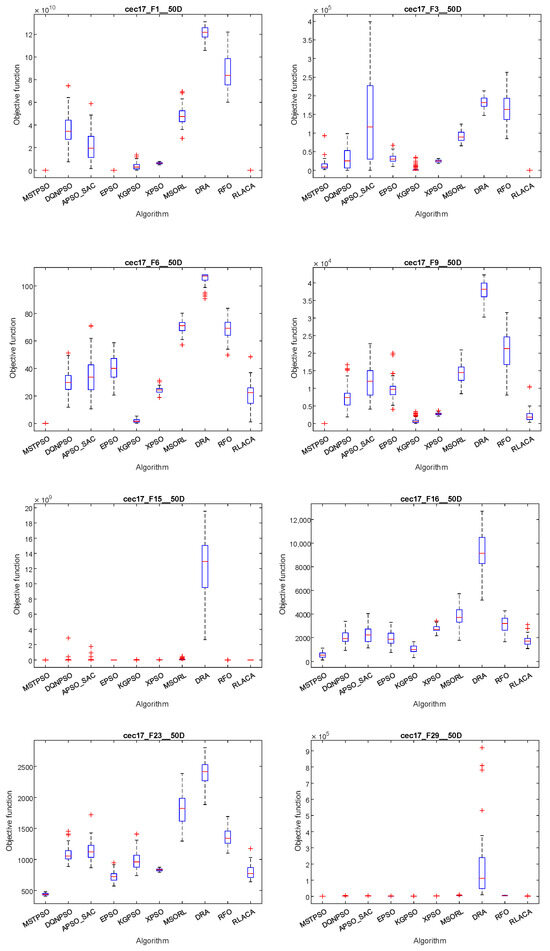
Figure 6.
Stability effect of MSTPSO with PSO variants in the CEC2017 (50-D).
4.5. Significance Test Analysis (Wilcoxon Rank-Sum Test)
To further verify the statistical superiority of MSTPSO, Table 7 presents the Wilcoxon signed-rank test results of ten algorithms on the CEC2017 benchmark functions under 10-, 30-, and 50-dimensional settings. A significance level of 0.05 was used to determine whether the performance differences are statistically meaningful, and the p-values obtained from the Wilcoxon test indicate the degree of significance. Here, “+” denotes that MSTPSO significantly outperforms the compared algorithm, “−” indicates significant inferiority, and “≈” represents no significant difference. Compared with advanced variants such as DQNPSO, APSO_SAC, XPSO, and DRA, MSTPSO achieved statistically superior results on nearly all test functions, with complete wins across all dimensions against XPSO and DRA. Against EPSO, KGPSO, and MSORL, MSTPSO also maintained clear statistical superiority with only a few non-significant cases. Compared with RFO and RLACA, MSTPSO is slightly better at low dimensions and achieves greater superiority at 30-D and 50-D. Overall, the Wilcoxon results confirm that MSTPSO significantly outperforms most representative PSO variants across the majority of test functions and dimensions, verifying the statistical reliability of its performance gains.
4.6. Ablation Study on Topology Structures
4.6.1. Multi-Topology Ablation
To verify the contribution of each topology in MSTPSO, three ablation versions are tested: MSTPSO1 removes the FIPS topology, MSTPSO2 removes the small-world topology, and MSTPSO3 removes the exemplar topology. Their optimization performance on the 10- and 30-dimensional CEC2017 functions is compared with the full MSTPSO, as shown in Table 8.

Table 8.
Experiments of MSTPSO algorithm and change action algorithm on 10D and 30D.
The results show that MSTPSO achieves the best average ranking in both dimensions, confirming the effectiveness of the multi-topology integration in balancing global search and local convergence. The average rankings of MSTPSO are 2.31 in 10-D and 2.22 in 30-D, significantly better than the ablation versions. MSTPSO1 shows a clear decline in 10-D, especially on unimodal and multimodal functions, indicating the critical role of the FIPS topology in maintaining diversity and avoiding premature convergence. MSTPSO2 performs worse in multiple functions, particularly in 30-D, with an average rank of 3.81, demonstrating the importance of the small-world topology for global exploration. MSTPSO3 shows performance similar to MSTPSO2 but still inferior to the full version, especially on complex functions. Overall, MSTPSO’s superior performance validates the importance of multi-topology integration.
4.6.2. Ablation of Stagnation Detection and Hierarchical Response Mechanism
As shown in Table 9, the average ranking results indicate that introducing stagnation detection and the hierarchical response mechanism further improves overall performance in different dimensions. The complete algorithm achieves average ranks of 1.33, 1.43, and 1.47 in 10-D, 30-D, and 50-D, respectively, outperforming the version without this module. The improvement is particularly evident in high-complexity problems. On unimodal functions, both versions converge quickly, but MSTPSO ranks significantly higher in 10-D and 50-D, showing faster convergence and better escape ability. For multimodal functions, stagnation detection enhances global exploration, and in 30-D and 50-D, the average rankings are much better than the baseline, indicating higher solution quality and stability in complex spaces. For hybrid and composition functions, the advantage is most significant, with the complete MSTPSO achieving markedly better average rankings in 10-D and 30-D. These results confirm that stagnation detection and hierarchical response are key modules for improving MSTPSO’s robustness and adaptability in high-dimensional optimization.

Table 9.
Friedman ranking of four individual stagnation threshold parameters.
To evaluate the impact of stagnation detection thresholds on the stability of the algorithm, a parameter sensitivity study was conducted on the CEC2017 30-D and 50-D test suites, with the Friedman average rankings shown in Table 10, Table 11 and Table 12. The individual stagnation threshold , the population stagnation threshold , and the lower velocity bound were set within the ranges 10, 15, 20, 30, 5, 10, 15, 20 and , , , respectively. The experimental results show that the performance of MSTPSO remains stable within these parameter ranges, with only slight fluctuations in the average rankings. The configuration , and achieves the best average rankings in both the 30-D and 50-D cases.

Table 10.
Experiments of MSTPSO algorithm and stop detection module on 10-D, 30-D and 50-D.

Table 11.
Friedman ranking of the stagnation threshold parameters for four groups.

Table 12.
Friedman ranking of lower bound parameters at three speeds.
5. Conclusions
This paper proposes a multi-topology Particle Swarm Optimization algorithm controlled by Q-learning (MSTPSO). The method introduces a reinforcement learning–driven adaptive topology selection mechanism into the standard PSO framework, enabling particles to dynamically switch among FIPS, small-world, and exemplar-set topologies to balance global exploration and local exploitation. Meanwhile, a diversity-entropy regulation mechanism is designed to maintain population diversity, and, based on stagnation detection, DE perturbations combined with a global best restart strategy are incorporated to avoid premature convergence and enhance local search capability. Unlike most existing RL-PSO variants, which mainly use reinforcement learning to adapt inertia weight or learning factors, the proposed method focuses on dynamic topology selection and improves performance through the combination of dual-layer experience replay, stagnation detection, and DE perturbations, thus complementing existing approaches in mechanism design. Systematic experiments on the CEC2017 benchmark functions demonstrate that MSTPSO achieves superior performance on unimodal, multimodal, hybrid, and composite functions across four dimensionalities (10, 30, 50, and 100). Compared with various advanced PSO variants, the proposed algorithm attains faster convergence, higher solution accuracy, and better stability, showing particularly strong robustness on high-dimensional complex functions. Further ablation studies reveal that the Q-learning-based topology selection mechanism significantly improves overall convergence quality, while the stagnation-driven DE perturbation and global restart strategy effectively enhance the ability to escape local optima. Nevertheless, some limitations remain. First, the Q-learning parameter settings may require task-specific adjustment and show certain sensitivity. Second, computing diversity entropy and pairwise distance matrices incurs higher computational cost for large populations and high-dimensional problems. Finally, current experiments are limited to benchmark functions, and the applicability of the algorithm to complex constrained optimization and real engineering problems requires further investigation. Future work may proceed in several directions: (1) optimizing the reinforcement learning control strategy to reduce parameter sensitivity and improve efficiency on large-scale, high-dimensional problems; (2) extending the algorithm to more complex scenarios such as constrained, dynamic, and multiobjective optimization to further verify its generality; (3) exploring parallel computing and hardware acceleration methods, such as GPU computing and distributed architectures, to enhance scalability; and (4) applying the algorithm to real engineering tasks—including industrial scheduling, image and vision inspection, and path planning—to validate its practical value.
Author Contributions
X.H., conceptualization; work preparation; S.W., conceptualization; methodology; software; validation; formal analysis; investigation; resources; data curation; visualization; writing—original draft preparation; writing—review and editing; X.L., work preparation; data curation; T.W., conceptualization; supervision; writing—review and editing; project administration; funding acquisition; G.Q., conceptualization; supervision; Z.Z., writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article; our code is released at https://github.com/shenweiwang767-ai/MSTPSO.git, accessed on 15 October 2025.
Acknowledgments
The authors gratefully acknowledge the support from the Scientific Research Project of the Department of Education of Guangdong Province (Grant No. 2022ZDZX3034) and the Key Platform and Research Project for Ordinary Universities of Guangdong Province (Grant No. 2024ZDZX1009). The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tanabe, R.; Fukunaga, A. Success-history based parameter adaptation for differential evolution. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 71–78. [Google Scholar]
- Liu, Y.; Liu, J.; Ding, J.; Yang, S.; Jin, Y. A surrogate-assisted differential evolution with knowledge transfer for expensive incremental optimization problems. IEEE Trans. Evol. Comput. 2023, 28, 1039–1053. [Google Scholar] [CrossRef]
- Lambora, A.; Gupta, K.; Chopra, K. Genetic algorithm—A literature review. In Proceedings of the 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019; pp. 380–384. [Google Scholar]
- Ngo, L.; Ha, H.; Chan, J.; Nguyen, V.; Zhang, H. High-dimensional Bayesian optimization via covariance matrix adaptation strategy. arXiv 2024, arXiv:2402.03104. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, H.; Wang, W.; Huang, Z.; Zhou, X.; Xu, M. Artificial bee colony algorithm based on adaptive neighborhood search and Gaussian perturbation. Appl. Soft Comput. 2021, 100, 106955. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, San Diego, CA, USA, 25–27 March 1998; IEEE World Congress on Computational Intelligence (Cat. No. 98TH8360). pp. 69–73. [Google Scholar]
- Eberhart, R.; Shi, Y. Particle swarm optimization and its applications to VLSI design and video technology. In Proceedings of the 2005 IEEE International Workshop on VLSI Design and Video Technology, Suzhou, China, 28–30 May 2005; p. xxiii. [Google Scholar]
- Ratnaweera, A.; Halgamuge, S.K.; Watson, H.C. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients. IEEE Trans. Evol. Comput. 2004, 8, 240–255. [Google Scholar] [CrossRef]
- Chen, Q.; Li, C.; Guo, W. Railway passenger volume forecast based on IPSO-BP neural network. In Proceedings of the 2009 International Conference on Information Technology and Computer Science, Kiev, Ukraine, 25–26 July 2009; Volume 2, pp. 255–258. [Google Scholar]
- Liu, H.R.; Cui, J.C.; Lu, Z.D.; Liu, D.Y.; Deng, Y.J. A hierarchical simple particle swarm optimization with mean dimensional information. Appl. Soft Comput. 2019, 76, 712–725. [Google Scholar] [CrossRef]
- El-Kenawy, E.S.; Eid, M. Hybrid gray wolf and particle swarm optimization for feature selection. Int. J. Innov. Comput. Inf. Control 2020, 16, 831–844. [Google Scholar]
- Adamu, A.; Abdullahi, M.; Junaidu, S.B.; Hassan, I.H. An hybrid particle swarm optimization with crow search algorithm for feature selection. Mach. Learn. Appl. 2021, 6, 100108. [Google Scholar] [CrossRef]
- Khan, T.A.; Ling, S.H. A novel hybrid gravitational search particle swarm optimization algorithm. Eng. Appl. Artif. Intell. 2021, 102, 104263. [Google Scholar] [CrossRef]
- Lin, A.; Liu, D.; Li, Z.; Hasanien, H.M.; Shi, Y. Heterogeneous differential evolution particle swarm optimization with local search. Complex Intell. Syst. 2023, 9, 6905–6925. [Google Scholar] [CrossRef]
- Lin, A.; Li, S.; Liu, R. Mutual learning differential particle swarm optimization. Egypt. Inform. J. 2022, 23, 469–481. [Google Scholar] [CrossRef]
- Chen, H.; Shen, L.Y.; Wang, C.; Tian, L.; Zhang, S. Multi Actors-Critic based particle swarm optimization algorithm. Neurocomputing 2025, 624, 129460. [Google Scholar] [CrossRef]
- Zhongxing, L.; Fangxi, Z.; Bingchen, L.; Shaohua, X. Quality monitoring of tractor hydraulic oil based on improved PSO-BPNN. J. Chin. Agric. Mech. 2024, 45, 140. [Google Scholar]
- Huang, Y.; Li, W.; Tian, F.; Meng, X. A fitness landscape ruggedness multiobjective differential evolution algorithm with a reinforcement learning strategy. Appl. Soft Comput. 2020, 96, 106693. [Google Scholar] [CrossRef]
- Lu, L.; Zheng, H.; Jie, J.; Zhang, M.; Dai, R. Reinforcement learning-based particle swarm optimization for sewage treatment control. Complex Intell. Syst. 2021, 7, 2199–2210. [Google Scholar] [CrossRef]
- Janson, S.; Middendorf, M. A hierarchical particle swarm optimizer and its adaptive variant. IEEE Trans. Syst. Man Cybern. Part 2005, 35, 1272–1282. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhang, J.; Ji, W.; Sun, X.; Zhang, L. Particle swarm optimization algorithm with self-correcting and dimension by dimension learning capabilities. J. Chin. Comput. Syst. 2021, 42, 919–926. [Google Scholar]
- Xia, X.; Gui, L.; He, G.; Wei, B.; Zhang, Y.; Yu, F.; Wu, H.; Zhan, Z.H. An expanded particle swarm optimization based on multi-exemplar and forgetting ability. Inf. Sci. 2020, 508, 105–120. [Google Scholar] [CrossRef]
- Jiang, S.; Ding, J.; Zhang, L. A personalized recommendation algorithm based on weighted information entropy and particle swarm optimization. Mob. Inf. Syst. 2021, 2021, 3209140. [Google Scholar] [CrossRef]
- Engelbrecht, A.P. Computational Intelligence: An Introduction; Wiley Online Library: Hoboken, NJ, USA, 2007; Volume 2. [Google Scholar]
- Liu, Q.; Van Wyk, B.J.; Sun, Y. Small world network based dynamic topology for particle swarm optimization. In Proceedings of the 2015 11th International Conference on Natural Computation (ICNC), Zhangjiajie, China, 15–17 August 2015; pp. 289–294. [Google Scholar]
- Zeng, N.; Wang, Z.; Liu, W.; Zhang, H.; Hone, K.; Liu, X. A dynamic neighborhood-based switching particle swarm optimization algorithm. IEEE Trans. Cybern. 2020, 52, 9290–9301. [Google Scholar] [CrossRef]
- Pan, L.; Zhao, Y.; Li, L. Neighborhood-based particle swarm optimization with discrete crossover for nonlinear equation systems. Swarm Evol. Comput. 2022, 69, 101019. [Google Scholar] [CrossRef]
- Li, T.; Shi, J.; Deng, W.; Hu, Z. Pyramid particle swarm optimization with novel strategies of competition and cooperation. Appl. Soft Comput. 2022, 121, 108731. [Google Scholar] [CrossRef]
- Li, W.; Liang, P.; Sun, B.; Sun, Y.; Huang, Y. Reinforcement learning-based particle swarm optimization with neighborhood differential mutation strategy. Swarm Evol. Comput. 2023, 78, 101274. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, J. Time domain waveform synthesis method of shock response spectrum based on PSO-LSN algorithm. J. Vib. Shock 2024, 43, 102–107. [Google Scholar]
- Tatsis, V.A.; Parsopoulos, K.E. Dynamic parameter adaptation in metaheuristics using gradient approximation and line search. Appl. Soft Comput. 2019, 74, 368–384. [Google Scholar] [CrossRef]
- Liu, Y.; Lu, H.; Cheng, S.; Shi, Y. An adaptive online parameter control algorithm for particle swarm optimization based on reinforcement learning. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 815–822. [Google Scholar]
- Yin, S.; Jin, M.; Lu, H.; Gong, G.; Mao, W.; Chen, G.; Li, W. Reinforcement-learning-based parameter adaptation method for particle swarm optimization. Complex Intell. Syst. 2023, 9, 5585–5609. [Google Scholar] [CrossRef]
- Hamad, Q.S.; Samma, H.; Suandi, S.A.; Mohamad-Saleh, J. Q-learning embedded sine cosine algorithm (QLESCA). Expert Syst. Appl. 2022, 193, 116417. [Google Scholar] [CrossRef]
- Hamad, Q.S.; Samma, H.; Suandi, S.A. Feature selection of pre-trained shallow CNN using the QLESCA optimizer: COVID-19 detection as a case study. Appl. Intell. 2023, 53, 18630–18652. [Google Scholar] [CrossRef]
- Wang, F.; Wang, X.; Sun, S. A reinforcement learning level-based particle swarm optimization algorithm for large-scale optimization. Inf. Sci. 2022, 602, 298–312. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, UK, 1998; Volume 1. [Google Scholar]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Qiang, W.; Zhongli, Z. Reinforcement learning model, algorithms and its application. In Proceedings of the 2011 International Conference on Mechatronic Science, Electric Engineering and Computer (MEC), Jilin, China, 19–22 August 2011; pp. 1143–1146. [Google Scholar]
- Awad, N.H.; Ali, M.Z.; Suganthan, P.N. Ensemble sinusoidal differential covariance matrix adaptation with Euclidean neighborhood for solving CEC2017 benchmark problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia/San Sebastian, Spain, 5–8 June 2017; pp. 372–379. [Google Scholar]
- Mendes, R.; Kennedy, J.; Neves, J. The fully informed particle swarm: Simpler, maybe better. IEEE Trans. Evol. Comput. 2004, 8, 204–210. [Google Scholar] [CrossRef]
- Wu, X.; Han, J.; Wang, D.; Gao, P.; Cui, Q.; Chen, L.; Liang, Y.; Huang, H.; Lee, H.P.; Miao, C.; et al. Incorporating surprisingly popular algorithm and euclidean distance-based adaptive topology into PSO. Swarm Evol. Comput. 2023, 76, 101222. [Google Scholar] [CrossRef]
- Aoun, O. Deep Q-network-enhanced self-tuning control of particle swarm optimization. Modelling 2024, 5, 1709–1728. [Google Scholar] [CrossRef]
- von Eschwege, D.; Engelbrecht, A. Soft actor-critic approach to self-adaptive particle swarm optimisation. Mathematics 2024, 12, 3481. [Google Scholar] [CrossRef]
- Yuan, Y.L.; Hu, C.M.; Li, L.; Mei, Y.; Wang, X.Y. Regional-modal optimization problems and corresponding normal search particle swarm optimization algorithm. Swarm Evol. Comput. 2023, 78, 101257. [Google Scholar] [CrossRef]
- Zhang, D.; Ma, G.; Deng, Z.; Wang, Q.; Zhang, G.; Zhou, W. A self-adaptive gradient-based particle swarm optimization algorithm with dynamic population topology. Appl. Soft Comput. 2022, 130, 109660. [Google Scholar] [CrossRef]
- Wang, X.; Wang, F.; He, Q.; Guo, Y. A multi-swarm optimizer with a reinforcement learning mechanism for large-scale optimization. Swarm Evol. Comput. 2024, 86, 101486. [Google Scholar] [CrossRef]
- Mozhdehi, A.T.; Khodadadi, N.; Aboutalebi, M.; El-kenawy, E.S.M.; Hussien, A.G.; Zhao, W.; Nadimi-Shahraki, M.H.; Mirjalili, S. Divine Religions Algorithm: A novel social-inspired metaheuristic algorithm for engineering and continuous optimization problems. Clust. Comput. 2025, 28, 253. [Google Scholar] [CrossRef]
- Braik, M.; Al-Hiary, H. Rüppell’s fox optimizer: A novel meta-heuristic approach for solving global optimization problems. Clust. Comput. 2025, 28, 1–77. [Google Scholar] [CrossRef]
- Liu, X.; Wang, T.; Zeng, Z.; Tian, Y.; Tong, J. Three stage based reinforcement learning for combining multiple metaheuristic algorithms. Swarm Evol. Comput. 2025, 95, 101935. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).