A GIN-Guided Multiobjective Evolutionary Algorithm for Robustness Optimization of Complex Networks
Abstract
1. Introduction
- The network robustness enhancement task is formulated as a multiobjective optimization problem, which simultaneously considers node robustness against targeted attacks and the cost of structural modifications;
- A GIN-based surrogate model is employed to efficiently approximate the expensive robustness evaluation. Compared to traditional surrogate models, the GIN model directly learns from graph-structured data. It has relatively few parameters, which makes it easier to train and particularly suitable for high-cost optimization problems with limited sample sizes;
- A novel surrogate-assisted multiobjective evolutionary algorithm is developed, in which a GIN model is employed to efficiently guide the search for robust network structures. Moreover, the GIN is iteratively updated via online learning to improve prediction accuracy during the optimization;
- Extensive experiments on various complex networks demonstrate that the proposed MOEA-GIN framework achieves superior performance.
2. Preliminary Knowledge
2.1. Complex Network
2.2. Multiobjective Robustness Optimization
2.3. Surrogate-Assisted Optimization
2.4. Graph Neural Networks
3. Proposed Algorithm
3.1. Framework
| Algorithm 1: MOEA-GIN. |
 |
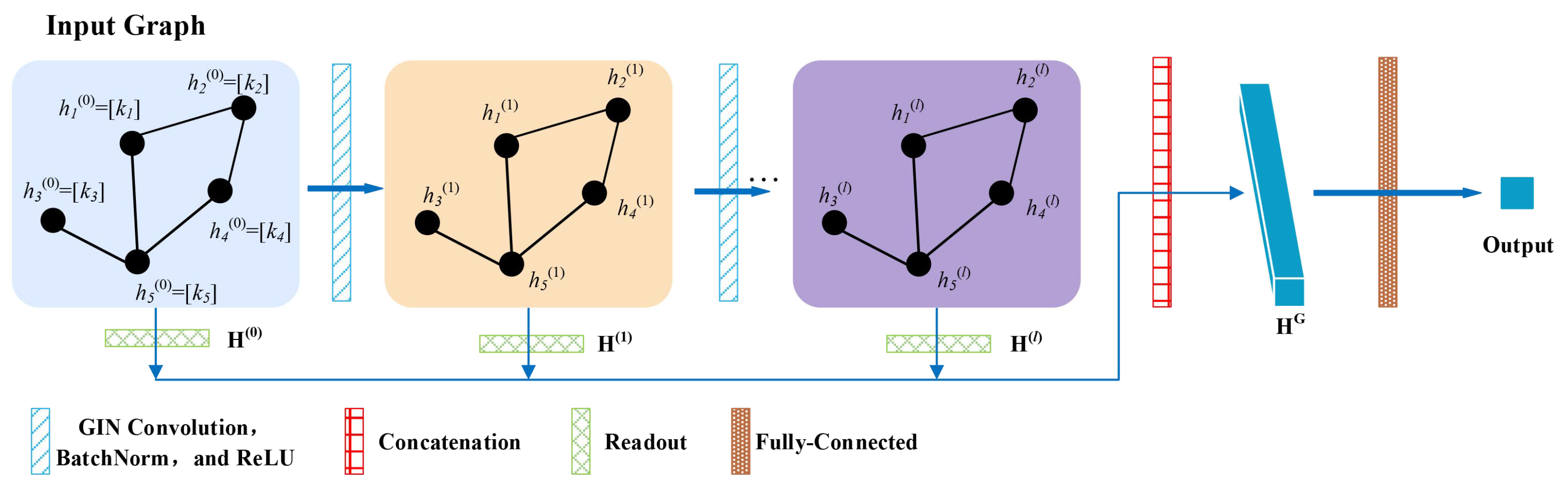
3.2. Model Construction
| Algorithm 2: Topological rewiring operator. |
 |
3.3. Evolutionary Optimization
| Algorithm 3: Initialization. |
 |
| Algorithm 4: Crossover operator. |
 |
| Algorithm 5: Mutation operator. |
 |
| Algorithm 6: Local search. |
 |
3.4. Online Learning
- Convergence-oriented strategy. This strategy selects individuals based on their dominance over solutions in . It is defined as the sum of the times that an individual is superior to other individuals in each objective, expressed as follows:where denotes the ith objective function (). is the set of solutions that have been evaluated using the real robustness function during the optimization process. By leveraging the reliable reference set, it enables the algorithm to select promising solutions that are likely near the true Pareto front, thus guiding the search more effectively. Moreover, if such individuals turn out to be false positives, their feedback can effectively guide model correction and reduce prediction bias.
- Diversity-oriented strategy. To promote exploration in unexplored regions, shift-based diversity estimation (SDE) [59] is employed to guide the sampling. For an individual (), SDE is calculated as follows:where represents the Euclidean distance between individuals, the function is used to quantify the similarity between and the individuals in , and is the shifted individual as follows:This strategy improves the coverage of the Pareto front by encouraging exploration in underrepresented regions. In addition, diverse samples can enhance the generation ability of the surrogate model and mitigate the risk of overfitting.
| Algorithm 7: Online learning. |
 |
4. Experimental Analysis
4.1. Experimental Setting
4.2. Validation and Verification of the Surrogate Model
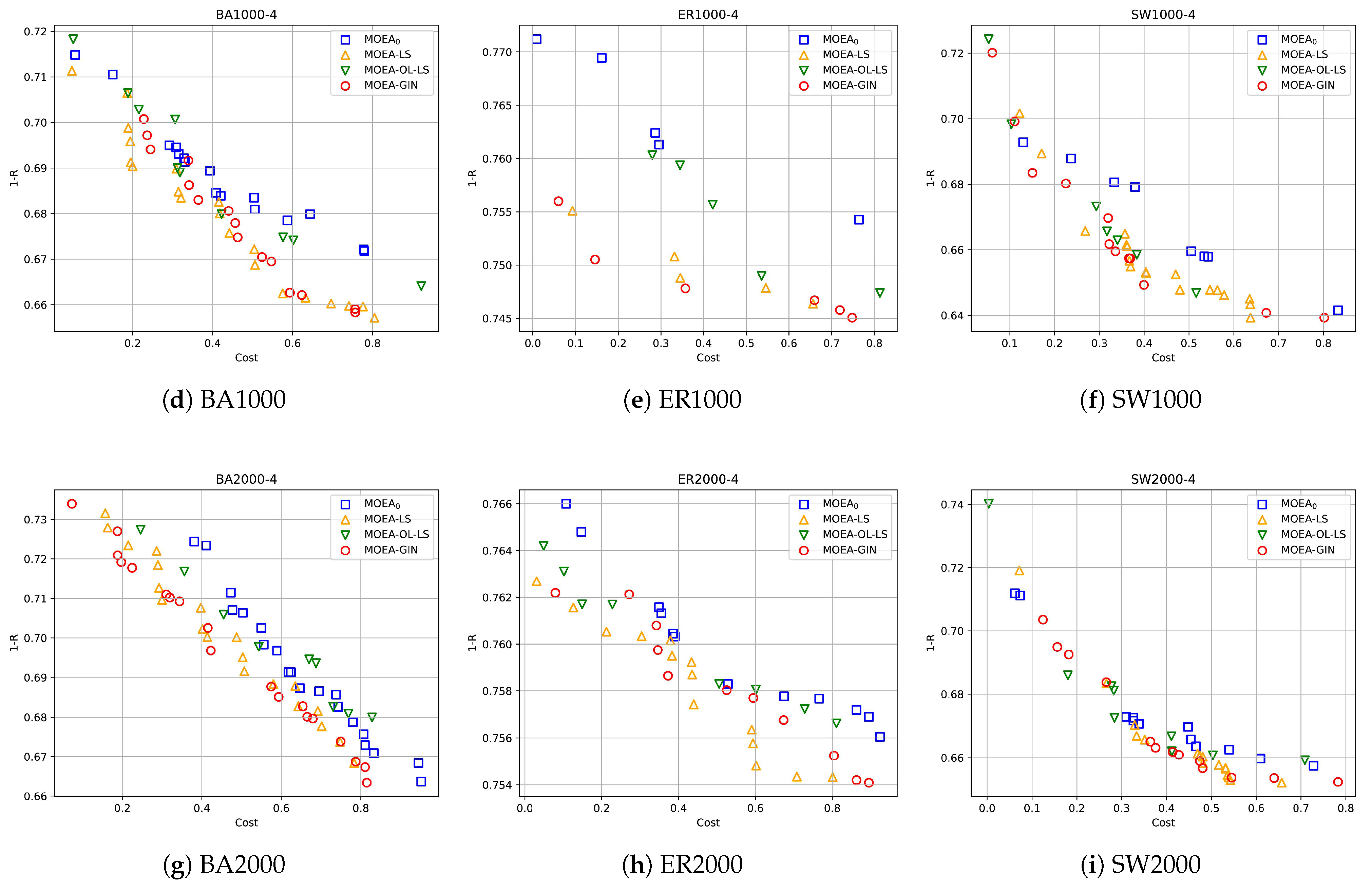
4.3. Experimental Results in Synthetic Networks
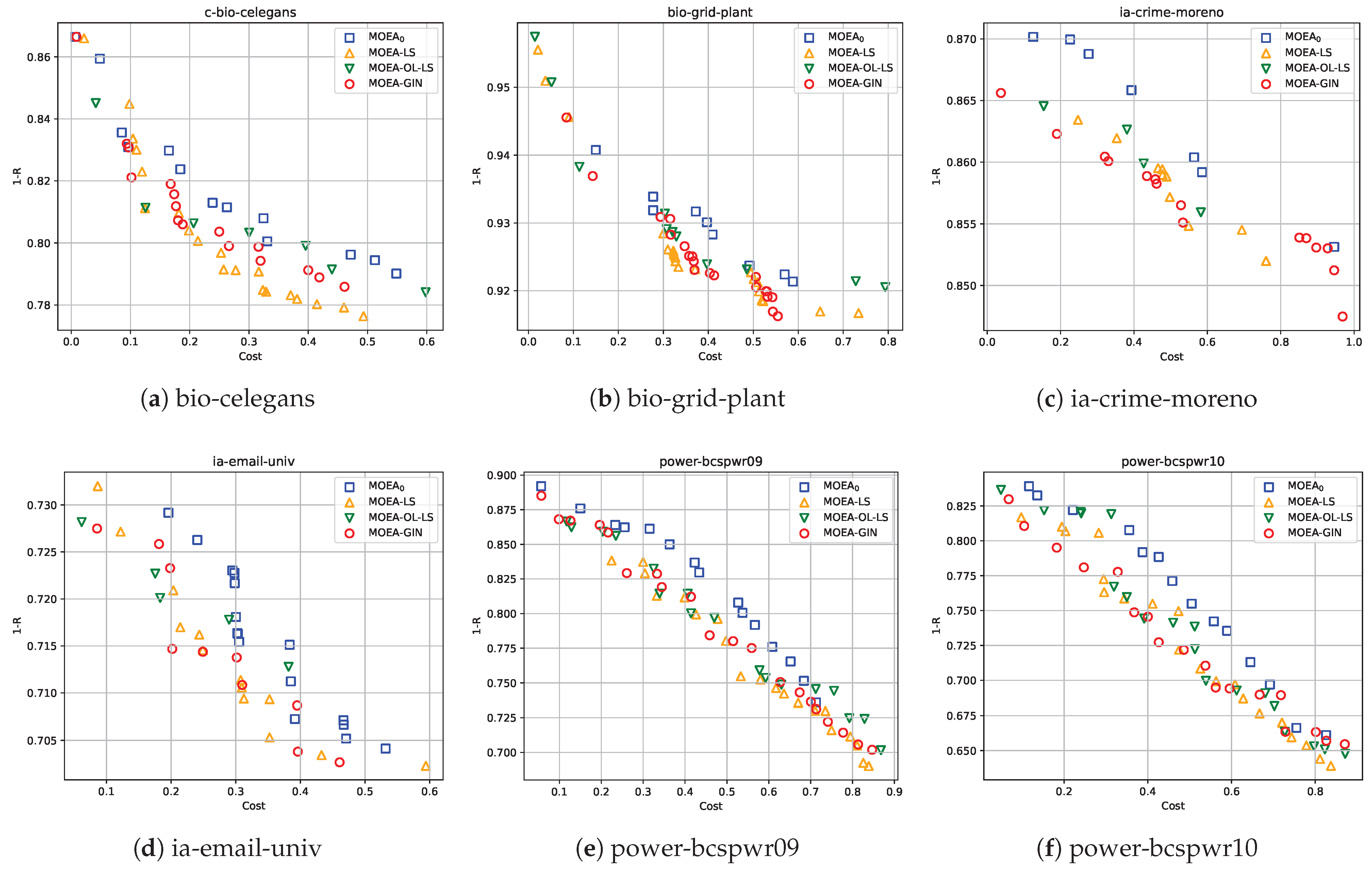
4.4. Experimental Results in Real-World Networks
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PS | Pareto set |
| PF | Pareto front |
| HV | Hypervolume |
| EA | Evolutionary algorithm |
| GNNs | Graph neural networks |
| GIN | Graph isomorphism network |
| MSE | Mean squared error |
| ER | Erdős–Rényi random graphs |
| BA | Barabási–Albert scale-free networks |
| SW | Watts–Strogatz small-world networks |
| LCC | Largest connected component |
| MOPs | Multiobjective optimization problems |
| MOEAs | Multiobjective evolutionary algorithms |
| SDE | Shift-based diversity estimation |
References
- Lou, Y.; Wang, L.; Chen, G. Structural Robustness of Complex Networks: A Survey of A Posteriori Measures [Feature]. IEEE Circuits Syst. Mag. 2023, 23, 12–35. [Google Scholar] [CrossRef]
- Grassia, M.; De Domenico, M.; Mangioni, G. Machine learning dismantling and early-warning signals of disintegration in complex systems. Nat. Commun. 2021, 12, 5190. [Google Scholar] [CrossRef]
- Ma, L.; Xu, L.; Fan, X.; Li, L.; Lin, Q.; Li, J.; Gong, M. Multifactorial evolutionary deep reinforcement learning for multitask node combinatorial optimization in complex networks. Inf. Sci. 2025, 702, 121913. [Google Scholar] [CrossRef]
- Zhou, D.; Hu, F.; Wang, S.; Chen, J. Power network robustness analysis based on electrical engineering and complex network theory. Phys. A Stat. Mech. Its Appl. 2021, 564, 125540. [Google Scholar] [CrossRef]
- Jiang, X.; Yan, H.; Li, B.; Zheng, S.; Huang, T.; Shi, P. Optimal Tracking of Networked Control Systems over the Fading Channel with Packet Loss. IEEE Trans. Autom. Control 2023, 69, 2652–2659. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Girvan, M. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar]
- Li, M.; Liu, J. A link clustering based memetic algorithm for overlapping community detection. Phys. A Stat. Mech. Its Appl. 2018, 503, 410–423. [Google Scholar] [CrossRef]
- Ulrik, B. On variants of shortest-path betweenness centrality and their generic computation. Soc. Netw. 2008, 30, 136–145. [Google Scholar]
- Malliaros, F.D.; Megalooikonomou, V.; Faloutsos, C. Fast robustness estimation in large social graphs: Communities and anomaly detection. In Proceedings of the 12th SIAM International Conference on Data Mining, SDM 2012, Anaheim, CA, USA, 26–28 April 2012; pp. 942–953. [Google Scholar] [CrossRef]
- Chan, H.; Akoglu, L. Optimizing network robustness by edge rewiring: A general framework. Data Min. Knowl. Discov. 2016, 30, 1395–1425. [Google Scholar] [CrossRef]
- Chen, L.; Xi, Y.; Dong, L.; Zhao, M.; Li, C.; Liu, X.; Cui, X. Identifying influential nodes in complex networks via Transformer. Inf. Process. Manag. 2024, 61, 103775. [Google Scholar] [CrossRef]
- Zhang, K.; Pu, Z.; Jin, C.; Zhou, Y.; Wang, Z. A novel semi-local centrality to identify influential nodes in complex networks by integrating multidimensional factors. Eng. Appl. Artif. Intell. 2025, 145, 110177. [Google Scholar] [CrossRef]
- Munikoti, S.; Das, L.; Natarajan, B. Scalable graph neural network-based framework for identifying critical nodes and links in complex networks. Neurocomputing 2022, 468, 211–221. [Google Scholar] [CrossRef]
- Wang, S.; Liu, J.; Jin, Y. Surrogate-Assisted Robust Optimization of Large-Scale Networks Based on Graph Embedding. IEEE Trans. Evol. Comput. 2020, 24, 735–749. [Google Scholar] [CrossRef]
- Wang, S.; Liu, J.; Jin, Y. A Computationally Efficient Evolutionary Algorithm for Multiobjective Network Robustness Optimization. IEEE Trans. Evol. Comput. 2021, 25, 419–432. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, R.; Zhang, Y.; Zhang, X. Adaptive population sizing for multi-population based constrained multi-objective optimization. Neurocomputing 2025, 621, 129296. [Google Scholar] [CrossRef]
- Ming, F.; Gong, W.; Wang, L.; Jin, Y. Constrained Multi-Objective Optimization with Deep Reinforcement Learning Assisted Operator Selection. IEEE/CAA J. Autom. Sin. 2024, 11, 919–931. [Google Scholar] [CrossRef]
- Zeng, A.; Liu, W. Enhancing network robustness against malicious attacks. Phys. Rev. E-Stat. Nonlinear, Soft Matter Phys. 2012, 85, 066130. [Google Scholar] [CrossRef]
- Schneider, C.M.; Moreira, A.A.; Andrade, J.S.; Havlin, S.; Herrmann, H.J. Mitigation of malicious attacks on networks. Proc. Natl. Acad. Sci. USA 2011, 108, 3838–3841. [Google Scholar] [CrossRef]
- Liang, J.; Ban, X.; Yu, K.; Qu, B.; Qiao, K.; Yue, C.; Chen, K.; Tan, K.C. A Survey on Evolutionary Constrained Multiobjective Optimization. IEEE Trans. Evol. Comput. 2023, 27, 201–221. [Google Scholar] [CrossRef]
- Zhou, M.; Liu, J. A memetic algorithm for enhancing the robustness of scale-free networks against malicious attacks. Phys. A Stat. Mech. Its Appl. 2014, 410, 131–143. [Google Scholar] [CrossRef]
- Tang, X.; Liu, J.; Zhou, M. Enhancing network robustness against targeted and random attacks using a memetic algorithm. Europhys. Lett. 2015, 111, 38005. [Google Scholar] [CrossRef]
- Tang, X.; Liu, J.; Hao, X. Mitigate Cascading Failures on Networks using a Memetic Algorithm. Sci. Rep. 2016, 6, 38713. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Liu, J.; Li, L.; Liu, Y.; Wang, H. A knowledge driven two-stage co-evolutionary algorithm for constrained multi-objective optimization. Expert Syst. Appl. 2025, 274, 126908. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, C.; Wu, X.; Zhou, Z.; Yan, X.; Gong, W. Utilizing feasible non-dominated solution information for constrained multi-objective optimization. Inf. Sci. 2025, 699, 121812. [Google Scholar] [CrossRef]
- Bai, W.; Dang, Q.; Wu, J.; Gao, X.; Zhang, G. Growing neural gas network based environment selection strategy for constrained multi-objective optimization. Inf. Sci. 2025, 698, 121774. [Google Scholar] [CrossRef]
- Sun, Y.; Zhou, X.; Yang, C.; Huang, T. Constrained multi-objective state transition algorithm via adaptive bidirectional coevolution. Expert Syst. Appl. 2025, 266, 126073. [Google Scholar] [CrossRef]
- Zhao, S.; Hao, X.; Chen, L.; Yu, T.; Li, X.; Liu, W. Two-stage bidirectional coevolutionary algorithm for constrained multi-objective optimization. Swarm Evol. Comput. 2025, 92, 101784. [Google Scholar] [CrossRef]
- Zhou, M.; Liu, J. A Two-Phase Multiobjective Evolutionary Algorithm for Enhancing the Robustness of Scale-Free Networks Against Multiple Malicious Attacks. IEEE Trans. Cybern. 2017, 47, 539–552. [Google Scholar] [CrossRef]
- Wang, S.; Liu, J. Designing comprehensively robust networks against intentional attacks and cascading failures. Inf. Sci. 2019, 478, 125–140. [Google Scholar] [CrossRef]
- Wang, S.; Liu, J. A Multi-Objective Evolutionary Algorithm for Promoting the Emergence of Cooperation and Controllable Robustness on Directed Networks. IEEE Trans. Netw. Sci. Eng. 2018, 5, 92–100. [Google Scholar] [CrossRef]
- Wu, H.; Chen, Q.; Chen, J.; Jin, Y.; Ding, J.; Zhang, X.; Chai, T. A Multi-Stage Expensive Constrained Multi-Objective Optimization Algorithm Based on Ensemble Infill Criterion. IEEE Trans. Evol. Comput. 2024; early access. [Google Scholar] [CrossRef]
- Wu, H.; Chen, Q.; Jin, Y.; Ding, J.; Chai, T. A Surrogate-Assisted Expensive Constrained Multi-Objective Optimization Algorithm Based on Adaptive Switching of Acquisition Functions. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 2050–2064. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, H.; Tian, Y.; Ma, H.; Zhang, X. Multigranularity Surrogate Modeling for Evolutionary Multiobjective Optimization with Expensive Constraints. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 2956–2968. [Google Scholar] [CrossRef] [PubMed]
- de Winter, R.; Bronkhorst, P.; van Stein, B.; Bäck, T. Constrained Multi-Objective Optimization with a Limited Budget of Function Evaluations. Memetic Comput. 2022, 14, 151–164. [Google Scholar] [CrossRef]
- Li, J.; Dong, H.; Wang, P.; Shen, J.; Qin, D. Multi-objective constrained black-box optimization algorithm based on feasible region localization and performance-improvement exploration. Appl. Soft Comput. 2023, 148, 110874. [Google Scholar] [CrossRef]
- Wauters, J.; Keane, A.; Degroote, J. Development of an adaptive infill criterion for constrained multi-objective asynchronous surrogate-based optimization. J. Glob. Optim. 2020, 78, 137–160. [Google Scholar] [CrossRef]
- Martínez-Frutos, J.; Herrero-Pérez, D. Kriging-based infill sampling criterion for constraint handling in multi-objective optimization. J. Glob. Optim. 2016, 64, 97–115. [Google Scholar] [CrossRef]
- Sun, J.; Zheng, W.; Zhang, Q.; Xu, Z. Graph Neural Network Encoding for Community Detection in Attribute Networks. IEEE Trans. Cybern. 2022, 52, 7791–7804. [Google Scholar] [CrossRef]
- Lou, Y.; He, Y.; Wang, L.; Chen, G. Predicting Network Controllability Robustness: A Convolutional Neural Network Approach. IEEE Trans. Cybern. 2022, 52, 4052–4063. [Google Scholar] [CrossRef]
- Lou, Y.; He, Y.; Wang, L.; Tsang, K.F.; Chen, G. Knowledge-Based Prediction of Network Controllability Robustness. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 5739–5750. [Google Scholar] [CrossRef]
- Zonghan, W.; Shirui, P.; Fengwen, C.; Guodong, L.; Chengqi, Z.; Philip S, Y. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4–24. [Google Scholar]
- Zhang, Y.; Li, J.; Ding, J.; Li, X. A Graph Transformer-Driven Approach for Network Robustness Learning. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 1992–2005. [Google Scholar] [CrossRef]
- Holme, P.; Kim, B.J.; Yoon, C.N.; Han, S.K. Attack vulnerability of complex networks. Phys. Rev. E-Stat. Physics, Plasmas, Fluids, Relat. Interdiscip. Top. 2002, 65, 14. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Jeong, H.; Barabási, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. In The Structure and Dynamics of Networks; Princeton University Press: Princeton, NJ, USA, 2011; Volume 9781400841356, pp. 349–352. [Google Scholar] [CrossRef]
- Shi, C.; Peng, Y.; Zhuo, Y.; Tang, J.; Long, K. A new way to improve the robustness of complex communication networks by allocating redundancy links. Phys. Scr. 2012, 85, 035803. [Google Scholar] [CrossRef]
- Kůdela, J.; Dobrovský, L. Performance Comparison of Surrogate-Assisted Evolutionary Algorithms on Computational Fluid Dynamics Problems. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer Nature: Cham, Switzerland, 2024; Volume 15149, pp. 303–321. [Google Scholar] [CrossRef]
- Homberg, T.; Mostaghim, S.; Hiwa, S.; Hiroyasu, T. Optimized Drug Design using Multi-Objective Evolutionary Algorithms with SELFIES. In Proceedings of the 2024 IEEE Congress on Evolutionary Computation, CEC 2024, Yokohama, Japan, 30 June–5 July 2024. [Google Scholar] [CrossRef]
- Wu, C.; Lou, Y.; Li, J.; Wang, L.; Xie, S.; Chen, G. A Multitask Network Robustness Analysis System Based on the Graph Isomorphism Network. IEEE Trans. Cybern. 2024, 54, 6630–6642. [Google Scholar] [CrossRef]
- Cheng, G.H.; Gary Wang, G.; Hwang, Y.M. Multi-Objective Optimization for High-Dimensional Expensively Constrained Black-Box Problems. J. Mech. Des. 2021, 143, 111704. [Google Scholar] [CrossRef]
- Yang, Z.; Qiu, H.; Gao, L.; Chen, L.; Liu, J. Surrogate-assisted MOEA/D for expensive constrained multi-objective optimization. Inf. Sci. 2023, 639, 119016. [Google Scholar] [CrossRef]
- Xu, K.; Jegelka, S.; Hu, W.; Leskovec, J. How powerful are graph neural networks? In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019.
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. 2017, 2017, 1025–1035. [Google Scholar]
- Veličkovi’veličkovi’c, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lì, P.; Bengio, Y.; Veličković, P.; Casanova, A.; Liò, P.; Cucurull, G.; et al. Graph attention networks. In Proceedings of the 6th International Conference on Learning Representations, ICLR 2018—Conference Track Proceedings, Vancouver, BC, Canada, 30 April–3 May 2018; pp. 1–12. [Google Scholar]
- Xu, K.; Li, C.; Tian, Y.; Sonobe, T.; Kawarabayashi, K.I.; Jegelka, S. Representation learning on graphs with jumping knowledge networks. In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholm, Sweden, 10–15 July 2018; Volume 12, pp. 8676–8685. [Google Scholar]
- Zhang, M.; Cui, Z.; Neumann, M.; Chen, Y. An end-to-end deep learning architecture for graph classification. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence, AAAI 2018, New Orleans, LA, USA, 2–7 February 2018; pp. 4438–4445. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Li, L.; Li, G.; Chang, L. On self-adaptive stochastic ranking in decomposition many-objective evolutionary optimization. Neurocomputing 2022, 489, 547–557. [Google Scholar] [CrossRef]
- Erdos, P.; Renyi, A. On the strength of connectedness of a random graph. Acta Math. Hung. 1961, 12, 261–267. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ï¿œsmall-worldï¿œ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Yao, W.; Jiang, T.; Chen, X. A multi-objective memetic algorithm for automatic adversarial attack optimization design. Neurocomputing 2023, 547, 126318. [Google Scholar] [CrossRef]
- Tian, Y.; Pan, J.; Yang, S.; Zhang, X.; He, S.; Jin, Y. Imperceptible and Sparse Adversarial Attacks via a Dual-Population-Based Constrained Evolutionary Algorithm. IEEE Trans. Artif. Intell. 2023, 4, 268–281. [Google Scholar] [CrossRef]
- Reis, M.J.C.S. Symmetry-Guided Surrogate-Assisted NSGA-II for Multi-Objective Optimization of Renewable Energy Systems. Symmetry 2025, 17, 1367. [Google Scholar] [CrossRef]
- Haddad, A.; Tlili, T.; Dahmani, N.; Krichen, S. Integrating NSGA-II and Q-learning for Solving the Multi-objective Electric Vehicle Routing Problem with Battery Swapping Stations. Int. J. Intell. Transp. Syst. Res. 2025, 23, 840–856. [Google Scholar] [CrossRef]
- Zhang, P.; Qian, Y.; Qian, Q. Multi-objective optimization for materials design with improved NSGA-II. Mater. Today Commun. 2021, 28, 102709. [Google Scholar] [CrossRef]
- Qi, Y.; Hou, Z.; Li, H.; Huang, J.; Li, X. A decomposition based memetic algorithm for multi-objective vehicle routing problem with time windows. Comput. Oper. Res. 2015, 62, 61–77. [Google Scholar] [CrossRef]
- Huang, J.; Wu, R.; Li, J. Efficient adaptive robustness optimization algorithm for complex networks. J. Comput. Appl. 2024, 44, 3530–3539. [Google Scholar]
- Bader, J.; Zitzler, E. HypE: An Algorithm for Fast Hypervolume-Based Many-Objective Optimization. Evol. Comput. 2011, 19, 45–76. [Google Scholar] [CrossRef]
- Collette, Y.; Siarry, P. Three new metrics to measure the convergence of metaheuristics towards the Pareto frontier and the aesthetic of a set of solutions in biobjective optimization. Comput. Oper. Res. 2005, 32, 773–792. [Google Scholar] [CrossRef]
- Lu, X.; Liu, Z.; Fan, Y.; Zhou, J. A Graph Convolutional Network Approach for Predicting Network Controllability Robustness. In Proceedings of the 2023 35th Chinese Control and Decision Conference (CCDC), Yichang, China, 20–22 May 2023; pp. 3544–3547. [Google Scholar] [CrossRef]
- Lou, Y.; Wu, R.; Li, J.; Wang, L.; Li, X.; Chen, G. A Learning Convolutional Neural Network Approach for Network Robustness Prediction. IEEE Trans. Cybern. 2023, 53, 4531–4544. [Google Scholar] [CrossRef]
- Lou, Y.; Wu, R.; Li, J.; Wang, L.; Chen, G. A Convolutional Neural Network Approach to Predicting Network Connectedness Robustness. IEEE Trans. Netw. Sci. Eng. 2021, 8, 3209–3219. [Google Scholar] [CrossRef]
- Rossi, R.A.; Ahmed, N.K. The network data repository with interactive graph analytics and visualization. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, AAAI’15, Austin, TX, USA, 25–30 January 2015; AAAI Press: Washington, DC, USA, 2015; pp. 4292–4293. [Google Scholar]


| Parameter | Description | Value |
|---|---|---|
| n | The size of the dataset | 200 |
| The size of the population | 20 | |
| The maximum number of evolutionary generations | 100 | |
| The probability of performing a crossover | ||
| The probability of performing a mutation | ||
| The probability of performing a local search | ||
| The maximum number of rewiring executions in the local search | 20 | |
| K | The number of sampled solutions | 2 |
| T | The interval for updating the surrogate model | 10 |
| The number of runs for each algorithm | 10 |
| Network | Algorithm | Prediction Error | Inference Time (s) | True Evaluation Time (s) |
|---|---|---|---|---|
| BA200 | GE_SU | 0.0162 ± (0.0015) | 1.46 | 3.18 |
| CNN | 0.0054 ± (0.0036) | 1.63 | ||
| GCN | 0.0106 ± (0.0015) | 0.69 | ||
| GIN | 0.0057 ± (0.0016) | 0.37 | ||
| BA500 | GE_SU | 0.0190 ± (0.0017) | 2.96 | 18.36 |
| CNN | 0.0069 ± (0.0045) | 6.50 | ||
| GCN | 0.0085 ± (0.0018) | 0.73 | ||
| GIN | 0.0050 ± (0.0015) | 0.39 | ||
| BA1000 | GE_SU | 0.0346 ± (0.0038) | 7.20 | 73.20 |
| CNN | 0.0163 ± (0.0017) | 15.75 | ||
| GCN | 0.0074 ± (0.0028) | 0.79 | ||
| GIN | 0.0043 ± (0.0012) | 0.44 | ||
| BA2000 | GE_SU | 0.0344 ± (0.0031) | 16.37 | 289.41 |
| CNN | 0.0132 ± (0.0021) | 45.89 | ||
| GCN | 0.0086 ± (0.0019) | 0.88 | ||
| GIN | 0.0057 ± (0.0022) | 0.51 | ||
| ER200 | GE_SU | 0.0097 ± (0.0020) | 1.37 | 3.06 |
| CNN | 0.0099 ± (0.0015) | 1.55 | ||
| GCN | 0.0075 ± (0.0012) | 0.70 | ||
| GIN | 0.0056 ± (0.0013) | 0.39 | ||
| ER500 | GE_SU | 0.0142 ± (0.0013) | 3.02 | 18.90 |
| CNN | 0.0090 ± (0.0020) | 6.59 | ||
| GCN | 0.0075 ± (0.0008) | 0.74 | ||
| GIN | 0.0048 ± (0.0015) | 0.41 | ||
| ER1000 | GE_SU | 0.0391 ± (0.0035) | 7.21 | 74.87 |
| CNN | 0.0137 ± (0.0014) | 16.75 | ||
| GCN | 0.0046 ± (0.0025) | 0.76 | ||
| GIN | 0.0053 ± (0.0012) | 0.44 | ||
| ER2000 | GE_SU | 0.0239 ± (0.0022) | 15.68 | 292.83 |
| CNN | 0.0160 ± (0.0034) | 46.83 | ||
| GCN | 0.0121 ± (0.0025) | 0.85 | ||
| GIN | 0.0050 ± (0.0010) | 0.53 | ||
| SW200 | GE_SU | 0.0161 ± (0.0024) | 1.43 | 3.07 |
| CNN | 0.0110 ± (0.0011) | 1.68 | ||
| GCN | 0.0055 ± (0.0018) | 0.70 | ||
| GIN | 0.0092 ± (0.0010) | 0.38 | ||
| SW500 | GE_SU | 0.0124 ± (0.0012) | 2.87 | 18.28 |
| CNN | 0.0101 ± (0.0010) | 7.64 | ||
| GCN | 0.0063 ± (0.0010) | 0.73 | ||
| GIN | 0.0085 ± (0.0009) | 0.40 | ||
| SW1000 | GE_SU | 0.0289 ± (0.0026) | 7.12 | 73.62 |
| CNN | 0.0124 ± (0.0012) | 16.75 | ||
| GCN | 0.0064 ± (0.0027) | 0.79 | ||
| GIN | 0.0051 ± (0.0019) | 0.43 | ||
| SW2000 | GE_SU | 0.0261 ± (0.0089) | 16.25 | 287.05 |
| CNN | 0.0184 ± (0.0024) | 46.04 | ||
| GCN | 0.0086 ± (0.0017) | 0.91 | ||
| GIN | 0.0036 ± (0.0014) | 0.51 |
| Network | Algorithm | HV | Δ | Runtime (s)/ |
|---|---|---|---|---|
| BA500 | MOEA0 | 0.3970 ± 0.0120 (−) | 0.0256 ± 0.0031 (≈) | 1.73 |
| MOEA-LS | 0.4404 ± 0.0296 (−) | 0.0323 ± 0.0042 (≈) | 6.24 | |
| MOEA-OL-LS | 0.4337 ± 0.0184 (−) | 0.0530 ± 0.0064 (−) | 2.31 | |
| MOEA-GIN | 0.4573 ± 0.0117 | 0.0243 ± 0.0027 | 2.39 | |
| ER500 | MOEA0 | 0.3453 ± 0.0133 (−) | 0.0376 ± 0.0048 (+) | 1.48 |
| MOEA-LS | 0.3712 ± 0.0096 (≈) | 0.0255 ± 0.0033 (+) | 6.26 | |
| MOEA-OL-LS | 0.3569 ± 0.0124 (−) | 0.0352 ± 0.0041 (≈) | 1.98 | |
| MOEA-GIN | 0.3798 ± 0.0085 | 0.0518 ± 0.0056 | 1.79 | |
| SW500 | MOEA0 | 0.4240 ± 0.0133 (−) | 0.0667 ± 0.0075 (−) | 1.44 |
| MOEA-LS | 0.4852 ± 0.0096 (+) | 0.0464 ± 0.0049 (−) | 5.74 | |
| MOEA-OL-LS | 0.4347 ± 0.0224 (−) | 0.0457 ± 0.0053 (−) | 2.64 | |
| MOEA-GIN | 0.4560 ± 0.0115 | 0.0359 ± 0.0042 | 1.81 | |
| BA1000 | MOEA0 | 0.3960 ± 0.0206 (−) | 0.0104 ± 0.0016 (≈) | 6.48 |
| MOEA-LS | 0.4332 ± 0.0170 (≈) | 0.0323 ± 0.0039 (−) | 22.71 | |
| MOEA-OL-LS | 0.4129 ± 0.0154 (−) | 0.0966 ± 0.0105 (−) | 7.11 | |
| MOEA-GIN | 0.4363 ± 0.0192 | 0.0257 ± 0.0029 | 5.63 | |
| ER1000 | MOEA0 | 0.4228 ± 0.0225 (−) | 0.1704 ± 0.0213 (−) | 5.86 |
| MOEA-LS | 0.4589 ± 0.0157 (≈) | 0.0838 ± 0.0091 (−) | 22.93 | |
| MOEA-OL-LS | 0.4353 ± 0.0194 (−) | 0.0807 ± 0.0094 (−) | 5.17 | |
| MOEA-GIN | 0.4606 ± 0.0106 | 0.0626 ± 0.0071 | 4.83 | |
| SW1000 | MOEA0 | 0.4038 ± 0.0168 (−) | 0.0917 ± 0.0098 (−) | 5.73 |
| MOEA-LS | 0.4532 ± 0.0153 (≈) | 0.0248 ± 0.0028 (+) | 21.78 | |
| MOEA-OL-LS | 0.4475 ± 0.0173 (−) | 0.0394 ± 0.0046 (≈) | 5.17 | |
| MOEA-GIN | 0.4568 ± 0.0105 | 0.0440 ± 0.0051 | 5.03 | |
| BA2000 | MOEA0 | 0.3973 ± 0.0138 (−) | 0.0216 ± 0.0018 (≈) | 29.92 |
| MOEA-LS | 0.4151 ± 0.0092 (−) | 0.0252 ± 0.0017 (≈) | 94.77 | |
| MOEA-OL-LS | 0.3844 ± 0.0184 (−) | 0.0376 ± 0.0042 (−) | 25.12 | |
| MOEA-GIN | 0.4262 ± 0.0094 | 0.0157 ± 0.0016 | 19.05 | |
| ER2000 | MOEA0 | 0.3285 ± 0.0125 (−) | 0.0411 ± 0.0052 (≈) | 23.76 |
| MOEA-LS | 0.3663 ± 0.0085 (+) | 0.0419 ± 0.0046 (≈) | 90.83 | |
| MOEA-OL-LS | 0.3475 ± 0.0137 (−) | 0.0189 ± 0.0021 (+) | 18.36 | |
| MOEA-GIN | 0.3570 ± 0.0129 | 0.0493 ± 0.0054 | 15.06 | |
| SW2000 | MOEA0 | 0.4240 ± 0.0131 (−) | 0.0412 ± 0.0047 (−) | 22.68 |
| MOEA-LS | 0.4545 ± 0.0108 (≈) | 0.0598 ± 0.0062 (−) | 87.46 | |
| MOEA-OL-LS | 0.4332 ± 0.0118 (−) | 0.0855 ± 0.0093 (−) | 16.56 | |
| MOEA-GIN | 0.4504 ± 0.0094 | 0.0361 ± 0.0040 | 14.52 |
| Network | |||||
|---|---|---|---|---|---|
| bio-celegans | 453 | 2025 | 237 | 8 | 0.12 |
| bio-grid-plant | 1745 | 6196 | 142 | 7 | 0.12 |
| ia-crime-moreno | 829 | 1476 | 25 | 3 | 0.01 |
| ia-email-univ | 1133 | 5451 | 71 | 9 | 0.22 |
| power-bcspwr09 | 1723 | 4117 | 14 | 2 | 0.08 |
| power-bcspwr10 | 5300 | 13,571 | 13 | 3 | 0.09 |
| Network | Algorithm | HV | Δ | Runtime (s)/ |
|---|---|---|---|---|
| bio-celegans | MOEA0 | 0.3063 ± 0.0210 (−) | 0.0126 ± 0.0025 (+) | 1.44 |
| MOEA-LS | 0.3347 ± 0.0086 (≈) | 0.0197 ± 0.0039 (≈) | 4.75 | |
| MOEA-OL-LS | 0.3163 ± 0.0104 (−) | 0.0364 ± 0.0072 (−) | 2.25 | |
| MOEA-GIN | 0.3295 ± 0.0097 | 0.0274 ± 0.0054 | 1.53 | |
| bio-grid-plant | MOEA0 | 0.1574 ± 0.0170 (−) | 0.0414 ± 0.0082 (−) | 17.71 |
| MOEA-LS | 0.1875 ± 0.0093 (≈) | 0.0261 ± 0.0052 (≈) | 66.88 | |
| MOEA-OL-LS | 0.1765 ± 0.0136 (≈) | 0.0303 ± 0.0061 (−) | 10.32 | |
| MOEA-GIN | 0.1798 ± 0.0152 | 0.0190 ± 0.0038 | 8.34 | |
| ia-crime-moreno | MOEA0 | 0.2080 ± 0.0233 (−) | 0.1118 ± 0.0224 (−) | 4.06 |
| MOEA-LS | 0.2352 ± 0.0101 (−) | 0.0403 ± 0.0061 (≈) | 16.67 | |
| MOEA-OL-LS | 0.2280 ± 0.0165 (−) | 0.0771 ± 0.0154 (−) | 3.92 | |
| MOEA-GIN | 0.2581 ± 0.0129 | 0.0448 ± 0.0090 | 3.60 | |
| ia-email-univ | MOEA0 | 0.3542 ± 0.0152 (−) | 0.0195 ± 0.0039 (+) | 8.79 |
| MOEA-LS | 0.3979 ± 0.0061 (≈) | 0.0443 ± 0.0070 (−) | 32.00 | |
| MOEA-OL-LS | 0.3680 ± 0.0143 (−) | 0.0470 ± 0.0094 (−) | 9.58 | |
| MOEA-GIN | 0.3967 ± 0.0109 | 0.0296 ± 0.0059 | 8.33 | |
| power-bcspwr09 | MOEA0 | 0.2973 ± 0.0110 (−) | 0.0272 ± 0.0054 (≈) | 18.56 |
| MOEA-LS | 0.3303 ± 0.0108 (≈) | 0.0150 ± 0.0031 (≈) | 60.80 | |
| MOEA-OL-LS | 0.3208 ± 0.0080 (−) | 0.0169 ± 0.0034 (≈) | 19.28 | |
| MOEA-GIN | 0.3385 ± 0.0092 | 0.0145 ± 0.0029 | 14.02 | |
| power-bcspwr10 | MOEA0 | 0.3504 ± 0.0090 (−) | 0.0194 ± 0.0039 (≈) | 151.81 |
| MOEA-LS | 0.3951 ± 0.0062 (≈) | 0.0212± 0.0026 (−) | 539.52 | |
| MOEA-OL-LS | 0.3803 ± 0.0113 (−) | 0.0239 ± 0.0048 (−) | 83.10 | |
| MOEA-GIN | 0.3950 ± 0.0105 | 0.0154 ± 0.0031 | 71.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Li, L.; Cai, G. A GIN-Guided Multiobjective Evolutionary Algorithm for Robustness Optimization of Complex Networks. Algorithms 2025, 18, 666. https://doi.org/10.3390/a18100666
Li G, Li L, Cai G. A GIN-Guided Multiobjective Evolutionary Algorithm for Robustness Optimization of Complex Networks. Algorithms. 2025; 18(10):666. https://doi.org/10.3390/a18100666
Chicago/Turabian StyleLi, Guangpeng, Li Li, and Guoyong Cai. 2025. "A GIN-Guided Multiobjective Evolutionary Algorithm for Robustness Optimization of Complex Networks" Algorithms 18, no. 10: 666. https://doi.org/10.3390/a18100666
APA StyleLi, G., Li, L., & Cai, G. (2025). A GIN-Guided Multiobjective Evolutionary Algorithm for Robustness Optimization of Complex Networks. Algorithms, 18(10), 666. https://doi.org/10.3390/a18100666






