A Recursive Solution to the Global Maximum Minimum Cut Problem with a Fixed Sink

Abstract

In graph theory and network design, the minimum cut is a fundamental measure of system connectivity and communication capacity. While prior research has largely focused on computing the minimum cut for a fixed source–sink pair, practical scenarios such as data center communication often demand a different objective: identifying the source node whose minimum cut to a designated sink is maximized. This task, which we term the Global Maximum Minimum Cut with Fixed Sink (GMMC-FS) problem, captures the goal of locating a high-capacity source relative to a shared sink node that aggregates multiple servers. The problem is of significant engineering importance, yet it is computationally challenging as it involves a nested max–min optimization. In this paper, we present a recursive reduction (RR) algorithm for solving the GMMC-FS problem. The key idea is to iteratively select pivot nodes, compute their minimum cuts with respect to the sink, and prune dominated candidates whose cut values cannot exceed that of the pivot. By recursively applying this elimination process, RR dramatically reduces the number of max-flow computations required while preserving exact correctness. Compared with classical contraction-based and Gomory–Hu tree approaches that rely on global cut enumeration, the proposed RR framework offers a more direct and scalable mechanism for identifying the source that maximizes the minimum cut to a fixed sink. Its novelty lies in exploiting the structural properties of the sink side of suboptimal cuts, which leads to both theoretical efficiency and empirical robustness across large-scale networks. We provide a rigorous theoretical analysis establishing both correctness and complexity bounds, and we validate the approach through extensive experiments. Results demonstrate that RR consistently achieves optimal solutions while significantly outperforming baseline methods in runtime, particularly on large and dense networks.

1. Introduction

In graph theory and network optimization, the concept of a minimum cut plays a fundamental role in quantifying network reliability [1], communication bottlenecks [2], and resource allocation constraints [3]. Given a network represented as a capacitated undirected graph, the classic minimum cut problem focuses on identifying the smallest set of edges whose removal disconnects a designated pair of nodes—typically a source and a sink. This problem has been extensively studied and forms the basis of many important results, including the celebrated Max-Flow Min-Cut Theorem [3].

While traditional algorithms have concentrated on computing the minimum cut between a single source–sink pair [4,5,6,7], many emerging applications require a global view of network capacity. In particular, it is often important to identify the source node that can sustain the highest possible minimum cut to a fixed sink [8,9]. This leads to the Global Maximum Minimum Cut with Fixed Sink (GMMC-FS) problem: given a fixed sink node in a capacitated graph, find the source node whose minimum s–t cut is the largest among all possible sources. Applications of this problem arise in a variety of real-world network scenarios. For example, consider a communication network in which multiple base stations transmit data to a central controller. Selecting the base station whose connection to the controller has the largest minimum cut ensures the most reliable data delivery path, even under potential link or node failures. This idea naturally extends to other domains. In server provisioning and data center selection [10], the formulation assists in determining which server can sustain the highest aggregate throughput toward a fixed sink, thereby improving overall network utilization. In resilient data dissemination [11], the approach helps identify a source node that maintains service continuity under multiple link disruptions. Finally, in load-aware routing, the model facilitates balanced traffic distribution by selecting sources that provide the strongest connectivity margins to the sink.

The GMMC-FS problem can be naturally expressed as a nested max–min optimization [12], making it both conceptually and computationally more difficult than classical minimum cut computations. A naive approach would require solving a minimum cut problem from every other node to the sink, resulting in an excessive computational cost—especially in large or dense graphs. Furthermore, unlike the global minimum cut [13], the GMMC-FS problem lacks known deterministic polynomial-time algorithms with guaranteed optimality.

In this paper, we propose a recursive reduction (RR) algorithm for solving the GMMC-FS problem with provable correctness and practical efficiency. The key idea is to iteratively select a pivot source, compute its minimum cut with respect to the fixed sink, and then prune all vertices that cannot possibly exceed the pivot in cut value. By recursively applying this elimination process, the algorithm progressively reduces the candidate set of sources until only the maximizer remains. This design transforms an otherwise exhaustive enumeration of all source nodes into a streamlined recursive search, often requiring exponentially fewer max-flow computations in practice.

Our main contributions are summarized as follows:

• We formally define the Global Maximum Minimum Cut with Fixed Sink (GMMC-FS) problem, capturing a natural max–min connectivity formulation relevant to diverse applications.
• We design RR, a recursive reduction algorithm that leverages pivot-based elimination to efficiently solve the GMMC-FS problem. RR guarantees correctness while drastically reducing the number of max-flow computations compared to naive enumeration.
• We provide a rigorous theoretical analysis of RR, proving that it always identifies the optimal source and establishing both worst-case and expected complexity bounds.
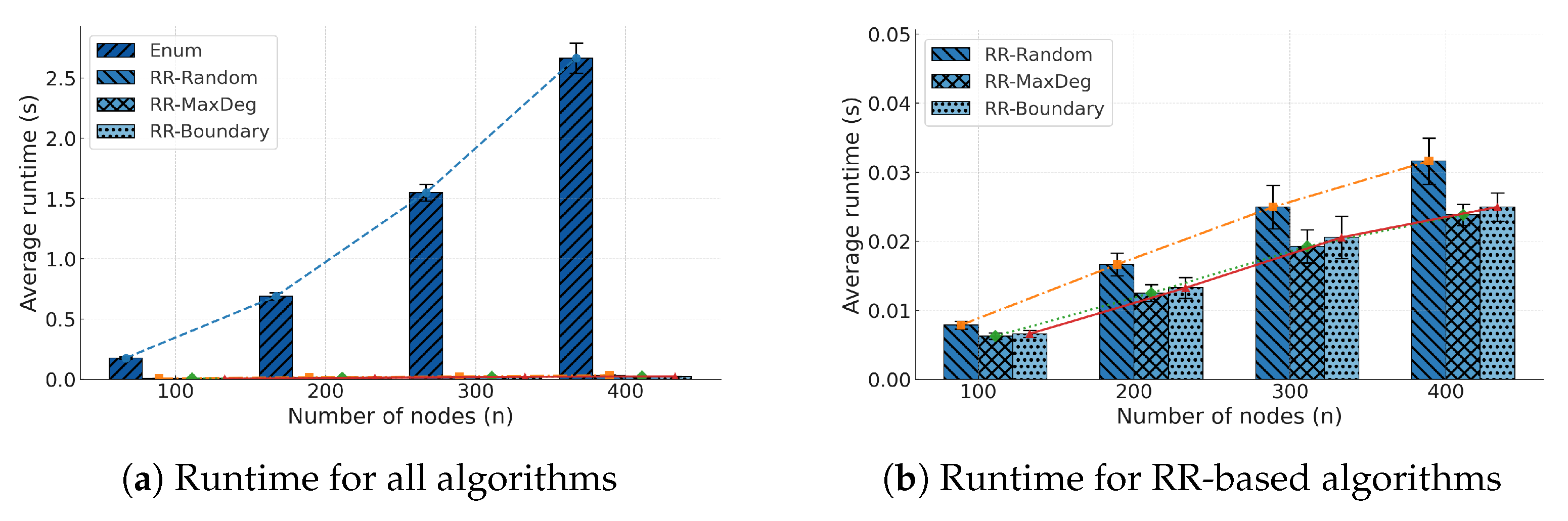
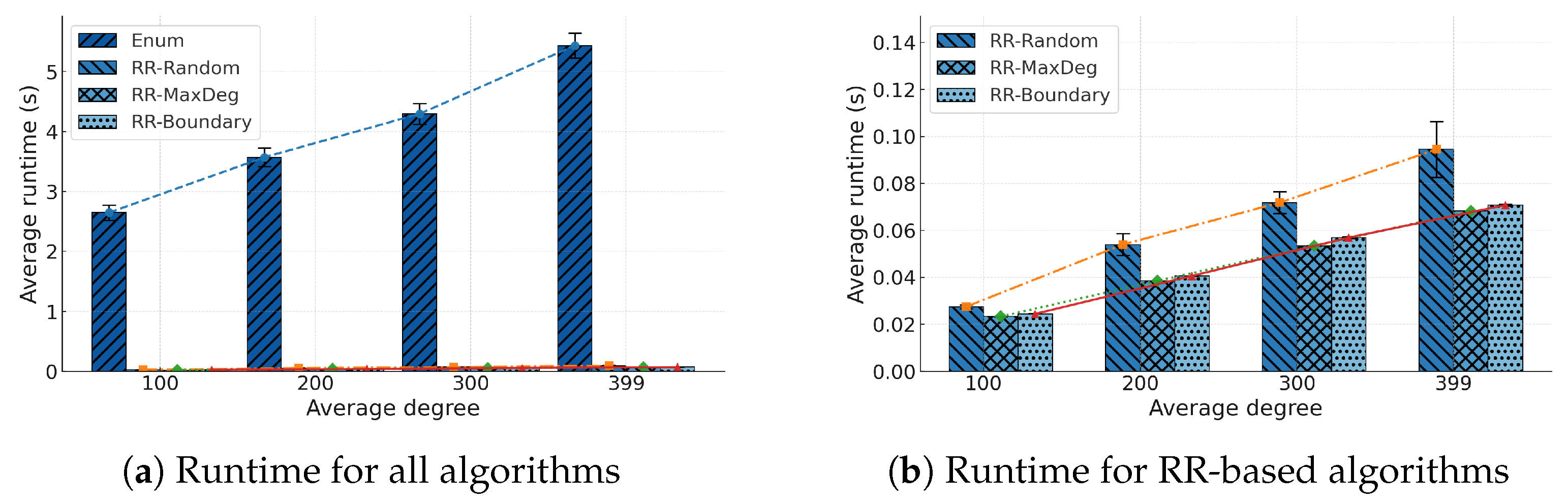
• We conduct extensive empirical evaluations across diverse graph topologies. Results demonstrate that RR consistently achieves optimal solutions with substantially reduced runtime relative to baseline methods, particularly on large and dense graphs.

The remainder of the paper is organized as follows. Section 2 formally defines the GMMC-FS problem and presents the necessary preliminaries. Section 3 introduces our RRA algorithm. Section 4 provides theoretical analysis, including correctness and complexity bounds. Section 5 presents experimental results with the baselines and varying scenarios. Section 6 introduces the related work and Section 7 concludes the paper.

2. Problem Definition and Preliminaries

We consider a capacitated undirected graph $G=(V,E)$, where V is the vertex set and E is the edge set, with the number of nodes $n=\left|V\right|$ and edges $m=\left|E\right|$. Each edge $e\in E$ has a non-negative capacity $c_e\ge 0$. Let $t\in V$ be a fixed terminal node, referred to as the sink. For any node $s\in V\setminus \left\{t\right\}$, define

$$f\left(s\right)=min\left\{\mathrm{cap}\left(\delta \right(X\left)\right):s\in X,t\notin X\right\},$$

where for any edge set $F\subseteq E$, $\mathrm{cap}\left(F\right):={\sum }_{e\in F}{c}_e$, and for any vertex subset $X\subseteq V$, $\delta \left(X\right):=\left\{\right\{u,v\}\in E:u\in X,v\notin X\}$. That is, $f\left(s\right)$ represents the minimum capacity of any cut that separates node s from the fixed sink t. The objective of the problem is to identify the source node

$$s^{★}=arg\underset{s\in V\setminus \left\{t\right\}}{max}f\left(s\right).$$

2.1. Relationship to Classical Min–Cut and Max–Flow

The GMMC-FS problem differs from the classical minimum cut problem, which seeks the smallest cut separating a single pair of nodes. In contrast, GMMC-FS is a max–min problem: it aims to identify the source node that has the highest possible minimum cut to a fixed sink. This makes the problem inherently more complex, as it involves evaluating multiple source candidates rather than a single cut.

By the max–flow min–cut theorem, $f\left(s\right)$ is equivalent to the value of the maximum flow from s to t. Therefore, solving the GMMC-FS problem can also be interpreted as identifying the node s that achieves the maximum value of the minimum capacity s–t cut (or equivalently, the maximum $s\to t$ flow).

2.2. Computational Challenge

A naive approach to solving the GMMC-FS problem would involve computing the minimum s–t cut (or maximum flow) for every $s\in V\setminus \left\{t\right\}$. Each such computation requires invoking a flow oracle, whose running time we denote by ${\mathsf{T}}_{\mathrm{flow}}(n,m)$, depending on the algorithm used (e.g., Edmonds–Karp [4], Dinic [5], Push–Relabel [6], or Orlin’s [7] algorithm). In dense graphs, where $m=\Theta \left(n^2\right)$, such computations for all nodes become very expensive.

Hence, a more efficient strategy is required to avoid exhaustively evaluating all possible source nodes, particularly for large-scale or dense networks. Our proposed approach addresses this challenge by using recursive reduction with the cut information, which narrows the search space while maintaining correctness guarantees.

2.3. Illustrative Example

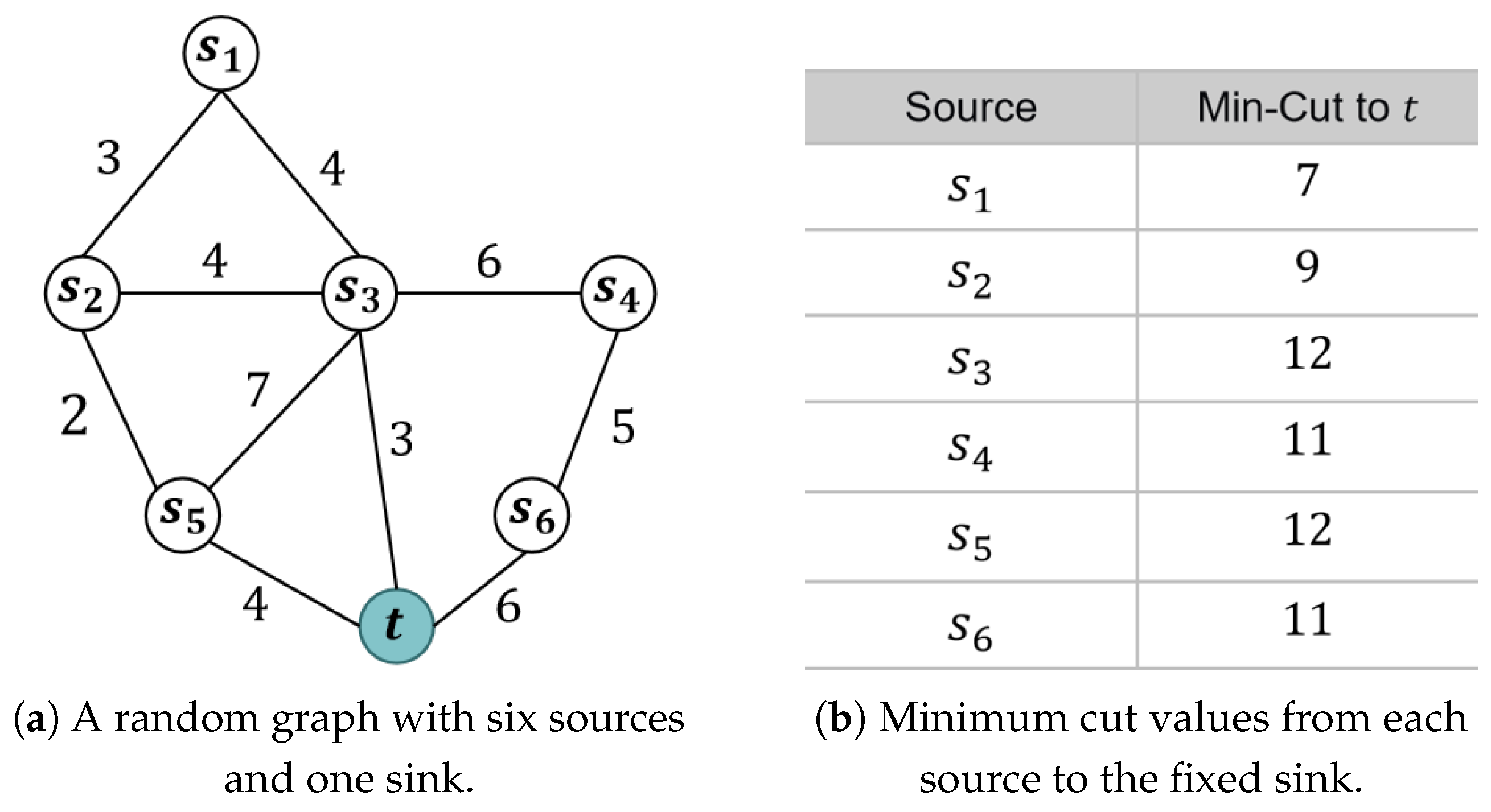
To better illustrate the structure and objective of the GMMC-FS problem, we provide a concrete example. Figure 1a shows a small undirected graph consisting of six source nodes $s_1,\dots ,s_6$ and one fixed sink node t. Each edge is labeled with its corresponding capacity, and all capacities are assumed to be non-negative integers. For each source node $s_i$, we compute the minimum $s_i$–t cut value, denoted $f\left(s_i\right)$. These values represent the smallest total capacity of edges that need to be removed to disconnect $s_i$ from t. The results are summarized directly in the associated Figure 1b.

This example highlights that different source nodes yield different minimum cut values to the sink. For instance, $f\left(s_3\right)=12$ and $f\left(s_5\right)=12$ are the highest, whereas $f\left(s_1\right)=7$ is the smallest. Therefore, the nodes $s_3$ and $s_5$ are optimal source nodes in this instance. The example demonstrates two key aspects of the GMMC-FS problem: (i) it illustrates the variability of connectivity strength between sources and the sink, and (ii) it shows that even on small graphs, computing all possible minimum cuts quickly becomes nontrivial, motivating the need for more efficient, scalable algorithms.

3. Recursive Reduction Algorithm

We now present the proposed recursive reduction (RR) algorithm, designed to efficiently identify the source node with the largest minimum s–t cut value in a capacitated undirected graph $G=(V,E)$. While a straightforward solution requires computing $\left|V\right|-1$ max-flow problems against a fixed sink t, RR leverages the structural properties of s–t cuts to eliminate groups of nodes at once, substantially reducing the number of required computations.

3.1. Algorithm Overview

The recursive reduction algorithm builds on the simple yet powerful observation that once the minimum cut between a chosen pivot node r and the sink t is computed, all other nodes lying on the same side of the cut as r cannot have a strictly larger cut value than r itself. These nodes can therefore be safely discarded from further consideration. By iteratively selecting pivots, evaluating their minimum cuts, and pruning entire subsets of vertices at each step, the algorithm progressively narrows the candidate set of sources. The search thus shifts from evaluating all possible sources to a recursive elimination process, which substantially reduces the number of max-flow computations required in practice while still guaranteeing that the true maximizer is preserved.

3.2. Algorithm Description

Let $\mathcal{C}\subseteq V\setminus \left\{t\right\}$ denote the current candidate set of sources. The algorithm begins with all non-sink vertices and iteratively selects one pivot from $\mathcal{C}$ according to a prescribed strategy, such as choosing the node of highest weighted degree (RR-MaxDeg), selecting randomly (RR-Random), or prioritizing boundary vertices revealed by previous cuts (RR-Boundary). For the chosen pivot, a minimum cut with respect to t is computed, and the resulting cut value $\kappa =f\left(r\right)$ is compared with the best solution found so far. If it improves upon the current record, both the maximum value and the corresponding source are updated. Next, the algorithm eliminates from $\mathcal{C}$ all nodes that lie on the same side of the cut as the pivot, since their cut values are upper bounded by the pivot’s. The process then continues with the reduced candidate set. Once $\mathcal{C}$ becomes empty, the algorithm returns the source achieving the largest recorded cut value. The full procedure is summarized in Algorithm 1.

Algorithm 1 Recursive reduction (RR) algorithm

Input: An undirected capacitated graph $G=(V,E)$ with a fixed sink t

Output: A source $s^{★}$ maximizing the s–t minimum cut value

1:   Initialize candidate set $\mathcal{C}\leftarrow V\setminus \left\{t\right\}$, best value $best\_val\leftarrow -\infty$, and $s^{★}\leftarrow ⌀$.   2:   while  $\mathcal{C}\ne \varnothing$  do   3:      Select a pivot $r\in \mathcal{C}$ according to a chosen strategy (e.g., random, maximum weighted degree, or boundary proximity).   4:      Compute the $r\to t$ minimum cut $(S,T)$ with $r\in S$, $t\in T$ and cut value $\kappa =f\left(r\right)$.   5:      if $\kappa >best\_val$ then   6:        Update $best\_val\leftarrow \kappa$ and $s^{★}\leftarrow r$.   7:      if $r\in S$ then   8:        $\mathcal{C}\leftarrow \mathcal{C}\cap (T\setminus \{t\left\}\right)$   9:      else 10:        $\mathcal{C}\leftarrow \mathcal{C}\cap (S\setminus \{t\left\}\right)$ 11:   return  $s^{★}$

3.3. Illustrative Example

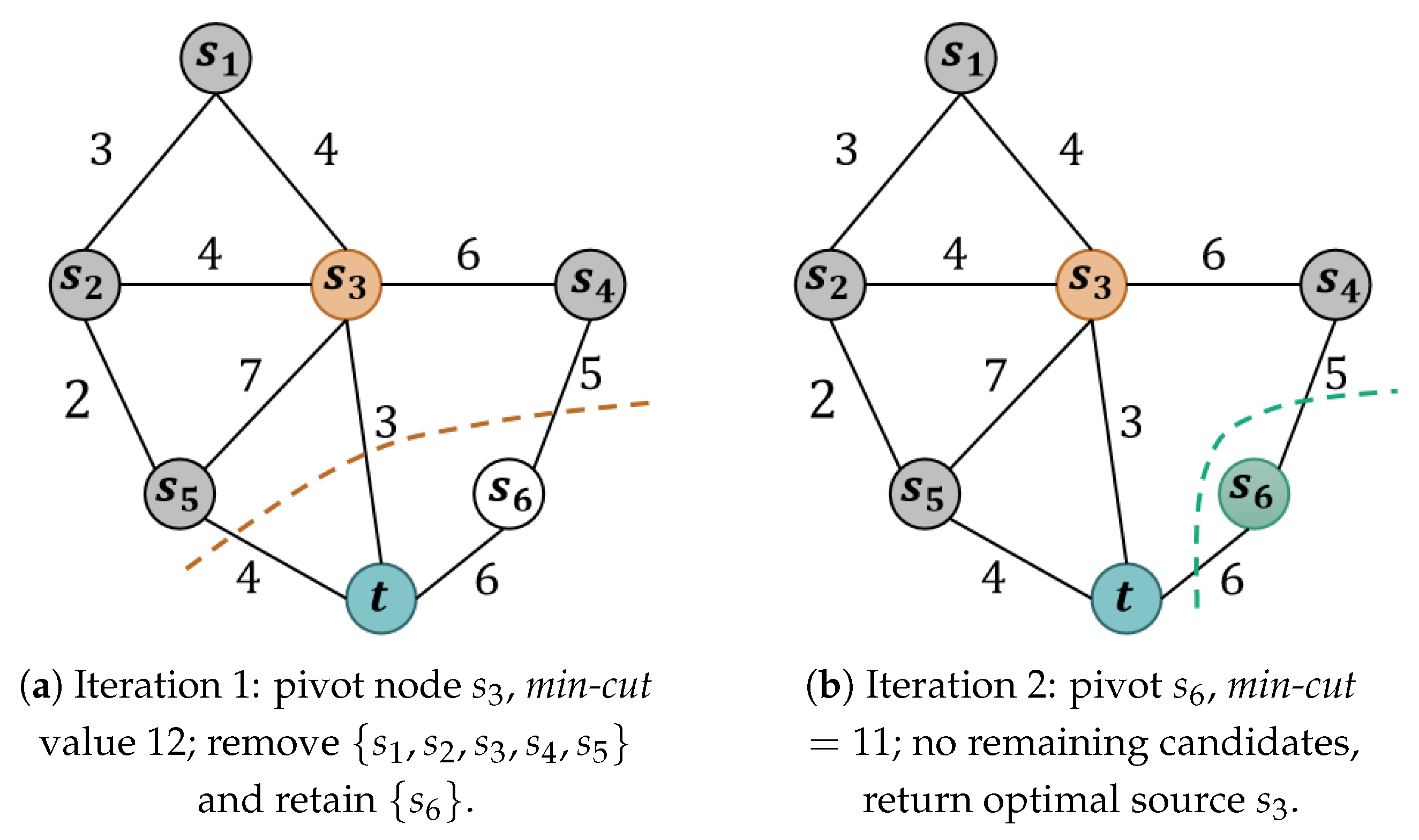
Figure 2, which adopts the same base graph as Figure 1, illustrates the recursive reduction process step by step. In the first iteration, the pivot node is selected as $s_3$ (colored orange) according to the maximum weighted degree strategy. The corresponding minimum $s_3$–t cut is shown in orange dashed lines, with cut value 12. All vertices on the same side of the cut as $s_3$, namely $\{s_1,s_2,s_3,s_4,s_5\}$, are removed from the candidate set since their cut values cannot exceed 12. The remaining candidate set reduces to $\left\{s_6\right\}$ (colored green).

In the second iteration, $s_6$ is the only remaining candidate. Its minimum cut shown in green dashed lines with t has value 11, which is strictly smaller than the current best value 12. Therefore, no update is made to the best solution. As the candidate set is now empty, the recursion terminates and the algorithm returns $s_3$ as the optimal source, achieving the global maximum minimum cut value of 12.

This example highlights the essence of the recursive reduction mechanism: by successively choosing pivots, evaluating their minimum cuts, and discarding dominated subsets, the candidate set shrinks rapidly while preserving correctness. In practice, this leads to substantial reductions in the number of max-flow computations compared to exhaustive enumeration.

3.4. Summary and Design Rationale

The recursive reduction (RR) algorithm is designed with two complementary goals: correctness and efficiency. Its correctness lies in the fact that each elimination step preserves the optimal source, a property that is formally established in Section 4.1. Its efficiency comes from recursive pruning: instead of exhaustively evaluating all $\left|V\right|-1$ possible sources, the algorithm progressively discards large subsets of candidates and quickly narrows the search space. As shown in Section 4.2, this mechanism guarantees that the expected number of iterations is only $\mathcal{O}(logn)$ on typical random graphs, yielding a total expected running time of $\mathcal{O}\left(logn·{\mathsf{T}}_{\mathrm{flow}}(n,m)\right)$, significantly improving over enumeration. This combination of provable optimality and practical efficiency constitutes the central design rationale of RR, making it a robust and scalable alternative to exhaustive max-flow computations.

4. Theoretical Analysis

We now establish the theoretical foundations of the recursive reduction (RR) algorithm. Our analysis is divided into two parts: first, we prove the correctness of the algorithm, showing that it always identifies a source node attaining the maximum s–t minimum cut value. Second, we analyze its computational complexity, contrasting the worst-case behavior with the typical performance observed in random graph models.

4.1. Correctness Guarantee

We now establish that Algorithm 1 always identifies a source node achieving the maximum s–t cut value. Recall that for any $s\in V\setminus \left\{t\right\}$,

$$f\left(s\right)=min\{\mathrm{cap}\left(\delta \left(X\right)\right):s\in X,t\notin X\},s^{★}=arg\underset{s\in V\setminus \left\{t\right\}}{max}f\left(s\right).$$

4.1.1. Safe Elimination via Pivot Cuts

At each iteration, the algorithm selects a pivot r and computes a minimum r–t cut $(S,T)$ with value $\kappa =f\left(r\right)$. Since every $u\in S$ is separated from t by the same cut, $f\left(u\right)\le f\left(r\right)$. Thus, if the true maximizer $s^{★}$ lies in S, then $f\left(s^{★}\right)=f\left(r\right)$ and the optimum has already been attained; otherwise, $s^{★}\in T$ and remains in the candidate set. Hence discarding S is always safe.

4.1.2. Invariant and Termination

This argument yields a simple invariant: after every iteration, either the optimum value has already been recorded, or the true maximizer remains in the candidate set. Since the candidate set shrinks strictly each round, the algorithm halts in at most $n-1$ iterations.

4.1.3. Main Theorem

Theorem 1 (Correctness of RR).

Upon termination, Algorithm 1 returns a source s with $f\left(s\right)=f\left(s^{★}\right)$.

Proof sketch. 

By the invariant, the optimum is never lost. When the candidate set becomes empty, the recorded best value must equal $f\left(s^{★}\right)$, and the corresponding source is returned. Formal details are deferred to Appendix A. □

4.2. Complexity Analysis

We analyze the iteration complexity of the RR framework. In each round of RR, a pivot vertex r is selected from the current candidate set $C\subseteq V\setminus \left\{t\right\}$, and the minimum r–t cut is computed to eliminate vertices. Since every iteration removes at least one candidate, in the worst case, RR halts after $n-1$ iterations. This $\Theta \left(n\right)$ bound is tight but arises only in highly adversarial constructions, and is rarely encountered in practice. We therefore focus on two more structured regimes where substantially faster convergence can be proved: (i) graphs where star cuts dominate the minimum cut structure, and (ii) graphs where every minimum cut is balanced. Finally, we present a unified upper bound that combines the two cases.

4.2.1. Star-Cut-Dominated Graphs

We first consider the regime where the minimum r–t cut typically isolates only the pivot vertex. Formally, for a vertex $r\in V$, we call the cut $\left(\right\{r\},V\setminus \{r\left\}\right)$ a star cut. In sparse random graphs, such star cuts dominate the cut structure with high probability.

Assumption 1 (Erdős–Rényi random graph with i.i.d. capacities).

Let $G\sim G(n,p)$ with $p\ge C_0\frac{logn}{n}$ for some absolute constant $C_0>1$. Each potential edge e independently exists with probability p. Edge capacities $\left\{c_e\right\}$ are i.i.d., independent of the topology, with mean $\mu >0$, variance ${\sigma }_c^2>0$, and finite third absolute moment.

Theorem 2 (Logarithmic iterations under star-cut dominance).

Under the above assumption, with high probability the minimum r–t cut is a star cut for every pivot r. Consequently, the RR algorithm terminates in $\mathcal{O}(logn)$ iterations in expectation.

Proof sketch. 

For a vertex r, write ${deg}_w\left(r\right):={\sum }_{e\in \delta \left(r\right)}{c}_e$ for the capacity of its star cut $\delta \left(r\right)$. Under i.i.d. edge capacities with mean $\mu$ and light tails (e.g., bounded or sub-Gaussian), ${deg}_w\left(r\right)$ concentrates around its expectation $\mathbb{E}\left[{deg}_w\left(r\right)\right]$ with high probability. Moreover, any r–t cut strictly larger than the star cut has a capacity larger by a constant factor with high probability; hence, star cuts dominate. Because pivots are symmetric and chosen uniformly at random from the candidate set, each iteration removes a uniformly random candidate, so the candidate set shrinks geometrically in expectation, which yields an expected $O(logn)$ number of iterations. □

4.2.2. Non-Star Balanced-Cut Graphs

We next consider graphs where star cuts are not dominant, but balanced cuts occur with non-negligible probability. Intuitively, as long as each iteration has a constant probability of producing a cut that eliminates a constant fraction of the candidate set, the algorithm still converges in logarithmically many rounds in expectation.

Assumption 2 (Balanced-cut condition).

There exist constants $\alpha ,\beta \in (0,1]$ such that for any iteration i and candidate set $C_i$, the pivot cut eliminates at least an α-fraction of $C_i$ with probability at least β.

Lemma 1 (Geometric shrinkage in expectation).

Under Assumption 2,

$$\mathbb{E}\left[\right|C_{i+1}|\mid C_i]\le (1-\alpha \beta )|C_i|.$$

Proof. 

If the balanced-cut event occurs (probability $\ge \beta$), then at least $\alpha |C_i|$ candidates are eliminated, yielding

$$|C_{i+1}|\le (1-\alpha )|C_i|.$$

Otherwise, fewer may be eliminated. Taking expectation over the two cases proves the stated inequality. □

Theorem 3 (Expected $\mathcal{O}(logn)$ iterations).

By iterating Lemma 1,

$$\mathbb{E}\left[\right|C_t\left|\right]\le {(1-\alpha \beta )}^t\left|C_0\right|\le e^{-\alpha \beta t}n.$$

Hence the expected number of iterations until termination satisfies

$$\mathbb{E}\left[\tau \right]=\mathcal{O}\left(\frac{1}{\alpha \beta }logn\right).$$

Thus, under the balanced-cut condition, RR terminates in expected $\mathcal{O}(logn)$ iterations. The overall expected running time is therefore

$$\mathbb{E}\left[T_{\mathrm{RR}}(n,m)\right]=\mathcal{O}\left(\frac{1}{\alpha \beta }logn·T_{\mathrm{flow}}(n,m)\right),$$

where $T_{\mathrm{flow}}(n,m)$ denotes the complexity of a maximum flow computation.

4.2.3. Complementary Upper Bound

Theorem 4 (Unified pathwise bound).

Let $N_{\mathrm{star}}$ denote the realized number of iterations in which the minimum cut is a star cut, and assume the remaining iterations satisfy the β-balanced condition. Then for every run, the total number of iterations R satisfies

$$R\le N_{\mathrm{star}}+⌈{log}_{1/(1-\beta )}n⌉.$$

Proof sketch. 

Each star-cut iteration eliminates one candidate, while each $\beta$-balanced iteration shrinks the candidate set by a constant fraction. Combining linear progress from $N_{\mathrm{star}}$ rounds with geometric progress from the balanced rounds yields the bound. □

In addition, if one introduces a probabilistic model of star-cut occurrence, taking expectations gives

$$\mathbb{E}\left[R\right]\le \mathbb{E}\left[N_{\mathrm{star}}\right]+{\displaystyle \frac{1}{\alpha \beta }}lnn.$$

If further each iteration produces a star cut with probability at least $\rho >0$, then

$$\mathbb{E}\left[N_{\mathrm{star}}\right]\le {\displaystyle \frac{n}{\rho }},$$

so that

$$\mathbb{E}\left[R\right]\le {\displaystyle \frac{n}{\rho }}+{\displaystyle \frac{1}{\alpha \beta }}lnn.$$

This shows that frequent star cuts ($\rho$ constant) keep the expected number of iterations logarithmic, while rare star cuts ($\rho \to 0$) lead to near-linear behavior.

4.2.4. Summary

The iteration complexity of RR depends on the structural properties of the underlying graph and detailed proofs are provided in Appendix B.

Table 1. Iteration complexity regimes of RR and representative graph families.

Graph Assumption	Iteration Complexity	Representative Families
None	$\Theta \left(n\right)$	Adversarial constructions
Star-cut-dominated	$\mathcal{O}(logn)$	Erdős–Rényi (ER)
$\beta$-balanced cuts	$\mathcal{O}(logn)$	Random regular (RRG), random geometric (RGG)
Mixed structure	$S+\mathcal{O}(logn)$	Watts–Strogatz (WS), Barabási–Albert (BA), stochastic block models (SBM)

summarizes the main regimes: in the worst case adversarial constructions graphs may require $\Theta \left(n\right)$ iterations, while star-cut-dominated or $\beta$-balanced graphs admit $\mathcal{O}(logn)$ convergence in expectation. Classical random graph families naturally align with these categories: ER graphs typically fall in the star-cut-dominated regime due to homogeneous degrees and weak clustering; RRG and RGG exhibit balanced partitions thanks to uniform connectivity and symmetry; while WS, BA, and SBM display mixed structures combining hubs, clustering, or community boundaries.

4.2.5. Discussion

The iteration complexity of RR is highly sensitive to the cut structure of the graph. Star-cut dominance and balanced cuts both lead to logarithmic performance, while the absence of such structure results in linear behavior.

A key algorithmic factor is the rule for selecting the pivot vertex r. Three natural strategies illustrate how pivoting interacts with graph structure:

• Uniform random selection. In symmetric settings such as Erdős–Rényi graphs, uniformly random pivots exploit star-cut dominance, leading to the expected $\mathcal{O}(logn)$ bound.
• Boundary-based selection. In graphs with balanced cuts, choosing pivots near the cut boundary increases the likelihood of large reductions in the candidate set, consistent with the $\beta$-balanced cut guarantee.
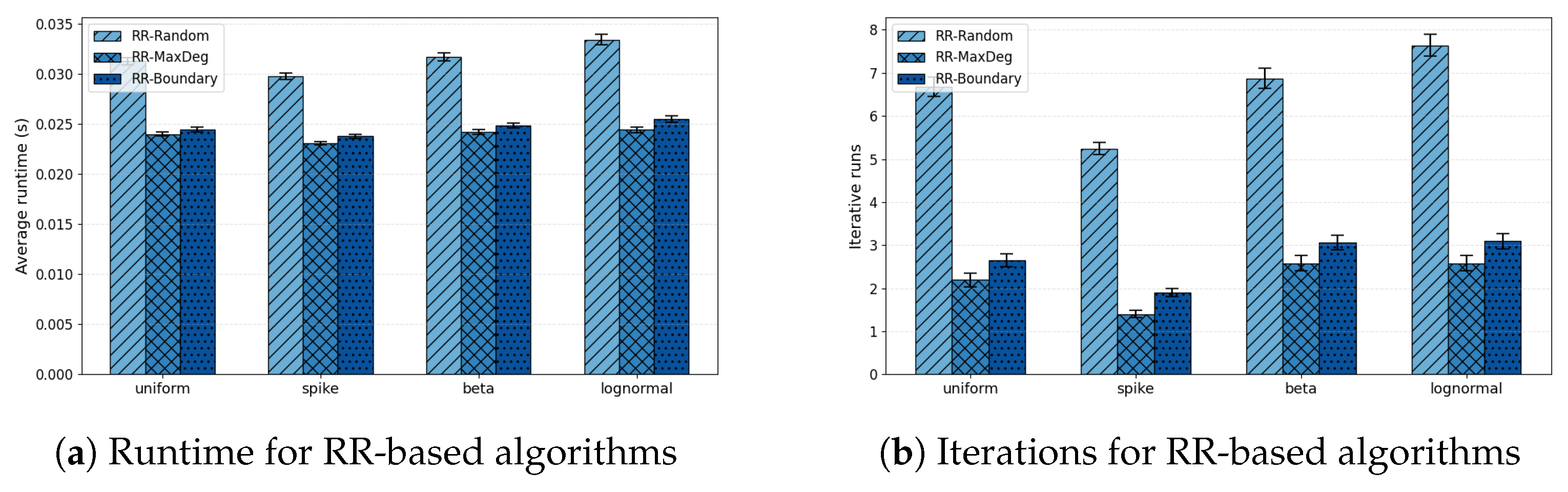
• Maximum-degree selection. Choosing the vertex with the highest weighted degree leverages structural heterogeneity, particularly in hub-dominated or scale-free graphs. This strategy significantly raises the chance of isolating a t-star cut, which both the theoretical analysis and empirical results show to yield the fastest convergence.

While poor pivot choices can in principle realize the pessimistic $\Theta \left(n\right)$ bound, such cases are rare in practice unless pivoting is adversarial. Overall, the pivot selection rule serves as the practical bridge between the structural regimes identified in theory and the observed efficiency of RR across diverse graph families.

5. Experimental Evaluation

5.1. Experimental Setup

We evaluate the proposed recursive reduction (RR) algorithm on synthetic graphs generated from the Erdős–Rényi (ER) random graph model $G(n,p)$, which has been widely used for analyzing algorithmic scalability under controlled structural conditions. In all ER instances we set $p=\overline{d}/(n-1)$, where $\overline{d}$ denotes the target average degree of the random graph and p is the corresponding edge probability (not to be confused with the pivot r). Edge capacities $\left\{c_e\right\}$ are sampled i.i.d. as $c_e\sim \mathrm{Unif}\{1,\dots ,20\}$, independent of the topology. Choosing $\mathtt{avg}\_\mathtt{deg}\ge C_{0}logn$ ensures $pn\ge C_{0}logn$, which matches the assumptions in Section 4.2 and yields connected graphs with high probability.

The comparison focuses on four algorithms:

• RR-Random: RR with pivot nodes selected uniformly at random.
• RR-MaxDeg: RR with pivot nodes chosen as those with the largest weighted degree.
• RR-Boundary: RR with pivot nodes chosen as the vertices closest to the most recently discovered cut boundary.
• Enum: A baseline that computes the s–t minimum cut for every $s\in V\setminus \left\{t\right\}$ using a standard max-flow routine, thereby guaranteeing optimality at the cost of maximal runtime.

Unless otherwise specified, we vary the number of nodes n, average degree $\overline{d}$, and capacity ranges to test scalability and robustness. Each data point represents the average over multiple independent ER graph realizations, ensuring statistical stability. Runtime is measured in wall-clock seconds. All max-flow computations are implemented using Dinic’s algorithm (worst-case complexity $O\left(V^{2}E\right)$).

5.2. Results and Analysis

5.2.1. Scalability with Graph Size

We evaluate scalability by varying the number of nodes $n\in [100,400]$ while fixing the average degree at $\overline{d}=99$. The results are summarized in Figure 3 and

Table 2. Average number of iterations for RR-based algorithms.

n	log n (Theory)	RR-Random	RR-MaxDeg	RR-Boundary
100	≈6.64	5.07	2.18	2.66
200	≈7.64	6.46	2.19	2.67
300	≈8.23	7.46	2.79	3.29
400	≈8.64	6.70	1.40	1.89

. Figure 3a shows that the baseline Enum exhibits rapidly increasing runtime as n grows, reflecting the fact that it requires $\Theta \left(n\right)$ independent max-flow computations and each invocation of Dinic’s algorithm becomes more expensive with larger graphs. In contrast, all RR variants remain below a few hundredths of a second even at $n=400$, demonstrating a clear scalability advantage. Figure 3b focuses on the RR-based methods: RR-MaxDeg consistently achieves the lowest runtime, followed closely by RR-Boundary, while RR-Random is somewhat slower but still far superior to Enum. The advantage of degree- and boundary-based pivoting is consistent with the theoretical analysis, which shows that increasing the likelihood of selecting a pivot with ${deg}_w\left(r\right)\ge {deg}_w\left(t\right)$ raises the probability of triggering the t-star event and thereby accelerates convergence.

Table 2 reports the average iteration counts required by each RR variant until convergence. All RR variants require only a handful of iterations, well below the $logn$ benchmark, providing strong empirical evidence for the logarithmic iteration bound established in Section 4.2. Among the strategies, RR-MaxDeg yields the fewest iterations across all tested sizes, RR-Boundary performs second best, and RR-Random incurs the largest number. This ordering parallels the runtime results in Figure 3b and is naturally explained by the star-dominance and two-star approximate symmetry established in our analysis: degree-based pivoting drives the constant probability $\beta$ close to one, boundary-based pivoting provides a moderate improvement, and random pivoting realizes the baseline constant. Although the average iteration counts fluctuate slightly with n rather than increasing monotonically, the overall runtime nonetheless grows with graph size because the cost of each max-flow call rises with n. These results confirm that the RR framework achieves consistently small iteration counts in practice, with the total runtime dominated by the complexity of the underlying max-flow oracle.

5.2.2. Sensitivity to Graph Density

The impact of graph density is examined by fixing the number of nodes at $n=400$ and varying the average degree $\overline{d}$ from 100 to 399, with edge capacities sampled i.i.d. as $c_e\sim \mathrm{Unif}\{1,\dots ,20\}$. Figure 4a reports the average runtime of all algorithms. The Enumeration baseline shows runtime growing nearly linearly with $\overline{d}$, consistent with the quadratic scaling of edge counts in dense Erdős–Rényi graphs and the repeated invocations of Dinic’s algorithm. By contrast, the RR-based approaches remain one to two orders of magnitude faster across the entire density spectrum, and their runtime curves increase only modestly with $\overline{d}$.

The differences among RR variants are highlighted in Figure 4b. RR-MaxDeg consistently achieves the lowest runtime across all densities, benefiting from pivot selections that favor highly connected nodes and thereby accelerate candidate elimination. RR-Boundary follows closely, with slightly higher runtimes that nonetheless remain well below those of RR-Random. The latter exhibits the steepest runtime growth among the three as $\overline{d}$ increases, reflecting the weaker structural guidance of random pivoting in dense topologies. Despite this relative disadvantage, even RR-Random substantially outperforms Enumeration by more than an order of magnitude.

These observations indicate that recursive pruning remains effective in the high-density regime. Structural pivot rules such as MaxDeg and Boundary are particularly advantageous, as they exploit connectivity patterns that are amplified with higher degrees, enabling the algorithm to maintain small iteration counts and controlled runtime growth.

5.2.3. Effect of Edge Capacity Distribution

We next evaluate the impact of edge capacity distributions while fixing $n=200$ and $\overline{d}=100$. Four representative families are considered: (i) Uniform$\{1,\dots ,20\}$, serving as a baseline with moderate variance; (ii) Spike, where a small fraction of edges are assigned very large capacities while the majority remain near the minimum, producing extreme variance; (iii) Beta, biased toward small capacities and emphasizing weaker links; and (iv) Lognormal, rescaled to $\{1,\dots ,20\}$, introducing a heavy right tail and pronounced heterogeneity.

Figure 5a reports runtimes for the three RR variants. Across all distributions, runtimes remain under $0.04$ seconds, confirming that efficiency is robust to capacity heterogeneity. Nevertheless, heavier-tailed distributions such as Spike and Lognormal incur slightly higher costs, reflecting more irregular cut structures that reduce pruning efficiency. Uniform and Beta distributions exhibit lower runtimes, consistent with their more balanced edge weights.

Figure 5b shows the corresponding iteration counts. The results parallel the runtime trends: RR-Random consistently requires the largest number of iterations, particularly under Lognormal and Spike where the probability of immediate elimination is reduced, while RR-MaxDeg and RR-Boundary achieve substantially smaller values across all cases. In every distribution, iteration counts remain within small constant factors of the logarithmic baseline, providing empirical support that the star-dominance and two-star approximate symmetry mechanisms are insensitive to the exact capacity distribution.

Overall, these findings demonstrate that RR maintains both correctness and near-logarithmic efficiency across a wide spectrum of capacity distributions. While extreme heterogeneity modestly increases runtime variance, pivot strategies that exploit degree or boundary information mitigate this effect and deliver consistently faster convergence than random pivoting.

5.2.4. Robustness to Structural Variability

To evaluate robustness across network structures, we fix the configuration at $n=200$ nodes, average degree $\overline{d}=100$, and edge capacities sampled i.i.d. as $c_e\sim \mathrm{Unif}\{1,\dots ,20\}$. Under this setting, one graph instance is generated from each of six classical random families: Erdős–Rényi (ER), Watts–Strogatz small-world graphs (WSs), Barabási–Albert preferential attachment graphs (BAs), random regular graphs (RRGs), random geometric graphs (RGGs), and stochastic block models (SBMs). These models capture a wide spectrum of structural features, ranging from homogeneous connectivity (ER, RRG) to strong clustering (WS, RGG), heavy-tailed degree distributions (BA), and explicit community organization (SBM).

Table 3. Average number of iterations of RR-based algorithms across different graph families.

Graph Family	log n (Theory)	RR-Random	RR-MaxDeg	RR-Boundary
ER	≈7.64	6.46	2.19	2.67
WS	≈7.64	6.54	2.98	3.50
BA	≈7.64	1.25	1.00	1.09
RRG	≈7.64	6.32	1.99	2.50
RGG	≈7.64	5.96	1.99	2.48
SBM	≈7.64	8.28	4.96	5.50

reports the average number of iterations of RR-based algorithms across the six graph families. The results confirm that the logarithmic iteration bound remains a reliable predictor across structurally diverse networks, although the precise iteration counts vary with topology. For ER and RRG, which closely match the assumptions of our theoretical model, the observed values of RR-Random are close to or slightly below the $logn$ benchmark, while RR-MaxDeg and RR-Boundary achieve substantially fewer iterations. For WS and RGG, where local clustering and geometric constraints reduce uniform expansion, iteration counts remain near the theoretical guideline but show moderate deviations, reflecting weaker star-dominance. The BA model demonstrates the opposite effect: the presence of high-degree hubs strongly accelerates convergence, so all RR variants terminate in nearly constant iterations, far below $logn$. In contrast, SBM exhibits the slowest convergence: explicit community bottlenecks degrade star-dominance, reducing the probability of the t-star event and leading to iteration counts moderately exceeding the $logn$ benchmark.

Across all families, RR-MaxDeg consistently yields the fewest iterations, confirming the benefit of exploiting degree heterogeneity. These variations align with the theoretical characterization and discussion in Section 4.2: the logarithmic expectation is robust under homogeneous random models, while heavy-tailed or community-structured graphs shift the effective constant $\beta$, producing either faster convergence (BA) or slower convergence (SBM).

6. Related Work

The study of network connectivity optimization has its roots in the classical maximum–flowand minimum cut problems. Foundational deterministic algorithms such as Edmonds–Karp [4] and Dinic [5], together with later improvements like Push–Relabel [6] and Orlin’s algorithm [7], provide efficient polynomial-time solutions for computing a single source–sink min-cut. However, applying these algorithms to all possible source nodes relative to a fixed sink, as required in the GMMC-FS problem, incurs $\Theta \left(n\right)$ flow computations. For dense graphs with $\left|E\right|=\Theta \left(\right|V{|}^2)$, this approach quickly becomes computationally infeasible.

Randomized contraction algorithms, pioneered by Karger [13] and refined in the Karger–Stein algorithm [8], shifted attention to the global minimum cut problem. These methods achieve near-optimal runtimes in unweighted graphs with high probability and have been extended through sparsification [14], dynamic contraction thresholds [15], and parallel implementations [16]. While highly successful for global connectivity, contraction-based methods do not directly address the fixed-sink max–min formulation, where the objective is to maximize the minimum cut over all sources to a designated sink.

For multi-terminal and all-pairs cut problems, the Gomory–Hu tree [2] offers a compact representation of all pairwise min-cuts using only $O\left(n\right)$ flow computations. Subsequent work has developed faster variants [9,17], as well as extensions to hypergraphs [18] and dynamic settings [19]. Despite their generality, Gomory–Hu-based approaches still require $\Theta \left(n\right)$ flow computations, which are unnecessarily expensive when only cuts relative to a fixed sink are needed, as in GMMC-FS.

Beyond theory, practical algorithm engineering has produced solvers optimized for large-scale graphs. For example, VieCut [20] integrates inexact preprocessing heuristics with exact cut routines to achieve significant speedups in practice. In distributed and parallel computation models, particularly the Congested Clique and MPC settings, researchers have developed near-optimal min-cut algorithms with sublinear round complexity [15,19], and streaming algorithms have been proposed for processing massive graphs under memory constraints [21,22]. These paradigms demonstrate strong scalability for general min-cut computations, but their overhead remains substantial for dense networks and fixed-sink formulations.

In networking applications, min-cut-based metrics have been widely adopted in traffic engineering [11], resilient server placement, and fault-tolerant multicast design. The max–min connectivity objective studied in robust network design [12,23] is conceptually related to GMMC-FS, as both focus on maximizing bottleneck connectivity to a sink or terminal. Existing approaches, however, either perform a sequence of full max-flow computations or rely on linear programming relaxations, both of which struggle to scale in high-density topologies.

In contrast to these prior approaches, the GMMC-FS problem—identifying the source node with the largest minimum cut to a fixed sink—has remained underexplored. Existing deterministic and randomized algorithms either solve the problem indirectly via exhaustive enumeration or rely on structures designed for global or all-pairs settings. Our work fills this gap by introducing the recursive reduction (RR) algorithm, which leverages pivot-based elimination and recursive pruning to reduce the candidate set aggressively. Rather than computing all $\left|V\right|-1$ flows, RR guarantees correctness while requiring only $O(logn)$ iterations in expectation on typical random graphs, as established in Section 4.1 and Section 4.2. This combination of provable optimality and practical scalability distinguishes RR from contraction-based min-cut algorithms and Gomory–Hu tree methods, offering the first exact and efficient solution tailored to the fixed-sink max–min cut problem.

7. Conclusions

This paper addressed the Global Maximum Minimum Cut with Fixed Sink (GMMC–FS) problem, which seeks the source node with the largest minimum cut to a designated sink in a capacitated undirected graph. To solve this problem efficiently, we proposed the recursive reduction (RR) algorithm, which applies a pivot-based elimination strategy to recursively prune dominated candidates while ensuring exact correctness. Specifically, we provided a rigorous theoretical analysis establishing both correctness and logarithmic expected complexity, and demonstrated through extensive experiments on synthetic and real-world graphs that RR consistently achieves the optimal solution with substantially lower runtime than classical enumeration. The results confirm that recursive pruning is highly effective in reducing the search space and that RR scales robustly across graph sizes, densities, and structures.

The proposed RR framework establishes a foundation for efficient max–min source selection in undirected static networks. A promising direction for future work is to extend RR to more general settings, particularly to directed or weighted dynamic graphs, where edge capacities or directions evolve over time. These extensions would enable the framework to handle asymmetric communication networks and time-varying topologies. Another promising direction is to integrate RR with approximation or learning-based strategies to further reduce computational costs on large-scale systems. Such developments could broaden the applicability of RR in dynamic and data-driven network optimization scenarios.