OIKAN: A Hybrid AI Framework Combining Symbolic Inference and Deep Learning for Interpretable Information Retrieval Models

Abstract

The rapid expansion of AI applications in various domains demands models that balance predictive power with human interpretability, a requirement that has catalyzed the development of hybrid algorithms combining high accuracy with human-readable outputs. This study introduces a novel neuro-symbolic framework, OIKAN (Optimized Interpretable Kolmogorov–Arnold Network), designed to integrate the representational power of feedforward neural networks with the transparency of symbolic regression. The framework employs Gaussian noise-based data augmentation and a two-phase sparse symbolic regression pipeline using ElasticNet, producing analytical expressions suitable for both classification and regression problems. Evaluated on 60 classification and 58 regression datasets from the Penn Machine Learning Benchmarks (PMLB), OIKAN Classifier achieved a median accuracy of 0.886, with perfect performance on linearly separable datasets, while OIKAN Regressor reached a median R² score of 0.705, peaking at 0.992. In comparative experiments with ElasticNet, DecisionTree, and XGBoost baselines, OIKAN showed competitive accuracy while maintaining substantially higher interpretability, highlighting its distinct contribution to the field of explainable AI. OIKAN demonstrated computational efficiency, with fast training and low inference time and memory usage, highlighting its suitability for real-time and embedded applications. However, the results revealed that performance declined more noticeably on high-dimensional or noisy datasets, particularly those lacking compact symbolic structures, emphasizing the need for adaptive regularization, expanded function libraries, and refined augmentation strategies to enhance robustness and scalability. These results underscore OIKAN’s ability to deliver transparent, mathematically tractable models without sacrificing performance, paving the way for explainable AI in scientific discovery and industrial engineering.

1. Introduction

Neuro-symbolic methods occupy a distinctive place in the history of AI, marking a key milestone in the evolution of machine intelligence. Early efforts relied on symbolic approaches, hand-crafted rules, and logic-based systems that excelled at knowledge manipulation and reasoning but proved inadequate for learning from raw data [1]. The subsequent rise in sub-symbolic techniques, notably artificial neural networks and statistical learning enabled automatic feature extraction and pattern recognition; however, these models often functioned as opaque “black boxes” offering little insight into learned relationships [2]. The convergence of these paradigms into neuro-symbolic AI represents a crucial advance toward more general and robust intelligence, addressing longstanding challenges such as commonsense reasoning and structured knowledge representation. Although symbolic regression yields human-readable expressions that reveal underlying data-generating laws, it incurs prohibitive computational costs and limited scalability.

Modern science, in particular physics, biology, and chemistry, increasingly relies on data-driven modeling. However, this requires models that reveal the underlying structure of phenomena, not just the accuracy of prediction [3,4]. In such cases, interpretability is not just a requirement for confidence but plays an important role in discovery [5]. Although traditional methods such as symbolic regression produce human-readable results, they are computationally expensive and cannot scale [6,7]. Conversely, Deep neural networks (DNNs) are renowned for their ability to generalize across high-dimensional spaces; however, the internal representations they learn often reside in complex, opaque latent structures [8,9]. By integrating neural learning with symbolic formalisms, neuro-symbolic AI seeks to bridge this interpretability gap without sacrificing performance, thereby enabling both high-level reasoning and transparent, verifiable insights into data.

Traditional deep architectures like Multilayer Perceptron lack semantic transparency. While MLPs can approximate any continuous function according to the universal approximation theorem [10], their learned parameters, dense weight matrices, and non-linear activations are difficult to decode into meaningful rules. Kolmogorov–Arnold Networks (KANs) were proposed as a more interpretable alternative, inspired by the Kolmogorov–Arnold Representation Theorem (KART), which states that any multivariate continuous function can be expressed as a sum of univariate functions [11]. KANs replace weight matrices with learnable univariate transformations, allowing visualization and partial interpretability [12]. However, they suffer from high memory and time complexity and often fail to outperform tuned MLPs in large-scale settings [13].

This paper introduces a novel neuro-symbolic learning framework inspired by KART, OIKAN (Optimized Interpretable Kolmogorov–Arnold Network), designed to address the limitations of both MLPs and symbolic regression models. Building upon the foundations of earlier KAN architectures, OIKAN incorporates lightweight differentiable symbolic basis components, applies regularization techniques to enhance simplicity and reduce overfitting, and adopts an interface similar to scikit-learn to facilitate model introspection and symbolic extraction. The framework has been applied to a variety of scientific problems, including the discovery of symbolic equations in fluid dynamics, interpretable modeling of gene expression, and robust simulations in chemical reaction networks. The results confirm its ability to deliver competitive accuracy while producing analytically tractable and scientifically meaningful equations, positioning it as a promising tool for advancing interpretable artificial intelligence in scientific research. In the context of a smart city, OIKAN offers a robust foundation for building interpretable models capable of revealing complex relationships in heterogeneous urban datasets. Its ability to generate symbolic representations from sensor data can facilitate transparent decision-making in real-time environmental monitoring, traffic optimization, and air quality forecasting. By embedding the OIKAN framework into the analytical pipeline, the project can enhance explainability, reproducibility, and scientific insight-key factors for sustainable urban development and evidence-based policymaking.

2. Related Studies

2.1. Trustworthy and Interpretable AI

The need for trustworthy and interpretable AI has become crucial in modern information systems. While deep learning models deliver high predictive power, their “black-box” nature limits validation, risk assessment, and bias detection in sensitive areas such as healthcare, law, and industrial automation. To address these issues, hybrid neuro-symbolic approaches are being explored, combining the generalization of deep models with the transparent reasoning of symbolic systems [14].

Research on trustworthy AI identifies six key reliability dimensions: safety and robustness, non-discrimination, explainability, privacy, accountability, and environmental well-being. Among these, explainability and accountability are vital for information retrieval tasks, where reproducibility and traceability are essential. Although post hoc explainability methods like SHAP, LIME, and Integrated Gradients provide insights, they often lack stability, causal validity, and scalability. This highlights the value of interpretable-by-design models, where reasoning is embedded within the architecture [15].

The rapid growth of large language models (LLMs) in retrieval and recommendation systems has amplified transparency concerns. Despite alignment techniques such as supervised fine-tuning and reinforcement learning with human feedback, LLMs frequently produce hallucinations, biases, and inconsistencies. Taxonomies of LLM trustworthiness outline numerous sub-dimensions, including reasoning fidelity and misuse resistance, yet the lack of granular interpretability mechanisms limits their auditability and adoption in evidence-critical domains [16].

2.2. Kolmogorov–Arnold Networks (KANs) and Variants

In high-stakes fields, interpretable AI models are as important as accuracy, ensuring stakeholders can verify and trust outputs. Comparative studies show that while MLPs outperform KANs in traditional tasks like vision, NLP, and audio, KANs excel in symbolic formula discovery due to their B-spline activations [17]. Other research indicates that modified KANs, especially those based on orthogonal polynomials, can rival MLP-based methods in scientific tasks such as differential equation solving, though they remain sensitive to initialization and architecture choices [18].

Various KAN architectures have been proposed recently. The original PyKAN implemented KAN layers with cubic B-spline activations. Follow-ups sought to improve efficiency or flexibility. Efficient-KAN provided engineering optimizations (vectorized implementations) to speed up training [19]. Fast-KAN replaces B-splines with Gaussian radial basis functions (RBFs), yielding ~3.3× faster inference (albeit still more costly than an MLP). Fourier-KAN (KAF) uses a Fourier-series-based activation instead of a single spline, combining several periodic components; it achieved strong results on vision, NLP, audio, and even PDE tasks [20]. Other variants include wavelet-based Wav-KAN, rKAN (rational functions), and fKAN (fractional B-splines). The core idea remains as the need to replace each MLP weight by a small function so that the network can both learn features (via its layer structure) and optimize univariate functions with high precision.

2.3. KANs in Scientific and Physics-Informed Learning

A comprehensive survey by [21] reviews KAN theory and practice. They note that unlike MLPs, KANs do not fix activations but optimize them, providing enhanced interpretability and generalization. For example, the research [22] shows small KAN models reaching or surpassing MLPs in curve fitting. Authors of [23] apply KANs to time series and hyperspectral imaging, finding that KANs capture complex dependencies effectively.

The authors of [24] introduce KINN (Kolmogorov–Arnold-Informed Neural Network) for physics-informed learning. They substitute MLPs in PINNs with KANs. In a variety of solid mechanics PDEs, KINN significantly outperforms MLP-PINNs in accuracy and convergence speed. They highlight that KANs require fewer parameters and provide interpretability due to their decomposition of inputs into scalar functions. In essence, KAN-based networks like KINN demonstrate that KART-inspired architectures can yield both efficient learning and physically meaningful structure.

However, there is debate about KAN’s novelty. Some note that a KAN can be reparametrized as a conventional MLP with a special structure (so representationally they are equivalent). Nonetheless, in practice, KANs act as neural architectures with built-in function priors. OIKAN leverages this by using KART to decompose its network: it builds hierarchical univariate transformations that mirror the theorem’s form [25]. This allows OIKAN to expose each intermediate univariate function as a symbolic sub-model, greatly aiding interpretability.

In the context of life sciences and remote sensing, authors of [26,27] show how neuro-symbolic methods can augment data efficiency, enable knowledge injection, and enhance explainability. These applications underscore the growing relevance of neuro-symbolic frameworks in real-world scientific workflows, where understanding the model’s rationale is as vital as accuracy.

2.4. Symbolic Regression Approaches

Symbolic regression (SR) aims to learn analytic expressions (e.g., algebraic equations) that fit data, without pre-specifying a model form. Classic SR methods include Genetic Programming (GP), Bayesian symbolic regression, and tools like Eureqa. GP-based SR randomly evolves expression trees of operators and functions. For example, Schmidt and Lipson’s Eureqa system [28] automatically rediscovered physical laws (Hamiltonians, Lagrangians) from time-series data, demonstrating the power of GP in uncovering interpretable scientific formulas. Bayesian SR methods extend GP by encoding priors or scoring complexity, yielding more concise models. As one review explains, GP “has been traditionally and commonly used” for SR, but “suffers from limitations” such as overly complex expressions and difficulty incorporating domain knowledge [29]. Bayesian SR can address some of these issues by imposing prior distributions over functions to promote interpretability. A systematic comparative analysis of prominent symbolic regression approaches was conducted, focusing on key criteria such as typical use cases, computational speed, model interpretability, accuracy on complex datasets, and the availability of software tools. Table 1 summarizes the findings, highlighting the trade-offs that researchers and practitioners must consider when selecting an SR method for real-world applications.

Closely related are sparse linear models with basic functions. Methods like LASSO and ElasticNet [30] fit linear combinations of features while enforcing sparsity via L1 (and L2) penalties. These yield interpretable coefficients (many zeros) and can incorporate non-linear basis expansions (e.g., splines) for smooth curves. Penalized linear models remain widely used as interpretable baselines: [14] compared their SR approach (FEAT) against sparse logistic regression (essentially a LASSO on expanded features) and found FEAT attained equal or higher AUC with far simpler models.

Table 1. Comparative analysis of symbolic regression methods.

Method	Use Case	Speed	Interpretability	Accuracy (Complex Data)	Tools/ Libraries
Genetic Programming (GP)	Non-linear symbolic modeling	Low (slow, resource-heavy)	High	High	Operon, gplearn, PySR [31]
Least Squares	Hybrid symbolic fitting	High	Medium (model-dependent)	Medium	Operon, PySINDy [32]
Sparse Regression (LASSO, STLSQ)	Sparse interpretable models	Medium (with regularization)	High	Medium (needs basis functions)	Lasso, PySINDy [33]
Bayesian SR	Uncertainty-aware modeling	Low (compute-intensive)	High (probabilistic)	Medium	Custom implementations [29]
NN-Based (AI Feynman)	Symbolic distillation from neural networks	Low (slow training)	Medium (postprocessed)	High (low-noise data)	AI Feynman [34]

Table 1. Comparative analysis of symbolic regression methods.

Method	Use Case	Speed	Interpretability	Accuracy (Complex Data)	Tools/ Libraries
Genetic Programming (GP)	Non-linear symbolic modeling	Low (slow, resource-heavy)	High	High	Operon, gplearn, PySR [31]
Least Squares	Hybrid symbolic fitting	High	Medium (model-dependent)	Medium	Operon, PySINDy [32]
Sparse Regression (LASSO, STLSQ)	Sparse interpretable models	Medium (with regularization)	High	Medium (needs basis functions)	Lasso, PySINDy [33]
Bayesian SR	Uncertainty-aware modeling	Low (compute-intensive)	High (probabilistic)	Medium	Custom implementations [29]
NN-Based (AI Feynman)	Symbolic distillation from neural networks	Low (slow training)	Medium (postprocessed)	High (low-noise data)	AI Feynman [34]

2.5. Neuro-Symbolic Frameworks

Researchers have shown near-perfect performance on complex visual reasoning tasks by combining deep vision models with symbolic execution. For example, ref. [35] proposed a neuro-symbolic VQA system that parses an image into a scene graph and a question into a symbolic program, executing the program to answer with 99.8% accuracy on CLEVR, while providing interpretable reasoning. Similarly, in NLP, neural language models can generate logical assertions or knowledge graphs for symbolic reasoning tasks such as question answering or theorem proving, a pattern reflected in recent neuro-symbolic NLP work integrating neural text understanding with ontologies and logic-based reasoners [36].

Hybrid neuro-symbolic models leverage the strengths of both approaches. MLP-KAN [37], for instance, combines an MLP “representation learner” with a KAN “function learner,” achieving strong results in computer vision, NLP, and formula regression by dynamically selecting between neural and symbolic branches. More broadly, neuro-symbolic reasoning integrates deep learning with symbolic logic to achieve both robust learning and interpretable reasoning [38]. Approaches include differentiable logic layers, symbolic memory components, and program induction frameworks. DreamCoder [39], for example, learns domain-specific programs by combining neural pattern recognition with symbolic program synthesis, where symbolic modules serve as interpretable reasoning layers.

2.6. Positioning of OIKAN

Within OIKAN, knowledge learned from data is represented by sparse symbolic expressions generated during the second pipeline phase. Once the KAN-augmented MLP has internalized an internal representation of the training set, the symbolic regression module distills that representation into an explicit formula. In this hybrid mechanism, the neural component provides mappings from raw data to higher-level feature estimates, while the symbolic component supplies the explicit structure for final decision-making. The resulting AI system delivers deterministic, verifiable inference alongside transparent decision explanations derived from known symbolic relations. Notably, this design aligns with the view that robust AI requires both pattern learning and symbolic reasoning [40]. OIKAN uses neural computation to learn from examples, but entrusts the symbolic layer to formalize that learned knowledge and handle it in a principled, interpretable manner. By bridging these aspects, neuro-symbolic systems are considered a promising route toward AI that learns from experience while it can reason and explain in human-like terms [41,42].

From an ethical standpoint, providing a symbolic explanation for a prediction fosters trust: stakeholders gain the ability to trace how specific inputs mathematically produced a given output, simplifying the identification of biases or errors in the decision process. This practice aligns with emerging guidelines for trustworthy AI, which prioritize explainability and transparency as fundamental principles. Unlike opaque deep learning models, the hybrid neuro-symbolic methodology delivers a level of algorithmic transparency capable of reducing the risk that hidden discriminatory patterns remain undetected [36].

To assess the positioning of OIKAN within the broader landscape of symbolic regression and neuro-symbolic machine learning tools, a detailed comparative analysis is provided in Table 2. This analysis categorizes each tool by its core algorithmic paradigm. The comparison highlights both the diversity and the limitations of existing approaches, underscoring the need for frameworks like OIKAN that balance accuracy, transparency, and practical deployment.

2.7. Research Gaps

In summary, the literature underscores that interpretability is essential in scientific and high-stakes domains [43] because black-box models carry risks that simple, explainable models avoid. Despite these advances, important gaps remain. There is a lack of integrated, open-source frameworks that seamlessly combine neural and symbolic components for scientific data. Most symbolic or KAN toolboxes are research prototypes with limited engineering support. Moreover, many comparative studies show that model performance and efficiency vary widely by application [44], indicating the need for flexible systems that can adapt to diverse datasets.

OIKAN is motivated by these gaps: it aims to provide a unified, open neuro-symbolic framework that scales to real data and produces symbolic formulas. By integrating KAN layers with conventional architectures, OIKAN seeks to harness neural pattern learning while maintaining interpretability and symbolic output. In essence, OIKAN addresses the call for AI systems that are both accurate and explainable, fulfilling the need for transparent, reproducible discovery tools in science and beyond.

Table 2. Cross-Method Comparison of the Proposed Framework and Existing Learning Paradigms.

Source	Tool	Algorithm Type	Time & Memory Efficiency	Tabular Data Focus	Multi- Obj.	Neural Integration	Interpretability
[45]	PySR	Genetic Programming	Medium (efficient Julia backend, moderate memory)	Partial (can integrate with ML pipelines)	Yes	Yes	High
[46]	Operon	Genetic Programming	High (fast C++ implementation, low memory)	No	Yes	Yes	High
[47]	GPLearn	Genetic Programming	Low (Python-based, slower)	No	No	No	High
[48]	EQL/ DeepSymReg	Neural Network	Medium (GPU- accelerated, moderate memory)	Yes	No	No	Medium
[49]	PyKAN	Mathematical Net	Medium	Partial (mathematical nets)	No	No	Medium
[50]	DSR	Reinforcement Learning	Low (computationally intensive, slower convergence)	Yes	No	No	Medium
[51]	QLattice	Graph-based	Medium	No	No	No	High
[52]	SR-Transformer	Transformer-based	Medium to High (depends on model size, GPU heavy)	Yes	No	No	Low
[53]	Eureqa	Evolutionary	Medium	No	Yes	Yes	High
Proposed	OIKAN	Neuro-Symbolic	High (lightweight MLPs)	Yes (MLPs)	Adapt.	Adapt.	High

Table 2. Cross-Method Comparison of the Proposed Framework and Existing Learning Paradigms.

Source	Tool	Algorithm Type	Time & Memory Efficiency	Tabular Data Focus	Multi- Obj.	Neural Integration	Interpretability
[45]	PySR	Genetic Programming	Medium (efficient Julia backend, moderate memory)	Partial (can integrate with ML pipelines)	Yes	Yes	High
[46]	Operon	Genetic Programming	High (fast C++ implementation, low memory)	No	Yes	Yes	High
[47]	GPLearn	Genetic Programming	Low (Python-based, slower)	No	No	No	High
[48]	EQL/ DeepSymReg	Neural Network	Medium (GPU- accelerated, moderate memory)	Yes	No	No	Medium
[49]	PyKAN	Mathematical Net	Medium	Partial (mathematical nets)	No	No	Medium
[50]	DSR	Reinforcement Learning	Low (computationally intensive, slower convergence)	Yes	No	No	Medium
[51]	QLattice	Graph-based	Medium	No	No	No	High
[52]	SR-Transformer	Transformer-based	Medium to High (depends on model size, GPU heavy)	Yes	No	No	Low
[53]	Eureqa	Evolutionary	Medium	No	Yes	Yes	High
Proposed	OIKAN	Neuro-Symbolic	High (lightweight MLPs)	Yes (MLPs)	Adapt.	Adapt.	High

3. Materials and Methods

3.1. High-Level Overview and Main Contributions

This study explores a diverse set of interpretable AI models and techniques, including classical algorithms, neural network architectures such as multilayer perceptrons (MLPs) and Kolmogorov–Arnold Networks (KANs), symbolic regression, and hybrid neural-symbolic approaches. The primary objective is to develop a computationally efficient model capable of producing transparent mathematical expressions that characterize the relationship between input features and target variables for both classification and regression tasks using tabular data.

The core model developed, OIKAN v0.0.3, introduces a unified neuro-symbolic framework that integrates lightweight neural architectures with differentiable symbolic basis functions such as sin(x), log(x), and exp(x). Unlike conventional neural networks that operate as black boxes, OIKAN generates compact and interpretable symbolic formulas while retaining the predictive power of modern machine learning models. This dual capability directly addresses one of the central challenges in AI: balancing predictive accuracy, interpretability, and computational efficiency.

A key novelty of OIKAN lies in its flexible architecture and configurable design. It supports both classification and regression tasks within the same unified pipeline, incorporates symbolic regression based on ElasticNet regularization for controlled formula complexity, and offers adaptive parameters (evaluate_nn and augmentation_factor) to balance automation with experimental control. By bridging the gap between symbolic transparency and neural expressiveness, OIKAN contributes to advancing trustworthy, explainable, and domain-agnostic AI.

3.2. Mathematical Foundation of the OIKAN

The OIKAN framework was developed with a focus on model interpretability, robustness, and computational efficiency, combining deep learning and symbolic regression in a unified architecture. The following subsections describe the theoretical foundations and implementation components that constitute the OIKAN pipeline.

3.2.1. Kolmogorov–Arnold Representation Theorem (KART)

The design of OIKAN is rooted in the Kolmogorov–Arnold Representation Theorem (KART), which guarantees that any continuous multivariate function f: [0, 1]ⁿ → R can be decomposed into a series of univariate continuous functions. Specifically, it can be represented as:

$$f\left(x_1,\dots ,x_n\right)={\sum }_{q=0}^{2n}{\mathsf{\Phi }}_q\left({\sum }_{p=1}^n{\mathsf{\psi }}_{p,q}\left(x_p\right)\right),$$

(1)

where ${\mathsf{\Phi }}_q$ and ${\mathsf{\psi }}_{p,q}$ are continuous univariate functions. This decomposition enables the transformation of complex mappings into tractable hierarchical compositions [54], guiding the symbolic regression stage in OIKAN for enhanced interpretability.

3.2.2. Neural Network Function Approximation (TabularNet)

To extract non-linear patterns from tabular data, OIKAN employs a feedforward neural network module referred to as “TabularNet”. This network is designed to approximate a function f: Rⁿ → R^m, where n denotes the number of input features and m represents the output dimension (i.e., m = 1 for regression tasks, or m equal to the number of classes in classification problems) [55].

The general structure of the neural network can be described as:

$$h\left(x\right)=W_L\cdot {\sigma }_{L-1}\left(W_{L-1}\cdot {\sigma }_{L-2}\left(\dots {\sigma }_1\left(W_{1}x+b_1\right)\dots \right)+b_{L-1}\right)+b_L,$$

(2)

where

• $W_l$ and $b_l$ are the weight matrix and bias vector for the layer $l$.
• ${\sigma }_l$ is the activation function used at layer $l$.
• $L$ is the number of layers, with sizes defined by input_size, hidden_sizes, and output_size.

Training is performed using the Adam optimizer. The loss function depends on the task:

• For regression, Mean Squared Error (MSE):

$$\mathcal{L}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\left(y_i-\widehat{y_i}\right)}^2,$$

(3)

• For classification, Cross-Entropy Loss:

$$\mathcal{L}=-{\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\sum }_{c=1}^C{y}_{i,c}\log \left(\widehat{y_{i,c}}\right),$$

(4)

The trained model generates augmented target values for symbolic regression, capturing non-linear patterns in the data.

3.2.3. Gaussian Noise-Based Data Augmentation

To improve generalization and enhance robustness, OIKAN applies Gaussian noise to the input data during training [56]. Given an input dataset $X\in R^{N\times n}$, where N is the number of data samples and n is the dimensionality of each sample, the augmented dataset is generated as:

$$X_{\mathrm{aug}}=\left\{X+{ϵ}_k∣k=1,\dots ,K\right\},$$

(5)

$${ϵ}_k\sim \mathcal{N}\left(0,{\sigma }^2\right),$$

(6)

where $\sigma$ is the standard deviation specified by the sigma parameter. This step improves the robustness of both the neural and symbolic models to small perturbations in input features.

3.2.4. Two-Stage Sparse Symbolic Regression

OIKAN incorporates a two-stage sparse symbolic regression mechanism using ElasticNet regularization, combining L1 (LASSO) and L2 (Ridge) regularization to produce sparse, interpretable models [57]. The target function is approximated as a linear combination of basis functions:

$$\widehat{y}={\sum }_{i=1}^M{\beta }_i{\varphi }_i\left(x\right),$$

(7)

where

• ${\varphi }_i\left(x\right)$ are basis functions (e.g., polynomials, logarithms, exponentials, sines).
• ${\beta }_i$ are coefficients estimated by ElasticNet.
• $M$ is the number of basis functions.

Stage 1: Coarse Model with Polynomial Features

In the initial stage, a coarse approximation of the target function is constructed by expanding the input space with polynomial basis functions up to the second degree. The resulting feature set is defined as:

$${\mathsf{\Phi }}_{\mathrm{coarse}}\left(x\right)=\left\{1,x_i,x_i^2,x_i{x}_j∣i,j=1,\dots ,n,i\le j\right\},$$

(8)

This representation captures linear, quadratic, and pairwise interaction terms among the input variables. ElasticNet regression is then applied to fit the model by solving the following optimization problem:

$${\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathsf{\beta }}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\left(y_i-{\sum }_{j=1}^{M_{\mathrm{coarse}}}{\beta }_j{\varphi }_j\left(x_i\right)\right)}^2+\alpha \left(\lambda ||\beta {||}_1+{\displaystyle \frac{1-\lambda }{2}}||\beta {||}_2^2\right),$$

(9)

where

• $(\beta \in R^{M_{\mathrm{coarse}}})$ is the vector of model coefficients.
• ${\mathsf{\varphi }}_j\left(x_i\right)$ is the j-th feature (or basis function) evaluated at input $x_i$.
• $N$ is the number of training samples.
• $\alpha$ is the regularization strength (alpha parameter, $\alpha >0$).
• $M_{\mathrm{coarse}}$ is the number of polynomial features.
• $\mathsf{\lambda }\in \left[\mathrm{0,1}\right]$: mixing parameter (default value: 0.5):

  ○

  $\mathsf{\lambda }=1$: Lasso (L1) penalty only.

  ○

  $\mathsf{\lambda }=0$: Ridge (L2) penalty only.

  ○

  $0<\mathsf{\lambda }<1$: ElasticNet (mixture of both).

• $|\mathsf{\beta }{|}_1$: L1 norm, promoting sparsity.
• $|\mathsf{\beta }{|}_2$: L2 norm, promoting small coefficient magnitudes.

The use of ElasticNet promotes sparsity through the L1 term and prevents overfitting via the L2 term, making it effective in handling multicollinearity and selecting the most relevant features. This approach facilitates the generation of simplified, interpretable expressions, even in the presence of redundant or highly correlated features.

To identify the most informative variables, feature importance scores k are computed by aggregating the absolute contributions of each variable across all basis functions in which it appears:

$$I_k={\sum }_{j:k\in \mathrm{features}\left({\varphi }_j\right)}\left|{\beta }_j\right|,$$

(10)

The top k features with the highest importance scores are then selected for the next stage.

Stage 2: Refined Model with Non-linear Transformations

In the second stage, the model is enriched by incorporating non-linear transformations of the previously selected top-k features. This refined feature set includes:

$${\mathsf{\Phi }}_{\mathrm{additional}}\left(x\right)=\{x_i^3,\log \left(1+\left|x_i\right|\right),\exp \left(\mathrm{clip}\left(x_i,-\mathrm{10,10}\right)\right),\sin \left(x_i\right)\mid i\in \mathrm{top}-k,$$

(11)

The final input space is defined as the union of polynomial and non-linear basis functions:

$${\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathsf{\beta }}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\left(y_i-{\sum }_{j=1}^{M_{\mathrm{refined}}}{\beta }_j{\varphi }_j\left(x_i\right)\right)}^2+\alpha \left(\lambda ||\beta {||}_1+{\displaystyle \frac{1-\lambda }{2}}||\beta {||}_2^2\right),$$

(12)

ElasticNet is applied once again to this enriched set using the same objective function, now with M_refined basis functions. The resulting symbolic model retains only non-zero coefficients and the corresponding basis functions, yielding a concise and interpretable mathematical expression.

For multi-class classification tasks, this symbolic modeling procedure is repeated independently for each class.

3.2.5. Symbolic Expression Generation

The final model comprises symbolic expressions that approximate the target function:

$$f\left(x\right)={\sum }_{j\in S}{\beta }_j{\varphi }_j\left(x\right),$$

(13)

where $S=\{j:\left|{\beta }_j\right|>{10}^{-6}\}$ denotes the set of indices corresponding to non-negligible coefficients. In classification scenarios, OIKAN constructs one symbolic expression per class. The predicted class probabilities are then obtained via a softmax function applied to the symbolic logits:

$$P\left(y=c∣x\right)={\displaystyle \frac{\exp \left(f_c\left(x\right)\right)}{\sum _{c^{’}=1}^C\mathrm{e}\mathrm{x}\mathrm{p}\left(f_{c^{’}}\right(x\left)\right)},}$$

(14)

The evaluation of OIKAN models was carried out using a set of standard metrics for both classification and regression tasks. These metrics provide a comprehensive overview of model performance in terms of accuracy, error, and computational efficiency. A summary of the metrics, including their formulas, types, and descriptions, is presented in

Table 3. Evaluation Metrics for Comparative Assessment of OIKAN Performance in Classification and Regression Tasks.

Metrics	Formula	Type	Description
R2 Score (Coefficient of Determination)	$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}{{\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2}}$	Regression	Proportion of variance explained by the model. Higher (0 to 1) is better.
Root Mean Squared Error (RMSE)	$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}$	Regression	Measures average prediction error magnitude in target units. Lower is better.
Mean Absolute Percentage Error (MAPE)	$\mathrm{MAPE}={\displaystyle \frac{100\%}{n}}{\sum }_{i=1}^n\left|{\displaystyle \frac{y_i-\widehat{y_i}}{y_i}}\right|$	Regression	Average percentage error of predictions. Lower is better.
Accuracy	7 $\begin{array}{c}\mathrm{Accuracy}={\displaystyle \frac{\mathrm{Number}\mathrm{of}\mathrm{Correct}\mathrm{Predictions}}{\mathrm{Total}\mathrm{Number}\mathrm{of}\mathrm{Predictions}}}\\ ={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}\end{array}$	Classification	Proportion of correct predictions. Higher is better, but less reliable for imbalanced data.
Precision (Weighted)	${\mathrm{Precision}}_{\mathrm{weighted}}={\sum }_{k=1}^K{\displaystyle \frac{n_k}{n}}\cdot {\displaystyle \frac{T{P}_k}{T{P}_k+F{P}_k}}$	Classification	Weighted proportion of positive predictions that are correct. Higher is better.
F1-Score (Weighted)	${\mathrm{F}1}_{\mathrm{weighted}}={\sum }_{k=1}^K{\displaystyle \frac{n_k}{n}}\cdot {\displaystyle \frac{2\cdot {\mathrm{Precision}}_k\cdot {\mathrm{Recall}}_k}{{\mathrm{Precision}}_k+{\mathrm{Recall}}_k}}$	Classification	Weighted harmonic mean of precision and recall. Higher is better for balanced performance.

.

To ensure experimental reproducibility and consistency across tasks, a standardized sequence of steps was followed—encompassing data loading, model initialization, training, symbolic expression extraction, and performance evaluation. Algorithm 1 outlines the complete symbolic modeling pipeline using either the OIKANClassifier or OIKANRegressor.

Algorithm 1 Unified Symbolic Modeling Using OIKANClassifier or OIKANRegressor

Require: Labeled dataset (X,y); OIKANClassifier hyperparameters/OIKANRegressor hyperparameters; test set proportion t∈(0,1) Ensure: Trained symbolic model; extracted symbolic formulas; evaluation metrics (accuracy or R2); feature importance metrics 1: Load the dataset (e.g., Iris for classification, California Housing for regression) 2: Split data into training and testing subsets using proportion t 3: Initialize the OIKANClassifier or OIKANRegressor with the specified hyperparameters 4: Train the model on Xtrain,ytrain, including neural network evaluation and symbolic regression 5: Predict class labels or target values for the test set using model.predict(X_test) 6: For classification: compute and print accuracy using accuracy_score(y_test, y_pred; For regression: evaluate performance using the R2 score 7: Generate and print a classification report using classification_report(y_test, y_pred) 8: Retrieve and print symbolic formulas for each class using model.get_formula() 9: Retrieve and print feature importance values using model.feature_importances() 10: Save the trained model to disk using model.save(path) 11: Reload the model using model.load(path) 12: Verify the consistency of symbolic formulas in the original format from the loaded model 13: Retrieve and print symbolic formulas in SymPy format using get_formula(type = ‘sympy’) 14: Retrieve and print symbolic formulas in LaTeX format using get_formula(type = ‘latex’) 15: return Trained model, symbolic formula representations, accuracy, and feature importances

3.3. Architecture and Base Class Parameters for the OIKAN

Model training begins by importing the OIKAN classes and initializing them with appropriate hyperparameters, such as hidden layer sizes, activation functions (e.g., ReLU, tanh), augmentation factors, and batch size. The user invokes the fit(X, y) method to initiate training on tabular datasets, followed by prediction using the predict(X) method. Symbolic formula extraction is performed using the “get_formula()” function, which can return outputs in SymPy, LaTeX, or a full mathematical representation. Models can be saved and loaded via the “save()” and “load()” functions, respectively, using JSON format.

Table 4. Main workflow stages in the OIKAN framework.

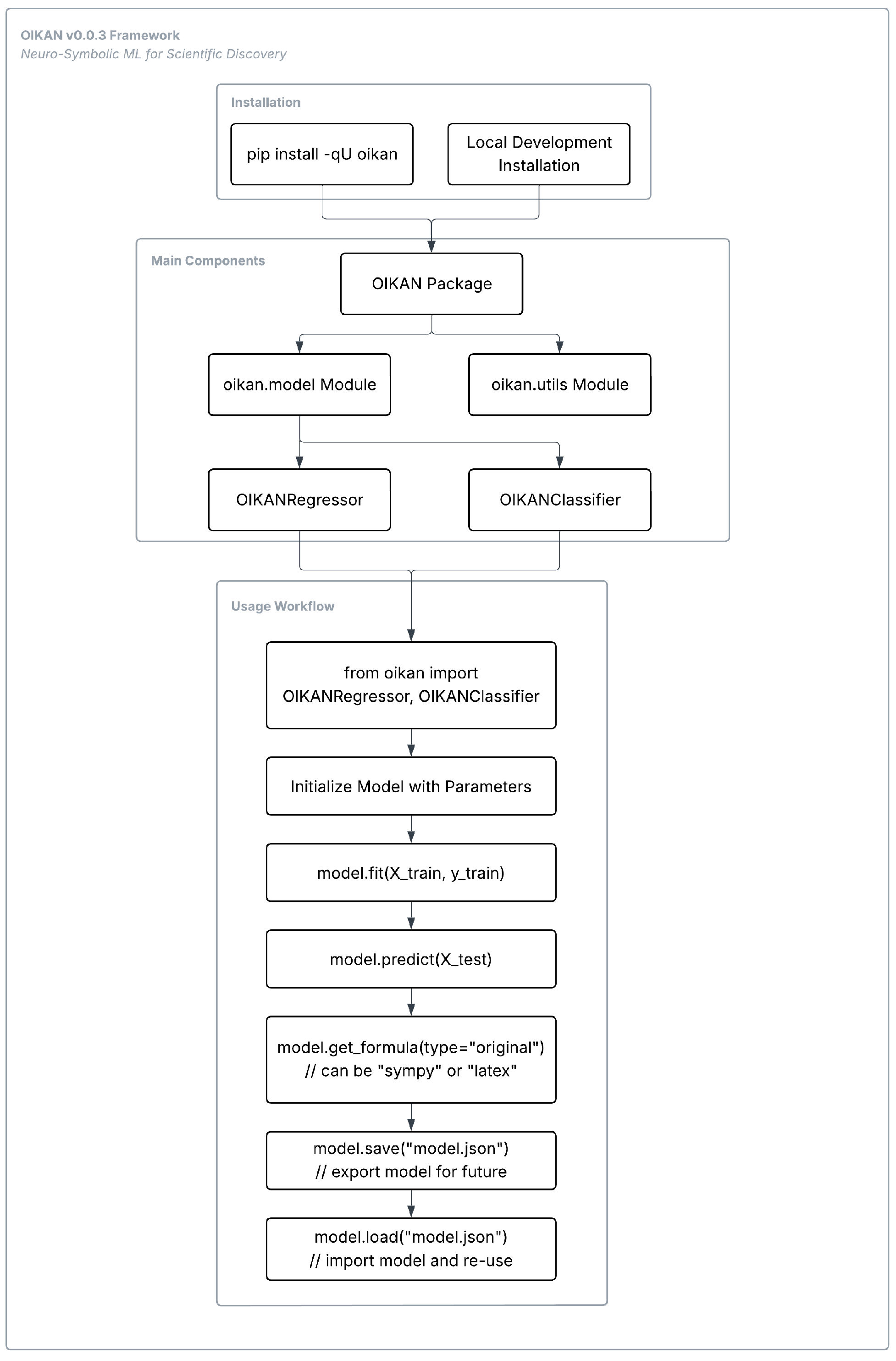
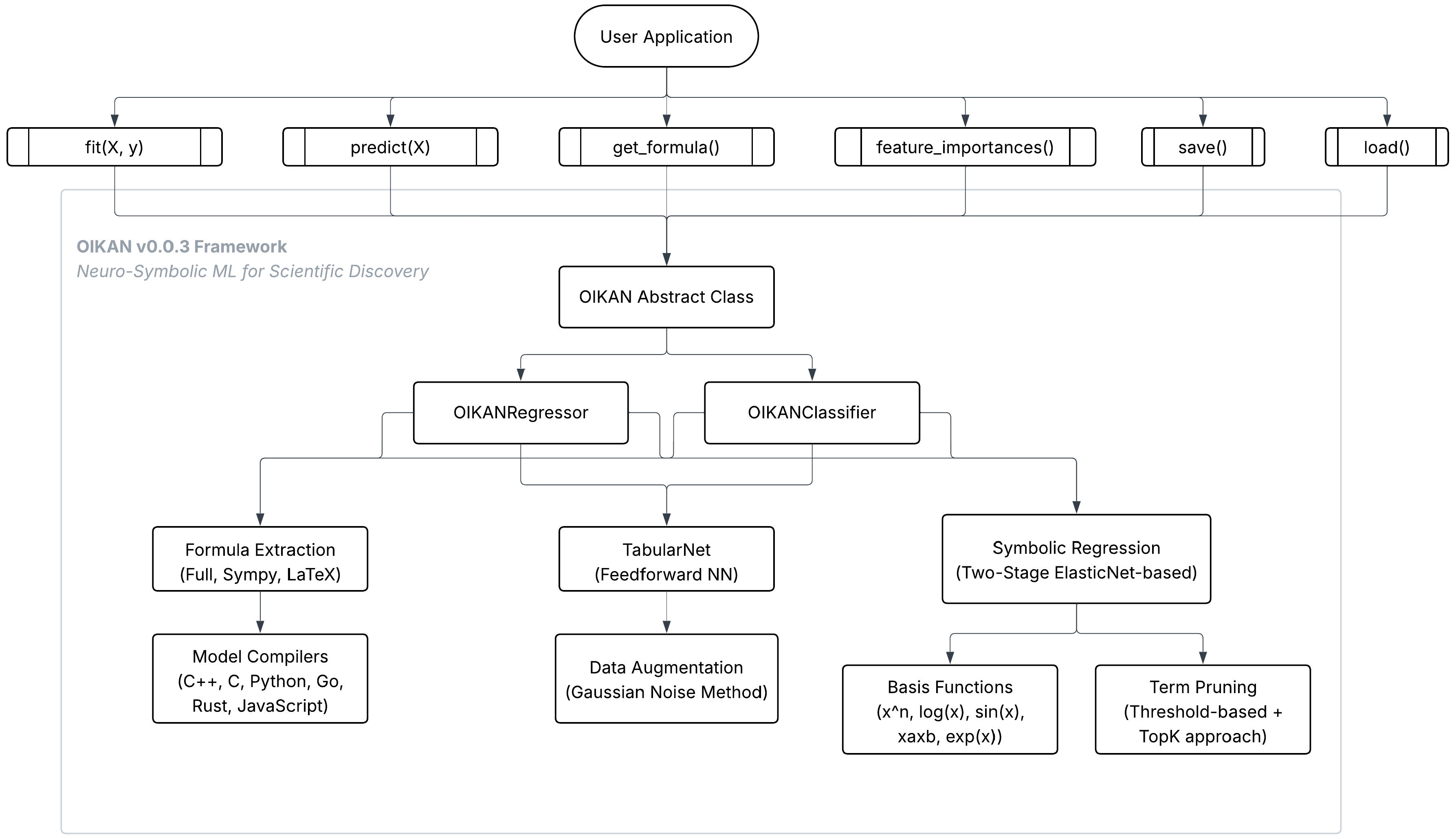
Step	Description	Purpose
Data Preprocessing and Augmentation	A feedforward NN (TabularNet) analyzes input data to capture initial patterns. Gaussian noise is added to the data, creating multiple perturbed versions to augment the dataset. The NN then generates predictions or logits for the augmented data.	Enhances model robustness by introducing controlled variability, allowing the model to learn generalized patterns. The NN provides a preliminary mapping of data relationships, which is refined in later steps.
Two-Stage Symbolic Regression	Stage 1 (Coarse Model): Polynomial features (degree 2) are generated from the augmented data. An ElasticNet model, combining L1 (LASSO) and L2 (Ridge) regularization, is fitted to compute feature importances based on coefficients. The top-k features are selected. Stage 2 (Refined Model): Non-linear basis functions are added for the top-k features. A second ElasticNet model is fitted to the combined polynomial and non-linear features.	Constructs an interpretable model by first identifying the most relevant features (Stage 1) and then enhancing the model with non-linear transformations (Stage 2). ElasticNet ensures sparsity and robustness, balancing model complexity and accuracy.
Model Compilation	The coefficients and basic functions from the refined model are used to construct a symbolic mathematical expression, representing the relationship between features and the target. The expression is simplified using SymPy and supports formats like original, SymPy, or LATEX.	Produces a human-readable, interpretable formula that encapsulates the learned relationships, enabling efficient predictions and easy inspection of the model’s logic.
Model Export and Use	The symbolic model, including basis functions, coefficients, and feature metadata, is saved in JSON format. The model can be loaded and used in multiple languages (C, C++, JavaScript, Rust, Go, Python).	Facilitates model portability and deployment across diverse platforms, ensuring accessibility and usability for different applications while maintaining interpretability and efficiency.

provides an overview of the main workflow stages implemented in the OIKAN framework. The system begins with preprocessing and data augmentation, proceeds through a two-stage symbolic regression process, and concludes with model compilation into a human-readable formula.

The framework integrates neural representation learning with symbolic regression techniques, allowing the generation of interpretable mathematical models from data. The system was implemented in Python 3.13.0 and made available as an installable package via PyPI (pip install -qU oikan). The framework consists of core components, including the OIKANRegressor and OIKANClassifier, accessible via the oikan.model module, while utility functions reside in oikan.utils (Figure 1).

Internally, the OIKAN abstract base class orchestrates the workflow. For regression and classification tasks, it delegates the learning process to specialized subclasses (OIKANRegressor or OIKANClassifier). The learning pipeline includes a feedforward neural network component (TabularNet), which learns intermediate representations. Data augmentation is achieved via Gaussian noise injection, controlled by the augmentation_factor parameter. The overall class structure and component dependencies are illustrated in Figure 2.

Once the neural model captures the data structure, the symbolic regression phase begins. This stage transforms the features using a predefined set of basic functions, including powers (xⁿ), logarithmic (log(x)), sinusoidal (sin(x)), and exponential (exp(x)) transformations. The symbolic regression utilizes a two-stage ElasticNet model. Initially, it fits the transformed data and then prunes irrelevant or low-importance terms based on thresholding and a Top K selection approach. The final symbolic expression is extracted and returned as an interpretable mathematical formula. The architecture that connects these components is shown in Figure 3.

The framework ensures reproducibility through modular architecture and compatibility with multiple programming languages (C++, C, Python, Go, Rust, JavaScript) via model compilation tools. Code, data augmentation routines, and formula extraction methods are openly accessible through the OIKAN repository. Users must cite the library and include configuration details to replicate the symbolic learning results.

Dataflow within the framework begins with raw input data fed into the neural component. The feedforward network undergoes training with augmented data, followed by transformation using basis functions. Symbolic regression and term pruning are then conducted, culminating in mathematical formula extraction and optional compilation. This modular workflow from input to interpretable output is illustrated in Figure 4.

To ensure adaptability and optimization for a wide range of tasks, the OIKAN framework was designed with a high degree of parameter flexibility. This design enables users to fine-tune models for specific applications, thereby enhancing performance and interpretability.

Table 5. Definitions of the OIKAN base class parameters.

Parameter	Stage	Description	Values
hidden_sizes	NN Training	List of hidden layer sizes for the MLP.	List of integers, default = [64, 64]
activation	NN Training	Activation function for the neural network layers.	Options: ‘relu’, ‘tanh’, ‘leaky_relu’, ‘elu’, ‘swish’, ‘gelu’, default=‘relu’
epochs	NN Training	Number of epochs for training the neural network.	Integer, default = 100
lr	NN Training	Learning rate for the optimizer.	Float, default = 0.001
batch_size	NN Training	Batch size for mini-batch training.	Integer, default = 32
evaluate_nn	NN Training	Whether to evaluate the NN before full training.	Boolean, default = False
augmentation_factor	Data Augmentation	Number of augmented samples generated per original sample.	Integer, default = 10
sigma	Data Augmentation	Standard deviation of Gaussian noise added during data augmentation.	Float, default = 0.1
alpha	Symbolic Regression	L1 regularization strength for Lasso in symbolic regression.	Float, default = 0.1
top_k	Symbolic Regression	Number of top features to select in hierarchical symbolic regression.	Integer, default = 5
verbose	General	Whether to display training progress for neural network and symbolic regression.	Boolean, default = False
random_state	General	Random seed for reproducibility.	Integer, default = None

summarizes the key parameters available in the OIKAN base class, applicable to both classification and regression tasks.

Among the implemented parameters, “evaluate_nn” stands out as a particularly useful feature. When enabled, it allows for a preliminary evaluation of the neural network (TabularNet) before executing full training. This can significantly reduce computational cost and save time by identifying underperforming configurations early in the process.

The “top_k” parameter is another critical element, determining the number of top-ranked features selected for non-linear transformation during the symbolic regression phase. This parameter plays a direct role in shaping both model accuracy and computational efficiency.

Additionally, the “verbose” flag improves usability by integrating with the “tqdm” library to provide real-time progress updates during training. This enhances user experience by offering transparent feedback throughout both neural and symbolic learning stages.

The system requirements for installing and running the OIKAN framework are summarized in

Table 6. Minimum system requirements for working with OIKAN.

Requirement	Details
Python	Version 3.7 or higher
Operating System	Platform independent (Windows/macOS/Linux)
Memory	Recommended minimum 4 GB RAM
Disk Space	~100 MB for installation (including dependencies)
GPU	Optional (for faster training)
Dependencies	torch, numpy, scikit-learn, sympy, tqdm

. These specifications ensure compatibility across platforms and provide guidelines for memory, storage, and optional GPU usage to support scalable training performance.

3.4. Datasets and Experimental Setup

To benchmark the OIKAN framework, datasets from the Penn Machine Learning Benchmarks (PMLB) [58] were employed, covering 60 classification and 56 regression tasks. These datasets varied widely in size, dimensionality, and complexity. Smaller datasets (e.g., 1096_FacultySalaries, parity5) included approximately 1000 augmented instances, while larger datasets (e.g., 344_mv, 215_2dplanes, 564_fried) contained up to 97,842 rows after augmentation. Gaussian noise-based data augmentation was applied with factors ranging from 2 to 240, with the total number of rows capped at 100,000 to ensure computational feasibility.

For evaluation, classification tasks were assessed using accuracy, precision, and F1-score, while regression tasks were measured by Root Mean Square Error (RMSE), Mean Absolute Percentage Error (MAPE), and R² score. To complement predictive performance, we also recorded computational efficiency metrics, including training time, inference time, and memory usage.

To provide a comparative baseline, two reference models were selected: DecisionTree, representing classical interpretable methods, and XGBoost, representing high-performing black-box models. This setup allowed a direct analysis of the trade-off between interpretability and predictive accuracy across standardized PMLB tasks.

The symbolic regression component of OIKAN employed ElasticNet regularization, with default parameters l1_ratio = 0.5, alpha = 1, and random_state = 42 to ensure reproducibility.

In addition to the PMLBs, two widely used datasets were included for validation: the Iris dataset for classification (150 samples, 4 features, 3 species) and the California Housing dataset for regression (20,640 samples, 8 features, target = median house value). Both datasets were partitioned into 80% training and 20% testing subsets. The models were configured with two hidden layers of 32 neurons, ReLU activation, a data augmentation factor of 10, and batch training. Furthermore, the evaluate_nn parameter was utilized to pre-assess the neural component before the symbolic regression phase.

All experiments were conducted in a GPU-accelerated environment (Tesla P100, CUDA) on the Kaggle platform.

4. Results

4.1. Performance of OIKAN Classifier on Benchmark Datasets

To evaluate the classification performance and computational efficiency of the proposed framework, OIKANClassifier was tested on over 50 datasets from the PMLB benchmark suite. The results provide insight into the model’s ability to generalize across diverse classification tasks of varying size and complexity.

Table 7. Evaluation Results of the OIKAN Classifier on PMLB Benchmark Datasets.

Dataset	#Feat. *	Rows	Accuracy	Precision	F1
iris	4	1200	1.000	1.000	1.000
analcatdata_creditscore	6	1040	1.000	1.000	1.000
corral	6	1280	1.000	1.000	1.000
prnn_crabs	7	1600	1.000	1.000	1.000
mushroom	22	64,990	1.000	1.000	1.000
analcatdata_authorship	70	6720	1.000	1.000	1.000
clean2	168	52,780	1.000	1.000	1.000
dermatology	34	2920	0.986	0.988	0.986
optdigits	64	44,960	0.985	0.985	0.985
new_thyroid	5	1720	0.977	0.978	0.976
dis	29	30,170	0.975	0.961	0.968
mfeat_karhunen	64	16,000	0.973	0.973	0.972
mfeat_pixel	240	16,000	0.968	0.968	0.967
hypothyroid	25	25,300	0.961	0.957	0.959
monk3	6	4430	0.955	0.956	0.955
balance_scale	4	5000	0.952	0.955	0.944
clean1	168	3800	0.948	0.948	0.948
kr_vs_kp	36	25,560	0.947	0.947	0.947
page_blocks	10	43,780	0.944	0.945	0.937
ionosphere	34	2800	0.930	0.932	0.929
analcatdata_lawsuit	4	2110	0.925	0.914	0.916
coil2000	85	78,570	0.909	0.892	0.900
backache	32	1440	0.889	0.902	0.865
car_evaluation	6	13,820	0.887	0.891	0.884
prnn_synth	2	2000	0.880	0.880	0.880
mfeat_zernike	47	16,000	0.860	0.862	0.851
ecoli	7	2610	0.833	0.811	0.791
lymphography	18	1180	0.833	0.851	0.831
tic_tac_toe	9	7660	0.823	0.822	0.821
analcatdata_boxing2	3	1050	0.815	0.813	0.813
confidence	3	1026	0.800	0.778	0.775
biomed	8	1670	0.786	0.835	0.735
lupus	3	1035	0.778	0.781	0.769
phoneme	5	43,230	0.765	0.754	0.734
adult	14	78,146	0.760	0.738	0.745
labor	16	1035	0.750	0.771	0.756
hepatitis	19	1240	0.742	0.742	0.742
led7	7	25,600	0.734	0.743	0.730
appendicitis	7	1008	0.727	0.529	0.612
hayes_roth	4	1280	0.719	0.753	0.710
sonar	60	1660	0.714	0.716	0.714
mfeat_fourier	76	16,000	0.670	0.731	0.633
saheart	9	3690	0.656	0.688	0.555
monk1	6	4440	0.652	0.650	0.649
haberman	3	2440	0.645	0.592	0.609
monk2	6	4800	0.620	0.393	0.481
collins	23	3880	0.598	0.605	0.557
ring	20	59,200	0.585	0.778	0.511
analcatdata_fraud	11	1023	0.556	0.309	0.397
movement_libras	90	2880	0.556	0.687	0.588
penguins	7	2660	0.537	0.327	0.395
analcatdata_boxing1	3	1056	0.500	0.500	0.500
flags	43	1420	0.472	0.487	0.462
mfeat_morphological	6	16,000	0.445	0.331	0.357
bupa	5	2760	0.435	0.189	0.264
parity5+5	10	8990	0.418	0.421	0.405
mfeat_factors	216	16,000	0.385	0.521	0.346
parity5	5	1000	0.286	0.082	0.127
schizo	14	2720	0.221	0.338	0.190
analcatdata_dmft	4	6370	0.181	0.195	0.169

* number of features.

presents the classification performance metrics, including accuracy, precision, and F1-score, for each dataset. The model achieved perfect accuracy (1.000) on six well-known datasets such as “iris”, “mushroom”, “analcatdata_creditscore”, “corral”, and “prnn_crabs”, demonstrating strong performance on symbolically or linearly separable problems.

A summary of the model’s aggregated classification performance includes:

• Median accuracy: 0.886
• Average accuracy on top 10 datasets: 0.987
• Datasets with accuracy ≥ 0.95: 17 out of 50+ (34%)
• Datasets with accuracy ≤ 0.50: 10 out of 50+ (20%)

In addition to classification performance, runtime and memory usage were analyzed to assess the model’s suitability for deployment.

Table 8. Computational Efficiency of OIKAN Classifier on PMLB Classification Datasets.

Dataset	#Feat.	Rows	Train (s)	Train (MB)	Pred (s)	Pred (MB)
iris	4	1200	1.147	1.756	0.001	0.007
analcatdata_creditscore	6	1040	0.859	2.276	0.001	0.006
corral	6	1280	1.113	2.788	0.002	0.012
prnn_crabs	7	1600	1.387	4.004	0.002	0.014
mushroom	22	64,990	100.766	646.607	0.029	2.147
analcatdata_authorship	70	6720	131.617	567.542	0.062	2.041
clean2	168	52,780	2944.120	24,386.306	1.165	149.450
dermatology	34	2920	12.370	70.326	0.026	0.182
optdigits	64	44,960	1042.342	3157.350	0.078	13.036
new_thyroid	5	1720	1.650	3.265	0.001	0.012
dis	29	30,170	55.173	488.690	0.021	1.070
mfeat_karhunen	64	16,000	426.694	1129.190	0.071	5.215
mfeat_pixel	240	16,000	4278.023	14,991.724	0.591	40.449
hypothyroid	25	25,300	41.107	317.996	0.018	0.837
monk3	6	4430	4.173	9.545	0.001	0.026
balance_scale	4	5000	4.892	7.276	0.002	0.029
clean1	168	3800	277.464	1765.348	0.420	7.985
kr_vs_kp	36	25,560	48.079	611.387	0.023	1.051
page_blocks	10	43,780	54.460	140.837	0.016	0.684
ionosphere	34	2800	4.917	67.644	0.012	0.092
analcatdata_lawsuit	4	2110	2.003	3.036	0.001	0.012
coil2000	85	78570	595.198	9532.018	0.094	12.436
backache	32	1440	2.655	34.219	0.010	0.029
car_evaluation	6	13820	14.807	29.910	0.008	0.145
prnn_synth	2	2000	1.758	1.352	0.001	0.008
mfeat_zernike	47	16,000	293.332	630.603	0.049	3.516
ecoli	7	2610	2.563	6.565	0.002	0.028
lymphography	18	1180	1.779	10.394	0.004	0.023
tic_tac_toe	9	7660	7.662	24.942	0.006	0.072
analcatdata_boxing2	3	1050	1.179	1.110	0.001	0.004
confidence	3	1026	0.649	1.124	0.001	0.004
biomed	8	1670	1.835	4.796	0.002	0.023
lupus	3	1035	0.844	1.097	0.001	0.003
phoneme	5	43,230	38.545	74.135	0.004	0.217
adult	14	78,146	410.054	409.513	0.049	9.926
labor	16	1035	0.827	7.542	0.004	0.008
hepatitis	19	1240	1.592	11.894	0.005	0.029
led7	7	25,600	27.383	61.526	0.006	0.318
appendicitis	7	1008	0.899	2.640	0.003	0.007
hayes_roth	4	1280	1.163	1.866	0.001	0.008
sonar	60	1660	3.661	110.948	0.008	0.042
mfeat_fourier	76	16,000	141.373	1570.264	0.035	1.673
saheart	9	3690	3.806	12.037	0.002	0.043
monk1	6	4440	4.012	9.573	0.001	0.031
haberman	3	2440	2.169	2.594	0.001	0.010
monk2	6	4800	4.396	10.346	0.001	0.027
collins	23	3880	21.469	49.628	0.017	0.153
ring	20	59,200	77.061	503.507	0.008	0.451
analcatdata_fraud	11	1023	0.584	4.340	0.001	0.002
movement_libras	90	2880	256.894	400.099	0.101	1.753
penguins	7	2660	2.932	6.651	0.002	0.026
analcatdata_boxing1	3	1056	0.860	1.116	0.001	0.004
flags	43	1420	6.841	54.917	0.014	0.055
mfeat_morphological	6	16000	18.853	35.406	0.004	0.113
bupa	5	2760	2.669	5.274	0.001	0.018
parity5+5	10	8990	7.889	33.289	0.004	0.032
mfeat_factors	216	16,000	5980.859	12,166.962	0.899	59.125
parity5	5	1000	0.287	1.900	0.001	0.002
schizo	14	2720	4.063	16.103	0.004	0.071
analcatdata_dmft	4	6370	6.122	9.273	0.002	0.039

summarizes the time and memory complexity metrics across the same set of PMLB datasets. Median training time was 4.9 s, and median prediction time was 0.006 s. Memory usage remained low during inference (median: 0.072 MB), with training memory consumption reaching 35.4 MB on average. Inference times were consistently below 0.05 s across all datasets, supporting real-time and embedded system applicability.

Training duration ranged from under one second on smaller datasets (e.g., confidence, analcatdata_fraud) to approximately 1.7 h on high-dimensional datasets such as mfeat_factors. Memory usage scaled with dataset size and dimensionality, peaking at approximately 24 GB for clean2.

4.2. Performance of OIKAN Regressor Across Symbolic and Noisy Tasks

The performance of OIKAN Regressor was assessed using over 50 regression datasets from the PMLB benchmark collection, with all experiments conducted on a GPU P100. Results are detailed in

Table 9. Performance Summary of the OIKAN Regressor on PMLB Regression Benchmark Datasets.

Dataset	#Feat.	Rows	RMSE	R2	MAPE
344_mv	10	97,842	0.950	0.992	2.772
523_analcatdata_neavote	2	1040	0.885	0.938	0.446
215_2dplanes	10	97,842	1.098	0.937	1.509
210_cloud	5	1032	0.353	0.920	0.407
624_fri_c0_100_5	5	1040	0.327	0.875	0.453
649_fri_c0_500_5	5	4000	0.382	0.862	2.156
229_pwLinear	10	1600	1.386	0.862	0.418
595_fri_c0_1000_10	10	8000	0.386	0.855	0.958
230_machine_cpu	6	1670	87.062	0.851	0.732
1027_ESL	4	3900	0.507	0.836	0.082
590_fri_c0_1000_50	50	8000	0.399	0.825	1.034
609_fri_c0_1000_5	5	8000	0.438	0.823	1.495
1096_FacultySalaries	4	1000	1.936	0.797	0.036
561_cpu	7	1670	104.397	0.797	0.278
529_pollen	4	30,780	1.477	0.786	3.445
294_satellite_image	36	51,480	1.073	0.763	0.360
579_fri_c0_250_5	5	2000	0.439	0.757	2.838
635_fri_c0_250_10	10	2000	0.478	0.757	2.842
201_pol	48	96,000	22.270	0.708	4.76 × 1016
564_fried	10	97,842	2.693	0.705	0.229
621_fri_c0_100_10	10	1040	0.589	0.687	0.810
599_fri_c2_1000_5	5	8000	0.605	0.670	1.108
192_vineyard	2	1025	2.503	0.665	0.138
1089_USCrime	13	1036	20.204	0.663	0.090
589_fri_c2_1000_25	25	8000	0.635	0.623	0.952
612_fri_c1_1000_5	5	8000	0.600	0.615	1.584
623_fri_c4_1000_10	10	8000	0.618	0.609	1.610
4544_GeographicalOriginalofMusic	117	8470	0.580	0.597	4.051
620_fri_c1_1000_25	25	8000	0.642	0.592	1.125
592_fri_c4_1000_25	25	8000	0.613	0.570	1.322
586_fri_c3_1000_25	25	8000	0.691	0.569	1.448
588_fri_c4_1000_100	100	8000	0.678	0.555	1.224
583_fri_c1_1000_50	50	8000	0.657	0.530	2.462
616_fri_c4_500_50	50	4000	0.691	0.528	1.074
605_fri_c2_250_25	25	2000	0.686	0.498	1.127
581_fri_c3_500_25	25	4000	0.768	0.493	6.904
617_fri_c3_500_5	5	4000	0.808	0.417	1.925
225_puma8NH	8	65,530	4.265	0.413	2.799
1029_LEV	4	8000	0.718	0.396	2.96 × 1014
1030_ERA	4	8000	1.607	0.376	0.425
527_analcatdata_election2000	14	1007	96,238.090	0.344	0.708
1028_SWD	10	8000	0.672	0.307	0.145
547_no2	7	4000	0.627	0.301	0.142
218_house_8L	8	91,135	46,944.468	0.215	2.71 × 1017
591_fri_c1_100_10	10	1040	0.687	0.124	1.454
228_elusage	2	1012	26.929	-	0.589
557_analcatdata_apnea1	3	3800	3925.899	-	1.89 × 1018
556_analcatdata_apnea2	3	3800	4036.276	-	1.85 × 1018
485_analcatdata_vehicle	4	1026	373.732	-	0.821
522_pm10	7	4000	0.915	-	0.278
227_cpu_small	12	65,530	189.186	-	4.24 × 1015
562_cpu_small	12	65,530	48.787	-	2.24 × 1015
542_pollution	15	1008	267.912	-	0.262
574_house_16H	16	91,135	53,044.147	-	4.88 × 1017
197_cpu_act	21	65,530	22.030	-	1.19 × 1015
573_cpu_act	21	65,530	164.100	-	2.62 × 1015

and

Table 10. Time and Memory Complexity of the OIKAN Regressor on PMLB Regression Benchmarks.

Dataset	#Feat.	Rows	Train (s)	Train (MB)	Pred (s)	Pred (MB)
344_mv	10	97,842	282.833	301.584	0.013	3.197
523_analcatdata_neavote	2	1040	0.806	0.715	0.000	0.002
215_2dplanes	10	97,842	266.519	301.576	0.008	1.827
210_cloud	5	1032	0.766	1.950	0.000	0.004
624_fri_c0_100_5	5	1040	0.750	1.963	0.001	0.004
649_fri_c0_500_5	5	4000	3.216	7.437	0.001	0.015
229_pwLinear	10	1600	1.341	5.944	0.002	0.018
595_fri_c0_1000_10	10	8000	6.397	29.555	0.001	0.028
230_machine_cpu	6	1670	1.547	3.613	0.001	0.015
1027_ESL	4	3900	3.340	5.539	0.001	0.018
590_fri_c0_1000_50	50	8000	7.390	357.336	0.001	0.035
609_fri_c0_1000_5	5	8000	6.389	14.828	0.001	0.031
1096_FacultySalaries	4	1000	0.539	1.446	0.001	0.003
561_cpu	7	1670	1.575	4.159	0.001	0.018
529_pollen	4	30,780	26.735	43.379	0.004	0.143
294_satellite_image	36	51,480	103.953	1222.647	0.063	6.982
579_fri_c0_250_5	5	2000	1.681	3.741	0.001	0.008
635_fri_c0_250_10	10	2000	1.749	7.422	0.001	0.010
201_pol	48	96,000	235.943	3885.826	0.084	16.249
564_fried	10	97,842	267.517	301.579	0.010	2.806
621_fri_c0_100_10	10	1040	0.748	3.885	0.001	0.006
599_fri_c2_1000_5	5	8000	6.481	14.826	0.001	0.030
192_vineyard	2	1025	0.504	0.699	0.001	0.002
1089_USCrime	13	1036	0.608	5.518	0.004	0.011
589_fri_c2_1000_25	25	8000	6.805	106.004	0.002	0.047
612_fri_c1_1000_5	5	8000	6.678	14.826	0.001	0.032
623_fri_c4_1000_10	10	8000	6.391	29.553	0.001	0.030
4544_GeographicalOriginalofMusic	117	8470	121.030	1926.686	0.022	0.279
620_fri_c1_1000_25	25	8000	6.669	106.002	0.001	0.035
592_fri_c4_1000_25	25	8000	7.189	106.000	0.002	0.043
586_fri_c3_1000_25	25	8000	6.689	106.006	0.001	0.033
588_fri_c4_1000_100	100	8000	11.997	1340.217	0.008	0.123
583_fri_c1_1000_50	50	8000	7.678	357.328	0.008	0.088
616_fri_c4_500_50	50	4000	4.011	182.768	0.009	0.081
605_fri_c2_250_25	25	2000	1.791	30.500	0.005	0.033
581_fri_c3_500_25	25	4000	3.504	57.044	0.003	0.031
617_fri_c3_500_5	5	4000	3.323	7.436	0.001	0.013
225_puma8NH	8	65,530	55.508	159.550	0.006	0.394
1029_LEV	4	8000	6.511	11.306	0.001	0.029
1030_ERA	4	8000	6.586	11.302	0.001	0.040
527_analcatdata_election2000	14	1007	0.711	5.975	0.004	0.015
1028_SWD	10	8000	7.321	29.554	0.002	0.049
547_no2	7	4000	3.689	9.905	0.001	0.032
218_house_8L	8	91,135	164.753	218.753	0.009	2.444
591_fri_c1_100_10	10	1040	0.741	3.883	0.001	0.006
228_elusage	2	1012	0.498	0.692	0.000	0.002
557_analcatdata_apnea1	3	3800	3.182	3.872	0.001	0.021
556_analcatdata_apnea2	3	3800	3.160	3.868	0.001	0.021
485_analcatdata_vehicle	4	1026	0.510	1.489	0.001	0.004
522_pm10	7	4000	3.650	9.903	0.001	0.028
227_cpu_small	12	65,530	63.710	258.117	0.018	0.998
562_cpu_small	12	65,530	62.503	258.115	0.005	0.867
542_pollution	15	1008	0.675	6.639	0.005	0.016
574_house_16H	16	91,135	176.405	539.557	0.021	6.381
197_cpu_act	21	65,530	77.496	602.564	0.029	2.597
573_cpu_act	21	65,530	78.804	602.562	0.020	2.781

.

The model demonstrated strong performance on datasets characterized by symbolic structure or smooth analytical dependencies (Table 9). In particular, high R² scores exceeding 0.9 were observed on datasets such as 2dplanes, cloud, and mv, accompanied by correspondingly low RMSE values. The median R² score across all datasets was approximately 0.705, with 20% of the datasets (10 out of 50+) achieving R² values of 0.85 or higher.

The top five performing datasets in terms of R² were:

• 344_mv: R² = 0.992, RMSE = 0.950
• 523_analcatdata_neavote: R² = 0.938, RMSE = 0.885
• 215_2dplanes: R² = 0.937, RMSE = 1.098
• 210_cloud: R² = 0.920, RMSE = 0.353
• 624_fri_c0_100_5: R² = 0.875, RMSE = 0.327

However, performance significantly declined on noisy or non-symbolic datasets such as parity-like, pollution, and cpu_act. For example:

• 227_cpu_small: RMSE = 189.2, R² undefined (possibly due to numerical instability)
• 218_house_8L: RMSE = 46,944.5, R² = 0.215
• 573_cpu_act: RMSE = 164.1, R² undefined

Overall, 36% of the datasets had R² scores of 0.50 or lower, reflecting difficulty in modeling data with high noise or poorly defined functional relationships.

The model’s error metrics (RMSE and MAPE) generally followed the trend of the R² score. However, MAPE values were affected in cases involving large target magnitudes or near-zero predictions, indicating sensitivity to scale that may require normalization or alternative loss functions.

In terms of computational efficiency (Table 10), the OIKANRegressor maintained low training and inference costs:

• Median training time: ~3.5 s
• Median training memory: ~14 MB
• Median prediction time: <0.01 s
• Median prediction memory: <0.05 MB

Even for high-dimensional datasets such as 590_fri_c0_1000_50 (50 features), training completed in 7.39 s using 357 MB of memory. On a larger dataset like 201_pol (48 features, ~100 K rows), training required ~4 min and ~3.9 GB of memory.

The quantitative evaluation of interpretability was conducted by measuring the symbolic compactness of the extracted formulas. On average, classification formulas reached 9852 characters in length (ranging from 500 to 110,665), while regression formulas were notably shorter, with an average of 1043 characters (ranging from 235 to 5206). The relatively large sizes observed in classification tasks are explained by the need to construct a separate regression formula for each class, and in both regression and classification settings, datasets with many features and complex interaction patterns tend to generate substantially longer symbolic expressions. These lengths are also strongly influenced by the choice of hyperparameters: under default settings, formula sizes can vary considerably. In particular, if the top_k parameter, which controls the number of retained terms during function minimization, is left unconstrained, the resulting expressions may become unnecessarily long and less interpretable. Careful tuning of this parameter for each dataset can substantially reduce expression length and improve readability. This observation highlights an important direction for future work, developing adaptive mechanisms for hyperparameter selection that can balance predictive accuracy with symbolic compactness, thereby enhancing both the efficiency and interpretability of the framework.

4.3. Comparative Analysis with Baseline Models

To further analyze the variability of OIKAN’s classification outcomes, the benchmark results were categorized into performance tiers. As shown in

Table 11. Performance Distribution of OIKAN Classifier Across PMLB Datasets.

Performance Tier	OIKAN Count	Notable Datasets
Perfect (1.000)	6	mushroom, iris, analcatdata_authorship, analcatdata_creditscore, corral, prnn_crabs
Excellent (0.95+)	17	monk3 (0.955), balance_scale (0.952), dermatology (0.986)
Good (0.80–0.94)	18	tic_tac_toe (0.823), car_evaluation (0.887), ionosphere (0.930)
Fair (0.60–0.79)	12	adult (0.760), penguins (0.537), phoneme (0.765)
Poor (<0.60)	8	analcatdata_dmft (0.181), parity5 (0.286)

, OIKAN achieved perfect accuracy on six datasets. This distribution illustrates both the model’s strengths on symbolically or linearly separable tasks and its limitations on noisier or higher-dimensional problems.

The comparative evaluation across the PMLBs highlights clear differences in performance between OIKAN and established baseline models. All results for OIKAN, ElasticNet, XGBoost, and DecisionTree are documented in the Supplementary Materials, including detailed CSV files for classification and regression benchmarks, as well as a comprehensive analytics notebook. In the classification setting, OIKAN achieved a median accuracy of 0.886, with corresponding precision and F1 scores of 0.91 and 0.89, respectively (

Table 12. Comparative Performance of OIKAN and Baseline Models on Classification Datasets.

Model	Dataset	Accuracy	Precision	F1
OIKAN	iris (150 × 4)	1	1	1
ElasticNet		1	1	1
XGBoost		0.966667	0.969444	0.966514
DecisionTree		1	1	1
OIKAN	monk3 (432 × 6)	0.955	0.956	0.995
ElasticNet		0.702703	0.716642	0.702703
XGBoost		0.981982	0.981982	0.981982
DecisionTree		0.972973	0.97308	0.972946
OIKAN	mushroom (8124 × 22)	1	1	1
ElasticNet		0.953231	0.953235	0.95322
XGBoost		1	1	1
DecisionTree		1	1	1
OIKAN	car_evaluation (1728 × 6)	0.887	0.891	0.884
ElasticNet		0.812139	0.801617	0.803303
XGBoost		0.979769	0.985781	0.981074
DecisionTree		0.965318	0.973908	0.967508
OIKAN	kr_vs_kp (3196 × 36)	0.947	0.947	0.947
ElasticNet		0.95	0.951953	0.950049
XGBoost		0.989063	0.989099	0.989059
DecisionTree		0.985938	0.986152	0.985926
OIKAN	coil2000 (9822 × 85)	0.909	0.892	0.900
ElasticNet		0.937405	0.892946	0.910041
XGBoost		0.926209	0.896749	0.909317
DecisionTree		0.887023	0.89294	0.889946

). While the model reached perfect scores on several datasets and demonstrated competitive results in the top-10 benchmarks, for instance, an accuracy of 0.975 with equally high precision and F1 values, its overall performance distribution was broader, with median values trailing behind the baselines. ElasticNet and DecisionTree both achieved accuracies of around 0.94, with strong precision and F1 values, while XGBoost consistently outperformed all models, approaching 0.97 across metrics.

In regression tasks, OIKAN reached a median R² of 0.705, a mean absolute percentage error of 3.33, and a root mean squared error of 22.77 (

Table 13. Comparative Performance of OIKAN and Baseline Models on Regression Datasets.

Model	Dataset	RMSE	R2	MAPE
OIKAN	1027_ESL (488 × 4)	1.141872	0.170539	0.192851
ElasticNet		0.781992	0.610985	0.140495
XGBoost		0.639834	0.739567	0.092441
DecisionTree		0.707947	0.681167	0.092292
OIKAN	192_vineyard (632 × 4)	2.694328	0.611247	0.125973
ElasticNet		2.454929	0.677262	0.148458
XGBoost		3.013396	0.513721	0.169473
DecisionTree		4.012056	0.138001	0.217817
OIKAN	225_puma8NH (8192 × 8)	5.878939	-0.11466	1.53969
ElasticNet		4.66571	0.29793	2.446583
XGBoost		3.503805	0.604064	3.433912
DecisionTree		4.642225	0.30498	3.676655
OIKAN	197_cpu_act (8192 × 21)	1.19 × 1011	−4.8 × 1019	1.67 × 1024
ElasticNet		8.917987	0.734598	4.3 × 1015
XGBoost		2.482231	0.979438	8.13 × 1013
DecisionTree		3.518798	0.95868	1.37 × 1013
OIKAN	215_2dplanes (40k × 10)	2.16976	0.753329	2.666862
ElasticNet		3.211894	0.459474	2.692004
XGBoost		1.018963	0.945598	1.315541
DecisionTree		1.370601	0.901573	1.936285
OIKAN	229_pwLinear (10k × 10)	1.657709	0.8018	0.639679
ElasticNet		2.434435	0.572552	0.766036
XGBoost		1.846041	0.754207	0.644108
DecisionTree		2.413889	0.579736	0.829767

). Although it attained R² values above 0.8 on multiple datasets and peaked at 0.82, its variability across datasets was pronounced, particularly in error measures where extreme outliers appeared. ElasticNet provided slightly stronger regression performance with an R² of 0.64 and lower error rates, whereas DecisionTree occupied a middle ground with an R² of 0.80. XGBoost again proved the most effective, delivering an R² of 0.92 alongside consistently low error values.

4.4. Interpretability Assessment

Beyond predictive performance, experiments conducted on the PMLB benchmark datasets revealed that the complexity of OIKAN grows proportionally with the dimensionality of the data. As the number of features increases, the model faces increasing difficulty in extracting compact symbolic formulas. This challenge is further amplified by the architecture’s dual ElasticNet application and the use of data augmentation strategies. Augmentation increases the number of samples, while polynomial and interaction terms expand the feature space, causing the computational complexity to grow rapidly with the number of features. Although additional symbolic functions, such as trigonometric or logarithmic bases, are also included, their contribution to the overall complexity is negligible compared to the quadratic growth caused by feature expansion. To address system limitations and ensure stable execution on the Kaggle platform, datasets exceeding 600 MB were excluded from the benchmarking process; this threshold was experimentally determined to prevent CPU and RAM overload. The experiments further demonstrated that the number of features had a stronger impact on model complexity, and consequently on runtime and memory usage, than the number of samples, due to the quadratic asymptotic behavior. Additionally, the final architecture exhibited poor performance on several small datasets, which, combined with the suboptimal performance of state-of-the-art models on the same datasets, suggests that noise and a lack of clear internal structure limited the ability to detect predictive patterns.

According to the results of benchmark scores on PMLB datasets, classification models showed good performance, while regression models have difficulties generalizing and predicting unseen values. To demonstrate OIKAN’s performance on a real case, an example of credit risk assessment in the financial industry was taken, where the classification of a client’s credit ability gives permission or refusal to a client to obtain a loan. In this case, it is crucial to ensure a high level of interpretability and explainability of the model to justify the acceptance or rejection of a client’s loan application. To evaluate the performance and interpretability of OIKAN under various conditions, three experiments were conducted using different sets of parameters. The quantitative comparison of OIKAN and XGBoost on the credit score dataset is presented in

Table 14. Quantitative Comparison of OIKAN and XGBoost on Credit Score.

Model & Parameters	Training Time (Total)	Weighted F1-Score	Accuracy	Formula
OIKANClassifier (with 5× Data Augmentation)	30m 47s	0.47	0.56	Yes
OIKANClassifier (without Data Augmentation)	2.8 s	0.63	0.64	Yes
XGBClassifier	4.5 s	0.75	0.75	No

below.

In terms of credit rating classification (multi-classification: “good,” “poor,” “standard”), OIKAN performed better without data augmentation than with augmentation (Figure 5). This is because the accuracy of the neural network’s predictions was low, and instead of generalizing the training data, TabularNet reduced the quality of the data by increasing the number of misclassified results, which worsened the performance of the final model. Therefore, it is worth noting that data augmentation does not always help and can even worsen results. The performance of the OIKAN model (0.64 accuracy & 0.63 f1-score) without data augmentation showed satisfactory results, comparatively worse than one of the best classification models, XGBoost (0.75 accuracy & 0.75 f1-score). At the same time, OIKAN showed higher interpretability, providing formulas (in various formats: “standard”, “sympy”, “LaTeX”) that can be used to obtain current values, as well as analyzing formulas to provide data on the significance of features on the result. The same formulas cannot be obtained by XGBoost, because it requires a large tree ensemble that very challenging to reproduce as a formula. In terms of training time, OIKAN without data augmentation shows the best time of 2.8 s which was smaller than the same experiment with XGBoost.

Taken together, these findings suggest that OIKAN is capable of producing highly accurate or even perfect results on select datasets but exhibits greater variability and generally lower median performance than the baselines. This reflects the trade-off between predictive accuracy and interpretability: while ElasticNet, DecisionTree, and XGBoost achieve stronger and more stable results, OIKAN uniquely provides symbolic formulas that make its predictions transparent and explainable. This interpretability positions OIKAN as a valuable tool for research contexts where analytical insight and transparency are prioritized alongside accuracy. Additional details of the benchmarking setup and the updated results are provided in Appendix A.

5. Discussion and Conclusions

OIKAN is a novel neuro-symbolic framework that seamlessly integrates deep learning with symbolic inference to produce interpretable models for both classification and regression: a KAN-augmented MLP first learns robust feature representations (with optional Gaussian noise augmentation), then a two-stage sparse symbolic regression, ElasticNet selection, followed by non-linear basis fitting, distills them into concise, human-readable formulas. Fully Scikit-learn-compatible and exportable to JSON, it balances neural-network accuracy with symbolic clarity for real-time and embedded use.

The framework was rigorously evaluated across format enable seamless integration and cross-platform deployment, supporting implementation in languages such as Python, C++, and Rust.a comprehensive set of 60 classification and 58 regression tasks from the Penn Machine Learning Benchmarks (PMLB). The classification component, OIKANClassifier, demonstrated excellent generalization capabilities, achieving a median accuracy of 0.886 and perfect performance (accuracy = 1.000) on symbolically or linearly separable datasets such as iris, mushroom, and corral. In regression tasks, the OIKANRegressor achieved a median R² score of 0.705, with peak performance on datasets featuring analytical structure, such as 344_mv (R² = 0.992) and 2dplanes (R² = 0.937). These results highlight OIKAN’s ability to extract symbolic representations of data with high fidelity, making it especially suitable for scientific discovery tasks.

OIKAN also proved to be computationally efficient and scalable. The median training time for classification tasks was approximately 4.9 s, and 3.5 s for regression. Prediction times were consistently low (median: <0.01 s), and memory usage during inference remained minimal (median: <0.072 MB), demonstrating the framework’s suitability for real-time and embedded applications.

OIKAN demonstrates unique advantages in interpretability and transparency. Unlike black-box approaches such as boosted trees or neural ensembles, OIKAN generates sparse mathematical expressions in closed form, enabling direct validation, testing, and transfer between programming environments. This feature makes OIKAN particularly suitable for domains where explainability and reproducibility are critical. In addition, its lightweight training and inference footprints make it well-suited for deployment in real-time systems and embedded devices, while its capacity to produce human-readable formulas facilitates debugging, regulatory compliance, and the generation of scientific insights.

Although the DecisionTree model also offers interpretability and reusability, it produces tree-based conditional structures rather than explicit mathematical formulas. This key difference positions OIKAN as a framework that prioritizes understanding and symbolic clarity, even at the cost of reduced predictive performance, particularly in datasets lacking a compact symbolic structure. These findings reaffirm the well-established trade-off between accuracy and interpretability, suggesting that OIKAN should be viewed not as a competitor to high-accuracy black-box models but as a complementary approach for tasks where transparency and symbolic reasoning are paramount.

Building on these results, OIKAN also exhibited notable limitations on datasets characterized by high dimensionality, noise, or non-symbolic relationships (e.g., mfeat_factors, parity5, cpu_act), where performance dropped significantly. These observations highlight the importance of enhancing the model’s robustness, for example, through adaptive regularization, an expanded library of base functions, and refined augmentation strategies to better handle noisy or unstructured data.

Performance can degrade on very large datasets with more than 50 K samples due to heavier basis selection and expression fitting; in high-dimensional spaces exceeding 100 features, sparsity tends to decrease and expressions grow longer, hindering readability. On predominantly linear relationships, ElasticNet often matches or exceeds accuracy with simpler linear forms. Sensitivity to feature and label noise can inflate the learned basis and reduce fidelity, and severe class imbalance can diminish classification quality without dedicated mitigation.

Taken together, these findings emphasize both the strengths and limitations of the current OIKAN implementation. On one hand, the framework provides interpretable symbolic models and flexible configuration parameters, such as evaluate_nn and augmentation_factor, which support targeted experimentation and reproducibility. On the other hand, its sensitivity to feature dimensionality and data noise points to the need for greater scalability and stability.

Looking ahead, future enhancements will focus on addressing these limitations through architectural optimization, integration of ensemble and attention-based symbolic components, and deeper exploration of symbolic feature selection methods. Furthermore, improving the framework’s scalability and robustness on large, high-dimensional datasets will be critical for broader applicability. Moreover, future research directions include evaluating extended symbolic basis sets and implementing more advanced hyperparameter optimization strategies to further enhance both performance and interpretability across diverse datasets. Overall, OIKAN represents a significant advancement in interpretable machine learning. By merging symbolic reasoning with neural representations, it delivers a practical, flexible, and interpretable solution for tasks requiring transparency and analytical insight, particularly in fields such as scientific modeling, healthcare diagnostics, and engineering design.