Binary Differential Evolution with a Limited Maximum Number of Dimension Changes
Abstract
1. Introduction
2. Current State of the Research Field
3. Proposed Algorithm
| Algorithm 1: NBDE Pseudocode |
| 1 Set parameters 2 Initialize Population 3 for iteration in range(MAX_EVAL) 4 for i in range(POP_SIZE): 5 Randomly select one individual from population ≠ i 6 Create v as a copy of i 7 Set ; 8 Select num_dim random dimensions j from the food source using a uniform distribution; 9 for each selected dimension j do: 10 if v[j] ≠ x_r1[j] 11 v[j] x_r1[j] 12 end 13 else 14 v[j] x_r1[j] 15 end 16 end 17 Create u as the result of the crossover between v and i 18 Apply selection between u and 19 end 20 end |
4. Materials and Methods
4.1. Selected Algorithms
4.2. Selected Problems
4.3. Data Generation Procedure
4.4. Parameter Configuration
4.5. Sensitivity Analysis Methodologic Procedures
4.6. Complexity Analysis Methodologic Procedures
5. Results and Discussion
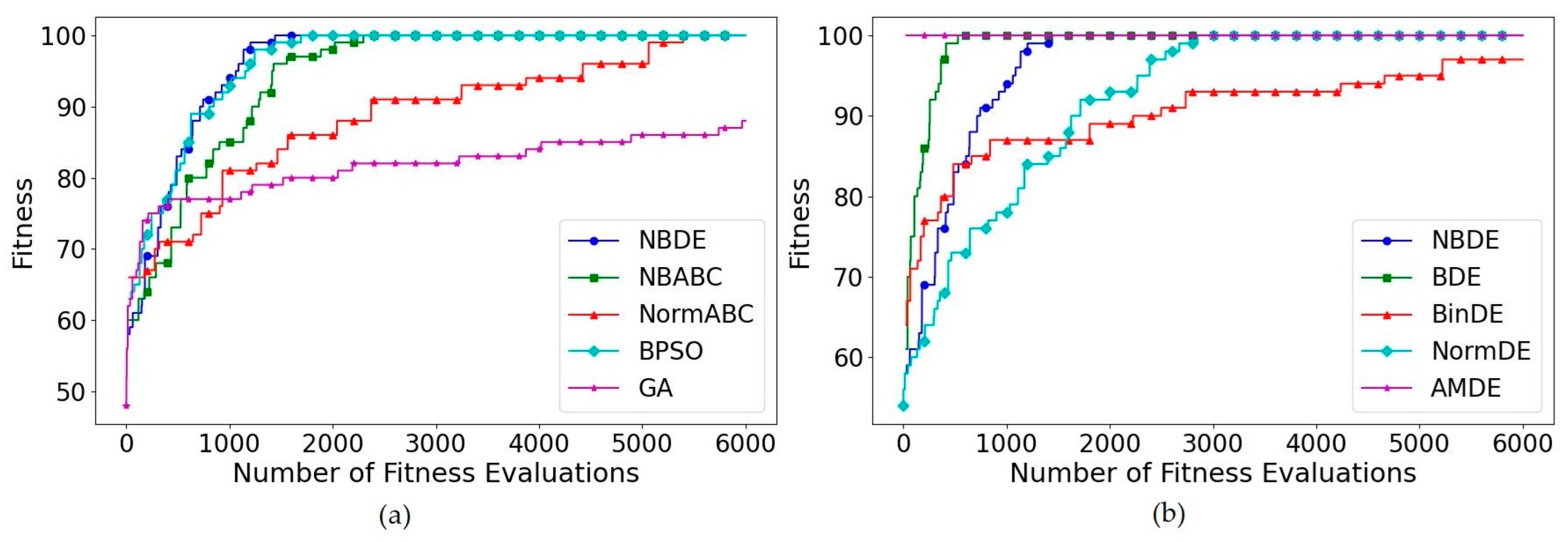
5.1. OneMax Problem
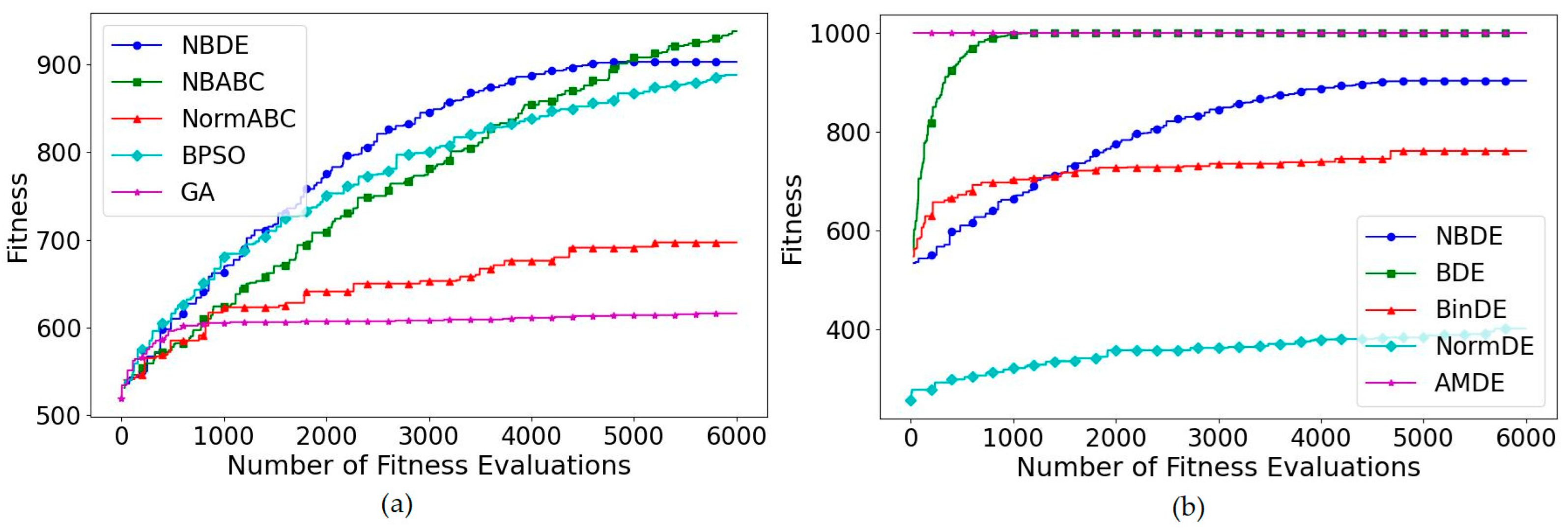
5.2. Knapsack Problem
5.3. Multidimensional Knapsack Problem
5.4. Multiple Knapsack Problem
5.5. Multiple Choice Knapsack Problem
5.6. Subset Sum Problem
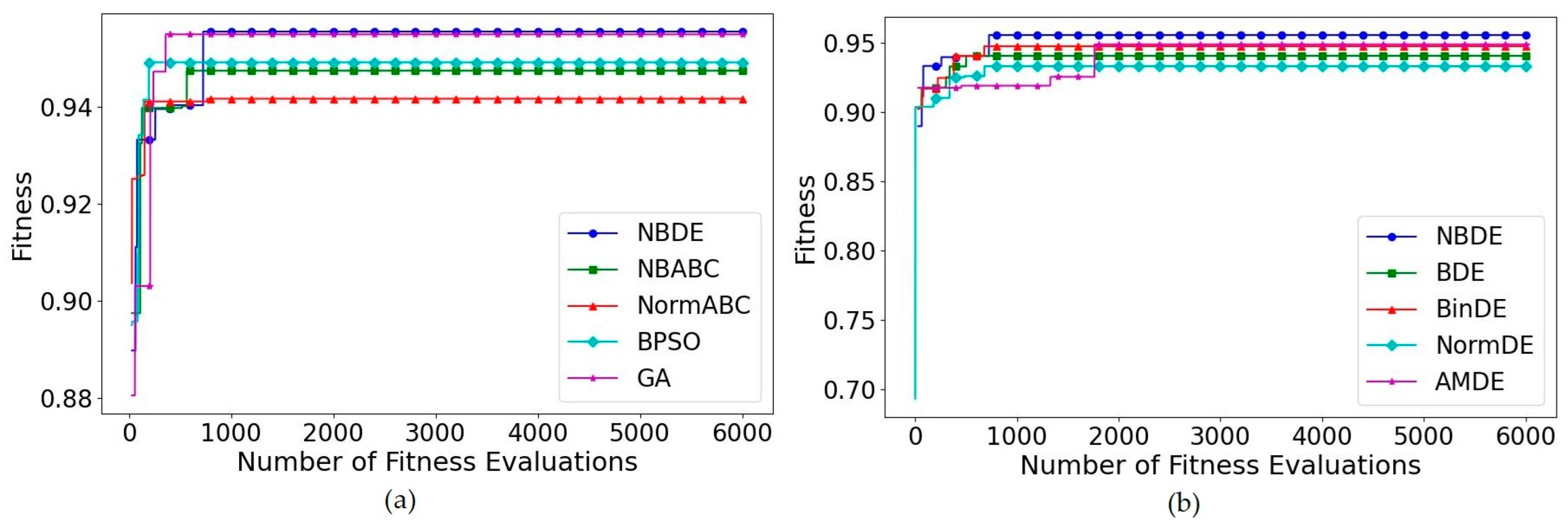
5.7. Feature Selection Problem
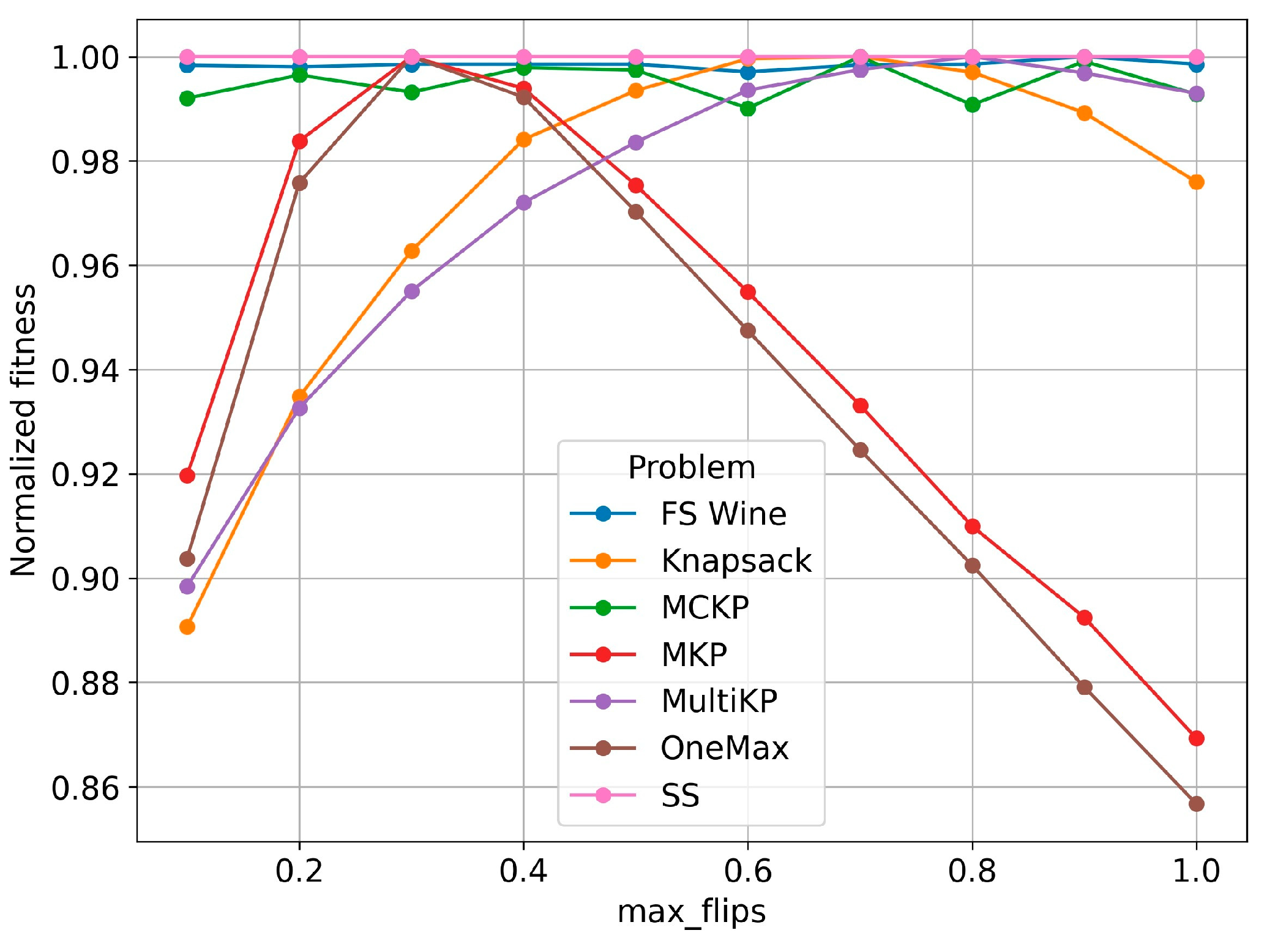
5.8. Sensitivity Analysis
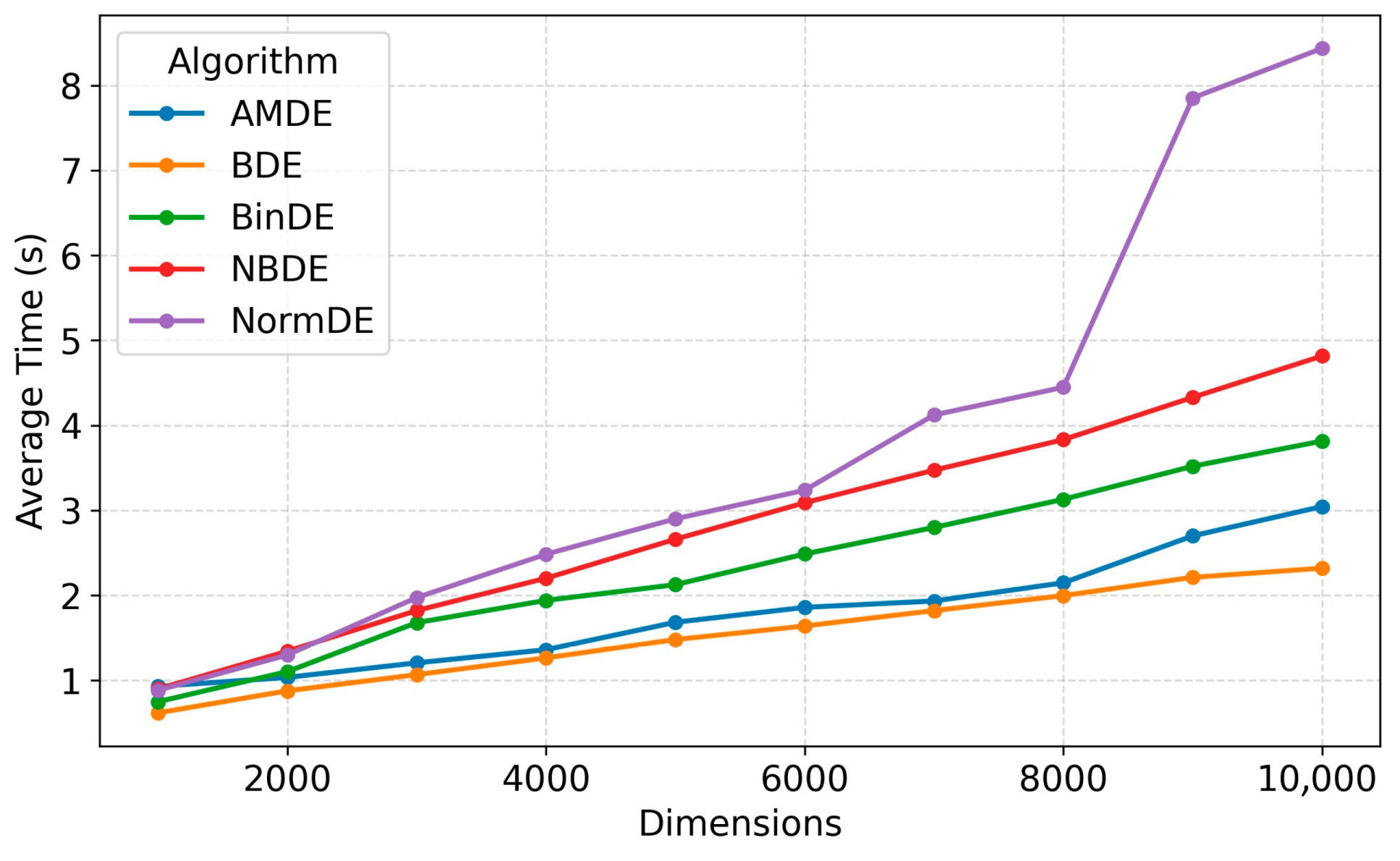
5.9. Complexity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMDE | Angle-Modulated Differential Evolution |
| BinDE | Binary DE |
| BDE | Binary Differential Evolution |
| BPSO | Binary Particle Swarm Optimization |
| CA | Complexity Analysis |
| DE | Differential Evolution |
| EAs | Evolutionary algorithms |
| EC | Evolutionary Computing |
| FS | Feature Selection |
| GA | Genetic Algorithm |
| KP | Knapsack Problem |
| KNN | K-Nearest Neighbours |
| MultiKP | Multidimensional Knapsack Problem |
| MKP | Multiple Knapsack Problem |
| MCKP | Multiple-Choice Knapsack Problem |
| NBABC | Novel Binary Artificial Bee colony Algorithm |
| NBDE | Binary Differential Evolution with a limited maximum number of dimension changes |
| NormABC | Normalized Binary Artificial Bee Colony |
| NormDE | Normalization DE |
| PSO | Particle Swarm Optimization |
| PEOs | Probability Estimator Operators |
| SA | Sensitivity Analysis |
| SS | Subset Sum |
References
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing, 2nd ed.; Springer: Amsterdam, The Netherlands, 2015. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Ali, I.M.; Essam, D.; Kasmarik, K. Novel binary differential evolution algorithm for knapsack problems. Inf. Sci. 2021, 542, 177–194. [Google Scholar] [CrossRef]
- He, X.; Han, L. A novel binary differential evolution algorithm based on artificial immune system. In Proceedings of the IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007. [Google Scholar] [CrossRef]
- Wang, L.; Pan, Q.-K.; Suganthan, P.N.; Wang, W.-H.; Wang, Y.-M. A novel hybrid discrete differential evolution algorithm for blocking flow shop scheduling problems. Comput. Oper. Res. 2010, 37, 509–520. [Google Scholar] [CrossRef]
- Fan, G.-M.; Huang, H.-J. A novel binary differential evolution algorithm for a class of fuzzy-stochastic resource allocation problems. In Proceedings of the 13th IEEE International Conference on Control & Automation, Ohrid, North Macedonia, 3–6 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 548–553. [Google Scholar] [CrossRef]
- He, Z.; Xiao, L.; Huo, Z.; Wang, T.; Wang, X. Fast minimization of fixed polarity Reed-Muller expressions. IEEE Access 2019, 7, 24843–24851. [Google Scholar] [CrossRef]
- He, Y.; Zhang, F.; Mirjalili, S.; Zhang, T. Novel binary differential evolution algorithm based on taper-shaped transfer functions for binary optimization problems. Swarm Evol. Comput. 2022, 69, 101022. [Google Scholar] [CrossRef]
- Wang, P.; Xue, B.; Liang, J.; Zhang, M. Feature selection using diversity-based multi-objective binary differential evolution. Inf. Sci. 2023, 626, 586–606. [Google Scholar] [CrossRef]
- Santana, C.J.; Macedo, M.; Siqueira, H.; Gokhale, A.; Bastos-Filho, C.J.A. A novel binary artificial bee colony algorithm. Future Gener. Comput. Syst. 2019, 98, 180–196. [Google Scholar] [CrossRef]
- Wu, C.Y.; Tseng, K.Y. Engineering optimization using modified binary differential evolution algorithm. In Proceedings of the 3rd International Joint Conference on Computational Sciences and Optimization (CSO 2010), Huangshan, China, 28–31 May 2010. [Google Scholar] [CrossRef]
- Wang, X.; Guo, P. A novel binary adaptive differential evolution algorithm for Bayesian network learning. In Proceedings of the 8th International Conference on Natural Computation, Chongqing, China, 29–31 May 2012. [Google Scholar] [CrossRef]
- Li, H.; Zhang, L. Solving linear bilevel programming problems using a binary differential evolution. In Proceedings of the 11th International Conference on Computational Intelligence and Security, Shenzhen, China, 19–20 December 2015. [Google Scholar] [CrossRef]
- Banitalebi, A.; Aziz, M.I.A.; Aziz, Z.A. A self-adaptive binary differential evolution algorithm for large scale binary optimization problems. Inf. Sci. 2016, 367–368, 487–511. [Google Scholar] [CrossRef]
- Xuan, M.; Li, L.; Lin, Q.; Ming, Z.; Wei, W. A modified decomposition-based multi-objective optimization algorithm for high dimensional feature selection. In Proceedings of the 7th IEEE International Conference on Cloud Computing and Intelligence Systems, Beijing, China, 26–27 June 2021. [Google Scholar] [CrossRef]
- Wei, W.; Xuan, M.; Li, L.; Lin, Q.; Ming, Z.; Coello Coello, C.A. Multiobjective optimization algorithm with dynamic operator selection for feature selection in high-dimensional classification. Appl. Soft Comput. 2023, 143, 110360. [Google Scholar] [CrossRef]
- Deng, C.S.; Zhao, B.Y.; Deng, A.Y.; Liang, C.Y. Hybrid-coding binary differential evolution algorithm with application to 0–1 knapsack problems. In Proceedings of the International Conference on Computer Science and Software Engineering (CSSE), Wuhan, China, 12–14 December 2008. [Google Scholar] [CrossRef]
- Xie, W.; Chi, Y.; Wang, L.; Yu, K.; Li, W. MMBDE: A two-stage hybrid feature selection method from microarray data. In Proceedings of the IEEE International Conference on Bioinformatics and Biomedicine, Houston, TX, USA, 9–12 December 2021. [Google Scholar] [CrossRef]
- He, X.; Zhang, Q.; Sun, N.; Dong, Y. Feature selection with discrete binary differential evolution. In Proceedings of the International Conference on Artificial Intelligence and Computational Intelligence (AICI), Shanghai, China, 7–8 November 2009. [Google Scholar] [CrossRef]
- Krause, J.; Lopes, H.S. A comparison of differential evolution algorithm with binary and continuous encoding for the MKP. In Proceedings of the BRICS Congress on Computational Intelligence and Brazilian Congress on Computational Intelligence (BRICS-CCI-CBIC), Ipojuca, Brazil, 8–11 September 2013. [Google Scholar] [CrossRef]
- Pampará, G.; Engelbrecht, A.P.; Franken, N. Binary differential evolution. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 16–21 July 2006. [Google Scholar]
- Engelbrecht, A.P.; Pampará, G. Binary differential evolution strategies. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Singapore, 25–28 September 2007. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), Orlando, FL, USA, 12–15 October 1997. [Google Scholar] [CrossRef]
- Parija, S.R.; Sahu, P.K.; Singh, S.S. Differential evolution for cost reduction in cellular network. In Proceedings of the International Conference on High Performance Computing and Applications (ICHPCA), Bhubaneswar, India, 22–24 December 2014. [Google Scholar] [CrossRef]
- Dhaliwal, J.S.; Dhillon, J.S. A binary differential evolution based memetic algorithm to solve profit based unit commitment problem. In Proceedings of the Power India International Conference (PIICON), Kurukshetra, India, 20–22 December 2018. [Google Scholar] [CrossRef]
- Gao, T.; Li, H.; Gong, M.; Zhang, M.; Qiao, W. Superpixel-based multiobjective change detection based on self-adaptive neighborhood-based binary differential evolution. Expert Syst. Appl. 2023, 212, 118811. [Google Scholar] [CrossRef]
- Bidgoli, A.A.; Ebrahimpour-Komleh, H.; Rahnamayan, S. A novel multi-objective binary differential evolution algorithm for multi-label feature selection. In Proceedings of the IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019. [Google Scholar] [CrossRef]
- Li, T.; Dong, H.; Sun, J. Binary differential evolution based on individual entropy for feature subset optimization. IEEE Access 2019, 7, 24109–24121. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, H.; Chen, W.; Xu, L.; Li, C.; Feng, Q. Near infrared feature waveband selection for fishmeal quality assessment by frequency adaptive binary differential evolution. Chemom. Intell. Lab. Syst. 2021, 217, 104393. [Google Scholar] [CrossRef]
- Chen, Y.; Xie, W.; Zou, X. A binary differential evolution algorithm learning from explored solutions. Neurocomputing 2015, 149, 1038–1047. [Google Scholar] [CrossRef]
- Zhang, L.; Li, H. BPSOBDE: A binary version of hybrid heuristic algorithm for multidimensional knapsack problems. In Proceedings of the 13th International Conference on Computational Intelligence and Security, Hong Kong, China, 15–17 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 54–58. [Google Scholar] [CrossRef]
- Pampara, G.; Engelbrecht, A.P. Binary artificial bee colony optimization. In Proceedings of the IEEE Symposium on Swarm Intelligence, Paris, France, 11–15 April 2011. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Ackley, D.H. A Connectionist Machine for Genetic Hillclimbing; Kluwer Academic Publishers: Boston, MA, USA, 1987. [Google Scholar]
- Xu, J.; Li, H.; Yin, M. Finding and exploring promising search space for the 0–1 multidimensional knapsack problem. Appl. Soft Comput. 2024, 164, 111934. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Delorme, M.; Iori, M.; Martello, S. Mathematical models and decomposition methods for the multiple knapsack problem. Eur. J. Oper. Res. 2019, 274, 886–899. [Google Scholar] [CrossRef]
- Lai, T.-C. Worst-case analysis of greedy algorithms for the unbounded knapsack, subset-sum and partition problems. Theor. Comput. Sci. 1993, 123, 215–220. [Google Scholar] [CrossRef]
- Zhong, T.; Young, R. Multiple choice knapsack problem: Example of planning choice in transportation. Eval. Program Plann. 2010, 33, 128–137. [Google Scholar] [CrossRef] [PubMed]
- Liao, C.; Yang, B. A novel multi-label feature selection method based on conditional entropy and its acceleration mechanism. Int. J. Approx. Reason. 2025, 185, 109469. [Google Scholar] [CrossRef]
- Google OR-Tools. Linear Solver Wrapper (CBC). Available online: https://developers.google.com/optimization/reference/python/linear_solver/pywraplp (accessed on 16 July 2025).
- Rojas, I.; González, J.; Pomares, H.; Merelo, J.; Castillo, P.; Romero, G. Statistical analysis of the main parameters involved in the design of a genetic algorithm. IEEE Trans. Syst. Man Cybern.—Part C Appl. Rev. 2002, 32, 31–37. [Google Scholar] [CrossRef]
- Weisberg, S. Applied Linear Regression, 4th ed.; Wiley: Hoboken, NJ, USA, 2014; ISBN 978-1-118-38608-8. [Google Scholar]
- Giannelos, S.; Zhang, T.; Pudjianto, D.; Konstantelos, I.; Strbac, G. Investments in electricity distribution grids: Strategic versus incremental planning. Energies 2024, 17, 2724. [Google Scholar] [CrossRef]
- Siqueira, H.; Boccato, L.; Attux, R.; Lyra Filho, C. Echo State Networks for Seasonal Streamflow Series Forecasting. In Intelligent Data Engineering and Automated Learning—IDEAL 2012. Lecture Notes in Computer Science; Yin, H., Costa, J.A.F., Barreto, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7435, pp. 222–229. [Google Scholar] [CrossRef]
- Castanho, M.J.P.; Lima, D.S.; Veiga, L.M.S.; Filho, M.C.F.; Neto, E.A.B.; Silva, I.N. Performance Evaluation of Bio-Inspired Algorithms in the Calibration of Linear Models for SoC Estimation in Li-Ion Batteries. Algorithms 2022, 15, 415. [Google Scholar] [CrossRef]
| Dataset | Instances | Features |
|---|---|---|
| Wine | 178 | 13 |
| Vehicle Silhouettes | 846 | 18 |
| Ionosphere | 351 | 34 |
| German Credit Data | 1000 | 20 |
| Breast Cancer Wisc. | 569 | 30 |
| Musk1 | 476 | 166 |
| Dimension | NBDE | NBABC | BPSO | NormABC | GA | binDE | NormDE | AMDE | BDE | |
|---|---|---|---|---|---|---|---|---|---|---|
| 100 | Fitness | 99.6 ± 0.6 | 100.0 ± 0.0 | 100.0 ± 0.0 | 98.4 ± 1.5 | 94.4 ± 2.1 | 94.6 ± 0.9 | 100.0 ± 0.0 | 100.0 ± 0.0 | 100.0 ± 0.0 |
| Wilcoxon | - | < | < | > | > | > | < | < | < | |
| Time | 1.0 ± 0.0 | 0.6 ± 0.0 | 2.4 ± 0.2 | 0.8 ± 0.1 | 0.1 ± 0.0 | 0.5 ± 0.1 | 0.5 ± 0.0 | 0.9 ± 0.0 | 0.4 ± 0.0 | |
| 500 | Fitness | 470.8 ± 5.1 | 497.8 ± 1.2 | 479.0 ± 4.1 | 377.4 ± 4.7 | 368.2 ± 7.7 | 396.7 ± 3.8 | 392.7 ± 5.4 | 500.0 ± 0.0 | 499.8 ± 0.4 |
| Wilcoxon | - | < | < | > | > | > | > | < | < | |
| Time | 3.1 ± 0.1 | 0.9 ± 0.0 | 10.9 ± 0.3 | 0.9 ± 0.0 | 0.1 ± 0.0 | 0.9 ± 0.0 | 0.7 ± 0.0 | 1.0 ± 0.0 | 0.5 ± 0.0 | |
| 1000 | Fitness | 895.4 ± 7.9 | 926.6 ± 6.8 | 873.2 ± 7.6 | 684.9 ± 7.1 | 663.8 ± 12.3 | 746.9 ± 4.2 | 694.8 ± 6.5 | 1000.0 ± 0.0 | 999.7 ± 0.6 |
| Wilcoxon | - | < | > | > | > | > | > | < | < | |
| Time | 5.9 ± 0.3 | 1.1 ± 0.0 | 21.9 ± 0.2 | 1.0 ± 0.0 | 0.1 ± 0.0 | 1.4 ± 0.5 | 1.0 ± 0.0 | 1.1 ± 0.0 | 0.6 ± 0.0 | |
| Dimension | NBDE | NBABC | BPSO | NormABC | GA | binDE | NormDE | AMDE | BDE | |
|---|---|---|---|---|---|---|---|---|---|---|
| 100 | Fitness | 11,985.4 ± 69.1 | 11,721.3 ± 76.4 | 11,823.8 ± 59.9 | 11,053.2 ± 115.7 | 10,506.4 ± 299.2 | 10,594.7 ± 132.8 | 11,577.7 ± 97.2 | 9393.0 ± 205.93 | 11,626.3 ± 153.24 |
| Wilcoxon | - | > | > | > | > | > | > | > | > | |
| Time | 1.32 ± 0.2 | 0.74 ± 0.1 | 2.47 ± 0.1 | 0.85 ± 0.0 | 0.16 ± 0.0 | 0.5 ± 0.0 | 0.62 ± 0.0 | 0.93 ± 0.0 | 0.53 ± 0.1 | |
| 500 | Fitness | 61,321.9 ± 490.9 | 57,798.6 ± 507.7 | 59,731.829 ± 520.5 | 51,992.9 ± 623.3 | 50,465.0 ± 1060.1 | 48,991.5 ± 534.4 | 53,127.1 ± 563.1 | 46,378.9 ± 617.1 | 45,769.6 ± 740.7 |
| Wilcoxon | - | > | > | > | > | > | > | > | > | |
| Time | 3.2 ± 0.2 | 0.94 ± 0.0 | 11.6 ± 0.4 | 0.9 ± 0.0 | 0.2 ± 0.0 | 0.6 ± 0.0 | 0.8 ± 0.0 | 1.0 ± 0.0 | 0.8 ± 0.2 | |
| 1000 | Fitness | 115,132.9 ± 860.4 | 107,356.2 ± 874.6 | 11,162.3 ± 1093.1 | 97,138.5 ± 672.9 | 94,388.3 ± 1597.9 | 90,167.0 ± 958.1 | 98,503.1 ± 718.7 | 87,811.3 ± 781.1 | 86,194.3 ± 1011.3 |
| Wilcoxon | - | > | > | > | > | > | > | > | ||
| Time | 5.5 ± 0.1 | 1.3 ± 0.0 | 23.4 ± 1.1 | 1.1 ± 0.0 | 0.2 ± 0.0 | 0.7 ± 0.1 | 1 ± 0.0 | 1.2 ± 0.0 | 0.8 ± 0.1 | |
| Dimension | NBDE | NBABC | BPSO | NormABC | GA | binDE | NormDE | AMDE | BDE | |
|---|---|---|---|---|---|---|---|---|---|---|
| 100 | Fitness | 3854.8 ± 25.9 | 3773.6 ± 35.3 | 3820.9 ± 32.2 | 3527.9 ± 54.2 | 3302.4 ± 121.5 | 3336.7 ± 45.2 | 3680.5 ± 40.1 | 2996.1 ± 60.8 | 3479.7 ± 102.5 |
| Wilcoxon | - | > | > | > | > | > | > | > | > | |
| Time | 1.4 ± 0.1 | 0.8 ± 0.0 | 2.9 ± 0.5 | 0.9 ± 0.0 | 0.2 ± 0.0 | 0.6 ± 0.1 | 0.7 ± 0.0 | 1.0 ± 0.0 | 0.5 ± 0.0 | |
| 500 | Fitness | 19,459.6 ± 148.9 | 18,180.0 ± 198.2 | 19,021.1 ± 173.6 | 16,578.6 ± 196.1 | 15,994.1 ± 408.1 | 15,496.8 ± 177.05 | 16,883.4 ± 203.4 | 14,867.9 ± 146.6 | 14,630.0 ± 273.8 |
| Wilcoxon | - | > | > | > | > | > | > | > | > | |
| Time | 3.7 ± 0.7 | 1.1 ± 0.1 | 11.8 ± 0.2 | 1.0 ± 0.1 | 0.2 ± 0.0 | 0.8 ± 0.0 | 0.9 ± 0.1 | 1.2 ± 0.1 | 0.1 ± 0.1 | |
| 1000 | Fitness | 35,906.2 ± 293.5 | 33,552.0 ± 304.1 | 35,143.3 ± 258.2 | 31,318.1 ± 261.3 | 30,694.4 ± 460.4 | 29,248.4± 264.1 | 31,685.1 ± 221.9 | 29,145.6 ± 215.3 | 28,427.6 ± 348.2 |
| Wilcoxon | - | > | > | > | > | > | > | > | > | |
| Time | 5.6 ± 0.2 | 1.4 ± 0.1 | 23.1 ± 0.4 | 1.2 ± 0.1 | 0.3 ± 0.0 | 1.0 ± 0.1 | 1.1 ± 0.1 | 1.3 ± 0.1 | 0.8 ± 0.1 | |
| Dimension | NBDE | NBABC | BPSO | NormABC | GA | binDE | NormDE | AMDE | BDE | |
|---|---|---|---|---|---|---|---|---|---|---|
| 100 | Fitness | 15,850.5 ± 65.0 | 15,898.6 ± 0.8 | 15,896.6 ± 5.4 | 15,484.2 ± 202.7 | 15,117.7 ± 243.9 | 15,252.8 ± 133.1 | 15,898.8 ± 0.4 | 15,873.6 ± 9.4 | 15,895.4 ± 7.0 |
| Wilcoxon | - | < | < | > | > | > | < | < | < | |
| Time | 1.9 ± 0.1 | 1.5 ± 0.1 | 3.1 ± 0.3 | 1.6 ± 0.1 | 1.0 ± 0.1 | 1.3 ± 0.2 | 1.4 ± 0.1 | 2.0 ± 0.1 | 1.7 ± 0.2 | |
| 500 | Fitness | 82,023.7 ± 727.2 | 85,299.5 ± 235.8 | 83,294.5 ± 506.9 | 66,775.4 ± 803.6 | 65,071.0 ± 1480.2 | 69,330.0 ± 592.8 | 69,242.4 ± 810.2 | 86,040.3 ± 90.8 | 86,195.3 ± 65.5 |
| Wilcoxon | - | < | < | > | > | > | > | < | < | |
| Time | 6.8 ± 0.3 | 4.6 ± 0.2 | 14.1 ± 0.4 | 4.0 ± 0.3 | 3.8 ± 0.2 | 4.5 ± 0.1 | 4.3 ± 0.3 | 6.7 ± 1.0 | 7.0 ± 0.5 | |
| 1000 | Fitness | 152,406.4 ± 1131.4 | 156,937.7 ± 987.7 | 150,174.0 ± 1130.4 | 118,066.7 ± 1266.0 | 114,228.8 ± 1811.5 | 127,659.9 ± 797.6 | 119,080.0 ± 847.5 | 168,043.9 ± 5.1 | 168,114.3 ± 95.5 |
| Wilcoxon | - | < | < | > | > | > | > | < | < | |
| Time | 12.5 ± 0.5 | 7.8 ± 0.2 | 27.9 ± 1.1 | 7.1 ± 0.5 | 6.9 ± 0.2 | 8.4 ± 1.0 | 7.8 ± 0.6 | 11.8 ± 0.6 | 14.0 ± 0.9 | |
| Dimension | NBDE | NBABC | BPSO | NormABC | GA | binDE | NormDE | AMDE | BDE | |
|---|---|---|---|---|---|---|---|---|---|---|
| 100 | Fitness | 1351.5 ± 36.12 | 1352.4 ± 40.48 | 1362.2 ± 40.70 | 1356.7 ± 45.97 | 1028.9 ± 135.20 | 1351.9 ± 41.35 | 1348.5 ± 39.73 | 1336.3 ± 39.20 | 1354.0 ± 38.38 |
| Wilcoxon | - | - | - | - | > | - | - | > | - | |
| Time | 2.1 ± 0.1 | 1.7 ± 0.0 | 3.8 ± 0.4 | 2.2 ± 0.3 | 1.3 ± 0.0 | 1.7 ± 0.2 | 2.1 ± 0.2 | 2.0 ± 0.1 | 1.7 ± 0.4 | |
| 500 | Fitness | 1373.6 ± 24.7 | 1371.3 ± 23.4 | 1365.3 ± 24.3 | 1370.9 ± 20.6 | 1171.2 ± 83.0 | 1366.1 ± 17.7 | 1376.14 ± 21.9 | 1370.9 ± 23.2 | 1367.3 ± 20.5 |
| Wilcoxon | - | - | - | - | > | - | - | - | - | |
| Time | 3.9 ± 0.2 | 2.0 ± 0.0 | 13.0 ± 0.8 | 2.4 ± 0.2 | 1.3 ± 0.1 | 1.9 ± 0.1 | 2.3 ± 0.2 | 2.1 ± 0.1 | 1.7 ± 0.0 | |
| 1000 | Fitness | 1391.7 ± 20.0 | 1390.5 ± 25.3 | 1384.9 ± 23.8 | 1390.5 ± 26.9 | 1195.9 ± 69.9 | 1385.8 ± 27.5 | 1387.3 ± 24.5 | 1387.5 ± 24.7 | 1381.6 ± 20.9 |
| Wilcoxon | - | - | - | - | > | - | - | > | > | |
| Time | 6.1 ± 0.2 | 2.3 ± 0.1 | 24.6 ± 0.5 | 2.3 ± 0.1 | 1.3 ± 0.0 | 2.1 ± 0.1 | 2.6 ± 0.2 | 2.2 ± 0.1 | 1.8 ± 0.2 | |
| Dimension | NBDE | NBABC | BPSO | NormABC | GA | binDE | NormDE | AMDE | BDE | |
|---|---|---|---|---|---|---|---|---|---|---|
| 100 | Fitness | 1726.0 ± 0.0 | 1726.0 ± 0.0 | 1415.3 ± 663.1 | 1726.0 ± 0.0 | 1725.9 ± 0.4 | 1725.8 ± 0.4 | 1726.0 ± 0.0 | 1725.8 ± 0.5 | 1726.0 ± 0.0 |
| Wilcoxon | - | - | > | - | > | > | - | > | - | |
| Time | 1.0 ± 0.2 | 0.7 ± 0.0 | 2.4 ± 0.1 | 0.8 ± 0.1 | 0.2 ± 0.0 | 0.5 ± 0.1 | 0.6 ± 0.0 | 0.8 ± 0.1 | 0.7 ± 0.1 | |
| 500 | Fitness | 8408.0 ± 0.0 | 8408.0 ± 0.0 | 8407.8 ± 0.4 | 8407.7 ± 0.5 | 8407.8 ± 0.6 | 0 ± 0.0 | 8407.9 ± 0.0 | 8406.3 ± 2.1 | 0.0± 0.0 |
| Wilcoxon | - | - | > | - | > | > | > | > | > | |
| Time | 2.8 ± 0.1 | 1.0 ± 0.1 | 16.3 ± 3.2 | 0.9 ± 0.1 | 0.2 ± 0.0 | 1.0 ± 0.3 | 0.7 ± 0.0 | 1.0 ± 0.1 | 0.8 ± 0.0 | |
| 1000 | Fitness | 17,401.0 ± 0.2 | 17,401.0 ± 0.1 | 0.0 ± 0.0 | 17,023.7 ± 2432.4 | 7307.9 ± 8587.8 | 0.0 ± 0.0 | 17,398.7 ± 2.5 | 17,398.4 ± 3.1 | 0.0 ± 0.0 |
| Wilcoxon | - | - | > | > | > | > | > | > | > | |
| Time | 2.7 ± 0.0 | 1.3 ± 0.0 | 33.1 ± 2.4 | 1.0 ± 0.0 | 0.2 ± 0.0 | 1.2 ± 0.2 | 1.4 ± 0.3 | 1.2 ± 0.2 | 0.8 ± 0.0 | |
| Dataset | NBDE | NBABC | BPSO | NormABC | GA | BinDE | NormDE | AMDE | BDE | |
|---|---|---|---|---|---|---|---|---|---|---|
| Wine | Fitness | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 |
| Wilcoxon | - | - | - | - | - | - | - | - | - | |
| SF | 3.2 ± 0.7 | 3.2 ± 0.7 | 3.3 ± 0.7 | 3.4 ± 0.8 | 3.2 ± 0.9 | 3.2 ± 0.9 | 3.2 ± 0.7 | 3.2 ± 0.7 | 3.4 ± 0.7 | |
| Accuracy | 0.9 ± 0. | 0.9± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 1.0 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | |
| Wilcoxon | - | - | - | - | - | - | < | - | - | |
| Time | 225.0 ± 4.6 | 226.4 ± 4.7 | 220.4 ± 1.4 | 221.0 ± 1.1 | 217.6 ± 1.4 | 229.6 ± 3.0 | 229.0 ± 0.8 | 220.1 ± 2.5 | 222.1 ± 5.6 |
| Dataset | NBDE | NBABC | BPSO | NormABC | GA | BinDE | NormDE | AMDE | BDE | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vehicle Silhouettes | Fitness | 0.7 ± 0.0 | 0.7 ± 0.0 | 0.7 ± 0.0 | 0.7 ± 0.0 | 0.7 ± 0.01 | 0.7 ± 0.001 | 0.7 ± 0.0 | 0.7 ± 0.0 | 0.7 ± 0.0 |
| Wilcoxon | - | < | < | < | - | < | < | > | > | |
| SF | 6.8 ± 0.6 | 6.7 ± 0.76 | 6.2 ± 0.79 | 6.9 ± 0.62 | 6.5 ± 0.7 | 7.0 ± 0.5 | 7.0 ± 0.3 | 6.4 ± 1.9 | 7.1 ± 0.7 | |
| Accuracy | 0.7 ± 0.0 | 0.7 ± 0.0 | 0.7 ± 0.0 | 0.7 ± 0.0 | 0.7± 0.0 | 0.7 ± 0.0 | 0.7 ± 0.0 | 0.7 ± 0.0 | 0.7 ± 0.0 | |
| Wilcoxon | - | > | > | > | > | > | < | > | - | |
| Time | 354.7 ± 5.6 | 344.1 ± 3.4 | 352.0 ± 56.6 | 350.2 ± 10.5 | 338.6 ± 17.3 | 360.1 ± 27.5 | 338.1 ± 7.4 | 337.1 ± 4.7 | 374.8 ± 12.3 |
| Dataset | NBDE | NBABC | BPSO | NormABC | GA | BinDE | NormDE | AMDE | BDE | |
|---|---|---|---|---|---|---|---|---|---|---|
| Ionosphere | Fitness | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.1 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 |
| Wilcoxon | - | < | - | < | > | > | < | > | > | |
| SF | 3.5 ± 0.7 | 3.7 ± 0.7 | 4.0 ± 1.0 | 3.9 ± 0.7 | 5.3 ± 1.6 | 6.8 ± 1.5 | 3.6 ± 0.6 | 3.0 ± 0.5 | 5.7 ± 1.8 | |
| Accuracy | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | |
| Wilcoxon | - | > | > | > | > | > | > | - | > | |
| Time | 292.6 ± 29.0 | 384.6 ± 1.9 | 282.6 ± 6.0 | 287.8 ± 1.9 | 285.0 ± 3.5 | 297.1 ± 41.0 | 289.5 ± 15.9 | 256.1 ± 4.6 | 285.0 ± 7.1 |
| Dataset | NBDE | NBABC | BPSO | NormABC | GA | BinDE | NormDE | AMDE | BDE | |
|---|---|---|---|---|---|---|---|---|---|---|
| German Credit Data | Fitness | 0.8 ± 0.0 | 0.8 ± 0.0 | 0.8 ± 0.0 | 0.8 ± 0.0 | 0.8 ± 0.0 | 0.7 ± 0.0 | 0.8 ± 0.0 | 0.7 ± 0.0 | 0.7 ± 0.0 |
| Wilcoxon | - | > | > | > | > | > | - | > | > | |
| SF | 14.4 ± 2.3 | 16.0 ± 3.03 | 18.7 ± 3.4 | 15.7 ± 2.8 | 19.9 ± 2.8 | 26.0 ± 3.0 | 10.8 ± 1.9 | 10.6 ± 3.7 | 31.6 ± 2.7 | |
| Accuracy | 0.7 ± 0.0 | 0.7 ± 0.0 | 0.9 ± 0.0 | 0.7 ± 0.0 | 0.7 ± 0.0 | 0.7 ± 0.0 | 0.7 ± 0.0 | 0.7 ± 0.0 | 0.7 ± 0.0 | |
| Wilcoxon | - | - | - | - | - | - | - | - | - | |
| Time | 287.5 ± 27.8 | 253.6 ± 12.3 | 263.8 ± 55.5 | 251.0 ± 14.6 | 253.8 ± 43.3 | 239.4 ± 3.5 | 389.6 ± 8.1 | 308.7 ± 9.6 | 248.2 ± 1.7 |
| Dataset | NBDE | NBABC | BPSO | NormABC | GA | BinDE | NormDE | AMDE | BDE | |
|---|---|---|---|---|---|---|---|---|---|---|
| Breast Cancer Wisconsin (Diagnostic) | Fitness | 1.0 ± 0.0 | 1.0 ± 0.0 | 0.9 ± 0.0 | 1.0 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 1.0 ± 0.0 | 0.9 ± 0.0 | 1.0 ± 0.0 |
| Wilcoxon | - | - | > | - | > | > | > | > | - | |
| SF | 3.0 ± 0.0 | 3.0 ± 0.0 | 3.0 ± 0.37 | 3.0 ± 0.0 | 2.9 ± 0.62 | 4.3 ± 0.6 | 3.0 ± 0.1 | 3.6 ± 1.0 | 3.0 ± 0.1 | |
| Accuracy | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | |
| Wilcoxon | - | > | > | - | > | > | - | - | - | |
| Time | 289.9± 14.2 | 282.4 ± 1.6 | 280.6 ± 2.4 | 291.0 ± 5.7 | 302.8 ± 33.2 | 301.2 ± 1.6 | 278.9 ± 6.5 | 274.5 ± 4.4 | 292.2 ± 11.5 |
| Dataset | NBDE | NBABC | BPSO | NormABC | GA | BinDE | NormDE | AMDE | BDE | |
|---|---|---|---|---|---|---|---|---|---|---|
| Musk1 | Fitness | 0.9 ± 0. | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.8 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.8 ± 0.0 |
| Wilcoxon | - | > | > | > | > | > | > | > | > | |
| SF | 59.6 ± 5.3 | 67.9 ± 6.0 | 59.8 ± 6.6 | 66.5 ± 6.5 | 70.5 ± 5.6 | 88.6 ± 6.2 | 28.6 ± 4.7 | 33.3 ± 9.5 | 112.0 ± 6.9 | |
| Accuracy | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.9 ± 0.0 | 0.89 ± 0.0 | 0.8 ± 0.02 | |
| Wilcoxon | - | - | > | - | > | > | < | > | > | |
| Time | 233.9 ± 20.2 | 226.7 ± 1.8 | 231.3 ± 31.0 | 221.5 ± 2.4 | 221.3 ± 2.3 | 231.0 ± 4.4 | 220.1 ± 1.4 | 215.6 ± 3.4 | 242.8 ± 1.8 |
| Algorithm | β |
|---|---|
| AMDE | 0.51 |
| BDE | 0.58 |
| BinDE | 0.7 |
| NBDE | 0.73 |
| NormDE | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filgueira, J.; Antonini Alves, T.; Santana, C.; Converti, A.; Bastos-Filho, C.J.A.; Siqueira, H. Binary Differential Evolution with a Limited Maximum Number of Dimension Changes. Algorithms 2025, 18, 621. https://doi.org/10.3390/a18100621
Filgueira J, Antonini Alves T, Santana C, Converti A, Bastos-Filho CJA, Siqueira H. Binary Differential Evolution with a Limited Maximum Number of Dimension Changes. Algorithms. 2025; 18(10):621. https://doi.org/10.3390/a18100621
Chicago/Turabian StyleFilgueira, Jade, Thiago Antonini Alves, Clodomir Santana, Attilio Converti, Carmelo J. A. Bastos-Filho, and Hugo Siqueira. 2025. "Binary Differential Evolution with a Limited Maximum Number of Dimension Changes" Algorithms 18, no. 10: 621. https://doi.org/10.3390/a18100621
APA StyleFilgueira, J., Antonini Alves, T., Santana, C., Converti, A., Bastos-Filho, C. J. A., & Siqueira, H. (2025). Binary Differential Evolution with a Limited Maximum Number of Dimension Changes. Algorithms, 18(10), 621. https://doi.org/10.3390/a18100621










