Integrating Structured Time-Series Modeling and Ensemble Learning for Strategic Performance Forecasting
Abstract
1. Introduction
2. Related Works
3. Materials and Analysis
3.1. Assumptions and Notations
3.1.1. Assumptions and Justifications
3.1.2. Notations
3.2. Feature Extraction
3.2.1. Characterization 1: Advantage Sport Effect
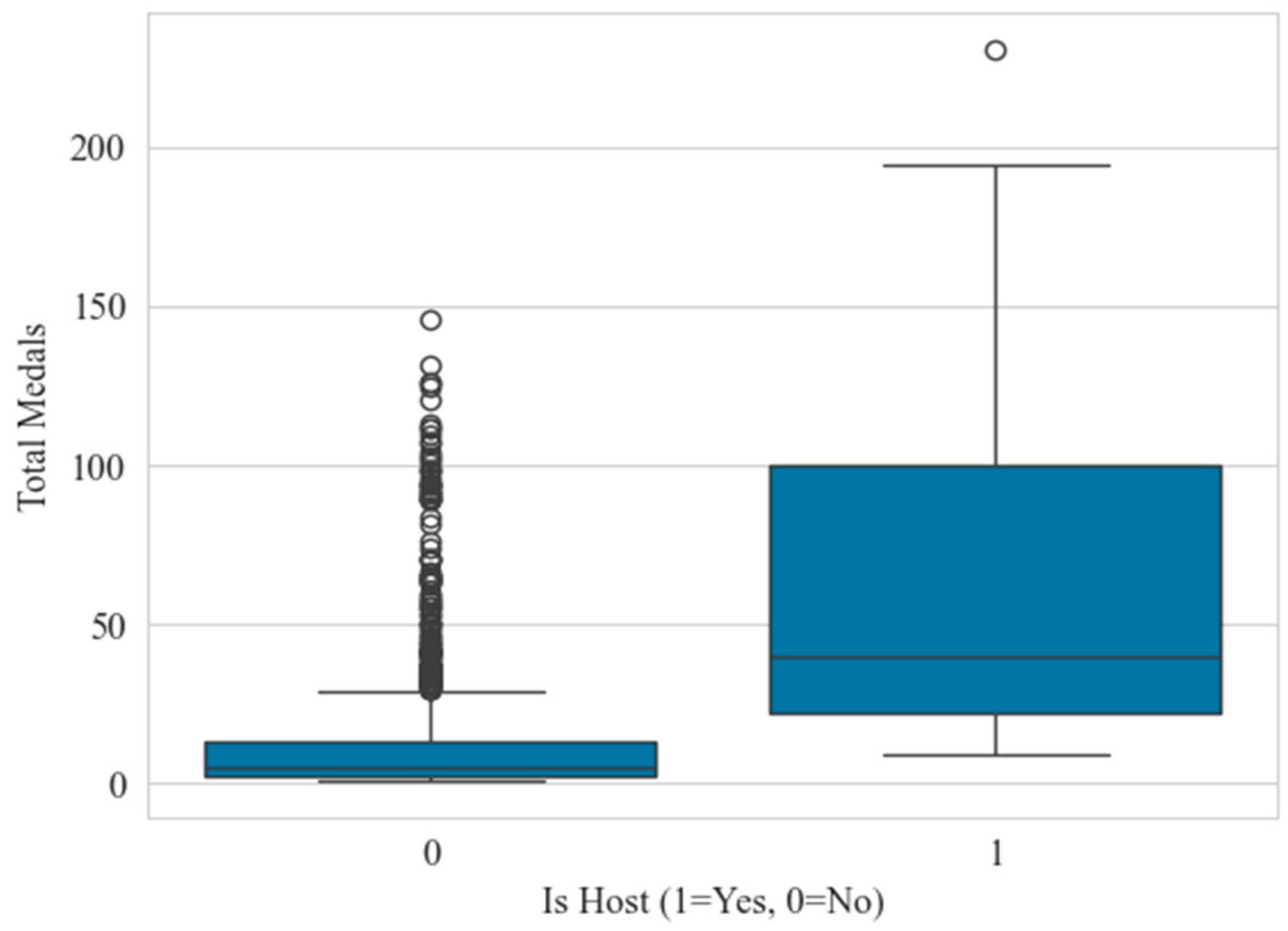
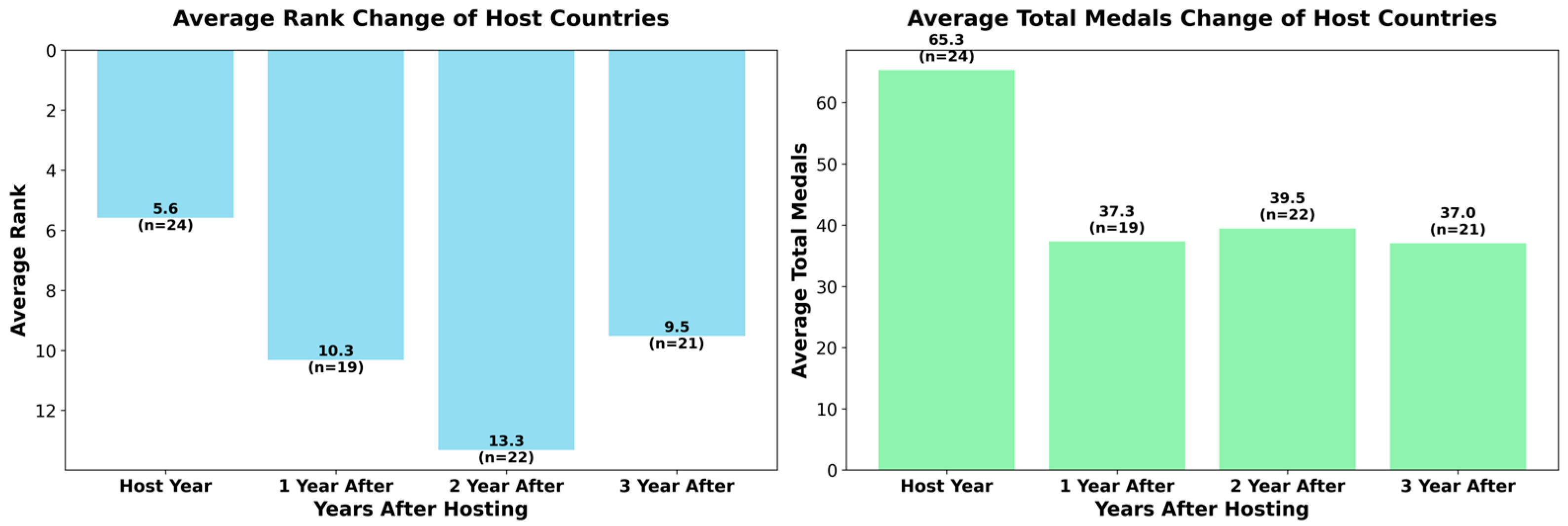
3.2.2. Characterization 2: Host Country Effect
3.2.3. Feature Engineering
4. Methods
4.1. Model Notations
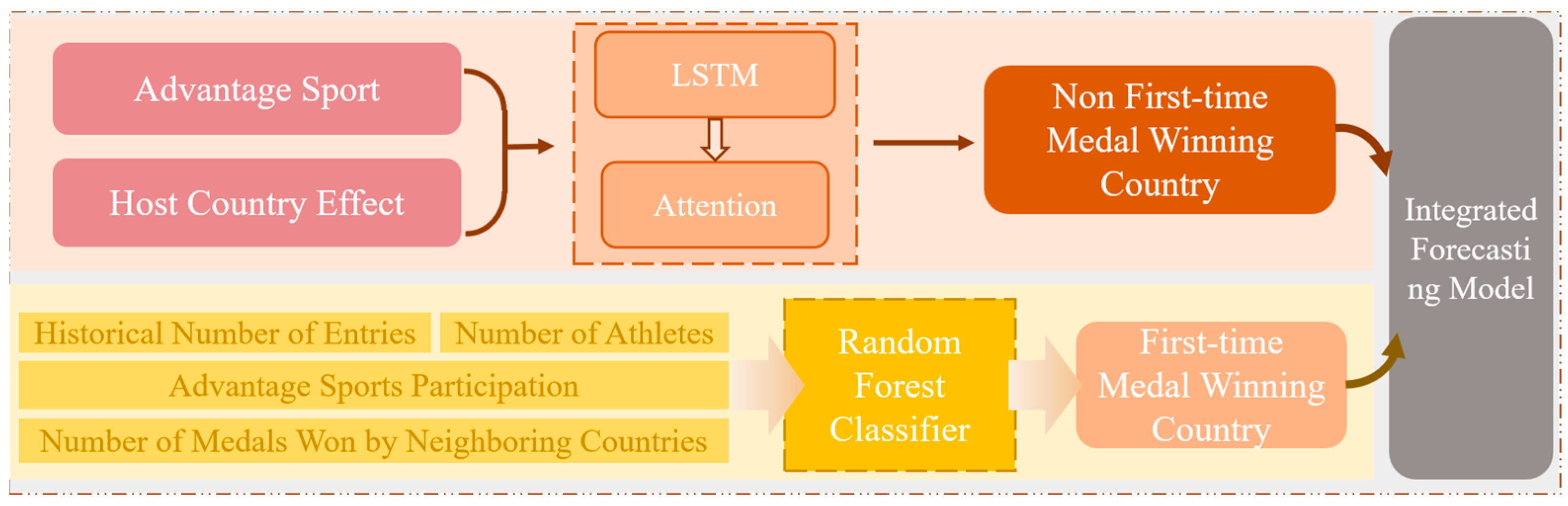
4.2. Model Structure
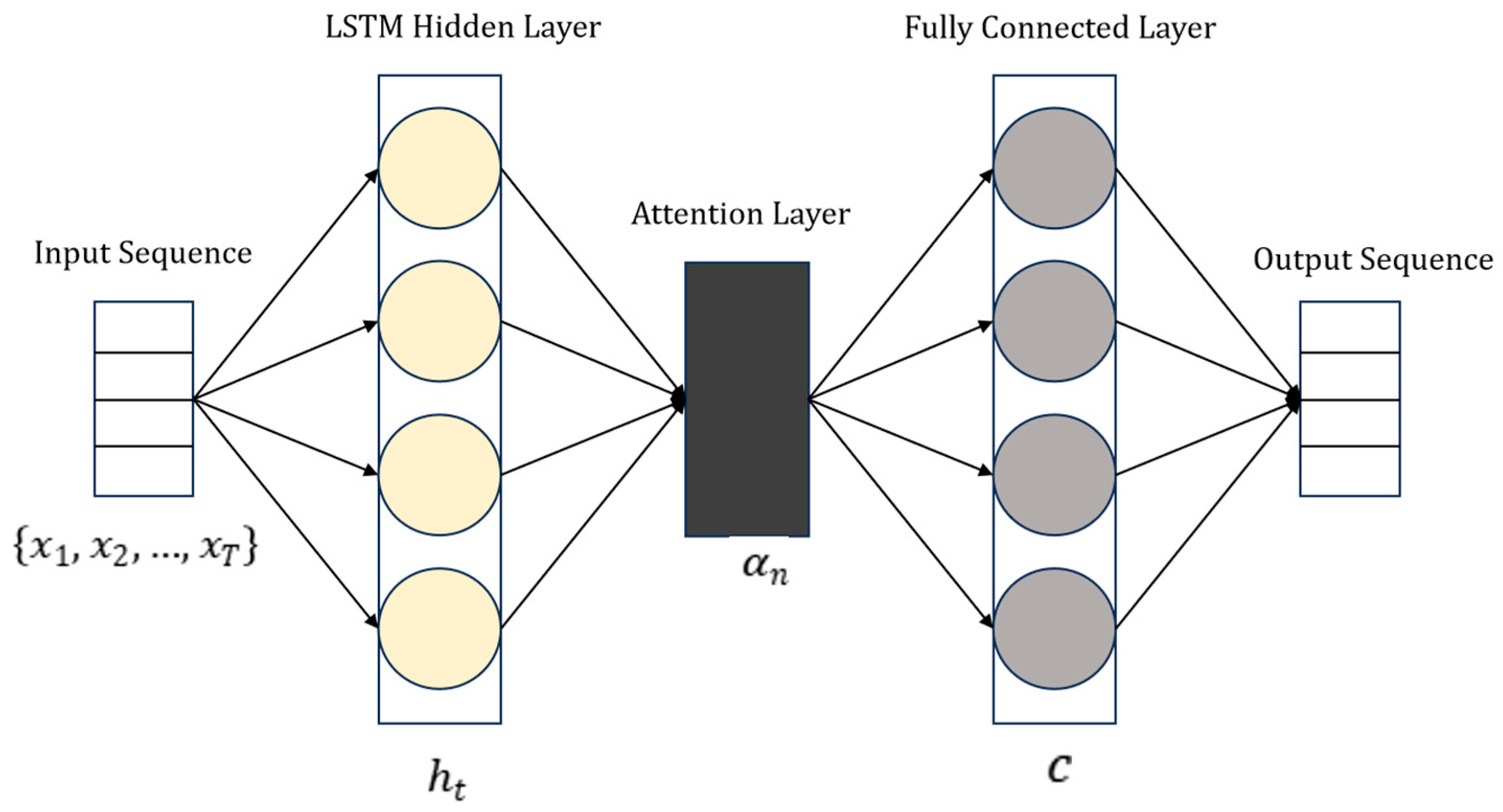
4.3. Prediction Model for Non-First-Time Medal-Winning Countries
- 1.
- LSTM gating calculation
- 2.
- Attention mechanism
4.4. Prediction Model for First-Time Medal-Winning Countries
- Historical Number of Entries (): Defined as the number of times country i has competed in previous Olympic Games ().
- Number of Athletes (): Defined as the number of athletes sent by country i in the current Olympics ().
- Advantage Sport Participation (): A binary indicator representing country i’s participation in sports identified as its advantage areas (e.g., track and field, swimming, etc.) in the current Olympics ().
- Number of Medals Won by Neighboring Countries (): Defined as the sum of medals won by countries geographically or economically clustered around country i in the current Olympics (), reflecting potential clustering effects.
4.5. Explainability Analysis
4.5.1. Theoretical Foundations of SHAP
4.5.2. Analysis of the Model Decision-Making Process
4.5.3. Interpretation of Feature Importance
5. Experiments
5.1. Data Preparation and Preprocessing
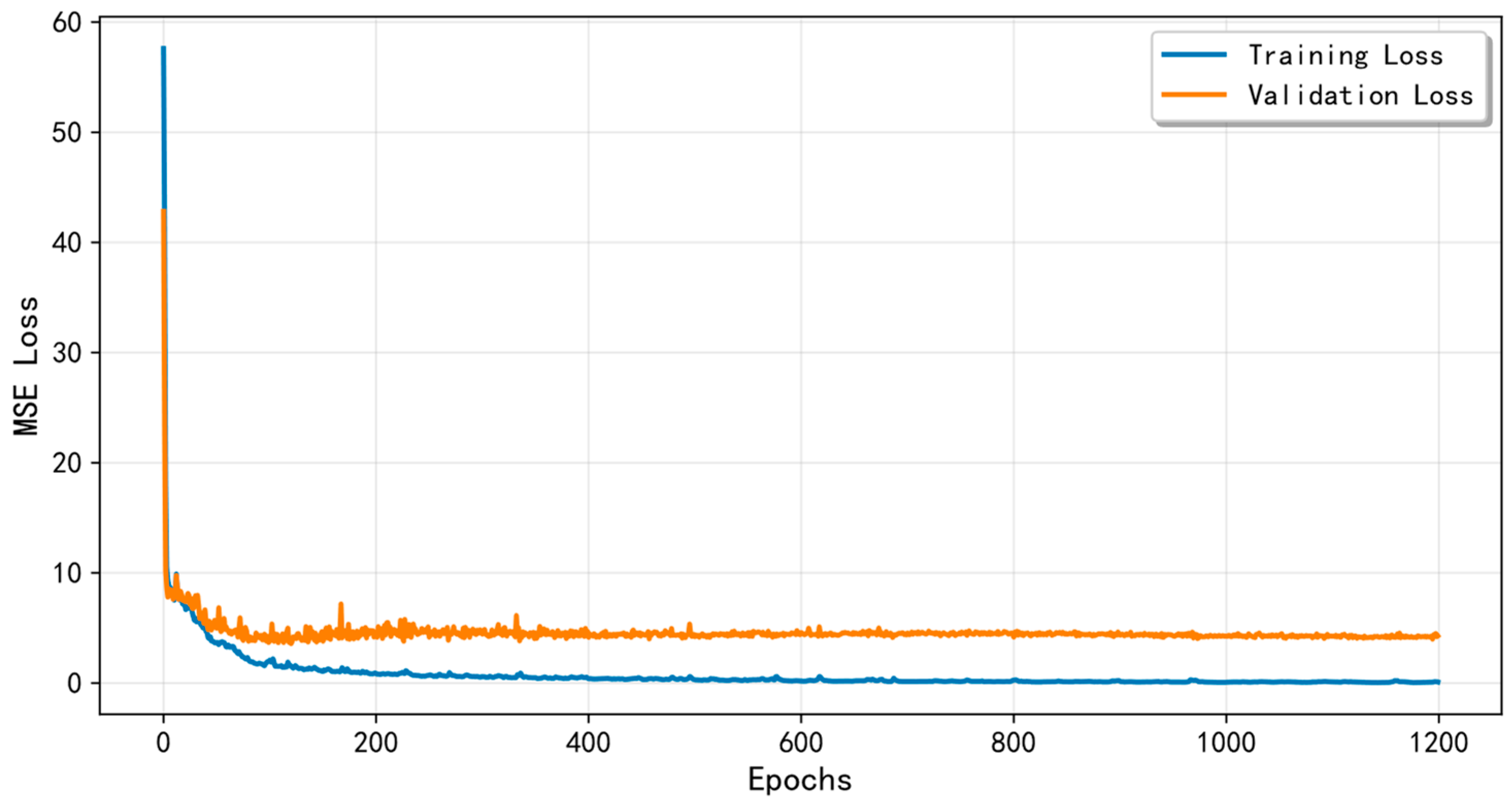
5.2. The Model Training
5.3. Medal Table Predictions for the 2028 Los Angeles Olympics
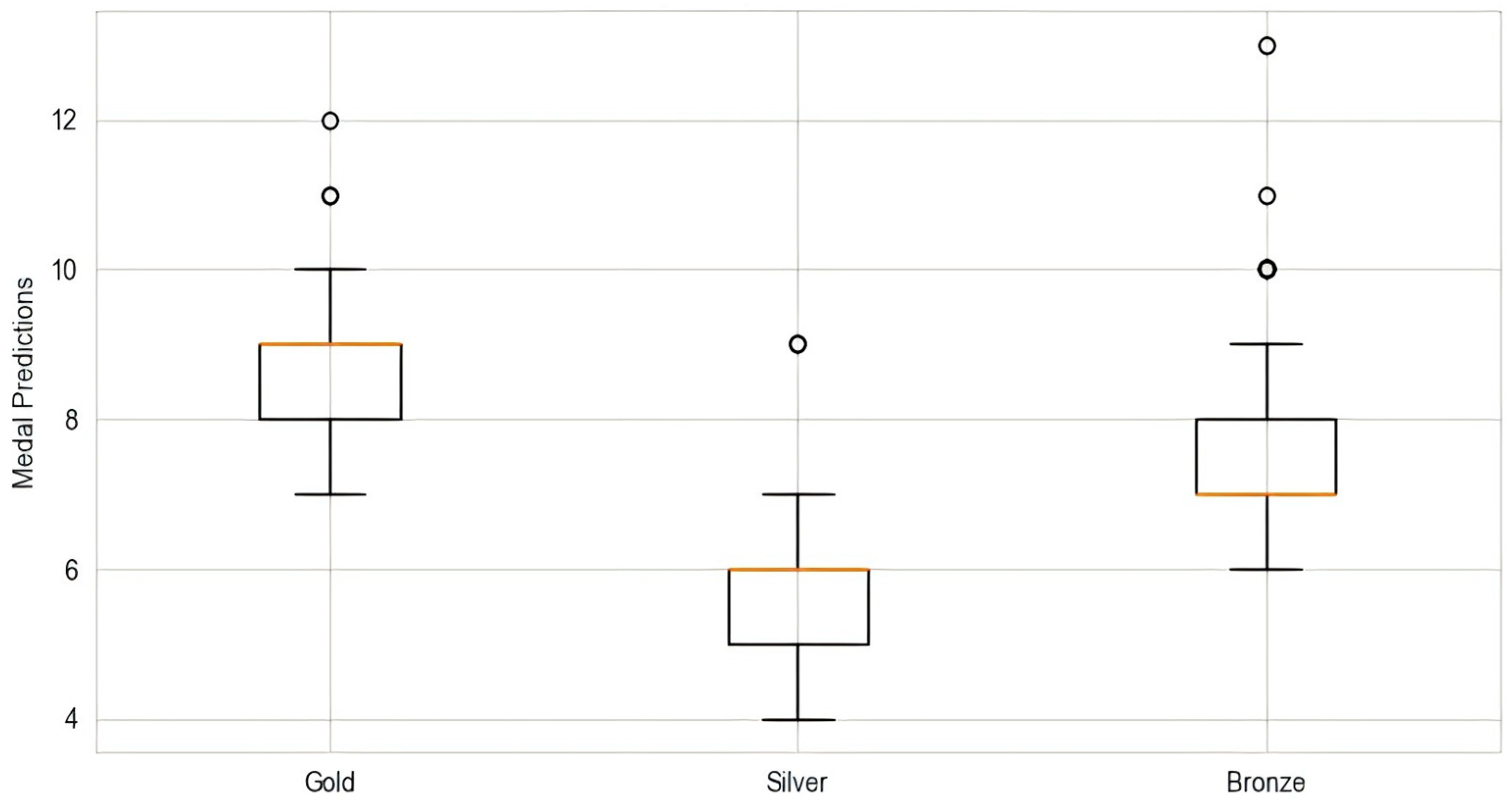
5.4. Countries Most Likely to Progress or Regress
6. Results
6.1. Performance Indicators Performances
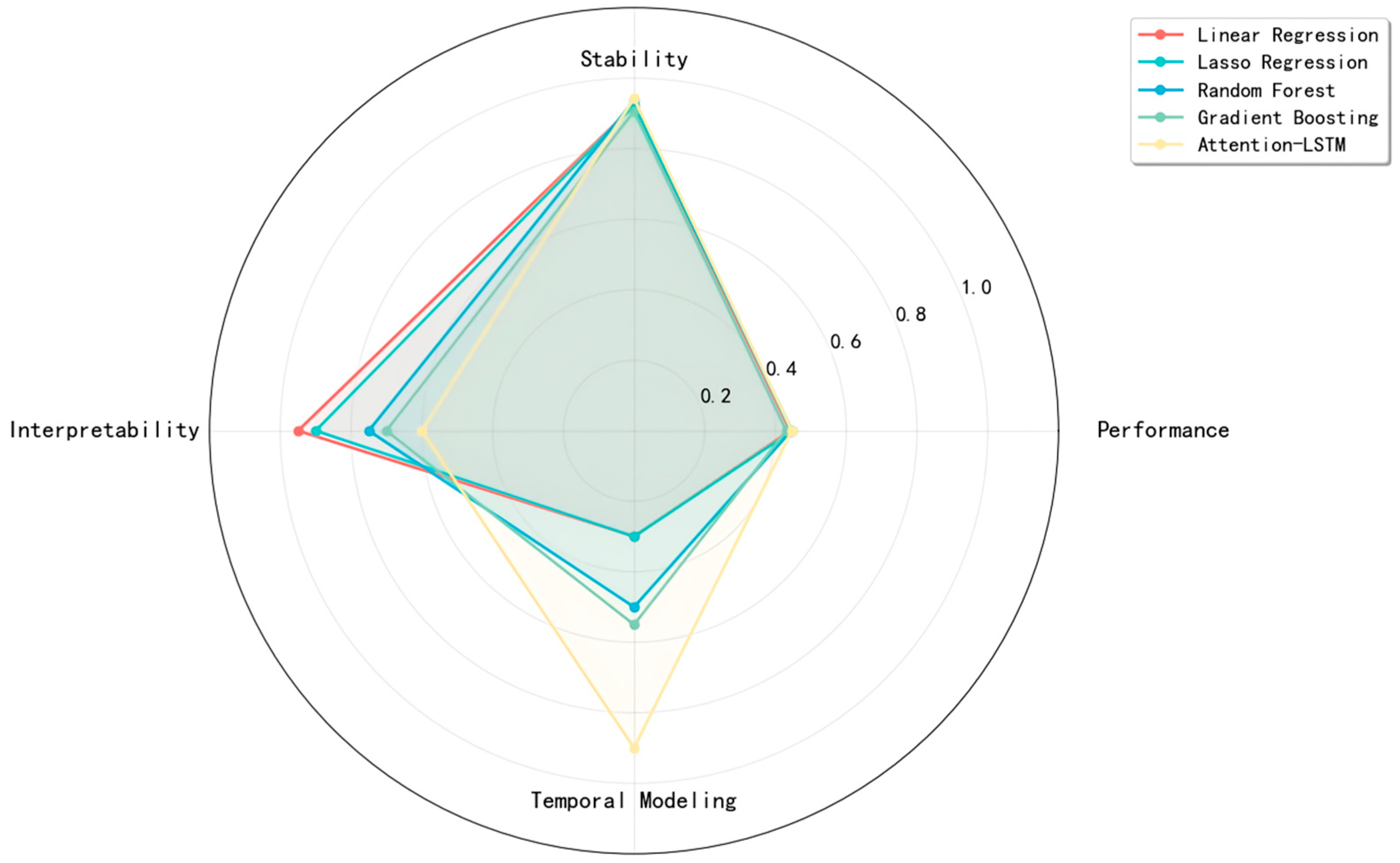
6.2. Stability Analysis
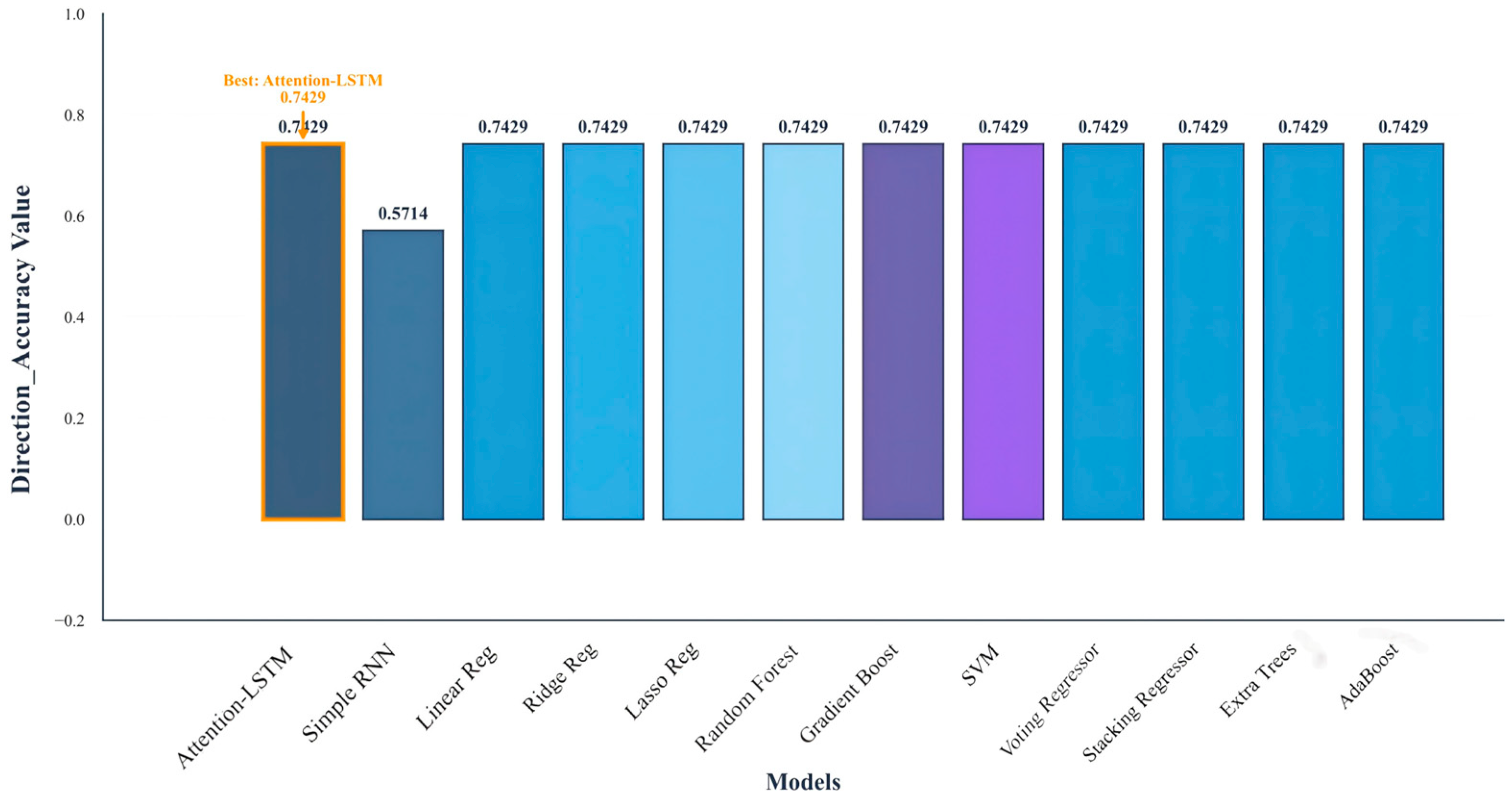
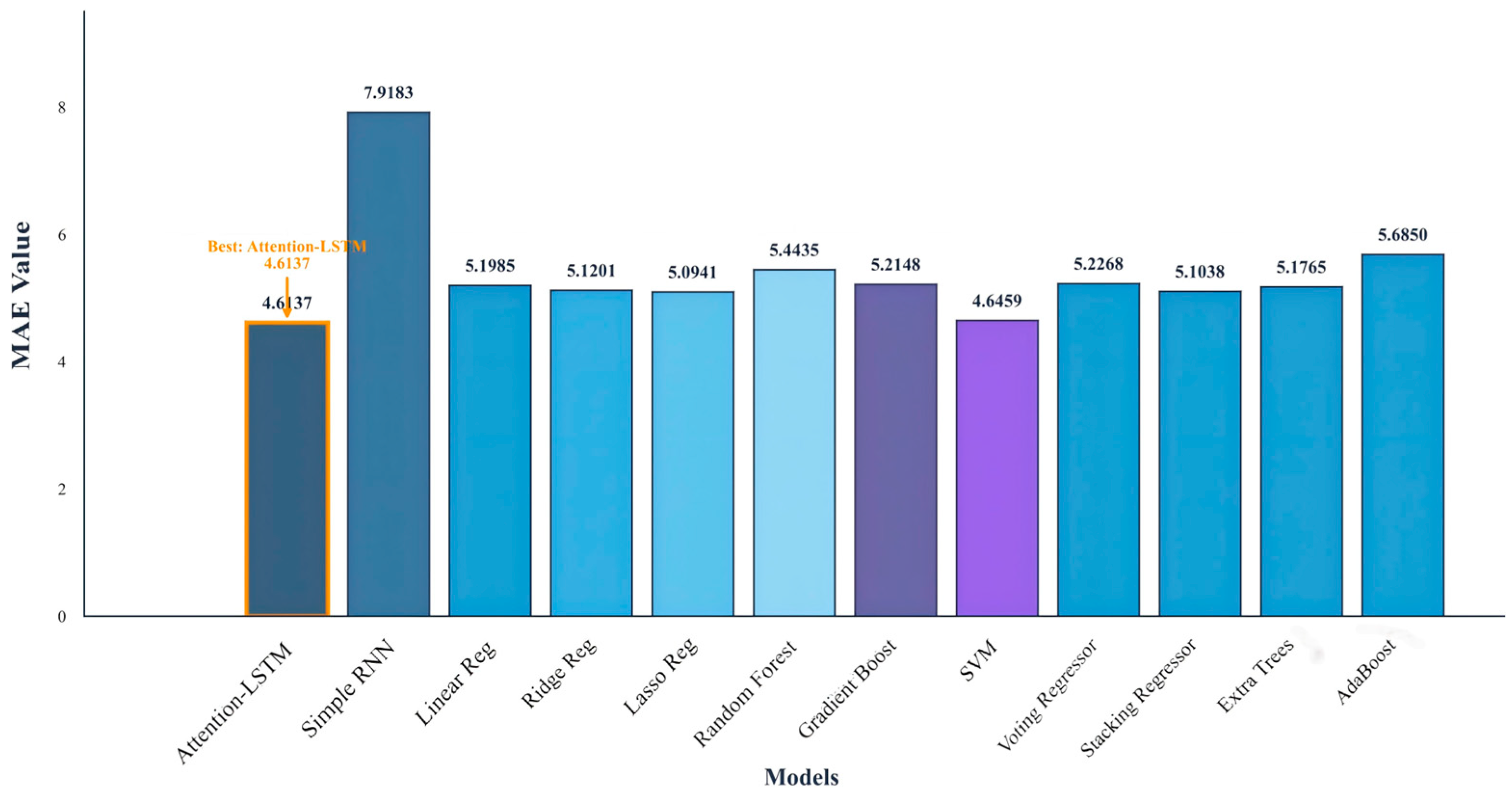
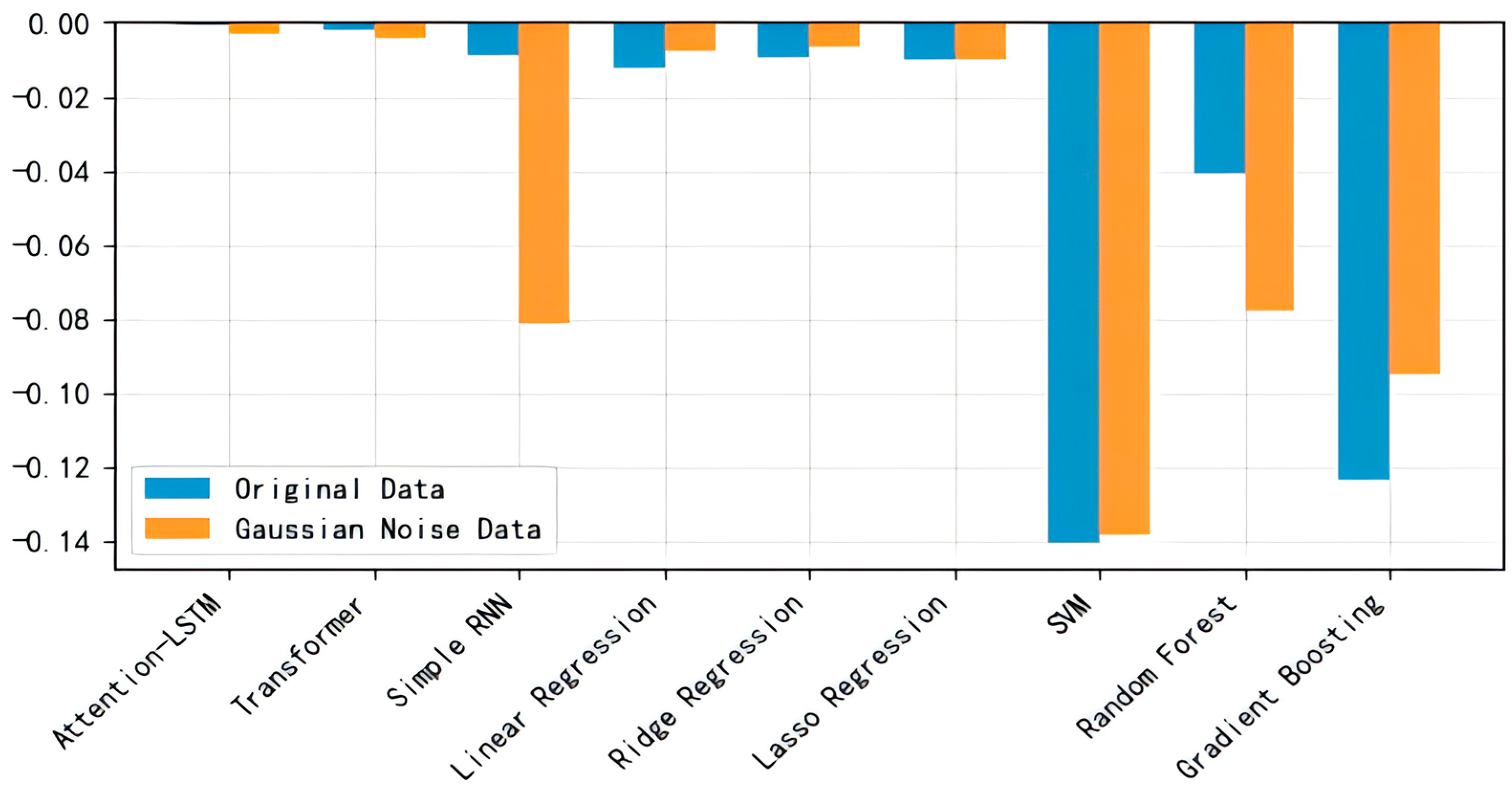
6.3. Comparative Experiment
6.4. Original Insights
- Capture the path-dependent effect of medal distribution.
- 2.
- Amplifying the impact of host countries.
- 3.
- Increasing the marginal cost of winning a medal.
- 4.
- Establish a new decision support framework.
- Strengths Assessment: Input historical data to obtain a potential map for each sport and a complete picture of your strengths and weaknesses.
- Resource Allocation: Based on the marginal revenue curve, scientific allocation of training resources maximizes the input-output ratio.
- Strategy Simulation: Predict the impact of the system reform on the distribution of medals and formulate a strategy to deal with it in advance to get a start.
- Breakthrough Detection: Monitor emerging countries’ strengths and adjust training to maintain a competitive edge.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ball, D.W. Olympic Games Competition: Structural Correlates of National Success. Int. J. Comp. Sociol. 1972, 13, 186–200. [Google Scholar] [CrossRef]
- Condon, E.M.; Golden, B.L.; Wasil, E.A. Predicting the success of nations at the Summer Olympics using neural networks. Comput. Oper. Res. 1999, 26, 1243–1265. [Google Scholar] [CrossRef]
- Lozano, S.; Villa, G.; Guerrero, F.; Cortés, P. Measuring the performance of nations at the Summer Olympics using data envelopment analysis. J. Oper. Res. Soc. 2002, 53, 501–511. [Google Scholar] [CrossRef]
- Tcha, M.; Pershin, V. Reconsidering Performance at the Summer Olympics and Revealed Comparative Advantage. J. Sports Econ. 2003, 4, 216–239. [Google Scholar] [CrossRef]
- Lui, H.-K.; Suen, W. Men, Money and medals: An Econometric analysis of the olympic games. Pac. Econ. Rev. 2008, 13, 1–16. [Google Scholar] [CrossRef]
- Baimbridge, M. Outcome uncertainty in sporting competition: The Olympic Games 1896–1996. Appl. Econ. Lett. 1998, 5, 161–164. [Google Scholar] [CrossRef]
- Hoffmann, R.; Ging, L.C.; Ramasamy, B. Public Policy and Olympic Success. Appl. Econ. Lett. 2002, 9, 545–548. [Google Scholar] [CrossRef]
- Calzada-Infante, L.; Lozano, S. Analysing Olympic Games through dominance networks. Phys. A Stat. Mech. Its Appl. 2016, 462, 1215–1230. [Google Scholar] [CrossRef]
- Kuper, G.H.; Sterken, E. Olympic Participation and Performance Since 1896. Available online: https://research.rug.nl/en/publications/olympic-participation-and-performance-since-1896-2 (accessed on 20 September 2025).
- Lessmann, S.; Sung, M.-C.; Johnson, J.E.V. Alternative methods of predicting competitive events: An application in horserace betting markets. Int. J. Forecast. 2010, 26, 518–536. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Hubáček, O.; Šourek, G.; Železný, F. Exploiting sports-betting market using machine learning. Int. J. Forecast. 2019, 35, 783–796. [Google Scholar] [CrossRef]
- Lim, B.; Zohren, S. Time-series forecasting with deep learning: A survey. Philos. Trans. R. Soc. A 2021, 379, 20200209. [Google Scholar] [CrossRef]
- Huebner, M.; Perperoglou, A. Performance Development From Youth to Senior and Age of Peak Performance in Olympic Weightlifting. Front. Physiol. 2019, 10, 1121. [Google Scholar] [CrossRef] [PubMed]
- Johnston, K.; Wattie, N.; Schorer, J.; Baker, J. Talent Identification in Sport: A Systematic Review. Sports Med. 2018, 48, 97–109. [Google Scholar] [CrossRef] [PubMed]
- Shen, C. A transdisciplinary review of deep learning research and its relevance for water resources scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Potharlanka, J.L.; Bhat M, N.B. Feature importance feedback with Deep Q process in ensemble-based metaheuristic feature selection algorithms. Sci. Rep. 2024, 14, 2923. [Google Scholar] [CrossRef]
- Xu, F.; Uszkoreit, H.; Du, Y.; Fan, W.; Zhao, D.; Zhu, J. Explainable AI: A Brief Survey on History, Research Areas, Approaches and Challenges. In Proceedings of the CCF International Conference on Natural Language Processing and Chinese Computing (NLPCC 2019), Dunhuang, China, 9–14 October 2019; Springer: Cham, Switzerland, 2019; pp. 563–574. [Google Scholar] [CrossRef]
- Liu, L.; Shih, Y.C.T.; Strawderman, R.L.; Zhang, D.; Johnson, B.A.; Chai, H. Statistical analysis of zero-inflated nonnegative continuous data. Stat. Sci. 2019, 34, 253–279. [Google Scholar] [CrossRef]
- Blasco-Moreno, A.; Pérez-Casany, M.; Puig, P.; Morante, M.; Castells, E. What does a zero mean? Understanding false, random and structural zeros in ecology. Methods Ecol. Evol. 2019, 10, 949–959. [Google Scholar] [CrossRef]
- Munkhdalai, L.; Munkhdalai, T.; Park, K.H.; Amarbayasgalan, T.; Batbaatar, E.; Park, H.W. An end-to-end adaptive input selection with dynamic weights for forecasting multivariate time series. IEEE Access 2019, 7, 99099–99114. [Google Scholar] [CrossRef]
- Hammami, Z.; Sayed-Mouchaweh, M.; Mouelhi, W.; Ben Said, L. Neural networks for online learning of non-stationary data streams: A review and application for smart grids flexibility improvement. Artif. Intell. Rev. 2020, 53, 6111–6154. [Google Scholar] [CrossRef]
- Parhizkar, T.; Rafieipour, E.; Parhizkar, A. Evaluation and improvement of energy consumption prediction models using principal component analysis based feature reduction. J. Clean. Prod. 2021, 279, 123866. [Google Scholar] [CrossRef]
- Richardson, R.R.; Birkl, C.R.; Osborne, M.A.; Howey, D.A. Gaussian Process Regression for In Situ Capacity Estimation of Lithium-Ion Batteries. IEEE Trans. Ind. Informat. 2019, 15, 127–138. [Google Scholar] [CrossRef]
- Kim, T.-Y.; Cho, S.-B. Predicting residential energy consumption using CNN-LSTM neural networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Streicher, T.; Schmidt, S.L.; Schreyer, D.; Torgler, B. Anticipated feelings and support for public mega projects: Hosting the Olympic Games. Technol. Forecast. Soc. Change 2020, 158, 120158. [Google Scholar] [CrossRef]
- Maennig, W.; Du Plessis, S. World Cup 2010: South African Economic Perspectives and Policy Challenges Informed by the Experience of Germany 2006. Contemp. Econ. Policy 2007, 25, 578–590. [Google Scholar] [CrossRef]
- Weinstock, D.S. Using the Herfindahl Index to measure concentration. Antitrust Bull. 1982, 27, 285–301. [Google Scholar] [CrossRef]
- Wikipedia Contributors. Summer Olympics All Cities. Available online: https://zh.wikipedia.org/wiki/File:Summer_olympics_all_cities.PNG (accessed on 20 September 2025).
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar] [CrossRef]
- Lewis, J.R. Multipoint scales: Mean and median differences and observed significance levels. Int. J. Hum.-Comput. Interact. 1993, 5, 383–392. [Google Scholar] [CrossRef]
- Singh, J.; Singh, G. Evaluating CNN and CNN-LSTM in Indian Stock Market Prediction. J. Manag. World Bus. Res. 2024, 2024, 217–237. [Google Scholar] [CrossRef]
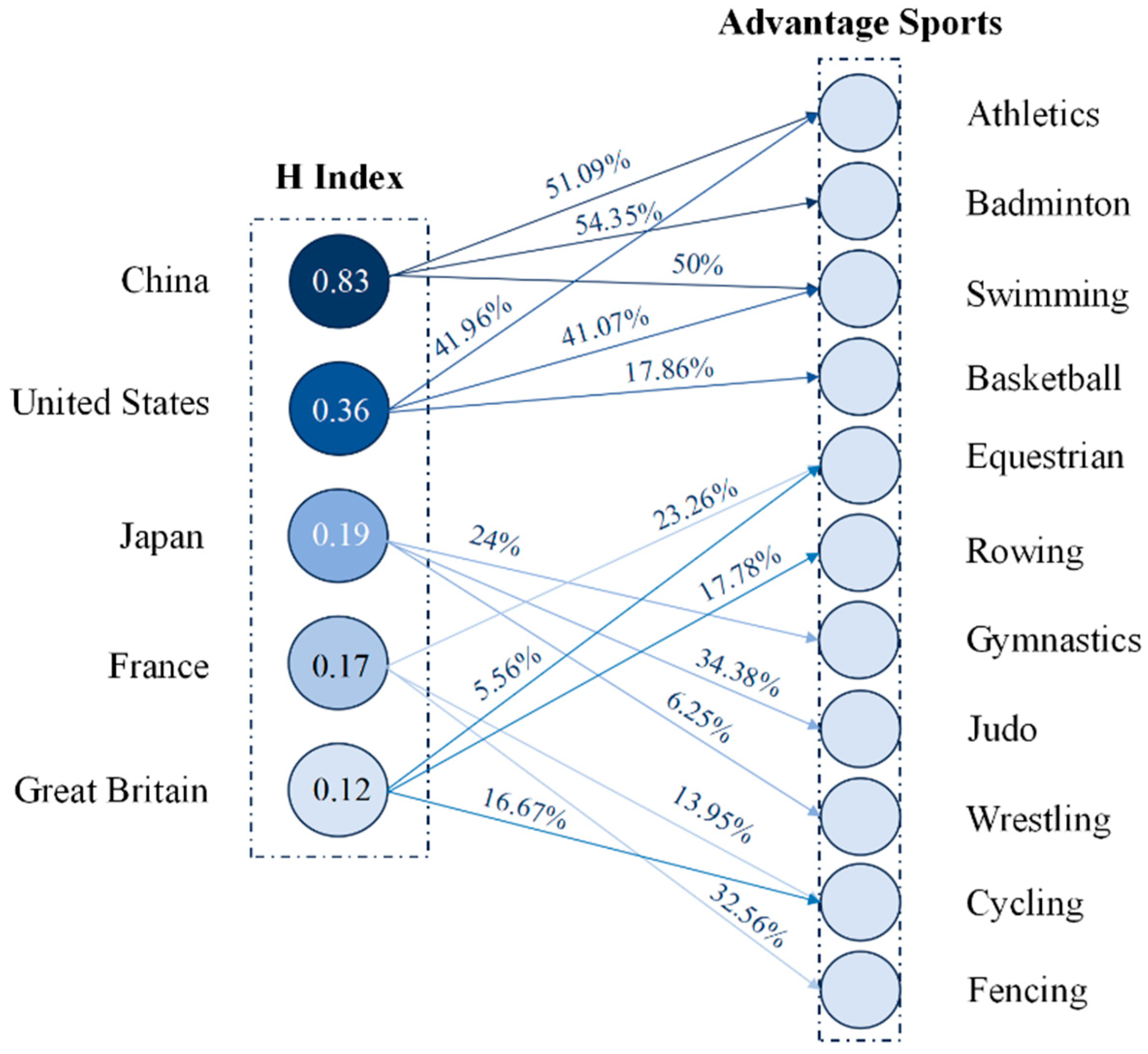
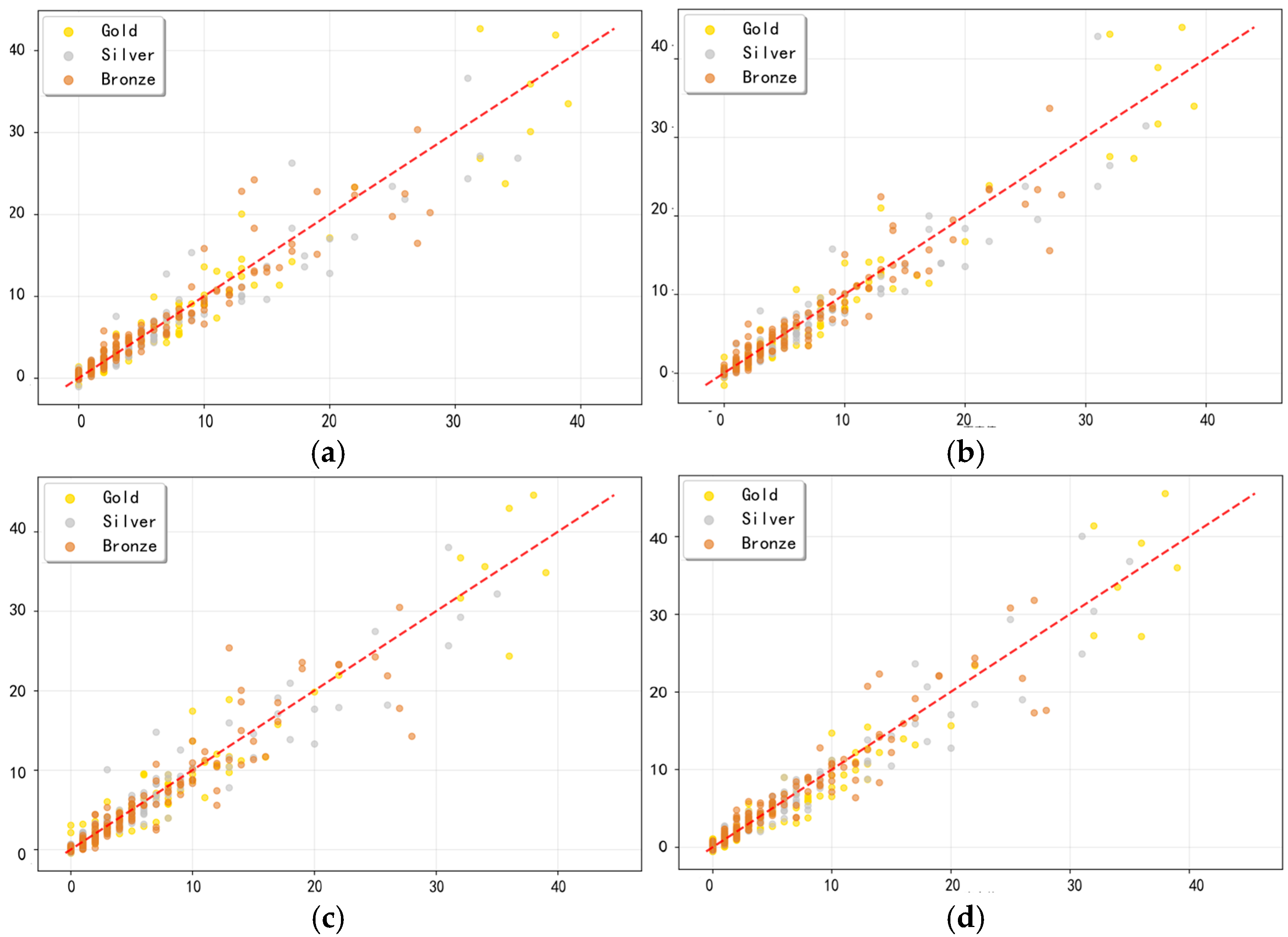
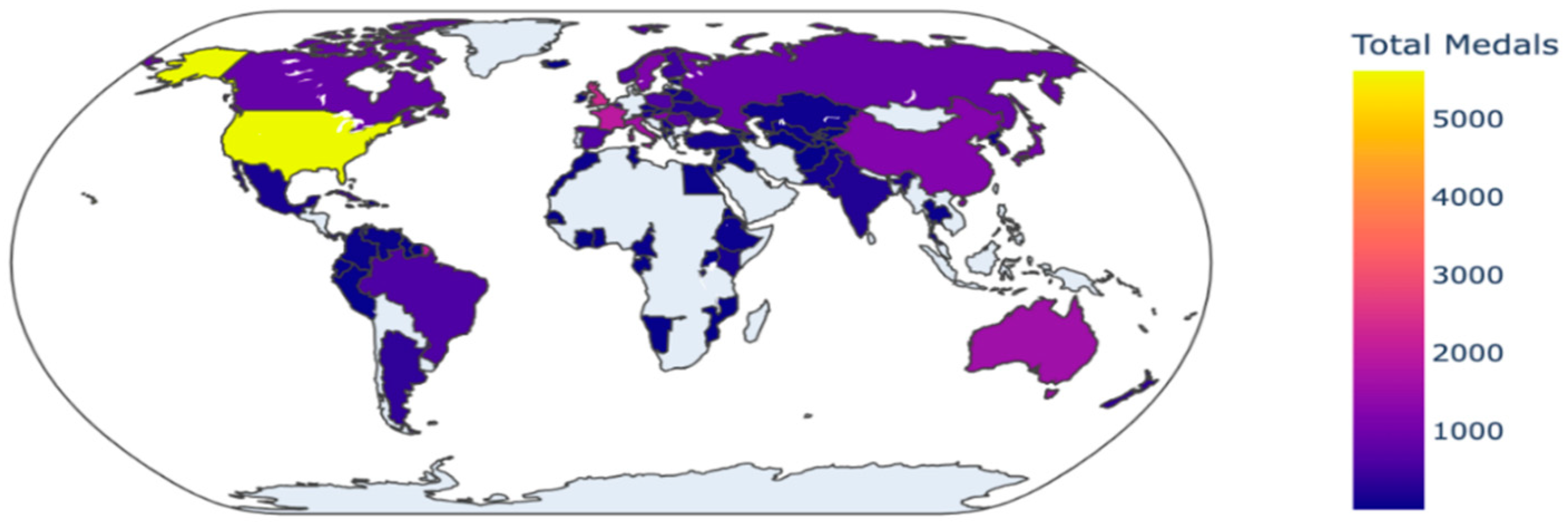
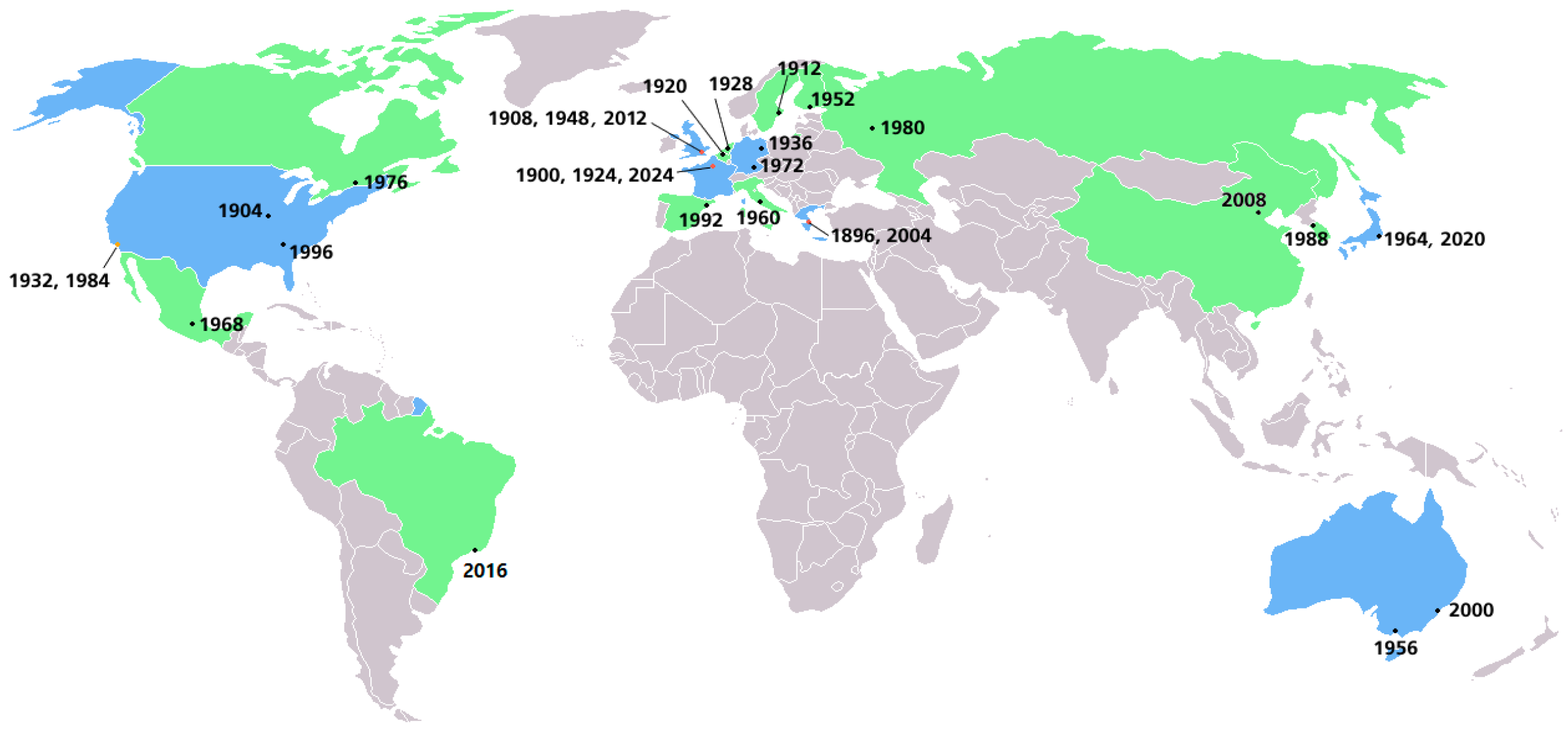
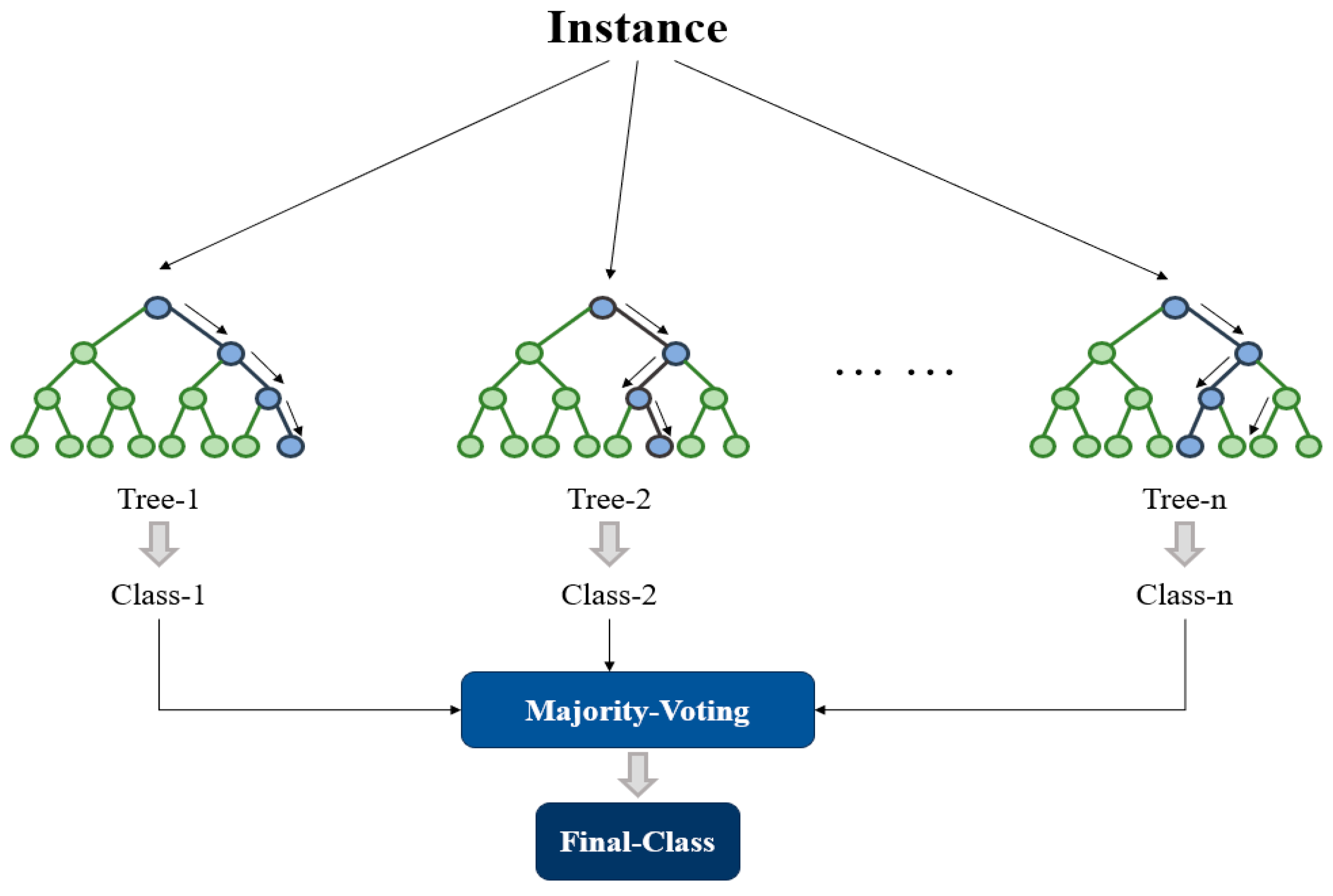
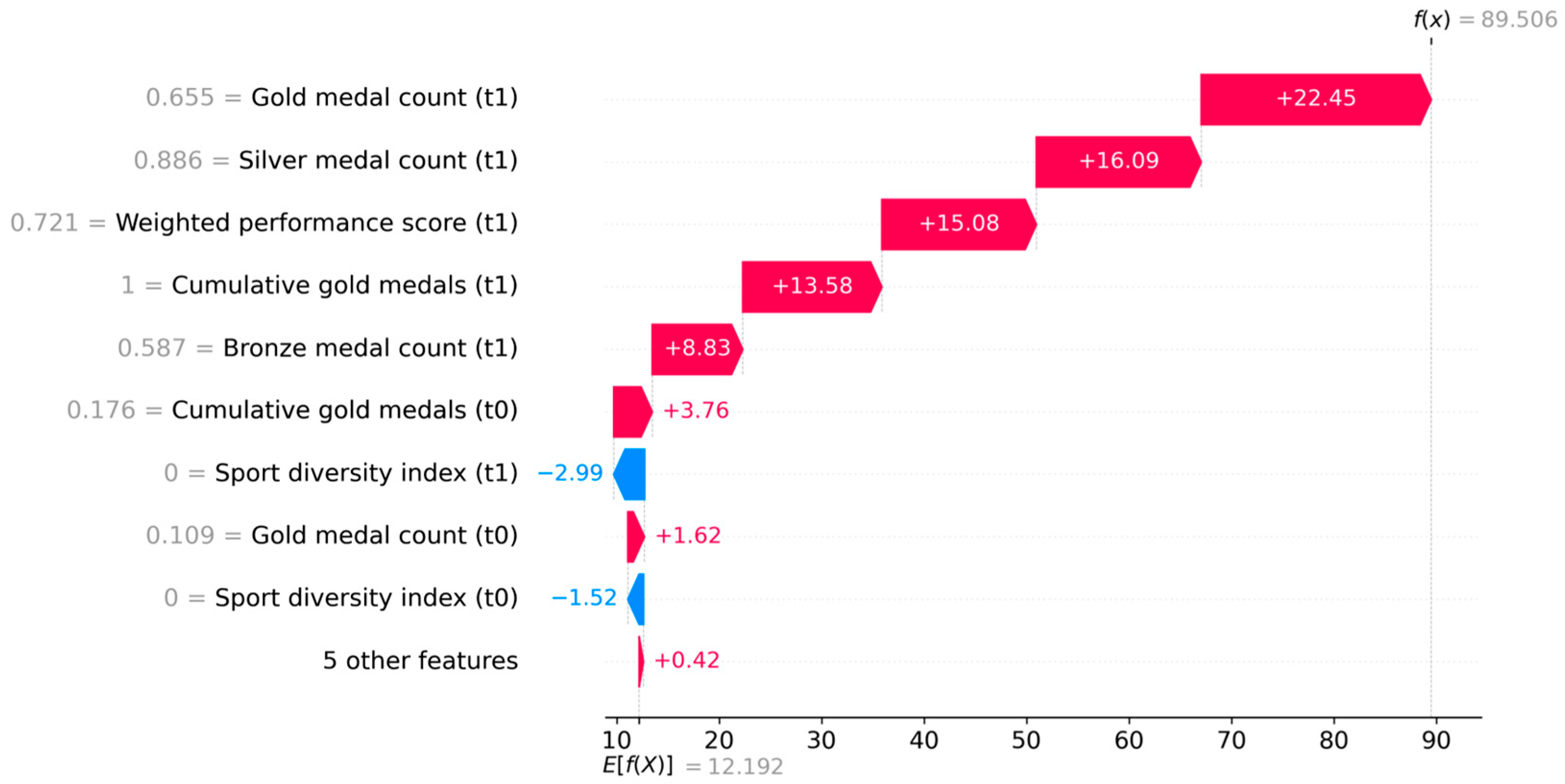
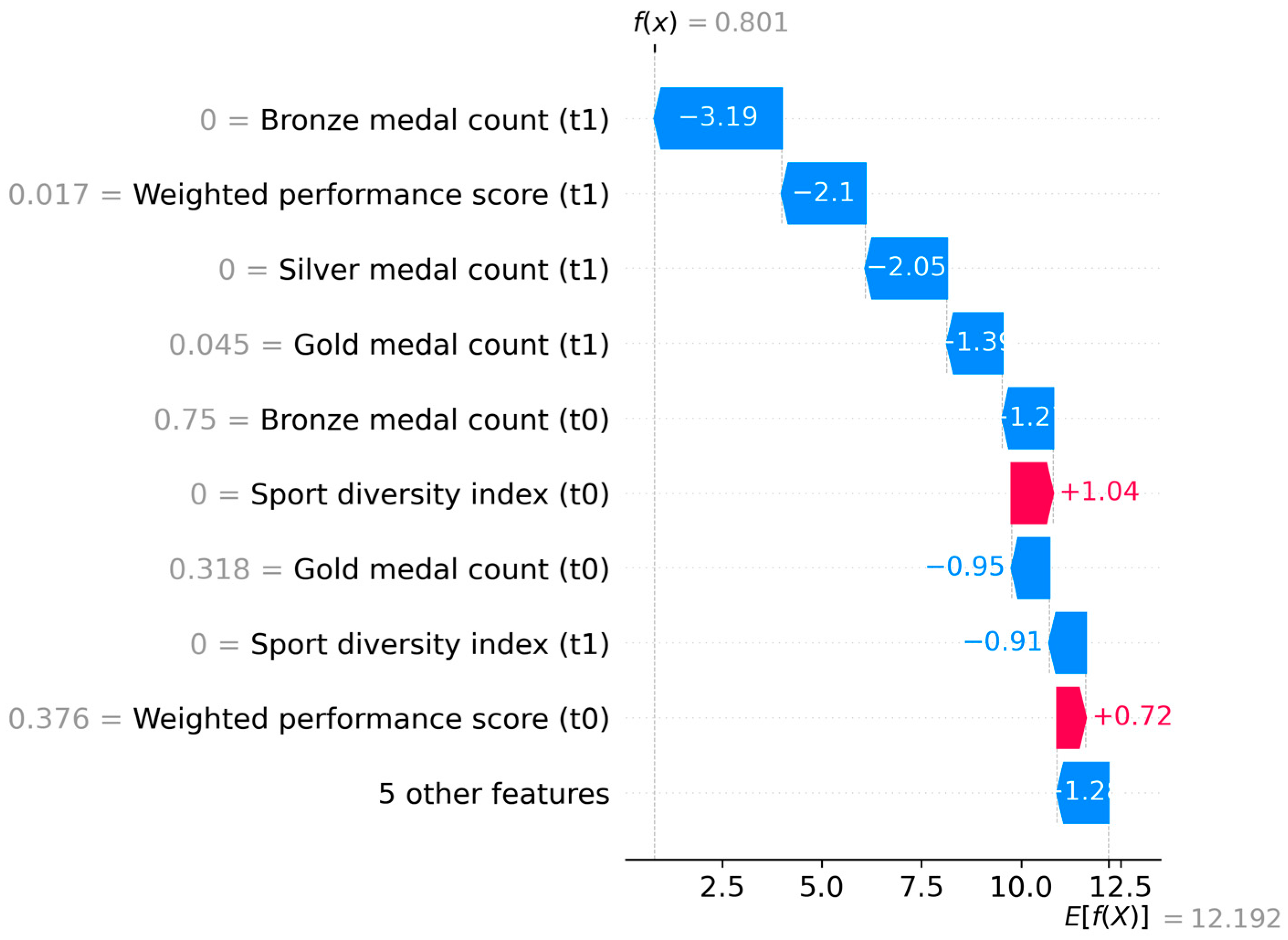
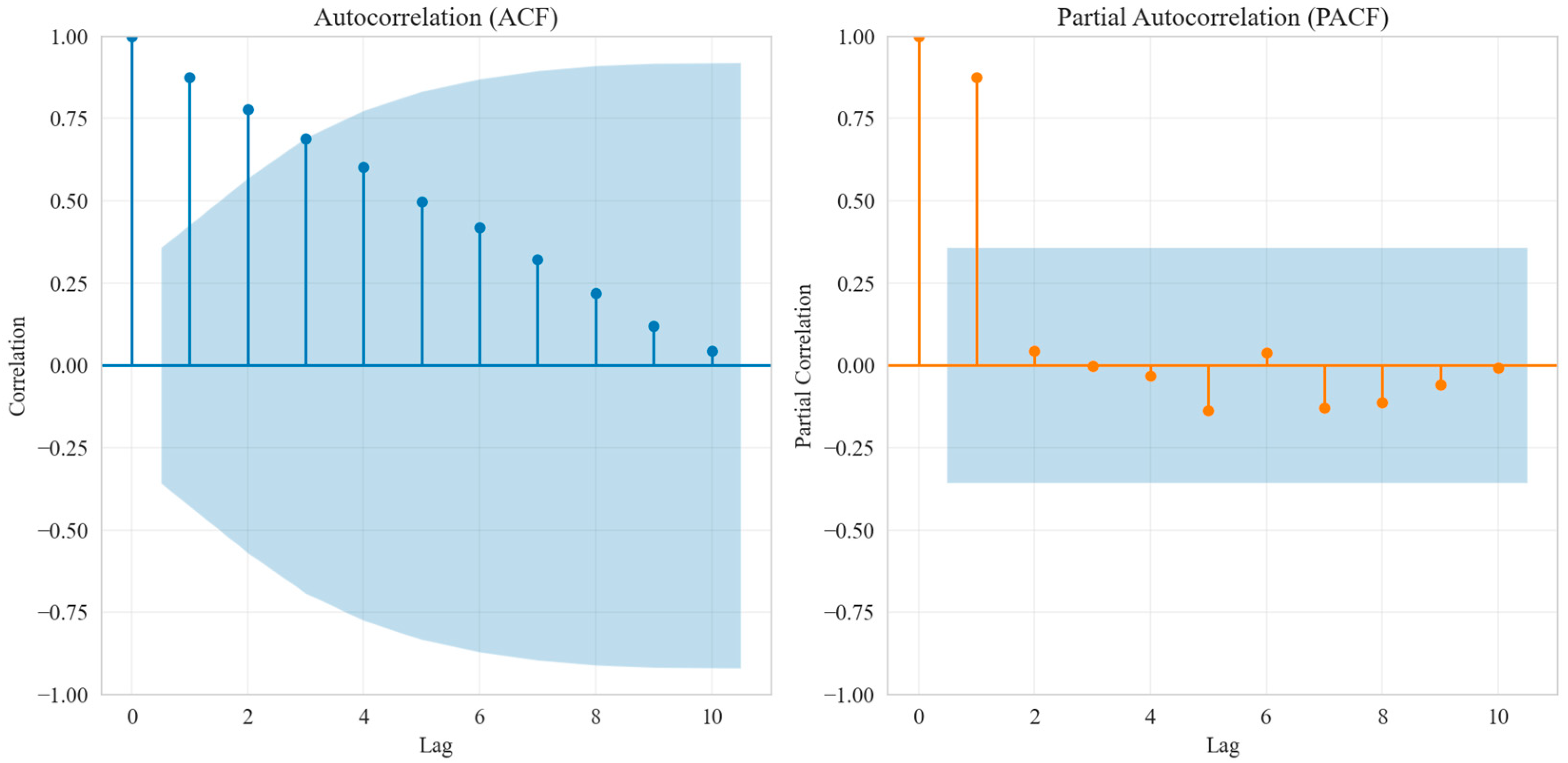
| Symbol | Description |
|---|---|
| loss function value | |
| MSE | Mean square error |
| R2 | Coefficient of determination |
| Experimental Setup | RMSE | MAE | R2 | MSE |
|---|---|---|---|---|
| Complete Model | 1.6941 | 0.8325 | 0.9255 | 2.8700 |
| 1.6709 | 0.8525 | 0.9280 | 2.7919 | |
| 1.7492 | 0.8680 | 0.9198 | 3.0597 | |
| Remove two indicators | 1.6133 | 0.8147 | 0.9322 | 2.6027 |
| Symbol | Description |
|---|---|
| time step | |
| time step | |
| Binary indicator (1 if host country) | |
| Binary indicator (1 for post-hosting years) | |
| DiD estimator of the host-country effect | |
| time step | |
| Input Gate, Forget Gate, Output Gate | |
| Candidate memory cell state | |
| , | Weighting matrix and bias terms for each gate control unit |
| Attention weighting | |
| Attention scoring function | |
| Context vector | |
| Actual values and predicted values |
| Ranking | Feature Name | Explanation | Importance Score | Relative Importance (%) |
|---|---|---|---|---|
| 1 | Gold | Number of gold medals | 1.8956 | 25.3 |
| 2 | Bronze | Number of bronze medals | 1.6157 | 21.6 |
| 3 | Weighted_Score | 1.5006 | 20.0 | |
| 4 | Silver | Number of silver medals | 1.3757 | 18.4 |
| 5 | Cumulative_Gold | Total Gold Medals | 0.8403 | 11.2 |
| 6 | Sport_Diversity | 0.8380 | 11.2 | |
| 7 | Is_Host | Whether it is the host country | 0.1366 | 1.8 |
| Hyperparameters | Description | Value |
|---|---|---|
| Hidden Size | Number of neurons in the hidden layer | 128 |
| Output Size | Predicts the number of gold, silver, and bronze medals | 3 |
| Optimizer | Optimization algorithm | Adam |
| Learning Rate | Step size controls the optimization speed | 0.001 |
| Batch Size | Number of samples per training batch | 64 |
| Epochs | Total number of training iterations | 400 |
| Loss Function | The function used to calculate error | MSELoss |
| Country | Predicted Probability | Confidence Interval |
|---|---|---|
| Yemen | 0.92 | [0.85, 0.97] |
| Chad | 0.88 | [0.81, 0.93] |
| Laos | 0.75 | [0.68, 0.82] |
| Bahrain | 0.63 | [0.56, 0.73] |
| South Sudan | 0.61 | [0.52, 0.70] |
| Rank | Nation | Gold Medal Prediction (Interval) | Silver Medal Predictions (Interval) | Bronze Medal Predictions (Range) | 2028 Predicted Ranking | Tendency |
|---|---|---|---|---|---|---|
| 1 | United States | 52 (48–56) | 42 (38–46) | 36 (32–40) | 1 | → |
| 2 | China | 43 (39–47) | 35 (31–39) | 30 (26–34) | 2 | → |
| 3 | France | 35 (30–40) | 28 (24–32) | 25 (20–30) | 3 | ↑2 |
| 4 | Japan | 33 (28–38) | 25 (20–30) | 22 (18–26) | 4 | ↑3 |
| 5 | Great Britain | 29 (25–33) | 31 (27–35) | 28 (24–32) | 5 | ↓1 |
| 6 | Germany | 27 (23–31) | 24 (20–28) | 20 (16–24) | 6 | ↓3 |
| 7 | Australia | 25 (21–29) | 22 (18–26) | 19 (15–23) | 7 | ↑1 |
| 8 | Russia | 18 (14–22) | 22 (18–26) | 20 (16–24) | 8 | ↓2 |
| 9 | Italy | 20 (16–24) | 18 (14–22) | 17 (13–21) | 9 | ↑1 |
| 10 | Netherlands | 19 (15–23) | 16 (12–20) | 15 (11–19) | 10 | ↑2 |
| Nation | Gold Medal 2024 | Silver Medal 2024 | Bronze Medal 2024 | Gold Medal 2028 | Silver Medal 2028 | Bronze Medal 2028 | Total Medal Change |
|---|---|---|---|---|---|---|---|
| United States | 45 | 38 | 30 | 52 | 42 | 36 | +15 |
| China | 38 | 32 | 28 | 43 | 35 | 30 | +8 |
| Japan | 27 | 21 | 20 | 33 | 25 | 22 | +9 |
| France | 22 | 17 | 15 | 35 | 28 | 25 | +9 |
| Nation | Gold Medal 2024 | Silver Medal 2024 | Bronze Medal 2024 | Gold Medal 2028 | Silver Medal 2028 | Bronze Medal 2028 | Total Medal Change |
|---|---|---|---|---|---|---|---|
| Russia | 25 | 30 | 28 | 18 | 22 | 20 | −13 |
| Germany | 20 | 18 | 25 | 15 | 16 | 18 | −6 |
| Model | Hyperparameters | Value |
|---|---|---|
| Attention-LSTM | hidden_size | 128 |
| learning_rate | 0.001 | |
| optimizer | Adam | |
| loss_function | MSE Loss | |
| epochs | 400 | |
| early_stopping_patience | 20 | |
| Transformer | d_model | 128 |
| learning_rate | 0.0005 | |
| weight_decay | 1 × 10−5 | |
| gradient_clipping | 1.0 | |
| epochs | 300 | |
| early_stopping_patience | 25 | |
| Simple RNN | hidden_size | 64 |
| learning_rate | 0.001 | |
| epochs | 200 | |
| Ridge Regression | alpha | 1.0 |
| Lasso Regression | alpha | 0.1 |
| Random Forest | n_estimators | 100 |
| random_state | 42 | |
| Gradient Boosting | n_estimators | 100 |
| random_state | 42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, L.; Wang, S.; Ji, J.; Yin, S.; Yasrab, R.; Zhou, C. Integrating Structured Time-Series Modeling and Ensemble Learning for Strategic Performance Forecasting. Algorithms 2025, 18, 611. https://doi.org/10.3390/a18100611
Tang L, Wang S, Ji J, Yin S, Yasrab R, Zhou C. Integrating Structured Time-Series Modeling and Ensemble Learning for Strategic Performance Forecasting. Algorithms. 2025; 18(10):611. https://doi.org/10.3390/a18100611
Chicago/Turabian StyleTang, Liqing, Shuxin Wang, Jintian Ji, Siyuan Yin, Robail Yasrab, and Chao Zhou. 2025. "Integrating Structured Time-Series Modeling and Ensemble Learning for Strategic Performance Forecasting" Algorithms 18, no. 10: 611. https://doi.org/10.3390/a18100611
APA StyleTang, L., Wang, S., Ji, J., Yin, S., Yasrab, R., & Zhou, C. (2025). Integrating Structured Time-Series Modeling and Ensemble Learning for Strategic Performance Forecasting. Algorithms, 18(10), 611. https://doi.org/10.3390/a18100611









