An Efficient and Accurate Adaptive Time-Stepping Method for the Landau–Lifshitz Equation
Abstract
:1. Introduction
2. Numerical Method
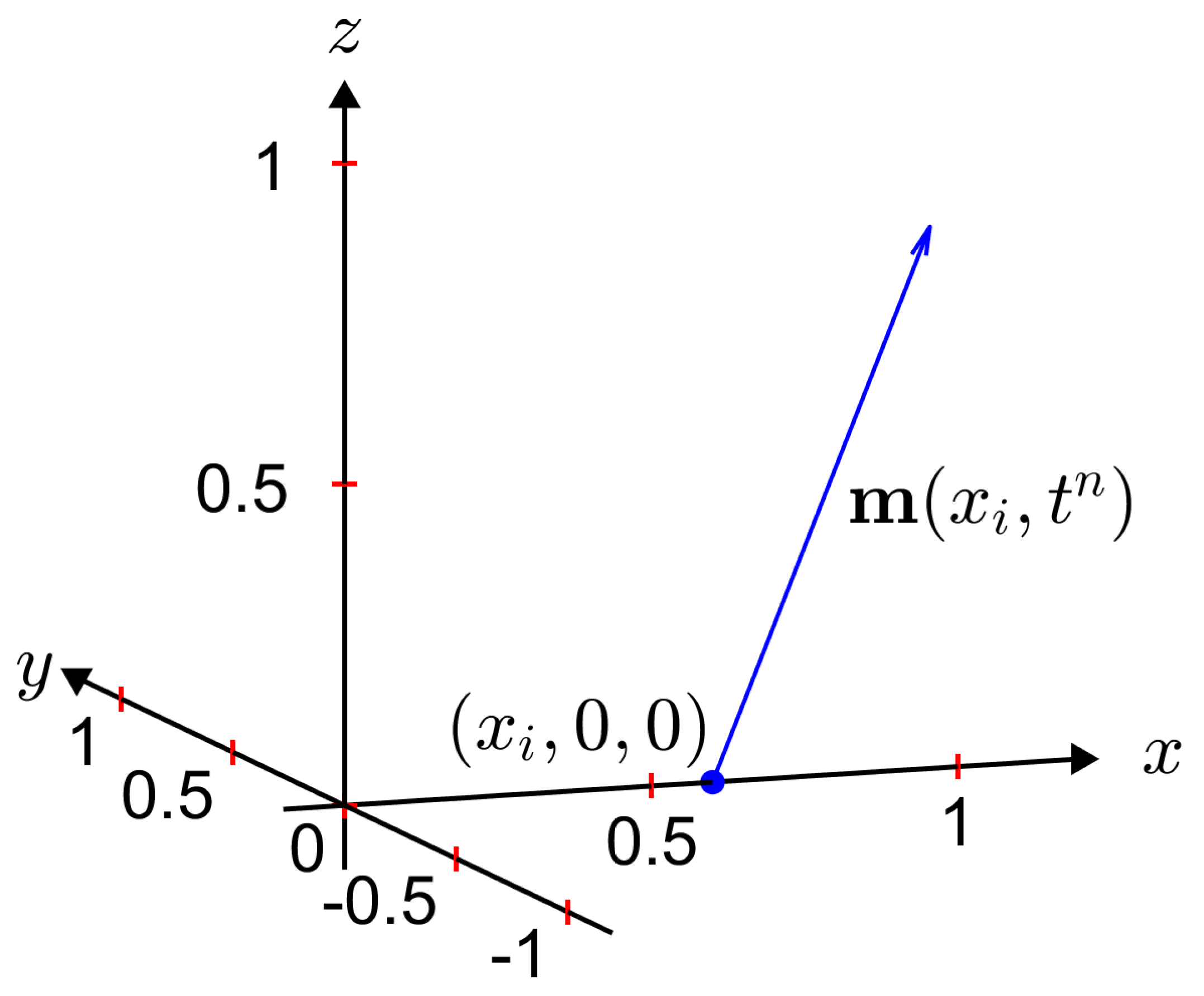
2.1. Discretization
2.2. Adaptive Time-Stepping Algorithm
| Algorithm 1: Adaptive scheme for the LL equation |
| INPUT endpoints ; number of grid points ; initial condition; final time T; tolerance ; maximum time step size ; forcing term . OUTPUT approximation of . Step 1 Initialization Set and For do , , Step 2 While (), do Steps 3–7. Step 3 For do . Use periodic boundary condition Step 4 Set . Step 5 Set ; . If , then . Step 6 Set . Step 7 Set . . Step 8 OUTPUT , , STOP. |
3. Computational Experiments
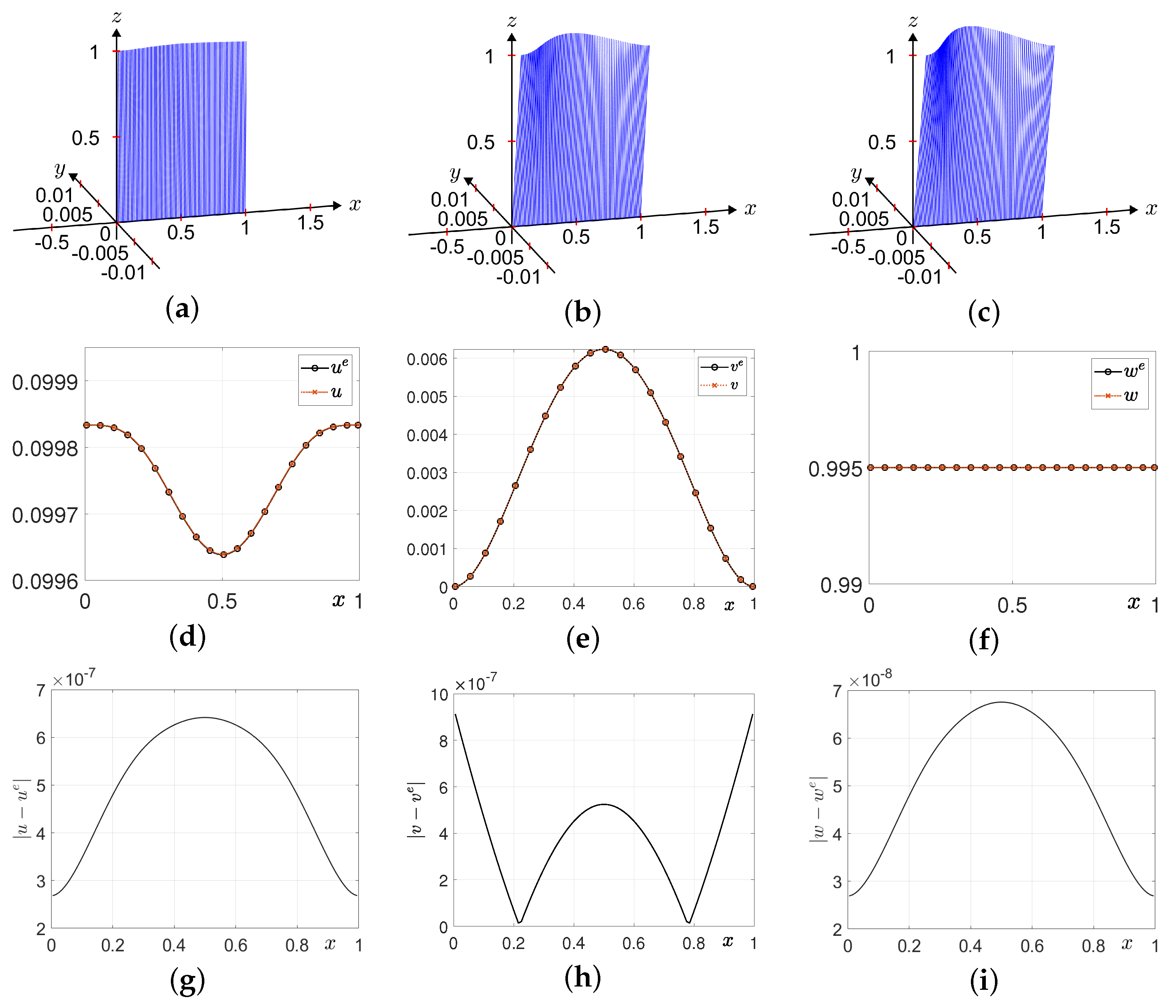
3.1. Without Forcing Term
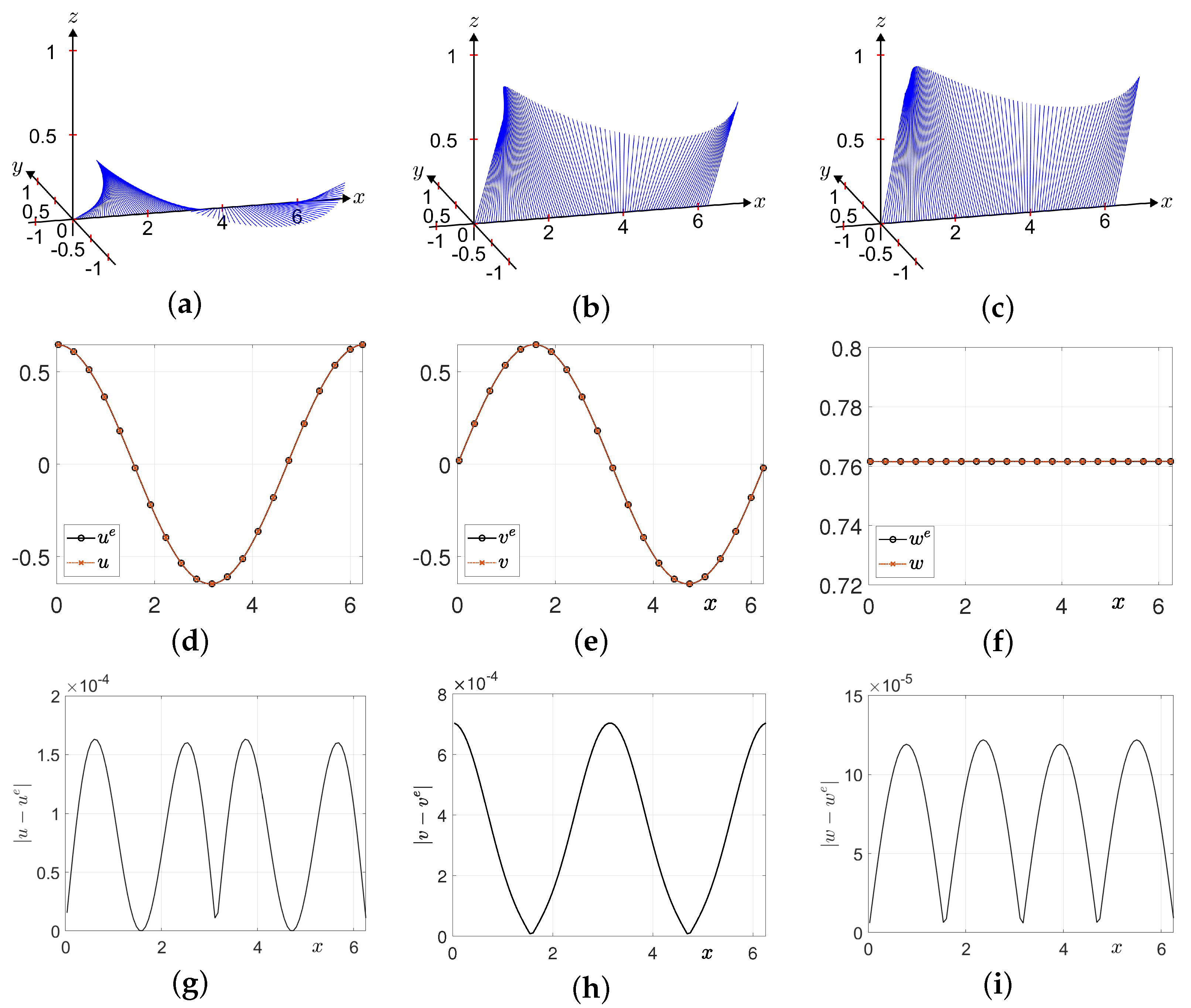
3.2. Periodic Forcing Term
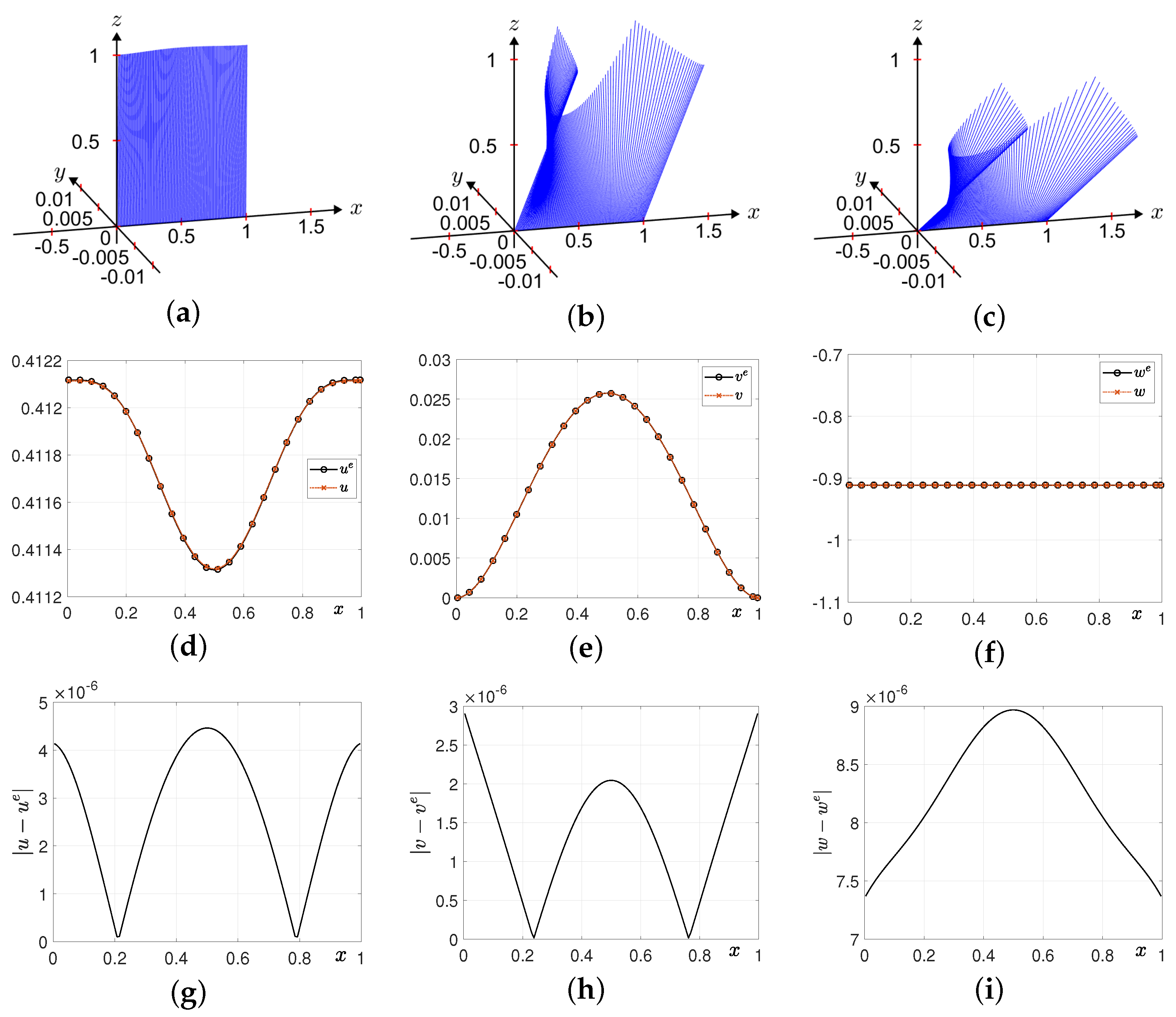
3.3. Non-Periodic Forcing Term
3.4. Damping Forcing Term
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameters | Description |
|---|---|
| Nx | number of grid points on the x-axis |
| Lx | minimum value on the x-axis |
| Rx | maximum value on the x-axis |
| h | space step size |
| T | final time |
| maxdt | maximum time step size |
| tol | tolerance |
clear; Nx=100; Lx=0; Rx=1; h=(Rx-Lx)/Nx; x=linspace(Lx+0.5*h,Rx-0.5*h,Nx); XX=(x.^2).*((1-x).^2); dXX=2*x-6*x.^2+4*x.^3; ddXX=2-12*x+12*x.^2; ue=@(t) sin(t).*cos(XX); ve=@(t) sin(t).*sin(XX); we=@(t) cos(t).*ones(1,Nx); T=1.e-1; maxdt=0.5*h^2; t=0; u=ue(0); v=ve(0); w=we(0); tol=1.e-7; while t<T Lapu(1)=(u(2)-2*u(1)+u(Nx))/h^2; Lapv(1)=(v(2)-2*v(1)+v(Nx))/h^2; Lapw(1)=(w(2)-2*w(1)+w(Nx))/h^2; for i=2:Nx-1 Lapu(i)=(u(i+1)-2*u(i)+u(i-1))/h^2; Lapv(i)=(v(i+1)-2*v(i)+v(i-1))/h^2; Lapw(i)=(w(i+1)-2*w(i)+w(i-1))/h^2; end Lapu(Nx)=(u(1)-2*u(Nx)+u(Nx-1))/h^2; Lapv(Nx)=(v(1)-2*v(Nx)+v(Nx-1))/h^2; Lapw(Nx)=(w(1)-2*w(Nx)+w(Nx-1))/h^2; fu=cos(XX).*cos(t)+(dXX.^2.*sin(XX)-ddXX.*cos(XX))*sin(t)*cos(t); fv=sin(XX).*cos(t)-(dXX.^2.*cos(XX)+ddXX.*sin(XX))*sin(t)*cos(t); fw=-sin(t)+ddXX*sin(t).^2; su=v.*Lapw-w.*Lapv-fu; sv=w.*Lapu-u.*Lapw-fv; sw=u.*Lapv-v.*Lapu-fw; en=max(sqrt(su.^2+sv.^2+sw.^2)); dt=0.99*tol/en; dt=min(dt,maxdt); if (t+dt>T) dt=T-t; end t=t+dt; nu=u-dt*su; nv=v-dt*sv; nw=w-dt*sw; u=nu; v=nv; w=nw; A=[u’ v’ w’]; for i=1:Nx B(i)=norm(A(i,:)); end u=u./B; v=v./B; w=w./B; end |
References
- Landau, L.; Lifshitz, E. On the theory of the dispersion of magnetic permeability in ferromagnetic bodies. Phys. Z. Sowjetunion 1935, 8, 101–114. [Google Scholar]
- Bertotti, G.; Mayergoyz, I.D.; Serpico, C. Analytical solutions of Landau–Lifshitz equation for precessional dynamics. Physica B 2004, 343, 325–330. [Google Scholar] [CrossRef]
- García-Ñustes, M.A.; Humire, F.R.; Leon, A.O. Self-organization in the one-dimensional Landau–Lifshitz–Gilbert–Slonczewski equation with non-uniform anisotropy fields. Commun. Nonlinear Sci. Numer. Simul. 2021, 96, 105674. [Google Scholar] [CrossRef]
- Jeong, D.; Kim, J. A Crank–Nicolson scheme for the Landau–Lifshitz equation without damping. J. Comput. Appl. Math. 2010, 234, 613–623. [Google Scholar] [CrossRef]
- Jeong, D.; Kim, J. An accurate and robust numerical method for micromagnetics simulations. Curr. Appl. Phys. 2014, 14, 476–483. [Google Scholar] [CrossRef]
- Sharma, H.; Borggaard, J.; Patil, M.; Woolsey, C. Performance assessment of energy-preserving, adaptive time-step variational integrators. Commun. Nonlinear Sci. Numer. Simul. 2022, 114, 106646. [Google Scholar] [CrossRef]
- Moumni, M.; Tilioua, M. A finite-difference scheme for a model of magnetization dynamics with inertial effects. J. Eng. Math. 2016, 100, 95–106. [Google Scholar] [CrossRef]
- Li, P.; Xie, C.; Du, R.; Chen, J.; Wang, X.P. Two improved Gauss-Seidel projection methods for Landau–Lifshitz–Gilbert equation. J. Comput. Phys. 2020, 401, 109046. [Google Scholar] [CrossRef]
- Jannelli, A. Adaptive numerical solutions of time-fractional advection–diffusion–reaction equations. Commun. Nonlinear Sci. Numer. Simul. 2022, 105, 106073. [Google Scholar] [CrossRef]
- Wang, X.P.; García-Cervera, C.J.; Weinan, E. A Gauss–Seidel projection method for micromagnetics simulations. J. Comput. Phys. 2001, 171, 357–372. [Google Scholar] [CrossRef]
- Dörfler, M. Quilted Gabor frames—A new concept for adaptive time-frequency representation. Adv. Appl. Math. 2011, 47, 668–687. [Google Scholar] [CrossRef]
- Alouges, F. A new finite element scheme for Landau–Lifshitz equations. Discrete Contin. Dyn. Syst. Ser. S 2008, 1, 187–196. [Google Scholar]
- Alouges, F.; Jaisson, P. Convergence of a finite element discretization for the Landau–Lifshitz equations in micromagnetism. Math. Models Methods Appl. Sci. 2006, 16, 299–316. [Google Scholar] [CrossRef]
- Mohammed, M.; Mouhcine, T. A finite element approximation of a current-induced magnetization dynamics model. J. Math. Model. 2022, 10, 53–69. [Google Scholar]
- Moumni, M.; Douiri, S.M.; Kim, J.S. Fourier-spectral method for the Landau–Lifshitz–Gilbert equation in micromagnetism. Results Appl. Math. 2023, 19, 100380. [Google Scholar] [CrossRef]
- Weinan, E.; Wang, X.P. Numerical methods for the Landau–Lifshitz equation. SIAM J. Numer. Anal. 2001, 39, 1647–1665. [Google Scholar]
- Yang, W.; Wang, D.; Yang, L. A stable numerical method for space fractional Landau–Lifshitz equations. Appl. Math. Lett. 2016, 61, 149–155. [Google Scholar] [CrossRef]
- Cimrák, I. A survey on the numerics and computations for the Landau–Lifshitz equation of micromagnetism. Arch. Comput. Methods Eng. 2007, 15, 1–37. [Google Scholar] [CrossRef]
- Bastos, J.P.A.; Sadowski, N. Magnetic Materials and 3D Finite Element Modeling; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Cai, Y.; Chen, J.; Wang, C.; Xie, C. Error analysis of a linear numerical scheme for the Landau–Lifshitz equation with large damping parameters. Math. Methods Appl. Sci. 2023, 46, 18952–18974. [Google Scholar] [CrossRef]
- Chen, J.; Wang, C.; Xie, C. Convergence analysis of a second-order semi-implicit projection method for Landa–Lifshitz equation. Appl. Numer. Math. 2021, 168, 55–74. [Google Scholar] [CrossRef]
- Yang, Y.B.; Jiang, Y.L. Unconditional optimal error estimates of linearized second-order BDF Galerkin FEMs for the Landau–Lifshitz equation. Appl. Numer. Math. 2021, 159, 21–45. [Google Scholar] [CrossRef]
- Fuwa, A.; Ishiwata, T.; Tsutsumi, M. Finite difference scheme for the Landau–Lifshitz equation. Jpn. J. Ind. Appl. Math. 2012, 29, 83–110. [Google Scholar] [CrossRef]
- Magaletti, F.; Gallo, M.; Perez, S.P.; Carrillo, J.A.; Kalliadasis, S. A positivity-preserving scheme for fluctuating hydrodynamics. J. Comput. Phys. 2022, 463, 111248. [Google Scholar] [CrossRef]
- Daribayev, B.; Mukhanbet, A.; Azatbekuly, N.; Imankulov, T. A quantum approach for exploring the numerical results of the heat equation. Algorithms 2024, 17, 327. [Google Scholar] [CrossRef]
- Krivovichev, G.V. Stability optimization of explicit Runge–Kutta methods with higher-order derivatives. Algorithms 2024, 17, 535. [Google Scholar] [CrossRef]
- Christou, M.A.; Papanicolaou, N.C.; Sophocleous, C. An efficient and highly accurate spectral method for modeling the propagation of solitary magnetic spin waves in thin films. Comput. Appl. Math. 2020, 39, 205. [Google Scholar] [CrossRef]
- Lee, C.; Park, J.; Kwak, S.; Kim, S.; Choi, Y.; Ham, S.; Kim, J. An adaptive time-stepping algorithm for the Allen–Cahn equation. J. Funct. Spaces 2022, 2022, 2731593. [Google Scholar] [CrossRef]
- Cheng, Q.; Shen, J. Length preserving numerical schemes for Landau–Lifshitz equation based on Lagrange multiplier approaches. SIAM J. Sci. Comput. 2023, 45, A530–A553. [Google Scholar] [CrossRef]
- He, J.; Yang, L.; Zhan, J. Temporal High-Order Accurate Numerical Scheme for the Landau–Lifshitz–Gilbert Equation. Mathematics 2024, 12, 1179. [Google Scholar] [CrossRef]
- De Laire, A. Recent results for the Landau–Lifshitz equation. SeMA J. 2022, 79, 253–295. [Google Scholar] [CrossRef]
- Atkinson, K.; Han, W.; Stewart, D.E. Numerical Solution of Ordinary Differential Equations, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Alshina, E.A.; Zaks, E.M.; Kalitkin, N.N. Optimal first-to sixth-order accurate Runge-Kutta schemes. Comput. Math. Math. Phys. 2008, 48, 395–405. [Google Scholar] [CrossRef]
- Ham, S.; Kim, J. Stability analysis for a maximum principle preserving explicit scheme of the Allen–Cahn equation. Math. Comput. Simul. 2023, 207, 453–465. [Google Scholar] [CrossRef]
- Lee, C.; Kwak, S.; Hwang, Y.; Kim, J. Accurate and efficient finite difference method for the Black–Scholes model with no far-field boundary conditions. Comput. Econ. 2023, 61, 1207–1224. [Google Scholar] [CrossRef]
- Dieguez, G.; Batistela, C.; Piqueira, J.R.C. Controlling COVID-19 spreading: A three-level algorithm. Mathematics 2023, 11, 3766. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Kwak, S.; Mohammed, M.; Kang, S.; Ham, S.; Kim, J. An Efficient and Accurate Adaptive Time-Stepping Method for the Landau–Lifshitz Equation. Algorithms 2025, 18, 1. https://doi.org/10.3390/a18010001
Kim H, Kwak S, Mohammed M, Kang S, Ham S, Kim J. An Efficient and Accurate Adaptive Time-Stepping Method for the Landau–Lifshitz Equation. Algorithms. 2025; 18(1):1. https://doi.org/10.3390/a18010001
Chicago/Turabian StyleKim, Hyundong, Soobin Kwak, Moumni Mohammed, Seungyoon Kang, Seokjun Ham, and Junseok Kim. 2025. "An Efficient and Accurate Adaptive Time-Stepping Method for the Landau–Lifshitz Equation" Algorithms 18, no. 1: 1. https://doi.org/10.3390/a18010001
APA StyleKim, H., Kwak, S., Mohammed, M., Kang, S., Ham, S., & Kim, J. (2025). An Efficient and Accurate Adaptive Time-Stepping Method for the Landau–Lifshitz Equation. Algorithms, 18(1), 1. https://doi.org/10.3390/a18010001








