Abstract
This study evaluates several maze generation algorithms applied to generate mazes in a game-based Android mobile application designed to support children in learning basic programming concepts and computational thinking. Each algorithm is assessed for its ability to generate solvable and educationally effective mazes, varying in complexity and size. Key findings indicate that Wilson’s and Aldous–Broder algorithms were identified as the most time inefficient. In comparison, Sidewinder and Binary Tree algorithms perform best for smaller mazes due to their straightforward traversal methods. The Hunt-and-Kill and Recursive backtracker algorithms maintain higher ratios of longest paths, making them suitable for the more complex maze generation required for advanced game levels. Additionally, the study explores various maze-solving algorithms, highlighting the efficiency of the recursive algorithm for simpler mazes and the reliability of Dijkstra’s algorithm across diverse maze structures. This research underscores the importance of selecting appropriate maze generation and solving algorithms to balance generation speed, path complexity, and navigational characteristics. While the study demonstrates the practical applicability of these algorithms in a mobile educational application, it also identifies limitations and suggests directions for future research.
1. Introduction
Among young learners, programming goes beyond simply writing code. It introduces them to computational thinking, which involves problem-solving using computer science concepts such as abstraction and decomposition. One way to teach children the basic programming concepts is through maze-based problems. A maze is a type of game in which a player navigates through branching pathways to find an exit or reach specific targets [1]. In the context of learning basic programming concepts, maze-based problems and games guide even the youngest learners on how to break down the problem into smaller tasks [2,3]. More precisely, this approach requires them to identify the sequence of steps required to navigate (e.g., move forward, move left, and move right) through the maze or game board to reach a certain point or complete a task. Depending on the child’s age, these games can be designed as unplugged activities, i.e., activities without the use of a computer and digital screens, activities with programmable robotic toys, mobile, web or desktop applications [4].
In digital games, the maze-making process involves designing the layout of paths and walls within the maze and various methods and algorithms exist to generate a maze [5]. Still, they generally fall into two categories: creating paths step by step within a maze initially enclosed by walls or constructing walls on an initially open field or space. Despite the number of well-known algorithms, the maze-making process remains a challenging area. This complexity arises from the need to balance algorithmic efficiency with creativity in design, ensuring that the generated mazes are not only solvable but also engaging and appropriately challenging for the intended audience. The integration of these algorithms into practical applications, such as games or educational tools, requires a deep understanding of user interaction, problem-solving strategies, and cognitive development, making the maze-making process a multidisciplinary challenge that extends beyond mere algorithmic design.
Yet, existing research on the application of maze generation algorithms and their efficiency in creating solvable and appropriate mazes for the mobile game-based learning of basic programming concepts among young children is scarce. Therefore, this paper explores the application of several different maze generation algorithms within a game-based Android mobile application designed and developed to teach basic programming concepts to children and aims to answer the following research questions:
- 1.
- How do different maze generation algorithms compare regarding time efficiency and space complexity in a mobile game-based learning environment?
- 2.
- Which algorithm is optimal for solving a generated maze in a mobile game-based learning environment?
- 3.
- What are the educational implications of using various maze generation algorithms in mobile applications designed to teach children basic programming concepts?
The developed Android mobile application enables players to guide a sketched dog character through a maze using simple commands such as moving up, down, left, and right. Mobile devices are chosen as the platform for this application because they are widely used and highly accessible, especially among younger users. Their portability allows children to engage with educational content in various settings, whether at home, in the classroom, or on the go. This flexibility makes learning more integrated into daily life, supporting continuous educational engagement and enhancing the overall learning experience. Several maze generation algorithms are integrated into the application and tested to determine their characteristics and mutual differences, ensuring they can generate mazes of varying complexity suitable for different levels of education. The algorithms are evaluated based on their time complexity, space complexity, and suitability for creating progressively challenging mazes, which are crucial for maintaining user engagement and promoting deeper learning.
The paper consists of six sections. Following the brief introduction, Section 2 covers the related work. Section 3 describes the developed maze-based mobile application for supporting children learning basic programming concepts. This section also gives a detailed overview of the implemented maze generation and solving algorithms. Section 4 provides a comparative analysis of the maze generation algorithms based on criteria such as time complexity, maze complexity, and suitability for different educational levels. In Section 5, the performance of various maze-solving algorithms is analyzed, focusing on their efficiency and effectiveness in different types of mazes generated by the application. The paper ends with a discussion and conclusion in Section 6, highlighting the strengths and limitations of each algorithm in the context of maze-based mobile educational applications and suggesting directions for future research.
2. Related Work
2.1. Fostering Computational Thinking and Programming Skills in Young Children through Maze-Based Games
Recently, there has been a growing focus on developing young children’s computational thinking skills. Computational thinking is a cognitive skill that utilizes fundamental computer science principles to address both technological and real-world problems [6], and programming has been a widely accepted method for enhancing learners’ computational thinking skills [7]. Papert [8] first introduced the concept of constructionism, where learners construct mental models to understand the world around them. This concept was the basis for various educational programming environments like LOGO [9], which allowed children to control a turtle character on the screen, thereby learning programming through visual feedback and immediate results. Later, Wing [6] emphasized the significance of computational thinking development for children and stated that it is as essential as reading, writing, and arithmetic. Moreover, research has shown that early childhood is a crucial time for development and learning [10,11,12], making it necessary to prioritize the cultivation of computational thinking in young children.
To support this approach, developing educational tools and games to introduce children to programming concepts has been a vibrant research area, where various methodologies and technologies have been explored to make learning engaging and effective. These efforts include developing and using visual programming languages that simplify coding for young learners, integrating game-based learning strategies to enhance motivation and retention, and using digital and physical tools, such as robotic toys and interactive apps, to reinforce computational thinking. Some of these approaches are described below.
Visual programming languages [13] and tools like Scratch (https://scratch.mit.edu/, accessed on 26 August 2024 Blockly (https://developers.google.com/blockly, accessed on 26 August 2024), and MIT App Inventor (https://appinventor.mit.edu/, accessed on 26 August 2024) have gained widespread adoption due to their intuitive drag-and-drop block-based interface that simplifies coding for beginners. They make programming accessible to a younger audience by reducing the syntactic complexity associated with traditional text-based programming languages [14]. They are rooted in the constructionist tradition, which emphasizes self-directed learning through art, games, and interactive stories [15]. These tools are often used to build simple games, offering an engaging way for learners to apply programming concepts in a creative and interactive context [16,17,18]. Game creation through visual programming languages involves tasks such as character movement, score keeping, and event handling, all of which reinforce foundational programming concepts like loops, conditionals, and variables. Moreover, the visual and interactive nature of game development helps to sustain motivation and interest, making the learning process enjoyable. As learners progress, they can gradually tackle more complex projects, eventually transitioning to more advanced programming environments with a solid understanding of the underlying logic and structure of programming. In some cases, they combine other technologies, such as augmented reality and virtual reality, to enhance computational thinking abilities while reducing the cognitive load [19,20]. This approach fosters a deeper connection between creativity and computational thinking, making it a powerful educational tool.
In general, game-based learning [21] has been recognized as an effective strategy for engaging children in educational activities [22,23], particularly in the domain of programming [24] and developing computational thinking [25]. It is usually defined as a game-like activity with specific learning objectives [26]. The existing research argues that the game-based approach increases motivation and player engagement and encourages risk-taking, trying new things, and exploration [21]. One of the most common approaches to supporting the development of computational thinking skills and introducing basic programming concepts to young children through games is solving maze-based problems. This contemporary approach engages children and helps develop their problem-solving and computational thinking skills [27]. Moreover, not only solving maze-based problems but constructing them through the use of visual programming languages encourages the development of computational thinking [28].
For preschoolers, this approach is usually applied as unplugged game activities [29] or play with screen-free robot toys [30]. In particular, an unplugged activity can be organized as a maze with obstacles taped on the floor or a maze drawn on paper, and children need to solve the problem step by step, i.e., by “coding” the pathway through the maze. Similarly, with haptic screen-free coding toys such as Code & Go® Robot Mouse (https://www.learningresources.com/item-stem-robot-mouse, accessed on 26 August 2024), they need to instruct, i.e., program, the robot toy to solve the maze problem.
In addition to the screen-free approach, a digital interface can be utilized to control the movement of the robotic toy or to interact with specially developed mobile, web, or desktop applications. As an example, commercial mobile applications such as Lightbot (https://lightbot.com/, accessed on 26 August 2024) and Kodable (https://www.kodable.com/, accessed on 26 August 2024) have been designed to teach programming logic through gameplay, where users solve puzzles by programming characters’ movements. Similar to visual programming languages, applications can integrate other innovative technologies, such as virtual reality [31], which have been demonstrated to enhance learning effectiveness. These technologies not only boost learning motivation but also have the potential to reduce cognitive load, making complex concepts more accessible and engaging for learners.
Regardless of the technology used, the objective of a maze-based game remains consistent: to provide a structured problem-solving environment that helps children learn basic programming skills and develop computational thinking. By navigating through mazes, children learn to break down complex problems into smaller, manageable tasks, reinforcing essential programming concepts and logical thinking. However, existing research indicates that factors such as age and gender may influence how effectively maze-based problems are applied [32,33]. This highlights the importance of offering differentiated tools and challenges tailored to various age groups and individual needs.
2.2. Maze Generation and Solving Algorithms
Maze generation algorithms are a key component in developing puzzle-based educational games, particularly those aimed at teaching programming and problem-solving skills. In his book, Buck [5] summarized and explained eleven maze generation algorithms: the recursive backtracker, Eller’s algorithm, Kruskal’s algorithm [34], Prim’s algorithm [35], the recursive division algorithm, the Aldous–Broder algorithm [32], Wilson’s algorithm [36], the Hunt and Kill algorithm, the Growing Tree algorithm, the Binary Tree algorithm, and the Sidewinder algorithm. However, the performance and suitability of these algorithms vary significantly based on the application’s requirements.
Over the years, programmers and researchers have analyzed, improved, adjusted, and proposed different maze generation algorithms to best suit the given situations. For example, in a comparative analysis of different maze generation algorithms, Mane et al. [37] studied Prim’s algorithm, Kruskal’s algorithm, the DFS algorithm (Depth First Search), Eller’s algorithm, Wilson’s algorithm, the Hunt and Kill algorithm, and the Aldous–Broder algorithm. They evaluated algorithms based on two parameters: the time taken by the algorithm to generate the maze, and the space complexity of the maze. Their research findings suggest that, on average, DFS is the fastest approach for producing and solving mazes. Similarly, Grabovšek [38] ranked different maze-generating algorithms according to their difficulty. He inspected several features, such as the number of visited intersections, dead ends, and overall steps of the solving agents. In this study, the Aldous–Broder and Wilson’s algorithms achieved the best results. Implementing dynamic maze generation in games is another crucial area, where the speed of generation is paramount. For instance, Hendrawan [39] examined three different implementations of the Growing Tree method for maze generation on Android mobile devices, concluding that the maze creation process operates efficiently on these devices. As for the new approaches, Bellou et al. [40] tried to create a perfect maze, where any two cells can be joined by a unique path. They proposed an original approach to classify mazes using the simple measures introduced by Buck [5], as well as the physical-based measures introduced by McClendon [41]. They designed two original maze generators, Prim and Kill, and Twist and Merge, and their study showed that the Twist and Merge algorithm is the best performingamong all the other algorithms.
On the other hand, Sadik et al. [42] elucidated how graph theory can be used to solve mazes. They compared BFS (Breadth First Search) and DFS algorithms, and their analysis suggests that the memory requirement for coding is higher in DFS than in BFS. Therefore, in the case of large mazes, BFS is more appropriate than DFS. If the maze contains several paths to reach the destination, DFS may be time-consuming. Thus, they suggested not to use DFS in those scenarios. Moreover, if the consideration point is to find the shortest path, then BFS is preferred over DFS. More recently, Martín-Nieto et al. [43] presented a new idea for solving mazes using graph theory. They elaborated on how to minimize the length of the optimal path formulated as a topology optimization problem by mapping a maze with finite elements and then, through the eigenvalues of the Laplacian matrix of the graph, imposing a constraint over the connectivity between the input and the output. Tjiharjadi et al. [44] conducted a systematic literature review focusing on research related to multi-agent systems, various maze-solving algorithms, and particularly multi-agent pathfinding. Their findings revealed that most multi-agent pathfinding applications were implemented in static environments with predefined target locations. Additionally, the majority of studies employed agents with individual goals, enabling distributed decision-making and distinct interests. Only a limited amount of research explored the capability to adapt environmental topologies, tasks, and other dynamic factors.
The diversity of the available algorithms highlights the range of strategies developers can employ to create engaging and challenging mazes. However, the performance and suitability of these algorithms depend significantly on the application’s specific requirements, such as the desired complexity, execution speed, and adaptability to dynamic environments. Moreover, there is very little research on the application and effectiveness of these algorithms on mobile devices and mobile applications designed to foster computational thinking and teach basic programming concepts to children.
3. Maze-Based Mobile Application for Learning Basic Programming Concepts
3.1. Application Overview
A game-based Android mobile application was developed to support children (age 5+) in learning basic programming concepts and encourage computational thinking. In this game, players guide a sketched dog character through a maze using simple commands such as moving up, down, left, and right. The game concept involves the player selecting a sequence of commands, which are then executed to guide a dog character through the maze, with the dog’s movement visually representing the command execution. At the end of the game, an image of either a happy or sad dog is displayed, depending on the outcome, specifically, whether the dog successfully reached its target, the doghouse. Subsequently, the child has the option to either replay a game of comparable complexity or advance to a more challenging one upon achieving accomplishment. A basic flow of the application is depicted in Figure 1.
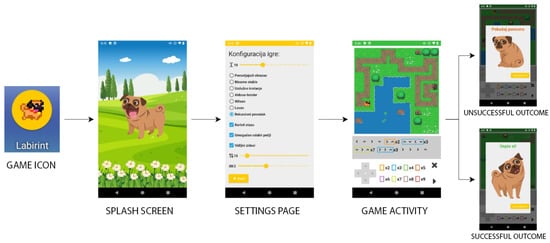
Figure 1.
Basic user flow of the mobile application, starting with the settings screen upon application launch, followed by the activity display, and concluding with a happy or sad dog image based on the game outcome.
As shown in Figure 2, the application’s main screen is structured into three distinct sections. The top section features the game board (i.e., maze), composed of a two-dimensional grid of cells. Each cell can be fenced off on each of the four sides by an obstacle, bearing in mind that the edge cells always have an outer fence on one or two sides. Several elements can be represented in each cell: dog, the dog’s house, path or road, water, grass, flowers, bush, stump, and rocks. The command area is directly below the game board, which displays the user’s selected sequence of commands. The bottom section of the interface provides the controls for interacting with the game. Through this section, a user manipulates the dog character’s movement by choosing from an assortment of pre-established instructions. A designated button initiates the execution of these commands, prompting the dog character to traverse the game board accordingly. Commands are highlighted in real time as the dog moves through the maze, offering immediate visual feedback on the effects of each action. This real-time command highlighting reinforces the understanding of cause-and-effect relationships inherent in programming logic.

Figure 2.
Layout of the application’s game activity, showing the maze in the top section, the middle gray section displaying the selected commands once the game starts, and the bottom section containing available controls and commands.
In the command area, the command input is facilitated by four buttons, which are shown as part of a game controller button. When the commands are clicked, they are added to the command area as shown in Figure 3. The interface features intuitive icons for each command, providing a straightforward user experience. Haptic feedback accompanies each button press, enhancing tactile interaction, while the selected commands are visually displayed in a designated interface area.
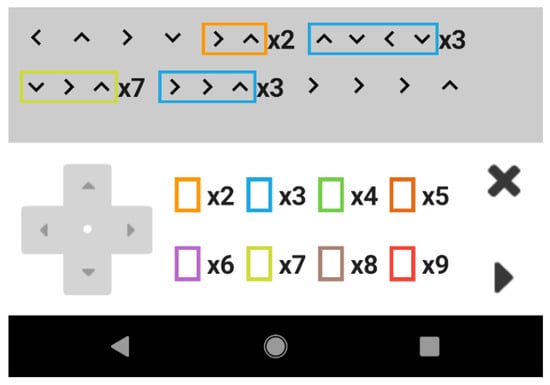
Figure 3.
Entry and overview of available commands in the command area.
Users can also make loops with a certain number of iterations, aiming to minimize the number of movement commands. Upon identifying a recurring pattern, the user can employ a loop to execute it, gaining insight into the practicality and efficacy of loops. The user selects these commands also by clicking on the appropriate button in the command area as shown in more detail in Figure 4.
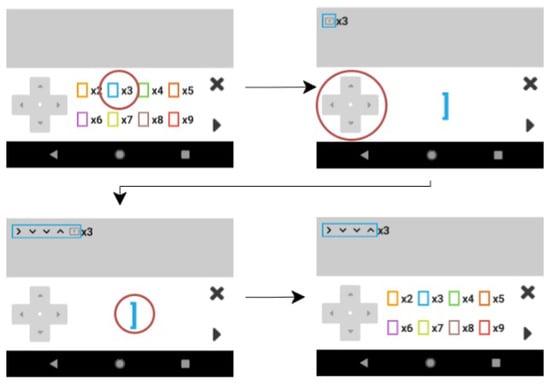
Figure 4.
Example of loop creation using the available commands. First, a player selects an adequate command representing the number of iterations (upper left), which is followed by entering the movement commands through the controller.
3.2. Maze Generation Algorithms
To display a route from the initial point to the final point (i.e., the dog’s house), it is imperative to create an algorithm that identifies the route and verifies the generated game scenario to ensure the maze can be solved. Moreover, the variety of maze complexities allows for adaptability in learning. Starting with simpler mazes and gradually increasing their difficulty can help children build on their knowledge incrementally, ensuring a solid understanding before moving to more complex tasks. In addition, the progressive challenge presented by different types of mazes can maintain interest and encourage continuous learning. The choice of maze type in a learning application is not just about creating a challenge but also about carefully crafting learning experiences that align with the child’s current level of understanding and readiness to advance to more complex concepts.
Launching the mobile application by selecting the game icon navigates to the game’s main menu, i.e., the settings page (see Figure 1). This menu allows users to customize the game settings and select the algorithm for generating the maze. The algorithm is then provided with input parameters such as the dimensions of the game board, the inclusion of water, and other relevant factors. The dimensions of the game board serve as the fundamental parameter for the level of difficulty, as larger boards allow for complex mazes and lengthier paths that necessitate a greater number of instructions to solve. Further, it is possible to define the length of the path that is generated.
Additionally, the game offers an option to generate a maze without a visible path. If the option for path generating is not chosen, the user has the freedom to navigate throughout the entire board within the boundaries of the maze’s structure. The purpose of this mode is to generate levels of escalating complexity, where the dog and his house are strategically positioned to ensure that the road connecting them is the longest route within the maze. The approach relies on constructing a maze structure that is characterized as a rectangular grid with an equal number of rows and columns. Employing such a framework ensures the achievement of effective level generation by preventing the creation of self-intersecting paths, a scenario that would not be feasible with a purely random approach. Both modes are depicted in Figure 5.
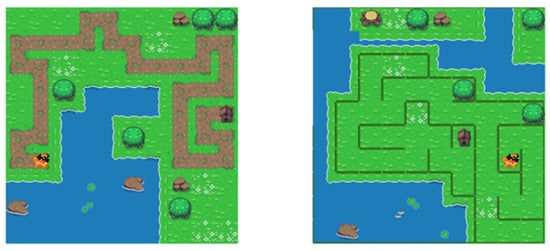
Figure 5.
Comparison of the two basic game versions: (left) with a visible path and (right) without a visible path through the maze.
In addition to allowing the manual selection of maze generation algorithms through the settings page, the game dynamically generates levels as the player progresses, gradually increasing in difficulty to sustain the child’s attention. Several algorithms were either adapted from existing maze generation techniques [5] or specifically designed, developed, and integrated into the mobile application to support maze generation. These algorithms are detailed in the following sections.
3.2.1. Repeating Pattern Algorithm
Creating game levels containing a clear and simple movement pattern is necessary to introduce users to the basics of pattern recognition. To ensure the creation of such levels, an algorithm was developed that generates the board. First, one direction is randomly selected from the four possibilities of diagonal movement within the game board from the starting position to the goal, i.e., northwest, northeast, southeast, or southwest. At the beginning, the basic structure of the game is defined. Using the data for direction and the number of moves, a correct and repeating sequence of commands is generated through a random selection method, constituting the solution for the created maze. The defined solution is then visualized by marking the starting and goal positions and drawing the path between them. The examples of generated mazes are depicted in Figure 6.
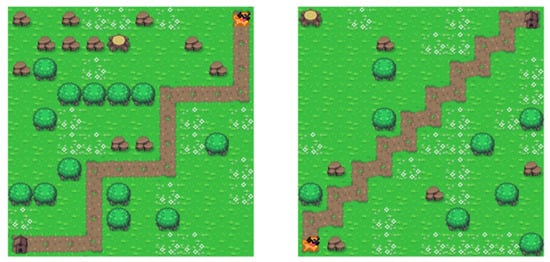
Figure 6.
Example of two mazes created with repeating pattern algorithm.
3.2.2. Random Selection Algorithm
The algorithm randomly traverses all cells of the game board. Based on a previously defined probability percentage parameter, it uses a random number generator to decide whether any of the cell’s edges should have the property of an obstacle. After the edges are defined, the algorithm passes through all the cells again. In this second pass, all cells whose edges have not initially been defined as obstacles and are adjacent to obstacles become obstacles themselves. The purpose of this action is to set the correct data for the data structure of each cell, which is necessary for the application to allow or restrict movement in a particular direction using the information contained in the data of the currently active cell. The application will allow movement in the desired direction if the common edge between the starting and destination cells does not contain an obstacle. The algorithm ensures that not all edges of the starting and destination cells are closed, which would create an unsolvable game. The edges of the game board are always defined as obstacles to prevent the moving object from going out of bounds. After defining the maze layout, the application proceeds to validate the solvability of the generated maze using a validation algorithm. If the validation shows that the generated game instance is unsolvable, the application discards the instance and all its data and starts generating a new instance. The example of the generated game is shown in Figure 7.
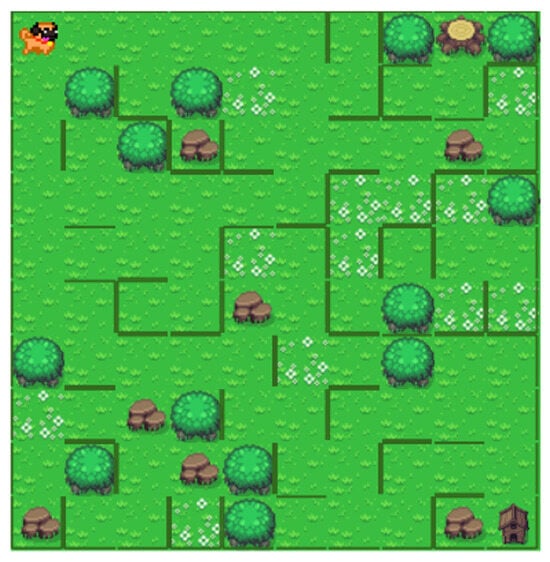
Figure 7.
Example of a maze created with random selection algorithm.
During the random generation process, situations arise where configurations of obstacles within solvable mazes create closed rooms that the player cannot access. To address this problem, an additional algorithm is created to detect these inaccessible parts and remove one of the obstacles separating the detected part from the rest of the maze. Starting from the initial position, the algorithm attempts to traverse all accessible cells by moving in random directions to ensure coverage of the entire maze. The drawback of using this method for maze generation is that it requires defining a relatively small percentage of obstacles within the maze. Any increase in the relative number of obstacles compared to the size of the maze increases the likelihood of creating an unsolvable maze. If it is determined that the maze is unsolvable, the generation and validation process is restarted. This process can take an exceptionally long time if a high percentage of obstacles is required in the game. After the algorithm completes the initial traversal, a search is initiated for any cells in the maze that have not been visited. If the algorithm finds a cell that has not been visited, it removes one of the obstacles separating the unvisited and visited cells. The process is then repeated from the beginning until all cells within the maze are marked as visited.
3.2.3. Binary Tree Algorithm
The Binary Tree algorithm is one of the most straightforward maze generation methods. The tree data structure represents the hierarchical relationships among interconnected nodes. Each node has a maximum of two child nodes, and these child nodes can also have their child nodes. Each node corresponds to a decision point for navigating through the maze. Selecting a child node signifies choosing the direction to take. The paths that connect the root and final nodes symbolize the routes within the maze. The adjusted algorithm for the described mobile application initiates its procedure by designating all cells obstructed in every direction. It then randomly selects two adjacent ways to traverse the board. In the subsequent stage, the process involves systematically selecting one of those directions and eliminating an obstruction in that chosen direction. Once the board’s edge is reached, the direction choice becomes obligatory. One of the advantages of this approach is creating a maze with a large number of branches. Since every node can have two children, creating complex mazes with many branched paths is possible. Furthermore, these mazes can be generated quickly because the decision of obstacles in a cell is independent of other cells. This algorithm creates solutions of mazes that are generally diagonal or contain long, continuous corridors [5]. These characteristics are desirable for more straightforward tasks and easier game levels. Figure 8 presents game examples generated with the Binary Tree algorithm.
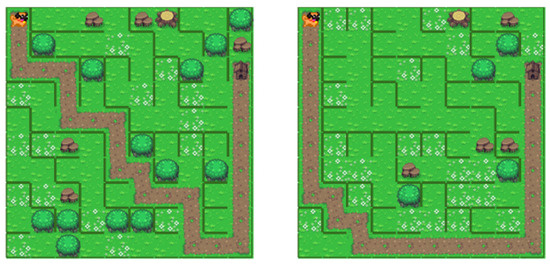
Figure 8.
Examples of mazes created with Binary Tree algorithm.
3.2.4. Sidewinder Algorithm
The Sidewinder algorithm [5] is similar to the Binary Tree algorithm because it uses two randomly chosen directions. The distinction lies in constructing a longitudinal series of interconnected cells. The algorithm starts in one of the edge cells depending on the direction, which is then added to the set. It then randomly chooses the next cell, removing the obstacle between them. If the cell is longitudinal to the previous one, it is added to the set. If the cell is transversal, the current set is closed, and a random cell is selected. The obstacle is then removed from the cell in the transversal direction towards the next cell, independent of the previous set, and added to a new set. The process is repeated until the algorithm reaches the last cell, where the longitudinal direction is impossible. A consequence of longitudinal mobility is that one side of the maze comprises a contiguous sequence of interconnected cells. This occurs due to the inability to select the transversal direction in the edge row, as it would result in going outside the boundaries. If that is not the desired outcome, the algorithm still holds an advantage over the Binary Tree approach, as it generates two rows instead. The mazes generated by this algorithm have discernible pathways in the horizontal direction, with short dead ends, making it particularly suitable for less complex mazes [5]. The examples of generated mazes are presented in Figure 9.
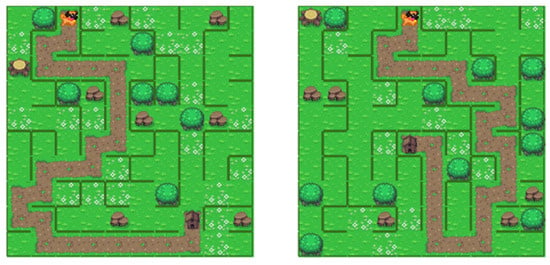
Figure 9.
Examples of mazes created with Sidewinder algorithm.
3.2.5. Aldous–Broder Algorithm
The Aldous–Broder algorithm [5] is a method of producing a uniform spanning tree. A spanning tree represents a structure that connects all the points of a graph. A uniform spanning tree is a tree that is chosen randomly and with the same probability within all the possible spanning trees in a given graph. Using this algorithm, it is possible to produce a maze by switching the points in the graph with cells of the maze and their connections with the borers of the cells. The algorithm creates the maze’s spanning tree, which determines the unique solution path through the maze. For its implementation, it is necessary to set the initial parameters of the variables. A list of cells visited by the algorithm is made, and a starting point for the algorithm is chosen. It starts from the starting point in one of four randomly chosen directions, considering the board’s edge as bounds. Every cell is assigned a sequential number. If the current cell has not been visited, the previous and current cell impediments are eliminated. The process persists until every cell has been visited. This algorithm has a couple of advantages: its relative simplicity in implementation and its minimal memory resource requirements for execution. Moreover, it generates trees that are consistent in shape, resulting in mazes that exhibit a significant level of unpredictability. An inherent limitation of the algorithm is its reliance on random direction selection, resulting in a significant time requirement for the algorithm to traverse all cells. This time requirement escalates proportionally with the size of the board. Given this factor, the approach is suitable for generating smaller mazes with negligible delay that does not compromise the user’s experience. The examples of generated boards are presented in Figure 10.
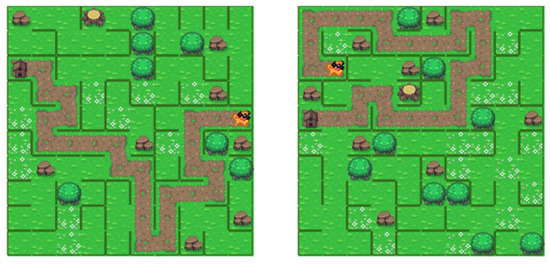
Figure 10.
Examples of mazes created with Aldous–Broder algorithm.
3.2.6. Wilson’s Algorithm
Like the previous algorithm, the Wilson algorithm [5] generates uniform spanning trees by randomly selecting the direction. The algorithm starts by randomly selecting a cell and then appending it to the list of visited cells. Subsequently, it chooses a cell at random but refrains from including it in the list at this point. The cell is the initial position for navigating the maze and begins an array of interconnected cells that link it to the previously marked visited cell. The algorithm randomly selects the direction for moving through the maze until it reaches the originally visited cell. It keeps track of the cells and determines which order they went through. If the algorithm encounters a previously visited cell, all the cells between the visits are ignored, the loop ends, and the algorithm proceeds as it did previously. When it reaches the originally visited cell, the algorithm enters the phase of connecting all the visited cells. All the visited cells are connected in the order the algorithm used. Subsequently, the search restarts by selecting another unvisited cell and repeating the procedure. The algorithm iterates the search and connects components until it traverses all the cells. This method differentiates itself from the Aldous–Broder algorithm by searching for previously visited cells. Hence, the process starts at a slower pace and gradually accelerates by constructing interconnected arrays of cells that have been visited. This algorithm is the antithesis of Aldous–Broder, as it initially operates at a high speed but gradually decelerates as it attempts to access the remaining unvisited cells. The examples of generated boards are presented in Figure 11.
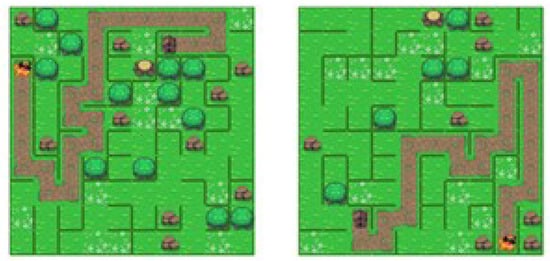
Figure 11.
Examples of mazes created with Wilson’s algorithm.
3.2.7. Hunt and Kill Algorithm
The Hunt and Kill algorithm [5] generates a maze that starts from a randomly chosen cell and moves to an unvisited neighboring cell while removing the obstacle. The direction is chosen randomly from the available directions that do not lead to a previously visited cell. The process continues until a dead end is reached, in which all the directions lead to the previously visited cell. Next, the hunt phase begins, during which the maze searches for an unvisited cell adjacent to a visited cell. If a cell of this nature is discovered, its barrier to the visited cell is eliminated, transforming it into a fresh initial location for the iterative first phase. The stages are then swapped until the hunt fails to locate an unvisited cell. The algorithm resembles the Aldous–Broder algorithm, but it distinguishes itself in the manner in which it selects directions. Specifically, this approach only permits ways that lead to cells that have not yet been visited. It results in a significant acceleration of maze creation. The mazes produced by this algorithm are distinguished by lengthy and curving corridors with relatively fewer dead ends than other methods. The examples of boards generated are presented in Figure 12.
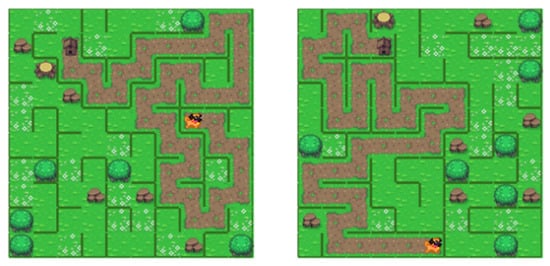
Figure 12.
Examples of mazes created with Hunt and Kill algorithm.
3.2.8. Recursive Backtracker
The Recursive backtracker algorithm [5], similar to the Hunt and Kill algorithm, uses restricted movement with random directions to enhance its efficiency. The process begins by selecting a cell at random, followed by the random selection of a direction. The obstacle between the cells is removed if the selected direction leads to a previously unvisited cell. If the current cell is surrounded by visited cells, the algorithm returns to the last cell with an unvisited neighbor and proceeds as before. The algorithm finishes when there are no cells with unvisited neighbors. It tracks the visited cells using a stack structure. The algorithm generates mazes more quickly than algorithms relying solely on random selection. This is achieved by utilizing the stack structure to keep track of the order in which cells are visited, reducing the time required to traverse the cells. This benefit becomes more pronounced as the size of the maze increases. The drawbacks of this approach include increased memory usage and the inability to guarantee a truly random labyrinth structure because using these limitations in the movement adds bias in maze generation. The examples of generated boards are presented in Figure 13.
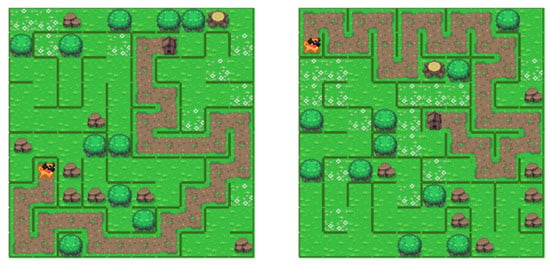
Figure 13.
Examples of mazes created with Recursive backtracker algorithm.
3.3. Algorithms for Solving Generated Mazes
The algorithms detailed below are used in the mobile application to verify the solvability of the generated game structure. If the algorithms indicate that the level is not solvable, the level generation algorithm requests the creation of a new structure. Based on the desired path length within the maze, the algorithms calculate and select the starting field position where the sketched dog character will be placed, the target field where the doghouse will be located, and the path connecting them. The path indicated in the data structure can be displayed as a trail within the game, depending on the selected menu option and the type of algorithm chosen for game structure creation. Regardless of whether the path is displayed, the calculated path is used to render the game board interface. The selection of visual elements on the defined path is restricted to ensure that no visual barrier, such as rocks or stumps, is drawn between the starting and target fields, which could confuse the user.
3.3.1. Recursive Algorithm
The generated maze is validated using an algorithm based on recursive calls. The algorithm is initially invoked for the starting cell from which the user begins the game. The algorithm calls itself again if the starting cell can transition to any of the four possible directions. In this subsequent call, the algorithm considers the adjacent cell next to the initial cell and has no barrier between them. The recursive call process repeats as long as the currently observed cell has at least one neighboring cell with which it does not share a barrier. If the algorithm encounters the target cell during verification, the validation process stops, and a positive result is returned. A positive result indicates an uninterrupted series of adjacent cells from the start to the target position. The algorithm can enter a loop if the created maze has multiple valid solutions for passing from the starting cell to the target cell. The algorithm might revisit already observed cells to find a valid path, thereby increasing the validation time and using the user’s device resources. A data structure tracks the list of visited cells to avoid this possibility. If the algorithm encounters a cell that has been previously checked, it returns a negative response to its previous caller. The calling algorithm can then attempt to validate using another free cell, if available. If no other cell is accessible, the algorithm returns a failed validation. One of the limitations of this algorithm is that in very complex mazes, the algorithm may take a significant amount of time to find a valid path. When the algorithm encounters a dead end, it identifies that path as invalid only upon reaching the end of the dead end.
3.3.2. Dead-End Filling Algorithm
A dead end within a maze is an uninterrupted path extending from a junction to a barrier that prevents further movement. The dead-end filling algorithm addresses this by identifying all dead-end cells surrounded by barriers on three sides. Once identified, the algorithm fills these paths back to the first junctions. This process is repeated iteratively, continually identifying and filling new dead ends. Ultimately, the algorithm ensures only the correct paths remain through the maze, assuming the maze is perfect and contains no loops. The advantages of using this algorithm include its relatively simple implementation and efficient execution. However, a limitation of the algorithm is that it cannot be used in mazes containing loops or mazes without dead ends, i.e., in imperfect mazes [39].
3.3.3. Customized Dijkstra’s Algorithm
Dijkstra’s algorithm [5] is a graph search algorithm used to find the shortest path between two nodes in a graph. This study employed a customized variant of this algorithm to analyze the mutual distances between individual cells of the maze. Using information on the number of steps required from a selected cell in the maze to all other cells provides an approximate evaluation of the maze’s difficulty. Since the path length from the starting cell to the target cell is one of the main characteristics of a maze, the length of this path can proportionally represent its difficulty. Therefore, this algorithm allows for adjusting the maze’s difficulty by changing the starting and target positions within the maze. Suppose the starting and target positions are fixed. In that case, it is possible to request the generation of a new maze if the currently generated one is deemed unsuitable, allowing for the creation of a lower- or higher-difficulty maze. The customized variant of the algorithm operates on the principle of flooding the maze from an arbitrary cell, which is assigned a distance of 0, i.e., the distance of the cell from itself. The algorithm then searches for all neighboring cells that have an open path with the starting cell. These cells are marked with a distance of 1 because it takes one step to reach them from the starting cell. The algorithm continues by searching for accessible neighbors for each cell at a distance of 1, which are then marked with a distance of 2. This process continues, identifying neighbors for each new neighboring cell until the algorithm has traversed all cells in the maze. Upon completion, the algorithm creates a data structure containing information on all cells’ distances from the selected cell in the maze. If the starting cell is the target cell of the maze, the created data structure allows for the examination of the maze solution, i.e., the shortest path from any point in the maze to the goal. The first step is to identify the distance of the cell from which the maze traversal begins. It is then sufficient to find a neighboring cell with an open path that has a distance less than the current cell’s distance and move to it. Repeatedly moving to the cell with a smaller number than the current one ensures a path to the target cell. This solution also represents the shortest path if the maze contains multiple possible solutions. In addition to finding the optimal maze solution, the algorithm can be adapted for other purposes that utilize distances between cells. If the goal is to find the most distant point from a given point, it is enough to examine the data structure and locate the highest number, whose position also marks the cell’s location in the maze. Using the algorithm twice enables the identification of the longest path within the maze between two cells. This is useful for creating, for example, the hardest variant of the game for a given maze, where one cell is marked as the starting point and another cell as the target. Any arbitrary cell within the maze is selected to find this path, and distances are calculated for it. Then, the cell farthest from the chosen one is identified. The identified cell becomes the new starting point, and the algorithm is repeated once more to calculate distances from the new cell. The path connecting the second starting cell and its farthest cell represents the longest path within the maze.
4. Analysis of Maze Generation Algorithms
Simulations were conducted to evaluate the performance of the aforementioned algorithms to determine characteristics and mutual differences and select the optimal algorithm for maze generation. For each algorithm, the requirement was set to create 100 mazes in the size range of the number of cells per page from 5 to 30 cells, matching the maximum size of the maze used in the developed mobile application. This resulted in mazes varying in size from 25 to 900 cells. The device used for measuring the performance of the algorithms was the Google Pixel with OS Android 10 (API version 29), which was introduced on the market in 2013.
4.1. Maze Generation Time Analysis
To analyze and compare the maze generation times of the implemented algorithms, the time taken to generate each of 100 mazes per algorithm was measured using a built-in software timer. Through data analysis, it was determined that Wilson’s algorithm and the Aldous–Broder algorithm stand out compared to the other methods (Figure 14). The time required to build the maze increased exponentially as the maze size increased. This impacts these algorithms most, as they need to visit every cell.
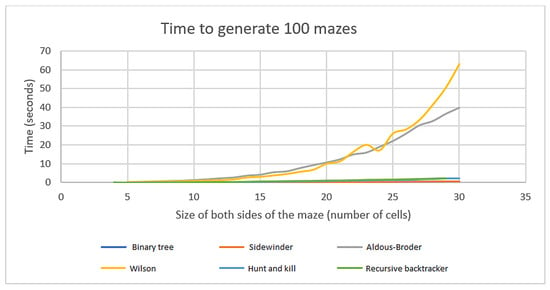
Figure 14.
Speed comparison of maze generation algorithms.
When applying a solely random approach to choose direction in algorithms, no additional data structures can affect this selection. One benefit of this technique would be eliminating bias in the maze generation process. The bias becomes apparent when generating a specific quantity of mazes using each algorithm as evidenced by corridors oriented in particular directions and variations in the length and quantity of dead ends. An instance of a discernible prejudice is the Sidewinder algorithm, which consistently produces a pathway of interconnected cells that adhere to a single edge of the maze. For the Binary Tree maze, there are consistently two passageways. Other algorithms can be divided into two groups when observing the time ratio to generate the maze and its size (Figure 15).
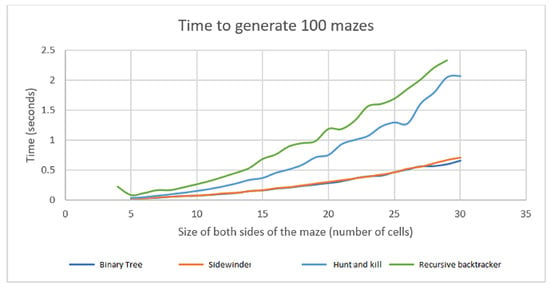
Figure 15.
Speed comparison of maze generation algorithms (without the Aldous–Broder and Wilson algorithms).
The Sidewinder and Binary Tree algorithms are the most efficient methods for achieving optimal results. This can be attributed to their comparatively uncomplicated execution and consecutive traversal of all the cells in the maze. The trade-off for achieving that level of speed is the previously mentioned bias. This bias is desirable in generating the starting levels with long straight corridors requiring simple solutions. Designing a visually captivating and intricate maze for advanced levels is crucial to enhancing the user’s engagement and maintaining their attention. Additionally, the Binary Tree and Sidewinder algorithms cannot remove cells from the maze. These algorithms require a proper grid that is fully accessible. Some cells could reach a dead end and stop if they are missing. Consequently, it is impossible to use these algorithms to create game boards with visually appealing elements, such as water. To generate those game boards, algorithms such as the Hunt and Kill and Recursive backtracker algorithms were used. Their characteristics demonstrate a favorable balance between the requirement to produce visually appealing and complex mazes, minimal bias, and a reasonable generation time. Thus, they are highly suitable for designing harder levels of the game.
4.2. Analysis of the Ratio of the Longest Path in the Maze Area
Mazes must be longer and more complex to create a progressive difficulty curve in the game. The size of the maze becomes the constraining factor in that procedure. An examination is undertaken to determine the optimal algorithm for efficiently using the available grid. A modified Dijkstra algorithm is used to determine the longest possible path within each generated maze. The path size is determined by counting the number of cells it contains and then calculating the ratio of those cells to the total number of cells. The graph for different algorithms is depicted in Figure 16.
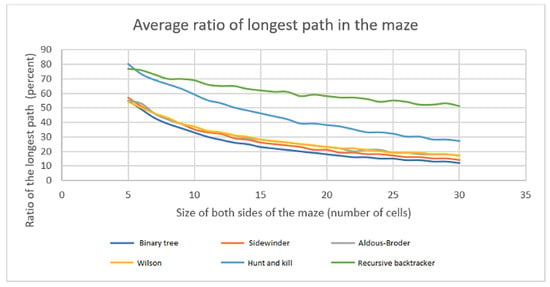
Figure 16.
Comparison of ratios of the longest path in the maze.
The relationship between maze size and the ratio of the longest path is easily understood: as the maze size increases, the ratio of the longest way decreases. The majority of algorithms yield comparable outcomes in this context. However, the Hunt and Kill algorithm and the Recursive backtracker method are particularly noteworthy. Their usage is significantly high. However, it declines with the size, albeit to a lesser extent compared to other methods. It is worth noting that the game’s first levels tend to be relatively simple and have short routes. Therefore, the demand for this aspect is not very crucial. However, as the game progresses to more difficult levels, this demand becomes more substantial and should be considered.
4.3. Analysis of the Share of Direct and Curved Movement
Introductory levels designed to familiarize users with the game should possess specific attributes. The solutions should be straightforward, with little changes in direction and a preference for long corridors of interconnected cells. These pathways facilitate the input of commands and loops more straightforwardly while reducing visual complexity to prevent the perception of the game from being excessively challenging. An analysis was conducted to determine appropriate algorithms for generating these levels. Each algorithm has generated a hundred mazes of varying sizes to compare the different methods of navigating through the maze. Given that the game chooses the path randomly, all cells have been adequately accounted for. The count of cells in the maze restricted to movement in only two perpendicular directions (east–west and north–south) was established, and the ratio of these cells to the total number of cells was computed. The findings are depicted in Figure 17.
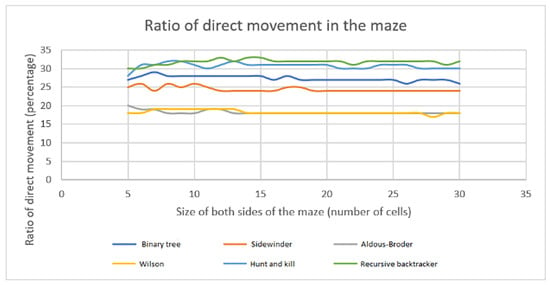
Figure 17.
Algorithm comparison of ratios of cells with direct movement in the area of the maze.
The analysis shows that the ratio described remains constant across different maze sizes, but it does vary based on the technique used. The Hunt and Kill algorithm and the Recursive backtracker method exhibit the highest ratio, within the 28 to 32 percent range. The Aldous–Broder and Wilson’s algorithms exhibit the smallest ratio, within the 18 to 20 percent range. Another factor to consider is the proportion of cells that necessitate a change in orientation. The higher the percentage, the more difficult the maze becomes, necessitating more commands to solve the problem. The pathways can be enhanced aesthetically and present a greater level of difficulty in the advanced stages of the game. The outcomes of the analysis from the simulation are presented in Figure 18.
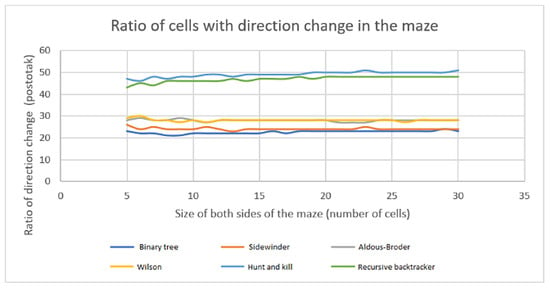
Figure 18.
Algorithm comparison of ratios of cells with direction change in the area of the maze.
Like the previous ratio, this ratio remains constant regardless of the maze size. The Hunt and Kill algorithm and the Recursive backtracker exhibit a noticeable disparity, ranging from 46 to 51 percent. In contrast, the other algorithms have a 21 to 30 percent ratio. The diagram presented in Figure 19 illustrates the mean proportion of movement types for each algorithm.
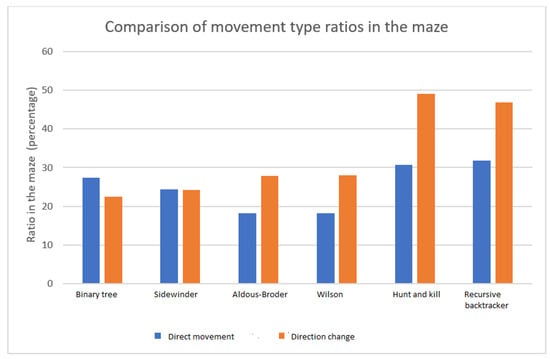
Figure 19.
Comparison of algorithm ratios by movement type.
Although the Hunt and Kill algorithm and the Recursive backtracker algorithm have the highest ratio of cells with unchanged direction, they also have a very high number of cells that require a change in direction. When aiming to design a simpler level, algorithms with a high ratio of direction cells that stay the same and a low ratio of cells that require a change in direction should be considered. The Binary Tree method and the Sidewinder algorithm are the most appropriate choices for meeting that requirement, and they should be employed to construct the initial levels. The Hunt and Kill algorithm and the Recursive backtracker method are the most optimal choices at advanced levels.
5. Analysis of Algorithms for Finding Maze Solutions
Choosing an optimal algorithm to solve the generated maze was necessary to optimize the application’s performance. The solving time of one hundred mazes generated with varying dimensions, ranging from 5 to 30 cells per axis, was analyzed. This process was performed for each algorithm and each instance of the maze, with the total duration calculated by summing up the individual times. The device utilized for the simulation remained unchanged from the preceding section. An examination of the solution time utilizing the Recursive call algorithm reveals that the time is comparable for the majority of algorithms, except for instances when the labyrinth is created by the Sidewinder algorithm, in which case, the time is even quicker when the Binary Tree algorithm generates the maze. For solving the maze with the dead-end filling algorithm, the solution size is similar regardless of which algorithm has been used to generate the maze. These are depicted in Figure 20.
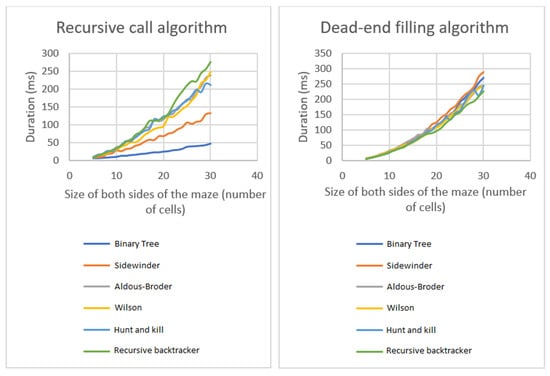
Figure 20.
Comparison of solution times: Recursive call algorithm (left) vs. dead-end filling algorithm (right).
Using the Dijkstra algorithm to compute distances consistently yields comparable results across all techniques (Figure 21). The exceptions are the generated Recursive backtracker mazes that require more time to solve. The times of solving the maze differ for a solving algorithm depending on the algorithm used to generate it. Therefore, an additional analysis is conducted.
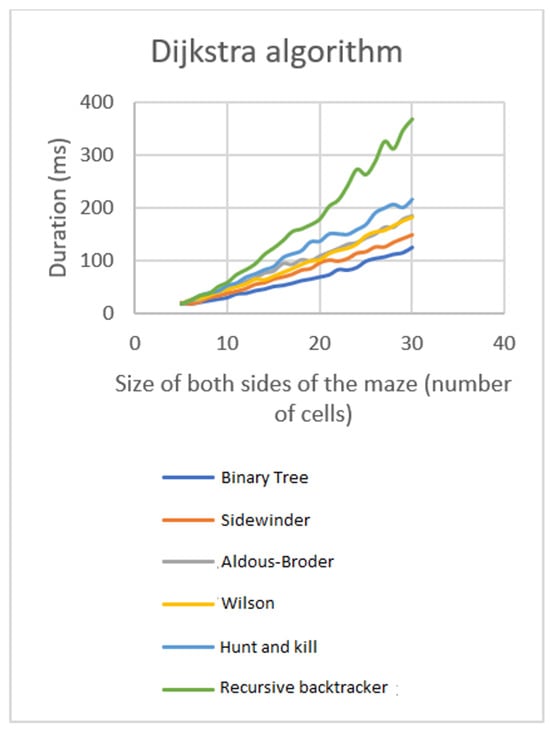
Figure 21.
Comparison of solution times for Dijkstra algorithm.
The Recursive call algorithm demonstrates the most optimal performance for mazes generated by the Binary Tree algorithm (Figure 22), whereas the dead-end filling algorithm exhibits the least favorable performance. Expanding the size of the maze amplifies this disparity. The Sidewinder algorithm mazes deliver comparable outcomes to the Binary Tree algorithm mazes, however, with a slightly inferior performance by the Recursive call algorithm that is closer to the Dijkstra algorithm. Both algorithms are appropriate for solving these mazes. The Binary Tree and Sidewinder algorithms show bias in their structure by producing elongated corridors extending along the edges. This bias also results in a significant number of dead ends, leading to suboptimal performance for the dead-end filling algorithm.
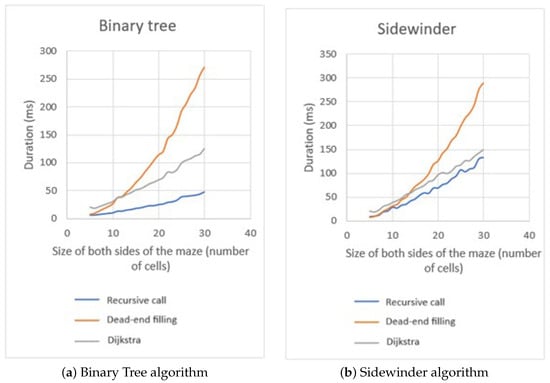
Figure 22.
Comparison of solution times: Binary Tree mazes (a) and Sidewinder mazes (b).
All methods demonstrate comparable efficiency when navigating through the mazes generated by the Aldous–Broder algorithm and the Wilson algorithm (Figure 23). Both algorithms utilize a predominantly random selection strategy to construct mazes, ensuring the avoidance of bias. The obtained results support this fact. Increasing the number of mazes enhances the diversity, preventing the solving algorithms from taking advantage of predictable patterns. If a particular algorithm demonstrates greater efficiency with one maze, the subsequent maze may present a higher difficulty level. When there are many mazes, the performance tends to level.
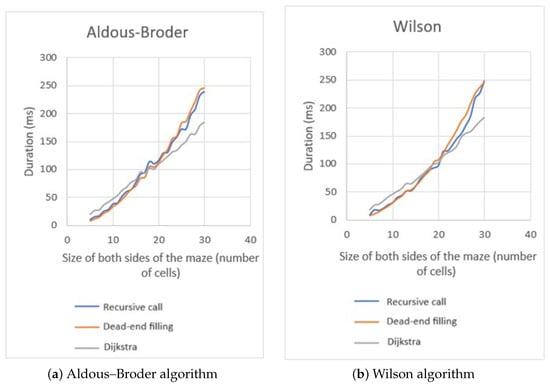
Figure 23.
Maze solving comparison of Aldous–Broder mazes (a) and Wilson mazes (b).
Comparable outcomes are demonstrated when the mazes are generated using the Hunt and Kill algorithm, which resembles the Aldous–Broder algorithm and utilizes random direction selection. The distinction lies in the necessity of choosing among unvisited cells. The distinction between the solving algorithms becomes evident when solving the recursive backtracker mazes (Figure 24). The dead-end filling algorithm repeatedly shows superior performance regardless of maze sizes. This is because these types of mazes contain limited pathways that lead to a dead end. By comparison, the mazes produced by the Binary Tree algorithm and the Sidewinder algorithm have numerous dead ends, whilst the Dead-end filling technique exhibits the poorest performance. Moreover, the Dijkstra method exhibits a slower performance mostly because these mazes contain a significant proportion of lengthy paths with minimal changes in direction within their structure.
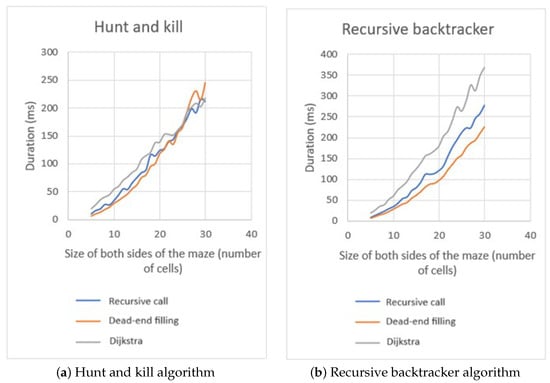
Figure 24.
Maze solving comparison of Hunt and kill mazes (a) and Recursive backtracker mazes (b).
6. Discussion and Conclusions
This paper presents a comparative analysis of various maze generation and solving algorithms implemented in an Android mobile application designed to help children aged five and above learn basic programming concepts and develop computational thinking skills. The application engages young learners by guiding a dog character through a maze using simple commands, providing an interactive and educational experience. By evaluating and comparing various maze generation algorithms within the context of a game-based mobile learning application, the research provides valuable insights into how different algorithms can be used to design and develop educational tools to foster computational thinking and programming skills in young learners. Compared to the existing research on maze generation algorithms, this paper contributes by evaluating existing and new algorithms in a different context, i.e., educational game design, and providing insights into which algorithms are best suited for different stages of learning basic programming concepts. The detailed comparison of various maze generation algorithms has highlighted their strengths and limitations in terms of time complexity, space complexity, and suitability for different educational contexts. Implementing these algorithms in a game-based mobile application has demonstrated their practical applicability.
Wilson’s and Aldous–Broder algorithms were identified as the most time inefficient. Their time complexity increases exponentially with maze size due to the necessity of visiting every cell. On the other hand, algorithms like Sidewinder and Binary Tree demonstrated the fastest generation times for smaller mazes due to their simpler, more direct traversal methods. Moreover, the longest path ratio decreases as the maze size increases across all algorithms. However, the Hunt and Kill and Recursive backtracker algorithms maintain a higher ratio of longest paths, making them suitable for generating progressively complex mazes crucial for advanced game levels.
In addition, the study underscores the importance of selecting the appropriate maze-solving algorithm based on the specific characteristics of the maze generation method used. The Recursive call algorithm is highly efficient for simpler, more predictable mazes, while the Dijkstra algorithm offers reliable performance across varied maze structures. Although less efficient in complex mazes, the dead-end filling algorithm can be beneficial in specific scenarios where dead-end paths are fewer. Future research should further explore these dynamics, particularly focusing on optimizing solving algorithms for more complex and unpredictable maze structures.
One of the primary implications is the importance of selecting the right maze generation algorithm based on the target audience’s skill level and the desired learning outcomes. Simpler algorithms like Binary Tree and Sidewinder are ideal for beginners due to their straightforward nature, offering mazes with less complexity and fewer dead-ends. These characteristics are conducive to helping young learners grasp basic programming concepts without becoming overwhelmed. On the other hand, more complex algorithms like Hunt and Kill and Recursive backtracker are better suited for advanced learners, as they generate mazes with greater complexity and longer paths, which can better challenge and develop problem-solving skills. Additionally, the study underscores the potential for these algorithms to be used in adaptive learning environments, where the difficulty of the mazes can be dynamically adjusted based on the learner’s progress. This adaptability can help maintain engagement and motivation, as the challenge level can be aligned with the learner’s growing abilities. Overall, the choice of maze generation algorithm should be guided by the application’s requirements, balancing factors such as generation speed, path complexity, and navigational characteristics to enhance the learning experience and maintain user engagement.
However, this study has several limitations. First, the comparative analysis of maze generation algorithms was conducted using a specific set of parameters and on a single type of mobile device. Variations in device capabilities and user interfaces could impact the algorithms’ performance. Future research should consider a broader range of devices and user interfaces to validate the generalizability of these findings.
While the study focused on the technical performance of maze generation algorithms, it did not extensively evaluate the pedagogical effectiveness of the generated mazes in enhancing programming skills and problem-solving abilities. The study lacks a comprehensive user-centered evaluation to assess how different maze complexities generated by these algorithms impact the actual learning experience of children. Factors such as user engagement, motivation, and learning outcomes were not directly measured, which limits the understanding of how well these algorithms serve the intended educational purpose.
Future research should address these limitations by testing a broader range of devices, adjusting algorithm parameters for diverse applications, and incorporating educational impact studies to validate and enhance the effectiveness of maze-based learning tools. Expanding the research to include a broader range of devices and operating systems would help generalize the findings and ensure that the educational tools developed are accessible and effective for a wide audience. This could involve testing the algorithms on devices with varying specifications and exploring how different input methods (e.g., touch, voice, and gestures) affect the learning experience.
Another important area for future research is the development of new algorithms or the modification of existing ones to create more tailored educational experiences. For instance, algorithms could be designed to generate mazes that gradually introduce new programming concepts or that adapt in real time to the learner’s performance, providing a personalized learning path.
Furthermore, the study suggests that the impact of different user interfaces and interaction methods on the effectiveness of maze-based learning tools should be examined. With the rise in new technologies such as augmented reality and virtual reality, future research could investigate how these technologies can be integrated with maze generation algorithms to create immersive and engaging learning environments.
These future research directions could significantly enhance the understanding and effectiveness of maze-based educational tools, ultimately contributing to better educational outcomes in the domain of computational thinking and programming for young learners.
Author Contributions
Conceptualization, M.Č., O.S. and I.D.; methodology, M.Č. and O.S.; software, M.Č.; validation, O.S., I.D. and D.C.; formal analysis, M.Č. and O.S.; investigation, M.Č.; resources, I.D. and D.C.; data curation, M.Č. and I.D.; writing—original draft preparation, M.Č. and O.S.; writing—review and editing, M.Č, O.S., I.D. and D.C.; visualization, M.Č., O.S. and I.D.; supervision, M.Č.; project administration, M.Č.; funding acquisition, I.D. and D.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the project “Application of VR technology and neural networks in the field of computer security and digital forensics” grant number NPOO2024-1. The project is financed by the Ministry of Science, Education, and Youth through EU funding (Recovery and Resilience Facility).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Matthews, W.H. Mazes and Labyrinths: Their History and Development; Courier Corporation: North Chelmsford, MA, USA, 1970. [Google Scholar]
- Brainin, E.; Shamir, A.; Eden, S. Robot programming intervention for promoting spatial relations, mental rotation and visual memory of kindergarten children. J. Res. Technol. Educ. 2022, 54, 345–358. [Google Scholar] [CrossRef]
- Demir, B.E.; Demir, F. Coding, Robotics and Computational Thinking in Preschool Education: The Design of Magne-Board. Avrupa Bilim Teknol. Derg. 2021, 23, 52–61. [Google Scholar] [CrossRef]
- Ching, Y.H.; Hsu, Y.C.; Baldwin, S. Developing Computational Thinking with Educational Technologies for Young Learners. TechTrends 2018, 62, 563–573. [Google Scholar] [CrossRef]
- Buck, J. Mazes for Programmers: Code your Own Twisty Little Passages; The Pragmatic Programmers, The Pragmatic Bookshelf: Dallas, TX, USA, 2015. [Google Scholar]
- Wing, J.M. Computational thinking. Commun. ACM 2006, 49, 33–35. [Google Scholar] [CrossRef]
- Macrides, E.; Miliou, O.; Angeli, C. Programming in early childhood education: A systematic review. Int. J. Child Comput. Interact. 2021, 32, 100396. [Google Scholar] [CrossRef]
- Papert, S. Mindstorms: Children, Computers, and Powerful Ideas; Basic Books, Inc.: New York, NY, USA, 1980. [Google Scholar]
- Abelson, H.; Goodman, N.; Lee, R. Logo Manual; MIT Libraries: Cambridge, MA, USA, 1974. [Google Scholar]
- Anderson, L.M.; Shinn, C.; Fullilove, M.T.; Scrimshaw, S.C.; Fielding, J.E.; Normand, J.; Carande-Kulis, V.G. The effectiveness of early childhood development programs: A systematic review. Am. J. Prev. Med. 2003, 24, 32–46. [Google Scholar] [CrossRef]
- Richter, L.M.; Daelmans, B.; Lombardi, J.; Heymann, J.; Boo, F.L.; Behrman, J.R.; Lu, C.; Lucas, J.E.; Perez-Escamilla, R.; Dua, T.; et al. Investing in the foundation of sustainable development: Pathways to scale up for early childhood development. Lancet 2017, 389, 103–118. [Google Scholar] [CrossRef]
- Essa, E.L.; Burnham, M.M. Introduction to Early Childhood Education; SAGE Publications: Thousand Oaks, CA, USA, 2019. [Google Scholar]
- Trakosas, D.; Tikva, C.; Tambouris, E. Visual programming and computational thinking environments for K-9 education: A systematic literature review. Int. J. Learn. Technol. 2023, 18, 94–121. [Google Scholar] [CrossRef]
- Maloney, J.; Resnick, M.; Rusk, N.; Silverman, B.; Eastmond, E. The Scratch Programming Language and Environment. ACM Trans. Comput. Educ. 2010, 10, 1–15. [Google Scholar] [CrossRef]
- Weintrop, D.; Wilensky, U. To Block or Not to Block, That is the Question: Students’ Perceptions of Blocks-Based Programming; ACM: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Yang, W.; Ng, D.T.K.; Su, J. The impact of story-inspired programming on preschool children’s computational thinking: A multi-group experiment. Think. Ski. Creat. 2023, 47, 101218. [Google Scholar] [CrossRef]
- Law, C.Y.; Goh, K.O.; Ooi, S.Y.; Chong, L.Y.; Siow, W.K.; Wong, B.J. Introducing Coding to Children with Scratch: A Pilot Study. In Proceedings of the Future Technologies Conference (FTC), San Francisco, CA, USA, 2–3 November 2023; Volume 4, pp. 362–371. [Google Scholar]
- Chatain, J.; Bitter, O.; Fayolle, V.; Sumner, R.W.; Magnenat, S. A Creative Game Design and Programming App. In Proceedings of the 12th ACM SIGGRAPH Conference on Motion, Interaction and Games, New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Huang, S.Y.; Tarng, W.; Ou, K.L. Effectiveness of AR Board Game on Computational Thinking and Programming Skills for Elementary School Students. Systems 2023, 11, 25. [Google Scholar] [CrossRef]
- Segura, R.; Pino, F.; Ogáyar, C.; Rueda, A. VR-OCKS: A virtual reality game for learning the basic concepts of programming. Comput. Appl. Eng. Educ. 2020, 28, 31–40. [Google Scholar] [CrossRef]
- Plass, J.L.; Homer, B.D.; Kinzer, C.K. Foundations of Game-Based Learning. Educ. Psychol. 2015, 50, 258–283. [Google Scholar] [CrossRef]
- Qian, M.; Clark, K.R. Game-based Learning and 21st century skills: A review of recent research. Comput. Hum. Behav. 2016, 63, 50–58. [Google Scholar] [CrossRef]
- Behnamnia, N.; Kamsin, A.; Ismail, M.A.B.; Hayati, S.A. A review of using digital game-based learning for preschoolers. J. Comput. Educ. 2023, 10, 603–636. [Google Scholar] [CrossRef]
- Theodoropoulos, A.; Lepouras, G. Digital Game-Based Learning and Computational Thinking in P-12 Education: A Systematic Literature Review on Playing Games for Learning Programming; IGI Global: Hershey, PA, USA, 2020; pp. 159–183. [Google Scholar] [CrossRef]
- Shute, V.J.; Sun, C.; Asbell-Clarke, J. Demystifying computational thinking. Educ. Res. Rev. 2017, 22, 142–158. [Google Scholar] [CrossRef]
- Shaffer, D.; Squire, K.; Halverson, R.; Gee, J. Video Games and the Future of Learning. Phi Delta Kappan 2005, 87, 104–111. [Google Scholar] [CrossRef]
- Werner, L.; Denner, J.; Campe, S.; Kawamoto, D. The fairy performance assessment: Measuring computational thinking in middle school. In Proceedings of the SIGCSE’12-Proceedings of the 43rd ACM Technical Symposium on Computer Science Education, Raleigh, NC, USA, 29 February–3 March 2012; ACM: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Nančovska Šerbec, I.; Ternik, Ž.; Koron, T.; Koron, A. Learning Programming Concepts through Maze Game in Scratch. In Proceedings of the 11th European Conference on Games Based Learning (ECGBL 2017), Graz, Austria, 5–6 October 2017. [Google Scholar]
- Jagušt, T.; Krzic, A.S.; Gledec, G.; Grgić, M.; Bojic, I. Exploring Different Unplugged Game-like Activities for Teaching Computational Thinking. In Proceedings of the 2018 IEEE Frontiers in Education Conference (FIE), San Jose, CA, USA, 3–6 October 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Papadakis, S. Robots and Robotics Kits for Early Childhood and First School Age. Learn. Technol. Libr. 2020, 14, 34. [Google Scholar] [CrossRef]
- Wernhuar, T.; Su, Y.C.; Ou, K.L. Development of a Virtual Reality Memory Maze Learning System for Application in Social Science Education. Systems 2023, 11, 545. [Google Scholar] [CrossRef]
- Aldous, D.J. The Random Walk Construction of Uniform Spanning Trees and Uniform Labelled Trees. Siam J. Discret. Math. 1990, 3, 450–465. [Google Scholar] [CrossRef]
- Guenaga, M.; Eguíluz, A.; Garaizar, P.; Gibaja, J. How do students develop computational thinking? Assessing early programmers in a maze-based online game. Comput. Sci. Educ. 2021, 31, 259–289. [Google Scholar] [CrossRef]
- Kruskal, J.B. On the Shortest Spanning Subtree of a Graph and the Traveling Salesman Problem. Proc. Am. Math. Soc. 1956, 7, 48–50. [Google Scholar] [CrossRef]
- Prim, R.C. Shortest connection networks and some generalizations. Bell Syst. Tech. J. 1957, 36, 1389–1401. [Google Scholar] [CrossRef]
- Wilson, D.B. Generating random spanning trees more quickly than the cover time. In Proceedings of the Symposium on the Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996. [Google Scholar]
- Mane, D.; Harne, R.; Pol, T.; Asthagi, R.; Shine, S.; Zope, B. An Extensive Comparative Analysis on Different Maze Generation Algorithms. Int. J. Intell. Syst. Appl. Eng. 2023, 12, 37–47. [Google Scholar]
- Gabrovšek, P. Analysis of maze generating algorithms. IPSI Trans. Internet Res. 2019, 15, 23–30. [Google Scholar]
- Hendrawan, Y. Comparison of Hand Follower and Dead-End Filler Algorithm in Solving Perfect Mazes. J. Phys. Conf. Ser. 2020, 1569, 022059. [Google Scholar] [CrossRef]
- Bellot, V.; Cautrès, M.; Favreau, J.M.; Gonzalez-Thauvin, M.; Lafourcade, P.; Le Cornec, K.; Mosnier, B.; Rivière-Wekstein, S. How to generate perfect mazes? Inf. Sci. 2021, 572, 444–459. [Google Scholar] [CrossRef]
- Mcclendon, M. The Complexity and Difficulty of a Maze. Bridg. Math. Connect. Art Music. Sci. 2001, 213–222. [Google Scholar]
- Sadik, A.M.J.; Dhali, M.A.; Farid, H.M.A.B.; Rashid, T.U.; Syeed, A. A Comprehensive and Comparative Study of Maze-Solving Techniques by Implementing Graph Theory. In Proceedings of the 2010 International Conference on Artificial Intelligence and Computational Intelligence, Sanya, China, 23–24 October 2010; Volume 1, pp. 52–56. [Google Scholar] [CrossRef]
- Martín-Nieto, M.; Castaño Torrijos, D.; Horta Muñoz, S.; Ruiz, D. Solving Mazes: A New Approach Based on Spectral Graph Theory. Mathematics 2024, 12, 2305. [Google Scholar] [CrossRef]
- Tjiharjadi, S.; Razali, S.; Sulaiman, H. A Systematic Literature Review of Multi-agent Pathfinding for Maze Research. J. Adv. Inf. Technol. 2022, 13, 1–10. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).