Abstract
The widespread adoption of the power grid has led to increased attention to load frequency control (LFC) in power systems. The LFC strategy of multi-source hybrid power systems, including hydroelectric generators, Wind Turbine Generators (WTGs), and Photovoltaic Generators (PVGs), with thermal generators is more challenging. Existing methods for LFC tasks pose challenges in achieving satisfactory outcomes in hybrid power systems. In this paper, a novel method for the multi-source hybrid power system LFC task by using an optimal active disturbance rejection control (ADRC) strategy is proposed, which is based on the combination of the improved linear quadratic regulator (LQR) and the ADRC controller. Firstly, an established model of a hybrid power system is presented, which incorporates multiple regions and multiple sources. Secondly, utilizing the state space representation, a novel control strategy is developed by integrating improved LQR and ARDC. Finally, a series of comparative simulation experiments has been conducted using the Simulink model. Compared with the LQR with ESO, the maximum relative error of the maximum peaks of frequency deviation and tie-line exchanged power of the hybrid power system is reduced by 96% and 83%, respectively, by using the proposed strategy. The experimental results demonstrate that the strategy proposed in this paper exhibits a substantial enhancement in control performance.
1. Introduction
With the advancement of the power industry, the power system has transformed into an intricate and extensive network consisting of numerous regions. Usually, when the electricity production meets consumption, the frequency will keep at a stable value. Since the loads of the electricity power system have varying values, the outputs of the power station should be adjusted to bring the frequency back to its set value as quickly as possible. An automatic control strategy should be constructed, which is called load frequency control (LFC). The LFC is an efficient and accurate control frame. When the power system is affected by an external disturbance, the frequency deviation is quickly reduced, and both the frequency and tie line exchange power are kept back to the set value by using this control strategy. Finally, the power system obtains a stable working state quickly [1]. This control strategy guarantees the maintenance of the rated values for frequency and tie-line power exchange, and a harmonious equilibrium between load demand and power generation supply can be achieved [2].
The primary concerns of the LFC mechanism can be categorized into two aspects: the structure design of the controller itself and the parameter tuning. The objective is to enhance the dynamic analysis performance of the power system, facilitating a quicker recovery of system frequency and stability in the presence of disturbances.
Various LFC methods have been proposed for traditional thermal power systems [3,4,5,6,7]. The PID and its variations have been extensively implemented across diverse domains [8]. A significant amount of time is dedicated to the adjustment of controller parameters. Intelligent optimization algorithms have been employed to optimize the parameters of the PID and its variations to enhance the performance [9,10]. Nevertheless, the inherent uncertainties present in power systems impede the achievement of desirable control outcomes. Thus, these controllers usually possess high orders, which present challenges in terms of practical implementation. To tackle these challenges, the utilization of sliding mode control has been implemented in order to mitigate system frequency deviations. This is primarily due to its prompt response and minimal overshoot. An enhanced sliding mode controller based on adaptive dynamic programming was proposed in [11]. This controller enables the online updating of weights to adaptively supplement control signals while also considering load variations and uncertainties in system parameters. Model predictive control is also widely utilized in LFC systems due to its adaptable modeling, rapid response characteristics, enhanced disturbance rejection capability, and superior stability performance [12,13]. For example, a distributed model predictive control approach is presented as the LFC control mechanism in an interconnected power system [12]. This strategy aims to achieve efficient coordination among various regions.
Active Disturbance Rejection Control (ADRC), a model-free control strategy, has garnered significant attention [14]. The ADRC controller, when compared to traditional PIDs and their variations, has several advantages. Firstly, it is independent of precise system mathematical models, thus requiring only minimal system information. Secondly, it demonstrates attributes such as rapid response, minimal overshoot, and strong robustness. The fundamental concept of ADRC involves reducing the reliance on model information and incorporating an estimation of the disturbance into the control strategy. The disturbances estimation takes into consideration the actual perturbations in the plant, uncertainties in the parameters of the model, and dynamics that are not accounted for in the model. A reduced-order linear ADRC controller is proposed for a three-control area system [15]. It demonstrates superior performance in terms of disturbance rejection when compared with PID-based controllers.
The integration of power systems across multiple regions and variations in tie-line power also requires a greater level of accuracy in control. As renewable energy sources like hydroelectric generators, Photovoltaic Generators (PVGs), and Wind Turbine Generators (WTGs) are gradually being integrated, traditional LFC methods encounter difficulties in maintaining efficient control. This is primarily attributed to the inherent occasionality and uncertainty associated with WTG and PVG [16]. Therefore, it is imperative to implement an appropriate LFC strategy to ensure the stability of the power system.
Since the variable nature and stochastic nature of wind and sunlight, the output powers of a WTG or PVG change indeterminately. Thus, the LFC mechanism of an electric power system with penetration of renewables should be reacted with electrical loads and outputs of generators [17]. In the context of a hybrid energy power system, the incorporation of the WTG and PVG introduces increased variability and unpredictability to the power system, thereby posing challenges to the LFC method. Previous research endeavors have also made attempts to address this matter [18,19,20,21,22,23,24,25]. A hybrid control strategy, consisting of a Linear Quadratic Regulator (LQR) and a generalized predictive controller, is introduced in reference [18]. The load variations were employed as quantifiable disturbances to attain frequency stability in hydroelectric power systems. The analysis failed to account for fluctuations in the load within the generating units themselves. A decentralized control strategy was proposed for the LFC task in the presence of renewable energy sources [19]. Their strategy of using the LQR with an ESO is utilized. However, the system failed to consider the feedback of errors, resulting in a notable increase in the frequency overshoot. For a microgrid, the case of delayed electric vehicle aggregators and renewable energy sources, including photovoltaic, wind, and fuel cells, was examined [20]. A novel approach for implementing a linear ADRC method, which is based on the ESO and a nonlinear feedback control law (NLFCL). This method demonstrated its effectiveness in reducing the impact of load disturbances and uncertainties arising from renewable energy sources.
For a more complex multi-area interconnected hybrid power system, WTG [21] or PVG [22,23] will be introduced separately. In this study, an LFC strategy of a hybrid power system with hydroelectric generators, WTGs, and PVGs with thermal generators is studied. It is more challenging work than the above-mentioned systems. The LQR shows good stability for uncertain systems [24], and ADRC shows strong disturbance rejection features [25]. In this research, a novel LFC mechanism for hybrid power systems is presented based on the optimal ADRC, which is a combination of an improved LQR with the ADRC.
Since the complexity of a multi-area interconnected hybrid power system, the state space model of the LFC target of the hybrid power system is established at first. Then, an LQR controller with the output weightings is designed as an optimal controller. Finally, the ADRC technique estimates the disturbances of plants and adjusts the power flows on the tie-line. This compensation is achieved without adding complexity to the designed model. Compared with the LQR with ESO, the relative errors of the maximum peaks of frequency deviation of the three regions of the established hybrid power system are reduced by 96%, 95%, and 96%, respectively, by using the proposed strategy. The relative errors of the maximum peaks of tie-line exchange power of the three regions of the established hybrid power system are reduced by 83%, 54%, and 76%, respectively, by using the proposed strategy.
The framework of this research is arranged as follows: The structure of the LFC strategy and the linearized models of LFC components in a multi-area interconnected hybrid power system are introduced in Section 2. The controller design of the proposed optimal ADRC is described in Section 3. The experimental results and analysis are given in Section 4. Finally, the conclusion and future directions are summarized in Section 5.
2. Dynamic Model of Load Frequency Control
2.1. Multi-Area Interconnected Power System
To ensure the stable control of frequency in the power system, it is imperative to accurately represent the fundamental dynamic characteristics of the system frequency through the construction of a suitable model. When the changes in load are insignificant, the LFC system can be effectively analyzed using a linear model. Therefore, the simplified linear models for all dynamic simulations are adopted in this paper.
In the regulation of a power system’s frequency, the primary control variable is the active power output of the generators. During periods of steady-state operation, it is expected that the active power will be synchronized with the load power. The interconnected power system is commonly composed of multiple control areas, which are interconnected through tie-lines to facilitate power exchange during regular operations. This interconnected arrangement helps address any discrepancies between power generation and demand. When confronted with a load change disturbance, the operation of the interconnected power system model aims to achieve two primary control objectives [26]. The primary goal is to maintain the load frequency deviation at or close to zero. The second objective is to maintain the tie-line power within the desired set value.
Taking a three-area interconnected power system, for instance, as shown in Figure 1, the LFC mechanism has the responsibility of maintaining power exchange between these areas within the scheduled limits. In essence, it is imperative that any alterations in the tie-line flow ΔPij remain at zero.
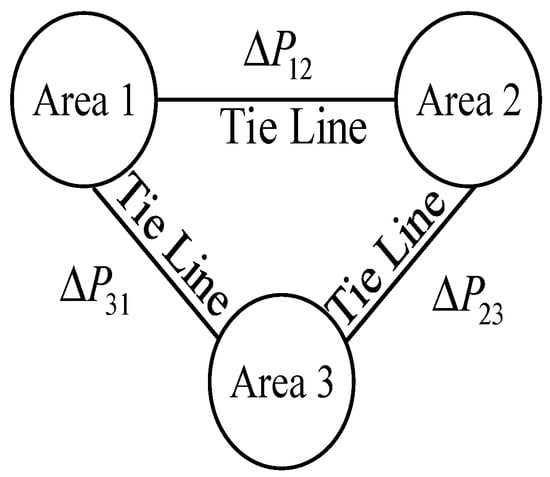
Figure 1.
The structure diagram of a three-area interconnected power system.
2.2. Load Frequency Control Model
The linearized model of a multi-area interconnected power system can be described in Figure 2, in which the i-th control region of a hybrid power system is described. In this diagram, each region is assumed to have ni generators. Each area has a participation factor αni and satisfies 0 ≤ αni ≤ 1; the sum of all regional participation factors is 1. ΔPL,i is the disturbance of power loads, and ΔPRES,i is the output power of renewable energy generators. Ri is the i-th unit droop feature. Bi is the frequency bias factor obtained from the gradient feature Ri,eq, via Bi = Di + 1/Ri,eq, where Di is the load-damping factor [19].
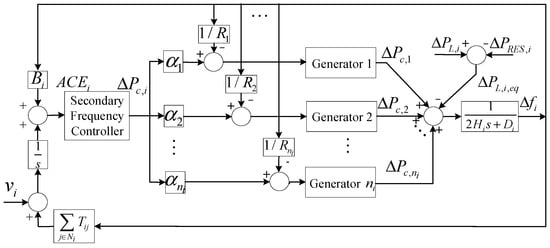
Figure 2.
Linearization model structure of the system in the i-th control area.
When quantifying the discrepancy arising from imbalances in power across multiple areas, the disruption encountered by the system is referred to as the Area Control Error (ACE) [27]. The ACE encompasses the deviation in power exchange between different control areas and the deviation in frequency within each area. The calculation formula can be represented as Equation (1).
where vi and are area interface signals. GA,i (s) is the transfer function from ΔPc,i to Δωi, which can be obtained by Equations (2) and (3) [28].
where Grm,i(s) is the transfer function of rotating mass inertia of the i-th region, GGT,i (s) is the transfer function governor and turbine, αij is the participated factor of the j-th generation unit, and Rj is the decline rate of the j-th generator.
2.3. Linearized Models for LFC Components
The linearized models of thermal turbine generators, hydroelectric generators, WTGs, and PVG are introduced in this subsection.
The transfer function of a reheat thermal generator is shown in Equation (4).
where TG, TCH, and TRH are the time constants of the governor, turbine, and reheating system separately. FHP is the fraction of the output power.
The linearized representation of the wind turbine generator can be expressed as Equations (5)–(7).
where Gwp (s) describes the changes in generated powers. KP1 is a gain of the actuator, and TP2 and KP2 are time constants of the process.
The linearized models of the photovoltaic generator are represented by Equations (8) and (9).
A hydraulic generator includes two cascaded transfer functions: a governor and a turbine. The linearized model of the hydraulic generator is represented by Equation (10).
3. The Proposed Control Strategy
The proposed control strategy is a combination of the LQR and ADRC; the diagram of the controller is shown in Figure 3. In a power system interconnected by i regions, an i-th controller is necessary. Thus, the strategy includes an ADRC and LQR-based LFC strategy to adjust the frequency deviation and the ACE within each control region. Given a hybrid power system model, the LQR is employed to effectively manage the overall errors of the ACEs and frequency deviations within a specified range. Additionally, the ADRC is utilized as a precise controller for the ACEs and frequency deviations. In this diagram, the upper half part is the ADRC strategy, and the lower part is the revised LQR strategy. The details of the Tracking Differentiator (TD) and NFCL blocks are given in [20].
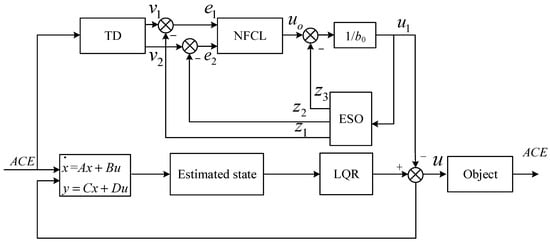
Figure 3.
Diagram of the proposed control strategy.
3.1. The Principle and Control Algorithm of ADRC
Han et al. [14] summarized the fundamental concepts of the ADRC strategy. The ADRC approach employs three key components: the TD, an ESO, and an NLFCL.
The principle of ADRC is based on its ability to estimate and compensate for disturbances. By incrementally augmenting the input signal throughout the transition process, the disparity in the output is minimized, enabling the system to attain a stable state without exceeding the desired value.
The second-order block diagram of the ADRC is depicted in Figure 3. In general, the determination of the order of the ADRC can be based on the characteristics of the controlled object. Higher orders of ADRC typically lead to improved control performance, albeit at the expense of increased complexity in implementation. After careful consideration of multiple factors, a second-order system is adopted. The system construction and integration are relatively simple, yet it successfully achieves the desired control effect. The mathematical representation of the second-order LADRC model is given by the following equation.
where u1 is the output value, ACE is the input value, b is the amplified factor, and f is the total disturbance of the system, as shown in Figure 3. Assume that,
The expression can be represented in the state space format, as depicted in Equation (13).
where A, B, E, C, and z are defined as depicted in Equation (14).
where b0 is the known parameter of the system.
The state space observer, known as the linear extended state observer (LESO) of Equation (11), is formulated according to Equation (15).
where L is the observer gain vector, which can be determined using established methods like the pole placement technique. In order to streamline the tuning process, the observer gains are parameterized as follows:
where ω0 is the observer bandwidth.
For the error feedback module, we also use the pole placement method, optimizing all controller poles at the same ωc bandwidth.
In summary, the optimization of three parameters, namely ωc, ω0, and b0, is necessary for the implementation of linear active disturbance rejection control.
3.2. Linear Quadratic Regulator
An LQR controller provides the optimal feedback control law for closed-loop systems in the presence of various uncertain factors, ensuring the high-performance design of the system [29]. Consider a state-space representation of the plant provided.
where x(t) is the system state vector.
The objective of an LQR controller is to compute an optimal control law vector, denoted as Kopt, which efficiently drives the system state from its current state to the desired state while minimizing energy consumption. The quadratic cost function is commonly represented in the following manner [30].
The weights on the output values y(t) and control input u(t) are defined by Q and R, respectively. Both Q and R are positive semi-definite matrices. N is the weighting value of y(t) and u(t). The singular positive solution P can be derived through the resolution of the Riccati equation.
The determination of the state feedback gain is achieved through the utilization of the following equation.
The ESO incorporates exogenous disturbances, non-modeled dynamics, and parameter uncertainties as part of its estimation process. It utilizes observation errors to extract disturbance information and estimate these extended states [30].
Suppose a disturbance is present at the input of the plant. The state-space representation of the plant can be described as follows:
The state-space representation of the internal model can be formulated as follows:
The value of k is determined to be set as 3 based on experience. The matrices Aw, Bw, and Cw are denoted as Equation (23). Substituting Equation (22) into Equation (21), the dynamics of the plant can be derived as Equation (24).
Therefore, the dynamics of the extended system can be represented as Equation (25).
By solving the previous equations, an estimation of the extended system state can be obtained.
The control strategy proposed in this work cancels the equivalent disturbance of the plant by utilizing the estimate provided by an ADRC system, which is shown in Equation (26).
where is the control value from the ADRC controller.
4. Experimental Results and Analysis
In this section, an investigation is conducted on a multi-source hybrid power system by using the proposed optimal ADRC method. The IEEE-39 Bus system with PVG and WTG was used as a baseline for the experiment [20]. This system has three control areas: WTGs and PVGs are added in certain nodes. Each control area has five generators. The G1, G4, and G9 are reheat thermal generators. The G2, G3, G5, G6, G7, G8, and G10 are hydroelectric generators. GWT and GPV are WTG and PVG separately. Area 1 includes G1, G2, G3, GWT1, and GPV1. Area 2 includes G4, G5, G6, G7, and GPV2. Area 3 includes G8, G9, G10, GWT2, and GPV2. All the experiments are finished on the Matlab/Simulink platform. The parameter values of the multi-area power system are given in Table 1. The participation factors of the generators of each area are given in Table 2, Table 3 and Table 4. The participation factor of the reheat thermal generator is 52% in all these three areas.

Table 1.
The System Parameter Values.

Table 2.
The participation Factors for area 1.

Table 3.
The participation Factors for area 2.

Table 4.
The participation Factors for area 3.
The total transfer function for each control area can be derived according to the model parameters and generator types given above, combined with the models of each generator in Section 2. This is a complex work. Model-wise-based methods require designing the controller according to the resulting precise model. The advantage of this proposed strategy is that the total transfer function model of the system does not need to be reduced. When the total disturbance of the system is estimated, so precise control can be implemented.
Comparative results of reducing frequency deviation and tie-line power variation using LQR, LQR with ESO [20], and the proposed method are presented and analyzed.
4.1. The Step-Load Disturbance
Suppose that the first region is interfered with by a step load disturbance at t1 = 5 s, = 1 p.u; t2 = 15 s, = 2 p.u and t3 = 25 s, = 1.5 p.u. The response results of the frequency deviation of the three regions are shown in Figure 4, Figure 5 and Figure 6, respectively. The tie-line power exchanges of the three regions are displayed in Figure 7, Figure 8 and Figure 9. The optimization results of different methods, such as LQR, ESO-LQR, and the proposed optimal ADRC, which is marked as ADRC-LQR, are also presented. In order to better observe the results of the comparison, the dramatically changed parts have been enlarged in the small images.
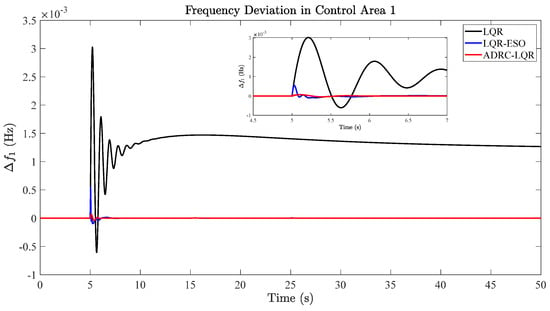
Figure 4.
Comparison results of frequency deviation in region 1.
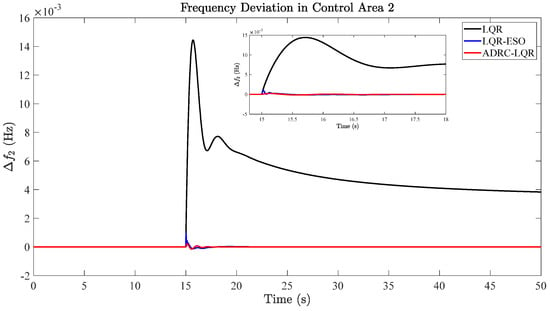
Figure 5.
Comparison results of frequency deviation in region 2.
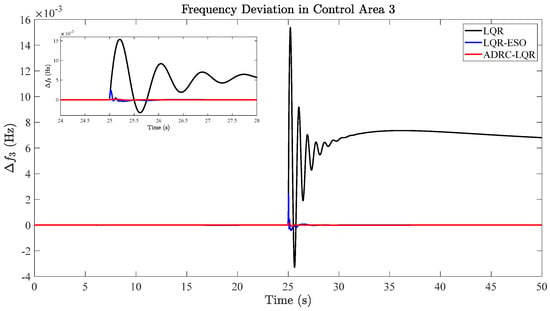
Figure 6.
Comparison results of frequency deviation in region 3.
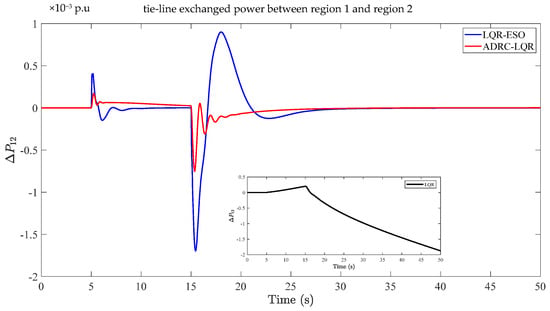
Figure 7.
Comparison results of tie-line exchanged power between region 1 and region 2.
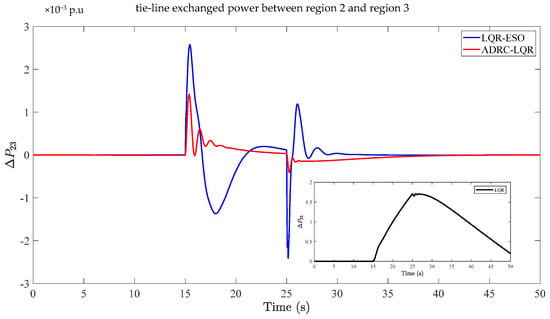
Figure 8.
Comparison results of tie-line exchanged power between region 2 and region 3.
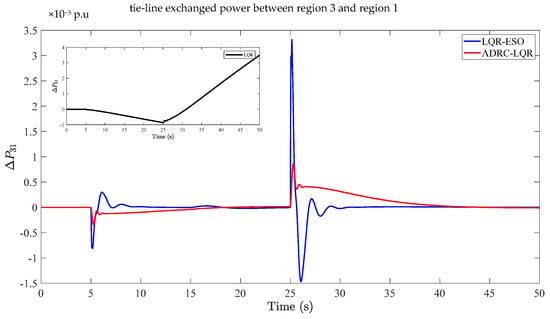
Figure 9.
Comparison results of tie-line exchanged power between region 3 and region 1.
In Figure 4, the steady-state error of region 1 is 1.25 × 10−3 Hz using the LQR method. The steady-state error is 0 when using the LQR with ESO and the proposed methods. From the enlarged small window, it can be seen that the frequency deviation of the LQR with ESO has four peaks from 5 to 5.5 s, among which the maximum peak value is 0.5 × 10−3 Hz. The method proposed in this paper has basically no fluctuation on the basis of error perturbation, and the maximum peak value is 0.02 × 10−3 Hz. Compared with the LQR with ESO, the relative error of the maximum peak is reduced by 96% by using the proposed strategy.
In Figure 5, the steady-state error of region 2 is 3.9 × 10−3 Hz by using the LQR method. The steady-state error is 0 when using the LQR with ESO and the proposed methods. From the enlarged small window, it can be seen that the frequency deviation of the LQR with ESO has two peaks from 15 to 15.3 s, among which the maximum peak value is 0.8 × 10−3 Hz. The method proposed in this paper has basically no fluctuation on the basis of error perturbation, and the maximum peak value is 0.04 × 10−3 Hz. Compared with the LQR with ESO, the relative error of the maximum peak is reduced by 95% by using the proposed strategy.
In Figure 6, the steady-state error of region 3 is 6.8 × 10−3 Hz using the LQR method. The steady-state error is 0 when using the LQR with ESO and the proposed methods. From the enlarged small window, it can be seen that the frequency deviation of the LQR with ESO has three peaks from 25 to 25.5 s, among which the maximum peak value is 2.0 × 10−3 Hz. The method proposed in this paper has basically no fluctuation on the basis of error perturbation, and the maximum peak value is 0.08 × 10−3 Hz. Compared with the LQR with ESO, the relative error of the maximum peak is reduced by 96% using the proposed strategy.
In Figure 7, the exchanged power between region 1 and region 2 does not reach a stable state within 50 s by using the LQR method. The system reached a stable state in 30 s, with four distinct peaks in the intermediate region, using the LQR with ESO. The absolute errors are 0.4 × 10−3 p.u, 0.2 × 10−3 p.u, 1.75 × 10−3 p.u, and 0.85 × 10−3 p.u, respectively. By using the method proposed in this paper, the system reached a stable state in 40 s. Four peaks can be found in the corresponding period, but the fluctuation range is significantly smaller, and the absolute errors are 0.18 × 10−3 p.u, 0.8 × 10−3 p.u, 0.3 × 10−3 p.u and 0.14 × 10−3 p.u. Compared with the LQR with ESO, the relative errors of the maximum peak fluctuation are reduced by 83% by using the proposed strategy.
In Figure 8, the exchanged power between region 2 and region 3 does not reach a stable state within 50 s when using the LQR method. The system reached a stable state in 40 s, with four distinct peaks in the intermediate region by using the LQR with ESO. The absolute errors are 2.6 × 10−3 p.u, 1.3 × 10−3 p.u, 2.4 × 10−3 p.u, and 1.1 × 10−3 p.u, respectively. By using the method proposed in this paper, the system reached a stable state in 32 s. Four peaks can be found in the corresponding period, but the fluctuation range is significantly smaller, and the absolute errors are 1.2 × 10−3 p.u, 0.4 × 10−3 p.u, 0.2 × 10−3 p.u, and 0.4 × 10−3 p.u. Compared with the LQR with ESO, the relative errors of the maximum peak fluctuation are reduced by 54% by using the proposed strategy.
In Figure 9, the exchanged power between region 3 and region 1 does not reach a stable state within 50 s by using the LQR method. The system reached a stable state in 40 s, with four distinct peaks in the central region. The absolute errors are 0.8 × 10−3 p.u, 0.3 × 10−3 p.u, 3.4 × 10−3 p.u, and 1.5 × 10−3 p.u, respectively. By using the proposed optimal ADRC, the system reached a stable state in 32 s, and four peaks can be found in the corresponding period, but the fluctuation range is significantly smaller, and the absolute errors are 0.3 × 10−3 p.u, 0.1 × 10−3 p.u, 0.8 × 10−3 p.u, and 0.3 × 10−3 p.u. Compared with the LQR with ESO, the relative errors of the maximum peak fluctuation are reduced by 76% by using the proposed strategy.
In conclusion, the LQR method proves inadequate in effectively controlling both frequency and interconnection line power. Under the LQR-ESO and the proposed ADRC-LQR methods, it is observed that both fi and in each region remain stable at zero during steady state operation. This indicates the consistent performance of the controllers in maintaining stability in this state. The ADRC-LQR method exhibits convergence approximately 3 s earlier than the LQR-ESO method.
Regarding the dynamic response, the proposed LFC system, which integrates the ADRC and LQR control methods, demonstrates the capability to efficiently attain the desired set value with minimal occurrence of overshoot and undershoot. This demonstration convincingly showcases the efficacy of the proposed methodology.
4.2. Random Disturbance
It is assumed that all control areas are equipped with a PVG functioning as a negative load and the variation in its irradiance is considered to be random. The load disturbance signals for each control area are illustrated in Figure 10. These signals consist of step, triangular, and parabolic patterns. It can be seen from Table 2, Table 3 and Table 4 that the proportion of new energy added in the three regions is basically balanced, and the same disturbance signal has little disturbance to the three regions. Figure 10 verifies the robustness of the proposed method to the three types of disturbance signals.
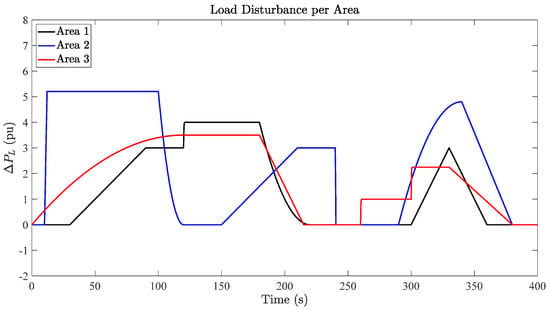
Figure 10.
Load disturbance for each control area.
The effectiveness of using the proposed optimal ADRC strategy is demonstrated in Figure 11. The proposed LFC strategy successfully keeps the frequency deviation near zero in all regions, even in the presence of load disturbances and unpredictable fluctuations in the functioning of the PVGs acting as negative loads. The area where the maximum frequency deviation is observed is area 3, with a value of only 3.7 × 10−4 Hz. Additionally, the proposed strategy effectively governs the power exchange between control areas through the tie-line in Figure 12. The maximum deviation in tie-line power is approximately 9.8 × 10−3 p.u.
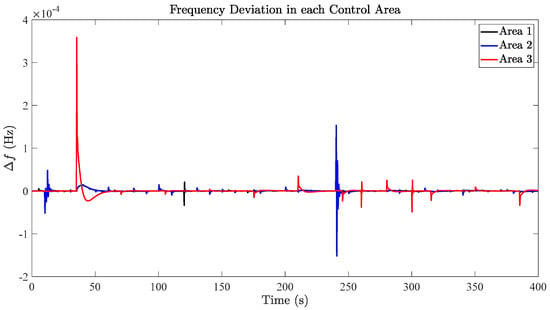
Figure 11.
Frequency deviation in each control area.
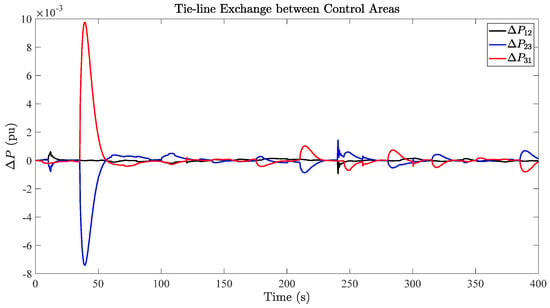
Figure 12.
Tie-line power exchange between control areas.
It can be seen from Figure 11 and Figure 12 that the control strategy proposed in this paper has a good effect on the three different disturbance signals. However, it can also be seen that these three signals have different effects on the system. The robustness of the system to the step signal is the strongest, and basically, the system has no fluctuation. For the other two nonlinear interference signals, the control effect is not as good as the step signal. Although the peak value is not large, it is also the direction of further improvement in the future.
5. Conclusions
For a multi-area hybrid power system, including WTG and PVG, the incorporation of wind power and solar power generations introduces increased variability and unpredictability to the power system. It is a challenge to work on the LFC task. In this paper, a novel optimal ADRC strategy is proposed to solve this problem. The contribution is summarized as follows: The three areas that interconnect hybrid power systems, including 2 WTGs and 3 PVGs, are established. The mathematical model is established and implemented on the Matlab/Simulink platform. The novel optimal ADRC is then proposed. Since the error feedback of ACEs is introduced into LQR, smaller frequency fluctuation and tie-line power deviation can be obtained. Thus, a combination of LQR and ADRC is proposed. Various experiments demonstrated the effectiveness of the proposed method. However, the tuning of parameters for the ADRC controller currently relies on manual experience. It is anticipated that an intelligent optimization algorithm will be incorporated in future developments. Additionally, it is worth exploring the implementation of more sophisticated control methods, such as those based on state space representation, as a means of enhancing the effectiveness of load frequency control (LFC) strategies in hybrid power systems. The objective of this study is to enhance the stability and performance of the load frequency control system, ensuring its robustness.
Author Contributions
Conceptualization, methodology, validation, and writing—review and editing, K.Z.; software, formal analysis, writing—original draft preparation, and resources, Y.W.; data curation, visualization, and investigation, B.L.; supervision and project administration, Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The public data that support the findings of this study are openly available in [Github] at [https://github.com/sergio-dorado/Decentralized-LFC-ADRC] (accessed on 31 July 2024).
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study, in the collection, analysis, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
References
- Cui, M.; Zhao, Y.; Cao, P.; Tang, Y.; Lu, Y. Load frequency control of interconnected hydrothermal power system based on FOPI + FOPD controller. Int. J. Dyn. Control 2024, 12, 1073–1085. [Google Scholar] [CrossRef]
- Khan, M.; Sun, H. Complete provision of MPC-based LFC by electric vehicles with inertial and droop support from DFIG-based wind farm. IEEE Trans. Power Deliv. 2022, 37, 716–726. [Google Scholar] [CrossRef]
- Marayati, M.; Farrukh, N.; Navinesshani, P.; Agileswari, A.; Aidil, A. Takagi-sugeno type 1–2 fuzzy linear output controller for two-area load frequency control. Syst. Soft Comput. 2024, 6, 200083. [Google Scholar]
- Li, X.; Ye, D. Event-based Distributed Fuzzy Load Frequency Control for Multi Area Nonlinear Power Systems with Switching Topology. IEEE Trans. Fuzzy Syst. 2022, 30, 4262–4272. [Google Scholar] [CrossRef]
- Vafamand, N.; Arefi, M.; Asemani, M.; Dragicevic, T. Decentralized Robust Disturbance-observer Based LFC of Interconnected Systems. IEEE Trans. Ind. Electron. 2022, 69, 4814–4823. [Google Scholar] [CrossRef]
- Wang, X.; Ding, D.; Dong, H.; Yi, X. PI-based Security Control Against Joint Sensor and Controller Attacks and Applications in Load Frequency Control. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 970–980. [Google Scholar] [CrossRef]
- Silani, A.; Cucuzzella, M.; Scherpen, J. Output Regulation for Load Frequency Control. IEEE Trans. Control Syst. Technol. 2022, 30, 1130–1144. [Google Scholar] [CrossRef]
- Khan, I.; Mokhli, H.; Mansor, N.; Illias, H.; Awalin, L.; Wang, L. New trends and future directions in load frequency control and flexible power system: A comprehensive review. Alex. Eng. J. 2023, 71, 263–308. [Google Scholar] [CrossRef]
- Lin, C.; Hu, B.; Shao, C. Event-triggered Load Frequency Control Based on Age-of-information. IEEE Trans. Power Syst. 2023, 38, 2348–2361. [Google Scholar] [CrossRef]
- Sari, A.; Sönmez, Ş.; Ayasun, S.; Kabalci, Y. Delay-dependent stability analysis of multi-area LFC-EVs system. IEEE Trans. Smart Grid 2023, 14, 2178–2188. [Google Scholar] [CrossRef]
- Daraz, A.; Malik, S.; Haq, I.; Khan, K.; Laghari, G.; Zafar, F. Modified PID controller for automatic generation control of multi-source interconnected power system using fitness dependent optimizer algorithm. PLoS ONE 2020, 15, 24–28. [Google Scholar] [CrossRef]
- Elkasem, A.; Khamies, M.; Hassan, M.; Agwa, A.; Kamel, S. Optimal design of TD-TI controller for LFC considering renewables penetration by an improved chaos game optimizer. Fractal Fract. 2022, 6, 220. [Google Scholar] [CrossRef]
- Mu, C.; Tang, Y.; He, H. Improved sliding mode design for load frequency control of power system integrated an adaptive learning strategy. IEEE Trans. Ind. Electron. 2017, 64, 6742–6751. [Google Scholar] [CrossRef]
- Han, J. Auto disturbance rejection controller and it’s applications. Control Decis. 1998, 13, 19–23. [Google Scholar]
- Zheng, Y.; Chen, Z.; Huang, Z.; Sun, M.; Sun, Q. Load frequency control of three-area interconnected power systems based on reduced-order active disturbance rejection controller. In Proceedings of the 2020 IEEE 9th Data Driven Control and Learning Systems Conference (DDCLS), Liuzhou, China, 20–22 November 2020; pp. 6–11. [Google Scholar]
- Chen, Z.; Zhu, J.; Li, S. Detection of False Data Injection Attacks on Load Frequency Control System with Renewable Energy Based on Fuzzy Logic and Neural Networks. J. Mod. Power Syst. Clean Energy 2022, 10, 1576–1587. [Google Scholar] [CrossRef]
- Muhammad, M.; Muhammad, I.; Sulman, S.; Hafiz, A.; Muhammad, S.; Muhammad, M. Load Frequency Control (LFC) Strategies in Renewable Energy-Based Hybrid Power Systems: A Review. Energies 2022, 15, 3488. [Google Scholar] [CrossRef]
- Campos-Peña, P.A.; Aliaga-Yauri, J.O.; Barrera-Esparta, D.L.; Gómez-Casasola, M.R. Performance comparison between LQR, GPC and ANFIS controllers for load frequency control in a small hydro power plant. In Proceedings of the 2022 IEEE International Conference on Automation/XXV Congress of the Chilean Association of Automatic Control (ICA-ACCA), Curicó, Chile, 24–28 October 2022; pp. 1–6. [Google Scholar]
- Dorado-Rojas, S.A.; Cortés-Romero, J.; Rivera, S.; Mojica-Nava, E. ADRC for Decentralized Load Frequency Control with Renewable Energy Generation. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar]
- Taghizadegan, N.; Babaei, F.; Safari, A. A linear active disturbance rejection control technique for frequency control of networked microgrids. Energy Syst 2024, 15, 807–826. [Google Scholar] [CrossRef]
- Liu, X.; Wang, C.; Kong, X.; Zhang, Y.; Wang, W.; Lee, K. Tube-based distributed MPC for load frequency control of power system with high wind power penetration. IEEE Trans. Power Syst. 2023, 39, 3118–3129. [Google Scholar] [CrossRef]
- Ozay, C.; Mustafa, S. Gorilla troops optimization-based load frequency control in PV thermal power system. Neural Comput. Appl. 2024, 36, 4179–4193. [Google Scholar]
- Ahmed, T.; Fahd, A.; Mohamed, M.; Mohamed, I.; Asmaa, F.; Mohamed, R.; Mahmoud, M.; Tarek, H. Adaptive Load Frequency Control in Microgrids Considering PV Sources and EVs Impacts: Applications of Hybrid Sine Cosine Optimizer and Balloon Effect Identifier Algorithms. Int. J. Robot. Control Syst. 2024, 4, 941–957. [Google Scholar]
- Wang, Q.; Lim, I.; Ye, Z.; Nie, Z. LQR approach to robust stabilization of state space systems with matched uncertainties. ISA Trans. 2023, 142, 420–426. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Nie, Z.; Shao, H.; Fang, H.; Luo, J. Active disturbance rejection control for non-minimum phase systems under plant reconstruction. ISA Trans. 2023, 134, 497–510. [Google Scholar] [CrossRef] [PubMed]
- Vedik, G.; Kumar, B.; Deshmukh, R.; Verma, R.; Shiva, C. Renewable energy-based load frequency stabilization of interconnected power systems using quasi-oppositional dragonfly algorithm. J. Control Autom. Electr. Syst. 2021, 32, 227–243. [Google Scholar] [CrossRef]
- Gündeş, A.; LKabuli, A. Load frequency control of multiarea interconnected power systems with time delays. IEEE Trans. Control Netw. Syst. 2022, 9, 625–634. [Google Scholar] [CrossRef]
- Fu, C.; Cai, F.; Wen, T. Decentralised load frequency control for power systems with communication delays via active disturbance rejection. IET Gener. Transm. Distrib. 2018, 12, 1397–1403. [Google Scholar] [CrossRef]
- Abdullahi, B. Hierarchical bi-level load frequency control for multi-area interconnected power systems. Int. J. Electr. Power Energy Syst. 2024, 155, 109600. [Google Scholar]
- Yin, X.; She, J.; Liu, Z.; Xiong, Y. Disturbance suppression and system design based on parallel-equivalent-input disturbance approach. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 3654–3665. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).