An Image Processing-Based Correlation Method for Improving the Characteristics of Brillouin Frequency Shift Extraction in Distributed Fiber Optic Sensors
Abstract
1. Introduction
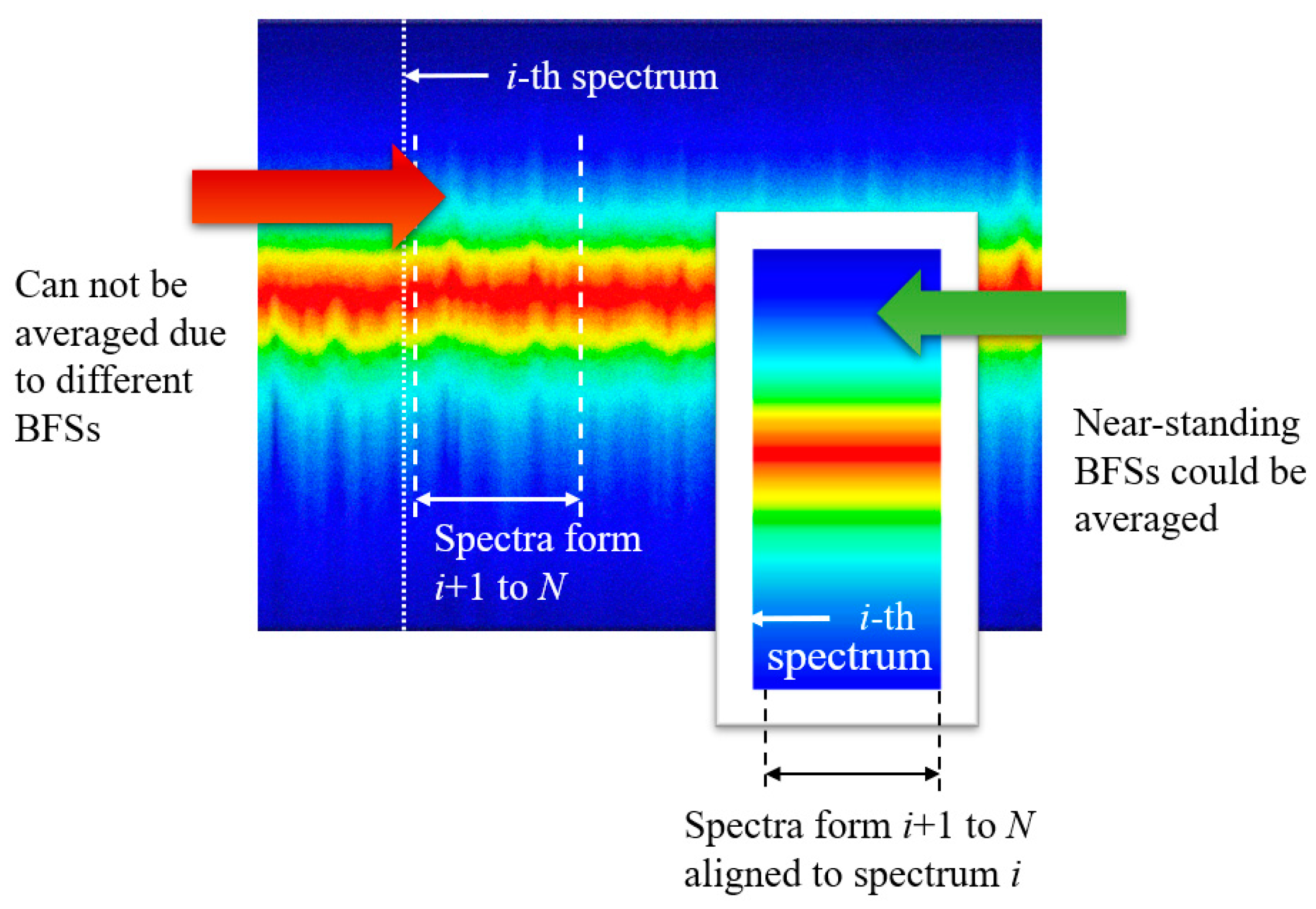
2. The Idea of the Proposed Method
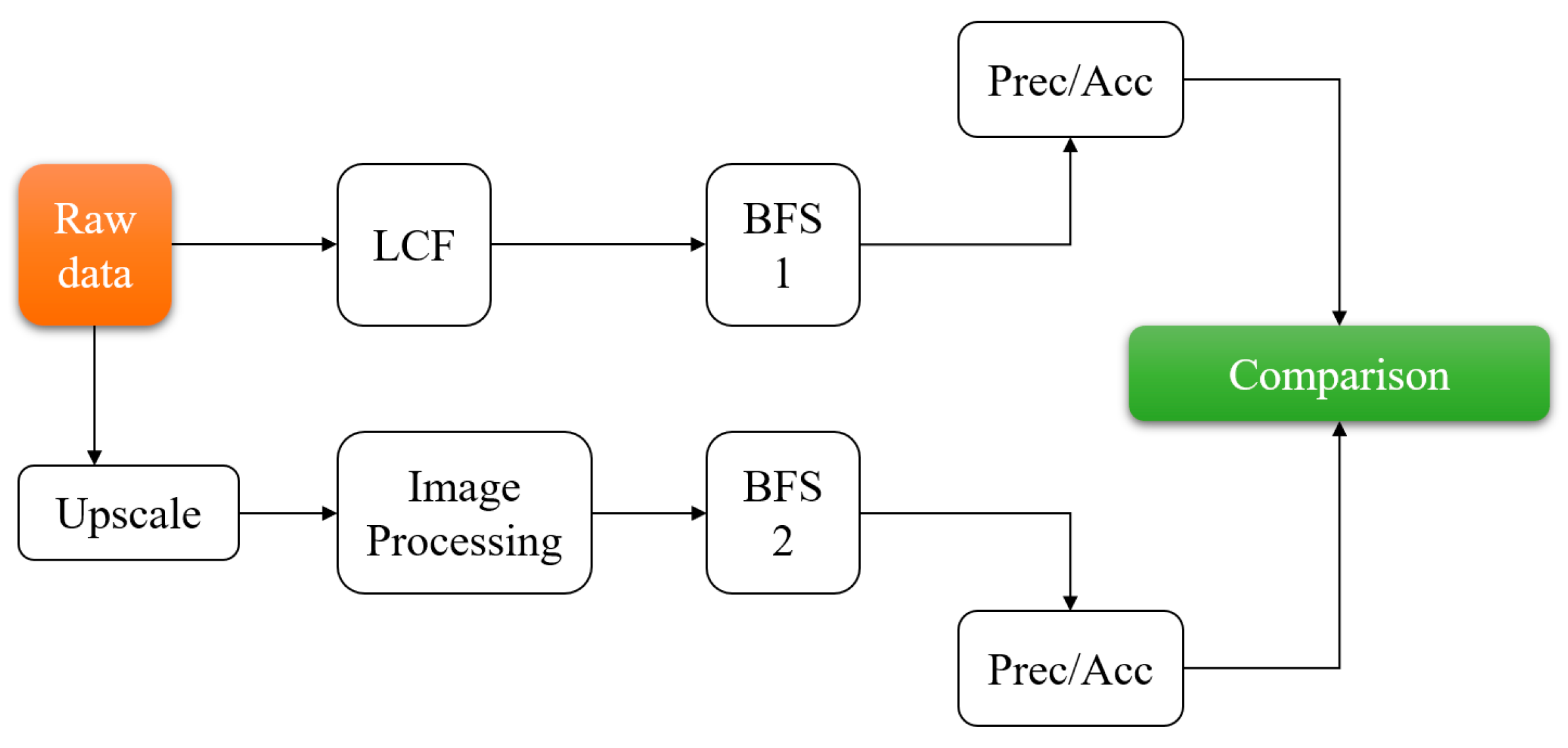
Description of Metrics for Comparing Algorithms
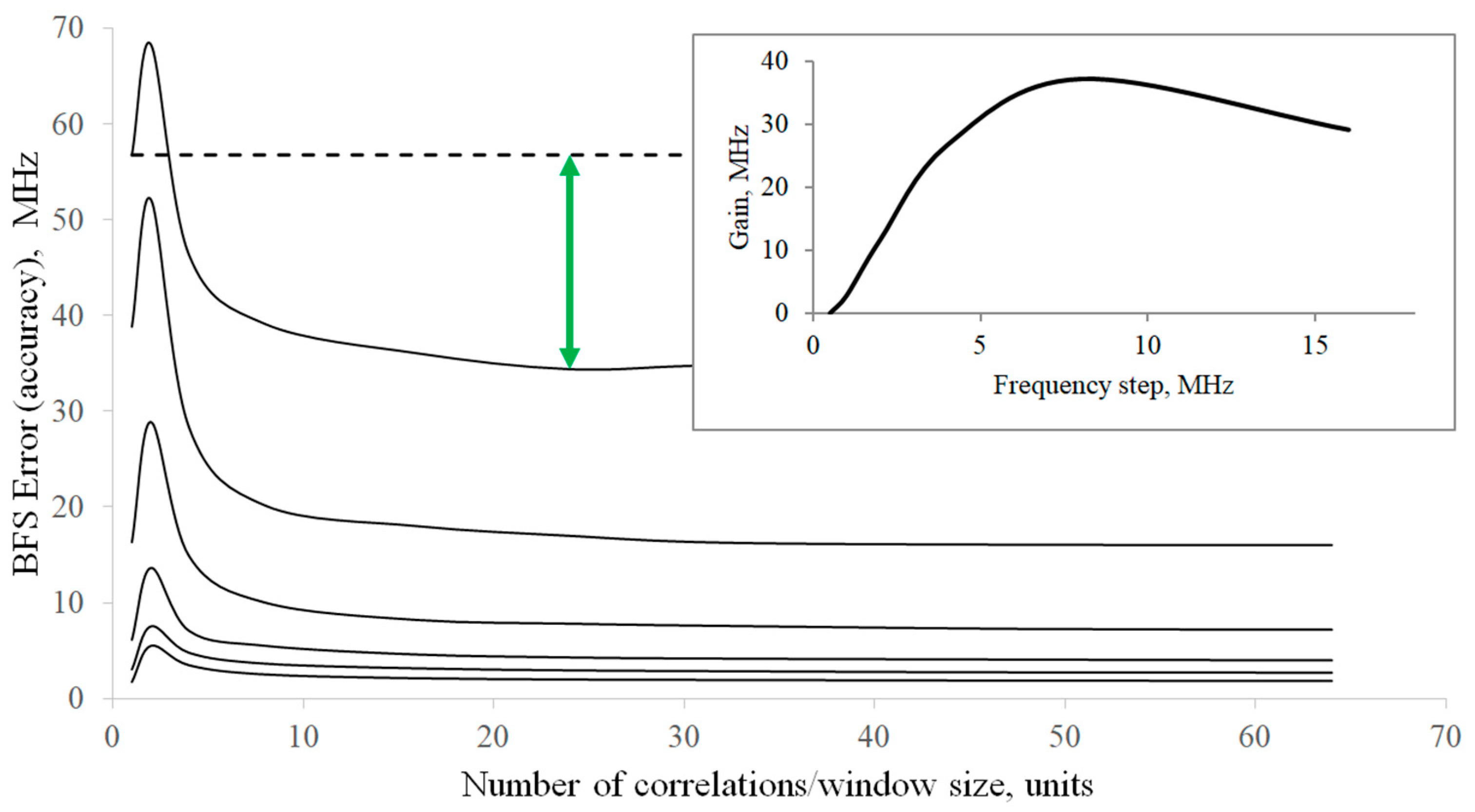
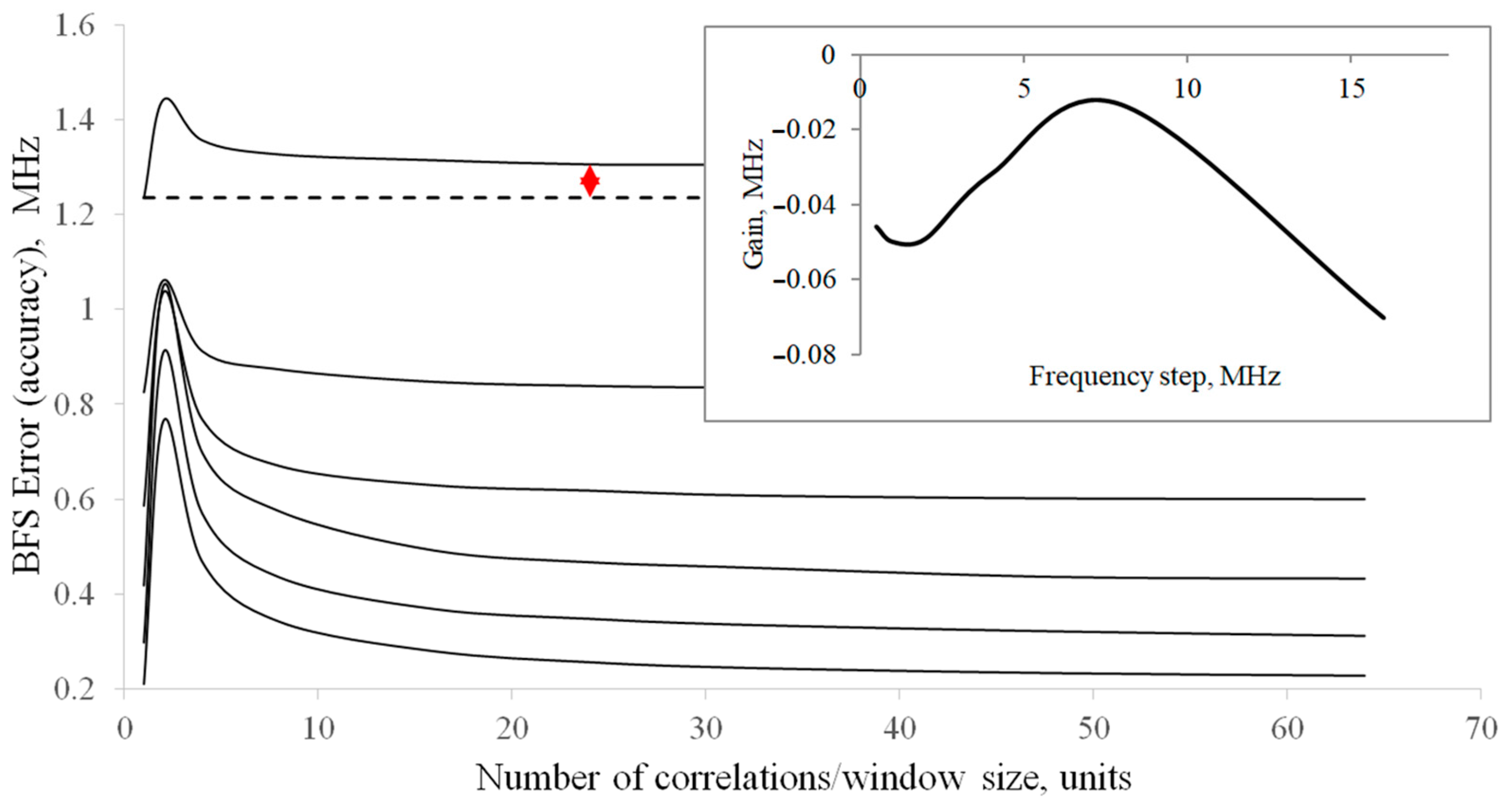
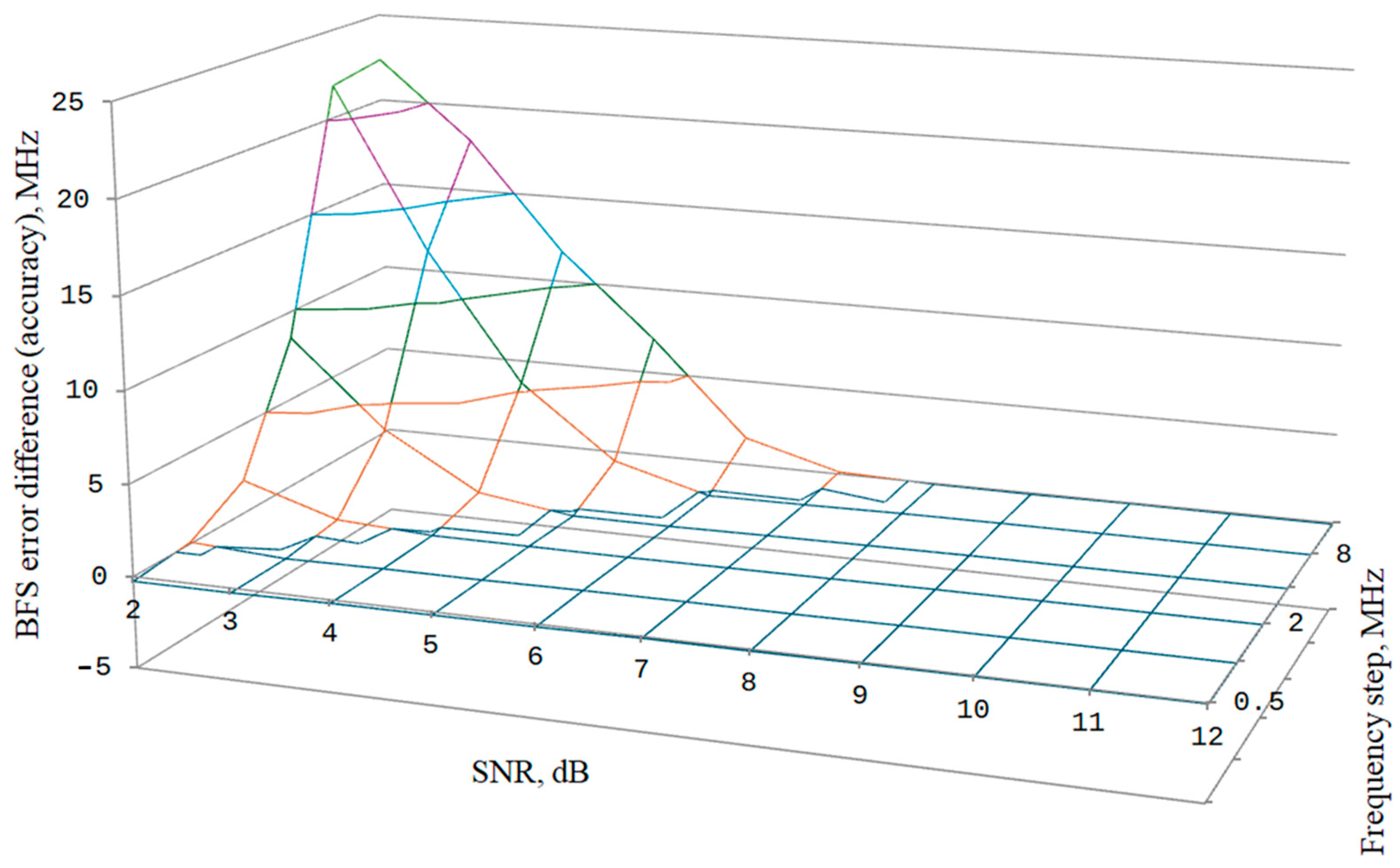
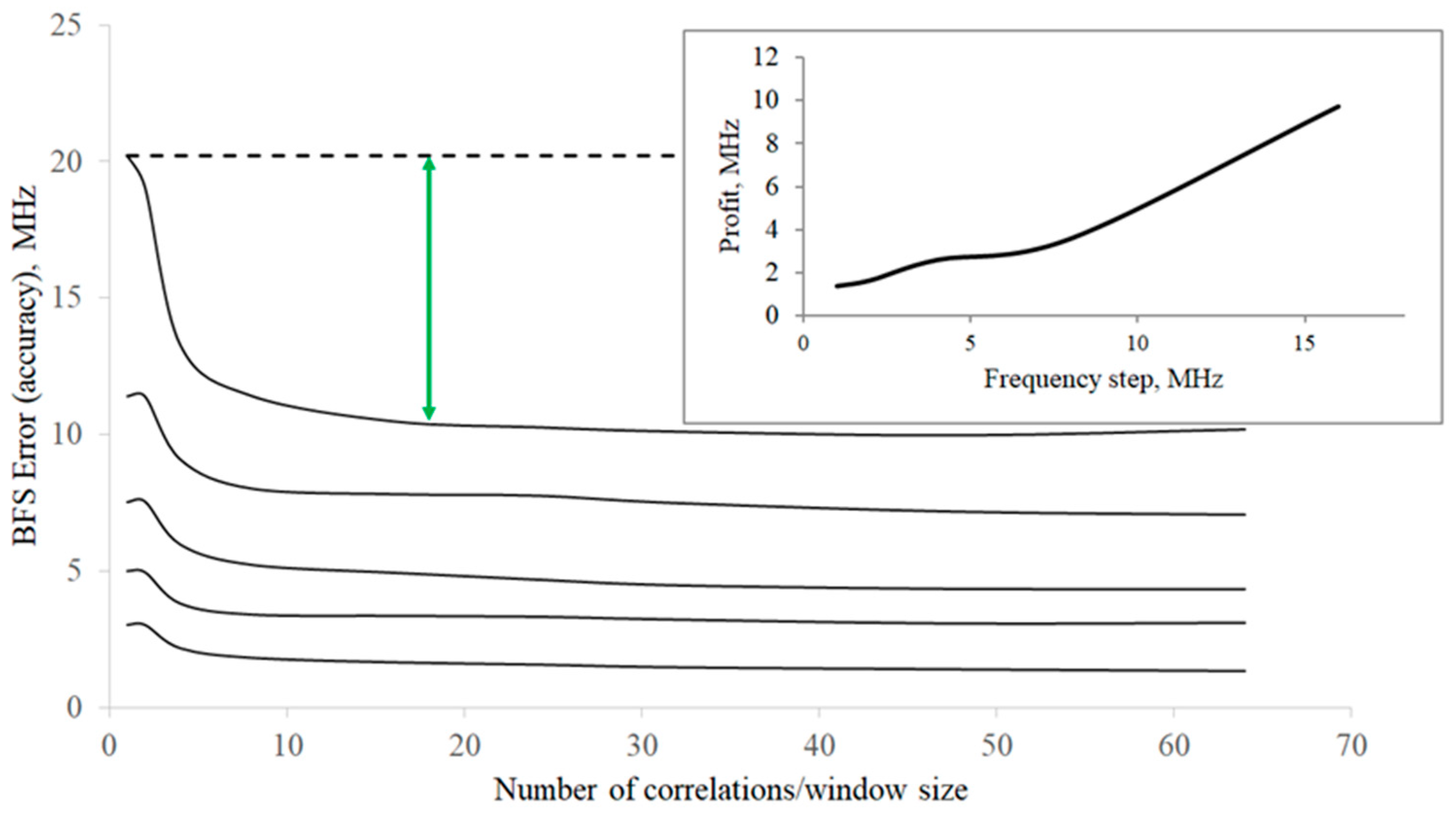
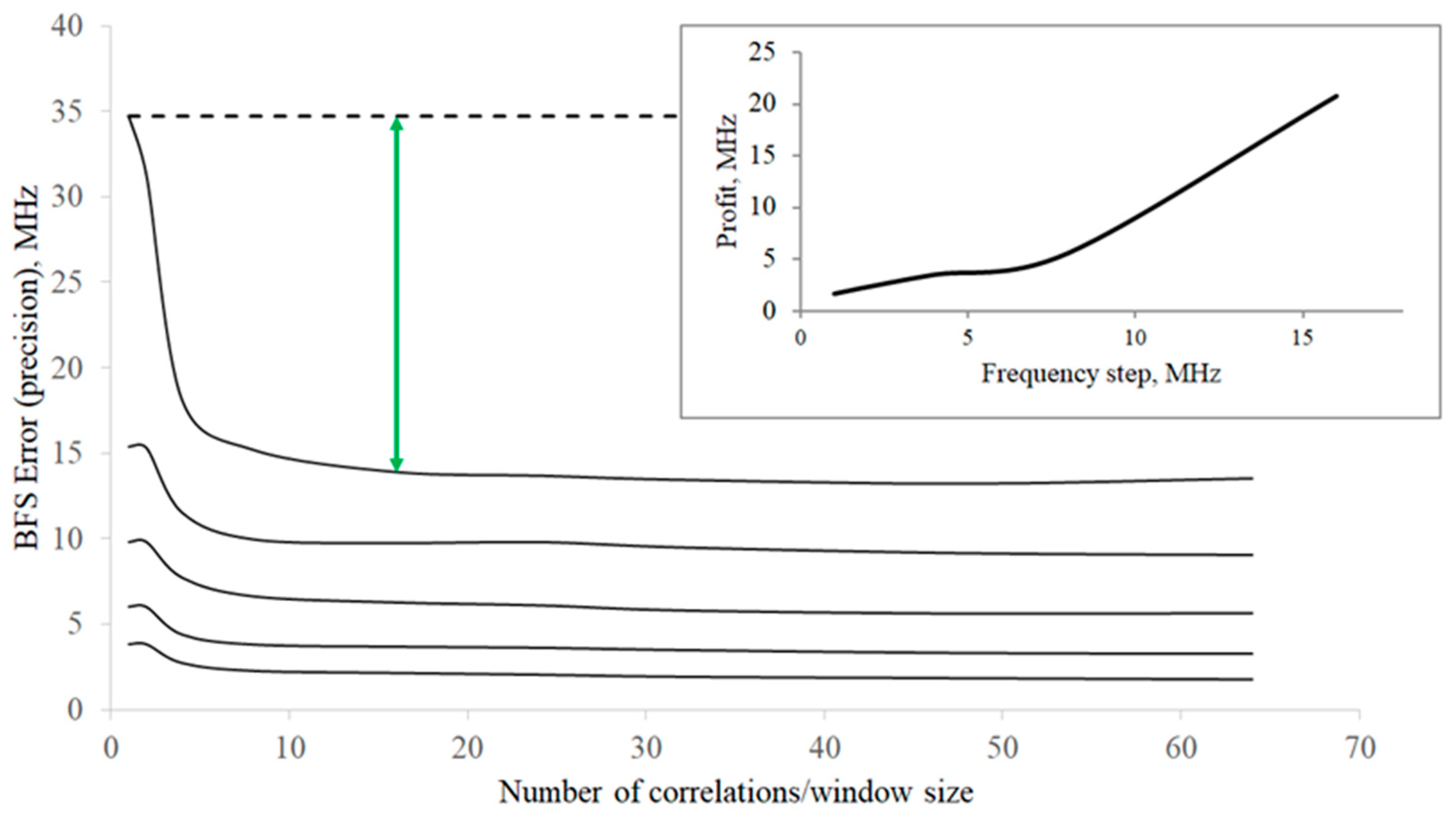
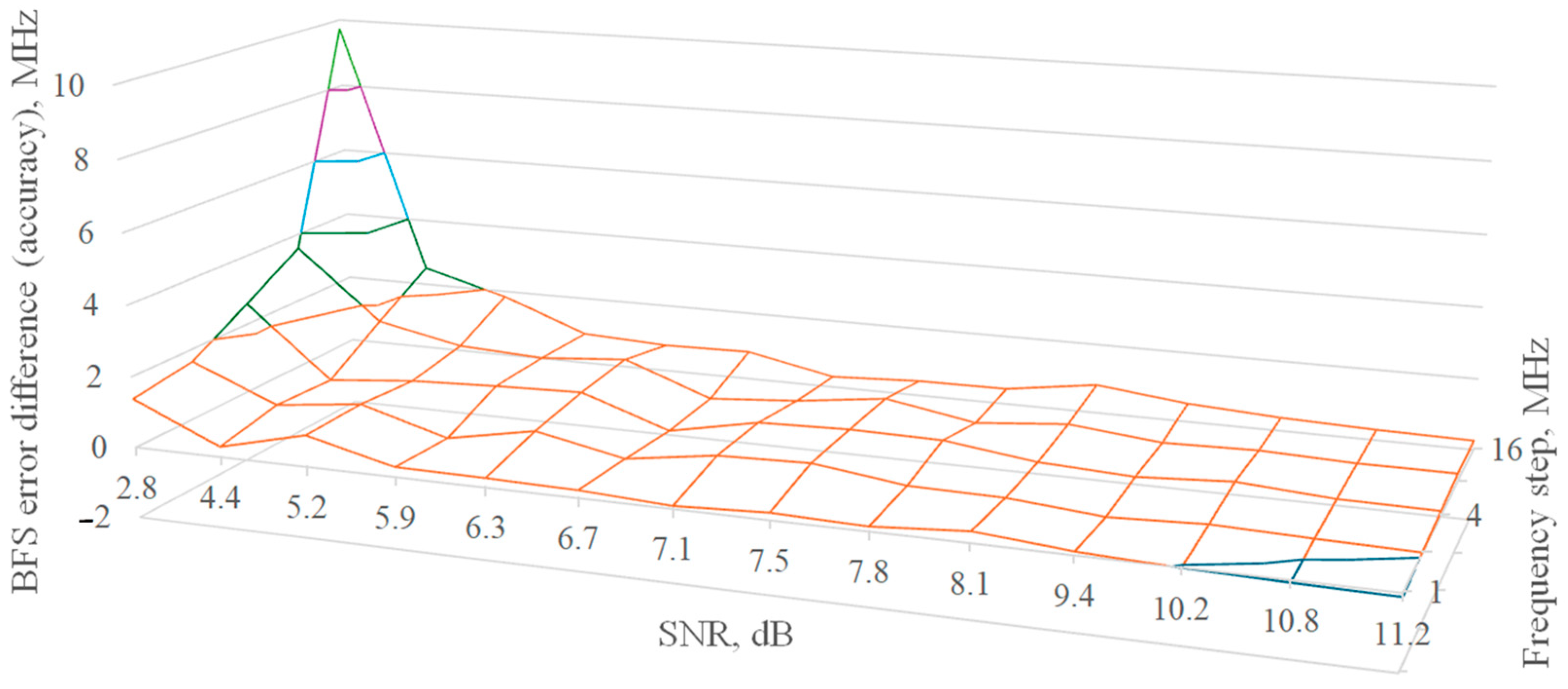
3. The Simulation and Its Results
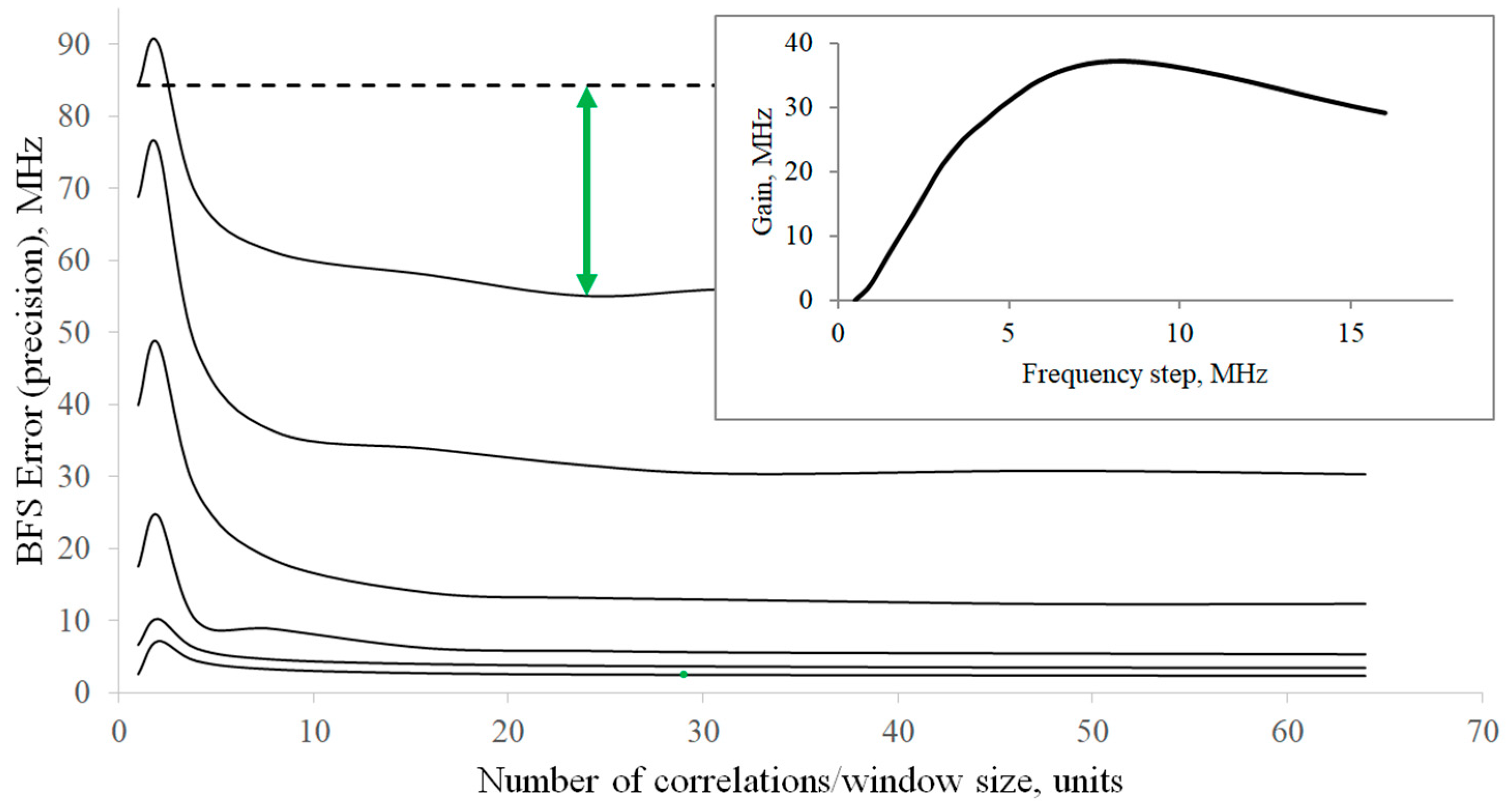
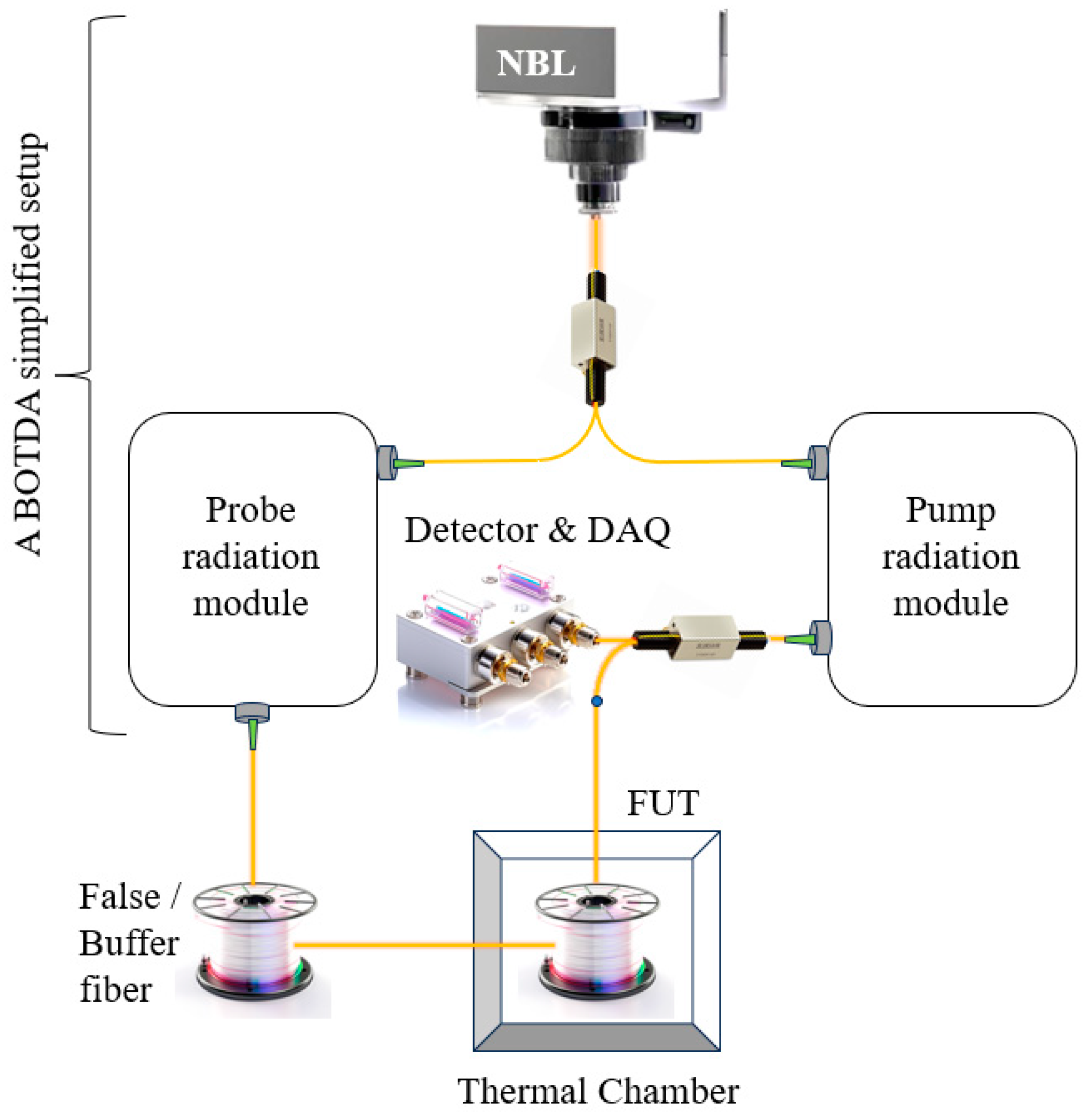
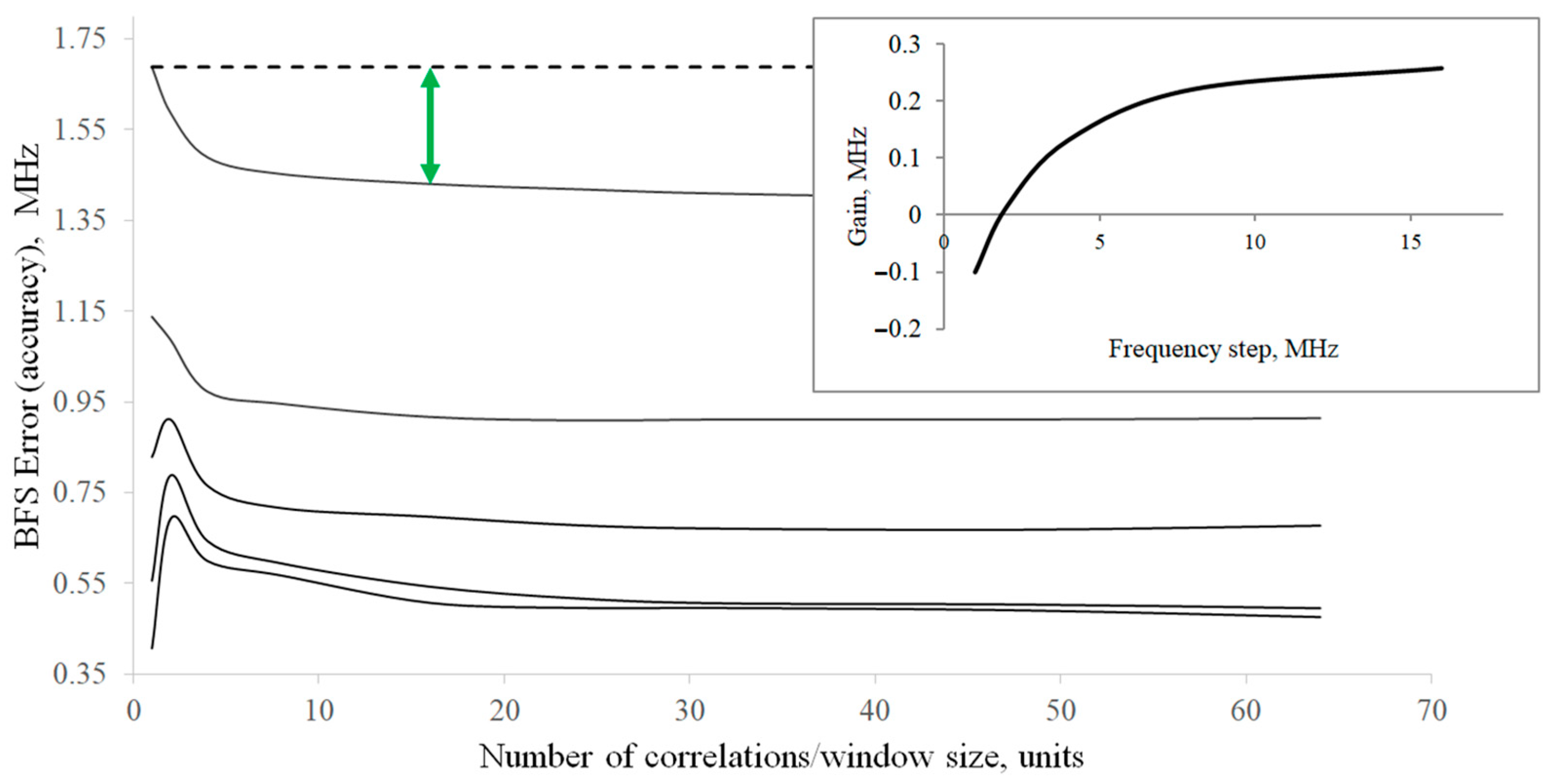
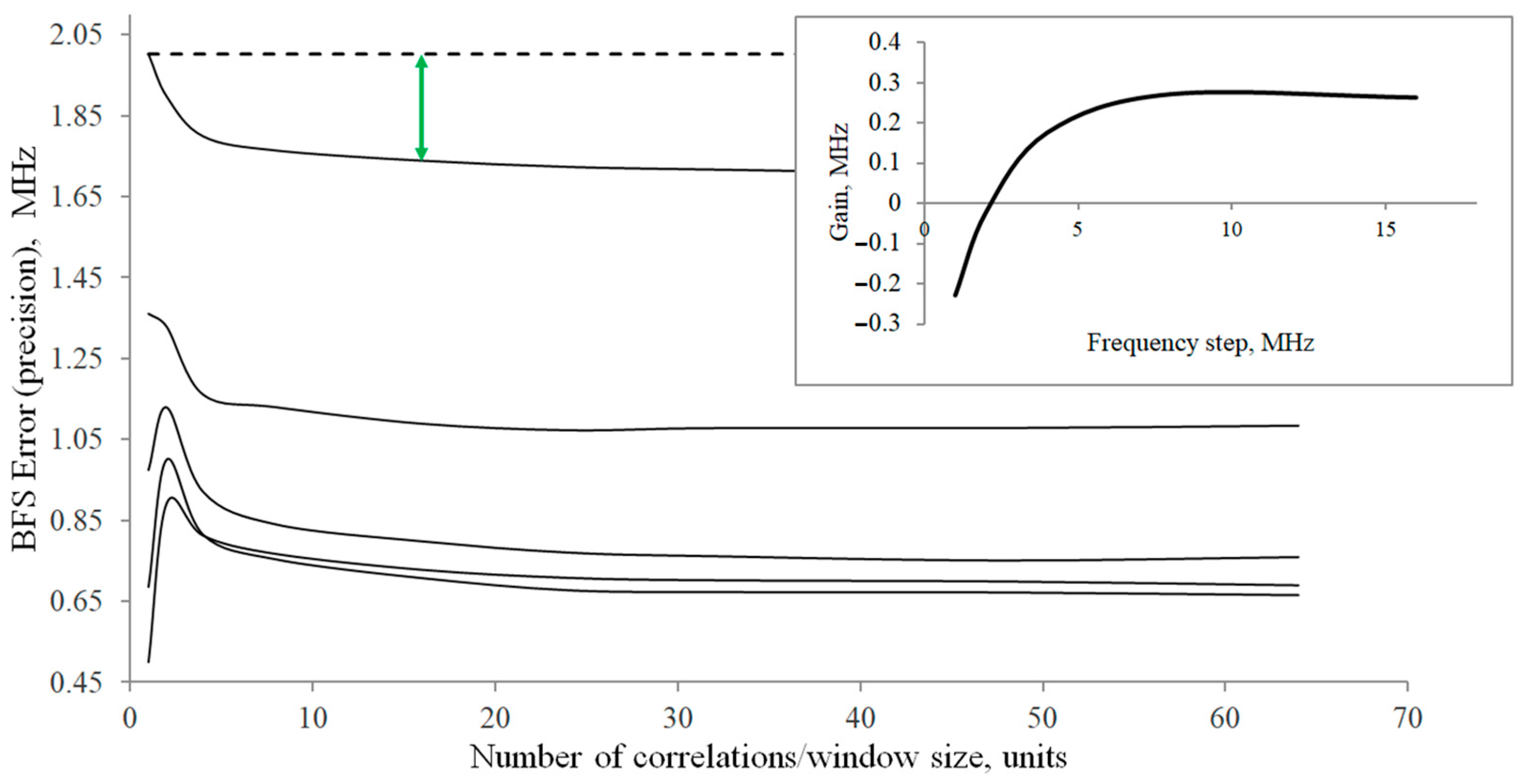
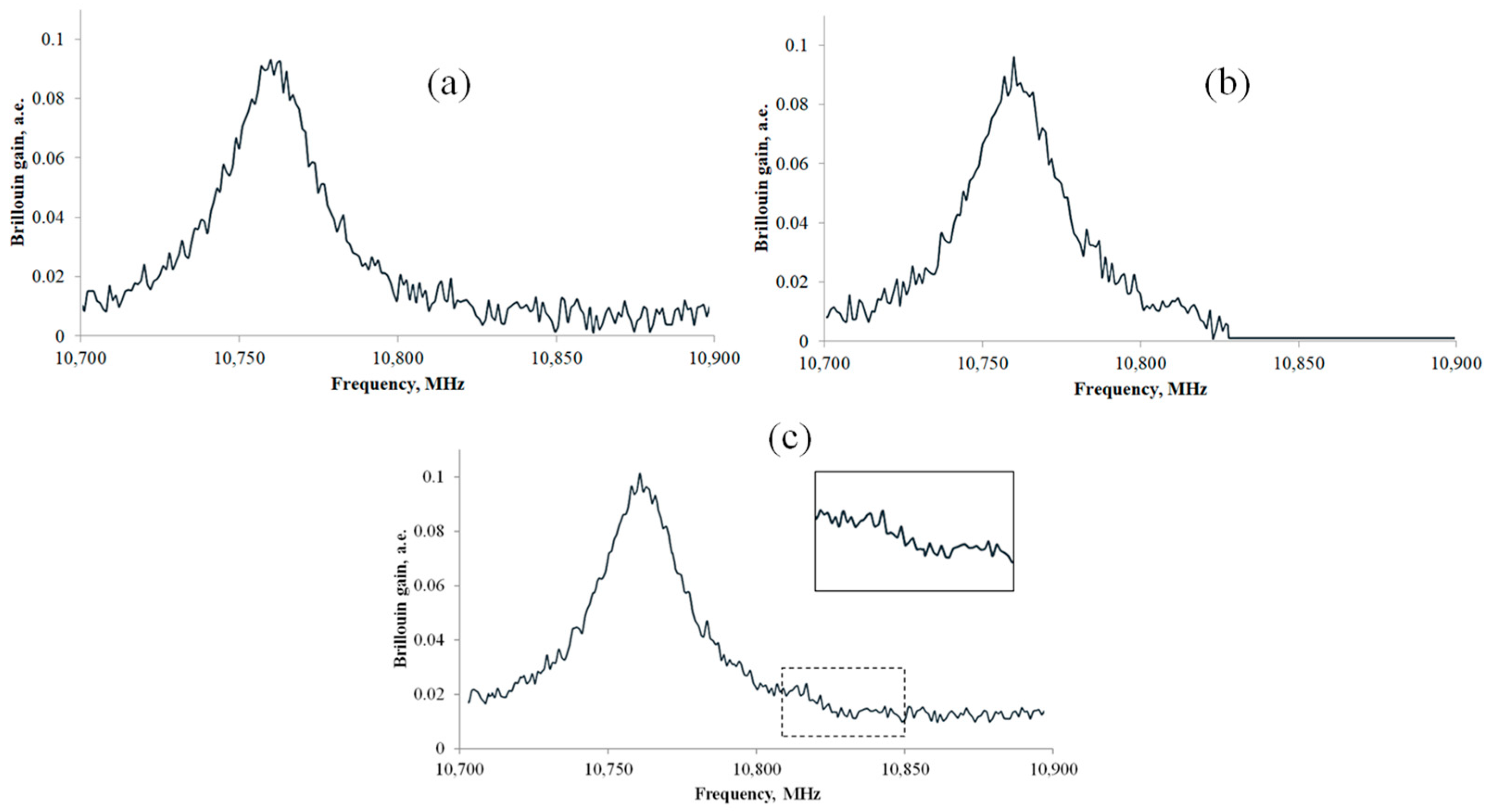
4. The Experiment and Its Results
5. Discussion
6. Conclusions
- It is imperative to optimize the algorithm to eliminate duplicate operations.
- Of particular interest is the alignment of spectra through the use of artificial intelligence rather than the traditional approach of calculating the correlation function.
- The calculation function is to be transferred to the hardware part of the device.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, Y.; Tian, H.; Jia, Z.; Chen, W.; Zhang, W.; Wang, C.; Zhou, T.; Li, L.; Hong, D.; Wang, Y.; et al. Distributed Partial Discharge Acoustic Signal Detection and Localization Technology for GIL with Built-in Fiber Optics. J. Light. Technol. 2024, 42, 5068–5076. [Google Scholar] [CrossRef]
- Kovalenko, D.; Sodnomay, A.; Alekseenko, Z.; Shelemba, I.; Lobach, I.; Firstov, S.; Melkumov, M. Loss-Compensated Dual-Source Raman-DTS with Bismuth- and Erbium-doped Fiber Amplifiers. In Optical Fiber Sensors Conference 2020 Special Edition; Paper T3.44; Cranch, G., Wang, A., Digonnet, M., Dragic, P., Eds.; OSA Technical Digest, Optica Publishing Group: Washington, DC, USA, 2020. [Google Scholar]
- Matveenko, V.P.; Serovaev, G.S.; Kosheleva, N.A.; Galkina, E.B. Investigation of fiber Bragg grating’s spectrum response to strain gradient. Procedia Struct. Integr. 2024, 54, 218–224. [Google Scholar] [CrossRef]
- Fu, C.; Xiao, S.; Meng, Y.; Shan, R.; Liang, W.; Zhong, H.; Liao, C.; Yin, X.; Wang, Y. OFDR shape sensor based on a femtosecond-laser-inscribed weak fiber Bragg grating array in a multicore fiber. Opt. Lett. 2024, 49, 1273–1276. [Google Scholar] [CrossRef]
- Höttges, A.; Rabaiotti, C.; Facchini, M. A Novel Distributed Fiber-Optic Hydrostatic Pressure Sensor for Dike Safety Monitoring. IEEE Sens. J. 2023, 23, 28942–28953. [Google Scholar] [CrossRef]
- Zhang, W.; Ni, X.; Wang, J.; Ai, F.; Luo, Y.; Yan, Z.; Liu, D.; Sun, Q. Microstructured Optical Fiber Based Distributed Sensor for In Vivo Pressure Detection. J. Light. Technol. 2019, 37, 1865–1872. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, Z.; Lin, Z.; Yao, Y.; Xiong, Y.; Tong, W.; Tang, M. Distributed twist sensing using frequency-scanning φ-OTDR in a spun fiber. Opt. Express 2023, 31, 17809–17819. [Google Scholar] [CrossRef]
- Gritsenko, T.V.; Chesnokov, G.Y.; Koshelev, K.I.; Khan, R.I.; Stepanov, K.V.; Valba, O.V.; Chernutsky, A.O.; Svelto, C.; Zhirnov, A.A.; Pnev, A.B.; et al. Optical Fiber Sensor for Real-Time Monitoring of Industrial Structures and Application to Urban Telecommunication Networks. In Proceedings of the 2023 IEEE International Conference on Metrology for eXtended Reality, Artificial Intelligence and Neural Engineering (MetroXRAINE), Milano, Italy, 25–27 October 2023; pp. 383–388. [Google Scholar] [CrossRef]
- Bengalskii, D.M.; Kharasov, D.R.; Fomiryakov, E.A.; Nikitin, S.P.; Nanii, O.E.; Treshchikov, V.N. Characterization of Laser Frequency Stability by Using Phase-Sensitive Optical Time-Domain Reflectometry. Photonics 2023, 10, 1234. [Google Scholar] [CrossRef]
- Yang, D.; Denney, T.; Bello, O.; Lazarus, S.; Vettical, C. Enabling Real-Time Distributed Sensor Data for Broader Use by the Big Data Infrastructures. Presented at the SPE Intelligent Energy International Conference and Exhibition, Aberdeen, Scotland, UK, 6 September 2016. [Google Scholar] [CrossRef]
- Sharma, J.; Santos, O.L.A.; Feo, G.; Ogunsanwo, O.; Williams, W. Well-scale multiphase flow characterization and validation using distributed fiber-optic sensors for gas kick monitoring. Opt. Express 2020, 28, 38773–38787. [Google Scholar] [CrossRef]
- Leite, T.M.; Freitas, C.; Magalhães, R.; da Silva, A.F.; Alves, J.R.; Viana, J.C.; Delgado, I. Decoupling of Temperature and Strain Effects on Optical Fiber-Based Measurements of Thermomechanical Loaded Printed Circuit Board Assemblies. Sensors 2023, 23, 8565. [Google Scholar] [CrossRef]
- Soga, K.; Luo, L. Distributed fiber optics sensors for civil engineering infrastructure sensing. J. Struct. Integr. Maint. 2018, 3, 1–21. [Google Scholar] [CrossRef]
- Franciscangelis, C.; Margulis, W.; Floridia, C.; Rosolem, J.B.; Salgado, F.C.; Nyman, T.; Petersson, M.; Hallander, P.; Hällstrom, S.; Söderquist, I.; et al. Vibration measurement on composite material with embedded optical fiber based on phase-OTDR. In Proceedings of the SPIE 10168, Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2017, Portland, OR, USA, 12 April 2017; p. 101683Q. [Google Scholar] [CrossRef]
- Stepanov, K.V.; Zhirnov, A.A.; Sazonkin, S.G.; Pnev, A.B.; Bobrov, A.N.; Yagodnikov, D.A. Non-Invasive Acoustic Monitoring of Gas Turbine Units by Fiber Optic Sensors. Sensors 2022, 22, 4781. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, L.; Fan, H. Influence of laser wavelength instability, polarization fading and phase fluctuation on local heterodyne detection wavelength scanning BOTDR. Optoelectron. Lett. 2023, 19, 200–204. [Google Scholar] [CrossRef]
- Li, M.; Xu, T.; Wang, S.; Hu, W.; Jiang, J.; Liu, T. Probe pulse design in Brillouin optical time domain reflectometry. IET Optoelectron. 2022, 16, 238–252. [Google Scholar] [CrossRef]
- Almoosa, A.S.K.; Zan, M.S.D.; Ibrahim, M.F.; Tanaka, Y.; Hamzah, A.E.; Arsad, N. Fast and accurate Brillouin frequency shift extraction in Brillouin optical time domain reflectometry (BOTDR) distributed fiber sensor by using ensemble machine learning algorithm. J. Phys. Conf. Ser. 2022, 2411, 012012. [Google Scholar] [CrossRef]
- Fu, Y.; Zhu, R.; Han, B.; Wu, H.; Rao, Y.-J.; Lu, C.; Wang, Z. 175-km Repeaterless BOTDA with Hybrid High-Order Random Fiber Laser Amplification. J. Light. Technol. 2019, 37, 4680–4686. [Google Scholar] [CrossRef]
- Peng, J.; Wang, T.; Zhang, Q.; Ge, X.; Zhu, Y.; Zhang, Y.; Zhang, J.; Li, J.; Zhang, M. High Spatial Resolution BOTDA Based on Deconvolution and All Phase Digital Filtering. IEEE Sens. J. 2024, 24, 10024–10030. [Google Scholar] [CrossRef]
- Hamzah, A.E.; Bakar, A.A.A.; Fadhel, M.M.; Sapiee, N.M.; Elgaud, M.M.; Hamzah, M.E.; Almoosa, A.S.K.; Naim, N.F.; Mokhtar, M.H.H.; Ali, S.H.M.; et al. Advancing the measurement speed and accuracy of conventional BOTDA fiber sensor systems via SoC data acquisition. Opt. Fiber Technol. 2024, 84, 103712. [Google Scholar] [CrossRef]
- Bogachkov, I.V.; Gorlov, N.I. Research of the Optical Fibers Structure Influence on the Acousto-Optic Interaction Characteristics and the Brillouin Scattering Spectrum Profile. J. Phys. Conf. Ser. 2022, 2182, 012088. [Google Scholar] [CrossRef]
- Krivosheev, A.I.; Barkov, F.L.; Konstantinov, Y.A.; Belokrylov, M.E. State-of-the-Art Methods for Determining the Frequency Shift of Brillouin Scattering in Fiber-Optic Metrology and Sensing. Instrum. Exp. Tech. 2022, 65, 687–710. [Google Scholar] [CrossRef]
- Poddubrovskii, N.R.; Lobach, I.A.; Kablukov, S.I. Microwave-free BOTDA based on a continuous-wave self-sweeping laser. Opt. Lett. 2024, 49, 282–285. [Google Scholar] [CrossRef] [PubMed]
- Lobach, I.A.; Kablukov, S.I.; Melkumov, M.A.; Khopin, V.F.; Babin, S.A.; Dianov, E.M. Single-frequency Bismuth-doped fiber laser with quasi-continuous self-sweeping. Opt. Express 2015, 23, 24833–24842. [Google Scholar] [CrossRef]
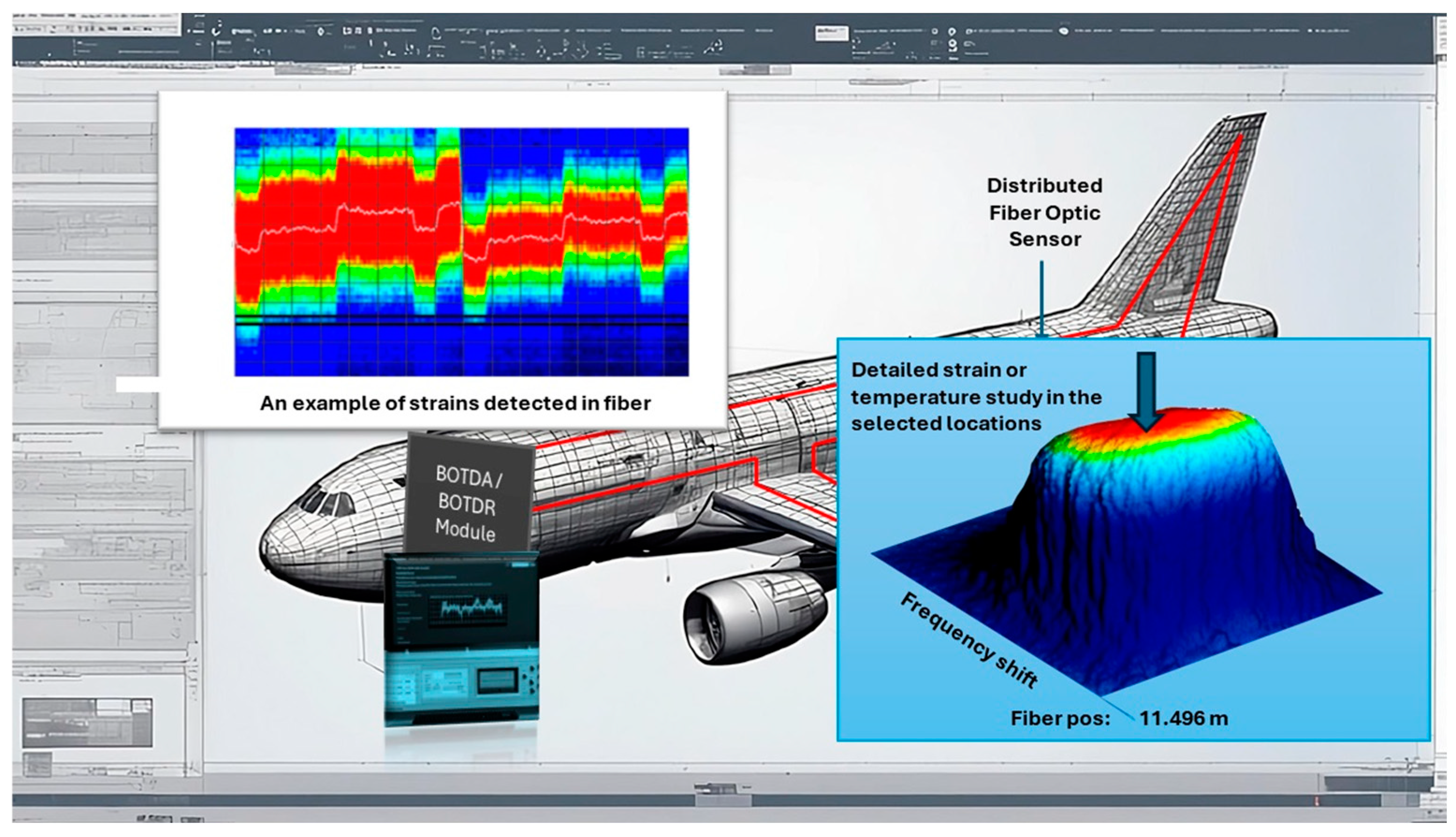
- Yari, T.; Nagai, K.; Takeda, N. Aircraft structural-health monitoring using optical fiber distributed BOTDR sensors. Adv. Compos. Mater. 2004, 13, 17–26. [Google Scholar] [CrossRef]
- Shimizu, T.; Yari, T.; Nagai, K.; Takeda, N. Strain measurement using a Brillouin optical time domain reflectometer for development of aircraft structure health monitoring system. In Proceedings of the SPIE 4335, Advanced Nondestructive Evaluation for Structural and Biological Health Monitoring, Newport Beach, CA, USA, 24 July 2001. [Google Scholar] [CrossRef]
- Sante, D.; Fibre, R. Optic Sensors for Structural Health Monitoring of Aircraft Composite Structures: Recent Advances and Applications. Sensors 2015, 15, 18666–18713. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Indust. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. J. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Lourakis, M.L.A.; Argyros, A.A. Is Levenberg-Marquardt the most efficient optimization algorithm for implementing bundle adjustment? In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05) Volume 1, Beijing, China, 17–21 October 2005; Volume 2, pp. 1526–1531. [Google Scholar] [CrossRef]
- Farahani, M.A.; Castillo-Guerra, E.; Colpitts, B.G. A Detailed Evaluation of the Correlation-Based Method Used for Estimation of the Brillouin Frequency Shift in BOTDA Sensors. IEEE Sens. J. 2013, 13, 4589–4598. [Google Scholar] [CrossRef]
- Barkov, F.L.; Konstantinov, Y.A.; Krivosheev, A.I. A Novel Method of Spectra Processing for Brillouin Optical Time Domain Reflectometry. Fibers 2020, 8, 60. [Google Scholar] [CrossRef]
- Farahani, M.A.; Colpitts, B.G.; Castillo-Guerra, E. Reduction of measurement time in BOTDA sensors using wavelet shrinkage. In Proceedings of the SPIE 7753, 21st International Conference on Optical Fiber Sensors, Ottawa, ON, Canada, 17 May 2011; p. 77532E. [Google Scholar] [CrossRef]
- Wang, B.; Wang, L.; Guo, N.; Zhao, Z.; Yu, C.; Lu, C. Deep neural networks assisted BOTDA for simultaneous temperature and strain measurement with enhanced accuracy. Opt. Express 2019, 27, 2530–2543. [Google Scholar] [CrossRef]
- Ruiz-Lombera, R.; Fuentes, A.; Rodriguez-Cobo, L.; Lopez-Higuera, J.M.; Mirapeix, J. Simultaneous Temperature and Strain Discrimination in a Conventional BOTDA via Artificial Neural Networks. J. Light. Technol. 2018, 36, 2114–2121. [Google Scholar] [CrossRef]
- Qu, S.; Qin, Z.; Xu, Y.; Cong, Z.; Wang, Z.; Liu, Z. Improvement of Strain Measurement Range via Image Processing Methods in OFDR System. J. Light. Technol. 2021, 39, 6340–6347. [Google Scholar] [CrossRef]
- Zhao, S.; Cui, J.; Wu, Z.; Tan, J. Accuracy improvement in OFDR-based distributed sensing system by image processing. Opt. Lasers Eng. 2020, 124, 105824. [Google Scholar] [CrossRef]
- Turov, A.T.; Barkov, F.L.; Konstantinov, Y.A.; Korobko, D.A.; Lopez-Mercado, C.A.; Fotiadi, A.A. Activation Function Dynamic Averaging as a Technique for Nonlinear 2D Data Denoising in Distributed Acoustic Sensors. Algorithms 2023, 16, 440. [Google Scholar] [CrossRef]
- Qian, X.; Wang, Z.; Sun, W.; Zhang, B.; He, Q.; Zhang, L.; Wu, H.; Rao, Y. Long-range BOTDA denoising with multi-threshold 2D discrete wavelet. In Proceedings of the Asia Pacific Optical Sensors Conference, Shanghai, China, 11–14 October 2016; OSA Technical Digest (online); paper W4A.24. Optica Publishing Group: Washington, DC, USA, 2016. [Google Scholar]
- Soto, M.A.; Ramírez, J.A.; Thévenaz, L. Intensifying the response of distributed optical fibre sensors using 2D and 3D image restoration. Nat. Commun. 2016, 7, 10870. [Google Scholar] [CrossRef] [PubMed]
- Qian, X.; Wang, Z.; Wang, S.; Xue, N.; Sun, W.; Zhang, L.; Zhang, B.; Rao, Y. 157km BOTDA with pulse coding and image processing. In Proceedings of the SPIE 9916, Sixth European Workshop on Optical Fibre Sensors, Limerick, Ireland, 30 May 2016; p. 99162S. [Google Scholar] [CrossRef]
- Soto, M.A.; Ramírez, J.A.; Thévenaz, L. Optimizing Image Denoising for Long-Range Brillouin Distributed Fiber Sensing. J. Light. Technol. 2018, 36, 1168–1177. [Google Scholar] [CrossRef]
- Li, B.; Jiang, N.; Han, X. Denoising of Brillouin Gain Spectrum Images for Improved Dynamic Measurements of BOTDR. IEEE Photon-J. 2023, 15, 6801808. [Google Scholar] [CrossRef]
- Hu, Y.; Shang, Q. Performance Enhancement of BOTDA Based on the Image Super-Resolution Reconstruction. IEEE Sens. J. 2021, 22, 3397–3404. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, J.; Wu, H.; Guo, N.; Zhu, T. Single shot OCC-BOTDA based on polarization diversity and image denoising. Opt. Lasers Eng. 2021, 137, 106368. [Google Scholar] [CrossRef]
- Wang, Q.; Bai, Q.; Liu, Y.; Wang, J.; Wang, Y.; Jin, B. SNR Enhancement for BOTDR With Spatial-Adaptive Image Denoising Method. J. Light. Technol. 2023, 41, 2562–2571. [Google Scholar] [CrossRef]
- Hamzah, A.E.; Zan, M.S.D.; Hamzah, M.E.; Fadhel, M.M.; Sapiee, N.M.; Bakar, A.A.A. Fast and Accurate Measurement in BOTDA Fiber Sensor Through the Application of Filtering Techniques in Frequency and Time Domains. IEEE Sens. J. 2024, 24, 4531–4541. [Google Scholar] [CrossRef]
- Soto, M.A.; Thévenaz, L. Modeling and evaluating the performance of Brillouin distributed optical fiber sensors. Opt. Express 2013, 21, 31347–31366. [Google Scholar] [CrossRef]
- Krivosheev, A.I.; Konstantinov, Y.A.; Barkov, F.L.; Pervadchuk, V.P. Comparative Analysis of the Brillouin Frequency Shift Determining Accuracy in Extremely Noised Spectra by Various Correlation Methods. Instrum. Exp. Tech. 2021, 64, 715–719. [Google Scholar] [CrossRef]
- Karapanagiotis, C.; Krebber, K. Machine Learning Approaches in Brillouin Distributed Fiber Optic Sensors. Sensors 2023, 23, 6187. [Google Scholar] [CrossRef] [PubMed]
- Barkov, F.L.; Krivosheev, A.I.; Konstantinov, Y.A.; Davydov, A.R. A Refinement of Backward Correlation Technique for Precise Brillouin Frequency Shift Extraction. Fibers 2023, 11, 51. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konstantinov, Y.; Krivosheev, A.; Barkov, F. An Image Processing-Based Correlation Method for Improving the Characteristics of Brillouin Frequency Shift Extraction in Distributed Fiber Optic Sensors. Algorithms 2024, 17, 365. https://doi.org/10.3390/a17080365
Konstantinov Y, Krivosheev A, Barkov F. An Image Processing-Based Correlation Method for Improving the Characteristics of Brillouin Frequency Shift Extraction in Distributed Fiber Optic Sensors. Algorithms. 2024; 17(8):365. https://doi.org/10.3390/a17080365
Chicago/Turabian StyleKonstantinov, Yuri, Anton Krivosheev, and Fedor Barkov. 2024. "An Image Processing-Based Correlation Method for Improving the Characteristics of Brillouin Frequency Shift Extraction in Distributed Fiber Optic Sensors" Algorithms 17, no. 8: 365. https://doi.org/10.3390/a17080365
APA StyleKonstantinov, Y., Krivosheev, A., & Barkov, F. (2024). An Image Processing-Based Correlation Method for Improving the Characteristics of Brillouin Frequency Shift Extraction in Distributed Fiber Optic Sensors. Algorithms, 17(8), 365. https://doi.org/10.3390/a17080365







