Optimization of Gene Selection for Cancer Classification in High-Dimensional Data Using an Improved African Vultures Algorithm

Abstract

This study presents a novel method, termed RBAVO-DE (Relief Binary African Vultures Optimization based on Differential Evolution), aimed at addressing the Gene Selection (GS) challenge in high-dimensional RNA-Seq data, specifically the rnaseqv2 lluminaHiSeq rnaseqv2 un edu Level 3 RSEM genes normalized dataset, which contains over 20,000 genes. RNA Sequencing (RNA-Seq) is a transformative approach that enables the comprehensive quantification and characterization of gene expressions, surpassing the capabilities of micro-array technologies by offering a more detailed view of RNA-Seq gene expression data. Quantitative gene expression analysis can be pivotal in identifying genes that differentiate normal from malignant tissues. However, managing these high-dimensional dense matrix data presents significant challenges. The RBAVO-DE algorithm is designed to meticulously select the most informative genes from a dataset comprising more than 20,000 genes and assess their relevance across twenty-two cancer datasets. To determine the effectiveness of the selected genes, this study employs the Support Vector Machine (SVM) and k-Nearest Neighbor (k-NN) classifiers. Compared to binary versions of widely recognized meta-heuristic algorithms, RBAVO-DE demonstrates superior performance. According to Wilcoxon’s rank-sum test, with a 5% significance level, RBAVO-DE achieves up to 100% classification accuracy and reduces the feature size by up to 98% in most of the twenty-two cancer datasets examined. This advancement underscores the potential of RBAVO-DE to enhance the precision of gene selection for cancer research, thereby facilitating more accurate and efficient identification of key genetic markers.

1. Introduction

Deoxyribonucleic Acid (DNA) makes up our genetic code, containing the recipe for our existence. Although every cell has the same DNA, each tissue structure is unique and serves a distinct purpose. The RNA transcription mechanism determines which genes in a cell are active, enabling RNA to be transformed into proteins responsible for the cell’s structure and functionality [1]. We analyze RNA-Seq gene expression data (GED) to determine genetic changes and evaluate disease biomarkers. Differential expression analysis identifies quantitative distinctions in gene expression, allowing us to categorize genes whose expression changes under various conditions. This method helps us understand illnesses and find ways to manage them. Gene expression profiling technologies have significantly developed over the years [2].

Two popular techniques are micro-array, which uses a hybridization-based approach, and RNA-Seq, which is based on next-generation sequencing. These technologies have demonstrated their value in advancing our understanding of gene expression [3]. Notable studies, such as those by Chen et al. [4] and Nunez et al. [5], have highlighted the potential of these techniques, while Wang et al. [6] have provided valuable insights into the RNA-Seq approach.

The two methods under consideration serve the purpose of quantifying gene expression for classification and statistical investigation. This paper has chosen the quantification data obtained through the next-generation sequencing (NGS)-based RNA-Seq approach because it offers more accuracy in detecting RNA quantification levels compared to micro-array data [7]. RNA-Seq has overcome several limitations of micro-array analysis, such as dependence on prior sequencing knowledge, which restricted the detection range [8,9]. Unlike micro-arrays, RNA-Seq does not require any previous knowledge and significantly expands the dynamic detection range. This enhancement improves the accuracy of results and enables the identification of a comprehensive set of genes, providing a precise understanding of disease biomarkers. As a result, RNA-Seq has emerged as a potent tool for researchers, offering valuable insights into the underlying molecular mechanisms of various diseases [10].

The “dimensionality curse” [11] has become a common challenge in contemporary times owing to the abundance of available data. This has caused a surge in the development of feature selection (FS) techniques and algorithms. FS algorithms can be classified into four distinct methods: filter, wrapper, embedded, and hybrid [12,13]. These approaches aim to identify the most informative features that can distinguish between different classes. In our case, we are concerned with identifying the genes linked to tumors.

The filter approach is a widely used technique in FS that involves evaluating the relevance of individual genes based on statistical scores. This method is known for its high accuracy in selecting the most satisfactory group of genes. Nevertheless, the filter approach has some limitations, as functioning on each gene individually ignores the interrelationships between genes, which can result in a local optima issue [14]. It is worth noting that the filter approach can be categorized into two sub-types—univariate and multivariate—with the latter considering the correlations between genes. Some examples of the filter approach include Relief [15], Fisher score [16], t-test [17], and information gain [18].

The wrapper method investigates all feasible gene subsets to test and create a subset of genes to determine their implications. A specific classifier is employed to determine the outcome of each subset, and the categorization technique is used multiple times for each assessment. Compared to the filter approach, the wrapper approach delivers superior performance by using a categorization technique that directs the learning procedure. However, this method requires substantial time and computational resources, especially when dealing with large-scale data [19].

Meta-heuristic methods (MHMs) are high-level heuristics used in mathematical optimization and computer science to find satisfactory solutions to optimization problems when information is imperfect or resources are limited [20]. MHMs sample a subset of solutions, making them useful for various optimization issues due to their few assumptions about the problem [21]. However, they do not guarantee globally optimal solutions. Many MHMs employ stochastic optimization, meaning the solution is based on random variables generated during the process [22].

Meta-heuristic methods (MHMs) are more practical than traditional iterative methods and optimization algorithms because they can explore a broader range of possible solutions. Consequently, MHMs have become a preferred strategy for solving optimization problems [23]. Numerous research papers have demonstrated that among the different wrapper methods, MHMs are well suited to address the feature selection (FS) issue. Stochastic methods, including MHMs, can produce optimal or near-optimal results quickly. They offer benefits such as flexibility, self-management without detailed mathematical properties, and the ability to assess numerous outcomes simultaneously. Various MHMs have recently been developed to solve the FS problem, providing reliable near-optimal solutions at significantly reduced computational costs [24].

Embedded FS methods utilize a learning technique to select appropriate genes that interact with the classification process. This method combines the FS technique as part of the learning model. The learning algorithm is trained with an initial attribute subset to estimate a measure for evaluating the rank values of attributes [25]. The ultimate goal is to decrease the computation time for reclassifying different subsets by incorporating the FS stage into the training process. Some techniques in this approach perform feature weighting based on regularization models with objective functions that minimize fitting errors while enforcing feature coefficients to be small or precisely zero. Examples of embedded methods are the First-Order Inductive Learner (FOIL) rule-based feature subset selection algorithm and SVM based on Recursive Feature Elimination (SVM-RFE) [26].

The hybrid method is a well-crafted technique that amalgamates the filter and wrapper methods to leverage the strengths of each. This approach begins with a filter that reduces the feature space dimensionality, generating multiple subsets with intermediate complexity. Subsequently, a wrapper is employed as a learning technique to choose the most suitable candidate subset [27]. The hybrid approach integrates the accuracy of wrappers and the efficiency of filters, resulting in an optimal methodology [28,29].

1.1. Motivation and Contributions

An effective global meta-heuristic optimization algorithm is presented in this paper, which is called the African Vultures Optimization (AVO) algorithm [30], which imitates the living and eating habits of African vultures. The proposed algorithm consists of four basic phases: population division into three groups—the best solution, the second-best solution, and the remaining solutions; famine-level measurement to formulate a mathematical model for the vultures’ exploitation, exploration, and transfer; exploration of vultures employing two strategies to allow vultures to cover large distances over extended periods to find food at random sites; and exploitation of vultures involving two sub-phases. Two distinct strategies are used in the first sub-phase: siege fight for strong vultures and rotational flight, which forms a spiral activity between the outstanding vulture and the rest. Two strategies are utilized in the second sub-phase: assembling vultures around the food source and a hostile siege fight, where vultures become more aggressive and attempt to steal food left behind by healthy vultures.

This study proposes an enhanced binary variant of the AVO technique, namely the RBAVO-DE technique, which is a productive approach that demonstrates accurate performance in handling the GS problem. At first, there is a high possibility that the recommended technique will steer clear of local optima and accomplish sufficient examination precision, quick convergence, and improved stability. Compared to recent MHMs, the proposed RBAVO-DE technique achieves enhanced efficacy by producing optimal or substantially optimal solutions for many of the analyzed situations. The Relief algorithm is utilized to identify only the related features to produce the final classification dataset. RBAVO-DE combines the Relief algorithm with the DE approach to increase exploration capability and obtain the best results within the solution space via repetitions. It also utilizes a transfer function to transform real position values into binary values. The RBAVO-DE approach makes sense in GS because it is simple to comprehend and implement, can deal with various optimization problems, produces valuable results in an acceptable amount of time, requires less computing power, and uses a small number of control parameters. This paper’s primary contributions are as follows:

• Level 3 data based on next-generation sequencing (RNA-Seq) have been pre-processed.
• The ability of the proposed AVO meta-heuristic algorithm to address the GS problem has not been investigated, as RNA-Seq GED has never been used with the AVO algorithm.
• To construct a binary version known as the RBAVO-DE algorithm, the AVO algorithm is altered and recreated.
• The proposed RBAVO-DE algorithm combines the binary variant of the AVO with a Relief approach and DE to improve the exploration ability of the search space and enhance the achieved optimal results.
• The proposed RBAVO-DE algorithm is applied to RNA-Seq GED for the first time.
• Several performance indicators, including average fitness, classification accuracy, number of selected genes, precision, recall, and F1-score, are used to assess the outcomes.
• A comparison is made between the impact of the presented RBAVO-DE algorithm, employing the two recommended ML classifiers (SVM and k-NN), and other algorithms in the literature.
• Twenty-two distinct cancer datasets are used to assess the proposed RBAVO-DE method, and the results are shown.
• The chosen genes are investigated using biomarkers associated with cancer.

1.2. Structure

This paper is structured into five main sections. Section 2 reviews previous research on FS using RNA-Seq GED. This is followed by Section 3, which offers an in-depth discussion of the RBAVO-DE algorithm, an enhanced version of AVO, including its parameters for addressing GS. Section 4 showcases the experimental findings compared to several recent MHMs. Lastly, Section 6 concludes this study and proposes avenues for future investigation.

2. Related Works

In this section, we discuss the literature that focuses on the methods researchers use to classify RNA-Seq GED, which typically has high dimensionality. To achieve optimal performance of classification methods, it is crucial to disregard irrelevant and unrelated genes; hence, selecting appropriate genes is a vital stage before utilizing ML and deep learning (DL) techniques [31] or any other classification techniques. In this regard, we have explored some relevant papers in this domain to accomplish the objective of RNA-Seq categorization for cancer identification.

Yaqoob et al. [32] introduced a cutting-edge technique for GS known as the Sine-Cosine–Cuckoo Search Algorithm (SCCSA), a hybrid method tailored to function alongside established ML models such as SVM. This innovative GS algorithm was evaluated using a breast cancer benchmark dataset, where its performance was meticulously analyzed and compared with other GS methodologies. To refine the selection of features, the minimum Redundancy Maximum Relevance method was initially applied as a preliminary filtering step. Subsequently, the hybrid SCCSA approach was deployed to further improve and fine-tune the GS process. The final stage involved using the SVM classifier to classify the dataset based on the selected genes. Considering the critical importance of GS in decoding complex biological datasets, SCCSA emerges as a crucial asset for the classification of cancer-related datasets.

Joshi et al. [33] introduced an innovative optimization strategy named PSO-CS integrated with DL for brain tumor classification. This method enhances the efficiency of the Particle Swarm Optimization (PSO) technique by incorporating the Cuckoo Search (CS) algorithm, optimizing the classification process. Following this optimization, PSO-CS utilizes DL to classify GED related to brain tumors, identifying various classes associated with specific tumors alongside the PSO-CS optimization method. By integrating the PSO-CS technique with DL, it significantly outperformed other DL and ML models regarding classification accuracy, as evidenced by various performance measures.

Mahto et al. [34] unveiled a groundbreaking approach for cancer classification through an integrated method based on CS-SMO (CS and Spider Monkey Optimization) for GS. Initially, the fitness function of the Spider Monkey Optimization (SMO) algorithm is modified using the CS algorithm. This modification leverages the strengths of both MHMs to identify a subset of genes capable of predicting cancer at an early stage. To further refine the accuracy of the CS-SMO algorithm, a pre-processing step, MRMR, is employed to reduce the complexity of cancer gene expression datasets. Subsequently, these gene subsets are processed using DL to classify different cancer types. The efficacy of the CS-SMO approach coupled with DL was evaluated using eight benchmark micro-array gene expression datasets for cancer, examining its performance across various measures. The CS-SMO method integrated with DL demonstrated superior classification accuracy across all examined large-scale gene expression datasets for cancer, outperforming existing DL and ML models.

Neggaz et al. [35] introduced an improved version of the manta ray foraging optimization, called MRFO-SC, which used trigonometric operators inspired by the sine-cosine (SC) algorithm to handle the GS issue. The k-NN model was used for gene-set selection. In addition, the statistical significance of the MRFO-SC was evaluated using Wilcoxon’s rank-sum test at a 5% significance level. The results were evaluated and compared with some recent MHMs. The comparison and experimental results confirmed the effective performance of the proposed MRFO-SC on high- and low-dimensional benchmark datasets by obtaining the greatest classification accuracy on 85% of the GS benchmark datasets.

Lyu et al. [36] explored cancer biomarkers by focusing on genes’ significance in their impact on classification. They followed a two-phase approach—data pre-processing and utilizing a convolutional neural network—to classify the type of tumor. In the second phase, they created heat maps for each category to identify genes related to pixels with the highest intensities in the heat maps. They then evaluated the selected genes’ pathways. During pre-processing, they removed the levels of gene expression that had not been modified during the GS phase, using a variance threshold of 1.19, which decreased the number of genes from 19,531 to 10,381. The final classification accuracy obtained was 95.59, which is good but could still be improved using a more effective FS methodology to further decrease data dimensionality.

Khalifa et al. [37] built on the aforementioned paper [36]. The focus of their study was on five types of cancer data: Uterine Corpus Endometrial Carcinoma (UCEC), Lung Squamous Cell Carcinoma (LUSC), Lung Adenocarcinoma (LUAD), Kidney Renal Clear Cell Carcinoma (KIRC), and Breast Invasive Carcinoma (BRCA). The benchmark dataset used for the study comprised 2086 records and 972 attributes. Each record provided detailed sample information, while each attribute included the RNA-Seq values for a specific gene, represented as RPKM (Reads Per Kilobase per Million) [38]. The researchers employed a mixed approach using binary PSO with the decision trees (BPSO-DT) method to pre-process the data. Out of 971 attributes, 615 were selected as the best attributes of RNA-SEquation The proposed method achieved an overall testing classification accuracy of 96.90%, as demonstrated by the suggested outcomes and evaluation measures used.

Xiao et al. [39] assessed their methodology using three RNA-Seq datasets: Stomach Adenocarcinoma (STAD), BRCA, and LUAD. Their approach relied on DL techniques, wherein they employed five classifiers and subsequently utilized the DL technique to ensemble each output of the five classifiers. This led to an improvement in the classification accuracy of all the predictions, with the BRCA dataset achieving 98.4% accuracy, STAD achieving 98.78% accuracy, and LUAD achieving 99.20% accuracy.

Liu et al. [40] used micro-array data and a hybrid approach to address the problem. Unlike the previously mentioned papers, they studied each cancer class separately. To assess performance, they employed four gene benchmarks related to small round blue cell tumors, colon cancer, lung cancer, and leukemia. Their proposed method used Relief as the pre-processing technique to eliminate genes with a lower correlation with the specific cancer class, followed by PSO as the search technique. Finally, they employed the SVM model to evaluate the classification accuracy of the selected subset of genes and obtain the conclusive optimum gene subset for each cancer type.

Based on the existing research, it seems that most studies using RNA-Seq GED are still in their early stages, with researchers attempting to implement and test various ideas in this promising area. While the literature contains a plethora of experiments employing multiple techniques, such as FS and DL recent methods, no single technique is perfect due to the high dimensionality of RNA-Seq GED. FS of RNA-Seq GED plays a crucial role in determining the relationship between a gene and its category. It is a critical pre-processing task for validating gene biomarkers of cancer and overcoming the dimensionality curse. Consequently, this study aims to introduce a new wrapper approach, the RBAVO-DE algorithm, and apply it to RNA-Seq data for the first time. It also compares the proposed algorithm’s effectiveness with that of other FS techniques.

3. Proposed RBAVO-DE for GS

An improved variant of AVO known as RBAVO-DE is proposed in this paper to discover the smallest relevant gene subsets from the classification process and to disregard irrelevant genes. RBAVO-DE utilizes a Relief-based binary AVO algorithm combined with the DE technique. RBAVO-DE’s primary feature is its ability to maximize accuracy while utilizing the fewest features possible. The proposed RBAVO-DE consists of two primary steps. First, there is a pre-processing step in which the Relief algorithm is used to determine which features are significant by assigning each feature a weight and then removing the features that are irrelevant and have the lowest weights. In the second step, the binary AVO algorithm and the DE technique are applied to identify the more pertinent and unique features. The AVO algorithm is prone to the local optimum trap when handling large-scale problems. The AVO algorithm incorporates the DE technique to prevent this.

The proposed RBAVO-DE algorithm for tackling the GS strategy requires applying the Relief algorithm, initializing, position boosting using the AVO algorithm, binary conversion, fitness appraisal, and integration with DE. The following subsections explain these steps.

3.1. Applying the Relief Algorithm for Feature Filtration

This step aims to pre-process the population using the Relief algorithm [41], which is considered a fast, easy, and efficient filtering technique for finding features related to one another. This algorithm’s primary goal is to find characteristics that differentiate sample values and group similar samples close together. As a result, the method depends on the weighted ranking of features, where a feature with a higher weight indicates better classification performance.

After choosing a sample randomly, the Relief algorithm examines two different kinds of closest samples: near-hit samples, which are associated with samples from the same class, and near-miss samples, which are associated with samples from other classes. The near-hit and near-miss values can be used to determine the features’ weights. To assess the importance in the classification process, the features’ weights are arranged from most significant to least significant. Finally, the features with the most significant weights are selected. The following formula can be used to determine the weight W for feature A:

$$W_A=\sum _{j=1}^N{\left(x_A^j-NM{\left(x^j\right)}_A\right)}^2-{\left(x_A^j-NH{\left(x^j\right)}_A\right)}^2.$$

(1)

where $W_A$ denotes the weight of feature A, $x_A^j$ denotes the value of feature A for data $x^j$, and N denotes the number of samples. The nearest data points to $x^j$ in the same or different classes are $NH\left(x^j\right)$ and $NM\left(x^j\right)$.

The Relief algorithm narrows its focus to only the necessary features and minimizes the search area to help the AVO algorithm find better features more quickly.

3.2. Initializing the Population

The proposed BAVO algorithm starts by randomly generating a population of N positions. A vector of dimensions D equivalent to the number of features in the original dataset describes each position as a possible solution at its constrained lower and upper bounds. This randomly initialized step, bounded within the $[-1,1]$ range for each position vector’s variable, uses the randomly produced position.

3.3. Boosting Positions via the AVO Algorithm

This paper presents the AVO algorithm [30], a meta-heuristic optimization algorithm inspired by vultures in Africa and their living and feeding behaviors. Based on fundamental ideas about vultures, the AVO algorithm is configured as follows: The African vulture population size is initially presumed by the AVO algorithm to consist of N vultures. The population of African vultures is then divided into three groups to reflect the primary natural function of vultures, based on the computed fitness function. The first group consists of the strongest vulture, which is the best solution; the second group contains a vulture weaker than the first, which is the second-best solution; and the final group encompasses the remaining weaker vultures, which are the worst solutions.

Based on the above, the proposed AVO algorithm is composed of four fundamental phases to simulate the behavior of different types of vultures. The following subsections clarify these phases.

3.3.1. Phase of Dividing the Population

The initial population is split into groups by assessing the solution’s fitness function. The best solution is chosen as the best vulture in the first group, while the second group contains the second-best solution. The third group contains the remaining solutions. As the solutions constantly strive to approach the best and second-best solutions, the population needs to be re-evaluated for each iteration, as follows:

$$R^g=\left\{\begin{array}{cc}BestVultur{e}_1^g,\hfill & \mathit{if}{pr}^g=L_1,\hfill \\ SecondBestVultur{e}_2^g,\hfill & \mathit{if}{pr}^g=L_2,\hfill \end{array}\right.$$

(2)

$${pr}^g={\displaystyle \frac{{\upsilon }^g}{{\sum }_{g=1}^N{\upsilon }^g}}.$$

(3)

The best vulture in the first group and the second-best vulture in the second group at the $g^{th}$ iteration are denoted by the expressions $BestVultur{e}_1^g$ and $SecondBestVultur{e}_2^g$, respectively. The probability of selecting the best solution for each group at the $g^{th}$ iteration is defined using the roulette wheel approach, as shown in Equation (3), ${pr}^g$. Two random parameters within the range $[0,1]$ are $L_1$ and $L_2$.

3.3.2. Phase of Measuring the Famine Level

This phase is utilized to formulate a mathematical model for the exploitation, exploration, and transfer among the vultures. When they are not famished, the vultures have a greater ability to search for food and can fly further. Furthermore, when famished, vultures cannot fly long distances in search of food and may become violent. The $i^{th}$ vulture’s famine level ($F_i^g$) during the $g^{th}$ iteration can be written as follows, which is used to develop a mathematical model for the vultures’ exploitation, exploration, and transfer:

$$F_i^g=(2\times rand+1)\times z\times \left(1-{\displaystyle \frac{g_i}{G_{max}}}\right)+t,$$

(4)

$$t=h\times \left({\sin }^w\left({\displaystyle \frac{\pi }{2}}\times {\displaystyle \frac{g_i}{G_{max}}}\right)+\cos \left({\displaystyle \frac{\pi }{2}}\times {\displaystyle \frac{g_i}{G_{max}}}\right)-1\right).$$

(5)

The vultures are presumably full since the variable $F_i^g$ shows the vultures’ shift from exploration to exploitation. A random number between 0 and 1 is called a $rand$. z denotes a random value within the interval $[-1,1]$. The current iteration number is denoted by $g_i$, while the maximum iteration number is denoted by $G_{max}$. Equation (5) calculates the t value to help solve complicated optimization problems more effectively and prevent reaching a local optimum. An arbitrary value within the interval $[-2,2]$ is represented by h. The probability of carrying out the exploration process is regulated by the predefined constant parameter w; the exploration likelihood grows as its value increases. Exploration is less probable as its value declines.

Equation (4) states that as the number of iterations increases, $F_i^g$ gradually lessens. As a result, the next step in the proposed AVO algorithm can be defined as follows:

$$\left\{\begin{array}{c}\mathit{Exploration}\mathit{phase}(\mathit{Search}\mathit{food}\mathit{in}\mathit{diverse}\mathit{areas}),\mathit{if}|F_i^g|\ge 1,\hfill \\ \mathit{Exploitation}\mathit{phase}(\mathit{Search}\mathit{food}\mathit{in}\mathit{surrounding}\mathit{area}),\mathit{if}|F_i^g|<1.\hfill \end{array}\right.$$

(6)

3.3.3. Phase of Exploration

The vultures are characterized by their great ocular ability to locate appropriate food during this phase. There are two different strategies used in this phase to enable vultures to travel great distances for lengthy periods to search for food in random locations. These locations are selected using a random number $ran{d}_{P_1}$ and a preset parameter $P_1$, both of which have values within the range $[0,1]$. In the exploration phase, the famine level $|F_i^g|$ is greater than or equal to 1. The exploration techniques are described as follows:

$$X_i^{g+1}=\left\{\begin{array}{cc}{R}^g-D_i^g\times F_i^g,\hfill & \mathit{if}ran{d}_{P_1}\le P_1,\hfill \\ R^g-F_i^g+rand\times ((UB-LB)\times rand+LB),\hfill & \mathit{if}ran{d}_{P_1}>P_1,\hfill \end{array}\right\}\mathit{if}\left|F_i^g\right|\ge 1,$$

(7)

$$D_i^g=|(2\times rand)\times R^g-X_i^g|.$$

(8)

where the upcoming updated position at the next ${(g+1)}^{th}$ iteration is denoted by $X_i^{g+1}$. The best vulture chosen for the current iteration g is denoted by $R^g$. This is determined using Equation (2). The vultures move randomly to protect the food from other vultures and to provide a high degree of randomness in their search behavior. $rand$ is a random value between zero and one. The variables’ upper bound is denoted by $UB$; their lower bound by $LB$; and the current position at the $g^{th}$ iteration is $X_i^g$.

3.3.4. Phase of Exploitation

In this phase, $|F_i^g|$ is less than 1. The proposed AVO algorithm’s efficacy is evaluated in two sub-phases that comprise the exploitation phase. Each of these sub-phases uses two different strategies. For each internal sub-phase, the appropriate strategy is chosen using two predefined parameters: $P_2$ for the first sub-phase and $P_3$ for the second, with values ranging from 0 to 1. These two internal sub-phases are explained as follows:

• First sub-phase of exploitation: This sub-phase applies two different strategies when $|F_i^g|$ is less than 1 and greater than or equal to $0.5$. The selection of one of these two strategies is made using a random value $ran{d}_{P_2}$ within the range $[0,1]$ and a specified parameter $P_2$.
  The initial strategy of this sub-phase is called siege fight, which involves sufficiently powerful and somewhat satiated vultures. More robust and healthier vultures try not to share food with others because they convene around a single food source. By swarming near the healthy vultures and engaging in small fights, the weaker vultures try to take food from them. Conversely, the second strategy is called rotational flight; it creates a spiral movement between a superior vulture and the others. The following illustrates the strategies for the first exploitation sub-phase:

  $$X_i^{g+1}=\left\{\begin{array}{cc}{D}_i^g\times (F_i^g+rand)-d_t^g,\hfill & \mathit{if}ran{d}_{P_2}\le P_2,\hfill \\ R^g-(S_1^g+S_2^g),\hfill & \mathit{if}ran{d}_{P_2}>P_2,\hfill \end{array}\right\}\mathit{if}1>\left|F_i^g\right|\ge 0.5,$$

  (9)

  $$d_t^g=R^g-X_i^g,$$

  (10)

  $$S_1^g=R^g\times \left({\displaystyle \frac{rand\times X_i^g}{2\pi }}\right)\times \cos \left(X_i^g\right),$$

  (11)

  $$S_2^g=R^g\times \left({\displaystyle \frac{rand\times X_i^g}{2\pi }}\right)\times \sin \left(X_i^g\right).$$

  (12)

  where the vulture’s next updated position at the next ${(g+1)}^{th}$ iteration is denoted by $X_i^{g+1}$, $D_i^g$ is defined using Equation (8), and $rand$ is an arbitrary value between 0 and 1. The distance $d_t^g$ between the vulture and one of the best two vultures is estimated using Equation (10); $R^g$ denotes the appropriate best vulture in the current $g^{th}$ iteration, which is computed using Equation (2); $S_1^g$ and $S_2^g$ are computed employing Equations (11) and (12), respectively; and $X_i^g$ denotes the current position at the $g^{th}$ iteration.
• Second sub-phase of exploitation: This sub-phase is carried out when $|F_i^g|$ is less than $0.5$. Various vulture species gather around the food supply and engage in many sieges and brawls during this sub-phase. This sub-phase employs two different strategies. A predefined parameter $P_3$ and an arbitrary value $ran{d}_{P_3}$, with values ranging from 0 to 1, are used to decide which of these two strategies to use.
  This sub-phase’s initial strategy is called assemble vultures around the food source. In this strategy, different kinds of vultures search for food and may compete near a single source. The second strategy is known as hostile siege fight. In this strategy, the vultures become more aggressive and try to plunder the leftover food from the healthy vultures by flocking around them in different ways. The healthy vultures, on the other hand, deteriorate and are unable to fend off the other vultures. The following illustrates the strategies for the second exploitation sub-phase:

  $$X_i^{g+1}=\left\{\begin{array}{cc}{\displaystyle \frac{A_1^g+A_2^g}{2}},\hfill & \mathit{if}ran{d}_{P_3}\le P_3,\hfill \\ R^g-\left|d_t^g\right|\times F_i^g\times Lev{y}_d,\hfill & \mathit{if}ran{d}_{P_3}>P_3,\hfill \end{array}\right\}\mathit{if}\left|F_i^g\right|<0.5,0.5,$$

  (13)

  $$A_1^g=BestVultur{e}_1^g-{\displaystyle \frac{BestVultur{e}_1^g\times X_i^g}{BestVultur{e}_1^g-{\left(X_i^g\right)}^2}}\times F_i^g,$$

  (14)

  $$A_2^g=\begin{array}{c}SecondBestVultur{e}_2^g-{\displaystyle \frac{SecondBestVultur{e}_2^g\times X_i^g}{SecondBestVultur{e}_2^g-{\left(X_i^g\right)}^2}}\times F_i^g,\hfill \end{array}$$

  (15)

  $$Lev{y}_d=0.01\times {\displaystyle \frac{\mu \times \sigma }{{\left|\nu \right|}^{\frac{1}{\beta }}}},$$

  (16)

  $$sigma={\left({\displaystyle \frac{\Gamma (1+\beta )\times \sin \left(\frac{\Pi \beta }{2}\right)}{\Gamma \left(1+\beta 2\right)\times \beta \times 2^{\left(\frac{\beta -1}{2}\right)}}}\right)}^{{\displaystyle \frac{1}{\beta }}}.$$

  (17)

  where the next updated position of the vulture at the next ${(g+1)}^{th}$ iteration, reflecting the assembly of vultures, is denoted by $X_i^{g+1}$. $A_1^g$ and $A_2^g$ are evaluated using, respectively, Equations (14) and (15). To increase the effectiveness of the AVO algorithm, $Lev{y}_d$ is the levy flight distribution function obtained using Equation (16). d is the dimensional space; $\sigma$ is defined by Equation (17), where $\beta =1.5$ is a constant value; and $\mu$ and $\nu$ are random numbers distributed equally within the range $[0,1]$.

3.4. Converting to Binary Nature

In the presented AVO algorithm, the positions are shown as real values. As such, they are not immediately applicable to the GS binary issue. Therefore, there is a need to convert these real position values into binary values to conform to GS’s binary nature and maintain the original algorithm’s structure. In this conversion, 1s represent the real values of the pertinent selected genes in the binarization vector, whereas 0s represent the real values of the unselected genes, which are not pertinent. At each iteration g, the following mathematical expression can be used to convert the real position $X_i^g$ to a binary position ${\left(X_i^g\right)}_{bin}$:

$${\left(X_i^g\right)}_{bin}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}{\mathbf{X}}_i^g>\delta ,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(18)

where an arbitrary threshold point within $[0,1]$ is represented by $\delta$. According to this fundamental binary conversion approach, the binary “1” (selected feature) replaces its real value if ${\left(X_i^g\right)}_{bin}$ is greater than $\delta$. On the other hand, if ${\left(X_i^g\right)}_{bin}$ is smaller than $delta$, its real value is set to the binary “0” (a feature that was not chosen).

3.5. Appraising the Fitness Function Value

Finding the fewest number of selected features and optimizing the classification accuracy of the available classifiers (k-NN and SVM models) are two conflicting objectives that should be balanced to achieve the best solution and determine its quality. Since the k-NN and SVM classifiers’ accuracies might be hampered if the number of selected features is lower than the optimal, the fitness function balances the selected features’ size and accuracy. The fitness function concentrates on lowering the classification error rate rather than accuracy, as follows:

$$\begin{array}{c}\hfill fit=w_1\times {Err}_{rate}+w_2\times {\displaystyle \frac{|{feat}_{picked}|}{\left|D\right|}},\\ \\ \hfill w_1\in [0,1],w_2=1-w_1.\end{array}$$

(19)

where ${feat}_{picked}$ denotes the number of selected features, D denotes the total number of features in the dataset, and ${Err}_{rate}$ represents the classification error rate from the k-NN and SVM classifiers. The classification accuracy importance and the number of selected features are denoted by the weight parameters $w_1$ and $w_2$, respectively. The values of $w_1$ ($0.99$) and $w_2$ ($0.01$) are determined through extensive trials conducted in previous studies [21,42,43].

3.6. Incorporating the DE Technique

DE [44] is characterized by its high efficiency and simplicity in finding a suitable solution for complex optimization problems. It can quickly produce value-added results. Three main processes—mutation, crossover, and selection—are necessary for DE. The differential mutation process seeks to produce a modified vector ${\upsilon }_i$ for each iteration’s solution vector. This can be computed mathematically as follows:

$${\overrightarrow{\upsilon }}_i={\overrightarrow{X}}_{r_1}+W_M({\overrightarrow{X}}_{r_2}-{\overrightarrow{X}}_{r_3})$$

(20)

Within the range [1, population size], three randomly selected asymmetric vectors are denoted by the symbols $X_{r_1},X_{r_2},$ and $X_{r_3}$. $W_M$ denotes the mutation weighting factor within the interval $[0,1]$.

After the mutation operation, DE performs a crossover operation to increase the population’s variety. An offspring vector $u_i$ is produced by combining values from the target vector $X_i$ and the altered vector ${\upsilon }_i$. The most commonly used and basic factor of crossover search is binary crossover, which has the following mathematical expression:

$$u_{i,d}=\left\{\begin{array}{cc}{\upsilon }_{i,d},\hfill & \mathrm{if}rand\le C_{R}ord=j_{rand},\hfill \\ X_{i,d},\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(21)

where a uniformly distributed random number $j_{rand}\in [1,2,...,D_X]$ is used to ensure that the mutated vector has at least one dimension. The possibility of crossing each element is calculated using the crossover rate $C_R$, frequently determined to be a big amount ($C_R$ = 0.9).

The selection operation is then carried out, as shown in Equation (22). Here, a comparison between the fitness function $f\left(X_i\right)$ of the target vector and the corresponding offspring vector $f\left(u_i\right)$ is performed, and the lowest-valued fitness function is kept for the upcoming iteration.

$$X_i=\left\{\begin{array}{cc}{u}_i,\hfill & \mathrm{if}f\left(u_i\right)<f\left(X_i\right)\hfill \\ X_i,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(22)

3.7. The Complete RBAVO-DE Algorithm

To handle the GS strategy, the steps of the recommended RBAVO-DE algorithm are described in the following subsections. The pseudo-code for the proposed RBAVO-DE algorithm is provided in Algorithm 1. A flowchart of the proposed RBAVO-DE algorithm is shown in Figure 1, illustrating its main steps.

Algorithm 1 The proposed RBAVO-DE algorithm.

Input:    N—total number of positions (size of population)    $G_{max}$—maximum number of permitted iterations    D—problem’s dimensional space    $LB$—lower bounds of variables    $UB$—upper bounds of variables    $C_R$—crossover rate    $W_M$—mutation weighting factor Output:    $X_{Best}$—the global best vulture’s position found while searching    $fit\left(X_{Best}\right)$—the global best fitness function value found, which should be lessened  1: Start  2:        Apply the Relief approach for selecting the related features and filtering them, as demonstrated in Section 3.1;  3:        Initialize a population of N positions, and provide the values of the necessary parameters ($L_1$, $L_2$, w, $P_1$, $P_2$, and $P_3$);  4:        Set a random position X in the initial population;  5:        Evaluate the fitness values $fit\left(X\right)$ for each position in the initial population;  6:        Arrange the positions in ascending order depending on their fitness function $fit\left(X\right)$;  7:        $g\leftarrow 1$;                                        ▹ Current number of iterations  8:        while $g<G_{max}$ do  9:              Assign the positions of both the first-best vulture $X_{Bes{t}_1}^g$ and the second-best vulture $X_{SecondBes{t}_2}^g$, as well as their fitness values $fit\left(X_{Bes{t}_1}^g\right)$ and $fit\left(X_{SecondBes{t}_2}^g\right)$, among all positions in the population; 10:            for vulture’s position $i=1:N$ do 11:                   Find the best vulture $R^g$ using Equation (2); 12:                   Adjust the vulture’s famine level $F_i^g$ using Equation (4); 13:                   Modify the levy flight distribution function $Lev{y}_d$ using Equation (16); 14:                   if $|F_i^g|\ge 1$ then 15:                         if $ran{d}_{P_1}\le P_1$ then 16:                               Amend the vulture’s position $X_i^{g+1}$ based on the first stage of the exploration phase using Equation (7); 17:                         else if $ran{d}_{P_1}>P_1$ then 18:                               Upgrade the vulture’s position $X_i^{g+1}$ based on the second stage of the exploration phase using Equation (7); 19:                         end if 20:                   else if $|F_i^g|<1$ then 21:                         if $|F_i^g|\ge 0.5$ then 22:                               if $ran{d}_{P_2}\le P_2$ then 23:                                     Adjust the vulture’s position $X_i^{g+1}$ based on the first condition of the first exploitation sub-phase using Equation (9); 24:                               else if $ran{d}_{P_2}>P_2$ then 25:                                     Amend the vulture’s position $X_i^{g+1}$ based on the second condition of the first exploitation sub-phase using Equation (9); 26:                               end if 27:                      else if $|F_i^g|<0.5$ then 28:                               if $ran{d}_{P_3}\le P_3$ then 29:                                     Upgrade the vulture’s position $X_i^{g+1}$ based on the first status of the second exploitation sub-phase using Equation (13); 30:                               else if $ran{d}_{P_3}>P_3$ then 31:                                    Adjust the vulture’s position $X_i^{g+1}$ based on the second status of the second exploitation sub-phase using Equation (13); 32:                               end if 33:                           end if 34:                       end if 35:                       $fit\left(X_i^{g+1}\right)\leftarrow$ Compute the fitness function value for $X_i^{g+1}$; 36:                       if $fit\left(X_i^{g+1}\right)<fit(X_i^g$) then 37:                           $X_i^g\leftarrow X_i^{g+1}$; 38:                           $fit\left(X_i^g\right)\leftarrow fit(X_i^{g+1}$); 39:                       end if 40:                   end for 41:                   Re-arrange the positions in ascending order depending on their fitness function $fit\left(X\right)$; 42:                   Detect the global best position $X_{Best}^{g+1}$ and its global best fitness value $fit\left(X_{Best}^{g+1}\right)$ when the current iteration $g+1$ is over; 43:                   Perform the DE technique for every position to ameliorate $X_{Best}^{g+1}$, as shown in Section 3.6; 44:                   $X_{Best}\leftarrow X_{Best}^{g+1}$; 45:                   $fit\left(X_{Best}\right)\leftarrow fit\left(X_{Best}^{g+1}\right)$; 46:                   $g\leftarrow g+1$; 47:       end while 48: End

4. Experimental Results and Discussion

This section presents the empirical findings of the proposed RBAVO-DE and its counterparts: Binary Artificial Bee Colony (BABC) [45], Binary Salp Swarm Algorithm (BSSA) [46], Binary PSO (BPSO) [47], Binary Bat Algorithm (BBA) [48], Binary Grey-Wolf Optimization (BGWO) [49], Binary Grasshopper Optimization Algorithm (BGOA) [50], Binary Whale Optimization Algorithm (BWOA) [51], Binary ASO (BASO) [52], Binary Bird Swarm Algorithm (BBSA) [53], Binary HGSO (BHGSO) [54], and Binary Harris Hawks Optimization (BHHO) [55]. The optimizers undergo evaluation through training and testing benchmarks, with conclusive results derived from the average values of the evaluation metrics. The benchmarks employed for assessing the performance of the proposed model are detailed in Section 4.1. The parameters used in the operational environments are outlined in Section 4.2. The metrics used for evaluation are described in Section 4.3. The analysis of the experimental outcomes is discussed in Section 4.4.

4.1. Dataset Description

In-depth experimental approaches and various wrapper algorithms were applied to twenty-two datasets of gene descriptions; the data comprise normalized Level 3 RNA-Seq gene expression data for twenty-two kinds of tumors from the Broad Institute. These data are publicly accessible and can be found in [56]. We adhered to the methodology described in [36] and observed discrepancies between the data referenced from GitHub in the paper and the figures reported within the document, which were sourced from the website. The website’s data included a mix of tumor and standard samples, whereas the paper treated the data uniformly as tumor samples. Consequently, we conducted a detailed examination of the data. Initially, the website offered various formats of the identical dataset we intended to analyze. Upon delving into the data, we encountered the following challenges:

• Certain genes are identified by ID but lack an associated symbol.
• Some genes are absent from the annotation file.
• There is a mix-up of samples, including both normal and tumor types.

Consequently, pre-processing was necessary to segregate and identify samples, distinguish between normal and tumor samples for use in binary classification, and streamline the GS process. We addressed the challenges above in the following manner:

• We looked up the corresponding gene symbol for each ID found in the annotation file.
• After cross-referencing with the annotating file, over one hundred genes were eliminated.
• Based on the sample report, every Excel sheet’s row was organized according to the kind of sample for binary classification.

Moreover, the Relief approach, as detailed in Section 3.1, was utilized in the pre-processing stage to calculate the weight of each gene within the benchmark. These weights were subsequently ordered from highest to lowest. Genes with lower weights were then removed. The Relief approach was useful for discarding genes that do not contribute to classification.

Following the pre-processing phase, the data were refined and ready for the GS process. Contrary to the approach used in [36], which tackled the multi-classification of all types of cancer together, we opted to analyze every cancer type individually for greater specificity.

Table 1. Datasets employed in this paper [57].

#	Cancer	Normal	Tumor
		Records	Records
1	Bladder Urothelial Carcinoma (BLCA)	19	408
2	Thyroid Cancer (THCA)	59	501
3	Cervical and Endocervical Cancers (CESCs)	3	304
4	Cholangiocarcinoma (CHOL)	9	36
5	Colon Adenocarcinoma (COAD)	41	458
6	Esophageal Cancer (ESCA)	13	184
7	Glioblastoma Multiforme (GBM)	5	153
8	Thymoma (THYM)	2	120
9	Head and Neck Squamous Cell Carcinoma
	(HNSC)	44	520
10	Kidney Chromophobe (KICH)	25	66
11	KIRC	72	533
12	Kidney Renal Papillary	32	290
	(KIRP)
13	Liver Hepatocellular Carcinoma (LIHC)	50	371
14	LUAD	59	515
15	LUSC	51	501
16	Pancreatic Adenocarcinoma (PAAD)	4	178
17	UCEC	35	176
18	Pheochromocytoma and	3	179
	Paraganglioma (PCPG)
19	Rectum adenocarcinoma (READ)	10	94
20	Sarcoma (SARC)	2	259
21	Skin Cutaneous Melanoma (SKCM)	1	103
22	STAD	37	415

[57] presents a comprehensive overview of all twenty-two tumor types and their respective sample counts. The number of features utilized in the benchmark datasets is 32,000 features (genes).

4.2. Parameter Setting

The proposed RBAVO-DE algorithm was compared against binary variants of different meta-heuristic optimizers, such as BABC, BSSA, BPSO, BBA, BGWO, BWOA, BBSA, BGOA, BHHO, BASO, and BHGSO. The critical parameters for the ML models employed in this study are detailed in

Table 2. The key parameters of the employed ML models.

Model	Parameters
SVM	Polynomial kernel $=2$
k-NN	Euclidean distance metric $k=5$ [21,58,59]

.

Within the proposed framework, the validity of the results was verified using a 10-fold cross-validation approach to ensure the reliability of the outcomes. This involved randomly dividing each dataset into two distinct subsets: 80% for training and the remaining 20% for testing. The training portion was employed to train the presented classifiers using optimization techniques, while the testing portion was used to evaluate the selected genes’ effectiveness. The parameters most commonly applied across all compared algorithms are summarized in

Table 3. Parameter configurations of all utilized optimizers.

Optimizer	Parameters
All optimizers	Execution count $=30$
	Maximum count of iterations $G_{max}=100$
	Size of population $N=10$
	Dimensionality D = The count of genes
	in the employed datasets
	Upper boundaries $UB$
	Lower boundaries $LB$
Proposed RBAVO-DE	Parameter $L_1=0.7$
	Parameter $L_2=0.2$
	Parameter $w=2$
	Parameter $P_1=0.6$
	Parameter $P_2=0.6$
	Parameter $P_3=0.5$
BSSA	Count of scroungers $SD=0.1\times N$
	Count of producers $PD=0.2\times N$
	Safety threshold $ST=0.8$
BABC	Count of employed bees $=16$
	Count of scout bees $=3$
	Count of onlooker bees $=4$
BPSO	Inertia weight $\left(\omega max=0.9\omega min=0.4\right)$
	Acceleration coefficients $\left(c_2=c_1=1.2\right)$
BBA	Loudness $A=0.8$
	Pulse emission rate $r=0.95$
	Lower and upper pulse frequencies $=0,10$
BWOA	a is linearly decreased from 2 to 0
	$p=0.5$
	$b=1.0$
BHHO	Rabbit energy $E\in [-1,1]$
BGWO	a is linearly decreased from 2 to 0
BGOA	$C_{\min }=0.00004$ and $C_{\max }=1$
BBSA	Frequency of flight $ff=10$
	Effect on birds’ vigilance
	Followed coefficient $fl$ = 0.5
	Probability of foraging for food $p=0.8$
	Acceleration coefficients $\left(c_1=c_2=1.5\right)$
	behaviors $\left(a_1=a_2=1.0\right)$
BASO	Depth weight $\alpha =50$
	Multiplier weight $\beta =0.2$
BHGSO	Count of clusters $=2$
	$\alpha =\beta =0.1$$K=1.0$, and $l_3=1E-02$
	$l_1=5E-03$, $l_2=1E+02$

. To execute all experiments in this paper, Python was utilized in a computational environment with a Dual Intel^® Xeon^® Gold 5115 2.4 GHz CPU and 128 GB of RAM on the Microsoft Windows Server 2019 operating system.

4.3. Evaluation Criteria

To evaluate the proposed RBAVO-DE’s effectiveness relative to other methods, each strategy was independently tested thirty times on each benchmark to ensure statistical validation of the results. For this purpose, the following established performance metrics for the GS issues were employed:

• Mean classification accuracy ($Mea{n}_{AC}$): This measure represents the accuracy of correctly classifying data, calculated by running the algorithm independently thirty times. It is determined in the following way:

  $$Mea{n}_{AC}=\sum _{k=1}^{30}\sum _{r=1}^{m}match(P{L}_r,A{L}_r)$$

  (23)
  In this formula, m denotes the number of samples in the test dataset, while $P{L}_r$ and $A{L}_r$ denote the predicted labels from the classifier and the actual class labels for sample r, respectively. The function $match(P{L}_r,A{L}_r)$ serves as a comparison mechanism, where if $P{L}_r$ is equal to $A{L}_r$, then $match(P{L}_r,A{L}_r)$ is assigned a value of 1; if they do not match, it is assigned a value of 0.
• Mean fitness $\left(Mea{n}_{Fi}\right)$: This measure calculates the average $meanFi$, achieved by running the proposed approach thirty times independently. It gauges the balance between lowering the classification error rate and minimizing the number of genes selected. A lower value indicates a superior solution, assessed based on fitness:

  $$MeanFi={\displaystyle \frac{1}{30}}\sum _{k=1}^{30}{f}_{*}^k$$

  (24)

  where $f_{*}^k$ shows the optimum fitness value achieved in the $k-th$ execution.
• Mean number of chosen genes $\left(MeanGe\right)$: This metric calculates the average number of genes chosen (or GS ratio) by running the proposed approach thirty times independently, and it is defined as follows:

  $$MeanFe={\displaystyle \frac{1}{30}}\sum _{k=1}^{30}{\displaystyle \frac{|d_{*}^k|}{\left|D\right|}}$$

  (25)
  Here, $|d_{*}^k|$ denotes the total count of genes chosen in the optimal solution for the $k^{th}$ execution, and $\left|D\right|$ represents the total number of genes present in the initial benchmark.
• Standard Deviation $\left(STDE\right)$: Based on the outcomes above, the overall average results derived from thirty separate executions of each optimizer on every benchmark were assessed for stability in the following manner:

  $$STDE=\sqrt{{\displaystyle \frac{1}{29}}\sum _{k=1}^{30}{(Y_{\ast }^k-Mea{n}_Y)}^2}$$

  (26)

  where Y shows the measure to be utilized, $Y\ast k$ denotes the measure value Y in the $k_{t}h$ run, and $Mea{n}_Y$ is the mean of the measure from thirty independent executions.

The data in the subsequent tables represent the mean values obtained from thirty independent executions, focusing on classification accuracy, the number of chosen genes, average fitness, precision, recall, and F1-score. The ensuing subsections thoroughly examine and discuss these experimental findings, with bold figures highlighting the optimal results.

4.4. Results of Comparing the Proposed RBAVO-DE with Various Meta-Heuristic Algorithms

The proposed RBAVO-DE approach with the SVM and k-NN models was compared with other recent meta-heuristic methods executed under the same conditions to show its superiority over its counterparts. The proposed RBAVO-DE algorithm was compared with binary variants of several optimizers, including BABC, BSSA, BPSO, BBA, BGWO, BWOA, BBSA, BGOA, BHHO, BASO, and BHGSO.

4.4.1. Results Employing the k-NN Model

Table 4. The results of the proposed RBAVO-DE algorithm and its counterparts using k-NN regarding average classification accuracy results.

Dataset	Metric	RBAVO-DE	BSSA	BABC	BPSO	BBA	BGWO	BWOA	BGOA	BHHO	BBSA	BASO	BHGSO
BLCA	Average	0.998	0.993	0.998	0.993	0.989	0.995	0.994	0.993	0.991	0.994	0.994	0.989
	STDE	0.004	0.006	0.005	0.006	0.003	0.006	0.006	0.006	0.005	0.006	0.006	0.002
CESC	Average	0.984	0.984	0.984	0.984	0.984	0.984	0.984	0.984	0.984	0.984	0.984	0.984
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
CHOL	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
COAD	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ESCA	Average	0.974	0.974	0.974	0.974	0.974	0.974	0.974	0.974	0.974	0.974	0.974	0.974
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
GBM	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
HNSC	Average	0.993	0.991	0.991	0.991	0.991	0.992	0.991	0.991	0.991	0.991	0.991	0.991
	STDE	0.004	0.002	0.002	0.000	0.000	0.002	0.000	0.000	0.000	0.002	0.000	0.000
KICH	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
KIRC	Average	0.998	0.993	0.994	0.992	0.992	0.994	0.992	0.994	0.993	0.993	0.993	0.992
	STDE	0.003	0.003	0.004	0.002	0.000	0.004	0.002	0.004	0.003	0.003	0.003	0.000
KIRP	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
LIHC	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
LUAD	Average	0.991	0.991	0.991	0.991	0.991	0.991	0.991	0.991	0.991	0.991	0.991	0.991
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
LUSC	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
PAAD	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
PCPG	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
READ	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
SARC	Average	0.981	0.981	0.981	0.981	0.981	0.981	0.981	0.981	0.981	0.981	0.981	0.981
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
SKCM	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
STAD	Average	0.999	0.996	0.999	0.996	0.989	0.996	0.995	0.997	0.992	0.995	0.996	0.989
	STDE	0.003	0.005	0.004	0.005	0.000	0.005	0.006	0.005	0.005	0.006	0.005	0.000
THCA	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
THYM	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
UCEC	Average	0.998	0.985	0.988	0.977	0.969	0.984	0.977	0.978	0.978	0.979	0.976	0.968
	STDE	0.008	0.012	0.013	0.006	0.011	0.012	0.006	0.008	0.009	0.009	0.005	0.011
Ranking	$\mathrm{W}\left|\mathrm{T}\right|\mathrm{L}$	$\mathbf{4}\left|\mathbf{18}\right|\mathbf{0}$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$

Boldface values denote the best results.

shows the results of the proposed RBAVO-DE algorithm and other optimization techniques employing the k-NN model, based on accuracy metrics compared under similar conditions. The experimental outcomes reveal that the proposed RBAVO-DE achieved the most promising outcomes in four benchmarks. It is noteworthy that all competitive methods, including the proposed RBAVO-DE employing the k-NN model, produced comparable outcomes across eighteen benchmarks.

The rest of the metrics for the k-NN model are shown in Appendix A.1. In terms of the average fitness values, the proposed RBAVO-DE algorithm demonstrated higher efficiency compared to its counterparts using the k-NN model under similar conditions. The RBAVO-DE algorithm yielded the lowest fitness results and the most competitive STDE across all benchmarks. Also, all utilized benchmarks are high-dimensional, demonstrating that the proposed RBAVO-DE can run effectively on all benchmarks regardless of size. The RBAVO-DE algorithm shows promise by effectively balancing exploitation and exploration of the search space, avoiding becoming trapped in local optima during iterations. Unlike many other algorithms that tend to become trapped, it demonstrated the ability to escape such traps.

Regarding the mean results for the genes selected by the proposed RBAVO-DE algorithm and its counterparts employing k-NN, the proposed RBAVO-DE algorithm surpassed the other methods across all benchmarks concerning the number of chosen genes. Furthermore, the RBAVO-DE’s capacity to identify significant genes is due to its effective exploration of possible areas while enhancing accuracy.

In terms of the mean precision of the proposed RBAVO-DE algorithm and its counterparts with k-NN, the proposed RBAVO-DE outperformed alternative approaches for three of the twenty-two datasets. For nineteen datasets, BWOA achieved similar results, while BABC, BPSO, BGWO, BGOA, and BHHO obtained results similar to those of the proposed RBAVO-DE. BASO and BHGSO, which produced the same outcomes as the proposed RBAVO-DE on seventeen datasets, ranked fourth. Ultimately, BBA ranked lowest among all approaches, producing similar outcomes to the proposed RBAVO-DE for fifteen datasets.

Regarding the mean recall of the proposed RBAVO-DE and its counterparts employing k-NN, RBAVO-DE outperformed the alternative approaches for three of the twenty-two datasets. On the other hand, BSSA, BABC, BPSO, BGWO, BWOA, BGOA, and BBSA produced the same outcomes as RBAVO-DE for 19 datasets, while BHHO achieved similar results for 18 datasets. BHGSO, which obtained the same outcomes as the proposed RBAVO-DE for seventeen datasets, ranked fourth. Ultimately, BASO and BBA ranked lowest among all approaches, producing similar results to RBAVO-DE for sixteen datasets.

With regard to the mean F1-score of the proposed RBAVO-DE and its counterparts employing k-NN, the proposed RBAVO-DE outperformed the alternative approaches for three of the twenty-two datasets. In contrast, for eighteen datasets, BSSA, BABC, BPSO, BGWO, BGOA, and BBSA produced the same outcomes as RBAVO-DE, while BWOA and BHHO produced comparable outcomes for seventeen datasets. BASO and BHGSO, which obtained the same outcomes for 16 datasets as the proposed RBAVO-DE, ranked fourth. Ultimately, BBA ranked lowest among all approaches, producing similar outcomes to the proposed RBAVO-DE for fourteen datasets.

4.4.2. Results Employing the SVM Model

Table 5. The results of the proposed RBAVO-DE algorithm and its counterparts employing SVM regarding average classification accuracy values.

Dataset	Metric	RBAVO-DE	BSSA	BABC	BPSO	BBA	BGWO	BWOA	BGOA	BHHO	BBSA	BASO	BHGSO
BLCA	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
CESC	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
CHOL	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
COAD	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ESCA	Average	0.986	0.975	0.977	0.974	0.974	0.977	0.974	0.975	0.975	0.975	0.974	0.974
	STDE	0.013	0.004	0.008	0.000	0.000	0.008	0.000	0.005	0.005	0.005	0.000	0.000
GBM	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
HNSC	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
KICH	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
KIRC	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
KIRP	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
LIHC	Average	1.000	1.000	1.000	1.000	0.9992	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.0029	0.000	0.000	0.000	0.000	0.000	0.000	0.000
LUAD	Average	0.993	0.991	0.991	0.991	0.991	0.991	0.991	0.991	0.991	0.991	0.992	0.991
	STDE	0.003	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.002	0.000
LUSC	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
PAAD	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
PCPG	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
READ	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
SARC	Average	0.994	0.986	0.989	0.986	0.981	0.989	0.987	0.986	0.984	0.986	0.984	0.981
	STDE	0.008	0.008	0.009	0.008	0.000	0.009	0.009	0.008	0.006	0.008	0.007	0.000
SKCM	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
STAD	Average	0.990	0.989	0.989	0.989	0.989	0.989	0.989	0.989	0.989	0.989	0.989	0.989
	STDE	0.003	0.000	0.000	0.000	0.002	0.000	0.000	0.000	0.002	0.000	0.000	0.000
THCA	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
THYM	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
UCEC	Average	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	STDE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
Ranking	$\mathrm{W}\left|\mathrm{T}\right|\mathrm{L}$	$\mathbf{4}\left|\mathbf{18}\right|\mathbf{0}$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$	$0\left|18\right|4$

Boldface numbers indicate the best results.

displays the outcomes of the proposed RBAVO-DE and various optimization techniques employing the SVM model concerning classification accuracy results assessed under identical running conditions. The experimental outcomes demonstrate that the proposed RBAVO-DE algorithm outperformed the other approaches by obtaining the most promising values for four datasets. All competitive methods, including the proposed RBAVO-DE employing SVM, obtained equivalent values across 18 benchmarks.

The rest of the metrics utilizing SVM are presented in Appendix A.2. Regarding the mean fitness values of the proposed RBAVO-DE and its counterparts employing the SVM model under equivalent running conditions, the proposed RBAVO-DE proved to be more efficient than the other methods. The proposed RBAVO-DE employing the SVM model yielded the lowest fitness values and the most competitive STDE across all benchmarks. Also, all utilized benchmarks are high-dimensional, demonstrating that the proposed RBAVO-DE can run effectively on all benchmarks regardless of size. The RBAVO-DE algorithm shows promise by effectively balancing exploitation and exploration of the search space, avoiding becoming trapped in local optima during iterations. Unlike many other algorithms that tend to become trapped, it demonstrated the ability to escape such traps.

Regarding the mean results for the genes selected by the proposed RBAVO-DE and its counterparts employing SVM, the proposed RBAVO-DE achieved more promising results than other techniques across all benchmarks utilized in this study. Also, the superiority of the proposed RBAVO-DE employing SVM in this context demonstrates its capability to effectively explore valuable regions of the search space while avoiding regions with non-feasible solutions.

With regard to the average precision values of the proposed RBAVO-DE and its counterparts employing SVM, the proposed RBAVO-DE outperformed the alternative approaches for three of the twenty-two datasets. On the other hand, for eighteen datasets, BABC, BGWO, BWOA, BBSA, and BASO yielded comparable results. For seventeen datasets, BSSA, BPSO, BGOA, and BHHO yielded results similar to those of RBAVO-DE, thereby ranking fourth. Ultimately, BBA ranked lowest among all approaches, producing similar outcomes to those of the proposed RBAVO-DE for twelve datasets.

In terms of the mean recall of the proposed RBAVO-DE method and its counterparts using SVM, the proposed RBAVO-DE outperformed the alternative approaches for three of the twenty-two datasets. In contrast, BPSO and BHHO performed similarly for eighteen datasets, while BSSA, BABC, BGWO, BWOA, BGOA, and BBSA produced the same results as the proposed RBAVO-DE for nineteen datasets. BHGSO, which obtained the same outcomes as RBAVO-DE for seventeen datasets, ranked fourth. In the end, BASO and BBA ranked lowest among all approaches, producing outcomes similar to those of RBAVO-DE for sixteen datasets.

Regarding the mean F1-score of the proposed RBAVO-DE algorithm and its counterparts employing SVM, the proposed RBAVO-DE outperformed the alternative approaches for five of the twenty-two datasets. On the other hand, BWOA produced outcomes similar to those of the proposed RBAVO-DE for seventeen datasets, while BSSA, BABC, BPSO, BGWO, BGOA, and BBSA produced comparable results for sixteen datasets. BHHO, which obtained the same outcomes as the proposed RBAVO-DE for fifteen datasets, ranked fourth. Ultimately, BBA ranked lowest among all approaches, producing similar outcomes to those of RBAVO-DE for 12 datasets.

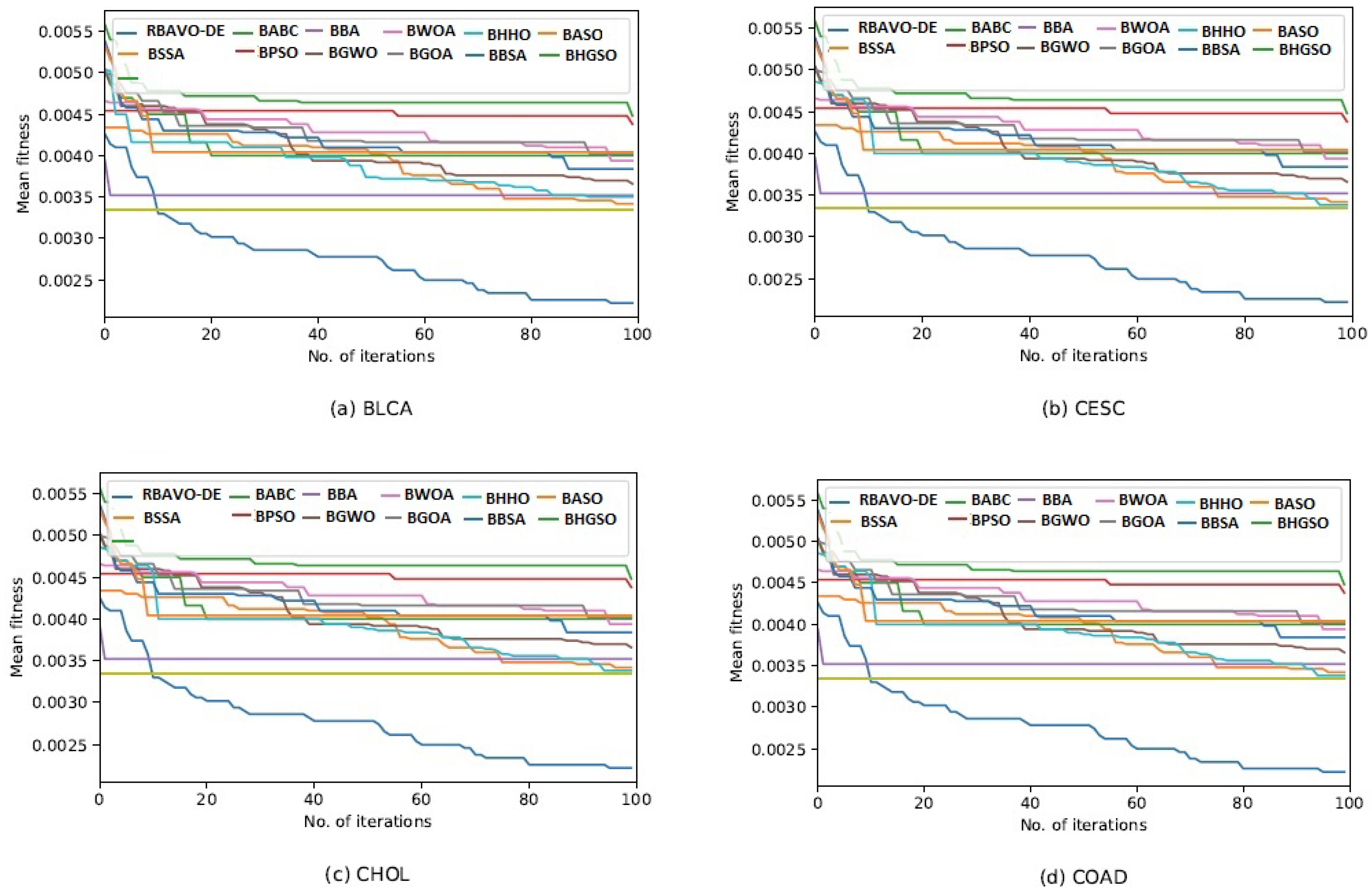
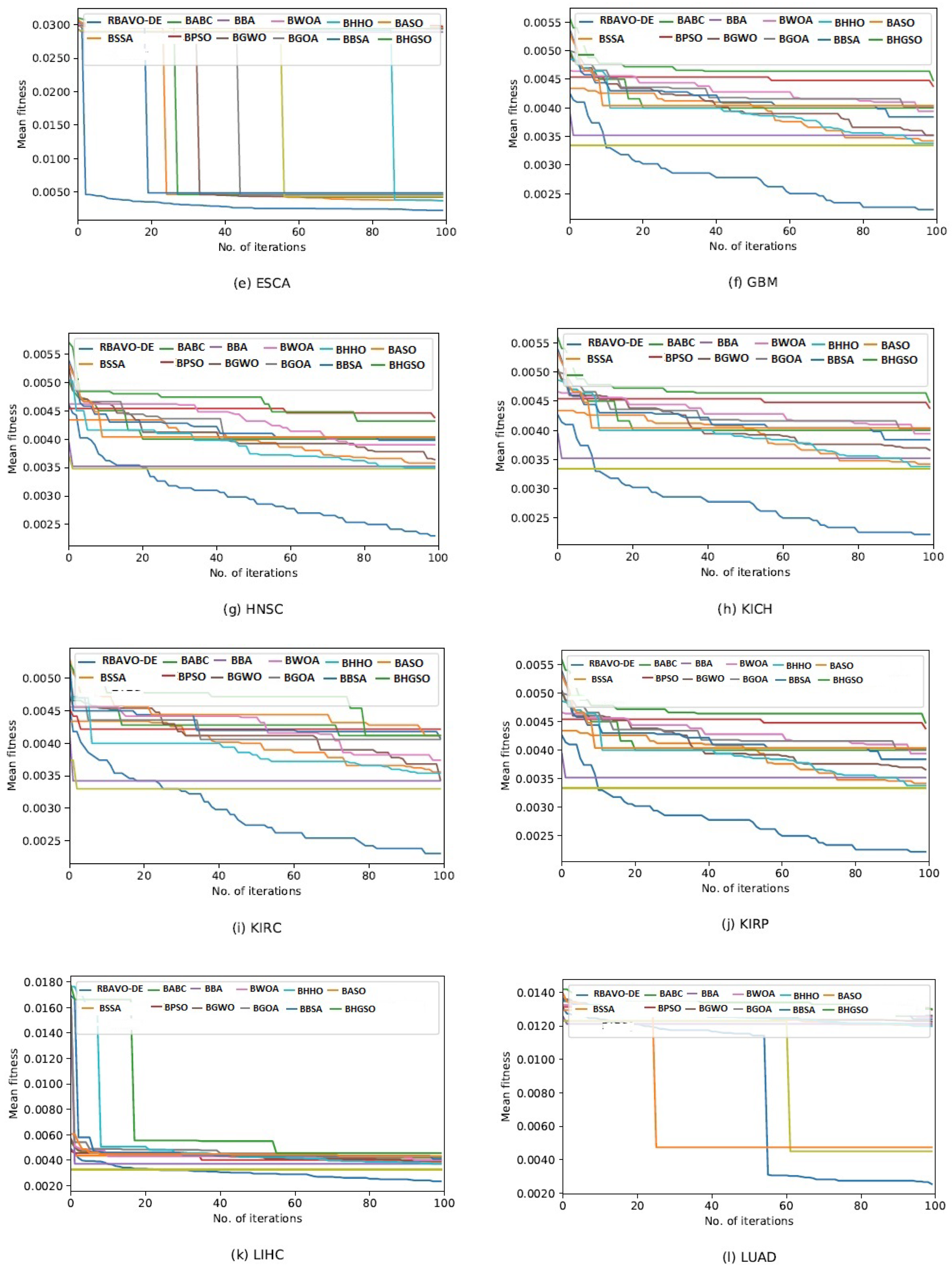
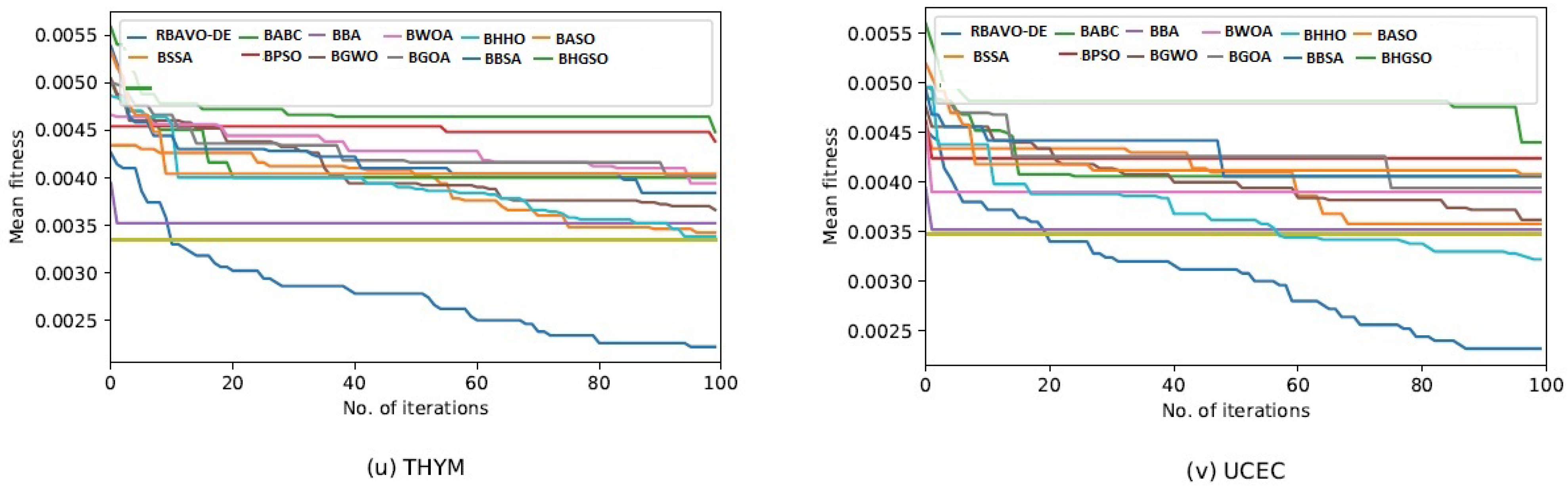
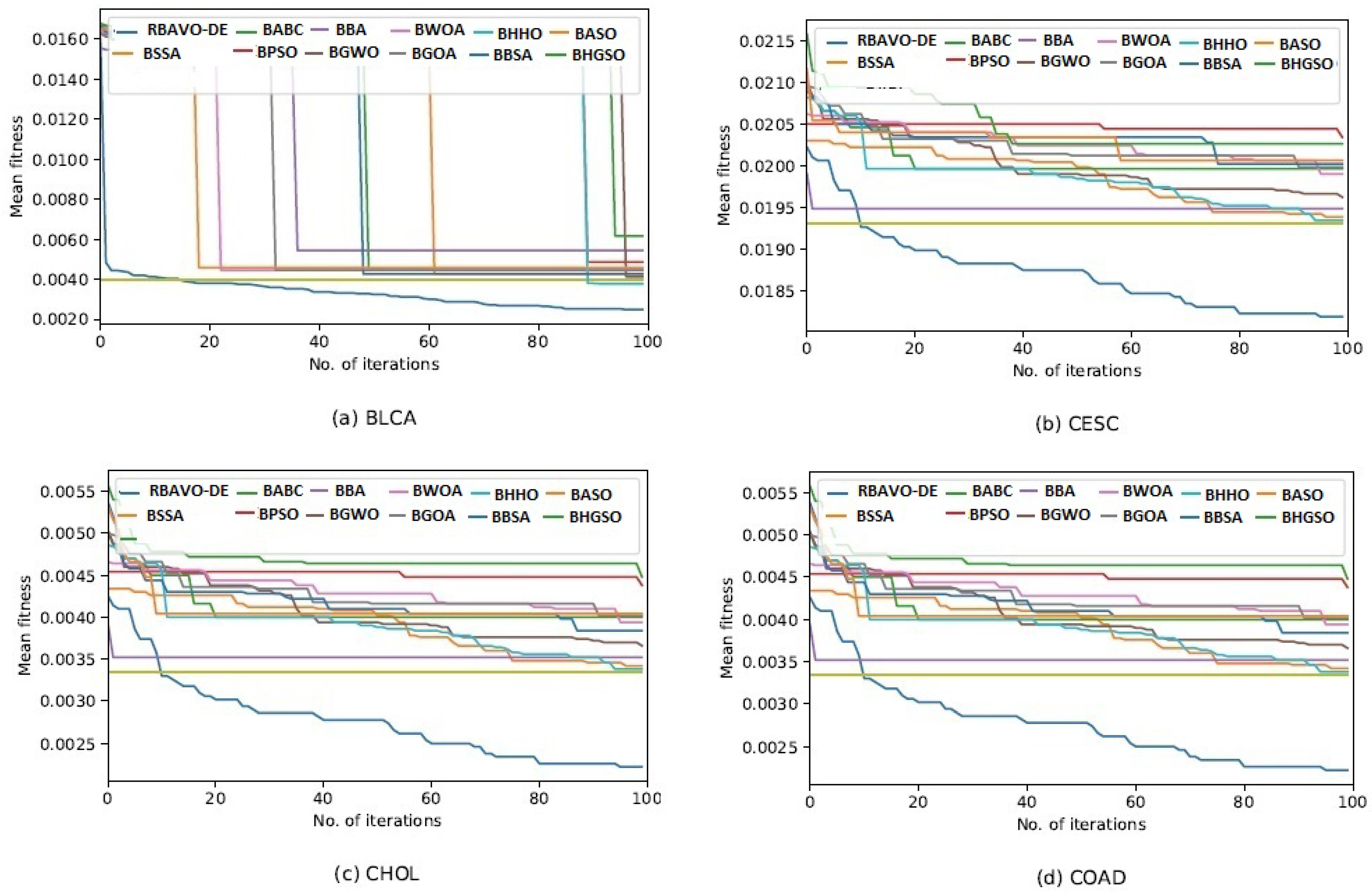
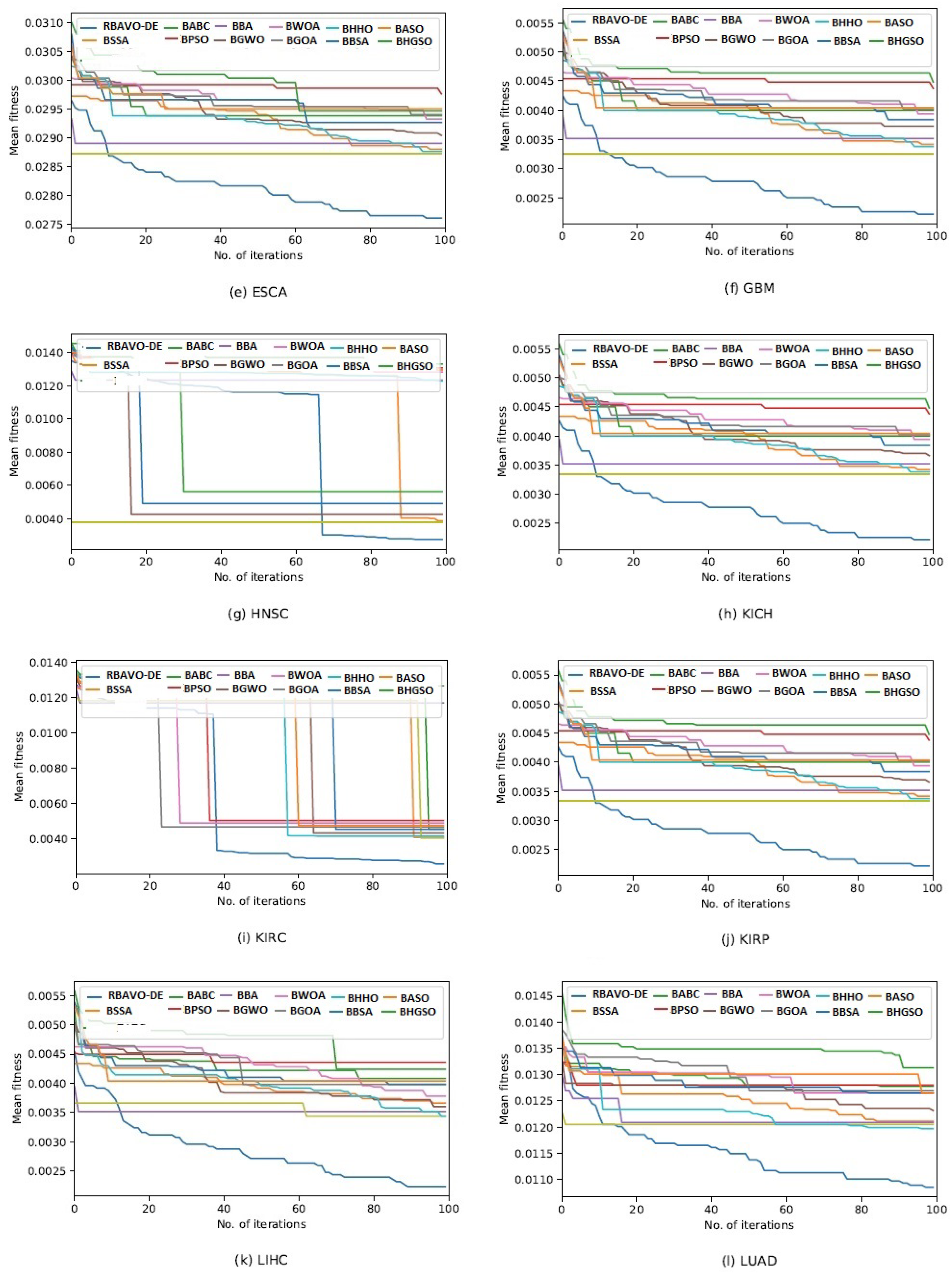
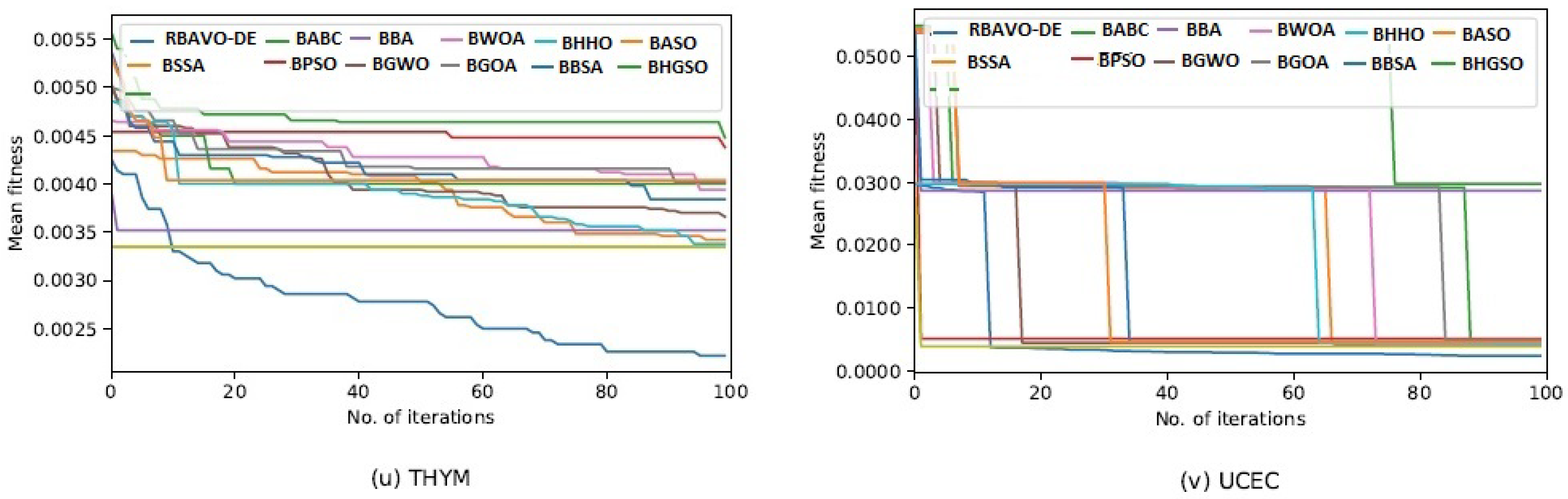
4.5. Convergence Analysis

It is evident in Appendix B [57] that the proposed RBAVO-DE employing the SVM and k-NN models attained optimum convergence behavior across all benchmarks. Therefore, the convergence performance of the proposed RBAVO-DE employing the SVM and k-NN models demonstrates its capability to reach optimal outcomes promptly while maintaining an efficient equilibrium between search and exploitation.

4.6. Wilcoxon’s Rank-Sum Test

This paper compares the fitness values achieved by the proposed RBAVO-DE and its counterparts pairwise using the Wilcoxon rank-sum test [60], which aims to determine whether there is a statistically significant difference between the different approaches. This test is a crucial tool for evaluating the success of the proposed algorithm. The Wilcoxon test is employed in hypothesis testing to compare matched data. It involves sorting the absolute differences in the outcomes of paired procedures on the $j^{th}$ of N issues. Next, the lowest value is found by summing the positive ($R^{+}$) and negative ($R^{-}$) rankings. The null hypothesis is rejected if the resultant significance level is less than 5%, and not rejected otherwise.

From examining the results of the comparison made between the RBAVO-DE and its counterparts pairwise using the Wilcoxon test, we found that all $R^{+}$ values equal 253, all $R^{-}$ values equal 0, and all p-values equal $4.768\times {10}^{-7}$ which are less than 0.05 (significance level of 5%). Hence, it can be concluded that the proposed RBAVO-DE employing SVM and k-NN performs better than any other algorithm in all cases. Therefore, all p-values less than 0.05 (significance level of 5%) offer compelling evidence that the outcomes of the proposed strategy are statistically significant and not just coincidental.

4.7. Computational Complexity of the RBAVO-DE Algorithm and Various Meta-Heuristic Algorithms

4.7.1. Computational Complexity of the Execution Time of the RBAVO-DE Algorithm

Each of RBAVO-DE’s five core steps can be analyzed separately to determine its computational complexity. These steps include filtering features, initializing the population, boosting and amending the position, appraising the fitness function, and using DE. Then, $O_{execute\_time}(RBAVO-DE)$ can be utilized to represent the overall computational complexity of the proposed RBAVO-DE algorithm. This can be computed using the following big-O notation formulas:

$$\begin{array}{cc}\hfill O_{execute\_time}(RBAVO-DE)=& O_{execute\_time}\left(\mathrm{Filtering} \mathrm{features}\right)+\hfill \\ \hfill & O_{execute\_time}\left(\mathrm{Initializing} \mathrm{population}\right)+\hfill \\ \hfill & O_{execute\_time}\left(\mathrm{Boosting} \mathrm{and} \mathrm{amending} \mathrm{position}\right)+\hfill \\ \hfill & O_{execute\_time}\left(\mathrm{Appraising} \mathrm{fitness} \mathrm{function}\right)+\hfill \\ \hfill & O_{execute\_time}\left(\mathrm{Incorporating} \mathrm{DE} \mathrm{technique}\right).\hfill \end{array}$$

(27)

Since N determines the population size, $G_{max}$ is the maximum number of iterations allowed, and D is the problem’s dimensional space. Hence,

• $O_{execute\_time}\left(\mathrm{Filtering} \mathrm{features}\right)=O_{execute\_time}\left(D\right)$.
• $O_{execute\_time}\left(\mathrm{Initializing} \mathrm{population}\right)=O_{execute\_time}\left(N\right)$.
• $O_{execute\_time}\left(\mathrm{Boosting} \mathrm{and} \mathrm{amending} \mathrm{position}\right)=O_{execute\_time}(G_{max}\times N\times D).$
• $O_{execute\_time}\left(\mathrm{Appraising} \mathrm{fitness} \mathrm{function}\right)=O_{execute\_time}(G_{max}\times N).$
• $O_{execute\_time}\left(\mathrm{Incorporating} \mathrm{DE} \mathrm{technique}\right)=O_{execute\_time}(N\times D).$

For that,

$$\begin{array}{c}{O}_{execute\_time}(RBAVO-DE)=O_{execute\_time}\left(D\right)+\hfill \\ O_{execute\_time}\left(N\right)+O_{execute\_time}(G_{max}\times N\times D)+\\ O_{execute\_time}(G_{max}\times N)+O_{execute\_time}(N\times D)=\\ \hfill O_{execute\_time}(G_{max}\times N\times D).\end{array}$$

4.7.2. Computational Complexity of the Memory Usage of the RBAVO-DE Algorithm

This involves measuring the amount of memory required by an algorithm to tackle a problem as the quantity of the input increases. It is frequently expressed as the additional memory needed by the algorithm beyond the input. It entails merging the following two primary elements:

• Memory usage of input variables: This is the amount of memory required for the algorithm to store the input data. There are 13 input variables related to the proposed RBAVO-DE algorithm, as follows: N, $G_{max}$, D, $LB$, $UB$, $C_R$, $W_M$, $L_1$, $L_2$, w, $P_1$, $P_2$, and $P_3$. Since each variable stores numerical values, 4 bytes of memory are utilized by each one. Consequently, the total memory usage complexity of these 13 input variables is 52 bytes ($13\times 4$ bytes $=52$ bytes). The memory usage complexity of the input values is constant.
• Additional memory usage: This shows how much more memory the algorithm needs in addition to the input. It includes the memory required for data structures, internal variables, and other components of the algorithm. Regardless of the size of the input, the RBAVO-DE algorithm requires a specific amount of extra memory. The following variables are involved:
  • The memory usage complexity consumed by $X_{initial}$ is $(4\times N\times D)$ bytes. This is because each position in the positions vector $X_{initial}$ requires 4 bytes of memory, and its size is $(N\times D)$, proportionate to the initial population of N positions with dimension size D. Because the amount of memory required rises linearly with the value $(N\times D)$, its memory use complexity is linear.
  • The variables $pr$, g, $F_i$, t, R, $D_i$, $d_t$, $S_1$, $S_2$, $A_1$, $A_2$, $sigma$, $fit\left(X_i\right)$, $fit\left(X_{Bes{t}_1}\right)$, $fit\left(X_{SecondBes{t}_2}\right)$, and $fit\left(X_{Best}\right)$ require 4 bytes of memory space each since they only represent numerical values. As a result, the total memory usage complexity of these 16 variables is 64 bytes ($16\times 4$ bytes $=64$ bytes). This memory usage complexity is constant.
  • The position vectors $BestVultur{e}_1$, $SecondBestVultur{e}_2$, $X_i$, $Lev{y}_d$, $\mu$, $\sigma$, $X_i^{bin}$, ${\upsilon }_i$, $X_{r_1}$, $X_{r_2}$, $X_{r_3}$, $u_i$, and $X_{Best}$ each require 4 bytes of memory space, and the size of each vector is D, proportionate to the dimension size of the acquired positions. As a result, the vectors at these 13 points have a total memory usage complexity of $(52\times D)$ bytes ($13\times 4\times D$ bytes). Since the memory needed grows linearly with the value D, its memory consumption complexity is linear.
  As a result, the overall memory usage complexity for all of the additional variables listed above is $(4\times N\times D)+64+(52\times D)$ bytes.

Lastly, the following formula can be used to determine the computational complexity of the overall memory usage of the proposed RBAVO-DE algorithm:

$$\begin{array}{c}\mathrm{Memory} \mathrm{usage} \mathrm{complexity}(\mathrm{RBAVO}-\mathrm{DE})=\mathrm{Input} \mathrm{values} \mathrm{memory} \mathrm{usage}+\hfill \\ \hfill \mathrm{Additional} \mathrm{memory} \mathrm{usage}=52+\left((4\times N\times D)+64+(52\times D)\right) \mathrm{bytes}.\end{array}$$

Keep in mind that there are constant bytes that are not taken into account. In big-O notation, the computational complexity of the total memory consumption of RBAVO-DE can be represented as $O_{memory\_usage}(RBAVO-DE)$. This can then be calculated in big-O notation after eliminating all constants in the following way:

$$\begin{array}{c}{O}_{memory\_usage}(RBAVO-DE)=O_{memory\_usage}\left(\mathrm{Input} \mathrm{values} \mathrm{memory} \mathrm{usage}\right)+\hfill \\ O_{memory\_usage}\left(\mathrm{Additional} \mathrm{memory} \mathrm{usage}\right)=\\ O_{memory\_usage}\left(1\right)+\left(O_{memory\_usage}(N\times D)+O_{memory\_usage}\left(1\right)+O_{memory\_usage}\left(D\right)\right)=\\ \hfill O_{memory\_usage}(N\times D).\end{array}$$

It can be difficult to compile a thorough comparison of the memory usage and execution time complexity of various meta-heuristic algorithms since these complexities might differ based on the particular implementation, size of the problem, and other operators. Furthermore, not all of the algorithms listed have comprehensive evaluations of the execution time and memory usage complexity available, and their properties may vary depending on the problem at hand.

5. Benefits and Drawbacks of the RBAVO-DE Algorithm

This part presents a balanced discussion of the benefits and drawbacks of the RBAVO-DE algorithm. The benefits of the RBAVO-DE algorithm can be listed as follows:

• High Accuracy in Classification: The RBAVO-DE algorithm has demonstrated high classification accuracy, achieving up to 100% in some cases. This is a noteworthy achievement, particularly regarding cancer datasets, as accurate gene selection can directly impact diagnostic and therapeutic outcomes.
• Effective Feature Size Reduction: The algorithm has shown remarkable capability in reducing the feature size by up to 98% while maintaining or improving classification accuracy. This dimensionality reduction is crucial for processing high-dimensional datasets efficiently.
• Robustness Across Diverse Datasets: The effectiveness of the RBAVO-DE algorithm across twenty-two cancer datasets indicates its robustness and adaptability to various genetic data characteristics. This versatility is beneficial for broader applications in genomics research.
• Superior Performance Over Competitors: When compared with binary variants of widely recognized meta-heuristic algorithms, RBAVO-DE stands out for its outstanding performance in accuracy and feature reduction, highlighting its innovative approach to gene selection.

On the other hand, the drawbacks of the proposed methodology can be listed as follows:

• Computational Complexity: The high dimensionality of the datasets and the iterative nature of meta-heuristic algorithms suggest that RBAVO-DE may have a significant computational cost. This aspect could limit its applicability in environments with constrained computational resources.
• Generalizability Concerns: Despite its success across various cancer datasets, the algorithm’s generalizability to other types of biological data or diseases remains to be thoroughly investigated. It is crucial to test RBAVO-DE in broader contexts to confirm its applicability beyond the datasets examined.
• Parameter Sensitivity: Like many meta-heuristic algorithms, RBAVO-DE might be sensitive to its parameter settings, affecting performance and efficiency. Detailed studies on the impact of different parameter configurations and strategies for their optimization could enhance the algorithm’s utility.

In summary, the RBAVO-DE algorithm represents a significant advancement in gene selection for cancer classification, with notable strengths in accuracy and efficiency. However, addressing its potential drawbacks through further research could broaden its applicability and improve its performance, making it an even more valuable tool in genomics and personalized medicine.

6. Conclusions and Future Directions

The RBAVO-DE approach proposed in this paper was the first to be implemented for handling GS issues in RNA-Seq gene expression data and determining potential biomarkers for different tumor classes to enhance the best solution discovered. The outcomes were promising, revealing that the proposed RBAVO-DE algorithm’s effectiveness and capabilities were significantly improved. SVM and k-NN, two widely used classification models, were employed to evaluate the efficacy of each set of selected genes. The proposed RBAVO-DE algorithm’s capability was compared to binary variants of eleven widely used meta-heuristic techniques to assess it on different tumor classes with various instances. The assessment was executed employing a combination of evaluation measures, such as average fitness, classification accuracy, the number of selected genes, precision, recall, and F1-score. The proposed RBAVO-DE algorithm using the SVM and k-NN classifiers achieved more promising results than other optimizers in handling GS issues. Despite the promising outcomes, this research opens several avenues for future exploration to further advance the field:

• Algorithmic Enhancements: Improving the algorithm’s efficiency and reducing computational complexity.
• Cross-disease Applicability: Testing the proposed algorithm on genetic data from various diseases beyond cancer.
• Comparative Analyses with Deep Learning Models: Evaluating RBAVO-DE against advanced deep learning models for genetic data analysis.
• Real-world Clinical Validation: Collaborating with clinical experts to validate the practical utility of selected genes in cancer treatment.
• Scalability and Parallelization: Enhancing the algorithm’s scalability through parallel computing to handle larger genetic datasets efficiently.
• Interdisciplinary Applications: Exploring the algorithm’s potential in other fields dealing with high-dimensional data, such as finance and environmental modeling.

In conclusion, while the RBAVO-DE algorithm represents a significant step forward in the field of gene selection for cancer classification, the paths outlined for future research highlight the potential for further advancements and broader applications of this work. Continued interdisciplinary collaboration and innovation will be crucial for unlocking the full capacity of gene selection methodologies to enhance healthcare outcomes and advance our understanding of complex diseases.