Pitfalls in Metaheuristics Solving Stoichiometric-Based Optimization Models for Metabolic Networks

Abstract

Flux Balance Analysis (FBA) is a constraint-based method that is commonly used to guide metabolites through restricting pathways that often involve conditions such as anaplerotic cycles like Calvin, reversible or irreversible reactions, and nodes where metabolic pathways branch. The method can identify the best conditions for one course but fails when dealing with the pathways of multiple metabolites of interest. Recent studies on metabolism consider it more natural to optimize several metabolites simultaneously rather than just one; moreover, they point out the use of metaheuristics as an attractive alternative that extends FBA to tackle multiple objectives. However, the literature also warns that the use of such techniques must not be wild. Instead, it must be subject to careful fine-tuning and selection processes to achieve the desired results. This work analyses the impact on the quality of the pathways built using the NSGAII and MOEA/D algorithms and several novel optimization models; it conducts a study on two case studies, the pigment biosynthesis and the node in glutamate metabolism of the microalgae Chlorella vulgaris, under three culture conditions (autotrophic, heterotrophic, and mixotrophic) while optimizing for three metabolic intermediaries as independent objective functions simultaneously. The results show varying performances between NSGAII and MOEA/D, demonstrating that the selection of an optimization model can greatly affect predicted phenotypes.

1. Introduction

Microalgae are photosynthetic cellular microorganisms that have been known since the beginning of time. They can be grown either in wastewater or in clean or salty waters; some strains, such as Dunaliella salina, can be grown in salty waters, and other strains, such as Chlorella vulgaris, are grown in fresh water and can survive high growing temperatures. Microalgae need a carbon source to carry out photosynthesis and produce their biomass. Carbon can be obtained as CO₂ from polluting sources, and they transform it into oxygen, circularly helping to reduce global warming [1].

Microalgae are large producers of biomass; inside there are metabolites such as lipids that in the future can be used as biofuels, amino acids and pigments that are currently used in the pharmaceutical and cosmetic industries, and proteins that are used as food supplements [2,3]. In addition, microalgae present biotechnological applications as bioremediation sources of water quality and have been used as alternatives for the removal of heavy metals due to some strains, such as Chlorella vulgaris and Scenedesmus obliquos, being able to absorb heavy metals such as Cadmium (Cd) and Lead (Pb) [4,5].

All the characteristics above make the study of the metabolism of microalgae attractive for metabolic engineering. This discipline focuses on the study of the topography of the network, the regulation of a metabolic pathway, the identification of bottlenecks, the determination of metabolic fluxes, and the elimination of side reactions by gene deletion [6].

In particular, various metabolic engineering techniques have been used to analyze pathways and optimize fluxes to manipulate metabolism and modify the fluxes towards a desired product and thus be able to add commercial value. However, metabolic fluxes cannot be measured in vivo; for this reason, modeling approaches are required to measure or predict them [7]. Among them are single-objective constraint-based approaches, such as FBA (Flux Balance Analysis), exact mathematical multi-objective, and heuristic-based approaches.

FBA is one of the most used techniques for studying cellular metabolism is the single-objective FBA approach based on constraints. This approach is widely used in the analysis of the fluxes of metabolic networks since it can be used even if kinetic data are not available, but it requires information on the stoichiometric data of the reactions present in the network, growth requirements, and parameter-specific measurement methods of the biological system, in particular the reconstruction of the metabolic network for the genome scale [8] that include all known reactions that are present in the studied organisms and the genes that encode each enzyme [9].

Cellular metabolism in metabolic modeling is described as the set of chemical reactions present in an organism. This is mathematically represented by a stoichiometric matrix, S, of size (m × n), where n are the reactions and m are the metabolites involved in each reaction, assigning a negative coefficient if it represents a reactant and a positive coefficient if it is a product, and a coefficient of zero means that the metabolite is not present in the reaction; each reaction will have a lower bound and an upper bound limiting the space of solutions or the maximum and minimum value of the allowed flux. The FBA seeks the linear optimization of an objective function; this function represents the linear combination of the fluxes that generally represents biomass production [10].

$$\begin{array}{c}\hfill \begin{array}{ccc}\mathrm{FBA}\hfill & maxF\left(v\right)=\hfill & v_{biomass}\hfill \\ & \mathrm{Subject} \mathrm{to}\hfill & \\ & & \mathrm{S}·v=0\hfill \\ & & {\mathrm{LB}}_j\le v_j\le U{B}_j,\forall j\in \{1,\dots ,n\}\hfill \end{array}\end{array}$$

(1)

Equation (1) defines the associated FBA linear optimization problem [11], where v is the flux vector across the reactions. The stoichiometric matrix $S_{m\times n}$ represents the metabolic network, where there exists a metabolite per row and a reaction per column. The value of the cell $S_{ij}$ is the stoichiometric coefficient of the metabolite i involved in reaction j [9], and $L{B}_j$ and $U{B}_j$ are the lower and upper bounds for the fluxes allowed in the metabolic system. The steady-state assumption is established by $Sv=0$ [12].

Its versatility has meant that FBA has been widely used in different organisms, including microalgae, bacteria, consortia of microorganisms, etc. An example of this is the prediction of cell growth of the cyanobacteria Synechocystis in [13]; it has also been used in the degradation of glucose by anaerobic digestion to predict the distribution of metabolites and reveal the transformation of carbon in order to evaluate the conversion of ethanol, propionic acid, and butyric acid into acetic acid [14]. FBA has served as a study in medicine, where flux activities were calculated to study differences in metabolic pathways, comparing breast cancer subtypes [15].

The FBA methodology has been used to evaluate metabolic fluxes in different strains of microalgae using three heterotrophic and mixotrophic autotrophic growth conditions. The first microalgae to use FBA was the microalgae Chlamydomonas reinhardtii [16], with which the first metabolic map was obtained. Later, the microalga Chlorella vulgaris was utilized for the study of lipid production [17]; both had biomass production as their sole objective function.

Although this approach has been widely used, the distribution of metabolites through the pathways is conditioned by the metabolites present in the objective function equation and in the experimental parameters; blocking some metabolic pathways results in a distribution of fluxes with zero values. Moreover, FBA has been widely used in the search for maximizing the production of compounds of interest, but cellular metabolism in its natural state does not guide metabolic pathways toward the production of a particular metabolite. In the search for a better understanding of microalgae metabolism, new optimization techniques have emerged, such as metaheuristics for multi-objective optimization [18]. These techniques seek a more uniform distribution and are closer to the reality of what happens at the metabolic level by simultaneously optimizing various functions with conflicting objectives.

Multi-objective optimization is generally based on the search for solutions to different conflicting objectives that must be optimized simultaneously. Multi-objective optimization is of great importance and has been carried out at a technological and scientific level. Some examples in the chemical industry have been reported in optimizing operating unit processes, biorefinery, reaction engineering, prevention and control, etc. [19]. It has also been utilized in the biology and medicine sector [20], and in metabolic engineering [18].

Multi-objective optimization contrasts with open-access Cobrapy FBA, which only maximizes or minimizes one objective function and where only one solution is obtained. In multi-objective optimization, a set of solutions is obtained. The solutions obtained are called non-dominated because no other solution in the search space is better than the others when all objectives are considered simultaneously. This set of solutions is known as Pareto optimal solutions [21].

Between the methods that have been used for multi-objective optimization of microorganisms are evolutionary algorithms such as NSGAII [18], MOMO, based on the Bio-objective model, and exact mathematical methods that spend a lot of computational resources [22].

Metaheuristic algorithms originate from the natural evolution of biological groups; they are part of artificial intelligence and are born from natural computing and heuristic methods (partial search algorithms). Compared to mathematical methods that generate a large computational expense, these methods provide sufficiently good solutions to an optimization algorithm with an acceptable computational time and space [23].

Multi-Objective Evolutionary Algorithms (MOEAs) are widely recognized in the scientific community as an approach to solving multi-objective optimization problems. In particular, the NSGAII (multi-objective EA based on non-dominated classification) proposed by [24] has been quite effective when handling two or three objectives [25,26]. The MOEA/D evolutionary algorithm based on decomposition is tested because it has the characteristic that it works correctly when there are more than three objective functions.

Previously, metaheuristic methods had been used to study the metabolism in [18]. The NSGAII algorithm was developed to optimize three objective functions, proteins, carbohydrates, and ${\mathrm{CO}}_2$, in a metabolic network of the microalga Chlamydomonas reinhardtii using the NSGAII algorithm, a coding scheme based on flux balance analysis (FBA). However, the algorithmic solution might be different for every optimization problem, a difference that can increase depending on how well the involved mathematical model explains the phenomena studied. Metabolic networks might not be exempt from such issues, and these works analyze distinct algorithms (NSGAII and MOEA/D) and distinct optimization models for metabolic networks (four multiobjective optimization approaches) from the perspective of the quality of solutions that might be achieved by them, and the convenience of the information provided. The study is carried out on two case studies that involve intricate conditions involving cycles, bifurcations, and reversible and irreversible reactions. The main contributions of this work include the development of three new multi-objective optimization models for metabolic networks, one new algorithmic solution based on decomposition, and an analysis that guides the proper identification of metaheuristics and models to solve the optimization process behind metabolisms.

The remainder of the document is structured as follows. Section 2 describes the metaheuristics used for the purpose of analysis in this research; particularly, it presents the overall definition and constituents. Section 3 details the novel optimization models for the metabolic networks proposed in this work. Section 4 discusses the original features included in the design of the NSGAII and MOEA/D used to solve the proposed optimization models. Section 5 and Section 6 describes the design of the experiments conducted to test the proposed optimization models and their metaheuristic solutions; it contains the definitions of the cases of studies along with the experiments and the results, concluding with a brief discussion of the observed data.

2. Materials and Methods

This work considers NSGAII and MOEA/D algorithms as the considered metaheuristics to tackle the optimization problem in metabolic networks. The general notion of the design of such algorithms is provided in the remainder of this section.

2.1. NSGAII Algorithm

NSGAII is a Multi-Objective Evolutionary Algorithm (MOEA) that utilizes non-dominated sorting and crowding distance to exert selective pressure toward the Pareto front [24]. The metaheuristic evolves an initial population of $P_0$ parents using common computable genetic operators such as mutation, crossover, and tournament selection that create a new offspring, $Q_t$, on each generation. To maintain elitism, the current population, $P_t$, is combined with the offspring $Q_t$, and a new population $P_{t+1}$ is chosen based on non-domination ranks and crowding distance to diversify and to break ties when necessary.

The three main components of NSGAII are its fast non-dominated sorting approach, the fast, crowded distance estimation procedure, and the simple crowded comparison operator. The general method derived from NSGAII can be depicted as follows:

• Initialization of population $P_o$ of size N using a uniform distribution.
• Create an offspring population $Q_t$ using binary tournament selection based on crowding-comparison operator, cross-over, and mutation performed on the parent population $\left(P_t\right)$, where subscript “t” denotes the number of generations. The offspring population and its parent population are combined to produce the entire population $R_t$, $R_t$ = $P_t$ + $Q_t$. The population $R_t$ will be of size 2N.
• Perform a fast nondominated sorting approach on the entire population $R_t$ to identify different fronts of objective functions. $F=fast-nondominated-sort\left(R_t\right)$, where $F=(F_0,F_1,F_2,\dots )$ will have in $F_0$ the non-dominated set of solutions of $R_t$ that best approximates the Pareto frontier.
• Construct a new parent population $\left(P_{t+1}\right)$ of size N from the obtained fronts $\left(F_i\right)$. This population of size N is now used for selection, cross-over, and mutation to create a new population $(Q_{t+i}$) of size N.
• The process must be repeated until the maximum number of iterations is reached.

2.2. MOEA/D

MOEA/D is a strategy based on decomposing the MOP multiobjective optimization problem (as defined in [27]) into a certain number of scalar optimization subproblems that are optimized simultaneously. Each subproblem is optimized using information that comes exclusively from its neighboring subproblems, achieving less computational complexity in each generation. There are several approaches to transforming a multi-objective problem into a scalar number of optimization problems. One of the most popular approaches is the MOEA/D proposed by [28], where the scalar optimization problems can be formulated as follows:

$$\begin{array}{c}\hfill \begin{array}{c}{g}^{te}(y\mid w_i,z)=max\left\{w_i\mid f_k\left(x\right)-z_k\mid \right\}\hfill \\ \mathrm{Subject}\mathrm{to}:x\in \mathrm{\Omega }\hfill \end{array},\end{array}$$

(2)

where $w=(w_1,w_2,\dots ,w_N)$ is a vector of weights and $w_i\ge 0$ for all $i=1,\dots ,k$, and the set $z=\{z_1,z_2,\dots ,z_k\}$ is the reference point, where $z_i=max\left\{f_i\left(x\right)\mid \times \in \omega \right\}$ for $i=1,\dots ,m$. For each Pareto optimal point $x^{*}$, there exists a vector of weights w, where $x^{*}$ is the optimal solution of 2.

MOEA/D performs for a certain number of generations, and during each generation it also exerts selective pressure toward the Pareto front using genetic operators such as mutation and crossover. The key element in this strategy is that offspring replace parents based on the scalar function and their closeness at each iteration until a final front is delivered by the algorithm.

3. Proposed Approaches

This work proposes three novel optimization models for metabolic networks that extend FBA to a multi-objective optimization problem. The models, called MOFBA₂, MOFBA₃, and MOFBA₄, represent improvements over the MOFBA₁ proposed in [18] and depicted in Equation (3). MOFBA₁ simultaneously optimizes a set of bioproducts $\{v_{b1},\dots v_{bm}\}$ instead of just one, keeps within bounds the reaction fluxes, and satisfies the steady state condition, i.e., they ensure that Sv = 0 (where the S is the stoichiometric matrix and v is the fluxes vector).

$$\begin{array}{c}\hfill \begin{array}{ccc}\mathrm{MOFBA}\hfill & maxF\left(v\right)=\hfill & \{v_{b_1},\dots ,v_{b_m}\}\hfill \\ & \mathrm{Subject}\mathrm{to}\hfill & \\ & & \mathrm{S}·v=0\hfill \\ & & {\mathrm{LB}}_j\le v_j\le U{B}_j,\forall j\in \{1,\dots ,n\}\hfill \end{array}\end{array}$$

(3)

MOFBA₁ is the optimization problem resulting from directly implementing the problem defined in Equation (3). It considers as many objective functions as sets of metabolites of interest. Likewise, it considers as many decision variables as reaction fluxes are needed to define the metabolic system. Note that, for an optimization approach, the search space depends on the decision variables, and based on this definition there is one for each possible flux, i.e., a metaheuristic must search proper flux values within the provided bounds of n distinct decision variables.

The conditions described in the previous paragraph characterize a common pitfall in designing solution strategies for optimization problems. The difficulty appears because metaheuristics might require larger running times to locate feasible solutions when the number of decision variables is large. This work considers this situation and proposes three new optimization models for metabolic networks that reduce the search space (i.e., the number of decision variables that a metaheuristic uses in the search). These models are integrated into an appropriate experimental design to demonstrate that, for quality purposes, it matters whose model one chooses to solve certain problems.

While details on the experiments are provided in further sections, the remainder of this section contains an in-depth description of the three novel MOFBAs proposed in this work, with a summary of their relevance and impact at the end.

3.1. MOFBA₂

In MOFBA₂, as in MOFBA₁, the objective functions to be optimized are the sets of metabolites of interest; hence, the number of objectives, m, is the same. On the other hand, MOFBA₂ considers a reduced set of decision variables consisting of only the reaction fluxes $\{v_{b1},\dots v_{bm}\}$ associated with the same metabolites of interest present in the objective function, and an additional one, v, that indicates which of the metabolites of interest leads the search. In other words, MOFBA₂ has $m+1$ decision variables instead of n. Equation (4) formally defines MOFBA₂.

$$\begin{array}{c}\hfill \begin{array}{ccc}\mathrm{MOFBA}\hfill & maxF\left(v\right)=\hfill & \{v_{b_1},\dots ,v_{b_m}\}\hfill \\ & \mathrm{Subject}\mathrm{to}\hfill & \\ & & \mathrm{FBA}(v_{bk},v)\mathrm{is}\mathrm{feasible}\hfill \\ & & {\mathrm{LB}}_j\le v_{b}i\le U{B}_j,\forall i\in \{1,\dots ,m\}\hfill \\ & & 1\le k\le m\hfill \end{array}\end{array}$$

(4)

MOFBA₂ describes a bilevel optimization model where the inner model optimizes the leading metabolite of interest, v, using FBA and delimits the bounds of the metabolites of interest to the ones defined in the outer model. The bounds of the remaining reactions are assumed to be known and fixed according to the analyzed metabolic network.

3.2. MOFBA₃

MOFBA₃ proposes a surrogate model to optimize metabolites of interest. The surrogate model searches for improving two well-known indicators: the Hypervolume (HV) and the Generational Distance (GD). These indicators reflect how well a solution converges to the Pareto front. While the HV must be maximized, the GD must be minimized.

MOFBA₃ has $m+1$ decision variables, the same ones of MOFBA₂, i.e., the reaction fluxes $\{v_{b1},\dots v_{bm}\}$ associated with the same metabolites of interest present in the objective function, and leading metabolite flux v. On the other hand, the number of objectives is always 2, no matter how many metabolites of interest are considered. The distinctive characteristic of this model is its surrogation; instead of directly searching for the proper flux values on the metabolites of interest, it uses indicators of performance in the multi-objective context (i.e., the HV and GD indicators). Equation (5) formally defines MOFBA₃.

$$\begin{array}{c}\hfill \begin{array}{ccc}\mathrm{MOFBA}\hfill & minF\left(v\right)=\hfill & -1HV(\{v_{b_1},\dots ,v_{b_m}\},R),DG(\{v_{b_1},\dots ,v_{b_m}\},Z_r)\hfill \\ & \mathrm{Subject}\mathrm{to}\hfill & \\ & & \mathrm{FBA}(v_{bk},v)\mathrm{is}\mathrm{feasible}\hfill \\ & & {\mathrm{LB}}_j\le v_{b}i\le U{B}_j,\forall i\in \{1,\dots ,m\}\hfill \\ & & 1\le k\le m\hfill \end{array}\end{array}$$

(5)

This optimization problem assumes that there exists a reference point, R, and a reference set, $Z_r$. Given that the management of FBA was under the COBRApy package, considering the limits on it, the reference point considered for this work is $R=\{1000,1000,\dots ,1000\}$. Also, given the availability of an FBA implementation due to the same package, the reference set $Z_r$ is formed by the set of optimal solutions formed by those obtained when solving FBA to optimality, having each metabolite of interest as optimized biomass.

3.3. MOFBA₄

MOFBA₄ is the last proposed optimization problem combining the ideas of MOFBA₂ and MOFBA₃. That is, it proposes to optimize not only the metabolites of interest but also the indicators HV and GD. The number of decision variables for this model remains as $m+1$, and the number of objectives is $m+3$. Equation (6) formally defines this optimization problem.

$$\begin{array}{c}\hfill \begin{array}{ccc}\mathrm{MOFBA}\hfill & minF\left(v\right)=\hfill & -1HV(\{v_{b_1},\dots ,v_{b_m}\},R),DG(\{v_{b_1},\dots ,v_{b_m}\},Z_r)(v_{b1},\dots ,v_{bm})\hfill \\ & \mathrm{Subject}\mathrm{to}\hfill & \\ & & \mathrm{FBA}(v_{bk},v)\mathrm{is}\mathrm{feasible}\hfill \\ & & {\mathrm{LB}}_j\le v_{b}i\le U{B}_j,\forall i\in \{1,\dots ,m\}\hfill \\ & & 1\le k\le m\hfill \end{array}\end{array}$$

(6)

3.4. Analysis

Table 1. Relevant features of MOFBA models for metabolic networks.

Model	No. Decision Variables	No. Objectives	Surrogate
MOFBA1	n	m	No
MOFBA2	$m+1$	m	No
MOFBA3	$m+1$	2	Yes
MOFBA4	$m+1$	$m+2$	Yes

summarizes the most notable features of the optimization models proposed in this work, and compares them against the MOFBA₁ proposed in [18]. The search space is greatly reduced in the novel models, and some of them use convergence information in their definition. The unique characteristics demonstrate the richness of the models that can be designed to solve a specific optimization problem.

The proposed MOFBAs cannot be solved with traditional linear solvers such as FBA. The alternatives are to use enumerative schemes or approximate approaches that allow one to obtain solutions belonging to the Pareto optimal frontier. In this sense, this research analyzed the use of metaheuristics that integrate FBA in their search process as an appropriate solution approach since they improve their approximation to the Pareto front in each iteration.

4. Metaheuristic Designs

This section presents the particular details required in this research for the implementation of the NSGAII and MOEA/D metaheuristics to solve the four optimization problems MOFBA₁, MOFBA₂, MOFBA₃, and MOFBA₄. These metaheuristics are based on the NSGAII and MOEA/D frameworks.

The metaheuristics considered require the definition of the following characteristics: (1) coding schemes; (2) fitness evaluation function; (3) genetic operators; and (4) constraint management strategy. The population initialization method for both strategies (NSGAII and MOEA/D) is random. The proposed design for the rest of these components to handle the novel MOFBAs is detailed in the remainder of this section. The novel adaptations for the NSGAII and MOEA/D frameworks include the clever computable representation of solutions associated with the coding schemes.

4.1. Coding Schemes

This work proposes the use of distinctive solution coding sets for each MOFBA (as defined in Equations (3)–(6). The coding schemes involve the definition of a data structure that represents a solution of the metabolic network. The script developed for experimentation is found in this Github repository (https://github.com/multiobjectiveoptimization2/MOFBAs, accessed on 24 June 2024).

For MOFBA₁ the data structure is a real-valued vector, $\mathcal{V}$. The coding scheme considered a metabolic network, $M_N$, constituted by a set of reactions, $\mathcal{V}$, and two subsets ${\mathcal{V}}^M,{\mathcal{V}}^b\subseteq \mathcal{V}$, where ${\mathcal{V}}^M\cap {\mathcal{V}}^b=\varnothing$, which represent the reactions of the metabolites of interest to a decision maker. Furthermore, let $v=(v_1,\dots ,v_n)$ be the flux vector for $\mathcal{V}$ and assume that there are initial lower and upper bounds, $L{B}_i,U{B}_i$, for each $v_i,1\le i\le n$. Then, the $\mathcal{W}$ encoding scheme proposes redefining the boundaries of each $v_i$ associated with a reaction in ${\mathcal{V}}^M\cup {\mathcal{V}}^b$ using two values $(I_i,{\mathrm{\Delta }}_i)$. The new limits are calculated as $L{B}_i^{new}=I_i$ and $U{B}_i^{new}=(U{B}_i-I_i){\mathrm{\Delta }}_i+I_i$. All remaining fluxes will keep their limits unchanged. In other words, the solution encodes boundary changes for FBA to solve ${\mathcal{M}}_N$ using a prespecified bioproduct, which in this work is assumed to be $v_1^b$. The resulting encoding vector W is of size $O\left(n\right)$, asymptotical in the number of reactions.

For MOFBA₂, MOFBA₃, and MOFBA₄, a vector of size $m+1$ is considered as the encoding scheme, where m is the number of objective functions. The first m elements of the vector are real variables whose value represents the upper limit of flux for each metabolite of interest in the associated reactions. The additional element is a single-objective optimization selector that takes values between 1 and m, indicating which metabolite is going to be optimized in turn. When it is a reversible reaction, the value in the indicated variable will be the same for the lower bound (but negative).

4.2. Fitness Evaluation Function

Between all MOFBA optimization problems, the fitness evaluation (or FEA) functions are considered a derived subset of the set composed of the values of the metabolite fluxes of interest, such as the Hypervolume and Generational Distance metrics. Since the required information on bioproducts is associated with specific reactions, the suitability of a solution obtained by metaheuristics on MOFBAs is evaluated considering their flux values. In MOFBA₁ and MOFBA₂, the criteria or objective functions to be optimized will be the reaction fluxes corresponding to the bioproducts of interest chosen in ${\mathcal{V}}^b$ and denoted as $(v_1^b,\dots ,v_m^b)$. In MOFBA₃, the Hypervolume and Generation Distance obtained from a solution, the reference point R, and the reference set Z_r, defined as follows, are optimized. The R point is the worst possible extreme value of fluxes, which is 1000 for any metabolite of interest, considering its definition for FBA, in widely used platforms, such as CobraPy. The set ${\mathrm{Z}}_r$ is made up of three points, which include the optimal fluxes obtained by solving the case in question using the FBA method by individually optimizing each metabolite of interest; therefore, if there are n objective functions, ${\mathrm{Z}}_r$ will have a cardinality of n. It is worth mentioning that when a leading bioproduct is required in MOFBA₂ to MOFBA₄, this is chosen derived from the value of one of the decision variables considered, as previously described.

4.3. Genetic Operators

These operators create new solutions by dynamically and randomly varying the values of the decision variables in the existing solutions. This selection was due to its success in solving problems involving decision variables with real values [29]. The operators chosen for NSGAII are mutation, crossover, and a simple but reliable random selection, respectively. The specific values of these parameters were taken from the literature and are shown in

Table 2. NSGAII implementation-specific parameters.

Parameter	Value
Polynomial Mutation	Probability = 1.0/d, where d is the number of decision variables.
	Distribution Index = 20
SBXCrossover	Probability = 100%
	Distribution Index = 20
Stoppage Criterion	until reaching 100,000 evaluations
Population Size	100

.

The operators chosen for MOEA/D for mutation and crossover were Polynomial mutation [30], with crossover by differential evolution. The selection strategy is simple but reliable, and the aggregation function used was the Tshebycheff distance. For a more extensive reference of operators, see [28]. The specific values of these parameters were taken from the literature and are shown in

Table 3. MOEA/D implementation-specific parameters.

Parameter	Values
Polynomial Mutation	Probability = 1.0/d, where d is the number of decision variables.
	Distribution Index = 20
Differential Evolution	CR = 1
	F = 0.5
	K = 0.5
Stoppage Criterion	Upon completion of 100,000 evaluations
Population Size	100

.

4.4. Constraint Management Strategy

This work uses the constraint management method proposed in [31] to generate selective pressure towards feasible solutions. As generations evolve in both metaheuristics, the competition between solutions will always prefer the feasible solution despite the non-domination state. In the long run, such a strategy tends to eradicate infeasible solutions in the final algorithm report. Multi-objective optimization is used when there are several objectives to optimize simultaneously. Several multi-objective evolutionary algorithms (MOEAs) exist, such as NSGAII and MOEA/D. Although they are used for optimizing multi-objective problems, they are significantly different. NSGAII is a non-dominated classification algorithm, while the MOEA/D algorithm is based on decomposition.

5. Design of Experiments

This subsection presents the set of experiments performed in order to validate the application of the proposed optimization models as tools to improve the understanding of microalgal metabolisms. In the field of research on effective solutions to multi-objective problems, experiments were conducted on two networks of the microalgae Chlorella vulgaris to evaluate the performance of different algorithms and the respective MOFBAs. The subsections present the case of studies, the experimental design, and the software details used in implementation, with the purpose of verifying the following hypotheses.

Hypotheses 0 (H₀).

It is not relevant to the selection of model and/or solution algorithm to optimize fluxes in a metabolic network.

5.1. Cases of Study

Compared to a previous investigation [18], two networks, glutamate metabolism and pigment flux distribution of the microalgae Chlorella vulgaris, were included in the two case studies; reversible and irreversible reactions were added, the representation of a reversible reaction using the intervals of lower bound fluxes of −1000 and upper bound 1000, and the irreversible ones with intervals of lower bound 0 to upper bound 1000. In addition, nodes were included where the metabolites bifurcate towards different routes, and cycles that are frequently presented in the metabolism of the cells.

5.1.1. Case of Study 1: Metabolic Network Chlorella vulgaris

The metabolic network of the microalga Chlorella vulgaris [17] was studied using NSGAII and MOEA/D algorithms for three different culture conditions: photoautotrophy (light + components), heterotrophy (component), and mixotrophy (CO₂ + light + component). 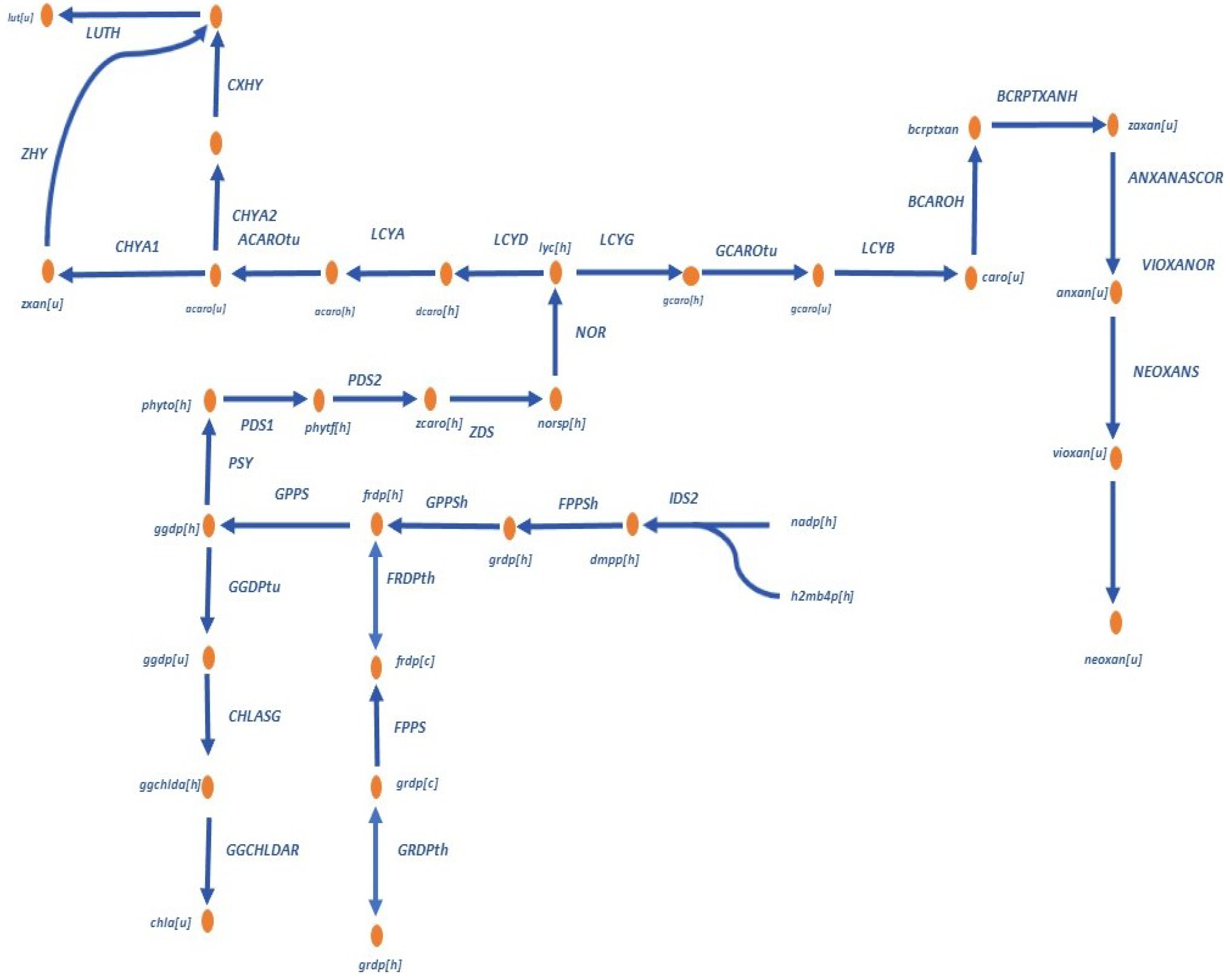Among the compounds that were used as nutrients for cultivation were the addition of nitrogen sources, such as NO₃ and NH₄, as well as sulfates, such as SO₄, Fe₂, and Magnesium. The different crop sources affect the production of metabolites. The following figure shows the distribution of pigments in the microalga C. vulgaris.

In this case, a part of the pigment distribution network will be studied since the distribution in microalgae such as C. vulgaris is of great importance in the study of pigment synthesis. The reactions involved in the metabolism are presented in Appendix A.1,

Table A1. Reactions derived from the synthesis of pigments in the metabolism of the microalgae C. vulgaris [17].

Name	Formula
FRDPth	frdp[h] ⇄ frdp[c]
GRDPth	grdp[h] ⇄ grdp[c]
ACAROtu	acaro[h] → acaro[u]
GCAROtu	gcaro[h] → gcaro[u]
GGDPtu	ggdp[h] → ggdp[u]
FPPS	grdp[c] + ipdp[c]→ frdp[c] + ppi[c]
FPPSh	grdp[h] + ipdp[h]→ frdp[h] + h[h] + ppi[h]
GGPS	frdp[h] + ipdp[h]→ ggdp[h] + h[h] + ppi[h]
GPPSh	dmpp[h] + ipdp[h]→ grdp[h] + h[h] + ppi[h]
IDS2	h[h] + h2mb4p[h] + nadph[h]→ dmpp[h] + h2o[h] + nadp[h]
ANXANASCOR	anxan[u] + ascb-L[u] → dhdascb[u] + h2o[u] + zaxan[u]
BCAROH	caro[u] + h[u] + nadph[u] + o2[u] → bcrptxan[u] + h2o[u] + nadp[u]
BCRPTXANH	bcrptxan[u] + h[u] + nadph[u] + o2[u] → h2o[u] + nadp[u] + zaxan[u]
CHYA1	acaro[u] + h[u] + nadph[u] + o2[u]→ h2o[u] + nadp[u] + zxan[u]
CHYA2	acaro[u] + h[u] + nadph[u] + o2[u]→ crpxan[u] + h2o[u] + nadp[u]
CXHY	crpxan[u] + h[u] + nadph[u] + o2[u]→ h2o[u] + lut[u] + nadp[u]
LCYB	gcaro[u] → caro[u]
LCYA	lyc[h] → dcaro[h]
LCYG	lyc[h] → gcaro[h]
NEOXANS	vioxan[u] → neoxan[u]
NOR	norsp[h] + o2[h] + pqh2[h] → 2 h2o[h] + lyc[h] + pq[h]
PDS1	phyto[h] + pq[h] → phytfl[h] + pqh2[h]
PDS2	phytfl[h] + pq[h] → pqh2[h] + zcaro[h]
PSY	2 ggdp[h]→ 2 h[h] + phyto[h] + 2 ppi[h]
VIOXANOR	ascb-L[u] + vioxan[u] → anxan[u] + dhdascb[u] + h2o[u]
ZDS	o2[h] + pqh2[h] + zcaro[h] → 2 h2o[h] + norsp[h] + pq[h]
ZHY	h[u] + nadph[u] + o2[u] + zxan[u]→ h2o[u] + lut[u] + nadp[u]
CHLASG	chlda[u] + ggdp[u]→ ggchlda[u] + h[u] + ppi[u]
GGCHLDAR	ggchlda[u] + 3 h[u] + 3 nadph[u]→ chla[u] + 3 nadp[u]
GGDR	ggdp[h] + 3 h[h] + 3 nadph[h] → 3 nadp[h] + pdp[h]
CHLBSG	chldb[u] + ggdp[u]→ ggchldb[u] + h[u] + ppi[u]

. This network includes the complexity of reversible and irreversible (FRDPth, GRDPth) reactions, nodes, and cycles, and are showed in the Figure 1.

5.1.2. Case of Study 2: Optimization Multiobjective of the Metabolic Network of Metabolism Glutamate of Microalgae Chlorella vulgaris

Metabolism consists of different metabolic pathways that are intertwined to form a more complex one. One such pathway is the distribution of fluxes of glutamate metabolism, which serves different functions, including amino acid synthesis.

This metabolic network represents great complexity due to the number of metabolites that branch at the central node and the presence of reversible reactions such as ASPATh and ASPNA1Th. This network was evaluated in three different growth conditions, autotrophy, heterotrophy, and mixotrophy, using the NSGAII and MOEA/D algorithms with their four MOFBAs. This metabolism is of great importance because the pathways for producing different products of interest, amino acids such as tyrosine, valine, leucine, etc., are involved, which can later be used to produce proteins. The reactions involved in the metabolism are presented in Appendix A.1,

Table A2. Reactions derived from the flux distribution associated to glutamate metabolism [17].

Name	Formula
GLNth	gln-L[c] + h[c] ⇄ gln-L[h] + h[h]
GALh	atp[h] + glu-L[h] + nh4[h] → adp[h] + gln-L[h] + h[h] + pi[h]
GLUS	glu-L[h] + h2o[h] + nad[h] → akg[h] + h[h] + nadh[h] + nh4[h]
GLUTRS	atp[h] + glu-L[h] + trnaglu[h] → amp[h] + glutrna[h] + h[h] + ppi[h]
GLUS(nadph)	akg[h] + gln-L[h] + h[h] + nadph[h] → 2 glu-L[h] + nadp[h]
ASPATh	akg[h] + asp-L[h] ⇄ glu-L[h] + oaa[h]
ASPNA1th	asp-L[c] + na1[c] ⇄ asp-L[h] + na1[h]
VALth	h[c] + val-L[c] ⇄ h[h] + val-L[h]
BCTA(val)h	akg[h] + val-L[h] → 3mob[h] + glu-L[h]
TYRTAh	34hpp[h] + glu-L[h] ⇄ akg[h] + tyr-L[h]
TYRth	h[c] + tyr-L[c] ⇄ h[h] + tyr-L[h]
BCTAh	3mop[h] + glu-L[h] ⇄ akg[h] + ile-L[h]
ILEth	h[c] + ile-L[c] ⇄ h[h] + ile-L[h]

. Figure 2 represents the distribution of fluxes associated with glutamate metabolism in the chloroplast and cytoplasm.

5.2. Experiments Definition

Defining a methodology based on metaheuristics that improve the metabolic network flux information provided by the FBA method by redefining Flux Balance Analysis as a Multi-objective Optimization Problem is possible; four experiments were proposed, summarized in the following

Table 4. Design of experiments to demonstrate metaheuristic support for understanding metabolism in microalgae.

Experiment	Objective	Variables Involved
Experiment1	Using different optimization models produces different results.	C. vulgaris, NSGAII, MOFA1, MOFBA2, MOFBA3, MOFBA4.
Experiment2	Demonstrate that the use of metaheuristics supports the understanding of microalgae metabolism.	C. vulgaris, FBA, NSGAII, MOFBA4
Experiment3	There are optimization algorithms more suitable for solving specific problems	C. vulgaris, NSGAII, MOEA/D, MOFBA4.
Experiment4	Validate that a random selection is not enough.	C. vulgaris, NSGAII, FBA, random.

.

Experiment 1 demonstrated that different multi-objective optimization models offer different results. The algorithm was set to NSGAII, the microalgae was modified to demonstrate the approach’s versatility, and finally, the four proposed optimization models were analyzed. For the cases studied, it was observed that the consistently best model was MOFBA₄, which was used in the subsequent experiments.

In Experiment 2, the algorithm, the microalgae, and the single-objective FBA model were compared against the multi-objective model defined by MOFBA₄. It was observed that the metabolism of a microalgae can be described with different fluxes, not one, and these can be controlled to obtain information on different metabolites of interest. This confirms the ease of adaptation of the proposed methods to different types of metabolic networks, considering different configurations.

Experiment 3 evaluated the performance of the NSGAII and MOEA/D algorithms on the same optimization problem. It was observed that, for the three objectives (i.e., three metabolites of interest) considered, NSGAII was the best. This result is consistent with the literature, given that for two or three objectives, NSGAII shows better performance than MOEA/D. This leaves open the question of whether MOEA/D will improve for a larger number of objectives, which is an open line of investigation for its application in the study of microalgal metabolic networks.

Experiment 4 shows that simple random sampling is not sufficient to obtain a better distribution of solutions, which is possible through the use of metaheuristics.

The metaheuristics NSGAII and MOEA/D were implemented with the aid of the jMetalPy framework [32]. The optimization models were developed in Python and used as part of the FBA implementation provided by the package COBRApy [33]. Graphics were recreated using the interface pyplot of matplotlib [34]. The computer used to run the experiments has a 64 bit 2.6 GHz processor with 32 RAM memory.

6. Results

This section summarizes the data obtained as a result of the implementation of the experiments described in Section 3.2. At the end, it provides a discussion over the achieved goals in the research. To visualize the results in Figure 3, Figure 4, Figure 5 and Figure 6, the matplotlib library was imported.

6.1. Experiment 1

En [18] showed that NSGAII presents better quality solutions than the classic FBA for three objective functions. Figure 3 shows the results of the experiment where the four variants described above, MOFBA₁, MOFBA₂, MOFBA₃, and MOFBA₄, for the NSGAII algorithm are tested, with the optimization of three objective functions of the pigment flux distribution of the microalgae Chlorella vulgaris. It can be observed that the different MOFBAs offer different behaviors to each other; MOFBA₁, MOFBA₃, and MOFBA₄ improve FBA. However, the best solution behavior was MOFBA₄ in Figure 3d as it provides more non-dominated solutions and maintains a good population diversity for the same population size environment.

Figure 3 shows the pigment flux distribution in the microalgae C. vulgaris; it can be seen that each variant of MOFBA offers different behaviors and all improve the FBA in Figure 3a–c, but the best behavior in the solutions can be observed in the variant of MOFBA₄ in Figure 3d.

Figure 3. Comparison between the NSGAII algorithm and the variants (a) MOFBA₁, (b) MOFBA₂, (c) MOFBA₃, and (d) MOFBA₄ in the distribution of pigment fluxes.

Figure 3. Comparison between the NSGAII algorithm and the variants (a) MOFBA₁, (b) MOFBA₂, (c) MOFBA₃, and (d) MOFBA₄ in the distribution of pigment fluxes.

6.2. Experiment 2

When comparing the performance of the NSGAII algorithm with the MOFBA₄ variant, Figure 4a and the classic single-objective optimization FBA in Figure 4b, it can be observed that the NSGAII-MOFBA₄ algorithm presents superiority by demonstrating that the information provided is improved by providing more solutions and, importantly, a significantly improved distribution. This enhanced distribution is particularly evident in Figure 3d and Figure 4a with two different metabolic networks studied, such as glutamate metabolism and the distribution of pigment fluxes in the microalgae C. vulgaris.

Figure 4. Comparison between (a) NSGAII-MOFBA₄ and (b) FBA in the distribution of fluxes associated with the glutamate metabolism of the microalgae Chlorella vulgaris.

Figure 4. Comparison between (a) NSGAII-MOFBA₄ and (b) FBA in the distribution of fluxes associated with the glutamate metabolism of the microalgae Chlorella vulgaris.

6.3. Experiment 3

Figure 5 presents the evaluation between the NSGAII, Figure 5a,c, and MOEA/D, Figure 5b,d, algorithms in the distribution of fluxes associated with glutamate metabolism and the distribution network and pigment fluxes with NSGAII, Figure 5c, and MOEA/D, Figure 5d, from the microalgae C. vulgaris with the variant of the MOFBA₄ algorithm. It was shown that the NSGAII algorithm has more solutions and better population diversity compared to MOEA/D. Metaheuristics are important; in this case, NSGAII is the best, which is consistent with the literature [35], because this algorithm works well with 2 and 3 objectives.

Figure 5. Comparison between the (a,c) NSGAII and (b,d) MOEA/D algorithms in the pigment distribution network and in the distribution of fluxes associated with glutamate metabolism of the microalgae Chlorella vulgaris.

Figure 5. Comparison between the (a,c) NSGAII and (b,d) MOEA/D algorithms in the pigment distribution network and in the distribution of fluxes associated with glutamate metabolism of the microalgae Chlorella vulgaris.

6.4. Experiment 4

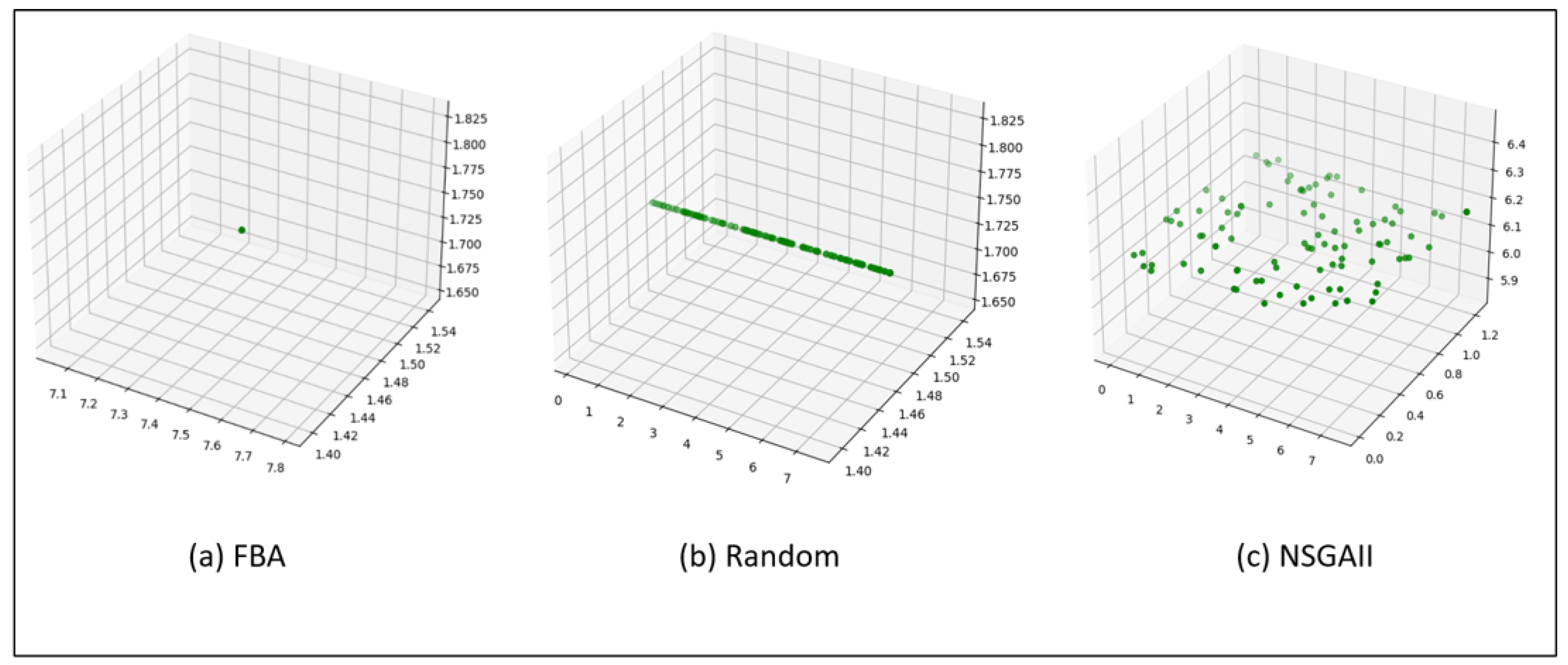
In addition to testing the different case studies with the FBA, NSGAII, and MOEA/D approaches, an experiment was carried out using a rapid random approach, which we call random, in the distribution of pigment flux in the microalgae C. vulgaris. Figure 6 shows the comparison between FBA, Figure 6a, random, Figure 6c, and NSGAII, Figure 6b. The random method, despite being fast, could not offer better results, Figure 6b, compared to what is presented in Figure 6c, NSGAII.

Figure 6. Comparison between the variants (a) FBA, (b) random, and (c) NSGAII in the microalgae C. vulgaris.

Figure 6. Comparison between the variants (a) FBA, (b) random, and (c) NSGAII in the microalgae C. vulgaris.

6.5. Statistic Analysis

Table 5. Distribution of fluxes in mmol h⁻¹ obtained by NSGA II, associated with the synthesis of pigments in the metabolism of the microalgae C. vulgaris.

Reaction	LB	UB	S1	S2	S3	S4
NADPH	0.000487	0.000487	0.000487	0.000487	0.000487	0.000487
IDS2	0	0.000487	7.42 × 10³	4.72 8	2.58 × 10−5	4.33 × 10−7
FPPSh	0	0.000487	7.42 × 10−5	4.72 × 10−5	2.58 × 10−5	4.33 × 10−7
GPPSh	0	0.000487	7.42 × 10−5	4.72 × 10−5	2.58 × 10−5	4.33 × 10−7
FRDPth	0	0	0	0	0	0
FPPS	0	0	0	0	0	0
GRDPth	0	0	0	0	0	0
GRDPH	0	0	0	0	0	0
GGPPS	0	0.000487	7.42 × 10−5	4.72 × 10−5	2.58 × 10−5	4.33 × 10−7
v1	0	0.000402078	0	0	0	0
GGDPtu	−0.0000849	0.0000849	7.42 × 10−5	4.72 × 10−5	2.58 × 10−5	4.33 × 10−7
CHLASG	0	0.0000742	7.42 × 10−5	4.72 × 10−5	2.58 × 10−5	4.33 × 10−7
GGCHLDAR	0	0.0000742	7.42 × 10−5	4.72 × 10−5	2.58 × 10−5	4.33 × 10−7
CHLAU	0	0.0000742	7.42 × 10−5	4.72 × 10−5	2.58 × 10−5	4.33 × 10−7
PSY	0	2.24 × 10−8	0	0	0	0
PDS1	−2.24 × 10−8	2.24 × 10−8	0	0	0	0
PDS2	−2.24 × 10−8	2.24 × 10−8	0	0	0	0
ZDS	−2.24 × 10−8	2.24 × 10−8	1.59 × 10−8	1.54 × 10−8	1.06 × 10−8	3.58 × 10−9
NOR	−2.24 × 10−8	2.24 × 10−8	1.59 × 10−8	1.54 × 10−8	1.06 × 10−8	3.58 × 10−9
v2	0.00	8.00 × 10−11	0	0	0	0
LCYG	−1.59 × 10−8	1.59 × 10−8	1.59 × 10−8	1.54 × 10−8	1.06 × 10−8	3.58 × 10−9
GCAROtu	−1.59 × 10−8	1.59 × 10−8	1.59 × 10−8	1.54 × 10−8	1.06 × 10−8	3.58 × 10−9
LCYB	−1.59 × 10−8	1.59 × 10−8	1.59 × 10−8	1.54 × 10−8	1.06 × 10−8	3.58 × 10−9
v3	0.00	1.24 × 10−8	1.24 × 10−8	1.20 × 10−8	7.10 × 10−9	1.00 × 10−10
BCAROH	−3.48 × 10−9	3.48 × 10−9	3.48 × 10−9	3.48 × 10−9	3.48 × 10−9	3.48 × 10−9
BCRPTXANH	−3.48 × 10−9	3.48 × 10−9	3.48 × 10−9	3.48 × 10−9	3.48 × 10−9	3.48 × 10−9
v4	0.00	6.16 × 10−9	6.16 × 10−9	6.16 × 10−9	6.16 × 10−9	6.16 × 10−9
ANXANAS	−2.68 × 10−9	2.68 × 10−9	−2.68 × 10−9	−2.68 × 10−9	−2.68 × 10−9	−2.68 × 10−9
v5	0.00	3.88 × 10−9	3.88 × 10−9	3.88 × 10−9	3.88 × 10−9	3.88 × 10−9
VIOXANOR	−2.41 × 10−9	2.41 × 10−9	−2.41 × 10−9	−2.41 × 10−9	−2.41 × 10−9	−2.41 × 10−9
v6	0.00	2.70 × 10−10	2.70 × 10−10	2.70 × 10−10	2.70 × 10−10	2.70 × 10−10
NEOXANS	−1.47 × 10−9	1.47 × 10−9	1.47 × 10−9	1.47 × 10−9	1.47 × 10−9	1.47 × 10−9
NEOXANU	0	1.47 × 10−9	1.47 × 10−9	1.47 × 10−9	1.47 × 10−9	1.47 × 10−9
LCYD	−6.42 × 10−9	6.42 × 10−9	0	0	0	0
LCYA	−6.42 × 10−9	6.42 × 10−9	0	0	0	0
v7	0.00	1.33 × 10−9	0	0	0	0
ACAROtu	−5.09 × 10−9	5.09 × 10−9	0	0	0	0
CHYA1	0	0	0	0	0	0
ZHY	0	0	0	0	0	0
CHYA2	0	5.09 × 10−9	0	0	0	0
CXHY	0	5.09 × 10−9	0	0	0	0
v8	0	3.35 × 10−9	−1.74 × 10−9	−1.74 × 10−9	−1.74 × 10−9	−1.74 × 10−9
LUTH	−1.74 × 10−9	1.74 × 10−9	1.74 × 10−9	1.74 × 10−9	1.74 × 10−9	1.74 × 10−9
LOROXANU	0	1.74 × 10−9	1.74 × 10−9	1.74 × 10−9	1.74 × 10−9	1.74 × 10−9
FRDPth	0	1	0	0	0	0

and

Table 6. Distribution of fluxes in mmol h⁻¹ obtained through FBA and the NSGAII-MOFBA₄ algorithm.

	Euclidean Distance between FBA and NSGAII-MOFBA4
Reaction.	FBA	MOFBA4	MOFBA4	MOFBA4
ACAROtu’	5.09 × 10−9	0	0	0
ANXANASCOR’	−2.68 × 10−9	−2.68 × 10−9	−2.68 × 10−9	−2.68 × 10−9
BCAROH’	3.48 × 10−9	3.48 × 10−9	3.48 × 10−9	3.48 × 10−9
BCRPTXANH’	3.48 × 10−9	3.48 × 10−9	3.48 × 10−9	3.48 × 10−9
CHLASG’	0	1.36106 × 10−9	2.35109 × 10−5	0.0000742
CHYA1’	0	0	0	0
CHYA2’	5.09 × 10−9	0	0	0
CXHY’	5.09 × 10−9	0	0	0
FPPS’	0	0	0	0
FRDPth’	0	0	0	0
GCAROtu’	1.59 × 10−8	7.94367 × 10−9	1.35944 × 10−8	1.59 × 10−8
GGCHLDAR’	0	1.36106 × 10−9	2.35109 × 10−5	0.0000742
GGDPtu’	0.000148102	1.36106 × 10−9	2.35109 × 10−5	0.0000742
GGPS’	0.000486596	1.36106 × 10−9	2.35109 × 10−5	0.0000742
GRDPth’	0	0	0	0
IDS1’	0.001459788	1.36106 × 10−9	2.35109 × 10−5	0.0000742
LCYA’	6.42 × 10−9	0	0	0
LCYB’	1.59 × 10−8	7.94367 × 10−9	1.35944 × 10−8	1.59 × 10−8
LCYD’	6.42 × 10−9	0	0	0
LCYG’	1.59 × 10−8	7.94367 × 10−9	1.35944 × 10−8	1.59 × 10−8
LUTH’	1.74 × 10−9	1.74 × 10−9	1.74 × 10−9	1.74 × 10−9
NEOXANS’	1.47 × 10−9	1.47 × 10−9	1.47 × 10−9	1.47 × 10−9
NOR’	2.24 × 10−8	7.94367 × 10−9	1.35944 × 10−8	1.59 × 10−8
PDS1’	2.24 × 10−8	0	0	0
PDS2’	2.24 × 10−8	0	0	0
PSY’	2.24 × 10−8	0	0	0
VIOXANOR’	−2.41 × 10−9	−2.41 × 10−9	−2.41 × 10−9	−2.41 × 10−9
ZDS’	2.24 × 10−8	7.94367 × 10−9	1.35944 × 10−8	1.59 × 10−8
ZHY’	0	0	0	0
Euclidean distance		0.001545861	0.001514586	0.001451344

shows that the proposed methods obtain feasible solutions; it is shown that they satisfy the conditions identified in [17] and FBA, thereby demonstrating the correlation of the solutions in silico and its ability to emulate results in different culture conditions. In Table 6 can be seen a comparison between the fluxes in mmol h⁻¹ obtained with FBA and NSGAII-MOFBA₄ and the Euclidean distance presented between them. Table 5 demonstrates that NSGAII presents great versatility to limit the parameters in the growing conditions through the lower bound and upper bound values, in addition to being able to simulate cycles and bifurcations between metabolic networks. Likewise, some feasible solutions corresponding to NSGAII with the MOFBA₄ variant and solutions obtained from the classic FBA are presented.

This section statistically validates that there is a difference when using different optimization problems or algorithms in order to show that the choice is relevant. To do this, it summarizes the results by comparing by Hypervolume (the proximity indicator to the Pareto Optimal front) to see whether or not there is a significant difference between the optimization models MOFBA₃ and MOFBA₄ and the NSGAII and MOEA/D algorithms.

The first analysis considers the models MOFBA₃ and MOFBA₄, sets the solution algorithm to NSGAII, and evaluates all networks. For the analysis, the Hypervolume was obtained from each of the 30 runs of the algorithm per problem. Using the non-parametric Wilcoxon signed rank test, with a confidence level of 95%, the $H_0$ was validated, which specifies that it is impossible to define a methodology based on metaheuristics that improves the information of metabolic network fluxes provided by the FBA method by redefining the Flux Balance Analysis as a Multi-objective Optimization Problem.

Table 7. Data were statistically analyzed to validate the differences between MOFBA₃ and MOFBA₄. The null hypothesis, $H_0$, was accepted when the p-value obtained was less than 0.05.

Glutamate Metabolism in C. vulgaris		Pigment Network in C. vulgaris
MOFBA4	MOFBA3	MOFBA4	MOFBA3
34.539	20.723	20.65	20.647
34.539	20.723	20.65	20.648
34.539	20.723	20.65	20.649
34.539	20.723	20.65	20.649
34.539	20.723	20.65	20.651
34.539	20.723	20.65	20.651
34.539	20.723	20.65	20.651
34.539	20.723	20.65	20.651
34.539	20.723	20.65	20.652
34.539	20.723	20.65	20.648
34.539	20.723	20.65	20.650
34.539	20.723	20.65	20.651
34.539	20.723	20.65	20.648
34.539	20.723	20.65	20.653
34.539	20.723	20.65	20.654
34.539	20.723	20.65	20.652
34.539	20.723	20.65	20.651
34.539	20.723	20.65	20.649
34.539	20.723	20.65	20.651
34.539	20.723	20.65	20.651
34.539	20.723	20.65	20.650
34.539	20.723	20.65	20.650
34.539	20.723	20.65	20.651
34.539	20.723	20.65	20.650
34.539	20.723	20.65	20.650
34.539	20.723	20.65	20.647
34.539	20.723	20.65	20.651
34.539	20.723	20.65	20.651
34.539	20.723	20.65	20.652
34.539	20.723	20.66	20.655
$H_0$	ACCEPTED	$H_0$	REJECTED

summarizes the results, showing the Hypervolume value on logarithmic scale per run for each network and the acceptance status of the $H_0$ in the last row. It can be seen that the hypothesis is rejected in almost all the metabolic networks analyzed. Except for /textitChlorella, it can be commented that the best optimization model is MOFBA₄.

The second analysis considers the NSGAII and MOEA/D algorithms, sets the optimization model to MOFBA₄, and evaluates all networks. For the analysis, the Hypervolume was obtained from each of the 30 executions of each algorithm on the solved problem. Using the non-parametric Wilcoxon signed rank test, with a confidence level of 95%, the $H_0$ was validated, which specifies that the difference in means between the samples is the same.

Table 8. Data were statistically analyzed to establish differences between the use of NSGAII and MOEA/D. The null hypothesis, $H_0$, was accepted when the p-value obtained was less than 0.05.

Glutamate Metabolism in C. vulgaris		Pigment Network in C. vulgaris
NSGAII	MOEA/D	NSGAII	MOEA/D
20.723	20.723	20.647	20.723
20.723	20.723	20.648	20.723
20.723	20.723	20.649	20.723
20.723	20.723	20.649	20.723
20.723	20.723	20.651	20.723
20.723	20.723	20.651	20.723
20.723	20.723	20.651	20.723
20.723	20.723	20.651	20.723
20.723	20.723	20.652	20.723
20.723	20.723	20.648	20.723
20.723	20.723	20.650	20.723
20.723	20.723	20.651	20.723
20.723	20.723	20.648	20.723
20.723	20.723	20.653	20.723
20.723	20.723	20.654	20.723
20.723	20.723	20.652	20.723
20.723	20.723	20.651	20.723
20.723	20.723	20.649	20.723
20.723	20.723	20.651	20.723
20.723	20.723	20.651	20.723
20.723	20.723	20.650	20.723
20.723	20.723	20.650	20.723
20.723	20.723	20.651	20.723
20.723	20.723	20.650	20.723
20.723	20.723	20.650	20.723
20.723	20.723	20.647	20.723
20.723	20.723	20.651	20.723
20.723	20.723	20.651	20.723
20.723	20.723	20.652	20.723
20.723	20.723	20.655	20.723
$H_0$	REJECTED	$H_0$	REJECTED

summarizes the results and shows each network’s Hypervolume value per run at the logarithmic scale and the acceptance status of $H_0$ in the last row. It can be seen that the hypothesis is rejected in all the metabolic networks analyzed. These results from both analyses confirm what was expected, that it is relevant to consider which optimization model to use, and which algorithm, because their performances when obtaining sets of solutions can be different.

Through the graphical results observed, mainly due to the volume and dispersion of the solutions obtained in all the algal metabolic networks considered, it is demonstrated that the proposed method based on multi-objective optimization resolved through metaheuristics offers better support for the analysis. On the other hand, the statistical analysis presented in this section demonstrates that it is relevant to consider the optimization model and the algorithm since these can contribute to different types of improvements. The statistical analyses presented here demonstrate that there can be a significant difference between optimization models and between metaheuristic algorithms.

6.6. Discussion

Almost no experiment has been done previously with the metabolism of microalgae, except for [18]. Although there are exact methodologies, evolutionary approaches require fewer computational resources in the field of multiple objectives; for example, it gives the advantage of using less time and memory. Approaches such as NSGAII and MOEA/D allow greater power of choice in the decision-making process due to the variety and number of solutions and the possibility of easier recognition of the most important fluxes in a network and their influence and impact, instead of not having a methodology.

Some additional insights emerge from the above results. Experiment 2 demonstrates the versatility of NSGAII to adapt to different circumstances and its ability to improve the analysis of the metabolic network given the greater number of solutions it produces for each of them. As demonstrated in Experiments 1 to 4, the analysis capacity of a metabolic network is improved by introducing the NSGAII algorithm.

The multi-objective optimization problems present in the literature currently consider different solution metrics. Experiment 1 compares the use of the NSGAII algorithm with the four variants of optimization problems, with the MOFBA₄ optimization problem being the most promising, by introducing different optimization strategies, such as optimizing not only the metabolites of interest but also Hypervolume and Generational Distance. Compared to MOFBA₃, which minimizes Hypervolume, in MOFBA₂ the decision variables are only the fluxes of the reactions of interest.

Although, in the case studies, NSGAII had a better graphically observable performance than MOEA/D, as occurred in Experiment 3, because the case studies had three objective functions and, according to the literature, NSGAII is better than MOEA/D when there are three functions objective, the possibility opens up of being able to use MOEA/D in networks where more than three objective functions need to be optimized. It can also be observed, through Experiment 4, that simply using a random sample solution is not enough to obtain a good set of solutions like using metaheuristics. However, special considerations must be taken to allow respect for restrictions or information of control desired by an interested individual.

The algorithms were tested on different microalgae strains, as seen in [18] with C. reinhardti, and in this research using C. vulgaris, in complex metabolic networks that contain cycles, bifurcations, and reversible reactions, it checks their viability in different metabolic networks, confirming that they can not only be used in a single microalgae. This leaves open the possibility of it being used in other types of species where there is a need to optimize more than one objective function.

7. Conclusions

The present research work carried out a study of metabolic fluxes in green microalgae. The objective was focused on verifying the suitability of in silico methods as support strategies for improving the analysis of metabolism in microalgae. Through the experiments developed, evidence was obtained that supports the following conclusions:

The study of metabolic fluxes in microalgae is improved through increasing the number of solutions that satisfy the conditions of a microalgae so that it can live. This is observable because, unlike traditional methods such as FBA that only offer a solution, which is expanded in a limited way through sensitivity analysis, it is greatly favored by integrating it into a methodology based on metaheuristics and multi-objective optimization problems; it increases both the number of fluxes that satisfy the conditions sought in the metabolic network, also simultaneously allowing the optimization of several metabolites of interest.

There is more than one alternative to analyzing a metabolic network by optimizing several metabolites of interest, with the FBA method as the core of the optimization process. The present work proposed four optimization models demonstrating this result, each offering analysis angles different from those that FBA offers.

It is possible to solve the optimization problems supporting the metabolic study by considering different evolutionary metaheuristics, and by obtaining significant results for the analysis. This is demonstrated using NSGAII and MOEA/D to solve the proposed optimization problems. In this study, NSGAII showed the best performance in general, which is consistent with the literature, by exclusively addressing the simultaneous optimization of three objectives. This shows that, for future work, the analysis of the best metaheuristic must be carried out before the study.

Solution search parameters can be controlled during the analysis of a metabolic network by adjusting the reaction boundaries. This contributes to further improving the study of microalgae since the definition of controlled environments is possible. This is observed in the validation process, where the parameters to generate solutions were limited to the values found in the work on in vivo specimens.

Selecting one algorithm or model to optimize a specific metabolic network can be troublesome and requires fine-tuning to identify the configuration that best fits the research interests of the metabolic engineering carried out. This is evident given the variation in the performance between algorithms and optimization models, or the different combinations tested in this research work.

A decision maker, e.g., a researcher in metabolic engineering, improves his decision-making capacity by visualizing a set of metabolic fluxes that satisfy the conditions specified for the metabolic network they study.