Motion Correction for Brain MRI Using Deep Learning and a Novel Hybrid Loss Function
Abstract
1. Introduction
- First, a new loss function was developed, which contains an L1 component for penalizing overall image artifacts and a total variation (TV) component to penalize the loss of image details such as boundaries. Accordingly, a two-stage training strategy was implemented to first minimize the overall motion artifacts and then consider both the residual motion-induced artifacts and the loss of image details such as boundaries.
- Second, the generalizability of the trained model was assessed using images with orientations and contrast different from those of the training data.
- Third, to ensure rigor and demonstrate clinical utility, in-depth evaluations were made using different levels of synthetic motions and in vivo data from patients, using both objective performance indices and subjective reading conducted by experienced clinicians. Motion-free images were also used to assess potential over-corrections made by the trained DL networks.
- Finally, to allow other researchers to reproduce our work or use the presented methods to process their own data, we have provided the code and sample data at https://github.com/MRIMoCo/DL_Motion_Correction (accessed on 10 October 2023).
2. Related Works
3. Materials and Methods
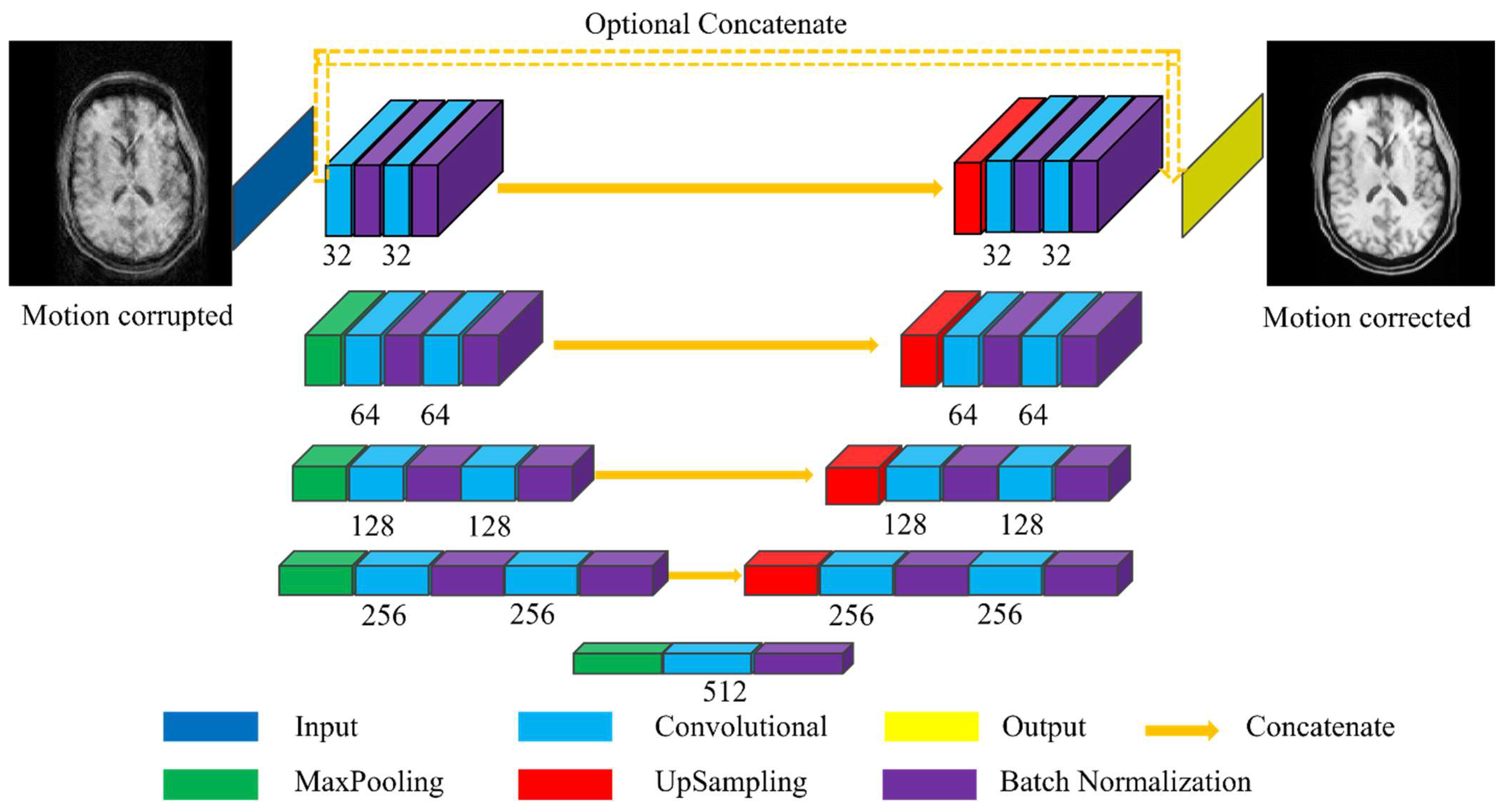
3.1. MC-Net
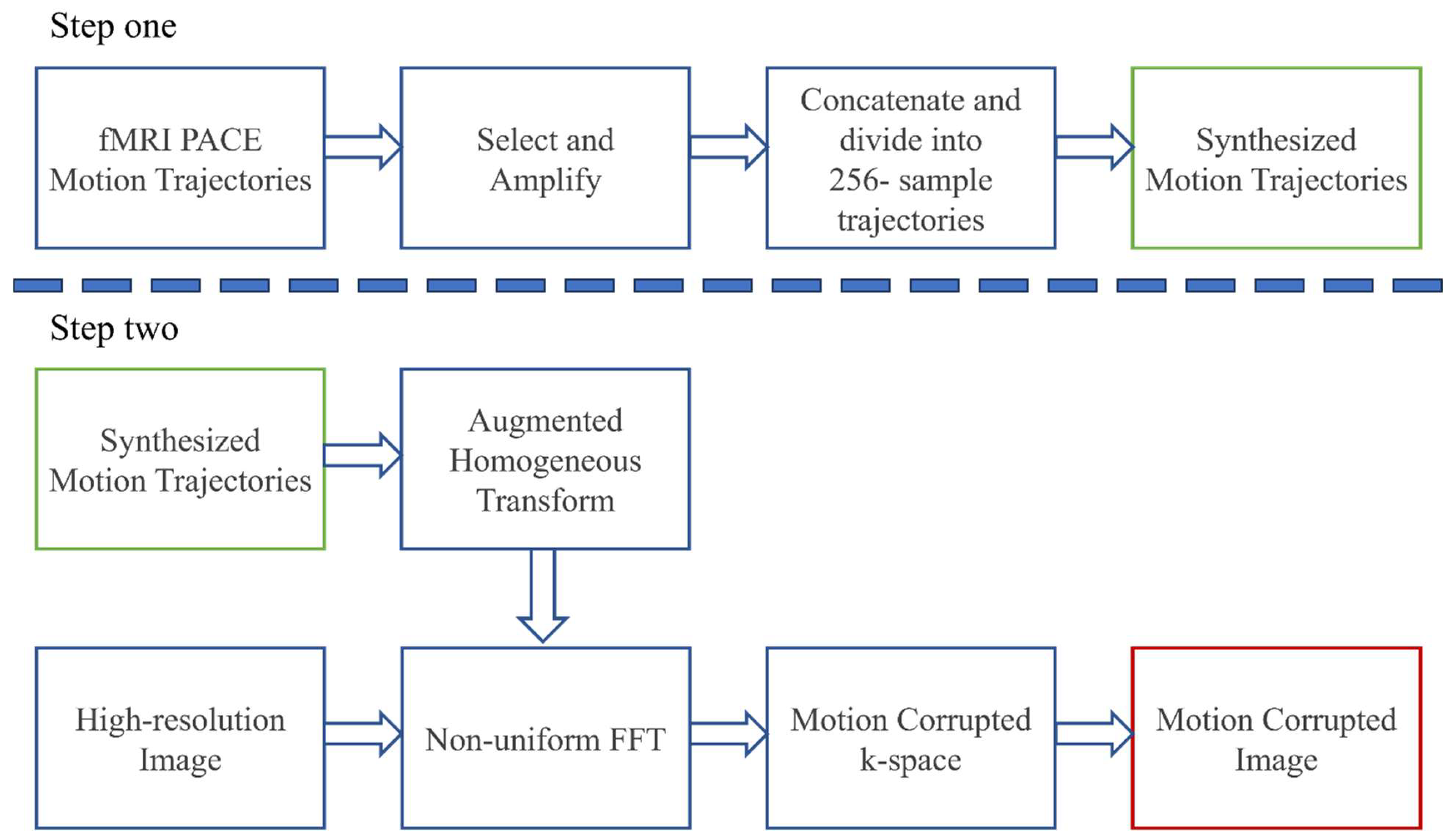
3.2. Motion-Corrupted Images
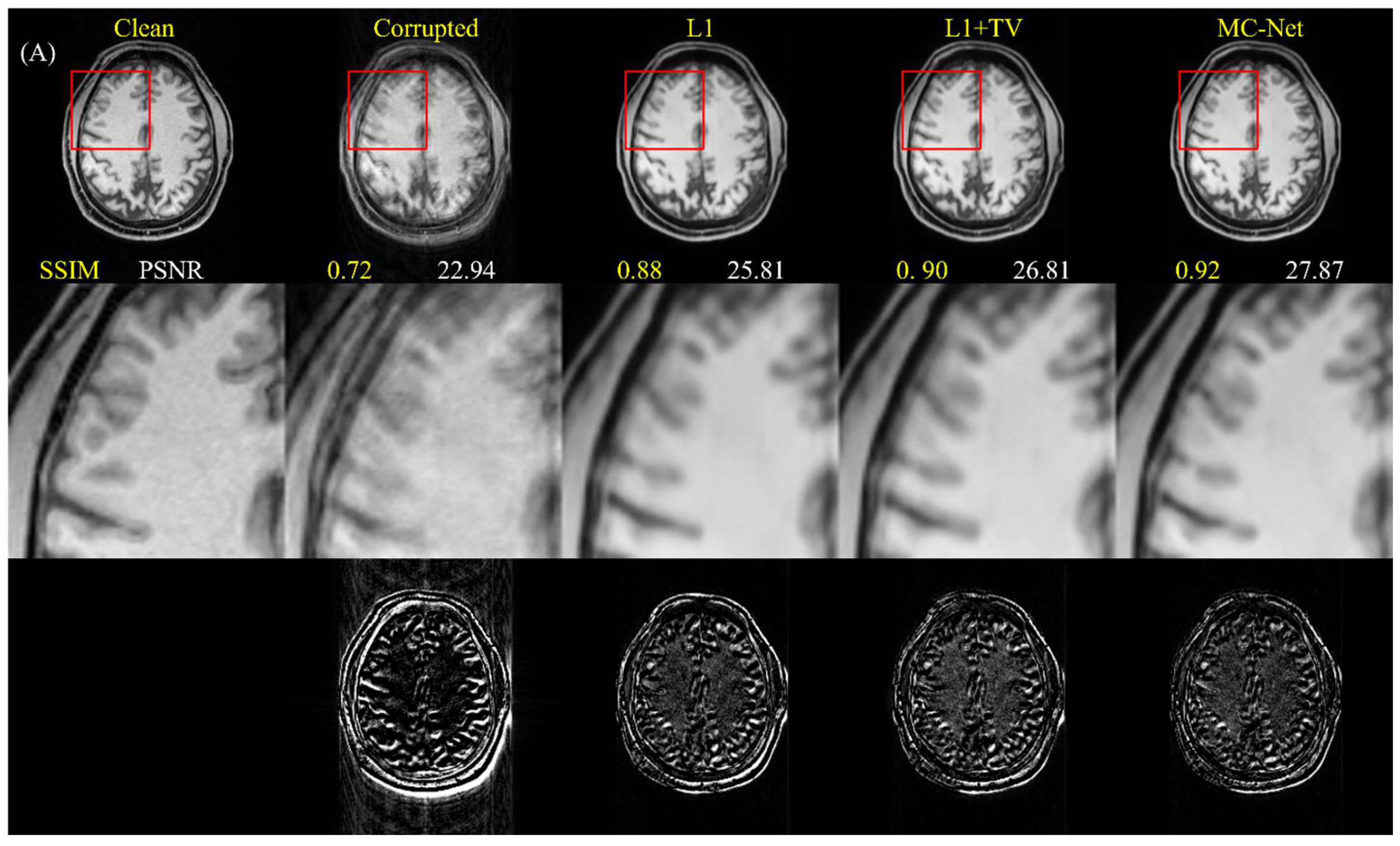
3.3. Quantitative Evaluation Metrics
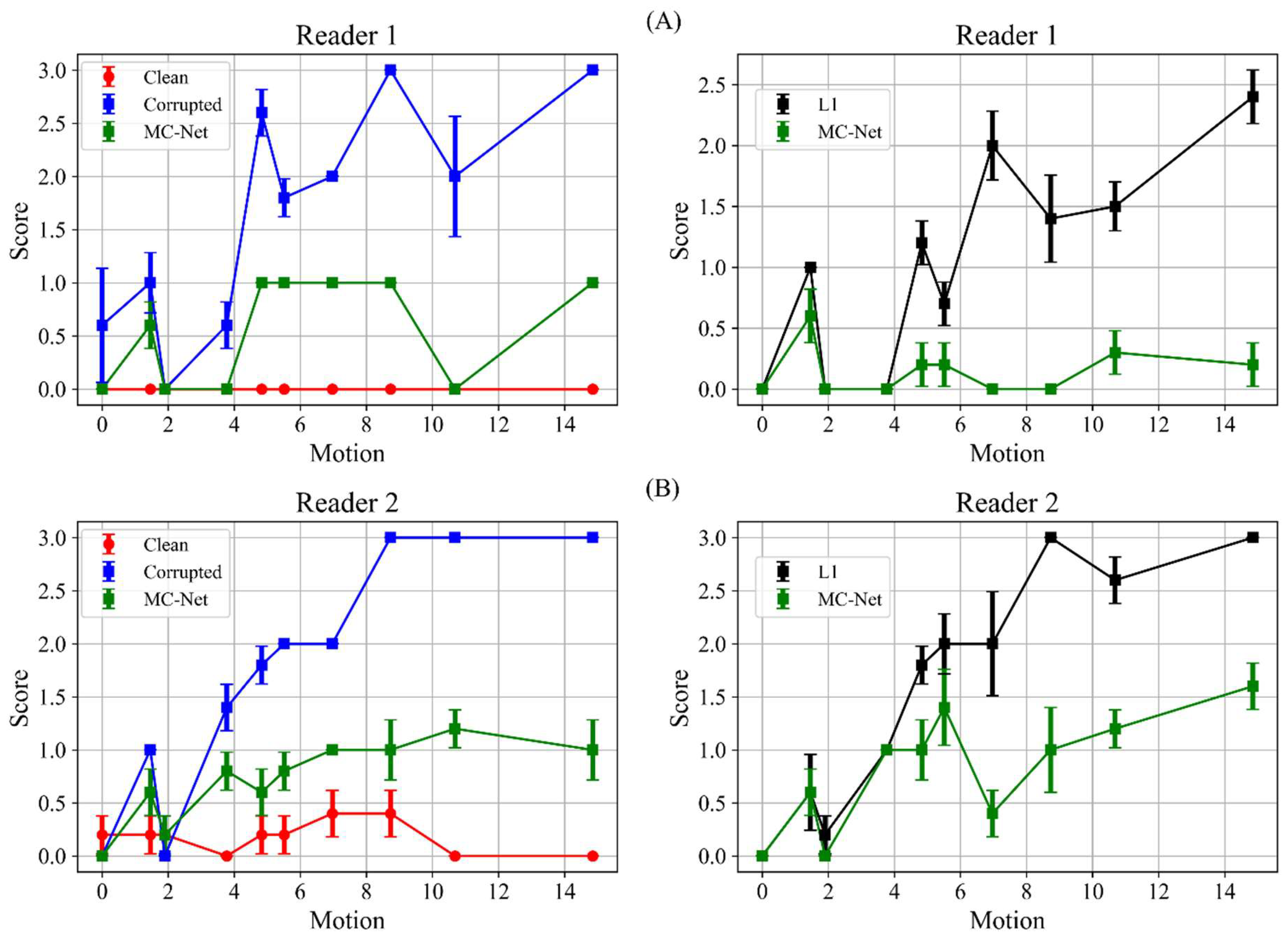
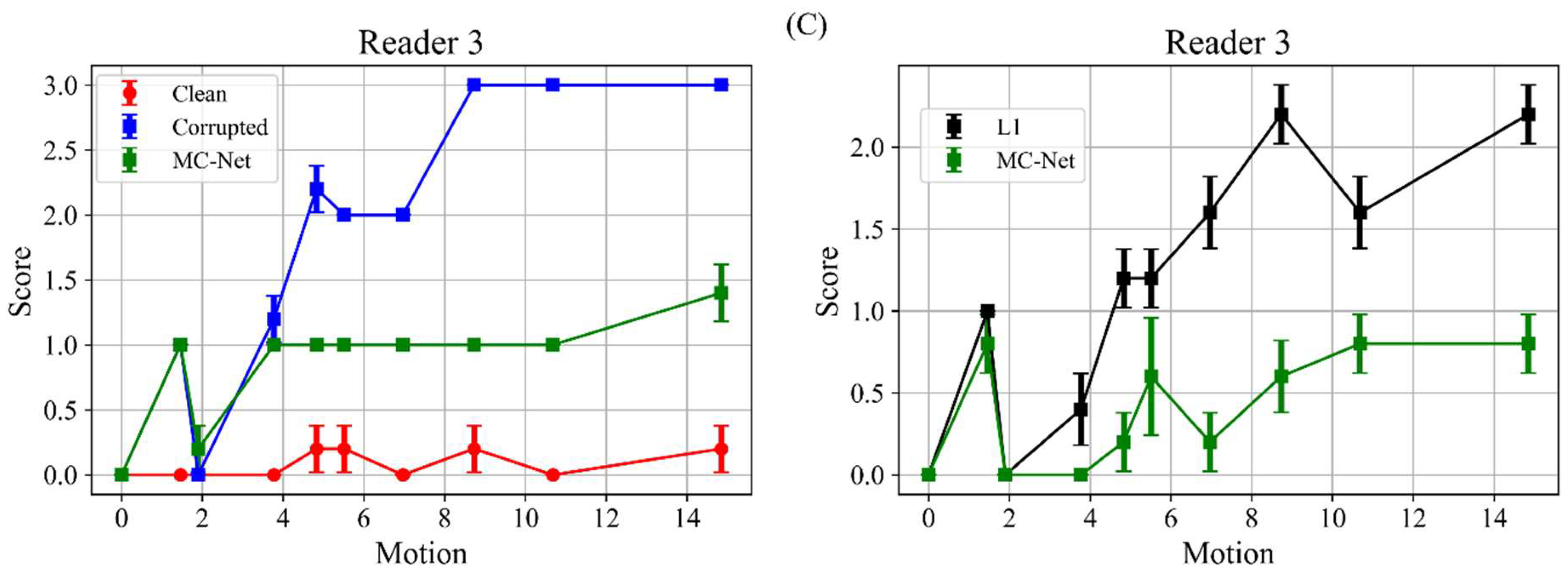
3.4. Visual Reading Scores
3.5. Implementation Details
| Algorithm 1: The overall operation of training and testing MC-Net | |
| Step 1: | Initialize the weights of MC-Net (as shown in Figure 1) randomly, Initialize variable for early stopping: best_loss = infinity, counter = 0 |
| Step 2: | Define hyperparameters: Learning rate, Number of epochs, and Batch size, Patience for early stopping. |
| Step 3: | First stage training (L1 loss): for each epoch from 1 to number of epochs do for each batch do Compute the predicted output using the current parameters Compute the loss between predicted and actual outputs Compute gradients of the loss with respect to the model parameters Update model parameters using ADAMS optimization algorithm Check for early stopping: If validation loss is less than best_loss Update best_loss = validation loss Reset counter = 0 Else Increment counter If counter >= patience Exit training loop |
| Step 4: | Second stage training (L1 + TV loss): Take the MC-Net weight with best validation loss in Step 3 as initial weight. Repeat the same procedure as in Step 3. |
| Step 5: | Test the MC-Net: Fed test images into the MC-Net and then get the outputs. |
4. Results
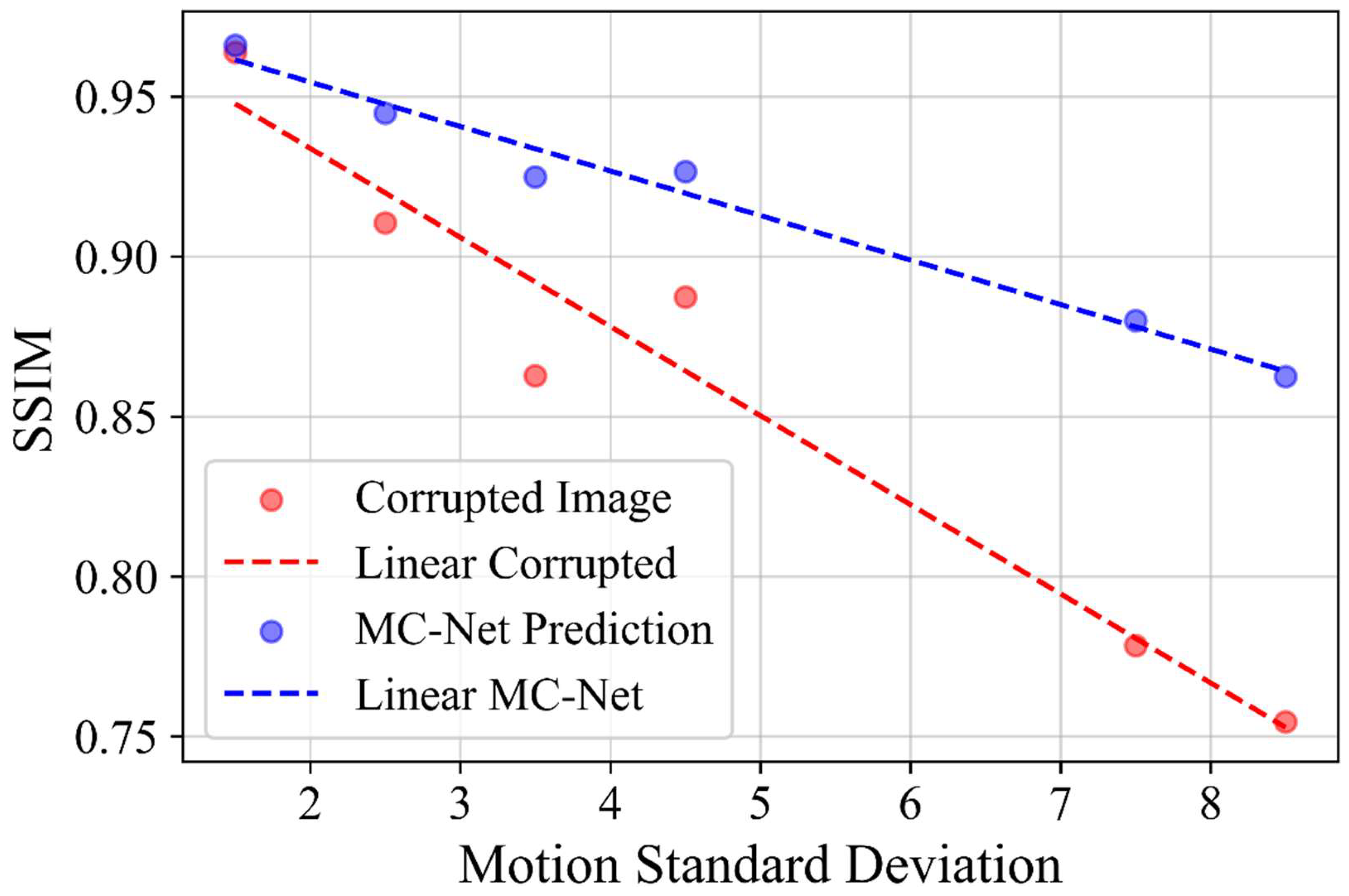
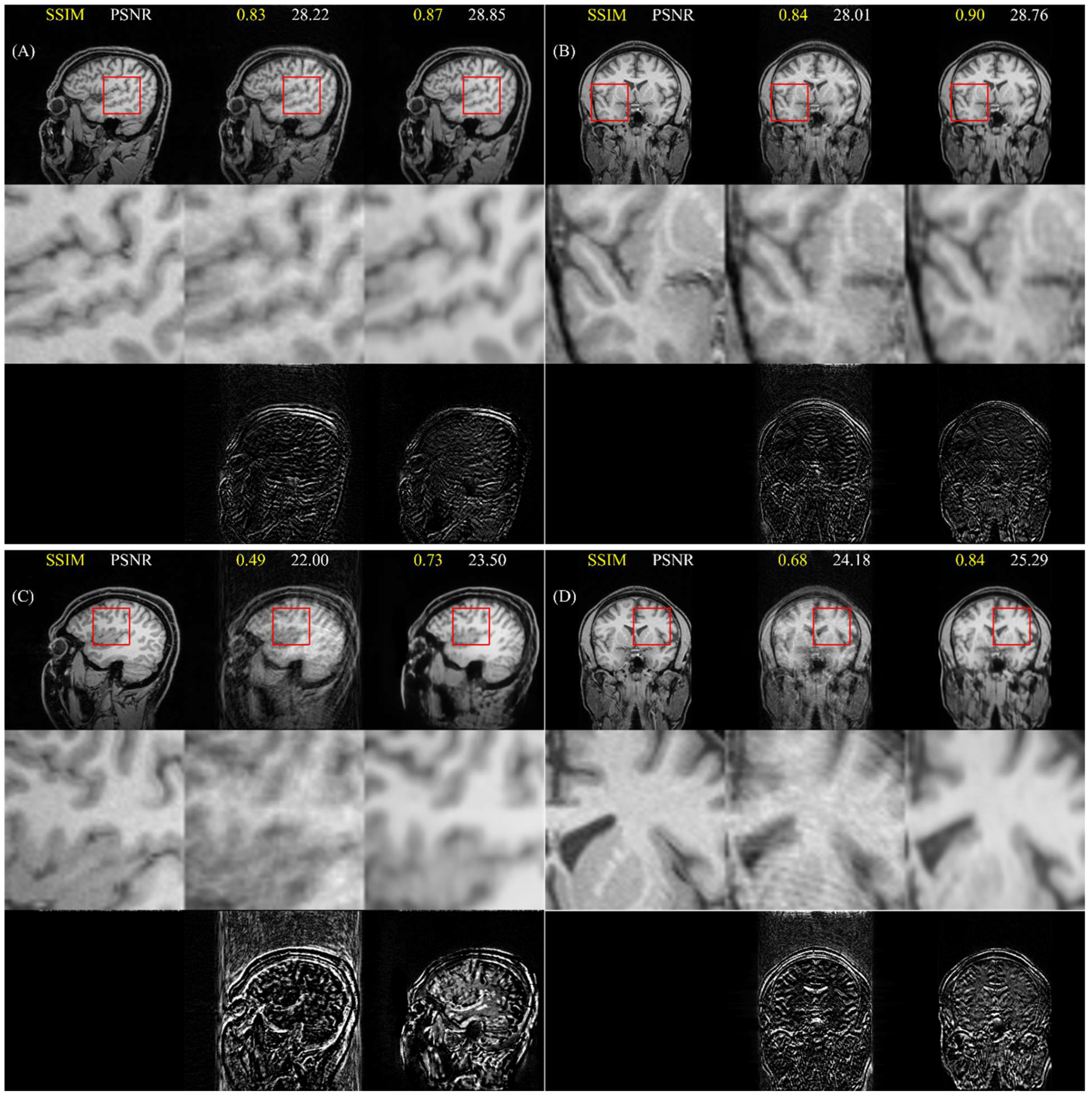
4.1. Quantitative Improvements for Motion-Corrupted Images
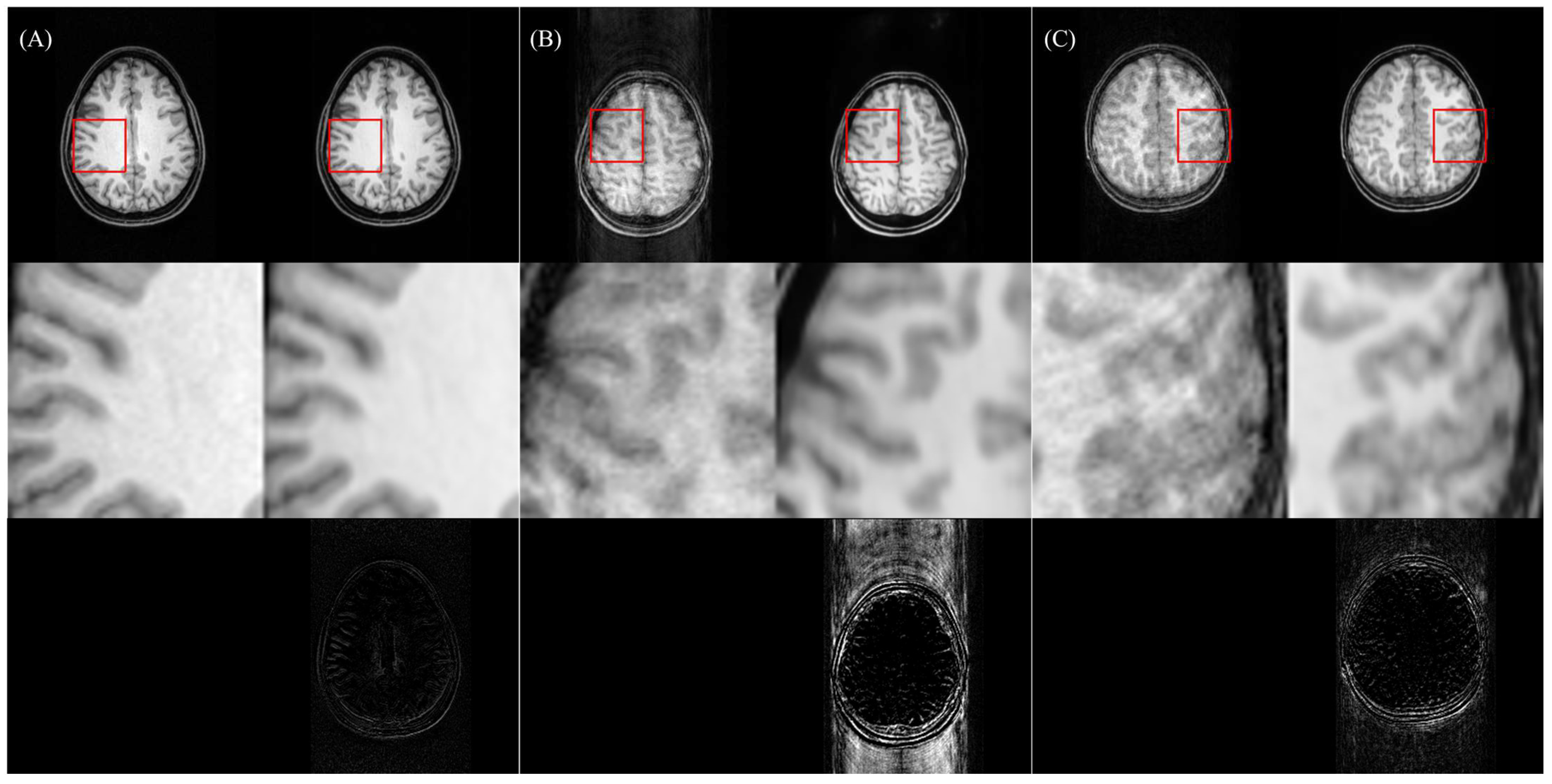
4.2. Effects on Artifact-Free Images
4.3. Visual Reading
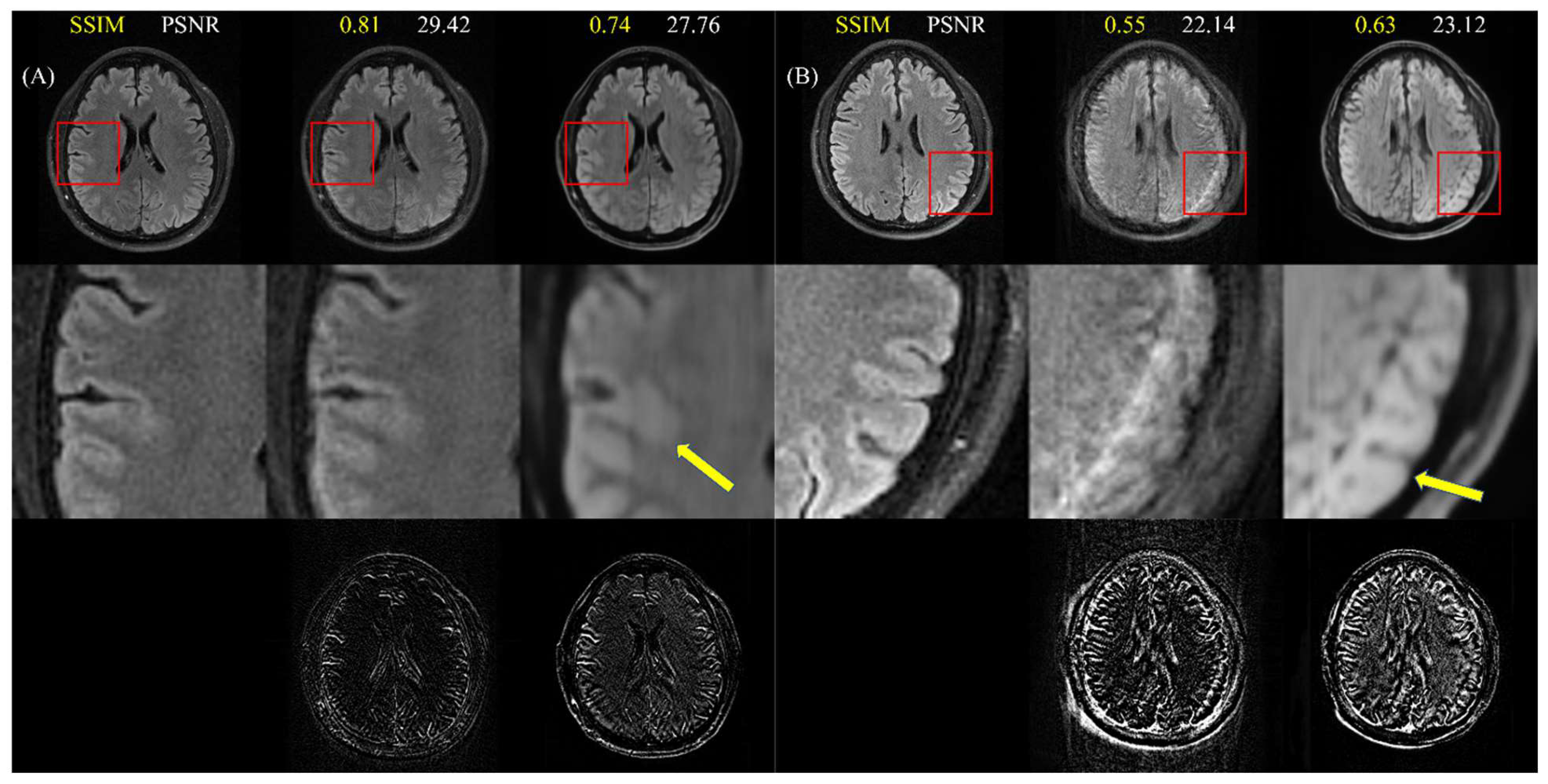
4.4. Cross-Dataset Generalization
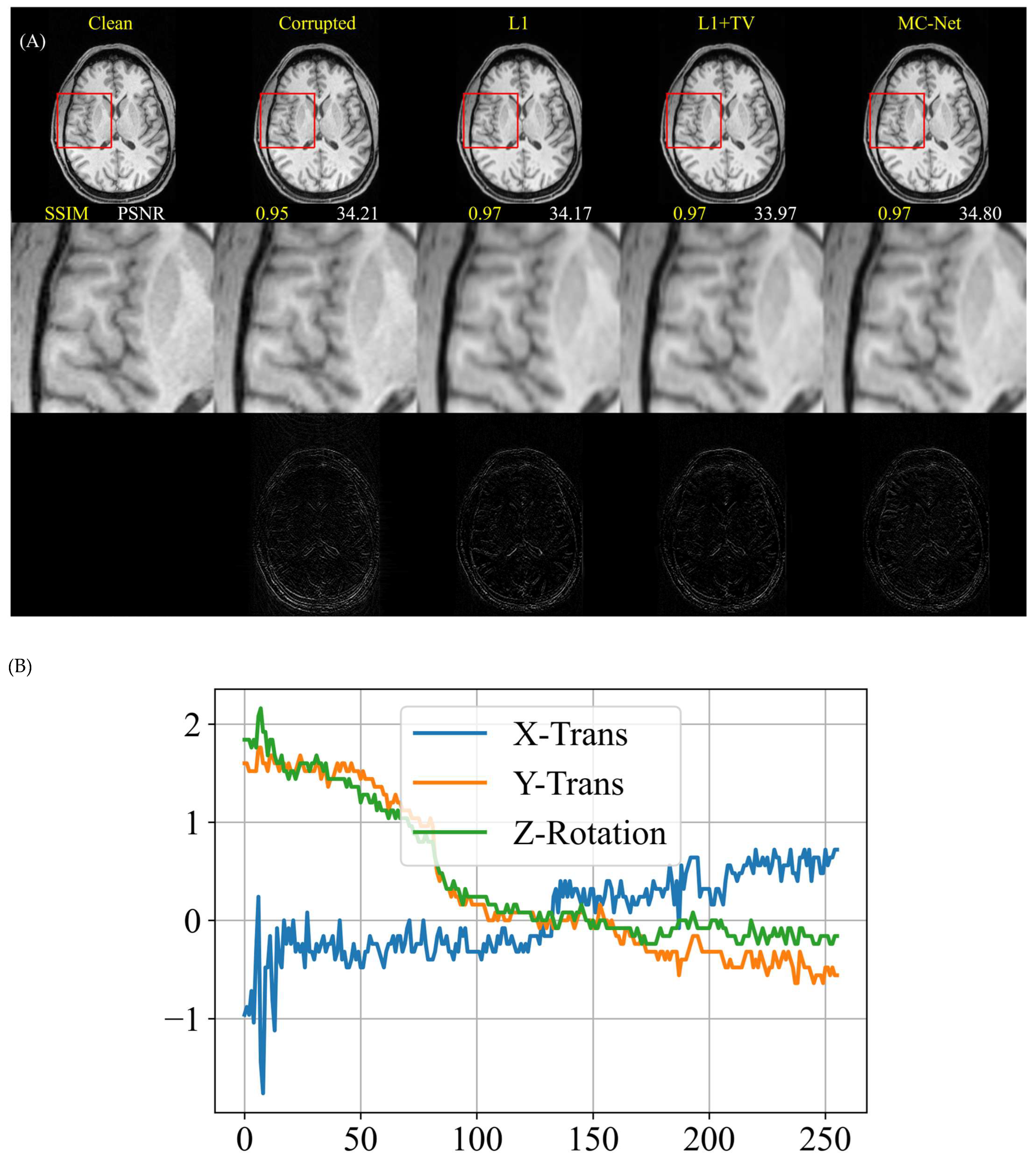
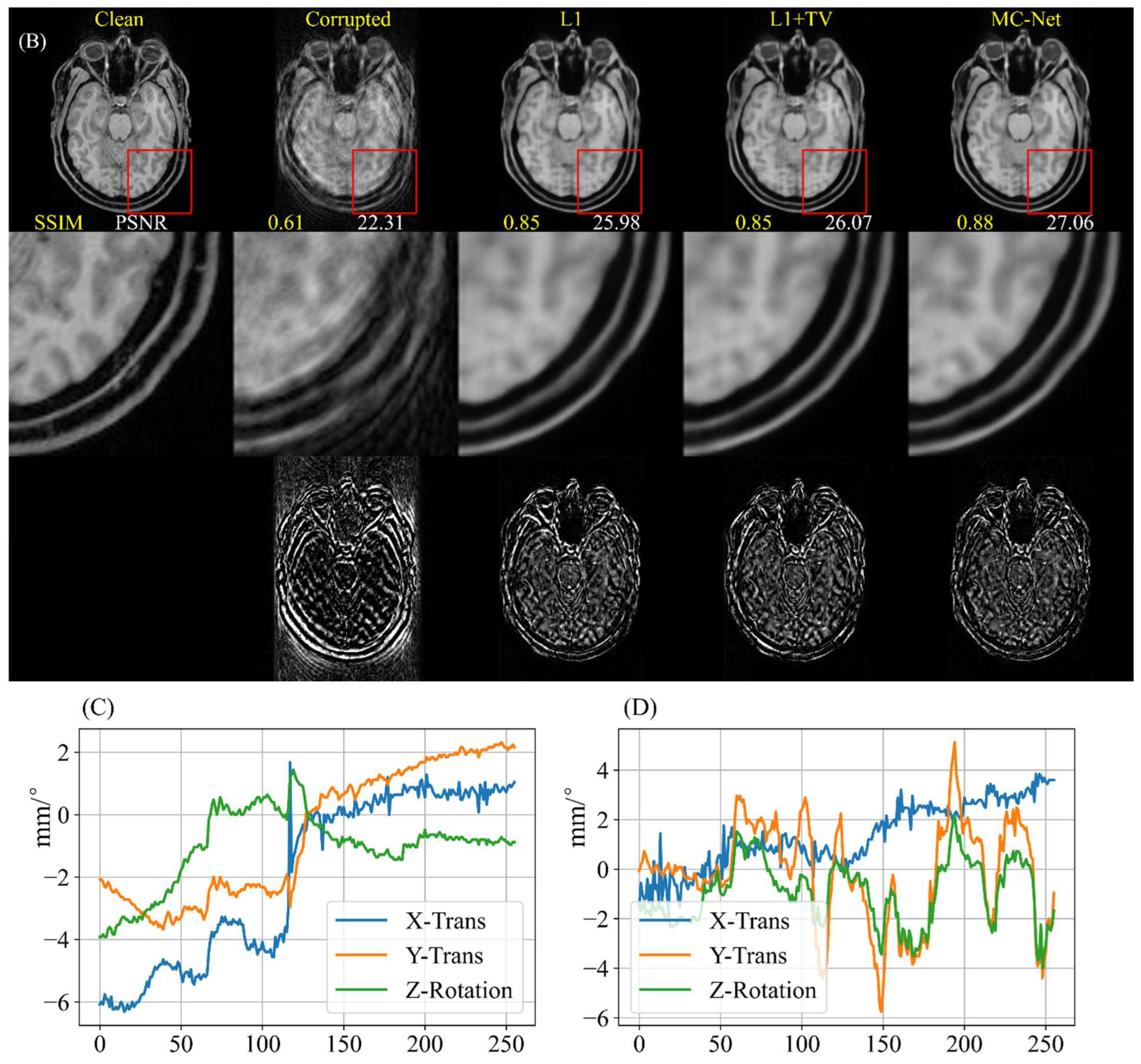
4.5. Images with Real (Non-Simulated) Motion
5. Discussion
5.1. Advantages of Two-Stage Training and Multiple-Loss Function
5.2. Comparison of Different DL Architectures
5.3. Performance on Test Set
5.4. Cross-Dataset Generalization
5.5. Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Küstner, T.; Armanious, K.; Yang, J.; Yang, B.; Schick, F.; Gatidis, S. Retrospective correction of motion-affected MR images using deep learning frameworks. Magn. Reson. Med. 2019, 82, 1527–1540. [Google Scholar] [CrossRef]
- Pawar, K.; Chen, Z.; Shah, N.J.; Egan, G.F. Suppressing motion artefacts in MRI using an Inception-ResNet network with motion simulation augmentation. NMR Biomed. 2019, 35, e4225. [Google Scholar] [CrossRef]
- Andre, J.B.; Bresnahan, B.W.; Mossa-Basha, M.; Hoff, M.N.; Smith, C.P.; Anzai, Y.; Cohen, W.A. Toward quantifying the prevalence, severity, and cost associated with patient motion during clinical MR examinations. J. Am. Coll. Radiol. 2015, 12, 689–695. [Google Scholar] [CrossRef]
- Skare, S.; Hartwig, A.; Mårtensson, M.; Avventi, E.; Engström, M. Properties of a 2D fat navigator for prospective image domain correction of nodding motion in brain MRI. Magn. Reson. Med. 2015, 73, 1110–1119. [Google Scholar] [CrossRef]
- Wallace, T.E.; Afacan, O.; Waszak, M.; Kober, T.; Warfield, S.K. Head motion measurement and correction using FID navigators. Magn. Reson. Med. 2019, 81, 258–274. [Google Scholar] [CrossRef]
- Zaitsev, M.; Maclaren, J.; Herbst, M. Motion artifacts in MRI: A complex problem with many partial solutions. J. Magn. Reson. Imaging 2015, 42, 887–901. [Google Scholar] [CrossRef]
- Maclaren, J.; Herbst, M.; Speck, O.; Zaitsev, M. Prospective motion correction in brain imaging: A review. Magn. Reson. Med. 2013, 69, 621–636. [Google Scholar] [CrossRef]
- Zahneisen, B.; Ernst, T. Homogeneous coordinates in motion correction. Magn. Reson. Med. 2016, 75, 274–279. [Google Scholar] [CrossRef]
- Usman, M.; Latif, S.; Asim, M.; Lee, B.-D.; Qadir, J. Retrospective motion correction in multishot MRI using generative adversarial network. Sci. Rep. 2020, 10, 4786. [Google Scholar] [CrossRef]
- Zhou, Z.; Shin, J.; Zhang, L.; Gurudu, S.; Gotway, M.; Liang, J. Fine-tuning convolutional neural networks for biomedical image analysis: Actively and incrementally. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7340–7351. [Google Scholar]
- Li, Y.; Yang, H.; Xie, D.; Dreizin, D.; Zhou, F.; Wang, Z. POCS-Augmented CycleGAN for MR Image Reconstruction. Appl. Sci. 2021, 12, 114. [Google Scholar] [CrossRef]
- Xie, D.; Li, Y.; Yang, H.; Bai, L.; Wang, T.; Zhou, F.; Zhang, L.; Wang, Z. Denoising arterial spin labeling perfusion MRI with deep machine learning. Magn. Reson. Imaging 2020, 68, 95–105. [Google Scholar] [CrossRef]
- Zhang, L.; Xie, D.; Li, Y.; Camargo, A.; Song, D.; Lu, T.; Jeudy, J.; Dreizin, D.; Melhem, E.R.; Wang, Z.; et al. Improving Sensitivity of Arterial Spin Labeling Perfusion MRI in Alzheimer’s Disease Using Transfer Learning of Deep Learning-Based ASL Denoising. J. Magn. Reson. Imaging 2022, 55, 1710–1722. [Google Scholar] [CrossRef]
- Zhang, L.; Mohamed, A.A.; Chai, R.; Guo, Y.; Zheng, B.; Wu, S. Automated deep learning method for whole-breast segmentation in diffusion-weighted breast MRI. J. Magn. Reson. Imaging 2020, 51, 635–643. [Google Scholar] [CrossRef]
- Zhang, L.; Arefan, D.; Guo, Y.; Wu, S. Fully automated tumor localization and segmentation in breast DCEMRI using deep learning and kinetic prior. In Proceedings of the Medical Imaging 2020: Imaging Informatics for Healthcare, Research, and Applications, Houston, TX, USA, 16–17 February 2020; Volume 11318, p. 113180Z. [Google Scholar]
- Balakrishnan, G.; Zhao, A.; Sabuncu, M.R.; Guttag, J.; Dalca, A.V. VoxelMorph: A learning framework for deformable medical image registration. IEEE Trans. Med. Imaging 2019, 38, 1788–1800. [Google Scholar] [CrossRef]
- Dalca, A.V.; Balakrishnan, G.; Guttag, J.; Sabuncu, M.R. Unsupervised learning of probabilistic diffeomorphic registration for images and surfaces. Med. Image Anal. 2019, 57, 226–236. [Google Scholar] [CrossRef]
- Johnson, P.M.; Drangova, M. Conditional generative adversarial network for 3D rigid-body motion correction in MRI. Magn. Reson. Med. 2019, 82, 901–910. [Google Scholar] [CrossRef]
- Hossbach, J.; Splitthoff, D.N.; Cauley, S.; Clifford, B.; Polak, D.; Lo, W.-C.; Meyer, H.; Maier, A. Deep learning-based motion quantification from k-space for fast model-based magnetic resonance imaging motion correction. Med. Phys. 2022, 50, 2148–2161. [Google Scholar] [CrossRef]
- Beljaards, L.; Pezzotti, N.; Rao, C.; Doneva, M.; van Osch, M.J.P.; Staring, M. AI-based motion artifact severity estimation in undersampled MRI allowing for selection of appropriate reconstruction models. Med. Phys. 2024, 51, 3555–3565. [Google Scholar] [CrossRef]
- Spieker, V.; Eichhorn, H.; Hammernik, K.; Rueckert, D.; Preibisch, C.; Karampinos, D.C.; Schnabel, J.A. Deep learning for retrospective motion correction in MRI: A comprehensive review. IEEE Trans. Med. Imaging 2023, 43, 846–859. [Google Scholar] [CrossRef]
- Zhang, L.; Luo, Z.; Chai, R.; Arefan, D.; Sumkin, J.; Wu, S. Deep-learning method for tumor segmentation in breast DCE-MRI. In Proceedings of the Medical Imaging 2019: Imaging Informatics for Healthcare, Research, and Applications, San Diego, CA, USA, 17–18 February 2019; Volume 10954, p. 109540F. [Google Scholar]
- Chollet, F. Deep Learning with Python; Manning: New York, NY, USA, 2018; Volume 361. [Google Scholar]
- Thesen, S.; Heid, O.; Mueller, E.; Schad, L.R. Prospective acquisition correction for head motion with image-based tracking for real-time fMRI. Magn. Reson. Med. 2000, 44, 457–465. [Google Scholar] [CrossRef]
- Greengard, L.; Lee, J.-Y. Accelerating the nonuniform fast Fourier transform. SIAM Rev. 2004, 46, 443–454. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Vallat, R. Pingouin: Statistics in Python. J. Open Source Softw. 2018, 3, 1026. [Google Scholar] [CrossRef]
- Shrout, P.E.; Fleiss, J.L. Intraclass correlations: Uses in assessing rater reliability. Psychol. Bull. 1979, 86, 420. [Google Scholar] [CrossRef]
- Chollet, F. Keras. GitHub. 2015. Available online: https://github.com/fchollet/keras (accessed on 11 November 2021).
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Prechelt, L. Early stopping-but when? In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 1998; pp. 55–69. [Google Scholar]
- Keskar, N.S.; Nocedal, J.; Tang, P.T.P.; Mudigere, D.; Smelyanskiy, M. On large-batch training for deep learning: Generalization gap and sharp minima. arXiv 2016, arXiv:1609.04836. [Google Scholar]
- Sommer, K.; Saalbach, A.; Brosch, T.; Hall, C.; Cross, N.M.; Andre, J.B. Correction of motion artifacts using a multiscale fully convolutional neural network. Am. J. Neuroradiol. 2020, 41, 416–423. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Yang, F.; Zhang, L.; Yu, S.; Prokhorov, D.; Mei, X.; Ling, H. Feature pyramid and hierarchical boosting network for pavement crack detection. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1525–1535. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Q.; Li, Y.; Ge, Q.; Shang, Y.; Song, D.; Wang, Z.; Shi, J. A two-stage multi-loss super-resolution network for arterial spin labeling magnetic resonance imaging. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Shenzhen, China, 13–17 October 2019; pp. 12–20. [Google Scholar]
- Wu, X.; Liu, M.; Cao, Y.; Ren, D.; Zuo, W. Unpaired learning of deep image denoising. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 352–368. [Google Scholar]
- Gatys, L.A.; Ecker, A.S.; Bethge, M. A neural algorithm of artistic style. arXiv 2015, arXiv:1508.06576. [Google Scholar] [CrossRef]
- Qiao, F.; Zhao, L.; Peng, X. Learning to learn single domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 12556–12565. [Google Scholar]
- Shamshad, F.; Khan, S.; Zamir, S.W.; Khan, M.H.; Hayat, M.; Khan, F.S.; Fu, H. Transformers in medical imaging: A survey. Med. Image Anal. 2023, 88, 102802. [Google Scholar] [CrossRef]
| Model | Corrupted | L1 | L1 + TV | Two-Stage | |
|---|---|---|---|---|---|
| SSIM | U | 0.773 ± 0.099 | 0.908 ± 0.036 | 0.910 ± 0.036 | 0.919 ± 0.033 |
| PSNR | U | 26.346 ± 3.315 | 29.005 ± 2.736 | 29.077 ± 2.713 | 29.717 ± 2.736 |
| SSIM | U + O | 0.773 ± 0.099 | 0.811 ± 0.078 | 0.811 ± 0.078 | 0.816 ± 0.077 |
| PSNR | U + O | 26.346 ± 3.315 | 26.938 ± 3.224 | 26.844 ± 3.216 | 27.056 ± 3.276 |
| Model | Clean Image | L1 | L1 + TV | Two-Stage | |
|---|---|---|---|---|---|
| SSIM | U | 1 | 0.959 ± 0.011 | 0.961 ± 0.009 | 0.967 ± 0.008 |
| PSNR | U | Inf | 36.697 ± 1.216 | 36.445 ± 1.080 | 37.403 ± 1.168 |
| SSIM | U + O | 1 | 0.999 ± 0.000 | 0.999 ± 0.001 | 0.999 ± 0.001 |
| PSNR | U + O | Inf | 47.004 ± 2.015 | 47.637 ± 2.713 | 45.490 ± 1.833 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Wang, X.; Rawson, M.; Balan, R.; Herskovits, E.H.; Melhem, E.R.; Chang, L.; Wang, Z.; Ernst, T. Motion Correction for Brain MRI Using Deep Learning and a Novel Hybrid Loss Function. Algorithms 2024, 17, 215. https://doi.org/10.3390/a17050215
Zhang L, Wang X, Rawson M, Balan R, Herskovits EH, Melhem ER, Chang L, Wang Z, Ernst T. Motion Correction for Brain MRI Using Deep Learning and a Novel Hybrid Loss Function. Algorithms. 2024; 17(5):215. https://doi.org/10.3390/a17050215
Chicago/Turabian StyleZhang, Lei, Xiaoke Wang, Michael Rawson, Radu Balan, Edward H. Herskovits, Elias R. Melhem, Linda Chang, Ze Wang, and Thomas Ernst. 2024. "Motion Correction for Brain MRI Using Deep Learning and a Novel Hybrid Loss Function" Algorithms 17, no. 5: 215. https://doi.org/10.3390/a17050215
APA StyleZhang, L., Wang, X., Rawson, M., Balan, R., Herskovits, E. H., Melhem, E. R., Chang, L., Wang, Z., & Ernst, T. (2024). Motion Correction for Brain MRI Using Deep Learning and a Novel Hybrid Loss Function. Algorithms, 17(5), 215. https://doi.org/10.3390/a17050215








