Research on a Fast Image-Matching Algorithm Based on Nonlinear Filtering

Abstract

Computer vision technology is being applied at an unprecedented speed in various fields such as 3D scene reconstruction, object detection and recognition, video content tracking, pose estimation, and motion estimation. To address the issues of low accuracy and high time complexity in traditional image feature point matching, a fast image-matching algorithm based on nonlinear filtering is proposed. By applying nonlinear diffusion filtering to scene images, details and edge information can be effectively extracted. The feature descriptors of the feature points are transformed into binary form, occupying less storage space and thus reducing matching time. The adaptive RANSAC algorithm is utilized to eliminate mismatched feature points, thereby improving matching accuracy. Our experimental results on the Mikolajcyzk image dataset comparing the SIFT algorithm with SURF-, BRISK-, and ORB-improved algorithms based on the SIFT algorithm conclude that the fast image-matching algorithm based on nonlinear filtering reduces matching time by three-quarters, with an overall average accuracy of over 7% higher than other algorithms. These experiments demonstrate that the fast image-matching algorithm based on nonlinear filtering has better robustness and real-time performance.

1. Introduction

With the widespread application of artificial intelligence technology, the influence of computer vision in the industrial field is increasing, and image matching based on vision theory has become a research hotspot in the field of computer vision. Image matching is of great value and significance in applications such as 3D scene reconstruction, target detection and recognition, video content tracking, pose estimation, motion estimation, and image recovery [1].

The key to image matching is feature band point extraction and description, in which the SIFT (Scale-invariant Feature Transform) algorithm was proposed by David [2] in 2004. Although the SIFT algorithm performs well in many applications, it also has some drawbacks. First, the computational complexity of the SIFT algorithm is high, especially when matching in large-scale image databases. Secondly, the feature vectors generated by the SIFT algorithm have high dimensionality and require a large amount of storage space. In addition, the SIFT algorithm is less stable to image transformations and more sensitive to occlusions and noise. Finally, the selection of key parameters in the SIFT algorithm is difficult and requires experience and trial and error to determine the appropriate values. Mikolajczyk et al. [3] adopted the GLOH (Gradient Location and Orientation Histogram) descriptor and used polar coordinates for feature descriptor construction, which has more accurate orientation estimation, more stable descriptor generation, and shorter descriptor lengths relative to the SIFT algorithm, and under the condition of reduced computation, the computation remains large and sensitive to noise and occlusion.

For the problem of the poor real-time performance of image-matching algorithms, Rublee E et al. proposed the ORB algorithm [4], a feature extraction algorithm based on FAST corner point detection and a BRIEF binary descriptor, which has a great improvement in speed, but performs poorly in dealing with images with high texture repetitions or lowtexture regions, and the short length of the descriptor may lead to an increase in matching errors. Yucheng Hu, Rui Ting et al. [5] proposed reducing the number of layers of a Gaussian pyramid and improving the SIFT operator to improve the time efficiency of feature point detection; Zhengshou Feng and Mei-Qing Wang [6] proposed extracting the corner points in an image by using the Harris corner-detection algorithm and describing these feature points using concentric circle descriptors, which reduces the total time needed for feature extraction and feature matching, but thenumber of feature points extracted is reduced; Weimin Li et al. [7] proposed a corner point indicatorthat improves upon Harris and can obtain a large number of feature points, but in terms of the descriptor and matching method, it is the same as the traditional SIFT matching algorithm, which will consume a lot of resources and time.

In order to improve the matching correctness of the image-matching algorithm, S Leutenegger et al. [8] proposed the BRISK algorithm, which uses a binary descriptor, significantly reduces computational complexity, and improvesmatching correctness, but its performance is not excellent in some extreme lighting changes, under high texture repetition, or in low-texture regions. Sheng Zhang and Wei Zhu [9] proposed a SIFT matching algorithm combined with RANSAC; this method uses the SIFT algorithm to extract and match the feature points of an image sequence, and then uses the RANSAC algorithm to eliminate the mismatched points, which improves the matching correctness rate to a certain extent, but there is also the problem of high resource occupancy in the process of descriptor generation. J. S. Sujin et al. improved image quality by adjusting the contrast thresholding and scaling the image, which they achieved by adjusting the size and contrast thresholding factors to produce a sufficient number of keypoints and enhance the correctness of the feature point matching, even in smooth, low-contrast, or small regions [10].

From the aspect of image feature-matching time and correctness rate, the above improved algorithms only improve upon one aspect, and cannot achieve a balance between correct matching rate and matching speed. In this paper, to address the above problems, a fast image-matching-improvement algorithm based on nonlinear diffusion is proposed to reduce image-matching time and improve the matching accuracy problem: first, the image is preprocessed with nonlinear diffusion filtering, which makes the scale space retain more feature information, and the scale space is constructed with the maximum downsampling value to reduce the computational cost while improving the accuracy of the selection of key points; second, the use of BRIEF feature descriptors [11] can greatly improve the computational efficiency and reduce the storage space; finally, we use the adaptive RANSAC algorithm to eliminate false matching points, to improve the accuracy of the algorithm proposed in this paper.

2. Theoretical Analysis

2.1. Nonlinear Diffusion Filtering

When constructing the scale space, the traditional construction method used is Gaussian filtering to smooth the image, which loses edge information. Nonlinear diffusion filtering [12] provides a superior solution, and is implemented by using the scale parameters of the image as thermal diffusion function scattering factors. This filtering method is generally solved by partial differential equations, while the differential equations are nonlinear in nature. Its scale space consists of multiple groups, and in each group, it contains several layers of the same size, which are obtained by nonlinear diffusion, layer by layer, and the next group is obtained by downsampling. Its mathematical expression is given below:

$$\frac{\partial L}{\partial t}=div(c(x,y,t),\nabla L)$$

(1)

where $L$ is the image luminance matrix, $div$ represents the dispersion function, and $\nabla$ represents the image gradient operator. The conduction function $c$ is carried over to the local structural properties for diffusion, where the conduction function is

$$c(x,y,t)=g(|\nabla L_{\sigma }(x,y,t)|)$$

(2)

Usually, the function $g$ is taken as the following equation:

$$g=\frac{1}{1+\frac{|\nabla L_{\sigma }{|}^2}{{\lambda }^2}}$$

(3)

Δ in Equation (2) is the gradient image of the image $L$ after Gaussian filtering, and the parameter $\lambda$ in Equation (3) is the range over which the contrast factor determines the spread of the function, and L is taken to be the value corresponding to 70% of the histogram in the literature [12].

In response to the issues caused by Gaussian filtering, including the blurring of image details and edges, reduced accuracy in feature point detection, and increased algorithm complexity and computational time when handling multi-scale pyramids, the use of nonlinear diffusion filtering offers the following advantages: firstly, it can remove noise more effectively without losing the target boundary and key detail information; secondly, it retains the edge information of the image, making it superior to Gaussian filtering in avoiding blurring and loss of information; and thirdly, it is able to reduce the scale while maintaining image clarity, quantize the featuresmore effectively, and improve the accuracy of the algorithm as well as increase the efficiency.

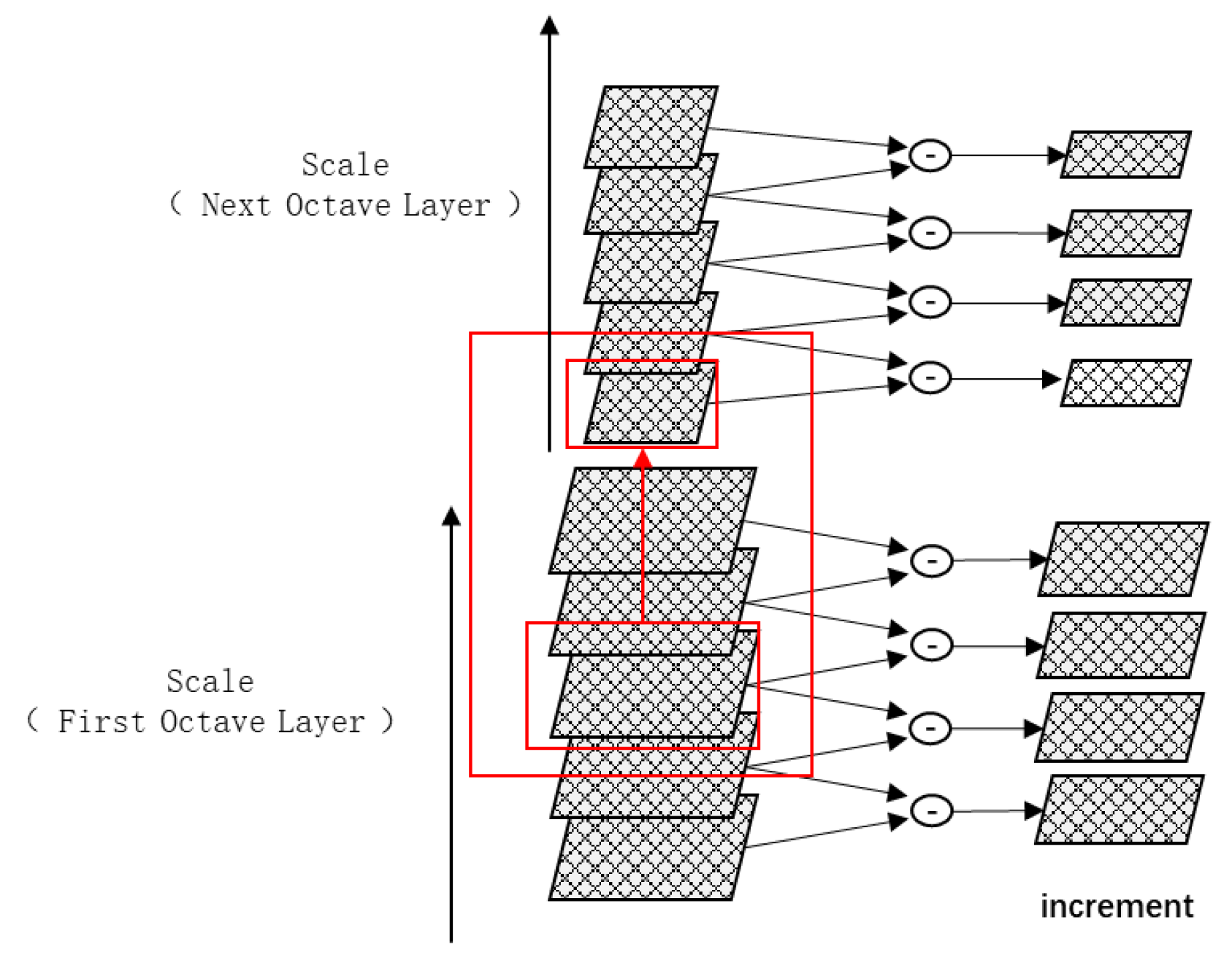
2.2. Downsampling

In the traditional SIFT matching algorithm, the author David Lowe uses averaging to downsample the image 2 to construct the scale space, which results in the loss of some of the feature information of the image and also suppresses the high-frequency information of the image. The average downsampling method may lead to distortion of the edges of the image. By changing the average sampling to maximum downsampling, the computation can be performed quickly with limited computational resources, and the important features of the image can be preserved by using maximum downsampling, as shown in Figure 1:

2.3. BRIEF Descriptor

Feature point descriptors are widely used in tasks such as target detection, image matching, image classification, object recognition, image retrieval, etc. Most of the applications run on limited resources, and to address the needs of fast computation, fast matching, and efficient storage, Michael Calonder, V Lepetit [13] and others proposed the BRIEF descriptor, which provides binary descriptions of feature points. The BRIEF algorithm, in comparison, has the advantages of fast computation speed, adjustable descriptor length, high robustness, and small storage space, especially in processing large-scale image data and real-time applications. Define the criterion $\tau$ for an image block $p$ of size $\mathrm{S}\times \mathrm{S}$ for

$$\tau (p;x,y)=\left\{\begin{array}{ll}1\hfill & p(x)\le p(y)\hfill \\ 0\hfill & \mathrm{others}\hfill \end{array}\right.$$

(4)

where $p(x)$ is the pixel grey value of the smoothed image block $p$ at $x={(u,v)}^T$ and $(x,y)$ is the pixel position information, and

$$f_{n_d}(p)={\displaystyle \sum _{1\le i\le n_d}{2}^{i-1}}\tau (p;x_i,y_i){)}_c$$

(5)

where $f_{n_d}(p)$ is the generated binary descriptor set, $n_d$ can be 128, 256, 512, etc., considering the speed and robustness, and $n_d=256$ in this paper.

2.4. Adaptive RANSAC Algorithm

The block diagram of the classical RANSAC algorithm consists of three stages: (1) the sampling modeling stage, where random samples are drawn to generate the model to be tested; (2) the model validation stage, where all the samples of the sample set are substituted into the model test one by one and the number of internal points is counted according to the error threshold w of the internal point determination; (3) and deriving the optimal model stage, where the number of internal points is compared with the model obtained from each iteration after M iterations and the model with the highest number of internal points is selected as the optimal mapping model for the two sample sets, wherein the determination method is as follows: for a model to be tested, the data sample points that satisfy the model within the error range are the internal points [14].

The adaptive RANSAC algorithm utilized in this paper can dynamically adjust thresholds during the model fitting process. Figure 2 illustrates the process of eliminating mismatched points in the fastimage-matching algorithm based on nonlinear filtering. The computational process is as follows [15]:

$$\left(\begin{array}{l}{x}_1\hfill \\ y_1\hfill \\ 1\hfill \end{array}\right)=\left(\begin{array}{lll}{a}_0\hfill & b_0\hfill & \Delta x\hfill \\ a_1\hfill & b_1\hfill & \Delta y\hfill \\ 0\hfill & 0\hfill & 1\hfill \end{array}\right)\left(\begin{array}{l}x\hfill \\ y\hfill \\ 1\hfill \end{array}\right)$$

(6)

where $(x,y)$ represents the coordinates of the original feature point corresponding to $(x_1,y_1)$, which representsthe target image feature point coordinates, where $a_0$, $a_1$, $b_0$ and $b_1$ correspond to the parameters of image scaling and image rotation, respectively, and $\Delta x$ and $\Delta y$ are the horizontal and vertical offsets of the image. Equation (6) can be calculated to conclude that the relationship between the original image and the matched image has six parameters, so it takes three feature points to be matched to obtain a unique solution. Therefore, this paper adopts the extraction of 3 feature point pairs for random sampling modelinand to ensure matching correctness, this paper sets the threshold of inner point determination to 1.

The RANSAC algorithm is used to randomly select three sets of data among all the data to estimate the mapping relationship between the datasets, with confidence probability $P$. To make sure that there are three sets of random samples in which all the matched pairs of points are endpoints, the number of sampling times M and the rate of endpoints $e$ need to satisfy the following conditions [16]:

$${(1-e^3)}^M=1-P$$

(7)

The main implementation process of pre-verification is to first randomly select three sets of samples from the entire set of samples $M$. If all three sets of sample data are inliers of the experimental model, then the remaining samples are tested in full. If the three sets do not meet the conditions, another three sets of samples are randomly selected from the entire set of sample data for retesting.

The key to the pre-test [17] lies in choosing the appropriate pre-test samples. The evaluation index in this paper uses the Euclidean distance for the experiment, by obtaining the value of the Euclidean distance for the ascending order of the ranking; the higher the ranking in the front, the better the matching effect. The 100 pairs of feature point groups with the results ranked in the front are used as the starting samples for the pre-test part. Since different images contain different content and features, if the c value is a definite value, it will lead to a decrease in the correctness of the matching; in this paper, to solve this problem, we use the adaptation and inspection process, as shown in Figure 2.

In the first step, three groups of feature band point pairs are randomly selected from all the feature band point pairs, which are subjected to linear validation and region comparison validation [18], and the affine transformation operator $n_1$ is established for the selected feature point pairs.

In the second step, updating of the $c$ value is carried out; if $n_1$ is greater than the $c$ value, the value of $n_1$ will be changed to $c$, and at the same time, the remaining feature band points will be verified, and vice versa The three groups of feature point pairs will be re-selected. Updating the $c$ value through this process can effectively improve the robustness of the algorithm.

For the model $H_0$, after passing the pre-test, all the remaining feature points will be detected, and the logarithmic number of filtered feature points $n_2$ will also be derived; then, the sum of $n_1$ and $n_2$ will be the number of points within the feature points of the algorithm $N_{found}$. If $N_{best}$ is less than $N_{found}$, then $N_{found}$ will be assigned to $N_{best}$ and the value of $M$ will be updated based on Equation (7), where $\epsilon$ is

$$\epsilon =\frac{N_{best}}{N}$$

(8)

where $N$ is the total number of feature points; conversely, we return to re-random sampling. The loop is ended when the affine transform operator $c$ is greater than $M$, and the optimal model $H$ is obtained.

The RANSAC algorithm needs to manually set the sampling times, thresholds, etc., and the settings of these parameters have a great impact on the effectiveness of the algorithm In this paper, by introducing adaptive updating of the logarithm of the feature points $c$ and the number of interior points $N_{best}$, this algorithm can improve the model’s robustness and adaptability to different images.

3. Experimental Results and Analysis

In this paper, the Bark, Bikes, Leuven, Boat, and Graf image sets from the Mikolajcyzk image dataset are used to test the robustness and real-time performance of the fast image-matching algorithm based on the nonlinear filtering method proposed in this paper, and at the same time, we conduct comparative experiments with the SIFT, SURF, BRISK, and ORB algorithms [19]. The test environment is Intel(R) Core(TM) i5-7200U [email protected] Windows 10 operating system, and the experimental compilation environment is Pycharm 2020 with python programming.

3.1. Image Information Comparison and Evaluation

The processes of constructing scale spaces varies between different algorithms, which include building an image pyramid and employing specific downsampling techniques. SIFT and SURF utilize Gaussian blurring and the GaussianLaplace filter for pyramid construction, respectively, and both apply average downsampling. In contrast, BRISK and ORB deviate from traditional Gaussian pyramids by creating scale spaces through direct downsampling, where each layer of the image is formed by simply removing pixels. This section describes the comparative experiments conducted to analyze the methods of Gaussian blurring + average downsampling and nonlinear diffusion filtering + maximum downsampling.

The above figure shows the boat image boat-1 in the Mikolajcyzk image dataset. Figure 3a adopts the Gaussian filter function + average downsampling method; it can be seen that the blurring effect cannot be controlled, and the edges and textures are not well processed, which will cause greater interference in later feature point extraction. Figure 3b adopts the Gaussian filter function + maximum downsampling method, and it can be seen that the edges and texture are improved compared with the image contour in Figure 3a, but the blurring effect of the overall image cannot be controlled, and the edges and texture are not well processed, which will cause a greater interference in the feature point extraction in the later stage. Figure 3c adopts the Gaussian filter function + average downsampling method, and it can be seen that the blurring effect cannot be controlled, and the edges and texture are not well processed, which will cause a greater interference. Figure 3b adopts the Gaussian filter function + maximum downsampling, from which it can be seen that the edges and textures are improved compared with the image contour in Figure 3a, but the overall image is still blurred. Figure 3c adopts nonlinear diffusion filtering + average downsampling, from which it can be seen that the edges and textures of the image contour are still blurred, but the clarity has been improved compared with that of the image contour in Figure 3a. The clarity of the image contour is improved compared to that in Figure 3a. Figure 3d uses nonlinear diffusion filtering + maximal downsampling, which retains more image details and texture information compared to Gaussian filtering, which retains the image information more effectively. It can be seen that the combination of nonlinear diffusion filtering and maximum downsampling has the best effect.

3.2. Robustness Evaluation

Image-processing algorithms maintain their ability to accurately and reliably identify similarities between corresponding points, regions, or features in different images, achieving effective matching capabilities even when confronted with various complex environmental conditions, image rotations, deformations, changes in illumination, viewpoint variations, and scale changes, among other factors. The robustness of such algorithms is assessed by performing feature point matching across diverse scenarios, thereby gauging their resilience under a range of challenging circumstances.

The following formula is used to calculate the correctness of the five algorithms to match the correctness rateand judge the robustness of the algorithm [20]:

$$P=N_b/N_c$$

(9)

where the matching correctness is $P$, $N_b$ is the correct match remaining after eliminating the incorrect matches, and the total number of coarse matches is $N_{\mathrm{c}}$.

The Mikolajcyzk dataset is used in our experiments, and this experiment uses the Bark, Bikes, Leuven, Boat, and Graf image sets in this dataset, which contain factors such as image rotation, distortion, illumination change, perspective change, scale change, etc., and each image set contains six images. Each algorithm uses the first image in each set as a sample image and uses the remaining five images as the images to be matched for the matching test. The following table shows the average correctness of the different algorithms on the Mikolajcyzk image dataset, as well as the total average correctness.

Through an analysis of the data in

Table 1. Average matching correctness of test image sets.

Methodologies	Bark	Bikes	Leuven	Boat	Graf	Average
SIFT	78.90	86.03	86.26	76.00	83.80	82.20
SURF	70.72	85.72	85.34	67.30	67.03	75.22
BRISK	78.91	86.05	91.92	76.63	81.57	83.02
ORB	46.67	94.64	86.68	60.52	53.31	68.36
Our	91.83	96.21	93.28	81.22	92.90	91.09

, it can be concluded that the proposed fast image-matching algorithm based on nonlinear filtering exhibits excellent overall performance on this dataset. The total average correctness rate of the fastimage-matching algorithm based on nonlinear filtering is higher than that of other algorithms. In the Bark dataset with clearly visible texture features, the average correctness rate of matches is 12.86% higher than that of the SIFT algorithm. In the Bikes and Leuven datasets with lighting changes, the fast image-matching algorithm based on nonlinear filtering achieves an average correctness rate 10.18% higher than that of the SIFT algorithm. In the grayscale and rotation-changed Boat dataset, the fast image-matching algorithm based on nonlinear filtering outperforms the SIFT algorithm, with an average correctness rate that is 5.22% higher. In the Graf dataset with changes in viewpoint, the fast image-matching algorithm based on nonlinear filtering achieves an average correctness rate 8.89% higher than that of the SIFT algorithm. Additionally, the improved algorithm also surpasses the other three algorithms in scenarios involving texture features, lighting changes, grayscale transformation, rotation, and changes in viewpoint.

In this paper, we take the Graf image set as an example to show the matching effect of the traditional SIFT matching algorithm and the fast image-matching algorithm based on nonlinear filtering, as shown in Figure 4.

Figure 4 shows the feature point-matching test in the Graf images, with green indicating correct matches and red indicating incorrect matches. Figure 4a presents the results of the SIFT feature-matching algorithm and RANSAC algorithm, while Figure 4b shows the results of the fast image-matching algorithm based on nonlinear filtering. In this algorithm, an adaptive RANSAC algorithm is employed. From Figure 4a, it can be observed that there are numerous cross mismatches in the SIFT algorithm, indicating incorrect matches. Compared to SIFT, the adaptive RANSAC algorithm in the fast image-matching algorithm based on nonlinear filtering effectively reduces incorrect matches, thereby enhancing accuracy.

Figure 5a depicts the Bark image dataset from the Mikolajczyk image library, designed to assess the robustness of algorithms to tree bark texture under various rotation conditions. This dataset features diverse textures covering the bark characteristics of trees, aiming to simulate real-world challenges for evaluating algorithm performance in practical scenarios. From Figure 5a, it can be observed that the improved algorithm proposed in this paper performs significantly better under image rotation conditions compared to the BRISK, ORB, SIFT, and SURF algorithms. In comparison to the SIFT algorithm, the improved algorithm in this paper achieves an average correctness rate that is 12.28% higher.

Figure 5b,c depict scenes of lighting changes and image blurring in the Bikes and Leuven datasets, respectively. From Figure 5b, it is evident in the Bikes dataset that the fast image-matching algorithm based on nonlinear filtering consistently outperforms the other algorithms in terms of the correctness rate for each match. In Figure 5c, within the Leuven dataset, the correctness rates for the first three sets of image matches are higher than those of the other four algorithms, and although there are fluctuations when matching with images 1–5, the correctness rate is comparable to that of the other four algorithms. Overall, the fast image-matching algorithm based on nonlinear filtering performs better than other algorithms in scenarios involving lighting changes and image blurring.

Figure 5d displays the Boat grayscale rotation dataset. The experimental results indicate that each algorithm processes the images in grayscale and performs feature matching under different rotation angles and focal lengths. From the correctness rates of the first three sets of image matches, it can be observed that all five algorithms exhibit a decreasing trend. However, the improved algorithm proposed in this paper consistently maintains a higher correctness rate compared to the other four algorithms. When matching features with images 1–5, there is a noticeable decrease in correctness rate for the fast mage-matching algorithm based on nonlinear filtering, yet it still outperforms the ORB algorithm, maintaining a 5.23% higher average correctness rate compared to the SIFT algorithm.

Figure 5e presents the correctness rate of matches in the Graf image dataset from the Mikolajczyk image library. This dataset is primarily used to test and evaluate the robustness of image feature point-matching algorithms in the face of varying viewpoints and angle changes. It aims to accurately measure and compare the stability and adaptability of different image feature-matching algorithms from multiple perspectives and dimensions to maintain high-precision matches. The experimental results indicate that when facing different viewpoints and angle changes, the overall correctness rate on each image dataset is higher than that of the ORB, SURF, and BRISK algorithms. Furthermore, the correctness rate is more than 9.1% higher than that of the SIFT algorithm.

The implementation of a fast image-matching algorithm based on nonlinear diffusion filtering for scale-space construction, coupled with maximum downsampling, has shown significant performance enhancements across the following five key datasets: Bark, Bikes, Leuven, Boat, and Graf. This improved algorithm employs nonlinear diffusion filters to accentuate feature edges, effectively highlighting and preserving valuable image details across various scales while minimizing information loss through maximum downsampling. The result is efficient feature matching in scenes with rich textures, such as tree bark in the Bark dataset, as well as in scenarios with rotational changes, such as the Boat dataset. Moreover, it provides robust performance even with significant lighting variations, as seen in the Bikes and Leuven datasets, and substantial viewpoint differences, as in the Graf dataset. This advancement showcases the applicability and efficiency of the fast image-matching algorithm based on nonlinear filtering across a diverse range of real-world application settings.

3.3. Real-Time Evaluation

In this section, four algorithms, SIFT, SURF, BRISK, and ORB, are compared; 1000 feature points are extracted in two images; and the results of 30 tests are averaged to arrive at a final performance evaluation. The test results are displayed in Figure 6, where the horizontal coordinates indicate the feature point detection time (FPDT), descriptor construction time (DT), descriptormatching time (DMT), and total operation time (OMT) of the algorithms, respectively. The vertical coordinate shows the time consumption of the nonlinear diffusion filtering-based algorithm with the other four algorithms at each stage, which visually compares the efficiency of different algorithms at each processing stage.

The experimental results reveal that overall, the ORB and the fast image-matching algorithm based on nonlinear filtering presented in this paper are distinguished by their time efficiency in all aspects, surpassing the speed of the other three algorithms. The fast image-matching algorithm employing nonlinear filtering proposed in this article closely matches the ORB algorithm in terms of time consumption for various tasks. Furthermore, the average time consumption of each task is four–five times lower than that of the traditional SIFT algorithm. The total operation time (OMT) is more than six times faster than that of the SIFT algorithm, marginally quicker than the rest of the algorithms.

4. Conclusions

In the practical applications of computer vision, feature detection and matching play crucial roles in various scenarios. This paper addresses the issue of inaccurate feature point extraction in areas with indistinct textures when constructing scale spaces using Gaussian filtering. To better preserve image edge details, nonlinear diffusion filtering combined with maximum downsampling is utilized. Given the considerable storage requirements for each key point’s scale, orientation, and feature descriptor, this paper introduces the BRIEF descriptor. This helps reduce storage needs and increase matching speed. Additionally, the robustness and accuracy of the fast image-matching algorithm, based on nonlinear filtering, are enhanced by adopting the adaptive RANSAC algorithm. The experimental results demonstrate that the fast image-matching algorithm based on nonlinear filtering achieves a matching correctness rate of over 81% on the Mikolajcyzk test dataset, which is more than 7% higher than the other algorithms. In terms of real-time performance, this algorithm matches the speed of ORB and is significantly faster than the other methods. In conclusion, the fast image-matching algorithm based on nonlinear filtering shows outstanding performance in both speed and accuracy.