An Iris Image Super-Resolution Model Based on Swin Transformer and Generative Adversarial Network
Abstract
1. Introduction
1.1. Research Questions
1.2. Contributions and Paper Outline
- (1)
- The paper introduces a unique model by combining residual Swin Transformer blocks with sub-pixel convolutional progressive upsampling. The model effectively addresses the relationship between global information in images while minimizing information loss during the reconstruction process.
- (2)
- The method incorporates adversarial learning into the model to provide more effective constraints on texture recovery. This addition enables the generated images to exhibit higher-frequency details, resulting in more realistic and visually appealing results.
- (3)
- A combination of multiple loss functions was employed, including perceptual loss, adversarial loss and the loss function utilizing the norm. This integrated loss function design aids in balancing the quality, structure, and visual perceptual aspects of the generated images during training. By merging multiple loss functions, this paper presents an effective training approach that enhances the precision and realism of generated images.
2. Related Work
3. Method
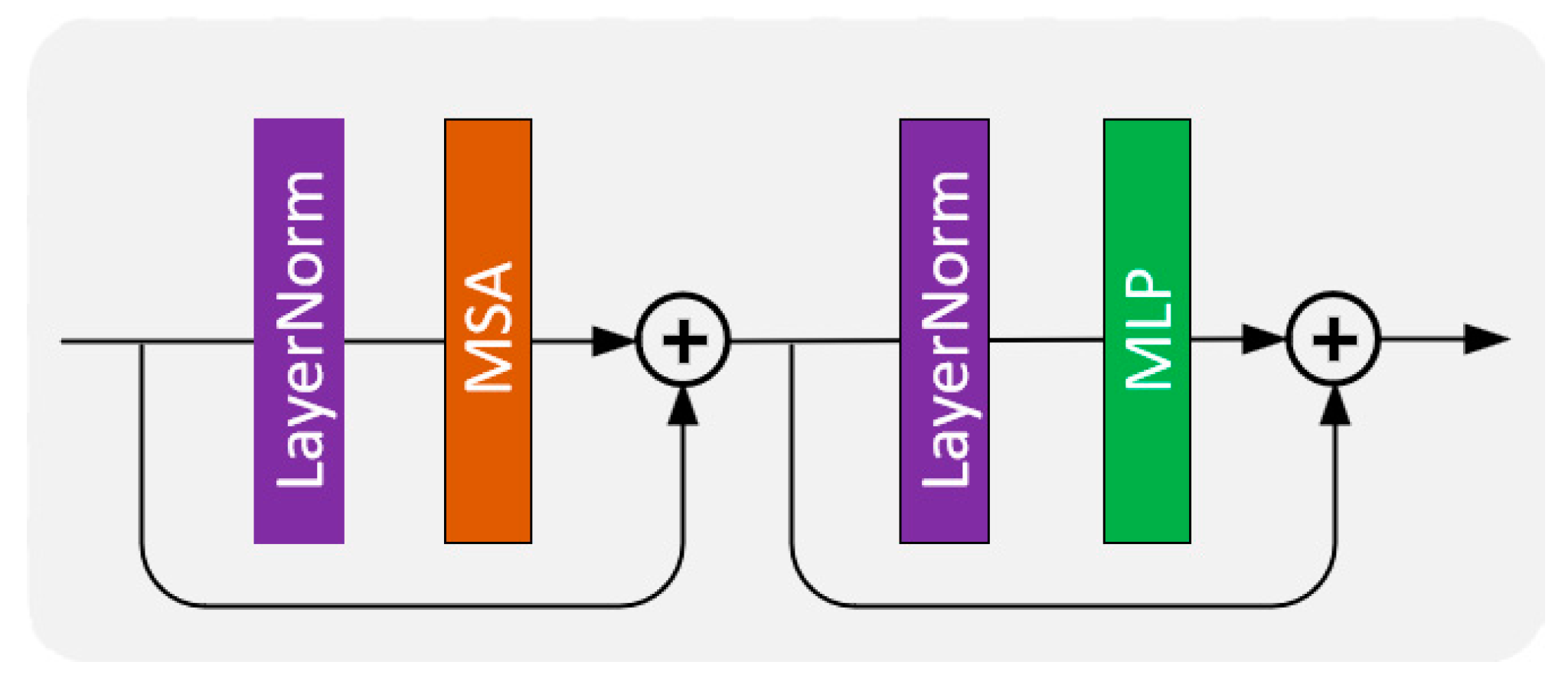
3.1. Model Architecture
3.2. Adversarial Architecture
3.3. Loss Function
4. Experiments and Results
4.1. Datasets
4.2. Implementation Details
4.2.1. Data Preparation
- (1)
- Use the open-source OSIRIS [20] to acquire the circle parameters of the original iris images.
- (2)
- Generate high-resolution images (HR images, 224 × 224): use the bicubic interpolation method to resize the iris images to a radius of 105 pixels and subsequently crop images into a resolution of 224 × 224 centered around the center of the pupil.
- (3)
- Generate low-resolution images (LR images, 56 × 56): low-resolution images with a resolution of 56 × 56 pixels are generated by bicubic interpolation downsampling of HR images with a resolution of 224 × 224.
- (4)
- Save all images as 24-bit color, bmp format.
4.2.2. Parameters
4.2.3. Metrics
4.3. Results
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Parker, J.A.; Kenyon, R.V.; Troxel, D.E. Comparison of interpolating methods for image resampling. IEEE Trans. Med. Imaging 1983, 2, 31–39. [Google Scholar] [CrossRef] [PubMed]
- Blu, T.; Thévenaz, P.; Unser, M. Linear interpolation revitalised. IEEE Trans. Image Process. 2004, 13, 710–719. [Google Scholar] [CrossRef] [PubMed]
- Keys, R. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 184–199. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision 2021, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Van Gool, L.; Timofte, R. Swinir: Image restoration using swin transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision 2021, Montreal, BC, Canada, 11–17 October 2021; pp. 1833–1844. [Google Scholar]
- Chen, X.; Wang, X.; Zhou, J.; Qiao, Y.; Dong, C. Activating more pixels in image super-resolution transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2023, Vancouver, BC, Canada, 17–24 June 2023; pp. 22367–22377. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2016, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- Wang, Y.; Perazzi, F.; McWilliams, B.; Sorkine-Hornung, A.; Sorkine-Hornung, O.; Schroers, C. A fully progressive approach to single-image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops 2018, Salt Lake City, UT, USA, 18–23 June 2018; pp. 864–873. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Change Loy, C. Esrgan: Enhanced super-resolution generative adversarial networks. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops 2018, Munich, Germany, 8–14 September 2018; pp. 63–79. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Dosovitskiy, A.; Brox, T. Generating images with perceptual similarity metrics based on deep networks. In Proceedings of the Advances in Neural Information Processing Systems 29 (NIPS 2016), Centre Convencions Internacional Barcelona, Barcelona, Spain, 5–10 December 2016; pp. 658–666. [Google Scholar]
- Goodrich, B.; Arel, I. Reinforcement learning based visual attention with application to face detection. In Proceedings of the 2012 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Providence, RI, USA, 16–21 June 2012; pp. 19–24. [Google Scholar]
- Taud, H.; Mas, J.F. Multilayer perceptron (MLP). In Geomatic Approaches for Modeling Land Change Scenarios; Springer: Cham, Switzerland, 2018; pp. 451–455. [Google Scholar]
- CASIA Iris Image Database. Available online: http://biometrics.idealtest.org/index.jsp#/datasetDetail/4 (accessed on 5 October 2022).
- Othman, N.; Dorizzi, B.; Garcia-Salicetti, S. OSIRIS: An open source iris recognition software. Pattern Recognit. Lett. 2016, 82, 124–131. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimisation. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sheikh, H.R.; Sabir, M.F.; Bovik, A.C. A statistical evaluation of recent full reference image quality assessment algorithms. IEEE Trans. Image Process. 2006, 15, 3440–3451. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Blau, Y.; Mechrez, R.; Timofte, R.; Michaeli, T.; Zelnik-Manor, L. The 2018 PIRM challenge on perceptual image super-resolution. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops 2018, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Ma, C.; Yang, C.Y.; Yang, X.; Yang, M.H. Learning a no-reference quality metric for single-image super-resolution. Comput. Vis. Image Underst. 2017, 158, 1–16. [Google Scholar] [CrossRef]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a “completely blind” image quality analyser. IEEE Signal Process. Lett. 2012, 20, 209–212. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2016, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Blau, Y.; Michaeli, T. The perception-distortion tradeoff. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2018, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6228–6237. [Google Scholar]




















| Bicubic | SRCNN | ESRGAN | SwinIR | HAT | IrisDnet | SwinIris | SwinGIris | |
|---|---|---|---|---|---|---|---|---|
| PSNR | 31.4261 | 31.6137 | 31.9372 | 33.6537 | 34.7421 | 31.5786 | 34.5798 | 33.5663 |
| SSIM | 0.8102 | 0.8063 | 0.8301 | 0.8703 | 0.8927 | 0.7994 | 0.8857 | 0.8639 |
| PI | 8.1907 | 9.1302 | 6.3256 | 7.9390 | 7.8452 | 6.0320 | 7.7257 | 5.9280 |
| LR | SRCNN | ESRGAN | SwinIR | HAT | IrisDnet | SwinIris | SwinGIris | |
|---|---|---|---|---|---|---|---|---|
| EER(VGG) | 2.9474 | 2.4737 | 1.7895 | 1.3158 | 1.0526 | 1.1053 | 1.1632 | 0.8421 |
| EER(ResNet) | 2.0526 | 0.8947 | 0.5263 | 0.4737 | 0.4211 | 0.4211 | 0.4737 | 0.2632 |
| EER(DenseNet) | 1.2632 | 0.6842 | 0.3684 | 0.4210 | 0.2105 | 0.2105 | 0.4211 | 0.1579 |
| Bicubic | SRCNN | ESRGAN | SwinIR | HAT | IrisDnet | SwinIris | SwinGIris | |
|---|---|---|---|---|---|---|---|---|
| PSNR | 33.4895 | 34.4581 | 34.8884 | 36.0513 | 36.3218 | 34.1663 | 35.8515 | 34.7214 |
| SSIM | 0.8339 | 0.8563 | 0.8905 | 0.9036 | 0.9152 | 0.8629 | 0.9011 | 0.8883 |
| PI | 8.2088 | 8.1540 | 6.3844 | 6.9119 | 7.6180 | 6.2439 | 6.8485 | 6.1892 |
| LR | SRCNN | ESRGAN | SwinIR | HAT | IrisDnet | SwinIris | SwinGIris | |
|---|---|---|---|---|---|---|---|---|
| EER(VGG) | 4.8600 | 3.4806 | 2.5119 | 2.6761 | 3.4007 | 2.3200 | 2.5143 | 2.0995 |
| EER(ResNet) | 3.3600 | 1.9818 | 1.4101 | 1.3997 | 4.5828 | 1.3088 | 1.3595 | 1.1200 |
| EER(DenseNet) | 2.1200 | 1.2952 | 0.8583 | 0.9402 | 0.9001 | 0.7203 | 0.8199 | 0.6000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, H.; Zhu, X.; Cui, J.; Jiang, H. An Iris Image Super-Resolution Model Based on Swin Transformer and Generative Adversarial Network. Algorithms 2024, 17, 92. https://doi.org/10.3390/a17030092
Lu H, Zhu X, Cui J, Jiang H. An Iris Image Super-Resolution Model Based on Swin Transformer and Generative Adversarial Network. Algorithms. 2024; 17(3):92. https://doi.org/10.3390/a17030092
Chicago/Turabian StyleLu, Hexin, Xiaodong Zhu, Jingwei Cui, and Haifeng Jiang. 2024. "An Iris Image Super-Resolution Model Based on Swin Transformer and Generative Adversarial Network" Algorithms 17, no. 3: 92. https://doi.org/10.3390/a17030092
APA StyleLu, H., Zhu, X., Cui, J., & Jiang, H. (2024). An Iris Image Super-Resolution Model Based on Swin Transformer and Generative Adversarial Network. Algorithms, 17(3), 92. https://doi.org/10.3390/a17030092






