Abstract
The particle swarm optimization (PSO) algorithm is widely used for optimization purposes across various domains, such as in precision agriculture, vehicular ad hoc networks, path planning, and for the assessment of mathematical test functions towards benchmarking different optimization algorithms. However, because of the inherent limitations in the velocity update mechanism of the algorithm, PSO often converges to suboptimal solutions. Thus, this paper aims to enhance the convergence rate and accuracy of the PSO algorithm by introducing a modified variant, which is based on a hybrid of the PSO and the smell agent optimization (SAO), termed the PSO-SAO algorithm. Our specific objective involves the incorporation of the trailing mode of the SAO algorithm into the PSO framework, with the goal of effectively regulating the velocity updates of the original PSO, thus improving its overall performance. By using the trailing mode, agents are continuously introduced to track molecules with higher concentrations, thus guiding the PSO’s particles towards optimal fitness locations. We evaluated the performance of the PSO-SAO, PSO, and SAO algorithms using a set of 37 benchmark functions categorized into unimodal and non-separable (UN), multimodal and non-separable (MS), and unimodal and separable (US) classes. The PSO-SAO achieved better convergence towards global solutions, performing better than the original PSO in 76% of the assessed functions. Specifically, it achieved a faster convergence rate and achieved a maximum fitness value of −2.02180678324 when tested on the Adjiman test function at a hopping frequency of 9. Consequently, these results underscore the potential of PSO-SAO for solving engineering problems effectively, such as in vehicle routing, network design, and energy system optimization. These findings serve as an initial stride towards the formulation of a robust hyperparameter tuning strategy applicable to supervised machine learning and deep learning models, particularly in the domains of natural language processing and path-loss modeling.
1. Introduction
The particle swarm optimization (PSO) algorithm is a widely recognized swarm intelligence-based optimization technique, extensively applied to diverse optimization problems [1,2,3]. For example, in precision agriculture, PSO and other optimization algorithms can be used to identify specific plants affected by diseases, thus enabling the targeted application of pesticides or the elimination of unwanted weed growth [4,5,6]. In vehicular ad hoc networks, optimization algorithms play a role in determining the optimal route for vehicle navigation amid numerous possibilities from source to destination [7,8,9]. Furthermore, during the development of optimization algorithms, the initial evaluation of such algorithms typically involves applying them to standard mathematical test functions to gauge their performance [10]. Other examples include the use of optimization techniques in solving the traveling salesman problem [7,8,9,11,12] and in path planning areas [13,14]. These examples illustrate the many application areas in which optimization algorithms, like PSO, can be effectively utilized to yield societal benefits.
The PSO algorithm operates by guiding a population of particles through the search space iteratively, with the objective of locating the optimal solution [15]. In this case, the search space refers to the population of all possible solutions to the problem under consideration. Specifically, each particle represents a potential solution to the problem, with its position in the search space representing a candidate solution. The PSO algorithm then updates each particle’s position iteratively, guided by both its own best position (referred to as personal best or pbest) and the best position among its neighboring particles [15]. Initially, each particle is assigned a random velocity, propelling it into the optimization hyperspace. Consequently, every particle maintains a record of its hyperspace coordinates, which are tied to its best solution found so far (pbest). Simultaneously, the entire swarm of particles collectively monitors the optimal solution and its location in hyperspace, referred to as the global best (gbest) [16]. In an n-dimensional search space, the position and velocity of a particle indexed by i at some present iteration cycle t are determined by the following equations [17]:
where and are the velocity control parameters, and and are random numbers generated differently. Therefore, the position of the particles is updated as expressed in Equation (4):
Many variants of the PSO algorithm exist in the literature, designed to enhance its performance. Noteworthy among these is the constriction factor PSO (CFPSO) [18,19], developed to mitigate premature convergence, a common issue in conventional PSO. CFPSO uses a constriction factor to regulate the particle velocity, thereby curbing excessive growth. This mechanism aids in preserving population diversity and safeguards against premature convergence to sub-optimal solutions.
Similarly, a popular variant of the PSO algorithm is the hybrid PSO, which amalgamates PSO with other optimization techniques to enhance its performance. Some studies advocate for the fusion of PSO with differential evolution (DE) to create a hybrid PSO-DE algorithm [20,21]. This hybrid approach combines PSO’s global search capabilities with DE’s local search abilities, resulting in an improved convergence speed and solution quality. Furthermore, research has delved into the concept of adaptive PSO, another common PSO variant that dynamically adjusts the algorithm’s parameters during optimization to enhance its performance [22,23]. Various strategies, such as altering the inertia weight or adapting the learning component, have been explored to fine-tune the PSO update equation. These adaptations serve to balance the exploration and exploitation phases of the algorithm, ultimately improving the convergence speed and accuracy.
Moreover, the multi-objective PSO is a specialized PSO modification tailored for solving multi-objective optimization problems [24,25,26]. Multi-objective optimization tasks involve the simultaneous consideration of conflicting objectives [24]. The multi-objective PSO employs a Pareto-based approach to generate a set of non-dominated individuals that represent the trade-offs between the different objectives. Essentially, the PSO algorithm and its variants stand as potent optimization techniques with widespread applications in solving diverse optimization problems, including mathematical test functions. The selection of a specific PSO variant hinges on the unique characteristics of the problem under investigation.
In this paper, based on the smell agent optimization (SAO) algorithm, we introduce a hybrid method, denoted as the PSO-SAO algorithm, aimed at enhancing the convergence accuracy of the original PSO algorithm. We achieved this by modifying the velocity update process of the original PSO through the incorporation of the trailing mode from the SAO algorithm (proposed in [27]). Hence, the specific objective of our study is to use the concept of the trailing mode in the SAO algorithm to continuously introduce agents to track molecules with higher concentrations, thus guiding the particles in the PSO towards optimal fitness locations. The velocity update process in PSO has been adapted to depend on a newly introduced parameter called the hopping frequency in PSO-SAO. This parameter dictates whether our hybrid algorithm uses the trailing mode or the standard PSO velocity update equation. The optimal value for the hopping frequency can be determined through experimental analysis, taking into consideration the specific application area of interest.
Our proposed PSO-SAO algorithm holds significant importance in the field of optimization techniques due to its ability to enhance convergence accuracy and efficiently navigate complex solution spaces. Its incorporation of the trailing mode from the SAO algorithm introduces adaptability, providing a promising approach for addressing optimization challenges. The algorithm’s potential applications span various domains, including precision agriculture, path loss prediction, path planning, machine learning, and deep learning models. By offering an effective tool for optimizing complex systems, the PSO-SAO algorithm creates opportunities for enhancing decision-making processes, resource utilization, and overall system performance in practical applications.
Therefore, in line with this concept, our study’s primary contribution revolves around the innovative integration of PSO with the trailing mode of SAO, resulting in an improved performance. To evaluate its robustness, we follow standard benchmark procedures [28] and assess the PSO-SAO algorithm across 37 standard benchmark test functions [29], comparing it to the original PSO and SAO algorithms. The remainder of this paper is structured as follows: Section 2 details the proposed PSO-SAO algorithm, Section 3 presents the results and discussions, and Section 4 provides the paper’s concluding remarks.
2. Hybridization of PSO and SAO Algorithms
This section provides a brief high-level summary of metaheuristics and then outlines our hybridization approach that combines the PSO algorithm with the trailing mechanism of the SAO algorithm. This hybridization aims to enhance the performance of the original PSO algorithm by addressing convergence issues towards suboptimal solutions.
Firstly, we note that metaheuristics are powerful problem-solving techniques used in various fields to find optimal or near-optimal solutions for complex problems. Unlike traditional mathematical optimization methods, which may struggle with highly nonlinear or combinatorial problems, metaheuristics are versatile and can efficiently explore solution spaces. These algorithms draw inspiration from natural processes or human behaviors to iteratively refine solutions. They employ strategies like population-based search, mutation, and selection to explore a wide range of possibilities and gradually converge towards better solutions. Here, we introduce the PSO-SAO algorithm, which is proposed for its ability to enhance the convergence accuracy and adaptability of the original PSO.
In developing the PSO-SAO approach, an initial population of randomly generated solutions is used to initiate the PSO process. Each solution (or particle) is associated with a random velocity and explores the optimization hyperspace. Each particle tracks its own position coordinates in hyperspace, denoted as the personal best (pbest). The swarm collectively maintains the overall best solution and its position in hyperspace, referred to as the global best (gbest). The position (x) and velocity (v) of particle i in an n-dimensional search space at a specific iteration cycle t are determined by Equations (1) and (2). The fitness of each particle is assessed, and their respective pbest and the population gbest values are updated using Equation (3), while particle positions are updated using Equation (4). Figure 1 provides an overview of the PSO implementation processes.
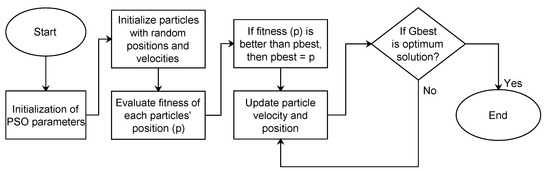
Figure 1.
PSO operational flow process.
Specifically, from Figure 1, the initial positions in the PSO algorithm are randomly assigned, and the particle fitness at these positions is evaluated. Then, the velocity is adjusted, and new positions are determined. Thereafter, the fitness of each particle is reevaluated, and the updated fitness is compared to the previous fitness, thus retaining the better value (i.e., smaller or larger value in the case of minimization or maximization problems, respectively). This process then updates the pbest and gbest positions. The PSO procedure then continues until the termination criteria are met. For performance analysis purposes, we classify the benchmark functions used in this work into three categories: unimodal and non-separable (UN), unimodal and separable (US), and multimodal and non-separable (MS), as summarized in Table 1. In this case, the unimodal functions have a single global optimum, aiding in assessing the exploitation capability of an algorithm, while multimodal functions possess multiple local optima, thus facilitating the evaluation of the exploration capability of an algorithm. Specifically, exploitation capability refers to the algorithm’s capacity to effectively utilize and exploit known information to maximize performance or achieve optimal results within a given context. It involves refining solutions and making incremental improvements by leveraging existing knowledge or resources. Conversely, exploration capability refers to the ability to search and explore new solutions within a problem space. This process involves discovering new information, potentially sacrificing immediate gains to uncover new possibilities or better solutions. Balancing exploitation and exploration capabilities is crucial, especially in optimization algorithms, as it determines the trade-off between refining known solutions and discovering potentially superior alternatives. Further details about the classification and benchmark test functions can be found in [27].

Table 1.
Mathematical benchmark test functions [26].
In order to improve the PSO’s efficiency and prevent it from converging to suboptimal values, we incorporated the trailing mechanism from the SAO, for which the full working mechanism of the SAO algorithm can be accessed in [27,30]. The SAO algorithm uses the phenomenon of smell and the intuitive trailing behavior of an agent to identify a smell source. The algorithm is inspired by the behavior of animals that use their sense of smell to locate food sources. The algorithm works by simulating the behavior of an agent that moves through a search space, leaving a trail of pheromones as it moves. The pheromones are then used to communicate information about the quality of the solutions found by the agent to other agents in the search space. The agents then use this information to guide their search towards better solutions. The algorithm is designed to balance exploration and exploitation of the search space, thus allowing it to find optimal solutions efficiently. The computational analysis of the SAO in [27,30] demonstrates the robustness of SAO in finding optimal solutions for mechanical, civil, and industrial design problems. The experimental results obtained showed that the algorithm leads to an improvement in solution quality by 10–20% of other selected metaheuristics while solving constraint benchmarks and engineering problems, with further details available in [27,30].
Thus, based on the performance of the SAO algorithm, it demonstrated a good balance between exploitation and exploration, which significantly influenced the effectiveness of any population-based algorithm. Consequently, as the PSO’s success relies heavily on the effectiveness of its velocity-computation technique and update process, there is potential for the trailing property of the SAO to be integrated into the PSO to prevent its convergence to suboptimal values. The trailing mode within the SAO algorithm carries significant importance as it directs agents from smell perception to evaporation locations. This mode captures both favorable and unfavorable odor molecules, which can serve as an occasional alternative to the position update behavior in PSO. The integration of this behavior in a hybrid algorithm will thus allow for dynamic position updates, using the solution found by the trailing behavior only if it surpasses the original PSO update solution. Moreover, this occasional switch eliminates the necessity of using velocity in the optimization process, facilitating a more extensive search. Furthermore, we note that in the trailing mode of the SAO, agents continuously track molecules with a higher concentration, hence directing them towards the best fitness location. The agents in the SAO algorithm possess olfaction capacities based on psychological and physical conditions, and the size of the olfactory lobe. A larger olfactory lobe favors exploitation, while a smaller lobe implies weaker olfaction. For the trailing mode to function, the odor must first evaporate in the agent’s direction, followed by the sniffing procedure to determine olfaction capacity, , which is calculated as follows [27]:
where is the agent’s fitness, denotes the fitness of an individual molecule, and N is the number of molecules. Equation (6) further defines the agent’s trailing behavior as follows:
where and are random numbers generated at distinct intervals. This trailing mechanism is proposed in our hybrid as an alternative position update strategy instead of the PSO update mechanism defined as follows:
where
and is calculated using Equation (6). The value of (termed the hopping frequency) determines whether our hybrid algorithm uses the trailing mode (Equation (6)) or the PSO velocity update equation (Equation (7)). Its value is determined experimentally, and is calculated using the normal distribution in the range (0, 1). Figure 2 presents a flowchart describing the complete working mechanism of the PSO-SAO algorithm. The control parameters, including the swarm size (i.e., population size), olfaction capacity (), hopping frequency (), coefficient vector, termination criteria , and initial velocity , are summarized in Table 2. The pseudocode for the hopping frequency trail update mechanism proposed for use in PSO-SAO is provided in Algorithm 1. The PSO-SAO algorithm is then evaluated to assess its effectiveness using 37 benchmark test functions listed in Table 1.
| Algorithm 1: Hopping frequency mechanism deployed in the PSO-SAO for position update |
|
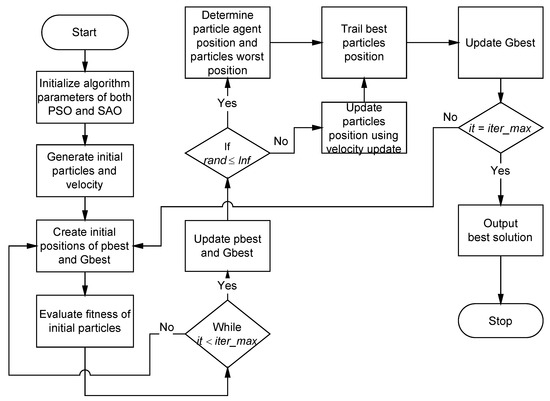
Figure 2.
Operation of the PSO-SAO algorithm.

Table 2.
Proposed algorithm control parameters.
3. Results and Discussion
This section presents the results of evaluating the PSO-SAO algorithm on benchmark test functions, as well as its comparison with the original PSO [1] and SAO algorithms [27]. Additionally, we report the fitness results of PSO-SAO on the benchmark functions for nine specified hopping frequencies. These results are essential to demonstrate the efficacy of the PSO-SAO algorithm’s search process.
Figure 3 and Figure 4 provide the outcomes of running each function 10 times with hopping frequencies ranging from 0.1 to 0.9, which were transformed to values from 1 to 9 in the charts. In particular, Figure 3 illustrates the minimization process for the PSO-SAO algorithm on the first benchmark function (Adjiman function) using varying hopping frequencies. Notably, PSO-SAO exhibits the fastest convergence at a hopping frequency of 8.
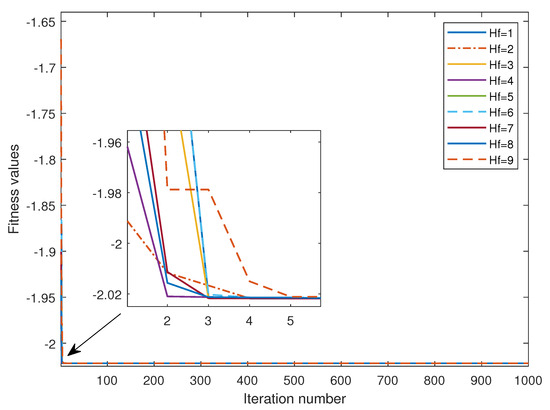
Figure 3.
Fitness values for the PSO-SAO on Adjiman test function showing convergence of all Hf.
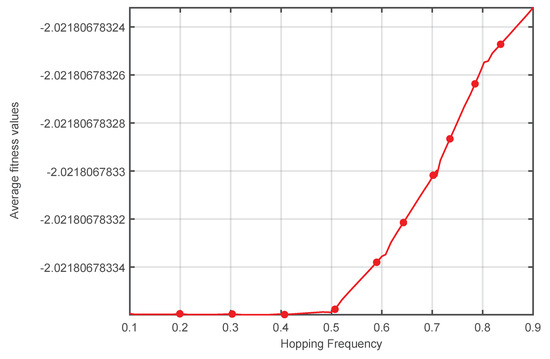
Figure 4.
Average fitness performance for the different hopping frequencies on Adjiman function (F1) for the PSO-SAO algorithm.
Figure 4 presents the average fitness plot for the nine hopping frequencies applied to the Adjiman function. It is apparent from Figure 4 that hopping frequencies between 0.1 and 0.5 yield identical average fitness values, while a hopping frequency of 0.9 produces the highest average fitness. This observation explains why the hopping frequency of 9 (on a scale of 1–10) achieves the best convergence rate in Figure 3. In this figure, the differences in the fitness values are indeed minimal, primarily because the Adjiman function considered here served as an easily solvable problem for the PSO-SAO algorithm. Nevertheless, we included it here because it broadly mirrors how the hopping frequency responds to numerous other functions. Furthermore, this difference in the fitness values only becomes more prominent when dealing with difficult problems with higher-dimensional and multimodal characteristics. Extensive analyses were conducted for all of the test functions in Table 1, with similar outcomes obtained as explained here, but due to space constraints, only the results for the Adjiman test function were reported.
Table 3 presents a comprehensive summary of the outcomes pertaining to both the average and standard deviation values for each algorithm when applied to the set of 37 functions. Notably, the PSO-SAO algorithm emerged as particularly successful in its ability to converge to global solutions, as highlighted by the use of the bold red font in Table 3. The ground truth global values, which served as benchmarks for assessing the performance of the algorithms, can be cross-referenced in Table 1. For instance, functions F1, F2, and F3, corresponding to the Adjiman, Beale, and Bird functions, respectively, exhibited true global solutions of −2.0218, 0, and −106.765, respectively, as documented in Table 1. Strikingly, a comparison of these global values with those attained by the PSO-SAO algorithm, as indicated in Table 3, revealed a good degree of approximation.

Table 3.
The fitness performance across functions 1 to 37. The red values represent the optimal values, i.e., the smallest absolute error, belonging to the algorithm that exhibits the best performance for each respective function.
The PSO-SAO algorithm achieved an average global solution of −2.0218 for the Adjiman function F1 (see Table 3). A similar result was obtained for SAO, with values of −2.0218 for F1. PSO, on the other hand, obtained an average of −2.0134, thus resulting in a larger error. These results highlight that both the PSO-SAO and SAO algorithms converged to the exact global solution with high precision (−2.0218) compared with the PSO algorithm. Other results can be observed for the other functions in Table 3.
We present a concise summary of algorithm rankings based on the number of functions for which they achieved optimal values in Table 4. It is important to note that the determination of optimal values was established through the calculation of the absolute errors between the average fitness values attained by each algorithm and the global solutions for each function, as presented in Table 1. The results indicate that the PSO-SAO algorithm achieved the highest ranking, demonstrating the best performance in 28 out of the 37 functions, resulting in a 76% success rate.

Table 4.
Ranking of the different algorithms based on the number of functions for which they achieved optimal values.
Summarily, it is shown that the PSO-SAO algorithm achieved global solutions for 76% of the standard benchmark test functions considered in our study, performing better than the SAO (with 62%) and PSO algorithms (with 41%). This demonstrates its potential and thus it can be deployed for solving engineering problems, for example, hyperparameter tuning in supervised machine learning models for different applications and problems.
4. Conclusions
This study presents the development of a hybrid modified particle swarm optimization (PSO-SAO) algorithm, which integrates the trailing mode of the smell agent optimization (SAO) algorithm to enhance the velocity update process of the original PSO algorithm. This hybridization aims to address the challenge of suboptimal convergence encountered in the standard PSO algorithm. The performance of the proposed hybrid PSO-SAO was assessed using 37 distinct benchmark test functions. Evaluation metrics comprised the determination of the best, average, worst, and standard deviation values for the different algorithms, followed by a comparative analysis against the performance of both the original PSO and SAO algorithms. The experimental results obtained revealed that the PSO-SAO achieved the best results in 71% of the 37 functions, followed by the SAO with 62% and the standard PSO with 41%. These findings substantiate the efficacy of the developed PSO-SAO. The primary challenge of the hybrid mechanism is the introduction of the increased computational complexity, which can potentially impact the system efficiency and performance. This challenge necessitates further research to optimize and mitigate the computational overhead. Nevertheless, our hybrid algorithm enhances existing research in optimization by demonstrating the combination of functions from two different optimization algorithms, thus leveraging their individual strengths to achieve improved solutions. This approach led to a robust and efficient optimization technique, thus offering solutions that may be superior to those obtained using the individual methods. Furthermore, it is essential to emphasize that this research serves as a preliminary step towards the establishment of a robust optimization approach for hyperparameter tuning in supervised machine learning models and deep learning models, specifically designed for natural language processing and pathloss modeling. Future investigations will extend the use of the developed PSO-SAO to address various engineering applications, including hyperparameter optimization in deep learning models, language translation, path loss modeling, and route planning, among others.
Author Contributions
Conceptualization, A.T.S. (Abdullahi T. Sulaiman), H.B.-S. and A.T.S. (Ahmed T. Salawudeen); methodology, H.B.-S., A.T.S. (Ahmed T. Salawudeen) and A.J.O.; writing—original draft preparation, H.B.-S. and A.T.S. (Ahmed T. Salawudeen); writing—review and editing, H.B.-S., A.J.O. and A.D.A.; supervision, M.B.M. and E.A.A.; funding acquisition, H.B.-S. and A.J.O. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to thank the Tertiary Education Trust Fund (TETFUND), Nigeria, for funding this research as part of the 2021 National Research Fund (NRF) grant cycle, under the project titled “A Novel Artificial Intelligence of Things (AIoT) Based Assistive Smart Glass Tracking System for the Visually Impaired” (TETF/DR&D/CE/NRF2021/SETI/ICT/00140/VOL.1). We would also like to thank the Image Processing and Computer Vision (IPCV) research group at Ahmadu Bello University Zaria, Nigeria, for their insightful comments and ideas that aided in the development of this study.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author. The data are not publicly available due to ethical reasons.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995. ICNN-95. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. J. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Juneja, M.; Nagar, S. Particle swarm optimization algorithm and its parameters: A review. In Proceedings of the 2016 International Conference on Control, Computing, Communication and Materials (ICCCCM), Allahbad, India, 21–22 October 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Rathod, S.; Saha, A.; Sinha, K. Particle Swarm Optimization and its applications in agricultural research. Food Sci. Rep. 2020, 1, 37–41. [Google Scholar]
- Mythili, K.; Rangaraj, R. Deep Learning with Particle Swarm Based Hyper Parameter Tuning Based Crop Recommendation for Better Crop Yield for Precision Agriculture. Indian J. Sci. Technol. 2021, 14, 1325–1337. [Google Scholar] [CrossRef]
- Raji, I.D.; Bello-Salau, H.; Umoh, I.J.; Onumanyi, A.J.; Adegboye, M.A.; Salawudeen, A.T. Simple deterministic selection-based genetic algorithm for hyperparameter tuning of machine learning models. Appl. Sci. 2022, 12, 1186. [Google Scholar] [CrossRef]
- Bello-Salau, H.; Onumanyi, A.; Sadiq, B.; Ohize, H.; Salawudeen, A.; Aibinu, M. An Adaptive Wavelet Transformation Filtering Algorithm for Improving Road Anomaly Detection and Characterization in Vehicular Technology. Int. J. Electr. Comput. Eng. (IJECE) 2019, 9, 3664–3670. [Google Scholar] [CrossRef]
- Bello-Salau, H.; Aibinu, A.M.; Wang, Z.; Onumanyi, A.J.; Onwuka, E.N.; Dukiya, J.J. An Optimized Routing Algorithm for Vehicle Ad-hoc Networks. Eng. Sci. Technol. Int. J. 2019, 22, 754–766. [Google Scholar] [CrossRef]
- Bello-Salau, H.; Onumanyi, A.J.; Abu-Mahfouz, A.M.; Adejo, A.O.; Mu’Azu, M.B. New Discrete Cuckoo Search Optimization Algorithms for Effective Route Discovery in IoT-Based Vehicular Ad-Hoc Networks. IEEE Access 2020, 8, 145469–145488. [Google Scholar] [CrossRef]
- Valdez, F.; Vazquez, J.C.; Melin, P.; Castillo, O. Comparative Study of the Use of Fuzzy Logic in Improving Particle Swarm Optimization Variants for Mathematical Functions Using Co-evolution. Appl. Soft Comput. 2017, 52, 1070–1083. [Google Scholar] [CrossRef]
- Zheng, R.Z.; Zhang, Y.; Yang, K. A transfer learning-based particle swarm optimization algorithm for the traveling salesman problem. J. Comput. Des. Eng. 2022, 9, 933–948. [Google Scholar]
- Zhong, Y.; Lin, J.; Wang, L.; Zhang, H. Discrete comprehensive learning particle swarm optimization algorithm with Metropolis acceptance criterion for the traveling salesman problem. Swarm Evol. Comput. 2018, 42, 77–88. [Google Scholar] [CrossRef]
- Song, B.; Wang, Z.; Zou, L. An Improved PSO Algorithm for Smooth Path Planning of Mobile Robots Using Continuous High-Degree Bezier Curve. Appl. Soft Comput. 2021, 100, 106960. [Google Scholar] [CrossRef]
- Song, B.; Wang, Z.; Zou, L. On Global Smooth Path Planning for Mobile Robots Using a Novel Multimodal Delayed PSO Algorithm. Cogn. Comput. 2017, 9, 5–17. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle Swarm Optimization: A Comprehensive Survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Yang, X.; Jiao, Q.; Liu, X. Center Particle Swarm Optimization Algorithm. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 March 2019; pp. 2084–2087. [Google Scholar] [CrossRef]
- Bansal, J.C. Particle Swarm Optimization. In Evolutionary and Swarm Intelligence Algorithms; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 11–23. [Google Scholar] [CrossRef]
- You, Z.; Chen, W.; He, G.; Nan, X. Adaptive Weight Particle Swarm Optimization Algorithm with Constriction Factor. In Proceedings of the 2010 International Conference of Information Science and Management Engineering (ISME), Shaanxi, China, 7–8 August 2010; IEEE: Piscataway, NJ, USA, 2010; Volume 2, pp. 245–248. [Google Scholar] [CrossRef]
- Lu, Y.; Liang, M.; Ye, Z.; Cao, L. Improved Particle Swarm Optimization Algorithm and Its Application in Text Feature Selection. Appl. Soft Comput. 2015, 35, 629–636. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, H.; Li, K.; Lin, Z.; Yang, J.; Shen, X.-L. A Hybrid Particle Swarm Optimization Algorithm Using Adaptive Learning Strategy. Inf. Sci. 2018, 436, 162–177. [Google Scholar] [CrossRef]
- Singh, A.; Sharma, A.; Rajput, S.; Bose, A.; Hu, X. An Investigation on Hybrid Particle Swarm Optimization Algorithms for Parameter Optimization of PV Cells. Electronics 2022, 11, 909. [Google Scholar] [CrossRef]
- Harrison, K.R.; Engelbrecht, A.P.; Ombuki-Berman, B.M.J.S.I. Self-Adaptive Particle Swarm Optimization: A Review and Analysis of Convergence. Swarm Intell. 2018, 12, 187–226. [Google Scholar] [CrossRef]
- Liang, X.; Li, W.; Zhang, Y.; Zhou, M.J.S.C. An Adaptive Particle Swarm Optimization Method Based on Clustering. Soft Comput. 2015, 19, 431–448. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.-W.; Cheng, J. Multi-Objective Particle Swarm Optimization Approach for Cost-Based Feature Selection in Classification. IEEE/ACM Trans. Comput. Biol. Bioinform. 2015, 14, 64–75. [Google Scholar] [CrossRef]
- Cui, Y.; Meng, X.; Qiao, J. A Multi-Objective Particle Swarm Optimization Algorithm Based on Two-Archive Mechanism. Appl. Soft Comput. 2022, 119, 108532. [Google Scholar] [CrossRef]
- Lin, Q.; Li, J.; Du, Z.; Chen, J.; Ming, Z. A Novel Multi-Objective Particle Swarm Optimization With Multiple Search Strategies. Eur. J. Oper. Res. 2015, 247, 732–744. [Google Scholar] [CrossRef]
- Salawudeen, A.T.; Mu’azu, M.B.; Yusuf, A.; Adedokun, E.A. A Novel Smell Agent Optimization (SAO): An Extensive CEC Study and Engineering Application. Knowl. Based Syst. 2021, 232, 107486. [Google Scholar] [CrossRef]
- Mahareek, E.A.; Cifci, M.A.; El-Zohni, H.; Desuky, A.S. Rhizostoma Optimization Algorithm and Its Application in Different Real-World Optimization Problems. Int. J. Electr. Comput. Eng. (IJECE) 2023, 13, 4317–4338. [Google Scholar] [CrossRef]
- Jamil, M.; Yang, X.S. A Literature Survey of Benchmark Functions for Global Optimisation Problems. Int. J. Math. Model. Numer. Optim. 2013, 4, 150–194. [Google Scholar] [CrossRef]
- Salawudeen, A.T.; Mu’azu, M.B.; Yusuf, A.; Adedokun, E.A. From Smell Phenomenon to Smell Agent Optimization (SAO): A Feasibility Study. In Proceedings of the International Conference on Global and Emerging Trends (ICGET 2018), Abuja, Nigeria, 2–4 May 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).