Applying Recommender Systems to Predict Personalized Film Age Ratings for Parents

Abstract

A motion picture content rating system categorizes a film based on its appropriateness for various audiences, considering factors such as portrayals of sex, violence, substance abuse, profanity, and other elements typically considered unsuitable for children or adolescents. This rating is usually coupled with a minimum desired age that the film is suitable for. In this work, we apply recommender systems to predict personalized film age ratings for parents. According to the proposed methodology, we reduce the personalized film age prediction problem to the classic item recommendation problem by applying a recommender system for each age film category. The recommender systems generate recommendations for each film age category. Finally, these recommendations are combined to provide the final age recommendation for the parent (user). The proposed methodology was applied to state-of-the-art recommender systems. In addition, we used them as baselines for comparing the direct application of a recommender system to the age prediction problem. This was achieved by treating each film as an item and assigning the given age as its rating. The experimental results highlight the efficiency of the proposed system when applied to a well-known real-world dataset.

1. Introduction

Extensive research has explored how media consumption and audiovisual content affect children. The literature indicates that a child’s psychological development is likely influenced by emotional stages and social factors [1,2,3,4]. Media influences children and adolescents according to the amount and type of content consumed, as well as factors such as age, genetics, interpersonal relationships, context, and societal influences [5,6,7].

Given that media content—such as sex, violence, or substance abuse—is generally considered inappropriate for children and adolescents, it is essential to classify films based on their suitability for different audiences. This classification is provided by age rating systems for films that are designed to inform viewers, particularly parents, about the suitability of the content of a movie for different age groups. These systems, used by organizations such as the Motion Picture Association (MPA) [8] and Common Sense Media (CSM) [9], evaluate elements such as violence, language, sexual content, and thematic material. By assigning films to categories like “PG” (Parental Guidance) or “R” (Restricted), age ratings help audiences make informed decisions about what is appropriate for children, teens, and adults to watch. Although these systems aim for consistency, cultural differences often lead to variations in ratings between countries. Parents often rely on media content classification systems, such as those provided by Common Sense Media [9], to help decide which films are appropriate for their children.

In countries like Australia, Canada, and Singapore, official government bodies determine the ratings, while in other countries such as Denmark, Japan, and the United States, industry committees handle the process with little to no official government involvement. However, there are differences between these media content classification systems as well as between countries that have applied them in films. However, since parents are responsible for preventing or not allowing films to be seen by their children, it makes sense to create a recommender system that can provide personalized age ratings based on the parents’ beliefs about the content of media for unseen films.

In this work, we apply recommender systems to predict personalized film age ratings for parents. This approach frames the problem as a ‘multiple recommendation task’ by using a recommender system that categorizes by age. In this work, we use the Common Sense Media dataset, where the age categories are $AC=\{2,3,\dots ,18\}$. Multiple recommender systems provide recommendations for each age category ($\{2,3,\dots ,18\}$) of a film. The system then predicts age recommendations for each category, which are combined to generate the final personalized recommendation for the parent. To our knowledge, this is the first work that solves the prediction problem of personalized film age ratings. Figure 1 shows the graphical abstract of the proposed system (multiple recommender systems—MRSs) with training and testing phases. Figure 2 illustrates the schematic representation of the proposed system architecture.

This paper is structured as follows: Section 2 reviews the related work for age rating systems and recommender systems. Section 3 introduces the main problem formulation surrounding a personalized film age rating (PFAR) that we study in this paper. Section 4 presents the proposed framework for the PFAR problem based on parental age ratings. Section 5 describes the experimental setup along with the results obtained. Finally, our conclusions are presented in Section 6.

2. Related Work

In the following, we review the related work for film age rating systems and recommender systems.

2.1. Film Age Rating Systems

Film age rating systems are used worldwide to provide guidance on the suitability of films for different age groups. These systems are generally established by governments or independent organizations and generally differ from country to country, based on cultural norms and concerns about media content. In the following, we provide a brief summary of some major film age rating systems.

• The MPAA (Motion Picture Association of America) was established in the USA. The MPAA is one of the most well-known film classification systems and has been in use since 1968 [8]. Its key ratings include the following

  –

  G (General Audience): Suitable for all ages.

  –

  PG (Parental Guidance): Some material may not be suitable for children.

  –

  PG-13: Parents are strongly advised that some content may be inappropriate for children under 13 years of age.

  –

  R (Restricted): Viewers under 17 years of age require an accompanying adult.

  –

  NC-17: No one 17 and under admitted.

• The BBFC (British Board of Film Classification) was established in the UK [10].
  The BBFC has been classifying films since 1912, offering ratings that guide the public and protect younger viewers:

  –

  U (Universal): Suitable for all.

  –

  PG (Parental Guidance): General viewing, but some scenes may be unsuitable for young children.

  –

  12A: Children under 12 years of age must be accompanied by an adult.

  –

  15: Only suitable for viewers aged 15 and older.

  –

  18: Only suitable for adults.

• CNC (Centre National du Cinéma et de l’Image Animée) was established in France [11].
  The French system, managed by the CNC, uses a stricter approach to age ratings, with a strong emphasis on protecting minors from harmful content:

  –

  U: Suitable for all.

  –

  10: Not recommended for children under 10.

  –

  12: Not recommended for children under 12.

  –

  16: Not recommended for children under 16.

  –

  18: Only suitable for adults.

• FSK (Freiwillige Selbstkontrolle der Filmwirtschaft) was established in Germany [12].
  The German film classification system is managed by the FSK and offers the following categories:

  –

  0: Suitable for all.

  –

  6: Suitable for ages 6 and older.

  –

  12: Suitable for ages 12 and older.

  –

  16: Suitable for ages 16 and older.

  –

  18: Only suitable for adults.

• The ACB (Australian Classification Board) was established in Australia [13] and has been in use since 1968.
  Australia’s film rating system offers the following categories:

  –

  G: Suitable for all.

  –

  PG: Parental guidance recommended for viewers under 15.

  –

  M: Recommended for viewers 15 and over.

  –

  MA15+: Restricted to viewers 15 and older unless accompanied by an adult.

  –

  R18+: Restricted to adult viewers (18+).

  –

  X18+: Explicit adult content.

Film age rating systems generally consider the following elements when assigning ratings: violence, sexual content, profanity, substance abuse, and themes (e.g., horror, suicide, etc.). Film age rating systems reflect the diverse cultural standards of different countries, aimed at protecting children and providing guidance to parents. Although there are similarities, the exact nature of these ratings can vary significantly, from permissiveness in one country to strict restrictions in another. The diversity of these classification systems affects the presented method since the proposed method can be adapted to any classification system providing different age classes. Furthermore, the high diversity of these classification systems underscores the utility of the proposed recommendation system in providing personalized recommendations, even for parents seeking advice on different age classes.

2.2. Recommender Systems

Recommender systems (RSs) gather information about user preferences for a set of items by collecting user ratings or monitoring user behaviors across various sources. This information is then used to generate predictions and provide personalized recommendations for items [14,15,16,17]. RSs have become increasingly popular in helping users make decisions more efficiently by leveraging diverse methods [18]. RSs have been successfully applied across a wide range of domains, including e-commerce products, web pages, news articles, social networks, movies, music, hotels, television shows, books, restaurants, and even social connections [17].

The problem that a recommender system aims to solve is as follows: Given a set of users (U), a set of items (I), e.g., movies, products, etc., and a set of ratings (R), e.g., evaluations, provided by users for items, the objective of a recommender system is to predict the rating for a user–item pair that is not present in R. In a typical RS, users create accounts and provide ratings for various items. Generally, as the number of users and ratings increases, the system improves its ability to deliver accurate predictions. However, when the available ratings data are extremely sparse (the sparsity problem) or when the system lacks information about the preferences of new users (the cold start problem) [19], most recommender systems struggle to provide reliable predictions. The primary function of RS is to predict the preference level that a user might have for a given item.

The literature offers a wide range of techniques for recommender systems. Below, we provide a concise overview of the most prominent ones. Broadly, recommender systems can be categorized into two primary types: collaborative filtering and content-based approaches.

Collaborative filtering (CF) relies solely on user preferences (e.g., ratings) for items to generate recommendations. In contrast, content-based recommender systems incorporate additional attributes related to both items and users (e.g., movie genres, content types, user demographics, etc.) to make suggestions. CF methods [20,21,22] analyze historical user behaviors and preferences to predict future interests. While these systems often face challenges such as data sparsity and the cold-start problem, they benefit from leveraging existing user-generated information, which is automatically collected as users interact with and rate items. Typically, user preferences are represented as numerical values within a predefined range. In memory-based CF approaches, recommendations are derived by correlating information through one of the following strategies [17]:

• Item-to-item correlation: Recommendations are based on similarities between items, utilizing their properties and associations.
• User-to-user correlation: Suggestions are generated based on demographic similarities among users.
• User-to-item correlation: Recommendations arise from matching users with items they have previously rated or expressed a preference for.

Model-based collaborative filtering recommendation systems employ a variety of techniques to construct predictive models, which are then used to provide recommendations. These approaches often leverage dimensionality reduction techniques (e.g., [23]), where latent variables are introduced to capture and explain co-occurrence patterns in the data. In this context, each user or item is represented as a vector, with the user’s vector encoding their set of ratings across all elements in the system. However, the inherent sparsity of these vectors makes it challenging to identify correlations between user–item pairs. To address this, various dimensionality reduction methods are utilized, such as singular value decomposition (SVD) [24], principal component analysis, probabilistic latent semantic analysis, and latent Dirichlet allocation [25]. Matrix factorization [26], a widely used dimensionality reduction technique, characterizes both items and users using vectors of latent factors inferred from item rating patterns. The degree of correlation between the latent factors of users and items drives the generation of recommendations.

SCoR [15] assigns synthetic coordinates to users and items (nodes), as proposed in [24,26]. However, instead of relying on the dot product, SCoR measures the Euclidean distance between a user and an item. Once the system converges, the distance between a user–item pair effectively predicts the user’s preference for that item. The SCoR framework offers several advantages: It eliminates the need for parameter tuning to achieve high performance and is more resilient to data sparsity than many other frameworks.

Various artificial neural network architectures have also been used in model-based recommendation systems [16,27]. Convolutional neural networks (CNNs) [28] have been utilized to process the output of pre-processing steps, such as the outer product of user and item ratings to generate a 2D interaction map. This approach enables the modeling of user–item interaction patterns and the capture of high-order correlations.

More recently, advancements in graph neural networks (GNNs) have leveraged embedding propagation to iteratively aggregate neighborhood embeddings. By stacking propagation layers, each node can access information from high-order neighbors, surpassing traditional methods that are typically limited to first-order neighbors [27]. In [29], a graph convolutional matrix completion approach was introduced, utilizing a graph autoencoder framework based on a differentiable message passing on a bipartite interaction graph. This method, combined with a bilinear decoder, predicts new ratings in the form of labeled edges. Additionally, the graph autoencoder framework is naturally extendable to incorporate side information for both users and items. In [16], neural network architectures were investigated for collaborative filtering. The authors proposed a general framework with three specific implementations: GMF, MLP, and NeuMF, which model user–item interactions in distinct ways. This work complements mainstream shallow models for collaborative filtering, opening new avenues for recommendation research utilizing deep learning.

Content-Based Recommender Systems analyze items (or their descriptions) to construct item representations and user profiles, which are then used to recommend new items to users [30]. The recommendation process involves matching user profile attributes with those of content items, resulting in an evaluation of user interests in specific items [31], which forms the basis for recommendations. Most content-based recommender systems rely on textual features to represent items and user profiles. Additionally, various hybrid methods combine multiple approaches to enhance recommendation performance [32].

This paper is structured as follows: Section 2 reviews the related work for age rating systems and recommender systems. Section 3 introduces the main problem formulation surrounding a personalized film age rating (PFAR) that we study in this paper. Section 4 presents the proposed framework for the PFAR problem based on parental age ratings. Section 5 describes the experimental results. Finally, our conclusions are presented in Section 6.

3. Problem Formulation

The prediction problem of personalized film age ratings for parents, viewed as a recommendation task, is formulated as follows: A set of users (U), e.g., parents, a set of items (I), such as films, and a set of age ratings ($AR$), such as evaluations by parents for films, is given. This dataset is divided into a training set and a test set. The training set is used to determine the system parameters. $AR\in AC$, where $AC$ denotes the set of age categories. Hereafter, without loss of generality, we will use the $AC$ from the Common Sense Media dataset; however, the problem can be applied to any other dataset.

The goal of this problem is to predict the age of a parent–film pair that is not in the training set ($TR$) but belongs to the test set ($TS$). To evaluate the systems, we use the root mean squared error (RMSE) [15,33], which is suitable for recommender systems because it measures inaccuracies across all ratings, whether negative or positive.

$$RMSE=\sqrt{E\{{(AR-\overline{AR})}^2\}}$$

(1)

where $AR$ denotes the set of age rating values (parents declared ratings) and $\overline{AR}$ denotes the set of age ratings produced by the recommendation algorithm for the test set. The lower the calculated RMSE, the better the prediction accuracy of the system.

4. Proposed Methodology

The proposed framework aims to address the problem of predicting personalized film age ratings for parents by employing multiple recommender systems (MRSs) tailored to individual age categories. This approach transforms the problem into a multi-faceted recommendation task, leveraging the strengths of modern recommender system algorithms. The methodology includes several stages: data transformation, training multiple models, and aggregating predictions to generate the final personalized rating. Below is a detailed explanation of the methodology:

According to the problem formulation, the given dataset consists of triples $(p,f,c(p,f\left)\right)$, where $p\in U, f\in I$ and $c(p,f)\in AC$ denote the parent id, film id and the age category of the film, f, according to the belief of the parent, p, respectively. The dataset is divided into the training ($TR$) and test set ($TS$). The proposed framework consists of training and testing phases (see Figure 1).

4.1. Training Phase

The pseudo-code of the training phase of the proposed method is presented in Algorithm 1. The input of the algorithm is the training set, $TR$, and the age category, $AC$. The output consists of the trained models for each recommender system $R{S}_i$, $i\in AC$, since we use a recommender system $R{C}_i$, $i\in AC$ for each age category, as shown in Figure 2. The training step includes both a dataset transformation stage and the actual training stage.

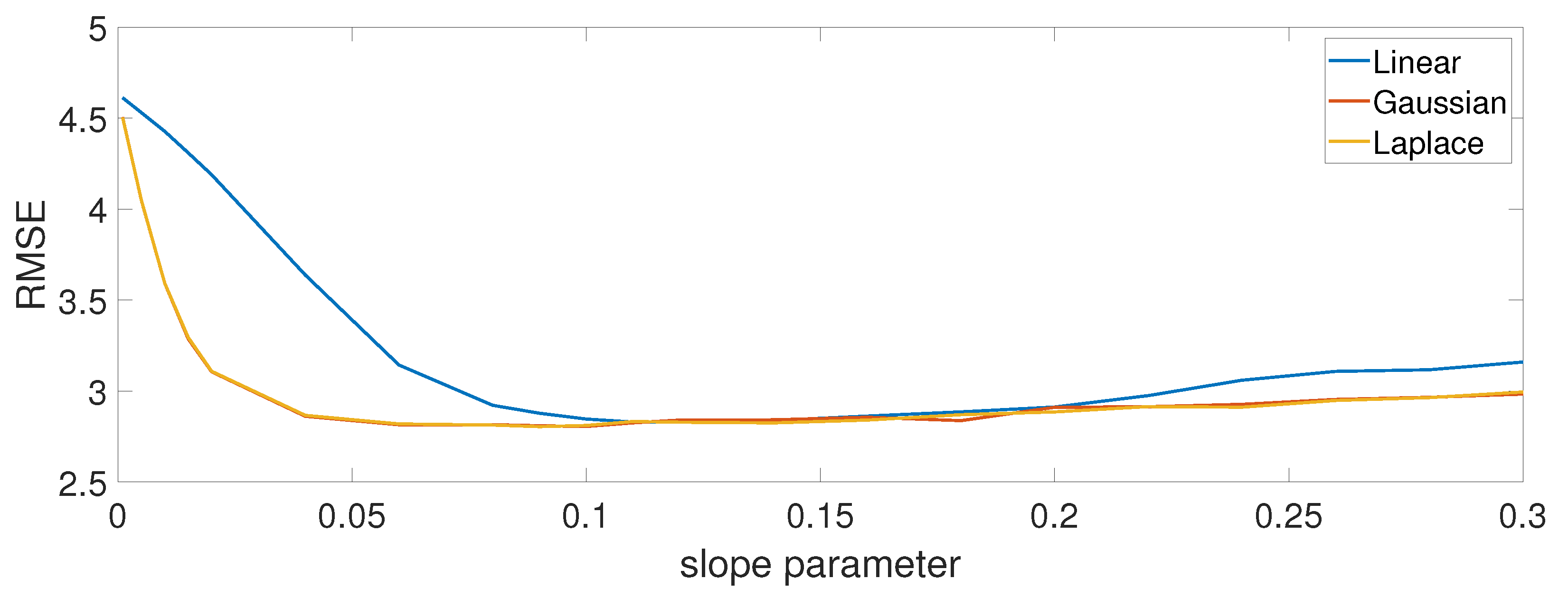
• The data transformation phase employs a modified, generalized version of one-hot encoding, in order to transform the age values into different age categories (see Figure 1). Therefore, to train each recommender system, $R{C}_i$, where $i\in AC$, we create $\left|AC\right|$ triples $(p,f,r_i(p,f))$ for any triplet $(p,f,c(p,f\left)\right)$ of the original training set. Here, $r_i(p,f)$ denotes the beliefs of the parent, p, and film, f, for the age category, i. According to the definition of $c(p,f)$, $r_i(p,f)$ can be defined by the following delta function, according to $c(p,f)$:

  $$r_i(p,f)=\left\{\begin{array}{cc}\hfill 1,\hfill & \hfill i=c(p,f)\hfill \\ \hfill 0,\hfill & \hfill \text{-}\hfill \end{array}\right.$$

  (2)
  However, better results are obtained when we allow non-zero values for values of i in the neighborhood of $c(p,f)$. As an example, one approach involves using a partially linear function $r_i(p,f)$ (triangular function), as defined in Equation (3), so that the belief of the parent gradually decreases as we move away from the selected age category $c(p,f)$:

  $$r_i(p,f)=max(0,1-\lambda ·|c(p,f)-i\left|\right)$$

  (3)

  where the parameter $\lambda \in (0,1]$ (e.g., $\lambda =0.2$) corresponds to the slope of the triangular function. It should be noted that when $\lambda =1$, we have the special case of the delta function.
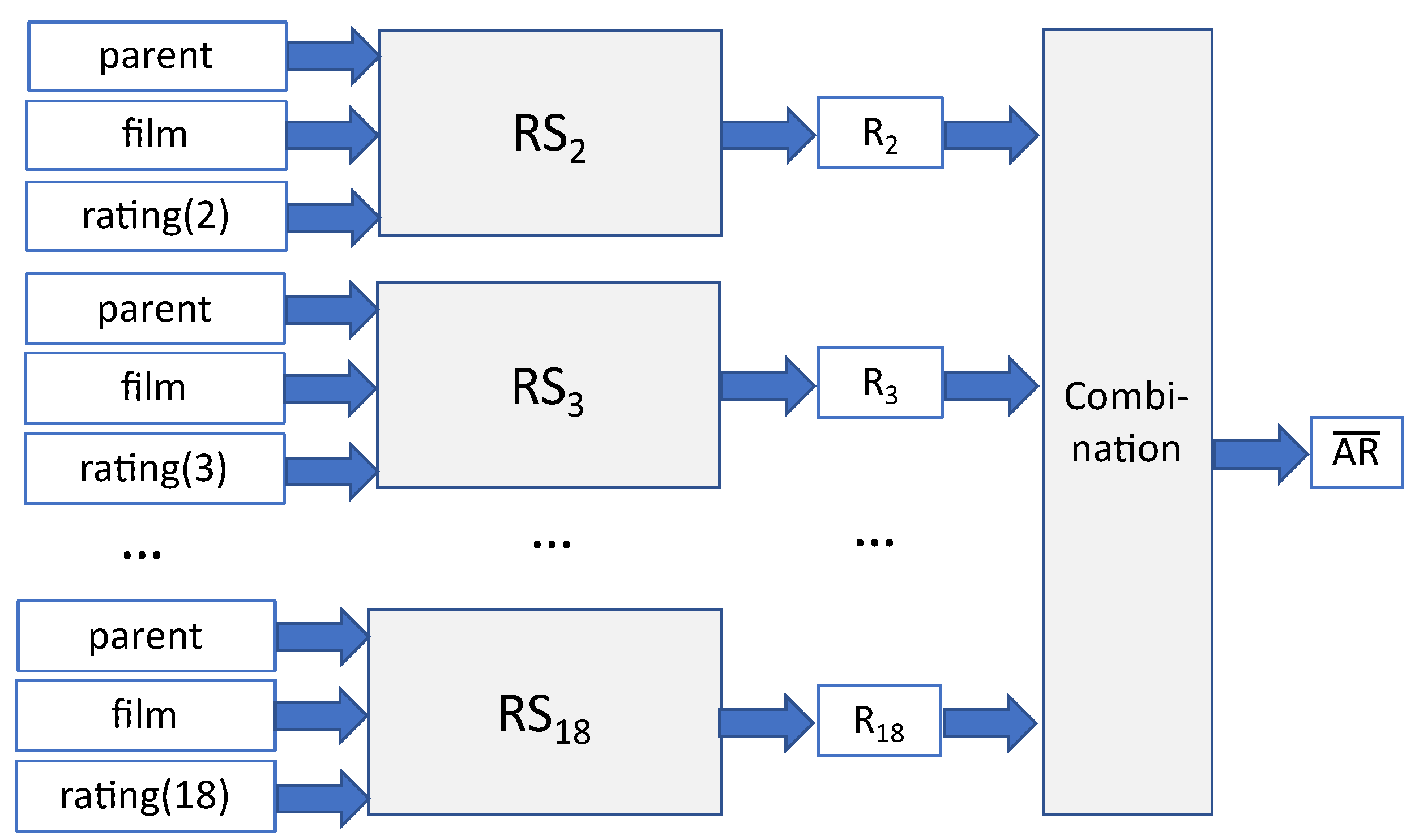
• According to the proposed methodology, the training set $S_i$ for each recommender system $R{S}_i$, $i\in AC$ defined on line 5 in Algorithm 1 is based on Equation (3). Finally, the trainRS procedure on line 7 in Algorithm 1 trains the recommender system $R{S}_i$ by using the training set $S_i$ (i.e., the $(p,f,r_i(p,f))$ triplets that correspond to the same age category).
  The final recommendation combines the resulting recommendations $R_i$ of the recommender systems $R{S}_i$, $i\in AC$ (see Figure 2). The output of each recommender system for a parent, p, and an item, f, corresponds to the predicted belief of that user that that item is appropriate for that age category. One natural way to combine the resulting recommendations, as conducted in classification problems, is to select the age category with the highest recommendation (see Equation (4)) to produce a single cage category as the final output, as follows:

  $$\overline{AR}=\underset{i\in AC}{argmax}{R}_i$$

  (4)
  However, taking into account that the age categories are numerical values, better results are obtained when we obtain the expected value of the recommendation, as defined in the following equation:

  $$\overline{AR}={\displaystyle \frac{{\displaystyle \sum _{i\in AC}}{R}_i·i}{{\displaystyle \sum _{i\in AC}}{R}_i}}$$

  (5)

Algorithm 1: The training phase of the proposed method.

input: $TR,AC$  output: $R{S}_i,i\in AC$

4.2. Testing Phase

The pseudo-code of the testing phase of the proposed method is provided in Algorithm 2. The input of the algorithm consists of a triplet $(p,f,c(p,f\left)\right)$ from the testing set, the age categories $AC$, and the $\left|AC\right|$ recommender systems $R{S}_i$, $i\in AC$ that were trained in the training phase of the method (see Algorithm 1). The output is the prediction of the age category. According to the proposed methodology, we combine the output $R_i$ of the recommendation of each recommender system $R{S}_i$ to obtain the expected value of the recommendations (see line 4 in Algorithm 2.   

Algorithm 2: The proposed application method of recommender systems to predict personalized film age ratings for parents. This algorithm shows the testing phase of the proposed method.

input: $P,I,c,AC$  output: $\overline{AR}$

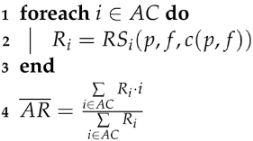5. Experimental Results

5.1. Dataset

We conducted our experiments using the age ratings provided by the users from the Common Sense Media site [9] (data were obtained from [9] and are available from [9], with permission from Common Sense Media). The site allows its users to specify their own age ratings on any movie they want. This enables our system to train its models on the personal age ratings provided by each user and predict personalized ratings on unrated movies, similar to how preference ratings are used in classic recommender system scenarios. The original dataset contains $50,781$ age classifications on $12,545$ movies, by $45,030$ users. The dataset was split randomly into training and test sets, with the test set containing approximately $6\%$ of the triplets of the dataset. Figure 3 shows the distribution of the various age values over all entries in the test set.

5.2. Performance Evaluation

We performed a wide range of experiments to evaluate the performance of the proposed system. All RMSE values reported are the average of five identical runs per value, with only minor differences between the averaged values observed in the second decimal digits.

We first performed several experiments on the shapes of the functions that generated the values $r_i(p,f)$. We employed three different types of functions, namely, the aforementioned linear function shown in Equation (3), a normal (Gaussian) distribution-like function, and a Laplace distribution-like function. In the last two cases, the maximum value was set to 1 (as in the linear function), while the variance and diversity parameters, respectively, were set to $1/\lambda$, which led to similar behavior of the $\lambda$ parameter in all three cases (i.e., the larger the value, the wider the range of non-zero values). We performed several experiments, using only the information contained in the original training set, in order to find the most efficient function to employ, as well as the optimal value of $\lambda$. The results of those experiments are shown in Figure 4. As expected, the Laplace and Gaussian functions performed similarly, with the Laplacian one yielding the best result for a $\lambda$ value of 0.9. One can also observe that both high and low values of $\lambda$ behaved poorly, which is to be expected. Low values of $\lambda$ do not differentiate the different age categories enough (due to a wide range of consecutive age categories receiving $r_i(p,f)$ values close to the highest one, whereas high $\lambda$ values lead to just one age category receiving a high $r_i(p,f)$ value, while the values of the rest will be almost zero (similar to Equation (2)). Having non-zero $r_i(p,f)$ values for age categories adjacent to $c(p,f)$ helps the recommender systems used in the following step to more easily “locate” the most accurate prediction.

Using the aforementioned parameter values, we then performed extensive experiments using two collaborative filtering recommender systems, namely SCoR [15] and NeuMF [16]. The experiments can be divided into the following three groups:

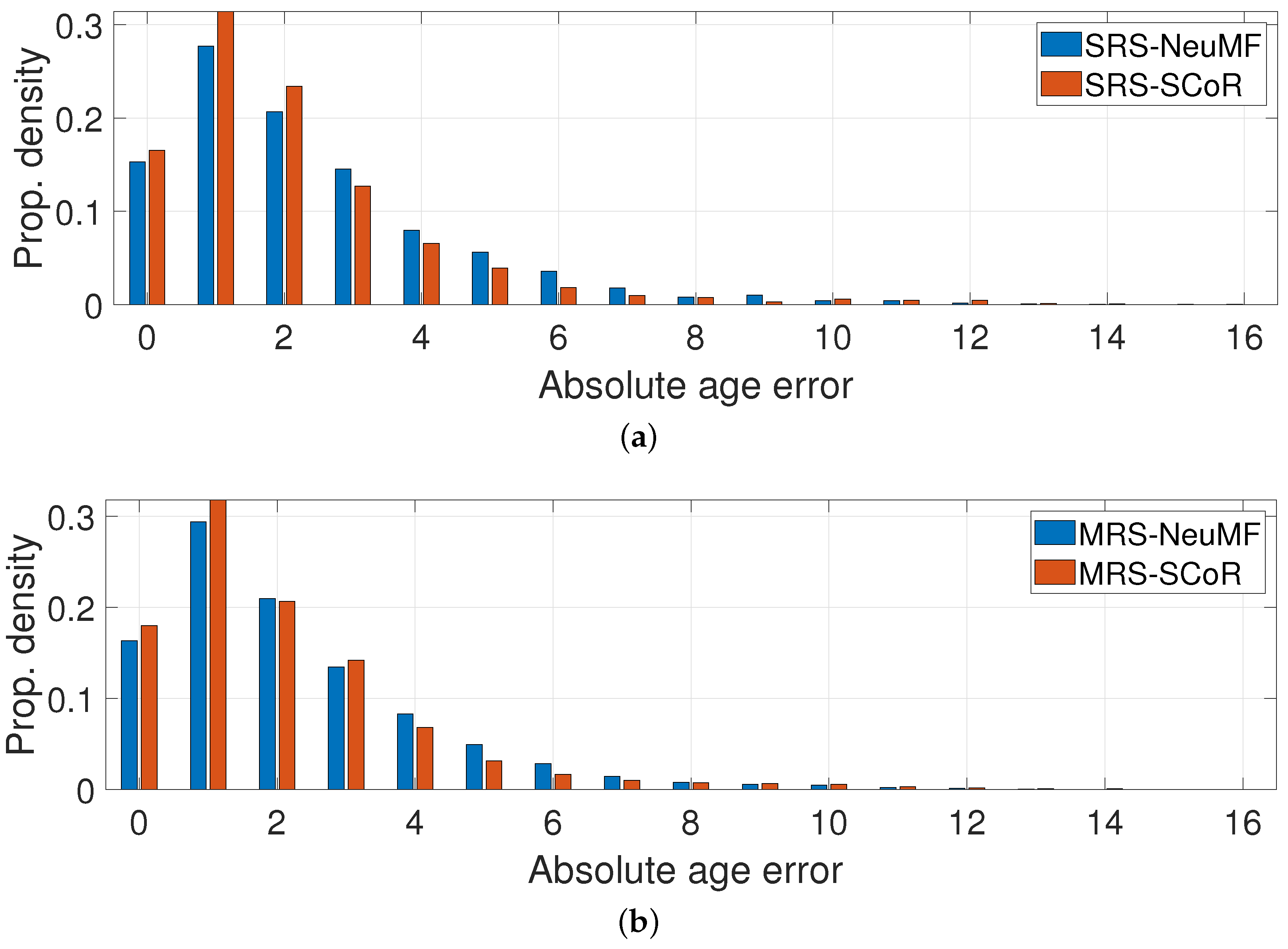
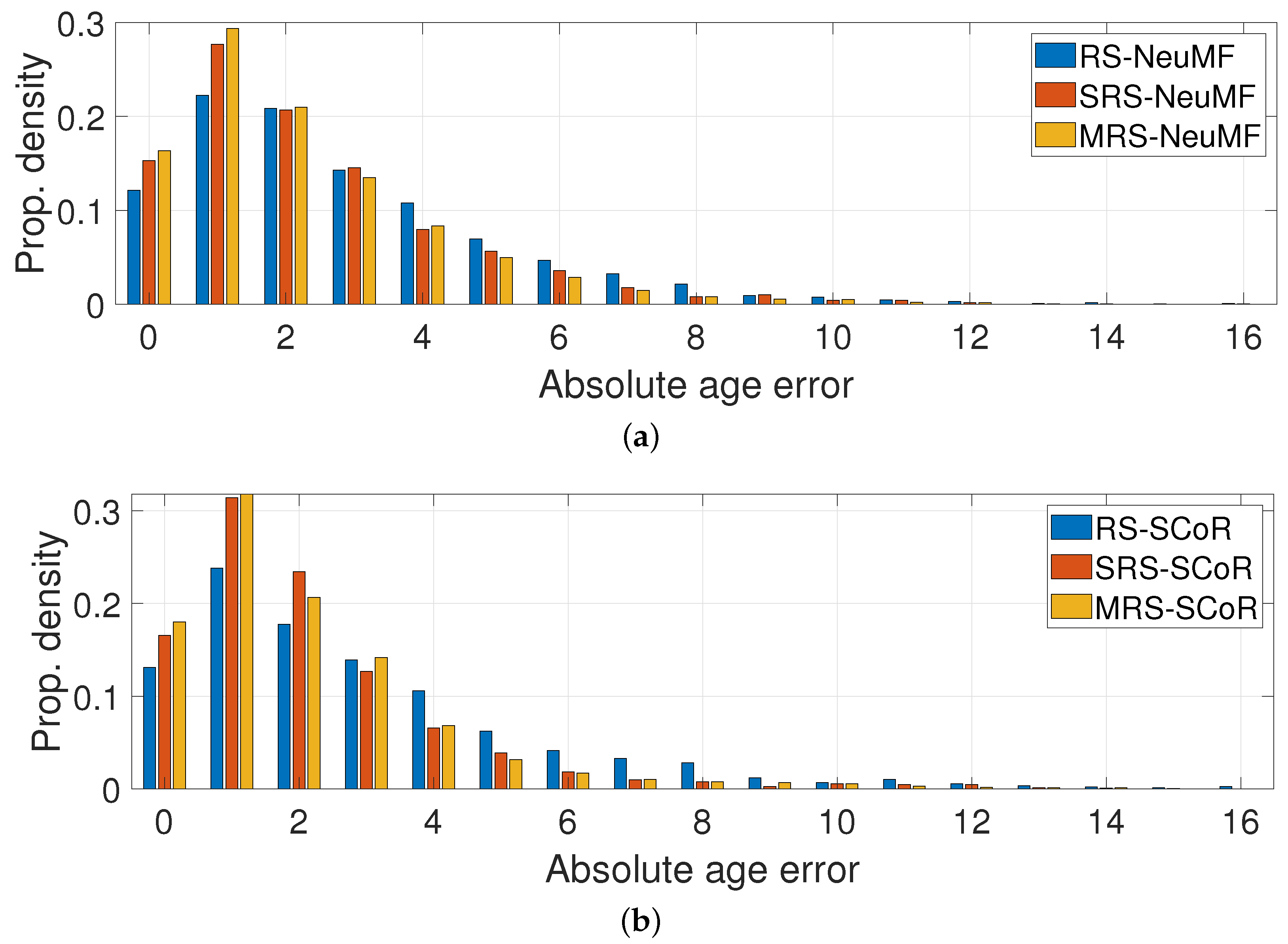
• In the first group (MRSs—multiple recommender systems), the approach used was the one described in this paper (see Figure 2).
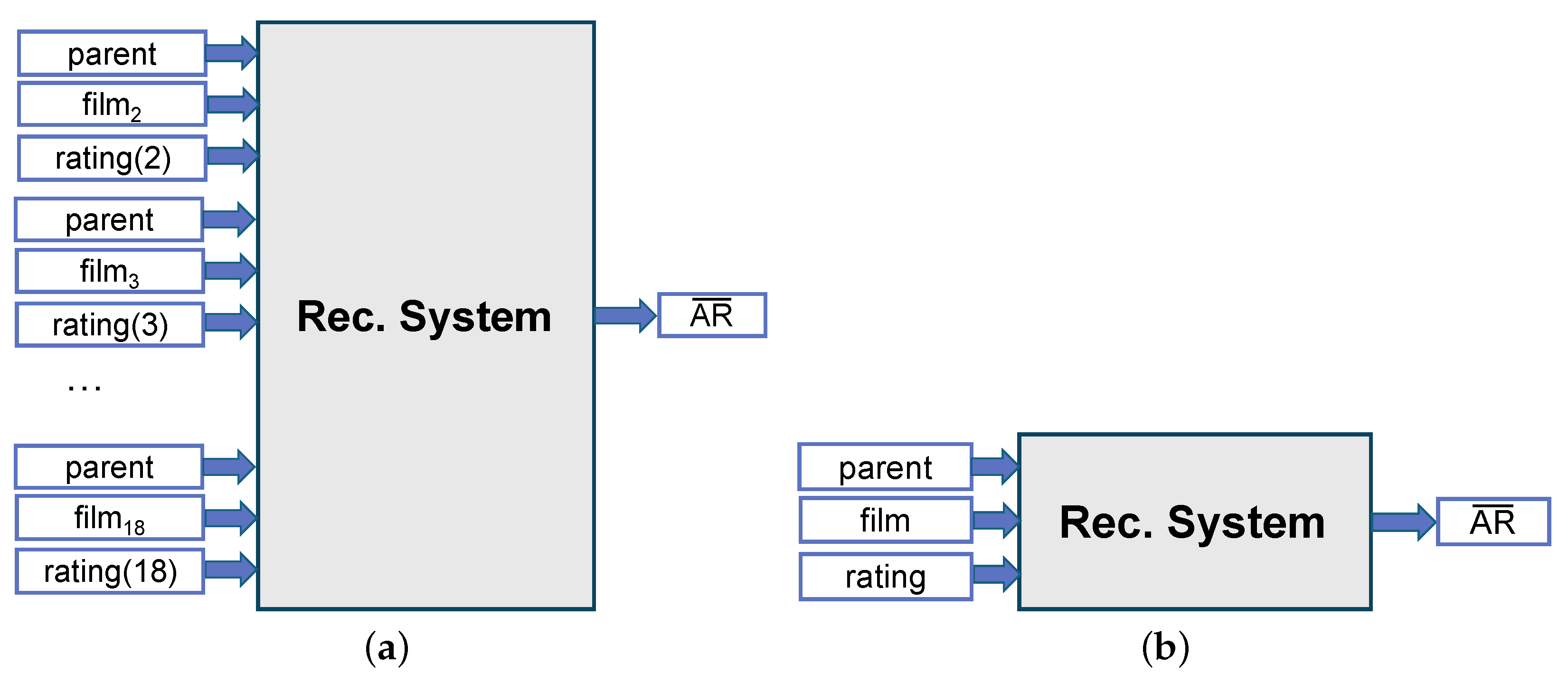
• The second group (SRS—single recommender system) was a variation of the first, where only one recommender system was used, which was trained on the data of all age categories, instead of a separate independent recommender system per age category (see Figure 5a).
• Finally, the “RS” group corresponds to the experiments performed without any dataset transformation, where both recommender systems used (SCoR and NeuMF) were trained on the original age values (see Figure 5b). Those experiments were performed in order to demonstrate the necessity of the data transformation in the first phase.

One can see in the results shown in

Table 1. RMSE values for each system.

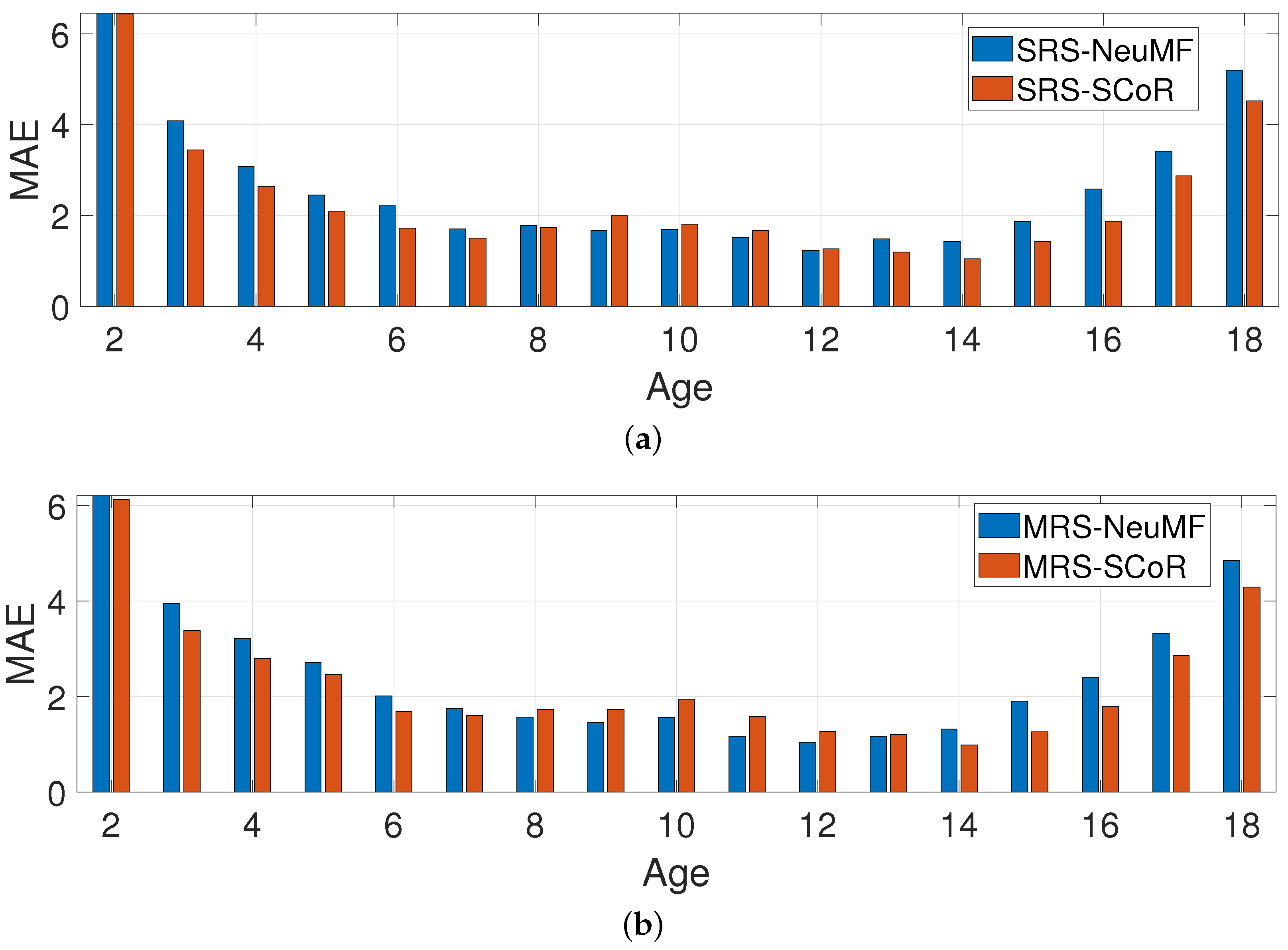
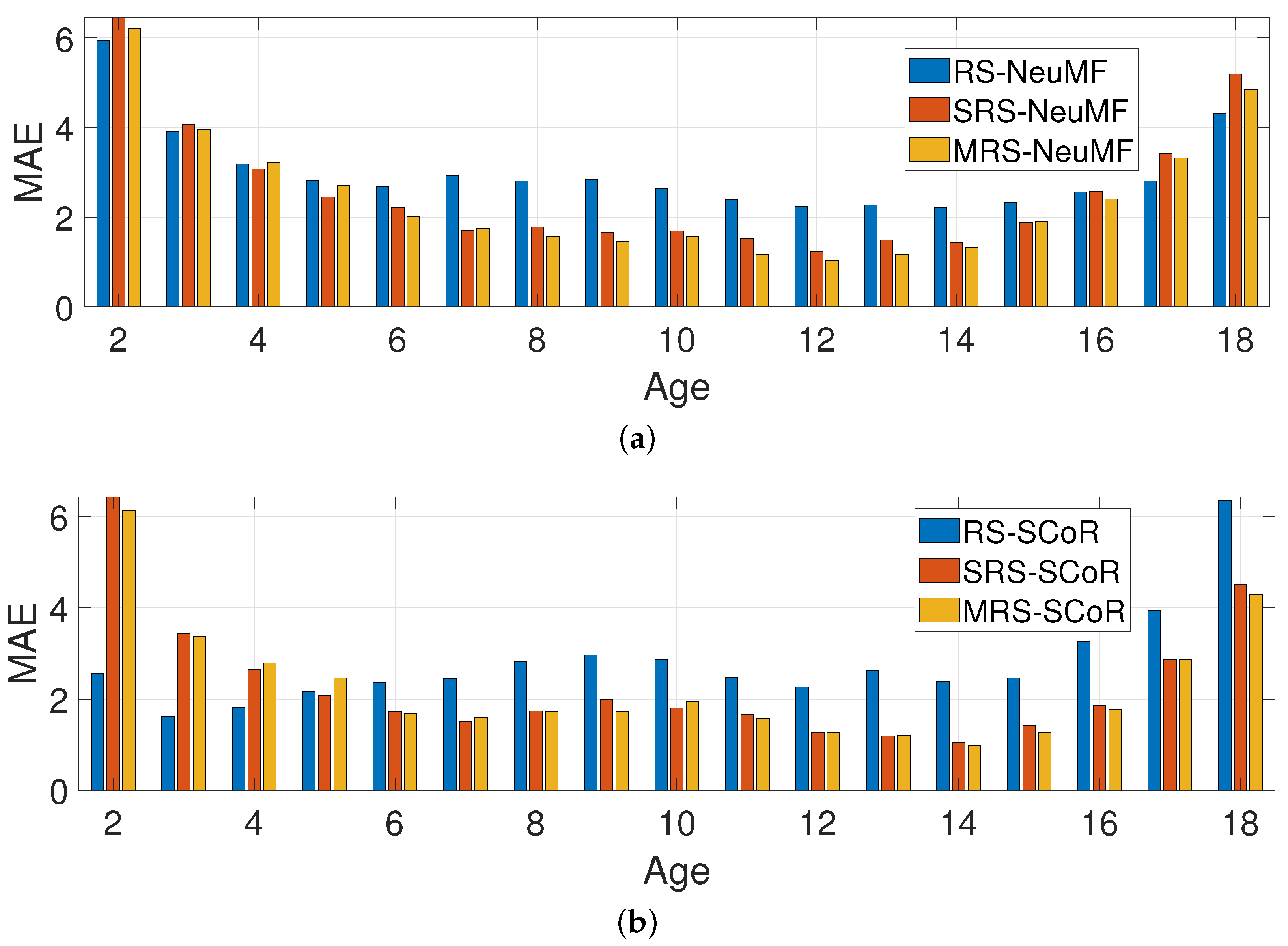
RMSE	RS	SRS	MRS
SCoR	3.99	2.88	2.83
NeuMF	3.67	3.14	2.93

that the MRS-SCoR combination outperforms the rest of the cases. In addition, it is noteworthy that the RMSE values between the SRS and MRS cases while using the same recommender system, which was expected. It is also important to note that not both recommender systems enjoyed similar improvements while employing the data transformation. At the same time, however, in both cases, those improvements are significant.

To gain deeper insight into the functioning of the suggested method, on each of the two recommender systems used, we also demonstrate the mean average error for all entries in the test file, per the “correct” age category. The results are presented in Figure 6. One can see that SCoR outperformed NeuMF in most age categories except for a narrow range in the middle of the entire age category range. One can also see that most expediencies appeared in the edge-age categories, which was to be expected, as those age values are the furthest away from the mean of the age category range.

In addition, Figure 7 displays the ratio of entries from the test file that were predicted with a given absolute error value (rounded to the closest integer). For instance, the ratio presented in the bars corresponding to the value of 0 on the x-axis shows the ratio of test file entries predicted with perfect accuracy. One can see that the MRS framework leads to slightly more test file entries with smaller errors. In addition, it is apparent that the SCoR recommender system benefits more from the proposed data transformation technique since its ratios on the smaller errors are higher; in contrast, its ratios on the higher errors are smaller than NeuMF.

We also present similar plots in order to compare the various frameworks (RS, SRS, MRS) on a given recommender system. These are shown in Figure 8 and Figure 9. In Figure 8, the benefit of the proposed technique (namely MRS but also SRS) is apparent for all age categories, compared to RS, except for the edge-age categories, where the use of the original age values (with no data transformation) leads to smaller errors. It is also noteworthy that RS-NeuMF exhibits similar behavior across both ends of the age category range, whereas RS-SCoR tends to perform poorly, particularly with the higher age category values. In Figure 9, the benefit of the proposed technique is also apparent, as it is shown that for both SCoR and NeuMF, the use of MRS (and SRS to a slightly smaller extent) leads to a higher ratio of entries for the test file, predicted with smaller absolute errors.

Finally, we performed experiments using the aforementioned parameter values (the Laplace-like function with $\lambda =0.9$), which provided the best RMSE values (see Table 1). These experiments were designed to compare the two methods of combining various recommendations into the final one (see Equations (4) and (5)). As mentioned before, Equation (5) produced the best results, specifically an RMSE of 2.83, as reported in Table 1, whereas the corresponding value while employing Equation (4) was 2.97.

6. Conclusions

This study presents a novel methodology that applies recommender systems (RSs) to predict personalized film age ratings for parents. By leveraging multiple RSs, with each RD tailored to a specific age category, our approach generates nuanced recommendations that align with personalized parental perceptions of age-appropriate content. The proposed system significantly outperformed single-system approaches in predictive accuracy, as demonstrated by experimental evaluations using the Common Sense Media dataset.

From a practical perspective, this methodology holds substantial implications for improving decision-making in digital platforms. Parents often grapple with selecting suitable content for their children, especially given the subjective and culturally diverse nature of age ratings. The personalized recommendations generated by our approach empower parents with tailored guidance, reducing the cognitive load associated with such decisions and enhancing user satisfaction. Furthermore, this system offers a flexible framework that can be adapted to other domains, such as educational tools, gaming platforms, and multimedia streaming services, where age-appropriate content is a concern.

The overall benefits of our approach include enhanced accuracy in recommendation generation, adaptability across varying datasets and cultural contexts, and scalability for integration into large-scale systems. By shifting the paradigm from generic age ratings to personalized recommendations, this methodology bridges the gap between standardized guidelines and individual parental preferences.

Future research could expand upon this work by applying the methodology to larger and more diverse datasets, exploring additional recommendation algorithms, and integrating feedback loops for continuous improvement. Moreover, cross-domain applications could be examined to validate the system’s versatility and robustness.

In conclusion, the proposed approach contributes to the field of personalized recommendation systems by addressing a specific, impactful challenge faced by parents. It also sets the foundation for further innovations in the broader domain of content classification and user-centric recommendation strategies.