Exploratory Study of a Green Function Based Solver for Nonlinear Partial Differential Equations

Abstract

This work explores the numerical translation of the weak or integral solution of nonlinear partial differential equations into a numerically efficient, time-evolving scheme. Specifically, we focus on partial differential equations separable into a quasilinear term and a nonlinear one, with the former defining the Green function of the problem. Utilizing the Green function under a short-time approximation, it becomes possible to derive the integral solution of the problem by breaking it into three integral terms: the propagation of initial conditions and the contributions of the nonlinear and boundary terms. Accordingly, we follow this division to describe and separately analyze the resulting algorithm. To ensure low interpolation error and accurate numerical Green functions, we adapt a piecewise interpolation collocation method to the integral scheme, optimizing the positioning of grid points near the boundary region. At the same time, we employ a second-order quadrature method in time to efficiently implement the nonlinear terms. Validation of both adapted methodologies is conducted by applying them to problems with known analytical solution, as well as to more challenging, norm-preserving problems such as the Burgers equation and the soliton solution of the nonlinear Schrödinger equation. Finally, the boundary term is derived and validated using a series of test cases that cover the range of possible scenarios for boundary problems within the introduced methodology.

1. Introduction

In this work, we explore the potential of the weak solution of a general partial differential equation (PDE) as an efficient, high-order numerical scheme. In particular, we are interested in PDEs that commonly arise in the modeling of continuum and physical media, such as balance-like differential equations. These equations relate the time variation of a physical magnitude to the spatial variation of its flux and the production or destruction terms—which tend to be nonlinear. This introductory approach serves as the first step towards a numerical methodology to solve such nonlinear PDEs with arbitrary boundary conditions by means of their weak or integral solution, defined by the Green function of the problem. Therefore, we first focus on the mathematical description of the integral solution, demonstrating how the Green function defines its properties and affects the initial and boundary conditions, before addressing the peculiarities of its numerical transposition into a time-evolving scheme. Finally, we demonstrate and validate the potential of the methodology through simple yet illustrative toy models.

Consequently, we have organized the paper into two main sections: a description of the mathematical foundations of the method and its translation into a numerical algorithm to solve the time-evolving problem. In the first section, we begin with the general integral expression of the solution and then separate each of its contributions, identifying a quasilinear term, a nonlinear term, and a boundary term, the details of which will be introduced and analyzed. The only strong assumption required for this methodology is the short-time approximation, i.e., that the time intervals at which we obtain the solution are separated by a short time-step, $\tau \ll 1$. This approximation is necessary for handling the integral terms numerically and, more importantly, for obtaining the Green function of the problem. Indeed, under this hypothesis, the Green function can be understood as the integral kernel of the solution, propagating or filtering the initial condition from one time frame to the next while satisfying the PDE and its boundary conditions. The nonlinear terms are then included by means of the variation of parameters technique, also through integration involving the Green function. Thus, this function arises as the key element for obtaining the solution to the problem, as it encapsulates the quasilinear part of the PDE. Consequently, we derive its closed analytical form for the PDEs of interest and provide a general series expansion in time for its appropriate implementation.

The numerical computation of the integral solution is consequently organized to follow the gradual levels of complexity inherent to the time-evolving solution: the quasilinear propagation of the initial condition, the integration of the nonlinear terms, and the boundary conditions. As can be deduced, the accuracy and convergence of the integral scheme depend on the appropriate implementation of the Green function; thus, each of these steps revolves around its interaction with the function. The first step involves defining the numerical Green function, which is deduced from its combination with a proper spatial representation of the discrete unknown function. We, therefore, introduce an efficient discretization that produces a numerical translation that is both accurate and straightforward, adapting a collocation scheme to ensure convergence and consistency. In this process, the usual Courant–Friedrichs–Lewy (CFL) number naturally arises as a non-dimensional group of the problem, showing the potential of the method for operating outside the usual limitations. Then, we study the nonlinear terms, requiring a numerical investigation of their integration over the time-step. As before, we introduce an interpolation methodology into the integral scheme. In particular, we adapt a numerical quadrature based on Runge–Kutta schemes. Finally, we examine the boundary term, showing how the numerical equivalent of the integral term becomes a localized contribution, which is easy to incorporate into the overall time-evolving scheme.

Being an exploratory study, we limit ourselves in this initial work to simple spatial domains—one-dimensional—in order to avoid overshadowing the behavior and performance of the method with the complexity of grid design.

To conclude this introduction, we present a brief historical review of the use of weak solutions as numerical methodologies to provide some context and rationale for the construction of the method presented in this work.

Some Historical Background on the Use of Integral Solutions as Numerical Schemes

The use of weak or integral schemes to solve PDEs has a long history, running parallel to the development of classical numerical schemes.

Notably, the foundational works of Wehner and Wolfer [1,2,3] introduced efficient numerical methods based on the Green function, incorporating theoretical advances like Path-sum techniques and stochastic differential equations, although constrained by the computational resources of their time.

Following these developments, Soler and Donoso [4,5] and others [6,7,8] applied similar methodologies, advancing Lagrangian particle methods. Drozdov [9,10] further linked the numerical Green function to probability distributions, while the Distributed Approximating Function theory (DAF) [11] provided a formal mathematical basis for propagating initial conditions. Among the many adaptations of this theory towards the use of weak solutions, we point out the work by Zhang and Wei [12], who developed and introduced the Discrete Singular Convolution (DSC) method, applying weak solutions to Navier–Stokes and fluid-like PDEs [13,14]. Furthermore, with the wave of more sophisticated numerical techniques, some of these works had interesting follow-ups with different discretization techniques, such as wavelets [15], integral kernels as substitutes of the Dirac delta [16], Fast transforms [17], Chebyshev discretization [18], Monte-Carlo simulations [19] and so on.

Among these, three prominent families of numerical methods are worth highlighting due to their relevance to our work.

The first of them being the Exponential Integral methods (ExpRK). These methods separate the PDE into quasilinear and nonlinear terms, using an exponential operator as the propagating element—similar to the Green function [20,21,22,23]. They are widely used for stiff problems, allowing us to implement arbitrary nonlinear terms with high levels of accuracy.

The next family of numerical methods are the Lagrangian or particle methods. These methods are highly versatile and often connected to weak solutions of PDEs. Recent advances, particularly in Smoothed Particle Hydrodynamics (SPH), have improved energy conservation, boundary conditions, and time integration [24,25,26].

The last family of methods are the Lattice Boltzmann (LB) methods. These methods provide a mesoscopic representation of dynamics and ability to simulate complex systems with high accuracy. This approach intertwines with the interpretation of the Green function as the probability distribution of the quasilinear operator, in the same manner that Fokker–Planck and Langevin equations are different scale representations of the problem. Therefore, while they are limited by the careful selection of parameters like relaxation times and time steps to ensure stability and accuracy, often validated through agreement with analytical solutions, they allow us to directly handle complex nonlinearities. Despite challenges in stability, particularly for coarse or under-resolved meshes, LB methods remain powerful tools for simulating nonlinear dynamics and exploring parameter spaces across a wide array of physical systems [27,28,29].

Modern refinements of these original methods include high-order integral algorithms for nonlinear problems (often applied to plasma physics) [30,31,32,33]. Moreover, with advances in Machine Learning and Quantum computing, new approaches are emerging to solve PDEs numerically while retaining physical meaning [34,35].

However, to the best of our knowledge, the apparently simple integral methodologies introduced by Wehner, Wolfer, Soler, and Donoso have yet to be fully revisited with modern discretization techniques like spectral and pseudo-spectral methods [36], discontinuous Galerkin methods [37,38], Residual Distribution [39], and the exploration on Birkhoff interpolation schemes [40,41].

As a result, this work aims to merge these original methodologies with appropriate numerical techniques, preserving their advantages—such as handling discontinuities and complex nonlinearities—while leveraging the Green function’s interpretation as transition probabilities to guide and simplify algorithm development.

2. Mathematical Foundations of the Method

The aim of the method is to solve balance-like partial differential Equations (PDEs) that can be cast without losing generality as:

$$\left({\displaystyle \frac{\partial }{\partial t}}-{\mathcal{L}}_{\overrightarrow{x},t}\right)u\left(\overrightarrow{x},t\right)={\mathfrak{A}}_{\overrightarrow{x},t}u\left(\overrightarrow{x},t\right)=\mathsf{\Phi }\left(\overrightarrow{x},t\right),$$

(1)

where u is the unknown function and $\overrightarrow{x}$ is the n-dimensional space under study. The time variable, t, is left separated from the dimensionality of the problem as the method is defined for time-evolving solutions. Hence, the operator ${\mathcal{L}}_{\overrightarrow{x},t}$ will include the spatial derivatives of the PDE and, when grouping spatial and temporal derivatives, we will refer to the more general operator, ${\mathfrak{A}}_{\overrightarrow{x},t}$.

A general, quasilinear (we use the quasilinear definition presented in [42]) differential spatial operator ${\mathcal{M}}_{\overrightarrow{x},t}$ can be defined as follows:

$${\mathcal{M}}_{\overrightarrow{x},t}=\sum _{i=1}^{o_2}{\overrightarrow{a}}_i\left(\overrightarrow{x},t\right)·{\displaystyle \frac{{\partial }^i}{\partial {\overrightarrow{x}}^i}},$$

(2)

where $o_2$ is the highest order of the spatial derivatives and ${\overrightarrow{a}}_i$ will be called transport coefficients. It is important to recall that their dimension will vary together with the order of the derivative to keep the general PDE as a scalar, i.e., the first-order derivative will require a vector transport coefficient, the second-order a matrix, the third a third-order tensor, and so on. Same thing goes for the product between the coefficient and the set of derivatives—it will be the standard inner product with the corresponding order of the derivative that is applied at. The highest order of the temporal derivative, $o_1$, is set equal to 1 for this work, therefore it is omitted through the derivation.

Finally, the function $\mathsf{\Phi }$ groups the rest of the terms of the equation that do not fit with the ones already described and will be called, for simplicity, non-homogeneous or nonlinear term (although it might be linear over some of the variables under study). This term can group not only arbitrary terms but also quasilinear terms that might fit into the definition of the operator (2).

In the following, we define the spatial operator of the PDE as the highest order derivative term, of order $o_2$, and the rest will be grouped into the $\mathsf{\Phi }$ term. This choice is justified not only for simplicity but also to reach a mathematical procedure and solutions of the problem in a systematic and consistent manner. Hence, the mathematical shape of the spatial operator of the PDE, ${\mathcal{L}}_{\overrightarrow{x},t}$, can be defined as follows,

$${\mathcal{L}}_{\overrightarrow{x},t}={\overrightarrow{\overrightarrow{a}}}_{o_2}\left(\overrightarrow{x},t\right)·{\displaystyle \frac{{\partial }^{o_2}}{\partial {\overrightarrow{x}}^{o_2}}}.$$

(3)

Together with Equation (1), a set of initial and boundary conditions will close the mathematical formulation of the problem object of this work. We define a mathematical control volume of study, $\mathcal{V}$, and its corresponding boundary surface, $\mathcal{S}$. This control volume is divisible in a differential sense, being $d\mathcal{V}$ its element of volume or differential volume and, in a same manner, $d\mathcal{S}$ the surface element or differential surface. The problem of interest will be an initial value problem (IVP), meaning that the boundary conditions in time are always set at the initial time frame, $t_0$.

The mathematical shape of the boundary conditions of the problem will vary depending on the spatial order of the PDE. For each $o_2$, and for different volumes of study, different allowed boundary conditions will arise, each one with their own peculiarities and mathematical shape. Thus, we leave their particular expression aside for the moment and they will be introduced afterwards for each specific problem.

2.1. Integral Solution of the Problem in Terms of the Green Function

We can define the solution of the initial value problem defined by Equation (1) and a set of boundary conditions by means of an integral scheme that separates the contributions of the different terms in play.

$$\begin{array}{cc}\hfill u\left(\overrightarrow{x},t\right)& =\int u\left({\overrightarrow{x}}^{\prime },t_0\right){\mathcal{G}}_{o_2}\left(\overrightarrow{x},t|{\overrightarrow{x}}^{\prime },t_0\right)d{V}^{\prime }\hfill \\ \hfill & +\int \int \mathsf{\Phi }\left({\overrightarrow{x}}^{\prime },t^{\prime }\right){\mathcal{G}}_{o_2}\left(\overrightarrow{x},t|{\overrightarrow{x}}^{\prime },t^{\prime }\right)d{\mathcal{V}}^{\prime }d{t}^{\prime }\hfill \\ \hfill & -\int \oint {\tilde{\overrightarrow{P}}}_{\mathcal{L}}\left[u\left({\overrightarrow{x}}^{\prime },t^{\prime }\right),{\mathcal{G}}_{o_2}\left(\overrightarrow{x},t|{\overrightarrow{x}}^{\prime },t^{\prime }\right)\right]·d{\overrightarrow{\mathcal{S}}}^{\prime }d{t}^{\prime }.\hfill \end{array}$$

(4)

where ${\mathcal{G}}_{o_2}$ is the Green function associated with the operator $\mathcal{L}$ and ${\tilde{\overrightarrow{P}}}_{\mathcal{L}}$ is the generalized flux or concomitant of the problem the shape of which will define the boundary conditions over the surface $\mathcal{S}$. This expression of the integral scheme is a generalization of what is usually presented as the weak solution of a PDE the details of which can be consulted in [43,44]. The tilde over the generalized flux refers to the adjoint problem, required as we will introduce to define the generalized Green theorem. We have selected a specific terminology to describe the spatio-temporal dependencies of the Green function, that follows a common physical interpretation of these functions: transition probabilities. As a result, we interpret the Green function as the Kernel that makes the initial information at state $\left({\overrightarrow{x}}^{\prime },t^{\prime }\right)$ propagate towards a final state, $\left(\overrightarrow{x},t\right)$.

Therefore, we can identify the three terms that define the time-evolving solution, being propagated from the initial time frame, $t_0$:

• The first term propagates the initial condition. Starting on time $t_0$, the Green function takes the information at the initial state and filters it through the integral, so the result satisfies the operator ${\mathcal{L}}_{\overrightarrow{x},t}$ as defined in Equation (3).
• The second integral contains all the mathematical terms that are left aside from the operator ${\mathcal{L}}_{\overrightarrow{x},t}$ and grouped on the nonlinear or non-homogeneous terms. This term is integrated through time and volume, meaning that it includes not only the values of the nonlinear terms at the initial state (like the first term) but also how their variation between states.
• The last term takes into account how the boundary conditions of the problem will contribute to the solution. Indeed, it is the surface integral of the adjoint surface flux (or concomitant function) defined by a pair of the unknown function and the Green function. As the shape of the concomitant will depend on the order of the operator, we will introduce it later for the operators of interest in this study.

Thus, obtaining the Green function and the expression of the generalized flux will provide a general expression for the solution of the problem. In particular, the Green function must satisfy the homogeneous partial differential equation of the problem, i.e., without the $\mathsf{\Phi }$ term and with a net flux equal to zero at the boundaries. Moreover, we can see that unless it has as initial condition a generalized Dirac delta function, expression (4) will not produce the unknown function for the limit when t tends towards $t_0$. These two conditions can be understood as the way to guarantee that the Green function does not introduce artificial, spurious information to the problem: neither through the spatial or temporal boundaries. While the fundamental mathematical operative under these assumptions can be extracted from reference [45], an appropriate study with the required details is left for a future extended work. For the purposes of this work, which aims to explore numerical implementation, only the final expressions used are introduced.

So the only term that appears in expression (4) that is not in an explicit form is the last one, that includes the boundary contributions. As it will be dependent of the operator $\mathcal{L}$, we need to state its order first, $o_2$, in order to fully develop the term. To do so, we first look at the definition of the concomitant function, $\overrightarrow{P}$ that the generalized Green theorem introduces,

$$\left.\begin{array}{c}\overrightarrow{\nabla }·\overrightarrow{P}\left(u,vs.\right)=u\mathcal{L}vs.-vs.\tilde{\mathcal{L}}u\\ \overrightarrow{\nabla }·\tilde{\overrightarrow{P}}\left(u,vs.\right)=u\tilde{\mathcal{L}}vs.-vs.\mathcal{L}u\end{array}\right\}⟶\tilde{\overrightarrow{P}}(u,v)=-\overrightarrow{P}(v,u),$$

(5)

where the tilde quantities refer to the mathematical problem defined by the adjoint operator and u and v stand for general test functions. Introducing the condition that the Green function’s flux must be zero at the boundaries—or, from the perspective of its boundary conditions, they must be the ones of the PDE but in a homogeneous expression—we can recover the possible boundary conditions for a given derivative order, $o_2$. For this initial exploration we will only look into the first two orders, $o_2=\left\{1,2\right\}$, that coincide, respectively, with the advective problem [44] and the diffusive one.

• First-order operator
  From expression (5) we can obtain the generalized flux, ${\overrightarrow{P}}_1\left(u,v\right)$ for the advective problem, and particularizing it for the boundary term of the integral scheme (4), we recover,

  $${\tilde{\overrightarrow{P}}}_1\left(u,{\mathcal{G}}_1\right)=-{\overrightarrow{a}}_{1}u{\mathcal{G}}_1⟶\int \oint {\overrightarrow{a}}_{1}u{\mathcal{G}}_1·d{\overrightarrow{\mathcal{S}}}^{\prime }dt.$$

  (6)
  Therefore, this operator will only allow for Dirichlet boundary conditions, imposed over the unknown function, u, and the Green function will necessarily be a generalized Dirac delta at the boundaries in the same way it was at the initial condition.
• Second-order operator
  On the other hand, this operator allows for Dirichlet, Neumann and Mixed boundary conditions as its generalized flux is,

  $${\tilde{\overrightarrow{P}}}_2\left(u,{\mathcal{G}}_2\right)=u\overrightarrow{\nabla }·\left({\overrightarrow{\overrightarrow{a}}}_2{\mathcal{G}}_2\right)-{\mathcal{G}}_2{\overrightarrow{\overrightarrow{a}}}_2·\overrightarrow{\nabla }u.$$

  (7)
  Therefore, depending on which of the three possible kinds of boundary condition we wan to impose over the unknown function, we will need the Green function to cancel the rest. For example, if we want to impose a Dirichlet boundary condition over u the term with its derivative, i.e., the Neumann one, need to be canceled, therefore forcing the Green function to have also a Dirichlet boundary condition. Furthermore, the same logical procedure can be applied for Neumann boundaries, from which we can derive the already introduced condition: the Green function must satisfy the homogeneous version of the unknown function in order not to contribute with spurious information at the boundaries.

Consequently, the full explicitly defined integral scheme that defines the solution of the partial differential equation can be defined, for the First and Second operators as,

• First-order operator

  $$\begin{array}{cc}\hfill u\left(\overrightarrow{x},t\right)& =\int u\left({\overrightarrow{x}}^{\prime },t_0\right){\mathcal{G}}_1\left(\overrightarrow{x},t|{\overrightarrow{x}}^{\prime },t_0\right)d{\mathcal{V}}^{\prime }\hfill \\ \hfill & +\int \int \mathsf{\Phi }\left({\overrightarrow{x}}^{\prime },t^{\prime }\right){\mathcal{G}}_1\left(\overrightarrow{x},t|{\overrightarrow{x}}^{\prime },t^{\prime }\right)d{\mathcal{V}}^{\prime }d{t}^{\prime }\hfill \\ \hfill & +\int \oint \left[{\overrightarrow{a}}_{1}u\left({\overrightarrow{x}}^{\prime },t^{\prime }\right){\mathcal{G}}_1\left(\overrightarrow{x},t|{\overrightarrow{x}}^{\prime },t^{\prime }\right)\right]·d{\overrightarrow{\mathcal{S}}}^{\prime }d{t}^{\prime }.\hfill \end{array}$$

  (8)
• Second-order operator

  $$\begin{array}{cc}\hfill u\left(\overrightarrow{x},t\right)& =\int u\left({\overrightarrow{x}}^{\prime },t_0\right){\mathcal{G}}_2\left(\overrightarrow{x},t|{\overrightarrow{x}}^{\prime },t_0\right)d{\mathcal{V}}^{\prime }\hfill \\ \hfill & +\int \int \mathsf{\Phi }\left({\overrightarrow{x}}^{\prime },t^{\prime }\right){\mathcal{G}}_2\left(\overrightarrow{x},t|{\overrightarrow{x}}^{\prime },t^{\prime }\right)d{\mathcal{V}}^{\prime }d{t}^{\prime }\hfill \\ \hfill & -\int \oint \left[u\left({\overrightarrow{x}}^{\prime },t^{\prime }\right){\overrightarrow{\nabla }}^{\prime }·\left({\overrightarrow{\overrightarrow{a}}}_2{\mathcal{G}}_2\right)-{\mathcal{G}}_2{\overrightarrow{\overrightarrow{a}}}_2·{\overrightarrow{\nabla }}^{\prime }u\left({\overrightarrow{x}}^{\prime },t^{\prime }\right)\right]·d{\overrightarrow{\mathcal{S}}}^{\prime }d{t}^{\prime }.\hfill \end{array}$$

  (9)

Thus, it is only left to obtain the Green functions for each of the operators to fully close the mathematical problem and pass to its numerical implementation. To do so, we introduce the first of our hypothesis, the short-time approximation, that will allow for both an easier resolution of the problem and a straightforward numerical transposition regarding time-evolving solutions.

2.2. The Short-Time Approximation

We will now introduce our first strong hypothesis of the methodology, directly related to the numerical application of expression (4), that is that the time at which we are solving the unknown function, t, occurs after a short time step from the initial condition, at time $t_0$. In other words, we are interested in how this initial condition or information evolves after a small time step, $\tau \ll 1$, so that,

$$t-t_0=\tau \ll 1,dt=d\tau ,$$

(10)

and introducing this approximation into Equation (4) we get,

$$\begin{array}{cc}\hfill u\left(\overrightarrow{x},t_0+\tau \right)& =\int u\left({\overrightarrow{x}}^{\prime },t_0\right){\mathcal{G}}_{o_2}\left(\overrightarrow{x},t_0+\tau |{\overrightarrow{x}}^{\prime },t_0\right)d{\mathcal{V}}^{\prime }\hfill \\ \hfill & +{\int }_0^{\tau }\int \mathsf{\Phi }\left({\overrightarrow{x}}^{\prime },t_0+{\tau }^{\prime }\right){\mathcal{G}}_{o_2}\left(\overrightarrow{x},t_0+\tau |{\overrightarrow{x}}^{\prime },t_0+{\tau }^{\prime }\right)d{\mathcal{V}}^{\prime }d{\tau }^{\prime }\hfill \\ \hfill & -{\int }_0^{\tau }\oint {\tilde{\overrightarrow{P}}}_{\mathcal{L}}\left[u\left({\overrightarrow{x}}^{\prime },t_0+{\tau }^{\prime }\right),\mathcal{G}\left(\overrightarrow{x},t_0+\tau |{\overrightarrow{x}}^{\prime },t_0+{\tau }^{\prime }\right)\right]·d{\overrightarrow{\mathcal{S}}}^{\prime }d{\tau }^{\prime }\hfill \end{array}$$

(11)

This expression sets the ground for a time evolving numerical scheme where the initial time frame is updated every iteration, making the solution evolve forward in time. One interesting consequence of this approximation is how the dependencies of the Green function change for each of the terms, specially on the first integral term (the one that propagates the initial condition). Without losing generality, we can set ourselves in $t_0=0$, obtaining:

$$u\left(\overrightarrow{x},\tau \right)=\int u\left({\overrightarrow{x}}^{\prime },0\right){\mathcal{G}}_{o_2}\left(\overrightarrow{x},\tau |{\overrightarrow{x}}^{\prime },0\right)d{\mathcal{V}}^{\prime }+(\dots ).$$

(12)

As a result the short-time Green function will only depend on the initial and final spatial positions $\left(\overrightarrow{x},{\overrightarrow{x}}^{\prime }\right)$ and the time step $\tau$. Furthermore, the closer to the initial state the problem is, $\tau ⟶0$, the Green function will recover its initial condition, that is, a Dirac delta. Therefore, the smaller the time step is the more spatially bounded the Green function, a property that will come in handy on the development of a numerical scheme around it.

The rest of the terms in expression (4) are more directly affected by this approximation as they are integrals in time that take into account the contribution of the nonlinear terms and the boundary conditions through the time step. For a small time step, it is possible to simplify them by applying the first mean value theorem for definite integrals [46], reaching:

$$\begin{array}{cc}\hfill u\left(\overrightarrow{x},\tau \right)& =\int \left[u\left({\overrightarrow{x}}^{\prime },0\right){\mathcal{G}}_{o_2}\left(\overrightarrow{x}|{\overrightarrow{x}}^{\prime };\tau \right)+\tau \mathsf{\Phi }\left({\overrightarrow{x}}^{\prime },\mathfrak{t}\right){\mathcal{G}}_{o_2}\left(\overrightarrow{x},\tau |{\overrightarrow{x}}^{\prime },\mathfrak{t}\right)\right]d{\mathcal{V}}^{\prime }\hfill \\ \hfill & -\tau \oint {\tilde{\overrightarrow{P}}}_{\mathcal{L}}\left[u\left({\overrightarrow{x}}^{\prime },\mathfrak{t}\right),\mathcal{G}\left(\overrightarrow{x},\tau |{\overrightarrow{x}}^{\prime },\mathfrak{t}\right)\right]·d{\overrightarrow{\mathcal{S}}}^{\prime },\hfill \end{array}$$

(13)

where $\mathfrak{t}$ is an undefined time value between $t_0$ and $t_0+\tau$.

The time, $\mathfrak{t}$, can be chosen as the initial time step assuming a certain error as in the classic Euler Explicit schemes [47] to recover a similar formulation with the peculiarity of the presence of the Green function as an integral kernel,

$$\begin{array}{cc}\hfill u\left(\overrightarrow{x},\tau \right)& =\int \left[u\left({\overrightarrow{x}}^{\prime },0\right)+\tau \mathsf{\Phi }\left({\overrightarrow{x}}^{\prime },0\right)\right]{\mathcal{G}}_{o_2}\left(\overrightarrow{x}|{\overrightarrow{x}}^{\prime };\tau \right)d{\mathcal{V}}^{\prime }+\epsilon \hfill \\ \hfill & -\tau \oint {\tilde{\overrightarrow{P}}}_{\mathcal{L}}\left[u\left({\overrightarrow{x}}^{\prime },\mathfrak{t}\right),\mathcal{G}\left(\overrightarrow{x},\tau |{\overrightarrow{x}}^{\prime },\mathfrak{t}\right)\right]·d{\overrightarrow{\mathcal{S}}}^{\prime }.\hfill \end{array}$$

(14)

And, depending on the order of the operator and the kind of the boundary conditions it allows, the last term can be included also into the first integral, as an extra nonlinear term. We can therefore identify this group as an extended initial condition, where the nonlinear and boundary terms are added to the original initial condition to be then integrated through the Green function.

It can be observed then that the Green function is nothing but the spatio-temporal filter or interpolator that propagates the information or the extended initial condition in a way that satisfies the PDE. One important extra property can be derived from this idea, that is, the norm or the integral of the Green function over the volume of study in its primed variables must be equal to one. Otherwise, the filter or interpolator will introduce additional or spurious information on the unknown function, not conserving the amount of information available at the initial condition. This reinforces the idea of understanding the Green function as a transition probability as it behaves like one also in terms of its unitary norm. Moreover, this norm must be preserved after any time step as this property must be satisfied, so the area under the Green function on the primed spatial variables, ${\overrightarrow{x}}^{\prime }$ must be kept constant even for $\tau ⟶0$, which is automatically satisfied as the initial condition of the Green function is a Dirac delta, a function with a unitary norm over the primed variables.

2.3. Closed Expressions for the Green Function

Having defined the short time approximation, we are ready to obtain a solution for the Green function knowing that it must satisfy the original partial differential equation without the non-homogeneous terms and satisfying its homogeneous boundary conditions. We start by approximating the Green function at time t by a Taylor series, recovering,

$$\begin{array}{cc}\hfill \mathcal{G}\left(\overrightarrow{x},t|{\overrightarrow{x}}^{\prime },t^{\prime }\right)& =\mathcal{G}\left(\overrightarrow{x},t^{\prime }|{\overrightarrow{x}}^{\prime },t^{\prime }\right)+\left(t-t^{\prime }\right){\mathcal{G}}_t\left(\overrightarrow{x},t^{\prime }|{\overrightarrow{x}}^{\prime },t^{\prime }\right)+\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\left(t-t^{\prime }\right)}^2{\mathcal{G}}_{tt}\left(\overrightarrow{x},t^{\prime }|{\overrightarrow{x}}^{\prime },t^{\prime }\right)+(\dots )+{\displaystyle \frac{1}{n!}}{\left(t-t^{\prime }\right)}^n{\mathcal{G}}_{\left(n\right)}\left(\overrightarrow{x},t^{\prime }|{\overrightarrow{x}}^{\prime },t^{\prime }\right),\hfill \end{array}$$

(15)

where the subscript ${\mathcal{G}}_t$ indicates time derivative. In general, for a quasi linear operator as defined in expression (3) the transport coefficients $a_{o_2}$ will depend on space, $\overrightarrow{x}$, and time, t, so the expression of the time derivatives of the Green function higher than 1 will be the result of the successive application of the operator ${\mathcal{L}}_{\overrightarrow{x},t}$ and the complexity on the derivatives and number of terms will increase exponentially,

$${\mathcal{G}}_t={\mathcal{L}}_{\overrightarrow{x},t}\mathcal{G},{\mathcal{G}}_{tt}={\left({\mathcal{L}}_{\overrightarrow{x},t}\mathcal{G}\right)}_t={\left({\mathcal{L}}_{\overrightarrow{x},t}\right)}_t\mathcal{G}+{\mathcal{L}}_{\overrightarrow{x},t}{\mathcal{G}}_t={\left({\mathcal{L}}_{\overrightarrow{x},t}\right)}_t\mathcal{G}+{\mathcal{L}}_{\overrightarrow{x},t}^2\mathcal{G}.$$

(16)

Indeed, following the general Leibniz rule [48] we recover a general expression for the n-th derivative

$${\mathcal{G}}_{\left(n\right)}=\sum _{k=0}^{n-1}\left({\displaystyle \genfrac{}{}{0pt}{}{n-1}{k}}\right){\left({\mathcal{L}}_{\overrightarrow{x},t}\right)}_{(n-1-k)}{\mathcal{G}}_{\left(k\right)},$$

(17)

that will be applied recursively until the n-th-order is lowered to 1.

If the coefficients inside ${\mathcal{L}}_{\overrightarrow{x},t}$ do not depend on $\left(\overrightarrow{x},t\right)$, then the expansion simplifies considerably, being able to relate each time derivative to the successive application of the spatial operator:

$${\mathcal{G}}_t=\mathcal{L}\mathcal{G},{\mathcal{G}}_{tt}={\mathcal{L}}^2\mathcal{G},(\dots ),{\mathcal{G}}_{\left(n\right)}={\mathcal{L}}^n\mathcal{G}.$$

(18)

In this situation, if we substitute conditions (18) and the fact that the initial condition of the Green function will be a Dirac delta into the Taylor series expansion, Equation (15), we recover:

$$\mathcal{G}\left(\overrightarrow{x},t|{\overrightarrow{x}}^{\prime },t^{\prime }\right)=\stackrel{\mathrm{Exp}\left[\left(t-t^{\prime }\right)\mathcal{L}\right]}{\overbrace{\left[1+\left(t-t^{\prime }\right)\mathcal{L}+{\displaystyle \frac{1}{2}}{\left(t-t^{\prime }\right)}^2{\mathcal{L}}^2+(\dots )+{\displaystyle \frac{1}{n!}}{\left(t-t^{\prime }\right)}^n{\mathcal{L}}^n\right]}}\delta \left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right).$$

(19)

We stress that this result is only valid for operators whose transport coefficients do not depend on $\left(\overrightarrow{x},t\right)$, i.e., transport coefficients that are constant in space and time. In general, when the coefficients do present such dependencies, although we will still recover the exponential term, due to the Leibniz rule a number of extra terms or corrections to the solution will appear. Although these terms will modify the shape of the Green function, they will only begin to appear when the time derivative is applied over the operator itself, that is, starting at the second-order in the Taylor expansion.

Consequently, they will be a second-order contribution in time and, the lower the time step is, the lower the influence of these terms on the final solution. We can cast this new form of the Green function for a general, quasi linear operator as:

$$\mathcal{G}\left(\overrightarrow{x},t|{\overrightarrow{x}}^{\prime },t^{\prime }\right)=\left\{\mathrm{Exp}\left[\left(t-t^{\prime }\right){\mathcal{L}}_{\overrightarrow{x},t}\right]+{\mathsf{\Psi }}_{\mathcal{L}}\right\}\delta \left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right),\mathcal{O}\left({\mathsf{\Psi }}_{\mathcal{L}}\right)={(t-t^{\prime })}^2,$$

(20)

where ${\mathsf{\Psi }}_{\mathcal{L}}$ is this term that groups the aforementioned corrections or variations over the exponential term. It is important to point out that, thanks to the properties of the Dirac delta as a function, the dependencies on $\overrightarrow{x}$ of the terms inside the operator ${\mathcal{L}}_{\overrightarrow{x},t}$ and ${\mathsf{\Psi }}_{\mathcal{L}}$ can be either on $\overrightarrow{x}$ or ${\overrightarrow{x}}^{\prime }$.

The next step will be to expand the Dirac delta appearing in expression (20) in the basis of Eigenfunctions, ${\phi }_p\left(x\right)$, and Eigenvalues, ${\lambda }_p$, that correspond to the space at which we are looking for a solution, i.e., at the domain and quasilinear operator we are studying. This operation can be performed as long as the transport coefficient does not depend either on time or space, and while it might looks as a limitation, we will show how to implement these effects as corrections in the likes of the ${\mathsf{\Psi }}_{\mathcal{L}}$ term. Therefore, we can leave the expression of the Green function in a general form for closed an open domains as,

• Closed Domain

$$\mathcal{G}\left(\overrightarrow{x},t|{\overrightarrow{x}}^{\prime },t^{\prime }\right)=\sum _{p=-\infty }^{\infty }{\displaystyle \frac{{\phi }_p\left(\overrightarrow{x}\right){\phi }_p\left({\overrightarrow{x}}^{\prime }\right)}{{\left|{\phi }_p\right|}^2}}\mathrm{Exp}\left[{\lambda }_p\left(t-t^{\prime }\right)\right].$$

(21)

• Open Domain

$$\begin{array}{cc}\hfill \mathcal{G}\left(\overrightarrow{x},t|{\overrightarrow{x}}^{\prime },t^{\prime }\right)& ={\displaystyle \frac{1}{{\left(2\pi \right)}^3}}{\int }_{{\mathbb{R}}^3}\mathrm{Exp}\left[\mathbf{i}\overrightarrow{\omega }·\left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right)+\lambda \left(\overrightarrow{\omega }\right)\left(t-t^{\prime }\right)\right]d\mathsf{\Omega },\hfill \\ \hfill \lambda \left(\overrightarrow{\omega }\right)& ={\overrightarrow{\overrightarrow{a}}}_{o_2}·{\left(\mathbf{i}\overrightarrow{\omega }\right)}^{o_2},\hfill \end{array}$$

(22)

where, $\mathbf{i}$ is the imaginary unit, $\overrightarrow{\omega }$ is the three dimensional frequency vector corresponding to the spatial $\overrightarrow{x}$ and the expression for $\lambda$ is written in an oversimplified notation to avoid the structure of an $o_2$-th-order tensor. Recall that, we are using the frequency vector $\overrightarrow{\omega }$ as the open domain Eigenfunctions for an operator of any $o_2$-th-order collapse towards the Fourier kernel, $\mathrm{Exp}\left(\mathbf{i}\overrightarrow{\omega }\right)$ as the Dirac delta can be expanded as its Fourier transform.

Once we have the general expression for both the Closed domain and Open domain Green functions together with their short-time approximation as a Taylor series, we proceed to obtain the specific expressions of the Green functions for the operators of interest: the advection and the diffusion ones.

2.3.1. First-Order Operator: Advection Equation

For this problem, expression (22) becomes,

$${\mathcal{G}}_1\left(\overrightarrow{x},t|{\overrightarrow{x}}^{\prime },t^{\prime }\right)={\displaystyle \frac{1}{{\left(2\pi \right)}^3}}{\int }_{{\mathbb{R}}^3}\mathrm{Exp}\left\{\mathbf{i}\overrightarrow{\omega }·\left[\overrightarrow{x}-{\overrightarrow{x}}^{\prime }+{\overrightarrow{a}}_1\left(t-t^{\prime }\right)\right]\right\}d\mathsf{\Omega }=\delta \left[\overrightarrow{x}-{\overrightarrow{x}}^{\prime }+{\overrightarrow{a}}_1\left(t-t^{\prime }\right)\right].$$

(23)

As it can be observed, the Green function collapses into Dirac delta that takes information from point ${\overrightarrow{x}}^{\prime }$ and advects it towards point $\overrightarrow{x}$ that is placed at a distance ${\overrightarrow{a}}_1\left(t-t^{\prime }\right)$, hence the usual name advection equation. If the advection is not constant, we need to go for the Taylor series expansion, that particularized for the first-order operator can be defined as:

$$\begin{array}{cc}\hfill \mathcal{G}\left(\overrightarrow{x},\tau |{\overrightarrow{x}}^{\prime },0\right)& =\delta \left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right)+\tau {\overrightarrow{a}}_1\left(\overrightarrow{x},0\right)·\overrightarrow{\nabla }\delta \left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right)+{\displaystyle \frac{1}{2}}{\tau }^2{\overrightarrow{a}}_1^T{\overrightarrow{a}}_1\left(\overrightarrow{x},0\right):\overrightarrow{\nabla }\overrightarrow{\nabla }\delta \left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\tau }^2\left\{{\overrightarrow{a}}_{1,t}+{\overrightarrow{a}}_1·\left(\overrightarrow{\nabla }{\overrightarrow{a}}_1\right)\right\}·\overrightarrow{\nabla }\delta \left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right)+\mathcal{O}\left({\tau }^3\right)\hfill \\ \hfill & =\mathrm{Exp}\left[\tau {\overrightarrow{a}}_1\left(\overrightarrow{x},0\right)·\overrightarrow{\nabla }\right]\delta \left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right)+{\displaystyle \frac{1}{2}}{\tau }^2{\psi }_1+\mathcal{O}\left({\tau }^3\right).\hfill \end{array}$$

(24)

Being the order of the derivative equal to one, the correction terms are easier for this operator, allowing even to go for higher order exploration in order to increase the precision. Additionally, if the advection is the unknown function as in Burgers non-viscid Equation [49], then the first correction term simplifies even more, resulting in:

$${\overrightarrow{a}}_1=u\overrightarrow{I}⟶{\psi }_1\left({\overrightarrow{x}}^{\prime },t^{\prime }\right)=u_t+u\overrightarrow{I}·\overrightarrow{\nabla }u\left({\overrightarrow{x}}^{\prime },t^{\prime }\right)=0,$$

(25)

where $\overrightarrow{I}$ is a vector with ones on each component.

For the boundary conditions, the mathematical shape of this operator has some peculiarities that might complicate their implementation. The main reason for them is that its Eigenfunctions do not accept a closed domain form but a semi-open one, in the sense that each surface that limits the volume of study will advect or receive information from its surroundings in an independent manner. Yet, by linear combination of all the semi-opened domains a full closed domain problem can be recovered.

The shape of this Green function allows to define, within the short-time approximation, a region of influence of the boundaries, that isolates their evolution from the rest of the domain in the transition from the initial state, $\left(x^{\prime },t_0\right)$ to the short time one in the future, $\left(x^{\prime },t_0+\tau \right)$. This region will be defined by the advection coefficient, hence separating an inner region and a boundary one, with the magnitude $\tau {\overrightarrow{a}}_1$, as the main driver of the separation between zones.

Moreover, as the advection coefficient is a vector with a defined direction its interaction with the surface normal will define whether the information leaves the domain or enters it. That, while both conditions can be understood as Dirichlet boundary conditions, depending on the mathematical set of equations we are solving might imply some hidden relations between the variables being solved, as it happens in the case of Euler equations in fluid dynamics.

We can then classify the boundaries associated with the first-order operator into active or passive boundaries. Together with the classification, in Figure 1 we present an example for a boundary situation that combines both active and passive boundaries as the boundary condition is a sine function.

A positive advection will imply that the boundary acts as an active source and introduce information inside the domain, therefore an active boundary, and negative advection will mean that the solution at that boundary point will come from a source point inside the domain, hence, passive boundary (see Figure 1).

If a boundary has an advection equal to zero, i.e., a non-permeable wall condition, the situation will be equivalent to a passive boundary. The boundary point will simply accumulate the information being advected towards it and if there is no other additional term, the solution will diverge after all the information has been concentrated at the last point. This occurs, for example, in an impinging polluted flow facing a non-permeable wall, where the fluid advects the inert heavy particles of the pollutant towards the wall concentrating at the impinging point until they occupy a region where the some transversal advection appears, moving them outwards.

2.3.2. Second-Order Operator: Diffusion Equation

This operator corresponds to the well-known Heat transfer equation, that smooths down initial conditions through the spatial domain. From the perspective of the integral scheme, we start by characterizing the general open domain solution, Equation (22) for $o_2=2$.

$$\begin{array}{cc}\hfill {\mathcal{G}}_2\left(\overrightarrow{x},t|{\overrightarrow{x}}^{\prime },t^{\prime }\right)& ={\displaystyle \frac{1}{{\left(2\pi \right)}^3}}{\int }_{{\mathbb{R}}^3}\mathrm{Exp}\left[\mathbf{i}\overrightarrow{\omega }·\left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right)-{\overrightarrow{\overrightarrow{a}}}_2:{\overrightarrow{\omega }}^T\overrightarrow{\omega }\left(t-t^{\prime }\right)\right]d\mathsf{\Omega }\hfill \\ \hfill & ={\displaystyle \frac{1}{\sqrt{\left(det{\overrightarrow{\overrightarrow{a}}}_2\right){\left[4\pi \left(t-t^{\prime }\right)\right]}^3}}}\mathrm{Exp}\left[-{\displaystyle \frac{1}{4\left(t-t^{\prime }\right)}}\left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right){\overrightarrow{\overrightarrow{a}}}_2^{-1}{\left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right)}^T\right],\hfill \\ \hfill & {\overrightarrow{\overrightarrow{a}}}_2=a_2\overrightarrow{\overrightarrow{I}}⟶{\displaystyle \frac{1}{\sqrt{{\left[4a_2\pi \left(t-t^{\prime }\right)\right]}^3}}}\mathrm{Exp}\left[-{\displaystyle \frac{{\left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right)}^2}{4a_2\left(t-t^{\prime }\right)}}\right].\hfill \end{array}$$

(26)

So the open domain Green function (ODGF) of the second-order operator is a normalized Gaussian function, centered in zero under the variable $\left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right)$ and a standard deviation, ${\sigma }_2$, of

$${\sigma }_2=\sqrt{a_2\left(t-t^{\prime }\right)}.$$

(27)

It can be easily verified that the initial condition for the Green function is satisfied by this mathematical shape: When the final time frame tends to the initial one, the Dirac delta is recovered. The support of the Gaussian tends to zero concentrating its area at position $\left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right)$, defining the limit towards a zero standard deviation Gaussian as a usual representation of the Dirac delta [50].

Contrary to the first-order Green function, the Gaussian function is more numerically friendly to implement. Indeed as it is presented in expression (26) the solution of the open domain integral scheme (4) can be seen as a convolution operation of the extended initial condition with a smoothing function.

$$u\left(\overrightarrow{x},t_0+\tau \right)=\left\{{\mathcal{G}}_2\left(\tau \right)\ast \left[u\left(t_0\right)+\tau \mathsf{\Phi }\left(\mathfrak{t}\right)\right]\right\}\left(\overrightarrow{x}\right).$$

(28)

Thus, any non-essential discontinuity [51] present on the non-homogeneous terms or at the initial condition will not be transmitted into the next time frame, smoothed down by the Gaussian [52].

Going back into the short-time approximation, the Taylor series expansion of the problem, with a non-constant transport coefficient will result into:

$$\begin{array}{cc}\hfill & \mathcal{G}\left(\overrightarrow{x},\tau |{\overrightarrow{x}}^{\prime },0\right)=\delta \left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right)+\tau a_{2,ij}{\nabla }_i{\nabla }_j\delta \left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right)+{\displaystyle \frac{1}{2}}{\tau }^2{a}_{2,ij}{a}_{2,kl}{\nabla }_i{\nabla }_j{\nabla }_k{\nabla }_l\delta \left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\tau }^2\left\{\left(a_{2,ij,t}+a_{2,ij}{\nabla }_k{\nabla }_l{a}_{2,kl}\right){\nabla }_i{\nabla }_j+2a_{2,ij}{\nabla }_k{a}_{2,kl}{\nabla }_l{\nabla }_i{\nabla }_j\right\}\delta \left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right)+\mathcal{O}\left({\tau }^3\right)\hfill \\ \hfill & =\mathrm{Exp}\left[\tau {\overrightarrow{\overrightarrow{a}}}_2\left(\overrightarrow{x},0\right):\overrightarrow{\nabla }\overrightarrow{\nabla }\right]\delta \left(\overrightarrow{x}-{\overrightarrow{x}}^{\prime }\right)+{\displaystyle \frac{1}{2}}{\tau }^2{\psi }_2+\mathcal{O}\left({\tau }^3\right),\hfill \end{array}$$

(29)

where we have used Einstein’s notation for the first terms for simplicity. To clarify this solution even further, we present the 1D Taylor expansion too:

$$\begin{array}{cc}\hfill & \mathcal{G}\left(x,\tau |x^{\prime },0\right)=\delta \left(x-x^{\prime }\right)+\tau a_2{\partial }_{xx}\delta \left(x-x^{\prime }\right)+{\displaystyle \frac{1}{2}}{\tau }^2{a}_2^2{\partial }_{xxxx}\delta \left(x-x^{\prime }\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\tau }^2\left\{\left(a_{2,t}+a_2{\partial }_{xx}{a}_2\right){\partial }_{xx}+2a_2{\partial }_x{a}_2{\partial }_{xxx}\right\}\delta \left(x-x^{\prime }\right)+\mathcal{O}\left({\tau }^3\right)\hfill \\ \hfill & =\mathrm{Exp}\left[\tau a_2\left(x,0\right){\partial }_{xx}\right]\delta \left(x-x^{\prime }\right)+{\displaystyle \frac{1}{2}}{\tau }^2{\psi }_2+\mathcal{O}\left({\tau }^3\right).\hfill \end{array}$$

(30)

It can be concluded that, similarly to the first-order operator, the corrections are of order ${\tau }^2$ and they include the application of the PDE to the transport coefficient and extra order derivatives due to the general Leibniz rule. Placing the Green function into the integral scheme together with its corrections we see that all the derivatives applied to the Dirac delta will become derivatives over the extended initial condition. As a result, not only the initial condition but also the nonlinear terms will be affected by these corrections, altering the possible smoothing of discontinuities.

The closed domain Green function for this operator, on the other hand, becomes more cumbersome as its Eigenfunctions accept two boundaries, therefore expression (21) must be derived accordingly for each geometry and kind of boundary conditions. Yet, we can once again take profit of the short-time approximation to simplify the problem. If the Gaussian spread is confined, at least until a numerical value close to the numerical zero, then the effect of the Green function will be limited to that spread. Being its standard deviation defined by the time step, it is clear that as long as the Gaussian does not interact with the boundary regions, the open domain Green function we have derived so far will suffice to describe the temporal evolution of the problem. For which is again important to recall that, while the Gaussian is not a bounded function, its value converges towards it fast enough, numerically speaking we can reach double floating point precision for around $8.5\sigma$, thus defining an affectation region of the open domain of this size.

Close to the boundaries we can take profit of the shape of the Eigenfunctions of the second-order operator, that allow the summation (21) to be operated by means of Poisson summation’s formula, arising the well-known method of images [53]. This method develops the resulting Green function from the closed domain expression as linear combinations of reflections of the open domain one. As a result, we can achieve Dirichlet or Neumann boundary conditions by simply substracting or adding a reflection at the Boundary, interpreting the boundaries as mirrors. Furthermore, for a closed domain, the infinite summation is recovered in the same sense an infinite reflection will be obtained when confronting two standard mirrors. If we add to this idea the short-time approximation the problem simplifies even more as the mirrors will be far from each other and only one reflection will appear when the Gaussian—the open domain Green function—is close to the boundary. For example, the Dirichlet one dimensional semi-open Green function for this problem will be,

$${\mathcal{G}}_{sOD}\left(x,x^{\prime },\tau \right)={\displaystyle \frac{1}{\sqrt{4\pi a_2\tau }}}\left\{\mathrm{Exp}\left[-{\left({\displaystyle \frac{x-x^{\prime }}{4a_2\tau }}\right)}^2\right]-\mathrm{Exp}\left[-{\left({\displaystyle \frac{x+x^{\prime }}{4a_2\tau }}\right)}^2\right]\right\}.$$

(31)

where we see that the reflection is performed over the $x^{\prime }$ variable and it can be verified that, for the boundary point $x=0$, the Green function satisfies the Dirichlet homogeneous boundary conditions. In addition, in Figure 2 we present another example, this time a Neumann boundary reflection, to clarify visually how this problematic behaves.

Once again, we relate the size of the boundary region within the domain to the value of the transport coefficient and the time step, yet in the second-order operator the effect of the short-time approximation is less accused compared to the first-order one. Indeed, the boundary region of the first-order operator was defined as the furthest distance the boundary could advect information, i.e., $a_1\tau$ and in this case, it is the standard deviation of the Gaussian, or, to rephrase it in similar terms, the furthest distance the boundary can diffuse information, $\sqrt{a_2\tau }$. As a result, for the same time-step and same transport coefficients, the boundary region will be wider for the second-order than for the first one, as in the short-time approximation the time step will be always smaller than one.

We can extrapolate by induction (although this must be verified for higher orders) and postulate that the boundary region of an operator under the simplifications we are considering (that are, short-time approximation, semi-infinite domain, constant transport coefficient) will be defined by the roots of its derivative order, $o_2$, i.e., ${\left(a_{o_2}\tau \right)}^{1/o_2}$. Thus, the boundary region will become wider the higher the order of the operator under the short-time approximation.

In a general statement, we can conclude that the characteristic physical effect of the operator on the extended initial condition will be ruled by this parametric group. Alternatively, we can cast the Buckingham $\pi$ theorem [54] at the Green function PDE to show the same result. We will see in the numerical implementation of the integral scheme that it is from this group where the usual Courant–Friedrichs–Lewy number [55] is derived.

3. Numerical Implementation

Throughout this section we will explore how to effectively implement the aforementioned integral scheme, hence solving numerically the PDE. We will start from its most basic shape, i.e., an equation defined in an infinite, one dimensional domain without nonlinear terms, then we will increase progressively the difficulty of the problem.

Going through the previous section, we can identify the levels of complexity that will appear when obtaining the solution, being the simplest one a constant transport coefficient PDE, that might have an analytic solution available. Then, non-constant transport coefficients will be introduced, analyzing how they affect the Green function and the integral scheme already implemented. The last milestone will be the addition of the two time-integral terms, c.f., the nonlinear term and the one corresponding to the boundary conditions, looking into the possible definitions of the extended initial conditions.

Thus, the time evolution of the unknown function u with these simplifications can be reduced to solving the following integral,

$$u\left(x,t\right)={\int }_{-\infty }^{+\infty }{\mathcal{G}}_{o_2}\left(x,t|x^{\prime },t^{\prime }\right)u\left(x^{\prime },t^{\prime }\right)d{x}^{\prime }.$$

(32)

We recall the terminology introduced in the previous section: ${\mathcal{G}}_{o_2}$ is the Green function of the operator whose highest spatial derivative is of order $o_2$, and it takes information from the initial $x^{\prime },t^{\prime }$ state and propagates it towards the final $x,t$ state.

The numerical implementation of the Green function integral scheme requires a discretization of the variables that define its domain of interest. For our study, we have time and either space or frequency. As a result, the initial condition will be reconstructed from its discrete spatial values saved in arrays and its time evolving solution will consist on its propagation through the integral scheme (32). We will call the time step, i.e., the temporal difference between the initial and the final states, $\tau =t-t^{\prime }$ and, as long as the short-time approximation is satisfied we can assume $\tau \ll 1$ (see Section 2.2). Regarding the spatial or frequency discretization, its definition, the subsequent reconstruction of the initial condition and the time-evolving solution will define the numerical method together with the possible error associated with this operation.

For this initial exploratory work, we will only define a discrete numerical spatial grid of $2N+1$ points with the positions at which the initial condition and its subsequent time evolution will be represented. Each of the positions of this grid will have a one-to-one correspondence with its numerical coefficient, that will be saved in its corresponding array with $2N+1$ values. In particular, we define the following spatial discretization:

$$\begin{array}{cc}\hfill \left\{x\right\}& =x_i,i\in \left[-N,N\right],x_i\in \left[x_{-N},x_N\right]\hfill \\ \hfill \left\{t\right\}& =t_n,n\in \left[0,T\right],t_n\in \left[t_0,t_f\right]\hfill \\ \hfill \left\{u\right\}& =u_i^n=u\left(x_i,t_n\right).\hfill \end{array}$$

(33)

where N and T are the number of points of the spatial and temporal grids, respectively, and we have already selected $\tau$ as the timestep. Furthermore, i and n are indexes to go through the different discrete values in space and time, respectively. Both grid and time steps in principle do not need to be homogeneous through the discretization, yet for the short-time approximation to hold, the values of ${\tau }_n$ are required to be small. How small will be determined by the final time-evolving solution. Although in the first, most simplified starting point our domain is defined as open, we have a discrete, finite, spatial grid as we assume N is a finite integer. We can already foresee that this issue will become a source of error in the computation of the solution.

An important remark is that the nonlinear terms of the PDE might originate a disruption over these fundamental frequencies, breaking them into smaller values, so the minimum and maximum frequencies of the problem should be at least characterized before setting the numerical grid step.

3.1. Spatial Discretization

The chosen spatial discretization and its corresponding interpolation of the unknown function will drive the main error of the numerical method generating a the time evolving accumulated error, the evolution of which will be dependent of the timestep, $\tau$. The original works of Wehner and Wolfer [1,2,3] used a simple zero-th-order discretization were both the Green function and the unknown function were evaluated over each of the points when computing the time marching integral scheme. Furthermore, while it is possible to keep this methodology, or even improve it by means of a Chebyshev-like grid distribution, in order to define a general numerical methodology that can be extended to a high performance numerical solver with an important number of grid points, N, we will explore the application of the method by means of piecewise interpolation, trying to recover the usual methodology for numerical computation such as stencils definitions and parallelization capabilities.

Moreover, we choose a piecewise interpolation that, by optimizing the position of the grid points reduces the possible interpolation errors at the boundaries of the domain. Therefore, for the whole set of $2N+1$ points we are using, the interpolation will be of order $2q+1$, being able to increase or reduce this value in case additional precision or frequency representation are needed. The expression of the unknown function approximated by piecewise interpolants, $u_{pw}$, will be defined as,

$$\begin{array}{cc}\hfill u_{pw}\left(x,t\right)& =\sum _{i=-M+1}^{M-1}H\left(x,{\mathsf{\Omega }}_i\right)I_i\left(x,t\right)+H\left(x,{\mathsf{\Omega }}_{-M}\right)I_{-M}\left(x,t\right)+H\left(x,{\mathsf{\Omega }}_M\right)I_M\left(x,t\right),\hfill \\ \hfill & I_i\left(x,t\right)=\sum _{j=-q}^{q}u\left(x_{i+j},t\right)l_{p,j}\left(x-x_i\right),M=N-q,\hfill \\ \hfill & \mathsf{\Omega }=\left[a,b\right)⟶H\left(x,\mathsf{\Omega }\right)=\mathrm{Heaviside}\left(x-a\right)-\mathrm{Heaviside}\left(x-b\right),\hfill \end{array}$$

(34)

where H stands for the rectangular function that defines the domain of validity for each of the piecewise interpolations, ${\mathsf{\Omega }}_i$, and $l_{p,j}$ is the Lagrange polynomial distributed over the $2q+1$ points of the stencil and centered at each of the points $x_i$. Each of the domains of validity will be delimited by a set of N, intermediate points, $\left\{y_j\right\}$ in the following manner,

$${\mathsf{\Omega }}_{-N}=\left[-1,y_{-N+1}\right),{\mathsf{\Omega }}_i=\left[y_i,y_{i+1}\right),{\mathsf{\Omega }}_N=\left[y_{N-1},+1\right].$$

(35)

where the last domains of validity, i.e., ${\mathsf{\Omega }}_{\pm M}$ have been sliced too in q subdomains to apply systematically the following methodology, yet these new sliced subdomains will not be domains of validity by definition, as the last stencil is valid all over ${\mathsf{\Omega }}_M$. We have normalized the ending points of the numerical domain at $\pm 1$, yet the general $\left[x_{-N},x_N\right]$ can be easily recovered by a renormalization of the grid. The reason for this particular interpolation method is rather simple: it was shown by Hermanns Navarro [56] that the combination of collocation techniques and piecewise interpolation produce, for relative small ratios $q/N$, a set of grid points that distributes homogeneously at the center of the domain and then adapts at the boundary to avoid the interpolation errors in the likes of the Chebyshev–Gauss–Lobatto grid distribution.

To achieve such a grid distribution an iterative process is required as the mathematical problem has no analytic solution. The condition that is imposed is the usual equioscillation property [57] over a lower order, $2q$, piecewise interpolation defined using the $\left\{y_j\right\}$ points to then recover the actual grid point distribution, $\left\{x_i\right\}$ from their extrema.

We attempt to summarize the whole process in a mathematical description, only for half of the domain as the whole $2N+1$ grid distribution is symmetrical.

$$\begin{array}{cc}\hfill \left\{y_j\right\}:\left|G_{2q,i+1}\right|\left(x_{i+1},\overrightarrow{y}\right)& =\left|G_{2q,i}\right|\left(x_i,\overrightarrow{y}\right),\left\{x_i\right\}:\left\{\begin{array}{c}{\displaystyle \frac{d}{dx}}{G}_{2q,i}\left(x,\overrightarrow{y}\right)=0\hfill \\ \mathrm{subject}\mathrm{to}{x}_i\in {\mathsf{\Omega }}_i=\left[y_i,y_{i+1}\right)\hfill \end{array}\right.,\hfill \\ \hfill G_{2q,i}\left(x,\overrightarrow{y}\right)& =\prod _{j=1}^{2q}\left[x-{\zeta }_{s\left(i\right)+j}\right],\left\{{\zeta }_j\right\}=\{\underset{q\mathrm{times}}{\underbrace{-y_q,\dots ,-y_1}},y_1,\dots ,y_N\},\hfill \\ \hfill & s\left(i\right)=\{0,\dots ,N-q,\underset{q\mathrm{times}}{\underbrace{N-q,\dots N-q}}\},\hfill \end{array}$$

(36)

where $s\left(i\right)$ serves as a re-indexing for the half-domain problem, adapted from what was introduced by [56]. The equioscillation property has to be imposed over the canonical function [58] of the interpolation as it serves as a measure of its error,

$$\begin{array}{cc}\hfill R\left(x,q,{\mathsf{\Omega }}_i\right)=u\left(x,t\right)-u_{pw}\left(x,t\right)& ={\displaystyle \frac{1}{\left(2q+2\right)!}}G\left(x\right)u^{\left(2q+2\right)}\left(\zeta ,t\right),x\in {\mathsf{\Omega }}_i=\left[y_i,y_{i+1}\right)\hfill \\ \hfill & G\left(x\right)=\prod _{j=-N}^N\left(x-x_j\right).\hfill \end{array}$$

(37)

Recall that, as this expression is a consequence of the application of Rolle’s theorem, the derivative must be evaluated in some point $\zeta \left(x\right)$ in the interval we are doing the reconstruction, hence the only parameters we have to improve the error are the nodes defining the canonical function, $\left\{x_i\right\}$. Therefore, optimizing the function towards the reduction of its maximal absolute value will produce an optimized grid in what is called the minimax problem [59]. Regarding the specific solver we use for the iterative process, we apply the standard Levenberg–Marquardt algorithm as described in [60] that will have the error vector, $\overrightarrow{\epsilon }$, with N components as the cost function to be reduced to zero.

$${\epsilon }_i=∥{\displaystyle \frac{\left|G_{2q,i+1}\right|\left(x_{i+1},\overrightarrow{y}\right)}{\left|G_{2q,i}\right|\left(x_i,\overrightarrow{y}\right)}}-1∥.$$

(38)

We present in Figure 3 an example on how the iterative procedure produces an optimized grid and the shape of the canonical functions for both interpolations, the one defined over the $2q$ points where equioscillation must be achieved and the optimal one over which the unknown function will be discretized and interpolated.

In this figure we can see how the optimal grid $\left\{x_i\right\}$ already presents a two-zones distribution, with an almost homogeneous grid distribution close to the center of the domain.

We can actually force this kind of two-zones distribution by fine tuning the Hermanns Navarro algorithm and pre-imposing that this region will exist. As a result, we define a set of boundary points, b, that will be the ones optimized after the $N-b$ homogeneous ones, redefining the error vector, now of dimension b for the iterative process as,

$${\epsilon }_{b,i}=∥{\displaystyle \frac{\left|G_{2q,i}\right|\left(x_i,\overrightarrow{y}\right)}{\left|G_{2q,N_b-1}\right|\left(x_{N_b-1},\overrightarrow{y}\right)}}-1∥,i=N_b,\dots ,N$$

(39)

Hence, instead of imposing an equioscillation over the whole extrema of the $2q$ polynomials, we will impose the value of the already equioscillating homogeneous inner $N-b$ point distribution and obtain the points that adapt to it.

The algorithmic logic for the forced two-zones problem can be described in the following manner:

• Select the number of points b to be optimized and obtain the limit of the homogeneous zone, $N_b=N-b$, defining the grid step at this region as $\Delta x_h=N_b/N^2$.
• Obtain the value of $∥G_{2q,i}\left(x_i,\overrightarrow{y}\right)∥$ for an $x_i$ that does not require a stencil, $\overrightarrow{y}$, composed of points from the region to optimize. See the initial condition of Figure 3 as a visual key.
• Compute the error vector ${\epsilon }_{b,i}$ and perform the optimization process over the $2q$ interpolation with the b points as the only unknowns.

Therefore, we can define two separated regions, an inner, homogeneous, and a boundary one, for the whole $2N+1$ grid points. Furthermore, we can make these regions match with the ones we presented for the definition of the Green functions in the previous section, obtaining an inner region with open domain Green functions, homogeneous, hence simple, grid distribution and low interpolation error. Recall that with the piecewise interpolation only the first inner error lobes of the interpolation are being taken into account, see Figure 3. Furthermore, for a reduced number of points, b, the stencils that include them will be slightly more cumbersome to deal with, reaching a region where we will need to apply the semi-open Green function instead of the open one and, finally, take into account the boundary term of the integral scheme at the very last points. Nonetheless, these b points can be computed for a defined stencil q beforehand and implemented into the algorithm without paying any penalty in time computation for each time iteration of the solution.

An alternative discretization approach may be based on the introduction of moving meshes, as presented by Gao and Zhang [61], where the spatial discretization may be adapted to the nonlinear PDE’s evolution.

3.2. The Numerical Transposition of the Integral Scheme

As we introduced at the beginning of the section, we will proceed within increasing levels of complexity to solve numerical problems by means of the integral scheme, (11). Furthermore, we will start by a one dimensional open domain, that can be achieved by connecting both end of the boundaries, obtaining a circle as a domain. Therefore, the stencils defining the last points of the domain at each sides will be connected with each other, not requiring for any boundary region neither for the Green function nor the interpolation. We can write this simple first problem as,

$$\begin{array}{c}\hfill u\left(x,t_0+\tau \right)=\int {\mathcal{G}}_{o_2}\left(x-x^{\prime },\tau \right)v\left(x^{\prime },t_0\right)d{x}^{\prime }\\ \hfill v\left(x^{\prime },t_0\right)=u\left(x^{\prime },t_0\right)+\tau \mathsf{\Phi }\left(x^{\prime },t_0\right)\end{array}$$

(40)

where we have already introduced v as the extended initial condition, assuming that we will have a time marching error by assuming $\mathfrak{t}=t_0$ for the non-homogeneous terms.

All the forthcoming numerical examples on the performance of the algorithm have been implemented in FORTRAN language and computed under double precision, over 6 cores in parallel, each of them corresponding to a processor unit: Intel Core i7-87000K, 3.70 GHz.

3.2.1. Basic Time Evolving Scheme

The most straightforward problem we can define, containing the core parts of the methodology, is one where we do not have the non-homogeneous contribution, we are under a ring domain where the boundaries are connected, hence they do not contribute to the problem, and the transport coefficient is constant. We will start by the second-order operator, showing how the Courant–Friedrichs–Lewy number appears even for this simple problem. Introducing the numerical discretization,

$$\begin{array}{cc}\hfill u\left(x,t_0+\tau \right)& =\int {\mathcal{G}}_2\left(x-x^{\prime },\tau \right)\sum _{i=-N}^{N}H\left(x,{\mathsf{\Omega }}_i\right)\sum _{j=-q}^q{l}_j\left(x^{\prime }-x_i\right)u\left(x_{i+j},t_0\right)d{x}^{\prime }\hfill \\ \hfill & =\sum _{i=-N}^N\sum _{j=-q}^{q}u\left(x_{i+j},t_0\right){\int }_{y_i}^{y_{i+1}}{\mathcal{G}}_2\left(x-x^{\prime },\tau \right)l_j\left(x^{\prime }-x_i\right)d{x}^{\prime }\hfill \\ \hfill =& \sum _{i=-N}^N\sum _{j=-q}^{q}u\left(x_{i+j},t_0\right)w_{i,j}\left(x\right)\hfill \end{array}$$

(41)

Now, there are two possibilities to derive the weights of the time-marching solution, each of them determined by which of the mathematical definition of the Green function we select: the Taylor series expansion or the closed expression. Starting from this last one, with the appropriate changes of variable we can recover,

$$\begin{array}{cc}\hfill w_{i,j}\left(x\right)& ={\displaystyle \frac{1}{\sqrt{4\pi a_2\tau }}}{\int }_{y_i}^{y_{i+1}}{e}^{-\frac{1}{4}{\left(\frac{x-x^{\prime }}{a_2\tau }\right)}^2}{l}_j\left(x^{\prime }-x_i\right)d{x}^{\prime }={\displaystyle \frac{1}{\sqrt{4\pi }}}{\displaystyle \frac{1}{{\mathsf{\Pi }}_2}}{\int }_{-1/2}^{+1/2}{e}^{-{\left(\frac{\zeta -{\zeta }^{\prime }}{2{\mathsf{\Pi }}_2}\right)}^2}{l}_j\left({\zeta }^{\prime }\right)d{\zeta }^{\prime }\hfill \\ \hfill & \zeta ={\displaystyle \frac{1}{\Delta x}}\left(x-x_i\right),y_i=x_i-{\displaystyle \frac{\Delta x}{2}},y_{i+1}=x_i+{\displaystyle \frac{\Delta x}{2}},{\mathsf{\Pi }}_2={\displaystyle \frac{\sqrt{a_2\tau }}{\Delta x}}\hfill \end{array}$$

(42)

where ${\mathsf{\Pi }}_2$ is the Courant–Friedrichs–Lewy (CFL) number for the diffusive problem, also known as the diffusion number. As it can be expected, with the appropriate change of variables, i.e., centering the interpolation over the discretization point $x_i$, these weights are the same for the whole set of points and independent of i. Hence, they can be pre-computed without affecting the iterative process. Yet, the higher this value is, the more important the boundary terms of the defining integral will be. Now, with the definition of these weights we see how the value of this number defines the width of the Green function as it appears as its standard deviation, hence a CFL lower than $1/2$ will imply that the Gaussian is contained without being affected by the piecewise subdomains of validity.

If the time-evolved solution is also studied over the same grid points, i.e., we are interested only over the points $u\left(x_i,t_0+\tau \right)$, therefore, we can simplify the integral as $\zeta =0$, obtaining,

$$u\left(x_i,t_0+\tau \right)=\mathrm{Erf}\left({\displaystyle \frac{1}{4}}{\displaystyle \frac{1}{{\mathsf{\Pi }}_2}}\right)u\left(x_i,t_0\right)+\sum _{k=1}^q{\left(2{\mathsf{\Pi }}_2\right)}^{2k}{\displaystyle \frac{1}{\sqrt{\pi }}}\gamma \left({\displaystyle \frac{1}{2}}+k,{\displaystyle \frac{1}{16{\mathsf{\Pi }}_2^2}}\right){\delta }_{2q+1}^{2k}\left[u\right]\left(x=x_i\right),$$

(43)

where $\gamma$ is the lower incomplete gamma function [62], $\mathrm{Erf}$ is the usual Error function and ${\delta }_{2q+1}^{2k}\left[.\right]$ is the centered finite differences operator of order $2k$, defined over a stencil of $2q+1$ at point $x=x_i$ [63]. Now this definition is exact and takes into account all the possible interactions with the boundaries of the piecewise domain of validity as the integral is performed over the analytical expression of the Green function. If, on the contrary, we use the Taylor series expansion of the Green function, we recover a similar expression,

$${\int }_{y_i}^{y_{i+1}}{\mathcal{G}}_2\left(x-x^{\prime },\tau \right)l_j\left(x^{\prime }-x_i\right)d{x}^{\prime }=l_j\left(0\right)+{\mathsf{\Pi }}_2^2{\displaystyle \frac{d^2}{d{\zeta }^2}}{\left[l_j\left(\zeta \right)\right]}_{\zeta =0}+\dots +{\displaystyle \frac{1}{q!}}{\mathsf{\Pi }}_2^{2q}{\displaystyle \frac{d^{2q}}{d{\zeta }^{2q}}}{\left[l_j\left(\zeta \right)\right]}_{\zeta =0}.$$

(44)

With the resulting final expression of the time evolving solution defined as,

$$u\left(x_i,t_0+\tau \right)=u\left(x_i,t_0\right)+\sum _{k=1}^q{\mathsf{\Pi }}_2^{2k}{\displaystyle \frac{\left(2k\right)!}{\left(k\right)!}}{\delta }_{2q+1}^{2k}\left[u\right]\left(x=x_i\right)$$

(45)

Comparing the results obtained from the two expressions of the Green function, we appreciate the effect the ${\mathsf{\Pi }}_2$ number has on the computation of the solution and a perspective about the limit of the CFL different from its usual stability definition [64]. We can see this comparison in Figure 4, where the Logarithmic difference between the two possible weights is presented. Equation (45) does not take into account the interaction between the boundaries of the domain of validity ${\mathsf{\Omega }}_i$ and the Green function, resulting into a persistent error that will accumulate through time iterations. Furthermore, depending on the numerical scheme used, making the global error of the computed function divergent. Unfortunately, we cannot obtain a closed expression in general of the open domain Green function when we have a spatial dependent transport coefficient, therefore we will need to consider this limitation of the CFL in order not to introduce extra error into the time-evolving solution.

First-order operator follows the same logic we have introduced: the two possible expressions for the Green function are valid as long as the CFL number is bounded correctly. Yet, the fact that the first-order Green function behaves as a Dirac delta modifies the problem, breaking the integral (40) in the following manner,

$$\begin{array}{cc}\hfill u\left(x_i,t_0+\tau \right)& =\sum _{j=-q}^{q}u\left(x_{i+j},t_0\right){\int }_{y_i}^{y_{i+1}}{\mathcal{G}}_1\left(x-x^{\prime },\tau \right)l_j\left(x^{\prime }-x_i\right)d{x}^{\prime }\hfill \\ \hfill & =u\left(x_i,t_0\right)+\sum _{k=1}^q\left\{{\mathsf{\Pi }}_1^{2k}{\delta }_{2q+1}^{2k}\left[u\right]\left(x=x_i\right)+{\mathsf{\Pi }}_1^{2k-1}{\delta }_{2q+1}^{2k-1}\left[u\right]\left(x=x_i\right)\right\}.\hfill \end{array}$$

(46)

Which is the same expression we recover using the Taylor series expansion, being ${\mathsf{\Pi }}_1=a_1\tau /\Delta x$ the usual CFL number. There are two details to point out, regarding this last expression:

• The CFL number for a constant advection simply marks the frontier after which the integral term (46) is zero, i.e., the information is propagated outside of the domain of validity, i.e., outside of the corresponding ${\mathsf{\Omega }}_i$.
• In the case of non-constant advection the situation is more complicated, while the Green function is still a Dirac delta, its dependencies affects the integral, making it become a simple layer integral [65]. Therefore, using the exact, open domain Green function will produce a different result from the one obtained by the Taylor series, and their difference will be defined by the value of the CFL in a similar manner as in the second-order.

Having a non-constant transport coefficient will affect also to the Taylor series expansion, yet in a simpler manner: the values of ${\mathsf{\Pi }}_1$ will be time and spatial dependent in general, yet evaluated at time frame $t_0$ and at $x_i$,

$${\mathsf{\Pi }}_1\left(x_i\right)={\displaystyle \frac{a_1\left(x_i,t_0\right)\tau }{\Delta x}}$$

(47)

On the other hand, using the exact Green function will have the transport coefficient evaluated at the advected point, $x_i+a_1\left(x_i,t_0\right)\tau$, therefore defining a new grid position that requires evaluation. Using this new grid position as the starting point for the propagation of the next time frame simplifies the simple layer integral to the very same (46) solution with the CFL number evaluated at those points, with the corresponding local grid step in its definition. This is the starting point for the well-known Roe-like or Gudonov-like numerical schemes for solving advective equations, often applied to the Euler equations and perturbations over them towards the Navier–Stokes system [66]. Furthermore, in a similar manner, Lagrangian particle methods use this perspective of the information propagation to define the trajectories of their particles or grid points at which the rest of the solution is solved, see for example SPH methods [16].

We present an example of this simple test case for the diffusive and advective problems, for which it is possible to obtain an analytic solution—as a matter of fact, from the integral scheme—defined over a ring for different stencils and CFLs.

In this basic form, the algorithm is equivalent to a piecewise homogeneously interpolated partial differential equation, i.e., a finite difference scheme. Moreover, combining this homogeneous discretization with the Taylor series definition of the Green function we recover a numerical scheme that is equivalent explicit Euler scheme, where the time derivative has been expanded up to the order marked by the stencil.

The initial condition chosen for this problem is a sine that will advect and diffuse at a speed according to its frequency,

$$u\left(x,t_0\right)={\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}\sin \left(2\pi x\right)\to \left\{\begin{array}{cc}\hfill \mathrm{First}-\mathrm{order}& :u_1\left(x,t\right)={\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}\sin \left[2\pi x+\left(t-t_0\right)a_1\left(2\pi \right)\right]\hfill \\ \hfill \mathrm{First}-\mathrm{order}& :u_2\left(x,t\right)={\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}{e}^{-\left(t-t_0\right)a_2{\left(2\pi \right)}^2}\sin \left(2\pi x\right)\hfill \end{array}\right..$$

(48)

We will have then for the first-order equation a sine that travels through the ring periodically for the advection equation, and, for the diffusion equation a vanishing sine whose steady state is equal to 1/2.

The relative integrated error, ${\epsilon }_{\mathrm{Adv}},{\epsilon }_{\mathrm{Diff}}$, between the exact solution, Equation (48) and the one produced by the algorithm are presented for the advective and diffusive test cases on Figure 5 and Figure 6, respectively. This relative error is computed by numerically integrate the differences between the analytic and numerical solutions and refering it to the maximum value of the analytic solution at the corresponding time frame, t.

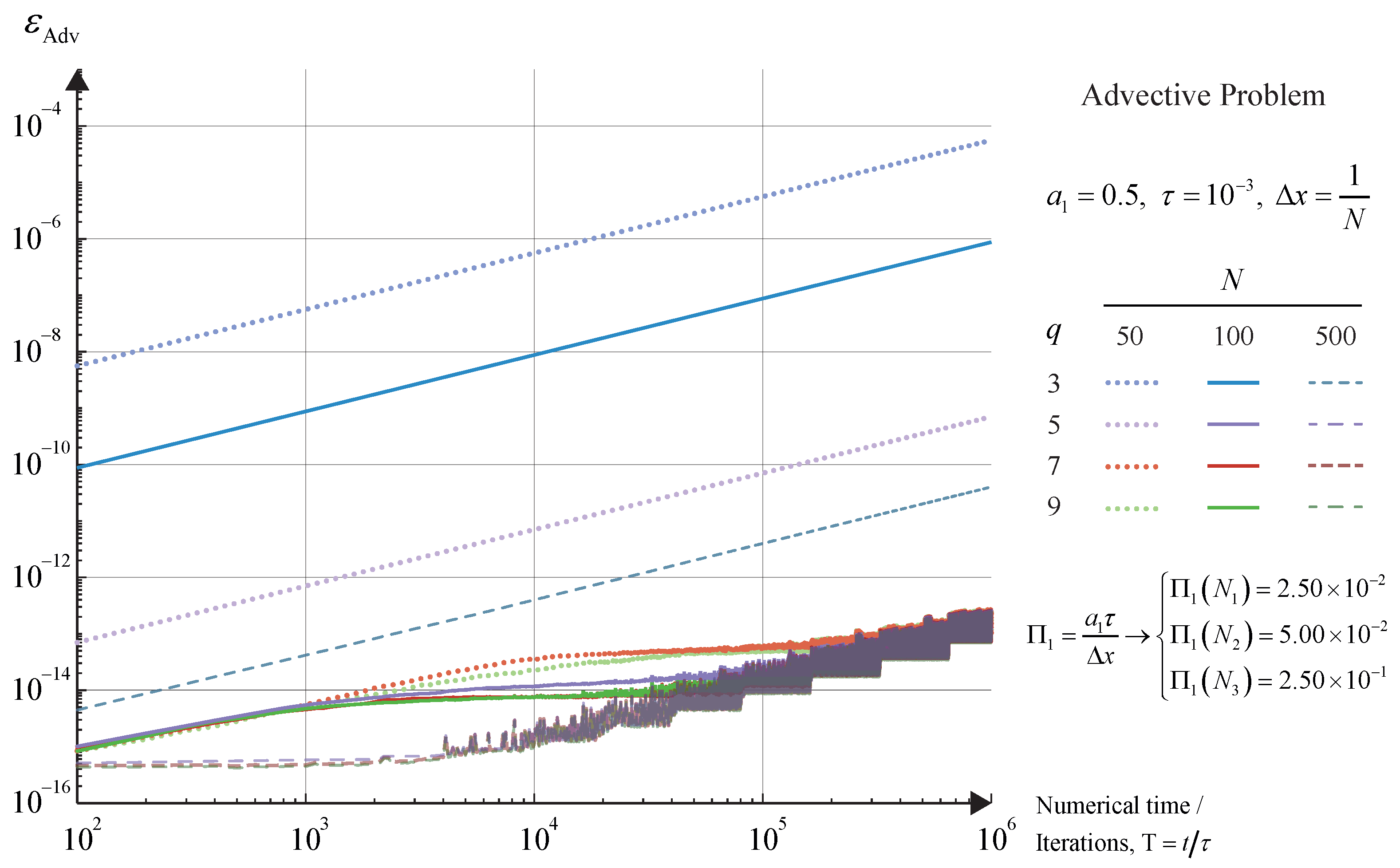
We compare the performance of the algorithm for several stencil sizes, defined by the parameter q and different CFL numbers, that are selected by means of the total number of points of the grid, N in order to perform an equivalent time-evolving comparison. From these results we can extract the behavior of the linear propagation of the algorithm, showing a fast convergence for the stencil size and a well behaved time evolving error, where, once the numerical precision is reached for a certain stencil. Due to the pseudospectra of the exponential matrix, which will be an approximation of that of the linear operators, the error accumulates with each time iteration, yet it does at a logarithm rate, hence it can be assumed to be controlled and so, the algorithm will produce a solution consistent with the exact one.

As the advective problem is a displacing sine, the established solution will be periodic, hence the propagation of the error will keep going, as it can be seen in Figure 5, even when it is the truncation error the one being propagated.

In the same perspective we can see that the influence of the CFL, as it is always kept low enough not to affect the stability of the solution, can only be appreciated for the diffusive problem, where the highest CFL (dashed lines) produce a significantly higher error than the rest while still remaining bounded. Moreover, the obtained solution improves due to the increase on number of points in the stencil, hence, the quality of each centered finite difference will increase as well, improving the final solution.

Although the computational performance of the algorithm and its optimization it is out of the scope of this work, the simulations performed to solve the diffusive and advective test cases took an order of magnitude of $2\times {10}^{-5}$ s per iteration for the highest order stencil, $q=10$ and of $2\times {10}^{-6}$ for $q=3$.

3.2.2. Non-Constant Transport Coefficients

In the situation where the transport coefficient, $a_{o_2}$, depends either on time or space we are forced to use the Taylor Series expansion of the Green function in order to introduce the correction terms, ${\psi }_{o_2}$. We use ${\psi }_{o_2}$ as the correction term that include the initial condition of the Green function, i.e., the Dirac delta, while in the previous section we use capital $\mathsf{\Psi }$ to refer to the correction terms without being applied to the initial condition. While it might be possible to obtain a closed Green function expression for certain Transport Coefficients, and it might be useful to understand the behavior of the PDE under study, the general situation will require for the Taylor series expression.

Starting from the second-order operator, we can introduce into the time marching scheme the correction terms from the expansion, c.f. Equation (30), in the following manner,

$$\begin{array}{c}\hfill {\psi }_2\left(x,x^{\prime }\right)=\left[\left({\left.{\displaystyle \frac{d{a}_2}{dt}}\right|}_{t=t_0}+a_2{\displaystyle \frac{d^2{a}_2}{d{x}^2}}\right){\displaystyle \frac{d^2}{d{x}^2}}+\left(2a_2{\displaystyle \frac{d{a}_2}{dx}}\right){\displaystyle \frac{d^3}{d{x}^3}}\right]\delta \left(x-x^{\prime }\right)\\ \hfill {\displaystyle \frac{1}{2}}{\tau }^2{\chi }_{2,j}={\displaystyle \frac{1}{2}}{\tau }^2{\int }_{y_i}^{y_i+1}{\psi }_2\left(x,x^{\prime }\right)l_j\left(x^{\prime }-x_i\right)d{x}^{\prime }\\ \hfill ={\displaystyle \frac{1}{2}}\left\{\left[{\mathsf{\Pi }}_2^2\left(x_i\right){\left.{\displaystyle \frac{d{\widehat{a}}_2}{d\mathfrak{t}}}\right|}_{\mathfrak{t}={\mathfrak{t}}_0}+{\mathsf{\Pi }}_2^4\left(x_i\right){\displaystyle \frac{d^2{\widehat{a}}_2}{d{\zeta }^2}}\right]{\displaystyle \frac{d^2}{d{\zeta }^2}}\left[l_j\left(\zeta \right)\right]+\left[2{\mathsf{\Pi }}_2^4\left(x_i\right){\displaystyle \frac{d{\widehat{a}}_2}{d\zeta }}\right]{\displaystyle \frac{d^3}{d{\zeta }^3}}\left[l_j\left(\zeta \right)\right]\right\}\left(\zeta =0\right),\end{array}$$

(49)

where we have introduced a non-dimensional set of variables to recover the CFL number evaluated at point $x_i$, taking profit that in general, both physically and mathematically, the transport coefficient for a purely diffusive equation is different from zero (see some examples of exceptions for this rule in [42]),

$${\mathsf{\Pi }}_2\left(x_i\right)={\displaystyle \frac{\sqrt{\tau a_2\left(x_i,t_0\right)}}{\Delta x}},{\widehat{a}}_2\left(x,t\right)={\displaystyle \frac{a_2\left(x,t\right)}{a_2\left(x_i,t_0\right)}},\mathfrak{t}={\displaystyle \frac{t}{\tau }},\zeta ={\displaystyle \frac{1}{\Delta x}}\left(x-x_i\right).$$

(50)

Recall that the while the correction terms ${\psi }_2$ are evaluated in the initial time frame as they are part of the Taylor series expansion of the Green function, they include also the temporal variation of the transport coefficient, that will be, in general, as small as the time step, making this term almost negligible under the short-time approximation.

As a result, the propagation of the unknown function due to the correction terms will be,

$$\begin{array}{c}\hfill u_{cor}\left(x_i,t_0+\tau \right)=\stackrel{{\mathsf{\Pi }}_2^2{f}_{ev,2}}{\overbrace{\left({\mathsf{\Pi }}_2^2{\displaystyle \frac{d{\widehat{a}}_2}{d\mathfrak{t}}}+{\mathsf{\Pi }}_2^4{\displaystyle \frac{d^2{\widehat{a}}_2}{d{\zeta }^2}}\right)}}{\delta }_{2q+1}^2\left[u\right]\left(x=x_i,t=t_0\right)+\\ \hfill \stackrel{{\mathsf{\Pi }}_2^4{f}_{odd,3}}{\overbrace{\left(6{\mathsf{\Pi }}_2^4{\displaystyle \frac{d{\widehat{a}}_2}{d\zeta }}\right)}}{\delta }_{2q+1}^3\left[u\right]\left(x=x_i,t=t_0\right),\end{array}$$

(51)

and, consequently, they can be introduced at the general scheme, c.f., Equation (45), as additional terms at the propagation. Therefore, each time step the three derivatives ${\displaystyle \frac{d{\widehat{a}}_2}{d\mathfrak{t}}},{\displaystyle \frac{d{\widehat{a}}_2}{d\zeta }},{\displaystyle \frac{d^2{\widehat{a}}_2}{d{\zeta }^2}}$ must be computed before the time propagation occurs. While originally these corrections were of order ${\tau }^2$, once the discretization appears this order of magnitude is piloted by both the CFL and the ${\delta }_{2q+1}$ operator. For a sufficiently small grid and a sufficiently well behaved unknown, as the ${\delta }_{2q+1}$ operator does not include the grid step in the definition we are using, the values produced by this operator will be of the order of its modulus of continuity [67] or any other measure of its regularity. Even in a situation where it produces a jump of order of the unity, these corrections will be still dominated by the order of magnitude of the CFL and, more important, the variation of the transport coefficient, that again, if it is smooth enough will produce bounded and correspondingly small corrections. Moreover, in a situation where we had a study a discontinuous transport coefficient that produce at any $x_i$ a jump on its derivatives, we could introduce analytically its variation at the moment we compute the integral, obtaining numerically controllable extra terms for each of the discontinuities introduced. We also point out that, if the transport coefficient $a_2$ satisfies a diffusion equation being its own diffusion coefficient, the even correction term will be zero.

The final propagation of the unknown function, including the corrections, for a second-order operator with non-constant transport coefficients can be written as,

$$\begin{array}{cc}\hfill u\left(x_i,t_0+\tau \right)=u\left(x_i,t_0\right)& +\sum _{k=1}^q{\mathsf{\Pi }}_2^{2k}\left(x_i,t_0\right)\left[{\displaystyle \frac{\left(2k\right)!}{k!}}+f_{ev,k}\left(x_i,t_0\right)\right]{\delta }_{2q+1}^{2k}\left[u\right]\left(x=x_i\right)\hfill \\ \hfill & +\sum _{k=1}^q{\mathsf{\Pi }}_2^{2k}\left(x_i,t_0\right)f_{odd,k}\left(x_i,t_0\right){\delta }_{2q+1}^{2k-1}\left[u\right]\left(x=x_i\right),\hfill \end{array}$$

(52)

where the terms $f_k$ will be, respectively, the odd and even correction terms, that will be composed of the derivatives of the transport coefficient evaluated at the point where we are computing the solution.

The correction terms for the first-order operator behave similarly, being piloted by the derivatives of the advection coefficient and the CFL number. Yet, as the transport coefficient of the first-order operator might be zero in some regions, we cannot choose $a_1\left(x_i,t_0\right)$ as the characteristic advection to make the expression non-dimensional. We therefore select a value, $a_{1,0}$, that will be considered as representative of the order of magnitude of the advection coefficient, resulting in the following correction expression,

$${\displaystyle \frac{1}{2}}{\tau }^2{\chi }_{1,j}={\displaystyle \frac{1}{2}}\left\{\left({\mathsf{\Pi }}_1{\left.{\displaystyle \frac{d{\widehat{a}}_1}{d\mathfrak{t}}}\right|}_{\mathfrak{t}={\mathfrak{t}}_0}+{\displaystyle \frac{1}{2}}{\mathsf{\Pi }}_1^2{\displaystyle \frac{d{\widehat{a}}_1^2}{d\zeta }}\right){\displaystyle \frac{d}{d\zeta }}\left[l_j\left(\zeta \right)\right]\right\}\left(\zeta =0\right),{\mathsf{\Pi }}_1={\displaystyle \frac{\tau a_{1,0}}{\Delta x}}$$

(53)

where we see again that the corrections will be zero if the advection coefficient satisfied the original PDE with a transport coefficient equal to itself, i.e., an inviscid Burgers equation. Under this non-dimensional grouping, the CFL is no longer a representation of how far the information is advected locally at every $x_i$, nonetheless, it still preserves the measure of how much the Taylor series expansion differs from the exact solution and, therefore, the stability of the global numerical method as in its classical definition. The propagation of the unknown function due to the correction terms will be,

$$u_{cor}\left(x_i,t_0+\tau \right)=\left({\displaystyle \frac{1}{2}}{\mathsf{\Pi }}_1{\displaystyle \frac{d{\widehat{a}}_1}{d\mathfrak{t}}}+{\displaystyle \frac{1}{4}}{\mathsf{\Pi }}_1^2{\displaystyle \frac{d{\widehat{a}}_1^2}{d\zeta }}\right){\delta }_{2q+1}^1\left[u\right]\left(x=x_i,t=t_0\right).$$

(54)

To which all the considerations regarding of their order of magnitude being related to the regularity of the function we introduced for the second-order operator are applicable. Despite being in general of low order of magnitude, as the presence of advective fronts that present steep slopes are common in mathematical modeling these corrections will be of higher importance than the diffusive ones. Moreover, being the first-order operator simpler to operate with, higher order corrections are easier to derive and implement too in case of such requirement.

We present an example of application for both an advective and a diffusive problem, with transport coefficients presenting steep variations so to highlight the correction terms. In particular, we choose the following transport coefficients,

$$a_1\left(x\right)=1-0.995{\sin }^6\left(2\pi x\right),a_2\left(x\right)={10}^{-5}+{\cos }^6\left(2\pi x\right)$$

(55)

and the following initial conditions:

$$u_1\left(x,0\right)=\sin \left(2\pi x\right),u_2\left(x,0\right)=\mathrm{Exp}\left(-{\displaystyle \frac{x^2}{4\times {10}^{-2}}}\right)$$

(56)

so that the time evolving solutions are affected by transport effects of different orders of magnitude, trapping the solution at the regions where the coefficients are close to zero.

We present in Figure 7 and Figure 8 the numerical solution of the test case together with the value of the propagated correction, that will follow the shape of the temporal evolution of the equation modulated by the correction terms.

We can confirm that, as we shown in Section 2.3, the corrections hold the order ${\tau }^2$ even at their most active region of space, allowing to neglect them depending the levels of accuracy desired for the solution and the particular problem. As a matter of fact, if the values of the transport coefficients are available in advanced, these corrections can be pre-calculated and incorporated into the Kernels without a penalization in the number of operations per iteration.

The computation of the corrections require for an additional (or several in the case of the diffusive ones) of the domain, hence increasing the number of memory accesses and operations of the algorithm, that will go in detriment of computational time. Nonetheless, thanks to parallelization it is possible to hold the order of magnitude, for the system of 6 cores we introduced at the beginning of the subsection, of ${10}^{-5}$ s for iteration for a number of total grid points of the order of ${10}^3$.

3.2.3. Non-Homogeneous Terms

Once we have defined and characterized the evolution of the initial condition of the problem through the numerical Green function, the next step is to add the propagation of the non-homogeneous terms, $\mathsf{\Phi }$ into the time-evolving solution. To do so, we need to compute the double integral, see Equation (13), that takes into account the propagation and variation of these terms through the time step $\tau$. While the spatial integral can be obtained in the same manner as we have already introduced, the temporal integral requires a numerical quadrature:

$$\begin{array}{c}\hfill u_{nh}\left(x_i,t+\tau \right)={\int }_0^{\tau }\int \mathsf{\Phi }\left(x^{\prime },t+{\tau }^{\prime }\right){\mathcal{G}}_{o_2}\left(x_i-x^{\prime },\tau -{\tau }^{\prime }\right)d{x}^{\prime }d{\tau }^{\prime }=\\ \hfill \sum _{k=1}^s\sum _{j=-q}^q{w}_j\left(\left.t_0+\tau \right|t_0+{\tau }_k\right)\mathsf{\Phi }\left(x_i,t+{\tau }_k\right),\end{array}$$

(57)

where we have used the same notation as we introduced for the Green functions to make explicit the time propagation between the time frame $t_0+{\tau }_k$ and the final one $t_0+\tau$.

For first-order, $s=1$, we recover the equivalent Euler method presented in Section 2.2: the weights will coincide with those of the initial condition causing both propagations—the initial condition and the non-homogeneous terms—be equivalent. Hence, we can group both terms, having an extended initial condition for the problem that evolves in time.

Increasing the order of the quadrature will imply propagations towards and from time frames between $t_0$ and $t_0+\tau$. Thus, requiring Runge–Kutta (RK) or $\theta$-like schemes [63] that allow to decrease the error combining them. In particular, the definition of such such schemes over an operator previously split into two parts, a linear and a nonlinear one, is the starting point for the exponential integrators, a family of numerical methods we introduced in Section 1, see for example [20,68] and the references within.

Their difficulty lies precisely in the split of the operator: while only the $u_{nh}$ integral requires to be approximated, in order to obtain the value of the nonlinear term at each of the intermediate s steps of the method we will need to propagate the whole solution towards them first. Moreover, once the non-homogeneous function is computed at those intermediate steps, the propagation towards $t=t_0+\tau$ must be done using a Green function that starts at these $t_0+{\tau }_k$ points, i.e., its transport coefficients and CFLs must be evaluated at these intermediate time frames and the two states for the Green function (the initial and final ones) must be defined accordingly. The control and reduction of the quadrature errors under these operators will require for adapted versions of Butcher tableau and the coefficients for high-order methods might not coincide with the classical ones.

For the explorative phase presented on this work we will limit ourselves to the midpoint method for the quadrature, that will serve also as an example of the implementation of these methods over the integral scheme, leaving the fourth-order equivalent Runge–Kutta and its adaptive versions for future works. Following the usual steps for the RK methods.

$$\begin{array}{c}\hfill t_0\to t_0+{\displaystyle \frac{\tau }{2}}:u_{mp}\left(x_i,t_0+{\displaystyle \frac{\tau }{2}}\right)=\\ \hfill \sum _{j=-q}^q{w}_j\left(\left.t_0+{\displaystyle \frac{\tau }{2}}\right|t_0\right)\stackrel{\mathrm{Extended}\mathrm{Initial}\mathrm{Condition}}{\overbrace{\left[u\left(x_{i+j},t_0\right)+{\displaystyle \frac{\tau }{2}}\mathsf{\Phi }\left(x_{i+j},t_0\right)\right]}},u_{mp}\left(x_i,t_0+{\displaystyle \frac{\tau }{2}}\right)\to \left\{\mathsf{\Phi }\left(x_{i+j},t_0+{\displaystyle \frac{\tau }{2}}\right)\right.,\\ \hfill a\left.\left(x_{i+j},t_0+{\displaystyle \frac{\tau }{2}}\right)\right\},a\left(x_i,t+{\displaystyle \frac{\tau }{2}}\right)⟶w_j\left(\left.t_0+\tau \right|t_0+{\displaystyle \frac{\tau }{2}}\right),\\ \hfill u\left(x_i,t+\tau \right)=u_{ic}+u_{nh}=\left\{\begin{array}{c}\hfill t_0\to t_0+\tau :u_{ic}\left(x_i,t+\tau \right)=\\ \hfill \sum _{j=-q}^q{w}_j\left(\left.t_0+\tau \right|t_0\right)u\left(x_{i+j},t_0\right)\\ \hfill t_0+{\displaystyle \frac{\tau }{2}}\to t_0+\tau :u_{nh}\left(x_i,t+\tau \right)=\\ \hfill \tau \sum _{j=-q}^q{w}_j\left(\left.t_0+\tau \right|t_0+{\displaystyle \frac{\tau }{2}}\right)\mathsf{\Phi }\left(x_{i+j},t_0+{\displaystyle \frac{\tau }{2}}\right)\end{array}\right.\end{array}.$$

(58)

where we see that, while the number of operations is doubled as two time propagations are required for each time step, the methodology will be highly simplified for a constant transport coefficient (or one that produce negligible corrective terms). Indeed, in this situation the Green function will only depend on the time frame explicitly, allowing for the weights to be precomputed, leaving only the value of the local transport coefficient $a\left(x_i\right)$ to be updated.

Recall that the RK methodology is only applied to solve the integral for the nonlinear terms, leaving the Taylor series expansion of the Green function as the usual extrapolation in time from the initial value. Yet, any multi-step technique can be applied too at the level of the general expression of the Green function, allowing to combine its error and step definition with the nonlinear integrals with a non-negligible level of complexity. This study ties again with the advances on exponential integrators and time-propagating solutions, and its in-depth analysis is left as a future line of research.

To show the performance of the midpoint adapted scheme and the wide range of possibilities for nonlinear terms, we present two test-cases: a nonlinear advection-diffusion equation where the norm must be conserved, and an equation with a soliton-like solution.

The first test case is the diffusive or viscid Burgers Equation [49], defined under a ring domain so there is no injection or destruction of information from the boundaries. Defining the PDE by means of its information current [69], $J\left(x,t\right)=1/2u-u_x$, we can show that its norm, $n\left(t\right)$ is conserved,

$$\begin{array}{cc}\hfill u_t& =-u{u}_x+\nu u_{xx}=-J_x,\hfill \\ \hfill n\left(t\right)={\int }_{-1}^{1}u\left(x^{\prime },t\right)d{x}^{\prime },n_t& ={\int }_{-1}^1{u}_t\left(x^{\prime },t\right)d{x}^{\prime }=J_1\left(t\right)-J_{-1}\left(t\right)=0⟶n=\mathrm{cte}.\hfill \end{array}$$

(59)

Therefore, we impose as an initial condition a normalized Gaussian that will evolve under the usual Burgers shock-like tendency: the higher values of the unknown function will advect as much as the value of the unknown function while the almost zero regions will remain still, grouping them into a front. This case is specially delicate as we are using a purely diffusive Green function, implementing the nonlinear advection through the $\mathsf{\Phi }$ term. There are two main advantages of using such Green function: there is no correction terms as the viscosity, i.e., the diffusive transport coefficient, is constant, and we can introduce any extra forcing terms into the problem without modifying the weights of the numerical scheme.

The typical shock-like evolution of the Burgers equation is shown clearly in Figure 9, where we also compare whether the numerical the numerical norm is conserved or not. To contrast the order of magnitude of the approximation we obtain the error between norms: the analytical (that for this example is equal to one) and the numerical one. Additionally, we take profit to compare how this error is altered by the inclusion of the RK scheme, showing a clear improvement of the order of magnitude when activating the scheme. Yet, as the error of the norm was already low enough, the duplication of the computational cost to reach these levels of accuracy must be a compromise when applying the methodology. Regarding the aforementioned computational cost of implementing the RK scheme, it will always be a compromise between how much the time grid can be increased, hence, saving a substantial number of iterations, versus the time spent in evaluating twice the domain for the half step and the final propagation. In the example of the Burgers equation, the order of magnitude for one iteration doubles or, depending whether we need to compute the corrections for a variable transport coefficient or not, it might quadruply.

For the soliton-like solution we select the nonlinear Schrödinger equation, that for an elastic potential presents a traveling wave solution, see [70]. To solve the wave function using the Green function scheme we have two possible paths: or we separate the nonlinear equation in its real and imaginary contributions, deriving two coupled diffusive equations to be solved or we use the closed definition of the Green function and introduce the imaginary diffusion before the discretization. As we want to show the capability of the scheme to hold the soliton solution, we select the first option, considering the numerical solution of the two equations—the real and the imaginary parts of the wave function—more challenging: two independent contributions of error will arise from their solution, affecting the required balance between functions to form the soliton. Operating with the nonlinear Schrödinger Equation [71] we recover,

$$\begin{array}{c}\hfill \mathbf{i}{\mathsf{\Psi }}_t=-{\displaystyle \frac{1}{2}}{\mathsf{\Psi }}_{xx}+Q\mathsf{\Psi }{\left|\mathsf{\Psi }\right|}^2\stackrel{\mathsf{\Psi }=u+\mathbf{i}v}{\to }\left\{\begin{array}{c}\hfill u_t=-{\displaystyle \frac{1}{2}}{v}_{xx}+Qvs.\left(u^2+v^2\right)\\ \hfill v_t=+{\displaystyle \frac{1}{2}}{u}_{xx}+Qu\left(u^2+v^2\right)\end{array}\right.,\\ \hfill \mathsf{\Psi }\left(x,0\right)=u_0\left(x\right)+\mathbf{i}{v}_0\left(x\right)={\varphi }_0{\displaystyle \frac{\mathrm{Exp}\left(\mathbf{i}{u}_{e}x\right)}{\mathrm{Cosh}\left(\sqrt{Q}{\varphi }_{0}x\right)}},{\varphi }_0=\sqrt{{\displaystyle \frac{u_e^2-2u_e{u}_p}{Q}}}\end{array}$$

(60)

where we have introduced already the initial condition that produces the traveling wave solution, $\mathsf{\Psi }\left(x,0\right)$. Furthermore, the parameters $P,Q,u_e,u_p$ are the standard parameters for soliton solutions as described in [70].

Hence, we have a crossed diffusion problem, where real part diffuses towards the imaginary one and vice versa, producing the pulsating behavior of the equation. Moreover, we have a production term due to the potential ${\left|\mathsf{\Psi }\right|}^2$ that will inject or destroy information into the time evolution of the problem depending on the modulus of the wave function, controlling the growth and the norm of its evolution. These production terms are also found on chemical advection-diffusion-reaction equations and, due to their high variability in time and their control over some of the conserved quantities of the problem tend to be cumbersome to deal with, see [72].

Additionally, for the nonlinear Schrödinger equation, the energy of the system must be also a conserved quantity according to Noether’s theorems [70], as a result we will have, apart from the general shape of the function, two numerical magnitudes that will serve as indicators of the quality of the time propagation scheme,

$$n\left(t\right)=\sum _{i=-N}^N\Delta x^{\prime }{\left|\mathsf{\Psi }\left(x_i,t\right)\right|}^2,e\left(t\right)=\sum _{i=-N}^N\Delta x^{\prime }\left({\left|{\mathsf{\Psi }}_x\left(x_i,t\right)\right|}^2-{\left|\mathsf{\Psi }\left(x_i,t\right)\right|}^4\right),$$

(61)

where the primes over the grid step indicate that the first and last points are multiplied only by half $\Delta x$.

We present in Figure 10 the temporal evolution of the wave function, the real and imaginary parts of which oscillate measured with each other in order to produce the same soliton envelope as its modulus. It is important to recall that, for imaginary diffusion the standard choices for to the numerical parameters are no longer applicable as the Green function is no longer a Gaussian. Nonetheless, we can still take profit of the Taylor series expansion to avoid this problematic and hold the same methodology we have introduced up to now. The only affectation will be at the CFL and the stability, indeed, if we look back at Equation (60) the diffusion is now imaginary, and one component diffuses into the other and viceversa. This is why we need to go to time steps as low as ${10}^{-12}$ to achieve a reasonable order of magnitude over the error of the conserved magnitudes, therefore increasing the computational cost of the whole simulation. While the order of magnitude of one time step is still the same as the one of the previous subsections, i.e., ${10}^5$ for high order stencils and $N\approx {10}^3$, to reach a dimensional time where we can appreciate the evolution of the initial condition we require several order of magnitude of iterations.

This is why the RK scheme for this application is critical as it allow to reduce significantly the number of iterations, up to two orders of magnitude according to the numerical experiments performed. In fact, for the parameters presented in Figure 11 the norm of the soliton was not conserved after a hundred iterations, producing an error of the order of the unknown function and losing the properties of the soliton as the traveling wave solution of the problem.

With these two test cases we have shown the performance of the RK scheme and how the nonlinear terms contribute to the solution, and more importantly, can be used effectively as a general term where to introduce the parts of the equation that are not the quasilinear operator that defines the Green function.

3.2.4. Boundary Conditions

The last contribution to the integral scheme is due to the boundary conditions, presenting a structure similar to the nonlinear terms: an integral through the time step of a propagated quantity. Yet, the quantity being propagated is of a discrete, source-like nature, breaking, so to speak, the usual integral form of the convolution.

For this exploratory study, we focus mainly on the second-order equation, utilizing the method of images [53], which serves as a foundational approach for further development. Consistent with this work, we operate under the short-time approximation, allowing us to separate the domain of study into two distinct regions, each with different Green functions: the inner domain, where both the theoretical and numerical frameworks we have presented hold, and the boundary region, where boundary effects influence both the theoretical (modifying the Green function expression) and numerical levels (requiring an optimized point distribution to mitigate interpolation errors). Thus, modifications are required at three levels within the algorithm: the expression of $\mathcal{G}$ across all three propagation terms, adjustments to the Lagrange-like interpolation weights due to the altered discrete points, and the contribution of the boundary integral term.

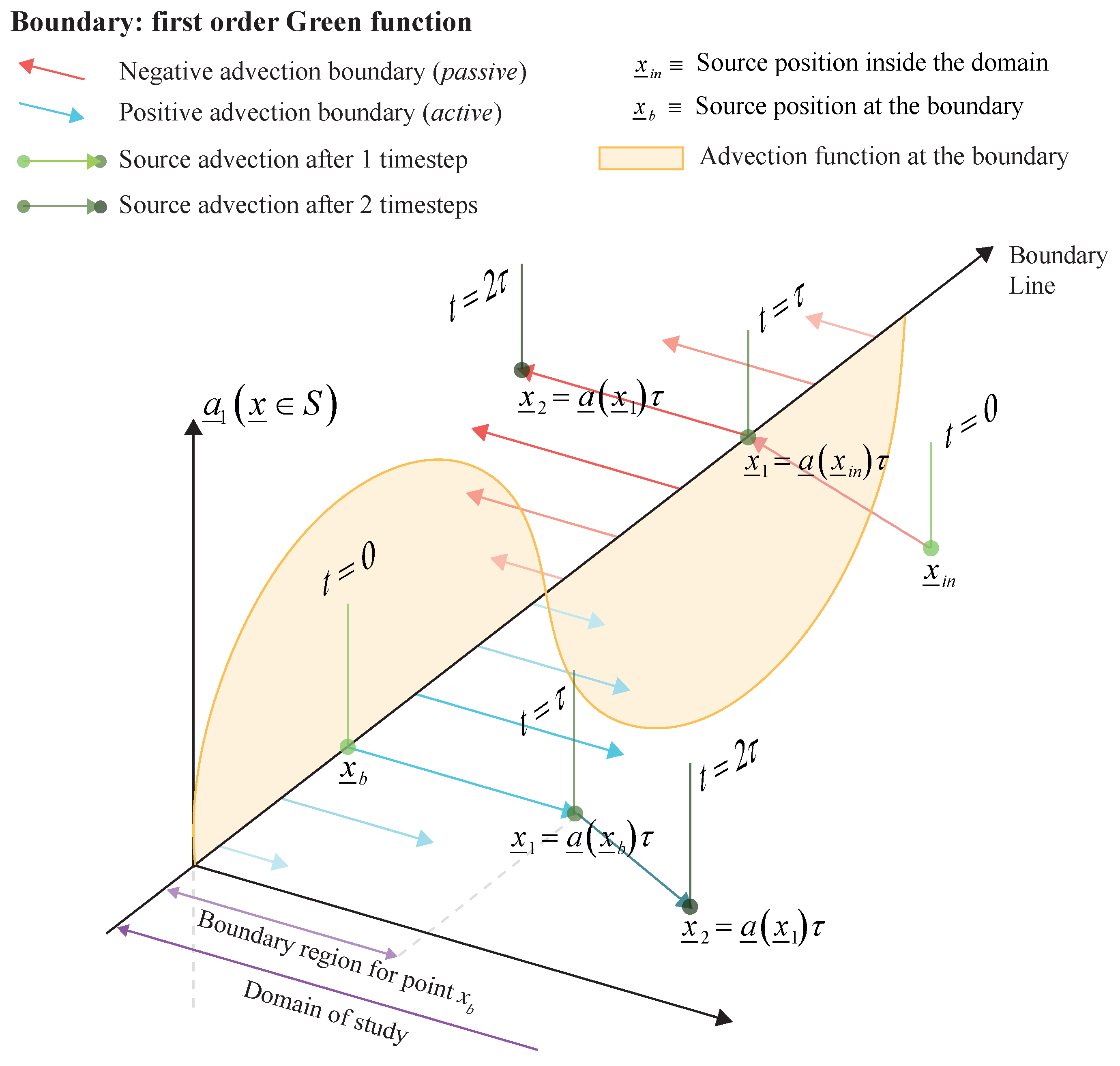
The first modification is rather straightforward since, for the second-order operator, the boundary reflects the Green function accordingly in order to satisfy the equivalent homogeneous boundary condition, see Figure 2. Furthermore, this reflection applies to both the closed expression of the Gaussian, c.f. expression (31), and the Taylor series expansion, with some precautions regarding the value of the diffusion coefficient. In general, if the transport coefficient is not constant, it will affect the expression of the Green function and the way the reflection occurs over the boundary as this coefficient will define the Eigenfunctions for the semi-open space of the approximated Green function, therefore, the affectation over the whole problem will be not negligible. Nonetheless, once again we take profit of both the short-time approximation and the perspective on how the Green function works as a transition probability to overcome this difficulty. In an abstract manner, we can think that the solution at future state $\left(x,t+\tau \right)$ as the sum of independent contributions from the past states, $\left(x^{\prime },t\right)$ being each of them defined by the Green function, that must be, at first-order, a Gaussian. Moreover, for each of the points $x_i$ in the future state, its solution will be propagated by a Gaussian-like Green function with its diffusion coefficient evaluated at this very same point $x_i$. Hence, from this perspective we can assume that each of the points $x_i$ will have their own Gaussian-like Green function and, accordingly, their reflection to satisfy the homogeneous boundary condition that is required. Writing the reflected Green function in terms of the Taylor series expansion we recover,

$${\mathcal{G}}_{2,sOD}\left(x,t+\tau |x^{\prime },t_0\right)=\left\{\mathrm{Exp}\left[\tau a_2\left(x,t_0\right){\displaystyle \frac{d^2}{d{x}^2}}\right]+{\displaystyle \frac{1}{2}}{\tau }^2{\psi }_2\right\}\left[\delta \left(x-x^{\prime }\right)\pm \delta \left(x-2x_b+x^{\prime }\right)\right]$$

(62)

where $x_b$ is the position of the boundary and the ± signs correspond, respectively, to the Dirichlet and Neumann homogeneous boundary conditions at the points.

From this perspective, we can therefore define the length of the $\mathit{physical}$ boundary region by means of the support of the reflected Green function, that, being a Gaussian-like function, will depend on the number of standard deviations, i.e., $\sqrt{\tau a_2}$ we want to consider. Moreover, this distance will be dependent of the value of the diffusion at the boundary $a_2\left(x_b,t\right)$, that might vary with time.

Following the same methodology as before, the next step is to integrate the Green function times the Lagrange polynomial over the domain of validity. In particular, for the numerical boundary region the integration is performed through the last stencils of the domain that include modified points to attenuate the error by means of the scheme presented in Section 3.1. As a result, the last stencil has a wider domain of validity, ${\mathsf{\Omega }}_M$, therefore, the integral will produce all the weights for the last stencil. Changing the points of the stencil will produce a different integral, and therefore, different weights than those computed in Equation (45). Consequently, the last point $x_i$ at which the weights are altered will be that defining the limit of the numerical boundary region. Hence, we can select the last $2q+1$ points as this limit.

Matching both numerical and analytical regions, we find a specific CFL number for the boundaries, or outer CFL, that will indicate how much of the reflected Gaussian interact with the inner boundary of ${\mathsf{\Omega }}_M$:

$${\mathsf{\Pi }}_{b,2}={\displaystyle \frac{a_2\left(x_b\right)\tau }{{\mathsf{\Omega }}_M}}.$$

(63)

As the standard CFL is defined over one single grid step, $\Delta x$, the outer CFL will in general be smaller than the inner one. Nevertheless, as there is no analytical solution for the grid distribution, this condition must be verified, specially for lower stencils.

One interesting consequence of using a piecewise interpolation together with the Green function is that, developing the integral as in Equation (42) for the last domain of validity, ${\mathsf{\Omega }}_M$, we obtain,

$$\begin{array}{c}\hfill u\left(x,t_0+\tau \right)=\\ \hfill \sum _{j=-q}^{q}u\left(x_{M+k}{t}_0\right){\int }_{y_M}^1{\mathcal{G}}_{2,sOD}\left(x-x^{\prime },\tau \right)\left[l_j\left(x^{\prime }-x_M\right)+R\left(x^{\prime },q,{\mathsf{\Omega }}_M\right)\right]d{x}^{\prime },\\ \hfill \forall x\in \left[y_M,1\right]\end{array}$$

(64)

where we have left explicit the error of the interpolation, $R\left(x^{\prime },q,{\mathsf{\Omega }}_M\right)$, as defined in (37). As we can see, the error at the boundary will be mitigated by the Green function, the more, the lower the value ${\mathsf{\Pi }}_{b,2}$ is.

The weights over the boundary points, $2q+1$ will be therefore case-dependent for each stencil and their closed expression must be pre-computed for every pair of values of N and q before the simulation is performed. Yet, they can still be defined in terms of Finite Difference operators. Indeed, for the non-reflected term, i.e., the one that contains the $\delta \left(x-x^{\prime }\right)$ in expression (62), we recover,

$$u\left(x_i,t+\tau \right)=u\left(x,t_0\right)+\left\{\begin{array}{c}\hfill \sum _{k=1}^q{\displaystyle \frac{\left(2k\right)!}{k!}}{\mathsf{\Pi }}_2^{2k}{\widehat{\delta }}_{2q+1}^{2k}\left[u\right]\left(x=x_i\right),\forall x_i/i\in \left[M-q+1,M\right]\\ \hfill \sum _{k=1}^q{\displaystyle \frac{\left(2k\right)!}{k!}}{\mathsf{\Pi }}_2^{2k}{\widehat{d}}_{2q+1,i-M}^{2k}\left[u\right]\left(x=x_i\right),\forall x_i/i\in \left[M+1,N\right]\end{array}\right.,$$

(65)

where the ${\widehat{\delta }}_{2q+1}^{2k}\left[.\right]$ operator is still the centered finite difference operator, yet defined over the last $2q+1$ points of the domain with the last half q points non-homogeneously distributed. Thus, it will produce different coefficients for different values of q. Furthermore, the hat indicates that each of the local grid steps, $\Delta x_i$ have been non-dimensionalized by the homogeneous $\Delta x$ in order to recover the same CFL number than we have on the other terms. The ${\widehat{d}}_{2q+1,i-M}^{2k}\left[.\right]$ operator corresponds to the de-centered finite difference operator, defined over $2q+1$ points and de-centered a number of points equal to $i-M$. These coefficients can be computed using the well-known Fornberg algorithm for the computation of finite differences [73], recalling that their grid step must be divided by the homogeneous $\Delta x$ before implementing them into the numerical scheme.

The reflection, on the other hand, only affects the boundary point, $x_b$, as the rest of the discrete reflections will remain outside of the domain of integration, i.e., ${\mathsf{\Omega }}_M$. This effect can be understood looking back at Figure 2, where we can identify the colored Gaussian as the explicit expression of the Green function and the Delta in its center can be seen as the Taylor series expansion of the Green function. Hence, while the reflection activates since the beginning of the boundary domain, the delta term only appears at the final value of the boundary point, imposing or codifying the Green function homogeneous condition over it. As a result, for the Dirichlet boundary condition, all the weights will be canceled at $x_b$ and in the Neumann boundary the weights will be doubled. Furthermore, this effect will be also transmitted at the non-homogeneous terms through the Green function, causing their propagation to also satisfy the homogeneous boundary condition.

We present two homogeneous examples in Figure 12 and Figure 13, with constant and variable diffusive coefficients, respectively. To recover these solutions, it is enough to follow the standard methodology we have introduced through this work, adding at the initial and last points the contribution of the reflection over the Green function, i.e., using the weights from (65) doubled at the Neumann Boundary point and of a null value for the Dirichlet one. Even in the situation of the time evolving and spatially variable diffusion coefficient, the scheme will include the weights for each of the propagation towards the boundary. While we will require to introduce the correction terms for the weights, specially to take into account for the temporal variation correction, the algorithm will still hold its simple shape: propagating the information from the stencil points towards the future value, regardless of whether we reach the end of the domain or not.

Finally, the last contribution of the boundary at the numerical scheme is its boundary term, that can be extracted from Equation (9). For the Dirichlet problem, its expression is rather straightforward as it is the only term that can affect the value of the unknown function at the boundary, $u\left(x_b,t_0+\tau \right)$ as the rest are null at $x_b$. Therefore, it must be equal to $u\left(x_b,t+\tau \right)-u\left(x_b,t\right)$, which is what we also recover analytically by developing the integral, i.e., deriving the Dirichlet Green function and applying it to the discretization of the unknown function at that point. This is why most of the numerical algorithms impose directly the Dirichlet boundary condition successfully without any extra regard on the affectation of the boundary over the rest of the domain. The Neumann boundary condition is also straightforward: all the terms of the integral disappear, leaving only the following,

$$u_{b,Neu}\left(x,t_0+\tau \right)={\int }_0^{\tau }{\mathcal{G}}_{2,sOD}\left(x,t_0+\tau |x_b,t_0+{\tau }^{\prime }\right)f_u\left(t_0+{\tau }^{\prime }\right)d{\tau }^{\prime }$$

(66)

where $f_u\left(t\right)=a_{2}du/dx$ is the usual flux or derivative imposed at the boundary for the unknown function. Hence, this term can be seen as the propagation of the flux that is injected to or extracted from the domain, which can be abstractly thought also as a discrete nonlinear term production/destruction term of the problem.

Finally, in Figure 14 we present an example where we use all three boundary contributions and required modifications to implement them into the scheme. In other words, we solve a Heat transfer equation with a space-dependent diffusion coefficient in the shape of a well in order to define clearly different regions of characteristic diffusion, and so, different heat propagation speeds. Furthermore, we set two boundary conditions: one time-evolving that increases the temperature of the left region of the domain up to a certain value progressively and another one at the left that serves as heat sink, i.e., a Dirichlet homogeneous condition. In particular, we select the following temperature law to heat the non-homogeneous boundary:

$$u_b\left(-1,t\right)=\left\{\begin{array}{cc}\hfill \sin \left(2\pi t\right),& 0\le t\le 0.5\hfill \\ \hfill 1,& 0.5\le t\hfill \end{array}\right.$$

(67)

Therefore, heat will take more time to evolve away from the domain, increasing the value of the temperature at the left-hand side more together with its slope or heat flux until it reaches the maximum possible. Regardless of the physical interpretation of this simple example, we have shown how to impose boundary conditions in an efficient manner and consistent with the chosen optimized discretization. Therefore, the explorative analysis of the method successfully achieves its first milestone: the definition of a consistent numerical algorithm that can be derived from the Green function of the problem.

This scheme sets the path for a wide range of possible boundaries to be imposed regardless of the problem we are dealing with as long as the boundary conditions are consistent with the order the Green function. In addition, as the contribution of the non-homogeneous terms and the boundaries are independent from the main propagation, we have shown that only the last point (or the last line or surface, deepening on which kind of boundary is under study) will be enough to deploy any kind of boundary law.

Finally, we point out that our results align, from a humble numerical perspective, with the efforts being performed to obtain a precise definition of boundaries from the perspective of Quantum Field Theory [74,75]. The most straightforward relation is the definition of boundary conditions as a discrete Dirac delta set at the boundary, from which they recover the Neumann term (two times the diffusion coefficient) in a more theoretically profound manner. Indeed, we can think of the boundary term that we have obtained as a non-homogeneous term, which by means of a Dirac delta, ${\delta }_{x-x_b}$, breaks the volumetric integral and transforms it into a surface, line, or point.

With this idea in mind, we could explore the possibility of defining internal boundary conditions, with the problem being that the stencils pointing towards them will be de-centered automatically. Moreover, if this internal boundary evolves in time, we will need to update all polynomial coefficients and stencils at every iteration. This may result in an arduous mathematical and numerical task, yet in line with applications intended for the particle or Lagrangian methodologies to solve PDEs [24].

4. Conclusions

Throughout this work, we have presented the numerical possibilities offered by the weak or integral solution of a nonlinear PDE when transposed into a numerical scheme, revisiting the original methods designed for Fokker–Planck equations and updating them into a more general algorithm. The only requirement for the original shape of the PDE is to have a separable quasilinear operator, which defines the Green function of the problem: a function that satisfies such a quasilinear PDE with homogeneous boundary conditions. The result of this exercise is an integral scheme where the Green function serves as the kernel propagating the different contributions of the solution in a defined state, $\left(x^{\prime },t_0\right)$, towards the next state—understood, within the short-time approximation, as the next time frame. Therefore, we can build an integral time-evolving numerical scheme defined by the difference between time frames, or time step, $\tau$, that will determine the quality of the numerical solution.

Under the short-time approximation, the Green function can be interpreted directly as a transfer function or, from a physical perspective, as a transition probability. Understanding its shape and properties allows one to predict how information evolves in time while satisfying the PDE, and moreover, to define zones of influence between past and future states. This allows for simplifications of the problem, the most straightforward being the separation of the domain of interest into different regions of influence. In this context, we can numerically define boundary and inner regions—zones within the domain that are unaffected by the boundary. As a result, the problem in the inner region is simplified and can be treated as an open domain, whereas the boundary regions are treated as semi-open. Under these assumptions, we derive the Green functions of the first- and second-order quasilinear operators in two different but equivalent ways: as discrete Dirac deltas, around which we extrapolate the operator using a Taylor series, and in a closed form, as the solution to its own PDE, i.e., the homogeneous version of the target PDE. Furthermore, at the boundary regions, the second-order operator allows for the application of the method of images, simplifying the process of deriving the semi-open Green function by reflecting it using the boundary as a mirror. With these two expressions established, the next step was to introduce a numerical discretization from which the time-evolving numerical algorithm could emerge. Depending on the shape of this discretization, we may find a solution with poor stability properties. Even when an appropriate discretization yields a low interpolation error, if the resulting discrete matrix does not exhibit suitable behavior or fails to correctly reproduce the time-marching behavior, it may cause indefinite growth over time. To mitigate these issues, we introduced and refined a grid optimization algorithm to ensure the equioscillation condition over a piecewise interpolation, following the methodology of Gauss–Lobato–Chebyshev quadrature. The main conclusion from this is that, outside of the boundary region (defined by the stencil size of the piecewise interpolation, $2q+1$), the optimal grid tends to approach a homogeneous discretization. Thus, we can separate the problem both numerically and analytically into inner and boundary problems, assuming that the inner points are defined with a constant grid and a domain of validity equal to half of the grid step. Incorporating this idea into the integral scheme and using a Lagrange-like interpolation, we developed a time-marching interpolation scheme over a stencil of size $2q+1$ with weights corresponding to the numerical transposition of the Green function. We then conducted an exploratory study to understand the limitations and behavior of these approximations by introducing mathematical complexity into the numerical scheme. To do so, we set ourselves in the simplest test case possible, a constant coefficient, linear PDE over a ring: the time-marching scheme will become the convolution of the Green function with the initial condition, hence, propagating it towards the next time frame. Yet, even for this simple test case we found that the domain of validity of the piecewise interpolation might interact with this convolution and, as the Green function is not in general a closed expression, would require us to set a limitation on the numerical group that determines the quality of the convolution, i.e., the Courant–Friedrichs–Lewy number (CFL). Once this limitation was satisfied, the next step in the exploration of the method was to analyze how a non-constant, non-homogeneous transport coefficient would affect both the closed expression of the Green function and its Taylor series expansion. To achieve this, we further developed the expansion, recovering the first correction terms, of order ${\tau }^2$, and tested them under constraining, steep transport coefficients to verify their order of magnitude and guarantee that the order ${\tau }^2$ held. Subsequently, the non-homogeneous contribution to the solution was introduced, representing a critical step as it is the malleable part of the method. If this contribution is handled properly, any PDE shape may be solved using this methodology so long as it presents a quasilinear term. To guarantee that the nonlinear term was handled appropriately, we adapted the midpoint rule, i.e., a second-order Runge–Kutta for its simplicity and improvement in quality of the result. Furthermore, we tested it in two cumbersome problems: the viscid Burgers equation, with a very low diffusion compared to its characteristic advection (in very generous choice of words, with a Reynolds number equal to ${10}^5$) and the norm and energy conserving soliton solution of the nonlinear Schödinger Equation (NLSE).

To further demonstrate the method’s robustness when coupled with the simplest of Runge–Kutta schemes, the classical shock-like behavior of the Burgers equation held without any Runge-like oscillations, preserving the norm of the initial condition (a normalized Gaussian) with a non-dimensional error up to ${10}^{-12}$ while preserving the order of magnitude of ${10}^{-5}$ s per iteration. The second problem, the soliton of the NLSE is particularly challenging as the diffusion coefficient in this equation is the imaginary unit, meaning that the real part of the wave function will diffuse over the imaginary and vice versa, creating the well-known oscillating properties for this equation. The quality of the approximation obtained is therefore lower than in the case of the Burgers equation, nonetheless, still numerically consistent. Moreover, after ${10}^9$ time iterations, both the norm and the energy of the soliton could be considered conserved within a non-dimensional variation of ${10}^{-3}$ and ${10}^{-5}$, respectively, over their analytical values.

Finally, we develop the boundary term for the second-order operator, to obtain a rather simple modification of the algorithm, only affecting the weights at the last domain of validity and the next q points due to the collocation algorithm we designed. Therefore, to test this result, we proposed three boundary test cases: two with homogeneous boundary conditions, with constant and spatio-temporal dependent transport coefficients, and one with non-homogeneous conditions. In both first cases, the boundary condition was achieved without a mayor analytical increase on complexity or computational time penalty over the algorithm definition. Only the weights of the last stencils are defined over the de-centered finite differences and the last point of the domain presents a modified scheme. Still, as the weights can be precomputed, together with the size and distribution of the last points $2q+1$ points not increasing the computational cost for the method. The last example was a time-evolving boundary condition at one of the boundaries, introducing information (or concretely, in the test case we studied, heat) at the left boundary that the Dirichlet homogeneous present at the right side will destroy.

As a general conclusion, this methodology shows promise for further exploration, allowing for the solution of complex problems involving nonlinear terms and time-evolving boundary conditions. While Lagrange piecewise interpolation and the optimized grid point have limitations for complex geometries, the simplicity and flexibility of the method warrant further investigation, particularly its adaptation for high-performance computing (HPC). Indeed, the coupling of this homogeneously distributed scheme with grid interpolators and the independence between boundary and inner regions might overcome this limitation.

Moreover, the convolution operation performed by this method is easily parallelizable/vectorizable, making it suitable for GPU implementation.

Future Works

We propose the following future lines of research, with the aim of expanding this work’s applications and optimizing the computational implementation of the algorithm while preserving its simplicity and high-order capabilities.

• Extension of the numerical method to wider and more ambitious high-dimensional problems.
• Development of a computationally efficient numerical scheme.
• Comprehensive study of boundary conditions and their classification.
• Comparison of different discretization techniques to show how the Green function interacts with other kinds of grid sets.
• Detailed development of the theoretical framework, including both the mathematical foundation and the numerical discretization of the Green function.
• Extension to higher-order operators in both time and space.