Improving the Generalization Abilities of Constructed Neural Networks with the Addition of Local Optimization Techniques
Abstract
1. Introduction
2. Method Description
2.1. Grammatical Evolution
- The set N contains the symbols denoted as non-terminal.
- The set T has the terminal symbols.
- The symbol stands for the start symbol of the grammar.
- The set P has all the production rules of the underlying grammar. These rules are used to produce terminal symbols from non-terminal symbols, and they are in the form or .
- Read the the next element V from the processed chromosome.
- Select the production rule that will be applied using the equation: Rule = V mod , where stands for the number of production rules that contains the current current non-terminal symbol.
2.2. The Proposed Algorithm
- 1.
- Initialization step.
- (a)
- Set as the generation counter.
- (b)
- Set as the maximum number of generations and as the number of chromosomes.
- (c)
- Set as the selection rate and as the mutation rate of the genetic algorithm.
- (d)
- Set as the number of chromosomes that will be selected to apply the local search optimization method on them.
- (e)
- Set as the number of generations that should pass before the application of the suggested local optimization technique.
- (f)
- Set as F the range of values within which the local optimization method can vary the parameters of the neural network.
- (g)
- Perform a random initialization of the chromosomes as sets of random integers.
- 2.
- Fitness Calculation step.
- (a)
- For do
- i.
- Produce the corresponding neural network for the chromosome , The production is performed using the procedure of Section 2.1. The vector denotes the set of parameters produced for the chromosome .
- ii.
- Set as the fitness of chromosome i. The set represents the train set.
- (b)
- EndFor
- 3.
- Genetic operations step.
- (a)
- Copy the best chromosomes according to their fitness values to the next generation.
- (b)
- Apply the crossover procedure. This procedure creates offsprings from the current population. Two chromosomes are selected through tournament selection for every created couple of ofssprings. These offsprings are created using the one-point crossover procedure, which is demonstrated in Figure 2.
- (c)
- Apply the mutation procedure. During this procedure, a random number is selected from uniform distribution for every element of each chromosome. If , then the current element is altered randomly.
- 4.
- Local search step.
- (a)
- If k mod = 0 then
- i.
- Set a set of chromosomes of the current population that are selected randomly.
- ii.
- For , apply the procedure described in Section 2.3 on chromosome .
- (b)
- Endif
- 5.
- Termination check step.
- (a)
- Set
- (b)
- If go to Fitness Calculation Step, else
- i.
- Obtain the chromosome that has the lowest fitness value among the population.
- ii.
- Produce the corresponding neural network for this chromosome. The vector denotes the set of parameters for the chromosome .
- iii.
- Obtain the corresponding test error for .
2.3. The Local Search Procedure
- 1.
- Set . This value denotes the total number of parameters for .
- 2.
- For do
- (a)
- Set , the left bound of the minimization for the parameter i.
- (b)
- Set , the right bound of the minimization for the parameter i.
- 3.
- EndFor
- 4.
3. Experimental Results
- 1.
- The UCI dataset repository, https://archive.ics.uci.edu/ml/index.php (accessed on 28 September 2024) [64].
- 2.
- The Keel repository, https://sci2s.ugr.es/keel/datasets.php (accessed on 28 September 2024) [65].
- 3.
- The Statlib URL http://lib.stat.cmu.edu/datasets/ (accessed on 28 September 2024).
3.1. The Used Classification Datasets
- 1.
- Appendictis, which is a dataset originated in [66].
- 2.
- Australian dataset [67], which is related to bank transactions.
- 3.
- Balance dataset [68], which has been used in a series of psychological experiments.
- 4.
- Circular dataset, which contains artificially generated data.
- 5.
- 6.
- Dermatology dataset [71], which is a dataset that contains measurements of dermatological deceases.
- 7.
- Ecoli dataset, which is a dataset that contains measurements of proteins [72].
- 8.
- Fert dataset, which is used to detect the relation between sperm concentration and demographic data.
- 9.
- Haberman dataset, which is a medical dataset related to breast cancer.
- 10.
- Hayes roth dataset [73].
- 11.
- Heart dataset [74], which is a medical dataset used for the prediction of heart diseases.
- 12.
- HeartAttack dataset, which is used for the detection of heart diseases.
- 13.
- HouseVotes dataset [75].
- 14.
- Liverdisorder dataset [76], which is a medical dataset.
- 15.
- 16.
- Mammographic dataset [79], which is a dataset related to the breast cancer.
- 17.
- Parkinsons dataset, which is used in the detection of Parkinson’s disease (PD) [80].
- 18.
- Pima dataset [81].
- 19.
- Popfailures dataset [82].
- 20.
- Regions2 dataset, which is used in the detection of hepatitis C [83].
- 21.
- Saheart dataset [84], which is a medical dataset used for the detection of heart diseases.
- 22.
- Segment dataset [85], which is a dataset related to image processing.
- 23.
- Spiral dataset, which is an artificial dataset.
- 24.
- Student dataset [86], which contains data from experiments conducted in Portuguese schools.
- 25.
- Transfusion dataset [87], which is a medical dataset.
- 26.
- Wdbc dataset [88].
- 27.
- 28.
- Eeg datasets, which is a dataset that contains EEG experiments [91]. The following distinct cases were used from this dataset: Z_F_S, Z_O_N_F_S, ZO_NF_S and ZONF_S.
- 29.
- Zoo dataset [92], which is used to classify animals.
3.2. The Used Regression Datasets
- 1.
- Abalone dataset [93].
- 2.
- Airfoil dataset, which is a dataset derived from NASA [94].
- 3.
- BK dataset [95], which contains data from various basketball games.
- 4.
- BL dataset, which contains data from an electricity experiment.
- 5.
- Baseball dataset, which is used to predict the average income of baseball players.
- 6.
- Concrete dataset [96].
- 7.
- Dee dataset, which contains measurements of the price of electricity.
- 8.
- FY, which is used to measure the longevity of fruit flies.
- 9.
- HO dataset, which appeared in the STALIB repository.
- 10.
- Housing dataset, which originated in [97].
- 11.
- Laser dataset, which contains data from physics experiments
- 12.
- LW dataset, which contains measurements of low weight babies.
- 13.
- MORTGAGE dataset, which is related to some economic measurements from the USA.
- 14.
- MUNDIAL, which appeared in the STALIB repository.
- 15.
- PL dataset, which is included in the STALIB repository.
- 16.
- QUAKE dataset, which contains data about earthquakes.
- 17.
- REALESTATE, which is included in the STALIB repository.
- 18.
- SN dataset, which contains measurements from an experiment related to trellising and pruning.
- 19.
- Treasury dataset, which deals with some factors of the USA economy.
- 20.
- VE dataset, which is included in the STALIB repository.
- 21.
- TZ dataset, which is included in the STALIB repository.
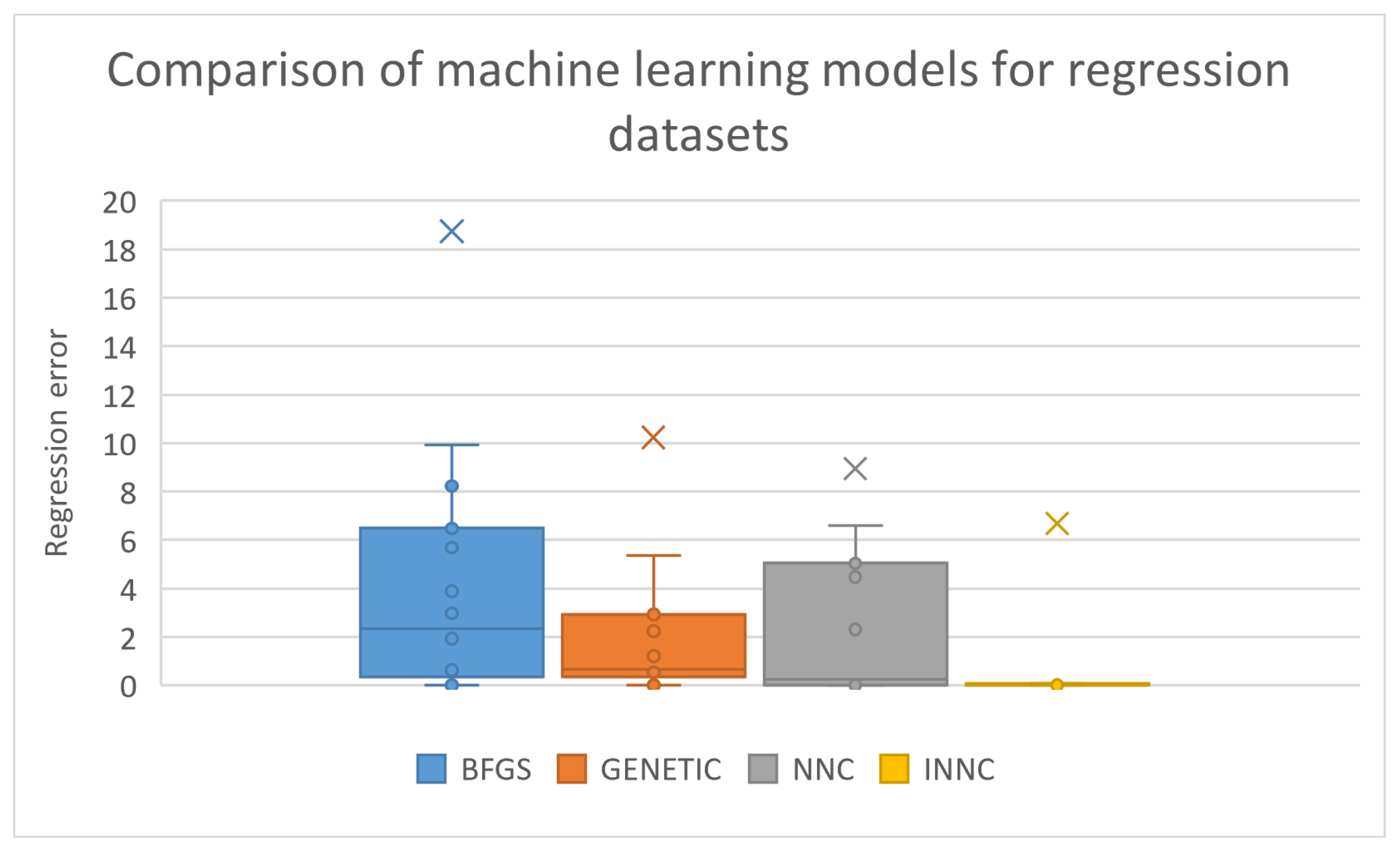
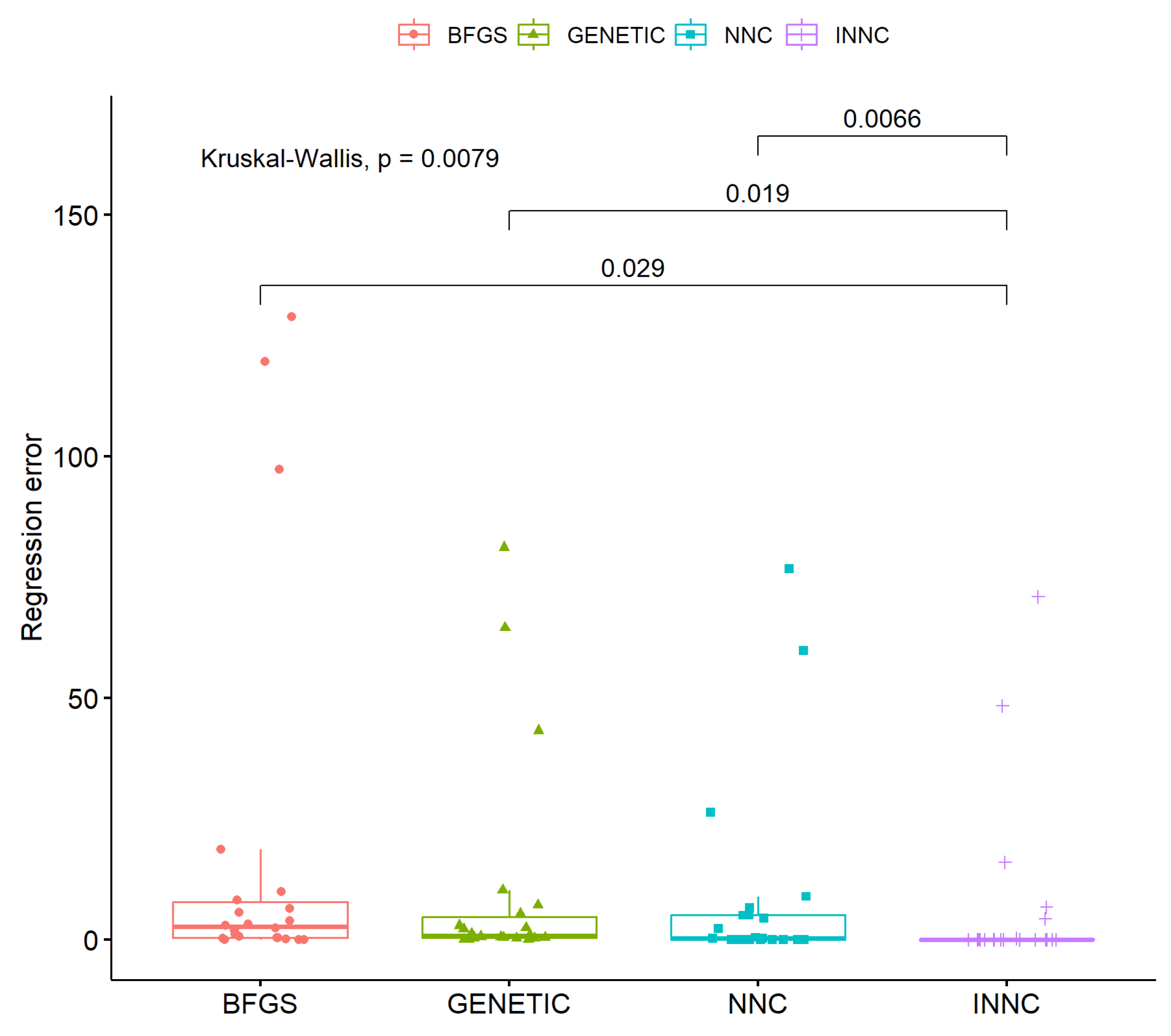
3.3. Experimental Results
- 1.
- The column BFGS represents the results obtained by the application of the BFGS method to train a neural network with processing nodes.
- 2.
- The column GENETIC represents the results produced by the training of a neural network with processing nodes using a genetic algorithm. The parameters of this algorithm are mentioned in Table 3.
- 3.
- The column NNC represents the results obtained by the neural construction technique.
- 4.
- The column INNC represents the results obtained by the proposed method.
- 5.
- The last row AVERAGE contains the average classification or regression error, as measured on all datasets.
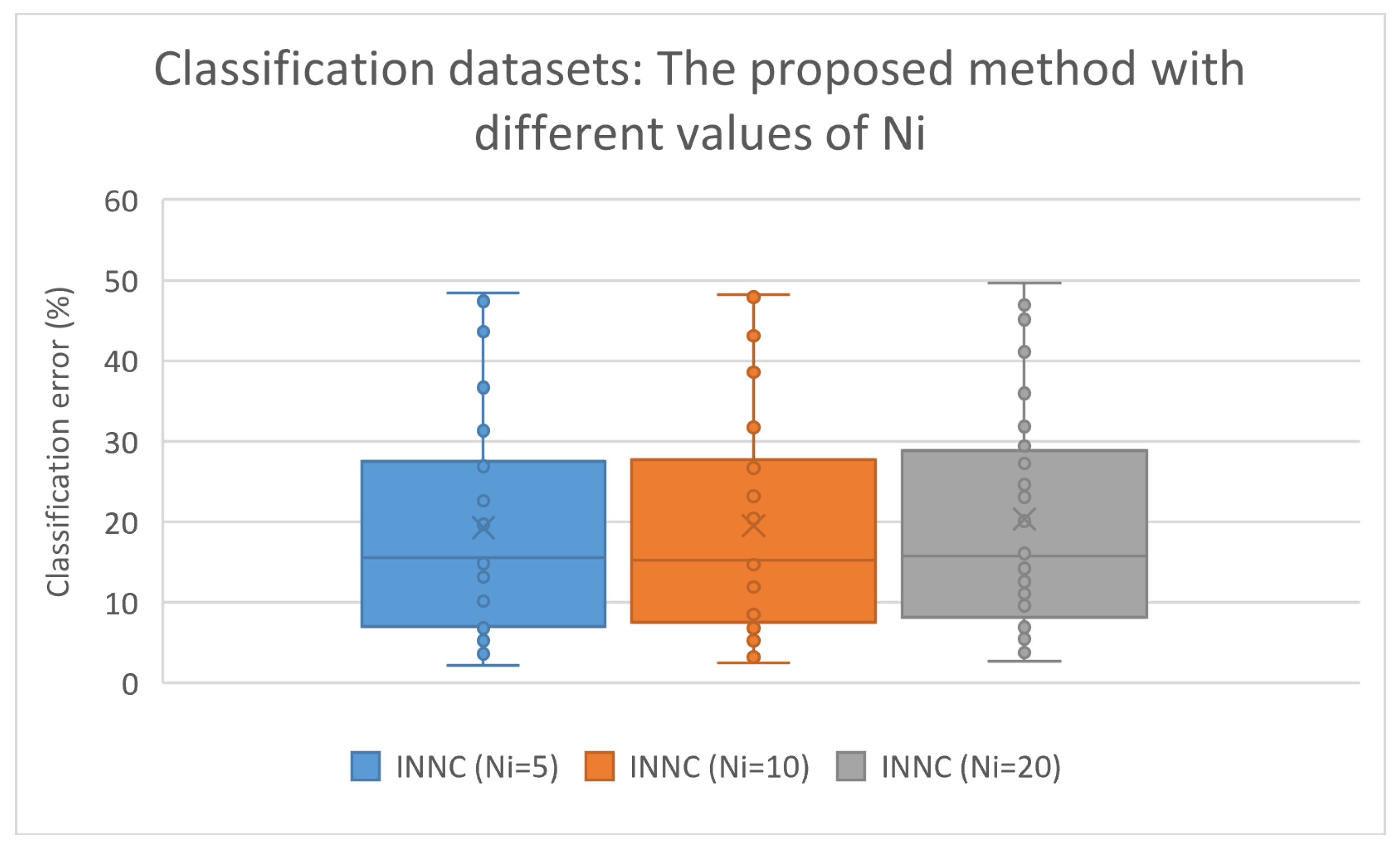
3.3.1. Experiments with the Parameter
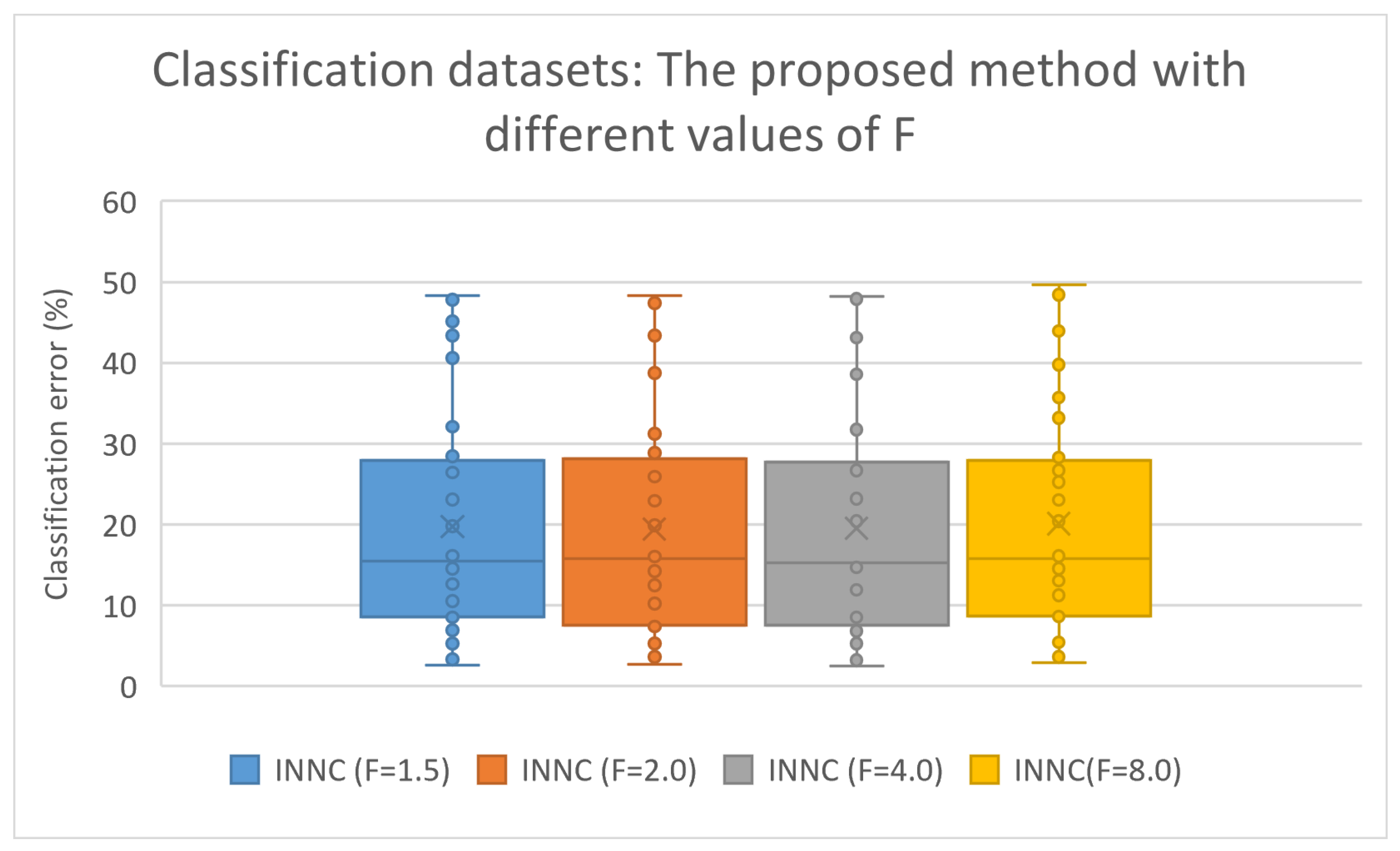
3.3.2. Experiments with the Parameter F
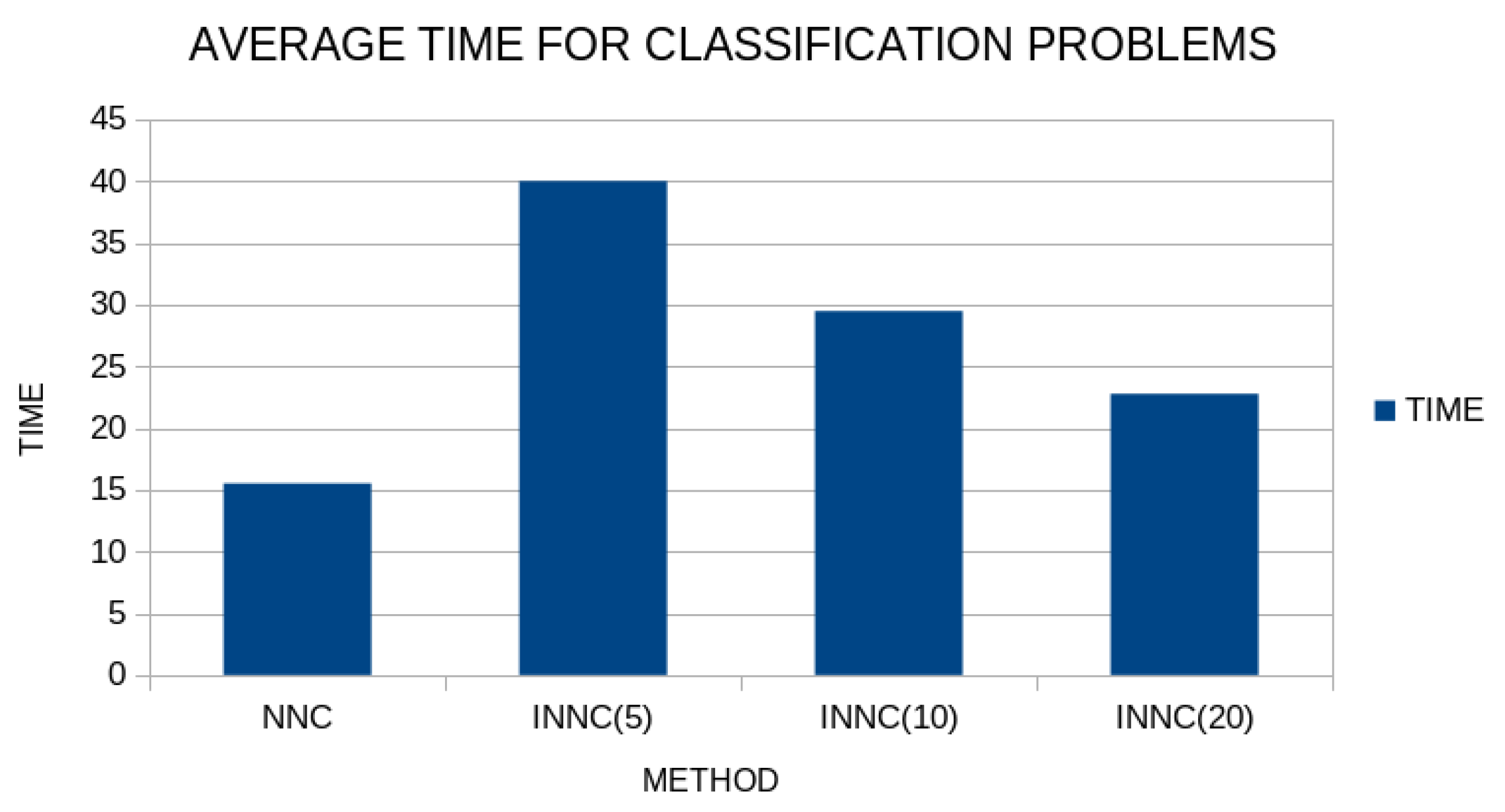
3.3.3. Experiments with the Used Local Search Optimizer
- 1.
- The column ADAM denotes the incorporation of the ADAM local optimization method [18] in the current technique.
- 2.
- The column LBFGS denotes the incorporation of the Limited Memory BFGS (L-BFGS) method [98] as the local search procedure.
- 3.
- The column BFGS represents the incorporation of the BFGS method, modified by Powell [63], as the local search procedure.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef]
- Suryadevara, S.; Yanamala, A.K.Y. A Comprehensive Overview of Artificial Neural Networks: Evolution, Architectures, and Applications. Rev. Intel. Artif. Med. 2021, 12, 51–76. [Google Scholar]
- Baldi, P.; Cranmer, K.; Faucett, T.; Sadowski, P.; Whiteson, D. Parameterized neural networks for high-energy physics. Eur. Phys. J. C 2016, 76, 1–7. [Google Scholar] [CrossRef]
- Carleo, G.; Troyer, M. Solving the quantum many-body problem with artificial neural networks. Science 2017, 355, 602–606. [Google Scholar] [CrossRef]
- Khoo, Y.; Lu, J.; Ying, L. Solving parametric PDE problems with artificial neural networks. Eur. J. Appl. Math. 2021, 32, 421–435. [Google Scholar] [CrossRef]
- Kumar Yadav, A.; Chandel, S.S. Solar radiation prediction using Artificial Neural Network techniques: A review. Renew. Sustain. Energy Rev. 2014, 33, 772–781. [Google Scholar] [CrossRef]
- Escamilla-García, A.; Soto-Zarazúa, G.M.; Toledano-Ayala, M.; Rivas-Araiza, E.; Gastélum-Barrios, A. Applications of Artificial Neural Networks in Greenhouse Technology and Overview for Smart Agriculture Development. Appl. Sci. 2020, 10, 3835. [Google Scholar] [CrossRef]
- Shen, L.; Wu, J.; Yang, W. Multiscale Quantum Mechanics/Molecular Mechanics Simulations with Neural Networks. J. Chem. Theory Comput. 2016, 12, 4934–4946. [Google Scholar] [CrossRef]
- Wei, J.N.; Duvenaud, D.; Aspuru-Guzik, A. Neural Networks for the Prediction of Organic Chemistry Reactions. ACS Cent. Sci. 2016, 2, 725–732. [Google Scholar] [CrossRef]
- Khosravi, A.; Koury, R.N.N.; Machado, L.; Pabon, J.J.G. Prediction of wind speed and wind direction using artificial neural network, support vector regression and adaptive neuro-fuzzy inference system. Sustain. Energy Technol. Assess. 2018, 25, 146–160. [Google Scholar] [CrossRef]
- Falat, L.; Pancikova, L. Quantitative Modelling in Economics with Advanced Artificial Neural Networks. Procedia Econ. Financ. 2015, 34, 194–201. [Google Scholar] [CrossRef]
- Namazi, M.; Shokrolahi, A.; Sadeghzadeh Maharluie, M. Detecting and ranking cash flow risk factors via artificial neural networks technique. J. Bus. Res. 2016, 69, 1801–1806. [Google Scholar] [CrossRef]
- Baskin, I.I.; Winkler, D.; Tetko, I.V. A renaissance of neural networks in drug discovery. Expert Opin. Drug Discov. 2016, 11, 785–795. [Google Scholar] [CrossRef]
- Bartzatt, R. Prediction of Novel Anti-Ebola Virus Compounds Utilizing Artificial Neural Network (ANN). Chem. Fac. Publ. 2018, 49, 16–34. [Google Scholar]
- Vora, K.; Yagnik, S. A survey on backpropagation algorithms for feedforward neural networks. Int. J. Eng. Dev. Res. 2014, 1, 193–197. [Google Scholar]
- Pajchrowski, T.; Zawirski, K.; Nowopolski, K. Neural speed controller trained online by means of modified RPROP algorithm. IEEE Trans. Ind. Inform. 2014, 11, 560–568. [Google Scholar] [CrossRef]
- Hermanto, R.P.S.; Nugroho, A. Waiting-time estimation in bank customer queues using RPROP neural networks. Procedia Comput. Sci. 2018, 135, 35–42. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. ADAM: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Kuo, C.L.; Kuruoglu, E.E.; Chan, W.K.V. Neural Network Structure Optimization by Simulated Annealing. Entropy 2022, 24, 348. [Google Scholar] [CrossRef]
- Reynolds, J.; Rezgui, Y.; Kwan, A.; Piriou, S. A zone-level, building energy optimisation combining an artificial neural network, a genetic algorithm, and model predictive control. Energy 2018, 151, 729–739. [Google Scholar] [CrossRef]
- Das, G.; Pattnaik, P.K.; Padhy, S.K. Artificial neural network trained by particle swarm optimization for non-linear channel equalization. Expert Syst. Appl. 2014, 41, 3491–3496. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, Y.; Chen, T. Back propagation neural network with adaptive differential evolution algorithm for time series forecasting. Expert Syst. Appl. 2015, 42, 855–863. [Google Scholar] [CrossRef]
- Salama, K.M.; Abdelbar, A.M. Learning neural network structures with ant colony algorithms. Swarm Intell. 2015, 9, 229–265. [Google Scholar] [CrossRef]
- Mirjalili, S. How effective is the Grey Wolf optimizer in training multi-layer perceptrons. Appl. Intell. 2015, 43, 150–161. [Google Scholar] [CrossRef]
- Aljarah, I.; Faris, H.; Mirjalili, S. Optimizing connection weights in neural networks using the whale optimization algorithm. Soft Comput. 2018, 22, 1–15. [Google Scholar] [CrossRef]
- Zhang, M.; Hibi, K.; Inoue, J. GPU-accelerated artificial neural network potential for molecular dynamics simulation. Comput. Phys. Commun. 2023, 285, 108655. [Google Scholar] [CrossRef]
- Varnava, T.M.; Meade, A.J. An initialization method for feedforward artificial neural networks using polynomial bases. Adv. Adapt. Data Anal. 2011, 3, 385–400. [Google Scholar] [CrossRef]
- Ivanova, I.; Kubat, M. Initialization of neural networks by means of decision trees. Knowl.-Based Syst. 1995, 8, 333–344. [Google Scholar] [CrossRef]
- Sodhi, S.S.; Chandra, P. Interval based Weight Initialization Method for Sigmoidal Feedforward Artificial Neural Networks. AASRI Procedia 2014, 6, 19–25. [Google Scholar] [CrossRef]
- Chumachenko, K.; Iosifidis, A.; Gabbouj, M. Feedforward neural networks initialization based on discriminant learning. Neural Netw. 2022, 146, 220–229. [Google Scholar] [CrossRef]
- Chen, Q.; Hao, W.; He, J. A weight initialization based on the linear product structure for neural networks. Appl. Math. Comput. 2022, 415, 126722. [Google Scholar] [CrossRef]
- Arifovic, J.; Gençay, R. Using genetic algorithms to select architecture of a feedforward artificial neural network. Phys. A Stat. Mech. Its Appl. 2001, 289, 574–594. [Google Scholar] [CrossRef]
- Benardos, P.G.; Vosniakos, G.C. Optimizing feedforward artificial neural network architecture. Eng. Appl. Artif. Intell. 2007, 20, 365–382. [Google Scholar] [CrossRef]
- Garro, B.A.; Vázquez, R.A. Designing Artificial Neural Networks Using Particle Swarm Optimization Algorithms. Comput. Intell. Neurosci. 2015, 2015, 369298. [Google Scholar] [CrossRef]
- Baker, B.; Gupta, O.; Naik, N.; Raskar, R. Designing neural network architectures using reinforcement learning. arXiv 2016, arXiv:1611.02167. [Google Scholar]
- Islam, M.M.; Sattar, M.A.; Amin, M.F.; Yao, X.; Murase, K. A New Adaptive Merging and Growing Algorithm for Designing Artificial Neural Networks. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2009, 39, 705–722. [Google Scholar] [CrossRef] [PubMed]
- O’Neill, M.; Ryan, C. Grammatical evolution. IEEE Trans. Evol. Comput. 2001, 5, 349–358. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Gavrilis, D.; Glavas, E. Neural network construction and training using grammatical evolution. Neurocomputing 2008, 72, 269–277. [Google Scholar] [CrossRef]
- Papamokos, G.V.; Tsoulos, I.G.; Demetropoulos, I.N.; Glavas, E. Location of amide I mode of vibration in computed data utilizing constructed neural networks. Expert Syst. Appl. 2009, 36, 12210–12213. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Gavrilis, D.; Glavas, E. Solving differential equations with constructed neural networks. Neurocomputing 2009, 72, 2385–2391. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Mitsi, G.; Stavrakoudis, A.; Papapetropoulos, S. Application of Machine Learning in a Parkinson’s Disease Digital Biomarker Dataset Using Neural Network Construction (NNC) Methodology Discriminates Patient Motor Status. Front. ICT 2019, 6, 10. [Google Scholar] [CrossRef]
- Christou, V.; Tsoulos, I.G.; Loupas, V.; Tzallas, A.T.; Gogos, C.; Karvelis, P.S.; Antoniadis, N.; Glavas, E.; Giannakeas, N. Performance and early drop prediction for higher education students using machine learning. Expert Syst. Appl. 2023, 225, 120079. [Google Scholar] [CrossRef]
- Toki, E.I.; Pange, J.; Tatsis, G.; Plachouras, K.; Tsoulos, I.G. Utilizing Constructed Neural Networks for Autism Screening. Appl. Sci. 2024, 14, 3053. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Tzallas, A.; Tsalikakis, D. NNC: A tool based on Grammatical Evolution for data classification and differential equation solving. SoftwareX 2019, 10, 100297. [Google Scholar] [CrossRef]
- Backus, J.W. The Syntax and Semantics of the Proposed International Algebraic Language of the Zurich ACM-GAMM Conference. In Proceedings of the International Conference on Information Processing, UNESCO, Paris, France, 15–20 June 1959; pp. 125–132. [Google Scholar]
- Ryan, C.; Collins, J.; O’Neill, M. Grammatical evolution: Evolving programs for an arbitrary language. In Genetic Programming. EuroGP 1998; Banzhaf, W., Poli, R., Schoenauer, M., Fogarty, T.C., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1391. [Google Scholar]
- O’Neill, M.; Ryan, M.C. Evolving Multi-line Compilable C Programs. In Genetic Programming. EuroGP 1999; Poli, R., Nordin, P., Langdon, W.B., Fogarty, T.C., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1598. [Google Scholar]
- Ryan, C.; O’Neill, M.; Collins, J.J. Grammatical Evolution: Solving Trigonometric Identities. In Proceedings of the Mendel 1998: 4th International Mendel Conference on Genetic Algorithms, Optimisation Problems, Fuzzy Logic, Neural Networks, Rough Sets, Brno, Czech Republic, 1–2 November 1998. [Google Scholar]
- Puente, A.O.; Alfonso, R.S.; Moreno, M.A. Automatic composition of music by means of grammatical evolution. In APL ’02: Proceedings of the 2002 Conference on APL: Array Processing Languages: Lore, Problems, and Applications Madrid, Spain, 22–25 July 2002; Association for Computing Machinery: New York, NY, USA, 2002; pp. 148–155. [Google Scholar]
- Dempsey, I.; Neill, M.O.; Brabazon, A. Constant creation in grammatical evolution. Int. J. Innov. Comput. Appl. 2007, 1, 23–38. [Google Scholar] [CrossRef]
- Galván-López, E.; Swafford, J.M.; O’Neill, M.; Brabazon, A. Evolving a Ms. PacMan Controller Using Grammatical Evolution. In Applications of Evolutionary Computation. EvoApplications 2010; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6024. [Google Scholar]
- Shaker, N.; Nicolau, M.; Yannakakis, G.N.; Togelius, J.; O’Neill, M. Evolving levels for Super Mario Bros using grammatical evolution. In Proceedings of the 2012 IEEE Conference on Computational Intelligence and Games (CIG), Granada, Spain, 11–14 September 2012; pp. 304–331. [Google Scholar]
- Martínez-Rodríguez, D.; Colmenar, J.M.; Hidalgo, J.I.; Micó, R.J.V.; Salcedo-Sanz, S. Particle swarm grammatical evolution for energy demand estimation. Energy Sci. Eng. 2020, 8, 1068–1079. [Google Scholar] [CrossRef]
- Sabar, N.R.; Ayob, M.; Kendall, G.; Qu, R. Grammatical Evolution Hyper-Heuristic for Combinatorial Optimization Problems. IEEE Trans. Evol. Comput. 2013, 17, 840–861. [Google Scholar] [CrossRef]
- Ryan, C.; Kshirsagar, M.; Vaidya, G.; Cunningham, A.; Sivaraman, R. Design of a cryptographically secure pseudo random number generator with grammatical evolution. Sci. Rep. 2022, 12, 8602. [Google Scholar] [CrossRef]
- Pereira, P.J.; Cortez, P.; Mendes, R. Multi-objective Grammatical Evolution of Decision Trees for Mobile Marketing user conversion prediction. Expert Syst. Appl. 2021, 168, 114287. [Google Scholar] [CrossRef]
- Castejón, F.; Carmona, E.J. Automatic design of analog electronic circuits using grammatical evolution. Appl. Soft Comput. 2018, 62, 1003–1018. [Google Scholar] [CrossRef]
- Araujo, L.; Martinez-Romo, J.; Duque, A. Discovering taxonomies in Wikipedia by means of grammatical evolution. Soft Comput. 2018, 22, 2907–2919. [Google Scholar] [CrossRef]
- Martín, C.; Quintana, D.; Isasi, P. Grammatical Evolution-based ensembles for algorithmic trading. Appl. Soft Comput. 2019, 84, 105713. [Google Scholar] [CrossRef]
- Moore, J.H.; Sipper, M. Grammatical Evolution Strategies for Bioinformatics and Systems Genomics. In Handbook of Grammatical Evolution; Ryan, C., O’Neill, M., Collins, J., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Peabody, C.; Seitzer, J. GEF: A self-programming robot using grammatical evolution. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; Volume 29. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Powell, M.J.D. A Tolerant Algorithm for Linearly Constrained Optimization Calculations. Math. Program. 1989, 45, 547–566. [Google Scholar] [CrossRef]
- Kelly, M.; Longjohn, R.; Nottingham, K. The UCI Machine Learning Repository. 2023. Available online: https://archive.ics.uci.edu (accessed on 18 February 2024).
- Alcalá-Fdez, J.; Fernandez, A.; Luengo, J.; Derrac, J.; García, S.; Sánchez, L.; Herrera, F. KEEL Data-Mining Software Tool: Data Set Repository, Integration of Algorithms and Experimental Analysis Framework. J. Mult.-Valued Log. Soft Comput. 2011, 17, 255–287. [Google Scholar]
- Weiss, S.M.; Kulikowski, C.A. Computer Systems That Learn: Classification and Prediction Methods from Statistics, Neural Nets, Machine Learning, and Expert Systems; Morgan Kaufmann Publishers Inc.: San Mateo, CA, USA, 1991. [Google Scholar]
- Quinlan, J.R. Simplifying Decision Trees. Int. J. Man-Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef]
- Shultz, T.; Mareschal, D.; Schmidt, W. Modeling Cognitive Development on Balance Scale Phenomena. Mach. Learn. 1994, 16, 59–88. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Jiang, Y. NeC4.5: Neural ensemble based C4.5. IEEE Trans. Knowl. Data Eng. 2004, 16, 770–773. [Google Scholar] [CrossRef]
- Setiono, R.; Leow, W.K. FERNN: An Algorithm for Fast Extraction of Rules from Neural Networks. Appl. Intell. 2000, 12, 15–25. [Google Scholar] [CrossRef]
- Demiroz, G.; Govenir, H.A.; Ilter, N. Learning Differential Diagnosis of Eryhemato-Squamous Diseases using Voting Feature Intervals. Artif. Intell. Med. 1998, 13, 147–165. [Google Scholar]
- Horton, P.; Nakai, K. A Probabilistic Classification System for Predicting the Cellular Localization Sites of Proteins. Int. Conf. Intell. Syst. Mol. Biol. 1996, 4, 109–115. [Google Scholar]
- Hayes-Roth, B.; Hayes-Roth, B.F. Concept learning and the recognition and classification of exemplars. J. Verbal Learn. Verbal Behav. 1977, 16, 321–338. [Google Scholar] [CrossRef]
- Kononenko, I.; Šimec, E.; Robnik-Šikonja, M. Overcoming the Myopia of Inductive Learning Algorithms with RELIEFF. Appl. Intell. 1997, 7, 39–55. [Google Scholar] [CrossRef]
- French, R.M.; Chater, N. Using noise to compute error surfaces in connectionist networks: A novel means of reducing catastrophic forgetting. Neural Comput. 2002, 14, 1755–1769. [Google Scholar] [CrossRef] [PubMed]
- Garcke, J.; Griebel, M. Classification with sparse grids using simplicial basis functions. Intell. Data Anal. 2002, 6, 483–502. [Google Scholar] [CrossRef]
- Dy, J.G.; Brodley, C.E. Feature Selection for Unsupervised Learning. J. Mach. Learn. Res. 2004, 5, 845–889. [Google Scholar]
- Perantonis, S.J.; Virvilis, V. Input Feature Extraction for Multilayered Perceptrons Using Supervised Principal Component Analysis. Neural Process. Lett. 1999, 10, 243–252. [Google Scholar] [CrossRef]
- Elter, M.; Schulz-Wendtland, R.; Wittenberg, T. The prediction of breast cancer biopsy outcomes using two CAD approaches that both emphasize an intelligible decision process. Med. Phys. 2007, 34, 4164–4172. [Google Scholar] [CrossRef]
- Little, M.A.; McSharry, P.E.; Hunter, E.J.; Spielman, J.; Ramig, L.O. Suitability of dysphonia measurements for telemonitoring of Parkinson’s disease. IEEE Trans. Biomed. Eng. 2009, 56, 1015–1022. [Google Scholar] [CrossRef]
- Smith, J.W.; Everhart, J.E.; Dickson, W.C.; Knowler, W.C.; Johannes, R.S. Using the ADAP learning algorithm to forecast the onset of diabetes mellitus. In Proceedings of the Symposium on Computer Applications and Medical Care; IEEE Computer Society Press: New York, NY, USA, 1988; pp. 261–265. [Google Scholar]
- Lucas, D.D.; Klein, R.; Tannahill, J.; Ivanova, D.; Brandon, S.; Domyancic, D.; Zhang, Y. Failure analysis of parameter-induced simulation crashes in climate models. Geosci. Model Dev. 2013, 6, 1157–1171. [Google Scholar] [CrossRef]
- Giannakeas, N.; Tsipouras, M.G.; Tzallas, A.T.; Kyriakidi, K.; Tsianou, Z.E.; Manousou, P.; Hall, A.; Karvounis, E.C.; Tsianos, V.; Tsianos, E. A clustering based method for collagen proportional area extraction in liver biopsy images. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBS), Milan, Italy, 25–29 August 2015; pp. 3097–3100. [Google Scholar]
- Hastie, T.; Tibshirani, R. Non-parametric logistic and proportional odds regression. JRSS-C (Appl. Stat.) 1987, 36, 260–276. [Google Scholar] [CrossRef]
- Dash, M.; Liu, H.; Scheuermann, P.; Tan, K.L. Fast hierarchical clustering and its validation. Data Knowl. Eng. 2003, 44, 109–138. [Google Scholar] [CrossRef]
- Cortez, P.; Gonçalves Silva, A.M. Using data mining to predict secondary school student performance. In Proceedings of the 5th FUture BUsiness TEChnology Conference (FUBUTEC 2008), EUROSIS-ETI, Porto Alegre, Brazil, 9–11 April 2008; pp. 5–12. [Google Scholar]
- Yeh, I.C.; Yang, K.J.; Ting, T.M. Knowledge discovery on RFM model using Bernoulli sequence. Expert Syst. Appl. 2009, 36, 5866–5871. [Google Scholar] [CrossRef]
- Wolberg, W.H.; Mangasarian, O.L. Multisurface method of pattern separation for medical diagnosis applied to breast cytology. Proc. Natl. Acad. Sci. USA 1990, 87, 9193–9196. [Google Scholar] [CrossRef] [PubMed]
- Raymer, M.; Doom, T.E.; Kuhn, L.A.; Punch, W.F. Knowledge discovery in medical and biological datasets using a hybrid Bayes classifier/evolutionary algorithm. IEEE Trans. Syst. Man Cybern. Part B Cybern. Publ. IEEE Syst. Man Cybern. Soc. 2003, 33, 802–813. [Google Scholar] [CrossRef]
- Zhong, P.; Fukushima, M. Regularized nonsmooth Newton method for multi-class support vector machines. Optim. Methods Softw. 2007, 22, 225–236. [Google Scholar] [CrossRef]
- Andrzejak, R.G.; Lehnertz, K.; Mormann, F.; Rieke, C.; David, P.; Elger, C.E. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Phys. Rev. E 2001, 64, 1–8. [Google Scholar] [CrossRef]
- Koivisto, M.; Sood, K. Exact Bayesian Structure Discovery in Bayesian Networks. J. Mach. Learn. Res. 2004, 5, 549–573. [Google Scholar]
- Nash, W.J.; Sellers, T.L.; Talbot, S.R.; Cawthor, A.J.; Ford, W.B. The Population Biology of Abalone (Haliotis Species) in Tasmania. I. Blacklip Abalone (H. rubra) from the North Coast and Islands of Bass Strait; Sea Fisheries Division, Technical Report 48; Sea Fisheries Division, Department of Primary Industry and Fisheries: Orange, NSW, Australia, 1994.
- Brooks, T.F.; Pope, D.S.; Marcolini, A.M. Airfoil Self-Noise and Prediction; Technical Report, NASA RP-1218; NASA: Washington, DC, USA, 1989.
- Simonoff, J.S. Smooting Methods in Statistics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Cheng Yeh, I. Modeling of strength of high performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar]
- Harrison, D.; Rubinfeld, D.L. Hedonic prices and the demand for clean ai. Environ. Econ. Manag. 1978, 5, 81–102. [Google Scholar] [CrossRef]
- Liu, D.C.; Nocedal, J. On the Limited Memory Method for Large Scale Optimization. Math. Program. B 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Gropp, W.; Lusk, E.; Doss, N.; Skjellum, A. A high-performance, portable implementation of the MPI message passing interface standard. Parallel Comput. 1996, 22, 789–828. [Google Scholar] [CrossRef]
- Chandra, R. Parallel Programming in OpenMP; Morgan Kaufmann: Cambridge, MA, USA, 2001. [Google Scholar]








| DATASET | INPUTS | CLASSES |
|---|---|---|
| APPENDICITIS | 7 | 2 |
| AUSTRALIAN | 14 | 2 |
| BALANCE | 4 | 3 |
| CIRCULAR | 5 | 2 |
| CLEVELAND | 13 | 5 |
| DERMATOLOGY | 34 | 6 |
| ECOLI | 7 | 8 |
| FERT | 9 | 2 |
| HABERMAN | 3 | 2 |
| HAYES ROTH | 5 | 3 |
| HEART | 13 | 2 |
| HEART ATTACK | 13 | 2 |
| HOUSEVOTES | 16 | 2 |
| LIVERDISORDER | 6 | 2 |
| IONOSPHERE | 34 | 2 |
| MAMMOGRAPHIC | 5 | 2 |
| PARKINSONS | 22 | 2 |
| PIMA | 8 | 2 |
| POPFAILURES | 18 | 2 |
| REGIONS2 | 18 | 5 |
| SAHEART | 9 | 2 |
| SEGMENT | 19 | 7 |
| SPIRAL | 2 | 2 |
| STUDENT | 5 | 4 |
| TRANSFUSION | 4 | 2 |
| WDBC | 30 | 2 |
| WINE | 13 | 3 |
| Z_F_S | 21 | 3 |
| Z_O_N_F_S | 21 | 5 |
| ZO_NF_S | 21 | 3 |
| ZONF_S | 21 | 2 |
| ZOO | 16 | 7 |
| DATASET | INPUTS |
|---|---|
| ABALONE | 8 |
| AIRFOIL | 5 |
| BASEBALL | 16 |
| BK | 4 |
| BL | 7 |
| CONCRETE | 8 |
| DEE | 6 |
| HO | 13 |
| HOUSING | 13 |
| FY | 4 |
| LASER | 4 |
| LW | 9 |
| MORTGAGE | 15 |
| MUNDIAL | 3 |
| PL | 2 |
| QUAKE | 3 |
| REALESTATE | 5 |
| SN | 11 |
| TREASURY | 15 |
| TZ | 60 |
| VE | 7 |
| PARAMETER | MEANING | VALUE |
|---|---|---|
| Chromosomes | 500 | |
| Generations | 200 | |
| Crossover rate | 0.10 | |
| Mutation rate | 0.05 | |
| Number of chromosomes that selected randomly | 20 | |
| Number of iterations before local search | 10 | |
| F | Magnitude of changes from local search | 4.0 |
| DATASET | BFGS | GENETIC | NNC | INNC |
|---|---|---|---|---|
| APPENDICITIS | 18.00% | 24.40% | 13.70% | 14.70% |
| AUSTRALIAN | 38.13% | 36.64% | 14.51% | 14.80% |
| BALANCE | 8.64% | 8.36% | 22.11% | 8.66% |
| CIRCULAR | 6.08% | 5.13% | 13.64% | 5.32% |
| CLEVELAND | 77.55% | 57.21% | 50.10% | 47.93% |
| DERMATOLOGY | 52.92% | 16.60% | 25.06% | 20.89% |
| ECOLI | 69.52% | 54.67% | 47.82% | 48.21% |
| FERT | 23.20% | 28.50% | 19.00% | 20.50% |
| HABERMAN | 29.34% | 28.66% | 28.03% | 26.70% |
| HAYES-ROTH | 37.33% | 56.18% | 35.93% | 31.77% |
| HEART | 39.44% | 26.41% | 15.78% | 14.74% |
| HEARTATTACK | 46.67% | 29.03% | 19.33% | 20.43% |
| HOUSEVOTES | 7.13% | 7.00% | 3.65% | 3.26% |
| IONOSPHERE | 15.29% | 15.14% | 11.12% | 11.92% |
| LIVERDISORDER | 42.59% | 37.09% | 33.71% | 31.77% |
| MAMMOGRAPHIC | 17.24% | 19.88% | 17.78% | 15.81% |
| PARKINSONS | 27.58% | 16.58% | 12.21% | 12.53% |
| PIMA | 35.59% | 34.21% | 27.99% | 24.00% |
| POPFAILURES | 5.24% | 4.17% | 6.74% | 6.44% |
| REGIONS2 | 36.28% | 33.53% | 25.52% | 23.18% |
| SAHEART | 37.48% | 34.85% | 30.52% | 28.09% |
| SEGMENT | 68.97% | 46.30% | 54.99% | 43.12% |
| SPIRAL | 47.99% | 47.67% | 48.39% | 43.99% |
| STUDENT | 7.14% | 5.61% | 5.78% | 4.55% |
| TRANSFUSION | 25.80% | 25.84% | 25.34% | 23.43% |
| WDBC | 29.91% | 7.87% | 6.95% | 4.41% |
| WINE | 59.71% | 22.88% | 14.35% | 9.77% |
| Z_F_S | 39.37% | 24.60% | 14.17% | 8.53% |
| Z_O_N_F_S | 65.67% | 64.81% | 49.18% | 38.58% |
| ZO_NF_S | 43.04% | 21.54% | 14.14% | 6.84% |
| ZONF_S | 15.62% | 4.36% | 3.14% | 2.52% |
| ZOO | 10.70% | 9.50% | 9.20% | 7.20% |
| AVERAGE | 33.91% | 26.73% | 22.50% | 19.52% |
| DATASET | BFGS | GENETIC | NNC | INNC |
|---|---|---|---|---|
| ABALONE | 5.69 | 7.17 | 5.05 | 4.33 |
| AIRFOIL | 0.003 | 0.003 | 0.003 | 0.002 |
| BASEBALL | 119.63 | 64.60 | 59.85 | 48.42 |
| BK | 0.36 | 0.26 | 2.32 | 0.07 |
| BL | 1.09 | 2.23 | 0.021 | 0.002 |
| CONCRETE | 0.066 | 0.01 | 0.008 | 0.005 |
| DEE | 2.36 | 1.01 | 0.26 | 0.23 |
| HO | 0.62 | 0.37 | 0.017 | 0.01 |
| HOUSING | 97.38 | 43.26 | 26.35 | 16.01 |
| FY | 0.19 | 0.65 | 0.058 | 0.042 |
| LASER | 0.015 | 0.59 | 0.024 | 0.005 |
| LW | 2.98 | 0.54 | 0.011 | 0.012 |
| MORTGAGE | 8.23 | 0.40 | 0.30 | 0.026 |
| MUNDIAL | 6.48 | 1.22 | 4.47 | 0.034 |
| PL | 0.29 | 0.28 | 0.045 | 0.022 |
| QUAKE | 0.42 | 0.12 | 0.045 | 0.04 |
| REALESTATE | 128.94 | 81.19 | 76.78 | 70.99 |
| SN | 3.89 | 0.40 | 0.026 | 0.023 |
| TREASURY | 9.91 | 2.93 | 0.47 | 0.066 |
| TZ | 3.27 | 5.38 | 5.04 | 0.03 |
| VE | 1.92 | 2.43 | 6.61 | 0.025 |
| AVERAGE | 18.75 | 10.24 | 8.94 | 6.69 |
| DATASET | INNC | INNC | INNC |
|---|---|---|---|
| APPENDICITIS | 14.50% | 14.70% | 14.20% |
| AUSTRALIAN | 14.48% | 14.80% | 14.58% |
| BALANCE | 7.63% | 8.66% | 11.71% |
| CIRCULAR | 5.25% | 5.32% | 5.87% |
| CLEVELAND | 48.41% | 47.93% | 49.66% |
| DERMATOLOGY | 19.66% | 20.89% | 23.11% |
| ECOLI | 47.39% | 48.21% | 48.09% |
| FERT | 20.80% | 20.50% | 20.90% |
| HABERMAN | 26.87% | 26.70% | 27.27% |
| HAYES-ROTH | 31.69% | 31.77% | 35.92% |
| HEART | 14.85% | 14.74% | 15.56% |
| HEARTATTACK | 20.10% | 20.43% | 20.07% |
| HOUSEVOTES | 3.87% | 3.26% | 3.78% |
| IONOSPHERE | 11.51% | 11.92% | 11.09% |
| LIVERDISORDER | 31.35% | 31.77% | 31.85% |
| MAMMOGRAPHIC | 16.25% | 15.81% | 16.06% |
| PARKINSONS | 13.16% | 12.53% | 12.58% |
| PIMA | 23.95% | 24.00% | 24.67% |
| POPFAILURES | 6.06% | 6.44% | 6.48% |
| REGIONS2 | 23.36% | 23.18% | 24.21% |
| SAHEART | 27.68% | 28.09% | 29.41% |
| SEGMENT | 43.79% | 43.12% | 46.91% |
| SPIRAL | 43.63% | 43.99% | 45.15% |
| STUDENT | 3.65% | 4.55% | 3.88% |
| TRANSFUSION | 22.62% | 23.43% | 23.89% |
| WDBC | 4.41% | 4.41% | 5.46% |
| WINE | 10.18% | 9.77% | 12.00% |
| Z_F_S | 7.70% | 8.53% | 9.63% |
| Z_O_N_F_S | 36.64% | 38.58% | 41.08% |
| ZO_NF_S | 6.84% | 6.84% | 6.90% |
| ZONF_S | 2.24% | 2.52% | 2.66% |
| ZOO | 6.30% | 7.20% | 7.70% |
| AVERAGE | 19.28% | 19.52% | 20.39% |
| DATASET | INNC | INNC | INNC |
|---|---|---|---|
| ABALONE | 4.38 | 4.33 | 4.45 |
| AIRFOIL | 0.002 | 0.002 | 0.002 |
| BASEBALL | 47.50 | 48.42 | 49.99 |
| BK | 0.64 | 0.07 | 1.86 |
| BL | 0.014 | 0.002 | 0.003 |
| CONCRETE | 0.005 | 0.005 | 0.005 |
| DEE | 0.22 | 0.23 | 0.23 |
| HO | 0.01 | 0.01 | 0.011 |
| HOUSING | 21.09 | 16.01 | 16.96 |
| FY | 0.046 | 0.042 | 0.19 |
| LASER | 0.004 | 0.005 | 0.005 |
| LW | 0.011 | 0.012 | 0.011 |
| MORTGAGE | 0.02 | 0.026 | 0.03 |
| MUNDIAL | 0.031 | 0.034 | 0.029 |
| PL | 0.022 | 0.022 | 0.022 |
| QUAKE | 0.045 | 0.04 | 0.037 |
| REALESTATE | 68.85 | 70.99 | 70.59 |
| SN | 0.023 | 0.023 | 0.024 |
| TREASURY | 0.063 | 0.066 | 0.073 |
| TZ | 0.029 | 0.03 | 0.031 |
| VE | 0.028 | 0.025 | 0.116 |
| AVERAGE | 6.81 | 6.69 | 6.89 |
| DATASET | INNC | INNC | INNC | INNC |
|---|---|---|---|---|
| APPENDICITIS | 14.80% | 14.20% | 14.70% | 15.00% |
| AUSTRALIAN | 14.58% | 14.56% | 14.80% | 14.54% |
| BALANCE | 8.52% | 8.68% | 8.66% | 9.35% |
| CIRCULAR | 5.92% | 5.46% | 5.32% | 5.43% |
| CLEVELAND | 48.35% | 47.38% | 47.93% | 49.62% |
| DERMATOLOGY | 19.80% | 20.09% | 20.89% | 21.66% |
| ECOLI | 47.76% | 48.30% | 48.21% | 48.42% |
| FERT | 21.20% | 21.20% | 20.50% | 20.90% |
| HABERMAN | 26.43% | 25.93% | 26.70% | 26.70% |
| HAYES-ROTH | 32.15% | 31.31% | 31.77% | 35.69% |
| HEART | 14.81% | 15.41% | 14.74% | 15.41% |
| HEARTATTACK | 21.20% | 19.90% | 20.43% | 20.40% |
| HOUSEVOTES | 3.35% | 3.65% | 3.26% | 3.65% |
| IONOSPHERE | 11.31% | 10.40% | 11.92% | 11.23% |
| LIVERDISORDER | 32.09% | 31.21% | 31.77% | 33.18% |
| MAMMOGRAPHIC | 16.15% | 16.05% | 15.81% | 16.07% |
| PARKINSONS | 12.63% | 12.47% | 12.53% | 13.05% |
| PIMA | 23.58% | 23.80% | 24.00% | 23.79% |
| POPFAILURES | 5.85% | 6.29% | 6.44% | 6.04% |
| REGIONS2 | 24.08% | 23.48% | 23.18% | 25.25% |
| SAHEART | 28.41% | 28.83% | 28.09% | 28.30% |
| SEGMENT | 45.12% | 43.37% | 43.12% | 43.93% |
| SPIRAL | 43.40% | 43.72% | 43.99% | 44.61% |
| STUDENT | 4.25% | 4.15% | 4.55% | 4.52% |
| TRANSFUSION | 23.09% | 22.93% | 23.43% | 23.05% |
| WDBC | 5.27% | 5.30% | 4.41% | 4.84% |
| WINE | 10.53% | 10.24% | 9.77% | 11.59% |
| Z_F_S | 9.20% | 7.57% | 8.53% | 8.63% |
| Z_O_N_F_S | 40.60% | 38.70% | 38.58% | 39.78% |
| ZO_NF_S | 6.90% | 7.68% | 6.84% | 6.56% |
| ZONF_S | 2.64% | 2.72% | 2.52% | 2.88% |
| ZOO | 8.60% | 7.40% | 7.20% | 8.90% |
| AVERAGE | 19.77% | 19.45% | 19.52% | 20.09% |
| DATASET | INNC | INNC | INNC | INNC |
|---|---|---|---|---|
| ABALONE | 4.49 | 4.43 | 4.33 | 4.66 |
| AIRFOIL | 0.002 | 0.002 | 0.002 | 0.002 |
| BASEBALL | 48.31 | 50.38 | 48.42 | 48.52 |
| BK | 0.06 | 0.21 | 0.07 | 0.02 |
| BL | 0.003 | 0.004 | 0.002 | 0.003 |
| CONCRETE | 0.005 | 0.005 | 0.005 | 0.005 |
| DEE | 0.23 | 0.23 | 0.23 | 0.23 |
| HO | 0.01 | 0.01 | 0.01 | 0.01 |
| HOUSING | 16.91 | 16.34 | 16.01 | 16.96 |
| FY | 0.042 | 0.043 | 0.042 | 0.043 |
| LASER | 0.005 | 0.005 | 0.005 | 0.004 |
| LW | 0.011 | 0.012 | 0.012 | 0.012 |
| MORTGAGE | 0.027 | 0.025 | 0.026 | 0.024 |
| MUNDIAL | 0.035 | 0.033 | 0.034 | 0.23 |
| PL | 0.022 | 0.022 | 0.022 | 0.022 |
| QUAKE | 0.036 | 0.037 | 0.04 | 0.036 |
| REALESTATE | 72.40 | 71.16 | 70.99 | 70.76 |
| SN | 0.024 | 0.024 | 0.023 | 0.024 |
| TREASURY | 0.07 | 0.068 | 0.066 | 0.068 |
| TZ | 0.029 | 0.031 | 0.03 | 0.031 |
| VE | 0.032 | 0.03 | 0.025 | 0.028 |
| AVERAGE | 6.80 | 6.81 | 6.69 | 6.75 |
| DATASET | ADAM | LBFGS | BFGS |
|---|---|---|---|
| APPENDICITIS | 14.60% | 14.60% | 14.70% |
| AUSTRALIAN | 14.78% | 15.29% | 14.80% |
| BALANCE | 16.89% | 11.47% | 8.66% |
| CIRCULAR | 10.79% | 8.15% | 5.32% |
| CLEVELAND | 49.10% | 48.45% | 47.93% |
| DERMATOLOGY | 22.32% | 23.03% | 20.89% |
| ECOLI | 48.15% | 49.48% | 48.21% |
| FERT | 18.10% | 20.10% | 20.50% |
| HABERMAN | 26.27% | 26.63% | 26.70% |
| HAYES-ROTH | 36.23% | 36.31% | 31.77% |
| HEART | 15.71% | 15.00% | 14.74% |
| HEARTATTACK | 21.33% | 20.07% | 20.43% |
| HOUSEVOTES | 3.39% | 3.39% | 3.26% |
| IONOSPHERE | 10.88% | 11.29% | 11.92% |
| LIVERDISORDER | 31.80% | 33.18% | 31.77% |
| MAMMOGRAPHIC | 16.71% | 16.30% | 15.81% |
| PARKINSONS | 12.10% | 12.32% | 12.53% |
| PIMA | 25.49% | 24.97% | 24.00% |
| POPFAILURES | 6.20% | 6.31% | 6.44% |
| REGIONS2 | 24.20% | 24.06% | 23.18% |
| SAHEART | 28.87% | 28.96% | 28.09% |
| SEGMENT | 50.16% | 46.63% | 43.12% |
| SPIRAL | 46.33% | 45.24% | 43.99% |
| STUDENT | 4.05% | 3.98% | 4.55% |
| TRANSFUSION | 24.74% | 24.56% | 23.43% |
| WDBC | 6.30% | 5.66% | 4.41% |
| WINE | 11.47% | 10.06% | 9.77% |
| Z_F_S | 12.33% | 10.92% | 8.53% |
| Z_O_N_F_S | 41.40% | 45.77% | 38.58% |
| ZO_NF_S | 11.26% | 9.83% | 6.84% |
| ZONF_S | 2.64% | 2.35% | 2.52% |
| ZOO | 8.50% | 8.70% | 7.20% |
| AVERAGE | 21.03% | 20.72% | 19.52% |
| DATASET | ADAM | LBFGS | BFGS |
|---|---|---|---|
| ABALONE | 4.73 | 4.49 | 4.33 |
| AIRFOIL | 0.003 | 0.003 | 0.002 |
| BASEBALL | 53.98 | 51.88 | 48.42 |
| BK | 0.05 | 0.08 | 0.07 |
| BL | 0.013 | 0.007 | 0.002 |
| CONCRETE | 0.006 | 0.006 | 0.005 |
| DEE | 0.24 | 0.23 | 0.23 |
| HO | 0.012 | 0.012 | 0.01 |
| HOUSING | 20.20 | 20.49 | 16.01 |
| FY | 0.042 | 0.042 | 0.042 |
| LASER | 0.012 | 0.005 | 0.005 |
| LW | 0.011 | 0.011 | 0.012 |
| MORTGAGE | 0.068 | 0.084 | 0.026 |
| MUNDIAL | 0.033 | 0.029 | 0.034 |
| PL | 0.031 | 0.023 | 0.022 |
| QUAKE | 0.036 | 0.037 | 0.04 |
| REALESTATE | 74.66 | 74.49 | 70.99 |
| SN | 0.025 | 0.024 | 0.023 |
| TREASURY | 0.114 | 0.084 | 0.066 |
| TZ | 0.03 | 0.08 | 0.03 |
| VE | 0.024 | 0.132 | 0.025 |
| AVERAGE | 7.35 | 7.25 | 6.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsoulos, I.G.; Charilogis, V.; Tsalikakis, D.; Tzallas, A. Improving the Generalization Abilities of Constructed Neural Networks with the Addition of Local Optimization Techniques. Algorithms 2024, 17, 446. https://doi.org/10.3390/a17100446
Tsoulos IG, Charilogis V, Tsalikakis D, Tzallas A. Improving the Generalization Abilities of Constructed Neural Networks with the Addition of Local Optimization Techniques. Algorithms. 2024; 17(10):446. https://doi.org/10.3390/a17100446
Chicago/Turabian StyleTsoulos, Ioannis G., Vasileios Charilogis, Dimitrios Tsalikakis, and Alexandros Tzallas. 2024. "Improving the Generalization Abilities of Constructed Neural Networks with the Addition of Local Optimization Techniques" Algorithms 17, no. 10: 446. https://doi.org/10.3390/a17100446
APA StyleTsoulos, I. G., Charilogis, V., Tsalikakis, D., & Tzallas, A. (2024). Improving the Generalization Abilities of Constructed Neural Networks with the Addition of Local Optimization Techniques. Algorithms, 17(10), 446. https://doi.org/10.3390/a17100446









