Abstract
This study reviews advanced methods for corrosion detection and characterization in pipes using thermography, with a focus on addressing the limitations posed by small datasets. Thermography captures temperature distributions on the surface of pipes to identify subsurface defects. The challenges of sequential data processing, neural network performance, feature extraction, and dataset size are discussed, with proposed solutions such as advanced algorithms, feature selection techniques, and data augmentation. Given the significant gap in the current literature, there is a need for larger, more diverse datasets to train more robust and accurate machine learning models. A case study combining experimental data with Finite Element Method (FEM) simulations demonstrates that augmenting datasets with synthetic data significantly improves defect detection accuracy. These findings highlight the potential of integrating thermography with machine learning to enhance defect detection, providing insights for future research and practical applications.
Keywords:
thermography; defect; subsurface; deep learning; machine learning; finite element analysis 1. Introduction
1.1. Thermography
Thermography is a non-destructive testing (NDT) technique that employs infrared thermography (IRT) to evaluate the thermal characteristics of materials and structures. Infrared cameras measure the infrared radiation emitted by objects, capturing variations that correspond to different surface temperatures. The underlying principle is that materials with varying thermal conductivities emit different levels of infrared radiation. By analyzing these radiation patterns, IRT can determine the apparent surface temperature and detect anomalies or subsurface defects [1]. Thermography methods can be categorized into two types: active and passive. Active thermography involves applying an external heat source to the specimen, while passive thermography relies on the specimen’s natural thermal emissions. The choice between active or passive thermography depends on the specific requirements of the testing scenario [2].
1.2. Subsurface Defects
Subsurface defects in materials significantly impact the strength, durability, and overall performance of these objects. Early detection is crucial for ensuring the safe and effective functioning of materials and structures. Non-destructive testing (NDT) methods evaluate the quality and condition of materials and structures without causing damage, allowing for regular and ongoing monitoring. This ensures that any potential issues are identified and addressed promptly [3].
1.3. Traditional Methods and Challenges
Traditional methods for subsurface defect detection include visual inspection, ultrasonic testing, and X-ray imaging. While these methods have proven effective, they often require significant time, specialized equipment, and can sometimes be intrusive. Visual inspections are subjective and dependent on the inspector’s experience. Ultrasonic and X-ray methods, although precise, involve complex equipment and safety concerns, particularly with radiation exposure [4].
1.4. Importance of Corrosion Detection
Corrosion in pipes is a critical issue in various industries, including oil and gas, water supply, and chemical processing. Corrosion can lead to leaks, structural failures, and significant economic losses. Therefore, early and accurate detection of corrosion is essential for maintaining the integrity and safety of infrastructure.
1.5. Objective and Significance of This Study
This paper aims to review state-of-the-art machine learning methods for characterizing subsurface defects using thermography, addressing the limitations posed by small datasets. By enhancing data through synthetic means, such as Finite Element Method (FEM) simulations, this study seeks to improve the robustness and accuracy of defect detection models. The findings underscore the potential of integrating thermography with machine learning to advance the field of corrosion detection and ensure safer and more efficient infrastructure maintenance. The paper is organized as follows: Section 2 provides a literature review of methods for characterizing subsurface defects by thermography. Section 3 discusses the challenges of subsurface defect characterization by thermography and state-of-the-art solutions to overcome these challenges. In Section 4, a case study is presented, demonstrating the automatic detection of subsurface defects in steel pipes using thermography and synthetic datasets.
2. Literature Review
The role of thermography in detecting and characterizing subsurface defects is significant, as this method allows for the identification of defects beneath the surface of materials and structures without causing any damage. This is particularly important in the assessment of critical infrastructure where disruptions to operations must be minimized. Recent advancements in thermography have led to the development of state-of-the-art methods providing improved accuracy and sensitivity for subsurface defect detection. Awareness of these new techniques is crucial for assessing the integrity of materials and structures, ensuring the continued safe and effective functioning of these critical assets [5].
Traditional methods for subsurface defect characterization include techniques based on the physical properties of materials [6]. Widely used traditional methods include linear regression, Gaussian regression, support vector machines (SVM) [7], polynomial approximation [8], and classification trees [9]. These methods model the relationship between thermal data features and defect characteristics, providing basic yet effective approaches for defect detection. Traditional machine learning methods are favored for their simplicity, stability, and interpretability. They tend to produce consistent results even with small variations in input data, and their decision-making processes are transparent, making them suitable for applications where accountability is critical [10]. Advancements in thermography have focused on enhancing the detection capabilities and accuracy of defect characterization. These improvements are driven by innovations in both hardware and software, including high-resolution infrared cameras and sophisticated data processing algorithms. Enhanced imaging techniques, such as lock-in thermography and pulsed thermography, have improved the resolution and depth of defect detection. Furthermore, integrating thermography with other NDT techniques like ultrasonic testing and X-ray imaging has resulted in more comprehensive assessments of material integrity. These advancements have expanded the applicability of thermography in various industrial settings, making it a more robust tool for subsurface defect detection [11,12].
Machine learning methods have revolutionized subsurface defect characterization by automating feature extraction and improving predictive accuracy. These methods can be broadly categorized into traditional machine learning techniques and deep learning approaches. Traditional techniques, as mentioned, offer interpretability and consistent performance with smaller datasets. However, deep learning has achieved state-of-the-art results in tasks such as image segmentation, speech recognition, and sequential data processing. The key advantages of deep learning include its ability to automatically learn relevant features from raw input data, reducing the need for manual feature engineering. Deep learning models are highly scalable and capable of handling large amounts of data, making them ideal for applications that require processing vast datasets. Moreover, these models can learn hierarchical representations of data, capturing complex relationships and patterns within the data.
Recent studies have demonstrated the efficacy of deep learning models in thermographic applications, with convolutional neural networks (CNNs) being successfully applied to segment thermal images and identify defect locations with high precision [13]. In recent years, the 1-D approach has been used, which corresponds to training the CNN with thermal temporal signals. This method has shown significant advantages in handling sequential thermal data, improving defect detection accuracy and computational efficiency. The 1-D CNN approach allows for the effective analysis of thermal profiles over time, making it particularly useful for applications where temporal thermal variations are critical [14,15].
Despite significant advancements, gaps in the current literature need to be addressed. One primary challenge is the limited availability of large, diverse datasets for training machine learning models. Small datasets restrict the performance and generalization capabilities of these models. The integration of synthetic data through techniques like Finite Element Method (FEM) simulations can augment datasets and enhance model robustness. Further research is needed to explore these avenues and develop more reliable and accurate defect detection systems.
3. Challenges of Subsurface Defect Characterization by Thermography
3.1. Sequential Data Processing
Sequential thermal data are pivotal in thermography methods like lock-in and pulsed thermography for defect detection, offering a time-resolved perspective that facilitates the identification of material defects such as cracks, voids, and delamination through the analysis of thermal process evolution. The acquisition and analysis of these data are vital for enhancing the reliability, safety, and performance of materials and components [16,17]. However, challenges such as data quality issues, the need for synchronization, high computational demands, and the complexity of data interpretation underscore the importance of advanced research.
Recent efforts in thermography for subsurface defect characterization have increasingly turned towards innovative neural network architectures to address these challenges. These architectures aim to enhance data processing speeds, accuracy, and overall quality in defect detection [18,19]. The Long Short-Term Memory Recurrent Neural Network (LSTM-RNN) architecture, for instance, is effective in capturing long-term dependencies in sequential data without succumbing to the vanishing gradient problem. Researchers, including Hu et al., have leveraged LSTM-RNN for automatic classification of common defects in materials such as honeycomb structures, achieving enhanced accuracy and reliable identification of defects by analyzing the thermal response over time [20].
Parallel to LSTMs, Gated Recurrent Unit (GRU) networks simplify the model structure while maintaining the ability to handle long-term dependencies effectively. This results in faster training times and reduced risk of overfitting [21]. GRUs have outperformed traditional RNNs and backpropagation networks in various sequential data modeling tasks, including defect depth recognition and quantification. Fang and Maldague demonstrated the effectiveness of GRUs in quantifying defect depths in composite materials using pulsed thermography, showcasing GRUs’ capability to process and analyze complex thermal datasets for accurate defect detection [22]. Figure 1 shows the structural differences between the LSTM and GRU architecture.
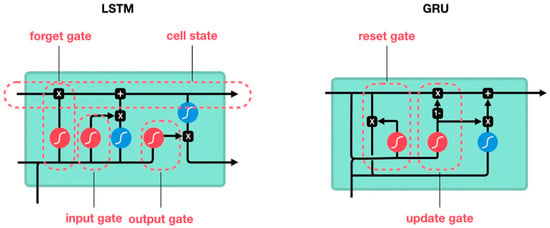
Figure 1.
Comparison of LSTM and GRU architecture [23].
In three-dimensional data analysis, 3D neural networks excel in processing 3D data, such as images and videos, enhancing object recognition, segmentation, and temporal changes handling. The introduction of a 3D convolutional neural network (CNN) model by Dong et al. [24], tailored for lock-in thermography in carbon fiber-reinforced polymer (CFRP), integrates spatial and temporal convolutional filters with batch-size independent group normalization, showcasing superior accuracy in detecting and estimating subsurface defect depths [25]. Figure 2 compares the architectures of 2D-CNN and 3D-CNN.
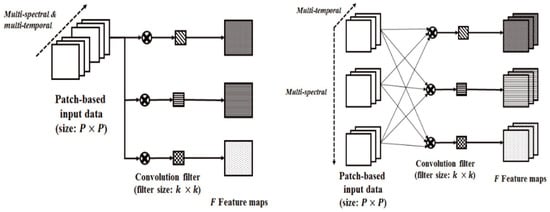
Figure 2.
Comparing the architecture of 2D-CNN and 3D-CNN [25].
3.2. Increasing Performance of the Deep Learning Method
Enhancing the performance of neural networks is pivotal for advancing thermography techniques, especially for subsurface defect characterization where precision and efficiency are paramount. The complexity of thermographic data, compounded by noise and inhomogeneous backgrounds, necessitates sophisticated neural network models. Neural Architecture Search (NAS) and hyperparameter tuning emerge as critical strategies for optimizing neural network architectures [26]. NAS systematically explores various architectures to find the most effective model for specific thermographic tasks, significantly boosting model accuracy [27]. For instance, Chen et al.’s utilization of NAS in multilayer perceptron models for defect classification achieved unparalleled accuracy [28]. Similarly, hyperparameter optimization techniques like Gray Wolf Optimization (GWO) fine-tune model parameters to optimize performance, as demonstrated by Chen et al. in classifying subsurface defects in carbon fiber-reinforced polymers [29].
3.3. Feature Extraction
Beyond architecture and parameter optimization, effective feature extraction is crucial for thermography applications. Techniques like Extended Blind End-Member and Abundance Extraction (EBEAE) [30] and Convolutional Autoencoders (CAEs) [31] have been instrumental in improving feature extraction. EBEAE enhances the identification and characterization of thermal features, leading to more accurate defect depth estimation in composite materials. Marani and Campos-Delgado’s work exemplifies EBEAEs’ effectiveness in extracting precise features from thermal maps for SVM classification [32]. CAEs, particularly in denoising and data enhancement roles, maintain deep spatial information while reducing noise, as seen in Li et al.’s improved DCAE (Data-enhanced Convolutional Autoencoders) model [33,34].
In addition to these methods, features can also be extracted using specific algorithms associated with different thermography techniques. Pulsed thermography features can be obtained by performing algorithms such as Thermal Signal Reconstruction (TSR) [35], Pulse Phase Thermography (PPT) [36], and Principal Component Analysis (PCA) [37]. These methods analyze the thermal response over time to identify and characterize subsurface defects. Lock-in thermography, on the other hand, allows for feature extraction by analyzing amplitude and phase maps obtained through lock-in (LI) algorithms. These maps provide detailed information about the thermal properties and the presence of defects within the material [38]. Incorporating these approaches enhances the capability to detect and quantify subsurface defects more accurately. By integrating a variety of feature extraction techniques, both traditional and advanced, we can improve the reliability and accuracy of thermographic inspections, thereby providing a more comprehensive assessment of material integrity.
Addressing the challenge of dataset size is paramount in machine learning, especially for thermography, where data diversity and volume directly influence model performance. Larger datasets enable training of more complex models, enhancing performance and reducing overfitting risks [39,40]. Innovative strategies include deep autoencoders, which leverage unsupervised learning to process and analyze thermographic data, identifying subtle, nonlinear patterns in noisy images. Liu et al.’s work with deep autoencoders facilitates detailed visualization of defect features and accurate identification in composite materials [41].
Semi-supervised learning, which utilizes both labeled and unlabeled data, enhances model performance and generalization, as demonstrated by Liu et al.’s semi-supervised framework for transient thermography [42]. Generative Adversarial Networks (GANs) address data scarcity by generating synthetic data that mimics real thermal images, augmenting existing datasets and improving model robustness [43]. Liu et al.’s application of GANs for thermal image augmentation highlights their potential in enhancing thermographic analysis [44], showing a flowchart suggested by the generative network for increasing the size of the dataset.
3.4. Dataset Augmentation
Dataset augmentation is a crucial technique in machine learning, particularly for thermography, where data diversity and volume significantly influence model performance. Several methods have been developed to augment datasets, each with its own advantages and limitations.
Generative Adversarial Networks (GANs) are powerful tools for generating new, synthetic data that mimic real data. GANs consist of two neural networks, a generator and a discriminator, that are trained simultaneously. The generator creates synthetic data, while the discriminator evaluates its authenticity. This adversarial process helps produce high-quality synthetic data that can be used to augment datasets, improving model robustness and performance, especially when dealing with small sample sizes [45,46]. However, training GANs can be complex and computationally intensive, and they require a significant amount of data to begin with [47].
U-Net is another advanced technique particularly useful for image segmentation tasks. Originally developed for biomedical image segmentation, U-Net has been adapted for various applications, including thermography. It works by capturing the context of an image through a contracting path and then enabling precise localization through an expansive path. U-Net can be used for data augmentation by generating segmented images from raw input, thereby increasing the diversity and volume of the training dataset [47].
Traditional methods such as image rotation, scaling, flipping, and cropping are also widely used to augment datasets. These techniques are relatively simple to implement and computationally inexpensive. They work by applying various transformations to the original images, thereby creating new training samples. While these methods can significantly increase the dataset size and help prevent overfitting, they do not add new information to the dataset as GANs do [48,49].
Table 1 shows the summary of challenges researchers face in subsurface defect characterization by machine learning algorithms with thermography and the state-of-the-art solutions they proposed to these challenges.

Table 1.
Challenges researchers face in subsurface defect characterization by machine learning algorithms with thermography and state-of-the-art solutions.
4. Case Study
This case study explores the detection and characterization of corrosion in steel pipes using thermography, emphasizing the usage of synthetic datasets to enhance machine learning model training. This methodology aims to improve the accuracy and reliability of defect detection in steel pipe insulation, addressing the challenges highlighted in the literature.
4.1. Experimental Setup
Infrared thermography (IRT) is a powerful technique for identifying defects within the insulation of steel pipes, with moisture presence being a key indicator of potential corrosion under insulation (CUI). Moisture ingress alters the insulation’s heat transfer coefficient, resulting in observable temperature variance in the pipe’s surface, crucial for pinpointing defect locations and extents. For this experiment, six different steel pipes of varying sizes and thicknesses were selected to create a diverse set of scenarios. The geometrical properties of each pipe are detailed in Table 2.

Table 2.
Dimension of the pipes.
To simulate moisture ingress and enhance realism, each pipe was insulated with fiberglass, selected for its widespread industrial use and favorable thermal properties. The insulation applied at a thickness of 12.7 mm (0.5 inches) was cut to create defects of varying sizes. These sections were saturated with water to 70% of their weight before being reattached to the pipes. An aluminum cladding, 0.76 mm (0.03 inches) thick, enveloped the insulation, mimicking operational insulation systems’ protective layer, providing mechanical protection and weather resistance. Figure 3 provides additional clarity on the geometrical positioning and dimensions of these defects relative to the pipes, aiding in the understanding of the simulated defect’s types and placements.

Figure 3.
Experimental setup showing the moisture simulation process. (a) Cut of insulation at planned geometry [50]. (b) Installation of wet insulation in cut regions [51].
A FLIR T650Sc thermal camera, with a high resolution of 640 × 480 pixels, was used to capture thermal images. In this study, median filtering was primarily used due to its simplicity and effectiveness in reducing noise without significantly affecting the important features of the thermal images. This preprocessing step ensured that the subsequent analysis and defect detection algorithms operated on clearer and more reliable data. Given the predefined locations of the defects, Regions of Interest (ROIs) were established based on these positions for later analysis. Figure 4 shows the defined ROI, based on the position and size of the defect, for pipe number 6. As can be seen, the position of the defect is known in the thermal image, so a circle which circumscribes the square is defined.
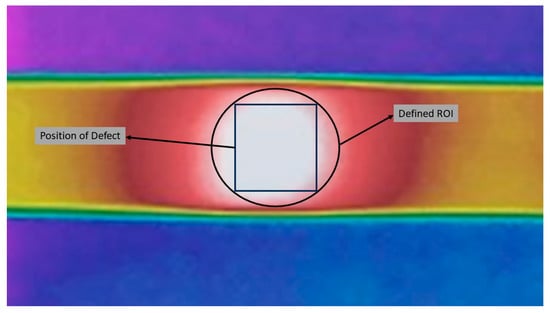
Figure 4.
Defined ROI for the thermal image of pipe number 6 and 12.7 cm defect [51].
4.2. Data Augmentation with FEM
To enhance the dataset and complement the experimental findings, this study’s setup was replicated within the COMSOL Multiphysics environment. This simulation aimed to precisely model the steel pipes, fiberglass insulation, and aluminum cladding, incorporating defects similar to moisture ingress to thoroughly analyze their thermal impact. The simulation was based on the assumption of material homogeneity across all components, with boundary conditions set to no heat loss at the pipe ends, reflecting the experimental setup. This approach ensured a focused analysis of the thermal behavior attributable to the introduced defects, aligning the computational model closely with the physical experiments.
Defects were introduced in the simulation by substituting sections of the original insulation with new material representing wet insulation. This method simulated various moisture levels, expanding the range of defect sizes from as small as 0.1 inches to as large as 5 inches, aiming to understand the impact of defect size on thermal performance more comprehensively. Table 3 details the range of simulated defect sizes for each pipe ID. The simulations used steady-state conditions to mirror the experimental setup, focusing on achieving a uniform thermal regime.

Table 3.
Range of simulated defects for each pipe ID.
To accurately model the wet insulation’s thermal properties, mixture rules were utilized. These rules allow for the calculation of effective thermal properties such as thermal conductivity (k), density (), and specific heat capacity at constant pressure () for the insulation, taking into account varying moisture contents. The equations used are as follows:
where
- and are the volume fractions of water and insulation, respectively, satisfying .
- , , and are the thermal conductivity, density, and specific heat capacity at constant pressure of water, respectively.
- , , and are the corresponding properties of the insulation material.
- This formulation provides a nuanced view of how moisture content influences the insulation’s thermal properties. These formulations allowed us to accurately model the thermal behavior of insulation with 70% wetness levels, directly correlating with the experimental conditions. Table 4 presents the material properties used in the simulation, including the base properties of steel, fiberglass insulation, water, and aluminum.
 Table 4. Thermophysical properties considered in the computational simulation.
Table 4. Thermophysical properties considered in the computational simulation.
The conduction occurs between solid phases in each material and at contact surfaces. The conduction heat transfer is governed by where is the conduction heat transfer coefficient, is the external temperature, and is the surface temperature. Inside the pipe, forced internal convection is set to replicate the experimental conditions, with the fluid being Mobil Therm 603. The convection heat transfer is described by where represents the heat transfer rate per unit area, is the convective heat transfer coefficient, is the fluid temperature, and is the solid surface temperature. The outer surface of the aluminum cladding experiences both natural convection with the ambient environment and radiation heat transfer, with a surface emissivity set at 0.9. The radiation heat transfer is governed by , where is the emissivity and is the ambient temperature.
Mesh size was set to automatic, allowing for finer mesh in areas with defects and around thin structures, while coarser mesh was applied elsewhere. This strategy optimized computational resource utilization.
The simulations were conducted under steady-state conditions to mimic the experimental setup, focusing on achieving a uniform thermal regime. Figure 5 showcases the simulation results for Pipe ID 1, featuring a defect characterized by 70% wetness and a size of 2.54 cm. These results highlight the thermal patterns and anomalies induced by the wet insulation defect.

Figure 5.
Simulation results for Pipe ID 1 with a 2.54 cm defect and 70% wetness [51].
4.3. Results and Discussion
4.3.1. Introduction to UNET+
The UNET+ model is an advanced convolutional neural network designed for image segmentation tasks. Its architecture includes a contracting path to capture context and a symmetric expanding path that ensures precise localization. The contracting path consists of repeated applications of convolutional layers followed by max-pooling for down-sampling, capturing high-level features and context information. Conversely, the expanding path uses transposed convolutions for up-sampling, restoring the spatial resolution of the features for accurate segmentation of fine details. UNET+ incorporates additional features such as residual connections, multi-scale feature integration, and attention mechanisms, improving upon the traditional UNET architecture. These enhancements enable the model to handle variations in defect size, shape, and contrast in thermographic images more effectively.
In the context of this work, the use of UNET+ is highly advantageous due to the complex nature of the thermal patterns associated with corrosion. Corrosion often manifests in irregular shapes and varying thermal contrasts, challenging simpler models to detect accurately. The multi-scale feature integration in UNET+ allows the model to consider both global and local features simultaneously, enhancing its ability to detect corrosion regardless of size or intensity. Additionally, the residual connections help mitigate the vanishing gradient problem during training, leading to a more stable and efficient learning process. These qualities make UNET+ not only suitable but also highly effective for detecting and characterizing corrosion in thermographic images of steel pipes.
In this study, the UNET+ model was trained on a combination of experimental and synthetic datasets. The experimental dataset consisted of thermal images captured from steel pipes with induced defects, while the synthetic dataset was generated using Finite Element Method (FEM) simulations to augment the available data. The training process involved several preprocessing steps, including normalization and augmentation techniques to enhance the model’s robustness. Figure 6 shows the UNET+ model architecture which is used in this research.
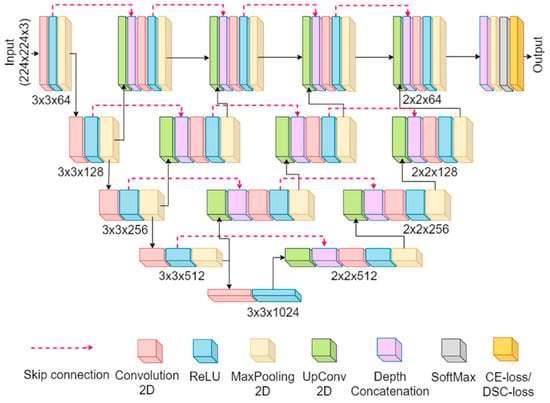
Figure 6.
UNET+ model architecture [52].
4.3.2. Results
The UNet+ model was trained under two scenarios to evaluate the impact of dataset composition on defect detection performance. Initially, the model was trained solely with 20 experimental images. The second scenario included 2000 synthetic images generated via FEM simulations, along with the 20 experimental images. Validation against unused experimental images provided a clear performance comparison. The performance of the UNET+ model was evaluated using metrics such as the F1 score, loss, and Mean Intersection over Union (Mean IoU). The F1 score is the harmonic mean of precision and recall, providing a balance between the two. Loss measures the difference between the predicted values and the actual values, indicating how well the model is performing. Mean IoU is a metric used for evaluating the accuracy of object detection models, calculated by dividing the intersection of the predicted and ground truth regions by their union [53,54]. Table 5 presents a comparison of these metrics for the model trained on the experimental dataset alone versus the combined dataset. The results indicate that incorporating synthetic data significantly improved the model’s performance, enhancing its accuracy and ability to generalize across unseen defect types and conditions.

Table 5.
Evaluation metrics of UNET+ for each dataset.
The inclusion of synthetic data in the training process addressed the common challenge of limited experimental data, resulting in a more robust and accurate model. The improved performance metrics demonstrate the value of data augmentation through FEM simulations. As shown in the learning curves (Figure 7), the UNET+ model trained on the FEM + experimental dataset exhibits steady improvement in accuracy throughout the training steps, reaching a final accuracy of approximately 0.88. In contrast, the model trained solely on the experimental dataset shows signs of overfitting, with accuracy plateauing and fluctuating around 0.85 after 10–14 steps. This indicates that while the model initially learns from the limited data, it eventually starts to memorize the training set rather than generalize to new data.
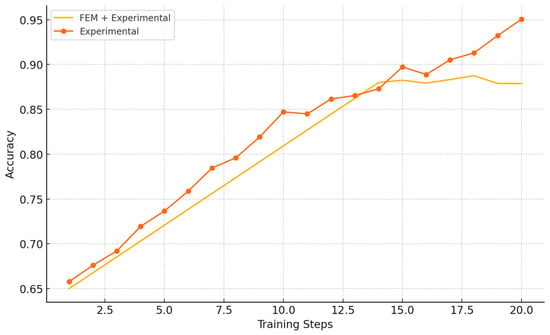
Figure 7.
Comparison of UNET+ model performance on different databases.
The performance metrics in Table 4 further corroborate these findings. The F1 score for the FEM + experimental dataset is 0.90, compared to 0.89 for the experimental dataset alone. The Mean IoU also saw a substantial increase from 0.66 to 0.87, and the loss for the FEM + experimental dataset was significantly lower at 0.26, compared to 0.57 for the experimental dataset. These results highlight that augmenting the training data with synthetic data from FEM simulations not only improves the overall accuracy and robustness of the model but also mitigates the risk of overfitting, ensuring better applicability to real-world scenarios.
5. Conclusions
This study demonstrated the effectiveness of integrating thermography with machine learning, particularly through the use of synthetic datasets, to improve the detection and characterization of corrosion in steel pipes. Key findings indicate that augmenting experimental data with Finite Element Method (FEM) simulations significantly enhances the performance of machine learning models, as evidenced by the improved metrics of the UNet model in detecting defects.
The implications of these findings are substantial, suggesting that the approach can overcome common challenges such as data scarcity and overfitting, thereby improving the reliability of defect detection in critical infrastructure. However, this study has limitations, including the dependency on the accuracy of synthetic data and the potential variations in real-world conditions that were not fully replicated in the simulations. Future work should focus on validating these findings with a broader range of materials and conditions, as well as exploring other machine learning architectures and augmentation techniques to further refine defect detection capabilities.
The contribution of this work to the field is significant, providing a robust framework for enhancing thermographic inspections using advanced data augmentation techniques. This methodology not only addresses current limitations in data availability but also offers practical applications in various industries where early and accurate defect detection is crucial for maintaining safety and performance. By integrating synthetic datasets, this approach sets a precedent for future research and development in non-destructive testing and condition monitoring, ultimately leading to more reliable and efficient maintenance strategies for critical infrastructure.
Author Contributions
Conceptualization, R.K.R., X.M. and C.I.-C.; methodology, R.K.R.; software, R.K.R.; validation, R.K.R.; formal analysis, R.K.R., X.M. and C.I.-C.; investigation, R.K.R., X.M. and C.I.-C.; resources, X.M. and C.I.-C.; data curation, X.M. and C.I.-C.; writing—original draft preparation, R.K.R.; writing—review and editing, R.K.R., X.M. and C.I.-C.; visualization, R.K.R.; supervision, X.M. and C.I.-C.; project administration, X.M.; funding acquisition, X.M. and C.I.-C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Natural Sciences and Engineering Council of Canada (NSERC), the CREATE oNDuTy Program (funding ref. number 496439-2017), the Canada Research Chair in Multipolar Infrared Vision (MIVIM), Department of Civil Engineering from Université Laval, and the MITACS Accelerate Program.
Data Availability Statement
All the data for this research are available at this link: https://github.com/reza7293/Thermography_CUI_FEM_data_augmentaition (accessed on 1 September 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Alhammad, M.; Avdelidis, N.P.; Ibarra Castanedo, C.; Maldague, X.; Zolotas, A.; Torbali, E.; Genest, M. Multi-label classification algorithms for composite materials under infrared thermography testing. Quant. InfraRed Thermogr. J. 2022, 21, 3–29. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C.; Tarpani, J.R.; Maldague, X.P.V. Nondestructive testing with thermography. Eur. J. Phys. 2013, 34, S91–S109. [Google Scholar] [CrossRef]
- Pozzer, S.; Rosa, F.D.; Pravia, Z.M.C.; López, F.; Maldague, X. Use of advanced thermographic signal processing techniques to improve the subsurface damage detection in concrete columns under varying solar exposure. In Thermosense: Thermal Infrared Applications XLIV; Avdelidis, N.P., Mendioroz, A., Eds.; SPIE: Bellingham, WA, USA, 2022; p. 28. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q.; Li, C.; Piao, Y.; Hou, N.; Hu, K. Characterization of surface and subsurface defects induced by abrasive machining of optical crystals using grazing incidence X-ray diffraction and molecular dynamics. J. Adv. Res. 2022, 36, 51–61. [Google Scholar] [CrossRef]
- Milovanović, B.; Banjad Pečur, I. Review of Active IR Thermography for Detection and Characterization of Defects in Reinforced Concrete. J. Imaging 2016, 2, 11. [Google Scholar] [CrossRef]
- Doshvarpassand, S.; Wu, C.; Wang, X. An overview of corrosion defect characterization using active infrared thermography. Infrared Phys. Technol. 2019, 96, 366–389. [Google Scholar] [CrossRef]
- Rodríguez-Martín, M.; Fueyo, J.G.; Gonzalez-Aguilera, D.; Madruga, F.J.; García-Martín, R.; Muñóz, Á.L.; Pisonero, J. Predictive Models for the Characterization of Internal Defects in Additive Materials from Active Thermography Sequences Supported by Machine Learning Methods. Sensors 2020, 20, 3982. [Google Scholar] [CrossRef]
- Nesteruk, D.; Vavilov, V.; Chulkov, A.; Burleigh, D. Simple and robust methodology of defect thermal characterization based on thermal quadrupoles and polynomial approximation. NDT E Int. 2021, 124, 102522. [Google Scholar] [CrossRef]
- Dudzik, S.; Dudek, G. Detection of thinning of homogeneous material using active thermography and classification trees. Metrol. Meas. Syst. 2021, 28, 89–105. [Google Scholar] [CrossRef]
- Lai, Y. A Comparison of Traditional Machine Learning and Deep Learning in Image Recognition. J. Phys. Conf. Ser. 2019, 1314, 012148. [Google Scholar] [CrossRef]
- Aldave, I.J.; Bosom, P.V.; González, L.V.; De Santiago, I.L.; Vollheim, B.; Krausz, L.; Georges, M. Review of thermal imaging systems in composite defect detection. Infrared Phys. Technol. 2013, 61, 167–175. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, Y.; Hu, S.; Wang, H.; Zhang, Y.; Ming, W. Progress in Active Infrared Imaging for Defect Detection in the Renewable and Electronic Industries. Sensors 2023, 23, 8780. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Fan, E.; Wang, P. Comparative analysis of image classification algorithms based on traditional machine learning and deep learning. Pattern Recognit. Lett. 2021, 141, 61–67. [Google Scholar] [CrossRef]
- Marani, R.; Palumbo, D.; Galietti, U.; D’Orazio, T. Deep learning for defect characterization in composite laminates inspected by step-heating thermography. Opt. Lasers Eng. 2021, 145, 106679. [Google Scholar] [CrossRef]
- Morelli, D.; Marani, R.; D’Accardi, E.; Palumbo, D.; Galietti, U.; D’Orazio, T. A Convolution Residual Network for Heating-Invariant Defect Segmentation in Composite Materials Inspected by Lock-in Thermography. IEEE Trans. Instrum. Meas. 2021, 70, 2515214. [Google Scholar] [CrossRef]
- Shaloo, M.; Schnall, M.; Klein, T.; Huber, N.; Reitinger, B. A Review of Non-Destructive Testing (NDT) Techniques for Defect Detection: Application to Fusion Welding and Future Wire Arc Additive Manufacturing Processes. Materials 2022, 15, 3697. [Google Scholar] [CrossRef]
- Chung, Y.; Lee, S.; Kim, W. Latest Advances in Common Signal Processing of Pulsed Thermography for Enhanced Detectability: A Review. Appl. Sci. 2021, 11, 12168. [Google Scholar] [CrossRef]
- Yousefi, B.; Sfarra, S.; Sarasini, F.; Castanedo, C.I.; Maldague, X.P.V. Low-rank sparse principal component thermography (sparse-PCT): Comparative assessment on detection of subsurface defects. Infrared Phys. Technol. 2019, 98, 278–284. [Google Scholar] [CrossRef]
- Fleuret, J.R.; Ebrahimi, S.; Ibarra-Castanedo, C.; Maldague, X.P.V. Independent Component Analysis Applied on Pulsed Thermographic Data for Carbon Fiber Reinforced Plastic Inspection: A Comparative Study. Appl. Sci. 2021, 11, 4377. [Google Scholar] [CrossRef]
- Hu, C.; Duan, Y.; Liu, S.; Yan, Y.; Tao, N.; Osman, A.; Ibarra-Castanedo, C.; Sfarra, S.; Chen, D.; Zhang, C. LSTM-RNN-based defect classification in honeycomb structures using infrared thermography. Infrared Phys. Technol. 2019, 102, 103032. [Google Scholar] [CrossRef]
- Xu, L.; Hu, J. A Method of Defect Depth Recognition in Active Infrared Thermography Based on GRU Networks. Appl. Sci. 2021, 11, 6387. [Google Scholar] [CrossRef]
- Zaini, N.; Ean, L.W.; Ahmed, A.N.; Malek, M.A. A systematic literature review of deep learning neural network for time series air quality forecasting. Environ. Sci. Pollut. Res. 2022, 29, 4958–4990. [Google Scholar] [CrossRef] [PubMed]
- Illustrated Guide to LSTM’s and GRU’s: A Step by Step. Available online: https://towardsdatascience.com/illustrated-guide-to-lstms-and-gru-s-a-step-by-step-explanation-44e9eb85bf21 (accessed on 28 May 2024).
- Dong, Y.; Xia, C.; Yang, J.; Cao, Y.; Cao, Y.; Li, X. Spatio-Temporal 3-D Residual Networks for Simultaneous Detection and Depth Estimation of CFRP Subsurface Defects in Lock-In Thermography. IEEE Trans. Ind. Inf. 2022, 18, 2571–2581. [Google Scholar] [CrossRef]
- Kim, Y.; Kwak, G.-H.; Lee, K.-D.; Na, S.-I.; Park, C.-W.; Park, N.-W. Performance evaluation of machine learning and deep learning algorithms in crop classification. Korean J. Remote Sens. 2018, 34, 811–827. [Google Scholar] [CrossRef]
- Kang, J.-S.; Kang, J.; Kim, J.-J.; Jeon, K.-W.; Chung, H.-J.; Park, B.-H. Neural Architecture Search Survey: A Computer Vision Perspective. Sensors 2023, 23, 1713. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Z.; Zhao, C.; Liu, J.; Yin, W.; Li, Y.; Wang, F.; Li, C.; Lin, Z. Depth Classification of Defects Based on Neural Architecture Search. IEEE Access 2021, 9, 73424–73432. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Z.; Yin, W.; Wang, Q.; Li, Y.; Zhao, C. Surface defect characterization and depth identification of CFRP material by laser line scanning. NDT E Int. 2022, 130, 102657. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Z.; Yin, W.; Zhao, C.; Wang, F.; Li, Y. A study on depth classification of defects by machine learning based on hyper-parameter search. Measurement 2022, 189, 110660. [Google Scholar] [CrossRef]
- Campos-Delgado, D.U.; Cruz-Guerrero, I.A.; Mendoza-Chavarría, J.N.; Mejía-Rodríguez, A.R.; Ortega, S.; Fabelo, H.; Callico, G.M. Nonlinear extended blind end-member and abundance extraction for hyperspectral images. Signal Process. 2022, 201, 108718. [Google Scholar] [CrossRef]
- Collison, S. Artificial Intelligence based breast thermography using radiomic feature extraction versus conventional manual interpretation of breast thermograms in the prediction of breast cancer: A multi-reader study. medRxiv 2023. [Google Scholar] [CrossRef]
- Li, X.; Ying, X.; Zhu, W.; Liu, W.; Hou, B.; Zhou, L. Nondestructive detection and analysis based on data enhanced thermography. Meas. Sci. Technol. 2022, 33, 064006. [Google Scholar] [CrossRef]
- Barbedo, J.G.A. Impact of dataset size and variety on the effectiveness of deep learning and transfer learning for plant disease classification. Comput. Electron. Agric. 2018, 153, 46–53. [Google Scholar] [CrossRef]
- Althnian, A.; AlSaeed, D.; Al-Baity, H.; Samha, A.; Dris, A.B.; Alzakari, N.; Abou Elwafa, A.; Kurdi, H. Impact of Dataset Size on Classification Performance: An Empirical Evaluation in the Medical Domain. Appl. Sci. 2021, 11, 796. [Google Scholar] [CrossRef]
- Maldague, X. Theory and Practice of Infrared Technology for Nondestructive Testing; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Ibarra-Castanedo, C.; Avdelidis, N.P.; Grinzato, E.G.; Bison, P.G.; Marinetti, S.; Chen, L.; Genest, M.; Maldague, X. Quantitative inspection of non-planar composite specimens by pulsed phase thermography. Quant. InfraRed Thermogr. J. 2006, 3, 25–40. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C.; González, D.; Klein, M.; Pilla, M.; Vallerand, S.; Maldague, X. Infrared image processing and data analysis. Infrared Phys. Technol. 2004, 46, 75–83. [Google Scholar] [CrossRef]
- Breitenstein, O.; Warta, W.; Langenkamp, M. Lock-In Thermography: Basics and Use for Evaluating Electronic Devices and Materials; Springer: Berlin/Heidelberg, Germany, 2010; Volume 10. [Google Scholar]
- Sharath, D.; Menaka, M.; Venkatraman, B. Defect Characterization Using Pulsed Thermography. J. Nondestruct. Eval. 2013, 32, 134–141. [Google Scholar] [CrossRef]
- Wei, Z.; Osman, A.; Valeske, B.; Maldague, X. Pulsed Thermography Dataset for Training Deep Learning Models. Appl. Sci. 2023, 13, 2901. [Google Scholar] [CrossRef]
- Liu, K.; Zheng, M.; Liu, Y.; Yang, J.; Yao, Y. Deep Autoencoder Thermography for Defect Detection of Carbon Fiber Composites. IEEE Trans. Ind. Inf. 2023, 19, 6429–6438. [Google Scholar] [CrossRef]
- Ouali, Y.; Hudelot, C.; Tami, M. An Overview of Deep Semi-Supervised Learning. June 2020. Available online: http://arxiv.org/abs/2006.05278 (accessed on 28 May 2024).
- Shorten, C.; Khoshgoftaar, T.M. A survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
- Liu, K.; Tang, Y.; Lou, W.; Liu, Y.; Yang, J.; Yao, Y. A thermographic data augmentation and signal separation method for defect detection. Meas. Sci. Technol. 2021, 32, 045401. [Google Scholar] [CrossRef]
- Lu, Y.; Chen, D.; Olaniyi, E.; Huang, Y. Generative adversarial networks (GANs) for image augmentation in agriculture: A systematic review. Comput. Electron. Agric. 2022, 200, 107208. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, Q.; Chen, J.; He, S.; Li, F.; Zhou, Z. A multi-module generative adversarial network augmented with adaptive decoupling strategy for intelligent fault diagnosis of machines with small sample. Knowl.-Based Syst. 2022, 239, 107980. [Google Scholar] [CrossRef]
- Wei, Z.; Osman, A.; Valeske, B.; Maldague, X. A Dataset of Pulsed Thermography for Automated Defect Depth Estimation. Appl. Sci. 2023, 13, 13093. [Google Scholar] [CrossRef]
- Makhlouf, A.; Maayah, M.; Abughanam, N.; Catal, C. The use of generative adversarial networks in medical image augmentation. Neural Comput. Appl. 2023, 35, 24055–24068. [Google Scholar] [CrossRef]
- Yu, H.; Wang, Q.F.; Shi, J.Y. Data augmentation generated by generative adversarial network for small sample datasets clustering. Neural Process. Lett. 2023, 55, 8365–8384. [Google Scholar] [CrossRef]
- Rezayiye, R.K.; Laurent, K.; Nooralishahi, P.; Ibarra-Castanedo, C.; Maldague, X. Thermal Data Augmentation Approach for the Detection of Corrosion in Pipes Using Deep Learning and Finite Element Modelling. In AITA 2023, Proceedings of the 17th International Workshop on Advanced Infrared Technology and Applications, Venice, Italy, 10–13 September 2023; MDPI: Basel, Switzerland, 2023; p. 20. [Google Scholar] [CrossRef]
- Rezayiye, R.K.; Ibarra-Castanedo, C.; Maldague, X. Enhancing Moisture-Induced Defect Detection in Insulated Steel Pipes through Infrared Thermography and Hybrid Dataset. Electronics 2024, 13, 1748. [Google Scholar] [CrossRef]
- Nillmani; Sharma, N.; Saba, L.; Khanna, N.N.; Kalra, M.K.; Fouda, M.M.; Suri, J.S. Segmentation-Based Classification Deep Learning Model Embedded with Explainable AI for COVID-19 Detection in Chest X-ray Scans. Diagnostics 2022, 12, 2132. [Google Scholar] [CrossRef]
- Everingham, M.; Eslami, S.M.A.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. The Pascal Visual Object Classes Challenge: A Retrospective. Int. J. Comput. Vis. 2015, 111, 98–136. [Google Scholar] [CrossRef]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).