Abstract
Encoding a dictionary into another representation means that all the words can be stored in the dictionary in a more efficient way. In this way, we can complete common operations in dictionaries, such as (1) searching for a word in the dictionary, (2) adding some words to the dictionary, and (3) removing some words from the dictionary, in a shorter time. Binary decision diagrams (BDDs) are one of the most famous representations of such encoding and are widely popular due to their excellent properties. Recently, some people have proposed encoding dictionaries into BDDs and some variants of BDDs and showed that it is feasible. Hence, we further investigate the topic of encoding dictionaries into decision diagrams. Tagged sentential decision diagrams (TSDDs), as one of these variants based on structured decomposition, exploit both the standard and zero-suppressed trimming rules. In this paper, we first introduce how to use Boolean functions to represent dictionary files and then design an algorithm that encodes dictionaries into TSDDs with the help of tries and a decoding algorithm that restores TSDDs to dictionaries. We utilize the help of tries in the encoding algorithm, which greatly accelerates the encoding process. Considering that TSDDs integrate two trimming rules, we believe that using TSDDs to represent dictionaries would be more effective, and the experiments also show this.
1. Introduction
A word is a string consisting of some symbols or characters, and a dictionary is a set that includes numerous words. A large dictionary can consist of millions of words. With the evolution of computer technology, in practical life, we use dictionaries in many places. For example, teachers store the names of all students in the school on their computers; this list of students is actually a dictionary, where each student’s name is a word. In order to solve practical problems, we often need to perform some common operations in dictionaries, three of which are, for example, (1) searching for a word in a dictionary, (2) adding words to a dictionary, and (3) removing words from a dictionary. In general, the time complexity of the above operations is . When the size of a dictionary (that is, the number of words) is too large, the above three operators are time-consuming and ineffective. Therefore, designing an effective method for operations in dictionaries is worth investigating.
An effective method for operations in dictionaries is to encode the dictionary into an efficient and compact representation. Some scholars have proposed a decision-diagram-based method of operation for dictionaries [1]. However, they have not provided any algorithms or implementations of the method. Following the above-mentioned idea, in this paper, we represent large dictionaries in decision diagrams and solve the common operations for dictionaries via operations in decision diagrams.
Binary decision diagrams (BDDs) are unique canonical forms that adhere to specific constraints, namely, ordering and reduction, ensuring that each Boolean function possesses a distinct BDD representation. This characteristic minimizes the storage requirements of BDDs and facilitates O(1) time equality tests on BDDs. After the emergence of the BDD, a variant known as the zero-suppressed BDD (ZDD) was introduced in [2]. ZDDs share similar characteristics with BDDs, such as canonicity and support for polynomial-time Boolean operations. The primary distinction between BDDs and ZBDDs lies in their respective reduction rules. Building on the applications of BDDs and ZBDDs, several extensions have been developed, including tagged BDDs (TBDDs) [3], chain-reduced BDDs (CBDDs) [1], chain-reduced ZDDs (CZDDs) [1], and edge-specified reduction BDDs (ESRBDDs) [4]. These extensions, which integrate two reduction rules, offer more compact representations compared to BDDs and ZDDs.
With the increasing maturity of decision diagram technology, people have begun to focus on research on applying decision diagrams to many fields. In ref. [1], the researchers successfully transformed a dictionary into BDDs and two variants of BDDs, CBDDs and CZDDs. They started from the following three points: (1) A Boolean function can be used to represent a binary number. (2) Decision diagrams can be used to represent Boolean functions. (3) Characters and symbols can be encoded into binary codes. Then, they considered the possibility of using decision diagrams to represent characters and symbols and implemented it. Finally, they encoded two dictionaries containing hundreds of thousands of words into three decision diagrams and provided data on the node count and time indicators. This confirms that encoding dictionaries into decision diagrams is a feasible research direction.
Hence, in this paper, we focus on applying another type of decision diagram, tagged sentential decision diagrams (TSDDs), into encoding dictionaries, and we first introduce TSDDs. To introduce TSDDs, we first introduce sentential decision diagrams (SDDs), which are decision diagrams based on structured decomposition [5], while BDDs are based on Shannon decomposition [6]. While BDDs are characterized by a total variable order, SDDs are defined by a variable tree (vtree), which is a complete binary tree with variables as its leaves, and apply standard trimming rules. Furthermore, in ref. [7], the researchers introduced the zero-suppressed variant of the SDD, known as the ZSDD, which also utilizes structured decomposition and applies zero-suppressed trimming rules instead of the standard trimming rules used in SDDs. ZSDDs offer a more compact representation for sparse Boolean functions compared to SDDs, while SDDs are better suited for homogeneous Boolean functions. To leverage the strengths of both SDDs and ZSDDs, ref. [8] devised a new decision diagram, the TSDD, which combines the standard and zero-suppressed trimming rules.
The contributions of our paper mainly include the following: (1) We propose an algorithm for encoding dictionaries into decision diagrams. We first transform a dictionary into a well-known data structure: the trie. With the help of tries, our algorithm can encode a dictionary into a decision diagram more efficiently than the method without tries. (2) We encoded 14 dictionaries into seven decision diagrams, i.e., BDDs, ZDDs, CBDDs, CZDDs, SDDs, ZSDDs, and TSDDs, in four ways, and we believe that TSDDs are the most suitable for representing dictionaries among all decision diagrams. We adopted TSDDs to represent dictionaries, and the experimental results show that TSDDs are more compact representations compared to other decision diagrams. (3) We also designed an algorithm that decodes a decision diagram and obtains the original dictionary. Our algorithm recursively restores each word in the dictionary and then saves these words together to obtain the original dictionary. Moreover, our algorithm can quickly complete the decoding process in most cases.
The rest of this paper is organized as follows. We first introduce the syntax and semantics of SDDs and ZSDDs. Section 3 introduces the syntax of TSDDs and the binary operation on TSDDs. In this section, we mainly introduce how to use a TSDD to denote a Boolean function and the trimming rules of TSDDs. Ref. [8] proposed a related definition of TSDDs. However, the researchers used three different semantics to explain SDDs, ZSDDs, and TSDDs. In fact, we believe that the difference in these decision diagrams mainly lies in the different trimming rules. These three decision diagrams can be explained with the same semantics. In this way, we can have a more intuitive understanding of these three decision diagrams and theoretically understand why TSDDs are more effective than SDDs and ZSDDs. Section 4 introduces how to use a Boolean function to represent a dictionary, the process of encoding a dictionary with the help of tries, and the decoding algorithm. An experimental evaluation comparing TSDDs with other decision diagrams appears in Section 5. Finally, Section 6 concludes this paper.
2. Preliminaries
Throughout this paper, we use lowercase letters (e.g., ) for variables and bold uppercase letters (e.g., ) for sets of variables. For a variable x, we use to denote the negation of x. A literal is a variable or a negated one. A truth assignment over is the mapping . We let be the set of truth assignments over . We say f is a Boolean function over , which is the mapping . We use (resp. ) for the Boolean function that maps all assignments to 1 (resp. 0).
Let and be two disjoint and non-empty sets of variables. We use f to denote a Boolean function and use to denote a Boolean function over the variable set . We say the set is an -decomposition of a Boolean function iff , where every (resp. ) is a Boolean function over (resp. ). A decomposition is compressed iff for . An -decomposition is called an -partition iff (1) for , (2) for , and (3) .
A vtree is a full binary tree whose leaves are labeled by variables, and we use to denote a vtree node. Then, we use to denote the left subtree of , while denotes the right subtree of . The set of variables appearing in the leaves of is denoted by . In addition, there is a special leaf node labeled by 0, which can be considered a child of any vtree node, and = ∅. The notation denotes that is a subtree of . In order to unify the definition, we use a tuple to denote a decision diagram in this paper and give the following definition.
Definition 1.
A decision diagram is a tuple s.t. , which is recursively defined as follows:
- α is a terminal node labeled by one of four symbols: , , ε, or ;
- α is a decomposition node satisfying the following:
- –
- Each is a decision diagram , where ;
- –
- Each is a decision diagram , where .
The size of is denoted by , and when is a terminal node and when . We use to denote the Boolean function that this decision diagram represents. Then, we give the definition of the syntax of decision diagrams.
Definition 2.
Let and be two vtrees, and let be a subtree of . The semantics of decision diagrams is inductively defined as follows:
- , .
- , .
- and satisfies the following conditions:
- –
- for .
- –
- for .
- –
- .
A sentential decision diagram (SDD) has the following further constraints based on the above definition of a decision diagram:
- If is a terminal node, then it must be one of the following:
- –
- .
- –
- .
- –
- , where must be a leaf vtree node.
- –
- , where must be a leaf vtree node and .
- If is a decomposable node, then .
Suppose that is an SDD; then, we know that if is a decomposable node. Hence, we use to denote an SDD in order to provide a more intuitive definition of compression and trimming rules. The compression and trimming rules for SDDs are proposed in [9], and we give them according to the above definition.
- Standard compression rule: if , then replace with , where .
- Standard trimming rules:
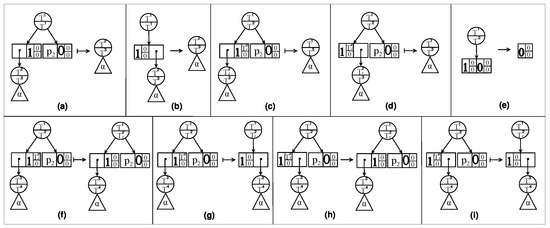
For Figure 1, we need to clarify the following content. For a decision diagram , when is a terminal node, the above three components are represented by a square, where is shown on the left side of the square, is in the upper-right corner, and is in the lower-right corner. When is a decomposition node, and are displayed as circles with outgoing edges pointing to the elements. Each element is represented by paired boxes, where the left box represents the prime , and the right box stands for the sub .
Compressed and trimmed SDDs were shown to be a canonical form of Boolean functions in [9]. Then, we show the syntax and semantics of ZSDDs in our definition. A ZSDD has different constraints based on the above definition of a decision diagram. First of all, it should be noted that we use to denote the root node of the whole vtree:
- If is a terminal node, then it must be one of the following:
- –
- .
- –
- .
- –
- , where must be a leaf vtree node.
- –
- , where must be a leaf vtree node.
The compression and trimming rules for ZSDDs are as follows:
Similar to SDDs, compressed and trimmed ZSDDs were also proven to be a canonical form of Boolean functions in [7]. SDDs are suitable to represent homogeneous Boolean functions, while ZSDDs are suitable to represent Boolean functions with sparse values.
3. Tagged Sentential Decision Diagrams
In this section, we will first introduce the syntax and semantics of TSDDs and the compression and trimming rules of TSDDs. Similar to SDDs and ZSDDs, we give the syntax and semantics based on the syntax and semantics of decision diagrams in Section 2. Then, we briefly introduce the binary operations on TSDDs and how to use these operations to construct a Boolean function.
3.1. Syntax and Semantics
TSDDs have different constraints compared to SDDs and ZSDDs based on the syntax and semantics of decision diagrams. Here, we give the following constraints.
Definition 3.
Let and be two vtrees s.t. and is a TSDD. Then,
- If α is a terminal node, then it must be one of the following:
- –
- , and .
- –
- , and (specifically, if , then ).
- –
- and must be a leaf vtree node, and .
- If α is a decomposition node, then must not be a leaf vtree node.
We can see that for a TSDD , must be a leaf vtree node or 0 if is a terminal node. We should note that we can directly construct some TSDDs. (1) The TSDDs and can be constructed. (2) The TSDDs and , where is a leaf vtree node, can be constructed. These two kinds of TSDDs are special TSDDs; that is, they are the foundation for constructing a TSDD to represent a Boolean function. For the second type of TSDDs, we know that is a leaf vtree node; that is, contains only one variable. Suppose that ; then, and .
3.2. Canonicity
TSDDs, as a variant of SDDs, apply trimming rules that integrate the trimming rules of SDDs and ZSDDs. Hence, the trimming rules of TSDDs include the trimming rules of SDDs and ZSDDs that are shown in Figure 1a–d, and we do not introduce them in the following definition. Hence, the trimming rules of TSDDs start from (e). In addition, these rules also include five new rules. We then show the compression and trimming rules for TSDDs as follows:
- Tagged compression rule: if , then replace with , where .
- Tagged trimming rules:
A TSDD is compressed (resp. trimmed) if no tagged compression (resp. trimming) rules can be applied to it. The canonicity of compressed and trimmed TSDDs was proved in [8].
3.3. Operations on TSDDs
The main operations on TSDDs include conjunction (∧), disjunction (∨), and negation (). The algorithm of the binary operations conjunction (∧) and disjunction (∨) was shown in [8]. Here, we show the negation algorithm on TSDDs in Algorithm 1.
| Algorithm 1: Negate |
 |
For special terminal nodes, which are the two kinds of TSDDs mentioned in Section 3.1, we can directly compute the resulting TSDD (Lines 1–2). For the other terminal nodes, we need to transform them into another form, namely, decomposable nodes (Line 3). And then, we apply to every element and construct the following elements: ; the resulting TSDD is (Lines 4–7). Finally, we apply compression and trimming rules to H (Line 8).
The binary operation is represented by , where ∘ represents ∧ or ∨, as shown in [8]. With these three operations, we can construct TSDDs to represent any Boolean function based on existing TSDDs. Here, we give an example. Given the Boolean function , we have the following initial TSDDs: , , , , , and , where and so on. The steps are as follows: (1) Let . (2) Let . (3) Let . (4) Let . Finally, we obtain TSDD F, where .
4. Encoding Dictionaries into TSDDs
A dictionary includes a large number of words, and we intend to transform it into a decision diagram that stores the whole dictionary. In this way, we can complete some common operations in the dictionary just by performing some binary operations on decision diagrams. When we want to verify whether a word exists in the dictionary, we just need to compute the result , where F is the decision diagram representing the dictionary, and G is the decision diagram representing the word. If the result is , then the word does not exist in the dictionary; otherwise, it exists in the dictionary. When we want to remove some words from the dictionary, we just need to construct the decision diagram G representing the set of words. And then, we compute the result , where F represents the dictionary. Changing the traversal process on dictionaries to several binary operations on decision diagrams can remove the traversal process. This is why we encode dictionaries into decision diagrams.
In this section, we first introduce the process of encoding a dictionary into a decision diagram in four different ways. Ref. [1] pointed out the use of tries when encoding dictionaries into decision diagrams but did not provide a detailed description of the process. Hence, we were inspired by them and designed our method of encoding dictionaries with the help of tries, which greatly accelerated the compilation process. In the following, we intend to explain in detail how to use tries to complete the encoding of a dictionary and present the algorithm for decoding TSDDs.
4.1. Four Encoding Methods
The key to our method is to establish the correspondence between letters and numbers so that we can use a string of numbers to represent a word. For example, the ASCII code, a famous encoding system, uses a number ranging from 0 to 127 to represent 128 characters. With the help of the ASCII code, we represent a letter with some variables by transforming the code into its binary representation. As we know, the ASCII code of the letter ‘A’ is 65, whose binary representation is ‘1000001’ with 7 bits. We represent the letter ‘A’ by 7 variables, ‘’, and consider the variable to be ‘0’ when the value is false and ‘1’ when the value is true. Hence, a letter needs 7 variables to be represented in the ASCII code. If a word consists of n letters, it needs 7*n variables in total to be represented.
However, there are many characters in the ASCII code that are often not used in most dictionaries, which means that it will cause significant redundancy if we use 7 bits to represent every letter. Suppose that a dictionary consists only of lowercase letters; that is, there are only 26 different letters in this dictionary. We number each letter in alphabetical order starting from 1, with the maximum number being 26, representing z. The number 26 just needs 5 bits to be represented, and its binary representation is ‘11010’, which means that a letter needs 5 variables to be represented. In this way, we reduce the number of variables required to represent a letter, and this code is called the compact code.
Compared with the ASCII code, the compact code can reduce the number of variables required to represent a letter. However, we need to make a protocol that specifies the correspondence between letters and numbers if we apply the compact code and records this correspondence in a table. This table is necessary for both encoding and decoding. Therefore, this table should be known as necessary information by all those who use compact encoding. The ASCCI code is an international standard that does not require additional space to store the correspondence between letters and codes. Hence, the universality of the ASCCI code is better than that of the compact code.
We use binary numbers to represent both the ASCII code and compact code for each letter, which means that the number of variables is the number of binary digits. Hence, we call this the binary way of encoding dictionaries. If the maximum value of the code is n, we can also use n variables to represent the code. For example, given the word zoo, there are two different letters, ‘z’ and ‘o’, in this word, and the word consists of three letters. Hence, we need six variables, , and , to represent it. and represent the first letter, and the first letter is ‘z’ if and , while it is ‘o’ if and . The other variables have similar meanings. Therefore, the word ‘zoo’ is represented by . We call this the one-hot way of encoding the dictionary. A word consisting of m letters needs n*m variables in total to represent it in one-hot encoding, while it just needs variables in total to represent it in a binary way.
4.2. Encoding with Tries
We can first encode every word in the dictionary into a TSDD one by one and then apply disjunction to these TSDDs to obtain the resulting TSDD that represents the whole dictionary. However, the process of encoding takes too much time, which is unacceptable to us. If the number of words in the dictionary exceeds 100,000, the encoding time will exceed two hours. Therefore, we first transform the dictionary into a trie, which is a multibranch tree, and then transform it into a TSDD. This can greatly accelerate the speed of encoding a dictionary.
A trie is a multibranch tree whose every node saves a letter, except for two special nodes. We know that a tree is a directed acyclic graph, and every node has its in- and out-degrees. In general, the in- and out-degrees of each node in a trie are both greater than 0, and these nodes all save a letter in them. However, there are two special nodes, one with an in-degree of 0 and the other with an out-degree of 0. We call the node with an in-degree of 0 the head and the node with an out-degree of 0 the tail. Both nodes do not save any letters. We can easily know that all paths in the trie must start from the head and end at the tail. A path represents a word in the dictionary, which means that the number of paths is the number of words in the trie.
We first introduce the algorithm for transforming a dictionary into a trie in Algorithm 2. We need to initialize the two special nodes, that is, the head node and the tail node , and a node , which is an empty node (Line 1). Then, we traverse each word in the dictionary, and in a loop, we let be the node (Lines 2–3). We perform the following operations on the letters in the word in order. The operation means we look for a node from successor nodes of that save the letter l. If such a node does not exist, we create a new node with NewNode(l) and let it be the successor node of trace with (Lines 4–8), and then we let be the node (Line 9). After all the letters have been accessed, we let be the successor node of (Line 10). Finally, the node is the resulting trie.
| Algorithm 2: ToTrie |
 |
After we obtain the trie, we need to compress it further. Firstly, the nodes in the trie need to be assigned an important parameter: depth; we denote a node as , where d stands for depth and l stands for letter. We first give the following definition.
Definition 4.
A trie node is defined as follows:
- if the node is the node .
- If is a node and is one of its children, then .
- Letters that appear sequentially in the path from the root to the leaf form a word.
The step of compressing the trie entails merging two nodes that have the same depth and meet certain conditions into one node. The conditions are as follows: (1) The two nodes save the same letter. (2) The two nodes have the same children nodes. We group all nodes by depth and merge nodes by group, starting from the deepest group.
Here, we give an example using a dictionary that contains six words: aco, cat, dot, purple, ripple, and zoo. The tries before and after merging the nodes are shown in Figure 2. There are two special nodes in the graph, namely, the root node with a depth of 0 and the tail node represented by a solid circle without a depth. Except for these two nodes, each other node stores a letter, and we stipulate that all paths representing words start at the root node and end at the tail node. Except for the tail node, all other nodes have a depth, and the maximum depth on a path is the number of letters in the word represented by that path. After we merge the nodes, we can see that the number of nodes has significantly decreased.
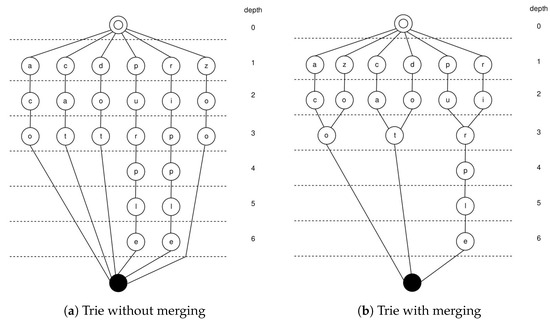
Figure 2.
Trie.
We then transform this trie into a TSDD, and the algorithm is shown in Algorithm 3. We first compute the number of variables in the TSDD and suppose that the maximum length of all words in the dictionary is n and the number of different letters in the dictionary is m. The number of variables is 128*n if we use the ASCII code in a one-hot way and 7*n if we use the ASCII code in a binary way. The number of variables is m*n if we use the compact code in a one-hot way and if we use the compact code in a binary way. Here, we explain the method that transforms a trie node into a TSDD node by using the ASCII code in a binary way, and we save the corresponding TSDD in the trie node. There are three steps in total. Let be a trie node. The steps are as follows: (1) We access each node from bottom to top and compute the result of applying disjoin on all the TSDDs that are saved in the successor nodes of and record this result as G, and Successor() represents all the successor nodes of the trie node (Lines 1–4). (2) We compute the TSDD GetTSDD(), which represents the letter saved in the trie node (Line 5). For example, if the letter l is ‘a’, the binary representation of the letter is ‘1100001’, and the related variables are . Of these variables, the variables that are marked as ‘1’ are . We need to construct the TSDD G that represents the Boolean function . (3) We compute the TSDD (Line 5). Then, we save this TSDD G in the trie node (Line 6). Similarly, we group all trie nodes based on depth and transform the nodes into TSDDs in the group in descending order of depth. We should note that if is the tail trie node, the TSDD saved in it is not fixed. The TSDD saved in the tail trie node is decided based on the depth of its parent node. Let the depth of the parent node be d and the TSDD saved in the tail node be G; then, . In addition, not all words consist of n letters. If a word consists of fewer than n letters, we use null characters to supplement the remaining positions. For the above example, if the letter saved in the trie node is a null character, then the Boolean function in step 2 is . Finally, the TSDD saved in the head trie node is the TSDD that represents the whole dictionary (Line 7).
| Algorithm 3: ToTSDD |
 |
For the other three encoding methods, the process is also similar, with only differences in the relevant variables. Similarly, it is necessary to perform a conjunction operation on the variables marked as 1 and the negation of variables marked as 0. The TSDD saved in the head trie node is what we want. At this point, the process of encoding a dictionary is complete.
4.3. Decoding
We use one code to represent a letter and then multiple codes to represent an entire word. On the contrary, we can also restore a word from a code string. The process of decoding a TSDD means restoring a string of code from the TSDD and then obtaining the corresponding words. After restoring all strings of codes, we can obtain the original dictionary.
Before explaining the decoding algorithm, we first introduce some operations. Given a depth d, we use List(d) to denote the set of all possible TSDDs, that is, the TSDDs representing the possible letters. In Section 4.1, we gave an example of how to represent the word zoo with six variables by using the compact code in a binary way. Now, we continue to use this example to illustrate the decoding process. In addition, the variables denote a null character when both and are assigned the value ’false’. Hence, there are three cases when the depth is 1. , where , , and are TSDDs, and , , and . We also use Letter(F) to denote the letter that the TSDD F represents; that is, is a null character, ‘z’, and ‘o’. Given the word ‘zo’, we stipulate that Push(‘zo’,‘o’) = ‘zoo’ and (‘zoo’) = ‘zo’. We use to denote the max depth in the dictionary. The algorithm is shown in Algorithm 4.
The initial inputs for this algorithm are the TSDD to be decoded, the empty word w, the empty dictionary , and the depth d = 1. Then, we make the operation , where G represents the letter that may appear in the word in order (Lines 1–2). If the result of is not false, we recursively add the next possible letter until we encounter a null character or reach the maximum depth (Lines 3–10). After the algorithm is completed, the dictionary is the result we want.
However, this algorithm is suitable for decision diagrams with fewer variables. We can decode decision diagrams that are encoded in a binary way but not decision diagrams that are encoded in a one-hot way. This is because the time for decoding a decision diagram that is encoded in a one-hot way exceeds one hour when the dictionary includes over 10,000 words. Hence, we need another effective algorithm to decode such decision diagrams. In this study, we did not conduct decoding-related experiments.
| Algorithm 4: Decode |
 |
5. Experimental Results
In this section, we first compare the speed of encoding a dictionary with and without tries to demonstrate the acceleration effect of tries on encoding a dictionary. We then encode 14 dictionaries into BDDs, ZDDs, CBDDs, CZDDs, SDDs, ZSDDs, and TSDDs with tries and compare the node count of decision diagrams and the time required for encoding the dictionaries into decision diagrams. All experiments were carried out on a machine equipped with an Intel Core i7-8086K 4 GHz CPU and 64 GB RAM. We used four encoding methods to conduct all experiments: compact code in a one-hot way, compact code in a binary way, ASCII code in a one-hot way, and ASCII code in a binary way.
The dictionaries we used are the English words in the file /usr/shar/dict/words on a MacOS system with 235,886 words with a length of up to 24 from 54 symbols, a password list with 979,247 words with a length of up to 32 from 79 symbols [10], and other word lists from the website at [11]. To compare the time for encoding dictionaries into TSDDs with and without tries, we separated the first 20,000, 30,000, and 40,000 words from the dictionary words to form four new dictionaries and encoded them into TSDDs. This is because, without the help of a trie, the encoding time would exceed two hours when the number of words exceeds 40,000. We used the same right linear vtree to complete the first experiment. Hence, the size and node count of TSDDs must be the same in this experiment with the same encoding method, and we only compared the encoding time. The results are shown in Table 1.

Table 1.
The time (secs.) for encoding dictionaries with and without tries.
We can see that all the experiments were completed within 10 s with the help of tries for these three dictionaries. When we did not rely on the help of tries, even the minimum encoding time reached 251.86 s (the compact code in a one-hot way for the dictionary with 20,000 words). When the number of words reaches 40,000, it even takes over 1000 s to encode the dictionary, which exceeds the time required for encoding the dictionary with the help of tries by more than a hundred times. It can be inferred that for dictionaries with more words, encoding them will take more time, which we cannot tolerate. Therefore, we can see that tries have excellent acceleration effects when we encode a dictionary, and it is necessary to rely on the help of tries when encoding dictionaries.
Then, the second experiment is as follows. Ref. [1] encoded two dictionaries, words and password, into four decision diagrams, i.e., BDDs, ZDDs, CBDDs, and CZDDs, in four ways and gave the number of nodes of decision diagrams and the encoding times for some data. Here, we use their data and record them in Table 2. For the other 12 dictionaries, they did not conduct any relevant experiments. Therefore, we extended their experiment by encoding the remaining twelve dictionaries into BDDs, ZDDs, CBDDs, and CZDDs in four ways and recording the node count and encoding time. We also encoded the 14 dictionaries into SDDs, ZSDDs, and TSDDs in four ways and then compared all decision diagrams using two categories of benchmarks: node count, the node count of decision diagrams, and time, the time for encoding a dictionary. The initial vtrees are all right linear trees. To reduce the node count of decision diagrams, we designed minimization algorithms for ZSDDs and TSDDs and applied them once to SDDs, ZSDDs, and TSDDs when over half of the words in the dictionary were encoded. The results of this experiment are shown in Table 2. Columns 1–2 report the names of the dictionaries and the word counts of the dictionaries. The names of the decision diagrams that represent the dictionaries are reported in column 3. Then, columns 4–11 report the node counts of decision diagrams and the encoding times using the four encoding methods. In our experiment, each dictionary contained over 100,000 words. In addition, we use ’–’ in place of data if the encoding time exceeded one hour.

Table 2.
The comparison of SDDs, ZSDDs, and TSDDs over 2 categories of benchmarks.
In general, the number of variables used in one-hot encoding is much larger than that in binary encoding, and the Boolean functions encoded in a one-hot way are more sparse than those encoded in a binary way when representing the same dictionary. For each dictionary, the node count of the decision diagram with the minimum node count among all decision diagrams for each encoding method is highlighted in bold so that readers can intuitively see which decision diagram performs the best in node count. We first consider the decision diagrams that are encoded with the compact code in a one-hot way. Taking the dictionary phpbb as an example, we can see that the ZDD and CZDD have the same and minimum node counts, while the CBDD has the second-smallest node count among all decision diagrams. The node count of the CBDD is 344,800, which is just 332 more than that of the BDD and CZDD. The node count of the ZSDD is larger than that of the ZDD, CZDD, and CBDD, and hence, it has the third-smallest node count. The node count of the TSDD is larger than that of the above decision diagrams. However, the node count still does not exceed 1.5 times the minimum value (the node count of ZDD or CZDD), that is, 446,421/344,468 = 1.29 < 1.5. The node counts of the SDD and BDD are much larger than those of the other decision diagrams, and the node count of the SDD is slightly smaller than that of the BDD. Hence, we can conclude that for the node count, among all the decision diagrams, the ZDD and CZDD have the best performance, and the performance of the CBDD, ZSDD, and TSDD is slightly inferior to that of the ZDD and CZDD, while the SDD and BDD perform the worst among all decision diagrams. For the encoding time, the performance of these decision diagrams is similar to that for the node count. We believe that the ZDD and CZDD take the minimum time to encode the dictionary. TSDDs perform worse than ZDDs and CZDDs in encoding time, while they are better than BDDs and SDDs. Although the performance of TSDDs is not very good when we encode in a one-hot way, it is not much worse than the best decision diagrams (ZDDs and CZDDs), and we can tolerate this drawback.
For the other 13 dictionaries, the performance of these decision diagrams for node count and time is similar to that for phpbb. We believe that the Boolean function that represents the dictionary in a one-hot way is a spare Boolean function, which makes the performance of ZDDs, CZDDs, CBDDs, ZSDDs, and TSDDs better than that of SDDs and BDDs. The decision diagrams that are encoded by the ASCII code in a one-hot way include more variables than those that are encoded by the compact code in a one-hot way. Because they are both encoded in a one-hot way, they have similar performance for the node count and encoding time.
For the decision diagrams that are encoded in a binary way, we focus on the performance of TSDDs. We can easily find that TSDDs have the minimum node count among all decision diagrams if we encode the same dictionary in a binary way, regardless of whether we use the compact code or ASCII code. Moreover, the node count of TSDDs may even be much smaller than that of other decision diagrams. For example, the node count of the TSDD that represents dutch-wordlist with the ASCII code in a binary way is 273,022, while the second-smallest node count is 976,921, which is more than 3 times larger than that of the TSDD. Although the encoding time of the TSDD is not the smallest among all decision diagrams, we believe that it is worth taking more time to encode the dictionaries into the TSDD, which has the minimum node count. Hence, we conclude that TSDDs are the most suitable decision diagrams for representing dictionaries in a binary way.
Finally, we make the following conclusions: (1) There is no decision diagram that has the minimum node count and encoding time for all dictionaries with all encoding methods. (2) TSDDs must have the minimum node count if we encode in a binary way, and the node count of TSDDs can be much smaller than those of other decision diagrams. (3) The node count of the TSDD is not more than 1.5 times that of the minimum node count for all dictionaries, except for walk-the-line, if we encode in the one-hot way. (4) Although the encoding time of TSDDs is not the best, for all dictionaries, we can encode them into TSDDs in four ways within half an hour, while it may take more than one hour for some dictionaries if we want to encode them into BDDs or SDDs in a one-hot way. Based on point 1, we find that there is no decision diagram that can perform better than all other decision diagrams in our experiments. Therefore, we need to find a decision diagram that is suitable for representing dictionaries among the seven decision diagrams. Based on points 2 and 3, we believe that, overall, TSDDs have the best performance in terms of the node count among all decision diagrams. Based on point 4, we believe that it is worthwhile to exchange some time for excellent performance in terms of the node count, which means that we intend to take more time to encode dictionaries into a more compact representation. In addition, we know that the number of variables of Boolean functions representing dictionaries encoded in a one-hot way is much larger than that in a binary way. With the increase in the word length, the number of variables will increase quickly. When we need to represent a large number by a Boolean function, a lot of variables are required if we represent it in a one-hot way. If a large number is represented in a binary way, only a small number of variables are required. Too many variables not only make management difficult but also require a lot of space to store. In general, people tend to represent large numbers in a binary way. We can see that TSDDs are the decision diagrams with the minimum node count and a suitable encoding time among the seven decision diagrams. Hence, we believe that TSDDs are more suitable for representing dictionaries.
6. Conclusions
In this paper, we have unified the definitions of semantics and syntax for SDDs, ZSDDs, and TSDDs based on Boolean functions, and our contributions are as follows: (1) We first propose an algorithm that encodes dictionaries into decision diagrams with the help of tries. To transform a dictionary into a decision diagram, we first transform the dictionary into a trie and then compress the trie, which can reduce the nodes of the trie. Then, we transform the trie into a decision diagram. Because we compress the trie, the number of operations on decision diagrams can be effectively reduced, which greatly accelerates the encoding speed. We have demonstrated through experiments that tries are of great help to our algorithm. (2) We then show that TSDDs are the decision diagrams that are more suitable for representing dictionaries. TSDDs had the smallest node count in our experiment when we encoded in a binary way and had a node count that was no more than 1.5 times that of the minimum node count among all decision diagrams in our experiments when we encoded in a one-hot way. In addition, the encoding time of TSDDs did not perform the best among all decision diagrams. However, we believe that it is worthwhile to exchange some encoding time for a smaller number of nodes. Hence, we believe that TSDDs are more suitable for representing dictionaries. (3) We also designed a decoding algorithm that transforms a decision diagram into the original dictionary. However, the decoding algorithm cannot decode decision diagrams encoded in a one-hot way.
By using TSDDs to represent the dictionary, we can complete common operations used on a dictionary with some binary operations on TSDDs. Hence, encoding dictionaries into TSDDs is very meaningful. Our study proposes an algorithm that transforms dictionaries into decision diagrams. However, our algorithm can still be further improved. In the future, we can continue our research in the following three directions: (1) We can search for a more compact way to represent symbols and characters by Boolean functions so as to reduce the number of variables. In this way, we can make the node count of decision diagrams smaller. (2) We can further improve the algorithms for reducing the node count and encoding time. If the node count of decision diagrams can be made small enough and the encoding time can be made short enough, decision diagrams will play a vital role in representing dictionaries. For example, we can use less storage space to store data consisting of symbols and characters by transforming them into decision diagrams. (3) On the other hand, our decoding algorithm needs to be improved so that it can decode decision diagrams encoded in a one-hot way in a short time. We believe that studying how to encode decision diagrams into dictionaries more efficiently will be very valuable in the future.
Author Contributions
Conceptualization, D.Z. and L.F. methodology, D.Z. and L.F.; software, D.Z.; validation, L.F. and Q.G.; formal analysis, Q.G.; investigation, D.Z.; resources, Q.G.; data curation, Q.G.; writing—original draft preparation, D.Z. and L.F.; writing—review and editing, D.Z., L.F. and Q.G.; visualization, D.Z.; supervision, L.F.; project administration, D.Z.; funding acquisition, Q.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Planning Project of Guangdong (2021B0101420003, 2020ZDZX3013, 2023A0505030013, 2022A0505030025, 2023ZZ03), the Science and Technology Planning Project of Guangzhou (202206030007), the Guangdong-Macao Advanced Intelligent Computing Joint Laboratory (2020B1212030003), and the Opening Project of Key Laboratory of Safety of Intelligent Robots for State Market Regulation (GQI-KFKT202205).
Data Availability Statement
Due to the involvement of our research data in another study, we will not provide details regarding where data supporting the reported results can be found.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bryant, R.E. Chain Reduction for Binary and Zero-Suppressed Decision Diagrams. J. Autom. Reason. 2020, 64, 1361–1391. [Google Scholar] [CrossRef]
- Minato, S. Zero-Suppressed BDDs for Set Manipulation in Combinatorial Problems. In Proceedings of the 30th International Design Automation Conference (DAC-1993), Dallas, TX, USA, 14–18 June 1993; pp. 272–277. [Google Scholar]
- van Dijk, T.; Wille, R.; Meolic, R. Tagged BDDs: Combining Reduction Rules from Different Decision Diagram Types. In Proceedings of the 17th International Conference on Formal Methods in Computer-Aided Design (FMCAD-2017), Vienna, Austria, 2–6 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 108–115. [Google Scholar]
- Babar, J.; Jiang, C.; Ciardo, G.; Miner, A. CESRBDDs: Binary decision diagrams with complemented edges and edge-specified reductions. Int. J. Softw. Tools Technol. Transf. 2022, 24, 89–109. [Google Scholar]
- Pipatsrisawat, K.; Darwiche, A. New Compilation Languages Based on Structured Decomposability. In Proceedings of the 23rd AAAI Conference on Artificial Intelligence (AAAI-2008), Chicago, IL, USA, 13–17 July 2008; pp. 517–522. [Google Scholar]
- Shannon, C.E. A Symbolic Analysis of Relay and Switching Circuits. Trans. Am. Inst. Electr. Eng. 1938, 57, 713–723. [Google Scholar] [CrossRef]
- Nishino, M.; Yasuda, N.; Minato, S.I.; Nagata, M. Zero-Suppressed Sentential Decision Diagrams. In Proceedings of the 30th AAAI Conference on Artificial Intelligence (AAAI-2016), Phoenix, AZ, USA, 12–17 February 2016; pp. 1058–1066. [Google Scholar]
- Fang, L.; Fang, B.; Wan, H.; Zheng, Z.; Chang, L.; Yu, Q. Tagged Sentential Decision Diagrams: Combining Standard and Zero-suppressed Compression and Trimming Rules. In Proceedings of the 38th IEEE/ACM International Conference on Computer-Aided Design (ICCAD-2019), Westminster, CO, USA, 4–7 November 2019; pp. 1–8. [Google Scholar]
- Darwiche, A. SDD: A New Canonical Representation of Propositional Knowledge Bases. In Proceedings of the 22nd International Joint Conference on Artificial Intelligence (IJCAI-2011), Catalonia, Spain, 16–22 July 2011; pp. 819–826. [Google Scholar]
- Bryant, R.E. Supplementary Material on Chain Reduction for Binary and Zero-Suppressed Decision Diagrams. 2020. Available online: http://www.cs.cmu.edu/~bryant/bdd-chaining.html (accessed on 5 December 2023).
- SecLists. Available online: https://github.com/danielmiessler/SecLists/tree/master (accessed on 8 December 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).