Abstract
Ambiguous optical illusions have been a paradigmatic object of fascination, research and inspiration in arts, psychology and video games. However, accurate computational models of perception of ambiguous figures have been elusive. In this paper, we design and train a deep neural network model to simulate human perception of the Necker cube, an ambiguous drawing with several alternating possible interpretations. Defining the weights of the neural network connection using a quantum generator of truly random numbers, in agreement with the emerging concepts of quantum artificial intelligence and quantum cognition, we reveal that the actual perceptual state of the Necker cube is a qubit-like superposition of the two fundamental perceptual states predicted by classical theories. Our results finds applications in video games and virtual reality systems employed for training of astronauts and operators of unmanned aerial vehicles. They are also useful for researchers working in the fields of machine learning and vision, psychology of perception and quantum–mechanical models of human mind and decision making.
1. Introduction
Optical illusions have fascinated humans since the ancient times [1,2,3] and served as both object of inspiration in arts [4,5] and paradigmatic topic of research in the fields of psychology and behavioural science [6,7,8,9,10,11,12,13]. Nowadays, when artificial intelligence (AI) is all around, a question arises whether a computer or robotic system can recognise optical illusions similarly to a human. Apart from a blue-skies research goal of creating a humanoid robot that both aesthetically resembles a human and can perceive the world as a human, a practicable model of human perception of optical illusions could revolutionise the way video games and spatial computing systems are designed [14], psychiatric illnesses are studied [15] and the effect of gravitation on cognition is investigated [16,17]. Moreover, establishing the psychological and physiological origin of perception of ambiguous figures promises to unlock the secrets of human decision making [9], also revealing a long-hypothesised but yet elusive link between human mental states and quantum mechanics [8,9,18,19,20,21,22,23].
We consider the Necker cube [2] shown in Figure 1a. A simple self-examination aimed to answer the question ‘Is the shaded face of the cube at the front or at the rear?’ results in a series of possible interpretations that randomly switch between ‘front’ and ‘rear’. When the sequence of the observed front–rear states, which in the following we denote as and , is recorded as a function of time as schematically shown in Figure 1b, one obtains a signal consisting of rectangular pulses of random duration. The temporal dynamics of the pulses will vary from one self-examination to another since the perception of optical illusions depends on the observer’s age and gender [24]. However, the general trend illustrated in Figure 1b is similar for all observers.
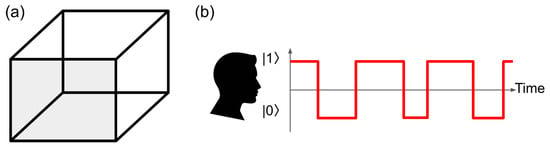
Figure 1.
(a) The Necker cube. The answer to the question ‘Is the shaded face of the cube at the front or at the rear?’ changes suddenly depending on the observer’s perception, giving rise to a series of rectangular pulses corresponding to the front, , and rear, , perceptual states of the cube shown in panel (b).
On the other hand, electroencephalograms recorded consistently with subjective inputs given by observers of the Necker cube and other ambiguous figures [25,26,27] suggest that the perception does not undergo an abrupt switching as sketched in Figure 1b but exhibits a rather continuous oscillation-like behaviour between the and states. Data speaking in favour of such a behaviour were also obtained in eye-tracking experiments, where both blink and movement of eye were associated with a perceptual reversal [6,28,29].
These experimental results indicate that the perceptual state may not exactly be or state but their combination. Mathematically, this scenario can be described as a superposition of and [9]. This intriguing observation has motivated the attempts to apply the methods of quantum mechanics and quantum computing to the analysis of human perception [9,21,30,31].
A quantum computer uses a quantum bit (qubit) that can be in states and . These states are analogous to the ‘0’ and ‘1’ binary states of a classical digital computer. However, a qubit exists in a continuum of states between and , i.e., its states are a superposition with .
When a quantum measurement is performed, a closed qubit system interacts in a controlled way with an external system from which the state of the qubit under measurement can be recovered. For example, using projective measurement operators and [32], the measurement probabilities for are and , which means that the qubit is in one of its basis states. Such a projective measurement can be visualised using the concept of the Bloch sphere where the qubit is projected on one of the coordinate axes (e.g., z-axis in Figure 2a).
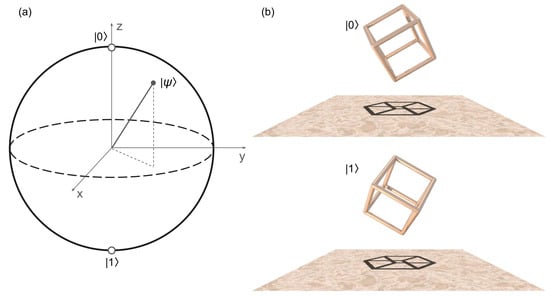
Figure 2.
(a) Projective measurement of a qubit. (b) Projective qubit-like measurement applied to the Necker cube. The two-dimensional shadows of the cubes are identical and perceived by an observer as an ambiguous Necker cube. Considering the shadows as a qubit-like superposition of and , we virtually project the shadows back to the three-dimensional space to obtain an unambiguous cube that corresponds to one of the basis states.
Computational algorithms based on measurements of the states of a qubit are exponentially faster than any possible deterministic classical algorithm [32]. Subsequently, it has been demonstrated that quantum mechanics can explain certain psychological and decision-making processes better than any classical model [9,31,33,34]. A large and growing body of research has provided significant evidence speaking in favour of this hypothesis [8,21,22,34,35,36,37,38,39,40,41,42,43,44,45,46,47].
In Figure 2b that was rendered using the physical ray-tracing software POV-Ray 3.7, we illustrate how the principle of projective qubit measurement can be generalised to the Necker cube. The two-dimensional (bottom) images in Figure 2b are the shadows cast by the three-dimensional cubes. However, while the three-dimensional cubes are visually different, the shadows cast by them are identical. Yet, the shadows are an ambiguous Necker cube with the alternating left and right faces (this can be seen by observing them for 5–10 s; some observers may also need to blink to notice the optical illusion [48]). Drawing an analogy with the projective measurement pictured in Figure 2a, in Figure 2b we consider the shadows as a qubit-like superposition of the two fundamental perceptual states of the cube and we virtually project these images back to the three-dimensional space to obtain an unambiguous (either or basis state) image of the cube.
It is noteworthy that the application of the concepts of qubit and superposition does not imply the existence of quantum processes in a biological brain. In fact, the analogy with a qubit serves as a mathematical model that can adequately describe the experimental data. At the same time, an ultimate verification of the accuracy of the quantum models is not practicable due to technical immaturity and high cost of quantum computers and adjacent technologies. Yet, from the neurobiological point of view, an idealised experiment would also include measurements conducted with a brain–computer interface that can decipher the human ‘thoughts’. Clearly, such complex tests are not yet feasible and they also raise ethics concerns.
Subsequently, much of the current research in this area has focused on artificial neural network modelling and digital twins of perception of optical illusions [25,49,50,51,52,53,54,55]. Some of these works have employed experimental electroencephalogram (EEG) and magnetoencephalography (MEG) data as the signals that are processed using a neural network model and then classified and correlated with experimental perceptual states of ambiguous figures [25,53,54,55]. In turn, works [50,51,56] have focused on the analysis of the dynamics of perception of the images of ambiguous figures using neural network architectures that exhibit chaotic behaviour. However, the results obtained in ref. [51] reproduce the results obtained in classical models of bistable perception, i.e., they do not predict any superposition of the two possible perceptual states of the Necker cube (quantum mechanical models of cognition and perception were not widely accepted when paper [51] was published). On the other hand, although paper [56] does not discuss the perception of ambiguous figures, the neural network model proposed in it reveals a possibility of superposition of two states in principle.
However, despite the advent of quantum mechanical models of perception and the previous attempts to study ambiguous figures using neural network algorithms, there have been no demonstrations of quantum neural network models of optical illusions. The concept of quantum neural networks has become an active topic of scientific research relatively recently owing to increasing maturity of quantum technologies [57,58,59,60,61]. Nevertheless, quantum neural network architectures have immediately demonstrated a number of advantages over the classical networks, including higher accuracy of outputs produced using just several qubits [62,63,64,65]. Thus, it is plausible that quantum neural network models of optical illusions will also outperform their classical counterparts.
Hence, in this present work, we construct a deep neural network that uses a quantum random generator to define the weights of the neural connections and we exploit it to model the perception of ambiguous figures. We demonstrate that the so-designed computational algorithm reproduces the hypothesised superposition of the possible perceptual states of the Necker cube. We also show that these results qualitatively agree with the predictions of a recently proposed quantum oscillator model of optical illusions [14].
Broadly speaking, the results presented in this paper may be used to enhance the ability of quantum neural networks to recognise and generate images of similarly looking human faces and fashion items [66,67], also being useful in the analysis of patterns of financial behaviours [68]. For example, optical illusion called #theDress has become a subject of scientific research in the fields neuroscience and vision science [69] following a viral online dispute between people who believed that the dress was blue and black and people who perceived its colours as white and gold. The quantum neural network model presented in this work should be applicable to #theDress because recent research works have also revealed that both #theDress and Necker cube are ambiguous figures [70].
The remainder of this paper is organised as follows. In Section 2, we present a detailed theoretical and technical discussion of the deep neural network algorithm proposed in this work. Then, in Section 3 we introduce a quantum oscillator model of perception of ambiguous figures. Then, in Section 4 we conduct a detailed comparative analysis of the results obtained using the neural network and the quantum oscillator model. Finally, we demonstrate the potential of our model to solve a wide range of practical problems.
2. Deep Neural Network Algorithm
The architecture of the neural network used in this work is illustrated in Figure 3. The network consists of an input layer that has input nodes, three hidden layers each of which has nodes and an output layer that has output nodes that are used to classify the perceptual state of the Necker cube. The weights of the connections of the network are updated using a cross-entropy-driven back-propagation algorithm [71,72]. The learning rate parameter used in all computations is .
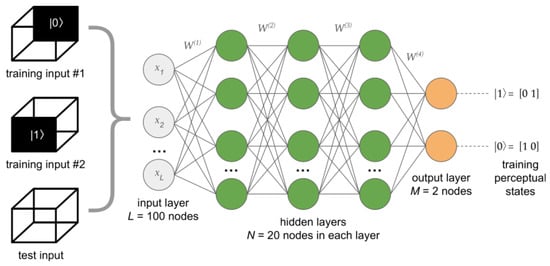
Figure 3.
Sketch of the deep neural network architecture used to model the perception of the Necker cube. The network consists of an input layer, three hidden layers and an output layer that has two nodes. Labels with denote the matrices of the weights of network connections. The network is trained using the images of the Necker cube with the shaded front and rear faces that correspond to and training states, respectively. Characters ‘’ and ‘’ are not part of the training images. The test input is an image of the ambiguous Necker cube. All input images consist of a total of 100 pixels. Individual pixels of each image form input vector with .
The activation function of the nodes of the hidden layers is represented by the Rectified Linear Unit (ReLU) that can be defined as [71,72]
where is the index denoting the sequential number of the input node and is the output from this node. As the activation function of the output nodes we choose the Softmax function that accounts not only for the weighted sum of the inputs to the given node but also for the inputs to the other output nodes [71,72]. This function is
where is the weighted sum of the input signals to the ith output node and M is the total number of the output nodes. The use of Equation (2) enables satisfying probability normalisation condition .
The network is trained using the following procedure [72]:
- Construct two output nodes that correspond to and perceptual states of the Necker cube;
- Initialise the weights of the neural network in the range from −1 to 1 using a random number generator;
- Enter input data and corresponding training data that encode the perceptual states of the Necker cube (the top and the middle illustrations on the left of Figure 3);
- Calculate error between output and target as ;
- Propagate output in the backward direction of the network and compute respective parameters of the hidden nodes using equations and , where index n denotes the sequential number of the hidden layer, prime denotes the derivative of the activation function and is the transpose of the matrix of weights corresponding to each relevant layer of the network.
- Repeat Step 5 until the back-propagation algorithm reaches the first hidden layer;
- Update the weights using learning rule , where are the weights between output node i and input node j of the nth layer and ;
- Repeat Steps 4–7 for all values of the training data set;
- Repeat Steps 4–8 until the neural network is trained with desired accuracy.
The exploitation process essentially reproduces Steps 1–3 [72]. We establish that it suffices to use 1000 epochs to obtain convergent results in all calculations.
The physical processes underpinning the dynamics of switching between the perceptual states of ambiguous figures remains a subject of debate [7,73]. One of the currently accepted theories suggests that the switching is likely to be explained by chaotic processes observed in nonlinear dynamical systems [51,56,74,75,76]. Indeed, broadly speaking, the brain is a dynamical system that exhibits a complex nonlinear and chaotic behaviour at multiple levels [77,78,79]. Subsequently, it is plausible that certain highly nonlinear and chaotic physical system can approximate the behaviour of a brain at least in principle [80].
To implement a chaotic dynamical behaviour in our model, we employ a quantum physical generator of random numbers [81,82] to define matrices that contain the weights of the connections of the neural network. Unlike the output of a pseudo-random generator such as the one described in ref. [83], a quantum generator produces truly random numbers [81,82]. In our model, this property implies that the neural network is not biased towards one of the possible perceptual states of the Necker cube and that its predictions do not repeat in time [84,85]. Furthermore, as with the purely classical neural network models [51,56], our quantum random generator-based neural network exhibits a truly chaotic dynamical behaviour [86] and therefore can be considered to be a chaos-driven system [51,56].
As illustrated in Figure 4, we first randomly generate , then we train the network on the data corresponding to the Necker cubes with the shaded faces, and then we exploit the trained neural network to predict the perceptual state of the ambiguous Necker cube. This procedure is repeated in a loop to plot the perceived states of the cube as a function of time.
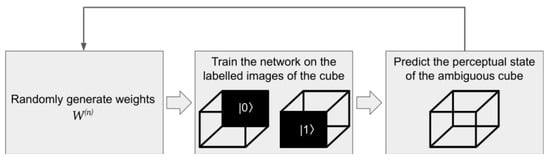
Figure 4.
Sketch of the recurring computation procedure that involves the generation of the connection weights using a random generator, training of the network and its exploitation to predict the perceptual state of the Necker cube. Characters ‘’ and ‘’ are not part of the training images.
Results: Predictions of the Neural Network Model
Figure 5 shows the prediction by the neural network model obtained as a result of 100 consecutive runs of the algorithm outlined in Figure 4. The states of the output nodes of the neural network were recorded at the end of each computational run and the respective results were plotted as a function of time (in arbitrary units). Therefore, every pair of data points that constitute the curves in Figure 5 was obtained using a unique initial set of neural weights obtained from a truly random quantum physical system [81,82].
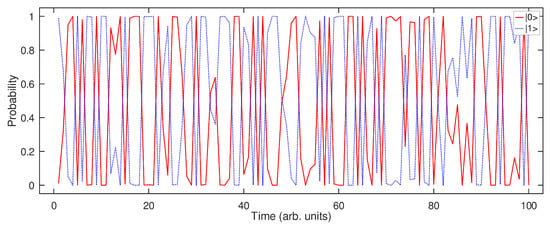
Figure 5.
Perceptual switching curves simulated by the neural network model using quantum random neural connection weights. The data produced by the two output nodes of the network are plotted using the solid and dotted curves, respectively. The data points with probability or correspond to the fundamental perceptual states of the Necker cube. The remaining data points are in a superposition of states and with .
We can observe a time-dependent switching between the two possible classical perception states of the cube that correspond to probability values zero and one on the y-axis of Figure 5. Importantly, the pattern of switching between one fundamental perceptual state to another is not abrupt, as often depicted in the literature and schematically shown in Figure 1b of this paper, but it involves certain intermediate states that are a superposition of the fundamental states.
Thus, the data produced by the neural network model speak in favour of plausibility of the previous theoretical results [9] and experimental evidence [25,26,27] demonstrating that the actual perception state is a superposition of the two fundamental states, and , of the Necker cube. Moreover, this result aligns with the current understanding of optical illusions and adjacent phenomena from the point of view of neuroscience. In fact, in the last four decades, many authors demonstrated that the perception of the Necker cube can be modelled as a continuous dynamical system subjected to random fluctuations [12,41,52,87,88,89,90,91,92,93,94,95]. Some of those approaches approximate the perception, drawing an analogy with physical wave-like phenomena where phase processes play a role [96] but the states of the model dynamical system gradually change in time.
Similar results were obtained using a quantum oscillator model of perception of ambiguous figures. In the following section, we overview the algorithm of that model and then compare its predictions with the result shown in Figure 5.
3. Quantum Oscillator Model of Perception of Ambiguous Figures
We model the dynamics of perception of the Necker cube using a harmonic motion of an electron trapped in a parabolic potential well (Figure 6a). This model is inspired by the quantum mechanical approach to human cognition proposed in ref. [9] and it captures the complex pattern of perception of the Necker cube [14].
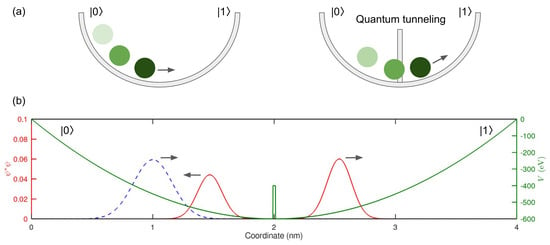
Figure 6.
(a) An electron trapped in a parabolic well behaves as a harmonic oscillator and it can pass through a barrier due to the quantum tunnelling effect. The arrows indicate the direction of movement. (b) Illustrative example (numerical simulation) of quantum tunnelling through a barrier. The dashed line denotes an snapshot of the incident Gaussian pulse. The solid line denotes the snapshots of the portions of the pulse that are reflected from and transmitted through the barrier (the green line, right y-axis). The labels and correspond to the perceptual states of the Necker cube. The arrows indicate the direction of propagation of the pulses with respect to the barrier.
A classical mechanics counterpart of this model is a small ball that rolls back and forth inside a bowl. While the ball does not have enough energy to surmount or penetrate a physical barrier inside the bowl, the electron may pass through the barrier due to the quantum tunnelling effect (Figure 6a).
We model the quantum tunnelling effect by solving the Schrödinger equation in a one-dimensional space [97],
where is a wave function, i is the imaginary unit, m is the mass of the electron, ℏ is Plank’s constant and is the parabolic potential well profile. We numerically solve Equation (3) using a finite-difference time-domain (FDTD) method [98] that represents the wave function as . We obtain
Representing coordinate x and time t as the vectors of discrete elements and , respectively, where k and n are integer numbers, and applying the Courant stability criterion [98], we define
Thus, a spatio-temporally discretised Equation (4) becomes
We model the electron as a Gaussian energy wave packet:
where is the wavelength, is the width of the Gaussian pulse and is the spatial coordinate of origin of the pulse. The amplitudes of the wave functions are normalised as
The probabilities of funding the electron in the and regions of the potential well are calculated as
where .
Using model parameters m, m and m, in Figure 6b we present the results of modelling of the electron tunnelling through a potential barrier. Calculating the modulus square of the wave function, we obtain the probability density of finding the electron at a certain position in the parabolic potential well. We can see that one part of the incident wave packet is reflected from the barrier but another part is transmitted through it. We label the left and right side of the parabolic potential well as and and associate them with the possible perceptual states of the Necker cube. In this particular demonstration simulation scenario, we obtain and .
Results: Predictions of the Quantum Oscillator Model
Figure 7 shows the results produced by the quantum oscillator model. We consider a single parabolic well (Figure 7a.i) and a double parabolic well with a barrier formed by two overlapping parabolic wells (Figure 7b.i). Assuming that the energy packet that represents the electron originates from the left side of the potential well (this corresponds to a visual cue to the cube orientation [9]), we simulate the dynamics of the oscillator in the time interval from 0 to 200 arbitrary units (these arbitrary units are different from those used in the neural network model). The result of this simulation is plotted in Figure 7a.ii, where the probability of finding the electron in the and regions of the potential well are denoted by the solid and dotted curves, respectively. The result of the simulation of the double parabolic well is presented in Figure 7b.ii.
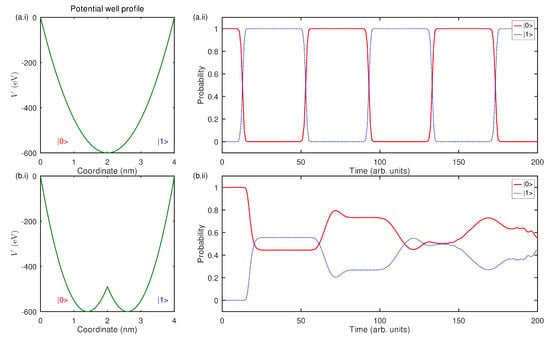
Figure 7.
(a) A single parabolic potential well model and the Necker cube perception switching predicted by it. (b) The respective double parabolic model with a barrier and its predictions. In both panels, labels and denote the fundamental perceptual states of the Necker cube. The time units used in this figure are different from those in Figure 5.
4. Discussion
4.1. Neural Network Model versus Quantum Oscillator Model
In Figure 7a.ii, we can see that the quantum oscillator model with a single potential well predicts a periodic switching between the two fundamental perceptual states, with a quick but not instantaneous change from one fundamental perceptual state to another. This result is in good agreement with the prediction of the previous quantum mechanical models proposed, for example, in Refs. [9,21], and it implies the existence of a superposition of the fundamental perceptual states. Qualitatively similar results are also predicted by the neural network, which can be seen in Figure 5 in the time intervals from approximately to .
Furthermore, a periodic switching between the two fundamental perceptual states predicted by the neural network model alternates with the periods of irregular switching between these states (e.g., from to approximately in Figure 5). This behaviour is qualitatively reproduced by the quantum oscillator model that uses the double periodic well with the barrier (Figure 7b.ii). We note that the time units used in the quantum oscillator model are different from those used in the neural network model, which means that the timescale of alternations between the perceptual states is different in these two models. This difference is inconsequential for the current discussion and, if needed, it can be eliminated using a different profile of the parabolic potential wells.
Thus, we conclude that the quantum oscillator model can reproduce the predictions of the neural network model provided that the outputs of the single and double parabolic potential well oscillators are combined together, which can be achieved, for example, by coupling them into a chain oscillator. While the discussion of an implementation of this approach is beyond the scope of this paper, the similarity of the outputs of the neural network model and the quantum oscillator model has a clear physical meaning: both models are dynamical systems that operate according to the fundamental laws of quantum mechanics [99,100,101].
Moreover, the results obtained using the neural network model speak in favour of the hypothesis that originates from the quantum oscillator model and that suggests that the phase change in the response of the dynamical system has the effect of eye blinking, an action known to induce a reversal of the perceptual state of the Necker cube [11,14,48]. Although this hypothesis has not been verified yet, it is known that the dynamics of eye blinks can be studied using the methods developed to investigate highly nonlinear and chaotic processes [102,103,104]. Hence, since the neural network model employs data produced by a generator of truly random numbers, its predictions should be consistent with the dynamics of the eye blink [84,105].
It is plausible that one can obtain, at least in principle, a quantitative agreement between two or more different models. However, such a comparison must be preceded by research aimed to compare the outcomes of a particular theoretical model with experimental psychological or neurobiological data. Although several attempts to conduct such studies have been undertaken (see, e.g., refs. [106,107,108]), a comprehensive validation of different models against the same experimental dataset is yet to be carried out.
4.2. Potential Applications in Artificial Intelligence and Virtual Reality Systems
The proposed neural network algorithm can be used as a model of optical illusions in filmmaking, architecture design and game development [4,109,110]. For example, the video game Superliminal uses forced perspective techniques that manipulate human visual perception to make an object appear larger or smaller than it actually is [111]. Typically, the design of such games requires an input from psychologists and experts in vision science, yet relying on subjective feedback provided by testers and professional video games players. The application of the model proposed in this work can help reduce the impact of subjectivity from game design procedures.
The models proposed in this work can be used in an advanced machine vision system intended to simulate the human perception and decision making. In particular, the so-designed machine vision system may be tasked to play a video game such as Superliminal and its actions can be compared with the actions of a human operator, providing a valuable feedback for engineers, neuroscientists and psychologists. Intriguingly, a number of recent research works have demonstrated that the psychological perception of game scenarios can also be modelled using the laws of physics [112]. Subsequently, the outcomes if this work can help improve deep learning models developed to play video games like a human [113,114].
The neural network model of optical illusions can be used to study the impact of weightlessness on the ability of astronauts to undertake complex tasks during and after spaceflights. On Earth, the majority of observers of ambiguous figures such as the Necker cube perceive one interpretation more often than the other. However, in weightlessness, this asymmetry gradually disappeared and, after spending several months in orbit, both interpretations have the same occurrence [16,17]. At present, such studies rely on experimental data that are often obtained in microgravity conditions or provided by individuals who experiences the effect of microgravity [115]. It is plausible that a virtual reality system that simulate the effect of microgravity on the ability of humans to perceive optical illusions will improve the fidelity of experimental results by reducing the effect of subjectivity. Such virtual reality systems can also enable anyone to experience the world thought the eyes of an astronaut.
The operation of unmanned aerial vehicles (UAVs), commonly known as drones, is another area where models of optical illusions may help extend the abilities of both humans and AI. For example, at present, the skills of human race drone operators significantly exceed the performance of the most advanced machine vision algorithms [116]. A better understanding of the ability of a human pilot to select appropriate motor commands from highly dynamic visual information may provide key insights for solving current challenges in vision-based autonomous navigation.
Yet, the neural network model of optical illusions can be used to validate certain neuroscience and psychological perception theories that are complimentary to the quantum mind hypothesis [117,118]. According to some mainstream theories, our subjective perception of the world is unitary coherent [119]. Here, unitary means that we perceive one interpretation at a time (e.g., one of the two possible states of the Necker cube) rather than a blur of the possible interpretations (i.e., we never see the two possible states of the cube together). In turn, coherent means that we perceive scenes that do not contain contradictory parts (e.g., we do not see a part of one cube and a part of another one at the same time).
However, such an intuitive approach contradicts the theories of optimal decision making and Bayesian brain [117,118]. These theories suggest that an optimal decision can be made only integrating the utility of all actions while considering all possible interpretations of sensory data.
To verify these alternative theories, a video game involving two scenarios was designed [119], where the players were first trained in a visually unambiguous scenario and then they played the same game but in an optical illusion scene that involved an image of the Necker cube. The proposed neural network model can be integrated with that game to address the weaknesses of the experiment identified in ref. [119].
5. Conclusions
This paper demonstrates the potential of a deep neural network algorithm powered by a quantum random number generator to simulate the human perception of optical illusions exemplified by the Necker cube. The results produced by the quantum neural network indicate that observers are likely to perceive a superposition of the fundamental perceptual states of the cube.
This finding aligns with the emerging psychology theories suggesting that certain psychological phenomena can be adequately described using such quantum mechanical concepts as qubit, superposition of states and projective measurement. In particular, we compare the results produced by the neural network with the predictions of a recently proposed quantum oscillator model of optical illusions and we establish that both models consistently predict a qubit-like superposition of perceptual states.
The proposed neural network model can be used in various AI systems ranging from video games and virtual reality and metaverse products, also being a useful tool for psychological and neuroscience studies. It can also be utilised to train astronauts and operators of UAVs to perform in visually challenging environments.
From the methodological point of view, the algorithm presented in this work is unique in terms of combining the emergent concept of quantum neural networks with quantum mechanical models of human mind and perception. This model can be further modified by incorporating the elements of biologically inspired artificial neural networks designed to understand certain functions of the brain [52,80,120]. Yet, the proposed quantum neural network architecture should be of interest to experts in machine learning and machine vision, which are the fields where quantum neural networks play an increasingly important role [121].
Finally, the images of the Necker cube can be used to test the performance of advanced neural network architectures such as reservoir computing (RC) systems [80,122,123,124]. Usually, RC systems are validated using nonlinear and chaotic time series, including Mackey–Glass time series and the Lorenz attractor [125,126]. Quantum RC systems are expected to forecast chaotic time series more efficiently than their classical counterparts [65], which means that more challenging test problems are needed. Therefore, since quantum RC systems are also efficient in completing complex classification tasks [65], a computational problem involving the recognition of the Necker cube and other ambiguous figures should be suitable for testing the performance of novel quantum RC algorithms.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The computational code of the neural network used in this work can be found at https://github.com/IvanMaksymov/DeepNeuralNecker (accessed on 8 January 2024).
Acknowledgments
The author acknowledges useful discussions with Ganna Pogrebna.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| artificial Intelligence | AI |
| electroencephalogram | EEG |
| finite-difference time-domain | FDTD |
| magnetoencephalography | MEG |
| rectified linear unit | ReLU |
| reservoir computing | RC |
| unmanned aerial vehicle | UAV |
References
- Shapiro, A.G.; Todorovic, D. The Oxford Compendium of Visual Illusions; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Necker, L.A. Observations on some remarkable optical phenomena seen in Switzerland; and on an optical phenomenon which occurs on viewing a figure of a crystal or geometrical solid. Lond. Edinb. Philos. Mag. J. Sci. 1832, 1, 329–337. [Google Scholar]
- Washburn, M.; Reagan, C.; Thurston, E. The comparative controllability of the fluctuations of simple and complex ambiguous perspective figures. Am. J. Psychol. 1934, 46, 636–638. [Google Scholar] [CrossRef]
- Fisher, G.H. Ambiguous figure treatments in the art of Salvador Dali. Percept. Psychophys. 1967, 2, 328–330. [Google Scholar] [CrossRef]
- Lindstrøm, T.C.; Kristoffersen, S. ‘Figure it out!’ Psychological perspectives on perception of migration period animal art. Nor. Archaeol. Rev. 2001, 34, 65–84. [Google Scholar] [CrossRef]
- Long, G.M.; Toppino, T.C. Enduring interest in perceptual ambiguity: Alternating views of reversible figures. Psychol. Bull. 2004, 130, 748–768. [Google Scholar] [CrossRef]
- Kornmeier, J.; Bach, M. The Necker cube–an ambiguous figure disambiguated in early visual processing. Vision Res. 2005, 45, 955–960. [Google Scholar] [CrossRef]
- Conte, E.; Khrennikov, A.Y.; Todarello, O.; Federici, A.; Mendolicchio, L.; Zbilut, J.P. Mental states follow quantum mechanics during perception and cognition of ambiguous figures. Open Syst. Inf. Dyn. 2009, 16, 1–17. [Google Scholar] [CrossRef]
- Busemeyer, J.R.; Bruza, P.D. Quantum Models of Cognition and Decision; Oxford University Press: New York, NY, USA, 2012. [Google Scholar]
- Stonkute, S.; Braun, J.; Pastukhov, A. The role of attention in ambiguous reversals of structure-from-motion. PLoS ONE 2012, 7, e37734. [Google Scholar] [CrossRef]
- Kornmeier, J.; Bach, M. Ambiguous figures—What happens in the brain when perception changes but not the stimulus. Front. Hum. Neurosci. 2012, 6, 51. [Google Scholar] [CrossRef]
- Runnova, A.E.; Hramov, A.E.; Grubov, V.V.; Koronovskii, A.A.; Kurovskaya, M.K.; Pisarchik, A.N. Theoretical background and experimental measurements of human brain noise intensity in perception of ambiguous images. Chaos Solitons Fractals 2016, 93, 201–206. [Google Scholar] [CrossRef]
- Meilikhov, E.Z.; Farzetdinova, R.M. Bistable perception of ambiguous images: Simple Arrhenius model. Cogn. Neurodyn. 2019, 13, 613–621. [Google Scholar] [CrossRef] [PubMed]
- Maksymov, I.S.; Pogrebna, G. Linking physics and psychology of bistable perception using an eye blink inspired quantum harmonic oscillator model. arXiv 2023, arXiv:2307.08758. [Google Scholar] [CrossRef]
- Basar-Eroglu, C.; Mathes, B.; Khalaidovski, K.; Brand, A.; Schmiedt-Fehr, C. Altered alpha brain oscillations during multistable perception in schizophrenia. Int. J. Psychophysiol. 2016, 103, 118–128. [Google Scholar] [CrossRef]
- Yamamoto, S.; Yamamoto, M. Effects of the gravitational vertical on the visual perception of reversible figures. Neurosci. Res. 2006, 55, 218–221. [Google Scholar] [CrossRef]
- Clément, G.; Allaway, H.C.M.; Demel, M.; Golemis, A.; Kindrat, A.N.; Melinyshyn, A.N.; Merali, T.; Thirsk, R. Long-duration spaceflight increases depth ambiguity of reversible perspective figures. PLoS ONE 2015, 10, e0132317. [Google Scholar] [CrossRef] [PubMed]
- Khrennikov, A. Quantum-like brain: “Interference of minds”. Biosystems 2006, 84, 225–241. [Google Scholar] [CrossRef]
- Mindell, A. Deep Democracy Exchange. Quantum Mind: The Edge Between Physics and Psychology. 2012. [Google Scholar]
- Wendt, A. Quantum Mind and Social Science; Cambridge University Press: Cambidge, UK, 2015. [Google Scholar]
- Atmanspacher, H.; Filk, T. A proposed test of temporal nonlocality in bistable perception. J. Math. Psychol. 2010, 54, 314–321. [Google Scholar] [CrossRef]
- Aerts, D.; Arguëlles, J.A. Human perception as a phenomenon of quantization. Entropy 2022, 24, 1207. [Google Scholar] [CrossRef]
- Kauffman, S.A.; Roli, A. What is consciousness? Artificial intelligence, real intelligence, quantum mind and qualia. Biol. J. Linn. Soc. 2022, 139, 530–538. [Google Scholar] [CrossRef]
- Lo, C.; Dinov, I. Investigation of optical illusions on the aspects of gender and age. UCLA USJ 2011, 24. [Google Scholar]
- Gaetz, M.; Weinberg, H.; Rzempoluck, E.; Jantzen, K.J. Neural network classifications and correlation analysis of EEG and MEG activity accompanying spontaneous reversals of the Necker cube. Cogn. Brain Res. 1998, 6, 335–346. [Google Scholar] [CrossRef] [PubMed]
- Piantoni, G.; Romeijn, N.; Gomez-Herrero, G.; Van Der Werf, Y.D.; Van Someren, E.J.W. Alpha power predicts persistence of bistable perception. Sci. Rep. 2017, 7, 5208. [Google Scholar] [CrossRef] [PubMed]
- Joos, E.; Giersch, A.; Hecker, L.; Schipp, J.; Heinrich, S.P.; van Elst, L.T.; Kornmeier, J. Large EEG amplitude effects are highly similar across Necker cube, smiley, and abstract stimuli. PLoS ONE 2020, 15, e0232928. [Google Scholar] [CrossRef] [PubMed]
- Choi, W.; Lee, H.; Paik, S.B. Slow rhythmic eye motion predicts periodic alternation of bistable perception. bioRxiv 2020. [Google Scholar] [CrossRef]
- Matsumiya, K.; Furukawa, S. Perceptual decisions interfere more with eye movements than with reach movements. Commun. Biol. 2023, 6, 882. [Google Scholar] [CrossRef]
- Atmanspacher, H.; Filk, T. The Necker-Zeno model for bistable perception. Top. Cogn. Sci. 2013, 5, 800–817. [Google Scholar] [CrossRef]
- Pothos, E.M.; Busemeyer, J.R. Quantum Cognition. Annu. Rev. Psychol. 2022, 73, 749–778. [Google Scholar] [CrossRef]
- Nielsen, M.; Chuang, I. Quantum Computation and Quantum Information; Oxford University Press: New York, NY, USA, 2002. [Google Scholar]
- Pothos, E.M.; Busemeyer, J.R. A quantum probability explanation for violations of ‘rational’ decision theory. Proc. R. Soc. B 2009, 276, 2171–2178. [Google Scholar] [CrossRef]
- Benedek, G.; Caglioti, G. Graphics and Quantum Mechanics–The Necker Cube as a Quantum-like Two-Level System. In Proceedings of the 18th International Conference on Geometry and Graphics, Milan, Italy, 3–7 August 2019; Cocchiarella, L., Ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 161–172. [Google Scholar]
- Yukalov, V.I.; Sornette, D. Entanglement production in quantum decision making. Phys. At. Nucl. 2010, 73, 559–562. [Google Scholar] [CrossRef][Green Version]
- Trueblood, J.S.; Busemeyer, J.R. A quantum probability account of order effects in inference. Cogn. Sci. 2011, 35, 1518–1552. [Google Scholar] [CrossRef]
- De Castro, A. On the quantum principles of cognitive learning. Behav. Brain Sci. 2013, 36, 281–282. [Google Scholar] [CrossRef]
- Martin, F.; Carminati, F.; Carminati, G.G. Quantum information theory applied to unconscious and consciousness. NeuroQuantology 2013, 11, 16–33. [Google Scholar] [CrossRef]
- Aerts, D.; Sozzo, S.; Tapia, J. Identifying quantum structures in the Ellsberg paradox. Int. J. Theor. Phys. 2014, 53, 3666–3682. [Google Scholar] [CrossRef]
- Khrennikova, P. A Quantum Framework for ‘Sour Grapes’ in Cognitive Dissonance. In Proceedings of the Quantum Interaction, Filzbach, Switzerland, 30 June–3 July 2014; Atmanspacher, H., Haven, E., Kitto, K., Raine, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 270–280. [Google Scholar]
- Conte, E.; Licata, I.; Alelú-Paz, R. A quantum neurological model of perception-cognition and awareness in ambiguous figures and the case of the Dalmatian dog. J. Behav. Brain Sci. 2015, 5, 61407. [Google Scholar] [CrossRef][Green Version]
- Broekaert, J.; Basieva, I.; Blasiak, P.; Pothos, E.M. Quantum-like dynamics applied to cognition: A consideration of available options. Philos. Trans. A Math. Phys. Eng. Sci. 2017, 375, 20160387. [Google Scholar] [CrossRef] [PubMed]
- Gronchi, G.; Strambini, E. Quantum cognition and Bell’s inequality: A model for probabilistic judgment bias. J. Math. Psychol. 2017, 78, 65–75. [Google Scholar] [CrossRef]
- Khrennikov, A.; Basieva, I.; Pothos, E.M.; Yamato, I. Quantum probability in decision making from quantum information representation of neuronal states. Sci. Rep. 2018, 8, 16225. [Google Scholar] [CrossRef]
- Rosen, S.M. The strange nature of quantum perception: To see a photon, one must be a photon. J. Mind Behav. 2021, 42, 229–270. [Google Scholar]
- Kovalenko, T.; Sornette, D. The Conjunction Fallacy in Quantum Decision Theory. In Credible Asset Allocation, Optimal Transport Methods, and Related Topics; Sriboonchitta, S., Kreinovich, V., Yamaka, W., Eds.; Springer: Cham, Switzerland, 2022; pp. 127–183. [Google Scholar]
- Ozawa, M.; Khrennikov, A. Application of theory of quantum instruments to psychology: Combination of question order effect with response replicability effect. Entropy 2020, 22, 37. [Google Scholar] [CrossRef]
- Ang, J.W.A.; Maus, G.W. Boosted visual performance after eye blinks. J. Vis. 2020, 20. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; McClelland, J.L. The Appeal of Parallel Distributed Processing. In Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Foundations; MIT Press: Cambridge, MA, USA, 1987; pp. 3–44. [Google Scholar]
- Inoue, M.; Nakamoto, K. Dynamics of cognitive interpretations of a Necker cube in a chaos neural network. Prog. Theor. Phys. 1994, 92, 501–508. [Google Scholar] [CrossRef][Green Version]
- Buesing, L.; Bill, J.; Nessler, B.; Maass, W. Neural dynamics as sampling: A model for stochastic computation in recurrent networks of spiking neurons. PLoS Comput. Biol. 2011, 7, e1002211. [Google Scholar] [CrossRef] [PubMed]
- Noest, A.J.; van Wezel, R.J.A. Dynamics of temporally interleaved percept-choice sequences: Interaction via adaptation in shared neural populations. J. Comput. Neurosci. 2012, 32, 177–195. [Google Scholar] [CrossRef] [PubMed]
- Araki, O.; Tsuruoka, Y.; Urakawa, T. A neural network model for exogenous perceptual alternations of the Necker cube. Cogn. Neurodyn. 2020, 14, 229–237. [Google Scholar] [CrossRef]
- Batmanova, A.; Kuc, A.; Maksimenko, V.; Savosenkov, A.; Grigorev, N.; Gordleeva, S.; Kazantsev, V.; Korchagin, S.; Hramov, A.E. Predicting perceptual decision-making errors using EEG and machine learning. Mathematics 2022, 10, 3153. [Google Scholar] [CrossRef]
- Kaneko, K. Chaotic but regular posi-nega switch among coded attractors by cluster-size variation. Phys. Rev. Lett. 1989, 63, 219–223. [Google Scholar] [CrossRef]
- Beer, K.; Bondarenko, D.; Farrelly, T.; Osborne, T.J.; Salzmann, R.; Scheiermann, D.; Wolf, R. Training deep quantum neural networks. Nat. Commun. 2020, 11, 808. [Google Scholar] [CrossRef]
- Bausch, J. Recurrent Quantum Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 1368–1379. [Google Scholar]
- Ezhov, A.A.; Ventura, D. Quantum Neural Networks. In Future Directions for Intelligent Systems and Information Sciences: The Future of Speech and Image Technologies, Brain Computers, WWW, and Bioinformatics; Kasabov, N., Ed.; Physica: Heidelberg, Germany, 2000; pp. 213–235. [Google Scholar]
- Abbas, A.; Sutter, D.; Zoufal, C.; Lucchi, A.; Figalli, A.; Woerner, S. The power of quantum neural networks. Nat. Comput. Sci. 2021, 1, 403–409. [Google Scholar] [CrossRef]
- Ngo, T.A.; Nguyen, T.; Thang, T.C. A survey of recent advances in quantum generative adversarial networks. Electronics 2023, 12, 856. [Google Scholar] [CrossRef]
- Fujii, K.; Nakajima, K. Harnessing disordered-ensemble quantum dynamics for machine learning. Phys. Rev. Appl. 2017, 8, 024030. [Google Scholar] [CrossRef]
- Govia, L.C.G.; Ribeill, G.J.; Rowlands, G.E.; Krovi, H.K.; Ohki, T.A. Quantum reservoir computing with a single nonlinear oscillator. Phys. Rev. Res. 2021, 3, 013077. [Google Scholar] [CrossRef]
- Mujal, P.; Martínez-Peña, R.; Nokkala, J.; García-Beni, J.; Giorgi, G.L.; Soriano, M.C.; Zambrini, R. Opportunities in quantum reservoir computing and extreme learning machines. Adv. Quantum Technol. 2021, 4, 2100027. [Google Scholar] [CrossRef]
- Dudas, J.; Carles, B.; Plouet, E.; Mizrahi, F.A.; Grollier, J.; Marković, D. Quantum reservoir computing implementation on coherently coupled quantum oscillators. NPJ Quantum Inf. 2023, 9, 64. [Google Scholar] [CrossRef]
- Sehrawat, A. Interferometric Neural Networks. arXiv 2023, arXiv:2310.16742. [Google Scholar]
- Sehrawat, A. Image Classification with CNN and QNN. Available online: https://github.com/ArunSehrawat/Image_classification_with_CNN_and_QNN (accessed on 28 November 2023).
- Zoufal, C.; Lucchi, A.; Woerner, S. Quantum Generative Adversarial Networks for learning and loading random distributions. NPJ Quantum Inf. 2019, 5, 103. [Google Scholar] [CrossRef]
- Aston, S.; Hurlbert, A. What #theDress reveals about the role of illumination priors in color perception and color constancy. J. Vis. 2017, 17. [Google Scholar] [CrossRef]
- Lafer-Sousa, R.; Conway, B.R. #TheDress: Categorical perception of an ambiguous color image. J. Vis. 2017, 17. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Kim, P. MATLAB Deep Learning with Machine Learning, Neural Networks and Artificial Intelligence; Apress: Berkeley, CA, USA, 2017. [Google Scholar]
- Lehky, S.R.; Westheimer, G. Binocular rivalry is not chaotic. Proc. R. Soc. B 1995, 259, 71–76. [Google Scholar]
- Sakai, K.; Katayama, T.; Wada, S.; Oiwa, K. Chaos causes perspective reversals for ambiguious patterns. In Proceedings of the Advances in Intelligent Computing—IPMU’94, Paris, France, 4–8 July 1994; Bouchon-Meunier, B., Yager, R.R., Zadeh, L.A., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; pp. 463–472. [Google Scholar]
- Shimaoka, D.; Kitajo, K.; Kaneko, K.; Yamaguchi, Y. Transient process of cortical activity during Necker cube perception: From local clusters to global synchrony. Nonlinear Biomed. Phys. 2010, 4, S7. [Google Scholar] [CrossRef]
- Chen, R.; Xiong, Y.; Zhuge, S.; Li, Z.; Chen, Q.; He, Z.; Wu, D.; Hou, F.; Zhou, J. Regulation and prediction of multistable perception alternation. Chaos Solitons Fractals 2023, 172, 113564. [Google Scholar] [CrossRef]
- Babloyantz, A. Chaotic Dynamics in Brain Activity. In Dynamics of Sensory and Cognitive Processing by the Brain; Başar, E., Ed.; Springer: Berlin/Heidelberg, Germany, 1988; pp. 196–202. [Google Scholar]
- McKenna, T.M.; McMullen, T.A.; Shlesinger, M.F. The brain as a dynamic physical system. Neuroscience 1994, 60, 587–605. [Google Scholar] [CrossRef] [PubMed]
- Korn, H.; Faure, P. Is there chaos in the brain? II. Experimental evidence and related models. C. R. Biol. 2003, 326, 787–840. [Google Scholar] [CrossRef] [PubMed]
- Maksymov, I.S. Analogue and physical reservoir computing using water waves: Applications in power engineering and beyond. Energies 2023, 16, 5366. [Google Scholar] [CrossRef]
- Symul, T.; Assad, S.M.; Lam, P.K. Real time demonstration of high bitrate quantum random number generation with coherent laser light. Appl. Phys. Lett. 2011, 98, 231103. [Google Scholar] [CrossRef]
- Haw, J.Y.; Assad, S.M.; Lance, A.M.; Ng, N.H.Y.; Sharma, V.; Lam, P.K.; Symul, T. Maximization of extractable randomness in a quantum random-number generator. Phys. Rev. Appl. 2015, 3, 054004. [Google Scholar] [CrossRef]
- Reiser, M.; Wirth, N. Programming in Oberon: Steps beyond Pascal and Modula; ACM Press: New York, NY, USA, 1992. [Google Scholar]
- Herring, C.; Palmore, J.I. Random number generators are chaotic. SIGPLAN Not. 1989, 24, 76–79. [Google Scholar] [CrossRef]
- Fan, F.; Wang, G. Learning from pseudo-randomness with an artificial neural network—Does God play pseudo-dice? IEEE Access 2018, 6, 22987–22992. [Google Scholar] [CrossRef]
- Brustein, R.; Oaknin, D.H. Classical dynamics of quantum fluctuations. Phys. Rev. D 2003, 67, 025010. [Google Scholar] [CrossRef]
- Matsuoka, K. The dynamic model of binocular rivalry. Biol. Cybern. 1984, 49, 201–208. [Google Scholar] [CrossRef]
- Lehky, S.R. An astable multivibrator model of binocular rivalry. Perception 1988, 17, 215–228. [Google Scholar] [CrossRef] [PubMed]
- Stollenwerk, L.; Bode, M. Lateral neural model of binocular rivalry. Neural Comput. 2003, 15, 2863–2882. [Google Scholar] [CrossRef] [PubMed]
- Moreno-Bote, R.; Rinzel, J.; Rubin, N. Noise-induced alternations in an attractor network model of perceptual bistability. J. Neurophysiol. 2007, 98, 1125–1139. [Google Scholar] [CrossRef]
- Shpiro, A.; Curtu, R.; Rinzel, J.; Rubin, N. Dynamical characteristics common to neuronal competition models. J. Neurophysiol. 2007, 97, 462–473. [Google Scholar] [CrossRef]
- Curtu, R.; Shpiro, A.; Rubin, N.; Rinzel, J. Mechanisms for frequency control in neuronal competition models. SIAM J. Appl. Dyn. Syst. 2008, 7, 609–649. [Google Scholar] [CrossRef] [PubMed]
- Gershman, S.J.; Vul, E.; Tenenbaum, J.B. Multistability and perceptual inference. Neural Comput. 2012, 24, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Panagiotaropoulos, T.I.; Kapoor, V.; Logothetis, N.K.; Deco, G. A common neurodynamical mechanism could mediate externally induced and intrinsically generated transitions in visual awareness. PLoS ONE 2013, 8, e0053833. [Google Scholar] [CrossRef]
- Gerstner, W.; Kistler, W.M.; Naud, R.; Paninski, L. Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Gladilin, E.; Eils, R. On the role of spatial phase and phase correlation in vision, illusion, and cognition. Front. Comput. Neurosci. 2015, 9, 45. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Quantum Mechanics; Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Sullivan, D.M. Electromagnetic Simulations Using the FDTD Method; IEEE Press: New York, NY, USA, 2000. [Google Scholar]
- Koch, R.; Lado, J.L. Neural network enhanced hybrid quantum many-body dynamical distributions. Phys. Rev. Res. 2021, 3, 033102. [Google Scholar] [CrossRef]
- Hendry, D.; Chen, H.; Feiguin, A. Neural network representation for minimally entangled typical thermal states. Phys. Rev. B 2022, 106, 165111. [Google Scholar] [CrossRef]
- Koch, R.; Lado, J.L. Designing quantum many-body matter with conditional generative adversarial networks. Phys. Rev. Res. 2022, 4, 033223. [Google Scholar] [CrossRef]
- Hampson, K.M.; Mallen, E.A.H. Chaos in ocular aberration dynamics of the human eye. Biomed. Opt. Express 2012, 3, 863–877. [Google Scholar] [CrossRef] [PubMed]
- Paprocki, R.; Lenskiy, A. What does eye-blink rate variability dynamics tell us about cognitive performance? Front. Hum. Neurosci. 2017, 11, 620. [Google Scholar] [CrossRef] [PubMed]
- Harezlak, K.; Kasprowski, P. Searching for chaos evidence in eye movement signals. Entropy 2018, 20, 32. [Google Scholar] [CrossRef] [PubMed]
- Rickles, D.; Hawe, P.; Shiell, A. A simple guide to chaos and complexity. J. Epidemiol. Community Health. 2007, 61, 933–937. [Google Scholar] [CrossRef] [PubMed]
- Aerts, D.; D’Hooghe, B.; Sozzo, S. A Quantum Cognition Analysis of the Ellsberg Paradox. In Proceedings of the Quantum Interaction, Aberdeen, UK, 26–29 June 2011; Song, D., Melucci, M., Frommholz, I., Zhang, P., Wang, L., Arafat, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 95–104. [Google Scholar]
- Aerts, D.; Sozzo, S.; Tapia, J. A Quantum Model for the Ellsberg and Machina Paradoxes. In Proceedings of the Quantum Interaction, Paris, France, 27–29 June 2012; Busemeyer, J.R., Dubois, F., Lambert-Mogiliansky, A., Melucci, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 48–59. [Google Scholar]
- Maksymov, I.S.; Pogrebna, G. The physics of preference: Unravelling imprecision of human preferences through magnetisation dynamics. arXiv 2023, arXiv:2310.00267. [Google Scholar] [CrossRef]
- Smith, N.E. A new angle on the freemish crate. Perception 1984, 13, 153–154. [Google Scholar] [CrossRef]
- Céspedes, P.; Cisternas, V.H. Necker. Available online: https://boardgamegeek.com/boardgame/203106/necker (accessed on 23 November 2023).
- Superliminal. Available online: https://store.steampowered.com/app/1049410/Superliminal/ (accessed on 23 November 2023).
- Khalid, M.N.A.; Iida, H. Objectivity and subjectivity in games: Understanding engagement and addiction Mechanism. IEEE Access 2021, 9, 65187–65205. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Kuperwajs, I.; Schütt, H.H.; Ma, W.J. Using deep neural networks as a guide for modeling human planning. Sci. Rep. 2023, 13, 20269. [Google Scholar] [CrossRef]
- Clément, G.; Skinner, A.; Lathan, C. Distance and size perception in astronauts during long-duration spaceflight. Life 2013, 3, 524–537. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, C.; Scaramuzza, D. Human-piloted drone racing: Visual processing and control. IEEE Robot. Autom. Lett. 2021, 6, 3467–3474. [Google Scholar] [CrossRef]
- Bernardo, J.M.; Smith, A.F.M. Bayesian Theory; John Wiley and Sons: New York, NY, USA, 2000. [Google Scholar]
- Doya, K.; Ishii, S.; Pouget, A.; Rao, R.P.N. Bayesian Brain; MIT Press: Cambridge, UK, 2007. [Google Scholar]
- Fox, C.W.; Stafford, T. Maximum utility unitary coherent perception vs. the Bayesian brain. Proc. Annu. Meet. Cogn. Sci. Soc. 2012, 34, 336. [Google Scholar]
- Maass, W.; Natschläger, T.; Markram, H. Real-time computing without stable states: A new framework for neural computation based on perturbations. Neural Comput. 2002, 14, 2531–2560. [Google Scholar] [CrossRef] [PubMed]
- Pira, L.; Ferrie, C. An invitation to distributed quantum neural networks. Quantum Mach. Intell. 2023, 5, 23. [Google Scholar] [CrossRef]
- Lukoševičius, M.; Jaeger, H. Reservoir computing approaches to recurrent neural network training. Comput. Sci. Rev. 2009, 3, 127–149. [Google Scholar] [CrossRef]
- Nakajima, K.; Fisher, I. Reservoir Computing; Springer: Berlin, Germany, 2021. [Google Scholar]
- Nakajima, M.; Inoue, K.; Tanaka, K.; Kuniyoshi, Y.; Hashimoto, T.; Nakajima, K. Physical deep learning with biologically inspired training method: Gradient-free approach for physical hardware. Nat. Commun. 2022, 13, 7847. [Google Scholar] [CrossRef]
- Gauthier, D.J.; Bollt, E.; Griffith, A.; Barbosa, W.A.S. Next generation reservoir computing. Nat. Commun. 2021, 12, 5564. [Google Scholar] [CrossRef]
- Maksymov, I.S.; Pototsky, A.; Suslov, S.A. Neural echo state network using oscillations of gas bubbles in water. Phys. Rev. E 2021, 105, 044206. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).