On Orthogonal Double Covers and Decompositions of Complete Bipartite Graphs by Caterpillar Graphs

Abstract

Nowadays, graph theory is one of the most exciting fields of mathematics due to the tremendous developments in modern technology, where it is used in many important applications. The orthogonal double cover $\left(ODC\right)$ is a branch of graph theory and is considered as a special class of graph decomposition. In this paper, we decompose the complete bipartite graphs $K_{x,x}$ by caterpillar graphs using the method of $ODC$s. The article also deals with constructing the $ODC$s of $K_{x,x}$ by general symmetric starter vectors of caterpillar graphs such as stars–caterpillar, the disjoint copies of cycles–caterpillars, complete bipartite caterpillar graphs, and the disjoint copies of caterpillar paths. We decompose the complete bipartite graph by the complete bipartite subgraphs and by the disjoint copies of complete bipartite subgraphs using general symmetric starter vectors. The advantage of some of these new results is that they enable us to decompose the giant networks into large groups of small networks with the comprehensive coverage of all parts of the giant network by using the disjoint copies of symmetric starter subgraphs. The use case of applying the described theory for various applications is considered.

1. Introduction

Graph theory occupies a special place in mathematics and is used in many areas of engineering to solve various problems, from describing the topologies of communication networks of autonomous vehicles [1] to medical research in eating disorders [2] and social interaction during pandemics [3].

Caterpillar graphs [4] are emphasized in graph theory due to their properties. They have gained their popularity since the 1970s and are still being studied. Moreover, they are studied not only in the context of their mathematical properties [5,6,7,8,9], but are also especially popular in chemistry [10], where they are used to describe benzenoid hydrocarbon molecules under the names benzenoid trees [11,12], alkane graphs, and Gutman trees [10,13]. Caterpillar graphs are also used to describe more complex graphs (for example, corona graphs [14]), leaf realization problems on graphs [15], and minimum spanning tree problems on graphs [16]. Currently, the use of such graphs in coding theory [17,18,19,20] is very popular, especially in the development of technologies for post-quantum cryptography [21]. The designations used in the paper are shown in

Table 1. Designations used in the paper.

Nomenclature
$K_{x,y}$	A complete bipartite graph with independent sets of sizes $x$ and $y.$
$\mathrm{g}\mathrm{c}\mathrm{d}$	The greatest common divisor.
$mG$	$m$ disjoint copies of $G$.
$G\cup H$	The disjoint union of $G$ and $H.$
$S_x$	A star with $x$ edges on $x+1$ vertices.
$P_x$	A path with $x$ vertices.
$K_1$	An isolated vertex.
$C(N;s_1,s_2,s_3)$	Three-dimensional circulant graph. $N$–number of nodes; $s_1,s_2,s_3$–generators.

.

Consider that $H\cong K_{x,x}$ and $\mathcal{G}=\{T_0$, $T_1$,…, $T_{x-1}$, $A_0$, $A_1$,…, $A_{x-1}\}$ be a collection that describes the $2x$ isomorphic subgraphs, $\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{n}$ $\mathrm{w}\mathrm{e}$ can call $\mathcal{G}$ an orthogonal double cover ($ODC$) of $K_{x,x}$ by $G,$ if the following two conditions are satisfied: (i) every edge of $K_{x,x}$ exists in two isomorphic subgraphs of $\mathcal{G}$ and (ii) for $\alpha ,\beta \in \{0,1,\dots ,x-1\},$ $\left|E\left(T_{\alpha }\right)\cap E\left(A_{\beta }\right)\right|=1$, and for $\alpha \ne \beta ,$ $\left|E\left(T_{\alpha }\right)\cap E\left(T_{\beta }\right)\right|=\left|E\left(A_{\alpha }\right)\cap E\left(A_{\beta }\right)\right|=0.$

The significance of graph decompositions can be exemplified as follows. By recognizing a graph’s structure through dividing a graph into more easily understood parts, decompositions can aid in our understanding of its structure [22]. By breaking down a graph into its connected parts, the number of distinct subgraphs present in the network can be defined. Via decompositions, the degree distribution and clustering coefficient of a graph can be identified. By breaking a graph down into its degree sequence, the distribution of degrees among the graph’s vertices can also be determined.

Decompositions can be applied to algorithms for the network flow analysis and graph coloring [23]. It is possible to find the maximum flow in a graph by breaking it down into its edge-disjoint path ways.

Decompositions are a topic of ongoing research in a graph theory causing numerous unanswered questions. Decompositions can be studied to gain new knowledge and understanding in this field. Furthermore, decompositions of graphs are a useful tool for understanding and analyzing graphs in general, and they have many real-world uses in many disciplines, including computer science [24], mathematics [25,26], and social science.

The existence of $ODC$s has been considered and generalized by many authors [27,28,29]. The importance of $ODC$ problems stems from solving database optimization problems; for example, when we look for specific information in a very large database, it takes too much time to find that information [30]. In [24], $ODC$s are related to several problems such as the statistical design of experiments and design theory. It can also be used to solve the routing problem in various network systems whose topologies are large regular graphs; for example, see works [31,32]. The specialists have solved the $ODC$ problem for various graphs such as circulant graphs, complete graphs, and complete bipartite graphs [33]. Note that these graphs are usually very large.

Definition 1.

Let$l\ge 2$ be integer. A caterpillar graph $C_l(w_1,w_2,\dots ,w_l)$ was obtained from a path  $P_l=u_1{u}_2\dots u_l$ by appending $w_i\ge 0$ necklace vertices to each  $u_i,$  $1\le i\le l.$

Example 1.

Figure 1 illustrates the path graph $P_4$ and how the graphs $C_4(2,2,1,1)$ and $C_4(1,3,2,2)$ can be obtained from $P_4.$

The following definition has been proposed in [34]. Let $H$ be a certain graph, the graph G-Path denoted by ${\mathbb{P}}_{m+1}\left(G\right)$, is a path of a set of vertices $\mathbb{V}=\{V_i:0\le i\le m\}$ and a set of edges $\mathbb{E}=\{E_i:0\le i\le m-1\}$ if and only if there exists the following two bijective mappings:

• ϕ: $\mathbb{E}\to \mathcal{H}$ defined by $\varphi \left(E_i\right)=H_i$, where $\mathcal{H}=\{H_0,H_1,\dots ,H_{m-1}\}$ is a collection of $m$ graphs; each one is isomorphic to the graph $G$.
• $\psi : \mathbb{V}\to \mathcal{A}$ defined by $\psi \left(V_i\right)=X_i$, where $\mathcal{A}=\{X_i:0\le i\le m:{\cap }_i{X}_i=\phi \}$ is a class of disjoint sets of vertices.

The graph ${\mathbb{P}}_6\left(K_{1,3}\right)$, the path of six sets of vertices and five edges of $K_{1,3}$, is shown in Figure 2.

Similarly, the caterpillar graph definition can be shown by replacing the path graph with the caterpillar graph in the previous definition. The caterpillar graph corresponding to the caterpillar $C_l(w_1,w_2,\dots ,w_l)$ will be denoted by ${\mathbb{C}}_l^{w_1,w_2,\dots ,w_l}\left(G\right)$.

In the main results section, several examples for the caterpillar graph are presented.

There are extensive studies in the literature for the $ODC$ of complete bipartite graphs such as the technique for constructing the $ODC$s of $K_{x,x}$ by copies of a graph, which is called the one-edge algorithm [35]. Additionally, there are many studies for constructing the $ODC$s of $K_{x,x}$ by special graphs such as the union of a cycle and a star, a special class of six caterpillars [36], and the disjoint union of complete bipartite graphs.

Several results of the $ODC$s of complete bipartite graphs can be generalized to mutually orthogonal graph squares that have many applications in design theory, graph-orthogonal arrays, and authentication codes [37]. Additionally, the techniques of constructing the $ODC$s are considered a tool for graph labeling called orthogonal labeling, which have many applications (for example, see [38]).

Motivated by all the previous results and the important applications of caterpillar graphs [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21], in this paper, we aim to decompose giant graphs for the special type of networks (complete bipartite graphs) by joint and disjoint copies of new generally symmetric graphs called caterpillar graphs.

The design of the study can be explained as follows: large complete bipartite networks and a symmetric starter vector method are applied to represent caterpillar graphs, which can be generated and used in many applications such as the analysis and decomposition of the large complete bipartite graphs (networks). The caterpillar graph used to decompose the complete bipartite graph are: the stars–caterpillar graph; the disjoint copies of cycles–caterpillars; the complete bipartite caterpillar graphs; and the disjoint copies of caterpillar paths. Additionally, we decompose the complete bipartite giant graph by the complete bipartite subgraphs and by the disjoint copies of complete bipartite subgraphs using general symmetric starter vectors. Note that the decomposition of a complete bipartite giant graph network through various joint and disjoint symmetric graphs manages to solve many relational database problems and analyze the relational database to speed up the information research. The symmetric starter vectors are chosen based on the nature of the problem to be solved or analyzed. This paper is the first to construct the $ODC$s by caterpillar graphs using general symmetric starter vectors. We obtained general results of a caterpillar graph for constructing the decompositions and $ODC$s of complete bipartite graphs while El-Shanawany et al. [36] constructed the $ODC$s of complete bipartite graphs by only a special class of six caterpillars. Based on works [39,40,41], we will use our new results (obtained in this paper) to design new kinds of topological structures in our future work.

In this paper, all graphs are undirected, without loops or multiple edges, and finite. We assume that $H\cong K_{x,x}$ with two sets of sizes $x$ each. For the complete bipartite graph $K_{x,x}$, the notation $v_j^i$ refers to the vertex $v^i,i\in {\mathbb{Z}}_x=\{0,1,\dots ,x-1\}$ that belongs to the set of vertices with number $j$ where $j\in \{0,1\}$ for $K_{x,x}$, which have two independent sets of vertices. Throughout the paper and for simplicity, we use the notation $i_j$ to represent the vertex $v_j^i.$ The length of an edge ${\gamma }_0{\chi }_1$ in $K_{x,x}$ is defined to be the difference $\chi -\gamma ,$ where $\chi ,\gamma \in {\mathbb{Z}}_x=\{0,1,2,\dots ,x-1\}$. Note that differences and sums are calculated in ${\mathbb{Z}}_x$ (i.e., sums and differences are calculated modulo $x$). For more illustration, the labeling of the vertices of $K_{3,3}$ is shown in Figure 3.

Several papers have generalized the $ODC$s to the mutually orthogonal graph squares; see, e.g., [42] and the references therein.

The rest of the paper is divided as follows. In Section 2, we show the definition and the construction of symmetric starters. The main results in eight theorems are presented in Section 3. An illustrative example of applying the proposed graph decomposition approach in a practical example for on-chip networks is given in Section 4. Finally, in Section 5, we provide the conclusion and summary of new results obtained.

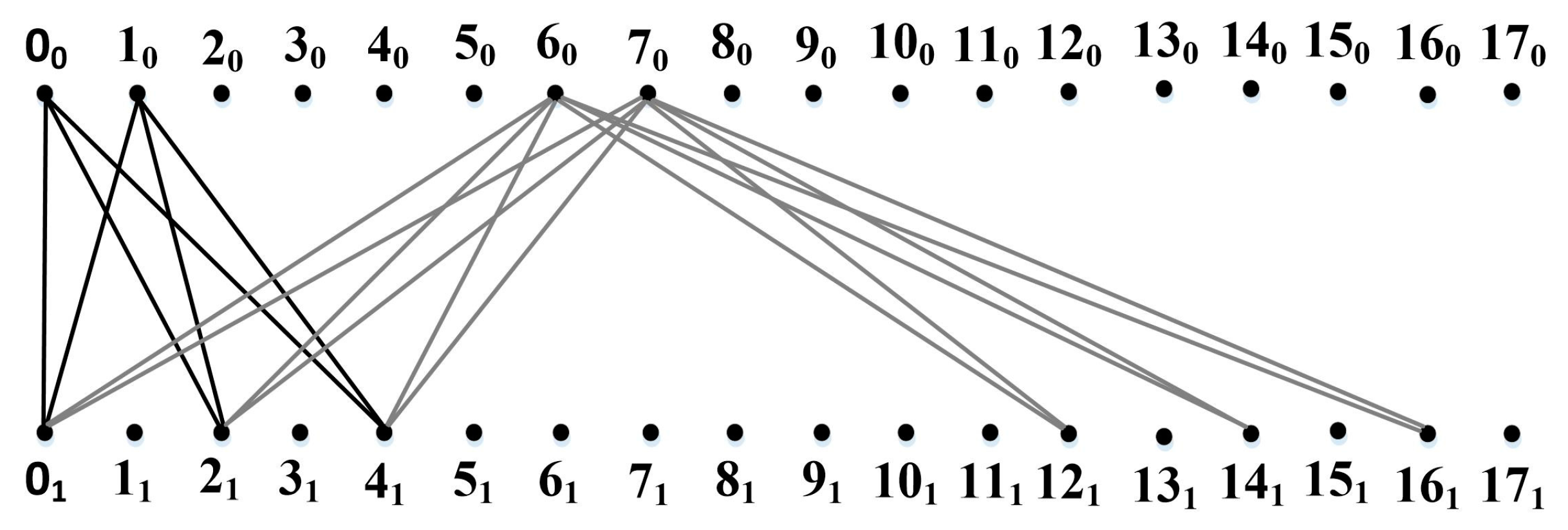
2. Symmetric Starters

Let $\mathcal{A}$ be a subgraph of $K_{x,x}$ and $\delta \in {\mathbb{Z}}_x$. Then, the graph $\mathcal{A}+\delta$ with $E(\mathcal{A}+\delta )=\left\{\right(\lambda +\delta ,\mu +\delta ):(\lambda ,\mu )\in E(\mathcal{A}\left)\right\}$ is called the $\delta$-translate of $\mathcal{A}$. $\mathcal{A}$ is called a half starter with respect to ${\mathbb{Z}}_x,$ if (i) $\left|E\left(\mathcal{A}\right)\right|=x$ and (ii) the lengths of all edges in $\mathcal{A}$ are mutually dissimilar and equal to ${\mathbb{Z}}_x$; that is, $\left\{d\right(e):e\in E(\mathcal{A}\left)\right\}={\mathbb{Z}}_x$. The following results have already been proven in the literature [22]:

• If $\mathcal{A}$ is a half starter, then the union of all translates of $\mathcal{A}$ forms an edge decomposition of $K_{x,x}$; that is, ${\cup }_{\delta \in {\mathbb{Z}}_x}E(\mathcal{A}+\delta )=E\left(K_{x,x}\right)$. Hereafter, a half-starter $\mathcal{A}$ can be represented by the vector $u\left(\mathcal{A}\right)=(u_{{\omega }_0},\dots .,u_{{\omega }_{x-1}})\in {\mathbb{Z}}_x^x.$ Two half-starter vectors $u\left({\mathcal{A}}_0\right)$ and $u\left({\mathcal{A}}_1\right)$ are said to be orthogonal if $\left\{u_{\alpha }\right({\mathcal{A}}_0)-u_{\alpha }({\mathcal{A}}_1):\alpha \in {\mathbb{Z}}_x\}={\mathbb{Z}}_x$.
• If two half-starter vectors $u\left({\mathcal{A}}_0\right)$ and $u\left({\mathcal{A}}_1\right)$ are orthogonal, then $\mathcal{G}=\{{\mathcal{A}}_{\delta ,\beta }:(\delta ,\beta )\in {\mathbb{Z}}_x\times {\mathbb{Z}}_2\}$ with ${\mathcal{A}}_{\delta ,\beta }={\mathcal{A}}_{\beta }+\delta$ is an $ODC$ of $K_{x,x}$. The subgraph ${\mathcal{A}}_s$ of $K_{x,x}$ with $E\left({\mathcal{A}}_s\right)=\left\{\right({\lambda }_0,{\mu }_1):({\mu }_0,{\lambda }_1)\in E(\mathcal{A}\left)\right\}$ is called the symmetric graph of $\mathcal{A}.$ If $\mathcal{A}$ is a half starter, then ${\mathcal{A}}_s$ is also a half starter. A half starter $\mathcal{A}$ is called a symmetric starter with respect to ${\mathbb{Z}}_x$ if the following vectors $u\left(\mathcal{A}\right)$ and $u\left({\mathcal{A}}_s\right)$ are orthogonal.
• Let $x$ be a positive integer and $\mathcal{A}$ a half starter represented by the vector $u\left(\mathcal{A}\right)=(u_{{\omega }_0},....,u_{{\omega }_{x-1}})$. Then, $\mathcal{A}$ is the symmetric starter if $\{u_{\omega }-u_{-\omega }+\omega :\omega \in {\mathbb{Z}}_x\}={\mathbb{Z}}_x$.

The symmetric starter can be used to decompose the balanced complete bipartite graphs $K_{x,x}$ by several graphs and relies on the idea of $\delta$-translate and half starters that are strongly related to Rosa’s labeling and his cyclic decompositions of the complete graph [25]. The symmetric starter vectors method is an easy method compared to the direct method, function-half starter method, and matrices method. Some graphs do not have a symmetric starter vector; so, the orthogonal double covers cannot be constructed by these graphs based on the symmetric starter method. Hence, the limitation of the method is that some classes of graphs cannot be represented by vectors; thus, we try to apply the methods above.

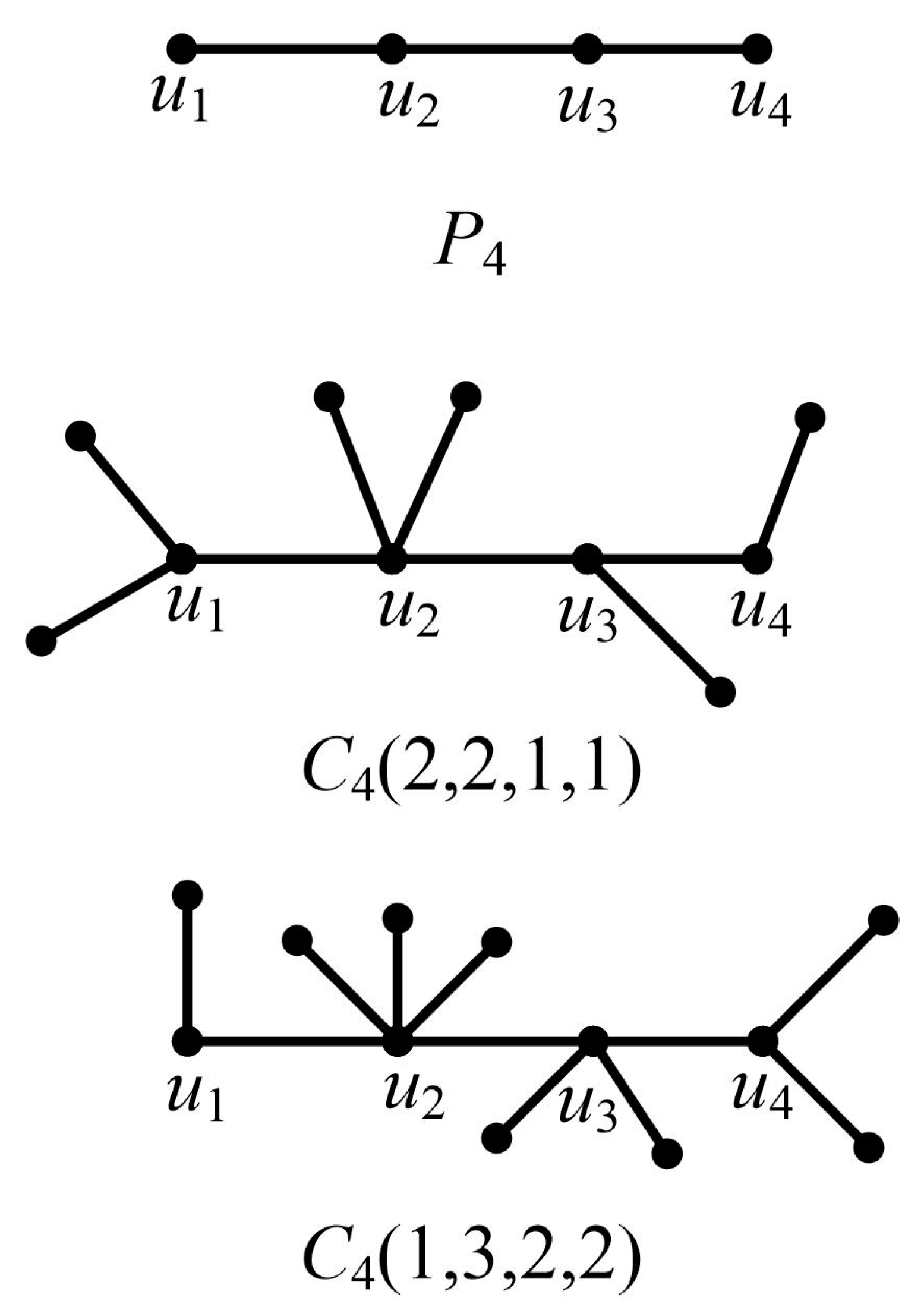
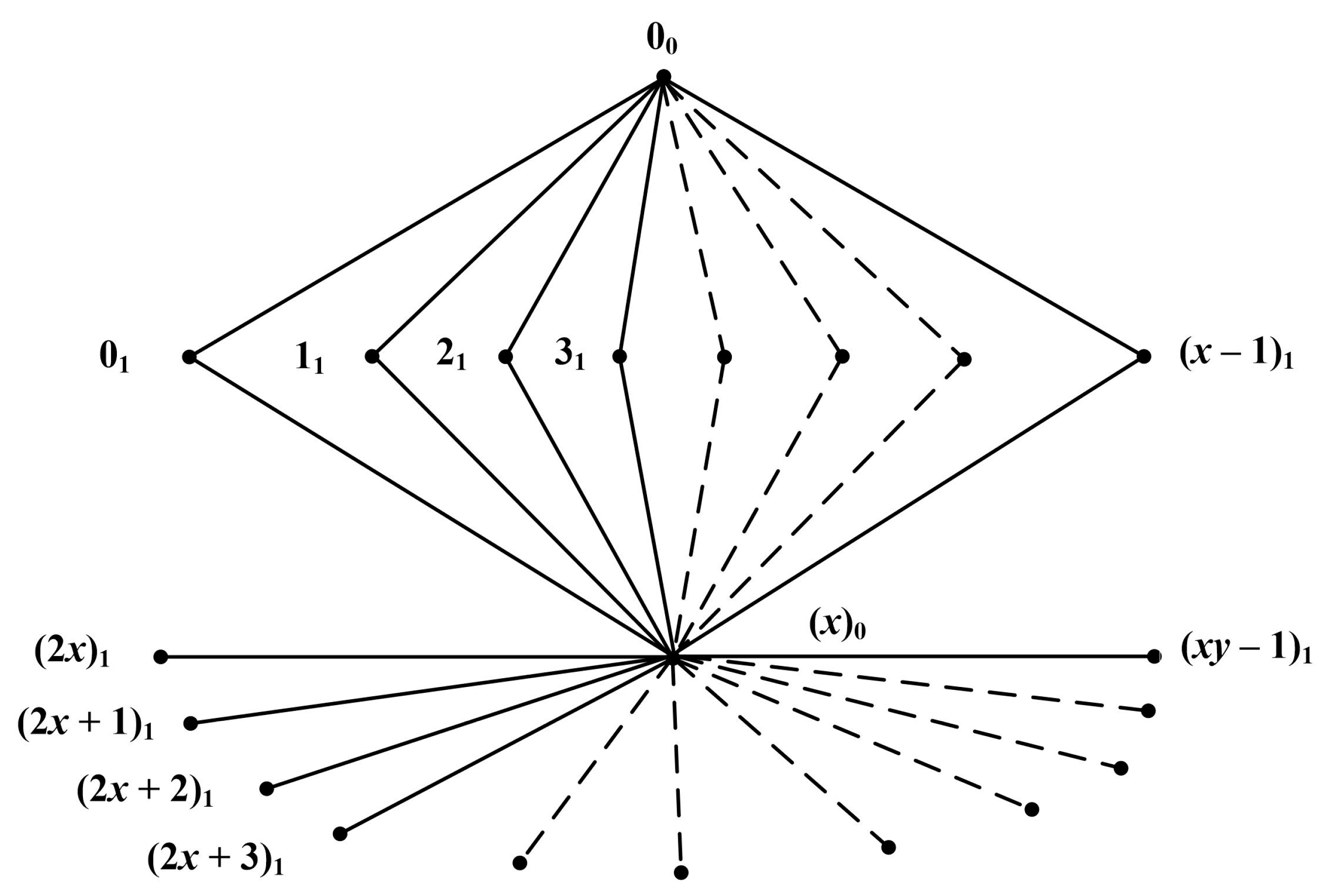
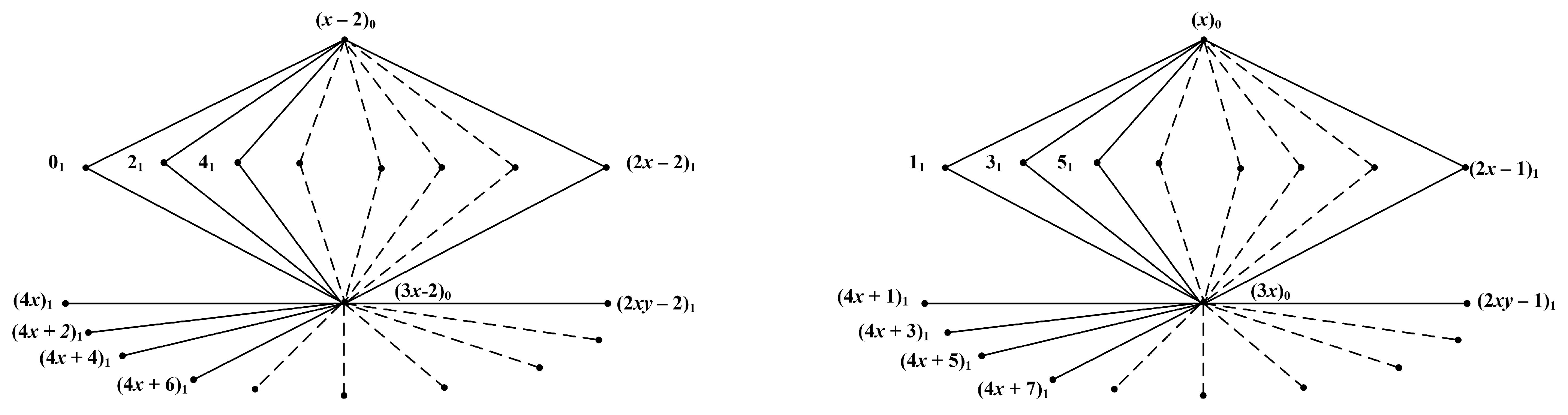
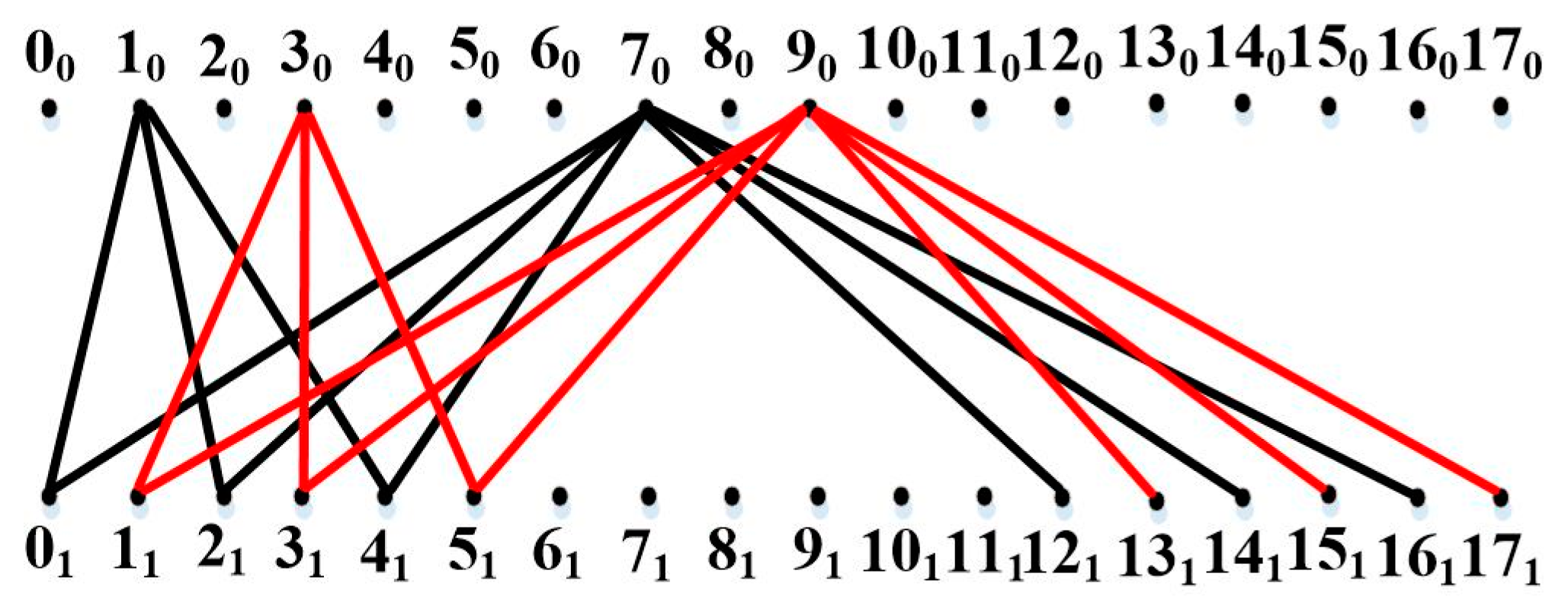
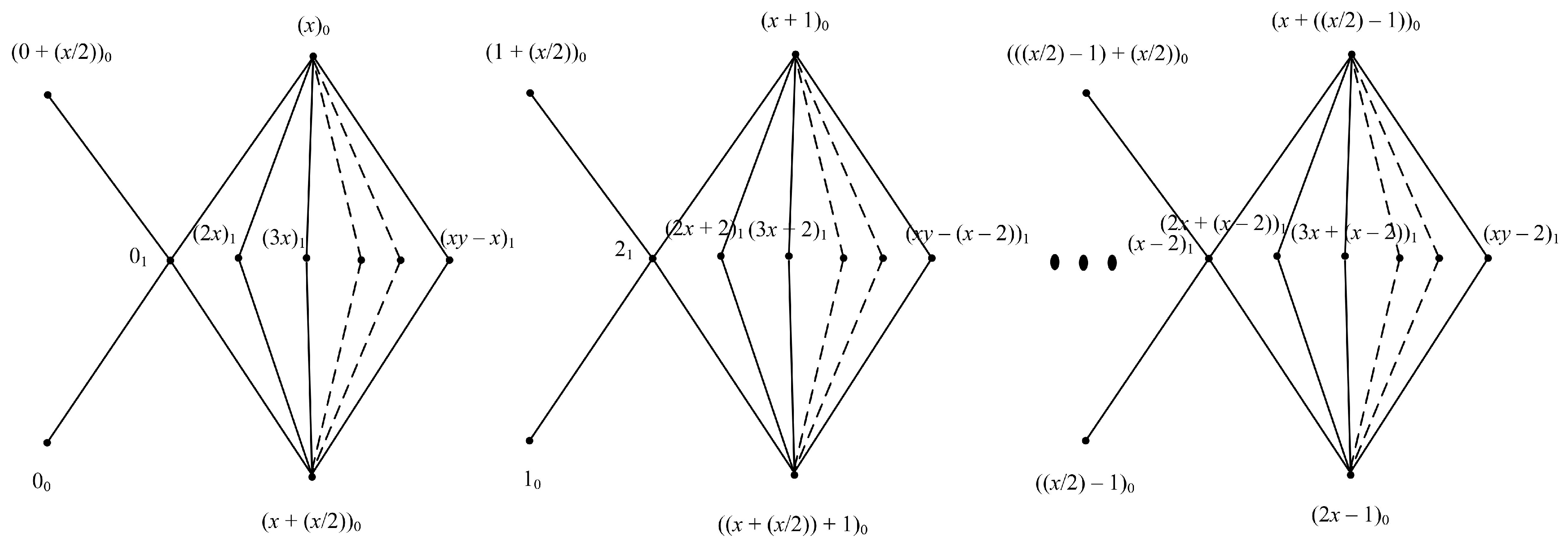
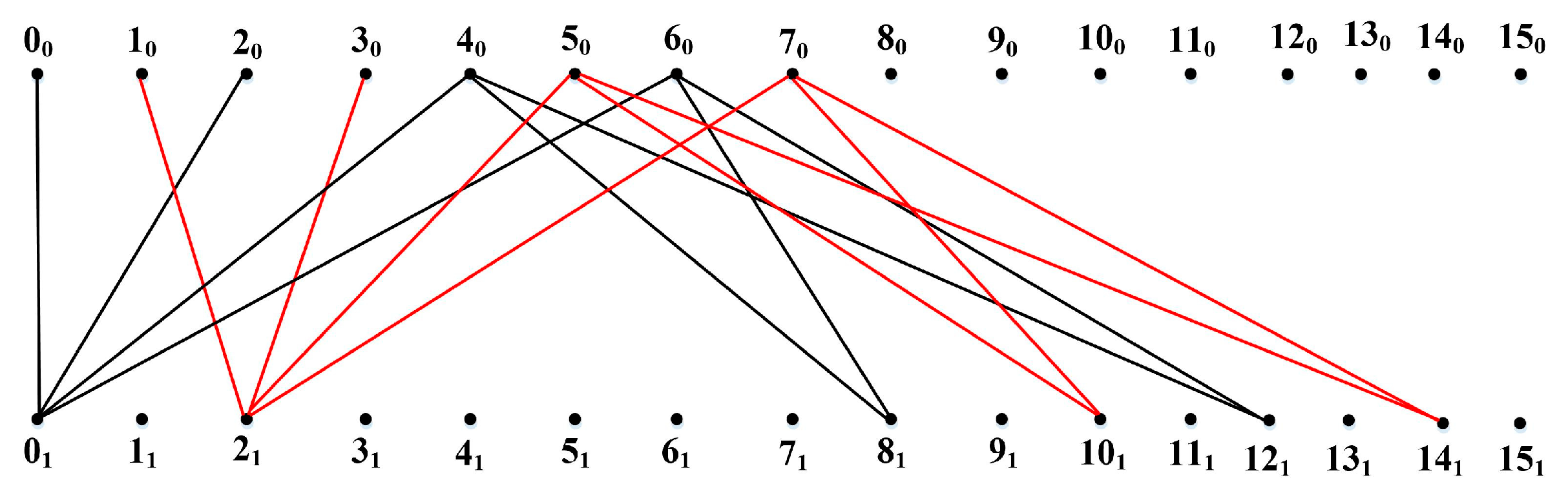
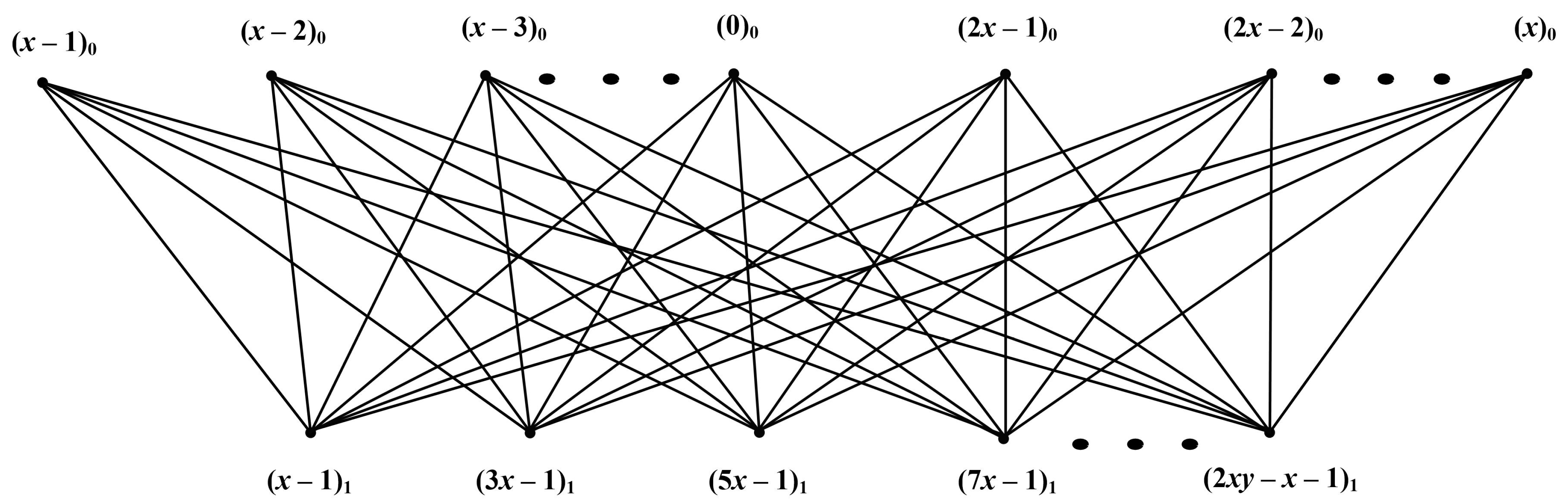
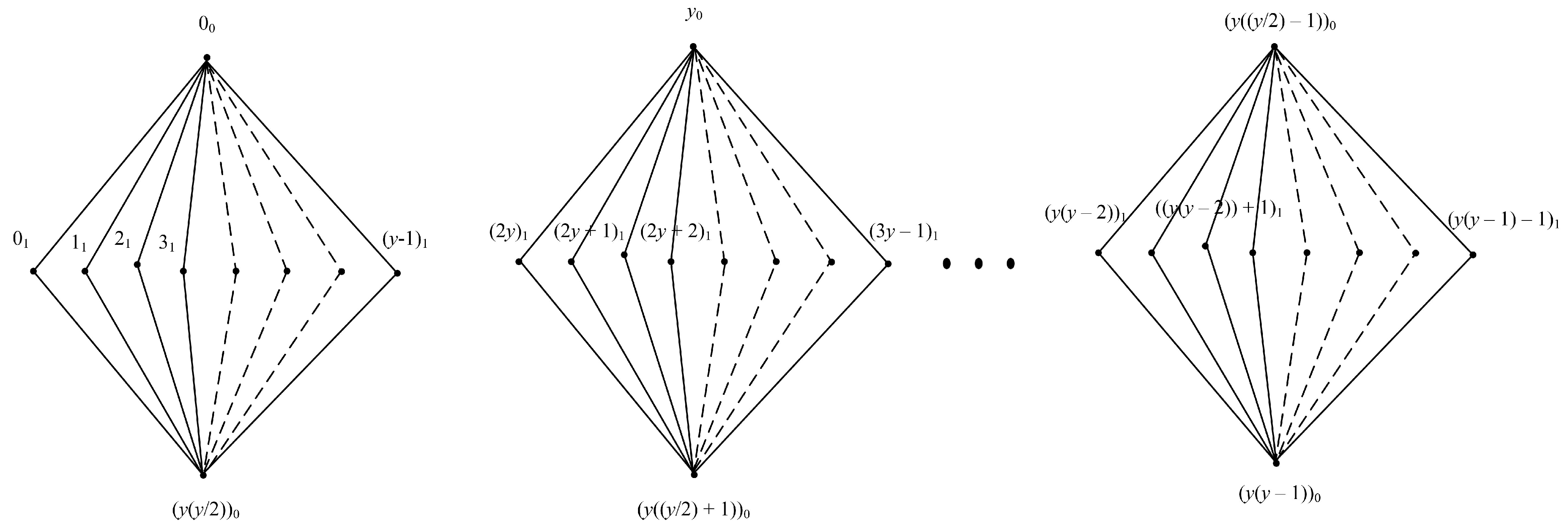
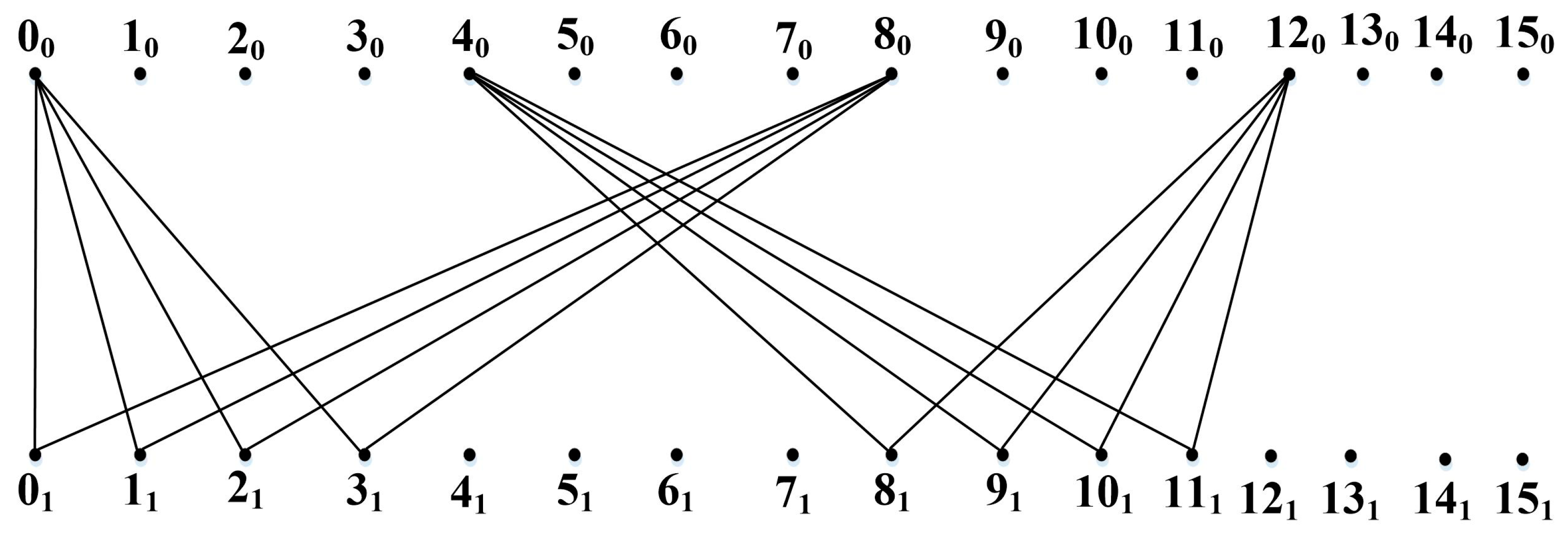
3. Main Results

In Theorem 1, we construct and prove the existence of the symmetric starter of an $ODC$ of $K_{xy,xy}$ by ${\mathbb{C}}_2^{1,y-2}\left(S_x\right)$ using a general symmetric vector. For more information, see Figure 4.

Theorem 1.

For all integers $y\ge 3$ and $x\ge 2$, then the vector $v\left({\mathbb{C}}_2^{1,y-2}\right(S_x\left)\right)=(0,0,\dots ,0,x,x,\dots ,x)\in {\mathbb{Z}}_{yx}^{yx}$, is a symmetric starter vector of an $ODC$ of $K_{xy,xy}$ by ${\mathbb{C}}_2^{1,y-2}\left(S_x\right)$.

Proof. 

From the vector $v\left({\mathbb{C}}_2^{1,y-2}\right(S_x\left)\right),$ we can define:

$$v_i=\left\{\begin{array}{ll}0& \mathrm{i}\mathrm{f} i<x,\mathrm{o}\mathrm{r}\\ x& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}\right.$$

(1)

Hence,

$$v_{-i}=\left\{\begin{array}{ll}x& \mathrm{i}\mathrm{f} 1\le i\le x(y-1),\mathrm{o}\mathrm{r}\\ 0& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}\right.$$

(2)

Then,

$$v_i-v_{-i}+i=\left\{\begin{array}{lll}0& \mathrm{i}\mathrm{f}& i=0,\mathrm{o}\mathrm{r}\\ i-x& \mathrm{i}\mathrm{f}& 1\le i<x,\mathrm{o}\mathrm{r}\\ i& \mathrm{i}\mathrm{f}& x\le i\le x(y-1),\mathrm{o}\mathrm{r}\\ i+x& & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}\right.$$

(3)

Note that $\{v_i-v_{-i}+i:i\in {\mathbb{Z}}_{yx}\}={\mathbb{Z}}_{yx}.$ □

Example 2 is a direct application of Theorem 1.

Example 2.

Let $y=4$ and $x=3;$ so, the vector $v\left({\mathbb{C}}_2^{1,2}\left(S_3\right)\right)=\left(0,0,0,3,3,3,3,3,3,3,3,3\right).$ Then, there exists an $ODC$ of $K_{12,12}$ by ${\mathbb{C}}_2^{1,2}\left(S_3\right)$. The edge set of $v\left({\mathbb{C}}_2^{1,2}\left(S_3\right)\right)$ is defined by $E\left({\mathbb{C}}_2^{1,2}\left(S_3\right)\right)=\left\{\right({{(v}_i)}_0,\left({v_i+i)}_1\right):i\in {\mathbb{Z}}_{12}\}=\{(0_0,0_1),(0_0,1_1),(0_0,2_1),(3_0,6_1),(3_0,7_1),(3_0,8_1),(3_0,9_1),(3_0,{10}_1),(3_0,{11}_1),(3_0,0_1),(3_0,1_1),$$(3_0,2_1)\},$ see Figure 5.

In Theorem 2, we construct the symmetric starter of an $ODC$ of $K_{2xy,2xy}$ by $2{\mathbb{C}}_2^{1,y-2}\left(S_x\right)$ using a general symmetric vector. There are two cases depending on the value of $x.$ For more information, see Figure 6 and Figure 7.

Theorem 2.

For all integers  $y\ge 3$ and  $x\ge 2,$ then the vector  $v\left(2{\mathbb{C}}_2^{1,y-2}\right(S_x\left)\right)=(x,x-2,x,x-2,\dots ,x,x-2,3x,3x-2,3x,3x-2,\dots ,3x,3x-2)\in {\mathbb{Z}}_{2xy}^{2xy},$ is a symmetric starter vector of an  $ODC$ of  $K_{2xy,2xy}$ by  $2{\mathbb{C}}_2^{1,y-2}\left(S_x\right).$

Proof. 

From the vector $v\left(2{\mathbb{C}}_2^{1,y-2}\right(S_x\left)\right),$ we can define:

$$v_i=\left\{\begin{array}{lll}x& \mathrm{i}\mathrm{f}& i=0,2,4,\dots ,2x-2,\mathrm{o}\mathrm{r}\\ x-2& \mathrm{i}\mathrm{f}& i=1,3,5,\dots ,2x-1,\mathrm{o}\mathrm{r}\\ 3x& \mathrm{i}\mathrm{f}& i=2x,2x+2,2x+4,\dots ,2yx-2,\mathrm{o}\mathrm{r}\\ 3x-2& \mathrm{i}\mathrm{f}& i=2x+1,2x+3,2x+5,\dots ,2yx-1.\end{array}\right.$$

(4)

Hence,

$$v_{-i}=\left\{\begin{array}{lll}3x-2& \mathrm{i}\mathrm{f}& i=1,3,5,\dots ,2yx-2x-1,\mathrm{o}\mathrm{r}\\ 3x& \mathrm{i}\mathrm{f}& i=2,4,6,\dots ,2yx-2x,\mathrm{o}\mathrm{r}\\ x-2& \mathrm{i}\mathrm{f}& i=2yx-2x+1,2yx-2x+3,\dots ,2yx-1,\mathrm{o}\mathrm{r}\\ x& \mathrm{i}\mathrm{f}& i=2yx-2x+2,2yx-2x+4,\dots ,2yx.\end{array}\right.$$

(5)

Then,

$$v_i-v_{-i}+i=\left\{\begin{array}{lll}0& \mathrm{i}\mathrm{f}& i=0,\mathrm{o}\mathrm{r}\\ i-2x& \mathrm{i}\mathrm{f}& i=1,2,3,\dots ,2x-1,\mathrm{o}\mathrm{r}\\ i& \mathrm{i}\mathrm{f}& i=2x,2x+1,2x+2,\dots ,2x(y-1),\mathrm{o}\mathrm{r}\\ i+2x& & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}\right.$$

(6)

Note that $\{v_i-v_{-i}+i:$  $i\in {\mathbb{Z}}_{2yx}\}={\mathbb{Z}}_{2yx}.$ □

Example 3 is a direct application of Theorem 2.

Example 3.

Let $y=3$ and $x=3;$ so, the vector $v\left(2{\mathbb{C}}_2^{1,1}\right(S_3\left)\right)=(3,1,3,1,3,1,9,7,9,7,9,7,9,7,9,7,9,7).$ Then, there exists an $ODC$ of $K_{\mathrm{18,18}}$ by $2{\mathbb{C}}_2^{\mathrm{1,1}}\left(S_3\right);$ for more information, see Figure 8.

Theorem 3.

Let $y\ge 3$ and $x\ge 2$ be integers, then, the vector $v\left({\mathbb{C}}_2^{1,y-2}\right(K_{2,x}\left)\right)=(0,1,0,1,\dots ,0,1,2x,2x+1,2x,2x+1,\dots ,2x,2x+1)\in {\mathbb{Z}}_{2xy}^{2xy}$, is a symmetric starter vector of an $ODC$ of $K_{2xy,2xy}$ by ${\mathbb{C}}_2^{1,y-2}\left(K_{2,x}\right).$

Proof. 

From the vector $v\left({\mathbb{C}}_2^{1,y-2}\right(K_{2,x}\left)\right)$, we can define:

$$v_i=\left\{\begin{array}{lll}0& \mathrm{i}\mathrm{f}& i=0,2,4,\dots ,2x-2,\mathrm{o}\mathrm{r}\\ 1& \mathrm{i}\mathrm{f}& i=1,3,5,\dots ,2x-1,\mathrm{o}\mathrm{r}\\ 2x& \mathrm{i}\mathrm{f}& i=2x,2x+\mathrm{2,2}x+4,\dots ,2yx-2,\mathrm{o}\mathrm{r}\\ 2x+1& \mathrm{i}\mathrm{f}& i=2x+1,2x+3,2x+5,\dots ,2yx-1.\end{array}\right.$$

(7)

Hence,

$$v_{-i}=\left\{\begin{array}{lll}2x+1& \mathrm{i}\mathrm{f}& i=1,3,5,\dots ,2yx-2x-1,\mathrm{o}\mathrm{r}\\ 2x& \mathrm{i}\mathrm{f}& i=\mathrm{2,4},6,\dots ,2yx-2x,\mathrm{o}\mathrm{r}\\ 1& \mathrm{i}\mathrm{f}& i=2yx-2x+1,2yx-2x+3,\dots ,2yx-1,\mathrm{o}\mathrm{r}\\ 0& \mathrm{i}\mathrm{f}& i=2yx-2x+\mathrm{2,2}yx-2x+4,\dots ,2yx.\end{array}\right.$$

(8)

Then,

$$v_i-v_{-i}+i=\left\{\begin{array}{lll}0& \mathrm{i}\mathrm{f}& i=0,\mathrm{o}\mathrm{r}\\ i-2x& \mathrm{i}\mathrm{f}& i=1,2,3,\dots ,2x-1,\mathrm{o}\mathrm{r}\\ i& \mathrm{i}\mathrm{f}& i=2x,2x+\mathrm{1,2}x+2,\dots ,2x(y-1),\mathrm{o}\mathrm{r}\\ i+2x& & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}\right.$$

(9)

Note that $\{v_i-v_{-i}+i:$  $i\in {\mathbb{Z}}_{2yx}\}={\mathbb{Z}}_{2yx}.$ □

Example 4.

Let $y=3$ and $x=3,$ so the vector $v\left({\mathbb{C}}_2^{\mathrm{1,1}}\right(K_{2,3}\left)\right)=(0,1,0,1,0,1,6,7,6,7,6,7,6,7,6,7,6,7).$ Then, there exists an $ODC$ of $K_{18,18}$ by ${\mathbb{C}}_2^{\mathrm{1,1}}\left(K_{2,3}\right)$; see Figure 9.

Theorem 4.

For all integers $x$ and $y\ge 3,$ and $gcd(x,3)=1,$ then the vector $v\left(x{\mathbb{C}}_2^{1,y-2}\right(K_{2,2}\left)\right)=(0,1,2,\dots ,2x-1,0,1,2,\dots ,2x-1,4x,4x+1,4x+2,\dots ,6x-1,\dots ,4x,4x+1,4x+2,\dots ,6x-1)\in {\mathbb{Z}}_{4xy}^{4xy}$ is a symmetric starter vector of an $ODC$ of $K_{4xy,4xy}$ by $x{\mathbb{C}}_2^{1,y-2}\left(K_{2,2}\right).$

Proof. 

From the vector $v\left(x{\mathbb{C}}_2^{1,y-2}\right(K_{\mathrm{2,2}}\left)\right)$, we can define:

$$v_i=\left\{\begin{array}{lll}0& \mathrm{i}\mathrm{f}& i=0 \mathrm{a}\mathrm{n}\mathrm{d} i=2x,\mathrm{o}\mathrm{r}\\ 1& \mathrm{i}\mathrm{f}& i=1 \mathrm{a}\mathrm{n}\mathrm{d} i=2x+1,\mathrm{o}\mathrm{r}\\ :& :& :\\ 2x-1& \mathrm{i}\mathrm{f}& i=2x-1 \mathrm{a}\mathrm{n}\mathrm{d} i=4x-1,\mathrm{o}\mathrm{r}\\ 4x& \mathrm{i}\mathrm{f}& i=4x,i=6x,\dots , i=4yx-2x, \mathrm{o}\mathrm{r}\\ 4x+1& \mathrm{i}\mathrm{f}& i=4x+1,i=6x+1,\dots ,i=4yx-2x+1, \mathrm{o}\mathrm{r}\\ :& :& :\\ 6x-1& \mathrm{i}\mathrm{f}& i=6x-1,i=8x-1,\dots , i=4yx-1.\end{array}\right.$$

(10)

Hence,

$$v_{-i}=\left\{\begin{array}{lll}6x-1& \mathrm{i}\mathrm{f}& i=1,i=1+2x,\dots , i=4yx-6x+1,\mathrm{o}\mathrm{r}\\ 6x-2& \mathrm{i}\mathrm{f}& i=2,i=2+2x,\dots ,i=4yx-6x+2,\mathrm{o}\mathrm{r}\\ :& :& :\\ 4x& \mathrm{i}\mathrm{f}& i=2x,i=4x,\dots , i=4yx-4x,\mathrm{o}\mathrm{r}\\ 2x-1& \mathrm{i}\mathrm{f}& i=4yx-4x+1 \mathrm{a}\mathrm{n}\mathrm{d} i=4yx-2x+1,\mathrm{o}\mathrm{r}\\ 2x-2& \mathrm{i}\mathrm{f}& i=4yx-4x+2 \mathrm{a}\mathrm{n}\mathrm{d} i=4yx-2x+2,\mathrm{o}\mathrm{r}\\ :& :& :\\ 0& \mathrm{i}\mathrm{f}& i=4yx-2x \mathrm{a}\mathrm{n}\mathrm{d} i=4yx.\end{array}\right.$$

(11)

Then,

$$v_i-v_{-i}+i=\left\{\begin{array}{lll}0& \mathrm{i}\mathrm{f}& i=0,\mathrm{o}\mathrm{r}\\ 2-6x+i& \mathrm{i}\mathrm{f}& i=1 \mathrm{a}\mathrm{n}\mathrm{d} i=2x+1,\mathrm{o}\mathrm{r}\\ 4-6x+i& \mathrm{i}\mathrm{f}& i=2 \mathrm{a}\mathrm{n}\mathrm{d} i=2x+2,\mathrm{o}\mathrm{r}\\ :& :& :\\ i-2x-2& \mathrm{i}\mathrm{f}& i=2x-1 \mathrm{a}\mathrm{n}\mathrm{d} i=4x-1,\mathrm{o}\mathrm{r}\\ i-4x& \mathrm{i}\mathrm{f}& i=2x,\mathrm{o}\mathrm{r}\\ i& \mathrm{i}\mathrm{f}& i=4x,i=6x,\dots ,i=4yx-4x,\mathrm{o}\mathrm{r}\\ i-2x+2& \mathrm{i}\mathrm{f}& i=4x+1,i=6x+1,\dots ,i=4yx-6x+1,\mathrm{o}\mathrm{r}\\ i-2x+4& \mathrm{i}\mathrm{f}& i=4x+2,i=6x+2,\dots ,i=4yx-6x+2,\mathrm{o}\mathrm{r}\\ :& :& :\\ i+2x-2& \mathrm{i}\mathrm{f}& i=6x-1,i=8x-1,\dots ,i=4yx-4x-1,\mathrm{o}\mathrm{r}\\ i+4x& \mathrm{i}\mathrm{f}& i=4yx-2x,\mathrm{o}\mathrm{r}\\ i+2x+2& \mathrm{i}\mathrm{f}& i=4yx-4x+1 \mathrm{a}\mathrm{n}\mathrm{d} i=4yx-2x+1,\mathrm{o}\mathrm{r}\\ i+2x+4& \mathrm{i}\mathrm{f}& i=4yx-4x+2 \mathrm{a}\mathrm{n}\mathrm{d} i=4yx-2x+2,\mathrm{o}\mathrm{r}\\ :& :& :\\ 6x-2+i& \mathrm{i}\mathrm{f}& i=4yx-2x-1 \mathrm{a}\mathrm{n}\mathrm{d} i=4x-1.\end{array}\right.$$

(12)

Note that $\{v_i-v_{-i}+i:$  $i\in {\mathbb{Z}}_{4yx}\}={\mathbb{Z}}_{4yx}$. □

Example 5.

Let $y=3$ and $x=2;$ so, the vector $v\left(2{\mathbb{C}}_2^{\mathrm{1,1}}\right(K_{\mathrm{2,2}}\left)\right)=(0,1,2,3,0,1,2,3,8,9,10,11,8,9,10,11,8,9,10,11,8,9,10,11)$. Then, there exists an $ODC$ of $K_{\mathrm{24,24}}$ by $2{\mathbb{C}}_2^{\mathrm{1,1}}\left(K_{\mathrm{2,2}}\right)$; see Figure 10.

In Theorem 5, we construct a symmetric starter of an $ODC$ of $K_{xy,xy}$ by $\frac{x}{2}{\mathbb{C}}_2^{1,y-2}\left(P_3\right)$ using a symmetric vector. For more illustration, see Figure 11.

Theorem 5.

Let $y\ge 3$ and $x\equiv 2,4 mod 6$ be integers, then, the vector $v\left(\frac{x}{2}{\mathbb{C}}_2^{1,y-2}\right(P_3\left)\right)=(0,1,2,\dots ,x-1,x,x+1,x+2,\dots ,2x-1,\dots ,x,x+1,x+2,\dots ,2x-1)\in {\mathbb{Z}}_{yx}^{yx}$ is a symmetric starter vector of an $ODC$ of $K_{xy,xy}$ by $\frac{x}{2}{\mathbb{C}}_2^{1,y-2}\left(P_3\right)$.

Proof. 

From the vector $v\left(\frac{x}{2}{\mathbb{C}}_2^{1,y-2}\right(P_3\left)\right)$, we can define:

$$v_i=\left\{\begin{array}{lll}0& \mathrm{i}\mathrm{f}& i=0,\mathrm{o}\mathrm{r}\\ 1& \mathrm{i}\mathrm{f}& i=1,\mathrm{o}\mathrm{r}\\ :& :& :\\ x-1& \mathrm{i}\mathrm{f}& i=x-1,\mathrm{o}\mathrm{r}\\ x& \mathrm{i}\mathrm{f}& i=x,i=2x,\dots , i=(y-1)x,\mathrm{o}\mathrm{r}\\ x+1& \mathrm{i}\mathrm{f}& i=x+1,i=2x+1,\dots ,i=(y-1)x+1,\mathrm{o}\mathrm{r}\\ :& :& :\\ 2x-1& \mathrm{i}\mathrm{f}& i=2x-1,i=3x-1,\dots , i=yx-1.\end{array}\right.$$

(13)

Hence,

$$v_{-i}=\left\{\begin{array}{lll}2x-1& \mathrm{i}\mathrm{f}& i=1,i=x+1,\dots , i=yx-2x+1,\mathrm{o}\mathrm{r}\\ 2x-2& \mathrm{i}\mathrm{f}& i=2,i=x+2,\dots , i=yx-2x+2,\mathrm{o}\mathrm{r}\\ :& :& :\\ x& \mathrm{i}\mathrm{f}& i=x,i=2x,\dots , i=yx-x,\mathrm{o}\mathrm{r}\\ x-1& \mathrm{i}\mathrm{f}& i=yx-x+1,\mathrm{o}\mathrm{r}\\ x-2& \mathrm{i}\mathrm{f}& i=yx-x+2,\mathrm{o}\mathrm{r}\\ :& :& :\\ 0& \mathrm{i}\mathrm{f}& i=yx.\end{array}\right.$$

(14)

Then,

$$v_i-v_{-i}+i=\left\{\begin{array}{lll}0& \mathrm{i}\mathrm{f}& i=0,\mathrm{o}\mathrm{r}\\ 3-2x& \mathrm{i}\mathrm{f}& i=1,\mathrm{o}\mathrm{r}\\ 6-2x& \mathrm{i}\mathrm{f}& i=2,\mathrm{o}\mathrm{r}\\ :& :& :\\ i-2& \mathrm{i}\mathrm{f}& i=x-1,\mathrm{o}\mathrm{r}\\ i& \mathrm{i}\mathrm{f}& i=x,i=2x,\dots , i=yx-x,\mathrm{o}\mathrm{r}\\ i-x+2& \mathrm{i}\mathrm{f}& i=x+1,i=2x+1,\dots , i=yx-2x+1,\mathrm{o}\mathrm{r}\\ i-x+4& \mathrm{i}\mathrm{f}& i=x+2,i=2x+2,\dots , i=yx-2x+2,\mathrm{o}\mathrm{r}\\ :& :& :\\ i+x-2& \mathrm{i}\mathrm{f}& i=2x-1,i=3x-1,\dots , i=yx-x-1,\mathrm{o}\mathrm{r}\\ i+2& \mathrm{i}\mathrm{f}& i=yx-x+1,\mathrm{o}\mathrm{r}\\ i+4& \mathrm{i}\mathrm{f}& i=yx-x+2,\mathrm{o}\mathrm{r}\\ :& :& :\\ i+2x-2& \mathrm{i}\mathrm{f}& i=yx-1.\end{array}\right.$$

(15)

Note that $\{v_i-v_{-i}+i:$  $i\in {\mathbb{Z}}_{yx}\}={\mathbb{Z}}_{yx}.$ □

Example 6 is a direct application of Theorem 5.

Example 6.

Let $y=4$ and $x=4;$ so, the vector $v\left(2{\mathbb{C}}_2^{1,2}\right(P_3\left)\right)=(0,1,2,3,4,5,6,7,4,5,6,7,4,5,6,7).$ Then, there exists an $ODC$ of $K_{16,16}$ by $2{\mathbb{C}}_2^{1,2}\left(P_3\right)$; see Figure 12 and Figure 13.

Theorem 6.

Let $y,x\ge 3$ be integers, then the vector $v\left({\mathbb{C}}_2^{1,y-2}\right(C_2(1,x-2)\left)\right)=(0,1,1,\dots ,1,x,x+1,x+1,\dots ,x+1,\dots ,x,x+1,x+1,\dots ,x+1)\in {\mathbb{Z}}_{xy}$ is a symmetric starter vector of an $ODC$ of $K_{xy,xy}$ by ${\mathbb{C}}_2^{1,y-2}\left(C_2\right(1,x-2\left)\right)$.

Proof. 

From the vector $v\left({\mathbb{C}}_2^{1,y-2}\right(C_2(1,x-2)\left)\right)$, we can define:

$$v_i=\left\{\begin{array}{lll}0& \mathrm{i}\mathrm{f}& i=0,\mathrm{o}\mathrm{r}\\ 1& \mathrm{i}\mathrm{f}& 1\le i<x,\mathrm{o}\mathrm{r}\\ x& \mathrm{i}\mathrm{f}& i=x,i=2x,i=3x,\dots ,i=yx-x, \mathrm{o}\mathrm{r}\\ x+1& & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}\right.$$

(16)

Hence,

$$v_{-i}=\left\{\begin{array}{lll}0& \mathrm{i}\mathrm{f}& i=0,\mathrm{o}\mathrm{r}\\ x& \mathrm{i}\mathrm{f}& i=x,i=2x,i=3x,\dots ,i=yx-x, \mathrm{o}\mathrm{r}\\ 1& \mathrm{i}\mathrm{f}& yx-x<i\le yx,\mathrm{o}\mathrm{r}\\ x+1& & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}\right.$$

(17)

Then,

$$v_i-v_{-i}+i=\left\{\begin{array}{lll}0& \mathrm{i}\mathrm{f}& i=0,\mathrm{o}\mathrm{r}\\ i-x& \mathrm{i}\mathrm{f}& 1\le i<x,\mathrm{o}\mathrm{r}\\ i& \mathrm{i}\mathrm{f}& x\le i\le yx-x,\mathrm{o}\mathrm{r}\\ i+x& \mathrm{i}\mathrm{f}& yx-x<i<yx.\end{array}\right.$$

(18)

Note that $\{v_i-v_{-i}+i:$  $i\in {\mathbb{Z}}_{yx}\}={\mathbb{Z}}_{yx}$.

Example 7 is a direct application of Theorem 6. □

Example 7.

Let $y=3$ and $x=5;$ so, the vector $v\left({\mathbb{C}}_2^{\mathrm{1,1}}\right(C_2(1,3)\left)\right)=(0,1,1,1,1,5,6,6,6,6,5,6,6,6,6).$ Then, there exists an $ODC$ of $K_{15,15}$ by ${\mathbb{C}}_2^{1,1}\left(C_2\right(1,3\left)\right)$; see Figure 14.

In Theorem 7, we construct a symmetric starter of an $ODC$ of $K_{2xy,2xy}$ by $K_{y,2x}$ using symmetric vectors. For more information, see Figure 15.

Theorem 7.

Let $y,x\ge 2$ be integers, then the vector $v\left(K_{y,2x}\right)=\left(\right(x-1),(x-2),(x-3),\dots ,0,(2x-1),(2x-2),(2x-3),\dots ,x,\dots ,(x-1),(x-2),(x-3),\dots ,0,(2x-1),(2x-2),(2x-3),\dots ,x)\in {\mathbb{Z}}_{2yx}^{2yx}$, is a symmetric starter vector of an $ODC$ of $K_{2xy,2xy}$ by $K_{y,2x}.$

Proof. 

From the vector $v\left(K_{y,2x}\right)$, we can define:

$$v_i=\left\{\begin{array}{lll}x-1& \mathrm{i}\mathrm{f}& i=0,i=2x,\dots , i=2yx-2x,\mathrm{o}\mathrm{r}\\ x-2& \mathrm{i}\mathrm{f}& i=1,i=2x+1,\dots , i=2yx-2x+1,\mathrm{o}\mathrm{r}\\ :& :& :\\ 0& \mathrm{i}\mathrm{f}& i=x-1,i=3x-1,\dots , i=2yx-x-1,\mathrm{o}\mathrm{r}\\ 2x-1& \mathrm{i}\mathrm{f}& i=x,i=3x,\dots , i=2yx-x,\mathrm{o}\mathrm{r}\\ 2x-2& \mathrm{i}\mathrm{f}& i=x+1,i=3x+1,\dots ,i=2yx-x+1,\mathrm{o}\mathrm{r}\\ :& :& :\\ x& \mathrm{i}\mathrm{f}& i=2x-1,i=4x-1,\dots , i=2yx-1.\end{array}\right.$$

(19)

Hence,

$$v_{-i}=\left\{\begin{array}{lll}x& \mathrm{i}\mathrm{f}& i=1,i=1+2x,\dots , i=2yx-2x+1,\mathrm{o}\mathrm{r}\\ x+1& \mathrm{i}\mathrm{f}& i=2,i=2+2x,\dots , i=2yx-2x+2,\mathrm{o}\mathrm{r}\\ :& :& :\\ 2x-1& \mathrm{i}\mathrm{f}& i=x,i=3x,\dots , i=2yx-x,\mathrm{o}\mathrm{r}\\ 0& \mathrm{i}\mathrm{f}& i=x+1,i=3x+1,\dots , i=2yx-x+1,\mathrm{o}\mathrm{r}\\ 1& \mathrm{i}\mathrm{f}& i=x+1,i=3x+1,\dots ,i=2yx-x+2,\mathrm{o}\mathrm{r}\\ :& :& :\\ x-1& \mathrm{i}\mathrm{f}& i=2x,i=4x,\dots , i=2yx.\end{array}\right.$$

(20)

Then,

$$v_i-v_{-i}+i=\left\{\begin{array}{lll}0& \mathrm{i}\mathrm{f}& i=0,\mathrm{o}\mathrm{r}\\ i-2& \mathrm{i}\mathrm{f}& i=1,i=1+2x,\dots , i=2yx-2x+1,\mathrm{o}\mathrm{r}\\ i-4& \mathrm{i}\mathrm{f}& i=2,i=2+2x,\dots , i=2yx-2x+2,\mathrm{o}\mathrm{r}\\ :& :& :\\ i-2x+2& \mathrm{i}\mathrm{f}& i=x-1,i=3x-1,\dots , i=2yx-x-1,\mathrm{o}\mathrm{r}\\ i& \mathrm{i}\mathrm{f}& i=x,i=2x,\dots , i=2yx-x,\mathrm{o}\mathrm{r}\\ i+2x-2& \mathrm{i}\mathrm{f}& i=x+1,i=3x+1,\dots , i=2yx-x+1,\mathrm{o}\mathrm{r}\\ i+2x-4& \mathrm{i}\mathrm{f}& i=x+2,i=3x+2,\dots , i=2yx-x+2,\mathrm{o}\mathrm{r}\\ :& :& :\\ i+2& \mathrm{i}\mathrm{f}& i=2x-1,i=4x-1,\dots , i=2yx-1.\end{array}\right.$$

(21)

Note that $\{v_i-v_{-i}+i:i\in {\mathbb{Z}}_{2yx}\}={\mathbb{Z}}_{2yx}.$ □

Example 8 is a direct application of Theorem 7.

Example 8.

Let $y=2$ and $x=4;$ so, the vector $v\left(K_{2,8}\right)=(3,2,1,0,7,6,5,4,3,2,1,0,7,6,5,4).$ Then, there exists an $ODC$ of $K_{16,16}$ by $K_{2,8}$; see Figure 16.

In Theorem 8, we construct a symmetric starter of an $ODC$ of $K_{y^2,y^2}$ by $\frac{y}{2}{K}_{2,y}$ using a general symmetric vector. For more illustration, see Figure 17.

Theorem 8.

Let $y\equiv 2 mod 6$ and $y\equiv 4 mod 6,$ then the vector $v\left(\frac{y}{2}{K}_{2,y}\right)=(0,0,..,0,y,y,..,y,2y,2y,..,2y,3y,3y,..,3y,\dots \dots ,y(y-1),y(y-1),..,y(y-1\left)\right)\in {\mathbb{Z}}_{y^2}^{y^2},$ is a symmetric starter vector of an $ODC$ of $K_{y^2,y^2}$ by $\frac{y}{2}{K}_{2,y}$.

Proof. 

From the vector $v\left(\frac{y}{2}{K}_{2,y}\right),$ we can define:

$$v_i=\left\{\begin{array}{lll}0& \mathrm{i}\mathrm{f}& i<y,\mathrm{o}\mathrm{r}\\ y& \mathrm{i}\mathrm{f}& y\le i<2y,\mathrm{o}\mathrm{r}\\ 2y& \mathrm{i}\mathrm{f}& 2y\le i<3y,\mathrm{o}\mathrm{r}\\ 3y& \mathrm{i}\mathrm{f}& 3y\le i<4y,\mathrm{o}\mathrm{r}\\ :& :& :\\ y(y-1)& \mathrm{i}\mathrm{f}& y(y-1)\le i<y^2.\end{array}\right.$$

(22)

Hence,

$$v_{-i}=\left\{\begin{array}{lll}y(y-1)& \mathrm{i}\mathrm{f}& 1\le i\le y,\mathrm{o}\mathrm{r}\\ y(y-2)& \mathrm{i}\mathrm{f}& y<i\le 2y,\mathrm{o}\mathrm{r}\\ y(y-3)& \mathrm{i}\mathrm{f}& 2y<i\le 3y,\mathrm{o}\mathrm{r}\\ y(y-4)& \mathrm{i}\mathrm{f}& 3y\le i<4y,\mathrm{o}\mathrm{r}\\ :& :& :\\ y(y-y)& \mathrm{i}\mathrm{f}& y(y-1)<i\le y^2.\end{array}\right.$$

(23)

Then,

$$v_i-v_{-i}+i=\left\{\begin{array}{lll}0& \mathrm{i}\mathrm{f}& i=0,\mathrm{o}\mathrm{r}\\ 0-y(y-1)+i& \mathrm{i}\mathrm{f}& 1\le i<y,\mathrm{o}\mathrm{r}\\ y-y(y-2)+i& \mathrm{i}\mathrm{f}& y<i<2y,\mathrm{o}\mathrm{r}\\ 2y-y(y-3)+i& \mathrm{i}\mathrm{f}& 2y<i<3y,\mathrm{o}\mathrm{r}\\ :& :& :\\ y(y-1)-y(y-y)+i& \mathrm{i}\mathrm{f}& y(y-1)<i<y^2,\mathrm{o}\mathrm{r}\\ y-y(y-1)+i& \mathrm{i}\mathrm{f}& i=y,\mathrm{o}\mathrm{r}\\ 2y-y(y-2)+i& \mathrm{i}\mathrm{f}& i=2y,\mathrm{o}\mathrm{r}\\ 3y-y(y-3)+i& \mathrm{i}\mathrm{f}& i=3y,\mathrm{o}\mathrm{r}\\ 4y-y(y-4)+i& \mathrm{i}\mathrm{f}& i=4y,\mathrm{o}\mathrm{r}\\ :& :& :\\ y(y-1)-y(y-(y-1\left)\right)+i& \mathrm{i}\mathrm{f}& i=y(y-1).\end{array}\right.$$

(24)

Note that $\{v_i-v_{-i}+i:$ $i\in {\mathbb{Z}}_{y^2}\}={\mathbb{Z}}_{y^2}$. □

Example 9 is a direct application of Theorem 8.

Example 9.

Let  $y=4;$ so, the vector$v\left(2K_{2,4}\right)=(0,0,0,0,4,4,4,4,8,8,8,8,12,12,12,12).$ Then, there exists an$ODC$ of $K_{16,16}$ by$2K_{2,4}$; see Figure 18.

Finally, we constructed the decompositions and $ODC$s of complete bipartite graphs $H$ by graphs $G.$ The results obtained in Section 3 are united in

Table 2. Summary of results based on Section 3.

$\mathit{H}$	$\mathit{G}$
$K_{y^2,y^2}$	$\frac{y}{2}{K}_{2,y}$
$K_{2xy,2xy}$	$K_{y,2x}$
$K_{xy,xy}$	${\mathbb{C}}_2^{1,y-2}\left(C_2\right(1,x-2\left)\right)$
$K_{xy,xy}$	$\frac{x}{2}{\mathbb{C}}_2^{1,y-2}\left(P_3\right)$
$K_{4xy,4xy}$	$x{\mathbb{C}}_2^{1,y-2}\left(K_{\mathrm{2,2}}\right)$
$K_{2xy,2xy}$	${\mathbb{C}}_2^{1,y-2}\left(K_{2,x}\right)$
$K_{2xy,2xy}$	$2{\mathbb{C}}_2^{1,y-2}\left(S_x\right)$
$K_{xy,xy}$	${\mathbb{C}}_2^{1,y-2}\left(S_x\right)$

as follows:

It should be emphasized again that the main advantage of the symmetric starter vectors method is that it is much easier to implement than, for example, the direct method, function-half starter method, and matrices method. However, it also has the limitation that some graphs do not have a symmetric starter; so, the orthogonal double covers cannot be constructed by these graphs based on the symmetric starter method. In these cases, it is not applicable, and alternative methods must be used.

4. Use Case

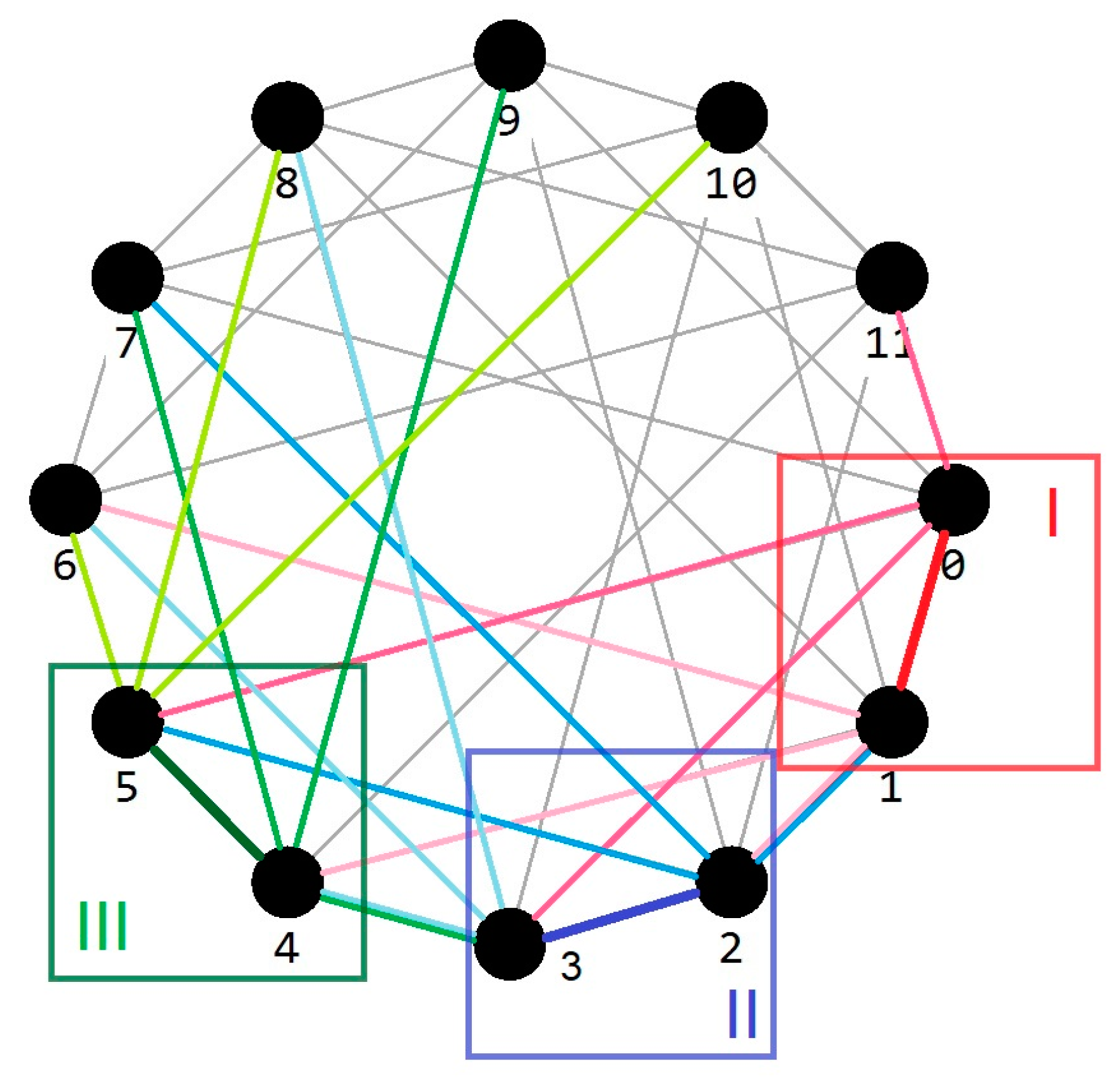
Consider various examples of how the developed theory can be applied in practice.

4.1. Local-to-Global Governments Public Elections

In the ‘Application’ section of work [43], an example of a task to analyze the election procedure of local governments in some countries is described. A model of relations between participants in the election process based on their portfolio and desired positions in the local government was built in the form of a graph, and a competition graph under interval-valued $m$-polar fuzzy environment to solve this problem was applied. Fuzzy competition graphs have a widespread use in various fields [44,45]. Using the proposed approach, the authors convincingly demonstrate how it is possible to plan the distribution of candidates for the appropriate positions in the local government so that they suit them best.

This task can be complicated and expanded if we accept the thesis that local governments (for example, from the level of cities or states) can win delegates to positions in the “global” government at the level, for example, of a country (parliament, council of a country, etc.). That is, if the basic approach is maintained, the problem can first be solved at the level of graphs of relations between local governments and then at the level of the graph above. However, if we represent the local relationship graph as a caterpillar graph, the description of the global relationship graph can be reduced to constructing $ODCs$ by caterpillar graphs using general symmetric starter vectors described and solved in this article (in general, a symmetric starter may not only be a caterpillar graph; ODS is good because the circulant is completely symmetrical to its vertices, i.e., all vertices are completely equal in terms of the election procedure). This means that the method from [43] can be applied to the entire global graph. This approach has the advantage that candidates for seats in local governments will be able to apply for positions in the governments of neighboring regions, thereby increasing variability and the ability to better match the right candidates for the right positions, as well as it is (theoretically) possible to achieve an acceleration of the calculations themselves.

4.2. On-Chip Communication Networks

Complete bipartite graphs are widely used in various areas of communication networks [26,46]. At the same time, if the network is large, there is a problem of finding routes and managing traffic in such networks [1,47]. It is solved, for example, by using the principle of small-world networks [48,49] by grouping nodes on a regular basis that are interconnected by the intensive communication traffic [32]. When referring to on-chip communication networks, the principles of organizing global networks using network-on-chip technology are then still supplemented by the use of communication buses [50,51,52], which have a very developed support at the level of CAD, IP cores, and their interfaces, and also are well-standardized.

The mathematical apparatus proposed in this paper allows for performing the decomposition of large graphs into simpler caterpillar graphs, whose features are the presence of the main route between nodes and branches from it. This route is very suitable for its implementation as a bus [53]. That is, in large graphs, separate sections (caterpillar subgraphs) which can be organized locally using communication buses can be distinguished.

Let us observe this concept with an example. It is known that in on-chip networks, there can be communication links of different bandwidths designed to transmit the traffic of different priorities and implement different levels of virtual channels [54]. The natural structure for complete bipartite graphs is to allocate circulant subgraphs for such tasks [55]. For example, in $K_{12,12}$, a circulant subgraph of the form $C(12;1,3,5)$ can be distinguished. The use of a ring circulant allows reflecting the local connectivity of neighboring routers in terms of location on the chip. Although such a circulant is much simpler than a complete bipartite graph, it nevertheless contains quite a lot of links, and the question is how to implement it as a communication environment on chip. Additionally, to implement routing, each router must store a routing table [56] for 12 nodes.

We propose to segment the graph along the outer ring into pairs of nodes, selecting from them $C_2(3,3)$; the main path is implemented by a high-performance bus [53], and the outer connections are implemented by links with a lower bandwidth. Thus, it is possible to reduce the size and number of routing tables (the number of segments (I, II, III, etc.) become 2-times less than nodes; one common table is stored per segment for two nodes). An illustration of such a partition is shown in Figure 19.

This approach can be applied to graphs with an even number of nodes. The length of the main path in caterpillar graphs must be less than the length of the second circulant generator.

5. Conclusions

We construct $ODC$s of $K_{x,x}$ by new general symmetric starter graphs and disjoint copies of symmetric starter graphs using general symmetric starter vectors of caterpillar graphs such as stars–caterpillar, the disjoint copies of cycles–caterpillars, the complete bipartite caterpillar graphs, and the disjoint copies of caterpillar paths. To the best of our knowledge, this paper is the first to construct the $ODC$s and decompositions of complete bipartite graphs using the caterpillar graph. The decomposition of giant graphs into large groups of small graphs allows us to quickly access information due to the ever-expanding growth of information represented by giant networks stored on massive servers using the disjoint copies of symmetric starter graphs compared to using one symmetric starter graph. The general symmetric starter vectors are very useful in many applications such as comprehensive coverage and the analysis of large networks relational databases, the statistical design of experiments, and design theory. It should be noted that not all the graphs have a symmetric starter. An illustrative example of applying the proposed graph decomposition approach in a practical example for on-chip networks is given. In the future, we will try to generalize the results obtained in this paper to the mutually orthogonal graph squares that have several applications in combinatorial design theory.