Abstract
Many real-world applications of the vehicle routing problem (VRP) are arising today, which range from physical resource planning to virtual resource management in the cloud computing domain. A common trait of these applications is usually the large scale size of problem instances, which require fast algorithms to generate solutions of acceptable quality. The basis for many VRP approaches is a heuristic which builds a candidate solution that may subsequently be improved by a local search procedure. Since there are many variants of the basic VRP model, specialised algorithms must be devised that take into account specific constraints and user-defined objective measures. Another factor is that the scheduling process may be carried out in dynamic conditions, where future information may be uncertain or unavailable or may be subject to change. When all of this is considered, there is a need for customised heuristics, devised for a specific problem variant, that could be used in highly dynamic environments. In this paper, we use genetic programming (GP) to evolve a suitable dispatching rule to build solutions for different objectives and classes of VRP problems, applicable in both dynamic and stochastic conditions. The results show great potential, since this method may be used for different problem classes and user-defined performance objectives.
1. Introduction
In the transport industry, planning and scheduling are of utmost importance to minimise expenses and provide a consistent quality of service. To adequately model real-world transportation and service delivery, a number of Vehicle Routing Problem (VRP) variants have been formulated. The underlying mathematical representation of such problems in operational research is dated from 1959 when it was defined in [1] as the “Truck Dispatching Problem”. This model includes a fleet of vehicles that need to travel in order to provide means of transportation or perform services at remote locations. VRP problems are a class of NP-hard discrete combinatorial optimisation problems and hence unlikely to be solvable in polynomial time [2].
In this paper, we focus on dynamic VRP scenarios [3,4], which include consideration of two important aspects in real-life applications: the availability and reliability of information. In most problem instances considered, all input is known beforehand, which corresponds to information availability. Furthermore, the information is considered static, and it is presumed that vehicle routes do not change while in execution.
In contrast to this, one can approach the problem with most of the input available, while also allowing that part of the information is revealed dynamically during execution (evolution of input data). This is considered to be a dynamic VRP, and may include additional information or changes in current requirements. Common sources of dynamic change are arrivals of new customer requests, changes in travel time due to current traffic conditions, as well as vehicle availability, such as the possible breakdown of vehicles.
Furthermore, regardless of the moment in time in which the information becomes available, during the execution actual values of VRP variables may also be subject to change. For instance, the expected travel time may be prolonged, or the customer request constraints may be altered due to unforeseen events. In this case, the problem is also considered to be stochastic, and final input and output values are only known after the schedule is executed. While we do not use stochastic modelling in this paper, we propose an approach that can also be used under stochastic conditions.
Dynamic conditions may also impose different criteria for schedule optimisation, such as the number of serviced requests in time (throughput), minimisation of response time or tardiness of service. Existing heuristics are not designed to optimise arbitrary criteria which could be defined by the user; it would be necessary to design a new heuristic to handle such a case. Therefore, selecting an appropriate algorithm and applying it in dynamic conditions is generally not straightforward.
Instead of manually selecting (or even guessing) which heuristic would be suitable in dynamic conditions, we propose to evolve (i.e., automatically generate) an appropriate heuristic, in the form of a dispatching rule, with the use of genetic programming [5]. This kind of approach is identified as a hyper-heuristic [6,7,8] since GP is searching the space of possible algorithms, rather than the space of possible routes. Genetic programming can evolve any form of an algorithm, provided a given definition of its building elements and a measure of algorithm quality (the fitness function). With this approach, we may create heuristics tailored to the problem at hand, regardless of the given performance objective and specific constraints [9,10,11].
The hyper-heuristic approach presented in this paper aims at providing the following:
- applicability in dynamic and stochastic VRP environments;
- an approach of generating dispatching rules to optimise routes for arbitrary user-defined criteria;
- possibility to generate solutions of acceptable quality for very large instances of VRP;
- the means of producing an initial solution that may be used for a subsequent decomposition approach.
To be able to achieve this, we identify and propose the following main contributions:
- definition of schedule generation algorithms and a learning environment for automatic development of VRP heuristics;
- definition of functional and terminal elements for two VRP variants: capacitated VRP (CVRP) and VRP with time windows (VRPTW);
- automated development of dispatching rules for static and dynamic instances of CVRP and VRPTW;
- automated optimisation of arbitrary criteria, such as soft constrained time windows and minimisation of vehicle time travel deviation.
It must be noted that the aim of this approach is not the generation of optimal or near-optimal solutions. If one is able to devote an arbitrary amount of time for creating the schedule, more efficient solutions can always be obtained by using improvement heuristics. However, if changes occur during the actual execution of the system (i.e., while vehicles are on route), one may not have enough time available to rebuild the rest of the schedule taking new information into account. Furthermore, most improvement heuristics are not easily accommodated to the fact that a partial schedule is already underway, and only the unfinished part must be optimised (constructive heuristics are readily applicable in this case).
On the other hand, using the hyper-heuristic approach, one is able to find simple heuristics that operate very fast and are suitable in both dynamic and stochastic conditions. Furthermore, by setting an appropriate performance measure, the user can generate customised heuristics that perform well given specific constraints or requirements.
The rest of the paper is organised as follows; in the following section the motivation and related work are briefly discussed. Section 3 describes the proposed approach and is central to the paper. Section 5 and Section 6 show the application of the hyper-heuristic to CVRP and VRPTW variants, respectively. Section 7 offers a discussion about the scalability and parameter sensitivity, as well as outlining some avenues for future research. Finally, Section 8 concludes the paper.
2. Motivation and Related Work
Since contemporary VRP problem instances include hundreds or thousands of requests, they are usually not amenable to be solved with exact methods. Instead, heuristic methods or fuzzy systems [12,13] are commonly used to provide a good enough solution which satisfies user-defined criteria. Heuristic methods may be further divided into two categories: the first group consists of search-based algorithms which search the space of solutions (routes) to find the best one. The second group are problem-specific constructive heuristics that build the solution using some features of the problem.
Search-based methods (such as evolutionary algorithms, ant colony optimisation, particle swarm optimisation, etc.) can be used to solve the VRP. Although the solutions obtained are often of a good quality, these methods require a substantial computational time to reach solutions of acceptable quality (since they search the entire solution space). Additionally, in dynamic conditions the search based methods usually have to be adapted in some way. In this case the search space considers only the pending requests, but the current condition of the system (e.g., vehicles currently on the way) must be taken into account by adding explicit or implicit constraints into the algorithm.
Constructive heuristics, on the other hand, directly build the solution and can therefore quickly react to changes in the environment, making them usable in dynamic conditions, since their computational complexity is almost negligible. However, it is often hard to select the most appropriate heuristic for the given VRP variant, objective criteria and problem instance, which is also evident in other problems, such as in scheduling [8,14].
A significant effort has been devoted to devising efficient solvers for the static variant of the vehicle routing problem. Various algorithms, mostly based on metaheuristics, have been used as optimisation techniques in the VRP domain [15]. Several survey papers outline in more detail the research conducted in the area of VRPs [16,17,18,19].
In [20] a tabu search optimisation is used to tackle the VRP problem with soft time windows, which means that lateness at a customer location is allowed but it incurs a certain penalty. The authors introduced a new neighbourhood structure, which has allowed the algorithm to achieve some of the best-known results on specific benchmark problems. A simulated-annealing-like-based local search was proposed in [21], which was applied to the VRP with time windows. The proposed method combined tabu search with simulated annealing and obtained results suggest that the method is comparable to other metaheuristic methods. Models describing different evolutionary methods for VRP were presented in [22,23]. The latter also introduced a two phase approach, in which a problem specific heuristic generates an initial solution in the first phase, which is then improved via local search in the second phase. The method was tested on several large scale problems and achieved a good performance on most of the problem instances. Ant-colony optimisation was used in [24], where the proposed approach is based on a parallel local search algorithm, once the solution space is decomposed into small enough instances. A decomposition technique which reduces the number of vehicles and can also be executed in parallel was described in several applications [25,26]. This approach requires a suitable initial solution to be constructed beforehand, and that part is mostly performed by a constructive heuristic method. Many of these solving procedures rely on a reasonably good initial solution, which is then improved with metaheuristics [27,28], local search algorithms [29], decomposition techniques and combinations of those. The incremental improvement approach is in most applications used only in static scheduling conditions, since the improvement algorithm usually operates on a fixed problem instance while it searches for a better solution. In this context, genetic programming was applied in [30] as a method for generation of new heuristic functions that can be used for constructing initial solutions for VRP with time windows, which were then improved with a decomposition approach. A hyper-heuristic method which selects existing heuristics for creating and improving a solution is proposed in [31]. The hyper-heuristic method is based on the iterative local search algorithm which determines the actions that need to be performed on the initial solution in order to improve it. The proposed method was compared to several approaches and the results show that it achieved better overall performance.
In dynamic conditions, on the other hand, the static approaches cannot usually be used without some adaptation. Since part of the customer information becomes available during the system execution, the problem instance can only be completely described at the end of the planning horizon. Therefore, no method can provide the optimal solution before the schedule is completed; instead, “optimal” choices can only be given for the current state of the system. Because of the previous, dynamic solvers usually rely on heuristic approaches that are able to quickly obtain a solution to the current state of the problem.
It is possible to adapt the improvement metaheuristic methods for use in dynamic conditions; in [32] the authors employ a parallel tabu search with many variants of possible routes. The existing routes are compared to new customer requests and a decision is made whether the request should be accepted or rejected. The authors experimented with dynamic VRP with and without time dependent travel times [33], and a similar approach was applied in [34]. A smaller number of applications also considered the stochastic variant of the VRPTW [35], in which new customer requests arrive over time. In order to tackle this problem the authors use probabilistic knowledge of the future and define a strategy which introduces dummy customers to better cover the entire territory.
Genetic algorithms (GA) were extensively used to solve static VRP instances, but have also been applied for the dynamic VRP [36] and pick up and delivery (PDP) problems [37]. In these applications, the GA is modified for use in dynamic conditions in the way that it is in fact constantly running concurrently with the execution of the system. The solutions produced by the GA are thus adapting on-the-fly to new information when it becomes available. Another metaheuristic, Ant Colony System (ACS), has also been used to solve the dynamic VRP in [38]. In this application, the scheduling horizon is a priori divided into time slices of equal duration, and a separate ACS is run for each time slice. Only the information related to the current time slice is taken into account, under the assumption that the requests can be postponed. Similar modifications by using ACS are used in [39]. In [40], an ACS is also applied for solving dynamic VRP with time windows, in a similar manner as in the previous two papers. The proposed ACO algorithm uses a joint solution construction mechanism, which constructs in parallel routes of the vehicles. The approach is combined with a local search procedure in order to improve its performance. The authors test the approach on problems with variable dynamics, which means that they vary the amount of orders that are known at the beginning of the system and those that are released over time. In [41] the dynamic VRP problem was tackled by using an evolutionary hyper-heuristic method which uses three different types of simple heuristic procedures for constructing and improving the schedule, and the order in which these heuristics are used and their parameters are optimised by using an evolutionary algorithm. The dynamic VRP with time windows and stochastic customers was considered in [42]. In order to tackle the dynamic problem, the authors propose a new decision rule, called GSA, which at each step chooses the next action to perform. The results demonstrate that the proposed method produces results comparable to the state of the art and that it leads to better decisions in a stochastic context. Genetic programming has also demonstrated its potential when applied to the dynamic pickup and delivery problem in [43]. The paper compared several genetic programming settings and problems with varying levels of dynamism, urgency and scale. The results show that the evolved heuristic obtained a competitive performance when compared to traditional approaches.
In all of these examples, the practitioner is bound by the time available to reach a decision for the next state of the system. While the current solution can always be improved given enough time, changes can occur in each moment after a single solution has been chosen, and the reaction time may be crucial in some applications. In the next section, we present the hyper-heuristic approach that aims to provide a solution in a negligible amount of time, taking into account current conditions and user-defined criteria. After the solution is obtained, it can also be modified using improvement heuristics if additional time is available.
3. Hyper-Heuristic Approach for VRP
3.1. Capacitated Vehicle Touting Problem
The capacitated VRP (CVRP) is described as follows: a set of n customers must be serviced from a central depot using vehicles of equal given capacity, denoted with Q. Each customer must be served by exactly one vehicle. A customer is defined with the following parameters:
- demand ;
- geographical data.
The scheduling task includes constructing a (minimal) number of routes, specifying the order in which vehicles are servicing disjunct sets of customers. The goal is usually to minimise the number of vehicles and the total distance, while the total demand for each route may not exceed the capacity of the vehicle which serves that route. In other words, for each route r the following condition must hold: , where m is the number of customers on route r.
3.2. Vehicle Routing Problem with Time Windows
The vehicle routing problem with time windows (VRPTW) is an extension of the VRP, defined in [44]. The VRPTW includes an additional constraint, which is that every customer must be serviced within a given time window . If a vehicle arrives earlier it must wait for the window opening time; if the vehicle arrives after the end of the time window, the solution is not valid. Every customer has the following parameters defined:
- ready time —window opening time;
- due date —window closing time;
- service time —time needed for the customer to be serviced;
- demand —customer capacity;
- geographical data.
Waiting time may be induced at customer v if the vehicle arrives at the customer before its window opening time. In both of these variants, usually two objective criteria are used: the primary is to minimize the number of vehicles and the secondary to reduce the total travel distance.
3.3. Generating Heuristics for VRP
The scheduling method applied in this work is priority scheduling, in which certain elements of the system are assigned priority values. In the classic scheduling theory, the typical elements are jobs (activities) and machines (resources), but the same logic can be applied to VRP scheduling with customers and vehicles. The choice of the next customer for a particular vehicle is based on the customer’s priority value, which may be determined dynamically. This type of scheduling algorithm is also called, variously, ‘dispatching rule’, ‘scheduling rule’ or just ‘heuristic’.
The term dispatching rule (DR), in a narrow sense, often represents only the priority function that assigns values to system elements [45]. For instance, in classic scheduling a scheduling process may be described with the statement ‘scheduling is performed using the shortest processing time (SPT) rule’, in which case jobs are sequenced in increasing order of their processing times. In VRP, a very simple heuristic may be the one that, for every vehicle, chooses the current closest customer as the next one. In terms of priority scheduling, we can say that the priority function applied to each customer is equal to that customer’s current distance.
While the method of assigning vehicles to customers based on priority values may be trivial, in some environments it is not necessarily so. This is particularly true in dynamic conditions, where orders may arrive over time or may not be serviced before some condition is met. Even when the priority function is defined, an additional procedure must be defined dictating how customers are serviced based on their priorities and possible system constraints.
In accordance to existing scheduling nomenclature, we name this component a meta-algorithm [9,10,46], or alternatively a schedule generation scheme (SGS) [47,48], which is a term commonly used in production scheduling. A meta-algorithm encapsulates the priority function, but the same meta-algorithm may be used with different priority functions and vice versa. In this work, the meta-algorithm is defined manually; the priority function, on the other hand, is evolved automatically with genetic programming and represented using appropriate functions and variables. This way, using the same meta-algorithm, different scheduling heuristics best suited for various criteria can be devised.
We propose two meta-algorithms, which differ by the way they construct the entire schedule, and consequently by the conditions they can be used in. The first meta-algorithm is a serial one, which builds the schedule incrementally by constructing routes one vehicle at a time. This approach is most commonly used in existing VRPs and is depicted in Algorithm 1.
| Algorithm 1 Serial VRP meta-algorithm |
|
We emphasise that the same meta-algorithm may be used for any VRP flavor; at the same time, the meta-algorithm does not depend on any concrete priority function, which means that many different priority functions can be used with the given meta-algorithm. As a consequence, the meta-algorithm can use priority functions which optimise different objectives. Note that the condition “valid customer” may have a very different meaning for different VRP variants. For instance, in CVRP this will only constrain the available choices to those customers whose demand does not exceed the remaining capacity of the current vehicle. For VRPTW, on the other hand, this will also constrain the choice to those customers which can be serviced in the defined time frame. The selection of the next valid customer to service is left entirely to the priority function. The definition of “best value” of the priority function is quite arbitrary, but in this case we use the lowest returned value as the best one (other options include the maximum value, minimum absolute value etc.). For instance, if the priority function equals simply the distance to the customer, then the same priority function will be evaluated for every possible customer, and the customer with the lowest priority value (the smallest distance) will be selected as the next customer for this vehicle.
Another meta-algorithm we propose is a parallel one that builds the schedule concurrently for every vehicle. This variant is defined as Algorithm 2. The parallel algorithm requires one important input, which is the current number of vehicles. If the given number of vehicles is insufficient to construct a valid schedule, then this value can be increased and the algorithm rerun. However, in our simulations this is not needed for the following reasons. While the serial meta-algorithm can be used in static conditions, where the schedule is constructed beforehand, it cannot be used during the actual execution of the system, for instance after an interruption has happened (such as a vehicle failure). In the case of dynamic conditions, we can use the parallel meta-algorithm to construct the remainder of the schedule, and in that case, the current number of vehicles is always known to the algorithm. The presented approach with the parallel meta-algorithm can also be used for stochastic VRP, where the actual parameter values are not known with certainty until the related event occurs. While we do not model a stochastic VRP in our experiments, the parallel algorithm can be readily applied in those conditions, since it builds the remainder of the schedule starting from any given moment in time with an arbitrary system state. Furthermore, for environments such as CVRP, the required minimum number of vehicles can always be determined beforehand based on given demand, vehicle capacity and other possible constraints.
| Algorithm 2 Parallel VRP meta-algorithm |
Input: number of vehicles to use
|
The time complexity of priority scheduling depends on the meta-algorithm, but it is in most cases negligible compared to search-based techniques, which allows using this method for on-line scheduling [49] and in dynamic conditions. It should be noted that the priority function must be previously evolved. The evolution process itself may take several hours on average, but this can always be performed offline, before the actual scheduling occurs.
3.4. Genetic Programming
Genetic programming [50] is an optimisation and machine learning method that uses simulation of evolution to automatically discover symbolic solutions (functions and programs) to the problem at hand. The main idea behind GP is that the solution to the problem may be represented as a (computer) program, in most applications in the form of a syntactic tree. The elements of the programs (tree nodes) must be predefined by the user and must be sufficient to describe the solution to the problem (e.g., mathematical and logical functions, variables, actions such as move forward, turn left etc.). In this case, we restrict the solutions to priority functions consisting of arithmetical and logic operators, as well as variables corresponding to the current VRP state. The algorithm randomly generates a set of trees (potential solutions) and evaluates each one on a predefined set of test cases. Test cases describe how well the candidate solution solves the given problem, e.g., how well does the function represented in the tree describe the data. In this paper, test cases will be represented by different VRP instances. Each potential solution thus receives its quality estimate - the fitness value - which is then used in the selection process.
The selection process imitates natural evolution where weaker solutions (individuals) are eliminated, and better individuals survive. Additionally, better individuals also participate in recombination, where two or more individuals are combined to form a new one. The algorithm also incorporates a mutation mechanism, where a single individual undergoes a random change, with a relatively small probability. The process continues, building new generations from old ones until a suitable termination criterion is reached. Termination criteria usually include finding a solution of the desired quality, evaluating a given number of potential solutions or running the algorithm for a predefined amount of time. The examples of human competitive results of genetic programming may be found in [51]. For priority functions evolution, the Evolutionary Computation Framework (ECF) http://ecf.zemris.fer.hr/ (accessed on 3 October 2022) was used.
3.5. Creating Priority Functions with GP
In this paper, genetic programming is used to automatically create the priority function used in the above meta-algorithms. The priority function is represented as a syntax tree, where inner nodes are operators and leaves are terminals (function inputs, domain variables). The operator and terminal set must be previously defined and they should give the GP information needed to construct an adequate priority function. In this work, we use the following operators (functional elements and inner nodes of a tree) listed in Table 1.

Table 1.
Functional elements used by GP.
This function set is based on our previous experience with GP, as well as on a small set of tuning experiments to estimate the efficiency of individual operators. Aside from these, we define a separate terminal set (set of variables, tree leaves) for each considered VRP variant. For example, all the variants will include the terminal dist, which simply gives the distance of the current considered vehicle to the current considered customer. This way, the GP is able to create new priority functions that match the current conditions and user-defined criteria. GP uses the standard tree representation to encode priority functions. An example of a random GP tree that denotes a potential priority function of a DR is shown in Figure 1 (the terminal sets are defined below).
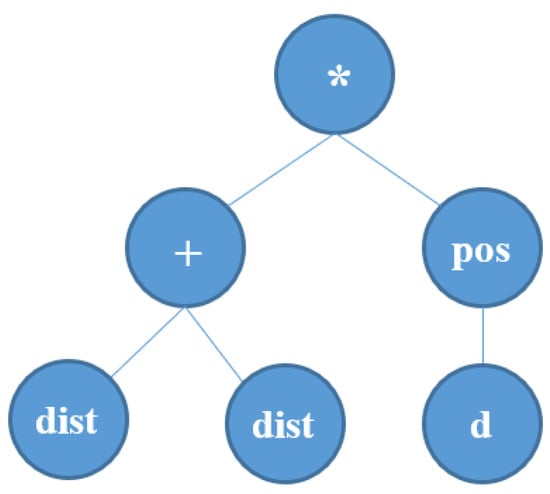
Figure 1.
An example GP tree representing a priority function .
GP creates a set of priority functions (individuals) in each generation, and each of those must be evaluated. The initial population is generated using the standard ramped half-and-half solution initialisation method. After the whole generation is evaluated, genetic operators (crossover, mutation and selection) are performed, thus producing the next generation of individuals (new candidate functions). The whole process is repeated until a predefined stopping criterion is met.
The evolutionary algorithm in this work uses a steady-state selection process, shown in Algorithm 3, where in each iteration only one individual from the population is replaced with a new one. The selection of the individual to be replaced is performed in a tournament of size three: the algorithm selects three individuals at random and eliminates the worst of those. The remaining tournament survivors are then used as parents to create a new individual using crossover. The crossover operators used are simple tree crossover, uniform crossover, size fair, one-point, and context preserving crossover [5], selected at random each time a crossover is performed. Following its creation, the new individual immediately undergoes mutation, which depends on the mutation rate parameter. In our experiments, this parameter equals 0.5, which results in five out of ten new individuals being mutated on average, and the operator is sub-tree mutation [5]. This kind of algorithm is convenient since it eliminates the need for specifying the crossover rate, and based on our previous experience provides a steady rate of convergence. Regarding the choice of genetic operators, in our previous experience with hyper-heuristic applications, different operators did not have a significant impact. In summary, we use the parameters for genetic programming as given in Table 2.
| Algorithm 3 Steady-state tournament selection |
|

Table 2.
Genetic programming parameters.
Finally, in all the experiments we evolve the candidate priority functions on the learning set of problem instances, selected for the given VRP flavor. Each individual is evaluated by optimising a selected criterion (number of vehicles, total distance, total tardiness, or combinations of these criteria) on each instance in the problem set. The total fitness value on the problem set is calculated as an aggregation of the individual fitness values obtained on each of the problem instances. However, the final set of evolved priority functions are evaluated on a separate test set of problem instances, which is a common procedure in machine learning. This cross-evaluation estimates the generalisation ability of the proposed approach, and separate learning and test sets are defined for every considered problem variant.
4. Experimental Setup
To test the proposed approach of automatically designing DRs for the VRP, the GP method described in the previous section is applied on two VRP problem variants: CVRP and VRPTW. Furthermore, both variants are investigated under static and dynamic case. The static case denotes the case in which all customers are known beforehand, meaning that all the information about the problem is known at the start of solving. On the other hand, in the dynamic case, not all customers are known at the start, but rather they become available as time progresses. In this case, we investigate the influence of different level of dynamism on the performance of the method, 5%, 25%, and 50%, which denote the number of customers that are not known up front and become available at a later point in time.
To test the approach for CVRP the problem instances proposed by Golden et al. are used [52], whereas for the VRPTW variant the instances proposed by Solomon are used [42]. Both problem sets are divided into a training set, which is used by GP to evaluate the rules during the evolution process, and a test set, which is used after training to evaluate the quality of the evolved rules on unseen instances and compare the results. The division of the problem sets is described in more detailed in the subsequent sections. The approaches are evaluated across several criteria that are commonly considered in VRP problems, which include the number of vehicles, total travelled distance, and total tardiness. These criteria are combined in different ways using a weighted linear combination, as will be outlined in more detail at the corresponding parts in the next two sections. Apart from these two criteria, another criterion called the distance deviation (more details about which are given in Section 6.3) is also used to demonstrate the ability of the approach to generate DRs for an arbitrarily defined user criterion. The results obtained by the proposed method are compared with the best known results for the problem instances known in the literature, as well as with simple manually designed DRs which present the most similar approach from the literature to the automatically developed DRs.
5. Solving CVRP with the Hyper-Heuristic Approach
In the optimisation used for the static variant of CVRP, a single objective criterion is defined in Equation (1) with the goal to minimise the total number of vehicles, multiplied with an arbitrary constant 10,000 and summed with travelled distance.
Using such objective criterion forces the heuristic on generating solutions with minimum number of vehicles and further minimising total travelled distance. Regardless of the actual objective used, we emphasise that the proposed method of automatic evolution of heuristics may be used with any conceivable performance measure.
5.1. Creating Dispatching Rules for CVRP
In addition to the functions defined in Table 1, in CVRP we define the following set of terminals (variables) that GP can use in the creation of candidate priority functions; these are shown in Table 3. All the terminals are self explanatory and correspond to the current vehicle, for which the decision is being made of which customer to visit next. In the table, the terminal ncc gives the value of the distance from the currently considered customer to the closest unserviced customer; i.e., this may be the next customer the vehicle could visit after the one being considered.

Table 3.
GP terminals for CVRP.
The experiments for CVRP were conducted on benchmark set from [52], which include 20 problem instances with 200 to 480 customers. Out of 20 instances, the first 10 were used as a learning set, while the remaining 10 served as the test set. In accordance with classical cross-validation used in other machine learning applications, the priority functions are first evolved on the learning test set. After that, all the presented results were obtained using only the instances from the test set.
Every learning experiment is repeated in 30 GP runs, and the 30 best individuals from those runs are evaluated on the test set. Both meta-algorithms were tested, but the results for the parallel variant were significantly worse than for the serial counterpart, so they are not presented in this section. This round of experiments is performed in static conditions, where it is expected that the serial meta-algorithm will exhibit better performance. Regardless of that, the parallel algorithm is the only choice when constructing the schedule in dynamic conditions, and the priority functions evolved with the serial algorithm can also be used in that case.
The results for 10 test cases from the dataset in terms of total travelled distance are given in Table 4. Note that the proposed approach is not meant to generate optimal or near-optimal solutions, but rather to produce adaptive schedules in a short amount of time. This property is additionally examined in the next subsection.

Table 4.
Total travelled distance—CVRP test set.
5.2. Evolved Heuristics in Dynamic CVRP
A dynamic VRP environment is simulated in the following manner: a given percentage of customer orders is not revealed at the beginning, and only becomes known at a certain point in time. Although there are many ways in which the dynamic environment could be emulated, such as the breakdown of vehicles and changes in travel time, we chose the commonly used variant as outlined in [40,42]. It should be noted that the proposed approach can cope with any type of dynamic disruption, by using the parallel meta-algorithm with the current number of vehicles (which can also be subject to change). For a problem instance with 200 customers, a varying percentage of orders (5, 25, and 50 percent) is only available at a later point in time, which corresponds to different levels of dynamism. The routes are generated on the fly using the evolved priority functions. The GP evolved solutions are compared with the “nearest neighbour” (NN) heuristic, which chooses the closest customer for every vehicle at every decision point. The number of vehicles is fixed to 15 according to [40]; because of this, the results in dynamic conditions show only the total travelled distance, since the vehicle count is the same for both heuristics. The results of this experiment are presented in Figure 2 and Table 5.
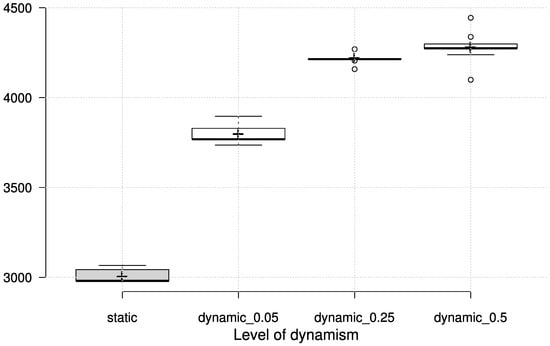
Figure 2.
Total travelled distance in dynamic CVRP—GP dispatching rules.

Table 5.
Total travelled distance—dynamic CVRP.
Since the dynamic differences include the appearance of new orders, we expect an increase in the total duration relative to the static solution. Although most of the GP-provided priority functions react better than the NN heuristic, there are some outliers which perform worse in dynamic conditions. This indicates that the training instances for GP should also be designed with a dynamic component, since all the training instances in the previous section were taken from a static benchmark.
6. Solving VRPTW with the Hyper-Heuristic Approach
When considering the static VRPTW model, we use the fitness function denoted in Equation (2) (same as for the CVRP) for optimisation of priority functions.
The experiments for VRPTW were conducted on Gehring and Homberger benchmark [53] containing problems with 200 to 1000 customers. For all problem instances, travel time and distance are equal to the corresponding Euclidean distance [54]. Separate experiments were conducted on groups with 200, 400, 600, 800 and 1000 customers; out of each group, 40 test instances were selected as the learning set, and 10 of the remaining instances were used as the test set. The learning process is performed in static conditions, while the dynamic variant is evaluated in the following subsection.
In addition to functional elements in Table 1, we define the following terminals for GP in the VRPTW environment, as given in Table 6. This terminal set is an extension of the terminals used in CVRP, with the addition of time-dependent information for each vehicle. The terminal waiting time denotes the amount of time the vehicle will have to wait for customer’s ready time (window opening) if it selects this customer for servicing next.

Table 6.
GP terminals for VRPTW.
After the learning phase, the resulting solutions were evaluated on the test set. Figure 3 shows the results obtained on a test set with 200 customers, but also presents the results of each group of priority functions obtained by learning on different learning set sizes. Since the results suggest that learning on a larger set of customers does not bring an improvement, we have evaluated the solutions, obtained on the learning set with a given number of customers, on each test set with a different number of customers. The purpose of this cross-evaluation was to identify any dependence of the number of customers in the learning phase on the effectiveness of priority functions on problem instances with a different customer number. The results in terms of box plots on the test set are given in Figure 4, with the circles representing outliers and the ’+’ symbol representing the average value.
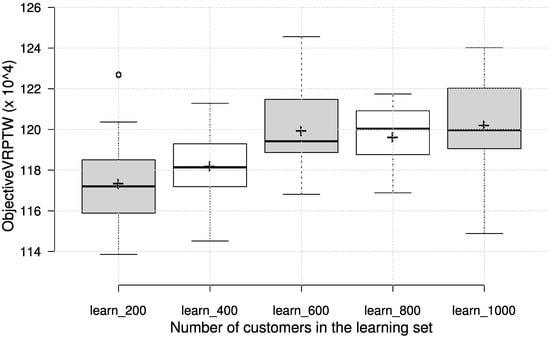
Figure 3.
Test results on VRPTW instances with 200 customers.
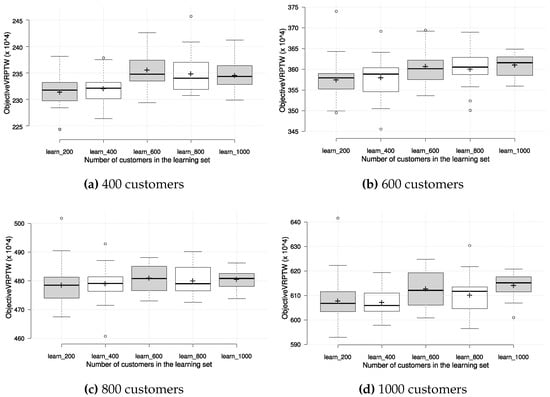
Figure 4.
Test results on VRPTW instances with different number of customers.
It can be observed that the number of customers in the learning set does not influence the final effectiveness to a great extent, which can be considered a good trait for scalability to larger instances. It is interesting to note, however, that the priority functions learned on a smaller number of customers generally achieve the best results, regardless of the number of customers in the test set. This is encouraging, since less time can be spent on learning with smaller number of customers, and still be able to obtain solutions that cope well with different problem sizes. To illustrate the absolute quality of the generated solutions, we compare the obtained number of vehicles on the test set with best known results for the chosen test set instances https://www.sintef.no/projectweb/top/vrptw/homberger-benchmark (accessed on 3 October 2023); the results are shown in Table 7.

Table 7.
Number of vehicles—VRPTW test set.
6.1. Evolved Heuristics in Dynamic VRPTW
Dynamic conditions for VRPTW are simulated in the same way as for the CVRP, where a given percentage of orders (5, 25 and 50 percent) is not known at the beginning, but revealed at a certain point in time. The dynamic scenario is simulated on the VRPTW test case with 200 customers, based on Solomon’s type “RC” example as outlined in [40,42]. Following the same recommendations, the number of vehicles is set to 15. Apart from the GP-evolved dispatching rules, we employ the “earliest first” rule (EF), which selects the customer whose servicing can be started the soonest (also taking into account the travel time to that customer), and the “most urgent first” rule (UF), which selects the customer whose window closing time (due date) is most urgent. The results for the GP priority functions in terms of total travelled distance are shown in Figure 5 and Table 8 along with the EF and UF heuristics.
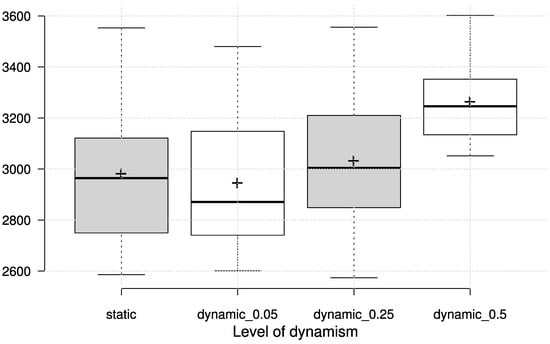
Figure 5.
Total travelled distance in dynamic VRPTW—GP dispatching rules.

Table 8.
Total travelled distance—dynamic VRPTW.
It can easily be seen that the GP-evolved priority functions manage to encapsulate the dynamic changes and adapt to new information. In this particular case, the “nearest neighbour” heuristic can also produce competitive travel distance, but at the same time incurs a number of unserviced orders (up to 26 for the most dynamic scenario), which makes it inappropriate in this setting.
6.2. Creating Heuristics for VRPTW with Soft Time Windows
As an example of adaptability of the proposed approach, we tackle the VRPTW variant with soft time constraints [55,56]. In this case, we allow the requests to be serviced outside the defined time window, but which induces additional cost. This cost is usually proportional to the time window violation, but the actual cost estimate may be formulated in any possible way.
To accommodate for soft time window constraints, the only change that must be made is the definition of a “valid customer” in the meta-algorithm. Instead of disregarding all customers that cannot be reached before the due date, we can introduce an additional amount of tolerance. In our experiments, the maximum time window tolerance is set to be twice as large as the denoted service time. This is completely arbitrary and may be defined to match the customer preferences, and even be modeled after individual customer constraints (e.g., delays at different types of customers incur different costs). Additionally, a variable tard is added to the GP set of terminals; this variable represents the tardiness of service if the current customer is selected (the value is zero if no tardiness is incurred if this customer is selected).
With these changes, the user can define a modified fitness function to measure the impact of tardiness of customers services. For the GP algorithm, the fitness function was modified as outlined in Equation (3), in which totalTardiness denotes the amount of time that the service at all customers has been delayed.
The weight factor denotes the magnitude of tardiness in relation to travelled distance, and equals 1 in this study. Note that this is also completely arbitrary and adaptive, since the tardiness cost may be additionally scaled to have a greater or smaller impact relative to other elements in the fitness.
The learning process with soft time windows was repeated on the same learning set as for the regular VRPTW. The results for this experiment were validated on the same test set of 10 problem instances with 200 customers and are shown in Table 9. The results are compared to best known values with hard time window constraints, as well as GP heuristic results (given in the first two rows of the table). When soft time constraints are introduced, we can perceive a slight decrease in the number of vehicles, which means the heuristic is able to reduce vehicle count with the increase in total service tardiness. At the same time, the total distance is not changed substantially, which shows the applicability of the devised priority functions. To further reduce the number of vehicles, an appropriate scaling factor associated with tardiness could be introduced by the user in the objective function.

Table 9.
VRPTW test set, 10 instances with 200 customers each—soft time windows.
6.3. Evolving Heuristics for an Arbitrary Optimisation Criterion
Since existing heuristics were usually designed to address certain criteria, they may not be appropriate for application under an arbitrary criteria defined in a concrete problem instance. Tackling an arbitrary optimisation criteria is possible with search-based metaheuristics such as evolutionary algorithms, but they exhibit already-described disadvantages in the dynamic scheduling scenario. As mentioned before, the proposed approach can produce routing heuristics for any conceivable objective measure, since the process of evolution is guided with an arbitrary fitness function. To apply this approach with an arbitrary optimisation criterion, the user must provide relevant parameters to calculate the objective value. These parameters may include information about the vehicles, their travel times and distances, or about servicing times at previous customers etc. In any case, we presume the schedule maker is able to collect information that is relevant to its designated criteria and provide that information to the learning algorithm.
To illustrate the applicability of this scenario, we introduce another optimisation criteria that considers the deviation of travel time of individual vehicles; this may be the case of a given fleet size, where vehicles should complete their respective routes in approximately the same time. The choice of this particular objective is entirely arbitrary and serves only as a case study. The objective function in this experiment is outlined in Equation (4), where distanceDeviation is calculated as mean squared deviation from the average travel time of all the vehicles in a single problem instance.
The results of this experiment are shown in Table 10. The upper half of the table shows the results obtained with the initial objective criterion for VRPTW, while the bottom half presents results with the above objective (both sets of results correspond to GP heuristics). It can be seen from the bottom half of the table that the travel time deviations are indeed smaller than in the case of total distance minimisation. It is somewhat surprising that this objective contributes to the decrease of total travelled distance; however, this is accomplished with the increase in the number of used vehicles.

Table 10.
VRPTW test set—minimisation of travel time deviation.
7. Discussion
7.1. Scalability
To estimate the applicability of this approach in the case of larger VRP instances, we apply a previously evolved priority function to different problem instances of increasing size. The data in the tested instances were obtained by using a VRPTW setting and randomly generating the input values for a given number of customers. A serial meta-algorithm was then used to build the entire solution from scratch for the given instance. The aim here was not to test the feasibility of the VRP solution, but rather to illustrate the speed at which a single solution can be built using the proposed approach. The results of this experiment are given in Table 11.

Table 11.
Schedule construction time depending on the number of customers (VRPTW).
It can be seen that the total duration approximately matches the quadratic dependency on the number of customers, which follows from the complexity of the meta-algorithm. Note that these results do not include the calculation of customer distances, which is presumed to be available beforehand, and can also be approximated with other existing methods.
7.2. Optimisation of GP Parameters
In Table 2 the parameters of GP were presented; most of the parameter values were chosen on the basis of our previous experience with GP. However, certain parameters related to the machine learning process were also tested in this context to estimate their influence.
The first parameter we tested was the stopping condition criterion, since it can influence the generalisation ability of the GP. If the evolution is too short, we may not still converge to an acceptable solution quality, and if it is too long, we may experience over-fitting to the learning data set. Figure 6 shows the performance of the evolved priority functions on the test set with regards to the number of fitness evaluations. It can be seen that the termination condition does not have a significant impact, but the choice of 25,000 evaluations proved to be the most efficient one.
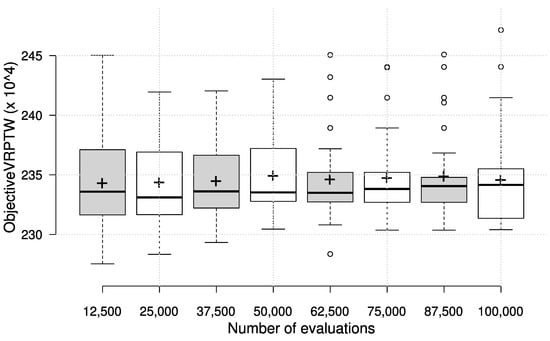
Figure 6.
Analysis of stopping criteria—test set performance by number of function evaluations.
Additionally, we experimented with different size of the learning set, i.e., the number of problem instances the GP used in the evolution. The results on the same test set, with different learning set sizes, are shown in Figure 7. Although the variations are not of great magnitude, this parameter does have a significant influence, and it would seem that the learning process benefits from a larger number of problem instances. Consequently, one should provide the GP with a sufficient amount of diverse instances for the best performance.
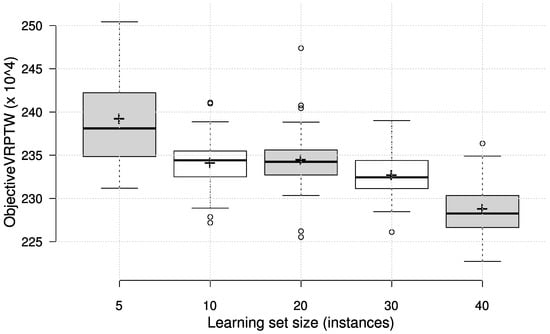
Figure 7.
Analysis of learning set size—test set performance.
7.3. Strengths and Weaknesses
As outlined through the text, the main advantage of the proposed approach is that it can automatically design DRs for various variants of the VRP and different user defined criteria, which can be nonstandard. This is important, since there is only a limited number of manual DRs proposed in the literature for VRPs, such as the nearest neighbour (NN) rule, earliest-first (EF) and urgent-first (UF) rule that were used as a baseline. Additional heuristics are available for different VRP variants, such as the Clarke–Wright algorithm that merges routes based on the saving distance [41], but which still needs to be adapted for use in dynamic conditions with a given number of vehicles. It is also not uncommon to use search-based methods in dynamic environments, but their utilisation depends on the rescheduling time complexity and adaptation is usually not trivial for different components of the schedule that are subject to change. Additionally, existing heuristics are tailored to satisfy specific commonly optimised criteria and they might not be efficient for a specific problem instance.
The experimental results demonstrated that the proposed method was able to generate DRs that perform better than existing rules. This is important as it shows limitations of existing rules, and outlines the need to evolve rules specialised for certain VRP flavors to obtain a better performance. Furthermore, the evolved DRs can be used both in static but also in dynamic conditions as well, which gives them a larger flexibility over search based methods (such as genetic algorithms and similar), which are usually mostly applied for static problem variants. Finally, the execution time of the proposed methods is quite small, even for larger problems, as opposed to other more sophisticated search-based methods.
However, the proposed methodology does not come without its issues. First of all, it is required to specify the terminal nodes used to evolve the rule, which does require certain domain knowledge, although it was demonstrated that already using simple operators leads to satisfactory results. Furthermore, the evolutionary process, i.e., the generation of new DRs is a time consuming process, which can take certain time to complete (up to a few hours). However, it must be stressed out that the idea of this method is to perform the generation of DRs prior to solving the problem, which then eliminates this long execution times when directly solving the problem. Finally, the performance of DRs when considering static problem variants is evidently worse than that of standard search-based methods. However, this is expected due to the difference in which they search for solutions. However, this problem can be amended by combining the proposed methodology with other improvement methods, some of which are mentioned in the next section as possibilities for future work.
8. Conclusions and Future Work
8.1. Conclusions
This paper presents an application of genetic programming for generating routing heuristics for different variants of VRP. The proposed approach falls into the category of hyper-heuristics, because a new heuristic is generated automatically for a given VRP environment and user defined objective measure. The solution is comprised of two parts: the first part is a meta-algorithm (or a schedule generation scheme), which is defined manually. Two meta-algorithms are given which can be used according to the scheduling conditions, under either static or dynamic conditions. The second part is the priority function, used by the meta-algorithm, which serves to match a vehicle to a specific customer. The priority function is created automatically using genetic programming, and can be tailored to specific criteria.
The results of the presented approach are new priority functions that can be used with an appropriate meta-algorithm, such as the two given in the paper. The priority functions can be evolved to optimise any conceivable user-defined criteria, and multi-objective optimisation is also possible. Once evolved, the priority functions can be used to generate routes in a small amount of time, which makes this approach applicable in on-line scheduling. While the goal of the approach is not finding the optimal solutions, it is an attempt to provide competitive results in variants where heuristics are available, and, what is more important, can help devise heuristics for new problem variants that may arise in everyday practice, where there are no adequate algorithms. The advantages of this approach are the applicability in dynamic as well as stochastic VRP environments since no information about the future of the system is used to construct the routes. The construction method is very fast, with a complexity quadratically dependent on the number of customers, which makes it a viable choice for large scale and highly dynamic VRP instances. Furthermore, the schedules obtained with this method may also serve as initial solutions to improvement heuristics, which may be employed if additional time is available.
8.2. Future Work
There are a lot of possibilities for the improvement of this approach; for instance, in our experiments we used only single-objective optimisation algorithms. Some problems naturally lend themselves to multiobjective optimisation, which is also the case with VRP variants. Separate objectives that can be individually observed include the number of vehicles, travel time and/or duration, customer response time and deviation, quality and tardiness of service etc. Previous studies show that it is possible to obtain high quality solutions that successfully optimize separate objective criteria and let the operator select the most appropriate heuristic [57,58,59]. What is more important, multiobjective heuristics can still manage to obtain solutions whose performance regarding a single criteria does not deteriorate compared to the ones evolved with single criteria optimisation.
Another research direction is the incorporation of rollout approach with the evolved constructive heuristics [60,61]. In this scenario, the meta-algorithm tests all possible decisions at the current moment in time (e.g., all valid customers are considered), and all subsequent decisions (later customers) are made using the priority function, creating the schedule up to the planning horizon. After such multiple simulations, the immediate decision that led to the best performance up to the planning horizon is made. Rollout can significantly improve the performance of constructive heuristics, with relatively simple modifications when creating a schedule. However, this is only possible under two conditions: firstly, if information about future service requests is available, and secondly, if there is additional time to spend on improving the initial solution. Still, this may prove to be one of the most effective ways of improving the quality of automatically created heuristics.
The hyper-heuristic approach is also amenable to other representations of priority functions: apart from the tree-based GP we used, other GP variants could be used to encode the priority function, such as Cartesian Genetic Programming [62], Gene Expression Programming [63], geometric semantic GP [64], dimensionally aware GP [65], and others [66]. Furthermore, different regression methods may be used instead of the GP representation, such as neural networks or Support Vector Regression (SVR).
Moreover, since the evolution produces not one, but a set of potential candidates for priority function, an ensemble approach can be utilised to try and improve the decision-making process [67]. Here, instead of a single priority function that can misjudge a situation, several functions combine their votes into a single decision for the next customer to service.
Author Contributions
Conceptualization, D.J., T.C. and D.D.; methodology, D.J. and D.D.; software, D.J., M.Đ. and K.B.; validation, D.J.; formal analysis, D.J.; investigation, D.J.; resources, D.J.; data curation, D.J. and J.F.; writing—original draft preparation, D.J. and M.Đ.; visualization, D.J.; supervision, D.J. and T.C.; project administration, K.B.; funding acquisition, D.J. and J.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported in part by Croatian Science Foundation under the project IP-2019-04-4333 and by the European Regional Development Fund under the project KK.01.2.1.01.0120.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dantzig, G.B.; Ramser, J.H. The Truck Dispatching Problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Lenstra, J.K.; Kan, A.H.G.R. Complexity of vehicle routing and scheduling problems. Networks 1981, 11, 221–227. [Google Scholar] [CrossRef]
- Pillac, V.; Gendreau, M.; Guéret, C.; Medaglia, A.L. A review of dynamic vehicle routing problems. Eur. J. Oper. Res. 2013, 225, 1–11. [Google Scholar] [CrossRef]
- Pavone, M.; Bisnik, N.; Frazzoli, E.; Isler, V. A Stochastic and Dynamic Vehicle Routing Problem with Time Windows and Customer Impatience. Mob. Netw. Appl. 2008, 14, 350–364. [Google Scholar] [CrossRef]
- Poli, R.; Langdon, W.B.; McPhee, N.F. A Field Guide to Genetic Programming; Lulu Enterprises, UK Ltd., 2008. Available online: http://gpbib.cs.ucl.ac.uk/gp-html/poli08_fieldguide.html (accessed on 29 May 2023).
- Burke, E.K.; Hyde, M.; Kendall, G.; Ochoa, G.; Özcan, E.; Woodward, J.R. A Classification of Hyper-heuristic Approaches. In International Series in Operations Research & Management Science; Springer: Berlin/Heidelberg, Germany, 2010; pp. 449–468. [Google Scholar] [CrossRef]
- Burke, E.K.; Gendreau, M.; Hyde, M.; Kendall, G.; Ochoa, G.; Özcan, E.; Qu, R. Hyper-heuristics: A survey of the state of the art. J. Oper. Res. Soc. 2013, 64, 1695–1724. [Google Scholar] [CrossRef]
- Branke, J.; Hildebrandt, T.; Scholz-Reiter, B. Hyper-heuristic Evolution of Dispatching Rules: A Comparison of Rule Representations. Evol. Comput. 2015, 23, 249–277. [Google Scholar] [CrossRef] [PubMed]
- Jakobović, D.; Marasović, K. Evolving priority scheduling heuristics with genetic programming. Appl. Soft Comput. 2012, 12, 2781–2789. [Google Scholar] [CrossRef]
- Đurasević, M.; Jakobović, D.; Knežević, K. Adaptive scheduling on unrelated machines with genetic programming. Appl. Soft Comput. 2016, 48, 419–430. [Google Scholar] [CrossRef]
- Branke, J.; Nguyen, S.; Pickardt, C.W.; Zhang, M. Automated Design of Production Scheduling Heuristics: A Review. IEEE Trans. Evol. Comput. 2016, 20, 110–124. [Google Scholar] [CrossRef]
- Peng, F.; Wang, Y.; Xuan, H.; Nguyen, T.V.T. Efficient road traffic anti-collision warning system based on fuzzy nonlinear programming. Int. J. Syst. Assur. Eng. Manag. 2021, 13, 456–461. [Google Scholar] [CrossRef]
- Nguyen, T.V.T.; Huynh, N.T.; Vu, N.C.; Kieu, V.N.D.; Huang, S.C. Optimizing compliant gripper mechanism design by employing an effective bi-algorithm: Fuzzy logic and ANFIS. Microsyst. Technol. 2021, 27, 3389–3412. [Google Scholar] [CrossRef]
- Đurasević, M.; Jakobović, D. Selection of dispatching rules evolved by genetic programming in dynamic unrelated machines scheduling based on problem characteristics. J. Comput. Sci. 2022, 61, 101649. [Google Scholar] [CrossRef]
- Toth, P.; Vigo, D. (Eds.) The Vehicle Routing Problem; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar] [CrossRef]
- Kumar, S.N.; Panneerselvam, R. A Survey on the Vehicle Routing Problem and Its Variants. Intell. Inf. Manag. 2012, 4, 66–74. [Google Scholar] [CrossRef]
- Lin, C.; Choy, K.; Ho, G.; Chung, S.; Lam, H. Survey of Green Vehicle Routing Problem: Past and future trends. Expert Syst. Appl. 2014, 41, 1118–1138. [Google Scholar] [CrossRef]
- Ritzinger, U.; Puchinger, J.; Hartl, R.F. A survey on dynamic and stochastic vehicle routing problems. Int. J. Prod. Res. 2015, 54, 215–231. [Google Scholar] [CrossRef]
- Mor, A.; Speranza, M.G. Vehicle routing problems over time: A survey. 4OR 2020, 18, 129–149. [Google Scholar] [CrossRef]
- Taillard, É.; Badeau, P.; Gendreau, M.; Guertin, F.; Potvin, J.Y. A Tabu Search Heuristic for the Vehicle Routing Problem with Soft Time Windows. Transp. Sci. 1997, 31, 170–186. [Google Scholar] [CrossRef]
- Li, H.; Lim, A. Local search with annealing-like restarts to solve the VRPTW. Eur. J. Oper. Res. 2003, 150, 115–127. [Google Scholar] [CrossRef]
- Schrimpf, G.; Schneider, J.; Stamm-Wilbrandt, H.; Dueck, G. Record Breaking Optimization Results Using the Ruin and Recreate Principle. J. Comput. Phys. 2000, 159, 139–171. [Google Scholar] [CrossRef]
- Mester, D.; Bräysy, O. Active guided evolution strategies for large-scale vehicle routing problems with time windows. Comput. Oper. Res. 2005, 32, 1593–1614. [Google Scholar] [CrossRef]
- Gambardella, L.M.; Taillard, E.; Agazzi, G. MACS-VRPTW: A Multiple Ant Colony System for Vehicle Routing Problems with Time Windows. Technical Report. 1999. Available online: https://people.idsia.ch/~luca/tr-idsia-06-99.pdf (accessed on 29 May 2023).
- Gulic, M.; Lucanin, D.; Skorin-Kapov, N. A two-phase vehicle based decomposition algorithm for large-scale capacitated vehicle routing with time windows. In Proceedings of the 2012 35th International Convention MIPRO, Opatija, Croatia, 21–25 May 2012; pp. 1104–1108. [Google Scholar]
- Bent, R.; Hentenryck, P.V. Spatial, Temporal, and Hybrid Decompositions for Large-Scale Vehicle Routing with Time Windows. In Principles and Practice of Constraint Programming–CP 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 99–113. [Google Scholar] [CrossRef]
- Gendreau, M.; Potvin, J.Y.; Bräumlaysy, O.; Hasle, G.; Løkketangen, A. Metaheuristics for the Vehicle Routing Problem and Its Extensions: A Categorized Bibliography. In Operations Research/Computer Science Interfaces; Springer: Berlin/Heidelberg, Germany, 2008; pp. 143–169. [Google Scholar] [CrossRef]
- Sánchez, F.F.S.; Lazo, C.A.L.; Quiñónez, F.Y.S. Comparative Study of Algorithms Metaheuristics Based Applied to the Solution of the Capacitated Vehicle Routing Problem. In Novel Trends in the Traveling Salesman Problem; IntechOpen: London, UK, 2020. [Google Scholar] [CrossRef]
- Arnold, F.; Sörensen, K. Knowledge-guided local search for the vehicle routing problem. Comput. Oper. Res. 2019, 105, 32–46. [Google Scholar] [CrossRef]
- Gulić, M.; Jakobović, D. Evolution of vehicle routing problem heuristics with genetic programming. In Proceedings of the 2013 36th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatia, Croatia, 19–24 May 2013; pp. 988–992. [Google Scholar]
- Mlejnek, J.; Kubalik, J. Evolutionary hyperheuristic for capacitated vehicle routing problem. In Proceedings of the 15th Annual Conference Companion on Genetic and Evolutionary Computation, Lisbon, Portugal, 15–19 July 2013. [Google Scholar] [CrossRef]
- Gendreau, M.; Guertin, F.; Potvin, J.Y.; Taillard, É. Parallel Tabu Search for Real-Time Vehicle Routing and Dispatching. Transp. Sci. 1999, 33, 381–390. [Google Scholar] [CrossRef]
- Ichoua, S.; Gendreau, M.; Potvin, J.Y. Vehicle dispatching with time-dependent travel times. Eur. J. Oper. Res. 2003, 144, 379–396. [Google Scholar] [CrossRef]
- Bent, R.W.; Hentenryck, P.V. Scenario-Based Planning for Partially Dynamic Vehicle Routing with Stochastic Customers. Oper. Res. 2004, 52, 977–987. [Google Scholar] [CrossRef]
- Ichoua, S.; Gendreau, M.; Potvin, J.Y. Exploiting Knowledge About Future Demands for Real-Time Vehicle Dispatching. Transp. Sci. 2006, 40, 211–225. [Google Scholar] [CrossRef]
- van Hemert, J.I.; Poutré, J.A.L. Dynamic Routing Problems with Fruitful Regions: Models and Evolutionary Computation. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2004; pp. 692–701. [Google Scholar] [CrossRef]
- Cheung, B.K.S.; Choy, K.; Li, C.L.; Shi, W.; Tang, J. Dynamic routing model and solution methods for fleet management with mobile technologies. Int. J. Prod. Econ. 2008, 113, 694–705. [Google Scholar] [CrossRef]
- Montemanni, R.; Gambardella, L.M.; Rizzoli, A.E.; Donati, A.V. Ant Colony System for a Dynamic Vehicle Routing Problem. J. Comb. Optim. 2005, 10, 327–343. [Google Scholar] [CrossRef]
- Rizzoli, A.E.; Montemanni, R.; Lucibello, E.; Gambardella, L.M. Ant colony optimization for real-world vehicle routing problems. Swarm Intell. 2007, 1, 135–151. [Google Scholar] [CrossRef]
- Necula, R.; Breaban, M.; Raschip, M. Tackling Dynamic Vehicle Routing Problem with Time Windows by means of ant colony system. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017. [Google Scholar] [CrossRef]
- Garrido, P.; Riff, M.C. DVRP: A hard dynamic combinatorial optimisation problem tackled by an evolutionary hyper-heuristic. J. Heuristics 2010, 16, 795–834. [Google Scholar] [CrossRef]
- Saint-Guillain, M.; Deville, Y.; Solnon, C. A Multistage Stochastic Programming Approach to the Dynamic and Stochastic VRPTW. In Integration of AI and OR Techniques in Constraint Programming; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 357–374. [Google Scholar] [CrossRef]
- van Lon, R.R.S.; Branke, J.; Holvoet, T. Optimizing agents with genetic programming: An evaluation of hyper-heuristics in dynamic real-time logistics. Genet. Program. Evolvable Mach. 2017, 19, 93–120. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithms for the Vehicle Routing and Scheduling Problems with Time Window Constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
- Ðurasević, M.; Jakobović, D. A survey of dispatching rules for the dynamic unrelated machines environment. Expert Syst. Appl. 2018, 113, 555–569. [Google Scholar] [CrossRef]
- Jakobović, D.; Budin, L. Dynamic Scheduling with Genetic Programming. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; pp. 73–84. [Google Scholar] [CrossRef]
- Kolisch, R. Serial and parallel resource-constrained project scheduling methods revisited: Theory and computation. Eur. J. Oper. Res. 1996, 90, 320–333. [Google Scholar] [CrossRef]
- Đurasević, M.; Jakobović, D. Comparison of schedule generation schemes for designing dispatching rules with genetic programming in the unrelated machines environment. Appl. Soft Comput. 2020, 96, 106637. [Google Scholar] [CrossRef]
- Pinedo, M.L. Scheduling; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Koza, J.R. Human-competitive results produced by genetic programming. Genet. Program. Evolvable Mach. 2010, 11, 251–284. [Google Scholar] [CrossRef]
- Golden, B.L.; Wasil, E.A.; Kelly, J.P.; Chao, I.M. The Impact of Metaheuristics on Solving the Vehicle Routing Problem: Algorithms, Problem Sets, and Computational Results. In Fleet Management and Logistics; Springer: Berlin/Heidelberg, Germany, 1998; pp. 33–56. [Google Scholar] [CrossRef]
- Gehring, H. A Parallel Hybrid Evolutionary Metaheuristic for the Vehicle Routing Problem with Time Windows. In Proceedings of the EUROGEN99; Springer: Berlin/Heidelberg, Germany, 1999; pp. 57–64. [Google Scholar]
- Deza, M.M.; Deza, E. Encyclopedia of Distances; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Taş, D.; Dellaert, N.; van Woensel, T.; de Kok, T. Vehicle routing problem with stochastic travel times including soft time windows and service costs. Comput. Oper. Res. 2013, 40, 214–224. [Google Scholar] [CrossRef]
- Calvete, H.I.; Galé, C.; Oliveros, M.J.; Sánchez-Valverde, B. A goal programming approach to vehicle routing problems with soft time windows. Eur. J. Oper. Res. 2007, 177, 1720–1733. [Google Scholar] [CrossRef]
- Đurasević, M.; Jakobović, D. Evolving dispatching rules for optimising many-objective criteria in the unrelated machines environment. Genet. Program. Evolvable Mach. 2017, 19, 9–51. [Google Scholar] [CrossRef]
- Xu, B.; Mei, Y.; Wang, Y.; Ji, Z.; Zhang, M. Genetic Programming with Delayed Routing for Multiobjective Dynamic Flexible Job Shop Scheduling. Evol. Comput. 2021, 29, 75–105. [Google Scholar] [CrossRef]
- Zhang, F.; Mei, Y.; Nguyen, S.; Zhang, M. Multitask Multiobjective Genetic Programming for Automated Scheduling Heuristic Learning in Dynamic Flexible Job-Shop Scheduling. IEEE Trans. Cybern. 2022, 1–14. [Google Scholar] [CrossRef]
- Goodson, J.C.; Ohlmann, J.W.; Thomas, B.W. Rollout Policies for Dynamic Solutions to the Multivehicle Routing Problem with Stochastic Demand and Duration Limits. Oper. Res. 2013, 61, 138–154. [Google Scholar] [CrossRef]
- Ðurasević, M.; Jakobović, D. Automatic design of dispatching rules for static scheduling conditions. Neural Comput. Appl. 2020, 33, 5043–5068. [Google Scholar] [CrossRef]
- Miller, J.F. Cartesian Genetic Programming. In Cartesian Genetic Programming; Springer: Berlin/Heidelberg, Germany, 2011; pp. 17–34. [Google Scholar] [CrossRef]
- Nie, L.; Shao, X.; Gao, L.; Li, W. Evolving scheduling rules with gene expression programming for dynamic single-machine scheduling problems. Int. J. Adv. Manuf. Technol. 2010, 50, 729–747. [Google Scholar] [CrossRef]
- Moraglio, A.; Krawiec, K.; Johnson, C.G. Geometric Semantic Genetic Programming. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; pp. 21–31. [Google Scholar] [CrossRef]
- Keijzer, M.; Babovic, V. Dimensionally Aware Genetic Programming. In Gecco-99, Proceedings of the Genetic and Evolutionary Computation Conference, Orlando, FL, USA, 13–19 July 1999; Springer: Berlin/Heidelberg, Germany, 1999; Volume 2, pp. 1069–1076. [Google Scholar]
- Planinic, L.; Backovic, H.; Durasevic, M.; Jakobovic, D. A Comparative Study of Dispatching Rule Representations in Evolutionary Algorithms for the Dynamic Unrelated Machines Environment. IEEE Access 2022, 10, 22886–22901. [Google Scholar] [CrossRef]
- Đurasević, M.; Gil-Gala, F.J.; Planinić, L.; Jakobović, D. Collaboration methods for ensembles of dispatching rules for the dynamic unrelated machines environment. Eng. Appl. Artif. Intell. 2023, 122, 106096. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).