Abstract
It is well-known that part of the neural networks capacity is determined by their topology and the employed training process. How a neural network should be designed and how it should be updated every time that new data is acquired, is an issue that remains open since it its usually limited to a process of trial and error, based mainly on the experience of the designer. To address this issue, an algorithm that provides plasticity to recurrent neural networks (RNN) applied to time series forecasting is proposed. A decision-making grow and prune paradigm is created, based on the calculation of the data’s order, indicating in which situations during the re-training process (when new data is received), should the network increase or decrease its connections, giving as a result a dynamic architecture that can facilitate the design and implementation of the network, as well as improve its behavior. The proposed algorithm was tested with some time series of the M4 forecasting competition, using Long-Short Term Memory (LSTM) models. Better results were obtained for most of the tests, with new models both larger and smaller than their static versions, showing an average improvement of up to 18%.
1. Introduction
Recurrent Neural Networks (RNN) have proved to be a powerful methodology to solve time series forecasting [1,2], due to their ability to adapt and recognize short-term and long-term correlations between input data sequences [3].
The capacity that these systems have, that is, how much they can learn and store knowledge, is determined among other features by their topology [4,5,6], made up of the number of units that they have and how these units are interconnected, which allows the system to acquire, store, and generalize knowledge. In addition to its topology, the capacity of the network is dependent on the training process that is used. Faced with this situation, the question arises about how the network should be designed, a situation that even today has not been resolved, can be provided some theoretical guidelines [7] that suggest what is likely to work or not work on a given problem, but, ultimately, it has been limited to a process of trial and error, based only on the experience of the designer.
Depending on these two factors: topology, and training, it is possible that the short-term memory effect occurs, which causes that, as the network processes more future elements of the series, the parameters that represent the knowledge of the behavior of the sequence in the long term can vanish [8]. This makes it necessary to update the network by adding the new observations acquired over time, a process normally addressed by discarding the previous model and retraining the network from scratch using the new data set. One neural model that successfully deals with vanishing gradients of long-term temporal sequences is the Long-Short Term Memory model (LSTM) [9]. LSTM model adds a constant error carrousel unit (CEC) that allows keeping gradients of data sequences for a long time.
Since time series sequences could suddenly change their complexity from one sample time to another, more or less neural units of the model can be needed to process dynamic data, and the LSTM efficiency and precision can be improved by adding functionalities inspired by concepts of biological brain neuroplasticity in the design and updating of architectures during the training time [10]. Some algorithms have been designed to simulate how synaptic connections are modified in biological neuronal networks and therefore how the number of neurons involved in a network is affected, developing techniques such as pruning [11] or growing [12], which represent brain plasticity. Brain plasticity describes the ability of brain areas or neuronal groups to respond functionally and neurologically to their environment, changing their activity in response to intrinsic or extrinsic stimuli by reorganizing their structures, giving them the possibility of growing and/or pruning synapses to fill functional deficiencies [13]. This is why, the objective of these techniques, growing and pruning, is to adapt the architecture of the networks that are already designed, increasing, or decreasing the number of neurons respectively, to deliver an efficient model that improves its performance. In this work the growing and pruning paradigm is developed using LSTM architectures to obtain LSTM models with better performance to solve time series forecasting problems.
Based on these methodologies, is proposed an algorithm that provides plasticity to an LSTM model. Which gives it the capacity to reduce or increase the number of neurons of its architecture in order to increase its precision and/or efficiency, applied to time series forecasting. This algorithm is a decision-making grow and prune paradigm, based on the calculation of the order of the data, being this, the way to simulate the stimulus presented in the environment, denoting to the network in which situations it should increase or reduce its connections, obtaining, as a result, a dynamic architecture that can facilitate its design and implementation, as well as improve its time series forecasting, obtaining reduced or larger models, but in both cases improving its performance. The algorithm consists of an automatized module that computes the order of the input data sequence, in this way the system will be able to detect the changes that the data presents. This calculation is carried out using Cao’s methodology [14], which is an improvement of the False Nearest Neighbor, (FNN) [15], for determining the minimum embedding dimension. After Cao’s order computation, a set of error metrics and a history of actions previously taken by the system will be fed into the decision-making policy to determine the next change that should be made in the LSTM topology. These changes can be apply: “pruning” eliminating connections of the network based on its magnitudes, “growing” activating connections, or increasing the number of neurons concerning the gradients or maintaining the network with its current structure.
Currently, the algorithm is designed to be applied when new information is obtained and the model needs to be retrained, a process that is called phase. At each phase, the decision policies will be activated and will indicate the modifications to be implemented in the topology during this process (training). This proposed methodology was tested using some time series obtained from the 2019 M4 contest daily training dataset [16]. A comparative analysis was performed to show the advantages of the methodology: the results obtained using a standard LSTM model were contrasted against those obtained using the dynamic architecture version of the LSTM.
The main contribution of this article is the proposal of a novel order-based schedule of dynamic topology for LSTM models, based on Cao’s order analysis of time series and the evolution of the forecasting error.
Where in most of the tests, improvements were presented by reducing the final error obtained, and in some cases, they also reduced the original architecture of the network. In the tests that did not present considerable improvements, a similarity in the error range to its static counterpart was maintained, but the number of connections was decreased.
Related Work
Since the design of neural networks is a dilemma in the field of artificial intelligence, some models that implement these growth and/or pruning methodologies have been proposed to address this problem.
However, using growing and pruning methodologies in RNN is difficult since these networks deal with time-varying data. Due to the above, common metrics that are used to decide to grow/prune network architectures that process static data are no longer applicable. For example: if the decision to prune the network is taken based on low values of gradients of some neurons, this could happen because those neurons are essential only to recognize key correlations between long-term data correlations, and that’s why they are just firing on the time that these correlations are presented in the data, which could not be frequent. On the other hand, a temporal decrease in the error value could indicate that the current architecture of the network is being enough to process the current data sequence. Nevertheless, the complexity of the time-varying data could change, and the network could require a sudden and critical increase of neurons which can be very computationally expensive.
So, there are a few approaches that present dynamic architecture RNN: among them is ”Nonlinear Identification Via Variable Structure Recurrent Neural Networks” [17], which shows an algorithm to perform nonlinear identification via variable structure RNN; here, the growth technique is applied, increasing the size of the network by introducing high-order connections, limiting itself to the minimum required to improve its performance during the analysis of the data available, but at the same time, it does not take into account the possibility of decreasing the number of connections to obtain compact networks, thus increasing the probability that the topology has redundant connections. Another algorithm that applies these methodologies seeking to obtain a dynamic topology is the model “Dynamic Generation of the Topology of an Artificial Neural Network of the Multilayer Perceptron Type“ [18], this addresses the situation by creating a dynamic tool that allows the user to design and modify a multilayer network by adding or removing synaptic connections using both pruning and growing techniques. Seeking to reduce the error by increasing or decreasing the connection nodes, but maintaining the decision only on the user and his design ability. “A Dynamic Ensemble Learning Algorithm for Neural Network” [19], is a model designed for classification problems, which looks to modify the topology starting from a multilayer neural network that will add more multilayer subnetworks that are designed in parallel, a process in which are added or deleted connections of the new subnet to be annexed. Generating these subnetworks automatically during the analysis process of the system eliminates user dependency, but with the particularity that the minimum possible model is a network with the addition of a sub-network, so the main model cannot be modified.
The model “Incremental Learning Using a Grow-and-Prune Paradigm with Efficient Neural Networks” [20] presents both methodologies, by proposing a consecutive growth paradigm followed by a pruning process that restores and eliminates redundant model connections. This algorithm was applied in convolutional networks, starting with a sparse network, and then applying the paradigm in its training process, but not taking into account the option to increase the number of units of the original model.
2. Theoretical Frameworks
One of the bases of the proposed algorithm is the calculation of the order of the data, thus seeking to obtain information on the inherent dynamics of the system. This calculation is carried out employing the methodology “Practical Method for Determining the Minimal Embedding Dimension of a Scalar Time Series” [14], which estimates the minimum embedded dimension based on the “False Nearest Neighbors” (FNN) [15] algorithm but looks for a more practical and simple way to obtain this metric.
2.1. Practical Method for Determining the Minimal Embedding Dimension of a Scalar Time Series
This method, proposed by Liangyue Cao [14], eliminates the need to make use of the threshold parameter used by the FNN algorithm (), which determines if the neighbor of a point is false or not, by describing it as a subjective parameter.
Let be a time series, and a -dimensional vector defined as.
where both and are values indicating the index of the original series data, where is the shift in the data and is the dimension under analyzed. Similar to the FNN algorithm is defined:
Being the relationship between the distance of a point and its nearest neighbor in a larger dimension and the distance between the same points (anchor point and its neighbor) but in the dimension of analysis . If qualifies as an embedded dimension, then any pair of close points in d must remain close in , if this is true these two points will be described as true neighbors, otherwise, they will be false neighbors. This is the base of the FNN algorithm. From this result, FNN determines the status of the neighbors by comparing the change ratio between both points with respect to a threshold , so Cao substituted this threshold by implementing the following equation:
This is the average of all distance ratios . Where only depends on and . In turn, is defined, which shows the variation of the averages during the expansions that exist from to .
where instead of using the threshold proposed in FNN, this method observes , which will stop changing when d is greater than a correct embed dimension so the minimum dimension will be .
2.2. Long Short-Term Memory (LSTM)
LSTM units are an extension of recurrent networks that allow them to remember their inputs for a longer period, resembling a computer’s memory. It can read, write, and delete information from its cell, saving information, and preventing it to vanish through time [21].
The cell decides whether to store or delete the information it is receiving based on a degree of importance that is assigned to it. This importance is assigned through the weights of the connections, so the LSTM learns over time to identify what part of the information is important and what is not. Implementing an internal state of the cell that will generate a long-term memory [22].
An LSTM neuron is composed of three gates: input, forget, and output, as shown in Figure 1. Which determines if a new input is allowed, which information is eliminated, or if it is allowed to affect the output at the current time.
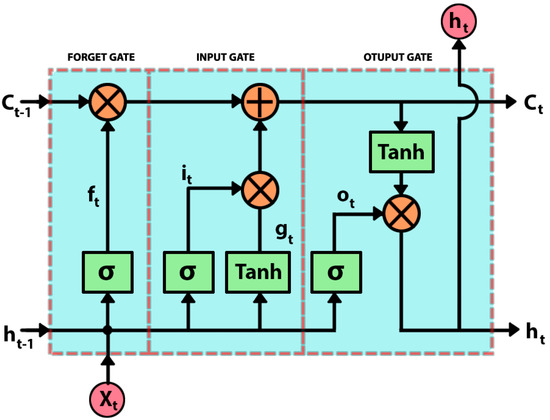
Figure 1.
LSTM neuron structure (Forget gate, Input gate, Output gate) stands for sigmoid function, the input data, and the current network output.
The first gate that appears from left to right in Figure 1 is the forget gate, which decides what information of the cell state () is going to be discarded, through a sigmoid function (σ).
where ( is the previous output of the unit, () is the input, () the forget gate weight matrix and () the gate bias. The output will be between a value ranged from 0 to 1, with 0 representing total elimination and 1 keeping the whole information. After this step, the input gate continues, which indicates what portion of the new information will be stored in the cell state. This gate is composed of two functions, one sigmoidal and the other hyperbolic tangent, which determines the degree of update of the state.
Being () and () the weight matrix for the input gate and () and () their respective bias. Thus obtained, the new state of the unit, by eliminating the unnecessary information and updating it with the new information acquired.
Finally determine the output of the unit (), which will be a version of the cell state filtered by the current input and the previous output. Where and are the weight matrix and bias for the output gate.
3. Dynamic Topology Method for RNN Based on Cao’s Order
This section describes the processes that make up the proposed dynamic structure algorithm for recurrent networks, segmented into five modules:
- Order analysis
- Growing
- Pruning
- Normal
- Decision-Making policy
As it was mentioned previously, the algorithm is based on the elaboration of a decision-making policy that allows determining the action to be carried out on the LSTM network architecture (growing, pruning, or normal) with respect to the evolution of the data during the update process, in such a way that it allows the network to dynamically adapt its architecture to maintain, transfer and distribute the knowledge to its next version. The flowchart of the methodology is illustrated in Figure 2.
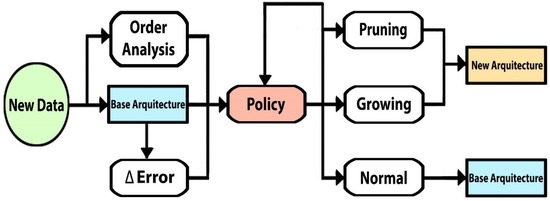
Figure 2.
Dynamic architecture algorithm for RNN flowchart.
Starting from the current architecture and weights of the network, the process of evolution of the topology continues. If the network is created from scratch, it will be initialized randomly creating a base model. Once is received a base model, the methodology analyzes the new training data determining the order of this sequence employing “Cao’s” algorithm to be introduced with other metrics in the decision policy that will select whether the network’s architecture will get into: (1) a growing process, creating new connections or new neurons based on the information of its gradients; (2) into a pruning process, deleting redundant connections based on the magnitudes of its connections; or (3) preserving its current topology.
These processes, the metrics used, and the decision-making policy are described in the following sections.
3.1. Order Analysis
When a sequence of new data is acquired, this is preprocessed by an algorithm that will calculate its order. The aim of analyzing the order of the series is to have a metric that allows visualizing the evolution that the data is presenting and thus, in parallel, to modify the structure of the network so that it can resemble approximately the same dynamics.
To calculate the order, the algorithm Practical Method for Determining the Minimum Embedding Dimension of Scalar Time Series proposed by Cao, described in Section 2, is used. This is an improvement to the algorithm False Nearest Neighbors.
3.2. Growing Phase
Once the new data set has been collected and analyzed, through the evolution policy, it is determined if the network should: (1) Grow its architecture, (2) Keep its current architecture or (3) Prune the network by deleting some connections.
To expand its topology, an increase in the network architecture is carried out by adding neurons or, in other cases, activating connections using a gradient-based growth algorithm. The methodology makes use of binary masks that distinguish the dropped connections in each of the weight tensors of their respective layers. Identifying with “0” the connections that are turned off and with “1” the active ones. These masks, in turn, have the objective of inhibiting the updating of non-active weights during the training process. This is divided into two steps, starting only with the new data set where the network growth will proceed and ending with a tuning training using the total data set (the previous data and the new ones collected) adapting the architecture to organize the new information available.
The network can present two possible scenarios when the decision to increase the topology has been taken, (1) the first occurs when the architecture has dropped connections, in this situation a percentage of the inhibited connections is reactivated. (2) If the network is fully connected, then, the growth of the network is carried out by adding neurons to the architecture.
3.2.1. Network Architecture Growth through Activation of Dropped Connections
The system allows the models to store their respective masks, so it can be identified if the network has non-activated connections. If this occurs, a sequential process is used to activate them. The growth of the network is determined by a rate parameter that tells the algorithm the percentage of the total units that must be activated in the network. In the experiments was used a 15% rate, which is applied every time that this process is made. This rate was chosen through experimentation.
Gradient evaluation: It starts with the calculation of the gradients of the dropped connections. These are calculated during training, where the gradients of all the weights are extracted during the backpropagation process, accumulating the gradients of only one epoch. It should be noted that the weights are not updated during this epoch. Then, the average of the resulting gradients is calculated.
Connection growth: The difference between the number of current connections and the percentage that must be initiated is calculated, obtaining as a result the number of dropped connections to be reactivated. This process is carried out for each set of weights of their respective layer. The connections with the highest gradients will be identified and then activated by changing their current value from 0 to 1 in their mask, that is, only the connections with the highest gradient will be activated until the percentage of active connections is completed. Seeking to have the most efficient connections that reduce the cost function.
Initialization: The new connections are initialized with the value resulting from the multiplication of the current training rate and their respective gradients, calculated in the previous step.
Once the new connections have been initialized, the updated model is trained using their masks, thus preventing the reactivation of the remaining dropped connections.
3.2.2. Network Architecture Growth by Adding New Neurons
If the model has all its connections activated but the method is indicating that the network must grow, a process of annexing new units is carried out to obtain a topology greater than the current one. Having the model, the option of increasing the number of the original model units. As in the previous situation, a sequential process is used starting with the calculation of gradients.
Gradient evaluation: Unlike what was previously explained, where the gradients were calculated and averaged only for the dropped connections since in this case they are all activated, the gradients are calculated and averaged, but respect to each layer, in order to identify which layer is the one that presents a greater gradient and try to reduce the cost function by introducing new units to the layer with the highest gradient.
Network expansion: Once the layer to be increased is determined, an expansion procedure must be carried out where one unit is added to the selected layer, expanding the connections of the neighbor units in the same and the next layer. To generate these connections, tensors are concatenated to the weight matrices in such a way that the missing connections are assembled. This procedure maintains the current values of the layers, thus avoiding the loss of knowledge of the model and being able to transfer it to its new version.
Initialization: To initialize the new tensors, a range of values is determined among which a value will be randomly assigned to each element of the tensor. This range is calculated with reference to the maximum and minimum value of each weight matrix, so each initialization will be dependent on the weight matrix. In this way, the aim is to prevent the new weights from presenting a bias away from the current search area, and having abrupt changes in the gradient values during training sessions.
In the end, the network is trained to adjust the values to the new data acquisition.
3.2.3. Growing Process
The growing phase is an iterative process. Divided into 3 steps.
In the beginning, the model received is trained for a small fixed number of epochs, this is made in order to obtain a metric that helps to compare the performance of the model and be able to distinguish if the growing process is improving the model. In the experiments, the metric used was the “root mean squared error” of the validation data during the training process, saving the best value reached.
Once this first step is done, the model grows using one of the two options explained before (Activation of dropped connections or Growth of neurons) using only the new data set and is trained during a fixed number of epochs. After this, the model is pruned 15% of its connections, letting the model grows in the next step, but now with the whole training set (the previous data and the new ones collected). Being this the second step.
The third step as it was mentioned before, reactive the 15% of the model that was pruned but now use the whole training set. Next, a tuning training is performed. During this, the metric root mean squared error is compared to the one saved in the first step, if this metric reaches a better result the training stops, the new best result and the weights are saved, and steps 2 and 3 are made again until the metric can’t reach a better result. At this moment, if the model didn’t grow a new neuron during the last step 2, the model will be set with the last weights saved, but if the model added a new neuron, the model will stay with the last set of weights trained during step 3.
This process gives the model the ability to grow iteratively as long as a better result can be achieved or until the model adds neurons three times.
3.3. Pruning Phase
Models presenting a large number of parameters are usually redundant [23], so there are methodologies to reduce this redundancy. In the proposed algorithm, a pruning policy is applied concerning the magnitudes of the weights. Where the weights with the smallest magnitudes will be inhibited, making an analogy to the disconnection of neural synapses.
As in the reactivation of connections, the same rate value is used to calculate the percentage of the network that will be pruned, in a similar way to the process described in the growth of connections, the number of connections to “turn off” will be the difference between the current deactivated connections and the ones remaining to reach the desired rate. The weights of the connections to be disabled are modified iteratively, assigning them to 0. Once the number of disconnections is reached, their new mask is calculated, updating the new disabled connections to 0.
Pruning Process
As in the growing process, the pruning phase is iterative. It’s made of 2 steps, being the first step the same as the one explained in the growing process, where the received model is trained and saves the best root mean squared error value of the validation set during this training. It’s necessary to mention that in both steps the whole training set is used, instead of only the new data acquired.
For the second step, the 15% of the model is pruned and then a tuning training is made, where the root mean squared errors are compared. If a better result is achieved the training is stopped, and the new best value and the weights are saved. This step is repeated until the model can’t reach a better value. When this happens the model is set with the last saved weight, which means, the model will reactive the 15% of the model before the 15% that couldn’t get a better result, this happens only if step 2 was made at least one time. If not, the model will be pruned and will keep the tuning weights.
The model can be pruned until 80% of the model is pruned, once this rate is reached, if the model keeps getting better results, the model will continue training but without pruning it.
3.4. Normal Phase
When the algorithm indicates that is not necessary to change the topology of the model a “normal phase” is run. In this phase, the model keeps its architecture, but the training process is changed. This phase can run two different options before training the model, in both processes just the whole training set is used.
The first one is used when the last action taken by the system was to prune the model. In this case, before the model is trained, a single 15% growing process is made, and after this, is made a single 15% pruning, in this way the system keeps the same topology, using a growing-pruning run. Once these two actions are done the model continues the training process.
The second option is applied when the last decision was growing or when the model has not presented any change (neither pruning nor growing). Like the first option, the topology is changed and recovered but this time a pruning-growing run is made, using the same rate as the first option (15%). In the end, the model is trained.
This change-recover policy helps the model to transfer the knowledge of the previous phase and reorganize the new information. This also avoids the model to be the same as a vanilla model if no variation under Cao’s method is presented.
3.5. Decision-Making Policy
The proposed algorithm is based on the union of the pruning and growth methodologies, and the order calculated by Cao’s method. To unify these methodologies, a system that indicates which one of the processes (growing, pruning, or normal) should be executed is proposed. Thus, implementing a decision-making policy that determines through some metrics the type of evolutionary process that the net should execute. The metrics used were: (1) the mean square error (MSE) at the time of model evaluation; (2) the value resulting from Cao’s order calculation; and (3) the previous decision made by the system about the type of evolution process executed. These metrics are compared between the last training run and the one before it, which allows us to observe the trend that the metrics are presenting, whether the error in the forecasting processes has been increased or decreased, and how the data dynamic is presented.
Phase: Each time that a new sequence of data is presented to the network is named a phase of the system.
Previous Decision: This describes the type of evolution process that the algorithm executed on each phase and is the first element taken into account to make the next decision about the type of network evolution that the system will execute.
Error: Continuing with the second element of comparison, it is the error calculated during the prediction of each phase. It is worth mentioning that the prediction is made concerning and during the acquisition of the new data, calculating the MSE error of each new pattern. In addition to the calculation of the error, the results in phases t-2 and t-1 are compared and it is determined if the error increased or decreased (∆ Error).
Cao: The next element taken into account to make a decision is the metric called “Cao”, which indicates the order presented by the new data sequence of the stage. Regarding the change presented between the new and last result, a suggestion of the following action that will be made is generated. If the order decreased compared to the previous one, pruning will be suggested, otherwise, if the order increases, growing will be requested.
Decision: Based on these metrics, a decision tree was made, which will evaluate element by element until it takes the final decision of what evolutionary process will be executed for the new data sequence training. Figure 3 shows the tree diagram. If the last decision made was to maintain the network architecture without modifications and run a normal phase (N), the last decision made that is growing (G) or pruning (P) with its respective branch in the decision tree will be taken into account instead of N, identifying it in Figure 3 with the symbol (X).
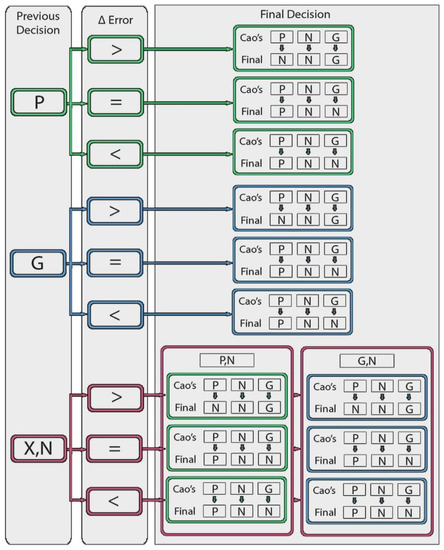
Figure 3.
Decision tree, [P = Pruning, G = Growing, N = Normal, X = Last decision different from N.
The following table illustrates an example of the decision-making process regarding each training phase and the three metrics used.
Table 1 shows training phases starting at phase 0 with the standard model and current data. The symbols G, P, and N indicate the type of evolutionary process that was executed, i.e., if the network was grown, pruned, or if it maintained its topology, respectively. Meanwhile stands for the value of the MSE of the phase. In this example are shown five phases, in Phase 0 the model was trained, and the error and Cao’s metrics were calculated. The models only can change after Phase 0. In Phase 1 Cao’s metric gave as result a bigger value than the one in Phase 0, because of this, the model suggested a growing run. The model ran Cao’s suggestion. After this, the error is calculated during the test process and continues with the next phase.

Table 1.
Decision-Making example by phases.
From Phase 2 the algorithm starts using the 3 metrics. In this phase the previous decision made was growing (Previous Decision row), the error calculated in Phase 1 is bigger than the one calculated in Phase 0 (∆ Error row, Phase 2), and Cao’s metric calculated in this phase is smaller than the phase before (Cao row, phase 1, Phase 2), which made the pruning suggest as can be seen in Cao’s suggest Phase 2. As a result of all this information, the algorithm applied a pruning run.
Phase 3 presented a bigger order than Phase 2 and even though Cao’s suggestion was, to apply a growing run, the algorithm didn’t apply it, instead, it ran a normal stage. Because the policy considers the 3 metrics used (Previous Decision, ∆ Error, and Cao’s suggest) and not only Cao’s suggest as can be seen in Figure 3. All the decisions starting from phase 2 use the decision tree. The last phase of the example used the same logic.
4. Results
To validate the proposed system, a comparison was made between Classic LSTM models (often called Vanilla LSTMs) and LSTM networks implemented with the proposed methodology, which will be named DyLSTM models to identify them. The test process and the results obtained are described below.
Dataset: The process makes use of some time series obtained from the M4 forecasting contest daily training dataset. The time series used by M4 were selected from the database ForeDeCk [24], which contains time series built from multiple and diverse sources. These series came from domains such as industries, services, tourism, imports & exports, demographics, education, labor & wage, government, households, bonds, stocks, insurance, loans, transportation, and natural resources & environment. This dataset has several time series that have different numbers of observations, due to this, were selected randomly 10 series with 1000 observations and 4 series with 4400 observations. Each series was partitioned into 10 divisions of equal sizes. In each stage, there will be 2 subsets, the first for training and the second for the prediction process (test).
Starting the model with the first division to consequently feed the system with the following divisions. Creating the training subset of the current phase, by joining the two subsets of the previous phase. In this way, the scenario of the acquisition of new data is simulated. Figure 4 shows the distribution that the data will present for each test.
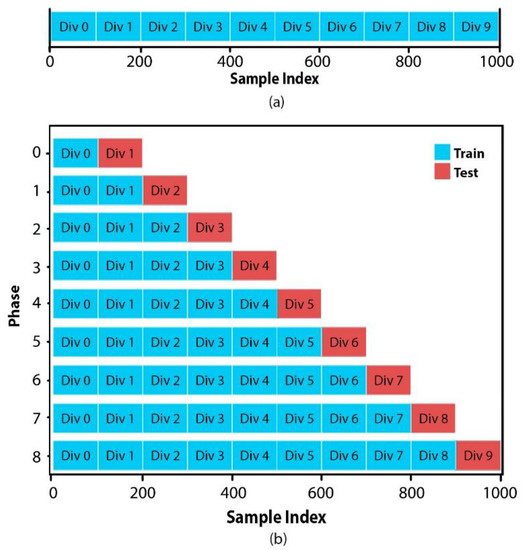
Figure 4.
Data distribution: (a) Data set divisions, (b) Train and Test subsets on each phase.
Training: In all the phases, the calculation of the order is carried out, as well as one of the three possible training processes is applied: “growing”, adding new units and/or reactivating connections; “pruning”, disabling connections; or “normal”, training and maintaining the current network architecture.
For the selection of the training process, is used the decision-making tree, described in the previous section, except for the first two phases. The first phase is the initialization of the models, in which they are trained with the first subset without any modification, keeping their respective current architectures. The second stage will only take into account the difference in the result that Cao’s methodology delivers in the current stage compared to the previous one, applying growing if the order change is greater, pruning if the order is decreased, or maintaining the architecture if the order did not change.
Cao: Originally, the calculation of Cao was made to the division that was added to the training subset, this being the test subset in the previous stage , but looking toward increasing the capacity of the Cao algorithm and giving context to the data was decided to expand its range. Calculating Cao now using windows, being the window of the phase () the union of the divisions and , to later make the comparison with the previous window () composed by the divisions and and thus be able to determine if there is an increase or decrease in the order. It is worth mentioning that this calculation method has a variation in the first two stages, wherein in the first stage, the order of the first division is calculated and in the second stage the order of the union of the first two divisions is calculated and compared with the result of the previous stage omitting the division union as it does not exist. Figure 5 exemplifies the process of moving the windows during the phases.
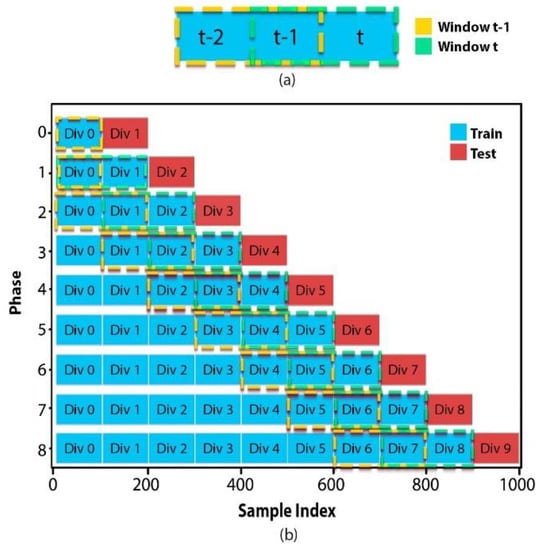
Figure 5.
Mobile window for order calculation: (a) Generation of windows, (b) Movement of windows on each phase.
4.1. Test
Five recurrent models made up of two hidden LSTM layers and an output layer with only one neuron were created. Each model has a different number of LSTM units in the two hidden layers. Obtaining “many to one” LSTM models with one step horizon. These will be compared with their counterparts that will apply the methodology proposed, presenting two groups of models (LSTM Vanilla and DyLSTM), having ten models at the end, where the first group will be trained commonly and the second will be trained with the decision policies. The initial architecture of DyLSMT models will be clones of the Vanilla models, so both groups will be initialized with the same architectures and weights as their counterparts. Table 2 shows the five models used with their respective architectures.

Table 2.
Models’ architecture.
In each phase, the models of both groups will be trained concerning their type of training and the forecasting process will be carried out with the corresponding subsets of the test, gathering the resulting error for each input pattern, ending with the calculation of the average of all the errors of the phase in their respective model. To later compare both versions and detect if an improvement was made.
Performance metrics: There are many metrics in the literature for the evaluation of forecasting methods, so it was decided to use the metrics used by the M4 which is the Overall Weighted Average (OWA) metric, which computes an average of two evaluation metrics, being the mean square error (MSE) and the symmetric mean absolute percentage error (sMAPE), the ones used, to achieve a higher level of objectivity. The equations for each of the metrics are shown next.
where is the forecast value and is the actual value.
4.2. Experimental Results
To determine as objectively as possible whether the dynamic model presents an improvement with respect to the Vanilla model, the OWA metric is used, calculated from the MSE average and the sMAPE average of all the phases and not only of the last one, since, the objective of the proposed method is the reduction of the metrics values and in some cases, the reduction and improvement of the model, keeping its error as close or better to a standard version in each retraining process (when new data is acquired), helped by a knowledge transfer process, between each new architecture.
In each of the 14 series, the error metrics (MSE and sMAPE) were calculated for each phase and model, ending with the average of all the phases to determine the OWA result among the 5 models.
To calculate OWA, the rates between the error metrics of the two models to be compared are added, in this case, since it seeks to determine if there is an improvement in the dynamic model, the OWA is calculated as follows.
where M is the vanilla version and MD is the proposed dynamic architecture version. If OWA is less than 1, it means that on average the model with the proposed algorithm has presented an improvement with respect to the Vanilla model. Where the difference to 1 is the average improvement percentage, that is, if the resulting value is 0.88, this would indicate that the model examined is 12% more accurate, taking MSE and sMAPE into account.
Figure 6 shows the evolution of the MSE error in each of the 10 models, the order obtained, and the decisions made at each phase during the first test (series 1). The regular lines describe the evolution of the errors obtained by the vanilla models and the dotted lines describe the errors acquired by the proposed models. The bars with the prefix TR show how the DyLSTM models were trained, and which change of architecture was run, being 0 as normal run, 1 as pruning run, and 2 as growing run being this metric measured in the right axes of the graph. The gray bar is the result of Cao’s method, which is also measured in the right axes of the graph. Each model has its own color code: blue for the first models, red for the second ones, orange for the third, purple for the fourth, and green for the fifth models.
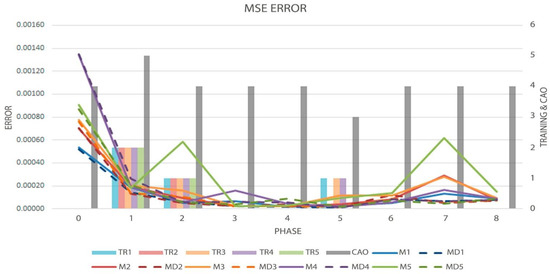
Figure 6.
Graph of the MSE metric (Solid and Dotted Lines, measured by left axis), Order evolution (CAO), and the decisions made by the algorithm (TR-Bars, the last two metrics measured by the right axis), in the first test.
Figure 7 displays how the DyLSTM models change their topology and the final rate they achieved at each phase. The rate is determined by the difference with the original architecture, being this the architecture of the vanilla model. So, if a DyLSTM model has a rate under 1 means that at that point the model is smaller than the Vanilla, as the same if the model has a bigger rate, the DyLSTM model has added new units.
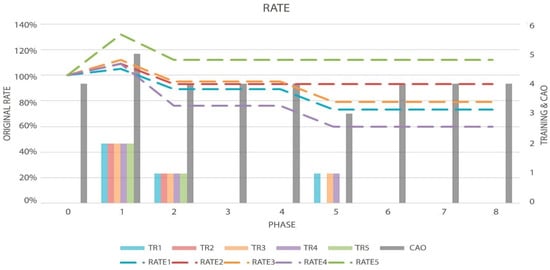
Figure 7.
Graph of the Topology Rate (Dotted Lines, measured by left axis), Order evolution (CAO), and the decisions made by the algorithm (TR-Bars, the last two metrics measured by the right axis) in the first test.
In Figure 6 can be seen that in Phase 1 the five models’ TR bars have a value of 2, which describes that the five models applied a growing run, and due to the models didn’t apply a pruning run before, the models added units. This gave in result bigger models than the originals, as can be seen in Phase 1 Figure 7, where their rates are greater than 100%. In phase 2 the five models applied a pruning run, this is described by the five TR bars with a value of 1, and the results of the rate changes, made in the topology are presented in Figure 7 Phase 2. Table 3 and Table 4 show the results of the MSE and sMAPE metrics of the first test, respectively. They show the model with its counterpart and the evolution of the metric on each phase, at the end, the average obtained from the complete test is shown.

Table 3.
Series 1 (MSE), order [Cao] and comparison between the 5 models [M] and their respective dynamic versions [MD], rate, and the decision made [TR] (Growth = 2, Pruning = 1, Normal = 0).

Table 4.
Series 1 (sMAPE), order [Cao], and comparison between the 5 models [M] and their respective dynamic versions [MD], rate, and the decision made [TR] (Growth = 2, Pruning = 1 Normal = 0).
Table 5 shows the results of the OWA calculation in each model, the final percentage of the dynamic architecture, with respect to the Vanilla version, as well as, the number of new units if they were added in the first test. Table 6 shows the result of Cao’s method on each phase of the 14 series. Table 7 summarizes the results of the average of the 14 tests performed three times. As can be seen in Table 7, it is just displayed the final rate of the model but is necessary to remember that the topology of the models changes according to the variation of the order of the series and the decisions made by the policy. So, the last rate might not be the same in all the past phases.

Table 5.
Metric (OWA). Final percentage (RATE) of the topology with respect to the initial model. (New units) Number of extra units added.

Table 6.
Cao’s method results from the 14 tests carried out.

Table 7.
Results of the 14 tests carried out.
5. Discussion
Through experimentation, certain variations of the method of the proposed algorithm were designed, such as the extension of the range of the windows for the calculation of the order, given that, initially, when only the new data was analyzed, our algorithm determined to make abrupt changes to the network topology since the system had a lack of context of the previous data. When it was determined the need to expand the amount of data, adding the previous data window to the current one, an improvement in order detection was obtained.
Another section that presented modifications in the experimentation process was the generation of the decision-making rules of the tree as its hierarchy. Looking to create a dependency between the decisions made over time and the evolution of the error metrics, the previous decision was assigned in the first position of the decision-making hierarchy followed by the error variation, thus presenting a distribution of rules that decreased or maintained the trend of the error.
It is important to note that in almost all of the 14 tests, our approach improved the results obtained by the vanilla LSTM models; in the cases that didn’t improve, the models keep almost the same performance as their counterparts. These cases were presented in five series (3, 4, 5, 11, 14) in just 7 models, where the worst model was presented in series 3, as can be seen in Table 7. During the experiments, in general, these results happened because in one of the phases, almost always after when a considerable change of order happened and a modification on the topology was made, the dynamic model had an error worse than the vanilla model, being this error enough to make on average that the dynamic model be worse in the whole test. As an example, Figure 8 and Table 8 and Table 9 is presented one of the tests of series 11, which had a major number of models with no improvement, where can be seen that models 1 and 4 had an error during phase 2 that avoided them to be on average, at the end, the same or better accuracy than the vanilla models, but getting a topology smaller than the original. Despite this fact, the models usually reduce their error by getting the same or better values than their counterparts during the next phases.
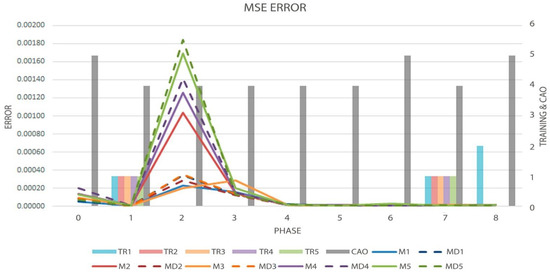
Figure 8.
Graph of the MSE metric (Solid and Dotted Lines, measured by left axis), Order evolution (CAO), and the decisions made by the algorithm (TR-Bars, the last two metrics measured by the right axis) in test eleven.

Table 8.
Series 11 (MSE), order [Cao], and comparison between the 5 models [M] and their respective dynamic versions [MD], rate, and the decision made [TR] (Growth = 2, Pruning = 1 Normal = 0).

Table 9.
Metric (OWA). Final percentage (RATE) of the topology with respect to the initial model. (New units) Number of extra units added, test eleven.
Other particularity presented in the experiments can be seen in tests 5 and 9, where the first phases, didn’t present changes of order as can be seen in Table 6, when this happens, the models can present the issue to be the same as their vanilla version, that’s why this issue was addressed using the normal phase training, giving the model the capability to manage the old knowledge and be able to distribute the new information over the whole architecture avoiding changing their topology. This implementation gave an improve over 40% in test 5 on models 2, 3, 4, and 5. Even though the dynamic model 1 didn’t present an accuracy improvement w.r.t Vanilla, it stays near the same performance as its counterpart. One of these results can be seen in Figure 9 and Figure 10 and Table 10, where it is presented the evolution of the MSE error and the rate of the architecture. Exemplifying the point described above, where architecture modifications are only seen in the last phases.
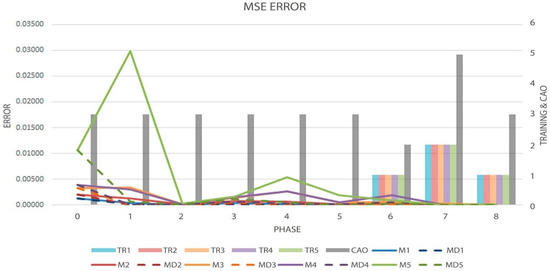
Figure 9.
Graph of the MSE metric (Solid and Dotted Lines, measured by left axis), Order evolution (CAO), and the decisions made by the algorithm (TR-Bars, the last two metrics measured by the right axis) in test five.
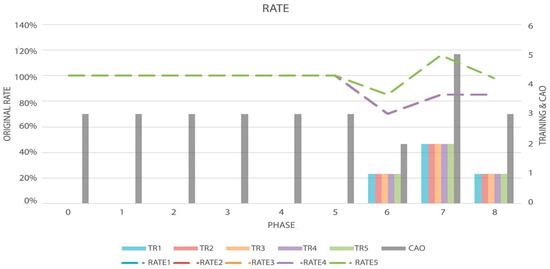
Figure 10.
Graph of the Topology Rate (Dotted Lines, measured by left axis), Order evolution (CAO), and the decisions made by the algorithm (TR-Bars, the last two metrics measured by the right axis) in test five.

Table 10.
Series 5 (MSE), order [Cao] and comparison between the 5 models [M] and their respective dynamic versions [MD], rate, and the decision made [TR] (Growth = 2, Pruning = 1 Normal = 0).
This process also helped in the situation described before, when a phase after a change of topology doesn’t get a good result. Being this training a way to reorganize the knowledge of the model and give better results in the next phases. This case is presented in Table 11, that is one of the results of series 4, which has a reduction of order in phase 1 and after this, the next 3 phases have an increase of order. As can be seen in Table 11 model 3 failed in phases 2 and 3, but even though this occurred the model achieved at the end a 9% improvement, this result can be seen in Table 12.

Table 11.
Series 4 (MSE), order [Cao], and comparison between the 5 models [M] and their respective dynamic versions [MD], rate, and the decision made [TR] (Growth = 2, Pruning = 1 Normal = 0).

Table 12.
Metric (OWA). Final percentage (RATE) of the topology with respect to the initial model. (New units) Number of extra units added, test four.
Unifying the three methods of training (pruning, growing, and normal) of the proposed system, makes the models able to identify a global trend of the data and get better results in later phases. Figure 11 shows the evolution of models 1 (Vanilla/DyLSTM) over phases 1 to 8 of series 4. This figure presents how model 1 trained with the proposed method acquires better results and anticipates trend changes meanwhile more phases have been processed.
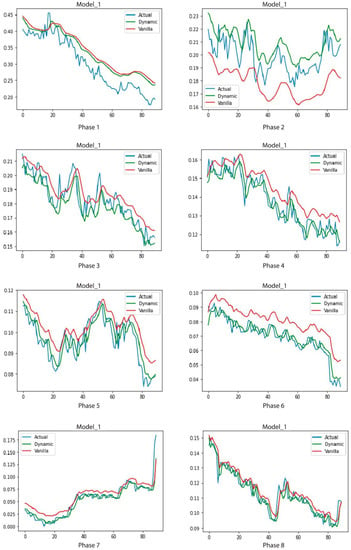
Figure 11.
Results of model 1 (Vanilla/DyLSTM) phases 1 to 8 in test four. Blue is the Actual timesereis, green is our proposed method and red is the vanilla model.
6. Conclusions and Future Work
In this work it was presented an algorithm that provides plasticity to recurrent neural networks, using as an example LSTM models applied to the time series forecasting, implementing (1) a growing paradigm based on gradients, (2) a pruning based on magnitudes, and (3) a reorganized knowledge normal phase, implemented through the use of decision policies, based on the calculation of the order of the data to train in each retraining process, when the database is updated.
Making use of some of the data series of the M4 competition, with 10 series of 1000 samples and 4 series with 4000 samples, where almost all the cases and models presented performance improvements by reducing the error function with respect to a static structure. Being the best result an improvement of around 40% between the 5 models and individually the best performance was obtained by the fifth model in series 5 with a 62% of improvement. Obtaining on average an improvement of up to 18%. In the cases that did not present considerable improvements, a similarity in the range of the error to its static counterpart was maintained and despite this, in the cases, where a reduction of order was presented, their architecture was notably reduced. As future work, the presented methodology is going to be improved by exploring new decision-making policies that allows their automatic updating based on the results obtained at each phase. It also looks forward implement a parallel process for predicting the order of the following data sequence, making the system more robust by giving it more information and anticipating the future behavior of the data. Furthermore, we will analyze the possibility to extend our approach by implementing the proposed method in other neural network models.
Author Contributions
Conceptualization, N.A.-D.; methodology, N.A.-D., D.S.N. and C.V.; software, D.S.N.; validation, C.V. and C.L.-F.; formal analysis, N.A.-D.; investigation, N.A.-D., D.S.N. and C.V.; resources, Carlos López-Franco.; writing—D.S.N.; writing—review and editing, N.A.-D. and C.V.; visualization, D.S.N.; supervision, N.A.-D. and C.V.; project administration, N.A.-D. and C.L.-F.; funding acquisition, C.L.-F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by CONACYT México grant number CB258068.
Data Availability Statement
Publicly available dataset was analyzed in this study. This data can be found here: [25].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Slawek, S. A hybrid method of exponential smoothing and recurrent. Int. J. Forecast. 2020, 36, 75–85. [Google Scholar]
- Khaldi, R.; El Afia, A.; Chiheb, R.; Tabik, S. What is the best RNN-cell structure to forecast each time series behavior? Expert Syst. Appl. 2023, 215, 119–140. [Google Scholar] [CrossRef]
- Peixeiro, M. Time Series Forecasting in Python, 1st ed.; Manning: New York, NY, USA, 2022; pp. 287–299. [Google Scholar]
- Haykin, S. Neural Networks and Learning Machines, 3rd ed.; Pearson: Hamilton, ON, Canada, 2009; pp. 1–45. [Google Scholar]
- Vapnik, V. Principles of Risk Minimization for Learning Theory. Adv. Neural Inf. Process. 1992, 4, 831–838. [Google Scholar]
- Byoung-Tak, Z. An Incremental Learning Algorithm That Optimizes Network Size and Sample Size in One Trial. IEEE Int. Conf. Neural Netw. 1991, 1, 215–220. [Google Scholar]
- Baum, E.; Haussler, D. What Size Net Gives Valid Generalization? Neural Comput. 1989, 1, 151–160. [Google Scholar] [CrossRef]
- Rehmer, A.; Kroll, A. On the vanishing and exploding gradient problem in Gated Recurrent Units. IFAC-PapersOnLine 2020, 53, 1243–1248. [Google Scholar] [CrossRef]
- Tsay, R.S.; Chen, R. Nonlinear Time Series Analysis, 1st ed.; Wiley: Hoboken, NJ, USA, 2019; pp. 173–184. [Google Scholar]
- Dai, X.; Yin, H.; Jha, N.K. Grow and Prune Compact, Fast and Accurate LSTMs. IEEE Trans. Comput. 2020, 69, 441–452. [Google Scholar] [CrossRef]
- Blalock, D.; Gonzalez Ortiz, J.J.; Frankle, J.; Guttag, J. What is the State of Neural Network Pruning? In Proceedings of the 3rd MLSys Conference, Austin, TX, USA, 2–4 March 2020. [Google Scholar]
- Fritzke, B. Growing cell structures—A self-organizing network for unsupervised and supervised learning. Neural Netw. 1994, 7, 1441–1460. [Google Scholar] [CrossRef]
- Benitez, E.M.S.; Pérez, M.Q.L. Plasticidad cerebral, una realidad neuronal. Rev. De Cienc. Médicas De Pinar Del Río 2019, 23, 599–609. [Google Scholar]
- Cao, L. Practical method for determining the minimum embedding dimension of a scalar time series. Elsevier Sci. 1997, 110, 43–50. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Am. Phys. Soc. 1992, 45, 3403–3411. [Google Scholar] [CrossRef] [PubMed]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. The M4 Competition: 100,000 time series and 61 forecasting methods. Int. J. Forecast. 2020, 36, 54–74. [Google Scholar] [CrossRef]
- Sanchez, E.N.; Felix, R.A. Nonlinear identification via variable structure recurrent neural networks. In Proceedings of the 15th Triennial World Congress, Barcelona, Spain, 21–26 July 2002. [Google Scholar]
- Tabares, H.; Branch, J.; Valencia, J. Generación dinámica de la topología de una red neuronal artificial del tipo perceptron multicapa, Revista Facultad de Ingenieria. Univ. De Antioq. 2006, 38, 146–162. [Google Scholar]
- Alam, K.M.R.; Siddique, N.; Adeli, H. A dynamic ensemble learning algorithm for neural networks. Neural Comput. Appl. 2019, 32, 8675–8690. [Google Scholar] [CrossRef]
- Dai, X.; Yin, H.; Jha, N.K. Incremental Learning Using a Grow and Prune Paradigm with Efficient Neural Networks. IEEE Trans. Emerg. Top. Comput. 2020, 10, 752–762. [Google Scholar] [CrossRef]
- Chollet, F. Deep Learning with Python; Manning Publications Co.: Shelter Island, NY, USA, 2018; pp. 202–216. [Google Scholar]
- Olah, C. Github-Understanding LSTM Networks. 27 August 2015. Available online: https://colah.github.io/posts/2015-08-Understanding-LSTMs/ (accessed on 20 October 2022).
- Denil, M.; Shakibi, B.; Dinh, L.; Ranzato, M.A.; De Freitas, N. Predicting Parameters in Deep Learning. Adv. Neural Inf. Process. Syst. 2013, 2, 2148–2156. [Google Scholar]
- Spiliotis, E.; Kouloumos, A.; Assimakopoulos, V.; Makridakis, S. Are forecasting competitions data representative of the reality? Int. J. Forecast. 2020, 1, 37–53. [Google Scholar] [CrossRef]
- Yogesh, S. Kaggle-M4 Forecasting Competition Dataset. 2020. Available online: https://www.kaggle.com/datasets/yogesh94/m4-forecasting-competition-dataset (accessed on 21 October 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).