Abstract
Combinatorial clustering based on the Ising model is drawing attention as a high-quality clustering method. However, conventional Ising-based clustering methods using the Euclidean distance cannot handle irregular data. To overcome this problem, this paper proposes an Ising-based kernel clustering method. The kernel clustering method is designed based on two critical ideas. One is to perform clustering of irregular data by mapping the data onto a high-dimensional feature space by using a kernel trick. The other is the utilization of matrix–matrix calculations in the numerical libraries to accelerate preprocess for annealing. While the conventional Ising-based clustering is not designed to accept the transformed data by the kernel trick, this paper extends the availability of Ising-based clustering to process a distance matrix defined in high-dimensional data space. The proposed method can handle the Gram matrix determined by the kernel method as a high-dimensional distance matrix to handle irregular data. By comparing the proposed Ising-based kernel clustering method with the conventional Euclidean distance-based combinatorial clustering, it is clarified that the quality of the clustering results of the proposed method for irregular data is significantly better than that of the conventional method. Furthermore, the preprocess for annealing by the proposed method using numerical libraries is by a factor of up to million × from the conventional naive python’s implementation. Comparisons between Ising-based kernel clustering and kernel K-means reveal that the proposed method has the potential to obtain higher-quality clustering results than the kernel K-means as a representative of the state-of-the-art kernel clustering methods.
1. Introduction
Ising machineshave been developed to solve combinatorial optimization problems in the past few years. D-Wave Systems, Inc., (Burnaby, Canada) is currently working on a Quantum Annealing (QA) machine that can solve the Ising model [1]. Additionally, conventional digital computers are also being utilized to perform special-purpose computations using the Ising model, such as Simulated Annealing [2], the simulated bifurcation algorithm [3], and so on [4,5]. In particular, Ising machines are expected to be applied to a wide range of fields such as vehicle routing problems [6], traffic flow optimization [7,8], air traffic management [9], control of automated guided vehicles [10], planning space debris removal missions [11], and machine learning [12,13,14].
One of the applications utilizing the Ising machines is combinatorial clustering. Clustering is a machine learning technique that involves grouping similar objects together based on their characteristics. Clustering aims to identify natural groupings in the data, which can help with tasks such as data compression, anomaly detection, and pattern recognition. There are two main types of clustering: hierarchical and non-hierarchical approaches. In hierarchical clustering, the data are organized into a tree-like structure, with the most similar objects grouped together at the bottom of the tree and progressively more dissimilar groups at higher levels. On the other hand, non-hierarchical clustering involves partitioning the data into a fixed number of clusters. This can be achieved through methods such as k-means clustering, where the data are partitioned into k clusters by minimizing the distance between each point and its assigned cluster centroid. Although non-hierarchical clustering is a powerful approach when the number of clusters is known, conventional non-hierarchical clustering makes it hard to find the globally optimum solution. This is because state-of-the-art clustering performs approximation by calculating the distance between the data point and the cluster centroid instead of the distance among data points.
Combinatorial clustering is a method that enables the calculation of the distance among data points [15]. Since Ising machines have the potential to accelerate such a time-consuming calculation, combinatorial clustering based on the Ising model is drawing attention because of its ability to obtain high-quality clustering results [16,17,18,19]. Ising-based combinatorial clustering typically employs the Euclidean distance as a measure of similarity. Nevertheless, numerous practical data possess irregular distributions that render clustering via Euclidean distance challenging.
To improve the quality and robustness of clustering, some different approaches have been developed. One is a clustering algorithm combining deviation-sparse fuzzy C-Means with neighbor information constraints [20]. The algorithm uses a deviation-sparsity regularization term to encourage sparsity in the clustering results by incorporating spatial information about neighboring data points. Such techniques can help feature selection and dimensionality reduction beyond performing only clustering. Viewpoint-based kernel fuzzy clustering with weight information granules [21] is another novel fuzzy clustering algorithm that combines kernel clustering with viewpoint-based clustering. The algorithm uses viewpoint-based clustering to identify initial clusters and then applies kernel clustering to refine them. Weight information granules are introduced to better capture the distribution of the data, and a regularization term is included to encourage sparsity in the clustering results. However, such clustering algorithms require minimization of objective functions and are still based entirely upon the approximation of minimizing them to save the computational complexity. Since such approximated methods fail to find the exact solution in many cases, Ising-based combinatorial clustering that potentially solves the exact solution has to be expanded to handle any distribution of data.
This paper suggests a solution for achieving combinatorial clustering capable of handling any irregular data. Specifically, the proposed method involves performing Ising-based kernel clustering by employing the kernel method on Ising machines to execute combinatorial clustering. The proposed method transforms irregular data onto the high-dimensional feature space by using an appropriate kernel function [22]. Here, it takes a lot of time to calculate the transformed data from the irregular input data. To accelerate this preprocess, this paper also discusses an efficient implementation of Ising-based kernel clustering for numerical libraries. Efficient representation to utilize numerical libraries is defined by matrix–matrix calculations.
The remainder of this paper is structured as follows: Section 2 provides an overview of Ising machines and combinatorial clustering. Section 3 proposes Ising-based kernel clustering and efficient implementation to utilize numerical libraries. Section 4 presents an evaluation of the proposed method with respect to quality and execution time. Section 5 describes the related work of the proposed method. Finally, Section 6 summarizes the main contributions of this paper.
2. Ising-Based Combinatorial Clustering
2.1. Ising Model
Equation (1) is a Hamiltonian of the Ising model. Ising machines search for the combination of variables that minimizes the energy of the Ising model in Equation (1).
The Ising model has the interactions between two different spins and the magnetic field of its own spin .
The Quadratic Unconstrained Binary Optimization (QUBO) model is an equivalent representation of the Ising model. Equation (2) is a Hamiltonian of the QUBO model. Here, binary variables are decision variables of the QUBO model. The Hamiltonian of the QUBO model is transformed from the Hamiltonian of the Ising model by .
The QUBO model also has the interactions between two different variables . In contrast to the Ising model, the QUBO model does not have any magnetic field but has another type of self-interaction because holds for . In addition, the coefficients of the Ising and QUBO models are stored in the matrix form. The matrix form is a unified interface that various Ising machines have adopted.
2.2. Combinatorial Clustering
Combinatorial clustering is one of the machine learning methods and minimizes the sum of intra-cluster distances among data points.
Well-known clustering methods such as K-means, K-means++, and spectral clustering perform quasi-optimization to reduce the computational complexity. Hence, quasi-optimized clustering methods cannot obtain the globally optimal clustering solution even with a sufficient computation time.
On the other hand,
combinatorial clustering can achieve high-quality clustering results. Finding the combination of data that minimizes the sum of intra-cluster distances guarantees that a globally optimal solution is found [15].
The objective function to minimize the sum of intra-cluster distances of combinatorial clustering is represented as Equation (3).
To perform combinatorial clustering, the number of clusters K is set in advance. indicates the coordinates of data point i. indicates the degree of similarities between two different data points i and j. Cluster assignments of data points are represented as when data point i belongs to cluster a.
Ising-based combinatorial clustering has been proposed to obtain the globally optimal solution [16].
Ising-based combinatorial clustering uses one-hot encoding to represent decision variables by using binary variables. Figure 1 is an overview of the one-hot encoding. The clustering results expressed in one-hot encoding represent a cluster to which a single datum belongs by using bits, whose number is the same as that of clusters.
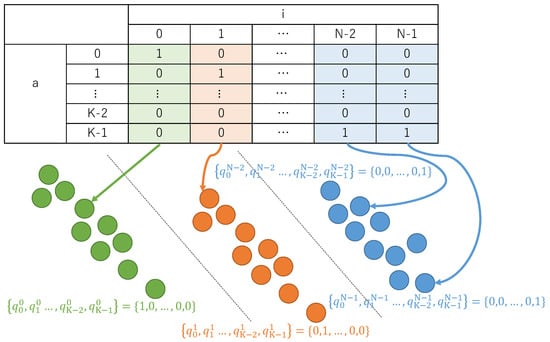
Figure 1.
An overview of one-hot encoding.
Equation (4) is a decision variable using one-hot encoding.
For , N is the number of data points, and K is the number of clusters. The one-hot encoding indicates that is 1 if data belongs to cluster , and 0 if it does not.
Equation (5) is the QUBO model of combinatorial clustering.
Here, the number of data points is represented as N. The Lagrange multiplier is introduced to combine the first and the second terms of Equation (5). The first term of Equation (5) is the objective function transformed from Equation (3) by using binary decision variables. The second term of Equation (5) is the constraint function that obliges each data point to belong to only one cluster. It is generally known that a sufficiently large Lagrange multiplier avoids violation of the constraint. In the case of combinatorial clustering, it is already revealed that the appropriate value of the Lagrange multiplier is when all the values of are normalized [16].
2.3. Problems
Ising-based combinatorial clustering has the potential to obtain the global optimal clustering results. However, conventional Ising-based combinatorial clustering cannot handle data with irregular distributions. This is because the conventional method uses the Euclidean distances as the degree of similarity. When the input data are mapped on the Euclidean space, combinatorial clustering can handle linearly separable data. However, conventional combinatorial clustering cannot handle non-linear separable data. Thus, irregular data are defined as the data for which linear decision boundaries cannot be drawn. Euclidean-based clustering methods assume that each cluster has equal variance, and decision boundaries are drawn linearly. Therefore, irregular data with heterogeneous variances among clusters or with no radial spread from the cluster center cannot be appropriately clustered.
One way to perform clustering of irregular data is to apply a kernel method to irregular data. The kernel method can perform clustering of irregular data by mapping the data onto a high-dimensional feature space.
In the case of quasi-optimal clustering methods, kernel clustering is widely used to obtain clustering results for any distributed data. However, Ising-based combinatorial clustering using the kernel method that can handle irregular data has not been proposed yet. Thus, it is required to consider the QUBO formulation for kernel clustering.
In addition, the preprocess for Ising-based computation takes a long time to calculate the coefficients of the QUBO problem. Ising-based clustering methods also require the calculation of the QUBO coefficients in Equation (5). To make matters complicated, Ising-based kernel clustering has to transform data onto the high-dimensional feature space. Thus, Ising-based kernel clustering requires more complex preprocessing calculations than conventional Ising-based combinatorial clustering.
3. Ising-Based Kernel Clustering
This paper extends Ising-based combinatorial clustering to minimize the high-dimensional space distance defined by the Gaussian kernel. The proposed method uses a Gram matrix and an appropriate kernel function to transform irregular data into linearly separable data. The Gram matrix is a matrix where each element is the distance between two data points in the high-dimensional feature space. The appropriate kernel function maps the input data onto the high-dimensional feature space.
Even though conventional Ising-based combinatorial clustering can potentially solve the exact solution for clustering problems based on the Euclidean distance, it cannot accept the Gram matrix determined by the kernel trick. This is because the Gram matrix has diagonal components in spite of the Euclidean distance matrix not having diagonal components. To process the Gram matrix by the Ising-based clustering, the objective function of combinatorial clustering, which works with distances between data points defined by Euclidean distances, is changed to an objective function including the Gram matrix. The objective function based on the Gram matrix is then transformed into a QUBO model.
On the other hand, the preprocess of creating the Gram matrix and calculating the kernel function takes a lot of time. To accelerate the preprocess, the preprocess in the Ising-based kernel clustering is implemented so as to utilize numerical libraries. Recent numerical libraries are designed to accelerate matrix calculations by solving them using parallel and distributed computing systems. Therefore, this paper discusses calculations for parallel and distributed computing systems.
3.1. Kernel Method for Combinatorial Clustering
In the kernel method, elements of a Gram matrix express the degree of similarities in the high-dimensional feature space between two data points. The elements of a Gram matrix are calculated by the following equation.
Hereinafter, is denoted as . The proposed method can calculate all necessary similarities in advance. This is because the proposed method is the optimization method using similarities among all data points. This method does not need to update any similarities in the calculation process. The calculation of similarities is performed for all pairs of data points. Thus, the Gram matrix is calculated by the following equation.
is a kernel matrix with elements calculated by the kernel function. is a K-dimensional vector whose i-th vector component represents an arithmetic mean among . The second and third terms of Equation (7) are derived from the second and third terms of Equation (6). in Equation (7) is a scalar that represents the arithmetic mean among all elements of the kernel matrix . Therefore, the elements of the fourth term in Equation (7) are equivalent to the fourth term of Equation (6) for each element . Switching the kernel function, called a kernel trick, enables the Gram matrix to represent various measures of similarities. requires the kernel trick to select the appropriate Mercer kernel defined by Mercer’s theorem. Mercer’s theorem determines that the available matrix used as the Gram matrix is only positive and semi-definite. The kernel function is defined so that the inner product matrix transformed from the original data is the symmetric Gram matrix. In this paper, the kernel function is given by the following Gaussian kernel.
in Equation (8) are the elements of the kernel matrix and are also calculated in the same way for all pairs of the data points. Thus, the kernel matrix is expressed by using a squared Euclidean distance matrix as follows, where has the elements of squared distances .
Here, is defined as the function that calculates Napier’s constant e to the power of each element in the matrix . Nowadays, numerical libraries implement such an exponential function to accelerate calculations. In addition, the same calculations of are performed as the scalar-matrix calculation in recent numerical libraries.
3.2. QUBO Formulation for Ising-Based Kernel Clustering
The kernel function transforms the elements of the Gram matrix into the degree of similarities among data points. Thus, combinatorial clustering using the Gram matrix provides global optimal clustering assignments. The elements of the Gram matrix are already transformed as distances in the high-dimensional data. Since the objective function of combinatorial clustering is the sum of intra-cluster similarities among data points, Equation (10) is the objective function of combinatorial clustering using the kernel method.
Equation (10) is a similar form to the first term of Equation (5). Although the distance matrix with elements has zero diagonal components, the Gram matrix with elements has non-zero diagonal components. Thus, the QUBO function for combinatorial clustering using the Gram matrix needs to be defined differently from the QUBO function for conventional combinatorial clustering using the Euclidean distance matrix.
Equation (10) can be expressed as Equation (11) by eliminating redundancy. This is because the Gram matrix is symmetric.
When the two data are in the same cluster, the elements of the Gram matrix are calculated. Equation (11) adds the element of the Gram matrix between the two data to the Hamiltonian when and are both 1.
However, Equation (11) has a minimum value when all binary variables are 0. This means that all the data do not belong to any cluster. To avoid this problem, the one-hot constraint that all the data should belong to only one cluster is given as Equation (12).
To satisfy Equation (12) for , the one-hot constraint function based on the QUBO model is shown in Equation (13).
The one-hot constraint function has also been used for combinatorial clustering based on the Euclidean distance. Therefore, combinatorial clustering based on the Ising model using the kernel method is represented in Equation (14).
is given by the method of the Lagrange multiplier. Violation of the constraint is avoided by providing a sufficiently large Lagrange multiplier.
3.3. QUBO Matrix Generation by Matrix–Matrix Calculations
To generate the QUBO matrix using matrix–matrix calculations, a binary decision vector is introduced. Each element of is defined as follows.
Here, the following five matrices are defined to discuss the matrix–matrix product form of Equation (14).
- is a K-dimensional identity matrix.
- is a K-dimensional upper triangular matrix with 0 for the diagonal components and 1 for the upper triangular components.
- is defined as a matrix with for the diagonal components and 0 for the other components.
- is a matrix consisting of only the diagonal components of the Gram matrix . has zero non-diagonal components.
- is a matrix consisting of only the upper triangular components of the Gram matrix . has zero diagonal and lower triangular components.
First, let us consider the matrix–matrix product form of calculating the similarities between two data points in the high-dimensional feature space. The first term of Equation (14) calculates the products among the diagonal components of the Gram matrix and the same two binary decision variables and . The second term calculates the products among the upper triangular components and two different binary decision variables and . Thus, the first and second terms of Equation (14) are transformed to Equation (16).
The operator ⊗ is the Kronecker product. The Kronecker product of matrices and generates a matrix as follows.
Equation (16) is calculated by using the calculation of Equation (17). The summation operators of , , and correspond to the matrices of , , and , respectively. and have the same sizes of . is the matrix with the size of . Since of Equation (15) is the vector with the size of , the size of the matrix is expanded to . As a result, Equation (16) can perform the same calculation of the first and second terms of Equation (14).
Second, let us consider the matrix–matrix QUBO generation form of the one-hot constraint. The third term of Equation (14) is represented as Equation (18) [18].
As well as the case in the matrix–matrix product form of calculating the Gram elements, the summation operators of , , and correspond to the matrices of , , , respectively. Hence, Equation (18) is represented as the matrix–matrix product form of Equation (19).
Equation (14) is expressed as the sum of the matrix–matrix product forms in Equations (16) and (19), as in Equation (20).
Recent numerical libraries are equipped with necessary functions for calculating the QUBO matrix . Therefore, the method of generating the QUBO matrix for kernel clustering by matrix–matrix calculations is effective to accelerate the preprocess for annealing methods.
The computational complexity of the proposed Ising-based kernel clustering is estimated to be at most. The complexity is mainly occupied by the process of solving the QUBO problem. When spins are given, SA takes the computational time of . Conversely, QA takes the computational time of . This paper uses the SA to solve the QUBO problem because the recent QA cannot yet solve the large problem at high computational precision. The kernel clustering by solving the QA is one of our main future directions.
The maximum preprocess times for annealing are estimated to be , , and for calculating the Gaussian kernel matrix (Equation (9)), the Gram matrix (Equation (7)), and the QUBO matrix (Equation (20)), respectively. Additionally, the preprocess is formulated in the matrix–matrix calculation to utilize the numerical libraries. Since the numerical libraries accelerate the preprocess, the actual computational time is reduced more.
Therefore, the proposed kernel clustering has a similar high computational complexity of as the conventional Euclidean-based Ising clustering. The proposed method can expand the system availability even without increasing the computational complexity. Conversely, Ising-based clustering methods have more computational complexity than state-of-the-art approximated clustering methods. The approximated clustering methods obtain at most the computational complexity of at the expense of finding a locally optimum solution. While the quasi-optimal clustering methods do not guarantee to provide the globally optimum solution, the Ising-based clustering methods have the potential to find a ground state. When the ground state of the clustering is required, the proposed method shows an ideal clustering one by leveraging the nature of Ising machines.
4. Evaluation
4.1. Experimental Environments
The proposed method is compared with Euclidean distance-based combinatorial clustering as the conventional method. Evaluations are conducted in terms of solution quality and execution time.
Both proposed and conventional combinatorial clustering based on the Ising model use an externally defined one-hot constraint [17,18]. This method is preferred over the internally defined one-hot constraint in the QUBO matrix, resulting in higher-quality clustering. The reason for this is that in the internally constrained method, the Lagrange multiplier is significantly larger than the coefficients of the objective function. As a result, the constraint function has a significant influence, and solutions that satisfy the one-hot constraint can be obtained. However, as the influence of the objective function is small, the quality of clustering results decreases [18]. To address this problem, this paper utilizes externally defining the one-hot constraint of Equation (12) while only minimizing the objective function of Equation (11). By using the externally-defined one-hot constraint method, combinatorial clustering with the QUBO function containing only the objective function and the externally defined one-hot constraint can achieve higher quality results than the method that has both the objective and constraint function in the QUBO function. The Ising-based kernel clustering method utilizes the coefficients of the objective function as the elements of the Gram matrix. Let us conduct the experiments by minimizing the Hamiltonian of Equation (16) while externally defining the one-hot constraint.
In the case of this paper, SA is used to search for the solution that minimizes the QUBO function for Ising-based kernel clustering. The SA algorithm is executed on a computing platform called SX-Aurora TSUBASA (Aurora) [23], which consists of a CPU (Intel Xeon 6126) and a VE (NEC Vector Engine Type 20B) [24]. In the SA algorithm on Aurora, the one-hot constraints are defined externally to the QUBO function, and the SA algorithm searches for solutions that allow multiple-bit flips [25]. Initially, SA searches for solutions with a single-bit flip, and once the one-hot constraint is satisfied, it then searches for only the solutions that satisfy the constraint using multiple-bit flips.
Parallel Tempering (PT) [26] is used in addition to SA on Aurora. PT assigns different temperatures to multiple SA processes, and each process independently executes SA in parallel. The purpose of this method is to improve the exploration of the solution space by allowing solutions to escape from local minima. During the PT search, solutions are probabilistically exchanged between different SA processes based on the temperature of each process. The number of parallel temperatures for PT is set to 8. The number of sweeps, which is a parameter indicating the number of times to search for a solution, is set to 100. The inverse temperature starts from at the beginning of the search and gradually increases to 50 at the end. NumPy v0.22.1 [27] is used as the numerical library to perform matrix–matrix calculations shown in Equations (7), (9) and (20).
The experiment uses four datasets generated through scikit-learn v1.0.2 [28]’s artificial data generation functions, and each dataset has 64 data points.
The clustering results are evaluated based on the Adjusted Rand Index (ARI), which measures the similarity between the clustering result and the correct label. ARI has a maximum value of 1 when all labels match, and the average value is calculated from 100 experiments.
4.2. Quality
Figure 2 shows the clustering results of the conventional method.
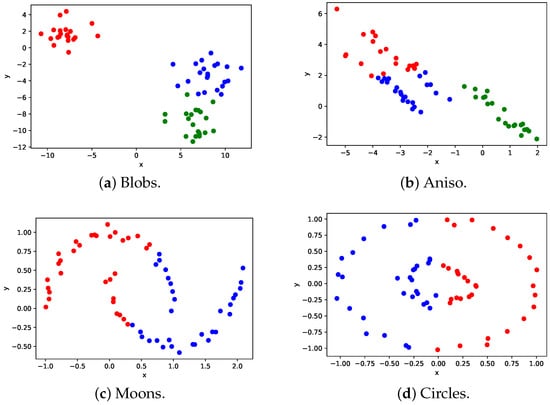
Figure 2.
Clustering results of the conventional method.
Figure 2a represents a dataset containing three clusters with equal variances, while Figure 2b depicts a dataset with clusters distributed anisotropically. Figure 2c shows a dataset comprising two half circles that interleave, while Figure 2d represents a dataset with a small circle inside a larger circle. In this paper, the datasets depicted in Figure 2a–d are referred to as Blobs, Aniso, Moons, and Circles, respectively, and the data points within different clusters are indicated with different colors.
Figure 2a illustrates that the conventional method is capable of clustering data with equal variances accurately. However, it fails to cluster data that are not equally distributed from the center, as depicted in Figure 2b–d. The conventional method tries to partition the data in a single linear line, making it impossible to achieve the desired clustering result.
Figure 3 shows the clustering results of the proposed method.
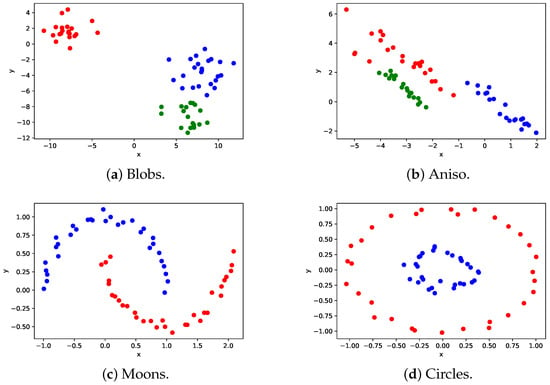
Figure 3.
Clustering results of the proposed method. Data points having the same color belong to the same cluster.
The parameters in Equation (8) for Figure 3a–d are set to 3.5, 0.55, 0.2, and 0.4, respectively, as these values produce the highest ARI. The clustering results in Figure 3a demonstrate that the proposed method can accurately cluster center-aggregated data, similar to the conventional method. Additionally, the proposed method can effectively cluster anisotropic and irregular data, as demonstrated in Figure 3b–d. This is due to the transformation of the data into linearly separable high-dimensional data through the kernel method.
Figure 4 shows ARI for each dataset to further evaluate the difference in quality between the proposed and conventional methods.
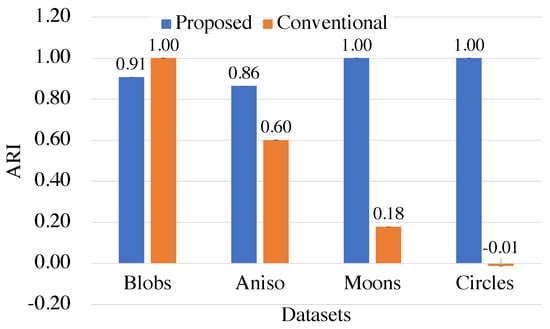
Figure 4.
The qualities of the proposed kernel-based and conventional Euclidean-based methods for different datasets.
The clustering results for the Blobs dataset show that the conventional method achieves a higher ARI than the proposed method. This is because the Blobs dataset can be linearly partitioned based on the Euclidean distance without any transformation. However, the proposed method still achieves a relatively high ARI of even by using the kernel method. On the other hand, for the Aniso, Moons, and Circles datasets, the proposed method outperforms the conventional method in terms of ARI. This is because the data transformation by the kernel method is effective for irregularly distributed data.
In order to achieve superior clustering results in combinatorial clustering using the kernel method, it is imperative to select the optimal parameter . Figure 5 vividly demonstrates the impact of varying on the clustering quality.
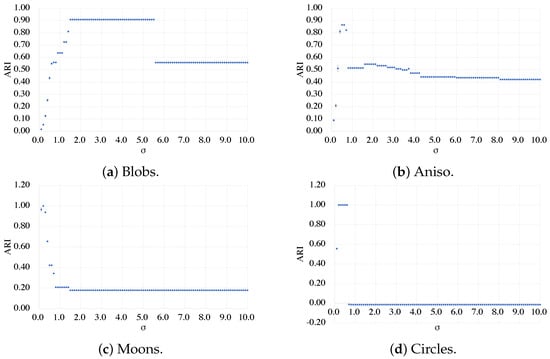
Figure 5.
ARI of combinatorial clustering using kernel method when is varied.
The results presented in Figure 5 are striking, demonstrating the crucial importance of selecting the correct parameter in the Ising-based combinatorial clustering using the kernel method. For instance, it is clear from Figure 5a that the Blobs dataset achieves remarkably high ARI for several , showcasing the versatility and flexibility of the proposed method in transforming the data to provide multiple decision boundaries. In contrast, Figure 5b–d show that Aniso, Moons, and Circles have a small range of maximum ARI, indicating a limited number of decision boundaries that can be achieved with the given parameter range. These findings underline the significance of selecting the optimal parameter to achieve high-quality results of Ising-based kernel clustering.
Next, Figure 6 shows the clustering results with the highest ARI of the proposed method and the conventional method on the dataset with six circles to evaluate the capability of the proposed method to handle any two or more clusters.
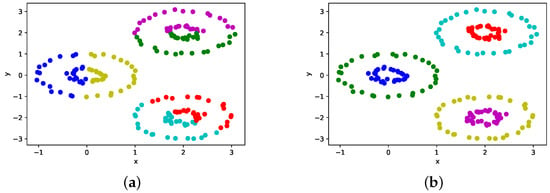
Figure 6.
The clustering results on the dataset with 6 circles. Data points having the same color belong to the same cluster. (a) The conventional Euclidean-based method; (b) the proposed kernel-based method.
The results show that the conventional method fails to cluster the data appropriately, while the proposed method successfully clusters the data even when the clusters have uneven variances and irregular shapes.
Furthermore, Figure 7 shows ARIs when changing the number of circles and the number of clusters. This experiment is carried out by changing the number of circles up to 6 in the Circles dataset. Then, the number of data points is also increased from 64 to 192.
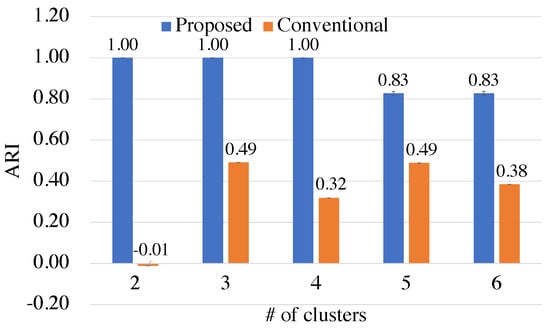
Figure 7.
The qualities of the proposed kernel-based and conventional Euclidean-based methods for different numbers of clusters.
Based on Figure 7, it is evident that the proposed method outperforms the conventional method across all the numbers of clusters considered. However, as the number of clusters increases, the mean ARI of the proposed method decreases. This is because SA converges to suboptimal solutions. To mitigate this issue, it is essential to fine-tune the parameters of SA, such as the number of sweeps or the way to schedule the inverse temperature, to obtain better results.
4.3. Execution Time
Figure 8 shows the total execution time of the preprocessing for annealing. These execution times include the times for generating the kernel, Gram, and QUBO matrices. Proposed indicates the proposed method that is defined by the matrix–matrix calculations for using numerical libraries. Conventional is the conventional implementation in which coefficients of the kernel, Gram, and QUBO matrices are calculated iteratively [22]. Internal and External indicate the internally-constrained and externally-constrained QUBO matrix-generating methods, respectively. The internally-constrained QUBO matrix contains coefficients of the Lagrange multiplier. Conversely, the externally-constrained QUBO matrix does not contain the coefficients of the Lagrange multiplier. The experiments are conducted by changing the number of data points from 8 to 1024.
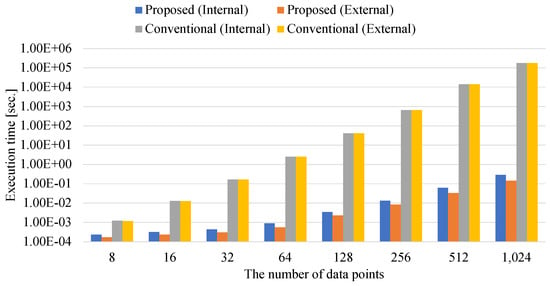
Figure 8.
Total execution time of preprocessing for annealing.
When the number of data points is eight, both internal and external Proposed methods are about 10 times faster than both internal and external Conventional methods. This is because the preprocess for annealing is represented as the matrix–matrix calculations to utilize numerical libraries. The numerical libraries can accelerate the matrix–matrix calculations by adopting techniques of distributed memory and highly parallel programming models. As the number of data points increases, the difference between Proposed and Conventional increases. The difference between the proposed and the conventional methods are at most million and million times when the number of data points is 1024. This is because the conventional method requires more instructions for calculating coefficients than the proposed method. The proposed method uses a numerical library to process calculations with a high level of parallelism. Moreover, numerical libraries are highly optimized to maximize machine performance by specializing in specific calculations. Conventional methods, on the other hand, are implemented in script languages such as Python to implement easily and are not specialized in bringing the best out of the performance. As a result, the proposed method achieves speedups of millions of times over the conventional method. Since the proposed method accelerates the preprocess for annealing methods, the matrix–matrix computation has the potential to solve large-scale Ising-based clustering problems.
To further investigate the effectiveness of matrix–matrix calculations in the preprocess for annealing, Figure 9, Figure 10, Figure 11 and Figure 12 show the breakdowns of the preprocess time. Figure 9 and Figure 10 show the execution times for calculating the kernel and Gram coefficients, respectively. Proposed uses the method of determining the coefficients of matrices by matrix–matrix calculations, as shown in Equations (7) and (9). Conventional calculates the coefficients sequentially by implementing Equations (6) and (8).
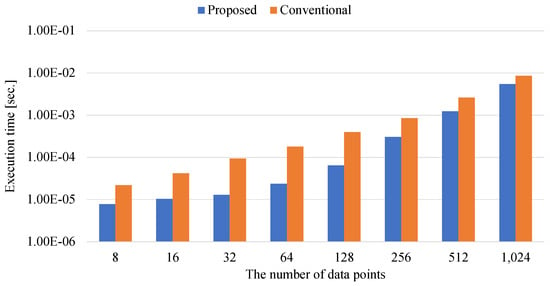
Figure 9.
The execution time of determining the Gaussian kernel coefficients.
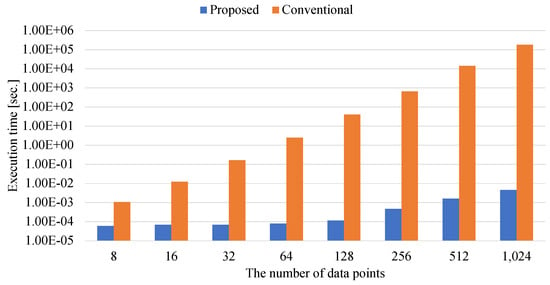
Figure 10.
The execution time of determining the Gram coefficients.
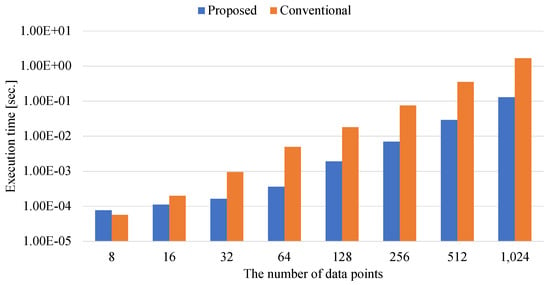
Figure 11.
The execution time of determining the elements of the externally-constrained QUBO matrix.
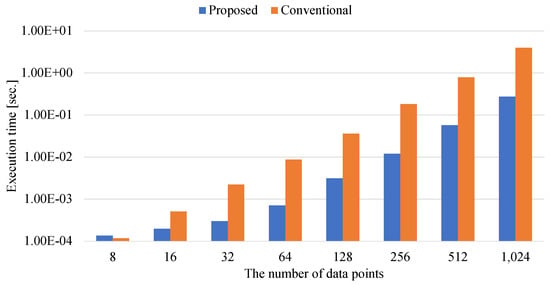
Figure 12.
The execution time of determining the elements of the internally-constrained QUBO matrix.
Figure 9 shows that the execution time for determining the coefficients of the kernel matrix is not so long. The acceleration rate of the proposed method to the conventional method is also small, ranging from to . This is because the proposed method determines the coefficients of kernel matrix by not matrix–matrix calculations but scalar–matrix calculation. As shown in Equation (9), an exponential operator and a multiplier is applied to the elements of the Gaussian kernel matrix only once to each element of the squared distance . Since the numerical library cannot be highly parallelized for scalar–matrix operation, the acceleration ratio of the proposed method to the conventional method is low.
Figure 10 also shows that Proposed is much faster than Conventional. This experimental result reveals that the matrix–matrix calculations is accelerated by the numerical library. In calculating the coefficients of the Gram matrix, the acceleration ratio of the proposed method to the conventional method is at most million. Since the process of generating the Gram matrix has multiple matrix–matrix calculations, the parallel calculation by the numerical library is effective.
Figure 11 and Figure 12 show the execution times for determining the elements of the externally-constrained and internally-constrained QUBO matrices.
When the number of data points is eight in Figure 11 and Figure 12, matrix–matrix calculations of the externally-constrained and internally-constrained QUBO matrix take longer than the conventional method. This is because multiple numerical functions of matrix–matrix calculations take constant overhead. Since the conventional methods do not have the overhead due to determining the QUBO coefficients, the conventional methods are faster than the proposed methods when the number of data points is small.
As the numbers of data points increase, the differences between the proposed and conventional methods increase in both cases of Figure 11 and Figure 12. The proposed methods for the externally-constrained and internally-constrained QUBO coefficients can achieve times that are and faster than the conventional methods for the externally-constrained and internally-constrained QUBO coefficients, respectively. Here, the acceleration ratio of generating the externally-constrained QUBO coefficients is smaller than that of generating the internally-constrained QUBO coefficients. This is because the internally-constrained QUBO coefficients require calculating both the coefficients of the Gram matrix and those of the Lagrange multiplier, while the externally-constrained QUBO coefficients require calculating only the coefficients of the Gram matrix. Since the conventional method for internally-constrained QUBO coefficients requires more complicated preprocesses, the proposed method for the internally-constrained QUBO coefficients is more effective than that for the externally-constrained QUBO coefficients. Thus, the speedup ratio for determining methods of the internally-constrained QUBO coefficients is higher than that for determining methods of the externally-constrained QUBO coefficients.
These discussions clarify that it is useful for the preprocess of annealing to use numerical libraries for the matrix–matrix calculations. The most effective part of the proposed method is determining the coefficients of the Gram matrix. The Gram coefficients are also used for the state-of-the-art kernel clustering methods other than Ising-based kernel clustering methods. While these state-of-the-art kernel clustering methods calculate the Gram coefficients among centroids and the other actual data points, Ising-based kernel clustering methods calculate the Gram coefficients among only the actual data points. Since all the Gram coefficients among the actual data points are calculated simultaneously in advance, calculating the Gram matrix for Ising-based kernel clustering methods can obtain a high level of parallelism by using the numerical libraries. The experiments clarify that utilizing matrix–matrix calculations for the Gram matrix is effective. Because the kernel methods are also useful in the field of other machine learning methods, such as linear regression, support vector machine, and K-nearest neighbor, the proposed matrix–matrix calculating method has the potential to accelerate these methods based on the Ising model.
4.4. Comparisons with Kernel K-Means
While the Ising-based kernel clustering optimizes the original objective function, kernel K-means clustering [29] as a representative of the state-of-the-art kernel clustering methods conducts quasi-optimization using the Gram elements. To reduce the computational cost, Kernel K-means calculates similarities among centroids , geometric center of clusters , and the other data points instead of similarities among all actual data points and .
Figure 13 and Figure 14 are comparisons between the proposed Ising-based kernel clustering and the kernel K-means. Figure 13 and Figure 14 show the ARIs and the execution times of each clustering method, respectively.
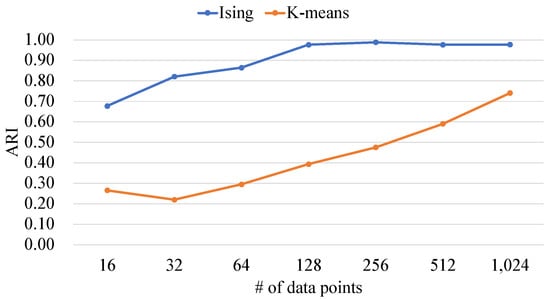
Figure 13.
The ARIs of the proposed Ising-based kernel clustering and kernel K-means.
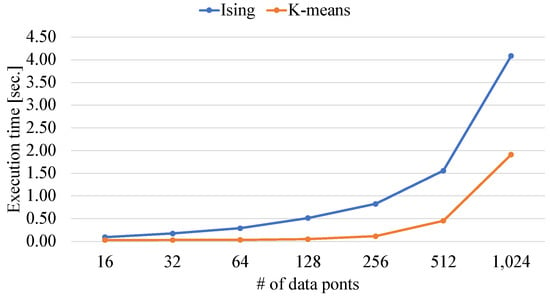
Figure 14.
Execution times of the proposed Ising-based kernel clustering and kernel K-means.
Figure 13 shows that the ARIs of the proposed method are higher than that of the conventional method. This is because the proposed method searches for the global optimal solution. Since the kernel K-means performs quasi-optimization, the probability of obtaining solutions with high accuracy is low.
Next, Figure 14 shows that the execution times of the proposed method are longer than that of the kernel K-means. This is because the proposed Ising-based kernel clustering takes a long time to determine the coefficients of the kernel, Gram, and QUBO matrices. Thus, Ising-based kernel clustering is useful in the situation where clustering results with higher accuracy are required even if it takes a longer time.
4.5. Experiments on Real Datasets
For further analysis, this section conducts experiments using practical real-world datasets. The Yale Face Database (YALE) [30] and the Japanese Female Facial Expression Dataset (JAFFE) [31] are used for the experiments, and their details are shown in Table 1. Furthermore, several facial image examples from YALE and JAFFE are presented in Figure 15 and Figure 16, respectively.

Table 1.
Description of the datasets.

Figure 15.
Samples of the Yale Face Database.
Figure 16.
Samples of the Japanese Female Facial Expression Dataset.
Clustering for the facial image dataset is a task that categorizes facial images of the same person into the same cluster. In this experiment, the proposed method is used to perform clustering for YALE and JAFFE datasets, and the performance is evaluated by comparing it with other non-Ising-based clustering methods.
The clustering performance is evaluated using Normalized Mutual Information (NMI). NMI is a normalization of the Mutual Information score to scale the results between 0 (no mutual information) and 1 (perfect correlation).
First, an experiment is conducted to investigate an appropriate parameter because the performance of the proposed method depends on the parameter . Next, the results are compared with state-of-the-art clustering methods. When performing clustering for complex image data, such as facial images, it is not always possible to convert the data structure to a linearly separable one with a single kernel. Therefore, multi-view methods using multiple kernels tend to show high performance [32]. Kang et al. [33] proposed Structured Graph Learning with Multiple Kernel (SGMK), which extends Structured Graph Learning to multiple kernel clustering and showed that SGMK outperforms many clustering methods, such as Spectral Clustering [34,35], Multiple Kernel K-means [36,37], and structure learning approaches [38,39]. Therefore, this paper compares the proposed method with SGMK from the viewpoint of NMI.
Figure 17 is the NMI of the proposed method for YALE and JAFFE datasets. The results show that the NMI performance of the proposed method did not change significantly when is varied for both the YALE and JAFFE datasets. This suggests that using a single Gaussian kernel to transform the data structure is not sufficient for facial image clustering and that using multiple kernels to select the most appropriate kernel is more effective than adjusting the parameters of the Gaussian kernel.
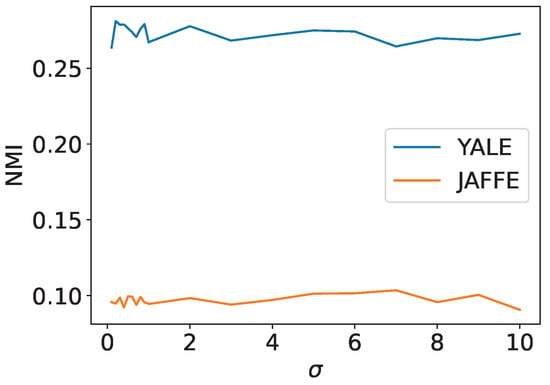
Figure 17.
The NMI of Ising-based kernel clustering for YALE and JAFFE datasets.
Table 2 shows that the Ising-based kernel clustering has lower NMIs than SGMK. This is because SGMK uses multiple kernels for data transformation and performs clustering based on the most suitable kernel, while Ising-based kernel clustering uses only a single Gaussian kernel.

Table 2.
The comparison of NMI between the Ising-based kernel clustering and SGMK.
Multi-view clustering methods that use multiple kernels to transform input data into linearly separable high-dimensional data are one of the most promising ways to perform kernel clustering for practical real-world data. While Ising-based kernel clustering has the potential to obtain the ground state for a given objective function of kernel clustering, selecting the most appropriate kernel is required before optimization. Thus, developing an algorithm for Ising-based kernel clustering that uses multiple kernels will be discussed in the future.
5. Related Work
In addition to Ising-based kernel clustering proposed in this paper, another way to perform clustering of irregular data is Ising-based binary clustering using the kernel method [40]. This method involves utilizing only one single decision boundary to linearly separate the data mapped onto a high-dimensional feature space. However, conventional Ising-based binary clustering utilizing the kernel method is limited to cases with only two clusters, rendering it impractical. The reason why binary clustering using the kernel method can only group data into two clusters is the use of decision variables representing a binary value. In contrast, the proposed method presented in this paper can be applied more generally across a wide range of applications to categorize irregular data into two or more clusters.
Combinatorial clustering based on the Ising model has also been utilized for semi-supervised clustering. Cohen et al. proposed constrained clustering, which employs various types of supervisory information [41], while Authur et al. proposed balanced clustering, ensuring that all clusters have the same number of data points [13,14]. The QUBO formulation employed in these semi-supervised clustering techniques can be converted into Equation (14). Consequently, the approach proposed in this paper that employs the kernel method can also be extended to semi-supervised clustering. When irregular data are given that are challenging to categorize, the inclusion of supervised information can be beneficial. Therefore, integrating the kernel method into semi-supervised clustering can enhance the practicality of combinatorial clustering. A promising area for future research would be to explore kernel clustering using supervisory information based on the Ising model.
6. Conclusions
Ising-based combinatorial clustering is receiving attention due to its quality of clustering. However, conventional Ising-based clustering methods cannot handle data with irregular distributions. To overcome this problem, this paper proposes an Ising-based combinatorial clustering method using a kernel method. The proposed method uses a kernel trick to convert various data onto high-dimensional data that can be clustered. This paper also resolves the problem of a high computation cost for the process of determining the coefficients of the kernel, Gram, and QUBO matrices by extracting the potential of highly parallelized numerical libraries.
First, the proposed method is compared with Euclidean distance-based combinatorial clustering as the conventional method. The experimental results show that the quality of the clustering results of the proposed method is significantly higher than that of the conventional method on irregular data. Moreover, the proposed method can obtain high-quality clustering results by selecting the appropriate parameter. Second, the proposed implementation using numerical libraries is compared with the naive implementation, where kernel, Gram, and QUBO coefficients are determined iteratively. Experimental results show that the proposed method is at most 12.4 million times faster than the conventional method. The experiments have also revealed the potential to solve large-scale Ising-based kernel clustering problems. Third, comparisons between the Ising-based kernel clustering and the kernel K-means show that the Ising-based kernel clustering is effective in the situation where higher-quality clustering results are required at the expense of a bit more time.
Finally, experiments on real-world datasets suggest that selecting the appropriate kernel is more important than parameter tuning for only one kernel. Even though the proposed method has the potential to minimize the given objective function of kernel clustering, it is needed to give the appropriate kernel to ensure maximum performance.
In future work, combining methods for ensemble clustering [42,43] that combine multiple clustering results or multiple kernels [33] to improve the accuracy and robustness of clustering will be discussed.
Author Contributions
Conceptualization, M.K. and K.K.; methodology, M.K. and K.K.; software, M.K.; validation, M.K.; formal analysis, M.K. and K.K.; investigation, M.K. and K.K.; resources, M.K.; data curation, M.K.; writing—original draft preparation, M.K.; writing—review and editing, M.K., K.K., M.S. and H.K.; visualization, M.K.; supervision, K.K., M.S. and H.K.; project administration, M.K., K.K., and H.K.; funding acquisition, M.K., K.K. and H.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by MEXT Next Generation High-Performance Computing Infrastructures and Applications R&D Program, entitled “R&D of A Quantum-Annealing- Assisted Next Generation HPC Infrastructure and its Applications,” Grants-in-Aid for Scientific Research (A) #19H01095, Grants-in-Aid for Scientific Research (C) #20K11838, Grants-in-Aid for JSPS Fellows #22J22908, and WISE Program for AI Electronics, Tohoku University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank Takuya Araki of NEC Corporation for his fruitful discussions and variable comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kadowaki, T.; Nishimori, H. Quantum annealing in the transverse Ising model. Phys. Rev. E 1998, 58, 5355. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Goto, H.; Tatsumura, K.; Dixon, A.R. Combinatorial optimization by simulating adiabatic bifurcations in nonlinear Hamiltonian systems. Sci. Adv. 2019, 5, eaav2372. [Google Scholar] [CrossRef] [PubMed]
- Aramon, M.; Rosenberg, G.; Valiante, E.; Miyazawa, T.; Tamura, H.; Katzgraber, H.G. Physics-inspired optimization for quadratic unconstrained problems using a digital annealer. Front. Phys. 2019, 7, 48. [Google Scholar] [CrossRef]
- Yamaoka, M.; Yoshimura, C.; Hayashi, M.; Okuyama, T.; Aoki, H.; Mizuno, H. A 20k-spin Ising chip to solve combinatorial optimization problems with CMOS annealing. IEEE J. Solid-State Circuits 2015, 51, 303–309. [Google Scholar]
- Irie, H.; Wongpaisarnsin, G.; Terabe, M.; Miki, A.; Taguchi, S. Quantum Annealing of Vehicle Routing Problem with Time, State and Capacity. In Quantum Technology and Optimization Problems; QTOP 2019; Lecture Notes in Computer Science; Feld, S., Linnhoff-Popien, C., Eds.; Springer: Cham, Switzerland, 2017; Volume 11413. [Google Scholar]
- Neukart, F.; Compostella, G.; Seidel, C.; Von Dollen, D.; Yarkoni, S.; Parney, B. Traffic flow optimization using a quantum annealer. Front. ICT 2017, 4, 29. [Google Scholar] [CrossRef]
- Ohzeki, M. Breaking limitation of quantum annealer in solving optimization problems under constraints. Sci. Rep. 2020, 10, 1–12. [Google Scholar] [CrossRef]
- Stollenwerk, T.; O’Gorman, B.; Venturelli, D.; Mandra, S.; Rodionova, O.; Ng, H.; Sridhar, B.; Rieffel, E.G.; Biswas, R. Quantum annealing applied to de-conflicting optimal trajectories for air traffic management. IEEE Trans. Intell. Transp. Syst. 2019, 21, 285–297. [Google Scholar] [CrossRef]
- Ohzeki, M.; Miki, A.; Miyama, M.J.; Terabe, M. Control of automated guided vehicles without collision by quantum annealer and digital devices. Front. Comput. Sci. 2019, 1, 9. [Google Scholar] [CrossRef]
- Snelling, D.; Devereux, E.; Payne, N.; Nuckley, M.; Viavattene, G.; Ceriotti, M.; Wokes, S.; Di Mauro, G.; Brettle, H. Innovation in Planning Space Debris Removal Missions Using Artificial Intelligence and Quantum-Inspired Computing. In Proceedings of the 8th European Conference on Space Debris, Darmstadt, Germany, 20–23 April 2021. [Google Scholar]
- Cohen, E.; Mandal, A.; Ushijima-Mwesigwa, H.; Roy, A. Ising-based consensus clustering on specialized hardware. In International Symposium on Intelligent Data Analysis; Springer: Cham, Switzerland, 2020; pp. 106–118. [Google Scholar]
- Arthur, D.; Date, P. Balanced k-Means Clustering on an Adiabatic Quantum Computer. Quantum Inf. Process. 2020, 20, 294. [Google Scholar] [CrossRef]
- Date, P.; Arthur, D.; Pusey-Nazzaro, L. QUBO formulations for training machine learning models. Sci. Rep. 2021, 11, 10029. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Kumar, V.; Bass, G.; Tomlin, C.; Dulny, J. Quantum annealing for combinatorial clustering. Quantum Inf. Process. 2018, 17, 39. [Google Scholar] [CrossRef]
- Kumagai, M.; Komatsu, K.; Takano, F.; Araki, T.; Sato, M.; Kobayashi, H. Combinatorial Clustering Based on an Externally-Defined One-Hot Constraint. In Proceedings of the 2020 Eighth International Symposium on Computing and Networking (CANDAR), Naha, Japan, 24–27 November 2020; pp. 59–68. [Google Scholar]
- Kumagai, M.; Komatsu, K.; Takano, F.; Araki, T.; Sato, M.; Kobayashi, H. An External Definition of the One-Hot Constraint and Fast QUBO Generation for High-Performance Combinatorial Clustering. Int. J. Netw. Comput. 2021, 11, 463–491. [Google Scholar] [CrossRef]
- Komatsu, K.; Kumagai, M.; Qi, J.; Sato, M.; Kobayashi, H. An Externally-Constrained Ising Clustering Method for Material Informatics. In Proceedings of the 2021 Ninth International Symposium on Computing and Networking Workshops (CANDARW), Matsue, Japan, 23–26 November 2021; pp. 201–204. [Google Scholar]
- Zhang, Y.; Bai, X.; Fan, R.; Wang, Z. Deviation-Sparse Fuzzy C-Means With Neighbor Information Constraint. IEEE Trans. Fuzzy Syst. 2019, 27, 185–199. [Google Scholar] [CrossRef]
- Tang, Y.; Pan, Z.; Pedrycz, W.; Ren, F.; Song, X. Viewpoint-Based Kernel Fuzzy Clustering With Weight Information Granules. IEEE Trans. Emerg. Top. Comput. Intell. 2022, 7, 342–356. [Google Scholar] [CrossRef]
- Kumagai, M.; Komatsu, K.; Sato, M.; Kobayashi, H. Ising-Based Combinatorial Clustering Using the Kernel Method. In Proceedings of the 2021 IEEE 14th International Symposium on Embedded Multicore/Many-Core Systems-on-Chip (MCSoC), Singapore, 20–23 December 2021; pp. 197–203. [Google Scholar]
- Yamada, Y.; Momose, S. Vector engine processor of NEC’s brand-new supercomputer SX-Aurora TSUBASA. In Proceedings of the Intenational symposium on High Performance Chips (Hot Chips2018), Cupertino, CA, USA, 19–21 August 2018; Volume 30, pp. 19–21. [Google Scholar]
- Komatsu, K.; Momose, S.; Isobe, Y.; Watanabe, O.; Musa, A.; Yokokawa, M.; Aoyama, T.; Sato, M.; Kobayashi, H. Performance evaluation of a vector supercomputer SX-Aurora TSUBASA. In Proceedings of the SC18: International Conference for High Performance Computing, Networking, Storage and Analysis, Dallas, TX, USA, 11–16 November 2018; pp. 685–696. [Google Scholar]
- Takano, F.; Suzuki, M.; Kobayashi, Y.; Araki, T. QUBO Solver for Combinatorial Optimization Problems with Constraints. Technical Report 4, NEC Corporation, 2019. Available online: https://ken.ieice.org/ken/paper/20191128b1rz/eng/ (accessed on 1 April 2023).
- Swendsen, R.H.; Wang, J.S. Replica Monte Carlo Simulation of Spin-Glasses. Phys. Rev. Lett. 1986, 57, 2607–2609. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Tzortzis, G.F.; Likas, A.C. The global kernel k-means algorithm for clustering in feature space. IEEE Trans. Neural Netw. 2009, 20, 1181–1194. [Google Scholar] [CrossRef]
- Belhumeur, P.; Hespanha, J.; Kriegman, D. Eigenfaces vs. Fisherfaces: Recognition using class specific linear projection. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 711–720. [Google Scholar] [CrossRef]
- Lyons, M.; Akamatsu, S.; Kamachi, M.; Gyoba, J. Coding facial expressions with Gabor wavelets. In Proceedings of the Third IEEE International Conference on Automatic Face and Gesture Recognition, Nara, Japan, 14–16 April 1998; pp. 200–205. [Google Scholar] [CrossRef]
- Liu, X. SimpleMKKM: Simple Multiple Kernel K-Means. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 5174–5186. [Google Scholar] [CrossRef] [PubMed]
- Kang, Z.; Peng, C.; Cheng, Q.; Liu, X.; Peng, X.; Xu, Z.; Tian, L. Structured graph learning for clustering and semi-supervised classification. Pattern Recognit. 2021, 110, 107627. [Google Scholar] [CrossRef]
- Ng, A.; Jordan, M.; Weiss, Y. On spectral clustering: Analysis and an algorithm. Adv. Neural Inf. Process. Syst. 2001, 14, 1–8. [Google Scholar]
- Huang, H.C.; Chuang, Y.Y.; Chen, C.S. Affinity aggregation for spectral clustering. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 773–780. [Google Scholar] [CrossRef]
- Du, L.; Zhou, P.; Shi, L.; Wang, H.; Fan, M.; Wang, W.; Shen, Y.D. Robust Multiple Kernel K-Means Using L21-Norm. In Proceedings of the 24th International Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015; pp. 3476–3482. [Google Scholar]
- Huang, H.C.; Chuang, Y.Y.; Chen, C.S. Multiple Kernel Fuzzy Clustering. IEEE Trans. Fuzzy Syst. 2012, 20, 120–134. [Google Scholar] [CrossRef]
- Kang, Z.; Peng, C.; Cheng, Q. Twin Learning for Similarity and Clustering: A Unified Kernel Approach. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 2080–2086. [Google Scholar]
- Nie, F.; Wang, X.; Huang, H. Clustering and Projected Clustering with Adaptive Neighbors. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; Association for Computing Machinery: New York, NY, USA, 2014; pp. 977–986. [Google Scholar] [CrossRef]
- Bauckhage, C.; Ojeda, C.; Sifa, R.; Wrobel, S. Adiabatic Quantum Computing for Kernel k = 2 Means Clustering; LWDA: Concord, MA, USA, 2018; pp. 21–32. [Google Scholar]
- Cohen, E.; Senderovich, A.; Beck, J.C. An Ising framework for constrained clustering on special purpose hardware. In Integration of Constraint Programming, Artificial Intelligence, and Operations Research; Hebrard, E., Musliu, N., Eds.; Springer: Cham, Switzerland, 2020; pp. 130–147. [Google Scholar]
- Huang, D.; Wang, C.D.; Peng, H.; Lai, J.; Kwoh, C.K. Enhanced Ensemble Clustering via Fast Propagation of Cluster-Wise Similarities. IEEE Trans. Syst. Man, Cybern. Syst. 2021, 51, 508–520. [Google Scholar] [CrossRef]
- Huang, D.; Wang, C.D.; Lai, J.H. Fast Multi-view Clustering via Ensembles: Towards Scalability, Superiority, and Simplicity. IEEE Trans. Knowl. Data Eng. 2023, 1–16, early access. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).