Abstract
In recent years, graph neural networks (GNNs) have played an important role in graph representation learning and have successfully achieved excellent results in semi-supervised classification. However, these GNNs often neglect the global smoothing of the graph because the global smoothing of the graph is incompatible with node classification. Specifically, a cluster of nodes in the graph often has a small number of other classes of nodes. To address this issue, we propose a graph-retraining neural network (GRNN) model that performs smoothing over the graph by alternating between a learning procedure and an inference procedure, based on the key idea of the expectation-maximum algorithm. Moreover, the global smoothing error is combined with the cross-entropy error to form the loss function of GRNN, which effectively solves the problem. The experiments show that GRNN achieves high accuracy in the standard citation network datasets, including Cora, Citeseer, and PubMed, which proves the effectiveness of GRNN in semi-supervised node classification.
1. Introduction
Convolutional neural networks (CNNs) achieve outstanding performance in a wide range of tasks that are based on Euclidean data including computer vision [1] and recommender systems [2,3]. However, an increasing number of application data are in the form of graph-structured non-Euclidean data, such as literature-citation networks and knowledge graphs. In this case, graph convolutional networks (GCNs) commonly outperform other models and are successfully applied in social analysis [4,5], citation networks [6,7,8], transport forecasting [9,10], and other promising fields. For example, in a literature-citation network, articles are usually presented as nodes and citation relationships as edges between nodes. When faced with the challenge of semi-supervised node classification on such non-Euclidean graph data, classical GCNs first extract and aggregate features of articles using the graph Fourier transform and the convolution theorem and then classify unlabeled articles based on graph convolution output features.
Graph neural networks (GNNs) are capable of reading prospective data from the network architecture. Graph convolution networks (GCNs), in which nodes learn their potential representations by aggregating features from neighboring nodes, have been shown to be effective and practical. For example, GCN [11] calculates the weight of aggregated neighbor nodes based on the degree of its nodes and its first-order neighbor nodes; GAT [12] injects the graph structure into the mechanism by performing masked attention, which means that the weight of aggregated neighbor nodes is a learnable parameter; GraphSAGE [13] uniformly samples a fixed number of neighbor nodes to aggregate information rather than using all neighbor nodes. MPNN [14] uses message-passing functions to unify almost all variants of the spatial graph neural network. However, a critical limitation is that the labels of nodes are independently predicted based on their representations and their neighbor-node representations. Each layer of the graph convolution neural network is a special kind of Laplace smoothing [6]. In other words, they attach importance to the smoothness of the nodes of the training set but neglect the smoothness of the whole network. Although C&S [15] and UniMP [16] perform smoothing of the predictions over the graph via label propagation, the representations are neglected in the smoothing process.
In this paper, we propose a novel approach called the graph-retraining neural network (GRNN), which conducts smoothing over the graph using a graph convolution neural network. The key idea behind the approach is similar to the expectation-maximum algorithm [17], alternating between a learning procedure and an inference procedure. It is different from GMNN [18], which contains a conditional random field [19] to model the joint distribution of the labels conditioned on representations. In the learning procedure, instead of maximizing the likelihood function, GRNN uses graph neural networks to train all node representations to minimize loss function or maximum accuracy, which can adjust the graph neural network’s weight. In the inference procedure, instead of calculating the expectations of the likelihood function, GRNN predicts all node labels using the final outputs of graph neural networks. Inspired by the idea of keeping the known representations at training nodes fixed [20,21], GRNN updates the predicted node labels by correcting the training labels in the inference procedure. To alleviate the problem that the expectation-maximum algorithm has a significant influence on the initially predicted labels, GRNN uses graph neural networks to train the training set and adjust the graph neural network’s weight as the initial weight. The architecture of GRNN alternating between a learning procedure and an inference procedure is illustrated in Figure 1.
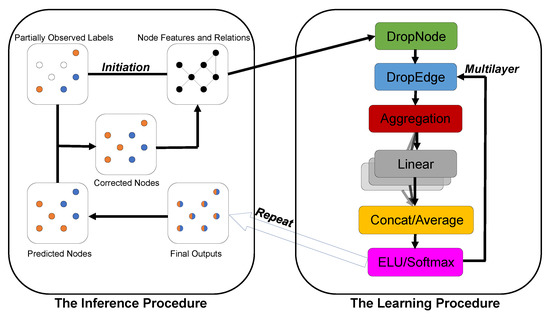
Figure 1.
The architecture of GRNN. Given the node features and relations, GRNN combines partially observed labels in the initial learning procedure, which is equivalent to the benchmark neural network. In the inference procedure, the predicted nodes are the index value of the maximum value of the final outputs, and the corrected nodes are corrected using the predicted nodes through partially observed labels. Finally, GRNN combines the corrected nodes and partially observed labels in the next learning procedure.
In general, there are three main contributions of the proposed GRNN to semi-supervised node classification. Firstly, to adapt to extending the message aggregation operation from the training set to the entire graph, we built a GRNN benchmark neural network that randomly deletes edges or nodes to improve robustness and uses multiple heads to improve stability. Secondly, a framework alternating between a learning procedure and an inference procedure was used in the process of global smoothing over the graph, which proved to be convergent. Thirdly, extensive experiments were conducted on standard datasets, including citation networks for the semi-supervised node classification task, to show that GRNN achieves superior performance.
2. Related Work
In this section, we briefly review previous work on graph-based semi-supervised classification, graph neural networks, and graph neural networks with a smoothing model.
2.1. Graph-Based Semi-Supervised Classification
Graph-based semi-supervised classification uses labels for predictions. For example, in label spreading [20], the label of each node is propagated to its neighbor nodes. The spectral graph transducer [22] is a variant of the k nearest-neighbor approach. The Gaussian random-field models [21] can also be regarded as a transductive version of the nearest-neighbor rule, in which the nearest labeled examples are determined using a random walk on the graph. However, these methods imply that the labeled nodes are at the center of node clusters while neglecting the labeled nodes that may be near the edge of the node clusters. Moreover, these methods do not fully exploit the representations that provide potential information for node classification.
2.2. Graph Neural Networks
Graph neural networks are roughly grouped into spectral-based approaches and spatial-based approaches [23]. The key idea of spectral-based approaches is to define a parameterized filter through a series of approximations and decompositions, including Fourier decomposition and wavelet decomposition [11,24,25,26]. As for the spatial-based approaches, they perform various aggregation operations directly on neighbor nodes and even multi-level neighbor nodes [12,13,27,28]. In essence, spectral-based and spatial-based approaches learn node features through neural networks combined with the encoding graph structure, and they are end-to-end training frameworks. However, graph neural networks usually neglect the correlation between labels. In other words, they do not attach importance to the global smoothing of the graph.
2.3. Graph Neural Networks with a Smoothing Model
Graph neural networks with a smoothing model usually perform a series of smoothing operations on the prediction results of graph neural networks. For instance, C&S [15] proposes error correction and smoothing prediction on the basis of simple base prediction. APPNP [29] and TPN [30] use graph neural networks to predict soft labels and then propagate them. GCN-LPA [31] uses label propagation algorithms to regularize graph neural networks. Furthermore, some smoothing models iteratively train graph neural networks. For example, GMNN [18] utilizes two graph neural networks for both inference and learning. Self-training [6] selects the prediction results with the highest confidence by comparing softmax scores and adds them to the training set to train iteratively. SPC-GNN [32] even integrates multiple graph neural networks for iterative training. Compared with these models, GRNN minimizes the smoothing error of the whole graph using graph neural networks.
3. Preliminary
3.1. Notations and Problem Definition
Let denote an undirected graph, in which V is the set of nodes, and E is the set of edges. There are nodes with features on each node represented by a real matrix , where p is the dimension of features, and edges with weights on each edge represented by the adjacency matrix of the graph. Additionally, suppose is the diagonal degree matrix (i.e., ) and is the one-hot-encoding matrix for labels in which q is the number of classes. In terms of dataset partition, the node-set V with an index of is divided into an unlabeled node set U and a labeled node set L composed of the training set and the validation set . Finally, the problem is to classify all the nodes. In other words, given G, X and , find the appropriate graph neural network f to satisfy so that the unlabeled nodes are classified by .
3.2. The Classical Graph Neural Networks
The classical graph neural networks are formulated as follows:
where is the hidden features of the -th node resulting from the -th graph neural hidden layer, is the learnable weight matrix of -th graph neural hidden layer, is the node set including the first-order neighbor nodes of the -th node and the -th node itself, is the weight between the -th node and the -th node of the -th graph neural hidden layer, and is a nonlinear activation function (e.g., ). GCN uses to obtain the weight between the -th node and the -th node, where is the degree of the node.
3.3. Residual Learning
Residual learning [33] is a widely used construction module of deep learning, which solves the problem of degradation when training very deep networks. Suppose x is the input feature, and is the residual function. The true and desired function is as follows:
The addition of and x is an element-by-element addition, but if the dimension of is different from that of x, linear mapping needs to be performed for x to match the dimensions of :
where W is the weight matrix. Residual learning can be realized in the form of a layer-hopping connection. In other words, the input features are directly added to the output features and then the activation function is used on the result, which makes the neural network easier to converge and optimize.
4. GRNN: Graph-Retraining Neural Network
In this section, we first introduce the structure of the benchmark neural network in detail and then derive the global smoothing model. Moreover, the loss function of GRNN is summarized by improving the smoothing model.
4.1. The Benchmark Neural Network
Since GCN has been demonstrated to be powerful and effective in the semi-supervised node classification of a graph, the benchmark neural network adopts its weight between connected nodes in graph learning. In addition, the benchmark neural network uses the dropout of the edges and nodes to improve the robustness of the model [34]. Specifically, given the node features , the message aggregation from distant j to source i can be expressed as follows:
where is a nonzero element of the normalized adjacency matrix, and is the learnable weight matrix of the -th graph neural hidden layer. Specifically, when , and when (where and is the random value from 0 to 1). when , and when (where and is the random value from 0 to 1).
After obtaining the graph-aggregation features, the benchmark neural network uses a concatenation operation to improve stability:
where ∥ is the C head concatenation operation, is a nonlinear activation function, and is assumed to be an exponential linear unit here.
Specifically, the benchmark neural network averages the multi-head output and then normalizes it in the last output layer as follows:
Finally, the loss function of the benchmark neural network is a cross-entropy error over the training set:
where is the benchmark neural network.
In summary, the benchmark neural network is different in the transition matrix of the message passing from GAT, and it is different in the multi-head operation and the dropout of edges and nodes from GCN.
4.2. The Smoothing Model
In the smoothing model, GRNN improves the accuracy of the base prediction by minimizing the global smoothing error over the graph. The key idea is to minimize the objective function over the graph using the graph neural network:
There are many unlabeled nodes in , which means that is unknown. To solve the problem, the unlabeled node-set is replaced by the prediction label of the graph neural network and the formula is as follows:
where returns the one-hot coding of the index of the vector maximum component (e.g., ).
However, in Equation (10) is non-differentiable. Therefore, GRNN calculates the equation through iteration that alternates between a learning procedure and an inference procedure. In the inference procedure, GRNN predicts all node labels using the benchmark neural network as follows:
In the learning procedure, GRNN uses the benchmark neural network to train all node features, and the objective is as follows:
Therefore, the loss function is as follows:
where .
Now, suppose is and show that the iterative loss function is convergent:
Additionally, is always greater than zero and monotonically decreasing so that is convergent, which implies that is convergent to Equation (10).
4.3. The Loss Function of GRNN
With the increase in the smoothing model iteration, the labeled labels are gradually ignored. Therefore, the loss function of GRNN is improved by combining Equations (8) and (15), and the formula is as follows:
where is a univariate function.
In order to eliminate the uncertainty of the system at the least cost, the univariate function satisfies the condition of the convex function. Furthermore, the univariate function also needs to satisfy in which if and only if , which avoids the loss value that is too close to zero resulting in gradient disappearance. There is a function satisfying the above conditions. Therefore, the loss function of GRNN is as follows:
The time complexity of a single benchmark neural network (GRNN-0) attention-head computing features can be expressed as . Therefore, the time complexity of a GRNN attention-head computing features can be expressed as , which shows that the time cost depends mainly on the GNNs and the number of iterations. Moreover, the complexity of GCN [11] and GAT [12] are and , respectively. Obviously, the complexity of GRNN-0 is slightly lower than that of GAT, and the complexity of GRNN is times of GCN.
The detailed GRNN algorithm is summarized in Algorithm 1.
| Algorithm 1 GRNN for semi-supervised node classification |
Initialization: ; ; repeat Compute using Equation (4) with ; for do Update base on Equation (5) with ; Update base on Equation (6); end for Compute (which is equivalent to ) using Equation (7); until The classification loss is minimized according to Equation (8); Compute using Equation (11); fordo repeat Compute using Equation (4) with ; for do Update base on Equation (5) with ; Update base on Equation (6); end for Compute (which is equivalent to ) using Equation (7); until The classification loss is minimized according to Equation (20); Update base on Equation (12); end for return(which is the subset of ) |
5. Experiments and Discussion
In this section, we perform a comparative evaluation of GRNN models against various baselines and previous approaches on four established graph-based benchmark tasks, and our model achieves or matches state-of-the-art performance across all of them. The section summarizes the six network datasets, experimental settings, and the results.
5.1. Datasets
The datasets used for evaluation include one webpage network Wiki dataset [35]; one large-scale citation network Arxiv dataset [36]; three standard citation network datasets, namely Cora, Citeseer, and PubMed [37] for transductive learning; and a protein–protein interaction [38] dataset for inductive learning. The Arxiv dataset and the standard citation network datasets are datasets with a network structure, where each node represents an article or publication and each edge represents the reference between connected nodes. The protein–protein interaction is composed of 24 graphs corresponding to various human tissues, where each node represents a protein and each edge represents the interaction between the proteins. Each node of Wiki represents a document, and each edge represents the link between connected nodes. Moreover, the self-loops of Wiki are removed, and the weight of each edge is set to 1. The detailed data about the standard citation network datasets and the protein–protein interaction dataset in this experiment are shown in Table 1.

Table 1.
Dataset statistics.
5.2. Baselines Methods
There are various traditional algorithms based on the random-walk model or state-of-the-art methods based on graph neural networks with neighbor-node aggregation for the citation network, the webpage network and the protein–protein interaction, which follows the experiment setup of previous works. In addition, a per-node shared multilayer perceptron (MLP) classifier or a label propagation algorithm (LP) is applied to the tasks, which highlights the importance of graph structure.
5.2.1. The Citation Network and the Webpage Network
There are some methods including skip-gram graph embedding model (DeepWalk) [39], graph attention network (GAT) [12], graph Markov neural network (GMNN) [18], adaptive graph smoothing network (AGSN) [40], full-graph attention neural network (FGANN) [41], Ricci curvature-based graph convolutional neural network (RCGCN) [42], label-consistency-based graph neural network (LC-GAT) [43], hierarchical graph convolutional network (H-GCN) [7], Chebyshev [26], graph convolutional network (GCN) [11], simplified graph convolutional network (SGC) [44], graph convolutional network via initial residual and identity mapping (GCNII) [45], deep adaptive graph neural network (DAGNN) [46], multi-granularity graph wavelet neural network (M-GWNN) [47], reverse graph learning for graph neural network (rGNN) [48], self-paced co-training of graph neural networks for semi-supervised node classification (SPC-CNN) [32], and a semi-supervised algorithm for scalable feature learning in networks (Node2vec) [49].
5.2.2. The Protein–Protein Interaction
For the protein–protein interaction, the methods used in this study include the inductive method named graph attention networks (GATs) and four various supervised GraphSAGE inductive methods, namely GraphSAGE-GCN (whose aggregation operation is similar to graph convolution neural network), GraphSAGE-mean (which aggregates neighbor nodes by taking the elementwise mean value of feature vectors), GraphSAGE-LSTM (which aggregates neighbor nodes by inputting neighbor features into an LSTM), and GraphSAGE-pool (which aggregates neighbor nodes by taking the elementwise maximization operation of transformed feature vectors) [13].
5.3. Experimental Settings
5.3.1. The Citation Network
A two-layer GRNN model was used on Cora and PubMed for semi-supervised node classification. The first layer was spliced into heads, and each head had features, which means that the first layer had a total of 128 features. In addition, the nonlinear activation function of the first layer was assumed to be an exponential linear unit. The second layer was used as the output layer for classification, which was only a single head that had q features. It is worth noting that only a one-layer GRNN model was used on Citeseer, and the architectural hyperparameters of GRNN were that the output layer averaged head outputs and each head had q features. Finally, the nonlinear activation function of the second layer was assumed to be a softmax activation to normalize the results. During training, the Adam SGD optimizer with an initial learning rate of as well as regularization with was used. Furthermore, the dropout of nodes with was applied to the input layer, and the dropout of edges with was applied to each layer. The architectural hyperparameters of GRNN on PubMed were a little different from the above architectural hyperparameters: The second layer averaged head outputs and each head had q features, and regularization was assumed to be , and the dropout of edges was . Last but not least, an early stopping strategy with a patience value of 200 epochs was applied for each iteration that alternated between a learning procedure and an inference procedure. The final accuracy of Cora and Citeseer was achieved on the 20th iteration, and the final accuracy of PubMed corresponding to the highest validation accuracy was achieved in 20 iterations.
For GCN+GRNN and GCNII+GRNN, we replaced the benchmark neural network of the GRNN model with GCN and GCNII, respectively, and the hyperparameters settings of GCN and GCNII were consistent with the recommendations in the original paper. For Cora, CiteSeer, and PubMed, the depths of GCN were 2, 2, and 2, respectively, while the depths of GCNII were 64, 32, and 16, respectively. The GCN+GRNN model used the same early stopping strategy as the GRNN model, while the GCNII+GRNN model used the early stopping strategy through which the final accuracy corresponding to the highest validation accuracy was achieved in 20 iterations.
For the large-scale citation network Arxiv, we used a four-layer network GCN with 16 hidden units and the Adam SGD optimizer with an initial learning rate of and regularization with 0. Moreover, the nonlinear activation function of the first layer was assumed as an exponential linear unit. The GCN+GRNN model used the early stopping strategy with which the final accuracy corresponding to the highest validation accuracy was achieved in 10 iterations.
5.3.2. The Protein–Protein Interaction
A seven-layer benchmark neural network was used for the protein–protein interaction. Each layer was spliced by heads, and each head had 256 features, which means that each layer had a total of 2048 features except for the last layer. In addition, the nonlinear activation function of each layer was assumed to be a rectified linear unit except the last layer. For the last layer, it was used as the output layer for prediction, which averaged head outputs, and each head had q features. Finally, the nonlinear activation function of the last layer was assumed to be a sigmoid activation to normalize the results. During training, the Adam SGD optimizer with an initial learning rate of was used, and each layer had a residual connection. Last but not least, an early stopping strategy with a patience of 200 epochs was also applied.
5.3.3. The Citation Network with Fewer Training Samples
For each run, we randomly split labels into a small set for training, a set with 500 samples for validation, and a set with 1000 samples for testing. We tested our model with , , , , , and training sizes on Cora and CiteSeer, and with , , , and training sizes on PubMed. The experimental settings of the GRNN model in the citation network with fewer training samples were the same as those in the standard citation network, except for the two-layer GRNN model on Citeseer. In addition, the GRNN model used the early stopping strategy through which the final accuracy corresponding to the highest validation accuracy was achieved in 20 iterations. For GCN, the hyperparameter settings were consistent with the recommendations in the original paper. Finally, we gathered data on the mean accuracy of over 10 runs in all result tables to make a fair comparison.
5.3.4. The Webpage Network
For each run, we randomly split labels into a set containing up to 5, 10, or 15 labeled nodes per class for training, a set containing up to 10 labeled nodes per class for validation, and a set containing the remaining nodes for testing. We used a two-layer network GRNN with 32 hidden units, the dropout of nodes with was applied to the input layer, and the dropout of edges with was applied to each layer. We used a two-layer network GCN with 32 hidden units for GCN+GRNN and a sixteen-layer network GCNII with 64 hidden units for GCNII+GRNN. Moreover, the nonlinear activation function of the first layer was assumed to be a linear rectification function, and the Adam SGD optimizer with an initial learning rate of and regularization with was used. Finally, the early stopping strategy through which the final accuracy corresponding to the highest validation accuracy was achieved in 10 iterations was also applied.
5.4. Result Analysis
The classification results of these baselines in origin papers, which compare with the results of GRNN and GRNN-0 (the benchmark neural network), are summarized in Table 2, Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8, where the highest accuracy in each column is highlighted in bold, and the second-highest values are underlined. Our methods are displayed at the bottom half of each table.

Table 2.
The performance comparison of GRNN with existing graph neural network methods (%).

Table 3.
Summary of micro-averaged F1 scores (%) on PPI.

Table 4.
Summary of classification accuracy (%) results with fewer training samples on Cora.

Table 5.
Summary of classification accuracy (%) results with fewer training samples on Citeseer.

Table 6.
Summary of classification accuracy (%) results with fewer training samples on PubMed.

Table 7.
Summary of classification accuracy (%) results on Wiki.

Table 8.
Summary of classification accuracy (%) results on Arxiv.
Analyzing Table 2 and Table 3, the results demonstrate that GRNN achieved superior performance on all four datasets. Specifically, GRNN achieved the best performance on Cora and the second-best performance on Citeseer and PubMed. GRNN improved on GRNN-0 by a margin of , , and on Cora, Citeseer, and PubMed, respectively. Moreover, GCN+GRNN improved on GCN by a margin of on Citeseer, and GCNII+GRNN improved on GCNII by a margin of on PubMed, which indicates that it is beneficial to reduce the global smoothing error over the graph by iteratively training the graph neural network. Furthermore, the result of the GRNN-0 model was higher than that of the GAT model on PPI, though the GRNN-0 model was the benchmark neural network of the GRNN model.
Analyzing Table 4, Table 5 and Table 6, the results verify the effectiveness of our GRNN model, consistently outperforming other state-of-the-art approaches by a large margin on a wide range of label rates across the three datasets. When the training size was small, the benchmark neural network GRNN-0, which is equivalent to the improved GCN, was much better than GCN in most cases. For example, GRNN-0 improved over GCN by and , with a labeling rate of , on Cora and CiteSeer, respectively, and improved over GCN by , with a labeling rate of on PubMed. When the training size grew, GRNN-0 was still better than GCN in most cases, demonstrating the effectiveness of the multi-head operation and the dropout of edges as well as nodes. Moreover, GRNN was better than GRNN-0, especially when the training size was small. For example, GRNN improved over GRNN-0 by and with a labeling rate of on Cora and CiteSeer, respectively, and improved over GRNN-0 by with a labeling rate of on PubMed. These also show that it is beneficial to reduce the global smoothing error over the graph by iteratively training the graph neural network.
Analyzing Table 7 and Table 8, with labeling rates of , , and on Wiki, it can be inferred that GRNN improved over GRNN-0 by , , and , respectively; GCN+GRNN improved over GCN by , , and , respectively; and GCNII+GRNN improved over GCNII by , , and , respectively. Moreover, GCN+GRNN only improved over GCN by on Arxiv, which indicates that the global smoothing model is not effective when the label rate is large.
6. Ablation Study
The results of the ablation study evaluating the contributions of the two techniques including the loss function and the number of iterations are presented in Figure 2. Specifically, the accuracy of the three datasets (Cora, Citeseer, and PubMed) trained by a two-layer GRNN model is demonstrated from two different loss functions (the global smoothing error is Equation (15), and the loss function of GRNN is determined using Equation (20)) and different iteration times. Two observations can be made from Figure 2. First, the prediction accuracy of the model using the loss function of GRNN was higher because the propagation of error nodes could be effectively avoided with the increase in the number of iterations, compared with the model using the global smoothing error function. Second, with the increase in the number of iterations, the prediction accuracy of the model using the loss function of GRNN improved until it became stable.
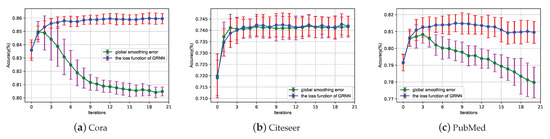
Figure 2.
Ablation study on the loss function and number of iterations.
Moreover, Figure 3 evaluating the contributions of GRNN with different layers shows that GRNN with two layers achieved stability and high accuracy in the standard citation network with the increase in the number of iterations. With the increase in the number of iterations, the effect of GRNN follows the law of diminishing marginal utility. Therefore, in the absence of current GPU computing capability integration, we recommend that the number of iterations be about four (and even only two).
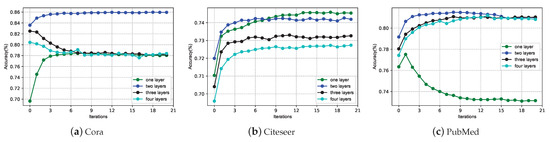
Figure 3.
Ablation study on the number of layers and iterations.
7. Discussion
In a broad sense, GNNs make full use of the feature that things of the same kind always gather together in the real network through message aggregation. Our GRNN model extends the message aggregation operation from the labeled nodes to all nodes, which is equivalent to label propagation with a minimum fitting error of the benchmark neural network. Moreover, our benchmark neural network GRNN-0 has a high dropout of nodes and edges, which aims to adapt to extending the message aggregation operation from the training set to the whole graph. Therefore, on the one hand, it is worth exploring more efficient benchmark neural networks to improve GRNN; for instance, a simpler benchmark neural network is beneficial to reduce the number of calculations of GRNN. On the other hand, in the future, more research is needed on how to optimize the loss function of GRNN to make the GRNN model converge faster.
In future work, we plan to exploit hypergraphs that are natural extensions of graphs and hypergraph neural networks that use the hypergraph structure for data modeling [51,52,53,54]. In addition, it is worth studying the loss function of GRNN to generalize the GRNN model to hypergraph neural networks, which helps to deal with multimodal data, including visual connections, text connections, and social connections. Finally, it is important to overcome the problem of computational inefficiency caused by the complex data structure of hypergraphs and the idea of the EM algorithm in the GRNN model.
8. Conclusions
We proposed a graph-retraining neural network (GRNN) that performs the smoothing operation over the graph by alternating between a learning procedure and an inference procedure to make the semi-supervised classification. In the learning procedure, the benchmark neural network uses the dropout of edges and nodes to improve robustness and uses the concatenation operation to improve stability. In the inference procedure, we highlighted the derivation and convergence of the global smoothing error function. In addition, we established a new loss function by eliminating the uncertainty of the system at the lowest cost. Our experimental results using standard citation network and protein–protein interaction datasets revealed the effectiveness of GRNN.
Author Contributions
Conceptualization, J.L. and S.F.; methodology, J.L. and S.F.; software, J.L.; validation, J.L.; formal analysis, J.L. and S.F.; investigation, J.L.; resources, J.L. and S.F.; data curation, J.L.; writing—original draft preparation, J.L.; writing—review and editing, J.L. and S.F.; visualization, J.L.; supervision, S.F.; project administration, S.F.; funding acquisition, S.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Natural Science Foundation of China (61572233), the National Key R&D Program of China (2020YFA0712500), and the Guangdong Basic and Applied Basic Research Foundation (2022A1515011267).
Data Availability Statement
The public datasets and codes used in this experiment can be obtained here: https://github.com/ljh1718841/GRNN (accessed on 19 February 2023).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analysis, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Huang, G.; Liu, Z.; van der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar] [CrossRef]
- Liu, Q.; Zeng, Y.; Mokhosi, R.; Zhang, H. STAMP: Short-Term Attention/Memory Priority Model for Session-based Recommendation. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, KDD 2018, London, UK, 19–23 August 2018; pp. 1831–1839. [Google Scholar] [CrossRef]
- Liu, Q.; Yu, F.; Wu, S.; Wang, L. A Convolutional Click Prediction Model. In Proceedings of the 24th ACM International Conference on Information and Knowledge Management, CIKM 2015, Melbourne, VIC, Australia, 19–23 October 2015; pp. 1743–1746. [Google Scholar] [CrossRef]
- Li, C.; Goldwasser, D. Encoding Social Information with Graph Convolutional Networks forPolitical Perspective Detection in News Media. In Proceedings of the 57th Conference of the Association for Computational Linguistics, ACL 2019, Florence, Italy, 28 July–2 August 2019; pp. 2594–2604. [Google Scholar] [CrossRef]
- Qiu, J.; Tang, J.; Ma, H.; Dong, Y.; Wang, K.; Tang, J. DeepInf: Social Influence Prediction with Deep Learning. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, KDD 2018, London, UK, 19–23 August 2018; pp. 2110–2119. [Google Scholar] [CrossRef]
- Li, Q.; Han, Z.; Wu, X. Deeper Insights Into Graph Convolutional Networks for Semi-Supervised Learning. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, (AAAI-18), The 30th innovative Applications of Artificial Intelligence (IAAI-18), and The 8th AAAI Symposium on Educational Advances in Artificial Intelligence (EAAI-18), New Orleans, LA, USA, 2–7 February 2018; pp. 3538–3545. [Google Scholar]
- Hu, F.; Zhu, Y.; Wu, S.; Wang, L.; Tan, T. Hierarchical Graph Convolutional Networks for Semi-supervised Node Classification. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI 2019, Macao, China, 10–16 August 2019; pp. 4532–4539. [Google Scholar]
- Hui, B.; Zhu, P.; Hu, Q. Collaborative Graph Convolutional Networks: Unsupervised Learning Meets Semi-Supervised Learning. In Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020, The Thirty-Second Innovative Applications of Artificial Intelligence Conference, The IAAI 2020, Tenth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2020, New York, NY, USA, 7–12 February 2020; pp. 4215–4222. [Google Scholar]
- Diao, Z.; Wang, X.; Zhang, D.; Liu, Y.; Xie, K.; He, S. Dynamic Spatial-Temporal Graph Convolutional Neural Networks for Traffic Forecasting. In Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence, AAAI 2019, The Thirty-First Innovative Applications of Artificial Intelligence Conference, IAAI 2019, The Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2019, Honolulu, HI, USA, 27 January–1 February 2019; pp. 890–897. [Google Scholar] [CrossRef]
- Han, Y.; Wang, S.; Ren, Y.; Wang, C.; Gao, P.; Chen, G. Predicting Station-Level Short-Term Passenger Flow in a Citywide Metro Network Using Spatiotemporal Graph Convolutional Neural Networks. ISPRS Int. J. Geo Inf. 2019, 8, 243. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 1025–1035. [Google Scholar]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural Message Passing for Quantum Chemistry. In Proceedings of the 34th International Conference on Machine Learning, ICML 2017, Sydney, NSW, Australia, 6–11 August 2017; pp. 1263–1272. [Google Scholar]
- Huang, Q.; He, H.; Singh, A.; Lim, S.; Benson, A.R. Combining Label Propagation and Simple Models out-performs Graph Neural Networks. In Proceedings of the 9th International Conference on Learning Representations, ICLR 2021, Virtual Event, 3–7 May 2021. [Google Scholar]
- Shi, Y.; Huang, Z.; Feng, S.; Zhong, H.; Wang, W.; Sun, Y. Masked Label Prediction: Unified Message Passing Model for Semi-Supervised Classification. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, IJCAI 2021, Montreal, QC, Canada, 19–27 August 2021; pp. 1548–1554. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B Methodol. 1977, 39, 1–22. [Google Scholar]
- Qu, M.; Bengio, Y.; Tang, J. GMNN: Graph Markov Neural Networks. In Proceedings of the 36th International Conference on Machine Learning, ICML 2019, Long Beach, CA, USA, 9–15 June 2019; pp. 5241–5250. [Google Scholar]
- Lafferty, J.D.; McCallum, A.; Pereira, F.C.N. Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data. In Proceedings of the Eighteenth International Conference on Machine Learning (ICML 2001), Williamstown, MA, USA, 28 June–1 July 2001; pp. 282–289. [Google Scholar]
- Zhou, D.; Bousquet, O.; Lal, T.N.; Weston, J.; Schölkopf, B. Learning with Local and Global Consistency. In Proceedings of the Advances in Neural Information Processing Systems 16 Neural Information Processing Systems, NIPS 2003, Vancouver and Whistler, BC, Canada, 8–13 December 2003; pp. 321–328. [Google Scholar]
- Zhu, X.; Ghahramani, Z.; Lafferty, J.D. Semi-Supervised Learning Using Gaussian Fields and Harmonic Functions. In Proceedings of the Machine Learning, Proceedings of the Twentieth International Conference (ICML 2003), Washington, DC, USA, 21–24 August 2003; pp. 912–919. [Google Scholar]
- Joachims, T. Transductive Learning via Spectral Graph Partitioning. In Proceedings of the Machine Learning, Proceedings of the Twentieth International Conference (ICML 2003), Washington, DC, USA, 21–24 August 2003; pp. 290–297. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef] [PubMed]
- Hammond, D.K.; Vandergheynst, P.; Gribonval, R. Wavelets on graphs via spectral graph theory. Appl. Comput. Harmon. Anal. 2011, 30, 129–150. [Google Scholar] [CrossRef]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral Networks and Locally Connected Networks on Graphs. In Proceedings of the 2nd International Conference on Learning Representations, ICLR 2014, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering. In Proceedings of the Advances in Neural Information Processing Systems 29: Annual Conference on Neural Information Processing Systems 2016, Barcelona, Spain, 5–10 December 2016; pp. 3837–3845. [Google Scholar]
- Monti, F.; Boscaini, D.; Masci, J.; Rodolà, E.; Svoboda, J.; Bronstein, M.M. Geometric Deep Learning on Graphs and Manifolds Using Mixture Model CNNs. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 5425–5434. [Google Scholar] [CrossRef]
- Bai, L.; Jiao, Y.; Cui, L.; Hancock, E.R. Learning aligned-spatial graph convolutional networks for graph classification. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Würzburg, Germany, 16 September 2019; pp. 464–482. [Google Scholar]
- Klicpera, J.; Bojchevski, A.; Günnemann, S. Predict then Propagate: Graph Neural Networks meet Personalized PageRank. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Chiang, W.; Liu, X.; Si, S.; Li, Y.; Bengio, S.; Hsieh, C. Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Networks. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, KDD 2019, Anchorage, AK, USA, 4–8 August 2019; pp. 257–266. [Google Scholar] [CrossRef]
- Wang, H.; Leskovec, J. Unifying Graph Convolutional Neural Networks and Label Propagation. arXiv 2020, arXiv:2002.06755. [Google Scholar]
- Gong, M.; Zhou, H.; Qin, A.K.; Liu, W.; Zhao, Z. Self-Paced Co-Training of Graph Neural Networks for Semi-Supervised Node Classification. IEEE Trans. Neural Netw. Learn. Syst. 2022; Early Access. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Rong, Y.; Huang, W.; Xu, T.; Huang, J. DropEdge: Towards Deep Graph Convolutional Networks on Node Classification. In Proceedings of the 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Yang, C.; Liu, Z.; Zhao, D.; Sun, M.; Chang, E.Y. Network Representation Learning with Rich Text Information. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, IJCAI 2015, Buenos Aires, Argentina, 25–31 July 2015; pp. 2111–2117. [Google Scholar]
- Hu, W.; Fey, M.; Zitnik, M.; Dong, Y.; Ren, H.; Liu, B.; Catasta, M.; Leskovec, J. Open Graph Benchmark: Datasets for Machine Learning on Graphs. In Proceedings of the Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, Virtual, 6–12 December 2020. [Google Scholar]
- Sen, P.; Namata, G.; Bilgic, M.; Getoor, L.; Gallagher, B.; Eliassi-Rad, T. Collective Classification in Network Data. AI Mag. 2008, 29, 93–106. [Google Scholar] [CrossRef]
- Zitnik, M.; Leskovec, J. Predicting multicellular function through multi-layer tissue networks. Bioinformatics 2017, 33, i190–i198. [Google Scholar] [CrossRef] [PubMed]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. DeepWalk: Online learning of social representations. In Proceedings of the The 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’14, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar] [CrossRef]
- Zheng, R.; Chen, W.; Feng, G. Semi-supervised node classification via adaptive graph smoothing networks. Pattern Recognit. 2022, 124, 108492. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, H.; Tao, S. Semi-supervised classification via full-graph attention neural networks. Neurocomputing 2022, 476, 63–74. [Google Scholar] [CrossRef]
- Wu, W.; Hu, G.; Yu, F. Ricci Curvature-Based Semi-Supervised Learning on an Attributed Network. Entropy 2021, 23, 292. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Huang, J.; Hou, L.; Shen, H.; Gao, J.; Cheng, X. Label-Consistency based Graph Neural Networks for Semi-supervised Node Classification. In Proceedings of the 43rd International ACM SIGIR conference on research and development in Information Retrieval, SIGIR 2020, Virtual Event, 25–30 July 2020; pp. 1897–1900. [Google Scholar] [CrossRef]
- Wu, F., Jr.; Souza, A.; Zhang, T.; Fifty, C.; Yu, T.; Weinberger, K.Q. Simplifying Graph Convolutional Networks. In Proceedings of the 36th International Conference on Machine Learning, ICML 2019, Long Beach, CA, USA, 9–15 June 2019; pp. 6861–6871. [Google Scholar]
- Chen, M.; Wei, Z.; Huang, Z.; Ding, B.; Li, Y. Simple and Deep Graph Convolutional Networks. In Proceedings of the 37th International Conference on Machine Learning, ICML 2020, Virtual Event, 13–18 July 2020; pp. 1725–1735. [Google Scholar]
- Liu, M.; Gao, H.; Ji, S. Towards Deeper Graph Neural Networks. In Proceedings of the KDD ’20: The 26th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Virtual Event, 23–27 August 2020; pp. 338–348. [Google Scholar] [CrossRef]
- Zheng, W.; Qian, F.; Zhao, S.; Zhang, Y. M-GWNN: Multi-granularity graph wavelet neural networks for semi-supervised node classification. Neurocomputing 2021, 453, 524–537. [Google Scholar] [CrossRef]
- Peng, L.; Hu, R.; Kong, F.; Gan, J.; Mo, Y.; Shi, X.; Zhu, X. Reverse Graph Learning for Graph Neural Network. IEEE Trans. Neural Netw. Learn. Syst. 2022; Early Access. 2022. [Google Scholar] [CrossRef] [PubMed]
- Grover, A.; Leskovec, J. node2vec: Scalable Feature Learning for Networks. In Proceedings of the Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar] [CrossRef]
- Sun, K.; Lin, Z.; Zhu, Z. Multi-Stage Self-Supervised Learning for Graph Convolutional Networks on Graphs with Few Labeled Nodes. In Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020, The Thirty-Second Innovative Applications of Artificial Intelligence Conference, IAAI 2020, The Tenth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2020, New York, NY, USA, 7–12 February 2020; pp. 5892–5899. [Google Scholar]
- Feng, Y.; You, H.; Zhang, Z.; Ji, R.; Gao, Y. Hypergraph Neural Networks. In Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence, AAAI 2019, The Thirty-First Innovative Applications of Artificial Intelligence Conference, IAAI 2019, The Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2019, Honolulu, HI, USA, 27 January–1 February 2019; pp. 3558–3565. [Google Scholar] [CrossRef]
- Gao, Y.; Feng, Y.; Ji, S.; Ji, R. HGNN+: General Hypergraph Neural Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 3181–3199. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Liu, Y. A Survey on Hyperlink Prediction. arXiv 2022, arXiv:2207.02911. [Google Scholar] [CrossRef]
- Huang, J.; Yang, J. UniGNN: A Unified Framework for Graph and Hypergraph Neural Networks. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, IJCAI 2021, Virtual Event, 19–27 August 2021; pp. 2563–2569. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).