Accelerating the Sinkhorn Algorithm for Sparse Multi-Marginal Optimal Transport via Fast Fourier Transforms
Abstract
1. Introduction
1.1. Our Contributions
1.2. Outline of the Paper
2. Notation
3. Multi-Marginal Optimal Transport
Entropy Regularization
| Algorithm 1 Sinkhorn iterations for the problem |
|
4. Sparse Cost Functions
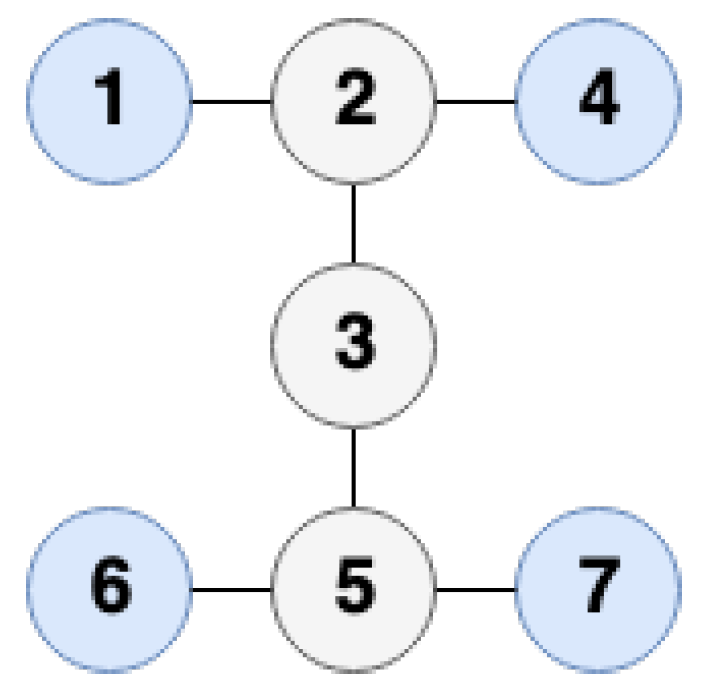
4.1. Tree Structure
| Algorithm 2 Sinkhorn algorithm for tree structure |
|
4.2. Circle Structure
| Algorithm 3 Sinkhorn algorithm for circle structure |
|
5. Non-Uniform Discrete Fourier Transforms
| Algorithm 4 NFFT-based fast summation |
|
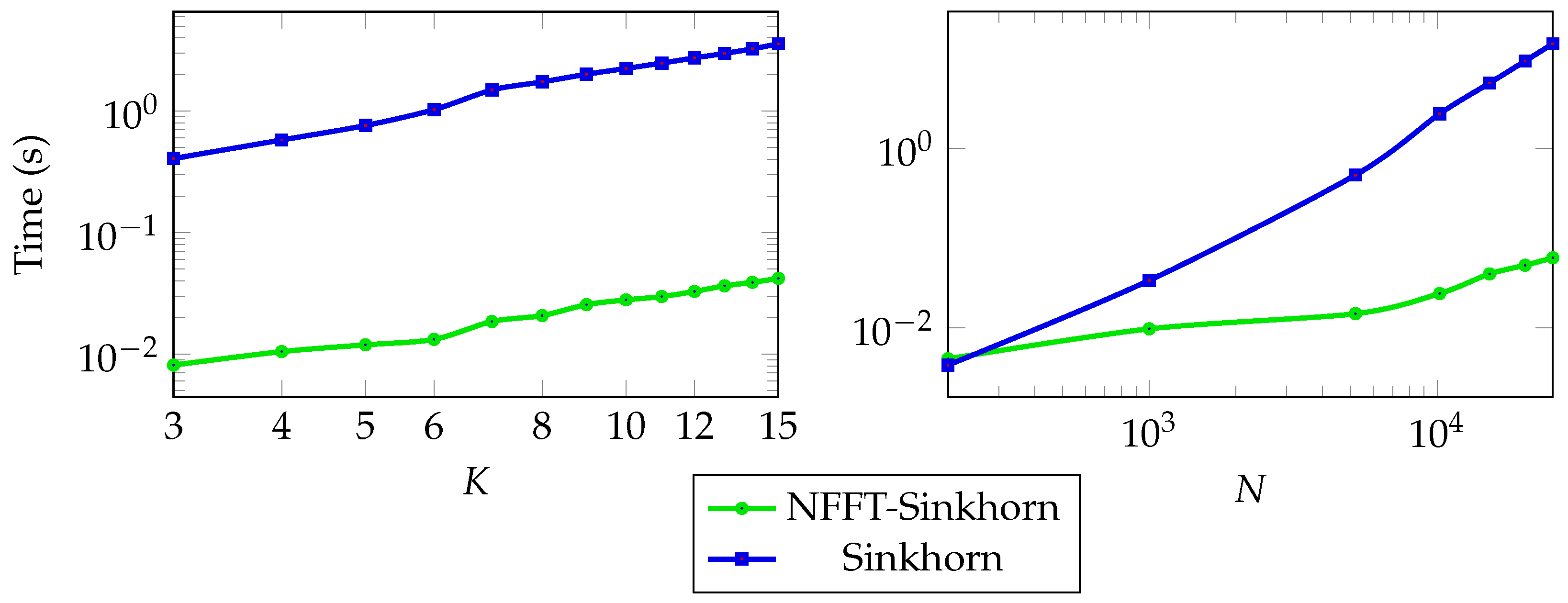
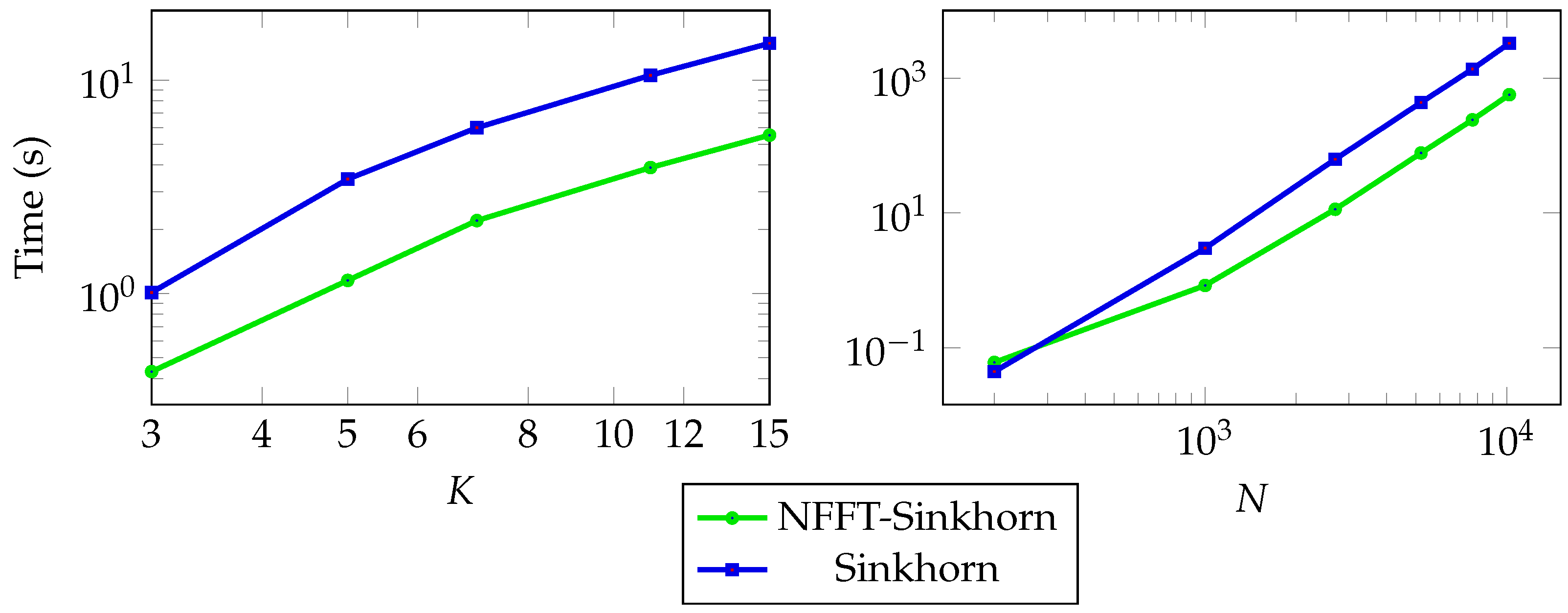
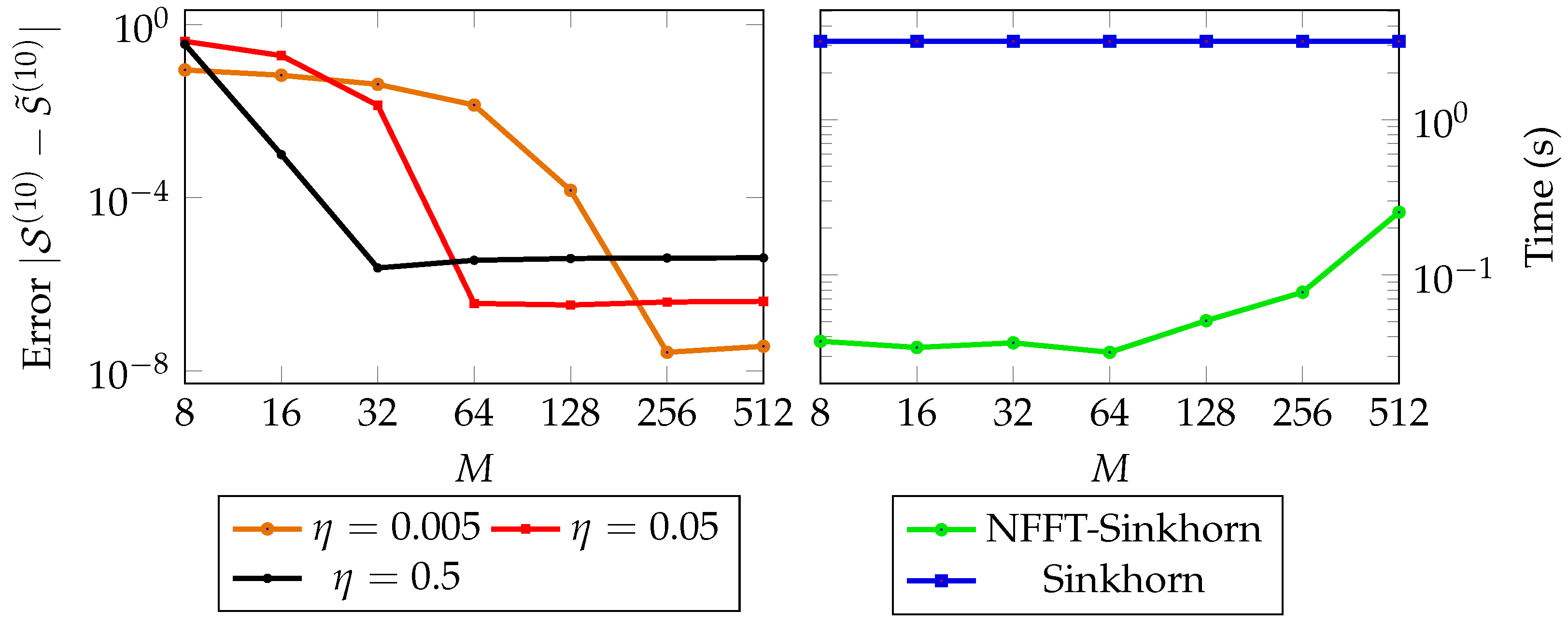
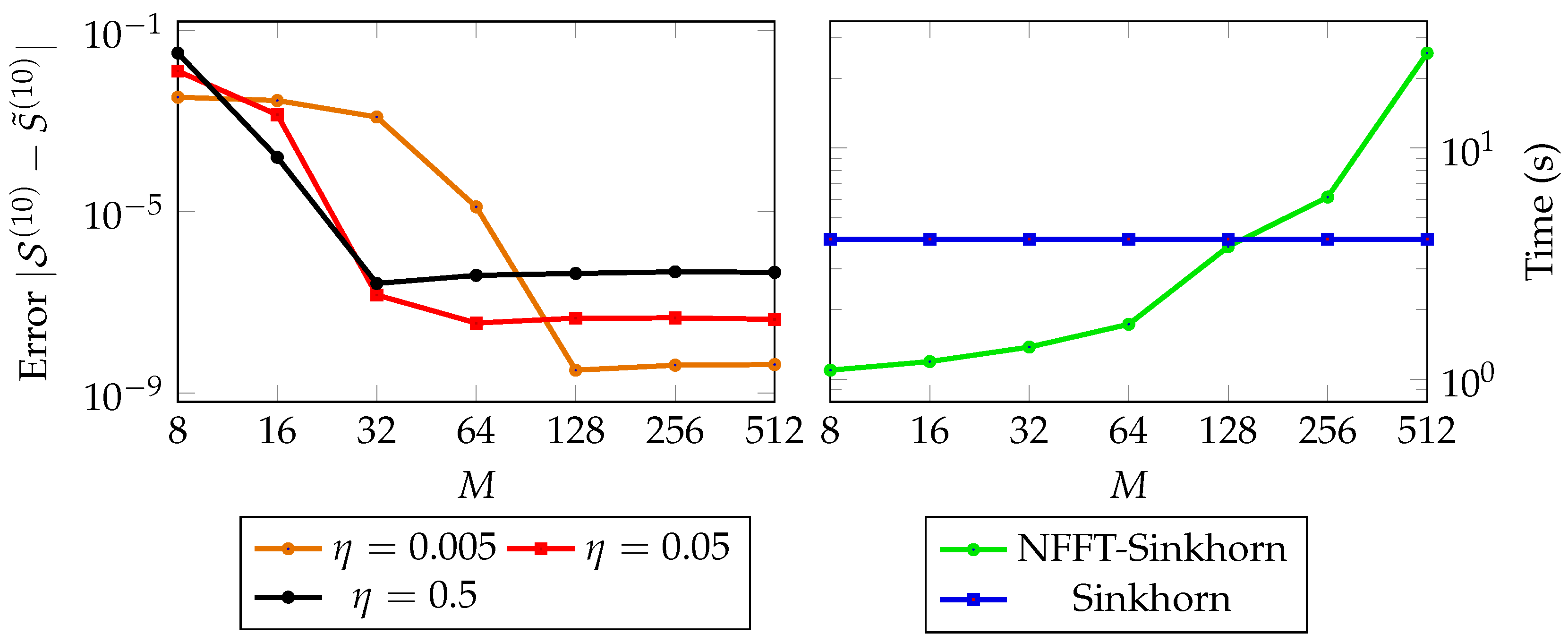
6. Numerical Examples
6.1. Uniformly Distributed Points
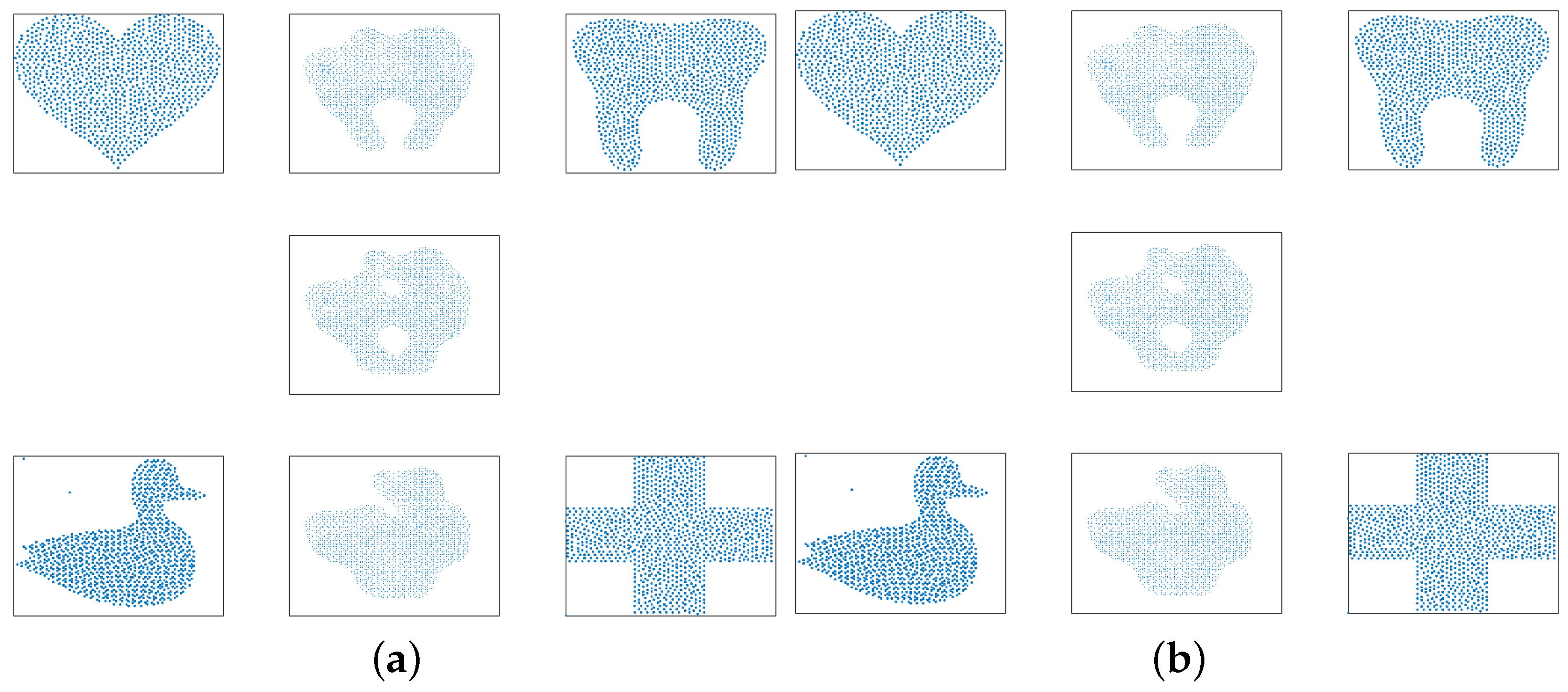
6.2. Fixed-Support Wasserstein Barycenter for General Trees
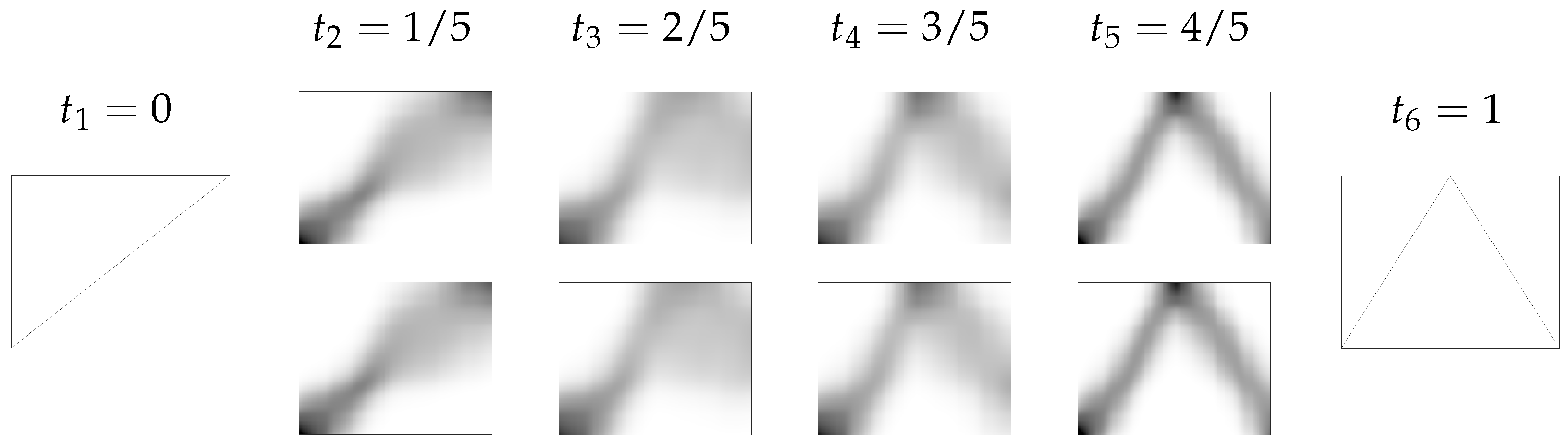
6.3. Generalized Euler Flows
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peyré, G.; Cuturi, M. Computational Optimal Transport: With Applications to Data Science. Found. Trends Mach. Learn. 2019, 11, 355–607. [Google Scholar] [CrossRef]
- Villani, C. Optimal Transport: Old and New; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Beier, F.; von Lindheim, J.; Neumayer, S.; Steidl, G. Unbalanced multi-marginal optimal transport. arXiv 2021, arXiv:2103.10854. [Google Scholar]
- Bonneel, N.; Peyré, G.; Cuturi, M. Wasserstein barycentric coordinates: Histogram regression using optimal transport. ACM Trans. Graph. 2016, 35, 71. [Google Scholar] [CrossRef]
- Tartavel, G.; Peyré, G.; Gousseau, Y. Wasserstein loss for image synthesis and restoration. SIAM J. Imaging Sci. 2016, 9, 1726–1755. [Google Scholar] [CrossRef]
- Thorpe, M.; Park, S.; Kolouri, S.; Rohde, G.K.; Slepčev, D. A transportation Lp distance for signal analysis. J. Math. Imaging Vis. 2017, 59, 187–210. [Google Scholar] [CrossRef] [PubMed]
- Vogt, T.; Lellmann, J. Measure-valued variational models with applications to diffusion-weighted imaging. J. Math. Imaging Vis. 2018, 60, 1482–1502. [Google Scholar] [CrossRef]
- Carlier, G.; Oberman, A.; Oudet, E. Numerical methods for matching for teams and Wasserstein barycenters. ESAIM M2AN 2015, 49, 1621–1642. [Google Scholar] [CrossRef]
- Galichon, A. Optimal Transport Methods in Economics; Princeton University Press: Princeton, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Dolinsky, Y.; Soner, H.M. Martingale optimal transport and robust hedging in continuous time. Probab. Theory Relat. Fields 2014, 160, 391–427. [Google Scholar] [CrossRef]
- Dolinsky, Y.; Soner, H.M. Robust hedging with proportional transaction costs. Financ. Stoch. 2014, 18, 327–347. [Google Scholar] [CrossRef]
- Frisch, U.; Matarrese, S.; Mohayaee, R.; Sobolevski, A.N. A reconstruction of the initial conditions of the universe by optimal mass transportation. Nature 2002, 417, 260–262. [Google Scholar] [CrossRef]
- Haasler, I.; Ringh, A.; Chen, Y.; Karlsson, J. Multimarginal optimal transport with a tree-structured cost and the Schrödinger bridge problem. SIAM J. Control Optim. 2021, 59, 2428–2453. [Google Scholar] [CrossRef]
- Kantorovich, L. On the translocation of masses. Manag. Sci. 1958, 5, 1–4. [Google Scholar] [CrossRef]
- Lin, T.; Ho, N.; Cuturi, M.; Jordan, M.I. On the complexity of approximating multimarginal optimal transport. J. Mach. Learn. Res. 2022, 23, 1–43. [Google Scholar]
- Pass, B. Multi-marginal optimal transport and multi-agent matching problems: Uniqueness and structure of solutions. Discret. Contin. Dyn. Syst. 2014, 34, 1623–1639. [Google Scholar] [CrossRef]
- Pass, B. Multi-marginal optimal transport: Theory and applications. ESAIM M2AN 2015, 49, 1771–1790. [Google Scholar] [CrossRef]
- Benamou, J.-D.; Carlier, G.; Nenna, L. A numerical method to solve multi-marginal optimal transport problems with Coulomb cost. In Splitting Methods in Communication, Imaging, Science, and Engineering; Springer: Cham, Switzerland, 2016; pp. 577–601. [Google Scholar]
- Neumayer, S.; Steidl, G. From optimal transport to discrepancy. In Handbook of Mathematical Models and Algorithms in Computer Vision and Imaging: Mathematical Imaging and Vision; Chen, K., Schönlieb, C.-B., Tai, X.-C., Younces, L., Eds.; Springer: Cham, Switzerland, 2021; pp. 1–36. [Google Scholar] [CrossRef]
- Terjék, D.; González-Sánchez, D. Optimal transport with f-divergence regularization and generalized Sinkhorn algorithm. arXiv 2021, arXiv:2105.14337. [Google Scholar]
- Blondel, M.; Seguy, V.; Rolet, A. Smooth and sparse optimal transport. In Proceedings of Machine Learning Research, Proceedings of the Twenty-First International Conference on Artificial Intelligence and Statistics, Playa Blanca, Spain, 9–11 April 2018; Volume 84, pp. 880–889. [Google Scholar]
- Lorenz, D.A.; Manns, P.; Meyer, C. Quadratically regularized optimal transport. Appl. Math. Optim. 2021, 83, 1919–1949. [Google Scholar] [CrossRef]
- Genevay, A.; Cuturi, M.; Peyré, G.; Bach, F. Stochastic optimization for large-scale optimal transport. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Curran Associates Inc.: Red Hook, NY, USA, 2016; pp. 3440–3448. [Google Scholar] [CrossRef]
- Ammari, H.; Garnier, J.; Millien, P. Backpropagation imaging in nonlinear harmonic holography in the presence of measurement and medium noises. SIAM J. Imaging Sci. 2014, 7, 239–276. [Google Scholar] [CrossRef][Green Version]
- Altschuler, J.M.; Boix-Adsera, E. Polynomial-time algorithms for multimarginal optimal transport problems with structure. Math. Program. 2022, in press. [Google Scholar] [CrossRef]
- Benamou, J.-D.; Carlier, G.; Cuturi, M.; Nenna, L.; Peyré, G. Iterative bregman projections for regularized transportation problems. SIAM J. Sci. Comput. 2015, 37, A1111–A1138. [Google Scholar] [CrossRef]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; Adaptive Computation and Machine Learning; The MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Alaya, M.Z.; Bérar, M.; Gasso, G.; Rakotomamonjy, A. Screening Sinkhorn algorithm for regularized optimal transport. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Curran Associates Inc.: Red Hook, NY, USA, 2019. [Google Scholar] [CrossRef]
- Cuturi, M. Sinkhorn distances: Lightspeed computation of optimal transport. In Advances in Neural Information Processing Systems; Burges, C.J.C., Bottou, L., Welling, M., Ghahramani, Z., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2013; Volume 26. [Google Scholar]
- Knopp, P.; Sinkhorn, R. Concerning connegative matrices and doubly stochastic matrices. Pac. J. Math. 1967, 21, 343–348. [Google Scholar] [CrossRef]
- Potts, D.; Steidl, G. Fast summation at nonequispaced knots by NFFTs. SIAM J. Sci. Comput. 2003, 24, 2013–2037. [Google Scholar] [CrossRef]
- Potts, D.; Steidl, G.; Nieslony, A. Fast convolution with radial kernels at nonequispaced knots. Numer. Math. 2004, 98, 329–351. [Google Scholar] [CrossRef]
- Nestler, F.; Pippig, M.; Potts, D. Fast Ewald summation based on NFFT with mixed periodicity. J. Comput. Phys. 2015, 285, 280–315. [Google Scholar] [CrossRef]
- Hielscher, R.; Quellmalz, M. Optimal mollifiers for spherical deconvolution. Inverse Probl. 2015, 31, 085001. [Google Scholar] [CrossRef]
- Alfke, D.; Potts, D.; Stoll, M.; Volkmer, T. NFFT meets Krylov methods: Fast matrix-vector products for the graph Laplacian of fully connected networks. Front. Appl. Math. Stat. 2018, 4, 61. [Google Scholar] [CrossRef]
- Lakshmanan, R.; Pichler, A.; Potts, D. Fast Fourier transform boost for the Sinkhorn algorithm. arXiv 2022, arXiv:2201.07524. [Google Scholar]
- Solomon, J.; de Goes, F.; Peyré, G.; Cuturi, M.; Butscher, A.; Nguyen, A.; Du, T.; Guibas, L. Convolutional Wasserstein distances: Efficient optimal transportation on geometric domains. ACM Trans. Graph. 2015, 34, 1–11. [Google Scholar] [CrossRef]
- Strössner, C.; Kressner, D. Low-rank tensor approximations for solving multi-marginal optimal transport problems. arXiv 2022, arXiv:2202.07340. [Google Scholar]
- Benamou, J.-D.; Carlier, G.; Nenna, L. Generalized incompressible flows, multi-marginal transport and Sinkhorn algorithm. Numer. Math. 2019, 142, 33–54. [Google Scholar] [CrossRef]
- Beiglböck, M.; Léonard, C.; Schachermayer, W. A general duality theorem for the Monge-Kantorovich transport problem. Studia Math. 2012, 209, 151–167. [Google Scholar] [CrossRef]
- Elvander, F.; Haasler, I.; Jakobsson, A.; Karlsson, J. Multi-marginal optimal transport using partial information with applications in robust localization and sensor fusion. Signal Process. 2020, 171, 107474. [Google Scholar] [CrossRef]
- Marino, S.D.; Gerolin, A. An optimal transport approach for the Schrödinger bridge problem and convergence of Sinkhorn algorithm. J. Sci. Comput. 2020, 85, 27. [Google Scholar] [CrossRef]
- Plonka, G.; Potts, D.; Steidl, G.; Tasche, M. Numerical Fourier Analysis; Applied and Numerical Harmonic Analysis; Birkhäuser: Basel, Switzerland, 2018. [Google Scholar] [CrossRef]
- Dutt, A.; Rokhlin, V. Fast Fourier transforms for nonequispaced data II. Appl. Comput. Harmon. Anal. 1995, 2, 85–100. [Google Scholar] [CrossRef]
- Beylkin, G. On the fast Fourier transform of functions with singularities. Appl. Comput. Harmon. Anal. 1995, 2, 363–381. [Google Scholar] [CrossRef]
- Keiner, J.; Kunis, S.; Potts, D. Using NFFT3—A software library for various nonequispaced fast Fourier transforms. ACM Trans. Math. Softw. 2009, 36, 19. [Google Scholar] [CrossRef]
- Nestler, F. Parameter tuning for the NFFT based fast Ewald summation. Front. Phys. 2016, 4, 28. [Google Scholar] [CrossRef]
- Bassetti, F.; Gualandi, S.; Veneroni, M. On the computation of Kantorovich-Wasserstein distances between 2d-histograms by uncapacitated minimum cost flows. arXiv 2018, arXiv:1804.00445. [Google Scholar]
- Cuturi, M.; Doucet, A. Fast computation of wasserstein barycenters. In Proceedings of the 31st International Conference on International Conference on Machine Learning, Beijing, China, 21–26 June 2014; Volume 32, pp. II–685–II–693. [Google Scholar]
- Rabin, J.; Peyre, G.; Delon, J.; Bernot, M. Wasserstein barycenter and its application to texture mixing. In Scale Space and Variational Methods in Computer Vision; Bruckstein, A.M., Romeny, B.M.t.H., Bronstein, A.M., Bronstein, M.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 435–446. [Google Scholar]
- von Lindheim, J. Approximative algorithms for multi-marginal optimal transport and free-support Wasserstein barycenters. arXiv 2022, arXiv:2202.00954. [Google Scholar]
- Takezawa, Y.; Sato, R.; Kozareva, Z.; Ravi, S.; Yamada, M. Fixed support tree-sliced Wasserstein barycenter. arXiv 2021, arXiv:2109.03431. [Google Scholar]
- Agueh, M.; Carlier, G. Barycenters in the Wasserstein space. SIAM J. Math. Anal. 2011, 43, 904–924. [Google Scholar] [CrossRef]
- Flamary, R.; Courty, N.; Gramfort, A.; Alaya, M.Z.; Boisbunon, A.; Chambon, S.; Chapel, L.; Corenflos, A.; Fatras, K.; Fournier, N.; et al. Pot: Python optimal transport. J. Mach. Learn. Res. 2021, 22, 1–8. [Google Scholar]
- Brenier, Y. The least action principle and the related concept of generalized flows for incompressible perfect fluids. J. Amer. Math. Soc. 1989, 2, 225–255. [Google Scholar] [CrossRef]
- Brenier, Y. The dual least action problem for an ideal, incompressible fluid. Arch. Ration. Mech. Anal. 1993, 122, 323–351. [Google Scholar] [CrossRef]
- Brenier, Y. Minimal geodesics on groups of volume-preserving maps and generalized solutions of the euler equations. Comm. Pure Appl. Math 1997, 52, 411–452. [Google Scholar] [CrossRef]

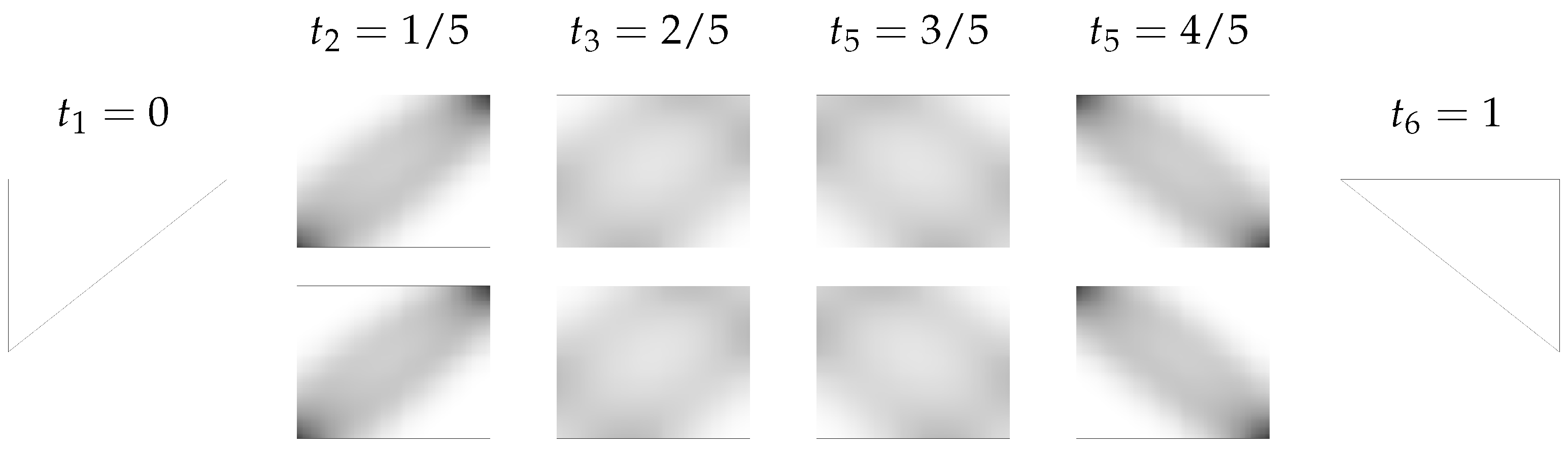
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ba, F.A.; Quellmalz, M. Accelerating the Sinkhorn Algorithm for Sparse Multi-Marginal Optimal Transport via Fast Fourier Transforms. Algorithms 2022, 15, 311. https://doi.org/10.3390/a15090311
Ba FA, Quellmalz M. Accelerating the Sinkhorn Algorithm for Sparse Multi-Marginal Optimal Transport via Fast Fourier Transforms. Algorithms. 2022; 15(9):311. https://doi.org/10.3390/a15090311
Chicago/Turabian StyleBa, Fatima Antarou, and Michael Quellmalz. 2022. "Accelerating the Sinkhorn Algorithm for Sparse Multi-Marginal Optimal Transport via Fast Fourier Transforms" Algorithms 15, no. 9: 311. https://doi.org/10.3390/a15090311
APA StyleBa, F. A., & Quellmalz, M. (2022). Accelerating the Sinkhorn Algorithm for Sparse Multi-Marginal Optimal Transport via Fast Fourier Transforms. Algorithms, 15(9), 311. https://doi.org/10.3390/a15090311





