Abstract
This paper presents and analyzes a programming tool that implements a method for classification and function regression problems. This method builds new features from existing ones with the assistance of a hybrid algorithm that makes use of artificial neural networks and grammatical evolution. The implemented software exploits modern multi-core computing units for faster execution. The method has been applied to a variety of classification and function regression problems, and an extensive comparison with other methods of computational intelligence is made.
1. Introduction
Many problems from various research areas can be considered as classification or regression problems, such as problems from physics [1,2,3,4], chemistry [5,6,7], economics [8,9], pollution [10,11,12], medicine [13,14], etc. These problems are usually tackled by learning models such as Artificial Neural Networks [15,16], Radial Basis Function (RBF) networks [17,18], Support Vector Machines (SVM) [19], Parse-matrix evolution [20], Multilevel Block Building [21], Development of Mathematical Expressions [22], etc. A review of the methods used in classification can be found in the work of Kotsiantis et al. [23].
Learning data are usually divided into two parts: training data and test data. Learning models adjust their parameters, taking the training data as input, and are evaluated on the test data. The number of learning model parameters directly depends on the dimension of the input problem (number of features) and this means that for large problems, large amounts of memory are required to store and manage the learning models. In addition, as the number of parameters of the computational models grows, a longer time is required to adjust the parameters. Moreover, as the dimension of the data grows, more samples (patterns) are required in order to achieve high learning rates. A discussion on how the dimensionality of the input problems affects the effectiveness of neural networks is presented in [24]. A common approach to reduce the dimension of the input data is the Principal Component Analysis (PCA) technique [25,26,27] or the Minimum redundancy Feature Selection (MRMR) technique [28,29]. Furtheromre, Wang et al. [30] proposed an auto-encoder based dimensionality reduction method for large datasets. An overview of dimensionality reduction techniques can be found in the work of Ayesha et al. [31].
The current article describes the method and the software associated with a feature construction method based on grammatical evolution [32], which is an evolutionary process that can create programs in any programming language. The described method constructs subsets of features from the original ones using non-linear combinations of them. The method is graphically illustrated in Figure 1. Initially, the method was described in [33], and it has been utilized in a variety of cases, such as spam identification [34], fetal heart classification [35], epileptic oscillations in clinical intracranial electroencephalograms [36], classification of EEG signals [37], etc.
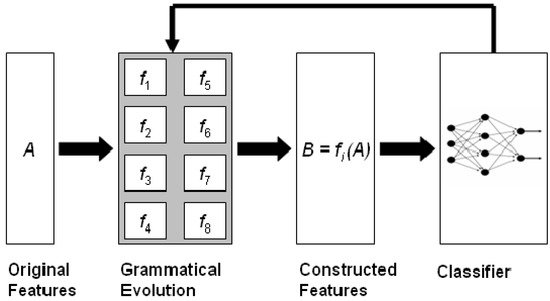
Figure 1.
Schematic representation of the feature construction technique.
Feature construction methods have been thoroughly examined and analyzed in the relevant literature such as the work of Smith and Bull [38], where tree genetic programming is used to construct artificial features. Devi uses the Simulated Annealing method [39] to identify the features that are most important for data classification. Neshatian et al. [40] construct artificial features using an entropy based fitness function for the associated genetic algorithm. Li and Yin use another evolutionary approach for feature selection using gene expression data [41]. Furthermore, Ma and Teng proposed [42] a genetic programming approach that utilizes information gain ratio (IGR) to construct artificial features.
The proposed software has been implemented in ANSI C++ utilizing the freely available library of QT from https://www.qt.io (accessed on 18 August 2022). The user should supply the training and test data of the underlying problem as well as the desired number of features that will be created. The evaluation of the constructed features can be made using a variety of machine learning models, and the user can easily extend the software to add more learning models. Moreover, the software has a variety of command line options to control the parameters of the learning models or to manage the output of the method. Finally, since the process of grammatical evolution can require a lot of execution time, parallel computation is included in the proposed software through the OpenMP programming library [43].
The proposed method differs from similar ones as it does not require any prior knowledge of the objective problem and can be applied without any change to both classification problems and regression problems. In addition, the method can discover any functional dependencies between the initial features and can drastically reduce the number of input features, significantly reducing the time required to train the subsequent machine learning model.
Related freely available software packages on feature selection and construction are also the Mlpack package [44], which implements the PCA method; the GSL software package obtained from https://www.gnu.org/software/gsl/doc/html/index.html (accessed on 18 August 2022), which also implements the PCA method, among others; the MRMR package writen in ANSI C++ by Hanchuan Peng [28,29]; etc.
The rest of this article is organized as follows: in Section 2, the grammatical evolution procedure is briefly described and the proposed method is analyzed; in Section 3, the proposed software is outlined in detail; in Section 4, a variety of experiments are conducted and presented; and finally in Section 5, some conclusions and future guidelines are discussed.
2. Methods
In this section, a brief overview of grammatical evolution, its applications and its advantages is given and then presented: the creation of artificial features using grammatical evolution, the first phase of the method where features are constructed and evaluated, and the second phase of the method, where the characteristics from the first phase are evaluated.
2.1. Grammatical Evolution
Grammatical evolution is a biologically inspired procedure that can create artificial programs in any language. In grammatical evolution, the chromosomes enclose production rules from a BNF (Backus–Naur form) grammar [45]. These grammars are usually described as a set , where
- N is the set of non-terminal symbols.
- T is the set of terminal symbols.
- S is a non-terminal symbol defined as the start symbol of the grammar.
- P is a set of production rules in the form or .
In order for grammatical evolution to work, the original grammar is expanded by enumerating all production rules. For example, consider the modified grammar of Figure 2. The symbols that are in <> are considered as non-terminal symbols. The numbers in parentheses are the production sequence numbers for each non-terminal symbol. The constant N is the original number of features for the input data. In grammatical evolution, the chromosomes are expressed as vectors of integers. Every element of each chromosome denotes a production rule from the provided BNF grammar. The algorithm starts from the start symbol of the grammar and gradually produces some program string by replacing non-terminal symbols with the right hand of the selected production rule. The selection of the rule has two steps:

Figure 2.
BNF grammar of the proposed method.
- Take the next element from the chromosome and denote it as V.
- Select the next production rule according to the the scheme Rule = V mod R, where R is the number of production rules for the current non-terminal symbol.
For example, consider the chromosome
and . The steps of mapping this chromosome to the valid expression are illustrated in Table 1.

Table 1.
Steps to produce a valid expression from the BNF grammar.
Initially, grammatical evolution was used in cases of learning functions [46,47] and solving trigonometric identities [48], but then it was also applied in other fields such as automatic composition of music [49], construction of neural networks [50,51], automatic constant creation [52], evolution of video games [53,54], energy demand estimation [55], combinatorial optimization [56], cryptography [57], etc.
A key advantage of the grammatical evolution is its easy adaptability to a wide range of problems, as long as the grammar of the problem and a fitness method are provided. No additional knowledge of the problem is required such as using derivatives. Furthermore, the method can be easily parallelized, since it is essentially a genetic algorithm of integer values. However, there are a number of disadvantages that must be taken into account when using the technique. In principle, in many cases a chromosome may not be able to produce a valid expression in the underlying grammar if its elements run out. In this case, wrapping an effect can be executed, but it is not always certain that this can again provide a valid solution. Moreover, another important issue is the initialization of the chromosomes of grammatical evolution. Usually the rules are very few in number and therefore, different numbers on the chromosomes may produce the same rules.
In the next subsection, the steps of producing artificial features from the original ones are provided and discussed.
2.2. The Feature Construction Procedure
The proposed technique is divided into two phases: in the first phase, new features are constructed from the old ones using grammatical evolution and in the second phase, these new features modify the control set, and a machine learning model is applied to the new control set. The following procedure is executed in order to produce features from the original ones for a given chromosome X:
- SplitX into parts.
- For, denote each part as .
- For every part , construct a feature using the grammar given in Figure 2.
Every feature is considered as a mapping function that transforms the original features to a new one. For example, the feature
is a non-linear function that maps the original feature into . Let . The mapping procedure will create the value .
2.3. The Feature Construction Step
This is the first phase of the proposed method and it has the following steps:
- 1
- Initialization step.
- (a)
- Read the train data. The train data contain M patterns as pairs , where is the actual output for pattern .
- (b)
- Set , the maximum number of generations.
- (c)
- Set , the number of chromosomes.
- (d)
- Set , the selection rate.
- (e)
- Set, the desired number of features.
- (f)
- Set , the mutation rate.
- (g)
- Initialize the chromosomes of the population. Every element of each chromosome is initialized randomly in the range [0, 255].
- (h)
- Set iter = 1.
- 2
- Genetic step.
- (a)
- For do
- i
- Create, using the procedure of Section 2.2, a set of for the corresponding chromosome .
- ii
- Transform the original train data to the new train data using the previously created features. Denote the new train set as .
- iii
- Apply a learning model C (such as RBF) to the new data and calculate the fitness as
- iv
- Apply the selection procedure. During selection, the chromosomes are classified according to their fitness. The best chromosomes are transferred without changes to the next generation of the population. The rest will be replaced by chromosomes that will be produced at the crossover.
- v
- Apply the crossover procedure. During this process, chromosomes will be created. Firstly, for every pair of produced offsprings, two distinct chromosomes (parents) are selected from the current population using tournament selection: First, a subset of randomly selected chromosomes is created and the chromosome with the best fitness value is selected as parent. For every pair of parents, two new offsprings and are created through one point crossover as graphically shown in Figure 3.
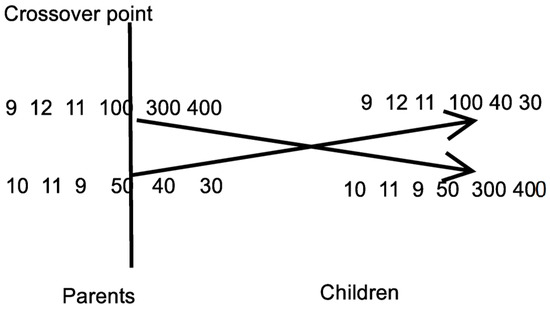 Figure 3. Example of one-point crossover.
Figure 3. Example of one-point crossover. - vi
- Apply the mutation procedure. For every element of each chromosome, select a random number and alter the corresponding chromosome if .
- (b)
- End For
- 3
- Set iter = iter + 1.
- 4
- If, goto Genetic Step, else terminate and obtain as the best chromosome in the population.
2.4. The Feature Evaluation Step
During the feature evaluation step, the following steps are executed:
- Denote as the original test set.
- Obtain the best chromosome of the feature construction step.
- Construct features for using the procedure of Section 2.2.
- TransformT into using the previously constructed features.
- Apply a learning model such as RBF or a neural network to and obtain the test error.
3. The Software
The proposed method has been fully implemented in ANSI C++ and is freely available from the internet. This section also acts as a small manual for this software. It starts with the software installation instructions, then all the operating parameters of the software are presented and the use of the software is demonstrated through an analytical example.
3.1. Installation Procedure
The software is entirely written in ANSI C++ using the freely available QT programming library. The library can be downloaded from https://www.qt.io (accessed on 18 August 2022) As expected, the software can be installed on the majority of operating systems, even on mobile devices (Android, iOS, etc.). The program is freely available from https://github.com/itsoulos/QFc (accessed on 18 August 2022), and the user should issue the following commands under most UNIX systems to compile the project:
- Download QFc-master.zip from the above url
- gunzip QFc-master.zip
- cd QFc
- qmake.
- make
The final outcome of the previous steps is a command line program called qfc. This program has a series of command line parameters that is illustrated subsequently.
3.2. The Program qfc
The program qfc has a variety of command line options. All options are in the form key = value, where key is the name of the option and value is the actual option value. The main options of the program are:
- 1
- trainFile = filename, where filename is the full path to data containing the input train set. The file must be in the format of Figure 4. The integer number D denotes the number of features of the dataset, and M represents the number of patterns. In every subsequent line of the file, there should be the input pattern, and the final column is the real output (category) for the corresponding pattern.
 Figure 4. Example of input file for regression/classification.
Figure 4. Example of input file for regression/classification. - 2
- testFile = filename, where filename is the full path to data containing the input test set. The format of this file should be the same as the train data. The user should at least provide the train and test set in order to execute the program.
- 3
- features = n, set as the n the number of features that will be constructed by the method. The default value is 1.
- 4
- randomSeed = r, set as r the random seed generator. The default value for this parameter is 1, and the drand48() random generator of c++ language was used.
- 5
- featureCreateModel = model, the string parameter model sets the name of the used feature construction model. The default value is “rbf”, and accepted values are:
- (a)
- copy. With this value, no feature construction is done and the original dataset is used for training by the model specified by the option featureEvaluate Model.
- (b)
- rbf. This value is used to utilize a Radial Basis Function neural network for the evaluation of the constructed features.
- (c)
- neural. This value is used to use a neural network for the evaluation of the constructed features.
- (d)
- knn. A simple K-nearest neighbor (KNN) method is used [58].
- (e)
- osamaRbf. A simple RBF implementation as downloaded from https://github.com/osama-afifi/RBF-Radial-Basis-Function-Network (accessed on 18 August 2022).
- 6
- featureEvaluateModel = model, the string parameter model sets the name of the used model for the evaluation of the constructed features. The default value is “neural”, but other accepted values are: rbf, knn, osamaRbf, nnc. The value nnc refers to the Neural Network Construction model as proposed by Tsoulos et al. [59].
- 7
- threads = t, the number of OpenMP threads used. The default value is 1.
- 8
- neural_trainingMethod = m. This is the option that defines the method used for neural network training. The default value for m is “bfgs”, and accepted values are
- (a)
- bfgs. This value sets as a training method a BFGS variant of Powell [60].
- (b)
- lbfgs. This value sets as a training method the limited memory BFGS [61,62].
- (c)
- genetic. With this value, a simple genetic algorithm [63,64] is used to train the neural network.
- 9
- neural_weights = n, the weights used in neural networks. The default value is 1.
- 10
- knn_weights = n, the weights (neighbors) used in the knn model. The default value is 1.
- 11
- rbf_weights = n, the weights used in the rbf model.
- 12
- ge_chromosomes = n, the number of chromosomes in the grammatical evolution procedure. The default value is 500.
- 13
- ge_maxGenerations = n, the maximum number of generations for the grammatical evolution procedure. The default value is 200.
- 14
- ge_selectionRate = f, the selection rate used in the grammatical evolution procedure. The default value is 0.10 (10%).
- 15
- ge_mutationRate = f, the mutation rate used in the grammatical evolution procedure. The default value is 0.05 (5%).
- 16
- ge_length = n, the length of chromosomes in the grammatical evolution procedure. The default value is , where d is the number of features that will be created.
- 17
- genetic_chromosomes = n, the number of chromosomes used in the genetic algorithm for neural network training. The default value is 500.
- 18
- genetic_maxGenerations = n, the maximum number of generations for the genetic algorithm used for neural network training. The default value is 200.
- 19
- genetic_selectionRate = f, the selection rate used in the genetic algorithm of neural network training. The default value is 0.1 (10%).
- 20
- genetic_mutationRate = f, the mutation rate used in the genetic algorithm of neural network training. The default value is 0.05 (5%).
- 21
- bfgs_iterations = n, the maximum number of iterations for the BFGS method. The default value is 2001.
- 22
- export_train_file = f. The value f specifies the file where the training set will be exported after new features are constructed. The new file will have the same format and the same number of templates as the original, but the dimension will be changed to the one defined with the parameter features.
- 23
- export_test_file = f, the value f specifies the file where the test set will be exported after new features are constructed. The new file will have the same format and the same number of templates as the original, but the dimension will be changed to the one defined with the parameter features.
- 24
- export_cpp_file = f, where f is the output of the constructed features in the C++ programming language. As an example, consider the file outlined in Figure 5. The function fcMap() is a function with two array arguments:
 Figure 5. An example output file for the BL dataset.
Figure 5. An example output file for the BL dataset.- (a)
- The argument inx denotes an input pattern with the original dimension. For the case of BL dataset, the original dimension is 7.
- (b)
- The argument outx stands for the features created by the algorithm. In this case, outx[0] is the first feature and outx[1] is the second feature.
- 25
- help, prints a help screen and terminates the program.
3.3. Example Run
As an example run, consider the wdbc dataset located in the examples folder of the distribution. The following command:
- ./QFc --trainFile = examples/wdbc.train --testFile = examples/wdbc.test--features = 2 --ge_maxGenerations = 5--featureEvaluatedModel = rbf --threads = 8
will produce the following output
- Iteration: 1 Best Fitness: −52.1562
- Best program: f1(x) = (447.63 ∗ x7 − x14 + x15)
- Iteration: 2 Best Fitness: −52.1562
- Best program: f1(x) = (447.63 ∗ x7 − x14 + x15)
- Iteration: 3 Best Fitness: −51.8369
- Best program: f1(x) = (417.63 ∗ x7 − x14 + x15)
- Iteration: 4 Best Fitness: −51.7176
- Best program: f1(x) = (417.63 ∗ x7 − x14 + (48.07/(−486.503)) ∗ x14 + exp(55.884 ∗ x15))
- Iteration: 5 Best Fitness: −51.5149
- Best program: f1(x) = (417.63 ∗ x7 − x14 + x15 + x16 + log(((−9.863)/5.9) ∗ x30 + exp(sin(x5 + (417.63/07.54) ∗ x8 + 7.494 ∗ x29))))
- AVERAGES(TRAIN,TEST,CLASS): 57.241174 60.60288 29.473684%
4. Experiments
A series of experiments were performed in order to evaluate the reliability and accuracy of the proposed methodology. In these experiments, the accuracy of the proposed methodology against other techniques, the running time of the experiments, and the sensitivity of the experimental results to various critical parameters, such as the number of features or the maximum number of generations of the genetic algorithm, were measured. All the experiments were conducted 30 times with different seeds for the random number generator each time and averages were taken. All the experiments were conducted on an AMD Ryzen 5950X equipped with 128GB of RAM. The operating system used was OpenSUSE Linux, and all the programs were compiled using the GNU C++ compiler. In all the experiments, the parameter featureCreateModel had the value rbf, since it is the fastest model that could be used and it has high learning rates. For classification problems, the average classification error on the test set is shown and, for regression datasets, the average mean squared error on the test set is displayed. In all cases, 10-fold cross-validation was used, and the number of parameters for neural networks and for RBF networks was set to 10. The evaluation of the features constructed by grammatical evolution was made using the Function Parser library [65].
4.1. Experimental Datasets
The validity of the method was tested on a series of well-known datasets from the relevant literature. The main repositories for the testing were:
- The UCI Machine Learning Repository http://www.ics.uci.edu/~mlearn/MLRepository.html (accessed on 18 August 2022)
- The Keel repository https://sci2s.ugr.es/keel/ (accessed on 18 August 2022)
- The Statlib repository http://lib.stat.cmu.edu/datasets/ accessed on 18 August 2022).
The classification datasets are:
- Australian dataset [66], a dataset related to credit card applications.
- Alcohol dataset, a dataset about Alcohol consumption [67].
- Balance dataset [68], which is used to predict psychological states.
- Cleveland dataset, a dataset used to detect heart disease and used in various papers [69,70].
- Dermatology dataset [71], which is used for differential diagnosis of erythemato-squamous diseases.
- Glass dataset. This dataset contains glass component analysis for glass pieces that belong to six classes.
- Hayes Roth dataset [72]. This dataset contains 5 numeric-valued attributes and 132 patterns.
- Heart dataset [73], used to detect heart disease.
- HouseVotes dataset [74], which is about votes in the U.S. House of Representatives Congressmen.
- Liverdisorder dataset [75], used to detect liver disorders in peoples using blood analysis.
- Ionosphere dataset, a meteorological dataset used in various research papers [76,77].
- Mammographic dataset [78]. This dataset can be used to identify the severity (benign or malignant) of a mammographic mass lesion from BI-RADS attributes and the patient’s age. It contains 830 patterns of 5 features each.
- PageBlocks dataset. The dataset contains blocks of the page layout of a document that has been detected by a segmentation process. It has 5473 patterns with 10 features each.
- Parkinsons dataset, ref. [79], which is created using a range of biomedical voice measurements from 31 people, 23 with Parkinson’s disease (PD). The dataset has 22 features.
- Pima dataset [80], used to detect the presence of diabetes.
- PopFailures dataset [81], used in meteorology.
- Regions2 dataset. It is created from liver biopsy images of patients with hepatitis C [82]. From each region in the acquired images, 18 shape-based and color-based features were extracted, while it was also annotated from medical experts. The resulting dataset includes 600 samples belonging to 6 classes.
- Saheart dataset [83], used to detect heart disease.
- Segment dataset [84]. This database contains patterns from a database of seven outdoor images (classes).
- Sonar dataset [85]. The task here is to discriminate between sonar signals bounced off a metal cylinder and those bounced off a roughly cylindrical rock.
- Spiral dataset, which is an artificial dataset with two classes. The features in the first class are constructed as: and for the second class the used equations are:.
- Wine dataset, which is related to chemical analysis of wines [86,87].
- Wdbc dataset [88], which contains data for breast tumors.
- EEG dataset. As a real-world example, an EEG dataset described in [89,90] is used here. The dataset consists of five sets (denoted as Z, O, N, F, and S), each containing 100 single-channel EEG segments and each having a 23.6 sec duration. Sets Z and O have been taken from surface EEG recordings of five healthy volunteers with eye open and closed, respectively. Signals in two sets have been measured in seizure-free intervals from five patients in the epileptogenic zone (F) and from the hippocampal formation of the opposite hemisphere of the brain (N). Set S contains seizure activity, selected from all recording sites exhibiting ictal activity. Sets Z and O have been recorded extracranially, whereas sets N, F, and S have been recorded intracranially.
- Zoo dataset [91], where the task is to classify animals in seven predefined classes.
The regression datasets used are the following:
- Abalone dataset [92]. This dataset can be used to obtain a model to predict the age of abalone from physical measurements.
- Airfoil dataset, which is used by NASA for a series of aerodynamic and acoustic tests [93].
- Baseball dataset, a dataset to predict the salary of baseball players.
- BK dataset, used to estimate the points scored per minute in a basketball game.
- BL dataset, which is related to the effects of machine adjustments on the time to count bolts.
- Concrete dataset. This dataset is taken from civil engineering [94].
- Dee dataset, used to predict the daily average price of the electricity energy in Spain.
- Diabetes dataset, a medical dataset.
- FA dataset, which contains percentage of body fat and ten body circumference measurements. The goal is to fit body fat to the other measurements.
- Housing dataset. This dataset was taken from the StatLib library and it is described in [95].
- MB dataset. This dataset is available from Smoothing Methods in Statistics [96], and it includes 61 patterns.
- MORTGAGE dataset, which contains economic data information from the USA.
- NT dataset [97], which is related to the body temperature measurements.
- PY dataset [98], used to learn Quantitative Structure Activity Relationships (QSARs).
- Quake dataset, used to estimate the strength of an earthquake.
- Treasure dataset, which contains economic data information from the USA from 1 April 1980 to 2 April 2000 on a weekly basis.
- Wankara dataset, which contains weather information.
4.2. Experimental Results
The parameters for the used methods are listed in Table 2. In all tables, an additional row was added at the end showing the average classification or regression error for all datasets, and it is denoted by the name AVERAGE. The columns of all tables have the following meaning:

Table 2.
Experimental parameters.
- The column RBF stands for the results from an RBF network with H Gaussian units.
- The column MLP stands for the results of a neural network with H sigmoidal nodes trained by a genetic algorithm. The parameters of this genetic algorithm are listed in Table 2.
- The column FCRBF represents the results of the proposed method, when an RBF network with H Gaussian units was used as the evaluation model.
- The column FCMLP represents the results of the proposed method, when a neural network trained by a genetic algorithm was used as the evaluation model. The parameters of this genetic algorithm are listed in Table 2.
- The column FCNNC stands for the results of the proposed method, when the neural network construction model (nnc) was utilized as the evaluation model.
- The column MRMR stands for the Minimum Redundancy Maximum Relevance Feature Selection method with two selected features. The features selected by MRMR are evaluated using an artificial neural network trained by a genetic algorithm using the parameters of Table 2.
- The Principal Component Analysis (PCA) method, as implemented in Mlpack software [44], was used to construct two features. The features constructed by PCA are evaluated using an artificial neural network trained by a genetic algorithm using the parameters of Table 2.
The experimental results for the classification datasets are listed in Table 3, and for regression datasets in Table 4. Furtheromre, a comparison against MRMR and PCA is performed in Table 5 and Table 6, respectively.

Table 3.
Experimental results between the method and other techniques for the classification datasets.

Table 4.
Experiments for regression datasets.

Table 5.
Comparison against MRMR and PCA for the classification datasets.

Table 6.
Comparison against MRMR and PCA for the regression datasets.
Summarizing the conclusions of the experiments, one can say that the proposed method obviously outperforms the other techniques in most cases, especially in the case of regression datasets. In the case of data classification, there is a gain of the order of 30%, and in the case of regression data, the gain from the application of the proposed technique exceeds 50%. The gain in many cases from the application of the proposed technique can even reach 90%. In addition, the MRMR method seems to be superior in most cases to the PCA, possibly pointing the way for a future research on the combination of grammatical evolution and MRMR. Furthermore, among the three cases of models used to evaluate the constructed features (FCRBF, FCMLP, FCNNC), there does not seem to be any clear superiority of any of the three. However, we would say that the nnc method slightly outperforms the simple genetic algorithm.
In addition, one more experiment was done in order to establish the impact of the number of features on the accuracy of the proposed method. In this case, the RBF (FCRBF) network was used as the feature evaluator, and the number of generated features was in the interval [1…4]. The average classification error and the average regression error for all datasets are shown in Table 7. From the experimental results, the robustness of the proposed methodology is clearly visible, as one or two features seem to be enough to achieve high learning rates for the experimental data used.

Table 7.
Average errors regarding the number of features.
Furthermore, one more experiment was conducted to determine the effect of the maximum number of generations on the accuracy of the proposed method. Again, as an evaluator model, the RBF was used. The number of generations was varied from 50 to 400, and the average classification error and average regression error for all datasets were measured. The results for this experiment are presented in Table 8. Once again, the dynamics of the proposed method appear as a few generations are enough to achieve high learning rates.

Table 8.
Average error depending on the number of generations.
5. Conclusions
A feature construction method and the accompanying software were analyzed in detail in this paper. The software is developed in ANSI C++ and is freely available on the internet. The proposed technique constructs technical features from the existing ones by exploiting the possible functional dependencies between the features, but also the possibility that some of the original features do not contribute anything to the learning. The method does not require any prior knowledge of the objective problem and can be applied without any change to both regression and classification problems. The method is divided into two phases: in the first phase, a genetic algorithm using grammatical evolution is used to construct new features from the original ones. These features are evaluated for their accuracy with some machine learning model. However, this process can be very time consuming and as a consequence, fast learning models or parallel algorithms should be used. Radial basis networks were used in the first phase of the method during the experiments, which are known to have short training times, but other models could be used in their place. In the second phase of the method after the features are generated, a machine learning method is applied to them and the error on the test set is evaluated.
The user can choose between several learning models and can customize the course of the technique through a series of command line parameters. From the extensive execution of experiments and the comparison with other learning methods, the superiority of the proposed technique and its ability to achieve high learning rates even with a limited number of constructed features or a maximum number of iterations emerge. These results combined with the ability of the method to run on multiple threads through the OpenMP library make it ideal for learning large sets of data in a satisfactory execution time.
The method can be extended in several ways, such as:
- Incorporation of advanced stopping rules.
- Usage of more advanced learning models such as SVM.
- Addition of more input formats such as the ARFF format or CSV format.
- Incorporation of the MPI library [99] for a large network of computers.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The experiments of this research work were performed at the high-performance computing system established at Knowledge and Intelligent Computing Laboratory, Dept of Informatics and Telecommunications, University of Ioannina, acquired with the project “Educational Laboratory equipment of TEI of Epirus” with MIS 5007094 funded by the Operational Programme “Epirus” 2014–2020, by ERDF and national finds.
Conflicts of Interest
The author declares no conflict of interest.
References
- Metodiev, E.M.; Nachman, B.; Thaler, J. Classification without labels: Learning from mixed samples in high energy physics. J. High Energy Phys. 2017, 2017, 174. [Google Scholar] [CrossRef]
- Baldi, P.; Cranmer, K.; Faucett, T.; Sadowski, P.; Whiteson, D. Parameterized neural networks for high-energy physics. Eur. Phys. J. C 2016, 76, 235. [Google Scholar] [CrossRef]
- Valdas, J.J.; Bonham-Carter, G. Time dependent neural network models for detecting changes of state in complex processes: Applications in earth sciences and astronomy. Neural Netw. 2006, 19, 196–207. [Google Scholar] [CrossRef]
- Carleo, G.; Troyer, M. Solving the quantum many-body problem with artificial neural networks. Science 2017, 355, 602–606. [Google Scholar] [CrossRef]
- Güler, C.; Thyne, G.D.; McCray, J.E.; Turner, K.A. Evaluation of graphical and multivariate statistical methods for classification of water chemistry data. Hydrogeol. J. 2002, 10, 455–474. [Google Scholar] [CrossRef]
- Byvatov, E.; Fechner, U.; Sadowski, J.; Schneider, G. Comparison of Support Vector Machine and Artificial Neural Network Systems for Drug/Nondrug Classification. J. Chem. Inf. Comput. Sci. 2003, 43, 1882–1889. [Google Scholar] [CrossRef]
- Singh, K.P.; Basant, A.; Malik, A. Gunja Jain Artificial neural network modeling of the river water quality—A case study. Ecol. Model. 2009, 220, 888–895. [Google Scholar] [CrossRef]
- Kaastra, I.; Boyd, M. Designing a neural network for forecasting financial and economic time series. Neurocomputing 1996, 10, 215–236. [Google Scholar] [CrossRef]
- Leshno, M.; Spector, Y. Neural network prediction analysis: The bankruptcy case. Neurocomputing 1996, 10, 125–147. [Google Scholar] [CrossRef]
- Astel, A.; Tsakovski, S.; Simeonov, V.; Reisenhofer, E.; Piselli, S.; Barbieri, P. Multivariate classification and modeling in surface water pollution estimation. Anal. Bioanal. Chem. 2008, 390, 1283–1292. [Google Scholar] [CrossRef]
- Azid, A.; Juahir, H.; Toriman, M.E.; Kamarudin, M.K.A.; Saudi, A.S.M.; Hasnam, C.N.C.; Aziz, N.A.A.; Azaman, F.; Latif, M.T.; Zainuddin, S.F.M.; et al. Prediction of the Level of Air Pollution Using Principal Component Analysis and Artificial Neural Network Techniques: A Case Study in Malaysia. Water Air Soil Pollut. 2014, 225, 2063. [Google Scholar] [CrossRef]
- Maleki, H.; Sorooshian, A.; Goudarzi, G.; Baboli, Z.; Birgani, Y.T.; Rahmati, M. Air pollution prediction by using an artificial neural network model. Clean Technol. Environ. Policy 2019, 21, 1341–1352. [Google Scholar] [CrossRef]
- Baskin, I.I.; Winkler, D.; Tetko, I.V. A renaissance of neural networks in drug discovery. Expert Opin. Drug Discov. 2016, 11, 785–795. [Google Scholar] [CrossRef]
- Bartzatt, R. Prediction of Novel Anti-Ebola Virus Compounds Utilizing Artificial Neural Network (ANN). Chem. Fac. 2018, 49, 16–34. [Google Scholar]
- Bishop, C. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Park, J.; Sandberg, I.W. Universal Approximation Using Radial-Basis-Function Networks. Neural Comput. 1991, 3, 246–257. [Google Scholar] [CrossRef]
- Yu, H.; Xie, T.; Paszczynski, S.; Wilamowski, B.M. Advantages of Radial Basis Function Networks for Dynamic System Design. IEEE Trans. Ind. Electron. 2011, 58, 5438–5450. [Google Scholar] [CrossRef]
- Steinwart, I.; Christmann, A. Support Vector Machines, Information Science and Statistics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Luo, C.; Zhang, S.L. Parse-matrix evolution for symbolic regression. Eng. Appl. Artif. 2012, 25, 1182–1193. [Google Scholar] [CrossRef]
- Chen, C.; Luo, C.; Jiang, Z. A multilevel block building algorithm for fast modeling generalized separable systems. Expert Syst. Appl. 2018, 109, 25–34. [Google Scholar] [CrossRef]
- Rivero, D.; Blanco, E.F.; Pazos, A. DoME: A deterministic technique for equation development and Symbolic Regression. Expert. Appl. 2022, 198, 116712. [Google Scholar] [CrossRef]
- Kotsiantis, S.B.; Zaharakis, I.D.; Pintelas, P.E. Machine learning: A review of classification and combining techniques. Artif. Intell. Rev. 2006, 26, 159–190. [Google Scholar] [CrossRef]
- Verleysen, M.; Francois, D.; Simon, G.; Wertz, V. On the effects of dimensionality on data analysis with neural networks. In Artificial Neural Nets Problem Solving Methods; Mira, J., Álvarez, J.R., Eds.; IWANN 2003; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2687. [Google Scholar]
- Erkmen, B. Tülay Yıldırım, Improving classification performance of sonar targets by applying general regression neural network with PCA. Expert Syst. Appl. 2008, 35, 472–475. [Google Scholar] [CrossRef]
- Zhou, J.; Guo, A.; Celler, B.; Su, S. Fault detection and identification spanning multiple processes by integrating PCA with neural network. Appl. Soft Comput. 2014, 14, 4–11. [Google Scholar] [CrossRef]
- Ravi Kumar, G.; Nagamani, K.; Anjan Babu, G. A Framework of Dimensionality Reduction Utilizing PCA for Neural Network Prediction. In Advances in Data Science and Management; Borah, S., Emilia Balas, V., Polkowski, Z., Eds.; Lecture Notes on Data Engineering and Communications Technologies; Springer: Singapore, 2020; Volume 37. [Google Scholar]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- Ding, C.; Peng, H. Minimum redundancy feature selection from microarray gene expression data. J. Bioinform. Comput. Biol. 2005, 3, 185–205. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, H.; Zhao, S. Auto-encoder based dimensionality reduction. Neurocomputing 2016, 184, 232–242. [Google Scholar] [CrossRef]
- Ayesha, S.; Hanif, M.K.; Talib, R. Overview and comparative study of dimensionality reduction techniques for high dimensional data. Inf. Fusion 2020, 59, 44–58. [Google Scholar] [CrossRef]
- O’Neill, M.; Ryan, C. Grammatical evolution. IEEE Trans. Evol. Comput. 2001, 5, 349–358. [Google Scholar] [CrossRef]
- Gavrilis, D.; Tsoulos, I.G.; Dermatas, E. Selecting and constructing features using grammatical evolution. Pattern Recognit. Lett. 2008, 29, 1358–1365. [Google Scholar] [CrossRef]
- Gavrilis, D.; Tsoulos, I.G.; Dermatas, E. Neural Recognition and Genetic Features Selection for Robust Detection of E-Mail Spam. In Advances in Artificial Intelligence; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3955, pp. 498–501. [Google Scholar]
- Georgoulas, G.; Gavrilis, D.; Tsoulos, I.G.; Stylios, C.; Bernardes, J.; Groumpos, P.P. Novel approach for fetal heart rate classification introducing grammatical evolution. Biomed. Signal Process. Control. 2007, 2, 69–79. [Google Scholar] [CrossRef]
- Smart, O.; Tsoulos, I.G.; Gavrilis, D. George Georgoulas Grammatical evolution for features of epileptic oscillations in clinical intracranial electroencephalograms. Expert Syst. Appl. 2011, 38, 9991–9999. [Google Scholar] [CrossRef][Green Version]
- Tzallas, A.T.; Tsoulos, I.; Tsipouras, M.G.; Giannakeas, N.; Androulidakis, I.; Zaitseva, E. Classification of EEG signals using feature creation produced by grammatical evolution. In Proceedings of the 24th Telecommunications Forum (TELFOR), Belgrade, Serbia, 22–23 November 2016; pp. 1–4. [Google Scholar]
- Smith, M.G.; Bull, L. Genetic Programming with a Genetic Algorithm for Feature Construction and Selection. Genet. Program. Evolvable Mach. 2005, 6, 265–281. [Google Scholar] [CrossRef]
- Devi, V.S. Class Specific Feature Selection Using Simulated Annealing. In Proceedings of the Mining Intelligence and Knowledge Exploration, MIKE 2015, Hyderabad, India, 9–11 December 2015; Prasath, R., Vuppala, A., Kathirvalavakumar, T., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2015; Volume 9468. [Google Scholar]
- Neshatian, K.; Zhang, M.; Andreae, P. A Filter Approach to Multiple Feature Construction for Symbolic Learning Classifiers Using Genetic Programming. IEEE Trans. Evol. Comput. 2012, 16, 645–661. [Google Scholar] [CrossRef]
- Li, X.; Yin, M. Multiobjective Binary Biogeography Based Optimization for Feature Selection Using Gene Expression Data. IEEE Trans. Nanobiosci. 2013, 12, 343–353. [Google Scholar] [CrossRef]
- Ma, J.; Teng, G. A hybrid multiple feature construction approach for classification using Genetic Programming. Appl. Soft Comput. 2019, 80, 687–699. [Google Scholar] [CrossRef]
- Dagum, L.; Menon, R. OpenMP: An industry standard API for shared-memory programming. IEEE Comput. Sci. Eng. 1998, 5, 46–55. [Google Scholar] [CrossRef]
- Curtin, R.R.; Cline, J.R.; Slagle, N.P.; March, W.; Ram, P.; Mehta, N.A.; Gray, A.G. MLPACK: A Scalable C++ Machine Learning Library. J. Mach. Learn. 2013, 14, 801–805. [Google Scholar]
- Backus, J.W. The Syntax and Semantics of the Proposed International Algebraic Language of the Zurich ACM-GAMM Conference. In Proceedings of the International Conference on Information Processing, UNESCO, Unesco, Paris, 15–20 June 1959; pp. 125–132. [Google Scholar]
- Ryan, C.; Collins, J.; O’Neill, M. Grammatical evolution: Evolving programs for an arbitrary language. In Genetic Programming. EuroGP 1998; Banzhaf, W., Poli, R., Schoenauer, M., Fogarty, T.C., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1391. [Google Scholar]
- O’Neill, M.; Ryan, M.C. Evolving Multi-line Compilable C Programs. In Genetic Programming. EuroGP 1999; Poli, R., Nordin, P., Langdon, W.B., Fogarty, T.C., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1598. [Google Scholar]
- Ryan, C.; O’Neill, M.; Collins, J.J. Grammatical evolution: Solving trigonometric identities. In Proceedings of the Mendel, 4th International Mendel Conference on Genetic Algorithms, Optimization Problems, Fuzzy Logic, Neural Networks, Rough Sets, Brno, Czech Republic, 24–26 June 1998. [Google Scholar]
- Puente, A.O.; Alfonso, R.S.; Moreno, M.A. Automatic composition of music by means of grammatical evolution. In Proceedings of the APL ’02: Proceedings of the 2002 Conference on APL: Array Processing Languages: Lore, Problems, and Applications, Madrid, Spain, 22–25 July 2002; pp. 148–155. [Google Scholar]
- Campo, L.M.L.; Oliveira, R.C.L.; Roisenberg, M. Optimization of neural networks through grammatical evolution and a genetic algorithm. Expert Syst. Appl. 2016, 56, 368–384. [Google Scholar] [CrossRef]
- Soltanian, K.; Ebnenasir, A.; Afsharchi, M. Modular Grammatical Evolution for the Generation of Artificial Neural Networks. Evol. Comput. 2022, 30, 291–327. [Google Scholar] [CrossRef]
- Dempsey, I.; Neill, M.O.; Brabazon, A. Constant creation in grammatical evolution. Int. J. Innov. Appl. 2007, 1, 23–38. [Google Scholar] [CrossRef]
- Galvün-Lüpez, E.; Swafford, J.M.; Neill, M.O.; Brabazon, A. Evolving a Ms. PacMan Controller Using Grammatical Evolution. In Applications of Evolutionary Computation; EvoApplications 2010; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6024. [Google Scholar]
- Shaker, N.; Nicolau, M.; Yannakakis, G.N.; Togelius, J.; O’Neill, M. Evolving levels for Super Mario Bros using grammatical evolution. In Proceedings of the 2012 IEEE Conference on Computational Intelligence and Games (CIG), Granada, Spain, 11–14 September 2012; pp. 304–331. [Google Scholar]
- Martünez-Rodrüguez, D.; Colmenar, J.M.; Hidalgo, J.I.; Micü, R.J.V.; Salcedo-Sanz, S. Particle swarm grammatical evolution for energy demand estimation. Energy Sci. Eng. 2020, 8, 1068–1079. [Google Scholar] [CrossRef]
- Sabar, N.R.; Ayob, M.; Kendall, G.; Qu, R. Grammatical Evolution Hyper-Heuristic for Combinatorial Optimization Problems. IEEE Trans. Evol. Comput. 2013, 17, 840–861. [Google Scholar] [CrossRef]
- Ryan, C.; Kshirsagar, M.; Vaidya, G.; Cunningham, A.; Sivaraman, R. Design of a cryptographically secure pseudo random number generator with grammatical evolution. Sci. Rep. 2012, 12, 8602. [Google Scholar] [CrossRef]
- Fix, E.; Hodges, J.L. Joseph, Discriminatory Analysis. Nonparametric Discrimination: Consistency Properties; USAF School of Aviation Medicine: Randolph Field, TX, USA, 1951. [Google Scholar]
- Tsoulos, I.; Gavrilis, D.; Glavas, E. Neural network construction and training using grammatical evolution. Neurocomputing 2008, 72, 269–277. [Google Scholar] [CrossRef]
- Powell, M.J.D. A Tolerant Algorithm for Linearly Constrained Optimization Calculations. Math. Program. 1989, 45, 547–566. [Google Scholar] [CrossRef]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Byrd, R.; Nocedal, J.; Schnabel, R. Representations of Quasi-Newton Matrices and their use in Limited Memory Methods’. Math. Program. 1994, 63, 129–156. [Google Scholar] [CrossRef]
- Michaelewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer: Berlin, Germany, 1996. [Google Scholar]
- Kaelo, P.; Ali, M.M. Integrated crossover rules in real coded genetic algorithms. Eur. J. Oper. Res. 2007, 176, 60–76. [Google Scholar] [CrossRef]
- Nieminen, J.; Yliluoma, J. Function Parser for C++, v2.7. Available online: http://warp.povusers.org/FunctionParser/ (accessed on 18 August 2022).
- Quinlan, J.R. Simplifying Decision Trees. Int. J. Man-Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef]
- Tzimourta, K.D.; Tsoulos, I.; Bilero, I.T.; Tzallas, A.T.; Tsipouras, M.G.; Giannakeas, N. Direct Assessment of Alcohol Consumption in Mental State Using Brain Computer Interfaces and Grammatical Evolution. Inventions 2018, 3, 51. [Google Scholar] [CrossRef]
- Shultz, T.; Mareschal, D.; Schmidt, W. Modeling Cognitive Development on Balance Scale Phenomena. Mach. Learn. 1994, 16, 59–88. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Jiang, Y. NeC4.5: Neural ensemble based C4.5. IEEE Trans. Knowl. Data Eng. 2004, 16, 770–773. [Google Scholar] [CrossRef]
- Setiono, R.; Leow, W.K. FERNN: An Algorithm for Fast Extraction of Rules from Neural Networks. Appl. Intell. 2000, 12, 15–25. [Google Scholar] [CrossRef]
- Demiroz, G.; Govenir, H.A.; Ilter, N. Learning Differential Diagnosis of Eryhemato-Squamous Diseases using Voting Feature Intervals. Artif. Intell. Med. 1998, 13, 147–165. [Google Scholar]
- Hayes-Roth, B.; Hayes-Roth, B.F. Concept learning and the recognition and classification of exemplars. J. Verbal Learning Verbal Behav. 1977, 16, 321–338. [Google Scholar] [CrossRef]
- Kononenko, I.; üimec, E.; Robnik-üikonja, M. Overcoming the Myopia of Inductive Learning Algorithms with RELIEFF. Appl. Intell. 1997, 7, 39–55. [Google Scholar] [CrossRef]
- French, R.M.; Chater, N. Using noise to compute error surfaces in connectionist networks: A novel means of reducing catastrophic forgetting. Neural Comput. 2002, 14, 1755–1769. [Google Scholar] [CrossRef]
- Garcke, J.; Griebel, M. Classification with sparse grids using simplicial basis functions. Intell. Data Anal. 2002, 6, 483–502. [Google Scholar] [CrossRef]
- Dy, J.G.; Brodley, C.E. Feature Selection for Unsupervised Learning. J. Mach. Learn. Res. 2004, 5, 845–889. [Google Scholar]
- Perantonis, S.J.; Virvilis, V. Input Feature Extraction for Multilayered Perceptrons Using Supervised Principal Component Analysis. Neural Process. Lett. 1999, 10, 243–252. [Google Scholar] [CrossRef]
- Elter, M.; Schulz-Wendtland, R.; Wittenberg, T. The prediction of breast cancer biopsy outcomes using two CAD approaches that both emphasize an intelligible decision process. Med. Phys. 2007, 34, 4164–4172. [Google Scholar] [CrossRef] [PubMed]
- Little, M.A.; McSharry, P.E.; Hunter, E.J.; Ramig, L. Suitability of dysphonia measurements for telemonitoring of Parkinson’s disease. IEEE Trans. Biomed. Eng. 2009, 56, 1015–1022. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.W.; Everhart, J.E.; Dickson, W.C.; Knowler, W.C.; Johannes, R.S. Using the ADAP learning algorithm to forecast the onset of diabetes mellitus. In Proceedings of the Symposium on Computer Applications and Medical Care, Orlando, FL, USA, 7–11 November 1988; IEEE Computer Society Press: Washington, DC, USA; American Medical Informatics Association: Bethesda, MD, USA, 1988; pp. 261–265. [Google Scholar]
- Lucas, D.D.; Klein, R.; Tannahill, J.; Ivanova, D.; Brandon, S.; Domyancic, D.; Zhang, Y. Failure analysis of parameter-induced simulation crashes in climate models. Geosci. Model Dev. 2013, 6, 1157–1171. [Google Scholar] [CrossRef]
- Giannakeas, N.; Tsipouras, M.G.; Tzallas, A.T.; Kyriakidi, K.; Tsianou, Z.E.; Manousou, P.; Hall, A.; Karvounis, E.C.; Tsianos, V.; Tsianos, E. A clustering based method for collagen proportional area extraction in liver biopsy images. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Milan, Italy, 25–29 August 2015; Art. No. 7319047. pp. 3097–3100. [Google Scholar]
- Hastie, T.; Tibshirani, R. Non-parametric logistic and proportional odds regression. JRSS-C (Appl. Stat.) 1987, 36, 260–276. [Google Scholar] [CrossRef]
- Dash, M.; Liu, H.; Scheuermann, P.; Tan, K.L. Fast hierarchical clustering and its validation. Data Knowl. Eng. 2003, 44, 109–138. [Google Scholar] [CrossRef]
- Gorman, R.P.; Sejnowski, T.J. Analysis of Hidden Units in a Layered Network Trained to Classify Sonar Targets. Neural Netw. 1988, 1, 75–89. [Google Scholar] [CrossRef]
- Raymer, M.; Doom, T.E.; Kuhn, L.A.; Punch, W.F. Knowledge discovery in medical and biological datasets using a hybrid Bayes classifier/evolutionary algorithm. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2003, 33, 802–813. [Google Scholar] [CrossRef]
- Zhong, P.; Fukushima, M. Regularized nonsmooth Newton method for multi-class support vector machines. Optim. Methods Softw. 2007, 22, 225–236. [Google Scholar] [CrossRef]
- Wolberg, W.H.; Mangasarian, O.L. Multisurface method of pattern separation for medical diagnosis applied to breast cytology. Proc. Natl. Acad. Sci. USA 1990, 87, 9193–9196. [Google Scholar] [CrossRef]
- Andrzejak, R.G.; Lehnertz, K.; Mormann, F.; Rieke, C.; David, P.; Elger, C.E. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Phys. Rev. E 2001, 64, 061907. [Google Scholar] [CrossRef]
- Tzallas, A.T.; Tsipouras, M.G.; Fotiadis, D.I. Automatic Seizure Detection Based on Time-Frequency Analysis and Artificial Neural Networks. Comput. Neurosci. 2007, 2007, 80510. [Google Scholar] [CrossRef]
- Koivisto, M.; Sood, K. Exact Bayesian Structure Discovery in Bayesian Networks. J. Mach. Learn. Res. 2004, 5, 549–573. [Google Scholar]
- Nash, W.J.; Sellers, T.L.; Talbot, S.R.; Cawthor, A.J.; Ford, W.B. The Population Biology of Abalone (_Haliotis_ species) in Tasmania. I. Blacklip Abalone (_H. rubra_) from the North Coast and Islands of Bass Strait, Sea Fisheries Division; Technical Report No. 48; Department of Primary Industry and Fisheries, Tasmania: Hobart, Australia, 1994; ISSN 1034-3288. [Google Scholar]
- Brooks, T.F.; Pope, D.S.; Marcolini, A.M. Airfoil Self-Noise and Prediction. Technical Report, NASA RP-1218. July 1989. Available online: https://ntrs.nasa.gov/citations/19890016302 (accessed on 18 August 2022).
- Yeh, I.C. Modeling of strength of high performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
- Harrison, D.; Rubinfeld, D.L. Hedonic prices and the demand for clean ai. J. Environ. Econ. Manag. 1978, 5, 81–102. [Google Scholar] [CrossRef]
- Simonoff, J.S. Smooting Methods in Statistics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Mackowiak, P.A.; Wasserman, S.S.; Levine, M.M. A critical appraisal of 98.6 degrees f, the upper limit of the normal body temperature, and other legacies of Carl Reinhold August Wunderlich. J. Am. Med. Assoc. 1992, 268, 1578–1580. [Google Scholar] [CrossRef]
- King, R.D.; Muggleton, S.; Lewis, R.; Sternberg, M.J.E. Drug design by machine learning: The use of inductive logic programming to model the structure-activity relationships of trimethoprim analogues binding to dihydrofolate reductase. Proc. Nat. Acad. Sci. USA 1992, 89, 11322–11326. [Google Scholar] [CrossRef]
- Graham, R.L.; Woodall, T.S.; Squyres, J. Open MPI: A Flexible High Performance MPI. In Parallel Processing and Applied Mathematics; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3911, pp. 228–239. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).