New Step Size Control Algorithm for Semi-Implicit Composition ODE Solvers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Using Variable-Step Integration with Composition Schemes
2.2. Semi-Implicit CD Method
2.3. Semi-Explicit Modification of Midpoint Method
2.4. Truncation Error Estimators for Composition ODE Solvers
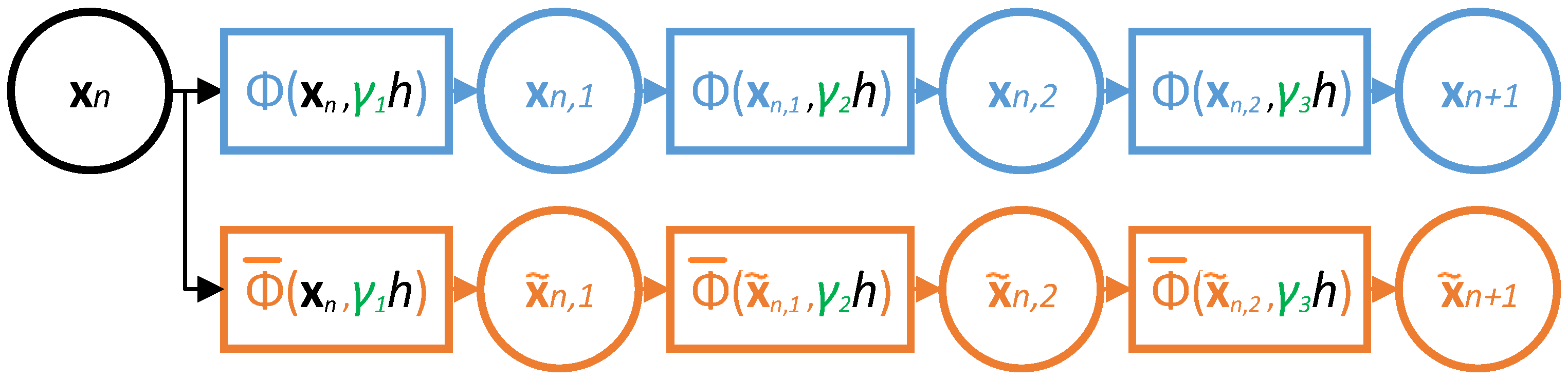
2.5. Embedded Error Estimators in Composition Schemes
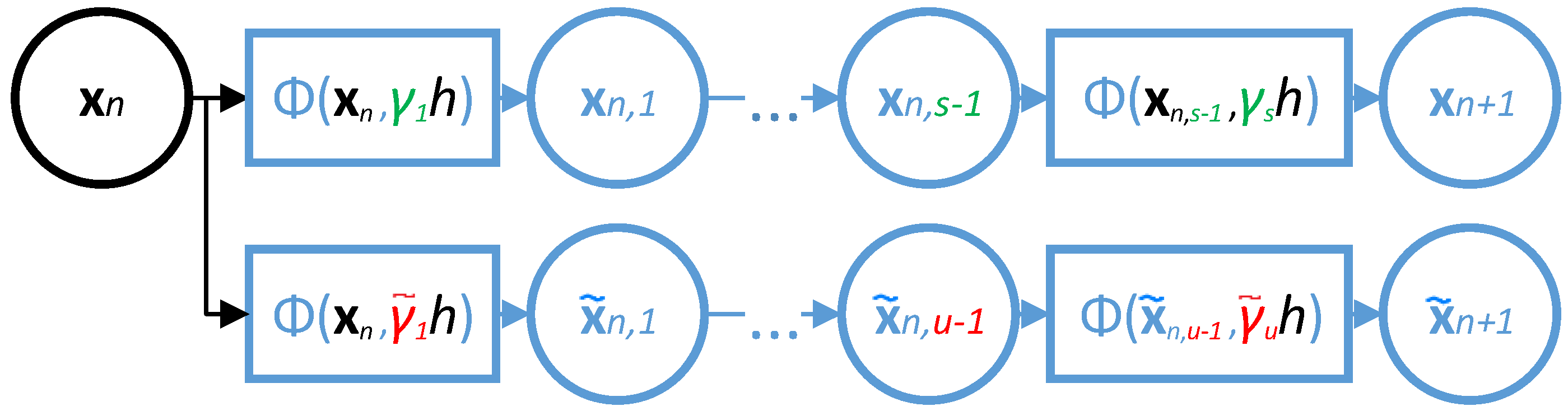
2.6. New Technique to Estimate Local Truncation Error
| Algorithm 1. Pseudocode for the proposed step size control algorithm |
| Begin Algorithm |
| 1 Setn, h; |
| 2 Set vector of composition coefficients γ; |
| 3 Set s as number of composition stages; |
| 4 |
| 5 Begin FOR i = 1, …, s |
| 6 Calculate a new value of h using formula h = hγ [i]; |
| 7 Calculate xn+ 0.5n using semi-explicit D method with |
| step size h/2; |
| 8 n using explicit Euler method |
| n+ 0.5; |
| 9 n+ 1n using semi-implicit D method with |
| n+ 0.5; |
| 10 End FOR cycle; |
| 16 Choose new step value h; |
| 18 End DO-WHILE cycle; |
| End Algorithm |
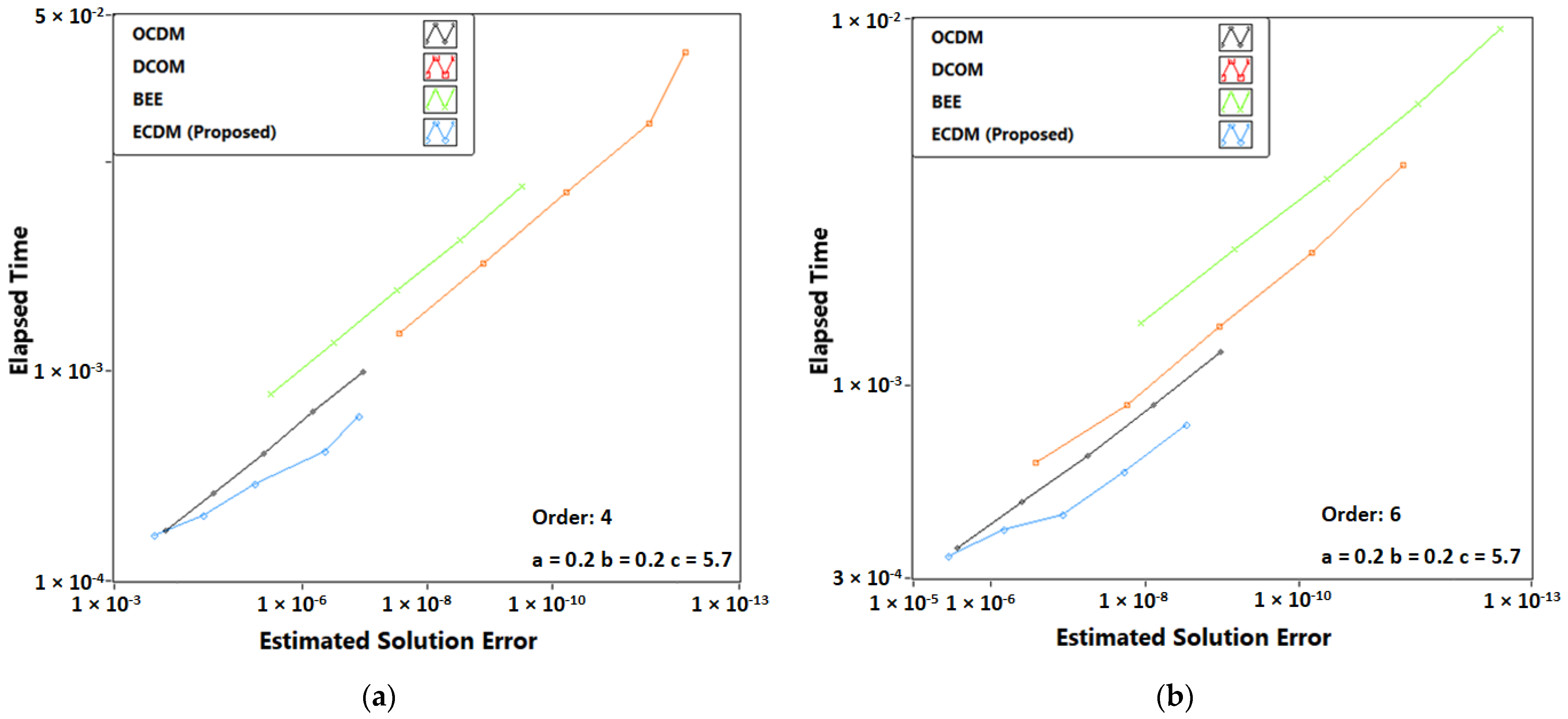
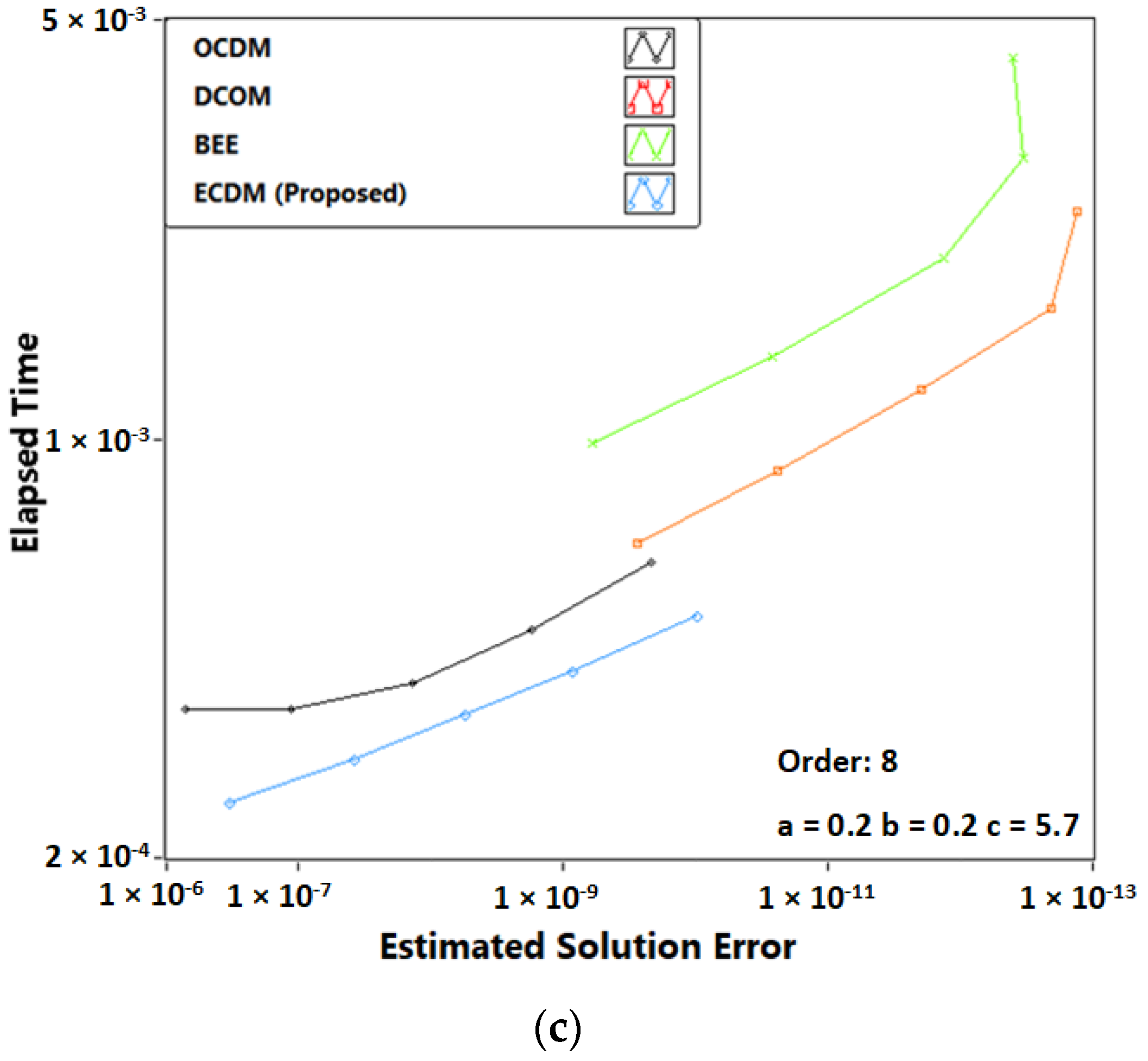
3. Results
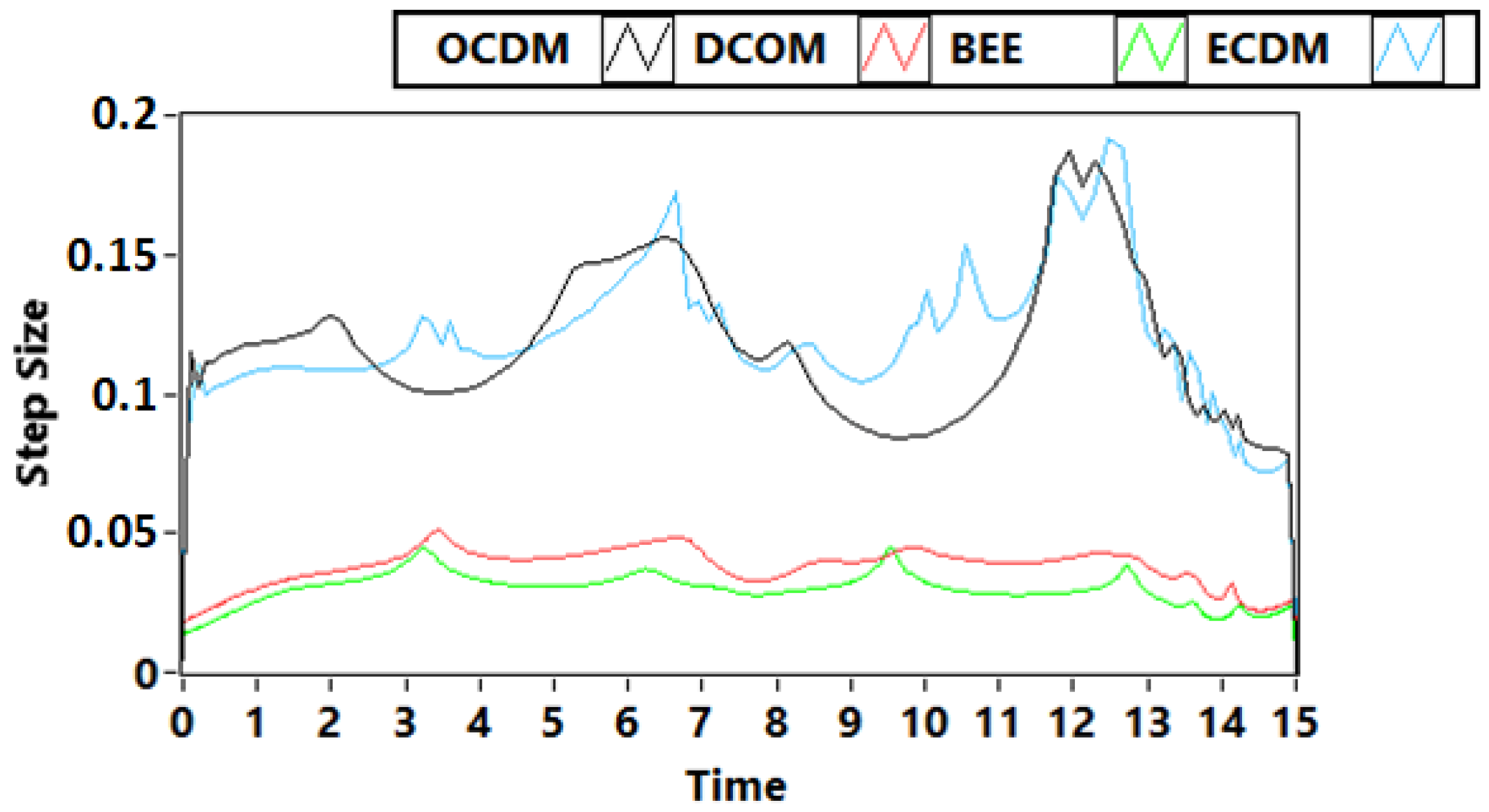
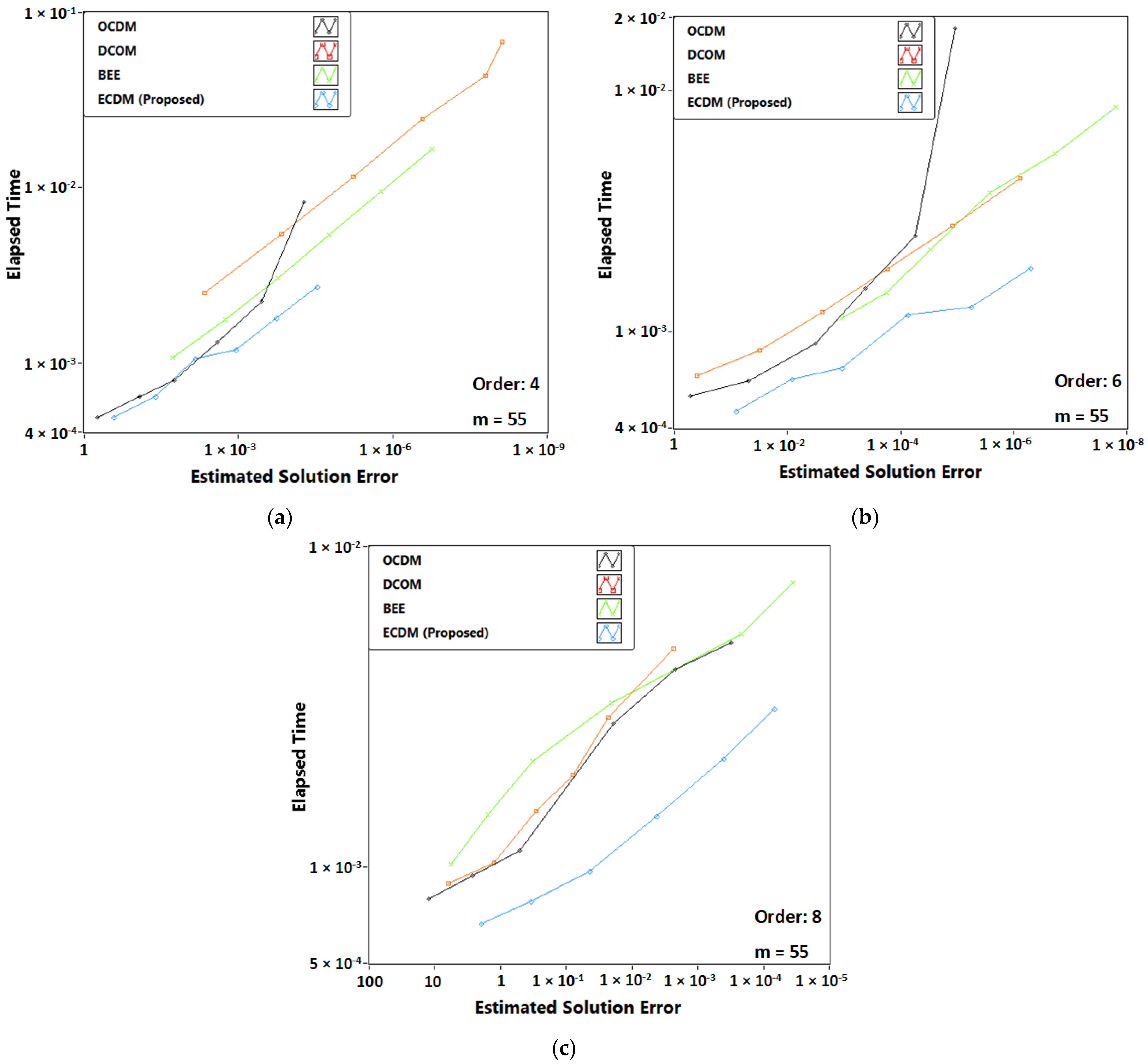
3.1. Problem 1: Rössler System
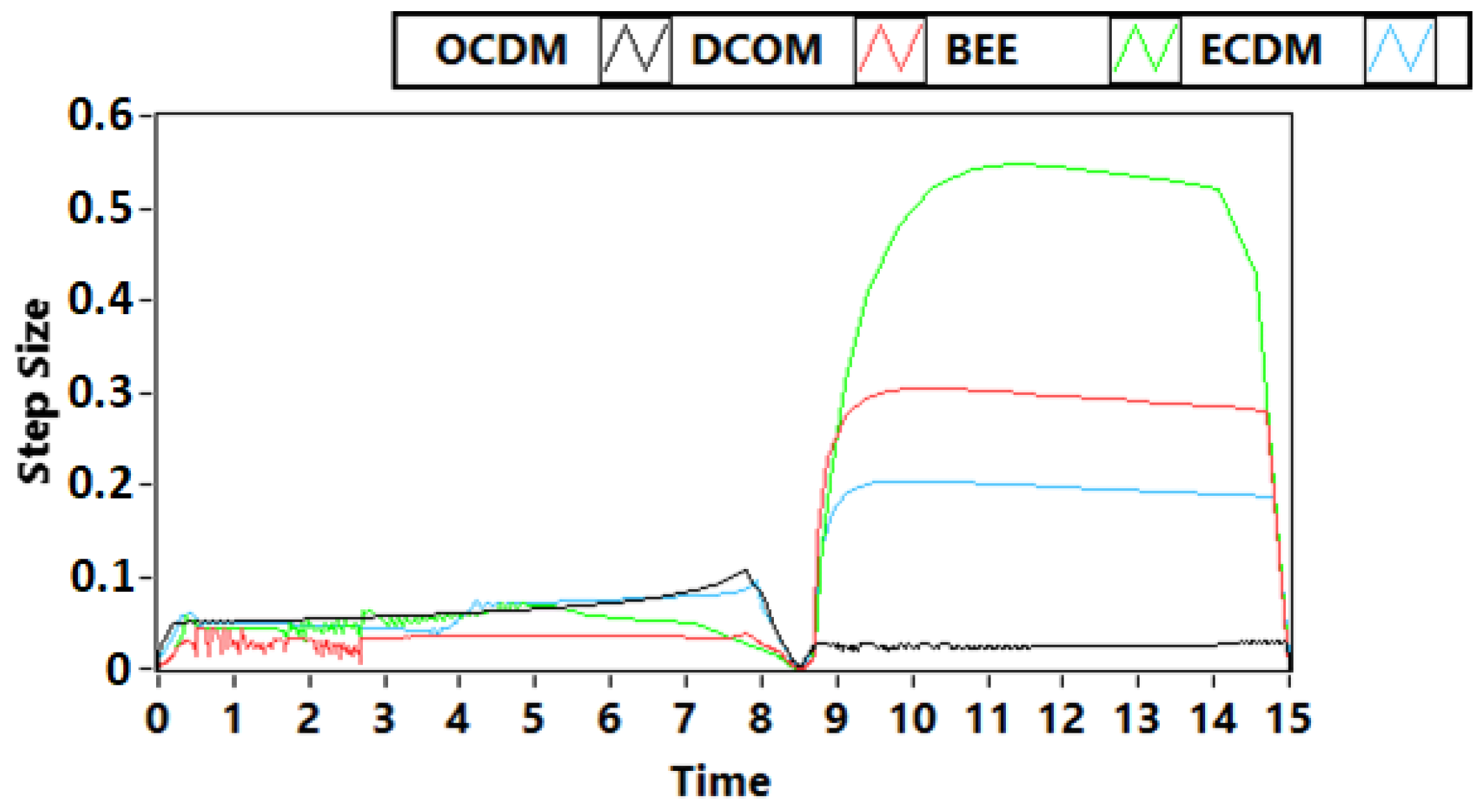
3.2. Problem 2: Van der Pol Oscillator
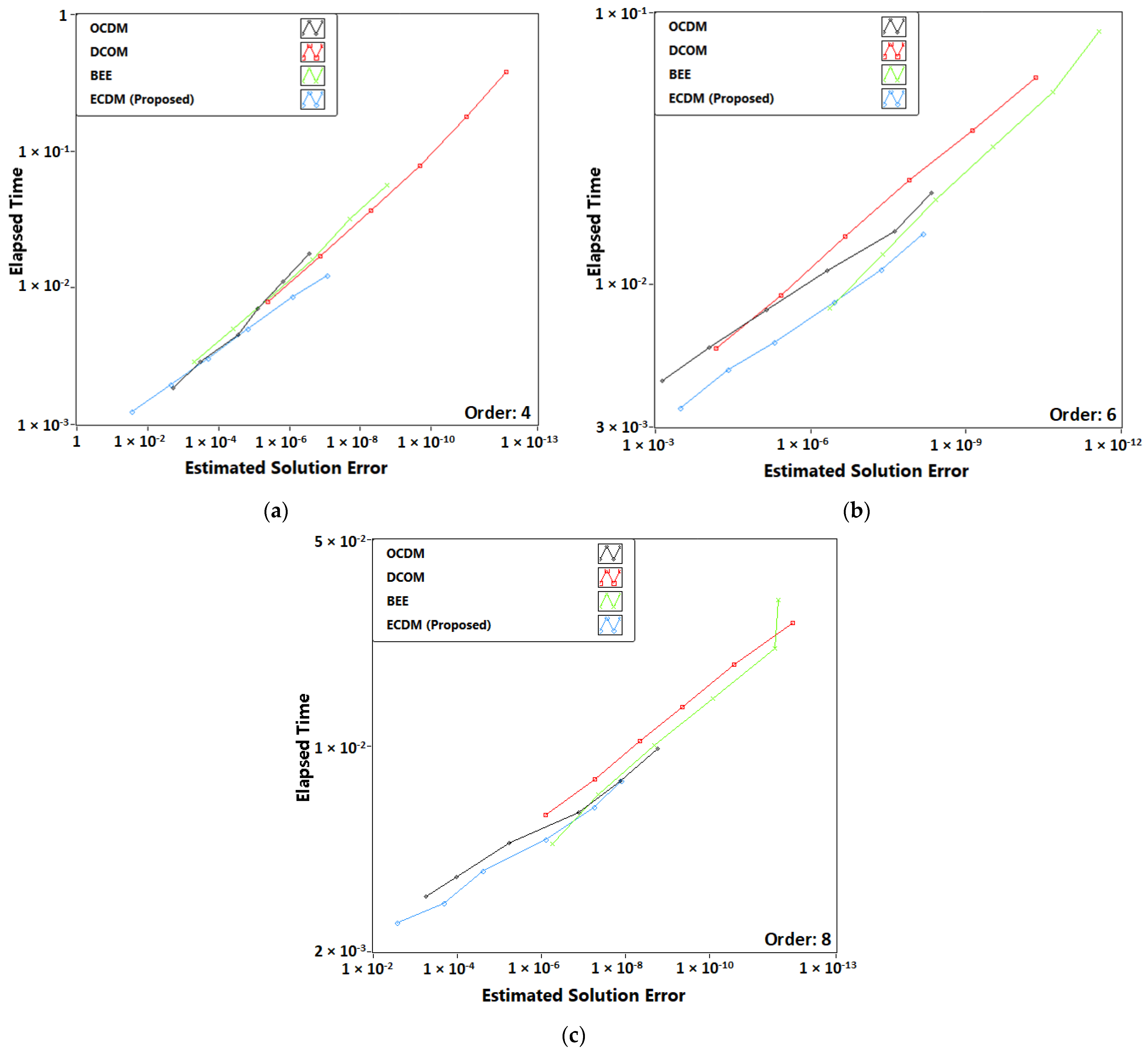
3.3. Problem 3: Two-Body Problem
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sofroniou, M.; Spaletta, G. Derivation of symmetric composition constants for symmetric integrators. Optim. Methods Softw. 2005, 20, 597–613. [Google Scholar] [CrossRef]
- Haier, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Leimkuhler, B.; Reich, S. Simulating Hamiltonian Dynamics (No. 14); Cambridge University Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Roulet, J.; Choi, S.; Vaníček, J. Efficient geometric integrators for nonadiabatic quantum dynamics. II. The diabatic representation. J. Chem. Phys. 2019, 150, 204113. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, H. Construction of higher order symplectic integrators. Phys. Lett. A 1990, 150, 262–268. [Google Scholar] [CrossRef]
- Suzuki, M. Fractal decomposition of exponential operators with applications to many-body theories and Monte Carlo simulations. Phys. Lett. A 1990, 146, 319–323. [Google Scholar] [CrossRef]
- Murua, A.; Sanz–Serna, J.M. Order conditions for numerical integrators obtained by composing simpler integrators. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1999, 357, 1079–1100. [Google Scholar] [CrossRef]
- Butusov, D.N.; Ostrovskii, V.Y.; Karimov, A.I.; Andreev, V.S. Semi-explicit composition methods in memcapacitor circuit simulation. IJERTCS 2019, 10, 37–52. [Google Scholar] [CrossRef]
- Blanes, S.; Casas, F.; Thalhammer, M. Splitting and composition methods with embedded error estimators. Appl. Numer. Math. 2019, 146, 400–415. [Google Scholar] [CrossRef] [Green Version]
- Kahan, W.; Li, R.C. Composition constants for raising the orders of unconventional schemes for ordinary differential equations. Math. Comput. 1997, 66, 1089–1099. [Google Scholar] [CrossRef] [Green Version]
- Hairer, E.; Wanner, G.; Nørsett, S.P. Solving Ordinary Differential Equations I. Nonstiff Problems; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Butusov, D. Adaptive Stepsize Control for Extrapolation Semi-Implicit Multistep ODE Solvers. Mathematics 2021, 9, 950. [Google Scholar] [CrossRef]
- Butusov, D.; Tutueva, A.; Fedoseev, P.; Terentev, A.; Karimov, A. Semi-implicit multistep extrapolation ODE solvers. Mathematics 2020, 8, 943. [Google Scholar] [CrossRef]
- Süli, E.; David, F.M. An Introduction to Numerical Analysis; Cambridge University Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Hairer, E.; Lubich, C. Extrapolation at stiff differential equations. Numer. Math. 1988, 52, 377–400. [Google Scholar] [CrossRef]
- Rössler, O. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Van der Pol, B. «On relaxation-oscillations», The London, Edinburgh and Dublin Phil. Mag. J. Sci. 1927, 2, 978–992. [Google Scholar] [CrossRef]
- Moo, K.W.; Senu, N.; Ismail, F.; Suleiman, M. New phase-fitted and amplification-fitted fourth-order and fifth-order Runge-Kutta-Nyström methods for oscillatory problems. Abstr. Appl. Anal. 2013, 2013, 939367. [Google Scholar] [CrossRef]

| s1ord2 | |
| 1 | |
| s5ord4 | |
| 0.414490771794375737142354063 | |
| −0.65796308717750294856941625 | |
| s7ord6 | |
| 0.78451361047755726382 | |
| 0.23557321335935813368 | |
| −1.1776799841788710069 | |
| 1.3151863206839112189 | |
| s17ord8 | |
| 0.13020248308889008088 | |
| 0.56116298177510838456 | |
| −0.38947496264484728641 | |
| 0.15884190655515560090 | |
| −0.39590389413323757734 | |
| 0.18453964097831570709 | |
| 0.25837438768632204729 | |
| 0.29501172360931029887 | |
| −0.60550853383003451170 | |
| Order | Initial Conditions | T | Step Size | Tolerance | ||
|---|---|---|---|---|---|---|
| Min | Start | Max | ||||
| 4 | (1.6; 0; −0.1) | 15 | 1 | |||
| 6 | (1.6; 0; −0.1) | 15 | 1 | |||
| 8 | (1.6; 0; −0.1) | 15 | 1 | |||
| Order | Tolerance | Total Number of Steps | |||
|---|---|---|---|---|---|
| OCDM | DCOM | BEE | ECDM | ||
| 4 | 86 | 662 | 186 | 71 | |
| 134 | 1423 | 328 | 100 | ||
| 210 | 3063 | 581 | 151 | ||
| 330 | 6598 | 1031 | 231 | ||
| 522 | 14,213 | 1831 | 359 | ||
| 6 | 146 | 191 | 307 | 138 | |
| 199 | 301 | 484 | 177 | ||
| 273 | 475 | 766 | 219 | ||
| 377 | 751 | 1212 | 296 | ||
| 524 | 1188 | 1920 | 405 | ||
| 8 | 61 | 118 | 116 | 55 | |
| 68 | 158 | 168 | 67 | ||
| 84 | 217 | 244 | 83 | ||
| 107 | 299 | 357 | 104 | ||
| 137 | 414 | 522 | 132 | ||
| Order | Initial Conditions | T | Step Size | Tolerance | ||
|---|---|---|---|---|---|---|
| Min | Start | Max | ||||
| 4 | (1.15; 0) | 15 | 1 | |||
| 6 | (1.15; 0) | 15 | 1 | |||
| 8 | (1.52; 0) | 15 | 1 | |||
| Order | Tolerance | Total Number of Steps | |||
|---|---|---|---|---|---|
| OCDM | DCOM | BEE | ECDM | ||
| 4 | 115 | 823 | 232 | 133 | |
| 162 | 1760 | 395 | 187 | ||
| 258 | 3790 | 687 | 376 | ||
| 442 | 8039 | 1206 | 445 | ||
| 777 | 14,159 | 2133 | 698 | ||
| 1748 | 22,080 | 3795 | 1009 | ||
| 6 | 95 | 119 | 177 | 106 | |
| 136 | 169 | 265 | 145 | ||
| 218 | 253 | 404 | 198 | ||
| 372 | 395 | 635 | 282 | ||
| 674 | 624 | 1005 | 414 | ||
| 2164 | 991 | 1595 | 621 | ||
| 8 | 56 | 90 | 80 | 65 | |
| 67 | 117 | 113 | 82 | ||
| 92 | 166 | 169 | 118 | ||
| 237 | 245 | 266 | 170 | ||
| 306 | 355 | 438 | 253 | ||
| 377 | 560 | 602 | 336 | ||
| Order | Initial Conditions | T | Step Size | Tolerance | ||
|---|---|---|---|---|---|---|
| Min | Start | Max | ||||
| 4 | (1; 0; 0; 1) | 50 | 1 × 10−4 | 5 × 10−3 | 1 | 1 × 10−4–1 × 10−9 |
| 6 | (1; 0; 0; 1) | 50 | 1 × 10−4 | 5 × 10−3 | 1 | 1 × 10−6–1 × 10−11 |
| 8 | (1; 0; 0; 1) | 50 | 1 × 10−4 | 5 × 10−3 | 1 | 1 × 10−5–1 × 10−10 |
| Order | Tolerance | Total Number of Steps | |||
|---|---|---|---|---|---|
| OCDM | DCOM | BEE | ECDM | ||
| 4 | 177 | 986 | 335 | 156 | |
| 279 | 2121 | 593 | 246 | ||
| 441 | 4567 | 1053 | 389 | ||
| 697 | 9837 | 1871 | 615 | ||
| 1102 | 21,192 | 3324 | 972 | ||
| 1744 | 45,655 | 5910 | 1539 | ||
| 6 | 309 | 442 | 745 | 289 | |
| 427 | 699 | 1179 | 401 | ||
| 593 | 1106 | 1868 | 547 | ||
| 823 | 1751 | 2959 | 759 | ||
| 1143 | 2774 | 4689 | 1048 | ||
| 1587 | 4395 | 7430 | 1452 | ||
| 8 | 88 | 234 | 197 | 83 | |
| 113 | 322 | 288 | 106 | ||
| 146 | 444 | 421 | 136 | ||
| 187 | 611 | 616 | 175 | ||
| 241 | 849 | 904 | 226 | ||
| 310 | 1179 | 1325 | 290 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fedoseev, P.; Pesterev, D.; Karimov, A.; Butusov, D. New Step Size Control Algorithm for Semi-Implicit Composition ODE Solvers. Algorithms 2022, 15, 275. https://doi.org/10.3390/a15080275
Fedoseev P, Pesterev D, Karimov A, Butusov D. New Step Size Control Algorithm for Semi-Implicit Composition ODE Solvers. Algorithms. 2022; 15(8):275. https://doi.org/10.3390/a15080275
Chicago/Turabian StyleFedoseev, Petr, Dmitriy Pesterev, Artur Karimov, and Denis Butusov. 2022. "New Step Size Control Algorithm for Semi-Implicit Composition ODE Solvers" Algorithms 15, no. 8: 275. https://doi.org/10.3390/a15080275
APA StyleFedoseev, P., Pesterev, D., Karimov, A., & Butusov, D. (2022). New Step Size Control Algorithm for Semi-Implicit Composition ODE Solvers. Algorithms, 15(8), 275. https://doi.org/10.3390/a15080275







