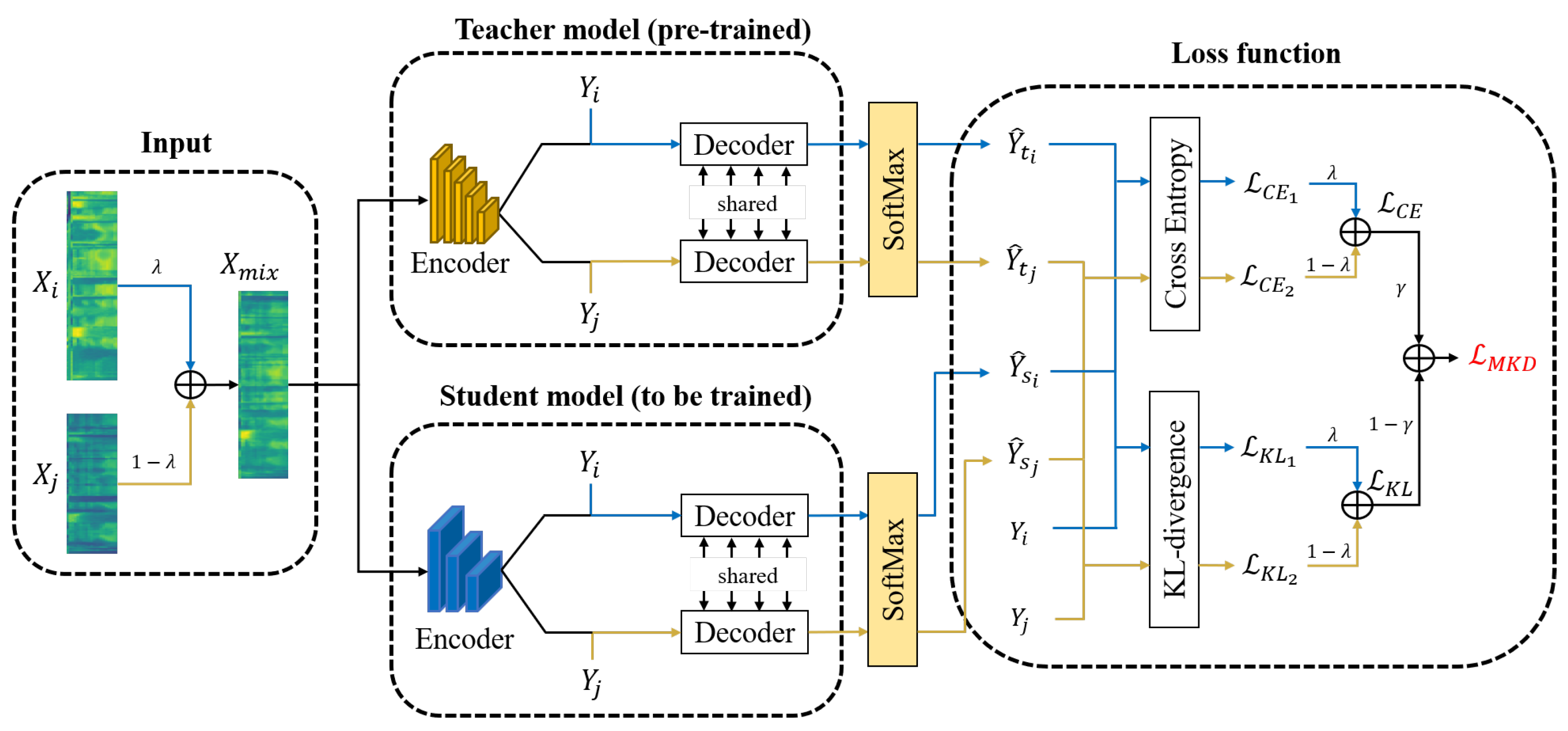
This section introduces the Mixup-based knowledge distillation, with Speech-Transform -er as the baseline. Firstly, the Transformer-based ASR model is introduced. Then, the detail of how to integrate Mixup into ASR model is explained. Finally the Mixup-based knowledge distillation method is proposed.
3.1. Speech-Transformer
In this work, Speech-Transformer is chosen as the baseline for
and
. Speech-Transformer is a Transformer-based neural network for speech recognition which consists of encoder
E and decoder
D. The spectrogram
X serves as the input of
E. Each
X is a two-dimensional matrix whose size is
, where
F is the number of frequency and
T denotes the number of frame.
E encodes the spectrogram by self-attention mechanism. The result of
E is a two-dimensional embedding
.
D decodes the embedding sequence
e based on the corresponding label sequence
Y. Finally, the decoder output goes through a Softmax classifier to generate the probability distribution of each character. The whole process can be summarized as:
where
represent the hidden layers in encoder
E.
are the hidden layers of decoder
D.
y denotes the one-hot encoding of a character in the whole sequence
Y. Finally, each
y is grouped as the output sequence
.
3.2. Mixup in Speech-Transformer
A robust end-to-end speech recognition model is insensitive to noise. Transformer has become the most popular baseline model for sequence-to-sequence problems due to its ability of modeling long-term dependency, but the complexity of Transformer-based model is extremely high. The dependence on data volume of Transformer is much higher than that of recurrent neural network. Thus, overfitting becomes a severe problem for Transformer-based methods in a limited-data setting. Data augmentation is an efficient tool to improve the robustness of neural networks, especially for low-resource speech recognition.
Mixup is a prevailing data augmentation method for supervised learning tasks. It trains a model on a linear combination of pairs of inputs and their targets to make the model more robust to adversarial samples. In this setting, the model can achieve more accurate rate under mixed noise. Mixup is computed as follows:
where
,
are the input vectors, and
,
are the corresponding targets.
and
are randomly sampled from dataset
.
is sampled by a
distribution
with
. The generated pair
is added into training dataset
D.
For classification problems, Mixup can effectively improve the robustness of the model by smoothing loss landscapes. However, Mixup cannot be directly applied in speech recognition because the length of audio differs from each other which makes it difficult to calculate by Equation (
2). Another reason is that the target sequence of each audio is discrete, and the linear combination of discrete data is meaningless. These two issues need to be addressed for most sequence-to-sequence problems.
In order to apply Mixup to speech recognition, Mixup is modified at the input level and the loss level, respectively. For input, two raw audios are mixed at the frame level. Before mixture, the shorter input will be padded to the same length as the longer one. Thus, the length of augmented sample equals .
A loss level mixture is adopted by mixing two loss function regarding the output. In general, the CTC loss function and the Cross-Entropy (CE) loss function are commonly used in end-to-end speech recognition. CE is adopted in Transformer-based model. For Speech-Transformer, the output of Transformer decoder is sent to a softmax classifier. The result of softmax layer becomes one of the input of CE loss. CE loss is calculated by Equation (
3).
where
denotes the output of ASR model for each character, and
N is the length of
Y.
The frame sequence and target are aligned by attention mechanism in Speech-Tran- sformer which makes the output of softmax layer synchronized with label sequence.
After integrating Mixup into
CE, the mixture of the
CE loss becomes:
where
is the same weight as in the input.
Theorem 1. For cross-entropy loss function, the mixture of the labels equals to the mixture of the CE loss.
The mixed CE loss, respectively calculates the CE loss and with label sequence and . Then, and are linearly combined with . This method is equivalent to interpolating the labels and directly.
3.3. MKD: Mixup-Based Knowledge Distillation
Knowledge distillation is commonly adopted in model compression for speech recognition. Knowledge distillation utilizes a teacher–student network structure that exploits soft labels from the teacher model to guide student network learning. However, this framework is subject to the amount of available data. In particular, tasks with fewer samples provide less opportunity for the student model to learn from the teacher. Even with a well-designed loss function, the student model is still prone to overfitting and effectively mimicking the teacher network on the available data. Existing data augmentation have been explored to combine with teacher–student network, improving the efficiency of knowledge distillation. Unlike other methods of data augmentation, Mixup is a data-agnostic approach which means no prior knowledge is required for augmentation. This brings an convenience for low-resource speech recognition to generate task-specific data.
Labels generated by Mixup are smoother than original one-hot labels. However, these soft labels don’t include mutual information between each category. On the other hand, soft labels generated from teacher network could reflect the relationship between similar labels, which have more mutual information than one-hot encoding. The two arguments above inspired us to integrate Mixup into teacher–student framework to improve the data efficiency of knowledge distillation.
In our teacher–student framework, the architecture of student model is the same as teacher model . There is only a difference in parameter scale between teacher model and student model in homogeneous neural networks. First, the input goes through the teacher model . The teacher model is trained by original CE loss.
The output of Softmax layer in
serves as the soft label of each frame. The student model is encouraged to imitate the prediction from teacher network by minimizing the
KL distance:
Considering that the original cross-entropy is helpful for training the student network. The student network is trained with
CE loss in usual way as well. The final loss
of student model is the linear combinations of
CE loss and
KL loss:
For softmax-level knowledge distillation, the distillation loss is calculated for k-th frame, and is composed of the accumulation of each frame loss.
When optimizing the teacher–student framework by Mixup, the label sequences
,
are served as one of the input to the Decoder of the teacher model to obtain their soft labels
,
, respectively. As shown in
Figure 1, when training the student network, the output of student network
,
are used to calculate the
and
. Equation (
4) is applied to generate
for each frame. However, the mixture of
is different from that of
because the KL-divergence
is not linear for the label
Y. To solve this problem, a novel loss function
is proposed to approximate
.
It could be proved that
is an upper bound on the
using the properties of convex functions. The proof of Equation (
7) is given below.
Theorem 2. The upper bound on the KL-divergence of is equivalent to the mixture of the KL-divergence.
After obtaining
and
, a factor
is applied to balance two loss functions. The final loss
is the combination of
KL-divergence and
CE loss: