A Preliminary Study on the Resolution of Electro-Thermal Multi-Physics Coupling Problem Using Physics-Informed Neural Network (PINN)
Abstract
:1. Introduction
2. Materials and Methods
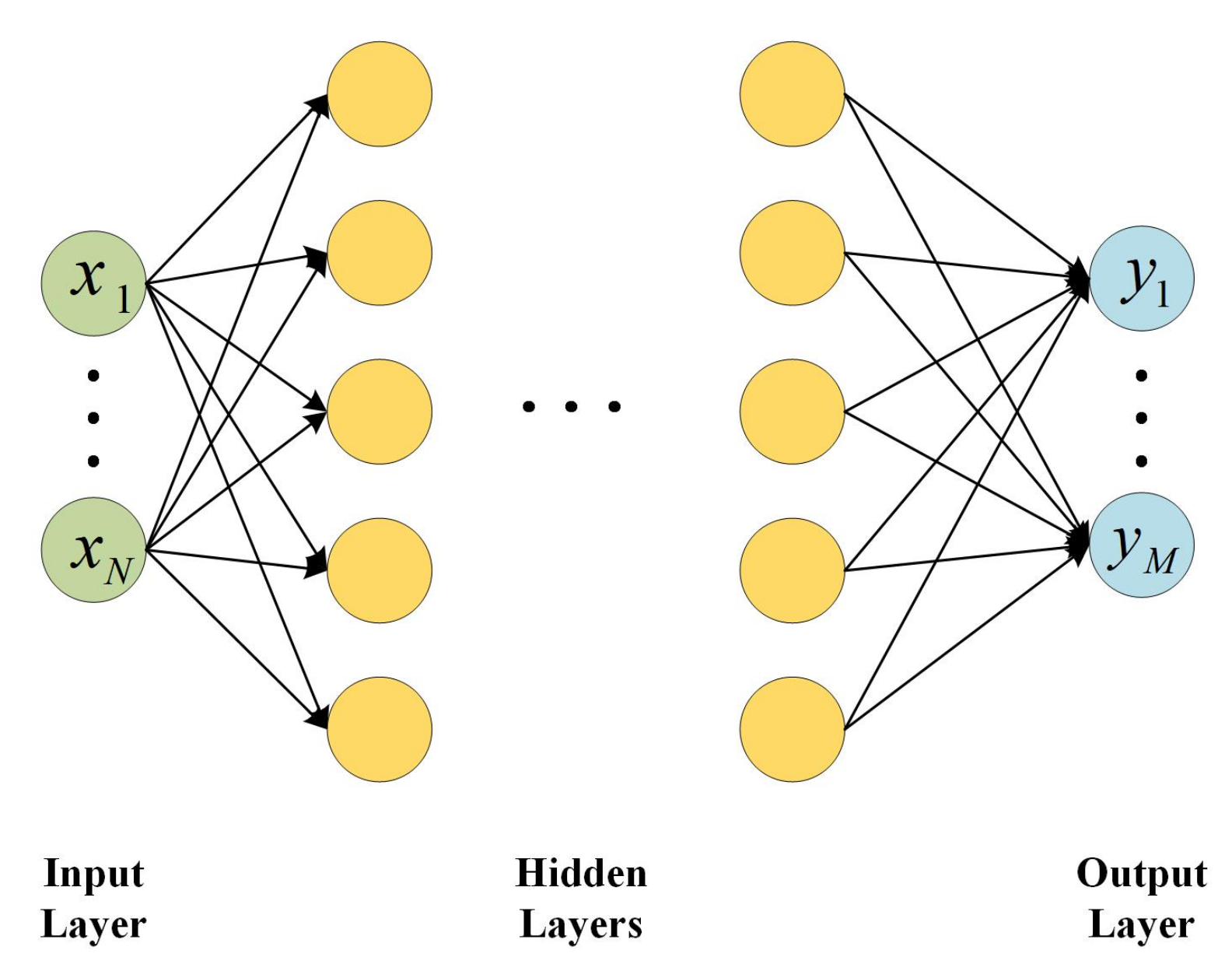
2.1. DNN
2.2. PINN
2.3. PINNs for the Electro-Thermal Coupling Problem
3. Experiments and Results
3.1. Electro-Thermal Coupling Problem
A Rectangle Electro-Thermal Coupling Problem
3.2. The Comparison between FEM and PINN
3.3. Empirical Properties of the PINN
3.3.1. The Effect of Depth and Width of the Network on the Training Time
3.3.2. Effect of Number of Samples on the Prediction Error and Training Time
4. Discussions
- PINN embeds physical constraints into the loss function of the neural network by using automatic differentiation. The imposition of the “hard” boundary makes the approximate solution automatically meet the Dirichlet boundary, which accelerates the convergence speed and improves the prediction accuracy [1].
- In addition to the advantage of being mesh-free, PINN can also generalize the construction process of various PDEs. On top of that, classical methods, such as FEM, can only obtain the solution on discrete points, while further interpolation is required for other points. This property makes the solution of the state variables at the interpolated points less accurate. For PINN, when considering the points that do not appear in the training set, there is no need to conduct an interpolation scheme to obtain the solutions.
- With the help of automatic differentiation, the derivative of each state variable can be easily calculated. Hence, the derivative distribution is smooth. However, for the first-order FEM, the first derivative of the state variable inside of an element is constant, which makes the derivative distribution discontinuous.
- Based on the experimental results, the convergence speed of PINN gradually increases as the size of the neural network goes up at the beginning. However, when it reaches a certain point, the improvement in computation time stagnates or even becomes worse. In addition, when studying the number of training samples influence on the convergence speed, except the case where the sampling points are too few, the convergence speed increases as the number of training samples increases; however, when it reaches a certain number, the improvement in convergence speed stagnates or even becomes worse.
- According to our experiments, although the PINN offers unique advantages for solving PDEs, its computational efficiency is an obvious disadvantage compared to FEM. Therefore, figuring out how to accelerate the training of PINN is an important research topic. Ref. [40] introduced an efficient approach based on adaptive sampling strategy, which speeds up the computation of the PINN. In [19], parallel calculation of the PINN was successfully implemented, which can easily handle any complex regional problems, but the improvement in computing time is still on the way. Huang et al. [41] realized speeding up convergence for high-frequency wavefields solutions by using the information from a pre-trained model instead of initializing the PINN randomly.
- PINN can be conveniently utilized to generate a surrogate model in the parametric analysis. In [42], the authors conducted a sensitivity analysis experiment. They first trained the PINN with merely a few values of a specific parameter and then utilized the trained neural network to predict the solution to this parameter within a range. The result is less accurate but still useful for the specific condition, which shows the possibility of PINN in tackling this kind of issue; we will work on this subject in our future study.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schiassi, E.; Furfaro, R.; Leake, C.; Florio, M.; Mortari, D. Extreme Theory of Functional Connections: A Fast Physics-Informed Neural Network Method for Solving Ordinary and Partial Differential Equations. Neurocomputing 2021, 457, 334–356. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, L.; Zhou, L.; Zhang, J. HEp-2 Cell Image Classification with Deep Convolutional Neural Networks. IEEE J. Biomed. Health Inform. 2016, 21, 416–428. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, Y.; Schuster, M.; Chen, Z.; Le, Q.; Norouzi, M.; Macherey, W.; Krikun, M.; Cao, Y.; Gao, Q.; Macherey, K.; et al. Google’s Neural Machine Translation System: Bridging the Gap between Human and Machine Translation. arXiv 2016, arXiv:1609.08144. [Google Scholar]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Kingsbury, B. Deep Neural Networks for Acoustic Modeling in Speech Recognition: The Shared Views of Four Research Groups. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Oishi, A.; Yagawa, G. Computational mechanics enhanced by deep learning. Comput. Methods Appl. Mech. Eng. 2017, 327, 327–351. [Google Scholar] [CrossRef]
- Gong, R.; Tang, Z. Investigation of convolutional neural network U-net under small datasets in transformer magneto-thermal coupled analysis. COMPEL Int. J. Comput. Math. Electr. 2020, in press. [Google Scholar] [CrossRef]
- Lee, H.; Kang, I.S. Neural algorithm for solving differential equations. J. Comput. Phys. 1990, 91, 110–131. [Google Scholar] [CrossRef]
- Lagaris, I.E.; Likas, A. Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Networks 1998, 9, 987–1000. [Google Scholar] [CrossRef] [Green Version]
- Psichogios, D.C.; Ungar, L.H. A hybrid neural network-first principles approach to process modeling. AIChE J. 1992, 38, 1499–1511. [Google Scholar] [CrossRef]
- Sirignano, J.; Spiliopoulos, K. DGM: A deep learning algorithm for solving partial differential equations. J. Comput. Phys. 2017, 375, 1330–1364. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Zhang, Z. A mesh-free method for interface problems using the deep learning approach. JCoPh 2020, 400, 108963. [Google Scholar] [CrossRef]
- He, C.; Hu, X.; Mu, L. A Mesh-free Method Using Piecewise Deep Neural Network for Elliptic Interface Problems. arXiv 2020, arXiv:2005.04847. [Google Scholar]
- Berg, J.; Nyström, K. A unified deep artificial neural network approach to partial differential equations in complex geometries. Neurocomputing 2017, 317, 28–41. [Google Scholar] [CrossRef] [Green Version]
- Ovcharenko, O.; Kazei, V.; Mahesh, K.; Peter, D.; Alkhalifah, T. Deep learning for low-frequency extrapolation from multi-offset seismic data. Geophysics 2019, 84, 1–64. [Google Scholar] [CrossRef] [Green Version]
- Sun, B.; Alkhalifah, T. ML-descent: An optimization algorithm for FWI using machine learning. In Proceedings of the SEG 89th Annual Meeting, San Antonio, TX, USA, 15–20 September 2020. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-Informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations. J. Comput. Phys. 2018, 378, 686–707. [Google Scholar] [CrossRef]
- Song, C.; Alkhalifah, T.; Bin Waheed, U. Solving the frequency-domain acoustic VTI wave equation using physics-informed neural networks. Geophys. J. Int. 2021, 225, 846–859. [Google Scholar] [CrossRef]
- Meng, X.; Li, Z.; Zhang, D.; Karniadakis, G.E. PPINN: Parareal physics-informed neural network for time-dependent PDEs. Comput. Methods Appl. Mech. Eng. 2020, 370, 113250. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Karniadakis, G.E. Extended Physics-Informed Neural Networks (XPINNs): A Generalized Space-Time Domain Decomposition Based Deep Learning Framework for Nonlinear Partial Differential Equations. Commun. Comput. Phys. 2020, 28, 2002–2041. [Google Scholar]
- Jagtap, A.D.; Kharazmi, E.; Karniadakis, G.E. Conservative physics-informed neural networks on discrete domains for conservation laws: Applications to forward and inverse problems. Comput. Methods Appl. Mech. Eng. 2020, 365, 113028. [Google Scholar] [CrossRef]
- Song, C.; Alkhalifah, T.; Waheed, U.B. A versatile framework to solve the Helmholtz equation using physics-informed neural networks. Geophys. J. Int. 2021, 228, 1750–1762. [Google Scholar] [CrossRef]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A deep learning library for solving differential equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Fang, Z.; Zhang, J.; Yang, X. A Physics-Informed Neural Network Framework For Partial Differential Equations on 3D Surfaces: Time-Dependent Problems. arXiv 2021, arXiv:2103.13878. [Google Scholar]
- Hu, X.; Buris, N.E. A Deep Learning Framework for Solving Rectangular Waveguide Problems. In Proceedings of the 2020 IEEE Asia-Pacific Microwave Conference (APMC), Hong Kong, 8–11 December 2020; pp. 409–411. [Google Scholar]
- Alkhalifah, T.; Song, C.; Bin Waheed, U.; Hao, Q. Wavefield solutions from machine learned functions constrained by the Helmholtz equation. Artif. Intell. Geosci. 2021, 2, 11–19. [Google Scholar] [CrossRef]
- Waheed, U.B.; Haghighat, E.; Alkhalifah, T.; Song, C.; Hao, Q. PINNeik: Eikonal solution using physics-informed neural networks. Comput. & Geosci. 2021, 155, 104833. [Google Scholar]
- Guo, Y.; Cao, X.; Liu, B.; Gao, M. Solving Partial Differential Equations Using Deep Learning and Physical Constraints. Appl. Sci. 2020, 10, 5917. [Google Scholar] [CrossRef]
- Yang, Y.; Perdikaris, P. Adversarial uncertainty quantification in physics-informed neural networks. J. Comput. Phys. 2019, 394, 136–152. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Lu, L.; Guo, L.; Karniadakis, G.E. Quantifying total uncertainty in physics-informed neural networks for solving forward and inverse stochastic problems. J. Comput. Phys. 2019, 397, 108850. [Google Scholar] [CrossRef] [Green Version]
- Pun, G.; Batra, R.; Ramprasad, R.; Mishin, Y. Physically informed artificial neural networks for atomistic modeling of materials. Nat. Commun. 2019, 10, 2339. [Google Scholar] [CrossRef]
- Niaki, S.A.; Haghighat, E.; Campbell, T.; Poursartip, A.; Vaziri, R. Physics-informed neural network for modelling the thermochemical curing process of composite-tool systems during manufacture. Comput. Methods Appl. Mech. Eng. 2021, 384, 113959. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Networks 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Marrero, C.O.; Perdikaris, P.; Tartakovsky, G.D.; Barajas-Solano, D. Physics-Informed Deep Neural Networks for Learning Parameters and Constitutive Relationships in Subsurface Flow Problems. Water Resour. Res. 2020, 56, e2019WR026731. [Google Scholar] [CrossRef]
- Rao, C.; Sun, H.; Liu, Y. Physics-Informed Deep Learning for Computational Elastodynamics without Labeled Data. J. Eng. Mech. 2021, 147, 04021043. [Google Scholar] [CrossRef]
- Leake, C.; Mortari, D. Deep Theory of Functional Connections: A New Method for Estimating the Solutions of Partial Differential Equations. Mach. Learn. Knowl. Extr. 2020, 2, 37–55. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baydin, A.; Pearlmutter, B.; Radul, A.; Siskind, J. Automatic differentiation in machine learning: A survey. J. Mach. Learn. Res. 2018, 18, 1–43. [Google Scholar]
- Mckay, M.; Conover, R.J.B.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. Comput. Sci. 2014. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. J. Mach. Learn. Res. 2010, 9, 249–256. [Google Scholar]
- Nabian, M.A.; Gladstone, R.J.; Meidani, H. Efficient training of physics-informed neural networks via importance sampling. Comput. Civ. Infrastruct. Eng. 2021, 36, 962–977. [Google Scholar] [CrossRef]
- Huang, X.; Alkhalifah, T. PINNup: Robust neural network wavefield solutions using frequency upscaling and neuron splitting. arXiv 2021, arXiv:2109.14536. [Google Scholar]
- Haghighat, E.; Raissi, M.; Moure, A.; Gomez, H.; Juanes, R. A deep learning framework for solution and discovery in solid mechanics: Linear elasticity. arXiv 2020, arXiv:2003.02751. [Google Scholar]








| Property | Steady Electric Field | Thermal Field |
|---|---|---|
| Lowest Loss | 9.97 × | 9.84 × |
| Time(s) | 101 | 109 |
| Depth | 1 | 2 | 4 | 6 | |
|---|---|---|---|---|---|
| Width | |||||
| 5 | 20,000 | 8539 | 5126 | 5193 | |
| 10 | 13,120 | 4832 | 2634 | 3046 | |
| 20 | 8791 | 2239 | 1430 | 1591 | |
| 30 | 7493 | 1993 | 1146 | 1584 | |
| 60 | 5958 | 1161 | 1343 | 2936 | |
| Depth | 1 | 2 | 4 | 6 | |
|---|---|---|---|---|---|
| Width | |||||
| 5 | 1129 | 547 | 410 | 497 | |
| 10 | 739 | 311 | 211 | 293 | |
| 20 | 495 | 144 | 115 | 153 | |
| 30 | 422 | 128 | 92 | 152 | |
| 60 | 335 | 75 | 108 | 286 | |
| Number | 10 | 100 | 500 | 1000 | 5000 | 10,000 | |
|---|---|---|---|---|---|---|---|
| Property | |||||||
| Time (s) | 35 | 97 | 91 | 74 | 97 | 101 | |
| RMSE | 1.59 | 5.60 | 1.09 | 5.14 × | 7.07 × | 5.48 × | |
| Epoch | 551 | 1508 | 1123 | 1066 | 1480 | 1539 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Xu, X.; Yan, S.; Ren, Z. A Preliminary Study on the Resolution of Electro-Thermal Multi-Physics Coupling Problem Using Physics-Informed Neural Network (PINN). Algorithms 2022, 15, 53. https://doi.org/10.3390/a15020053
Ma Y, Xu X, Yan S, Ren Z. A Preliminary Study on the Resolution of Electro-Thermal Multi-Physics Coupling Problem Using Physics-Informed Neural Network (PINN). Algorithms. 2022; 15(2):53. https://doi.org/10.3390/a15020053
Chicago/Turabian StyleMa, Yaoyao, Xiaoyu Xu, Shuai Yan, and Zhuoxiang Ren. 2022. "A Preliminary Study on the Resolution of Electro-Thermal Multi-Physics Coupling Problem Using Physics-Informed Neural Network (PINN)" Algorithms 15, no. 2: 53. https://doi.org/10.3390/a15020053
APA StyleMa, Y., Xu, X., Yan, S., & Ren, Z. (2022). A Preliminary Study on the Resolution of Electro-Thermal Multi-Physics Coupling Problem Using Physics-Informed Neural Network (PINN). Algorithms, 15(2), 53. https://doi.org/10.3390/a15020053







