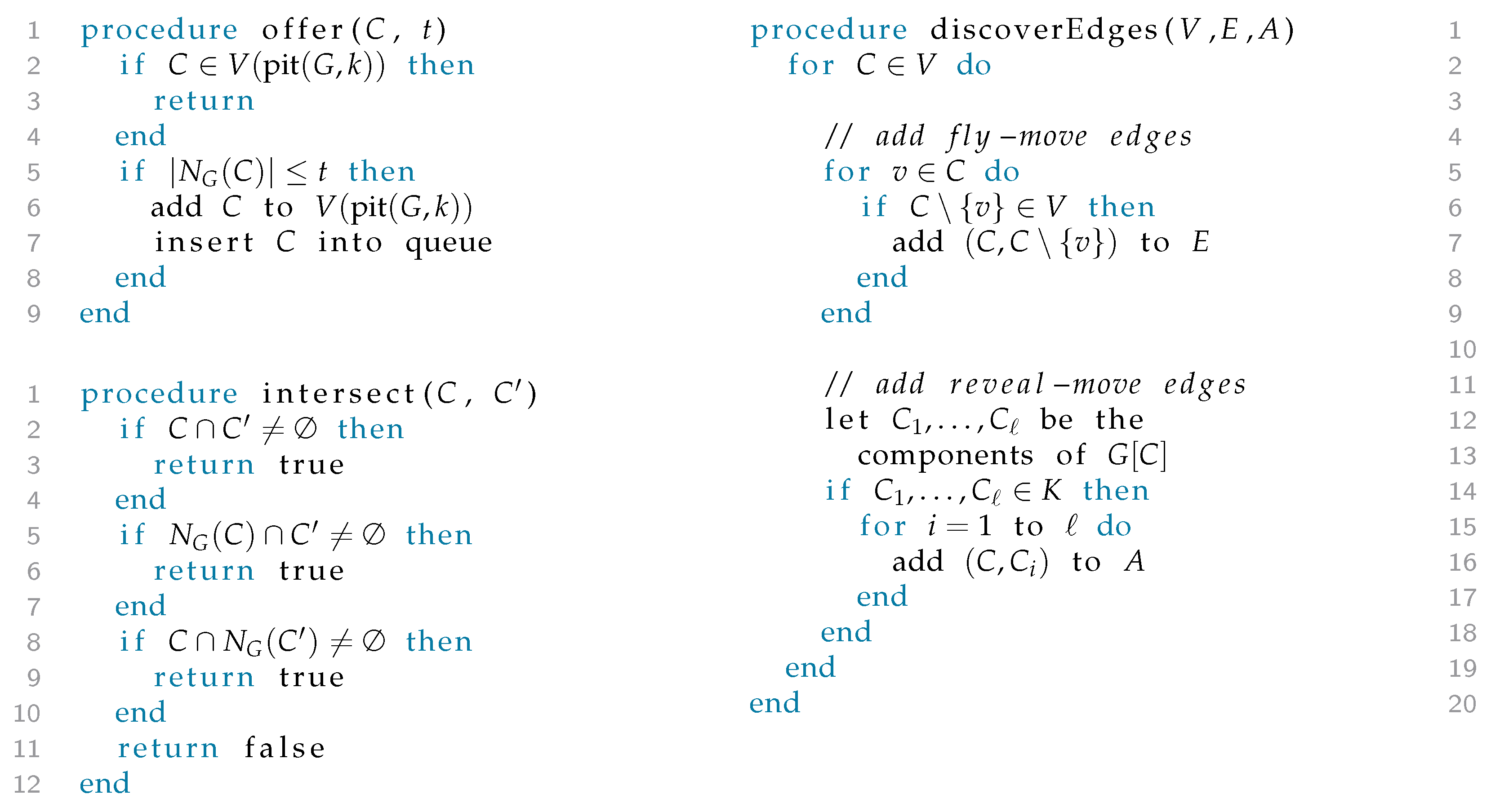Recent Advances in Positive-Instance Driven Graph Searching ^†

Abstract

Research on the similarity of a graph to being a tree—called the treewidth of the graph—has seen an enormous rise within the last decade, but a practically fast algorithm for this task has been discovered only recently by Tamaki (ESA 2017). It is based on dynamic programming and makes use of the fact that the number of positive subinstances is typically substantially smaller than the number of all subinstances. Algorithms producing only such subinstances are called positive-instance driven (PID). The parameter treedepth has a similar story. It was popularized through the graph sparsity project and is theoretically well understood—but the first practical algorithm was discovered only recently by Trimble (IPEC 2020) and is based on the same paradigm. We give an alternative and unifying view on such algorithms from the perspective of the corresponding configuration graphs in certain two-player games. This results in a single algorithm that can compute a wide range of important graph parameters such as treewidth, pathwidth, and treedepth. We complement this algorithm with a novel randomized data structure that accelerates the enumeration of subproblems in positive-instance driven algorithms.

1. Introduction

Graph decompositions are an important tool in modern algorithmic graph theory that provide a structured representation of a graph. A graph decomposition comes along with a width measure that indicates how well a graph can be decomposed. Many problems that presumably cannot be solved in polynomial time on general graphs can be solved efficiently on graphs that admit a certain decomposition of small width [1].

The most prominent example of a width measure is treewidth, which (on an intuitive level) measures the similarity of a graph to a tree. This parameter is a cornerstone of parameterized algorithms [2] and its success has led to its integration into many different fields. For instance, treewidth has been studied in the context of machine learning [3,4,5], model-checking [6,7], SAT-solving [8,9,10], QBF-solving [11,12], CSP-solving [13,14], or ILPs [15,16,17,18,19]. Tools such as Jdrasil [20] that compute tree decompositions of minimum width or that try to find good heuristic solutions are actively used, for instance, in the analysis of large SPARQL query logs [21] or in propositional model counting [22,23,24]. A large-scale experimental study that classifies real-world data sets according to their treewidth was recently performed by Maniu, Senellart, and Jog [25].

However, treewidth is often too general and we require more restrictive width measures in order to obtain an algorithmic advantage [26,27]. Close relatives of treewidth are the width measures pathwidth and treedepth, which (again on an intuitive level) measure the similarity of the graph to a path or a star, respectively. These graph parameters can be naturally ordered in the sense that some of them are more restrictive than others, that is, a graph of bounded treedepth has bounded pathwidth as well, and a graph of bounded pathwidth has also bounded treewidth. Tools that compute treedepth decompositions of small width can be used to efficiently solve the mixed Chinese postman problem [26] or to design algorithms for mixed integer linear programs [28]. Pathwidth was recently used as structural parameter to prove that the well-known vertex cover problem can be solved in polynomial time with high probability on hyperbolic random graphs (which are frequently used to model real-world networks) [29].

No matter which of these width measures we wish to utilize for a task at hand, we have to be able to compute it quickly. More crucially, most algorithms also need a witness in the form of a decomposition. A lot of theoretical research has been performed in this direction [30,31] and width measures such as treewidth can even be computed in linear fpt-time by Bodlaender’s famous algorithm [32]. Unfortunately, it is known that this algorithm does not work in practice due to huge constants [33] (the same holds for similar algorithms for the other width measures). When it comes to implementations, small progress has been made with classical exact exponential time algorithms, which are only able to solve graphs with about 50–100 vertices. See, for instance, the QuickBB algorithm for treewidth [34], the algorithm by Coudert, Mazauric, and Nisse for pathwidth [35], or a recent branch-and-bound algorithm for treedepth [36]. More progress was made with heuristics, see, for instance, [37,38,39] for treewidth, the algorithm by Kobayashi et al. for pathwidth [40], and Section 24 in [41] for treedepth. We may argue that, indeed, a heuristic is sufficient, as the attached solver will work correctly independently of the width of the provided decomposition—and the heuristic may produce a decomposition of “small enough” width. However, even a small error, something as “off by 5”, may put the parameter to a computationally intractable range, as the dependency on the width is usually at least exponential. For instance, it was observed that small changes (even by just one or two) in the width of a tree decomposition can have a huge impact on the inference time in probabilistic networks [42]. A similar effect was observed in recent advances of implementing a lightweight model checker for a fragment of MSO [7], where it turned out to be beneficial to invest additional time in order to obtain an optimal tree decomposition rather than relying on faster heuristics. It is therefore a natural and important task to build practical fast algorithms to determine parameters such as the treewidth, pathwidth, or treedepth of a graph exactly.

To tackle this issue, the fpt-community came up with a contest, the Parameterized Algorithms and Computational Experiments (PACE) challenge [43,44,45], with the goal of finding new exact algorithms to determine the exact treewidth or treedepth of a graph. Besides many, one important result of the challenge was a new combinatorial algorithm due to Tamaki, which computes the treewidth of an input graph exactly and astonishingly fast on a wide range of instances. An implementation of this algorithm by Tamaki himself [46] won the corresponding track in the PACE challenge in 2016 [43] and an alternative implementation due to Larisch and Salfelder [47] won in 2017 [44]. In 2020, many participants adapted the original algorithm to treedepth [45,48,49].

Tamaki’s original algorithm is based on a dynamic program by Arnborg, Corneil, and Proskurowski [50] for computing tree decompositions. This algorithm has a game theoretic characterization that can be used to generalize the algorithm to other width measures such as treedepth. Tamaki has improved his algorithm for the second iteration of the PACE by applying his framework to the algorithm by Bouchitté and Todinca [51,52], see, for instance, [53] for a recent evaluation of this version of the algorithm. While Bouchitté and Todinca’s algorithm has a game theoretic characterization as well [54], it is still unclear how it can be generalized to other width measures.

We focus on Tamaki’s first algorithm and characterize it in a unifying way that allows us to compute not just the treewidth of a graph but, with the same algorithm, the pathwidth, treedepth, q-branched treewidth, and dependency treewidth as well. Perhaps even more importantly, our description of the algorithm in a game theoretic framework is simple and intuitive and can be implemented quite directly. In fact, our treewidth and treedepth solvers Jdrasil and PID${}^{\star }$ are based on this characterization [20,49]. The detailed contributions of this paper are the following:

• Contribution I: A Simple Description of Tamaki’s First Algorithm.
  We describe Tamaki’s algorithm as a well-known graph searching game. This provides a link to known theory and allows us to analyze the algorithm in depth.
• Contribution II. Extending Tamaki’s Algorithm to Other Parameters
  The game theoretic point of view allows us to extend the algorithm naturally to various other parameters—including pathwidth and treedepth.
• Contribution III: A Novel Randomized Data Structure.
  The bottleneck in positive-instance driven algorithms is the enumeration of already computed solutions. We present a lazily constructed randomized data structure that, in contrast to existing data structures for this task, provides a guarantee that certain useless solutions are not enumerated with high probability.

1.1. Related Work

The concepts of pathwidth and treewidth were rediscovered several times in the literature [55,56,57]. Treedepth was discovered and analyzed by Nešetřil and de Mendez in their study of sparsity [58]. The game theoretic characterization of treewidth goes back to Seymour and Thomas [59]. Kirousis and Papadimitriou have studied a similar game for pathwidth [60], and Giannopoulou, Hunter and Thilikos have studied game theoretic approaches for treedepth [61]. The generalized version of this game, which we will use in this paper, was introduced by Fomin, Fraigniaud, and Nisse [62].

The potential success of positive-instance driven algorithms was demonstrated by Tamaki, who implemented a positive-instance driven version of Arnborg, Corneil, and Proskurowski’s treewidth algorithm for the PACE 2016 [46]. This algorithm outperformed all other submissions (including one by the authors) by far [43]. The winning algorithm of the PACE 2017 also “is basically Hisao Tamakis implementation” [44,47]. Tamaki later adapted his algorithm to the algorithm by Bouchitté and Todinca in his pioneering work introducing positive-instance driven dynamic programming [52]. Ongoing research constantly improves the performance of this version of the algorithm [39,53,63].

Positive-instance driven dynamic programming also played a key role in many submissions for the PACE 2020, where the goal was to compute the treedepth of a graph rather than the treewidth [45], for instance, in the winning submission by Trimble [48]. However, it should be noted that in contrast to treewidth, the dominance of positive-instance driven algorithms compared to other strategies (such as enumerating minimal separators [64,65]) was less dramatic for the computation of treedepth [45].

Besides the development of dedicated algorithms for these graph parameters, there is also ongoing research in implementing a unifying way of computing all these parameters using sat or maxsat solvers. See, for instance, [20,66,67,68,69,70,71].

1.2. Organization of This Paper

We provide some preliminaries about graphs and their decompositions in Section 2. We then invite the reader, in Section 3, to a gentle introduction to positive-instance driven graph searching with the example of computing the treedepth of a graph—while not directly necessary for the remaining paper, this section should make it easier to follow the more general approach presented later on. Section 4 lifts the game theoretic approach to a unifying algorithm that allows us to compute not just the treewidth or treedepth of a given graph but also its pathwidth and dependency treewidth. The somewhat technical proof of Theorem Section 4.5 is only sketched within the main text and we dedicate Appendix A to fill in the details.

After the main part of the paper, in Section 5 we identify a bottleneck of the positive-instance driven graph searching approach that was observed experimentally in various solvers. We extend a known data structure used by such algorithms, called block sieve, with a randomized component based on the well-known color coding technique. We illustrate the gained performance exemplarily in our treedepth solver PID${}^{\star }$ in Section 6.

We conclude our findings and discuss further research directions in Section 7.

1.3. Difference to the Conference Paper

This paper is an extended version of our paper Positive-Instance Driven Dynamic Programming for Graph Searching presented at WADS 2019 [72]. In the conference version, we already presented the unifying approach now discussed in Section 4. Because of this, the structure and content of this section have barely changed. In the present work, we improve the presentation of the algorithm and extend the approach further to directed treewidth (Section 4.6).

A new contribution, compared to [72], is the gentle introduction to positive-instance driven graph searching in Section 3. It is based on insights we gained during the development of our treedepth solver PID${}^{\star }$ [49] and its aim is to help the reader in following the more general algorithm presented later.

A new technical contribution is the lazily constructed randomized data structure (dubbed color coding sieve) presented in Section 5. The most expensive part of a positive-instance driven algorithm (be it for treewidth, treedepth, or any other width measure) is the enumeration of already computed positive subproblems that are compatible with each other [20,48,49,52,63]. Previous solvers use a data structure called block sieves to accelerate this process, which are basically set tries that store the positive subproblems and that can prune some non-compatible elements during the enumeration process. However, set tries are cumbersome and do not provide any guarantees on the number of non-compatible elements that actually get pruned. Our color coding sieves, in contrast, are (i) much more compact, as they are lazily constructed, (ii) use randomization to provide a guarantee that non-compatible elements are pruned with high probability, and (iii) allow a trade-off between the time spend in the data structure and the amount of elements that will be pruned. We extend this theoretical analysis by an implementation of the data structure in our treedepth solver PID${}^{\star }$ and an experimental evaluation (Section 6).

2. Preliminaries: Graphs and Their Decompositions

A digraph $G=(V(G),E(G))$ is a tuple containing a set $V(G)$ of vertices and a binary edge relation $E(G)\subseteq \{(v,w)\mid v\ne w\wedge v,w\in V\}$. The neighborhood of a vertex $v\in V(G)$ is defined as $N_G(v)=\{w\mid (v,w)\in E(G)\}$ and we define $N_G\left[v\right]=N_G(v)\cup \left\{v\right\}$. For a set $X\subseteq V$, we write $N_G(X)={\cup }_{x\in X}N(x)$ and $G\setminus X=(V(G)\setminus X,E(G)\setminus \{e\in E(G)\mid X\cap e\ne \varnothing \})$ for the graph obtained by deleting the vertices in X from G. The subgraph induced by X is defined as $G\left[X\right]=G\setminus (V(G)\setminus X)$. If G is clear from the context, we may simply refer to $V(G)$ and $E(G)$ as V and E, respectively, and we may drop the subscript “G” in the other definitions. A graph is undirected if its edge relation is symmetric and we may write abbreviations like $\{u,v\}\in E$ instead of $(u,v),(v,u)\in E$ for such graphs.

Graph Decompositions

Let $G=(V,E)$ be an undirected graph. A tree decomposition $(T,\iota )$ of G is a tree T and a mapping $\iota$ from the nodes of T to subsets of V (which we call bags) such that (i) for every $v\in V$, the set $\{x\mid v\in \iota (x)\}$ is non-empty and connected in T, and (ii) for every edge $\{v,w\}\in E$ there is a node y in T with $\{v,w\}\subseteq \iota (y)$. The width of a tree decomposition is the maximum size of one of its bags minus one. The treewidth $\mathrm{tw}(G)$ is the minimum width over all tree decompositions of G and its pathwidth $\mathrm{pw}(G)$ is the minimum width over all tree decompositions of G in which T is a path. Furthermore, its treedepth $\mathrm{td}(G)$ is the minimum width over all tree decompositions in which T can be rooted in such a way that for all nodes x, y of T we have $\iota (x)⊊\iota (y)$ if y is a descendant of x. Finally, its q-branched treewidth ${\mathrm{tw}}_{\mathrm{q}}(G)$ is the minimum width over all tree decompositions of G that can be rooted such that there are at most q vertices with more than one descendant on any root-leaf path. Intuitively, the treewidth of a graph measures how similar the graph is “to being a tree”, in the same sense pathwidth measures the similarity to a path and treedepth the similarity to a star. The q-branched treewidth allows to study the phase transition between the pathwidth and the treewidth of a graph. Loosely speaking, we can study the trade-off between the width of a decomposition and its “complexity”. A path decomposition has the highest width, but it is not “complex”. In contrast, a tree decomposition has the smallest width but may be arbitrary “complex”, as it may contain a large number of nodes of high degree. It is well known that we have $\mathrm{tw}(G)\le \mathrm{pw}(G)\le \mathrm{td}(G)\le \mathrm{tw}(G)·{log}_{2}n$ [58] and, by definition, we have $\mathrm{tw}(G)={\mathrm{tw}}_{\infty }(G)$ and $\mathrm{pw}(G)={\mathrm{tw}}_0(G)$. Figure 1 shows an example graph with multiple tree decompositions that minimize the various invariants defined above.

Another important variant of these parameters is dependency treewidth, which is used primarily in the context of quantified Boolean formulas [12]. Intuitively, this notion captures the idea that vertices in the graph are dependent on each other and thus need to be processed in a certain order. More formally, for a graph $G=(V,E)$ and a partial order ⋖ of V, the dependency treewidth $\mathrm{dtw}(G)$ is the minimum width of any tree decomposition $(T,\iota )$ with the following property: Consider the natural partial order ${\le }_T$ that T induces on its nodes, where the root is the smallest elements and the leaves form the maximal elements; define for any $v\in V$ the node $F_v(T)$ that is the ${\le }_T$-minimal node t with $v\in \iota (t)$ (which is well defined); then define a partial order ${<}_{\mathcal{T}}$ on V such that $u{<}_{\mathcal{T}}v$ if, and only if, $F_u(T){\le }_T{F}_v(T)$; finally, for all $u,v\in V$, it must hold that $F_u(T){<}_T{F}_v(T)$ implies that $u⋖v$ does not hold.

There are multiple generalizations of treewidth for digraphs. We will use the so-called D-width, which was introduced by Safari [73] and is based on D-decompositions. Such a decomposition is a tuple $(T,\iota )$ as above, but with the conditions that (i) for every strongly connected subset $S\subseteq V$ there is at least one x in T with $\iota (x)\cap S\ne \varnothing$, and (ii) the subgraph of T induced by $\left\{\right\{x,y\}\mid \iota (x)\cap \iota (y)\cap S\ne \varnothing \}$ is connected. The D-width of a digraph G, denoted by $\overrightarrow{\mathrm{tw}}(G)$, is the minimal width of any D-decomposition of G.

3. A Gentle Introduction to Positive-Instance Driven Graph Searching

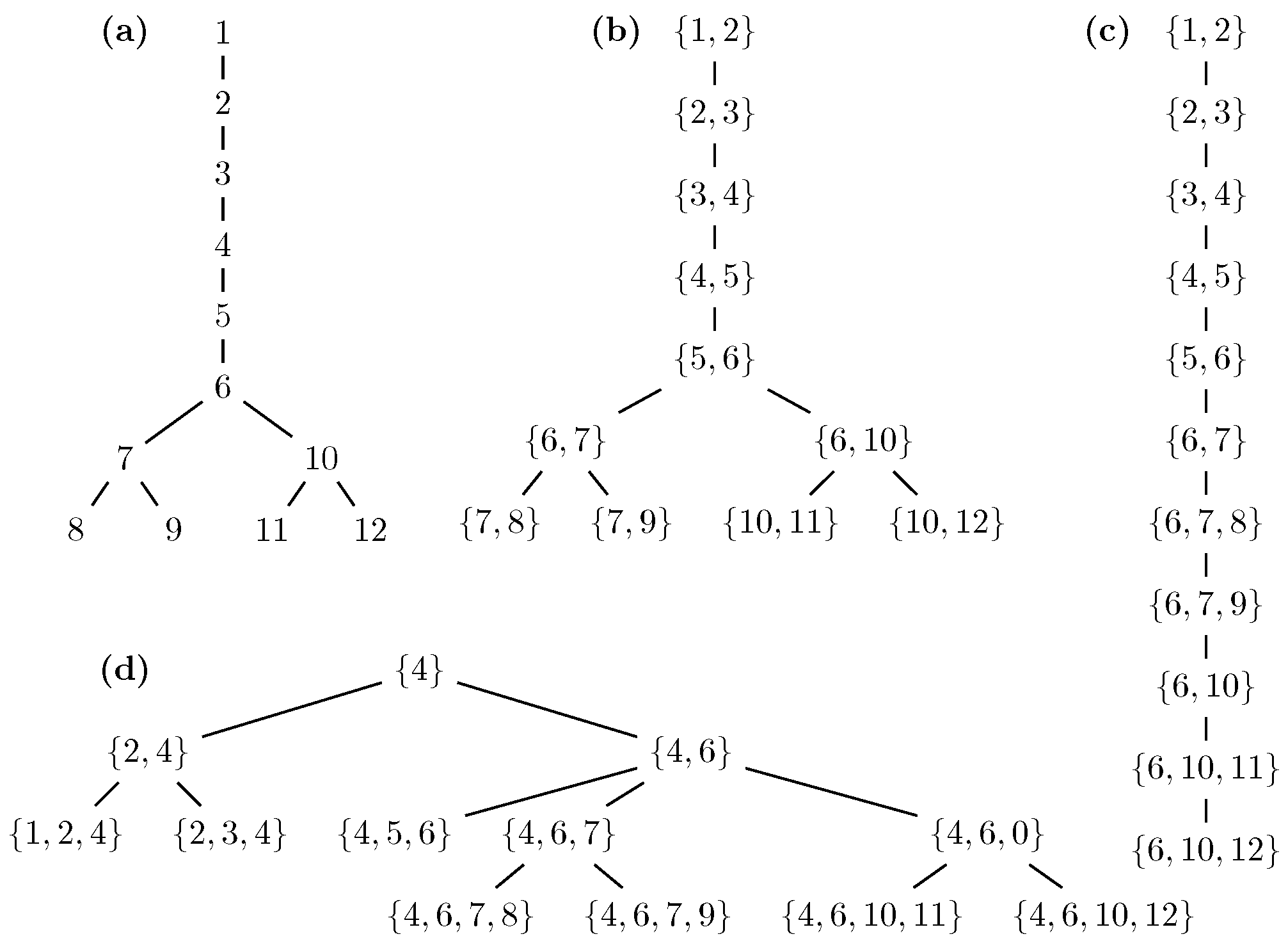
Before we describe a unifying algorithm that can compute all the graph decompositions shown in Figure 1, we will illustrate the positive-instance driven graph searching technique in a simpler example. Our goal in this section is to describe a game theoretic positive-instance driven algorithm for the width measure treedepth alone. For that end, let us use the following equivalent definition of this parameter: the treedepth of a graph $G=(V,E)$ is the minimum height of a rooted forest F such that G is a subgraph of the closure of F. This forest is called a treedepth decomposition of G. Since the treedepth of a graph is the maximum treedepth of its connected components, we can restrict ourselves to connected graphs. In this case, a treedepth decomposition of G is an elimination tree.

3.1. Graph Searching

Many graph decompositions have game theoretic characterizations in the form of vertex pursuit-evasion games [74]. Such games, which are also known as graph searching or cops and robber, are played by two players on an undirected graph $G=(V,E)$. In the game for treedepth, the first player places a team of ksearchers iteratively on the vertices of G, while the second player controls a single fugitive that hides in a connected component. The game is played in rounds as follows [61,75]: Initially, the fugitive hides in the vertex set $C=V$ (which we assume to be connected). The vertices in C are said to be contaminated. In each round, both players perform one action:

• The searchers pick a vertex $v\in C$ on which they want to place the next searcher. We say they clean the vertex v.
• The fugitive responds by picking a component $C^{\prime }$ of $G[C\setminus \{v\left\}\right]$. The contaminated area is reduced to $C^{\prime }$ and the game proceeds only on this subgraph.

The game ends when the contaminated area shrinks to the empty set or if the searchers have placed all k members of their team and C is still non-empty. In the first case, the graph was cleaned and the fugitive was caught; in the second case, the fugitive escaped. The searchers win if they catch the fugitive, otherwise the fugitive wins. Note that in this version of the game, the searchers are not allowed to remove an already placed searcher from the graph. The game is therefore monotone and always ends after, at most, k rounds. Further observe that the fugitive is visible in the sense that the searchers know in which connected component she hides—in contrast, an invisible fugitive could hide in subgraphs that are not connected (which notably complicates the arguments). The game is illustrated in Figure 2 on a small graph with eight vertices.

The configurations of this game are blocks, which are tuple $(C,\rho )$ with $\rho \in \mathbb{N}$ and $C\subseteq V$ being a connected subgraph with $|N(C)|+\rho \le k$. Informally, C is the (connected) contaminated area, and $\rho$ is the number of remaining searchers. We require $|N(C)|+\rho \le k$ as the neighborhood of C has to be cleaned in order to have C as contaminated area. We denote the set of blocks of the game played on a graph G with k searchers by $\mathcal{B}(G,k)$. Two blocks $(C_1,{\rho }_1)$ and $(C_2,{\rho }_2)$ intersect if $C_1\cap C_2\ne \varnothing$, $N_G(C_1)\cap C_2\ne \varnothing$ or $C_1\cap N_G(C_2)\ne \varnothing$. The start configuration of the game is $(V,k)$ and the winning configurations for the searchers are $(\varnothing ,\rho \ge 0)$. We say the searchers have a winning strategy on a block $(C,\rho )$ if, starting with configuration $(C,\rho )$, they can ensure to reach a winning configuration no matter how the fugitive acts. The set of blocks that guarantee such a strategy is the winning region, which we denote by $\mathcal{R}(G,k)\subseteq \mathcal{B}(G,k)$—the elements in this region are said to be positive. The connection between the game and the width measure treedepth is established by the following fact:

Fact 1 ([61]).

Let $G=(V,E)$ be a graph and $k\in \mathbb{N}$. Then $(V,k)\in \mathcal{R}(G,k)⟺\mathrm{td}(G)\le k$.

3.2. Simple Positive-Instance Driven Graph Searching

By Fact Section 3.1, it is sufficient to compute the set $\mathcal{R}(G,k)$ in order to test whether the treedepth of G is at most k. One way of doing so would be to first compute $\mathcal{B}(G,k)$, then build an auxiliary graph on top of this set, and finally compute $\mathcal{R}(G,k)$ by solving reachability queries on this auxiliary graph. We can estimate the number of configurations with $\left|\mathcal{B}(G,k)\right|\le (k+1)·n^{k+1}$, as there are $n^k$ possible ways of placing k searchers on an n-vertex graph—at most n connected components adjacent to a separator—and we have $\rho \in \{0,\cdots ,k\}$. Therefore, the sketched algorithm achieves a run time of $n^{O(k)}$, which is not feasible in practice for even moderate values of k.

To make the game theoretic approach feasible, we present an output-sensitive algorithm that computes just $\mathcal{R}(G,k)$— without “touching” the rest of $\mathcal{B}(G,k)$. Figure 3 illustrates why we may hope that $\mathcal{R}(G,k)$ is smaller than $\mathcal{B}(G,k)$. In the remainder of this section, we will develop some intuition about how to compute the set $\mathcal{R}(G,k)$. The formal details are postponed to the unifying version of the algorithm in the next section.

Surely, we cannot start at some block, say $(V,k)$, and just simulate the game in a top-down fashion—we could touch a lot of blocks in $\mathcal{B}(G,k)\setminus \mathcal{R}(G,k)$ without even noticing it (in Figure 3, that would mean starting a graph traversal from s, which could explore any leg of the spider). After all, we do not know whether $(V,k)\in \mathcal{R}(G,k)$. We do know, however, that $(\varnothing ,0)$ is a winning configuration (vertex t in Figure 3). So, let us start with the set $\mathcal{R}=\left\{(\varnothing ,0)\right\}$ and then try to grow it to $\mathcal{R}(G,k)$ in a bottom-up fashion. We can first ask which configurations of the game lead to $(\varnothing ,0)$, i. e., what are configurations in which the searchers immediately win in the next round? These are the configurations $(\{v\},1)$ with $|N(v)|<k$, as in these the searchers can surround the fugitive and have a searcher left to place it on top of her (in Figure 3, this corresponds to the predecessor of t).

Now, assume that we have currently a set $\mathcal{R}\subseteq \mathcal{R}(G,k)$ that had already grown a little. What does a configuration $(C,\rho )\in \mathcal{R}(G,k)\setminus \mathcal{R}$ that is “close to” $\mathcal{R}$ look like (that is, we wish to traverse the s-t-path of Figure 3 in reverse direction)? The set C is connected by definition and, since the searchers have a winning strategy from $(C,\rho )$, there is a vertex $v\in C$ such that $G[C\setminus \{v\left\}\right]$ has connected components $C_1,\cdots ,C_q$ ($q=1$ is possible) with $(C_i,\rho -1)\in \mathcal{R}$ for all $i\in \{1,\cdots ,q\}$. To find $(C,\rho )$, we first guess the vertex v, scan the sets of pairwise non-intersecting blocks $X\subseteq \{(C^{\prime },{\rho }^{\prime })\in \mathcal{R}\mid v\in N_G(C^{\prime })\wedge {\rho }^{\prime }<\rho \}$, and generate the new blocks $\left({\bigcup }_{(C^{\prime },{\rho }^{\prime })\in X}{C}^{\prime }\cup \left\{v\right\},1+{\max }_{(C^{\prime },{\rho }^{\prime })\in X}{\rho }^{\prime }\right)$. Note that we can prune a set X if $\left|\left(N_G({\bigcup }_{(C^{\prime },{\rho }^{\prime })\in X}{C}^{\prime }\right)\right|>k-{\max }_{(C^{\prime },{\rho }^{\prime })\in X}{\rho }^{\prime }$, as this neighborhood has to be cleaned by the searchers before they clean one of the components $C^{\prime }$. This will be utilized by the randomized data structure that we develop later in Section 5. Figure 4 illustrates this step of the algorithm, which we call a glue operation. We refer the reader who is interested in the details of implementing this algorithm for treedepth efficiently to the description of our solver PID${}^{\star }$ [49]. In the next section, we present a formal and more general version of the sketched strategy—which does not just work for treedepth, but for treewidth, pathwidth and many other width measures, too.

3.3. Alternative Characterization

Let us briefly sketch an interpretation of the algorithm without the game theoretic point of view. One can think of it as a procedure that, given a connected graph $G=(V,E)$, lists ever growing treedepth decompositions of subgraphs of G. In detail, a collection ${\mathcal{T}}_d$ of trees of depth at most d for some $d\ge 1$ is managed—starting with the trivial trees of depth 1 (i. e., single vertices) we have ${\mathcal{T}}_1\subseteq V$. Then, for ever larger d, the set ${\mathcal{T}}_d$ is computed by picking a new root $r\in V$ and a collection of previously computed trees $\mathcal{S}\subseteq {\bigcup }_{i=1}^{d-1}{\mathcal{T}}_i$, and by arranging the trees of $\mathcal{S}$ to a new tree by connecting their roots to r. Of course, in order to obtain a valid treedepth decomposition, the elements of $\mathcal{S}$ must be pairwise disjoint and non-adjacent. The selection of the set $\mathcal{S}$ is what was the glue operation and what will be a universal step in the algorithm presented in the next section, and the value d corresponds to $k-\rho$ and will be the distance that we will compute. Let us stress out that, in this characterization, the trees in $\mathcal{S}$ are, indeed, trees and thus connected. This is an invariant that the following algorithm cannot guarantee for all parameters but which improves the performance of the algorithm if met.

3.4. Execution Modes

It is worth noting that positive-instance driven algorithms only solve the problem for a fixed k. Hence, to obtain an optimal treedepth decomposition (or any other decomposition), one has to run the algorithm for various values of k. The order in which these values are tested is called the execution mode of the algorithm. Positive-instance driven algorithms differ from other strategies with respect to values that are “easy”. For instance, branch-and-bound algorithms usually solve the problem quickly if k overestimates the optimal value. However, overestimating k means more positive subproblems, making these instances hard for positive-instance driven algorithms. On the other hand, underestimating the optimal value yields instances that are usually hard but that are solved quickly by positive-instance driven algorithms as there are only few positive instances. Positive-instance driven graph searching is, thus, especially suited to compute lower bounds [63]. Therefore, the typical execution mode is to start with $k=1$ and to increase this lower bound until either an optimal solution was found or a heuristically obtained upper bound is met [48,49].

4. A Unifying Take on Positive-Instance Driven Graph Searching

Our goal is to generalize the algorithm that we just sketched in Section 3.2 to other graph measures such as treewidth and pathwidth. When we generalize from treedepth to other parameters, there are two main obstacles that we have to face. First, the sketched algorithm for treedepth “guessed” a root vertex in every iteration and glued already computed blocks to it. In more flexible graph decompositions such as tree decompositions, the root no longer is a single vertex but a set of up to k vertices. Clearly, we cannot guess such a set and, hence, have to compute it implicitly. Second, the treedepth algorithm explicitly carried the number of remaining searchers $\rho$ around (they were part of the blocks). In more flexible graph measures, we may remove and reuse already placed searchers and, thus, have to encode this information in a different way. We will handle this issue by splitting the computation into two phases, where the first phase mainly computes a configuration graph (intuitively, this graph contains blocks for various values of $\rho$) and where the second phase then computes distances in this configuration graph (hence, computes best possible $\rho$-values for the blocks). However, let us postpone the fiddling with distance queries to Section 4.5 and focus solely on the more general search game in the first part of this section.

We study graph searching in a setting proposed by Fomin, Fraigniaud, and Nisse [62]. The input is again an undirected graph $G=(V,E)$ and a number $k\in \mathbb{N}$, and the question is whether a team of k searchers can catch an invisible fugitive on G by the following set of rules: At the beginning, the fugitive picks a connected component C of G in which she hides—since the fugitive is invisible, in contrast to Section 3.2, the game is continued on G and not on $G\left[C\right]$ and we say that the set V is contaminated. In each round, the player now follows a similar procedure as in the previous game, but the searchers have a larger set of possible moves:

• The searchers perform one of the following:
  • Place a searcher on a contaminated vertex;
  • Remove a searcher from a vertex;
  • Reveal the current position of the fugitive.
• The fugitive responds as follows:
  • If the searchers place or remove a searcher, the fugitive adapts her connected component by adding or removing the vertex, respectively. (This may join multiple components or disconnect the current component, in which case the fugitive selects one of the resulting connected components).
  • If the searchers perform a reveal, the fugitive responds by uncovering her current connected component C. The contaminated area is reduced to C.

We follow the same terminology as before, i. e, we say a contaminated vertex becomes clean if a searcher is placed on it. In contrast to the previous game, a vertex v may now become recontaminated if a searcher is removed from it and there is a contaminated vertex adjacent to v. The searchers win the game if they manage to clean all vertices, i. e., if they catch the fugitive; the fugitive wins if, at any point, a recontamination occurs or if she can escape infinitely long. Note that this implies that the searchers have to catch the fugitive in a monotone way. A priori, one could assume that the later condition gives the fugitive an advantage (recontamination could be necessary for the cleaning strategy); however, a crucial result in graph searching is that “recontamination does not help” in all variants of the game that we consider [59,61,76,77,78].

4.1. Entering the Arena and the Colosseum

Our primary goal is to determine whether the searchers have a winning strategy. A folklore algorithm for this task is to construct an alternating graph called the arena: $\mathrm{arena}(G,k)=((V_s\cup V_f),E_{\mathrm{arena}})$ that contains for each position of the searchers ($S\subseteq V$ with $\left|S\right|\le k$) and each position of the fugitive ($f\in V$) two copies of the vertex $(S,f)$, one in $V_s$ and one in $V_f$ (see, for instance, Section 7.4 in [2]). Vertices in $V_s$ correspond to a configuration in which the searchers perform the next move (they are existential) and vertices in $V_f$ correspond to fugitive moves (they are universal). The edges $E_{\mathrm{arena}}$ are constructed according to all possible moves. The question is now whether there is an alternating path from a start configuration to some configuration in which the fugitive is caught. Since alternating paths can be computed in linear time ([79], Section 3.4), we immediately obtain an $O(n^{k+1})$ algorithm.

Modeling a configuration of the game as tuple $(S,f)$ comes, however, with a major drawback: The size of the arena does directly depend on n and k and does not depend on some further structure of the input. For instance, the arena of a path of length n and any other graph on n vertices will have the same size for any fixed value k. As the major goal of parameterized complexity is to gain insight into structural parameters beyond the input size n, such a fixed-size approach is not what we are looking for.

A bit counter intuitive, we will tackle this problem by, firstly, defining an alternating graph that is larger than the arena: the colosseum. As it befits for any good colosseum, it is not only larger but, in particular, “prettier” than the arena (which here means that it adapts to the input structure of the graph).

Once we can capture the structure in the colosseum, we will introduce yet another alternating graph that, finally, is actually small. This graph, which will be a subset of the colosseum, is called the pit—where only true champions can survive!

4.2. Simplifying the Game

Before we define all the locations of potential gladiator fights in graph theoretic terms, let us start with some simplifications of the game. We restrict the fugitive as follows: Since she is invisible, there is no need for her to take regular actions. Instead, the only moment when she is actually active is when the searchers perform a reveal. If C is the set of contaminated vertices, consisting of the induced components $C_1,\cdots ,C_{\ell }$, a reveal will uncover the component in which the fugitive hides and, as a result, reduce C to $C_i$ for some $1\le i\le \ell$. The only task of the fugitive is to answer a reveal with such a number i. The complete process of the searcher performing a reveal, the fugitive answering it, and finally of reducing C to $C_i$ is called a reveal-move.

We also restrict the searchers by the concept of implicit searcher removal. Let $S\subseteq V(G)$ be the set of vertices currently occupied by the searchers, and let $C\subseteq V(G)$ be the set of contaminated vertices. We call a vertex $v\in S$ covered if every path between v and C contains a vertex $w\in S$ with $w\ne v$.

Lemma 1.

A covered searcher can be removed safely.

Proof. 

As we have $N(v)\cap C=\varnothing$, the removal of v will not increase the contaminated area. Furthermore, v cannot be recontaminated at a later point, unless a neighbor of v becomes recontaminated as well (in which case the game would already be over). □

Lemma 2.

Only covered searchers can be removed safely.

Proof. 

Since for any other vertex $w\in S$ we have $N(w)\cap C\ne \varnothing$, the removal of w would recontaminate w and, hence, would result in a defeat of the searchers. □

Both lemmas together imply that the searchers never have to decide to remove a searcher but rather can do it implicitly. We restrict the possible moves of the searchers to a combined move of placing a searcher and immediately removing searchers from all covered vertices. This is called a fly-move. Observe that the sequence of original moves mimicked by a fly-move does not contain a reveal and, thus, may be performed independently of any action of the fugitive.

4.3. Building the Colosseum

We are now ready to define the colosseum. As for the arena, we could define it as an alternating graph. However, as only the searchers perform actions in the simplified game, we find it more natural to express this game as an edge-alternating graph—a generalization of alternating graphs. An edge-alternating graph is a triple $H=(V,E,A)$ consisting of a vertex set V, an existential edge relation $E\subseteq V\times V$, and a universal edge relation $A\subseteq V\times V$. The neighborhoods of a vertex v are the existential neighborhood $N_{\exists }(v)=\{w\mid (v,w)\in E\}$, the universal neighborhood $N_{\forall }(v)=\{w\mid (v,w)\in A\}$, and the complete neighborhood $N_H(v)=N_{\exists }(v)\cup N_{\forall }(v)$. An edge-alternating s-t-path is a set $P\subseteq V$ such that (i) $s,t\in P$ and (ii) for all $v\in P$ with $v\ne t$ we have either $N_{\exists }(v)\cap P\ne \varnothing$ or $\varnothing \ne N_{\forall }(v)\subseteq P$ or both. We write $s\prec t$ if such a path exists and define $\mathcal{R}(Q)=\{v\mid v\in Q\vee (\exists w\in Q:v\prec w)\}$ for $Q\subseteq V$ as the set of vertices on edge-alternating paths leading to Q. We say that an edge-alternating s-t-path P is q-branched if (i) H is acyclic and (ii) every (classical) directed path $\pi$ from s to t in H with $\pi \subseteq P$ uses at most q universal edges.

For $G=\left(V(G),E(G)\right)$ and $k\in \mathbb{N}$, the $\mathrm{colosseum}(G,k)$ is the edge-alternating graph H with $V(H)=\{C\mid \varnothing \ne C\subseteq V(G)\mathrm{and}|N_G(C)|\le k\}$ and the following edge sets: for all pairs $C,C^{\prime }\in V(H)$ there is an existential edge $e=(C,C^{\prime })\in E(H)$ if, and only if, $C\setminus \left\{v\right\}=C^{\prime }$ for some $v\in C$ and $|N_G(C)|<k$; furthermore, for all $C\in V(H)$ with at least two components $C_1,\cdots ,C_{\ell }$ we have universal edges $(C,C_i)\in A(H)$.

The nodes of the colosseum are called blocks and, thinking of Section 3.2, we have $V(H)=\mathcal{B}(G,k)$ (but note that the definition of “block” has slightly changed). The start configuration of the game is the block $C=V(G)$, i. e., all vertices are contaminated. We define $Q=\{\left\{v\right\}\subseteq V(G):|N_G(\left\{v\right\})|<k\}$ to be the set of winning configurations, as at least one searcher is available to catch the fugitive. Therefore, the searchers have a winning strategy if, and only if, $V(G)\in \mathcal{R}(Q)$ and we will therefore refer to $\mathcal{R}(Q)=\mathcal{R}(G,k)$ as the winning region (we did so similarly in Section 3.2, but we did not have the notation of edge-alternating graphs then). Observe that the colosseum is acyclic (that is, the digraph $(V(H),E(H)\cup A(H))$ is acyclic) as we have for every edge $(C,C^{\prime })$ that $\left|C\right|>|C^{\prime }|$, and observe that Q is a subset of the sinks of this graph. Hence, we can test if $V(G)\in \mathcal{R}(Q)$ in time $O(|\mathrm{colosseum}(G,k))|)$. Finally, note that the size of $\mathrm{colosseum}(G,k)$ may be of order $2^n$ rather than $n^{k+1}$, giving us a slightly worse overall runtime. This larger structure is required to encode that the fugitive is invisible.

4.4. Fighting in the Pit

The sketched algorithms have running time proportional to the size of the arena and the colosseum. Both of these auxiliary graphs might be large, as the arena has fixed size of order $O(n^{k+1})$ while the colosseum may even have size $O(2^n)$. Additionally, both graphs can contain unnecessary configurations, that is, configurations not part of the winning region. In the light of dynamic programming, this is the same as listing all possible configurations, and in the light of positive-instance driven dynamic programming, we would like to list only the positive instances—which is exactly the winning region $\mathcal{R}(Q)$.

The pit $\mathrm{pit}(G,k)$ inside the colosseum is now formally defined as the subgraph of $\mathrm{colosseum}(G,k)$ induced by $\mathcal{R}(Q)$, that is, as the induced subgraph on the winning region. The key insight is that $|\mathrm{pit}(G,k)|$ may be smaller than $|\mathrm{colosseum}(G,k)|$ or even $|\mathrm{arena}(G,k)|$ on various graph classes. Our primary goal for this section will therefore be the development of an algorithm that computes the pit in time depending only on the size of the pit (rather the size of the arena or the colosseum).

The algorithm traverses the colosseum “backwards” starting from the winning configurations Q and uncovering $\mathcal{R}(Q)$ layer by layer. In order to achieve this, we need to compute the predecessors of a block C. This is easy if C was reached by a fly-move as we can simply enumerate the n possible predecessors. Reversing a reveal-move, that is, finding the universal predecessors, is significantly more involved. A simple approach is to test for every subset of already explored configurations if we can “glue” them together—as we did in the sketched algorithm in Section 3.2. However, this results in an even worse runtime of $2^{|\mathrm{pit}(G,k)|}$. To avoid this exponential blow-up, we require the following structural property of the colosseum.

Definition 1 (Universal Consistent).

We say that an edge-alternating graph $H=(V,E,A)$ is universal consistent with respect to a set $Q\subseteq V$ if for all $v\in V\setminus Q$ with $v\in \mathcal{R}(Q)$ and $N_{\forall }(v)=\{w_1,\cdots ,w_r\}$ we have (1) $N_{\forall }(v)\subseteq \mathcal{R}(Q)$ and (2) for every $I\subseteq \{w_1,\cdots ,w_r\}$ with $\left|I\right|\ge 2$ there is a vertex $v^{\prime }\in V$ with $N_{\forall }(v^{\prime })=I$ and $v^{\prime }\in \mathcal{R}(Q)$.

Intuitively, Definition 1 implies that for every vertex with high universal-degree, there is a set of vertices that can be arranged in a tree-like fashion to realize the same adjacency relation. This allows us to glue only two configurations at a time and, thus, removes the exponential dependency. The definition is illustrated in Example 1.

Example 1.

Consider the following three edge-alternating graphs, where black edges are existential and the blue edges are universal. The set Q contains a single vertex that is highlighted. From left to right: the first graph is universal consistent, the second and third one are not. The second graph conflicts the condition that $v\in \mathcal{R}(Q)$ implies $N_{\forall }(v)\subseteq \mathcal{R}(Q)$, as the vertex on the very left is contained in $\mathcal{R}(Q)$ by the top path, while its universal neighbor on the bottom path is not contained in $\mathcal{R}(Q)$. The third graph conflicts the condition that $N_{\forall }(v)=\{w_1,\cdots ,w_r\}$ implies that for every $I\subseteq \{w_1,\cdots ,w_r\}$ with $\left|I\right|\ge 2$ there is a vertex $v^{\prime }\in V$ with $N_{\forall }(v^{\prime })=I$ and $v^{\prime }\in \mathcal{R}(Q)$ as witnessed by the vertex with three outgoing universal edges.

Lemma 3.

For every graph G and number k, the edge-alternating graph $\mathrm{colosseum}(G,k)$ is universal consistent.

Proof. 

For the first property, observe that “reveals do not harm”: Searchers that can catch the fugitive without knowing where she hides, certainly can do so if they know.

For the second property, consider any configuration $C\in V(H)$ that has universal edges to $C_1,\cdots ,C_{\ell }$. By definition, we have $|N_G(C)|\le k$ and $N_G(C_i)\subseteq N_G(C)$ for all $1\le i\le \ell$. Therefore, we have for every $I\subseteq \{1,\cdots ,\ell \}$ and $C^{\prime }={\cup }_{i\in I}{C}_i$ that $N_G(C^{\prime })\subseteq N_G(C)$ and $|N_G(C^{\prime })|\le k$ and, thus, $C^{\prime }\in V(H)$. □

The algorithm for computing the pit, see Figure 5 and Figure 6, runs in three phases: it first computes the set Q of winning configurations; then the winning region $\mathcal{R}(Q)$ (the vertices of $\mathrm{pit}(G,k)$); and finally, it computes the edges of $\mathrm{pit}(G,k)$.

Theorem 1.

The algorithm discover(G,k) finishes in at most $O\left({\left|\mathcal{R}(Q)\right|}^2·{\left|V\right|}^2\right)$ steps and correctly outputs $\mathrm{pit}(G,k)$.

Proof. 

The algorithm computes Q in phase I, the winning region $\mathcal{R}(Q)$ in phase II, and the edges of $\mathrm{colosseum}(G,k)[\mathcal{R}(Q)]$ in phase III. First observe that Q is correctly computed in phase I by the definition of Q.

For the correctness of the second phase, we show that the computed set $V(\mathrm{pit}(G,k))$ equals $\mathcal{R}(Q)$. Let us refer to the set $V(\mathrm{pit}(G,k))$ during the computation as K and observe that this is exactly the set of vertices inserted into the queue. We first show $K\subseteq \mathcal{R}(Q)$ by induction over the ith inserted vertex. The first vertex $C_1$ is in $\mathcal{R}(Q)$ as $C_1\in Q$. Now, consider a $C_i\in K$. It was either added in Line 18 or Line 24. In the first case, there was a vertex $\widetilde{C_i}\in K$ such that $C_i={\tilde{C}}_i\cup \left\{v\right\}$ for some $v\in N(\widetilde{C_i})$. By the induction hypothesis we have $\widetilde{C_i}\in \mathcal{R}(Q)$ and by the definition of the colosseum we have $(C_i,\widetilde{C_i})\in E(H)$ and, thus, $C_i\in \mathcal{R}(Q)$. In the second case, there were vertices $\widetilde{C_i},\widehat{C_i}\in K$ with $C_i={\tilde{C}}_i\cup \widehat{C_i}$. By the induction hypothesis, we have again ${\tilde{C}}_i,\widehat{C_i}\in \mathcal{R}(Q)$. Let $t_1,\cdots ,t_{\ell }$ be the connected components of $\widetilde{C_i}$ and $\widehat{C_i}$. Since the colosseum is universal consistent with respect to Q by Lemma 3, we have $t_1,\cdots ,t_{\ell }\in \mathcal{R}(Q)$. By the definition of the colosseum, we have $N_{\forall }(C_i)=t_1,\cdots ,t_{\ell }$ and, thus, $C_i\in \mathcal{R}(Q)$.

To see $\mathcal{R}(Q)\subseteq K$, consider for a contradiction the vertices of $\mathcal{R}(Q)$ in reversed topological order (recall that the colosseum is acyclic) and let C be the first vertex in this order with $C\in \mathcal{R}(Q)$ and $C\notin K$. If $C\in Q$, we have $C\in K$ by phase I and are complete, so assume otherwise. Since $C\in \mathcal{R}(Q)$, we have either $N_{\exists }(C)\cap \mathcal{R}(Q)\ne \varnothing$ or $\varnothing \ne N_{\forall }(C)\subseteq \mathcal{R}(Q)$. In the first case, there is a block $\tilde{C}\in \mathcal{R}(Q)$ with $(C,\tilde{C})\in E(H)$. Block $\tilde{C}$, thus, precedes C in the reversed topological order and, by the choice of C, we have $\tilde{C}\in K$. Therefore, at some point, $\tilde{C}$ is extracted from the queue and, in Line 18, C would be added to K, a contradiction.

In the second case, there are vertices $t_1,\cdots ,t_{\ell }\in \mathcal{R}(Q)$ with $N_{\forall }(C)=\{t_1,\cdots ,t_{\ell }\}$. By the choice of C, we have again $t_1,\cdots ,t_{\ell }\in K$. Since H is universal consistent with respect to Q, we have for every $I\subseteq \{1,\cdots ,\ell \}$ that ${\bigcup }_{i\in I}{t}_i$ is contained in $\mathcal{R}(Q)$. In particular, the vertices $t_1\cup t_2$, $t_3\cup t_4$, ⋯, $t_{\ell -1}\cup t_{\ell }$ are contained in $\mathcal{R}(Q)$, and these elements are added to K whenever the $t_i$ are processed (for simplicity, assume here that ℓ is a power of 2). Once these elements are processed, Line 24 will also add their union, that is, vertices of the form $(t_1\cup t_2)\cup (t_3\cup t_4)$. In this way, the process will add vertices that correspond to increasing subgraphs of G to K, resulting ultimately in adding ${\bigcup }_{i=1}^{\ell }{t}_i=C$ into K, which is the contradiction we have been looking for.

Once $\mathcal{R}(Q)$ is known, it is easy to compute the subgraph $\mathrm{colosseum}(G,k)[\mathcal{R}(Q)]$, that is, to compute the edges of the subgraph induced by $\mathcal{R}(Q)$. Phase III essentially iterates over all vertices and adds edges according to the definition of the colosseum.

For the runtime, observe that the queue will contain exactly the set $\mathcal{R}(Q)$ and, for every element extracted, we search through the current $K^{\prime }\subseteq \mathcal{R}(Q)$, which leads to the quadratic timebound of ${\left|\mathcal{R}(Q)\right|}^2$. Furthermore, we have to compute the neighborhood of every extracted element, and we have to test whether two such configurations intersect—both can easily be achieved in time $O(|V{|}^2)$. Finally, in phase III, we have to compute connected components of the elements in $\mathcal{R}(Q)$, but since this is possible in linear time per element, it is clearly possible in time $O\left(\left|\mathcal{R}(Q)\right|·{\left|V\right|}^2\right)$ for the whole graph. □

4.5. Distance Queries in Edge-Alternating Graphs

We have just discussed how to compute the pit for a given graph and $k\in \mathbb{N}$. The computation of graph measures such as treewidth now boils down to simple distance queries to this pit. To obtain an intuition of “distance” in edge-alternating graphs, think about such a graph as in our game and consider some vertex v. There is always one active player that may decide to take one existential edge (a fly-move in our game) or the player may decide to ask the opponent to make a move and, thus, has to handle all universal edges (a reveal-move in our game). From the point of view of the active player, the distance is thus the minimum over the minimum of the distances of the existential edges and the maximum of the universal edges.

Definition 2 (Edge-Alternating Distance).

Let $H=(V,E,A)$ be an edge-alternating graph with $v\in V$ and $Q\subseteq V$, let further $c_0\in \mathbb{N}$ be a constant, and ${\omega }_E:E\to \mathbb{N}$ and ${\omega }_A:A\to \mathbb{N}$ be weight functions. The distance $d(v,Q)$ from v to Q is inductively defined as $d(v,Q)=c_0$ for $v\in Q$ and otherwise:

$$d(v,Q)=\min \left(\underset{w\in N_{\exists }(v)}{min}(d(w,Q)+{\omega }_E(v,w)),\underset{w\in N_{\forall }(v)}{max}(d(w,Q)+{\omega }_A(v,w))\right).$$

Lemma 4.

Given an acyclic edge-alternating graph $H=(V,E,A)$, two weight functions ${\omega }_E:E\to \mathbb{N}$ and ${\omega }_A:A\to \mathbb{N}$, a source vertex $s\in V$, a subset of the sinks Q, and a constant $c_0\in \mathbb{N}$. The value $d(s,Q)$ can be computed in time $O(|V|+|E|+|A|)$ and a corresponding edge-alternating path can be output in the same time.

Proof of Lemma 4.

Since H is acyclic, we can compute a topological order of $(V,E\cup A)$ using the algorithm from [80]. We iterate over the vertices v in reversed order and compute the distance as follows. If v is a sink, we set:

$$d(v,Q)=\left\{\begin{array}{cc}{c}_0\hfill & \mathrm{if}v\in Q;\hfill \\ \infty \hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

If v is not a sink, we have already computed $d(w,Q)$ for all $w\in N(v)$ and, hence, can compute $d(v,Q)$ by the formula of the definition. Since this algorithm has to consider every edge once, the whole algorithm runs in time $O(|V|+|E|+|A|)$. A path from s to Q of length $d(s,Q)$ can be found by backtracking the labels starting at s. □

Being able to answer distance queries in the pit yields an easy way of computing graph measures that have game theoretic characterizations [61,62,76]. For instance, if we wish to compute a tree decomposition (there is no bound on the number of branches nor on the depth), we seek a winning strategy that may use an unbounded number of reveals and fly-moves—hence, we just can look for any path from the start configuration to Q. If we, instead, look for a path decomposition, we seek a tree decomposition without branches—hence, we need a winning strategy that does not use reveals and we can find one by introducing heavy weights on the universal edges. The following theorem collects graph measures that can be computed with similar arguments. We provide a sketch that illustrates how the weights have to be chosen within the main text; the interested reader finds the full (unfortunately somewhat technical) proof in Appendix A.

Theorem 2.

Given a graph G and an integer k, we can decide in time $O(|\mathrm{pit}(G,k+1){|}^2·|V{|}^2)$ whether G has { treewidth, pathwidth, treedepth, q-branched treewidth, dependency treewidth } at most k.

Proof. 

All five problems have game theoretic characterizations in terms of the same search game with the same configuration set [61,62,76]. More precisely, they condense to various distance questions within the colosseum by assigning appropriate weights to the edges.

• treewidth: To solve treewidth, it is sufficient to find any edge-alternating path from the vertex $C_s=V(G)$ to a vertex in Q. We can find a path by choosing ${\omega }_E$ and ${\omega }_A$ as $(x,y)\mapsto 0$, and by setting $c_0=0$.
• pathwidth: In the pathwidth game, the searchers are not allowed to perform any reveal [76]. Hence, universal edges cannot be used and we set ${\omega }_A$ to $(x,y)\mapsto \infty$. By setting ${\omega }_E$ to $(x,y)\mapsto 0$ and $c_0=0$, we again only need to find some path from $V(G)$ to Q with weight less than ∞.
• treedepth: In the game for treedepth, the searchers are not allowed to remove a placed searcher again [61]. Hence, the searchers can only use k existential edges. Choosing ${\omega }_E$ as $(x,y)\mapsto 1$, ${\omega }_A$ as $(x,y)\mapsto 0$, and $c_0=1$ is sufficient. We have to search a path of weight at most k.
• $\mathit{q}$-branched treewidth: For q-branched treewidth, we wish to use at most q reveals [62]. By choosing ${\omega }_E$ as $(x,y)\mapsto 0$, ${\omega }_A$ as $(x,y)\mapsto 1$, and $c_0=0$, we have to search for a path of weight at most q.
• dependency treewidth: This parameter is, in essence, defined via graph searching game that is equal to the game we study with some fly- and reveal-moves forbidden. Forbidding a move can be achieved by setting the weight of the corresponding edge to ∞ and by searching for an edge-alternating path of weight less than ∞. □

4.6. Extending the Algorithm to Directed Treewidth

D-width has a game theoretic characterization based on the following version of the game: The searchers and the fugitive now play on a digraph G, the searchers have unlimited reveals ($q=\infty$), and the fugitive is restricted to move inside strongly connected components (i. e., she can only reach vertices from which there is path back to her current position). Let D-search $(G)$ be the minimal number of searchers required to catch the fugitive in a monotone way. In contrast to the games we have considered previously, the number of required searchers may be reduced if we allow non-monotone strategies [81]. However, this is not relevant for the D-width, as we have:

Fact 2 ([81]).

D-search (G)$=\overrightarrow{\mathrm{tw}}(G)+1$.

Similar to the undirected games, we can construct a colosseum H, where each vertex $C\in V(H)$ corresponds to a configuration of the game. We put an existential edge from $C_1$ to $C_2$ when we can transform $C_1$ to $C_2$ by placing a searcher in $C_1$ and by removing all covered searchers (i. e., all searchers that stand on vertices v with $v\notin N_G(C_2)$). A universal edge is put from C to all its strongly connected components $C_1,\dots ,C_r$.

Observation 1.

Apart from G now being directed, not much changes for the colosseum. In particular, it is easy to see that it is still an acyclic edge-alternating graph. Thus, we can compute the pit in it using Theorem 1.

Corollary 1.

Given a digraph $G=(V,E)$ and an integer k, we can test whether or not we have $\overrightarrow{\mathrm{tw}}(G)\le k$ in time $O(|\mathrm{pit}(G,k){|}^2·|V{|}^2)$.

Proof. 

Compute the pit for the directed graph using Theorem 1; weight the edges with ${\omega }_E$ and ${\omega }_A$ as $(x,y)\mapsto 0$, and set $c_0=0$ (as for undirected treewidth in Theorem Section 4.5). Find a shortest edge-alternating path from V to the sinks of the pit using Lemma 4. □

5. Color Coding Sieves

The bottleneck in practical implementations of the presented algorithm is the enumeration of compatible blocks that can be glued (Line 22 and 23 in Figure 5). The same problem was observed in the positive-instance driven algorithms for treewidth [52] and treedepth [48]. Both used so called block sieves to tackle this problem.

These sieves are data structures based on set tries [82] allowing for an efficient enumeration over blocks that are possible candidates. More precisely, if K is the set of already computed blocks and the algorithm from Figure 5 reaches Line 22 with a block C, a block sieve shall efficiently enumerate a set $K^{\prime }\subseteq K$ such that all $C^{\prime }\in K$ for which the algorithm reaches Line 24 are contained in $K^{\prime }$ while $|K\setminus K^{\prime }|$ is maximized. Trivially, one could store K as list and just test for every element whether it is compatible (this is exactly what Figure 5 does). A block sieve improves this naive idea by storing the sets in a tree that represents intersections. Hence, while enumerating the output, one can prune some parts of the tree (of K) and, thus, has to consider only a subset of $K^{\prime }\subseteq K$. Tamaki presented this idea for the first time [52] and a more involved version was used by Trimble [48]. However, both implementations came with the drawback that they do not provide any guarantee on how well they sieve. We provide a randomized data structure for which we can provide tight bounds for the probability that certain unnecessary blocks are pruned. Furthermore, we show how to derandomize this data structure using the well-known color coding technique and obtain an implementation of the block sieve data structure that correctly prunes all of these blocks.

Another disadvantage of set tries is the overhead introduced by managing a tree structure of sets compared to, say, storing the blocks in a simple list or array. During the development of our treedepth solver PID${}^{\star }$ for PACE 2020, we actually observed that block sieves can negatively impact the performance of positive-instance driven solvers on instances of medium size [49].

In this section, we develop a randomized data structure that gives us the performance advantage of block sieves, reduces the overhead introduced by the set tries, and provides provable guarantees on the sieve quality. Color coding sieves apply different filter strategies successively to divide the set of all blocks into smaller and smaller sets. These sets often become small enough to be stored in simple lists. Only if these lists become too large, we divide them into multiple lists via a random choice. If such a separation happens frequently, the data structure converges into a classical set trie.

We assume a total order < on V, that is, $V=\{1,2,\cdots ,n\}$. Furthermore, we denote the smallest vertex in a set $C\subseteq V$ by $\min (C)$. Observe that < implies a partial order ⋖ on subgraphs where $C_1⋖C_2$ if, and only if, $\min (C_1)<\min (C_2)$. The color coding sieve will be used to store the set $\mathcal{R}(Q)=V(\mathrm{pit}(G,k))$, which, as before, consists of blocks C. The first operation supported by our data structure is the insertion operation that inserts a block C to the set represented by the data structure and is denoted by insert(C).

The second operation is used to speed up Line 22 in Listing 5. For a fixed block C, we have to enumerate all blocks $C^{\prime }$ that (i) do not intersect C (procedure intersect(C, $C^{\prime }$) in Figure 6) and that (ii) satisfy $|N_G(C\cup C^{\prime })|\le k$ (procedure offer(C, t) in Figure 6). Recall that two blocks intersect if $C\cap C^{\prime }\ne \varnothing$, $N_G(C)\cap C^{\prime }\ne \varnothing$ or $C\cap N_G(C^{\prime })\ne \varnothing$.

Definition 3.

A block $C^{\prime }$ is compatible with respect to a block C if all of the following holds:

• $C⋖C^{\prime }$;
• $|N_G(C\cup C^{\prime })|\le k$;
• $C\cap C^{\prime }=\varnothing$, $N_G(C)\cap C^{\prime }=\varnothing$, and $C\cap N_G(C^{\prime })=\varnothing$.

The set of all blocks that are compatible to C is denoted by $\mathrm{comp}(C)$.

In light of this definition, query operation query(C) should return a super set of $\mathrm{comp}(C)$. To support efficient implementation of such queries, a color coding sieve stores a set of blocks in three levels. Each level filters the blocks by making use of one of the three items of Definition 3.

The level-1 sieve partitions the blocks into sets $S_i=\{C\in \mathcal{R}\mid 2^i\le \min (C)<2^{i+1}\}$ for $i\in \{0,\cdots ,logn-1\}$ to make use of the partial ordering ⋖. We choose this partition because there are in general many more blocks with $\min (C)=1$ than with $\min (C)=n$.

Each set $S_i$ is stored as a level-2 sieve of depth γ. These sieves are the eponym for the data structure and partition $S_i$ by making use of $\gamma$ colorings ${\mathsf{color}}_1,\dots ,{\mathsf{color}}_{\gamma }$. Each coloring assigns two colors, say blue and orange, to the vertices of G. Let ${\mathrm{orange}}_j$ and ${\mathrm{blue}}_j$ be the set of orange and blue vertices according to ${\mathsf{color}}_j$, respectively. The set $S_i$ is partitioned into sets $S_i[\ell ]$, where $\ell =({\ell }_1,\dots ,{\ell }_{\gamma })\in {\{0,\dots ,k\}}^{\gamma }$. A block C belongs to $S_i[\ell ]$ if, and only if, the number of orange neighbors w. r. t. ${\mathsf{color}}_j$ is exactly ${\ell }_j$, that is,

$$\begin{array}{c}\hfill S_i[\ell ]=\{C\in S_i:|N_G(C)\cap {\mathrm{orange}}_j|={\ell }_j\mathrm{for}\mathrm{all}j\in \{1\dots ,\gamma \}\}.\end{array}$$

The idea is that whenever we query a block C with $[r_1,r_2,\dots ,r_{\gamma }]$ blue neighbors, we only have to search for compatible blocks in those sets $S_i[{\ell }_1,\dots ,{\ell }_{\gamma }]$ with ${\ell }_j+r_j\le k$.

Finally, the sets $S_i[\ell ]$ are stored as level-3 sieves, which are lazily built random set tries. Initially, we store the set $S_i[\ell ]$ as a list. If the size of the list grows too large, i. e., $|S_i[\ell ]|>\mathsf{\Theta }$ for a threshold $\mathsf{\Theta }$, we pick a random vertex $x\in V$ and divide $S_i[\ell ]$ into $\{C\in S_i[\ell ]\mid x\in C\}$ and $\{C\in S_i[\ell ]\mid x\notin C\}$. These sets are then recursively managed by new level-3 sieves. Observe that a level-3 sieve degenerates into a set trie with random order after n splits. However, because of the other sieve levels, we hope for far fewer recursive steps in the level-3 sieves.

5.1. Insert a Block to the Color Coding Sieve

Inserting a block C is straight forward: Every sieve adds it to the corresponding sieves of the next level. In detail, the level-1 sieve would add C to the sieve $S_i$ with $2^i\le \min (C)<2^{i+1}$. The level-2 sieve, on the other hand, counts, for $j=1,\dots ,\gamma$, the number ${\ell }_j$ of orange neighbors of C and adds the block to $S_i[\ell ]$. Finally, this level-3 sieve follows a path from the root in the trie to a leaf by checking for vertices on that path whether they are in C. Then C is added to the list stored at the leaf, which eventually is split if it grows too large.

5.2. Query the Color Coding Sieve

To answer query(C), we need to iterate through the sieves. For the level-1 sieve, let q be such that $2^q\le \min (C)<2^{q+1}$. As we only need to find blocks $C^{\prime }$ with $C⋖C^{\prime }$, we can focus our search on the sets $S_i$ with $i\ge q$. In order to sieve out elements on level 2, let C have $r_j$ blue neighbors (w. r. t. ${\mathsf{color}}_j$). We only need to consider sets $S_i[{\ell }_1,\dots ,{\ell }_{\gamma }]$ with ${\ell }_j+r_j\le k$ for all $j\in \{1,\cdots ,\gamma \}$.

Finally, for level-3 sieves, if $S_i[\ell ]$ is a list, we simply output that list. If $S_i[\ell ]$ is split into $X=\{C^{\prime }\in S_i[\ell ]\mid x\in C\}$ and $\overline{X}=\{C^{\prime }\in S_i[\ell ]\mid x\notin C\}$ for a vertex $x\in V$, we have to investigate these sets recursively. If $x\in C$, we only have to recur in $\overline{X}$, as we seek blocks that are disjoint from C. Otherwise, we have to search in both sets.

The data structure is illustrated in Figure 7 together with the steps corresponding to an insert and a query. The following lemma states that the color coding sieve is, in fact, a block sieve: the output of query(C) contains all blocks that are compatible to C.

Lemma 5.

After a sequence of insertions has inserted a set K of blocks to a color coding sieve that corresponds to a graph $G=(V,E)$ and $k\in \mathbb{N}$, we have $\mathrm{comp}(C)\subseteq \mathrm{query}(C)$ for all possible blocks C.

Proof. 

All three levels of the color coding sieve manage a partition of the set of blocks they contain and, thus, of K. We argue that any $C^{\prime }\in \mathrm{comp}(C)$ is output on query(C). The proof is by contradiction, so assume $C^{\prime }$ is pruned by one of the sieves.

If $C^{\prime }$ is pruned on level 1, it must have been in a set $S_i$ with $2^i\le \min (C^{\prime })\le 2^{i+1}$ and $i<q$ for $2^q\le \min (C)\le 2^{q+1}$. Thus, $C^{\prime }⋖C$ and, hence, $C^{\prime }$ is not compatible with respect to C by property 1 of being compatible.

Now, assume $C^{\prime }$ was pruned by the level-2 sieve. Then $C^{\prime }$ was stored in a set $S_i[{\ell }_1,\cdots ,{\ell }_{\gamma }]$ that was not explored. Hence, there must be an index $j\in \{1,\cdots ,\gamma \}$ and a number $r_j\ge 0$ with ${\ell }_j+r_j>k$ such that $N_G(C\cup C^{\prime })$ contains at least ${\ell }_j$ orange and $r_j$ blue vertices with respect to ${\mathsf{color}}_j$. This is a witness for $|N_G(C\cup C^{\prime })|>k$ and, thus, a contradiction to property 2 of being compatible.

Finally, if $C^{\prime }$ was pruned by the level-3 sieve, then clearly the sieve contains multiple layers (otherwise the whole list is output). The only way the sieve prunes is that it had split its list with a vertex $x\in V$ and $x\in C$. Since $C^{\prime }$ was pruned, we have $x\in C^{\prime }$ and, hence, $C\cap C^{\prime }\ne \varnothing$—a contradiction to property 3 of being compatible. □

5.3. Optimizing Level-2 Sieves

We have not yet specified the colorings used in level 2. In the following, we first consider randomized colorings and then make use of color coding for derandomization. Using the guarantees provided by this technique, we obtain a provable running time bound for the level-2 sieve. We are interested in the probability that a block $C^{\prime }$ with $|N_G(C\cup C^{\prime })|>k$ is part of the output if we use random colorings.

Lemma 6.

Let $\gamma =1$ and fix some blocks C and $C^{\prime }$ with $|N_G(C\cup C^{\prime })|>k$. If ${\mathsf{color}}_1$ is chosen randomly, the probability that $C^{\prime }$ is output by query(C) is at most

$$\begin{array}{c}\hfill 1-\frac{k+1}{2^{k+1}}.\end{array}$$

Proof of Lemma 6

Let $\widehat{k}=\left|N_G(C\cup C^{\prime })\right|\in \{k+1,\dots ,2k\}$ and let ${\mathsf{color}}_1$ be a randomly sampled coloring. Note that $C^{\prime }$ is output by query(C) if, and only if, $\beta (C)+\omega (C^{\prime })\le k$, where we define $\beta (C):=\left|\right\{v\in N_G(C)\mid \mathsf{color}(v)=\mathrm{blue}\}$ as the number of blue neighbors and $\omega (C)$ equivalently as the number of orange neighbors.

A coloring is called good if $\beta (C)+\omega (C^{\prime })>k$ as it allows to discard $C^{\prime }$. A vertex $v\in N_G(C\cup C^{\prime })$ is good if either $\mathsf{color}(v)=\mathrm{blue}$ and $v\in N_G(C)$ or $\mathsf{color}(v)=\mathrm{orange}$ and $v\in N_G(C^{\prime })$. Hence, a coloring is good if at least $k+1$ vertices are good. Note that all vertices in $N_G(C)\cap N_G(C^{\prime })$ are good (as each vertex is colored). In the following, we thus assume that $N_G(C)\cap N_G(C^{\prime })=\varnothing$, which is the worst case. As each coloring occurs with probability $2^{-\widehat{k}}$, the probability to hit a good coloring is then exactly

$$\begin{array}{c}\hfill {\left(2^{\widehat{k}}\right)}^{-1}\sum _{i=k+1}^{\widehat{k}}\left(\genfrac{}{}{0pt}{}{\widehat{k}}{i}\right).\end{array}$$

Hence, the probability of hitting a non-good coloring (and outputting $C^{\prime }$) is at most

$$\begin{array}{c}\hfill 1-\frac{{\sum }_{i=k+1}^{\widehat{k}}\left(\genfrac{}{}{0pt}{}{\widehat{k}}{i}\right)}{2^{\widehat{k}}}=\frac{{\sum }_{i=0}^k\left(\genfrac{}{}{0pt}{}{\widehat{k}}{i}\right)}{2^{\widehat{k}}}.\end{array}$$

This term is maximized for $\widehat{k}=k+1$, as the denominator grows faster than the nominator. Hence, the probability to output $C^{\prime }$ is at most

$$\begin{array}{c}\hfill \frac{{\sum }_{i=0}^k\left(\genfrac{}{}{0pt}{}{\widehat{k}}{i}\right)}{2^{\widehat{k}}}\le \frac{{\sum }_{i=0}^k\left(\genfrac{}{}{0pt}{}{k+1}{i}\right)}{2^{k+1}}=1-\frac{k+1}{2^{k+1}}.\end{array}$$

□

If we choose all $\gamma$ colorings randomly and independent, we obtain:

Corollary 2.

Fix some blocks C and $C^{\prime }$ with $|N_G(C\cup C^{\prime })|>k$. If ${\mathsf{color}}_1,{\mathsf{color}}_2,\dots ,{\mathsf{color}}_{\gamma }$ are chosen randomly and independent, the probability that $C^{\prime }$ is output by query(C) is at most

$$\begin{array}{c}\hfill {(1-\frac{k+1}{2^{k+1}})}^{\gamma }.\end{array}$$

We can now increase $\gamma$ until the term ${(1-\frac{k+1}{2^{k+1}})}^{\gamma }$ is below a tolerable threshold. If we add sufficiently many colorings, we may obtain the same result with deterministic colors that are produced by hash functions (that is, the level-2 sieve can be derandomized).

Definition 4.

For two natural numbers n and k, an $(n,k,2)$-universal coloring family is a set Λ of functions $\lambda :\{1,\dots ,n\}\to \{\mathrm{orange},\mathrm{blue}\}$ such that for every subset $S\subseteq \{1,\dots ,n\}$ of size $\left|S\right|=k$ and for every mapping $\mu :S\to \{\mathrm{orange},\mathrm{blue}\}$, there is at least one function $\lambda \in \Lambda$ with $\mu (s)=\lambda (s)$ for all $s\in S$.

It is well-known that such families can be constructed via hash functions.

Theorem 3 

(Theorem 13.41 in [83]). For all natural numbers n and k, an $(n,k,2)$-universal coloring family Λ of size $|\Lambda |\le 2^{O(k)}·{log}^2(n)$ can be found in time $2^{O(k)}·n·{log}^2(n)$.

Let $\Lambda$ be $(n,k,2)$-universal coloring family and assume that we operate the level-2 sieve with $\gamma =|\Lambda |$ colorings such that each of the colorings is produced by one of the hash functions in $\Lambda$. Now assume we perform query(C) and fixate any block $C^{\prime }$ with $|N_G(C\cup C^{\prime })|>k$. By the properties of $(n,k,2)$-universal coloring families, there is at least one coloring in $\Lambda$ that colors the vertices in $C\cup C^{\prime }$ in such a way that $N(C)$ contains at least ℓ orange vertices, $N(C^{\prime })$ contains at least r blue vertices, and $\ell +r>k$. Hence, the level-2 sieve prunes $C^{\prime }$ and, therefore, prunes all blocks that are incompatible to C by property 2 of being compatible. We collect this finding in form of the following theorem:

Theorem 4.

There is a computable function $f:\mathbb{N}\to \mathbb{N}$ such that for any graph G on n vertices and any $k\in \mathbb{N}$, the level-2 sieve can be implemented deterministically with $\gamma =f(k)·\mathrm{poly}(n)$ colors. When a block C is queried, this sieve prunes all stored blocks $C^{\prime }$ with $|N_G(C\cup C^{\prime })|>k$.

5.4. Pruning Queries in Level-3 Sieves

If the level-3 sieve degenerates into a set trie, we can use the structure of the trie to prune queries. Consider a node p of the trie and observe that the path from p to the root defines two sets $R_p$ and $F_p$ of required and forbidden vertices, respectively. Each block $C^{\prime }$ stored in the subtrie rooted at p fulfills $R_p\subseteq C^{\prime }$ and $F_p\cap C^{\prime }=\varnothing$. Hence, if $\min (R_p)\le \min (C)$, we do not have to explore p or its children. Define a pin to be a vertex $v\in V$ with $v\in F_p$ and $N_G(v)\cap R_p\ne \varnothing$, and let $P_p$ be the set of pins at p. Note that all blocks stored in the subtrie rooted at p are adjacent to v and, thus, we can prune the search if $v\in C$ as all blocks then intersect with C. Pins become neighbors of glued blocks and, hence, we can also prune if $|N_G(C)\cup P_p|>k$.

6. Experimental Evaluation of Color Coding Sieves

In this section, we experimentally evaluate the performance gain of a positive-instance driven algorithm when equipping it with a color coding sieve. We exemplarily do so by adding the color coding sieve (with $\gamma =1$ and randomly generated coloring) to our treedepth solver PID${}^{\star }$ that is built on the algorithms developed within this paper [49]. A comparison of PID${}^{\star }$ with other state-of-the-art treedepth solvers was recently performed in the light of PACE 2020 and can be found in [45].

We perform the experiments on a computer equipped with 64 GB of RAM and an AMD Ryzen Threadripper 3970X with 32 cores of 3.7 Ghz each and with 144 MB of combined cache. The system runs on Ubuntu 18.04.5 LTS, 64bit. We let the solver run on two benchmark sets: the well-known DIMACS graph coloring instances (see [34,84] for an overview of these instances in light of treewidth), and the instances that were used in the exact track of the treedepth challenge PACE 2020 [45]. Both solvers (without and with color coding sieves) were run for 10 min on each instance. The results of the experiment are illustrated as scatter plots in Figure 8 (the left one corresponds with the DIMACS instances, the right one to the PACE 2020 instances).

As one can observe, the color coding sieve generally improves the performance of the solver. Just on a few outlier instances, the solver cannot utilize this data structure, which is probably due to many non-compatible blocks that have a small neighborhood and, thus, are not pruned by the level-2 sieve. We can also observe that the obtained speedup is larger on the PACE 2020 instances than on the DIMACS instances. The PACE instances were generally harder to solve for PID${}^{\star }$ and contained more blocks. Hence, the solver can utilize the color coding sieve better on this benchmark set.

6.1. Color Coding Sieves on Hyperbolic Random Graphs

In this section, we investigate the potential performance boost obtained by using coloring coding sieves on hyperbolic random graphs. We use the same experimental setup as in the last section and, again, equip our treedepth solver PID${}^{\star }$ [49] with the color coding sieve data structure. In contrast to the last section, we will now:

• Vary the used layers and the number of colorings $\gamma$;
• Run the solver on random graphs rather than predefined benchmark sets.

For this experiment, we use hyperbolic random graphs, which are known to replicate many structural properties of real-world networks [85,86]. Loosely speaking, these graphs are generated by sampling points randomly in a disk (these are the vertices) and by connecting points by an edge if their hyperbolic distance is smaller than some predefined threshold.

We generated a set of 210 hyperbolic random graphs using the Hyperbolic Graph Generator [87]. The generator expects six parameters that we set as shown in

Table 1. Parameters of the used hyperbolic graph generator [87]. We set the number of vertices to a range in which the instances are tractable but challenging for the solver PID${}^{\star }$. The expected average degree is $k_1$ for $n\in \{100,110,120\}$, $k_2$ for $n\in \{130,140\}$, $k_3$ for $n\in \{150,160\}$, and $k_4$ for $n\in \{170,180,190,200\}$. For each combination of n and the corresponding $k_i$, we generated six instances with random seed $s\in \{1,\cdots ,6\}$ yielding 210 instances. The remaining parameters of the generator are set to their default value.

number of nodes	$n\in \{100,110,120,\cdots ,200\}$
expected average degree	$k_1\in \{10,20,30\}$, $k_2\in k_1\cup \left\{40\right\}$, $k_3=k_2\cup \left\{50\right\}$, $k_4\in \{3,5\}$
expected power-law exponent	2 (default)
square root of curvature	1 (default)
temperature	0 (default)
seed	$i\in \{1,2,\cdots ,6\}$

. The solver PID${}^{\star }$ was used with the four configurations explained in

Table 2. Four configurations of PID${}^{\star }$ used in the experiment.

Configuration	Meaning
-wo	Color coding sieves are not used.
-trie	Only the lazy set tries are used.
-color-1	All three sieves are used and $\gamma =1$.
-color-2	All three sieves are used and $\gamma =2$.

, whereby the level-2 sieves always use uniformly sampled random colorings.

All configuration of the solver were run on all instances for at most 30 min. The results of the experiment are illustrated in a cumulative distribution function plot in Figure 9. Various interesting findings are contained in the plot: First, we can observe that the core solver without any sieve layer (-wo) cannot fully utilize the provided 30 min time window. All instances solved by this configuration are solved within 20 min and, indeed, afterwards the amount of blocks becomes too large to be enumerated naively.

Second, we see the small (and expected) disadvantage of solvers with color coding sieves (-trie and -color-1) compared to the core algorithm (-wo) on “easy” instances (that can be solved in a minute or less). Of course, using involved data structures comes with an overhead and, if there are simply not enough blocks, we may not overcome this disadvantage with the improvements provided by the data structure. However, we can also observe that the performance of the solver with lazily built tries (-trie) and with the full color coding sieve (-color-1) quickly outperforms the core solver on the remaining instances. For the same reason as mentioned above, the lazily built set trie alone is better than the whole sieve on “medium hard” instance (solvable in about five minutes). Then, on even harder instances with more blocks, the additional layers can be utilized and the full color coding sieve provides the overall best performance.

Third, we can observe that, on this test set, choosing $\gamma >1$ (-color-2) has no positive effect compared to using $\gamma =1$ (-color-1). Adding more colorings increases the overhead of the data structure and, thus, a negative effect is expected if a layer cannot be fully utilized. Here, we conclude that on instances that are currently tractable for the solver, there are not enough blocks such that a second random partition sufficiently improves the enumeration of compatible blocks. However, we can also observe that the trend is positive, i. e., the overhead of a second coloring is reduced more and more on harder instances. We thus conjecture that, if the solver can be tuned to solve larger instances, the positive effect of $\gamma >1$ colorings, theoretically provided by Corollary 2, will also have a positive impact in practical implementations.

6.2. Sieve-Quality of the Individual Layers

So far, we measured the performance boost obtained by adding a color coding sieve to PID${}^{\star }$ with respect to the overall time the solver needs to solve an instance. In this section, we rather focus on the quality of the individual layers of the sieve. That is, we do not measure the time used to solve an instance but measure the amount of blocks that a sieve filtered.

In more detail, we measure the total number of blocks generated by PID${}^{\star }$ (that is, the total number of blocks inserted into the sieve) and the number of compatible blocks that were filtered from the output of the sieve (over the complete run of the solver). We compare this number with the number of loaded blocks, which is the number of blocks returned by the sieve. Of course, all compatible blocks are loaded, but (if the sieve works poorly) many other blocks may be loaded, too. We measure the performance of the sieve as the fraction of falsely loaded blocks over all non-compatible blocks. See

Table 3. Variables used to describe the performance of a sieve. The values t, c and ℓ are considered over a complete run of the solver for a given instance, e. g., summed over various values for the target width k.

Variable	Meaning	Comment
t	Total number of blocks.
c	Number of compatible blocks.	$c\le t$
ℓ	Number of blocks loaded by the sieve.	$c\le \ell \le t$
$\alpha$	Performance as $\alpha =1-\frac{\ell -c}{t-c}$	$\alpha =0$ for a trivial sieve $\alpha =1$ for a perfect sieve

for the exact terminology.

Observe that, in the light of Corollary 2 and Theorem 3, the performance of a color coding sieve converges to 1 if $\gamma$, the number of colorings, converges to infinity. See Figure 10 for an illustrative example.

For the following experiments, we only use a single layer of the color coding sieve and make all measurements with respect to a complete run of the solver for a given instance (i. e., summed over various values of the target width k). Since we aim to obtain a good estimation of the actual performance of the various sieves via experimental means, we consider rather difficult instances in this section. First, in

Table 4. Overview of the performance of PID${}^{\star }$ if a single layer of the color coding sieve is used. The columns n, m, and td describe the number of vertices and edges, as well as the treedepth of the corresponding graph. The columns labeled “Level-i” indicate that a level-i sieve is used (and none of the other layers). In this case, the level-2 sieve is used with $\gamma =1$ and the level-3 sieve is used in its plain version (without any improvements). Columns labeled with $\gamma =c$ indicate that a level-2 sieve with c colorings was used (the “random” colorings were generated with a seeded pseudo-random generator, that is, the first coloring of the $\gamma =3$ sieve is the same as the coloring of the $\gamma =1$ sieve and the first three colorings of the $\gamma =6$ sieve are the ones of the $\gamma =3$ sieve), and the column “imp. Level-3” corresponds to a level-3 sieve with the improvements discussed after Theorem 3. In each row, the sieve with the best performance on this instance is highlighted.

				$\mathbf{\alpha }$ of ⋯
Graph	n	m	td	Level-1	Level-2	$\mathbf{\gamma }=3$	$\mathbf{\gamma }=6$	Level-3	imp. Level-3
$\mathrm{grid}\_4\times 4$	16	24	7	$0.00$	$0.22$	$0.41$	0.63	$0.25$	$0.34$
$\mathrm{grid}\_5\times 5$	25	40	9	$0.00$	$0.20$	$0.49$	0.66	$0.46$	$0.65$
$\mathrm{grid}\_6\times 6$	36	60	11	$0.02$	$0.26$	$0.52$	$0.70$	$0.62$	0.81
$\mathrm{grid}\_7\times 7$	49	84	13	$0.07$	$0.29$	$0.59$	$0.78$	$0.69$	0.92
$\mathrm{grid}\_8\times 8$	649	112	15	$0.12$	$0.31$	$0.62$	$0.81$	$0.72$	0.96

, we consider $n\times n$-grid graphs, which are well-known to be difficult for various graph decomposition algorithms. Secondly, we hand-crafted a set of instances that are particularly difficult for the positive-instance driven approach. Let a $(n,d,c)$-spider be the graph obtained by the following procedure: start with a star with n leaves, then replace every edge by a path with d vertices, and finally replace every vertex by a clique on c vertices that is fully-connected to the vertices of adjacent cliques. (Intuitively, a star is a worst-case instance for the positive-instance driven approach, as initially only the leaves are positive subproblems and, by trying to glue them together, the solver has to explore all $2^n$ subsets of the leaves. By stretching and thickening the edges, we enforce that this behaviour stays the same and circumvent heuristics internally used by the solver.) The corresponding experiment is summarized in

Table 5. Same as Table 4, but on spider-graphs rather than grids.

				$\mathbf{\alpha }$ of ⋯
Graph	n	m	td	Level-1	Level-2	$\mathbf{\gamma }=3$	$\mathbf{\gamma }=6$	Level-3	imp. Level-3
$\mathrm{spider}\_(10,5,5)$	255	1760	20	$0.00$	$0.23$	$0.38$	0.51	$0.04$	$0.13$
$\mathrm{spider}\_(10,10,5)$	505	3510	25	$0.03$	$0.18$	$0.35$	0.49	$0.05$	$0.22$
$\mathrm{spider}\_(10,10,6)$	606	5115	30	$0.03$	$0.16$	$0.34$	0.44	$0.05$	$0.19$
$\mathrm{spider}\_(20,10,3)$	606	2403	15	$0.11$	$0.16$	$0.38$	0.57	$0.03$	$0.33$
$\mathrm{spider}\_(30,10,5)$	1505	10510	25	$0.15$	$0.14$	$0.31$	0.42	$0.02$	$0.34$

. Finally, we performed the experiment on a set of instances from the PACE 2020 benchmark set [45] (see Section 6). The results are presented in

Table 6. Same as Table 4, but on instances from the PACE 2020 benchmark set [45].

				$\mathbf{\alpha }$ of ⋯
Graph	n	m	td	Level-1	Level-2	$\mathbf{\gamma }=3$	$\mathbf{\gamma }=6$	Level-3	imp. Level-3
$\mathrm{exact}\_057$	50	75	13	$0.19$	$0.31$	$0.65$	$0.87$	$0.77$	0.97
$\mathrm{exact}\_077$	66	120	12	$0.10$	$0.27$	$0.53$	$0.75$	$0.51$	0.83
$\mathrm{exact}\_078$	67	152	12	$0.04$	$0.12$	$0.26$	0.33	$0.13$	$0.20$
$\mathrm{exact}\_079$	68	83	9	$0.06$	$0.27$	$0.59$	0.71	$0.36$	$0.69$
$\mathrm{exact}\_083$	70	274	22	$0.16$	$0.33$	$0.63$	$0.79$	$0.67$	0.92

.

From the experimental data shown in Table 4, Table 5 and Table 6, we conclude three observations: First, the level-1 sieve alone does not much. This was expected, as this sieve has semantically the least function. It is intended as fast preprocessing for the other sieves. Secondly, the level-2 and level-3 sieve (a single random partition and a normal set trie) are relatively equivalent. While the former is better on spider graphs, the latter is better on instances from the PACE benchmark set. Our final observation is that both sieves greatly improve their performance if the extensions are added (more colorings for the level-2 sieve or the improvements discussed after Theorem 3 for the trie, respectively). Comparing the level-2 sieve with $\gamma =6$ to the improved trie leads again to a mixed picture in which both of the sieves are better than the other on some of the instances. We conclude that taking a random partitioning is a valuable alternative to a set trie.

The level-2 sieve has two advantages over the set trie: (i) it is comparatively easy to implement and comes with low constants and (ii) we can easily improve its performance by adding more colorings. On the downside, adding more colorings slows this sieve down. Hence, if we need a large $\gamma$, a set trie becomes the better choice.

7. Conclusions and Outlook

Treewidth is one of the most useful graph parameters that is successfully used in many different areas. The positive-instance driven dynamic programming paradigm has led to the first practically relevant algorithm for this parameter, as well as for its close relative treedepth. We formalized such algorithms in the general setting of graph searching, which has allowed us to provide a clean and simple formulation and to extend the algorithm to many natural graph parameters.

With a few modifications of the colosseum, our approach can also be used for the notion of special treewidth [88]. We assume that a similar modification may also be possible for other parameters such as spaghetti treewidth [89].

We also extended the block sieve data structure to a randomized multi-level sieve that is constructed lazily and that utilizes the well-known color coding technique. By modifying the number of colorings used, we can change the probability that a non-compatible block is pruned by the sieve. Hence, introducing more and more colors makes it unlikely that non-compatible blocks are output by the sieve. On the theoretical side, we may derandomize the data structure and obtain a guarantee that certain non-compatible blocks are filtered.

Experiments have revealed that the color coding sieve in general increases the performance of our treedepth solver PID${}^{\star }$. For the instances that are currently tractable by the solver, a single random coloring provides the best overall performance, but we expect that on harder instances the theoretical guarantees of using more colorings will result in a positive practical impact. An interesting next step would be to implement the color coding sieve in state-of-the-art treewidth solvers such as [20,53,63], which currently perform slightly better than the state-of-the-art treedepth solvers [44,45].