Algorithms for Detecting and Refining the Area of Intangible Continuous Objects for Mobile Wireless Sensor Networks
Abstract
:1. Introduction
2. Related Works
3. Proposed Methods
3.1. Preliminaries and Assumptions
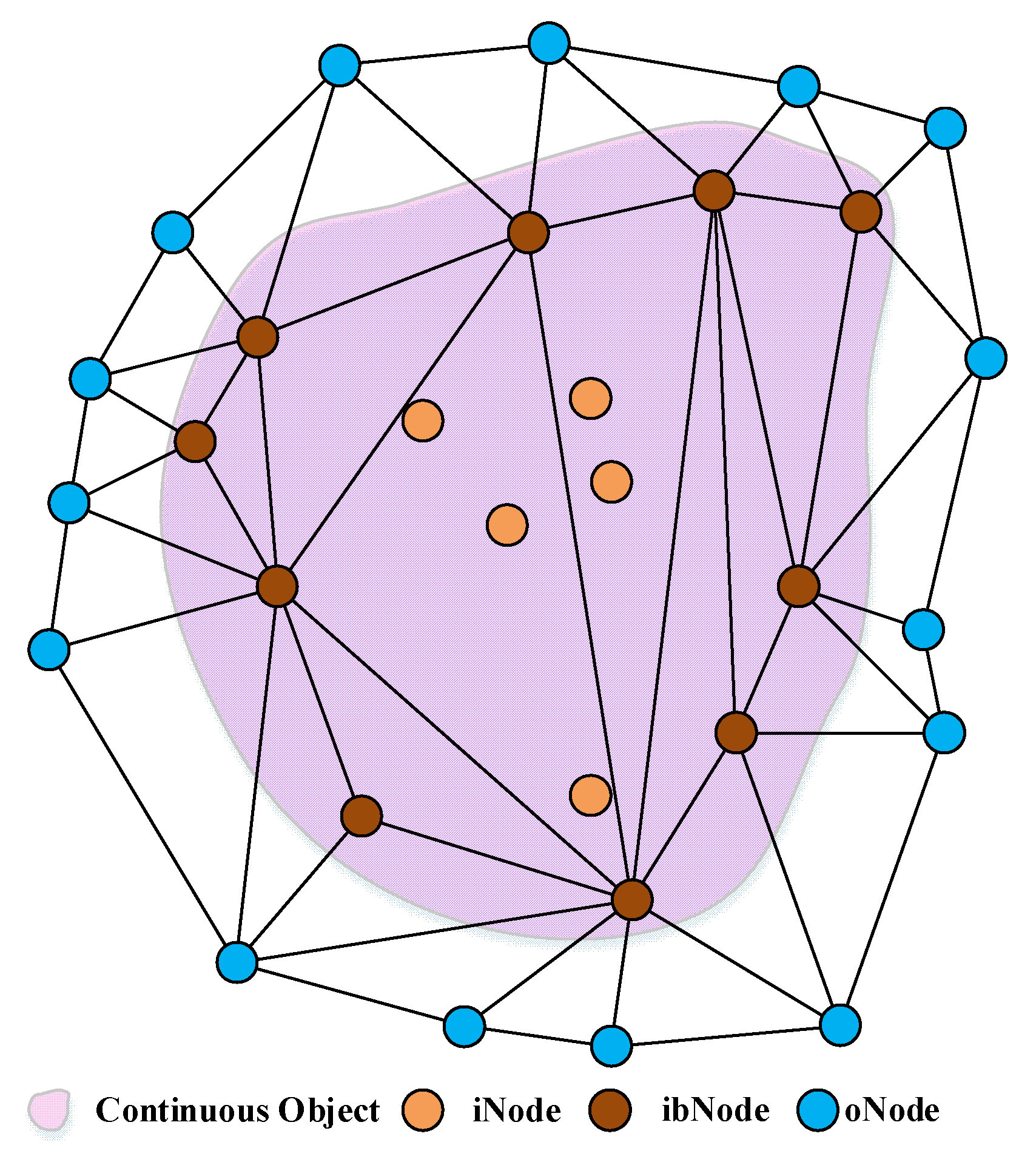
3.2. The Continuous Object Area Computation
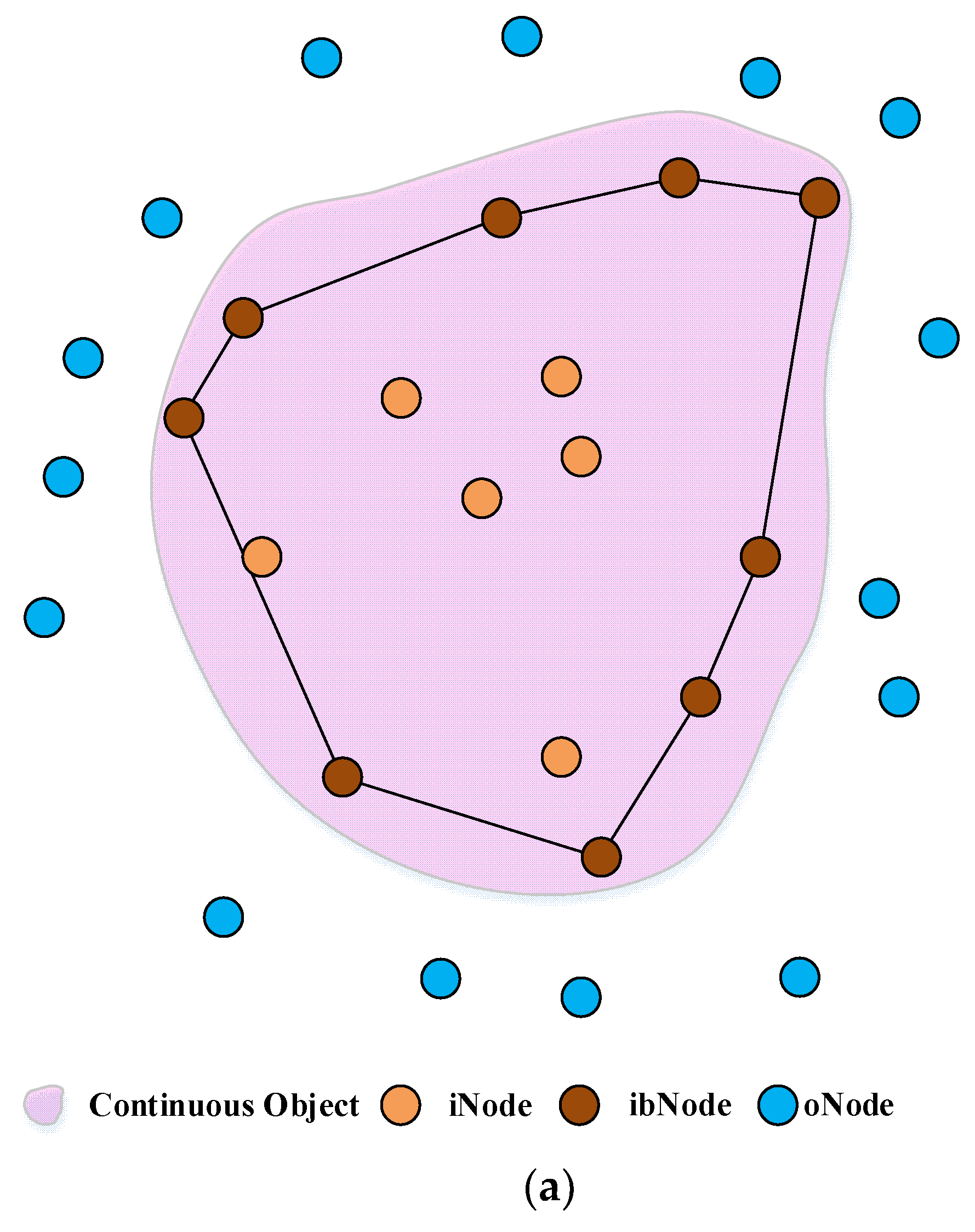
3.2.1. Compute the Rough Area of the Continuous Object
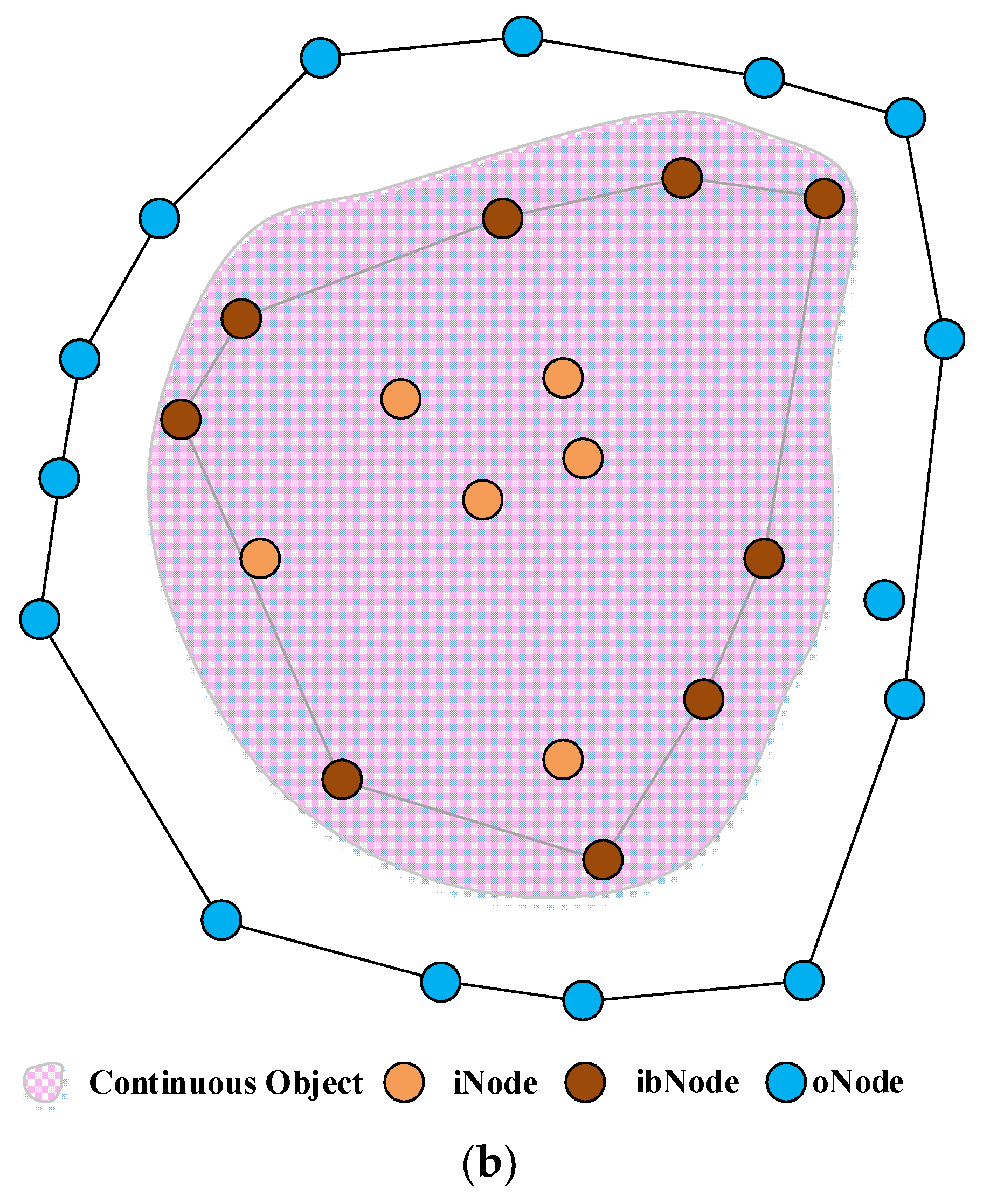
3.2.2. Refine the Enclosed Area with Mobile Sensors
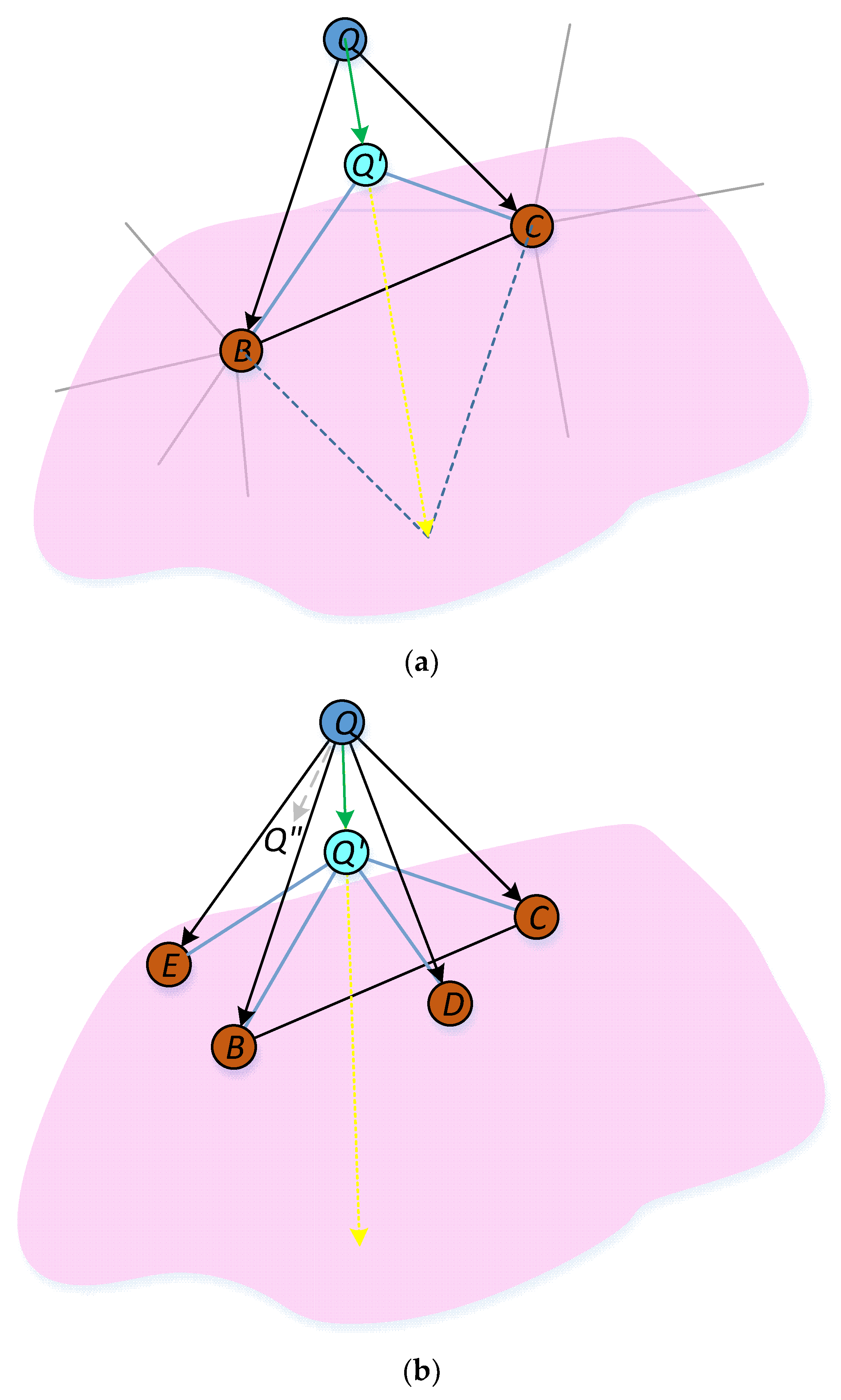
- Determine the moving direction for the sensors
- Determine the moving step size of the mobile sensors and location freeze mechanism
| Algorithm 1. The algorithm of the MDT. |
|
- MCH: Refine by updating the boundary nodes.
| Algorithm 2. The algorithm of the MCH. |
|
4. Simulation Results
4.1. Environment Setup
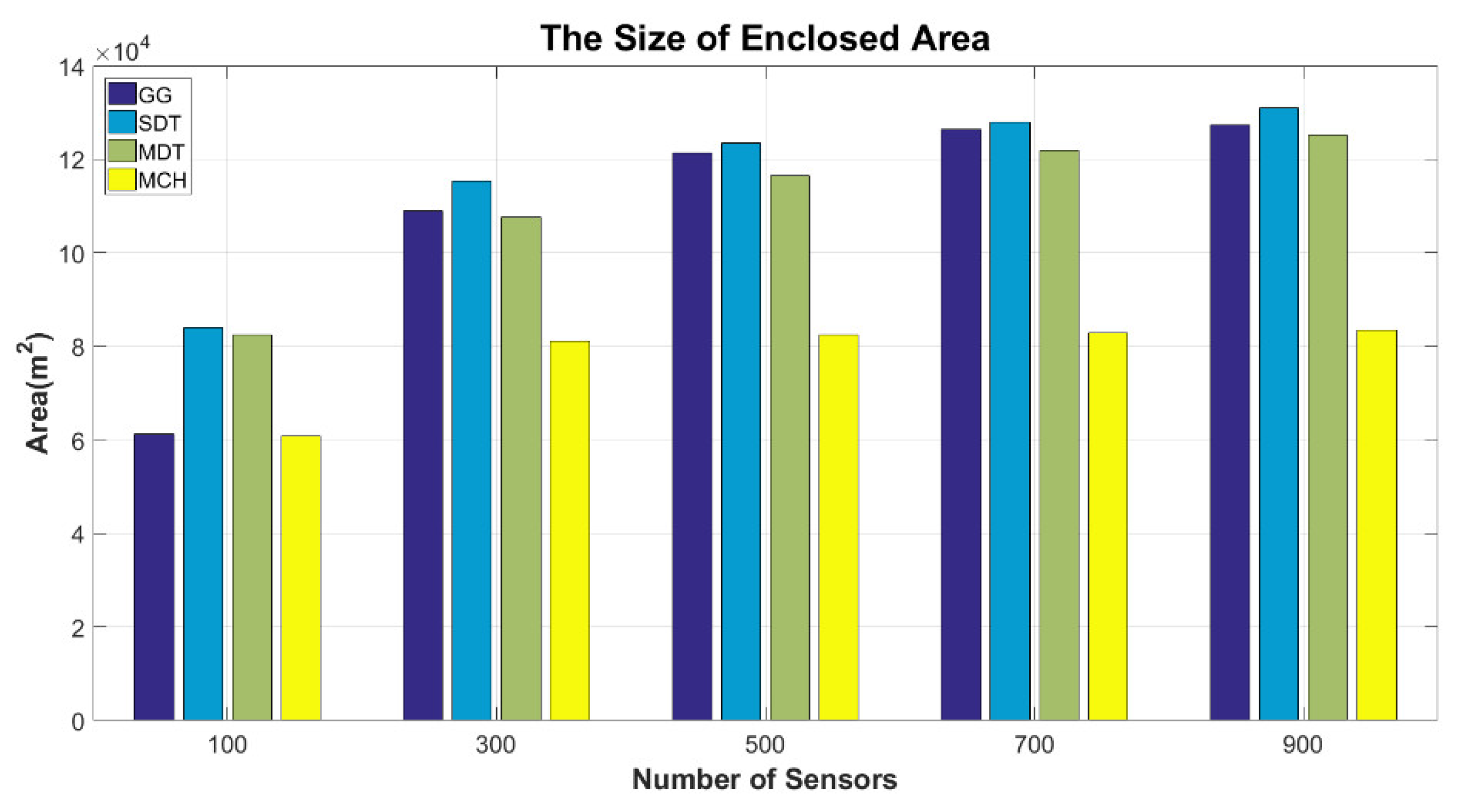
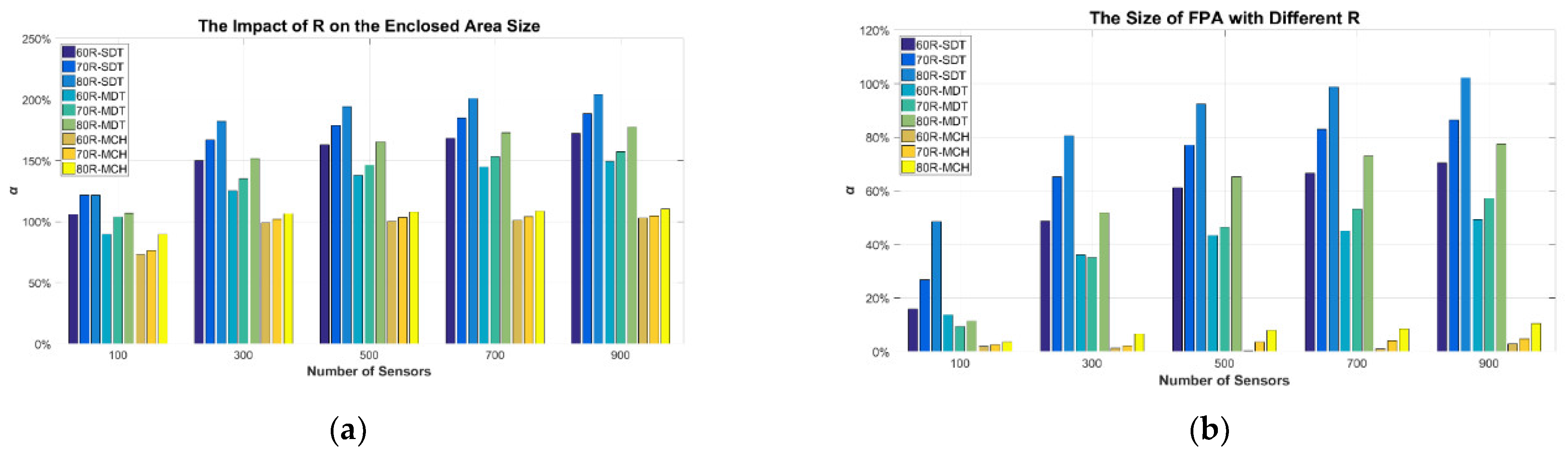
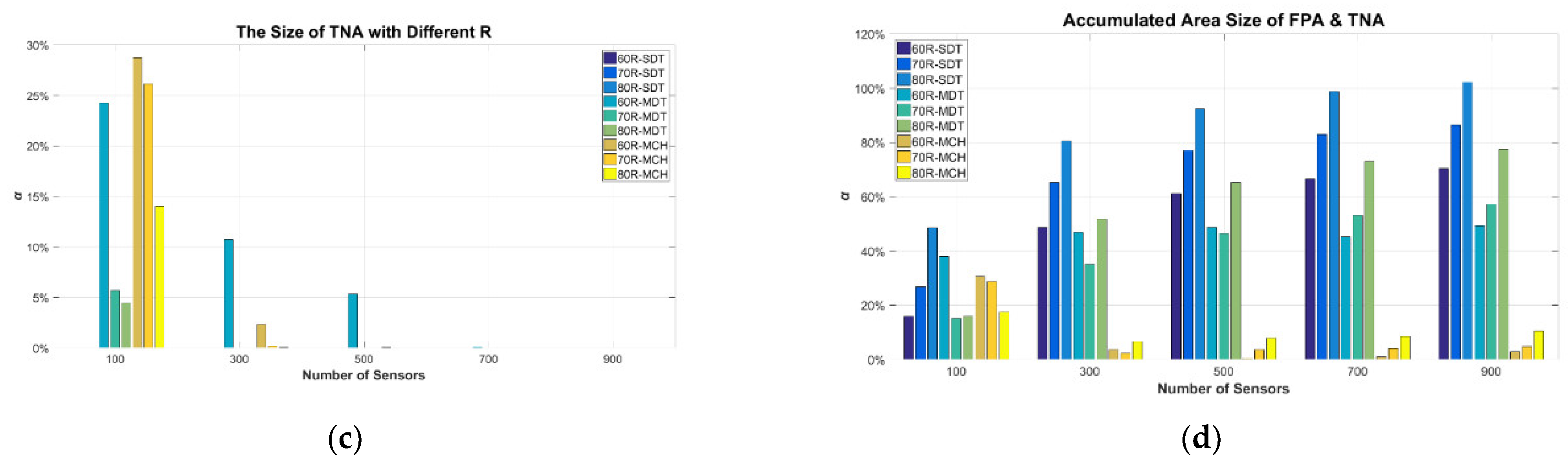
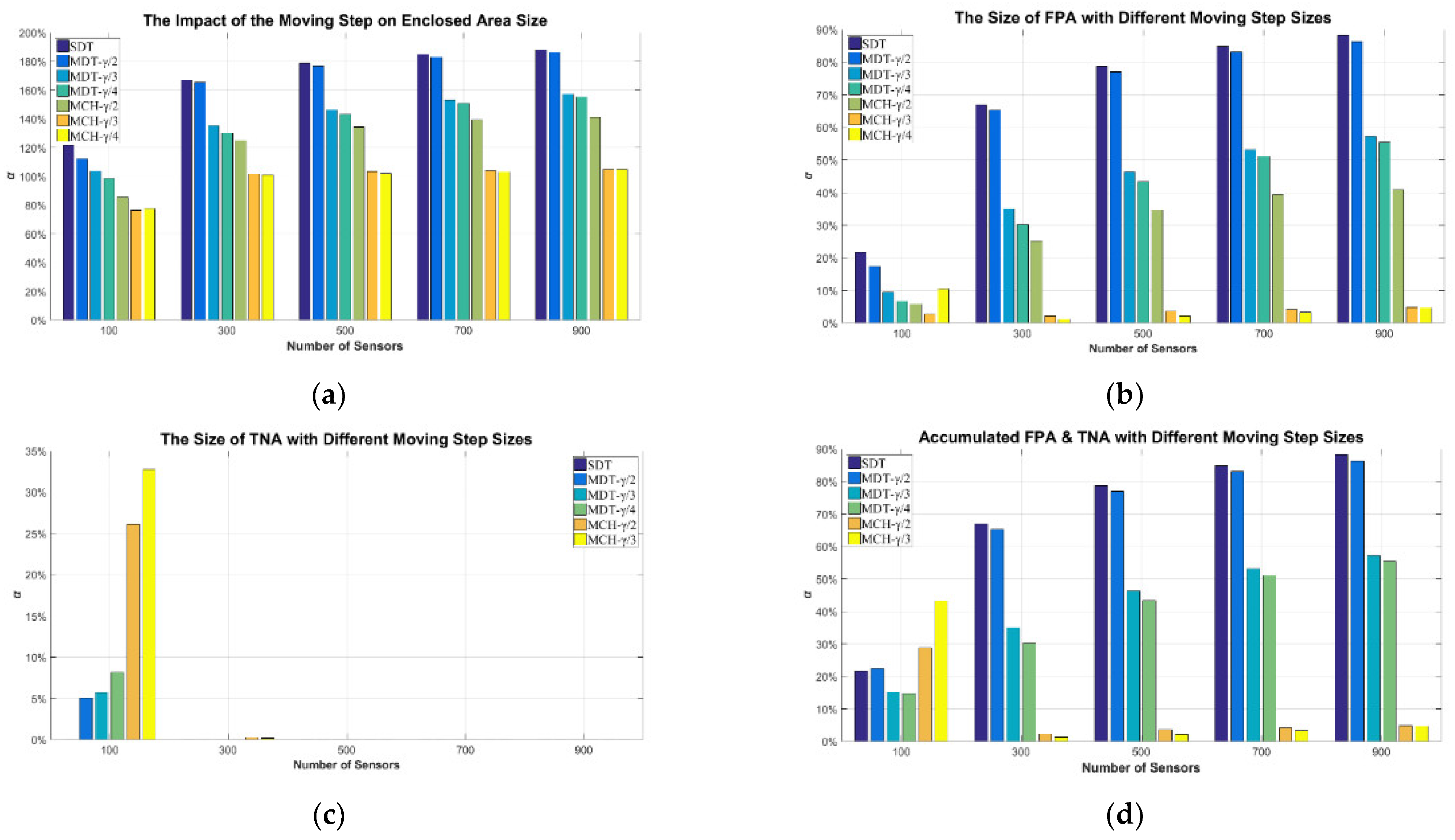
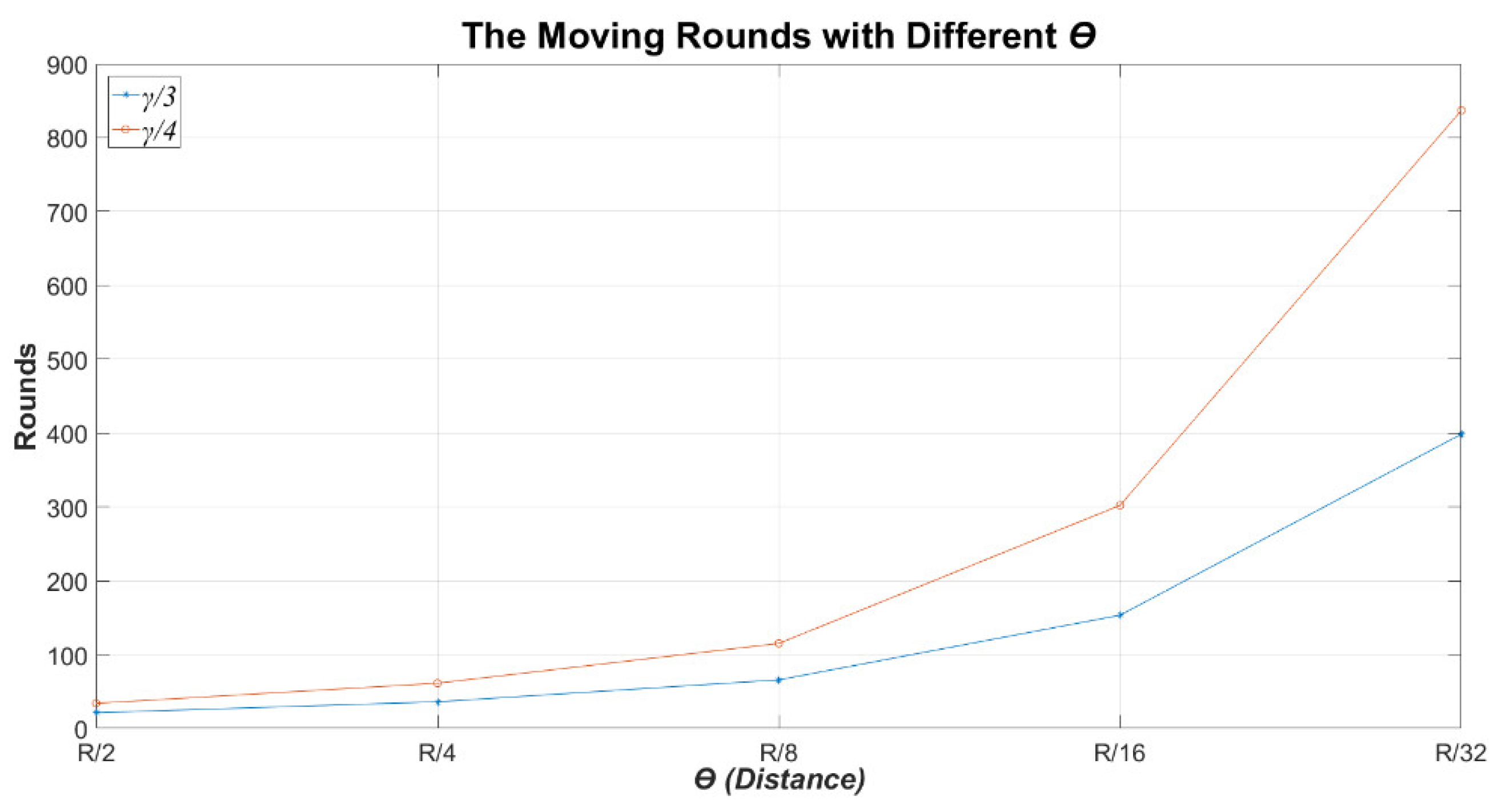
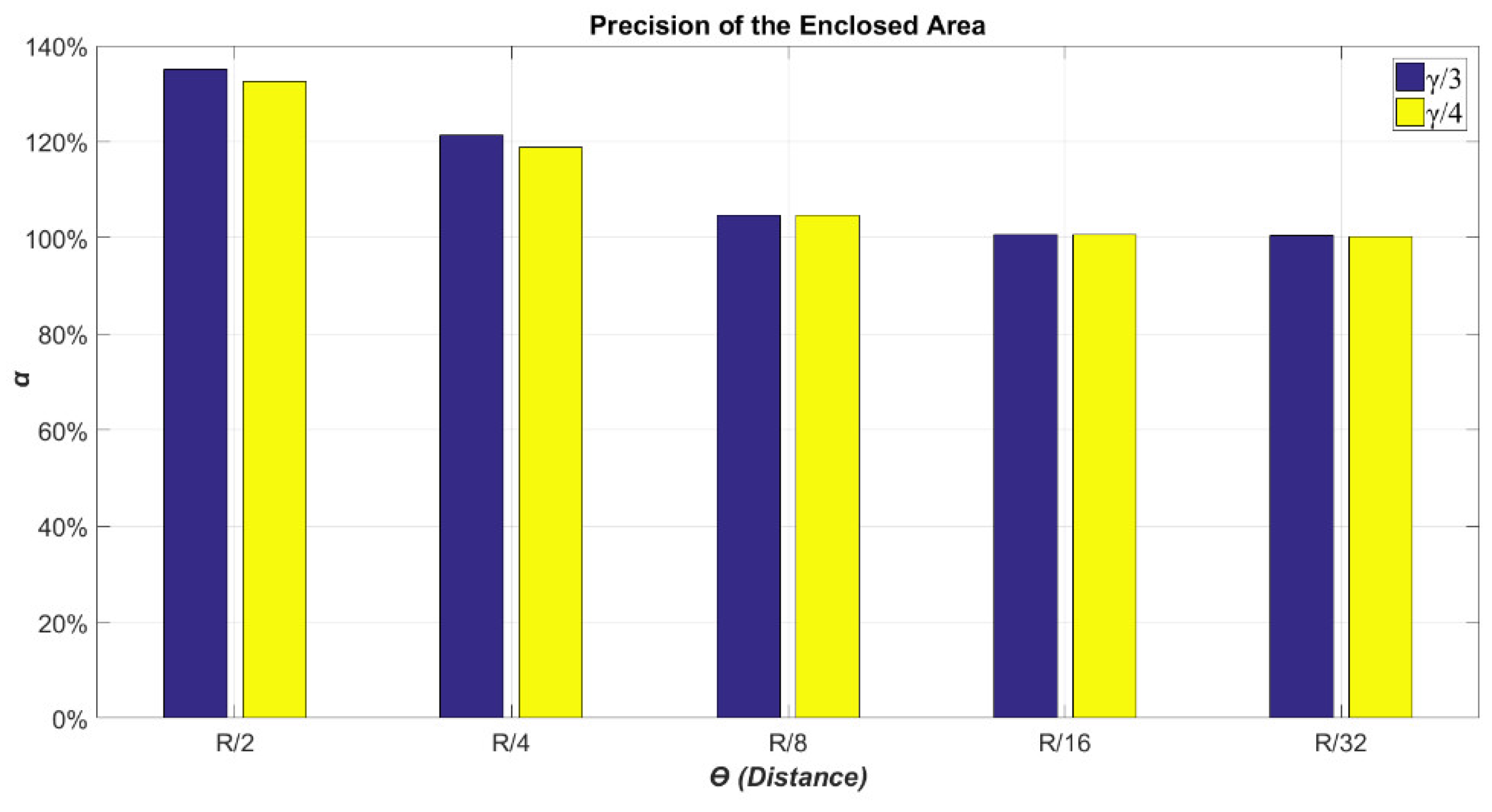
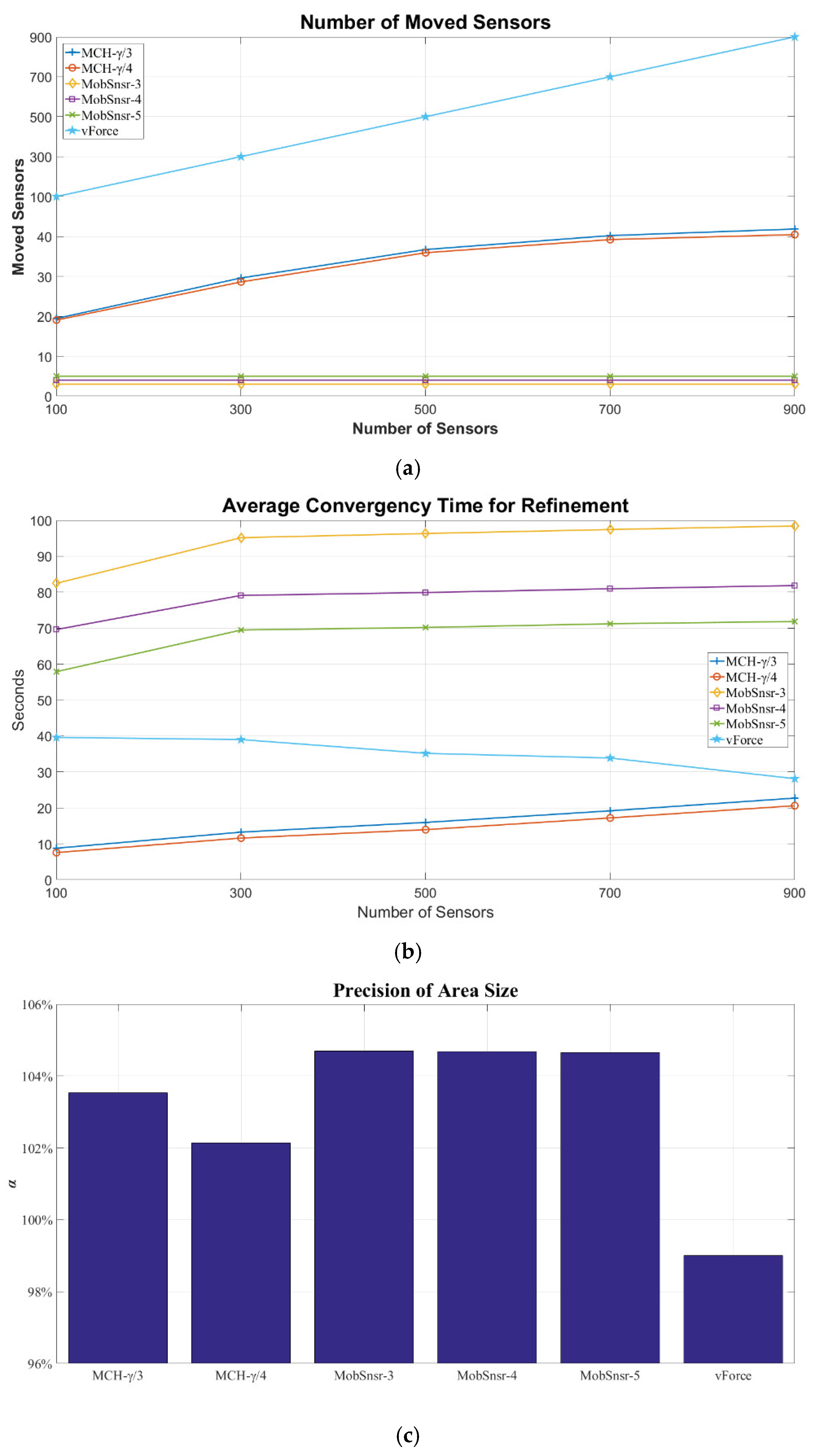
4.2. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Ji, X.; Zha, H.; Metzner, J.J.; Kesidis, G. Dynamic cluster structure for object detection and tracking in wireless ad-hoc sensor networks. In Proceedings of the IEEE International Conference on Communications, Paris, France, 20–24 June 2004; pp. 3807–3811. [Google Scholar]
- Chang, W.; Lin, H.; Cheng, Z. CODA: A Continuous Object Detection and Tracking Algorithm for Wireless Ad Hoc Sensor Networks. In Proceedings of the 5th IEEE Consumer Communications and Networking Conference, Las Vegas, NV, USA, 10–12 January 2008; pp. 168–174. [Google Scholar]
- Shen, J.; Han, G.; Jiang, J.; Sun, N.; Shu, L. An energy-efficient tracking scheme for continuous objects in duty-cycled wireless sensor networks. In Proceedings of the IEEE International Conference on Consumer Electronics, Taipei, Taiwan, 6–8 June 2015; pp. 150–151. [Google Scholar]
- Park, B.; Park, S.; Lee, E.; Kim, S.H. Detection and Tracking of Continuous Objects for Flexibility and Reliability in Sensor Networks. In Proceedings of the IEEE International Conference on Communications, Cape Town, South Africa, 23–27 May 2010; pp. 1–6. [Google Scholar]
- Gabriel, K.R.; Sokal, R.R. A New Statistical Approach to Geographic Variation Analysis. Syst. Biol. 1969, 18, 259–278. [Google Scholar] [CrossRef]
- Toussaint, G.T. The relative neighbourhood graph of a finite planar set. Pattern Recognit. 1980, 12, 261–268. [Google Scholar] [CrossRef]
- Rognant, L.; Chassery, J.M.; Goze, S.; Planes, J.G. The Delaunay constrained triangulation: The Delaunay stable algorithms. In Proceedings of the IEEE International Conference on Information Visualization, London, UK, 14–16 July 1999; pp. 147–152. [Google Scholar]
- Li, X.Y.; Calinescu, G.; Wan, P.J.; Wang, Y. Localized Delaunay triangulation with application in ad hoc wireless networks. IEEE Trans. Parallel Distrib. Syst. 2003, 14, 1035–1047. [Google Scholar]
- Yao, C.C. On Constructing Minimum Spanning Trees in k-Dimensional Spaces and Related Problems. SIAM J. Comput. 1982, 11, 721–736. [Google Scholar] [CrossRef] [Green Version]
- Diao, J.; Zhao, D.; Wang, J.; Nguyen, H.M.; Tang, J.; Zhou, Z. Energy-Efficient Boundary Detection of Continuous Objects in IoT Sensing Networks. IEEE Sens. J. 2019, 19, 8303–8316. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, Y.; Yi, X.; Chen, C.; Ping, H. Accurate Boundary Detection and Refinement for Continuous Objects in IoT Sensing Networks. IEEE Commun. Mag. 2019, 57, 93–99. [Google Scholar] [CrossRef]
- Kundu, S.; Das, N. Event boundary detection and gathering in wireless sensor networks. In Proceedings of the Applications and Innovations in Mobile Computing (AIMoC), Kolkata, India, 12–14 February 2015; pp. 62–67. [Google Scholar]
- Shu, L.; Mukherjee, M.; Wu, X. Toxic gas boundary area detection in large-scale petrochemical plants with industrial wireless sensor networks. IEEE Commun. Mag. 2016, 54, 22–28. [Google Scholar] [CrossRef]
- Ping, H.; Zhou, Z.; Rahman, T.; Duan, Y. Localization and tracking of continuous objects boundary area leveraging planar-ization algorithms in duty-cycled wireless sensor networks. In Proceedings of the 43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 5–8 November 2017; pp. 8476–8481. [Google Scholar]
- Zhang, Y.; Yi, X.; Zhou, Z.; Shu, L. A Mechanism for Continuous Object Boundary Region Detection and Prediction in Hybrid WSN. In Proceedings of the IEEE 27th International Symposium on Industrial Electronics (ISIE), Cairns, Australia, 13–15 June 2018; pp. 1296–1301. [Google Scholar]
- Sun, Z.; Wang, H.; Chen, Y.; Shu, L.; Mukherjee, M. Understanding the impact of planarized proximity graphs on toxic gas boundary area detection. In Proceedings of the International Conference on Recent Advances in Signal Processing, Telecom-munications & Computing (SigTelCom), Da Nang, Vietnam, 9–11 January 2017; pp. 109–114. [Google Scholar]
- Shu, L.; Chen, Y.; Sun, Z.; Tong, F.; Mukherjee, M. Detecting the Dangerous Area of Toxic Gases with Wireless Sensor Networks. IEEE Trans. Emerg. Top. Comput. 2017, 8, 137–147. [Google Scholar] [CrossRef]
- van Beers, W.C.M.; Kleijnen, J.P.C. Kriging interpolation in simulation: A survey. In Proceedings of the Winter Simulation Conference, Washington, DC, USA, 5–8 December 2004; p. 121. [Google Scholar]
- Sharma, V.; You, I.; Kumar, R. Energy efficient data dissemination in multi-UAV coordinated wireless sensor networks. Mob. Inf. Syst. 2016, 2016, 8475820. [Google Scholar] [CrossRef] [Green Version]
- Sharma, V.; Sabatini, R.; Ramasamy, S. UAVs assisted delay optimization in heterogeneous wireless networks. IEEE Commun. Lett. 2016, 20, 2526–2529. [Google Scholar] [CrossRef]
- Huang, S.-C.; Chang, C.-C.; Chang, H.-Y. Incremental Mobile Sensor Deploying Method for Intangible Event Region De-tection in Wireless Sensor Networks. In Proceedings of the International Conference on Networking and Network Applica-tions (NaNA 2016), Hakodate, Japan, 23–25 July 2016; pp. 360–364. [Google Scholar]
- Krzysztoń, M.; Niewiadomska-Szynkiewicz, E. Intelligent Mobile Wireless Network for Toxic Gas Cloud Monitoring and Tracking. Sensors 2021, 21, 3625. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S.-C.; Huang, C.-H. Algorithms for Detecting and Refining the Area of Intangible Continuous Objects for Mobile Wireless Sensor Networks. Algorithms 2022, 15, 31. https://doi.org/10.3390/a15020031
Huang S-C, Huang C-H. Algorithms for Detecting and Refining the Area of Intangible Continuous Objects for Mobile Wireless Sensor Networks. Algorithms. 2022; 15(2):31. https://doi.org/10.3390/a15020031
Chicago/Turabian StyleHuang, Shih-Chang, and Cong-Han Huang. 2022. "Algorithms for Detecting and Refining the Area of Intangible Continuous Objects for Mobile Wireless Sensor Networks" Algorithms 15, no. 2: 31. https://doi.org/10.3390/a15020031
APA StyleHuang, S.-C., & Huang, C.-H. (2022). Algorithms for Detecting and Refining the Area of Intangible Continuous Objects for Mobile Wireless Sensor Networks. Algorithms, 15(2), 31. https://doi.org/10.3390/a15020031





